Leveraging Seawater Thermal Energy Storage and Heat Pumps for Coupling Electricity and Urban Heating: A Techno-Economic Analysis

Abstract

This paper presents an economic assessment of seawater thermal energy storage (TES) integrated with industrial heat pumps to couple renewable electricity generation with urban district heating networks. Using Amsterdam as a case study, we develop a techno-economic model leveraging real-world data on electricity prices, heat demand, and system costs. Our findings show that large-scale TES using seawater as a storage medium significantly enhances district heating economics through energy arbitrage and operational flexibility. The optimal configuration yields a net present value (NPV) of EUR 466 million over 30 years and a payback period under 6 years. Thermal storage increases NPV by 17% compared to systems without storage, while within-day load shifting further boosts economic value by 23%. Accurate demand and price forecasting is critical, as forecasting errors can reduce NPV by 13.7%. The proposed system is scalable and well suited for coastal cities, offering a sustainable, space-efficient solution for urban decarbonization and addressing renewable energy overproduction.

1. Introduction

Despite the decreasing costs of renewable energy sources, many cities worldwide struggle to meet their decarbonization targets. One key challenge hindering the broader adoption of wind and solar energy is the mismatch between the timing of electric energy production and local demand. Renewable energy production is highly volatile depending on weather conditions, while a city’s energy needs, have their daily and weekly patterns, and also seasonal unbalances. The latter, in the case of continental and temperate climates like Amsterdam, the object of our test case, already peaks during the winter months and the increasing heating sector electrification will enhance the unbalance. Considering the future expansion in the production of renewables, these misalignments, jointly with an increasing share of renewable energy sources and lack of large-scale electric energy storage, can result in surplus clean electric energy being curtailed, which could limit their economic attractiveness compared to fossil fuels.

To address this challenge and facilitate the transition to a net-zero future, electric energy should be stored via long-duration energy storage (LDES) technologies. These solutions, massively deployed, can help stabilize energy markets and tap into the economic benefits of energy arbitrage, particularly in volatile electric energy price scenarios. LDES captures surplus energy when its production is high, such as during sunny or windy days, and delivers it when demand surges. Nevertheless, large-scale or massive deployment of electric LDES could be both costly and not sufficient to tackle the challenge alone, which is why the idea of indirectly storing the electric energy overproduction as heat via industrial heat pumps (HP) feeding thermal energy storage is a promising contender. It could benefit from relying on common technologies like heat exchangers and pumps, which reduce construction timelines and costs. The storage mediums, such as water, are abundant and environmentally friendly. It is also safer, unlike Li-ion battery storage of electric energy, which may bring fire hazards or other innovative solutions which may bring other types of hazards like the corrosive electrolyte (sulfuric acid) of vanadium redox flow batteries. The adopted solution using seawater also offers geographical flexibility when it comes to large scales, being easier to integrate into the urban design of sea towns. Furthermore, the durability of thermal energy storage technology is a significant asset. Thermal energy storage solutions are also experiencing a consistent trend toward lower installation costs and higher efficiency. The same is true for industrial heat pumps that are experiencing a continuous improvement in costs and performance, the latter helped by the possibility of using seawater as a cold source of heat, always far above zero degrees Celsius, which is not the case for ambient air during winter. Finally, the smart operation of so-defined thermal storage allows an effective coupling of electric and heating sectors, which could unlock substantial economic benefits for both markets.

A review of the literature reveals that solutions integrating large-scale industrial heat pumps with long-duration thermal energy storage, such as seawater storage, have started to appear both in innovative projects under development, such as the Helsinki Hot Heart [1], and in existing applications as shown by [2] in their extensive review. They highlight that seawater heat pumps of several MW size are deployed worldwide, reaching installations of hundreds of MW in both India and China, and conclude that further research is required for multi-energy and energy storage integration strategies. Ref. [3] explore the integration of seawater heat pumps in district heating systems in coastal towns, presenting relevant techno-economic assessments for North-European and Baltic countries. Here, alternative heat source scenarios are compared based on key parameters such as heat pump coefficient of performance (COP), heat costs, electricity consumption, and CO₂ emissions, although large-scale heat storage integration, including forecasting and optimization models, has not yet been considered. Other studies perform detailed techno-economic modeling of the operational management of conventional district heating power plants integrated with large-scale thermal energy storage, adhering to state-of-the-art operations research approaches [4]. Ref. [5] assess the massive deployment and integration of large-scale thermal energy storage with district heating at a national scale. Their study uses the open-source planning tool Balmorel, employing state-of-the-art optimization techniques, yet due to computational efficiency constraints, the assessment remains high level, using lumped typical weeks and constant efficiency for energy conversion units. Lastly, ref. [6] conduct a techno-economic assessment of large-scale heat pumps, considering variable demand, heat pump COP, and commodity prices, with optimal integration into district heating networks that also include large TES. They use the state-of-the-art, operations-research-based commercial software PLEXOS; however, their optimal management approach does not include sizing or load and price forecast models.

In this paper, we aim to combine the best aspects of the literature discussed above, targeting a trade-off between accuracy and computational burden. Our goal is to assess the potential economic gains from operating large-scale thermal energy storage fed by industrial seawater heat pumps and integrated with a hypothetical district heating network serving the entire city of Amsterdam. To achieve this, we develop a custom-made linear programming economic model that includes both the design and long-term operation of heat storage and time-variable COP for the heat pumps, leveraging the actual data on electricity prices and heat demand complemented by a forecast model. Our solution features essential aspects similar to those proposed in the Helsinki Hot Heart project [1], comprising an array of cylindrical basins positioned in the sea as artificial islands filled with seawater. Nevertheless, seawater storage could alternatively be replaced by more conventional pit thermal energy storage, though our chosen solution offers the added benefit of not occupying urban space. Our primary focus is the analysis of optimal sizing and energy arbitrage opportunities, emphasizing economic viability.

2. Materials and Methods

2.1. Thermal Storage in District Heating

Thermal energy storage (TES) is an essential component of district heating systems that provides a wide range of benefits [7]. TES allows for peak shaving as well as load shifting, meaning that excess heat generated during off-peak hours, either because the generation unit is not controllable or because it is more convenient to do so, like in the case of combined heat and power or heat generation via electricity, can be stored and used during peak hours when the demand for heat is higher. This helps to balance the supply and demand of heat, leading to a more stable and reliable district heating system.

By storing excess heat, TES reduces the need to produce heat during peak hours, which results in reduced energy consumption, increased energy efficiency, and could indirectly reduce greenhouse gas emissions. Such excess heat is otherwise wasted, or it is simply generated because it is more convenient to do so at that very moment, especially when having integration of thermal and electric infrastructure via combined heat and power or via heat pumps. Secondly, TES can help to reduce costs by enabling district heating systems to avoid, on the CapEx side, installing a generation capacity that will be utilized only during peak hours. Furthermore, on the OpEx side, less expensive off-peak electricity or heat sources could be used to generate and store heat for use during peak hours. This helps to lower energy bills for customers and reduces the cost of energy generation.

Overall, as we will show, TES allows to better capture the economic benefits from the coupling of electricity and thermal energy infrastructures, and thus the markets, by providing a way to buy or make use of self-produced electricity when it has lower cost, or even negative prices in the case of large overproduction in the region, and converting it to thermal energy, which can be stored at the costs lower than those for electricity storage and later sold or utilized as heat to customers when needed. The combination of TES with district heating becomes particularly convenient in comparison to what private citizens could implement independently, given the larger volume of heat involved, and thus the scale effect, more regular clustered consumption profiles, and also a larger variety of renewable energy sources that could be adopted, as well as heat generation units such as the seawater industrial heat pumps in our case.

2.2. Thermal Energy Storage Design

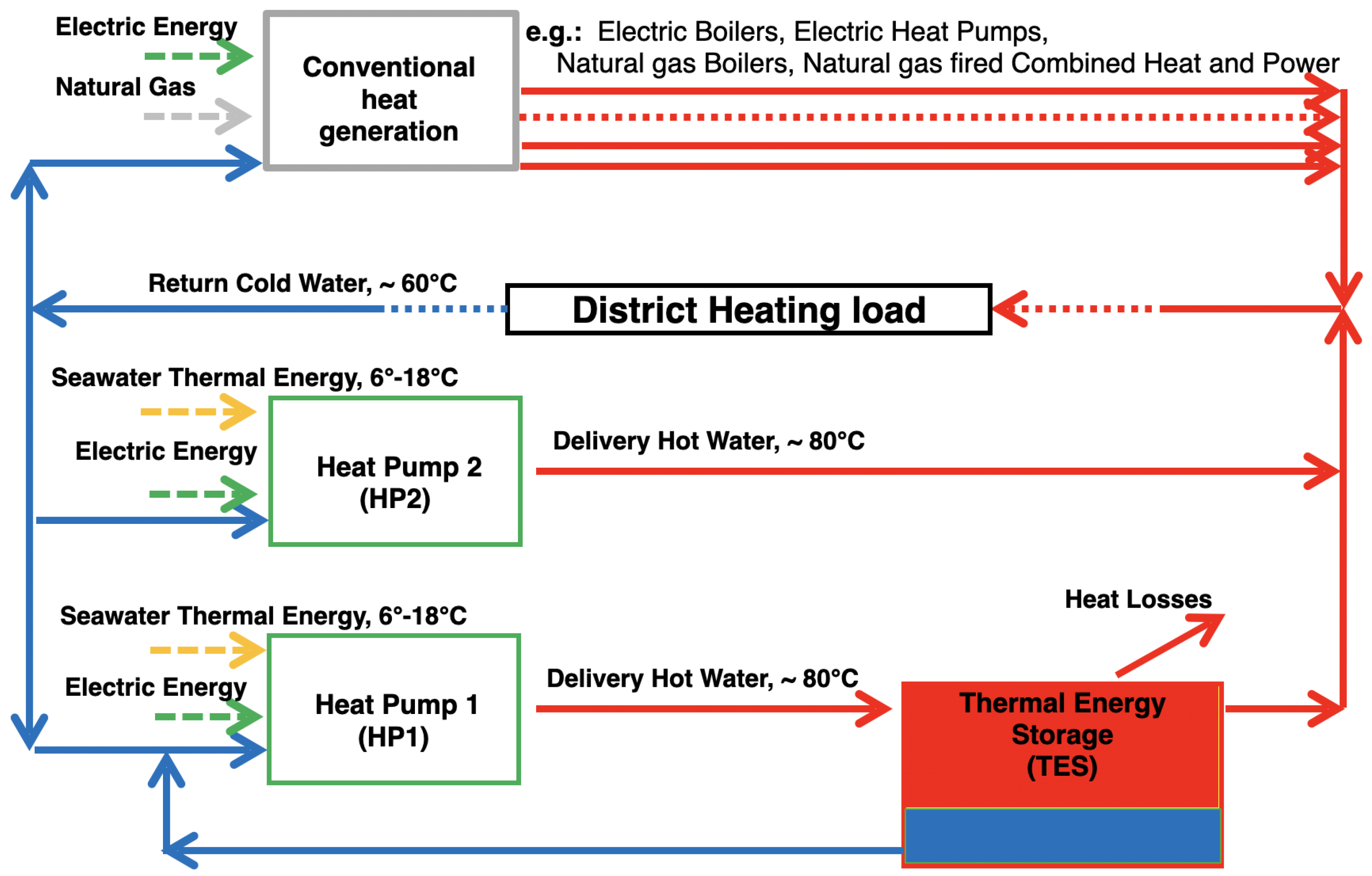
For this project, the technology that has been identified as a reference for thermal energy storage consists of large structures inside the seabed as shown in Figure 1. These capture volumes of water, insulating them from the rest of the sea and constituting an artificial island, both reducing construction costs and having a positive impact on the city by providing extra space for human activities. Such large cylinders filled with seawater could have diverse structures, ranging from excavated to floating, being like an artificial island and making use of seawater as a storage medium; see Figure 1. The operational characteristics of our proposed design, including cost parameters, are based on the previous research conducted by Carlo Ratti Associati and other partners for the “Hot Heart” project in Helsinki [1]. The working principle is similar to a standard pit heat storage, whereby most of the pit already exists thanks to the sea, and furthermore, we do not run into the typical problems of densely populated cities where there is no space available. Such TES ensures a long duration of stored energy up to seasonal heat storage [8]. In fact, pit thermal energy storage systems conventionally work by storing thermal energy in a borehole or pit that is dug deep into the ground, with a solid or liquid, such as water, storage medium. During times of excess energy a heat source—either thermal such as a solar collector, or electric via a heat pump—is used to accumulate heat energy in the pit. The heat energy is in fact transferred via an intermediate fluid, thermal vector such as water or antifreeze, and heat exchanger to the surrounding ground or underground water acting as the storage medium. When heat is needed, the thermal energy is retrieved from the ground by circulating the thermal vector through the heat exchanger in the pit. The fluid absorbs the stored thermal energy from the ground, which is then transferred to the district heating network, which is used for transferring heat to the city.

In this case, the proposed TES fed by industrial heat pumps could be seen as a large battery, “thermal battery”, which varies the usage of renewable electric energy. The main parameters are also summarized in

Table 1. Input parameters for the TES model.

Variables	Value	Units	Source
Cost of the structure ($C_s$)	200	EUR/MWh	[1]
Heat pump installation costs ($C_{hp}$)	1M	EUR/MW	[9]
Annual City Heat Demand, AMS	20,300	TJ	[10]
Annual City Heat Demand [High Growth Scenario]	24,650	TJ	[10]
Annual City Heat Demand [Low Growth Scenario]	21,650	TJ	[10]
National Heat Demand Profiles, NL	Time-series	MWh	[11]
Day-ahead Electricity Prices, NL	Time-series	EUR/MWh	ENTSO-e
Heat Selling Price	20	EUR/GJ	[12]
TES Operation and Maintenance Annual Cost ($C_s^{O\&M}$)	8	EUR/MWh	[13]
Heat Pump Fixed Annual Cost ($C_{hp}^{O\&Mf}$)	2000	EUR/MW	[13]
Heat Pump Variable Cost ($C_{hp}^{O\&Mv}$)	1.8	EUR/MWh	[13]

. The system analyzed is formed by the Tank, which stores water at a temperature of 80 °C, reaching its maximum value (SOC = 100%). Depending on the size, there will be different charge and discharge cycles that could start from daily, to accommodate electric price fluctuations with heat consumption profiles, ranging up to seasonal storage when reaching the maximum value after the summer period and discharging during the winter period. Heat Pump 1, $H{P}_1$, and Heat Pump 2, $H{P}_2$ are seawater industrial heat pumps, which means that they will take advantage, as a low-temperature heat source, of the heat provided by the seawater, which is always well above zero, during the winter as well. This heat will be boosted in quality, up to 80 °C and quantity summing up the electric energy consumed by the heat pumps, according to a coefficient of performance (COP) larger than 1. $H{P}_1$ first feeds the storage, while $H{P}_2$ is directly connected to the district heating network, which then reaches the customers’ houses in Amsterdam. The entire system is shown in Figure 2. The value of 80 °C is identified as a reasonable compromise for such a preliminary study because in the case of the extension of the Amsterdam district heating network to the whole city, it is high enough to not require too radical of a modification of the houses in order to reach comfort, as there is no need of floor heating, and it is at a temperature which can be already achieved by industrial heat pumps with reasonable COPs. Of course, the future Amsterdam district heating system will likely be a combination of low-temperature heat networks for fully refurbished buildings together with higher-temperature ones like ours, which therefore could be considered conservative to assess the solution impact.

2.3. Economic Model of Thermal Storage

In this section, we present a simplified economic model of thermal storage with two heat pumps described in the previous section. The analysis of the market potential is performed from the perspective of a monopolistic firm that serves the current district heating demand using conventional energy sources without storage, assuming that the system proposed here can be utilized as an alternative to partially fulfill such demand while taking existing prices as given.

In what follows, the economic model considers the following inputs for each time period $t=0,1,\dots ,T$: $P_E^t$, $P_H$, and $D_H^t$, which are the temporal data on electricity prices, fixed heat prices (EUR 47.38 per GJ), and city heat demand over the course of a year. In the first part of our analysis, we choose the model to be simulated at the daily frequency level. Later, in Section 3.3, we explore the more granular model, allowing for within-day load shifting.

2.3.1. Heat Demand Forecasting

In a real-life scenario, heat demand is not perfectly known in advance. Hence, optimizing the operation schedule of the thermal storage requires forecasting the demand. As our ground truth data on heat demand, we take the historical national heat demand profile for space and water heating available from [11], which computes heat demand profiles for the Netherlands by combining gas standard load profiles with the spatial temperature and wind speed reanalysis data as well as population geodata. 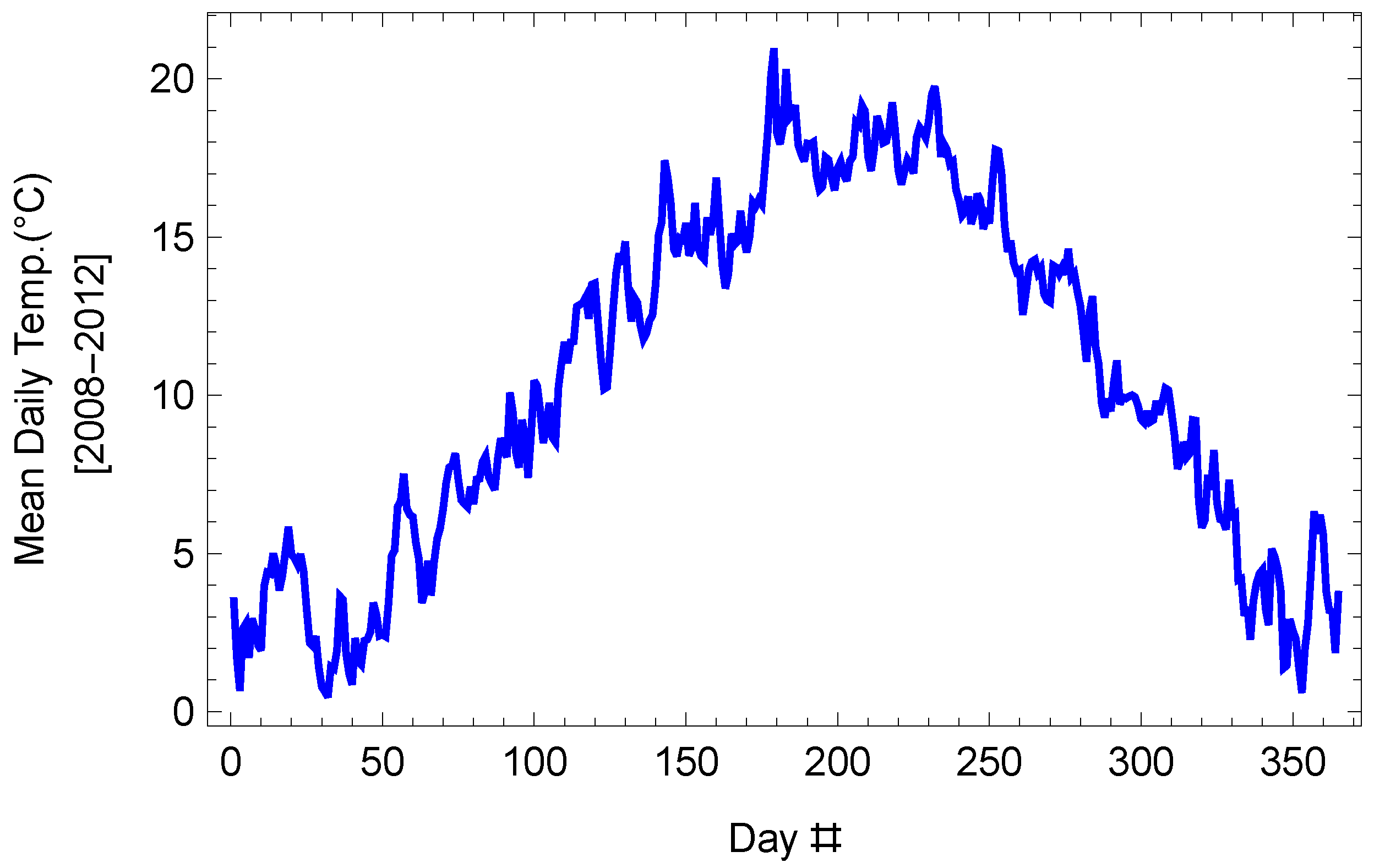Because we do not have access to the ground truth demand data in Amsterdam, we rescale the national estimates provided in [11] to match the total annual heat demand of Amsterdam (20300 TJ according to the “Amsterdam Heat Guide” report [10]), dividing it across the year in a way that matches the seasonal profile of the heat demand in the Netherlands. The resulting heat demand profiles from 2008 to 2013 are shown in Figure 3.

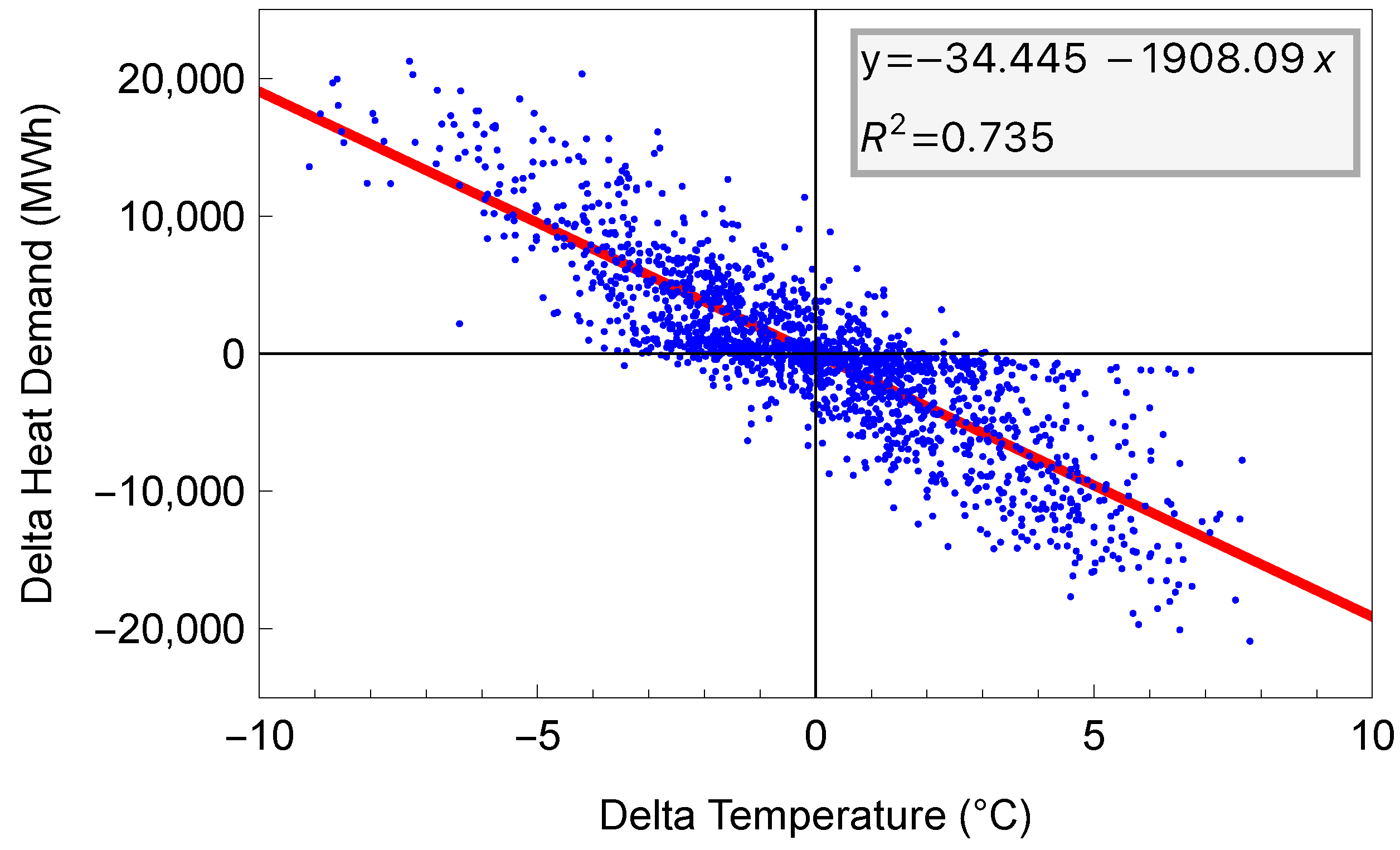
We choose the year 2013 as the case study for our forecasting model since it is the latest year available in our data. The forecast is constructed in three steps. First, we obtain the historical average mean demand for each day, using data for years 2008–2012, shown in Figure 4. In the second step, we take the historical daily ambient temperature data for Amsterdam (Figure 5) between 2008 and 2012, and estimate a regression model that predicts the deviations from the historical average mean heat demand using the corresponding deviations of the temperature from its historical average. The historic average temperature trend is shown in Figure 5, and the regression fit is shown in Figure 6.

The linear model shown in Figure 6 obtains a very high R-squared of 0.74. Therefore, we show that if the outdoor temperature is known perfectly in advance, one could predict the heat demand with high accuracy using the following equation:

$$\widehat{\mathrm{Demand}}\left(\mathit{day}\right)=\overline{\mathrm{HistoricMeanDemand}}\left(\mathit{day}\right)+\widehat{\Delta \mathrm{Demand}}\left(\mathit{day}\right)$$

(1)

where

$$\widehat{\Delta \mathrm{Demand}}\left(\mathit{day}\right)=-34.445-1908.09\times \Delta \mathrm{Temp}\left(\mathit{day}\right)$$

(2)

and $\Delta \mathrm{Temp}\left(\mathit{day}\right)$ denotes the difference between the historic average and actual temperature on a given day of the year.

However, weather forecasts are not precise, and their quality degrades over the prediction horizon. To account for this fact, we obtain the resulting forecast of the demand by adding noise to $\widehat{\mathrm{Demand}}\left(\mathit{day}\right)$ that has the same underlying variance as the demand itself. More specifically, we define

$$\widehat{\mathrm{DemandForecast}}\left(\mathit{day}\right)=\overline{\mathrm{HistoricMeanDemand}}\left(\mathit{day}\right)+\widehat{\Delta \mathrm{DemandForecast}}\left(\mathit{day}\right)$$

(3)

and

$$\widehat{\Delta \mathrm{DemandForecast}}\left(\mathit{day}\right)=0.{95}^{dt}\times \widehat{\Delta \mathrm{Demand}}\left(\mathit{day}\right)+(1-0.{95}^{dt})\times \mathbb{N}(0,V)$$

(4)

where $dt$ denotes the forecast horizon in days. For example, two weeks in advance $(dt=14)$, the forecast will roughly be 50% noise and 50% actual future weather data. An example of applying the resulting forecasting model is shown in Figure 7.

2.3.2. Electricity Price Forecasting

To optimize the schedule of thermal storage ahead of time, one also needs to obtain a forecast of electricity prices. For our case study, we obtain data on average day-ahead electricity prices in the Netherlands at the daily frequency from the beginning of 2020 to the end of 2021. We use prices from 2020 to obtain a forecast of prices throughout 2021—hence, prices in 2021 serve as the ground truth in our case.

Autoregressive models serve as the backbone of all statistical models of electricity prices, where no auxiliary data are required [14]. In particular, SARIMA models have been found effective in this context, and often serve as a baseline comparison for the more sophisticated data-driven methods [15,16,17,18]. We fit a SARIMA time-series process with two autoregressive lags and a seasonality component (of 32 days) on the price data from 2020. Then, for each given start date in 2021, we use a moving window of 60 days prior to this start date to obtain a forecast of the prices for the future dates in 2021, using the fitted SARIMA process to obtain the predictions. An example of applying the resulting forecasting model is shown in Figure 8.

To evaluate the effectiveness of the used forecasting method, we consider the symmetric mean absolute percentage error (sMAPE) as our reference metric. Based on this criterion (sMAPE = 37.08), our forecast performance is lower than the benchmark performance of the more tailored statistical methods in the literature, such as wavelet-ARIMA (WARIMA) or DSARIMA. For example, [19] consider the problem of price forecasting in the day-ahead market in Belgium using WARIMA and DSARIMA models and achieve sMAPE of 22.84–23.40, which is 38% lower than the performance of our model. That said, the objective of developing a state-of-the-art price forecasting model lies outside of the scope of this paper. Therefore, it is important to keep in mind that the results of our economic feasibility study that rely on price forecasting should be interpreted as a reasonable lower bound that can be improved upon with a more tailored forecasting approach. Additional diagnostic metrics are shown in

Table 2. Price prediction forecast accuracy.

Accuracy Metric	Value
sMAPE	37.08
MAPE	49.77
MAE	36.59
RMSE	50.87

.

2.3.3. Heat Pump COP Model

To reflect the dependence of the heat pump COPs, ${\eta }_1$ and ${\eta }_2$, on the variations in seawater temperature during the year, we use a well-established approximation that consists of the ideal HP efficiency, namely, the Carnot heat pump COP operating between these two temperatures, and thus the function of the temperature lift we want to provide, which has been multiplied by the second principle of thermodynamics efficiency assumed to be constant, equal to 0.4. Considering that a detailed model of the HP is not the object of this work and that the temperature lift is always below 80 °C, it is considered an acceptable approximation [20]:

$${\eta }_1^t={\eta }_2^t=\mathrm{COP}\left(t\right)=0.4\times {\displaystyle \frac{T_{\mathit{hot}}}{T_{\mathit{hot}}-T_{\mathit{cold}}^t}}$$

where $T_{\mathit{hot}}$ is set to 353.15 K (equivalent of 80 °C) and $T_{\mathit{cold}}^t$ is the average monthly seawater temperature obtained from historical sea surface temperature data [21].

2.3.4. Heat Supply and Storage Optimization Model

The optimization variables $\{H_D^t,H_S^t,H_C^t|t=0,1,\dots ,364\}$, $H{P}_1$ and $H{P}_2$ are defined as follows. In period $t=-1$, storage is charged at 0. In every period $t=0,1,\dots ,364$ corresponding to a given day of the year, the plant can discharge $H_D^t$ units of heat and has the option to upgrade it using heat pump 2 to supply $H_S^t$ to the district heating. The plant can also charge additional $H_C^t$ units of heat to store for later periods using heat pump 1. Both upgrading the supply and charging of the storage are constrained by the power of the installed heat pumps $H{P}_1$ and $H{P}_2$.

The arbitrage profit function is defined as follows, where ${\eta }_1^t$ and ${\eta }_2^t$ represent the COPs of heat pump 1 and heat pump 2:

$$\begin{array}{cc}\hfill AP{R}^t(H_D^t,H_S^t,H_C^t)& =H_S^t·P_H-{\displaystyle \frac{H_C^t·P_E^t}{{\eta }_1^t}}-(H_S^t-H_D^t)·{\displaystyle \frac{P_E^t}{{\eta }_2^t}}\hfill \end{array}$$

(5)

The annual arbitrage profit is calculated as the sum of the arbitrage profits for each time period during the year, and the total net present value of the system assuming a 30-year lifetime is calculated as

$$\begin{array}{cc}\hfill NPV(\{H_S^t,H_D^t,H_C^t\},H{P}_1,H{P}_2)& =-FC+\sum _{y=0}^{29}{\displaystyle \frac{{\sum }_{t=0}^{T}AP{R}^t-C^{O\&M}}{{(1+i)}^y}}\hfill \end{array}$$

(6)

Here, i denotes the interest rate, $FC$ denotes the investment costs for building a storage of a given size and with a given power of the two heat pumps:

$$FC(\{H_S^t,H_D^t,H_C^t\},H{P}_1,H{P}_2)=C_s\times \mathit{StorageSize}+C_{hp}\times (H{P}_1+H{P}_2)$$

where the storage size is determined by

$$\mathit{StorageSize}\left(\{H_D^t,H_C^t\}\right)=\underset{t=1,\cdots ,T}{max}{S}_t,$$

(7)

and $S_t$ is the state of charge at time t, which can be derived as

$$S_t=H_0{\alpha }^t-\sum _{\tau =0}^{t-1}{\alpha }^{t-\tau }\left(H_D^t-H_C^t\right),$$

(8)

with $alph{a}^t$ as the insulation efficiency at time t, and the annual operation and maintenance costs depend on the total storage size, the amount of energy charged via heat pumps, and the power of the heat pumps:

$$\begin{array}{c}\hfill C^{O\&M}\left(\{H_S^t,H_D^t,H_C^t\}\right)=C_s^{O\&M}\underset{t=1,\cdots ,T}{max}{S}_t+C_{hp}^{O\&Mf}\times (H{P}_1+H{P}_2)+\\ \hfill +C_{hp}^{O\&Mv}\times \sum _{t=1,\cdots ,T}(H_C^t+H_S^t-H_D^t)\end{array}$$

(9)

Algorithm 1: The optimization algorithm for the baseline model.

1. In period $\tau =0$, we choose the power of the two heat pumps $H{P}_1$ and $H{P}_2$, and complete storage schedule $\{H_D^t,H_S^t,H_C^t|t\in \{0,\cdots ,364\}\}$ to maximize NPV in Equation (6), using the actual heat demand and electricity prices for $t=0$, and their corresponding forecasts for $t>0$. 2. In period $\tau >0$, take $H{P}_1$ and $H{P}_2$ (chosen in step 1) and past storage schedule $\{H_D^t,H_S^t,H_C^t|t\in \{0,\cdots ,\tau -1\}\}$ as the given and maximize NPV with respect to the remaining free parameters: $\{H_D^t,H_S^t,H_C^t|t\in \{\tau ,\cdots ,364\}\}$, using the actual heat demand and electricity prices for $t\le \tau$, and their corresponding forecasts for $t>\tau$ (note that forecasts are updated in each period when new information becomes available). 3. Repeat step 2 until $\tau =364$

The optimization algorithm is outlined in Algorithm 1. Note that the optimization yields the optimal storage size derived from the optimal charging and discharging schedule (see Equation (7)), the optimal sizes of the two heat pumps, optimal operating schedules for charging and discharging the storage, and optimal heat supply levels. The optimization is subject to the following constraints:

C1

Demand: $H_S^t\le D_H^t$, the total heat supplied cannot exceed the available demand.

C2

No heat curtailment: $H_D^t\le H_S^t$, all the heat discharged has to be supplied to the district network.

C3

Storage with insulation efficiency $\alpha$ and initial charge $H_0$: The state of charge depletes by $(1-\alpha )$ every period (i.e., every day) and accumulates the difference between the heat that is charged and discharged:

$\forall t:H_D^t\le H_0{\alpha }^t-{\sum }_{\tau =0}^{t-1}{\alpha }^{t-\tau }(H_D^{\tau }-H_C^{\tau })$

For our baseline, we consider insulation with efficiency $\alpha =0.99$, corresponding to the daily depletion rate of the stored heat.

C4

The chosen power of heat pumps imposes two additional constraints:

$\forall t:H_C^t\le H{P}_2\times 24$, and $H_S^t-H_D^t\le H{P}_1\times 24$.

This economic model serves as the basis for analyzing the economic feasibility and performance of the thermal storage system coupled with seawater industrial heat pumps in the context of varying electricity prices, heat demand, and investment costs.

3. Results

3.1. Economic Viability

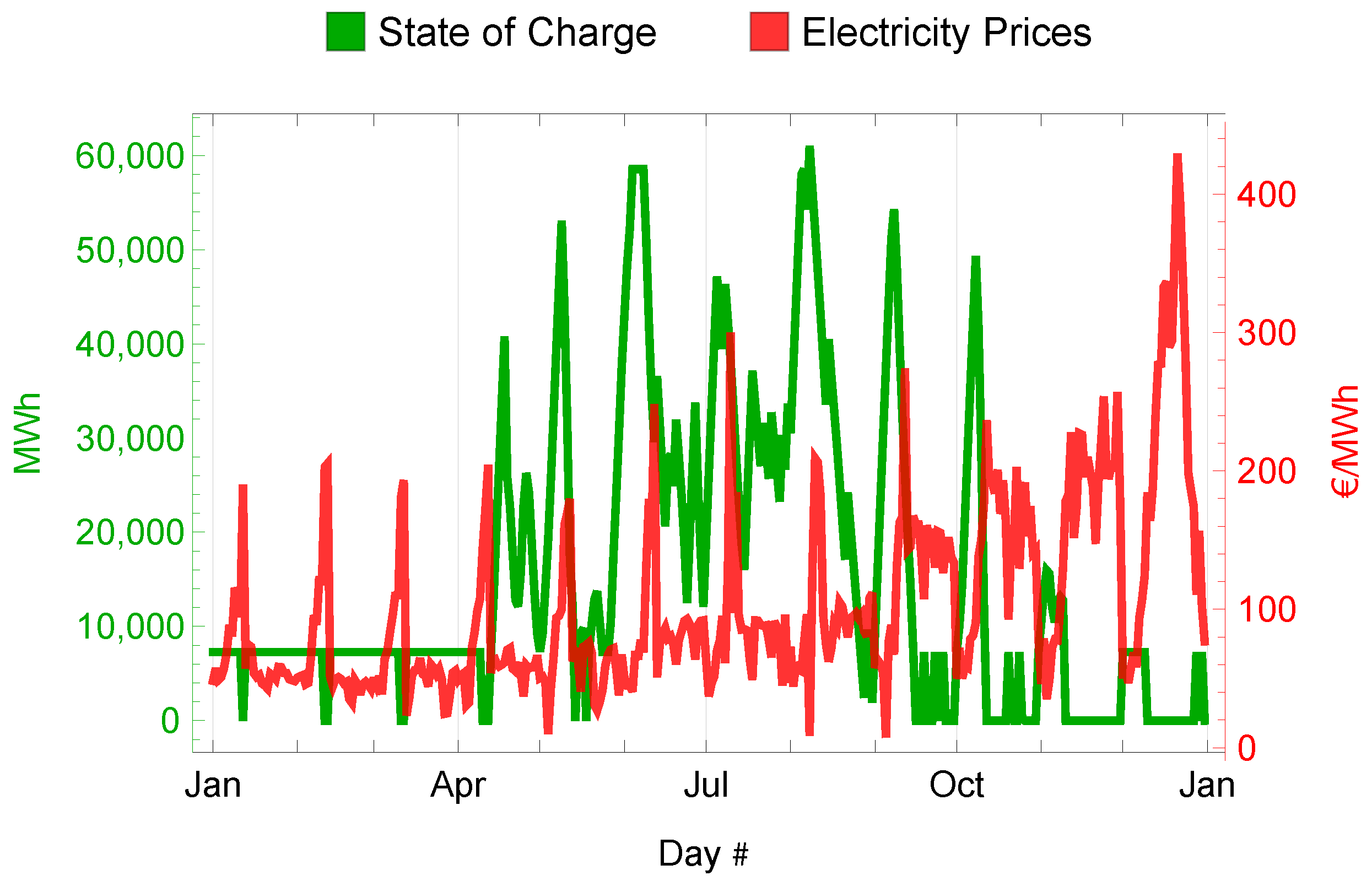
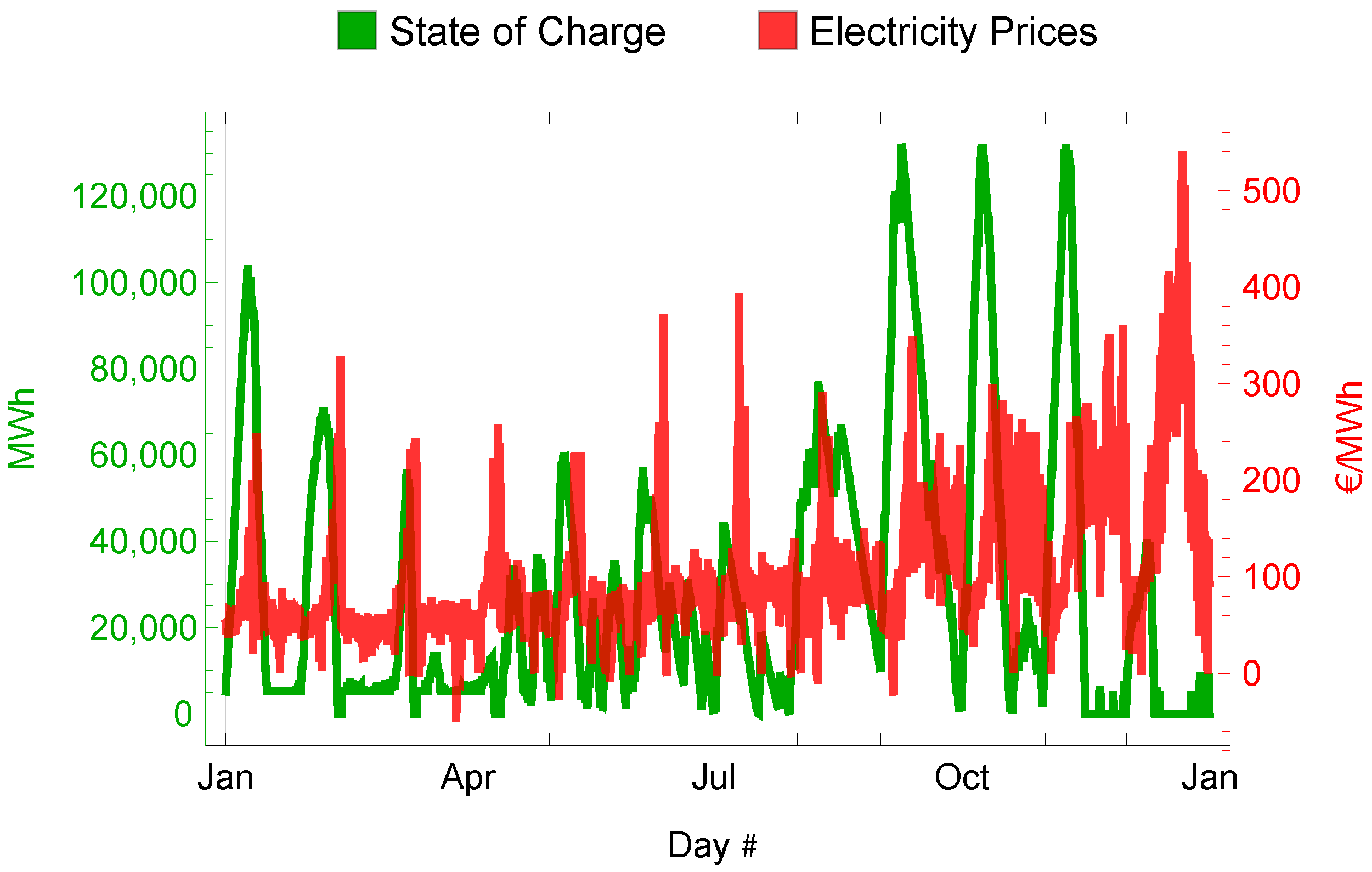
Figure 9 and Figure 10 present the key simulation results. We see that given the 2021 electricity and heat prices in the Netherlands, it would be economically viable to supply a substantial share of the total heating demand via the proposed seawater-cooled heat pumps; see the blue line. They are not utilized, in correspondence with the electricity price peaks, or else they are often at maximum power. We can also see that the optimal charging of the storage closely follows the electricity prices and exhibits a pattern that varies within the year. More in detail, we can see that it is charged before reaching peaks of electric energy costs and accordingly deeply discharged with the price surge. It happens about 10 times in a year, confirming the long-duration impact of this kind of energy storage, heat storage, which indirectly means electricity storage. This is the best trade-off between the price of electricity, helped by the better COP of the HPs in the hot periods, and the losses determined by keeping the storage filled, as it does not make it profitable to have it full for too long of a period, at 1 per cent of the stored energy each day.

Table 3. Output of the TES model: with and without storage.

Variables	With Storage		Without Storage		Units
	Baseline Model	Oracle Model	Baseline Model	Oracle Model
	(1)	(2)	(3)	(4)
Share of Demand Supplied	48 %	71%	49%	50%	%
Storage Size	61,013	149,605	-	-	MWh
Storage Volume	6.43M	2.62M	-	-	m3
Power of heat pump 1 ($H{P}_1$)	302.9	855.7	0	0	MW
Power of heat pump 2 ($H{P}_2$)	407.6	358.9	804.3	791.7	MW
Investment cost	723M	1.25B	804M	792M	EUR
Annual arbitrage	135M	202M	136M	135M	EUR
Annual O&M costs	8M	13M	7.69M	7.84M	EUR
Payback Period **	6	7	7	7	Years
Net Present Value *	466M	530M	397M	402M	EUR

* NPV is calculated assuming a lifespan of 30 years and a 10% discount rate. ** Payback period is calculated by dividing the total investment cost by the annual cash flow.

Column 1 summarizes the key outputs of the optimization. Overall, we find that thermal storage of about 61,000 MWh would be optimal and can provide substantial economic benefits. As seen from the table, it is optimal to utilize heat pump 2 (which is used to store additional energy in the tank) with a heat power of about 407 MW, and heat pump 1 with a heat power of about 303 MW. If we roughly divide the storage size by the heat pump 1, to which is connected, $H{P}_1$, we obtain about 200 h of duration of the nominal power it can discharge, which would be the same value whether we use the electric energy needed to fill it up or the electric power of the $H{P}_1$, neglecting the heat losses and different COP you have when shifting the usage in time. In this way, we can characterize the impact of the indirect electric energy storage adopted thanks to this solution.

This results in total investment costs of about EUR 723M, and annual operation and maintenance costs of about EUR 8M. This optimal configuration yields the corresponding annual arbitrage gain of about EUR 135M. In total, this amounts to the projected net present value of around EUR 466M, assuming a total life span of the system of 30 years and a 10% discount rate. Furthermore, a simple payback time below 6 years, makes this solution competitive also for unsubsidized industrial projects.

To assess the role of forecasting precision in the economic performance of our system, we also compare the results of our baseline model with those of an “oracle” model, in which both the heat demand and electricity prices are known perfectly in advance. Hence, it relies on the actual heat demand profile and electricity prices—as opposed to using the forecasts—to maximize the net present value of the proposed system over the 30-year horizon.

In Table 3, Column 2 shows the results of the optimization for the oracle model. Compared to the baseline model, we find that in the absence of uncertainty, a much larger storage size of about 150,000 MWh is preferred. This larger storage size is also complemented by the more powerful heat pump 1 that feeds the storage (856 MW), and the slightly less powerful heat pump 2 (359 MW). This leads to a heat supply profile of the oracle system that to some extent is similar to the supply profile of our baseline model, but it is both more intense and time-accurate with respect to the charging and discharging of the storage, in correspondence with the electricity price peaks. The first three peaks of electric energy, which do not imply any action in the baseline model, are accompanied by the charge and discharge of storage in the oracle model, and overall it is more precise and uses more storage in the other peaks (see Figure 11 and Figure 12). Overall, it supplies a larger share of the total demand during the high-demand months. Due to the larger storage size and a higher total power of the heat pumps, the oracle model also features substantially higher investment costs of about EUR 1.25B. The resulting net present value is also larger: EUR 530M compared to EUR 466M. Therefore, our baseline model that relies on imperfect forecasting performs relatively well in terms of capturing the economic benefits that arise from coupling the electric and heating infrastructures in Amsterdam. However, the losses from the forecasting errors are not negligible and constitute about 13.7% of the total NPV.

3.2. The Role of Storage

To further evaluate the role of thermal storage in generating economic benefits in the proposed system, we consider several additional results. More specifically, we perform the NPV optimization task for both the baseline and the oracle models shown in columns 1 and 2 of Table 3 but with an additional constraint that the storage size is zero. In this case, the arbitrage opportunities arise solely due to the heat pump 2 being used to convert electricity to heat and capture the price differential between heat and electricity prices without storage.

As can be seen from columns 3 and 4 in Table 3, thermal storage plays a significant role in the economic benefits generated by the proposed system. For the baseline model that relies on forecasting, we find that a system without storage generates about EUR 397M compared to EUR 466M with storage, and therefore storage increases NPV by about 17%. For the oracle model, the value added from storage appears to be larger at about 32% NPV: EUR 530M compared to EUR 402M. Therefore, we find substantial economic benefits from incorporating thermal storage. However, heat pumps still play a dominant role in capturing the price differentials between heat and electricity prices, and are responsible for more than 65% of the total NPV.

3.3. The Role Within-Day Load Shifting

Next, we evaluate the potential value added from using the proposed system for within-day load shifting. Compared to the previous sections, where our model was defined at the daily frequency, here, we utilize the hourly data on electricity prices and heat demand, and consider an analogous model with the exception that $\Delta t=4\mathrm{h}$ and the insulation efficiency per time increment is rescaled to $\sqrt[6]{0.99}$ (to match the daily insulation efficiency of 0.99 used in previous sections). Figure 13 shows the typical daily heat demand profile using hourly data obtained from [11], and we can see that is sufficiently well approximated by the daily heat demand measured using 4 h time windows. Furthermore, due to the substantially higher computational time, in this section, we only consider the oracle model and ignore the issue of forecasting.

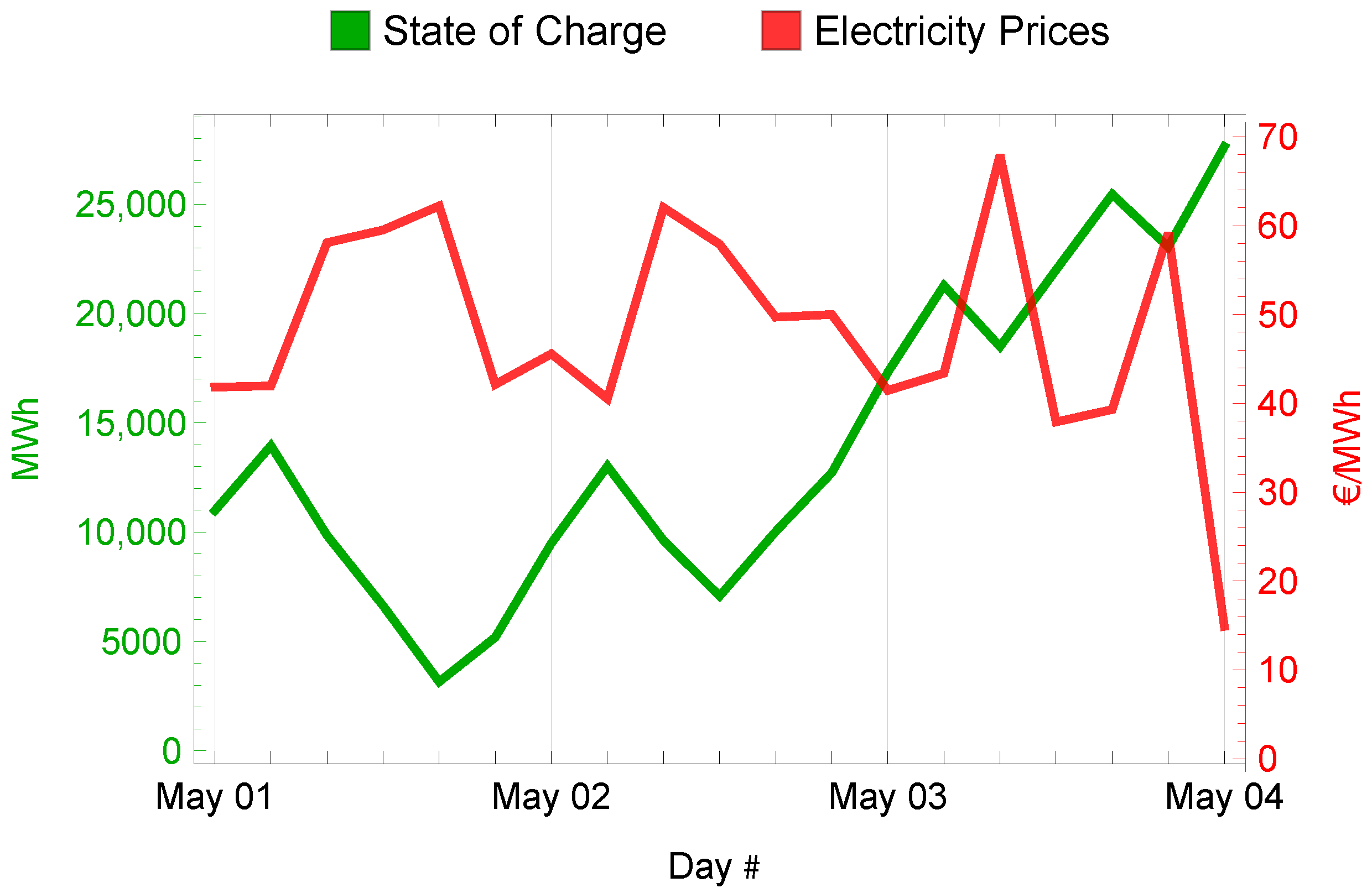
The results of the optimization show an optimal storage charging schedule that resembles a within-day load balancing pattern (see an example in Figure 14). The state of charge increases during the second half of the day when electricity prices are low, and depletes in the morning when electricity prices go up. Figure 15 and Figure 16 show the annual profile of heat supply and state of charge for this case.

As can be seen in

Table 4. TES model with within-day load shifting.

Variables	Oracle Model		Units
	With Storage	Without Storage
	(1)	(2)
Share of Demand Supplied	79%	48%	%
Storage Size	132,120	-	MWh
Storage Volume	5.68M	-	m3
Power of heat pump 1 ($H{P}_1$)	1297.1	0	MW
Power of heat pump 2 ($H{P}_2$)	106.6	753.7	MW
Investment cost	1.43B	754M	EUR
Annual arbitrage	236M	130M	EUR
Annual O&M costs	13.8M	7.4M	EUR
Payback Period **	7	7	Years
Net Present Value *	650M	394M	EUR

* NPV is calculated assuming a lifespan of 30 years and a 10% discount rate. ** Payback period is calculated by dividing the total investment cost by the annual cash flow.

, considering the additional benefits from within-day load shifting yields an optimized system that serves a larger share of total annual heat demand (79% compared to 71%), and utilizes a smaller storage size (about 132,000 MWh compared to 150,000 MWh). In this case, the optimal powers of the two heat pumps are disproportionally divided with a higher power of the heat pump feeding the storage (heat pump 1) compared to the heat pump 2. The overall investment costs in this case are larger at about EUR 1.43B. This yields higher annual arbitrage gains of EUR 236M, and ultimately results in a higher NPV of EUR 650M (which is a roughly 23% increase compared to EUR 530M obtained in the earlier sections). Hence, we find that considering the within-day load shifting substantially increases the economic value of our proposed system.

Finally, we investigate how the role of storage changes when within-day load shifting is considered. Column 2 in Table 4 shows the output of the optimization for the case when the storage size is set to zero. By comparing Columns 1 and 2, we see that once within-day load shifting is accounted for, storage plays a major role in generating the economic value of the proposed system: NPV increases from EUR 394M to EUR 650M, or roughly by 64% compared to the case without storage.

3.4. Insulated Islands Volume and Placement

The volume occupied by the heat storage are estimated in order to evaluate how impactful the proposed solution could be. At first, the mass of hot water $m_{\mathrm{water}}$ is assessed:

$$S_{\max }=m_{\mathrm{water}}·{\displaystyle \frac{c_{p,\mathrm{water}}}{3.6\times {10}^6}}·\Delta T_{\mathrm{stor}}\left(\mathrm{MWh}\right)$$

The maximum amount of energy resulting from the optimization of the storage size $S_{\max }$ is the outcome of the optimization model. The specific heat of water $c_{p,\mathrm{water}}$ is equal to 4.186 kJ/kg·K, and the difference in temperature between storage delivery (80 °C) and return (60 °C), $\Delta T_{\mathrm{stor}}$, is conservatively assumed to be 20 °C, but the return could actually be at a lower temperature.

By considering that $S_{\max }$ is between 61,013 and 149,605 MWh (Table 3 and Table 4) and assuming water density ${\rho }_{\mathrm{water}}$ equal to 1000 kg/m³, it is possible to derive the volume occupied by that mass of water:

$$V_{\mathrm{water}}={\displaystyle \frac{m_{\mathrm{water}}}{{\rho }_{\mathrm{water}}}}\left({\mathrm{m}}^3\right)$$

This results in roughly between 2.6 and 6.5 million cubic meters of water. Dividing by the volume of artificial islands assumed to have a 350 m diameter (D) and 10 m height (h)

$$V_{\mathrm{island}}={\displaystyle \frac{\pi ·D^2}{4}}·h\approx 962112\left({\mathrm{m}}^3\right)$$

This calculation gives us between three and seven islands. Such islands can hypothetically be placed to the east of the city center in the waters of IJmeer bordering Strandeiland as shown in Figure 17. One particular advantage of such a location is the proximity to the existing district heating network that connects Rieteilanden with the rest of the city. This is performed consistently with the marine traffic data taken from openseamap.org (accessed on 16 Septemver 2024), and placing all the islands jointly with the large centralized HP solution, to see its footprint. Such placement of the islands also benefits from the sea depth of around 8–9 m to the east of Strandeiland, meaning that only minimal excavation will be required. Nevertheless, in a real expansion and electrification of the Amsterdam district heating, we can foresee as a better solution smaller distributed HPs, and therefore distributed and eventually smaller artificial islands, so as to reach a better optimum with respect to the integration in the heat network, despite a slightly higher investment cost due to the higher number of smaller units.

4. Conclusions

The results of this study highlight the substantial economic potential of integrating large-scale seawater thermal energy storage (TES) with seawater industrial heat pumps within district heating networks as demonstrated in the case of Amsterdam. This proposed system not only addresses the challenge of aligning renewable energy production with urban heating demand but also represents a robust strategy for enhancing the economic viability of district heating decarbonization.

Our findings indicate that such an integrated TES plus heat pumps system can economically supply a significant portion of Amsterdam’s district heating demand. With an optimal storage size of approximately 61,000 MWh and $H{P}_1$ and $H{P}_2$ with about respectively 300 and 400 MW of heat power, the system is capable of capitalizing on electricity price fluctuations, as reflected in a projected net present value (NPV) of EUR 466 million over a 30-year lifespan. In addition to the impact of coupling thermal and electric infrastructures via heat pumps that often enables to produce heat at a lower price, the use of thermal storage emerges as a key factor in enhancing the economic performance of the system. A comparison between scenarios with and without storage shows a 17% increase in NPV when thermal storage is incorporated, underscoring its role in enabling energy arbitrage and providing operational flexibility. The capability to store thermal energy for extended periods allows the system to mitigate the inherent volatility in both electricity prices and heating demand, thereby stabilizing the overall operation of the district heating network and improving its economic viability.

The significance of storage is further emphasized when within-day load shifting is considered. By incorporating hourly adjustments in the storage and discharge schedule, the system can more effectively respond to short-term variations in electricity prices. This more granular approach not only improves overall system efficiency but also significantly increases the economic value of the TES. When within-day load shifting is integrated, the optimal storage size is slightly reduced, but the system’s NPV increases by approximately 23%, highlighting the enhanced role of storage in maximizing economic returns. Indeed, when accounting for within-day fluctuations, the presence of thermal storage leads to a 64% increase in NPV compared to a system without storage, demonstrating the crucial role that storage plays in capturing the full economic value of the proposed system.

Forecasting accuracy is also shown to be an important factor in realizing the full economic potential of the TES system. The comparison between the baseline model, which incorporates realistic forecasting errors, and an oracle model, which assumes perfect foresight, reveals that forecasting errors result in a 13.7% reduction in NPV. This finding underscores the importance of improving forecasting techniques to enhance the economic performance of the proposed seawater TES and heat pumps systems. As the precision of demand and price forecasts improves, the system’s ability to efficiently manage energy storage and distribution will become increasingly robust, further enhancing its financial returns.

These findings carry broader implications for urban decarbonization efforts, particularly in coastal cities like Amsterdam. The integration of seawater TES and heat pumps with district heating networks offers a scalable and sustainable solution for reducing reliance on fossil fuels. By utilizing seawater as both a storage medium and a heat source, the system minimizes environmental impact while addressing the spatial constraints typical of densely populated urban areas.

However, it is important to acknowledge certain limitations of this study. First, the modeling approach used in this paper does not account for all relevant factors, such as aging and loss problems created by seawater corrosion. Furthermore, the choice of the scheduling system has been dictated by the computational feasibility and represents a simplified algorithm that abstracts away from some of the practical considerations that can be considered in further research. For example, further research could consider incorporating more realistic constraints related to heat supply and storage, accounting for changes in storage temperature and outside air temperature. Additionally, to comprehensively assess the environmental gains of adopting this technology, it would be beneficial to incorporate the benefits derived from higher green energy utilization, particularly when renewable generation varies by season. This would align with Amsterdam’s commitment to green energy and provide a more holistic understanding of the potential impact of thermal energy storage on both the economy and the environment.

In conclusion, this study demonstrates the economic viability of integrating electric and thermal energy infrastructures via seawater industrial heat pumps feeding the district heating networks and enhancing its flexibility via long duration thermal energy storage, particularly in coastal cities like Amsterdam. By leveraging thermal storage for energy arbitrage and operational flexibility, the system effectively enhances economic returns and grid stability while supporting urban decarbonization. Beyond direct economic benefits, the strategic value of seawater TES in decarbonization efforts reinforces its long-term economic potential. By enabling a higher penetration of renewable and recovered heat in the energy mix, TES helps future-proof district heating systems against volatile fossil fuel prices and carbon costs.