A Numerical Analysis of Flow Dynamics Improvement in a Blower via Simple Integration of Bell Mouth and Nose Cone Structures
Abstract
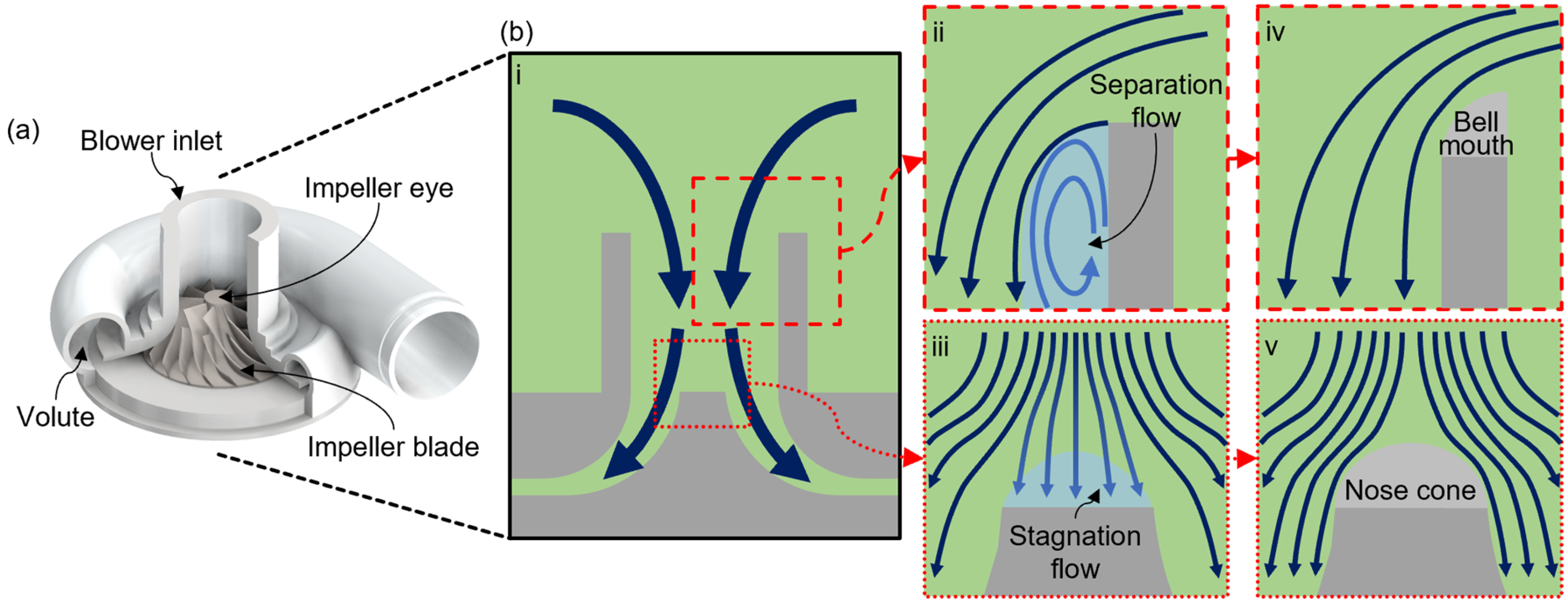
1. Introduction
2. Materials and Methods
2.1. Geometries of Analysis Models
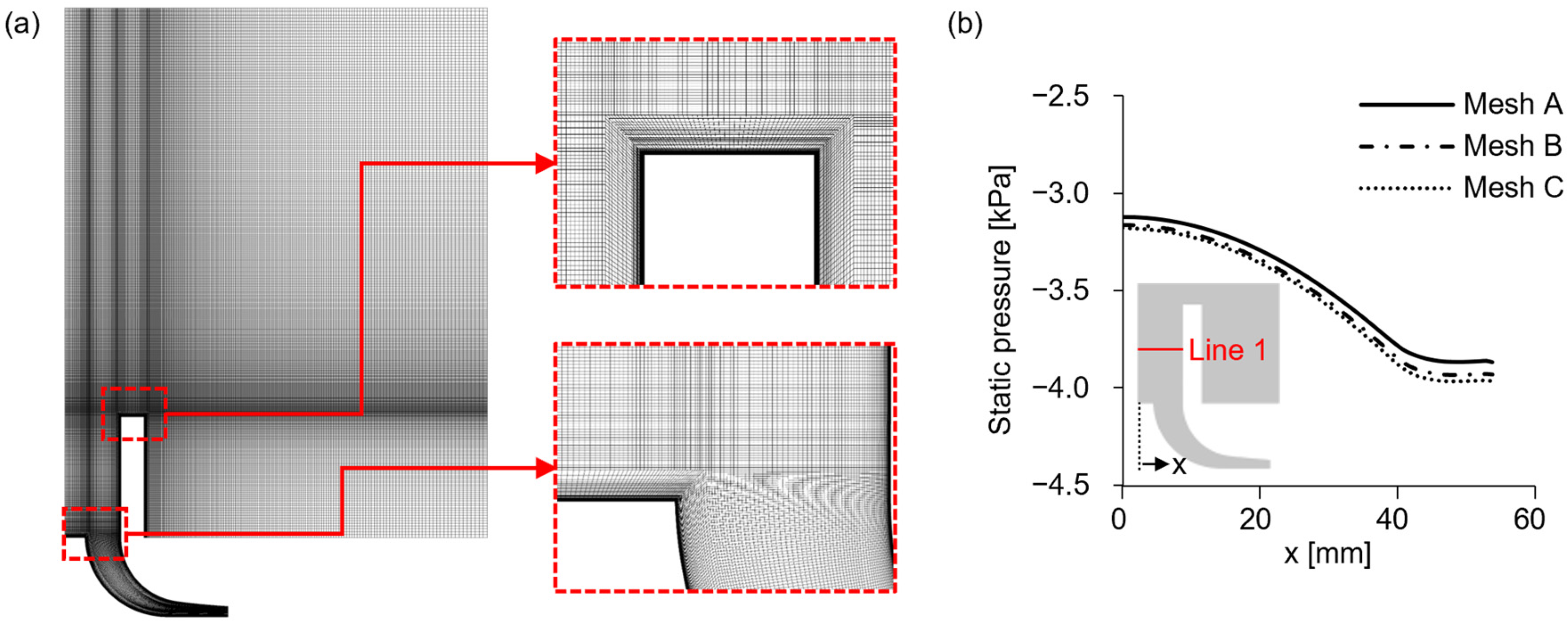
2.2. Numerical Model and Boundary Conditions
3. Results and Discussion
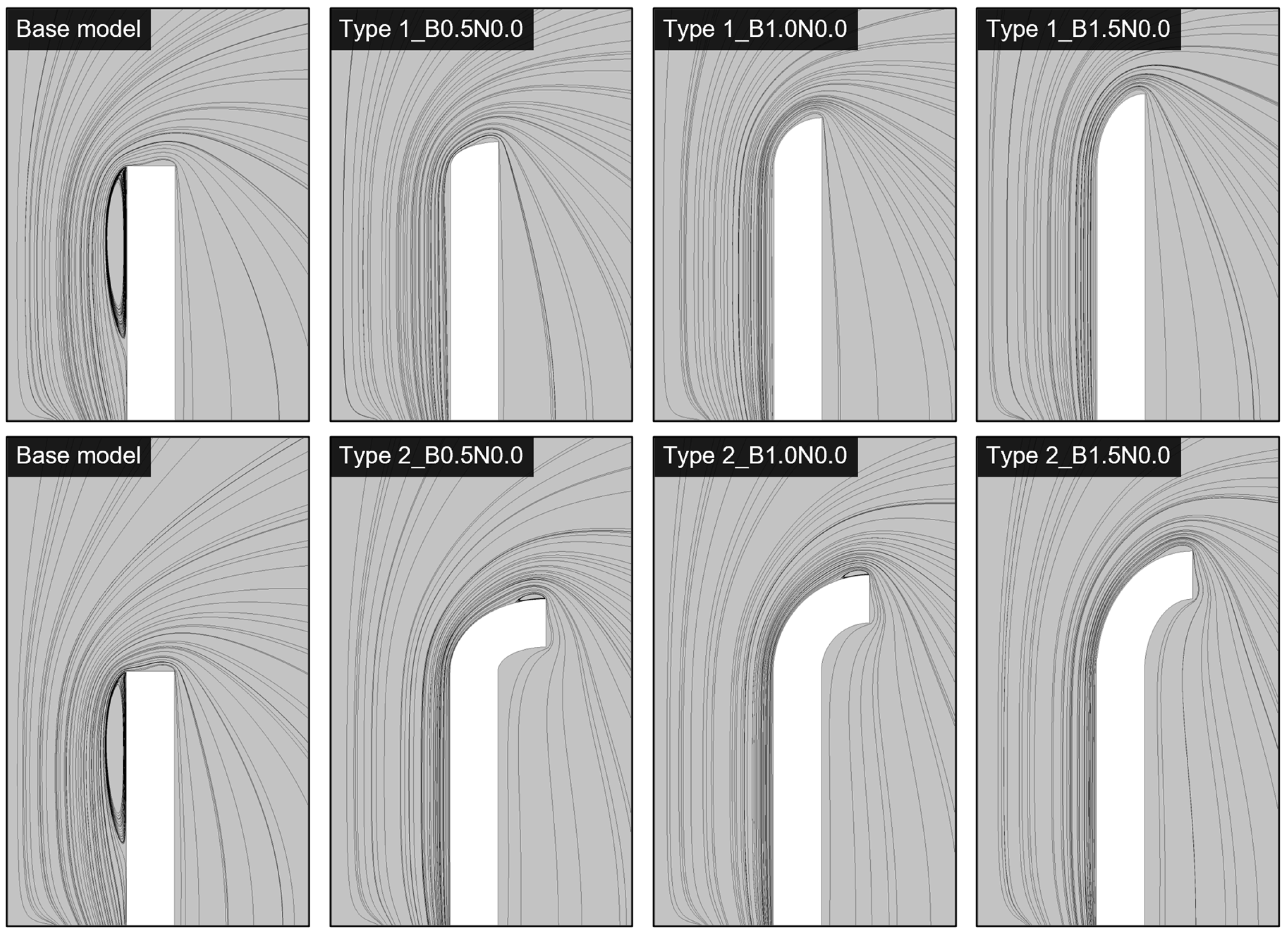
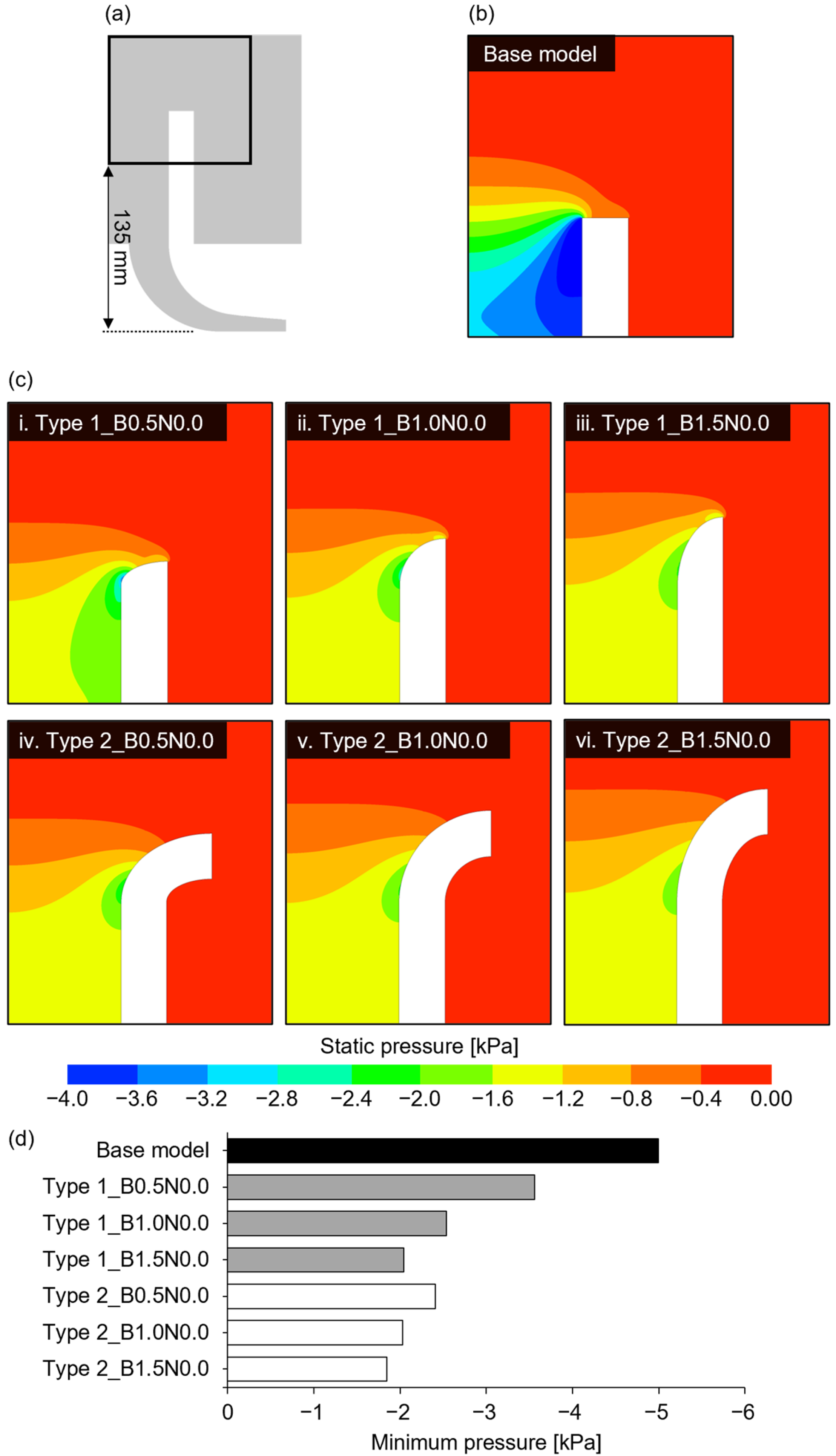
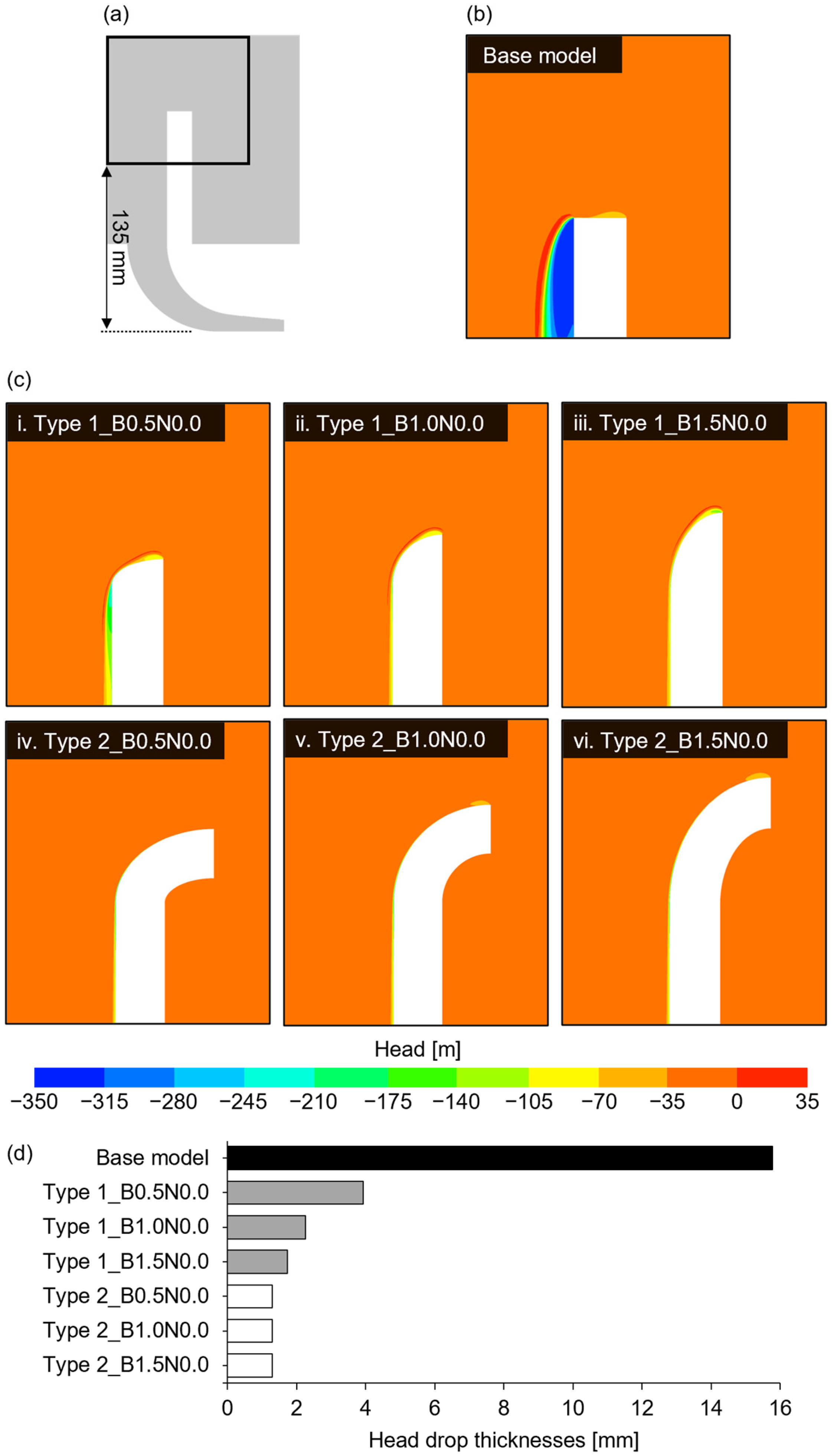
3.1. Bell Mouth Analysis
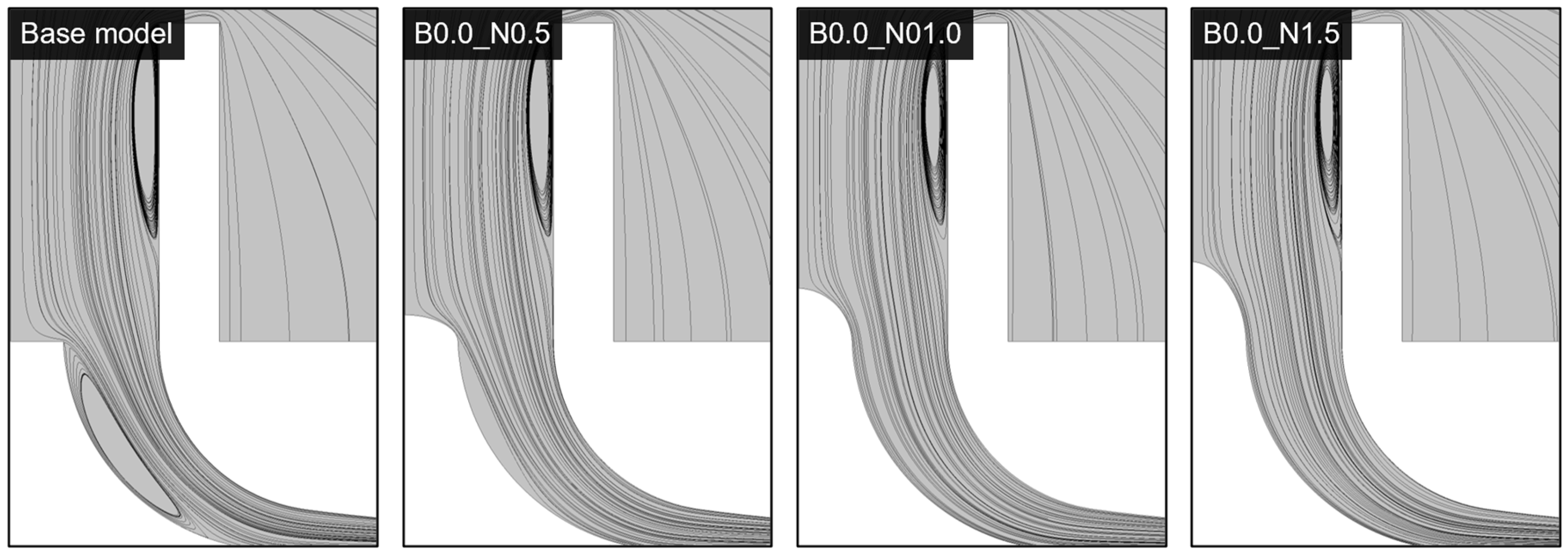
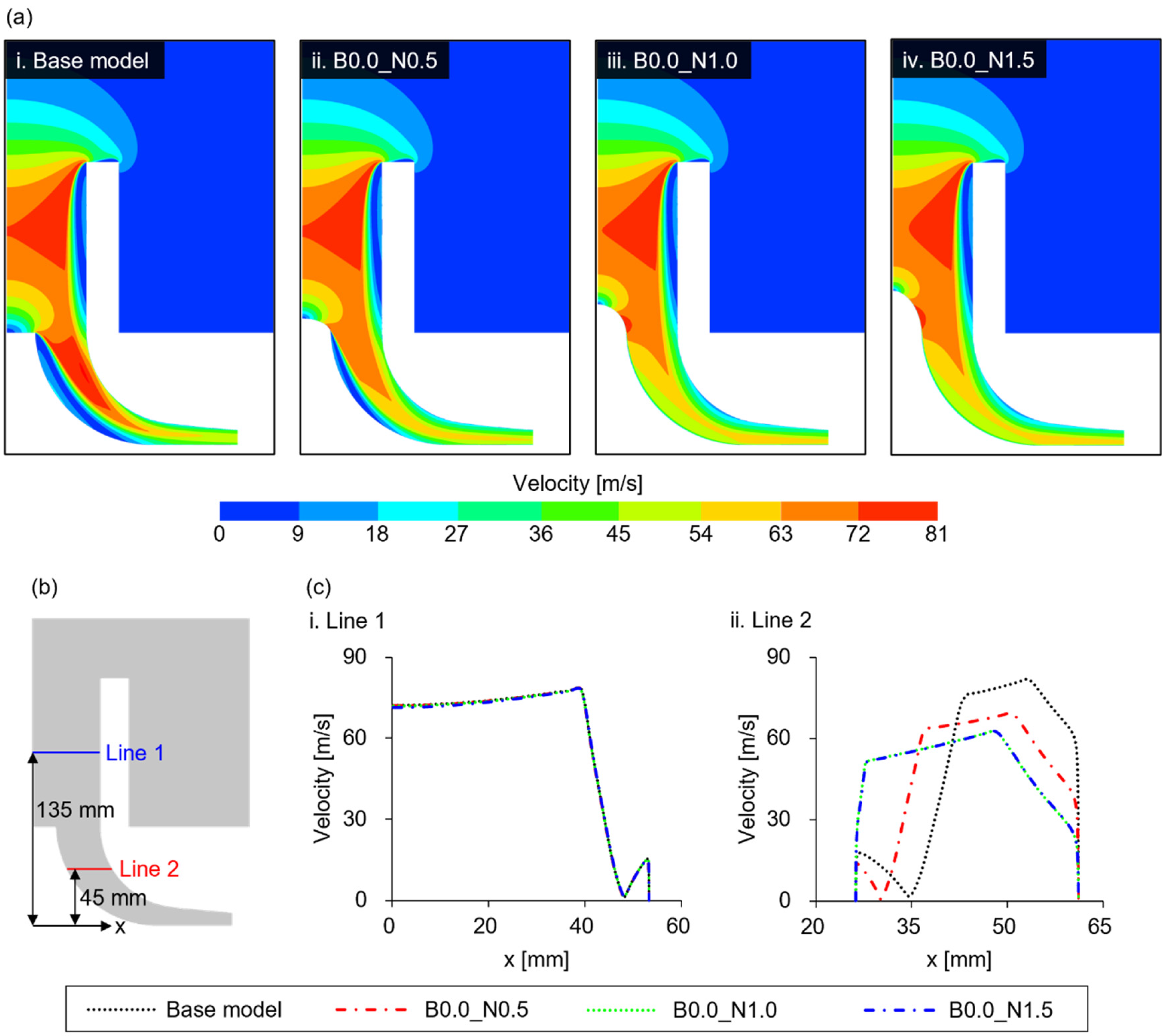
3.2. Nose Cone Analysis
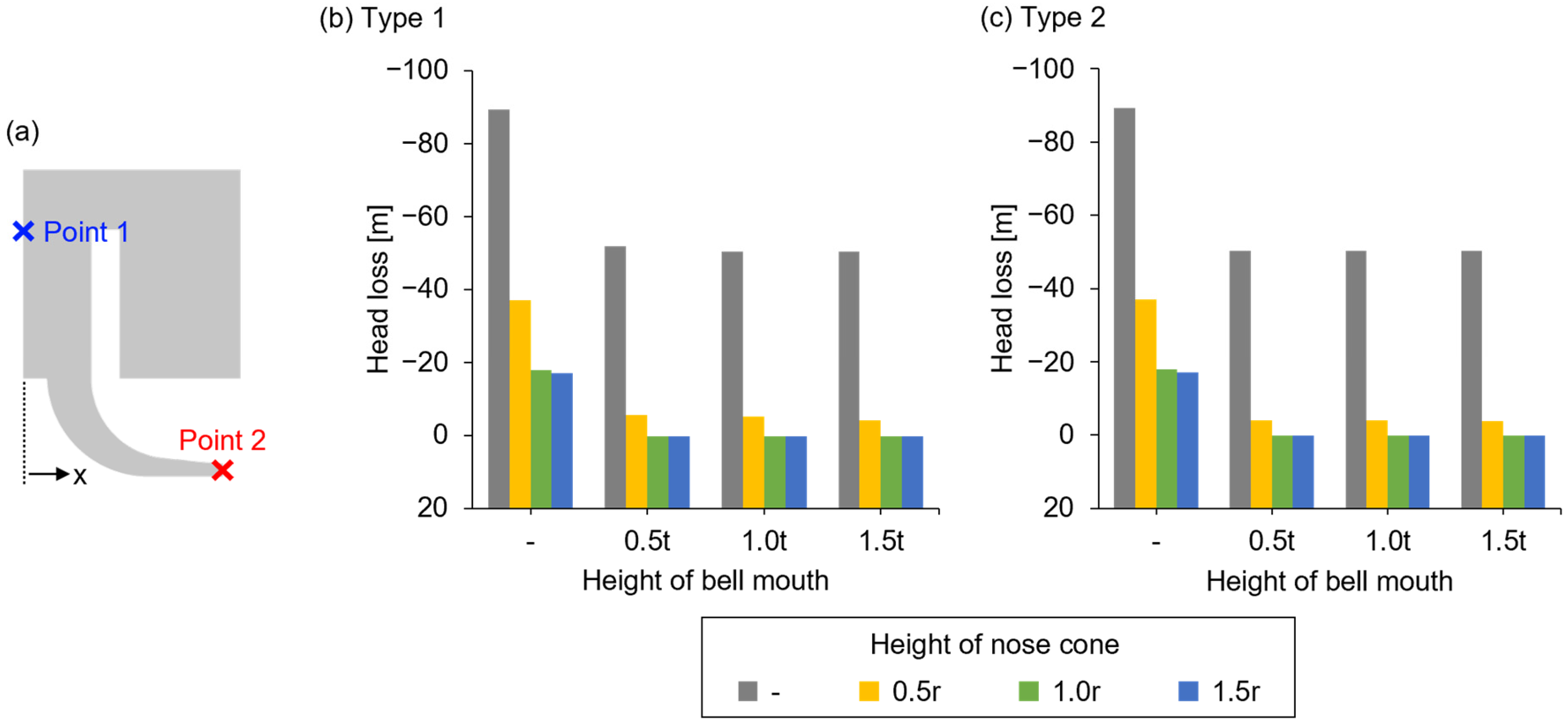
3.3. Combined Effect of the Bell Mouth and Nose Cone
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Crini, G.; Lichtfouse, E. Advantages and disadvantages of techniques used for wastewater treatment. Environ. Chem. Lett. 2019, 17, 145–155. [Google Scholar] [CrossRef]
- Longo, S.; d’Antoni, B.M.; Bongards, M.; Chaparro, A.; Cronrath, A.; Fatone, F.; Lema, J.M.; Mauricio-Iglesias, M.; Soares, A.; Hospido, A. Monitoring and diagnosis of energy consumption in wastewater treatment plants. A state of the art and proposals for improvement. Appl. Energy 2016, 179, 1251–1268. [Google Scholar] [CrossRef]
- Zhang, Z.; Kusiak, A. Models for Optimization of Energy Consumption of Pumps in a Wastewater Processing Plant. J. Energy Eng. 2011, 137, 159–168. [Google Scholar] [CrossRef]
- Afshar Ghotli, R.; Abdul Aziz, A.R.; Ibrahim, S.; Baroutian, S.; Arami-Niya, A. Study of various curved-blade impeller geometries on power consumption in stirred vessel using response surface methodology. J. Taiwan Inst. Chem. Eng. 2013, 44, 192–201. [Google Scholar]
- Lee, Y.T.; Lim, H.C. Performance assessment of various fan ribs inside a centrifugal blower. Energy 2016, 94, 609–622. [Google Scholar] [CrossRef]
- Imsaengsuk, J.; Sangsawangmatum, T.; Chantrasmi, T.; Nontakaew, U. Performance investigation of blower for mechanical ventilator using CFD. In AIP Conference Proceedings; AIP Publishing: Phuket, Thiland, 2024; Volume 3086. [Google Scholar]
- Abo Elyamin GR, H.; Bassily, M.A.; Khalil, K.Y.; Gomaa, M.S. Effect of impeller blades number on the performance of a centrifugal pump. Alex. Eng. J. 2019, 58, 39–48. [Google Scholar]
- Varun Ch, S.; Anantharaman, K.; Rajasekaran, G. Effect of blade number on the performance of centrifugal fan. Mater. Today Proc. 2023, 72, 1143–1152. [Google Scholar]
- Mandhare, N.A.; Karunamurthy, K. Investigation on Centrifugal Pump Performance for Various Nose-Cap Geometries. In Theoretical, Computational, and Experimental Solutions to Thermo-Fluid Systems: Select Proceedings of ICITFES 2020; Springer: Singapore, 2021; pp. 401–411. [Google Scholar] [CrossRef]
- Munson, B.R.; Okiishi, T.H.; Huebsch, W.W.; Rothmayer, A.P. Fundamentals of Fluid Mechanics, 7th ed.; Wiley: Singapore, 2013. [Google Scholar]
- Shaikh, J.S.; Pathan, K.A.; Kumar, K.; Khan, S.A. Effectiveness of Cone Angle on Surface Pressure Distribution along Slant Length of a Cone at Hypersonic Mach Numbers. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 104, 185–203. [Google Scholar]
- Dhumal, A.; Ambhore, N.; Tamkhade, P.; Marne, A.; Mujawar, N. Numerical Optimization for Aerodynamic Performance of Nose Cone of FSAE Vehicle through CFD. CFD Lett. 2024, 16, 161–171. [Google Scholar]
- Shah, V.K.; Ateeb, K.; Razzaq, M.; Varun, C.; Avinash, B. Determination of the optimum nose cone geometrical shape for supersonic missile. Mater. Today Proc. 2022, 64, 749–754. [Google Scholar] [CrossRef]
- Wu, H.; Tan, L.; Niu, W.; Song, Y.; Zhang, Y.; Wang, S.; Yan, S. A novel morphing nose cone for underwater gliders: Performance analysis, parameter optimization, and driving mechanism design. Appl. Ocean Res. 2024, 147, 104000. [Google Scholar] [CrossRef]
- Tiwari, A.; Patel, S.; Lad, A.; Mistry, C.S. Development of Bell Mouth For Low Speed Axial Flow Compressor Testing Facility. In Proceedings of the Asian Congress on Gas Turbines, Mumbai, India, 14–16 November 2016. [Google Scholar]
- Han, M.H.; Park, J.H.; Yang, J.S.; Yoon, S.Y.; Min, J.K. Shape optimization of bellmouth to improve flow uniformity under non-aligned inflow condition in gas turbine casing. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2400533. [Google Scholar]
- Sevinç, K. Aerodynamic design optimization of a bellmouth shaped air intake for jet engine testing purposes and its experiment based validation. J. Phys. Conf. Ser. 2021, 1909, 012028. [Google Scholar]
- Shrestha, U.; Choi, Y.-D. Bellmouth Shape Optimization for the Suppression of Flow Instability in a Pump Sump Model. KSFM J. Fluid Mach. 2021, 24, 49–57. [Google Scholar]
- Son, P.N.; Kim, J.W.; Byun, S.M.; Ahn, E.Y. Effects of inlet radius and bell mouth radius on flow rate and sound quality of centrifugal blower. J. Mech. Sci. Technol. 2012, 26, 1531–1538. [Google Scholar]
- Kim, S.; Heo, S.; Cheong, C.; Kim, T.H. Numerical and experimental investigation of the bell-mouth inlet design of a centrifugal fan for higher internal flow rate. J. Mech. Sci. Technol. 2013, 27, 2263–2273. [Google Scholar]
- Singh, A.P.; Kumar, A.; Akshayveer Singh, O.P. A novel concept of integrating bell-mouth inlet in converging-diverging solar chimney power plant. Renew. Energy 2021, 169, 318–334. [Google Scholar]
- Singh, A.P.; Kumar, A.; Akshayveer Singh, O.P. Natural convection solar air heater: Bell-mouth integrated converging channel for high flow applications. Build. Environ. 2021, 187, 107367. [Google Scholar]
- ANSYS Inc. ANSYS FLUENT Theory Guide 12.0 Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2015; Volume 15317. [Google Scholar]
- Deepak, N.R.; Ray, T.; Boyce, R.R. Evolutionary Algorithm Shape Optimization of a Hypersonic Flight Experiment Nose Cone. J. Spacecr. Rocket. 2012, 45, 428–437. [Google Scholar] [CrossRef]
- Gauer, M.; Paull, A. Numerical Investigation of a Spiked Blunt Nose Cone at Hypersonic Speeds. J. Spacecr. Rocket. 2012, 45, 459–471. [Google Scholar] [CrossRef]
- Whale, J. Design and construction of a simple blade pitch measurement system for small wind turbines. Renew. Energy 2009, 34, 425–429. [Google Scholar]
- Freere, P.; Sacher, M.; Derricott, J.; Hanson, B. A Low Cost Wind Turbine and Blade Performance. Wind. Eng. 2010, 34, 289–302. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Wang, Z. Influence of Blade Leading-Edge Shape on Cavitation in a Centrifugal Pump Impeller. Energies 2018, 11, 2588. [Google Scholar] [CrossRef]


| Height of Bell Mouth | Height of Nose Cone | Types of Bell Mouth | |
|---|---|---|---|
| (t = 21.61 mm) | (r = 19 mm) | Type 1 | Type 2 |
| - | - | Base model | |
| 0.5r | B0.0_N0.5 | ||
| 1.0r | B0.0_N1.0 | ||
| 1.5r | B0.0_N1.5 | ||
| 0.5t | - | Type 1_B0.5_N0.0 | Type 2_B0.5_N0.0 |
| 0.5r | Type 1_B0.5_N0.5 | Type 2_B0.5_N0.5 | |
| 1.0r | Type 1_B0.5_N1.0 | Type 2_B0.5_N1.0 | |
| 1.5r | Type 1_B0.5_N1.5 | Type 2_B0.5_N1.5 | |
| 1.0t | - | Type 1_B1.0_N0.0 | Type 2_B1.0_N0.0 |
| 0.5r | Type 1_B1.0_N0.5 | Type 2_B1.0_N0.5 | |
| 1.0r | Type 1_B1.0_N1.0 | Type 2_B1.0_N1.0 | |
| 1.5r | Type 1_B1.0_N1.5 | Type 2_B1.0_N1.5 | |
| 1.5t | - | Type 1_B1.5_N0.0 | Type 2_B1.5_N0.0 |
| 0.5r | Type 1_B1.5_N0.5 | Type 2_B1.5_N0.5 | |
| 1.0r | Type 1_B1.5_N1.0 | Type 2_B1.5_N1.0 | |
| 1.5r | Type 1_B1.5_N1.5 | Type 2_B1.5_N1.5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Yeom, J.; Baeck, S.; Lee, S.; Park, J.Y. A Numerical Analysis of Flow Dynamics Improvement in a Blower via Simple Integration of Bell Mouth and Nose Cone Structures. Energies 2025, 18, 1830. https://doi.org/10.3390/en18071830
Park J, Yeom J, Baeck S, Lee S, Park JY. A Numerical Analysis of Flow Dynamics Improvement in a Blower via Simple Integration of Bell Mouth and Nose Cone Structures. Energies. 2025; 18(7):1830. https://doi.org/10.3390/en18071830
Chicago/Turabian StylePark, Junseon, Jiun Yeom, Seongyeol Baeck, Seungjin Lee, and Joong Yull Park. 2025. "A Numerical Analysis of Flow Dynamics Improvement in a Blower via Simple Integration of Bell Mouth and Nose Cone Structures" Energies 18, no. 7: 1830. https://doi.org/10.3390/en18071830
APA StylePark, J., Yeom, J., Baeck, S., Lee, S., & Park, J. Y. (2025). A Numerical Analysis of Flow Dynamics Improvement in a Blower via Simple Integration of Bell Mouth and Nose Cone Structures. Energies, 18(7), 1830. https://doi.org/10.3390/en18071830








