Sample-Based Optimal Dispatch of Shared Energy Storage in Community Microgrids Considering Uncertainty
Abstract
1. Introduction
1.1. Related Works
1.2. Our Contributions
- We have constructed a community microgrid model with SES under deterministic and chance-constrained conditions with wind output uncertainty. The model is transformed into SRO and RSRO by introducing the concept of statistical feasibility. The uncertainty set is constructed and reconstructed based only on samples and constraint information, gradually reducing the conservatism of the proposed approach.
- The uncertainty in the objective function is handled using the sample average approximation (SAA) method, and the nonlinear terms in the constraints are dealt with using Slater’s condition, thereby enabling the practical solution of the proposed RSRO approach.
- The proposed approach is tested using a community example with three microgrids. Benchmarks and evaluation metrics are developed to verify the effectiveness of the approach. Compared with traditional approaches, the optimization results demonstrate the proposed approach’s superiority.
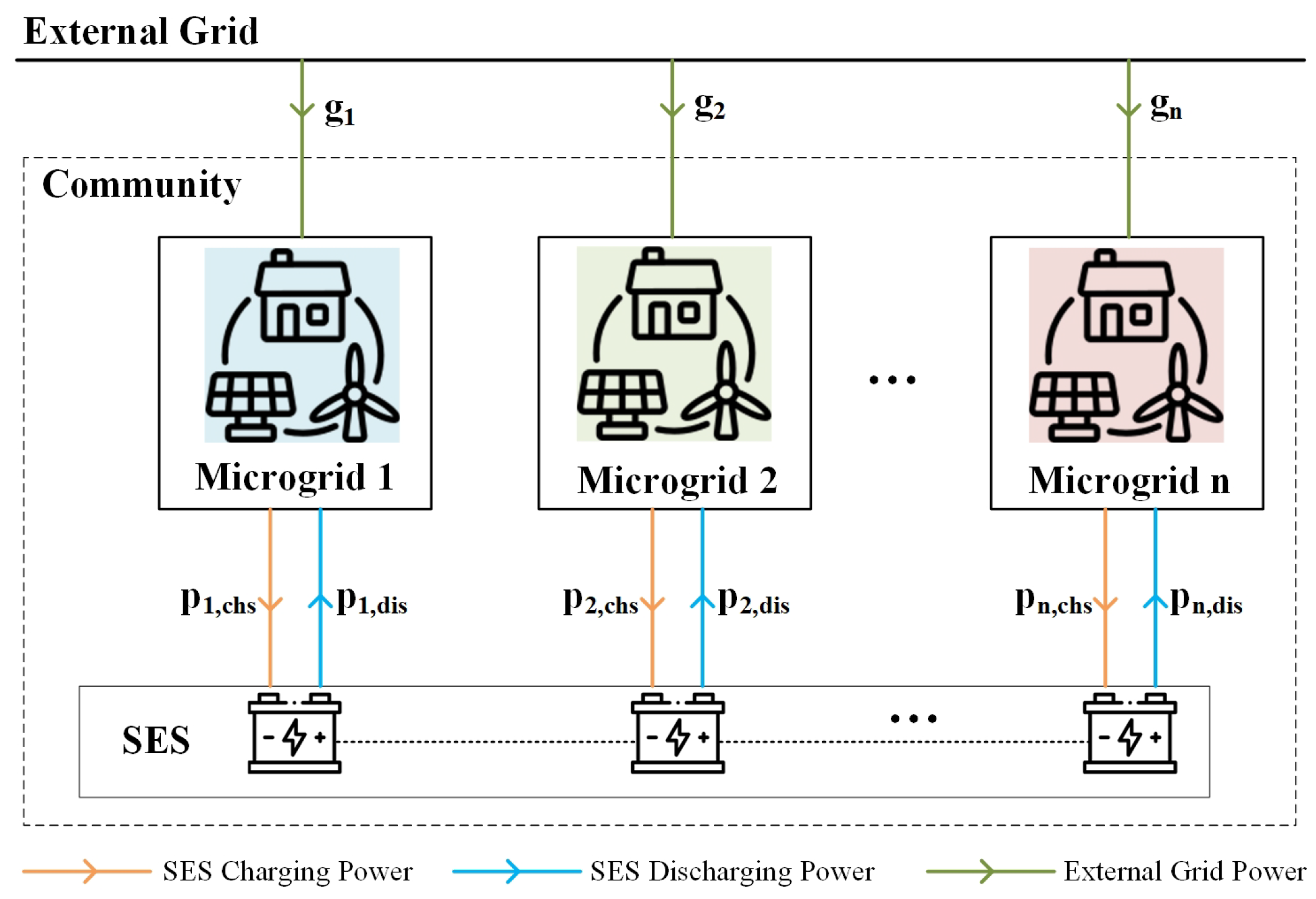
2. System Model
- The generation cost of renewable energy is assumed to be zero.
- The SES system can only charge or discharge at any given moment concerning each microgrid. However, its charging and discharging states can vary between different microgrids.
- The charging and discharging efficiency of the SES system is considered to be constant.
2.1. Deterministic Model
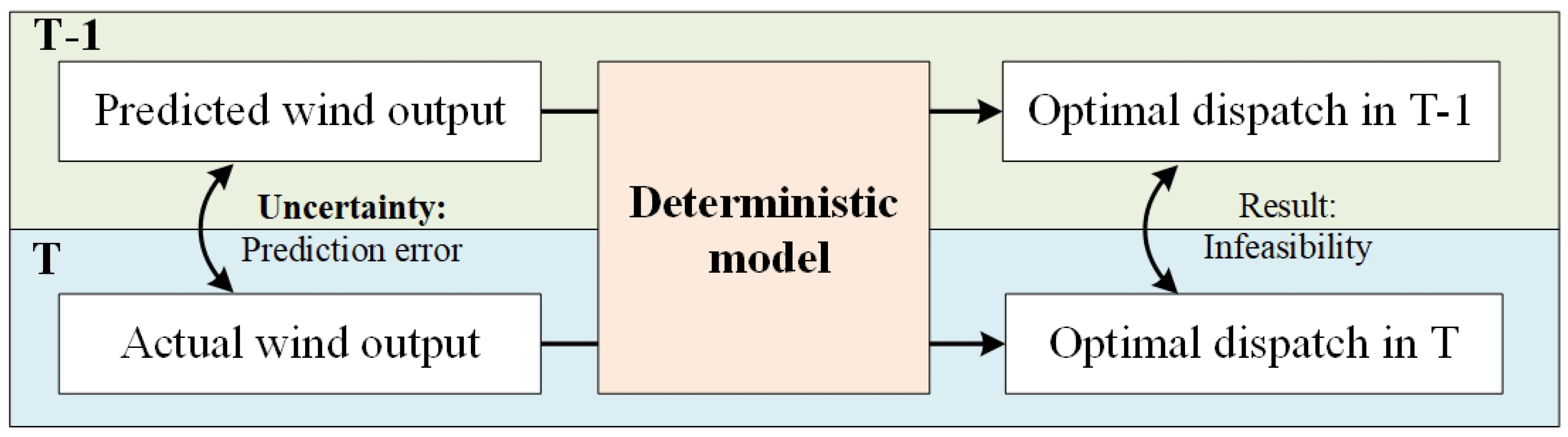
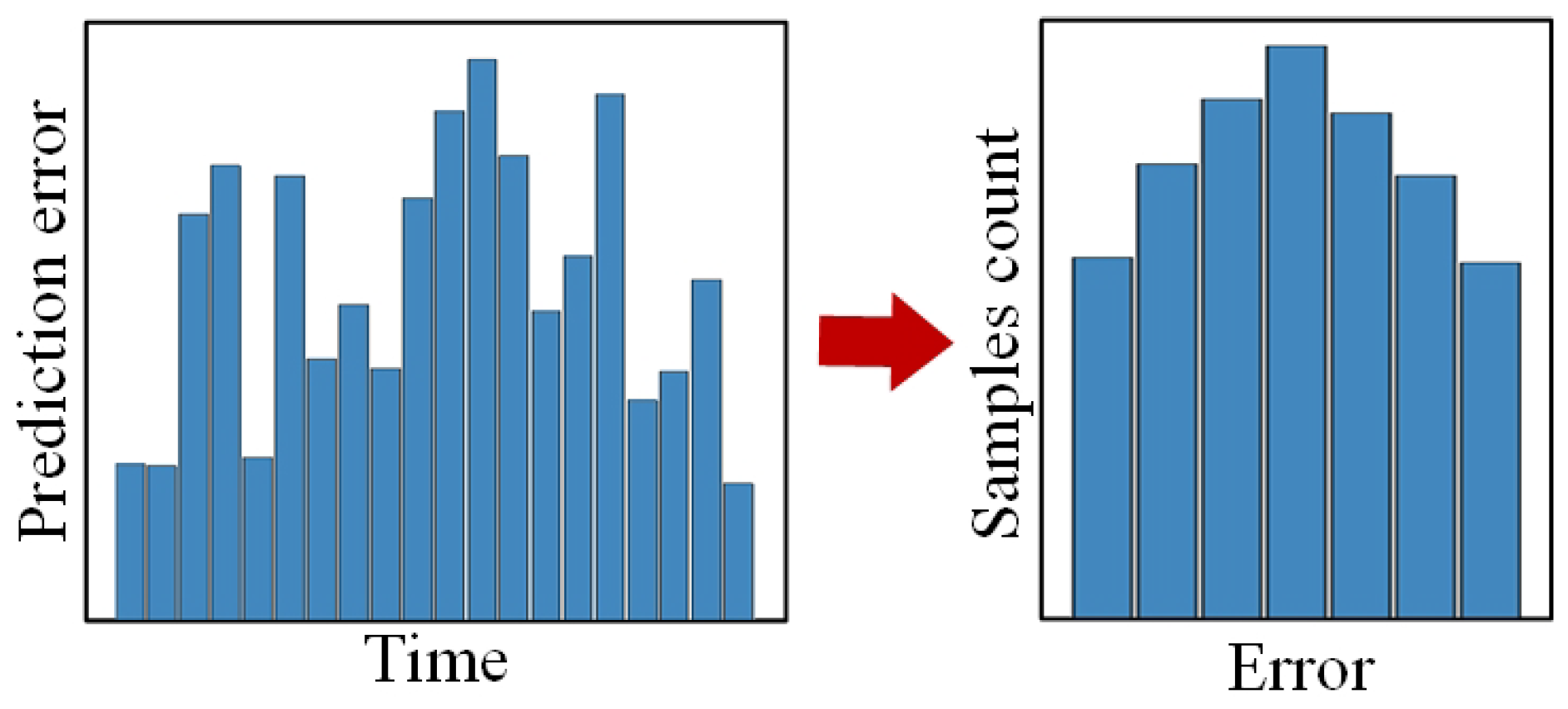
2.2. Uncertainty Analysis
2.3. Chance-Constrained Model
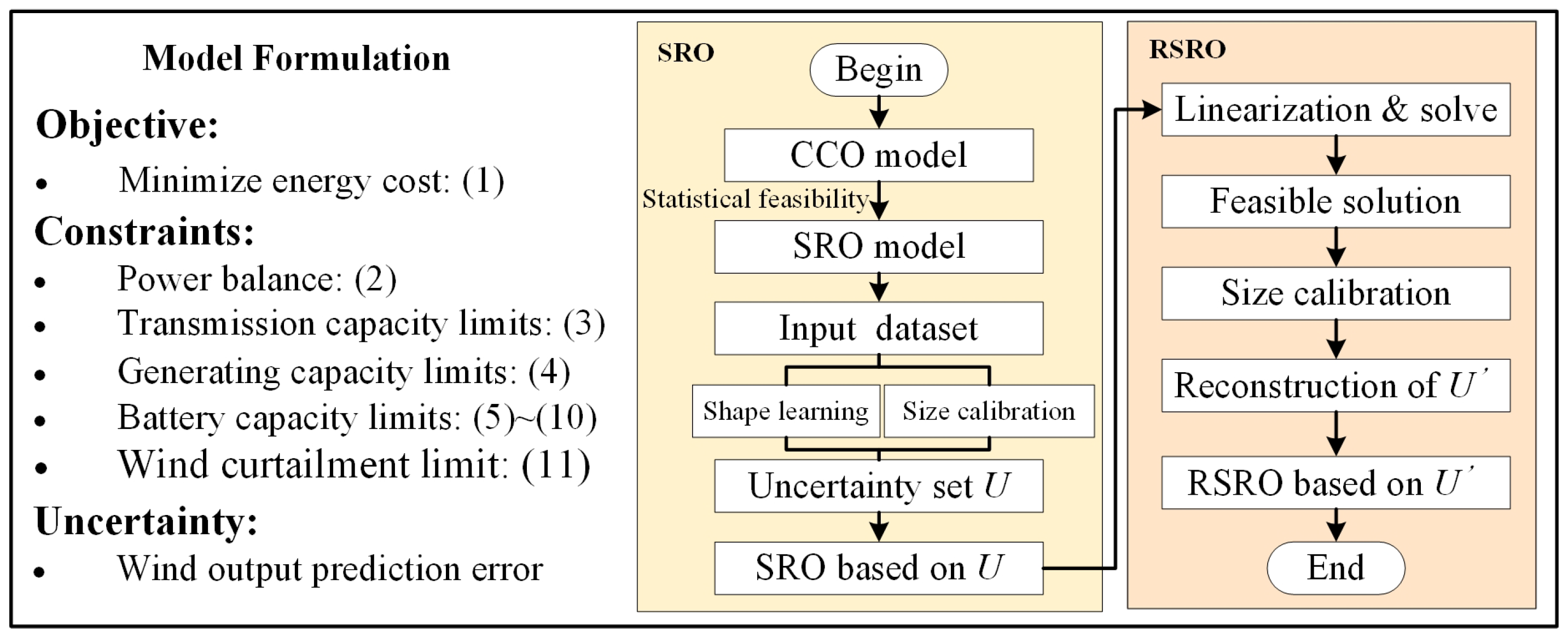
3. Sample-Based RO
3.1. Statistical Gurantee
3.2. Uncertainty Set Construction
- It is necessary to find the smallest possible uncertainty set that satisfies the given conditions, which means that should cover the high-probability regions (HPRs) [28] of . This approach will better capture the distributional characteristics of and reduce conservatism.
- The shape of the uncertainty set affects the complexity of the problem. In this study, with the shape of an ellipsoid is chosen to reduce the computational difficulty [29].
| Algorithm 1 Uncertainty Set Construction of SRO |
|
3.3. Uncertainty Set Reconstruction
| Algorithm 2 Uncertainty Set Reconstruction of RSRO |
|
4. Solution Methodology
4.1. Uncertainty in Objective Function
4.2. Linear Transformation for Robust Constraints
5. Numerical Studies
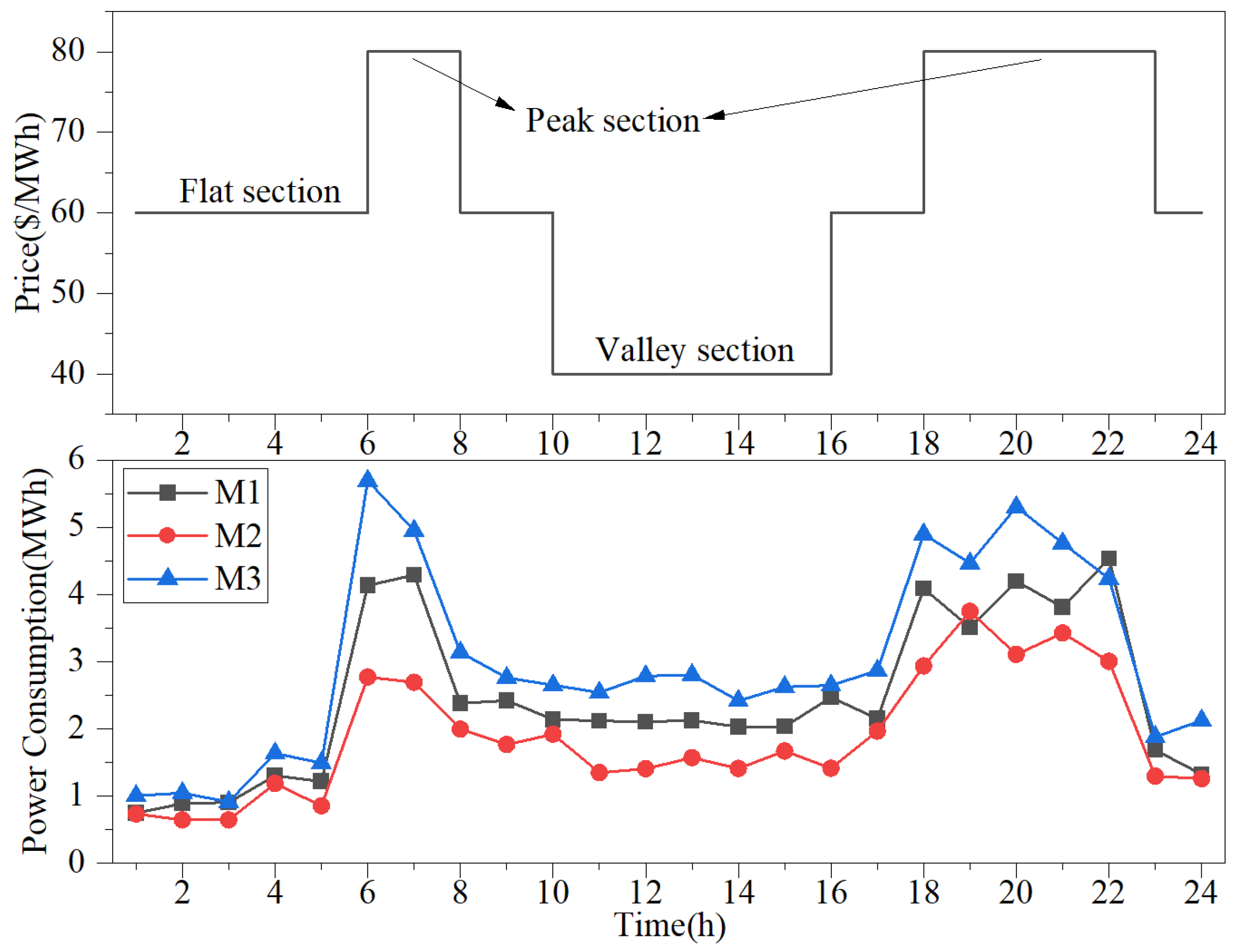
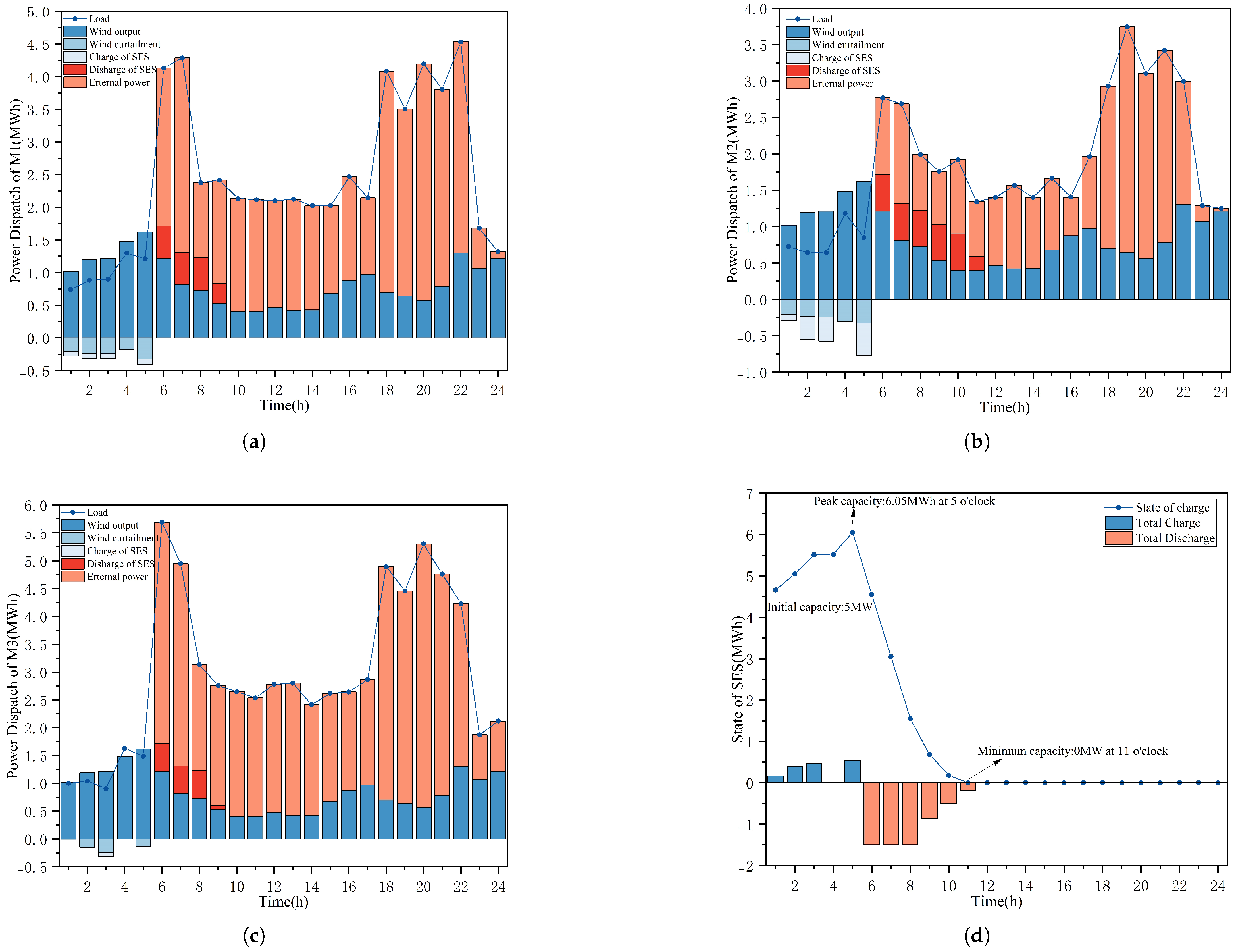
5.1. System Data and Analysis of Results
5.2. Benchmarks and Evaluation Metrics
- (1)
- The optimal baseline (OPT): OPT refers to deterministic optimization without forecast errors, where it is assumed that the output of renewable energy can be perfectly predicted, thereby achieving the optimal electricity cost.
- (2)
- Chance-constrained optimization (CC): The CC method is used for comparison, and it is assumed that the forecast errors of renewable energy output follow a Gaussian distribution.
- (3)
- (4)
- Sample-based robust optimization (SRO): SRO is the proposed robust optimization approach based on the concept of statistical feasibility. The uncertainty set is constructed solely from the samples.
- (5)
- Reconstructed sample-based RO (RSRO): RSRO is the approach proposed in this study, which performs robust optimization based on samples and reconstructed uncertainty sets.
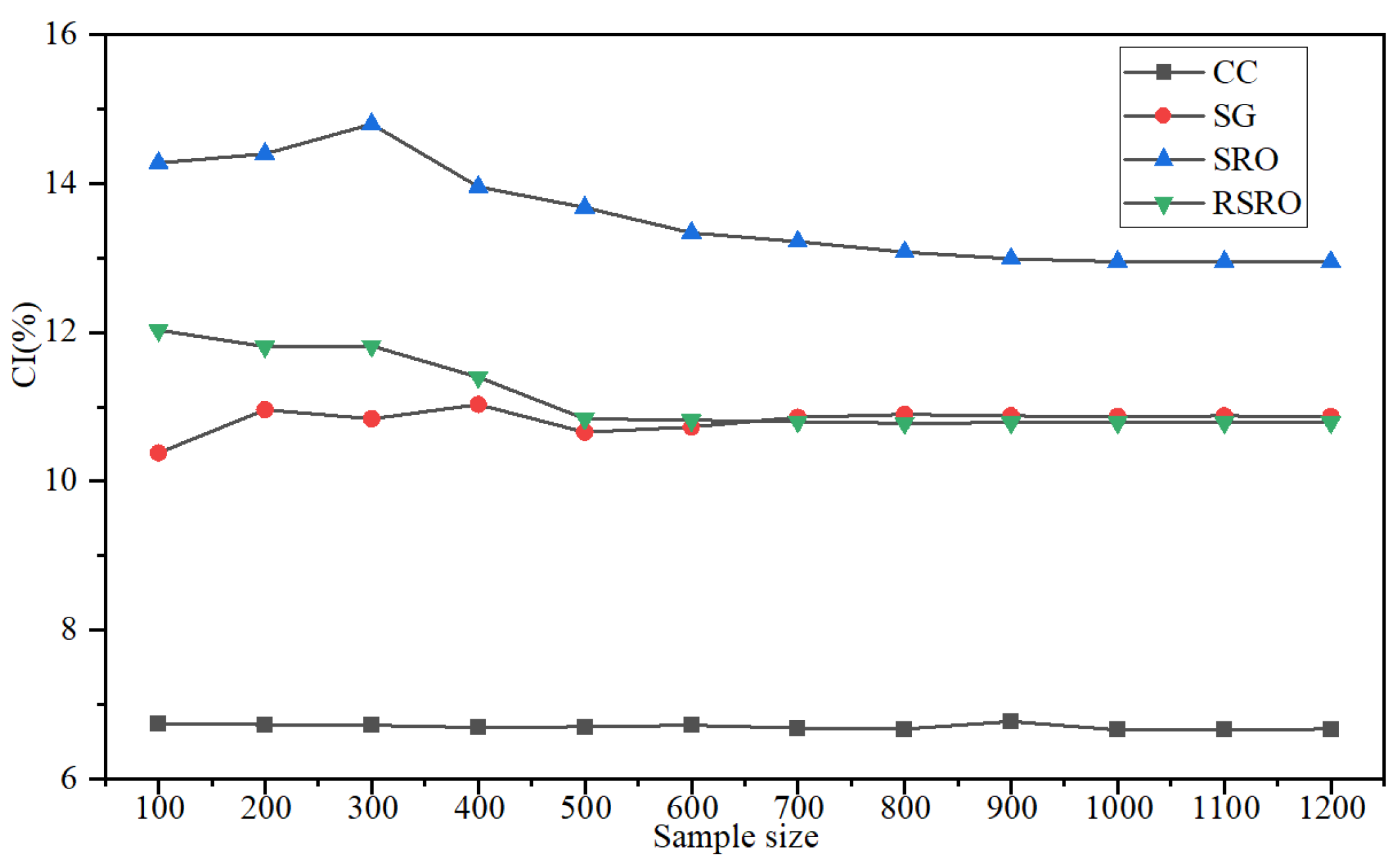
5.3. Performance Analysis with Varying Sample Sizes
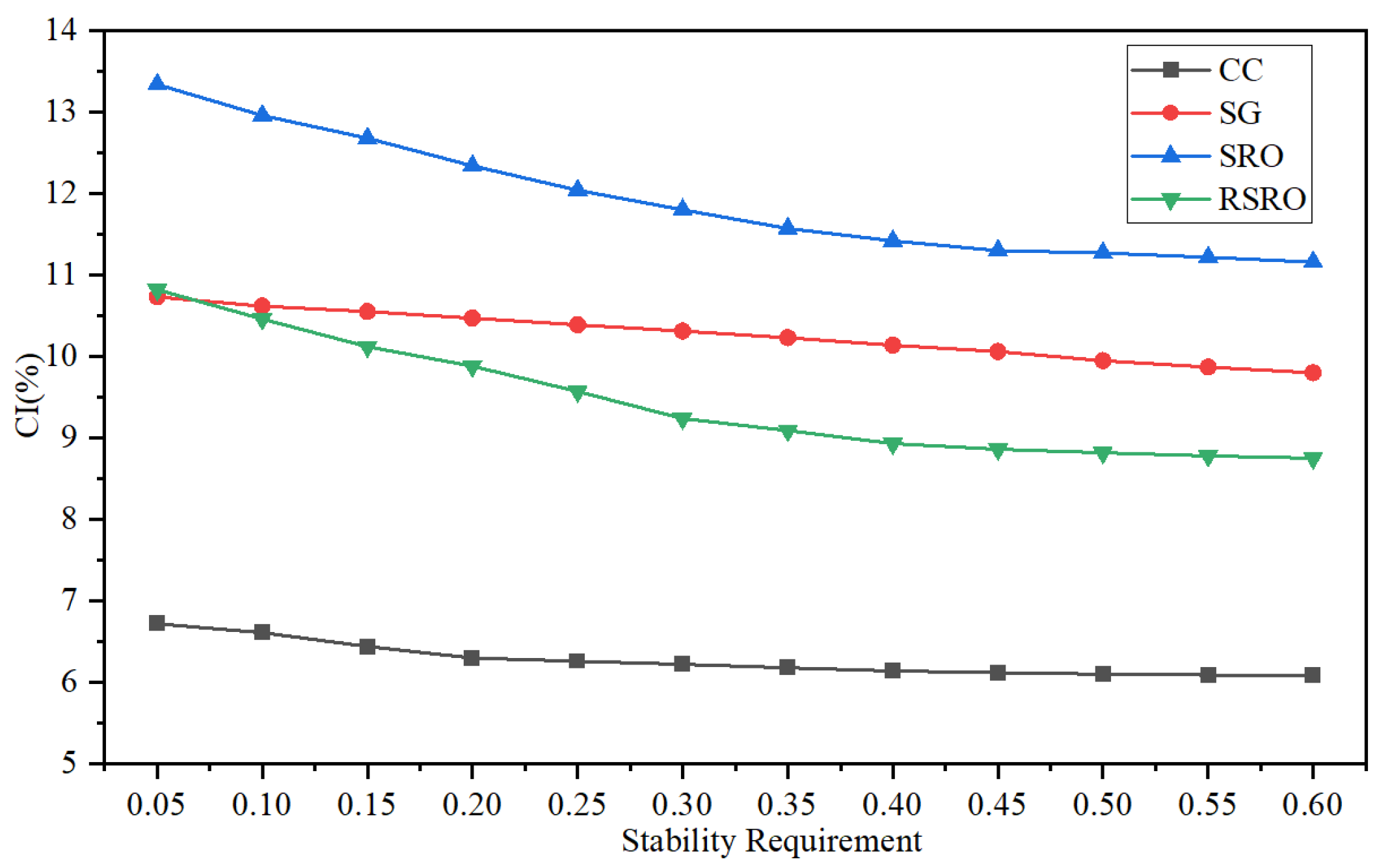
5.4. Performance Analysis with Varying Constraint Stability Requirements
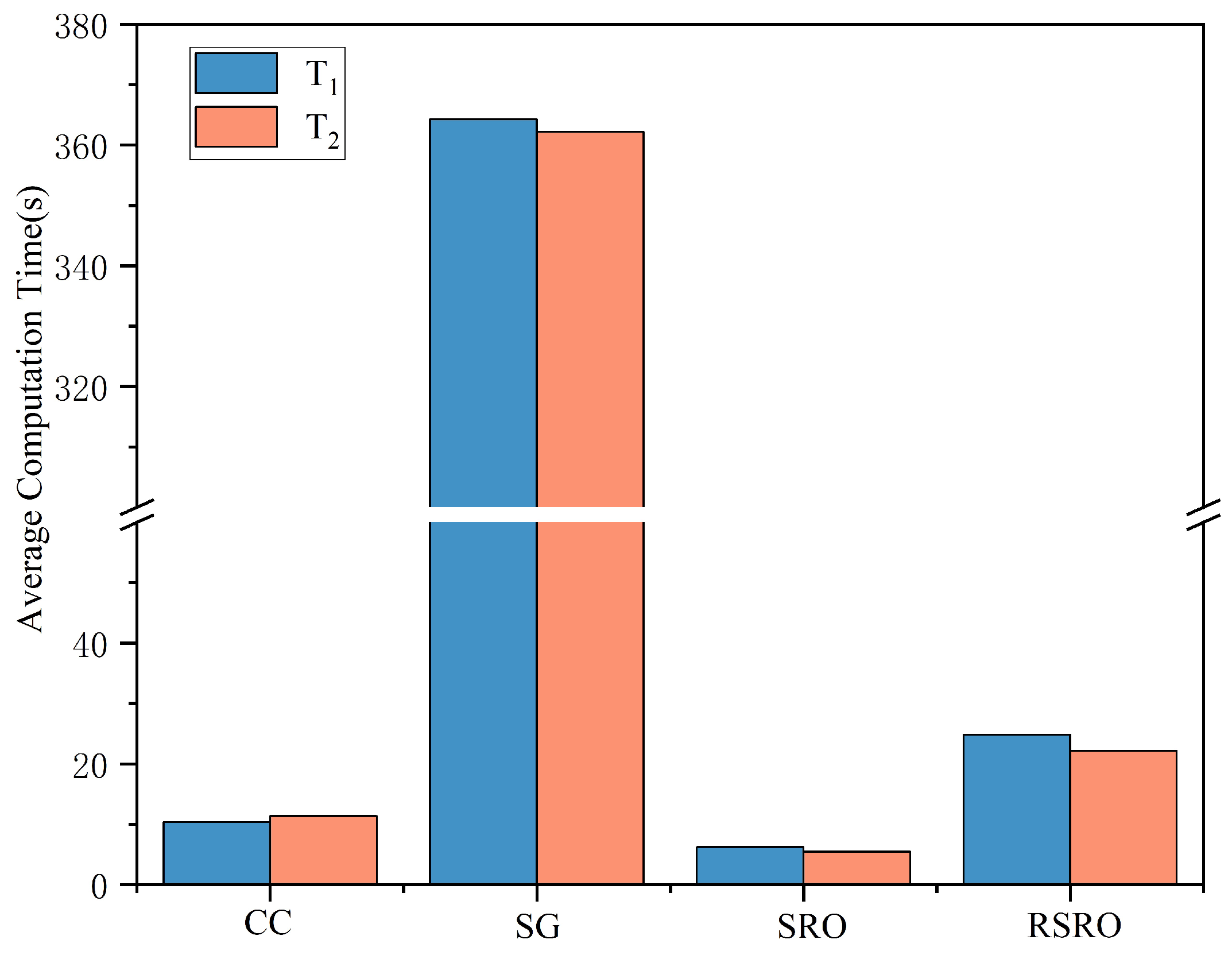
5.5. Evaluation of Computation Time
6. Conclusions
- The SES is charged from 0 to 5 h and discharged from 6 h until its capacity drops to 0. The peak capacity of SES reaches 6.05 MWh at 5 h.
- The proposed approach is compared with traditional methods like CC and SG. The results show that the SRO and RSRO approaches can obtain a 13.34% and 10.82% cost increase compared to OPT when .
- The proposed RSRO approach can maximize the utilization of the stability requirements of the optimization problem and can effectively reduce the conservatism of SRO. Meanwhile, the relatively low computational time ensures the efficiency of the proposed approach.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SES | Shared energy storage |
| CCO | Chance-constrained optimization |
| RO | Robust optimization |
| SO | Stochastic optimization |
| SRO | Sample-based RO |
| RSRO | Reconstructed sample-based RO |
| DRO | Distributed robust optimization |
| SAA | Sample average approximation |
References
- Wang, D.; Liu, N.; Chen, F.; Wang, Y.; Mao, J. Progress and prospects of energy storage technology research: Based on multidimensional comparison. J. Energy Storage 2024, 75, 109710. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Dong, L. Low carbon-oriented planning of shared energy storage station for multiple integrated energy systems considering energy-carbon flow and carbon emission reduction. Energy 2024, 290, 130139. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, B.; Sun, Q.; Wennersten, R. Application of energy storage in integrated energy systems—A solution to fluctuation and uncertainty of renewable energy. J. Energy Storage 2022, 52, 104812. [Google Scholar] [CrossRef]
- Reza, M.; Hannan, M.; Ker, P.J.; Mansor, M.; Lipu, M.H.; Hossain, M.; Mahlia, T.I. Uncertainty parameters of battery energy storage integrated grid and their modeling approaches: A review and future research directions. J. Energy Storage 2023, 68, 107698. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Bordons, C.; Tobajas, J.; Real-Calvo, R.; Santiago, I.; Grieu, S. Stochastic optimization of microgrids with hybrid energy storage systems for grid flexibility services considering energy forecast uncertainties. IEEE Trans. Power Syst. 2021, 36, 5537–5547. [Google Scholar] [CrossRef]
- Zhong, W.; Xie, K.; Liu, Y.; Xie, S.; Xie, L. Chance constrained scheduling and pricing for multi-service battery energy storage. IEEE Trans. Smart Grid 2021, 12, 5030–5042. [Google Scholar] [CrossRef]
- Jiang, W.; Lu, C.; Wu, C. Robust scheduling of thermostatically controlled loads with statistically feasible guarantees. IEEE Trans. Smart Grid 2023, 14, 3561–3572. [Google Scholar] [CrossRef]
- Bayram, I.S.; Abdallah, M.; Tajer, A.; Qaraqe, K.A. A Stochastic Sizing Approach for Sharing-Based Energy Storage Applications. IEEE Trans. Smart Grid 2017, 8, 1075–1084. [Google Scholar] [CrossRef]
- Dai, R.; Charkhgard, H.; Rigterink, F. A robust biobjective optimization approach for operating a shared energy storage under price uncertainty. Int. Trans. Oper. Res. 2022, 29, 1627–1658. [Google Scholar] [CrossRef]
- Han, O.; Ding, T.; Zhang, X.; Mu, C.; He, X.; Zhang, H.; Jia, W.; Ma, Z. A shared energy storage business model for data center clusters considering renewable energy uncertainties. Renew. Energy 2023, 202, 1273–1290. [Google Scholar] [CrossRef]
- Liu, D.; Cao, J.; Liu, M. Joint Optimization of Energy Storage Sharing and Demand Response in Microgrid Considering Multiple Uncertainties. Energies 2022, 15, 3067. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Yi, C.; Li, Z.; Xu, D. A Novel Shared Energy Storage Planning Method Considering the Correlation of Renewable Uncertainties on the Supply Side. IEEE Trans. Sustain. Energy 2022, 13, 2051–2063. [Google Scholar] [CrossRef]
- Zeng, L.; Gong, Y.; Xiao, H.; Chen, T.; Gao, W.; Liang, J.; Peng, S. Research on interval optimization of power system considering shared energy storage and demand response. J. Energy Storage 2024, 86, 111273. [Google Scholar] [CrossRef]
- Mehrjerdi, H.; Iqbal, A.; Rakhshani, E.; Torres, J.R. Daily-seasonal operation in net-zero energy building powered by hybrid renewable energies and hydrogen storage systems. Energy Convers. Manag. 2019, 201, 112156. [Google Scholar]
- Si, S.; Sun, W.; Wang, Y. A decentralized dispatch model for multiple micro energy grids system considering renewable energy uncertainties and energy interactions. J. Renew. Sustain. Energy 2024, 16, 015301. [Google Scholar]
- Lu, Y.; Alghassab, M.; Alvarez-Alvarado, M.S.; Gunduz, H.; Khan, Z.A.; Imran, M. Optimal distribution of renewable energy systems considering aging and long-term weather effect in net-zero energy building design. Sustainability 2020, 12, 5570. [Google Scholar] [CrossRef]
- Mohammadi, F.; Faghihi, F.; Kazemi, A.; Salemi, A.H. The effect of multi-uncertainties on battery energy storage system sizing in smart homes. J. Energy Storage 2022, 52, 104765. [Google Scholar]
- Walker, A.; Kwon, S. Design of structured control policy for shared energy storage in residential community: A stochastic optimization approach. Appl. Energy 2021, 298, 117182. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, L.; Guo, W.; Kang, Q.; Wu, Q. Chance Constrained Optimization in a Home Energy Management System. IEEE Trans. Smart Grid 2018, 9, 252–260. [Google Scholar] [CrossRef]
- Njema, G.G.; Ouma, R.B.O.; Kibet, J.K. A review on the recent advances in battery development and energy storage technologies. J. Renew. Energy 2024, 2024, 2329261. [Google Scholar]
- Liang, Z.; Chen, H.; Chen, S.; Wang, Y.; Zhang, C.; Kang, C. Robust Transmission Expansion Planning Based on Adaptive Uncertainty Set Optimization Under High-Penetration Wind Power Generation. IEEE Trans. Power Syst. 2021, 36, 2798–2814. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust convex optimization. Math. Oper. Res. 1998, 23, 769–805. [Google Scholar]
- Li, Y.; Hu, W.; Zhang, F.; Li, Y. Collaborative operational model for shared hydrogen energy storage and park cluster: A multiple values assessment. J. Energy Storage 2024, 82, 110507. [Google Scholar] [CrossRef]
- Siqin, Z.; Niu, D.; Li, M.; Gao, T.; Lu, Y.; Xu, X. Distributionally robust dispatching of multi-community integrated energy system considering energy sharing and profit allocation. Appl. Energy 2022, 321, 119202. [Google Scholar] [CrossRef]
- Agra, A.; Rodrigues, F. Distributionally robust optimization for the berth allocation problem under uncertainty. Transp. Res. Part B Methodol. 2022, 164, 1–24. [Google Scholar] [CrossRef]
- Hong, L.J.; Huang, Z.; Lam, H. Learning-based robust optimization: Procedures and statistical guarantees. Manag. Sci. 2021, 67, 3447–3467. [Google Scholar] [CrossRef]
- Lu, C.; Gu, N.; Jiang, W.; Wu, C. Sample-adaptive robust economic dispatch with statistically feasible guarantees. IEEE Trans. Power Syst. 2023, 39, 779–793. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ben-Tal, A.; Nemirovski, A. Robust optimization–methodology and applications. Math. Program. 2002, 92, 453–480. [Google Scholar] [CrossRef]
- Campi, M.C.; Garatti, S. The Exact Feasibility of Randomized Solutions of Uncertain Convex Programs. SIAM J. Optim. 2008, 19, 1211–1230. [Google Scholar] [CrossRef]
- Kleywegt, A.J.; Shapiro, A.; Homem-de Mello, T. The sample average approximation method for stochastic discrete optimization. SIAM J. Optim. 2002, 12, 479–502. [Google Scholar]
- Pagnoncelli, B.K.; Ahmed, S.; Shapiro, A. Sample average approximation method for chance constrained programming: Theory and applications. J. Optim. Theory Appl. 2009, 142, 399–416. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Arroyo, J.M. Bilevel programming applied to power system vulnerability analysis under multiple contingencies. IET Gener. Transm. Distrib. 2010, 4, 178–190. [Google Scholar] [CrossRef]
- Fang, W.; Yang, C.; Liu, D.; Huang, Q.; Ming, B.; Cheng, L.; Wang, L.; Feng, G.; Shang, J. Assessment of Wind and Solar Power Potential and Their Temporal Complementarity in China’s Northwestern Provinces: Insights from ERA5 Reanalysis. Energies 2023, 16, 7109. [Google Scholar] [CrossRef]
- Zeng, S.; Li, J.; Ren, Y. Research of time-of-use electricity pricing models in China: A survey. In Proceedings of the 2008 IEEE International Conference on Industrial Engineering and Engineering Management, IEEE, Singapore, 8–11 December 2008; pp. 2191–2195. [Google Scholar]
- Mitali, J.; Dhinakaran, S.; Mohamad, A. Energy storage systems: A review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Ma, X.Y.; Sun, Y.Z.; Fang, H.L. Scenario generation of wind power based on statistical uncertainty and variability. IEEE Trans. Sustain. Energy 2013, 4, 894–904. [Google Scholar] [CrossRef]
- Yan, R.; Wang, J.; Huo, S.; Qin, Y.; Zhang, J.; Tang, S.; Wang, Y.; Liu, Y.; Zhou, L. Flexibility improvement and stochastic multi-scenario hybrid optimization for an integrated energy system with high-proportion renewable energy. Energy 2023, 263, 125779. [Google Scholar] [CrossRef]



| Ref No. | Approach | Uncertainty Sources | Characterization Method | Distribution Independency | Statistical Feasibility |
|---|---|---|---|---|---|
| [10] | CC | wind output | normal distribution | × | × |
| [11,15] | SG | PV output | scenario generation | × | × |
| [14] | SG | PV output | Gaussian distribution | × | × |
| [18] | SG | PV output | Monte Carlo simulation | × | × |
| [12,13,20] | RO | wind and PV output | interval uncertainty | ✓ | × |
| [17] | RO | PV output | interval uncertainty | ✓ | × |
| [24] | RO | wind output | interval uncertainty | ✓ | × |
| [16] | RO | wind and PV output | Markov chain | ✓ | × |
| [24] | DRO | PV output | interval uncertainty | ✓ | × |
| our approach | SRO, RSRO | wind output | sample dataset | ✓ | ✓ |
| Unit | Price.peak | Price.flat | Price.valley | [37] | ||
| Value | 80 USD/MWh | 60 USD/MWh | 40 USD/MWh | 60 USD/MWh | 4 USD/MWh | 200 MW |
| Unit | / | [37] | ||||
| Value | 5 MW | 0.5 MW | 0.5 MW | 0.5 | 0.9 | 10 MWh |
| Approach | OPT | CC | SG | SRO | RSRO |
|---|---|---|---|---|---|
| Cost(USD) | 1257.66 | 1342.18 | 1392.61 | 1425.43 | 1393.74 |
| CI(%) | 0 | 6.72 | 10.73 | 13.34 | 10.82 |
| ACVR | 0 | 0.0529 | 0.0275 | 0.024 | 0.0419 |
| Size | CC (USD) | SG (USD) | SRO (USD) | RSRO (USD) |
|---|---|---|---|---|
| 100 | 1342.42 | 1388.21 | 1437.25 | 1408.96 |
| 200 | 1342.30 | 1395.50 | 1348.76 | 1406.19 |
| 300 | 1342.18 | 1393.99 | 1443.79 | 1406.32 |
| 400 | 1341.80 | 1396.38 | 1433.23 | 1401.03 |
| 500 | 1341.92 | 1391.73 | 1429.71 | 1393.99 |
| 600 | 1342.18 | 1392.61 | 1425.43 | 1393.74 |
| 700 | 1341.67 | 1394.24 | 1423.92 | 1393.49 |
| 800 | 1341.55 | 1394.75 | 1422.16 | 1393.24 |
| 900 | 1342.80 | 1394.49 | 1421.03 | 1393.30 |
| 1000 | 1341.42 | 1394.37 | 1420.53 | 1393.32 |
| 1100 | 1341.29 | 1394.49 | 1420.28 | 1393.24 |
| 1200 | 1341.55 | 1394.39 | 1420.33 | 1393.46 |
| Stability Requirement () | CC (USD) | SG (USD) | SRO (USD) | RSRO (USD) |
|---|---|---|---|---|
| 0.05 | 1342.18 | 1392.61 | 1425.43 | 1393.74 |
| 0.10 | 1340.79 | 1391.22 | 1420.65 | 1389.21 |
| 0.15 | 1338.65 | 1390.34 | 1417.13 | 1384.94 |
| 0.20 | 1336.89 | 1389.34 | 1412.86 | 1381.92 |
| 0.25 | 1336.39 | 1388.33 | 1409.08 | 1378.02 |
| 0.30 | 1335.89 | 1387.33 | 1406.06 | 1373.87 |
| 0.35 | 1335.38 | 1386.32 | 1403.17 | 1371.98 |
| 0.40 | 1334.88 | 1385.18 | 1401.29 | 1369.97 |
| 0.45 | 1334.63 | 1384.18 | 1399.78 | 1369.09 |
| 0.50 | 1334.38 | 1382.80 | 1399.40 | 1368.59 |
| 0.55 | 1334.26 | 1381.93 | 1398.77 | 1368.08 |
| 0.60 | 1334.13 | 1380.91 | 1398.02 | 1367.71 |
| n | 100 | 200 | 300 | 400 | 500 | 600 |
| Time (s) | 125.87 | 175.39 | 226.84 | 273.16 | 322.16 | 364.28 |
| n | 700 | 800 | 900 | 1000 | 1100 | 1200 |
| Time (s) | 417.95 | 461.39 | 559.85 | 606.24 | 662.38 | 712.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, K.; Xu, Q.; Li, S.; Xia, Y. Sample-Based Optimal Dispatch of Shared Energy Storage in Community Microgrids Considering Uncertainty. Energies 2025, 18, 1828. https://doi.org/10.3390/en18071828
Hua K, Xu Q, Li S, Xia Y. Sample-Based Optimal Dispatch of Shared Energy Storage in Community Microgrids Considering Uncertainty. Energies. 2025; 18(7):1828. https://doi.org/10.3390/en18071828
Chicago/Turabian StyleHua, Kui, Qingshan Xu, Shujuan Li, and Yuanxing Xia. 2025. "Sample-Based Optimal Dispatch of Shared Energy Storage in Community Microgrids Considering Uncertainty" Energies 18, no. 7: 1828. https://doi.org/10.3390/en18071828
APA StyleHua, K., Xu, Q., Li, S., & Xia, Y. (2025). Sample-Based Optimal Dispatch of Shared Energy Storage in Community Microgrids Considering Uncertainty. Energies, 18(7), 1828. https://doi.org/10.3390/en18071828








