Numerical Simulation and Optimization of a Chevron-Type Corrugated Solar Air Heater
Abstract
:1. Introduction
2. Methodology
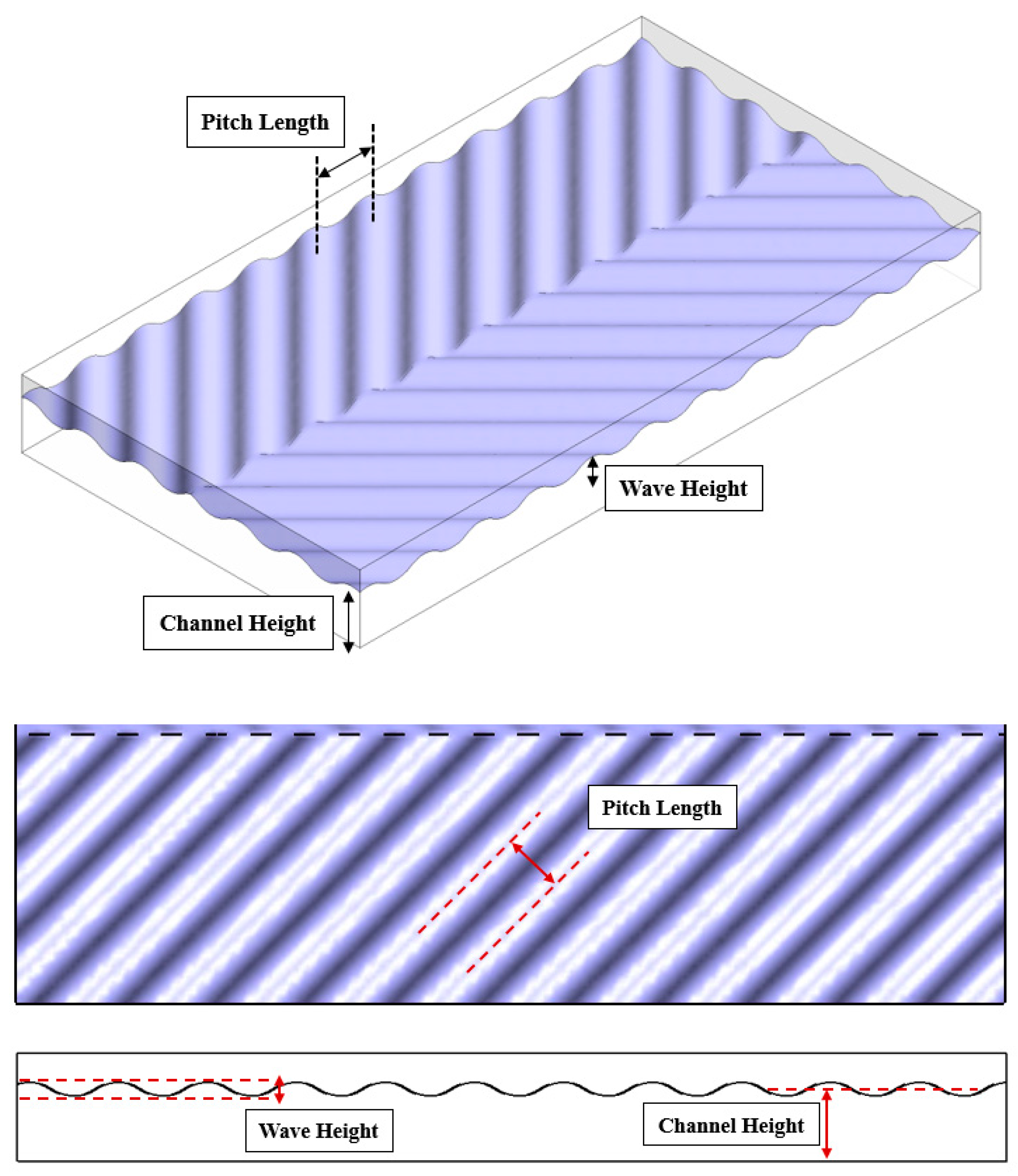
2.1. Geometry Definition
2.2. CFD Methodology
2.2.1. Materials
2.2.2. Boundary Conditions
2.2.3. Turbulence Model
2.3. Governing Equations
2.4. Performance Parameters
2.5. Grid Study
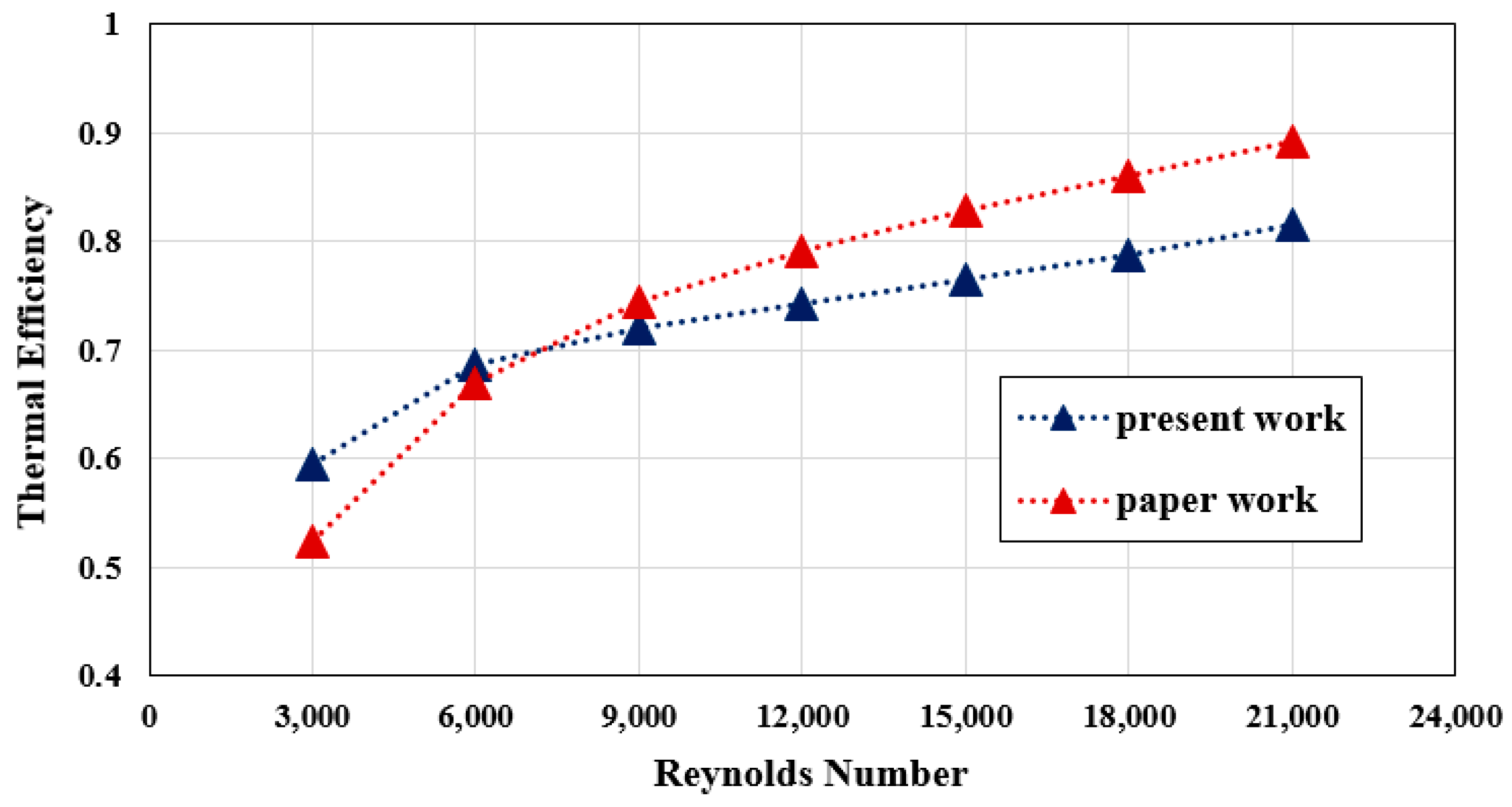
3. Validation
4. Results and Discussion
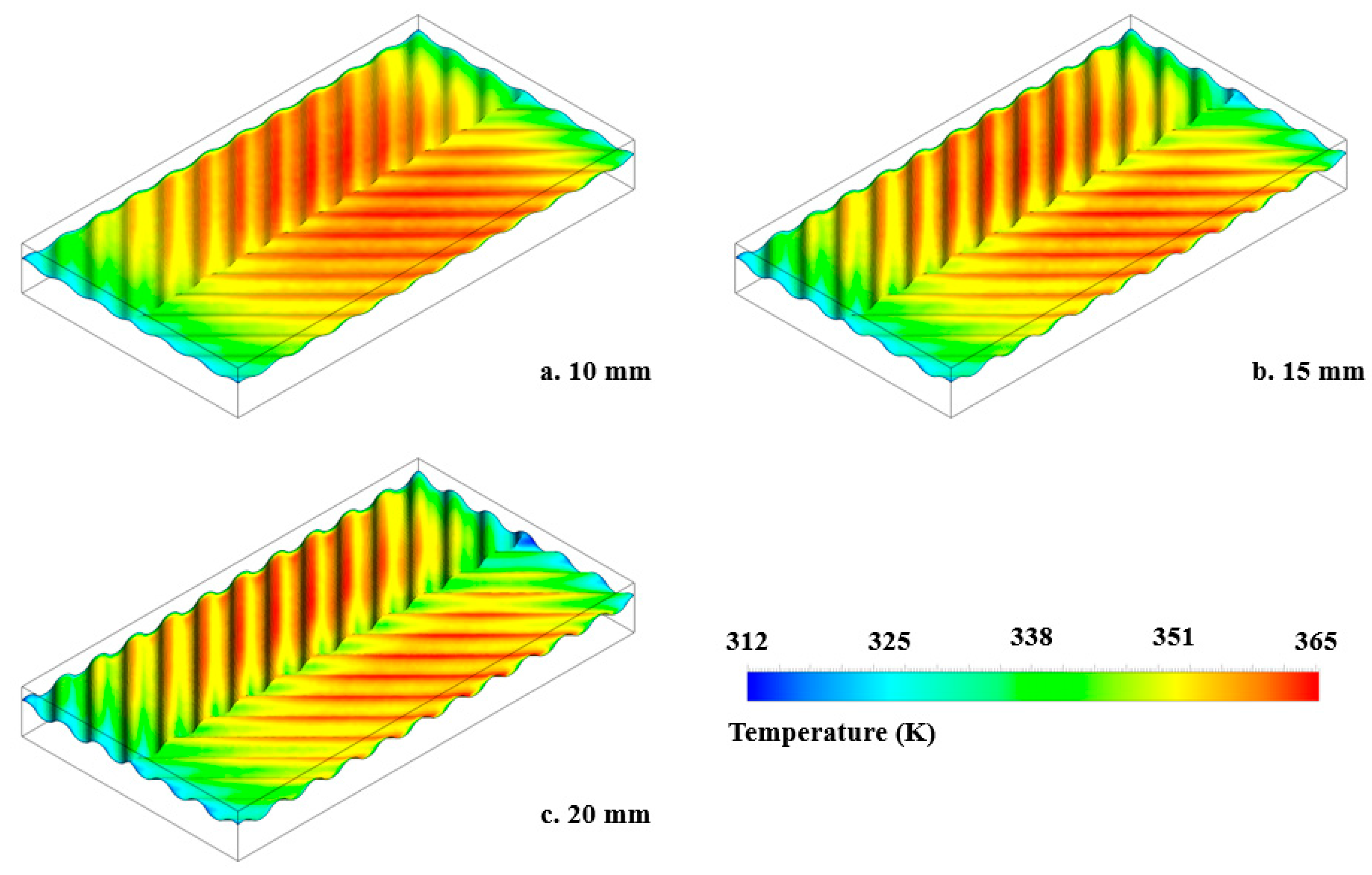
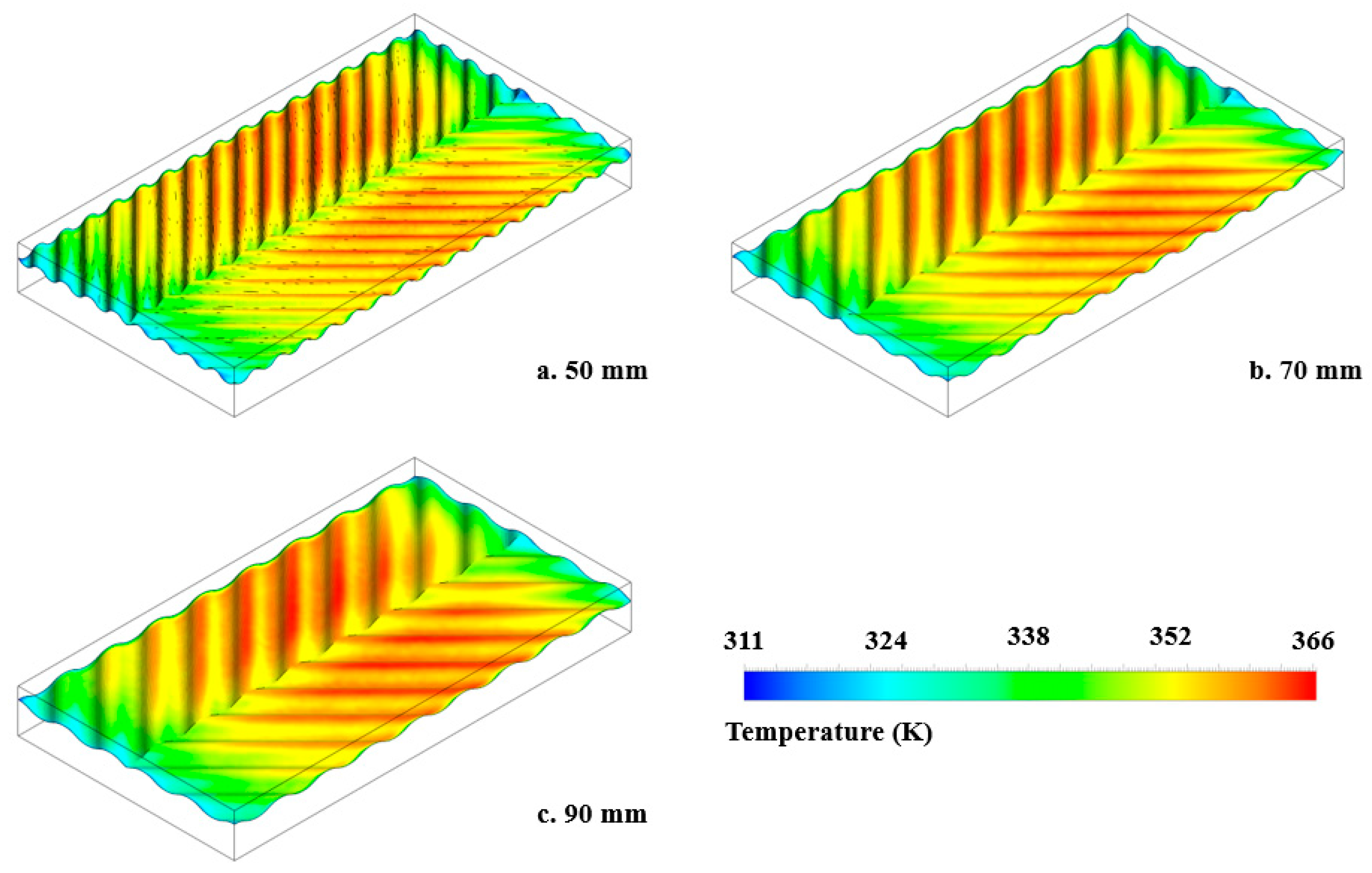
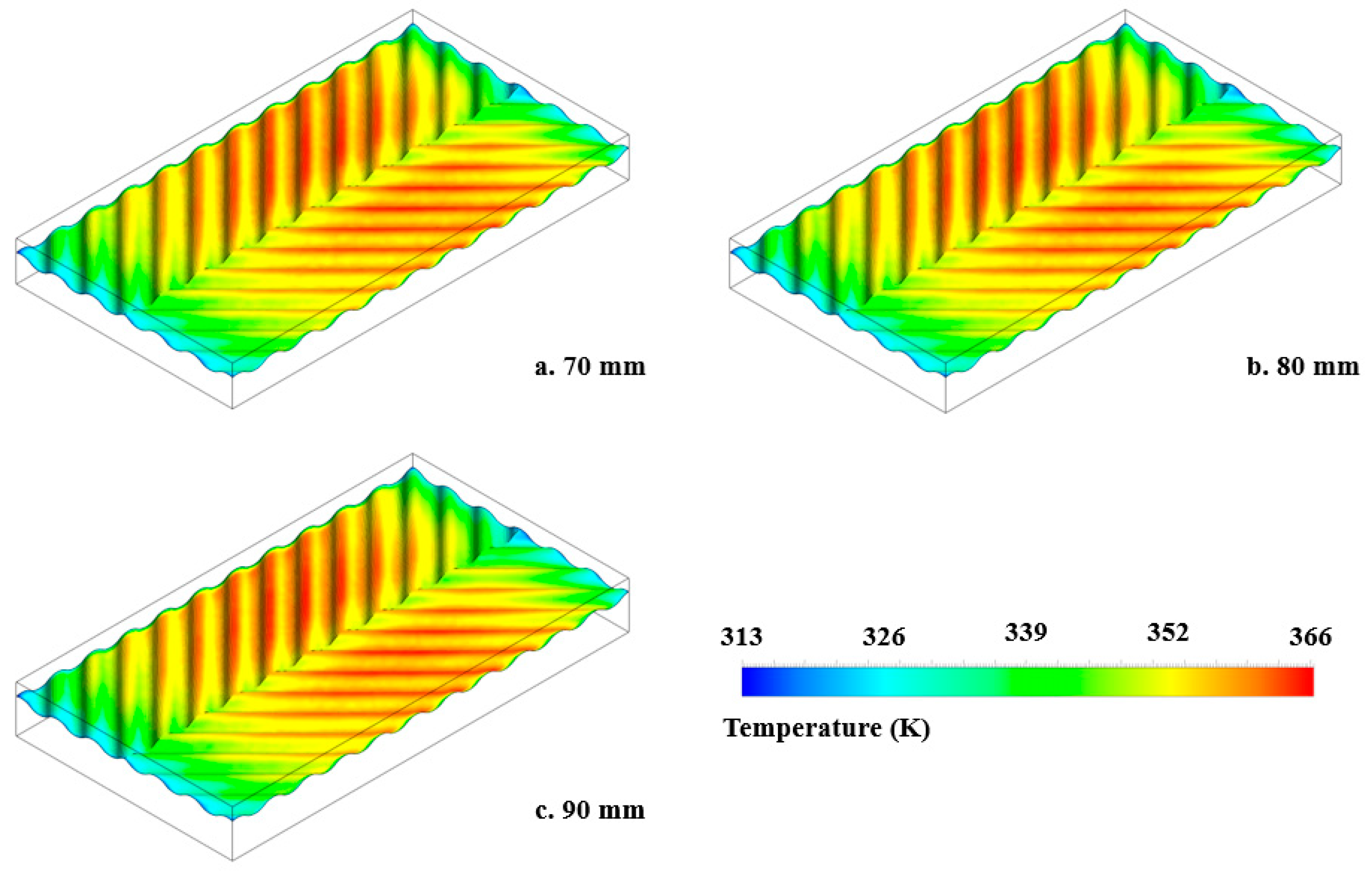
4.1. Thermal Analysis
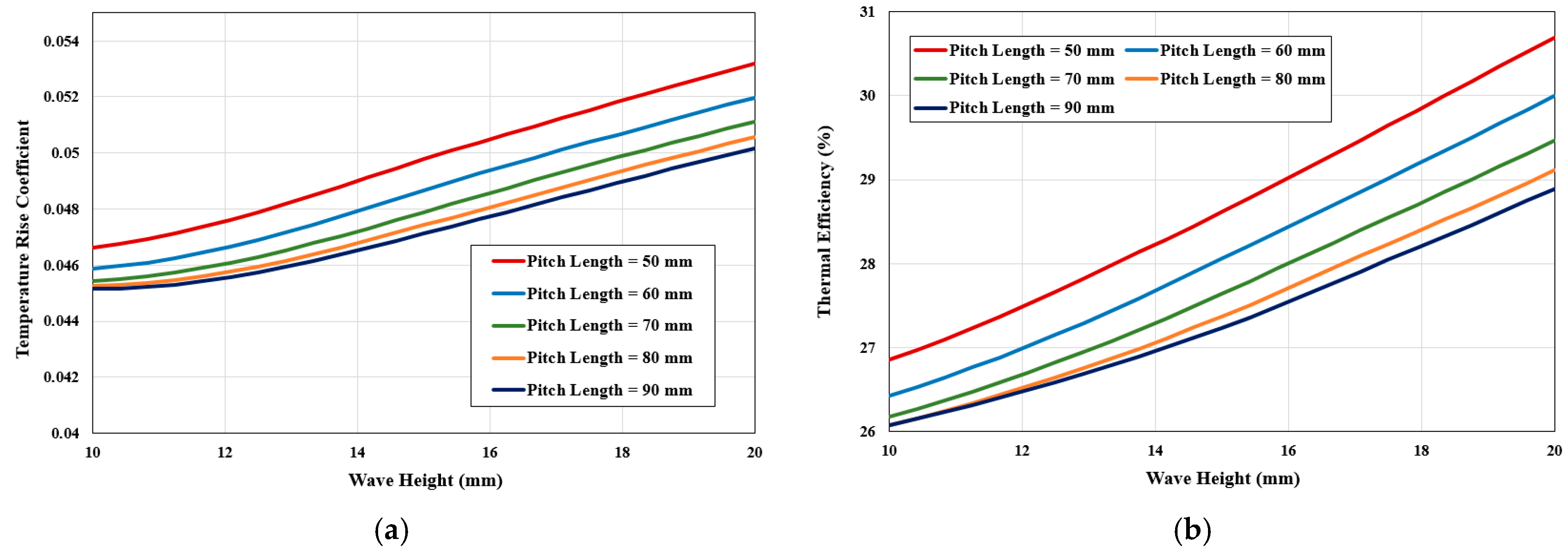
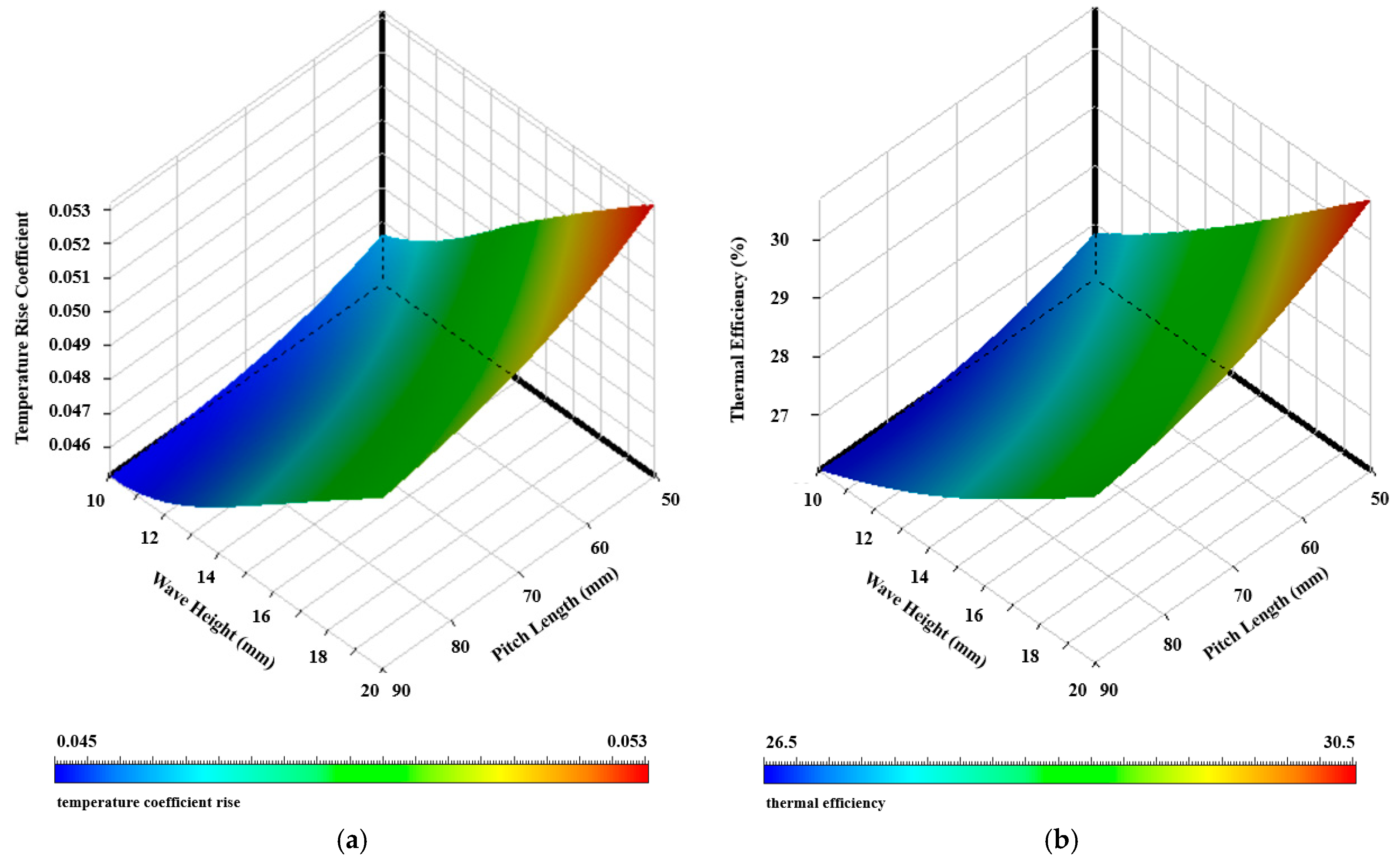
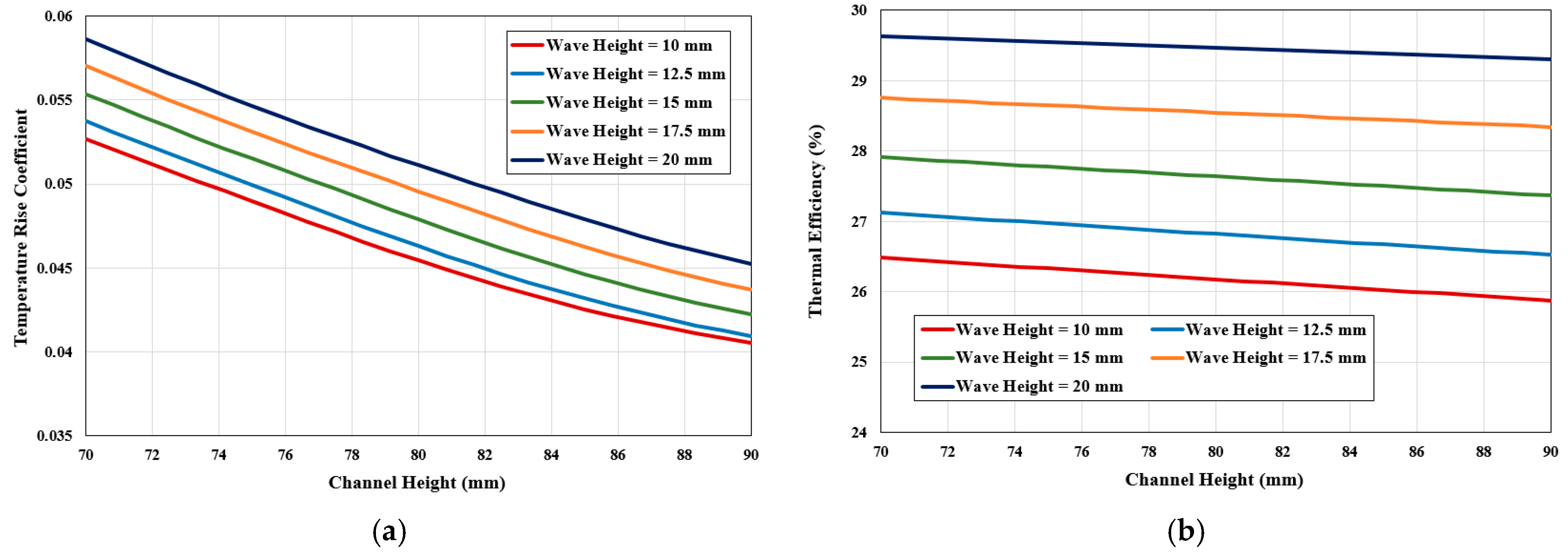
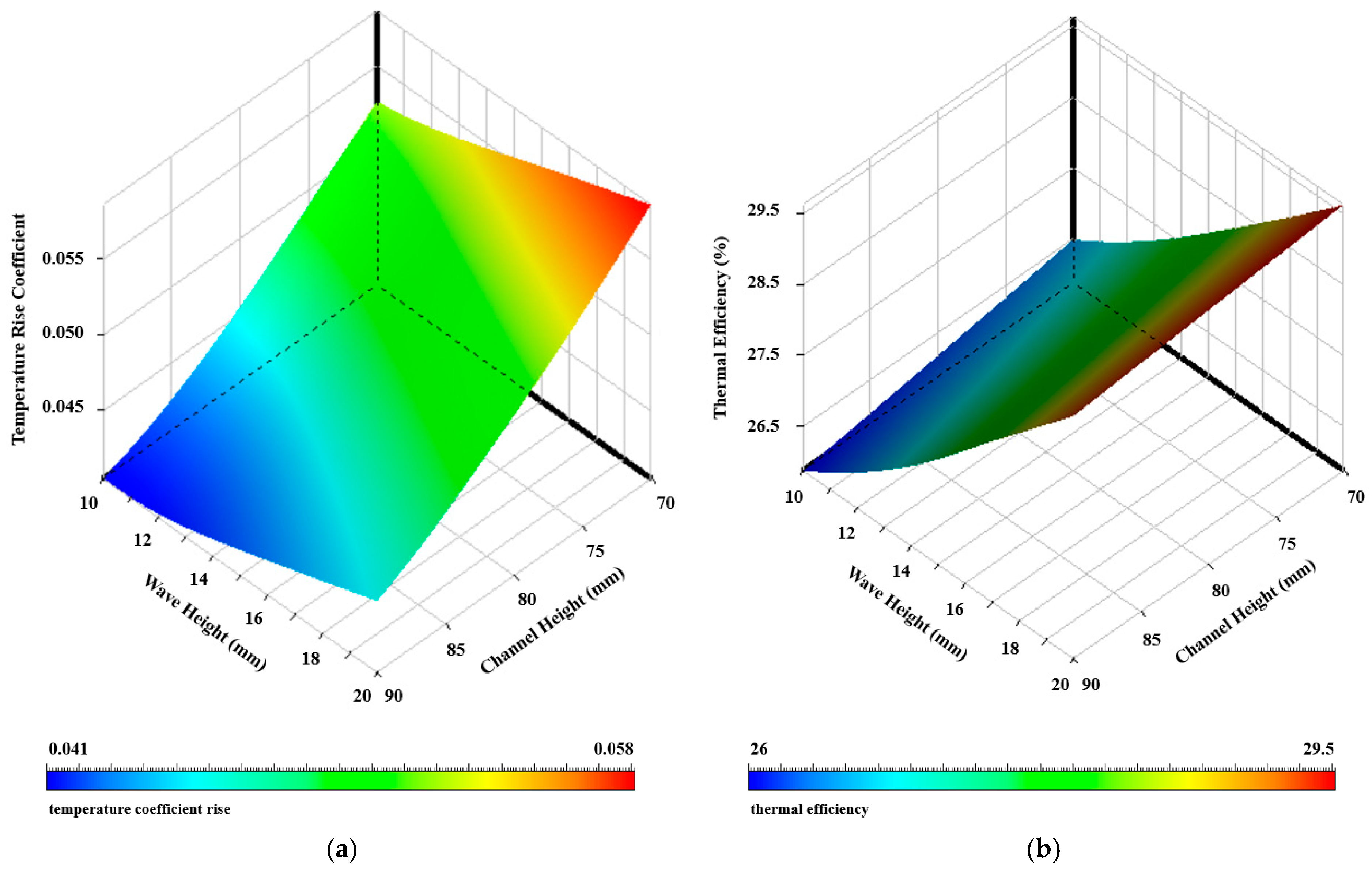
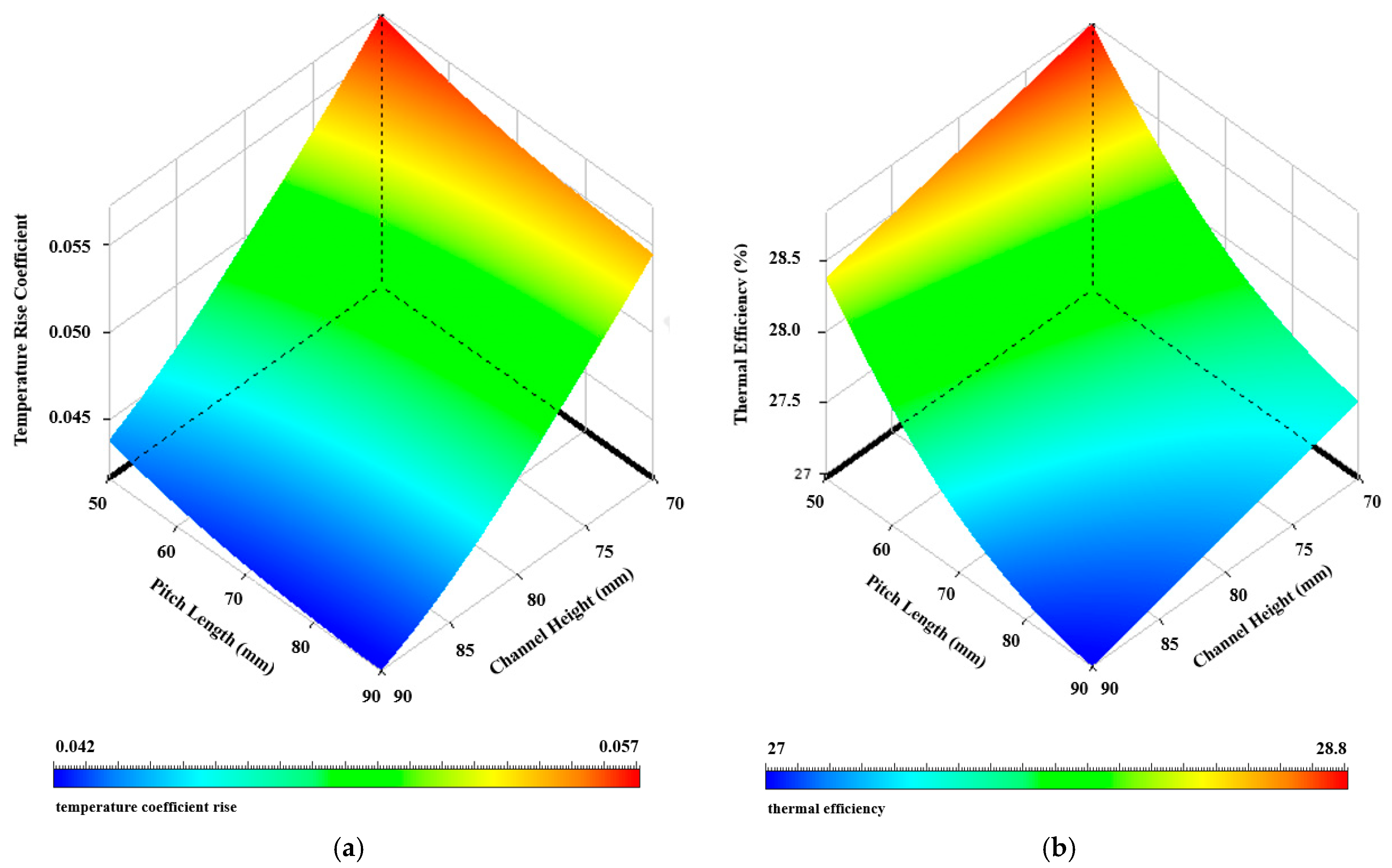
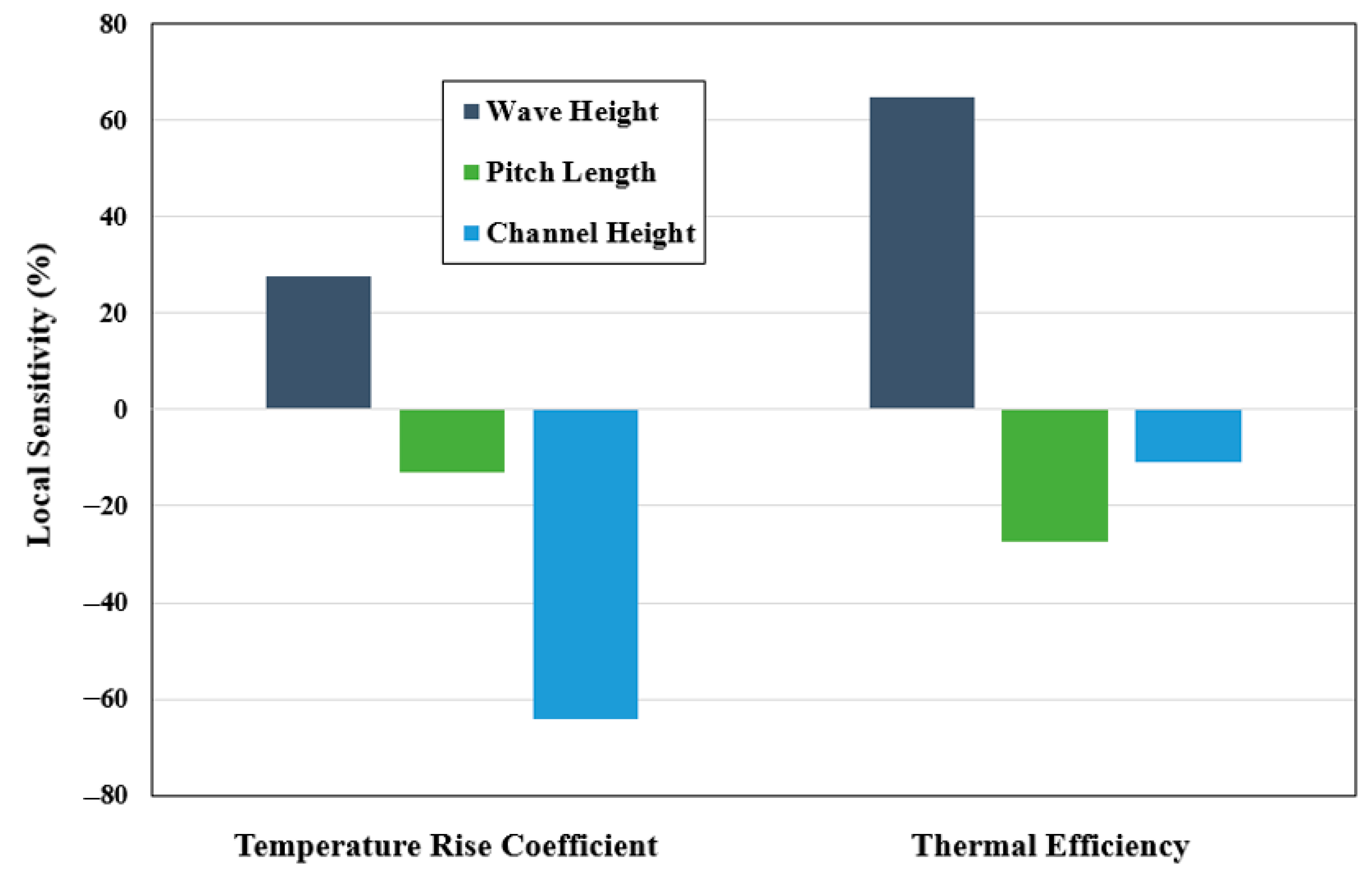
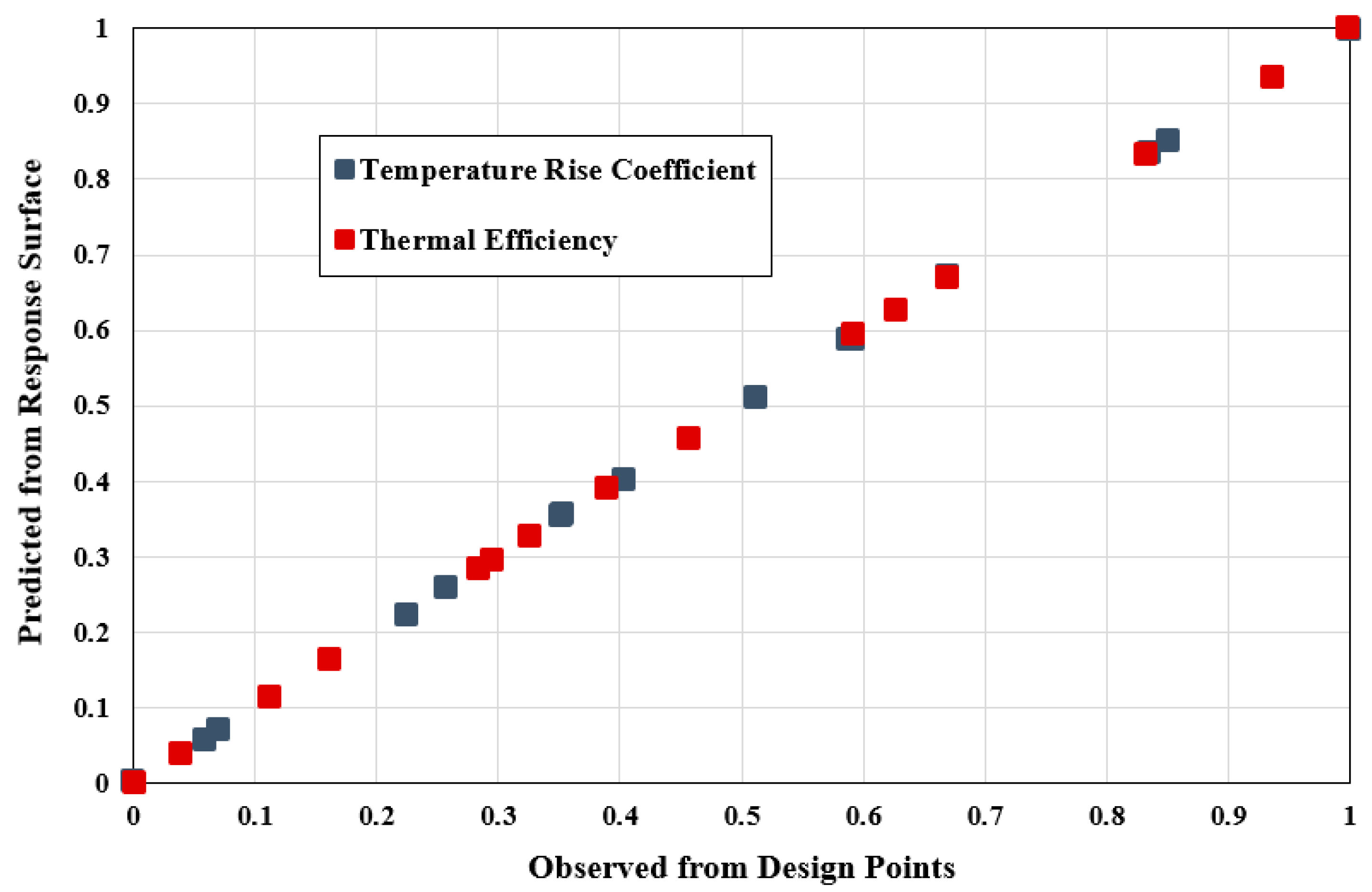
4.2. Optimization
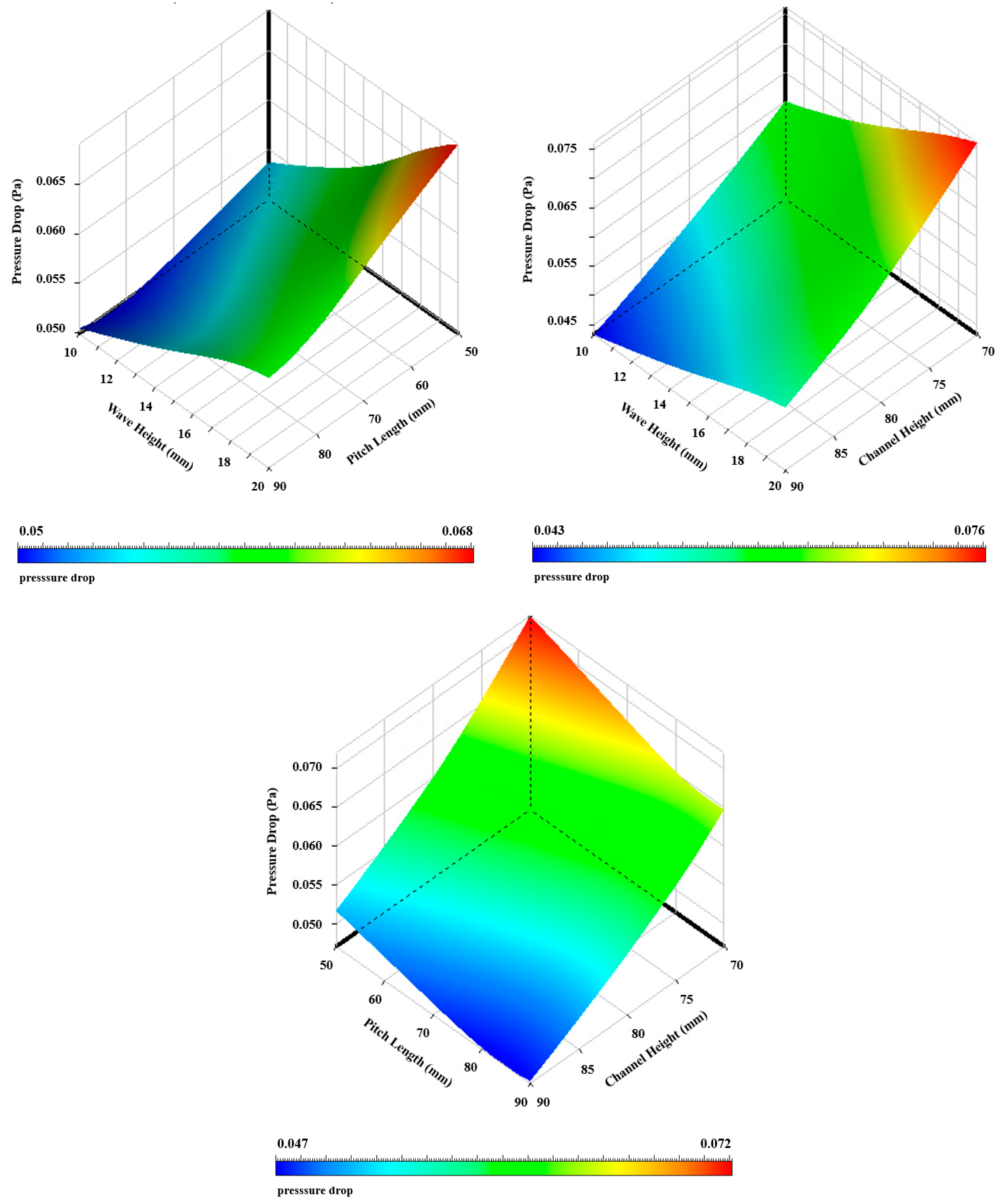
4.3. Pressure Analysis
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ap | area of absorber plate (m2) | r | direction vector |
| a | absorption coefficient | s | position vector |
| Bi | body force (N/m3) | T | air temperature (K) |
| Cpf | specific heat of air (J/kg.K) | Tfi | inlet air temperature (K) |
| Ct | temperature rise coefficient | Tfo | outlet air temperature (K) |
| e | specific internal energy (J/kg) | u, v, w | air velocity component (x,y,z) (m/s) |
| I | radiation intensity (W/m2) | ηth | thermal efficiency |
| k | thremal conductivity of air (W/mK) | μ | dynamic viscosity of air (kg/m.s) |
| ṁf | mass flow rate (kg/s) | ρ | air density (kg/m3) |
| n | refractive index | σs | scattering coefficient |
| P | pressure (Pa) | φ | phase function |
| Q̇c | incident solar radiation (W) | ω | solid angle (radians) |
| Q̇u | useful heat gained (W) |
References
- Panwar, N.L.; Kaushik, S.C.; Kothari, S. Role of renewable energy sources in environmental protection: A review. Renew. Sustain. Energy Rev. 2011, 15, 1513–1524. [Google Scholar] [CrossRef]
- Owusu, P.A.; Asumadu-Sarkodie, S. A review of renewable energy sources, sustainability issues and climate change mitigation. Cogent Eng. 2016, 3, 1167990. [Google Scholar] [CrossRef]
- Kannan, N.; Vakeesan, D. Solar energy for future world: A review. Renew. Sustain. Energy Rev. 2016, 62, 1092–1105. [Google Scholar] [CrossRef]
- Pourasl, H.H.; Barenji, R.V.; Khojastehnezhad, V.M. Solar energy status in the world: A comprehensive review. Energy Rep. 2023, 10, 3474–3493. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar thermal collectors and applications. Prog. Energy Combust. Sci. 2004, 30, 231–295. [Google Scholar] [CrossRef]
- Mund, C.; Rathore, S.K.; Sahoo, R.K. A review of solar air collectors about various modifications for performance enhancement. Sol. Energy 2021, 228, 140–167. [Google Scholar] [CrossRef]
- Saxena, A.; El-Sebaii, A.A. A thermodynamic review of solar air heaters. Renew. Sustain. Energy Rev. 2015, 43, 863–890. [Google Scholar] [CrossRef]
- Almutairi, K.; Almutairi, M.; Harb, K.; Marey, O.; Aungkulanon, P. An updated review on solar air heating systems. Sustain. Energy Technol. Assess. 2022, 53, 102573. [Google Scholar] [CrossRef]
- Markam, B.; Maiti, S. Artificial enhancer for small-scale solar air heater-A comprehensive review. Clean. Energy Syst. 2023, 4, 100046. [Google Scholar] [CrossRef]
- Hegde, A.K.; Pai, R.; Karanth, K.V. Performance augmentation of solar air heaters: A comprehensive analysis. Sol. Energy 2023, 253, 527–553. [Google Scholar] [CrossRef]
- Shrivastava, V.; Yadav, A.S.; Shrivastava, N. Comparative Study of the Performance of Double-Pass and Single-Pass Solar Air Heater with Thermal Storage. In Proceedings of the International Conference on Recent Advancements in Mechanical Engineering, Silchar, India, 8–9 July 2020; Springer Nature: Singapore, 2021. [Google Scholar] [CrossRef]
- Mohamed Salih, M.M.; Alomar, O.R.; Aziz Ali, F. An experimental investigation of a double pass solar air heater performance: A comparison between natural and forced air circulation processes. Solar Energy 2019, 193, 184–194. [Google Scholar] [CrossRef]
- Kabeel, A.E.; Hamed, M.H.; Omara, Z.M.; Kandeal, A.W. Solar air heaters: Design configurations, improvement methods and applications, A detailed review. Renew. Sustain. Energy Rev. 2017, 70, 1189–1206. [Google Scholar] [CrossRef]
- Chamoli, S.; Chauhan, R.; Thakur, N.S.; Saini, J.S. A review of the performance of double pass solar air heater. Renew. Sustain. Energy Rev. 2012, 84, 285–307. [Google Scholar] [CrossRef]
- Parsa, H.; Saffar-Avval, M.; Hajmohammadi, M.R. Improvement of solar air heaters performance with PCM-filled baffles and storage bed. Mech. Sci. 2023, 260, 108629. [Google Scholar] [CrossRef]
- Omojaro, A.P.; Aldabbagh, L.B.Y. Experimental performance of single and double pass solar air heater with fins and steel wire mesh as absorber. Appl. Energy 2010, 87, 3759–3765. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Koçyiğit, F. Energy and exergy analysis of a new flat-plate solar air heater having different obstacles on absorber plates. Appl. Energy 2010, 87, 3438–3450. [Google Scholar] [CrossRef]
- Potgieter, M.S.W.; Bester, C.R.; Bhamjee, M. Experimental and CFD investigation of a hybrid solar air heater. Sol. Energy 2020, 195, 413–428. [Google Scholar] [CrossRef]
- Singh, A.P.; Singh, O.P. Performance enhancement of a curved solar air heater using CFD. Sol. Energy 2018, 174, 556–569. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J.L. Heat transfer and fluid flow analysis of solar air heater: A review of CFD approach. Renew. Sustain. Energy Rev. 2013, 23, 60–79. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, M.H. CFD Analysis on the Thermal Hydraulic Performance of an SAH Duct with Multi V-Shape Roughened Ribs. Energies 2016, 9, 415. [Google Scholar] [CrossRef]
- Yusaidi, N.J.; Fauzan, M.F.; Abdullah, A.F.; Ibrahim, A.; Ishak, A.A. Theoretical and experimental investigations on the effect of double pass solar air heater with staggered-diamond shaped fins arrangement. Case Stud. Therm. Eng. 2024, 60, 104619. [Google Scholar] [CrossRef]
- Tanda, G. Performance of solar air heater ducts with different types of ribs on the absorber plate. Energy 2011, 36, 6651–6660. [Google Scholar] [CrossRef]
- Borah, P.P.; Pathak, K.K.; Gupta, A.; Roy, S.; Das, B. Experimental study of a solar air heater with modified absorber plate through square obstacles with threaded pin fins. Appl. Therm. Eng. 2023, 228, 120544. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, M.-H. Thermohydraulic performance of rectangular ducts with different multiple V-rib roughness shapes: A comprehensive review and comparative study. Renew. Sustain. Energy Rev. 2016, 54, 635–652. [Google Scholar] [CrossRef]
- Bhushan, B.; Singh, R. A review on methodology of artificial roughness used in duct of solar air heaters. Energy 2010, 35, 202–212. [Google Scholar] [CrossRef]
- Boulemtafes-Boukadoum, A.; Benzaoui, A. CFD based Analysis of Heat Transfer Enhancement in Solar Air Heater Provided with Transverse Rectangular Ribs. Energy Procedia 2014, 50, 761–772. [Google Scholar] [CrossRef]
- Mahanand, Y.; Senapati, J.R. Thermo-hydraulic performance analysis of a solar air heater (SAH) with quarter-circular ribs on the absorber plate: A comparative study. Int. J. Therm. Sci. 2021, 161, 106747. [Google Scholar] [CrossRef]
- Karim, M.A.; Hawlader, M.N.A. Performance investigation of flat plate, v-corrugated and finned air collectors. Energy 2006, 31, 452–470. [Google Scholar] [CrossRef]
- Gao, W.; Lin, W.; Liu, T.; Xia, C. Analytical and experimental studies on the thermal performance of cross-corrugated and flat-plate solar air heaters. Appl. Energy 2007, 84, 425–441. [Google Scholar] [CrossRef]
- Yehualashet, K.N.; Fatoba, O.; Asfaw, S.M. Experimental study and numerical analysis of thermal performance of corrugated plate solar collector. Mater. Today Proc. 2022, 62, 2849–2856. [Google Scholar] [CrossRef]
- Dović, D.; Palm, B.; Švaić, S. Generalized correlations for predicting heat transfer and pressure drop in plate heat exchanger channels of arbitrary geometry. Int. J. Heat Mass Transf. 2009, 52, 4553–4563. [Google Scholar] [CrossRef]
- Ham, J.; Kim, E.; You, N.; Cho, H. Comparison of thermal performance in solution heat exchangers with different chevron angles in absorption system. Case Stud. Therm. Eng. 2023, 51, 103598. [Google Scholar] [CrossRef]
- Varun; Siddhartha. Thermal performance optimization of a flat plate solar air heater using genetic algorithm. Appl. Energy 2010, 87, 1793–1799. [Google Scholar] [CrossRef]
- Salarpour, N.; Azadani, L.N. Optimization and evaluation of thermo-hydraulic performance of solar air heaters equipped with different roughness geometries. Case Stud. Therm. Eng. 2024, 61, 105037. [Google Scholar] [CrossRef]
- Mohammed, N.A.; Alwared, A.I.; Shakhir, K.S.; Sulaiman, F.A. Synthesis, characterization of FeNi3@SiO2@CuS for enhance solar photocatalytic degradation of atrazine herbicides: Application of RSM. Results Surf. Interfaces 2024, 16, 100253. [Google Scholar] [CrossRef]
- Matheswaran, M.M.; Arjunan, T.V.; Muthusamy, S.; Natrayan, L.; Panchal, H.; Subramaniam, S.; Khedkar, N.K.; El-Shafay, A.S.; Sonawane, C. A case study on thermo-hydraulic performance of jet plate solar air heater using response surface methodology. Case Stud. Therm. Eng. 2022, 34, 101983. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent 2023 R1, Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Shetty, S.P.; Madhwesh, N.; Vasudeva Karanth, K.V. Numerical analysis of a solar air heater with circular perforated absorber plate. Sol. Energy 2021, 215, 416–433. [Google Scholar] [CrossRef]
- Manjunath, M.S.; Vasudeva Karanth, K.; Yagnesh Sharma, N. Numerical Analysis of the Influence of Spherical Turbulence Generators on Heat Transfer Enhancement of Flat Plate Solar Air Heater. Energy 2017, 121, 616–630. [Google Scholar] [CrossRef]
- Arunkumar, H.S.; Kumar, S.; Vasudeva Karanth, K. Energy exergy and economic analysis of a multiple inlet solar air heater for augmented thermohydraulic performance. Therm. Eng. 2024, 246, 122981. [Google Scholar] [CrossRef]
- Ghritlahre, H.K.; Verma, M.; Parihar, J.S.; Mondloe, D.S.; Agrawal, S. A detailed review of various types of solar air heaters performance. Sol. Energy 2022, 237, 173–195. [Google Scholar] [CrossRef]
- Arunkumar, H.S.; Kumar, S.; Vasudeva Karanth, K. Experimental study on thermo-hydraulic performance of a solar air heater with rectangular perforated duct inserts. Sol. Energy 2021, 227, 179–189. [Google Scholar] [CrossRef]
- Korpale, V.S.; Deshmukh, S.P.; Mathpati, C.S.; Dalvi, V.H. Numerical simulations and optimization of solar air heaters. Therm. Eng. 2020, 180, 115744. [Google Scholar] [CrossRef]
- Qader, B.S.; Supeni, E.E.; Ariffin, M.K.A.; Abu Talib, A.R. RSM approach for modeling and optimization of designing parameters for inclined fins of solar air heater. Renew. Energy 2019, 136, 48–68. [Google Scholar] [CrossRef]



| Properties | Air | Aluminum | Glass |
|---|---|---|---|
| Density (kg/m3) | Equation (1) | 2719 | 2500 |
| Specific heat (J/kg·K) | 1006.43 | 871 | 800 |
| Thermal conductivity (W/m.K) | Equation (2) | 202.4 | 1.2 |
| Viscosity (kg/m·s) | Equation (3) | - | - |
| Emissivity | - | 0.9 | - |
| Refractive index | - | 1 | 1.53 |
| Number of Elements | 500,000 | 1,000,000 | 1,500,000 | 2,000,000 |
|---|---|---|---|---|
| Air temperature at outlet | 322.1 | 322.0 | 321.8 | 321.8 |
| Reynolds Number | Thermal Efficiency Present Study | Thermal Efficiency Reference Paper | Error Percentage |
|---|---|---|---|
| 3000 | 0.5949 | 0.5237 | 13.58 |
| 6000 | 0.6864 | 0.6697 | 2.49 |
| 9000 | 0.7203 | 0.7443 | 3.21 |
| 12,000 | 0.7433 | 0.7913 | 6.06 |
| 15,000 | 0.7650 | 0.8286 | 7.67 |
| 18,000 | 0.7884 | 0.8610 | 8.43 |
| 21,000 | 0.8151 | 0.8918 | 8.59 |
| Input Parameters | Output Parameters | ||||
|---|---|---|---|---|---|
| Case No. | Wave Height (mm) | Pitch Length (mm) | Channel Height (mm) | Temperature Rise Coefficient | Thermal Efficiency (%) |
| 1 | 15 | 70 | 80 | 0.0479 | 27.631 |
| 2 | 10 | 70 | 80 | 0.0454 | 26.178 |
| 3 | 20 | 70 | 80 | 0.0511 | 29.468 |
| 4 | 15 | 50 | 80 | 0.0497 | 28.615 |
| 5 | 15 | 90 | 80 | 0.0470 | 27.239 |
| 6 | 15 | 70 | 70 | 0.0533 | 27.912 |
| 7 | 15 | 70 | 90 | 0.0422 | 27.365 |
| 8 | 10.935 | 53.739 | 71.87 | 0.0525 | 27.195 |
| 9 | 19.065 | 53.739 | 71.87 | 0.0581 | 30.160 |
| 10 | 10.935 | 86.261 | 71.87 | 0.0511 | 26.479 |
| 11 | 19.065 | 86.261 | 71.87 | 0.0556 | 28.792 |
| 12 | 10.935 | 53.739 | 83.13 | 0.0420 | 26.685 |
| 13 | 19.065 | 53.739 | 83.13 | 0.0470 | 29.900 |
| 14 | 10.935 | 86.261 | 83.13 | 0.0410 | 26.019 |
| 15 | 19.065 | 86.261 | 83.13 | 0.0448 | 28.473 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqsair, U.F. Numerical Simulation and Optimization of a Chevron-Type Corrugated Solar Air Heater. Energies 2025, 18, 1821. https://doi.org/10.3390/en18071821
Alqsair UF. Numerical Simulation and Optimization of a Chevron-Type Corrugated Solar Air Heater. Energies. 2025; 18(7):1821. https://doi.org/10.3390/en18071821
Chicago/Turabian StyleAlqsair, Umar Fahed. 2025. "Numerical Simulation and Optimization of a Chevron-Type Corrugated Solar Air Heater" Energies 18, no. 7: 1821. https://doi.org/10.3390/en18071821
APA StyleAlqsair, U. F. (2025). Numerical Simulation and Optimization of a Chevron-Type Corrugated Solar Air Heater. Energies, 18(7), 1821. https://doi.org/10.3390/en18071821





