A Combined LPTN-FETM Approach for Dual-Mode Thermal Analysis of Composite Cage Rotor Bearingless Induction Motor (CCR-BIM) with Experimental Verification
Abstract
1. Introduction
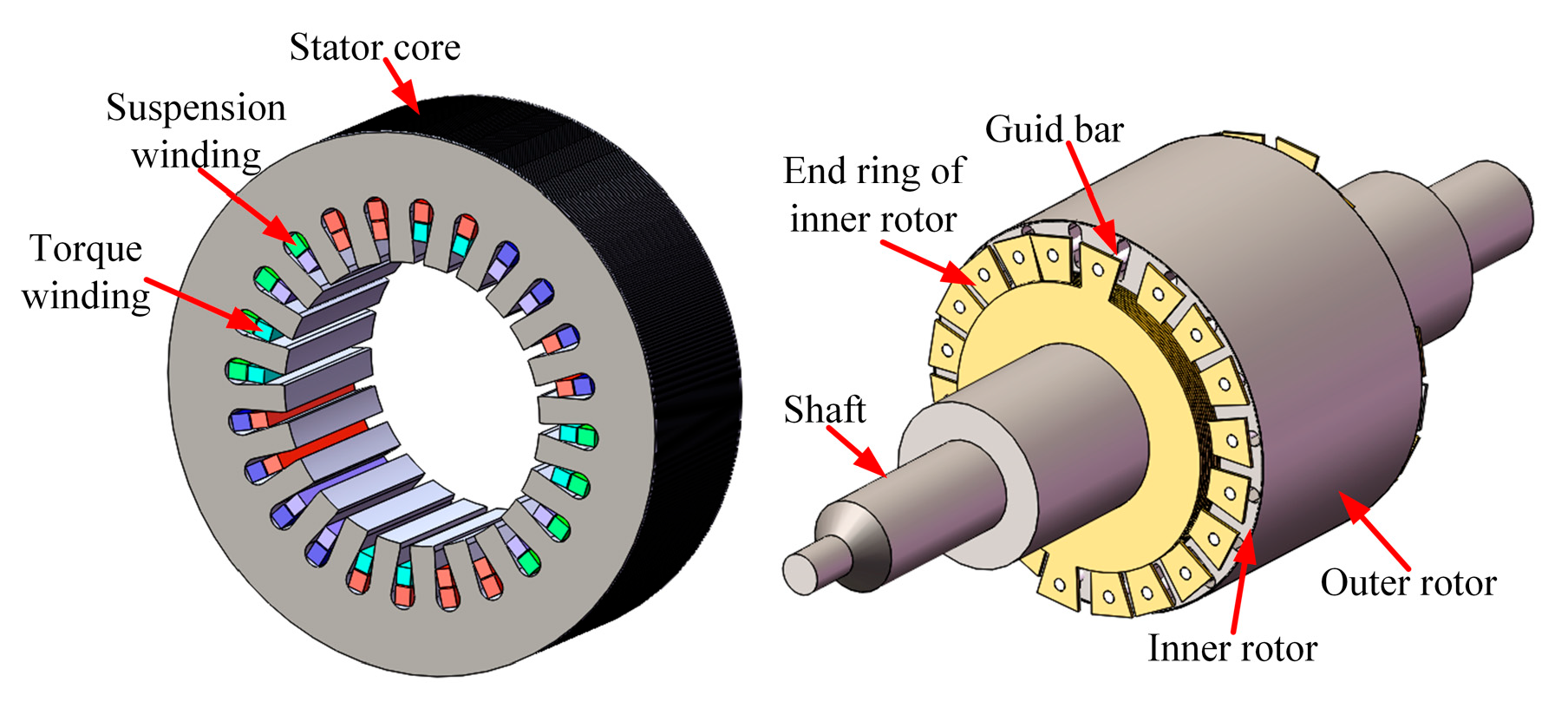
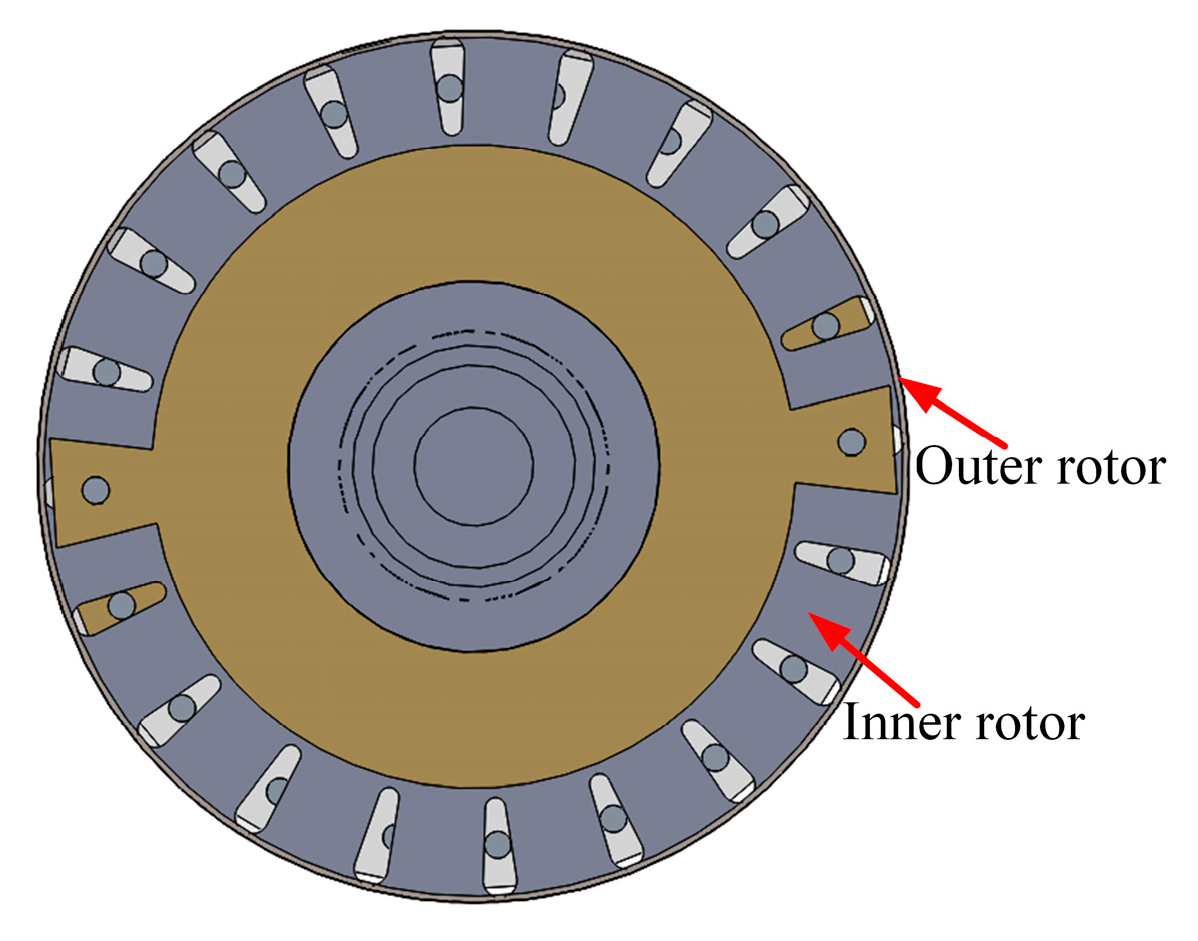
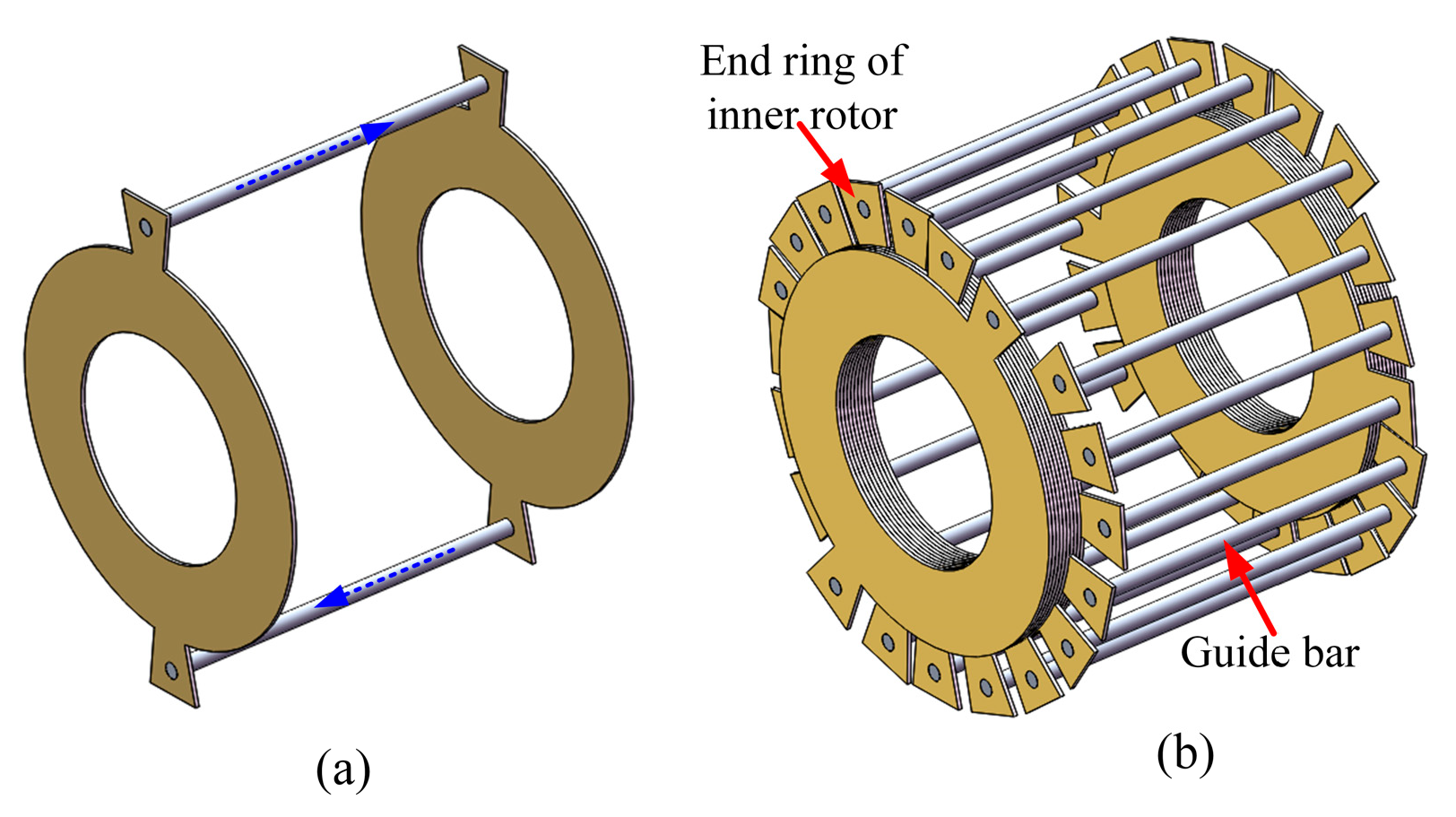
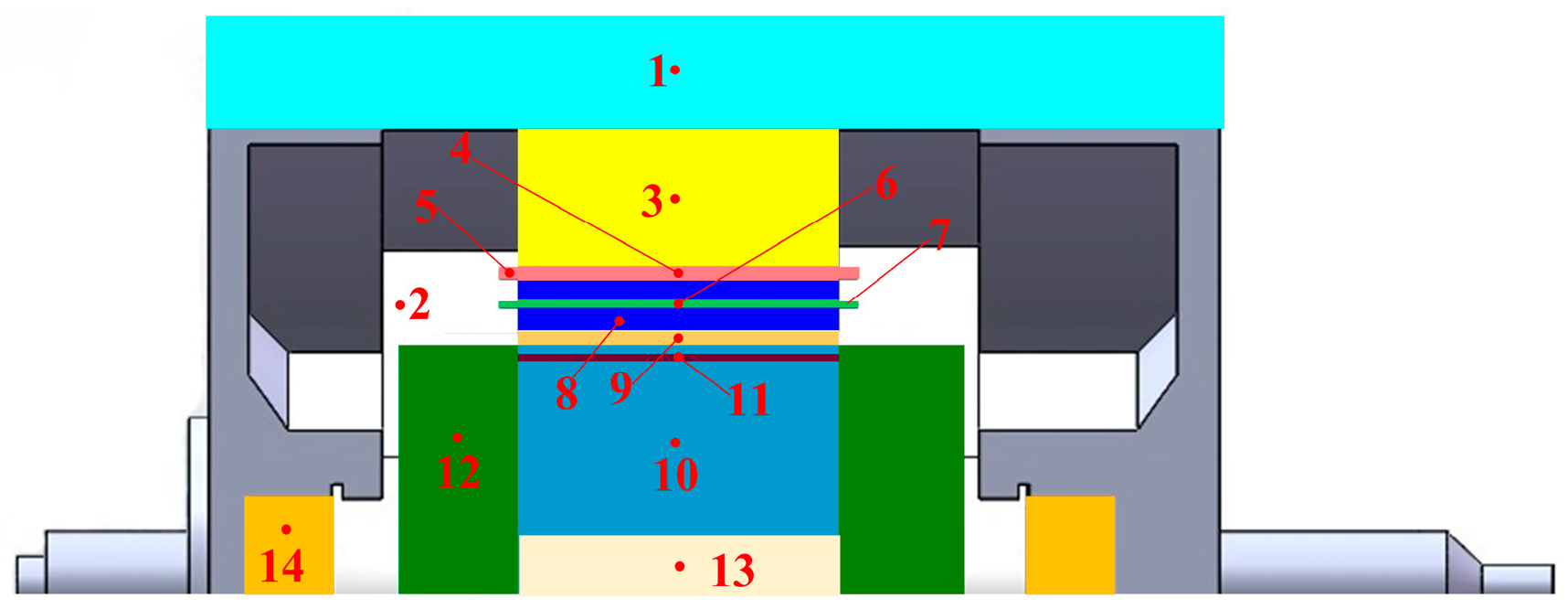
2. Basic Structure and Principle of CCR-BIM
3. LPTN Model of CCR-BIM
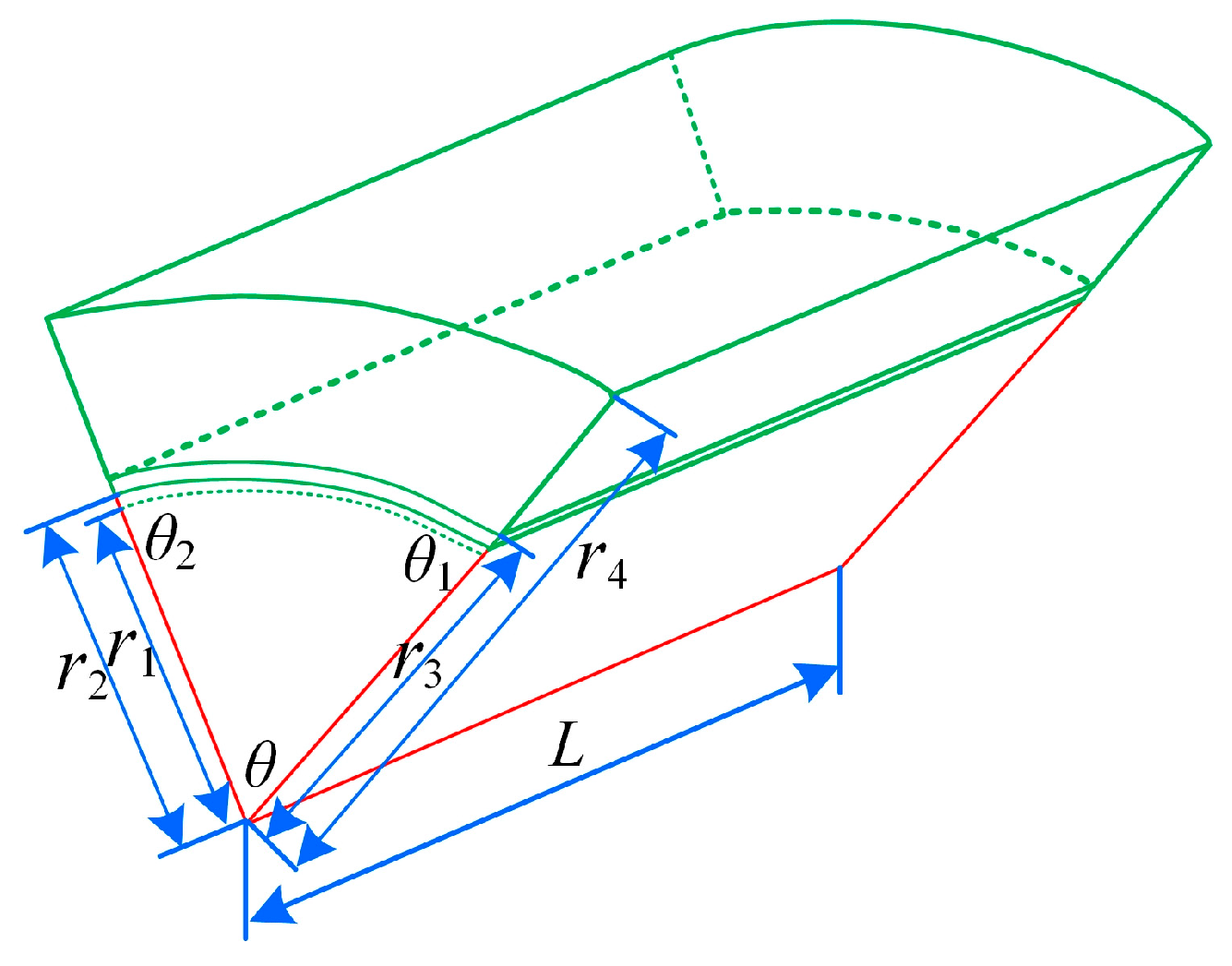
3.1. Modeling
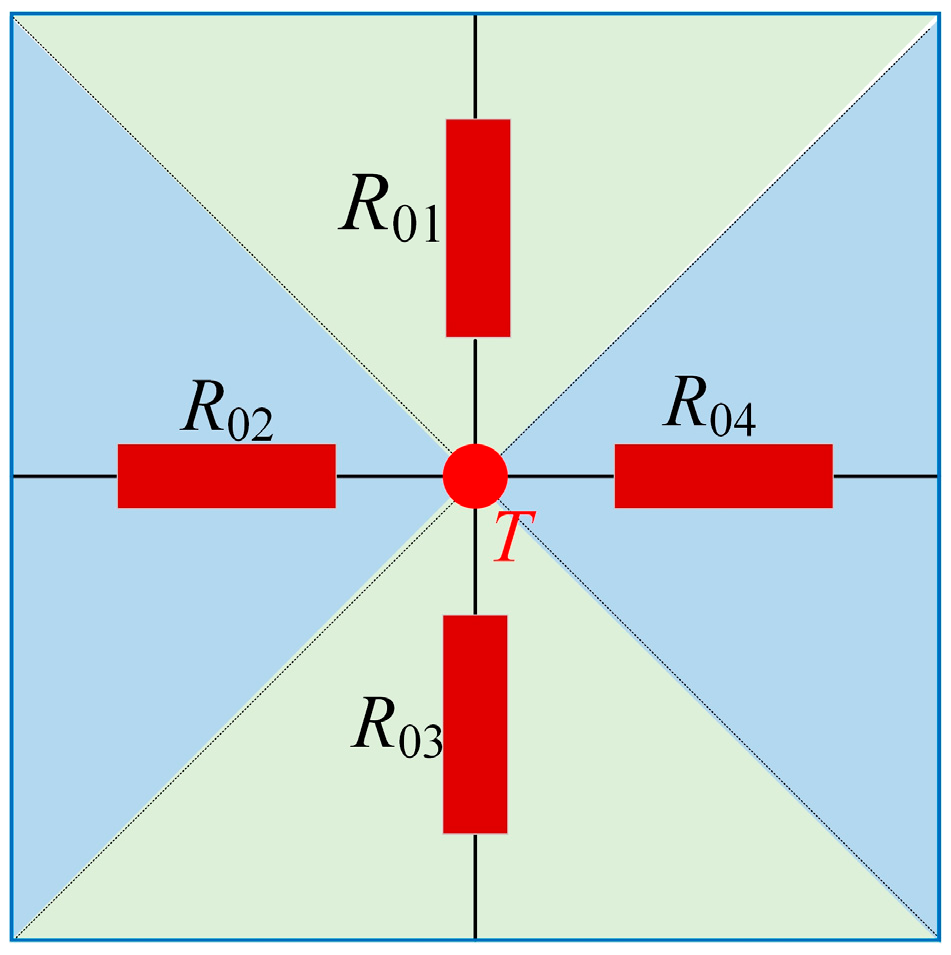
3.2. Thermal Resistance
3.3. Heat Sources
- (1)
- Copper loss of the two windings
- (2)
- Copper loss of the end ring
- (3)
- Iron loss of the stator core
- (4)
- Iron loss of the stator teeth
- (5)
- Eddy current loss of the outer rotor
- (6)
- Aluminum loss of rotor bar
3.4. Thermal Network Matrix
4. FETM Analysis of Motor Temperature Field
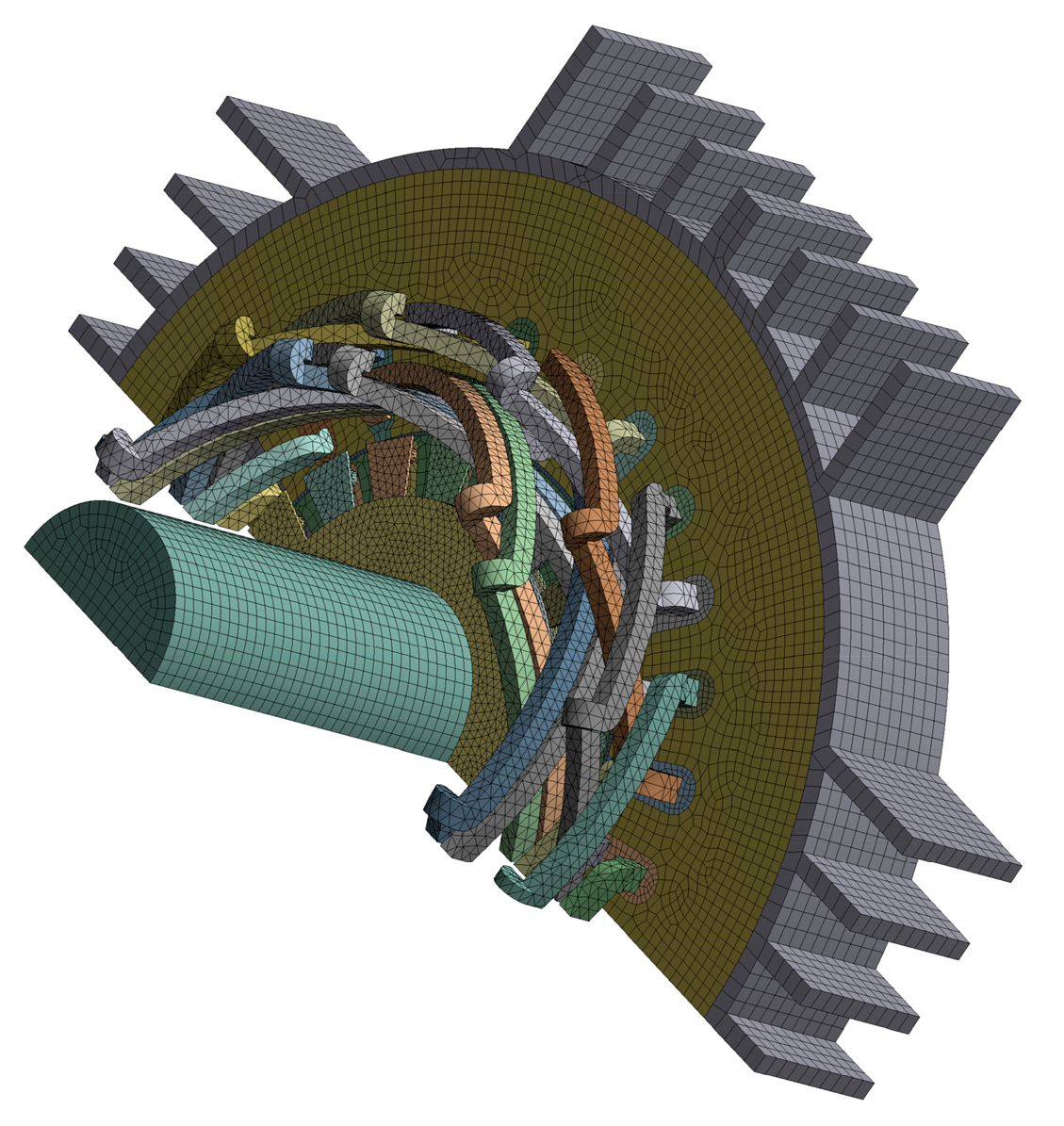
4.1. Finite Element Modeling
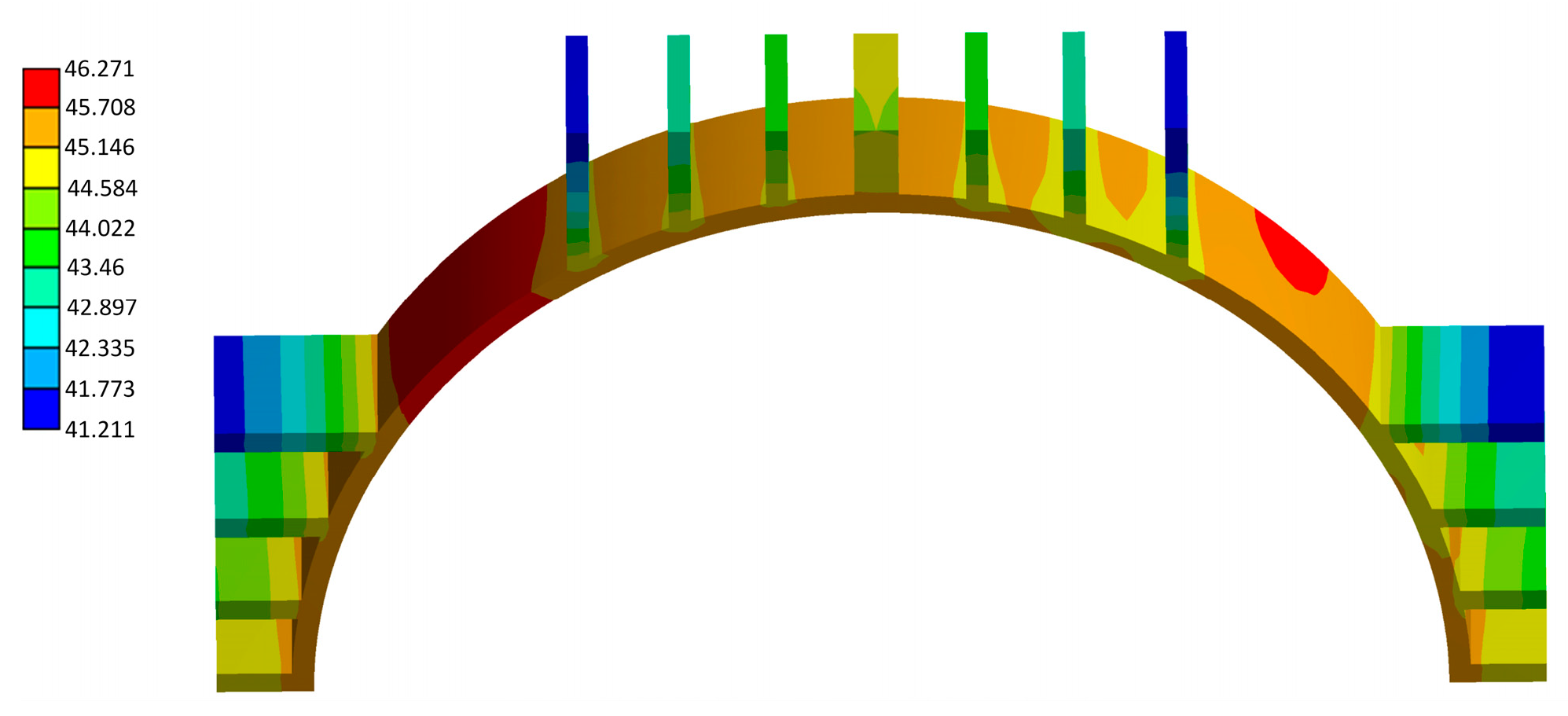
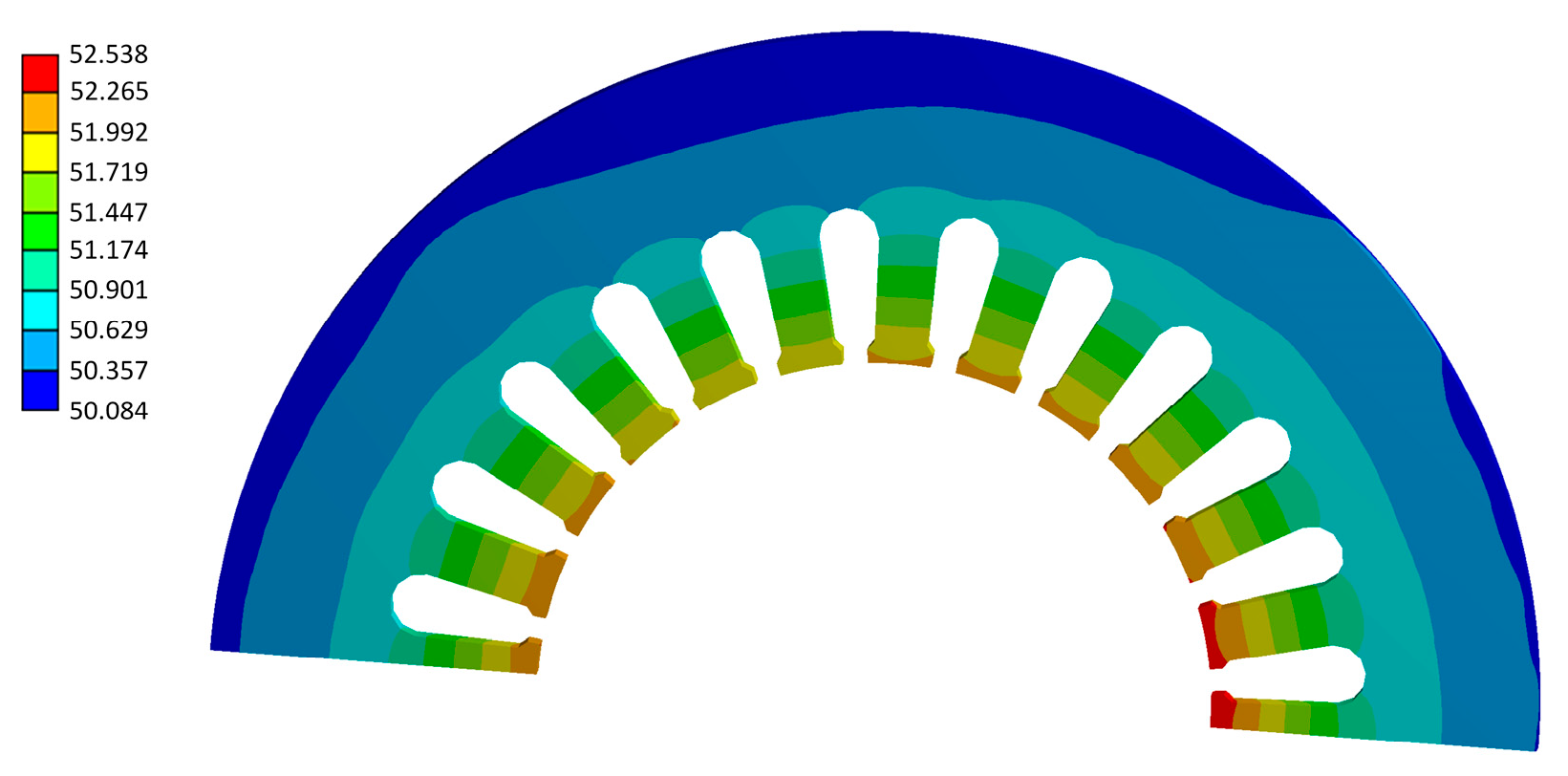
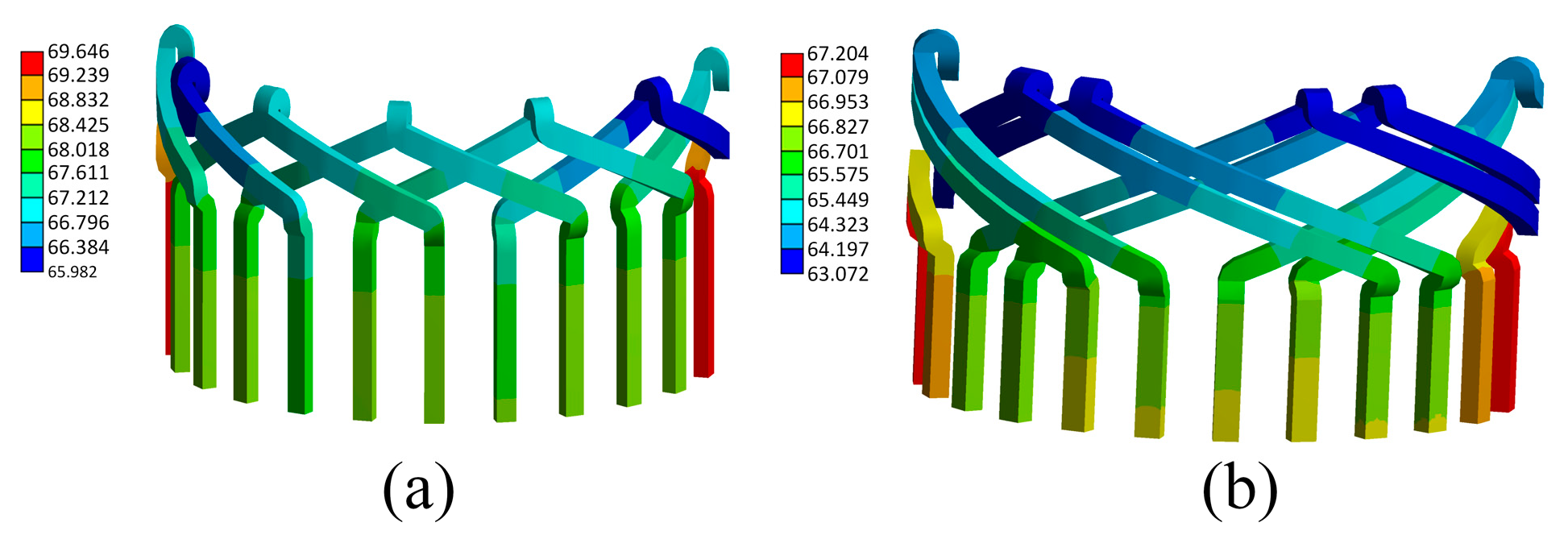
4.2. Simulation Results and Analysis of FETM
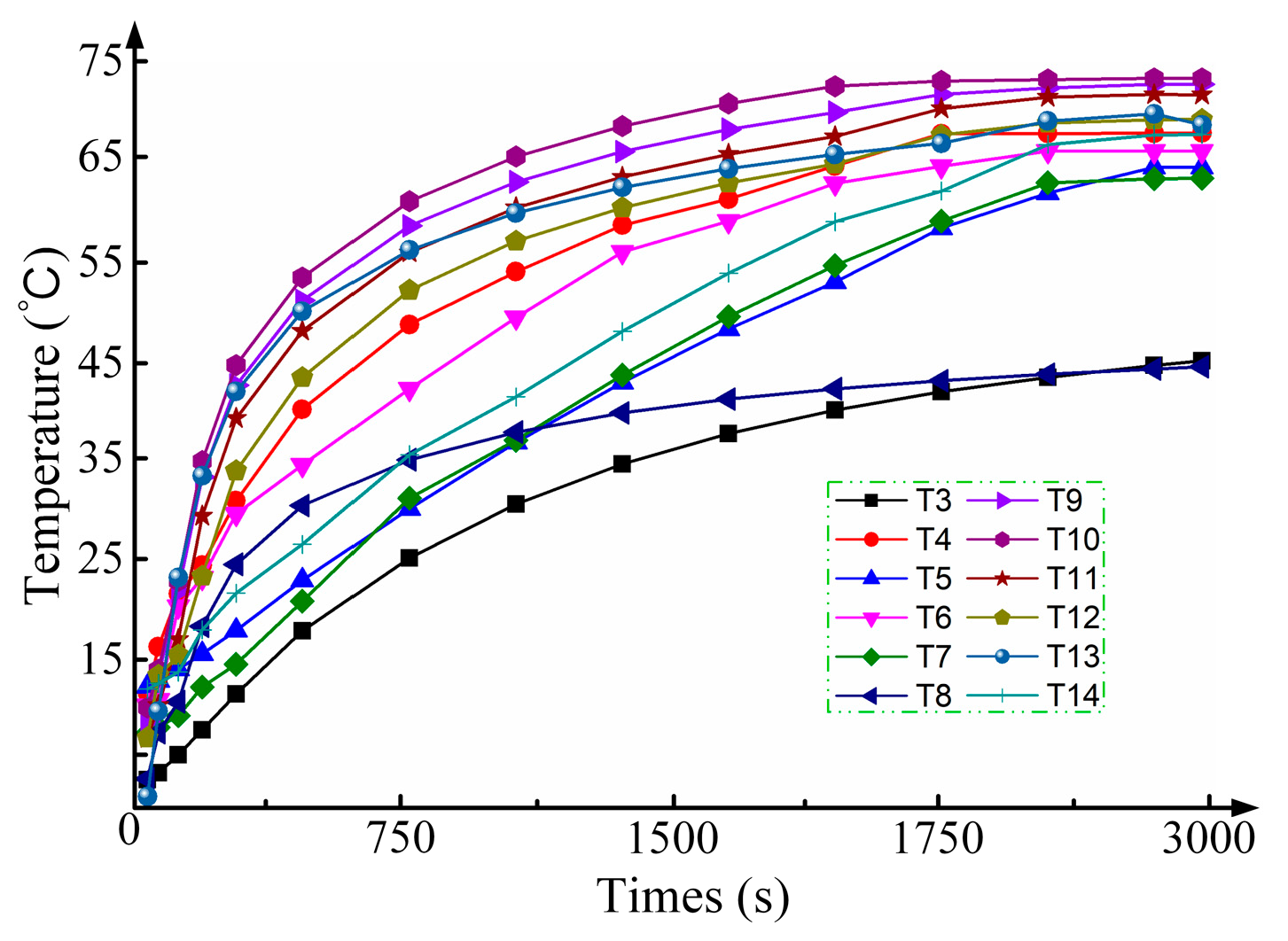
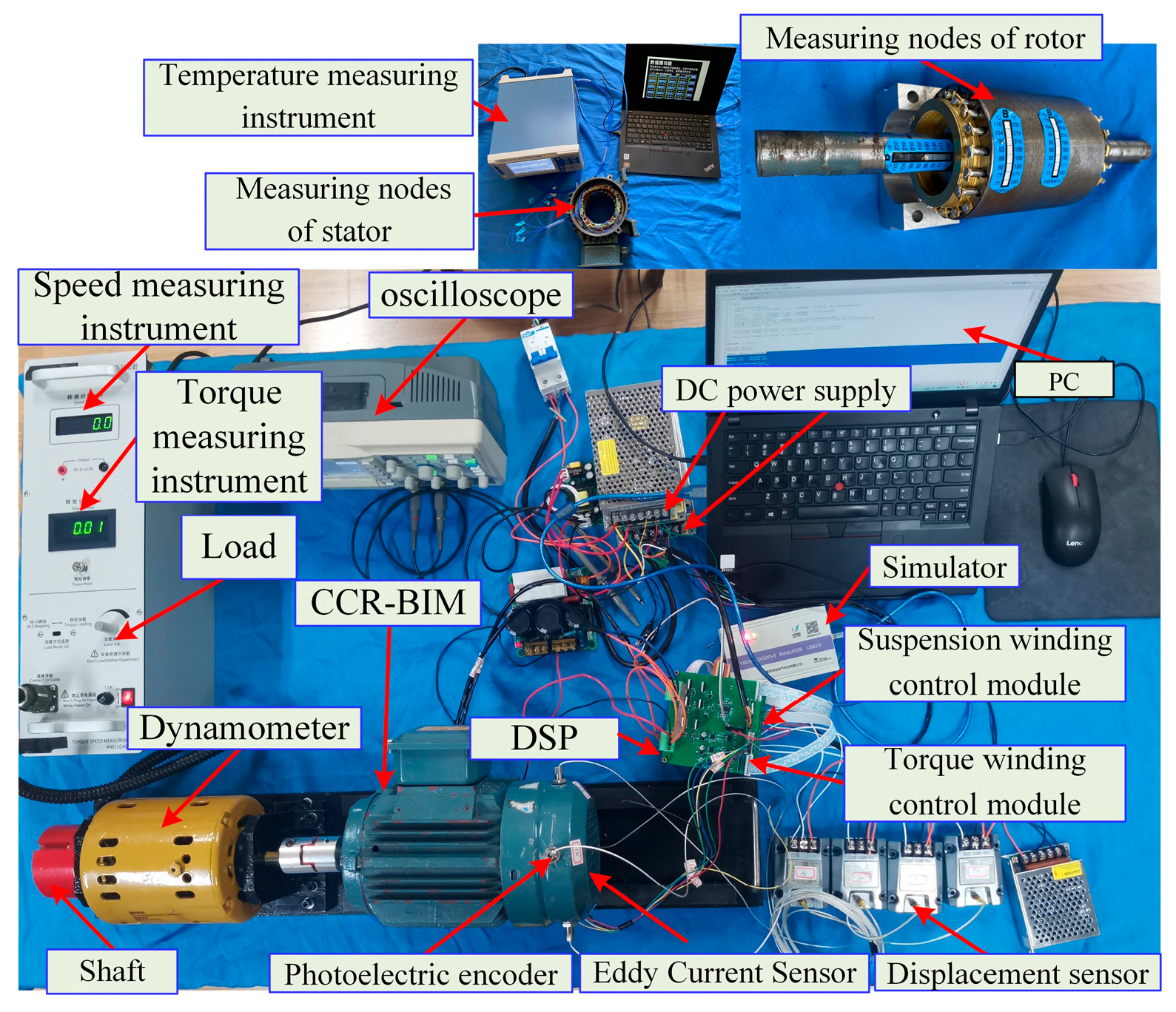
5. Temperature Test Platform of CCR-BIM
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tera, T.; Yamauchi, Y.; Chiba, A.; Fukao, T.; Rahman, M. Performances of bearingless and sensorless induction motor drive based on mutual inductances and rotor displacements estimation. IEEE Trans. Ind. Electron. 2006, 53, 187–194. [Google Scholar] [CrossRef]
- De Freitas Nunes, E.A.; Salazar, A.O.; Villarreal, E.R.L.; Souza, F.E.C.; Dos Santos, L.P.; Lopes, J.S.B.; Luque, J.C.C. Proposal of a Fuzzy Controller for Radial Position in a Bearingless Induction Motor. IEEE Access 2019, 7, 114808–114816. [Google Scholar] [CrossRef]
- Chen, J.; Fujii, Y.; Johnson, M.W.; Farhan, A.; Severson, E.L. Optimal Design of the Bearingless Induction Motor. IEEE Trans. Ind. Appl. 2020, 57, 1375–1388. [Google Scholar] [CrossRef]
- Victor, V.F.; Quintaes, F.O.; Lopes, J.S.B.; Junior, L.d.S.; Lock, A.S.; Salazar, A.O. Analysis and Study of a Bearingless AC Motor Type Divided Winding, Based on a Conventional Squirrel Cage Induction Motor. IEEE Trans. Magn. 2012, 48, 3571–3574. [Google Scholar] [CrossRef]
- Lu, C.; Yang, Z.; Sun, X.; Ding, Q.; Zhao, Q. A decoupling control of composite cage rotor bearingless induction motor based on SA-PSO support vector machine inverse. Int. Trans. Electr. Energy Syst. 2021, 31, e12988. [Google Scholar] [CrossRef]
- Kauh, S.; Hahn, S.-Y.; Lee, Y. Thermal analysis of induction motor with forced cooling channels. IEEE Trans. Magn. 2000, 36, 1398–1402. [Google Scholar] [CrossRef]
- Kokate, R.; Seele, J.; Park, C.; Mitsingas, C.; Schroen, E.; Kweon, C.-B. Thermal Modeling and Analysis of an Axial Flux Permanent Magnet Motor. In Proceedings of the AIAA AVIATION FORUM AND ASCEND 2024, Las Vegas, NV, USA, 29 July–2 August 2024. [Google Scholar]
- Ebrahimi, Y.; Feyzi, M.R. Lumped Parameter Thermal Model for Axial Flux Switched Reluctance Motors. Electr. Power Components Syst. 2017, 45, 2318–2326. [Google Scholar] [CrossRef]
- Arbab, N.; Wang, W.; Lin, C.; Hearron, J.; Fahimi, B. Thermal Modeling and Analysis of a Double-Stator Switched Reluctance Motor. IEEE Trans. Energy Convers. 2015, 30, 1209–1217. [Google Scholar] [CrossRef]
- Guo, B.; Huang, Y.; Guo, Y.; Zhu, J. Thermal Analysis of the Conical Rotor Motor Using LPTN with Accurate Heat Transfer Coefficients. IEEE Trans. Appl. Supercond. 2016, 26, 0611507. [Google Scholar] [CrossRef]
- Vahedi, P.; Ganji, B.; Afjei, E. Lumped thermal model for the multi-layer switched reluctance motor. IET Electr. Power Appl. 2020, 14, 1873–1885. [Google Scholar] [CrossRef]
- Chen, Q.; Zou, Z.; Cao, B. Lumped-parameter thermal network model and experimental research of interior pmsm for electric vehicle. CES Trans. Electr. Mach. Syst. 2017, 1, 367–374. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, J.; Guo, Y. Thermal Analysis of High-Speed SMC Motor Based on Thermal Network and 3-D FEA with Rotational Core Loss Included. IEEE Trans. Magn. 2009, 45, 4680–4683. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, W.; Li, Y.; Guo, J. Thermal Analysis of Axial Permanent Magnet Flywheel Machine Based on Equivalent Thermal Network Method. IEEE Access 2021, 9, 33181–33188. [Google Scholar] [CrossRef]
- Staton, D.; Popescu, M. Analytical thermal models for small induction motors. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2010, 29, 1345–1360. [Google Scholar] [CrossRef]
- Yu, W.; Hua, W.; Qi, J.; Zhang, H.; Zhang, G.; Xiao, H.; Xu, S.; Ma, G. Coupled Magnetic Field-Thermal Network Analysis of Modular-Spoke-Type Permanent-Magnet Machine for Electric Motorcycle. IEEE Trans. Energy Convers. 2020, 36, 120–130. [Google Scholar] [CrossRef]
- Ye, X.; Yang, Z.; Zhang, T. Modelling and performance analysis on a bearingless fixed-pole rotor induction motor. IET Electr. Power Appl. 2019, 13, 251–258. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Q.; Sun, X.; Lu, C. Design and Analysis of a Three-Speed Wound Bearingless Induction Motor. IEEE Trans. Ind. Electron. 2021, 69, 12529–12539. [Google Scholar] [CrossRef]
- Bu, W.; Huang, Y.; Li, Z.; Shi, H.; Shi, J. Diaplacement sensorless control strategy of bearingless induction motor. Int. J. Appl. Electromagn. Mech. 2017, 54, 597–610. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, C.; Sun, X.; Sun, Y. An Improved Dynamic Model for Bearingless Induction Motor Considering Rotor Eccentricity and Load Change. IEEE Trans. Ind. Electron. 2022, 69, 3439–3448. [Google Scholar] [CrossRef]
- Chen, W.; Wu, G.; Li, Y.; Ma, J. Coupled magnetic-thermal fields analysis using an adaptive single-mesh method. Int. J. Appl. Electromagn. Mech. 2019, 62, 45–57. [Google Scholar] [CrossRef]
- Zhao, W.; Cao, D.; Ji, J.; Huang, L.; Liu, T. A Generalized Mesh-Based Thermal Network Model for SPM Machines Combining Coupled Winding Solution. IEEE Trans. Ind. Electron. 2021, 68, 116–127. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, X.; Li, Y.; Zhang, Y.; Wang, J. Thermal Calculation on Brushless Doubly-fed Machines with a Magnetic Barrier Rotor. Proc. Chin. Soc. Electr. Eng. 2018, 38, 2745–2752. [Google Scholar] [CrossRef]
- Ahmed, F.; Ghosh, E.; Kar, N.C. Transient thermal analysis of a copper rotor induction motor using a lumped parameter temperature network model. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016; pp. 1–6. [Google Scholar]
- Amara, Y.; Wang, J.; Howe, D. Stator iron loss of tubular permanent-magnet machines. IEEE Trans. Ind. Appl. 2005, 41, 989–995. [Google Scholar] [CrossRef]
- Chen, M.; Zhuang, W.; Deng, S.; Zhu, C. Thermal analysis of the triple-phase asynchronous motor-reducer coupling system by thermal network method. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 2851–2861. [Google Scholar] [CrossRef]
- Benedik, B.; Duhovnik, J.; Rihtaršič, J.; Tavčar, J. Thermal model of through flow universal motor by means of lumped parameter network. Teh. Vjesn. 2017, 24, 405–412. [Google Scholar] [CrossRef][Green Version]
- Zhang, Y.; Ruan, J.; Huang, T.; Yang, X.; Zhu, H.; Yang, G. Calculation of Temperature Rise in Air-cooled Induction Motors Through 3-D Coupled Electromagnetic Fluid-Dynamical and Thermal Finite-Element Analysis. IEEE Trans. Magn. 2012, 48, 1047–1050. [Google Scholar] [CrossRef]




| Item | Value | Item | Value |
|---|---|---|---|
| Rated current of torque winding | 3 A | Turns of torque winding | 60 |
| Rated current of suspension winding | 0.8 A | Turns of suspension winding | 50 |
| Thickness of outer rotor | 0.35 mm | Stator outer diameter/inner diameter | 125/65 mm |
| Rated speed | 3000 rpm | Outer diameter of composite rotor | 64.4 mm |
| Core length | 83 mm | Shaft diameter | 20 mm |
| Material | Thermal Conductivity (W/m·K) | Specific Heat (J/kg·K) | Density (kg/m³) |
|---|---|---|---|
| Silicon Steel | 28.5 | 460 | 7650 |
| Copper (Winding) | 401 | 385 | 8960 |
| Aluminum (Bar) | 237 | 900 | 2700 |
| Shaft Steel | 43 | 475 | 7850 |
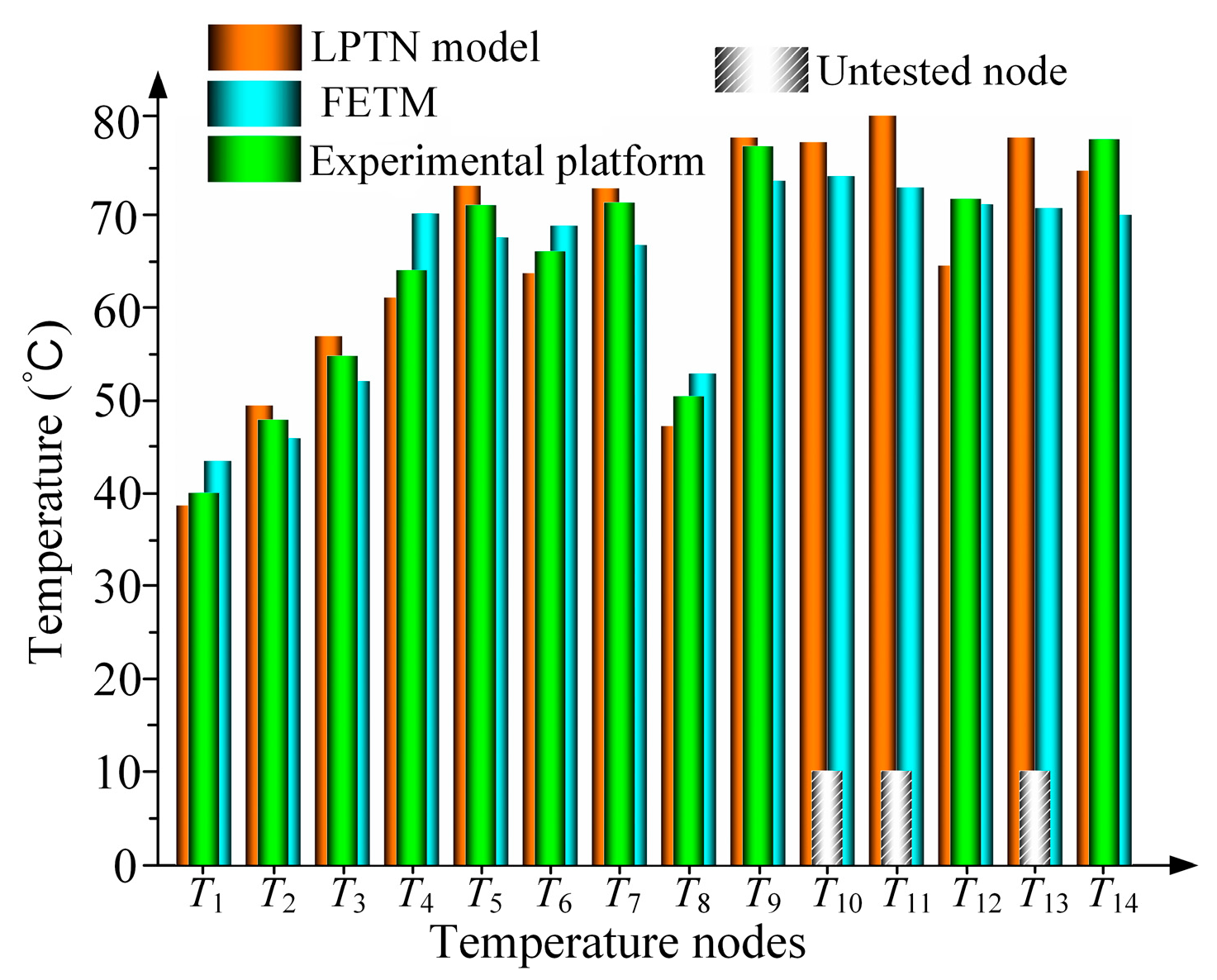
| Node | Temperature/°C | Node | Temperature/°C |
|---|---|---|---|
| T1 | 38.4 | T8 | 46.9 |
| T2 | 49.1 | T9 | 77.7 |
| T3 | 56.5 | T10 | 77.2 |
| T4 | 60.6 | T11 | 82.2 |
| T5 | 72.6 | T12 | 64.1 |
| T6 | 63.3 | T13 | 77.7 |
| T7 | 72.3 | T14 | 74.2 |
| Category | Specification |
|---|---|
| Software Platform | ANSYS Workbench 2020 R1 |
| Mesh Type | SOLID187 |
| Mesh Size | Critical Regions (Winding/Rotor): 0.5 mm; Non-critical Regions: 2 mm |
| Boundary Conditions | Ambient Temperature: 25 °C (Fixed) |
| Convergence Criteria | Relative Energy Error < 1 × 10−4 |
| Solver Settings | Steady-State (Newton–Raphson Iterative Method) |
| Node | Temperature/°C | Node | Temperature/°C |
|---|---|---|---|
| T1 | 43.2 | T8 | 52.5 |
| T2 | 45.6 | T9 | 73.1 |
| T3 | 52.9 | T10 | 73.6 |
| T4 | 69.6 | T11 | 72.4 |
| T5 | 67.1 | T12 | 70.6 |
| T6 | 68.3 | T13 | 70.2 |
| T7 | 66.3 | T14 | 68.5 |
| Node | Temperature/°C | Node | Temperature/°C |
|---|---|---|---|
| T1 | 39.7 | T8 | 50.1 |
| T2 | 47.6 | T9 | 76.8 |
| T3 | 54.4 | T10 | / |
| T4 | 63.6 | T11 | / |
| T5 | 70.5 | T12 | 71.2 |
| T6 | 65.6 | T13 | / |
| T7 | 70.8 | T14 | 77.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, C.; Lu, C.; Fang, J.; Zhang, J.; Cheng, J. A Combined LPTN-FETM Approach for Dual-Mode Thermal Analysis of Composite Cage Rotor Bearingless Induction Motor (CCR-BIM) with Experimental Verification. Energies 2025, 18, 1816. https://doi.org/10.3390/en18071816
Du C, Lu C, Fang J, Zhang J, Cheng J. A Combined LPTN-FETM Approach for Dual-Mode Thermal Analysis of Composite Cage Rotor Bearingless Induction Motor (CCR-BIM) with Experimental Verification. Energies. 2025; 18(7):1816. https://doi.org/10.3390/en18071816
Chicago/Turabian StyleDu, Chengtao, Chengling Lu, Jie Fang, Jinzhong Zhang, and Junhui Cheng. 2025. "A Combined LPTN-FETM Approach for Dual-Mode Thermal Analysis of Composite Cage Rotor Bearingless Induction Motor (CCR-BIM) with Experimental Verification" Energies 18, no. 7: 1816. https://doi.org/10.3390/en18071816
APA StyleDu, C., Lu, C., Fang, J., Zhang, J., & Cheng, J. (2025). A Combined LPTN-FETM Approach for Dual-Mode Thermal Analysis of Composite Cage Rotor Bearingless Induction Motor (CCR-BIM) with Experimental Verification. Energies, 18(7), 1816. https://doi.org/10.3390/en18071816







