Optimized Dimensioning and Economic Assessment of Decentralized Hybrid Small Wind and Photovoltaic Power Systems for Residential Buildings
Abstract
1. Introduction
1.1. Hybrid Power Generation from Small Wind Turbines and PV Systems
1.2. Optimized Dimensioning of HVAC Systems
1.3. Aim of This Work
2. Methodology
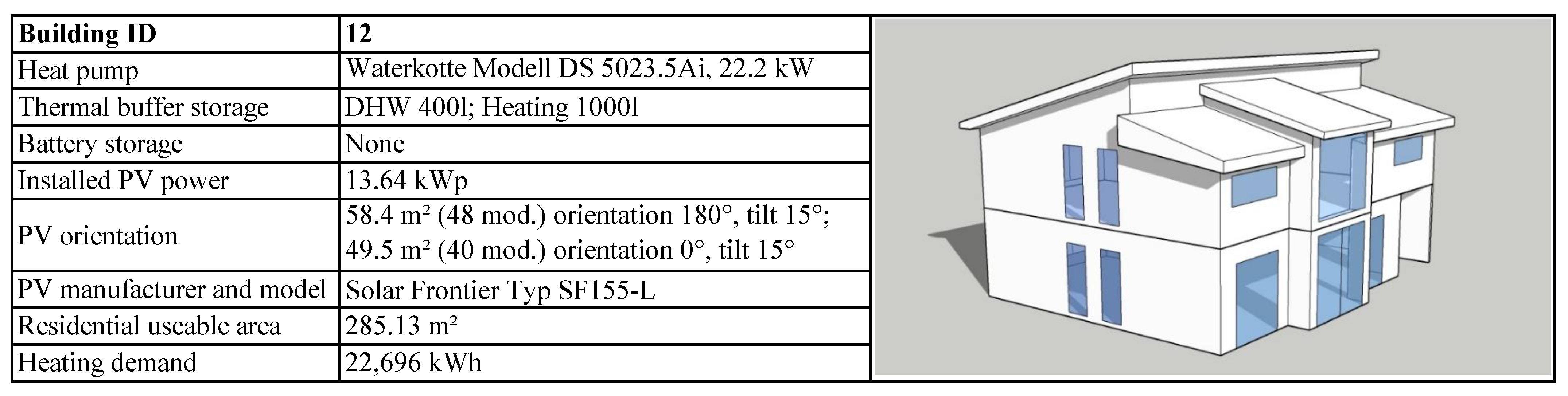
2.1. Boundary Conditions
| Location | Data Resolution | Data Source | Measurement Height [m] | Hub Height [m] | Roughness Exponent [-] |
|---|---|---|---|---|---|
| Aachen | 10 min | 5 | 10 | 0.16 | |
| Braunlage | 10 min | 8 | 15 | 0.28 | |
| Greifswald | 10 min | 5 | 10 | 0.28 | |
| Potsdam | 10 min | 18 | 15 | 0.28 | |
| Stuttgart | 30 min | CFD | 30 | 30 | no scaling |
| Wüstenrot | 1 h | Own measurements | 5 | 15 | 0.28 |
| Montreal | 1 h | 20 | 20 | no scaling |
2.2. Overall System Cost Function
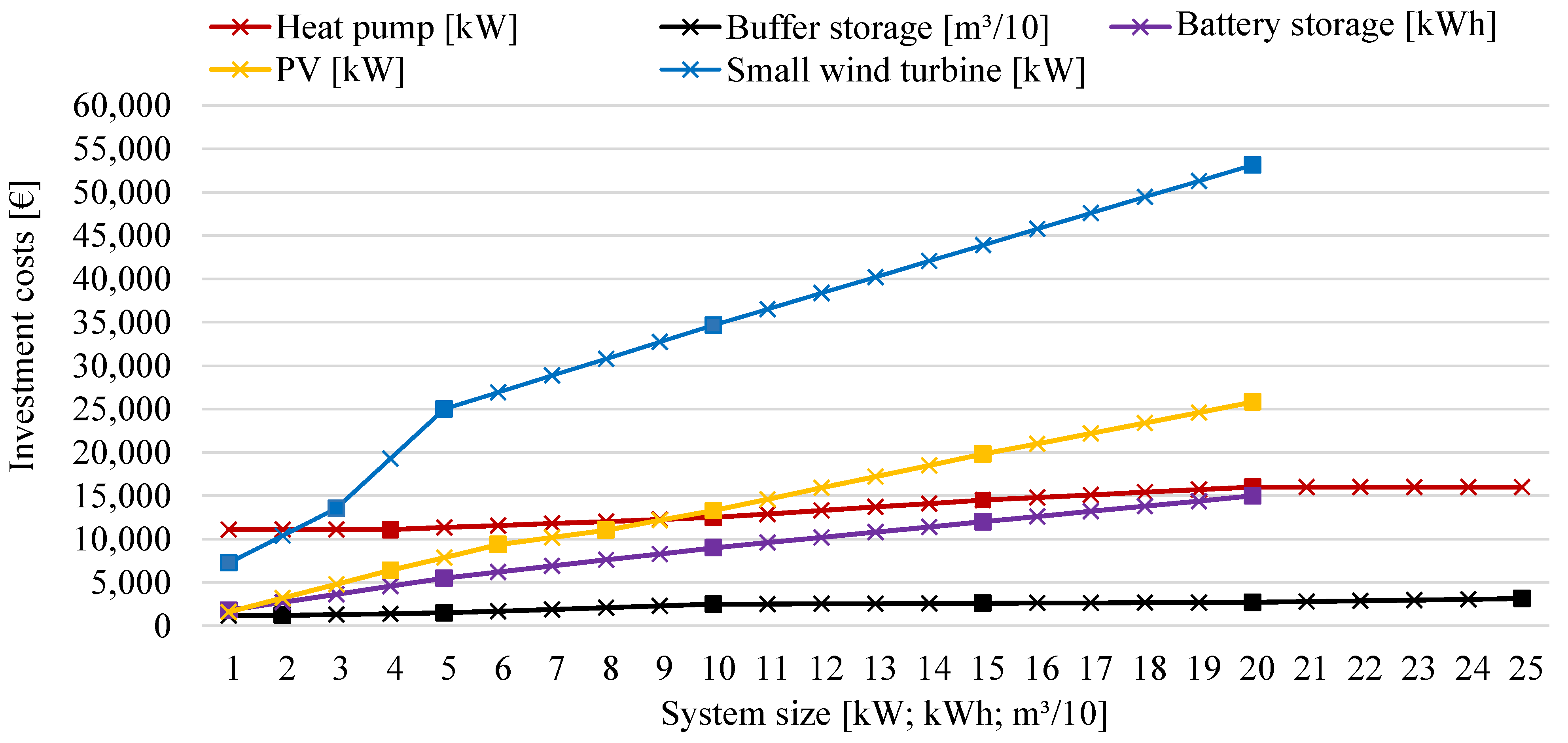
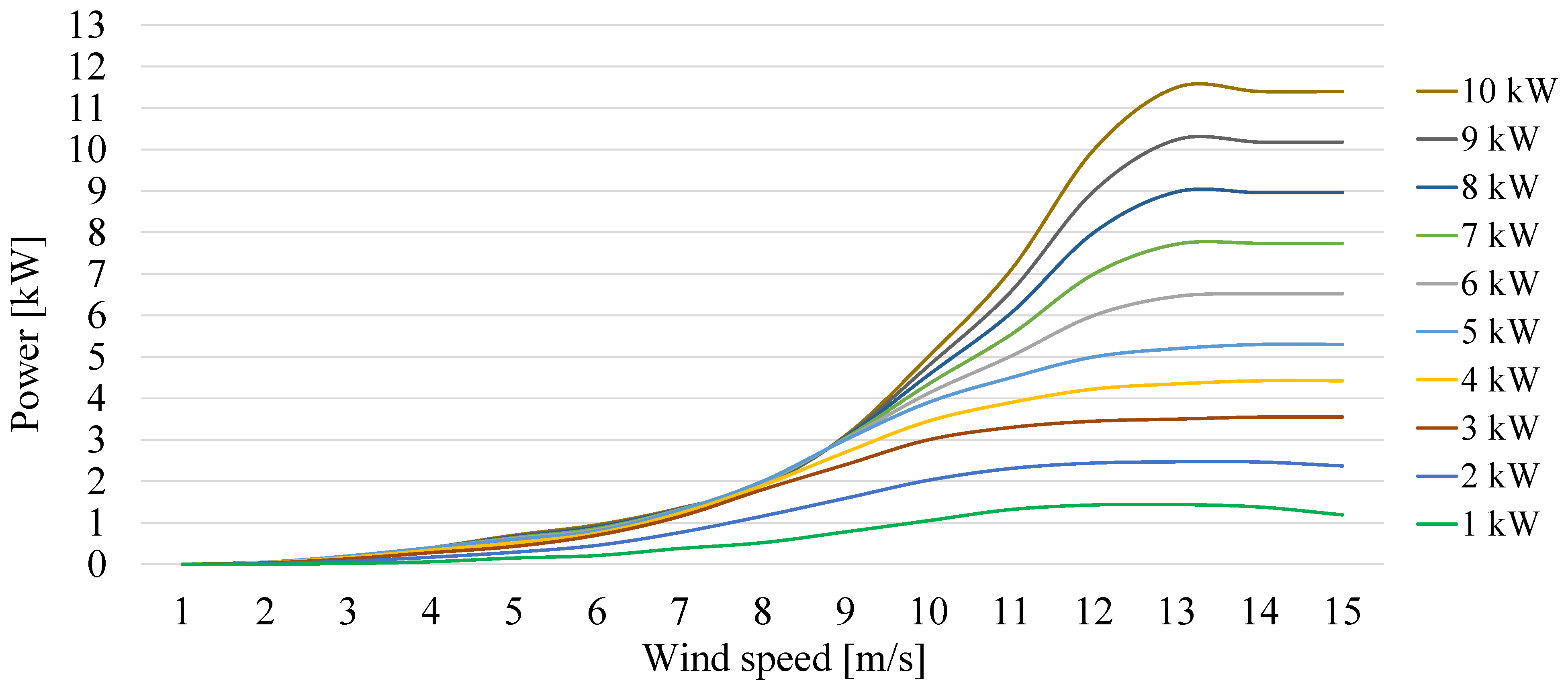
2.3. Investment Costs
3. Results
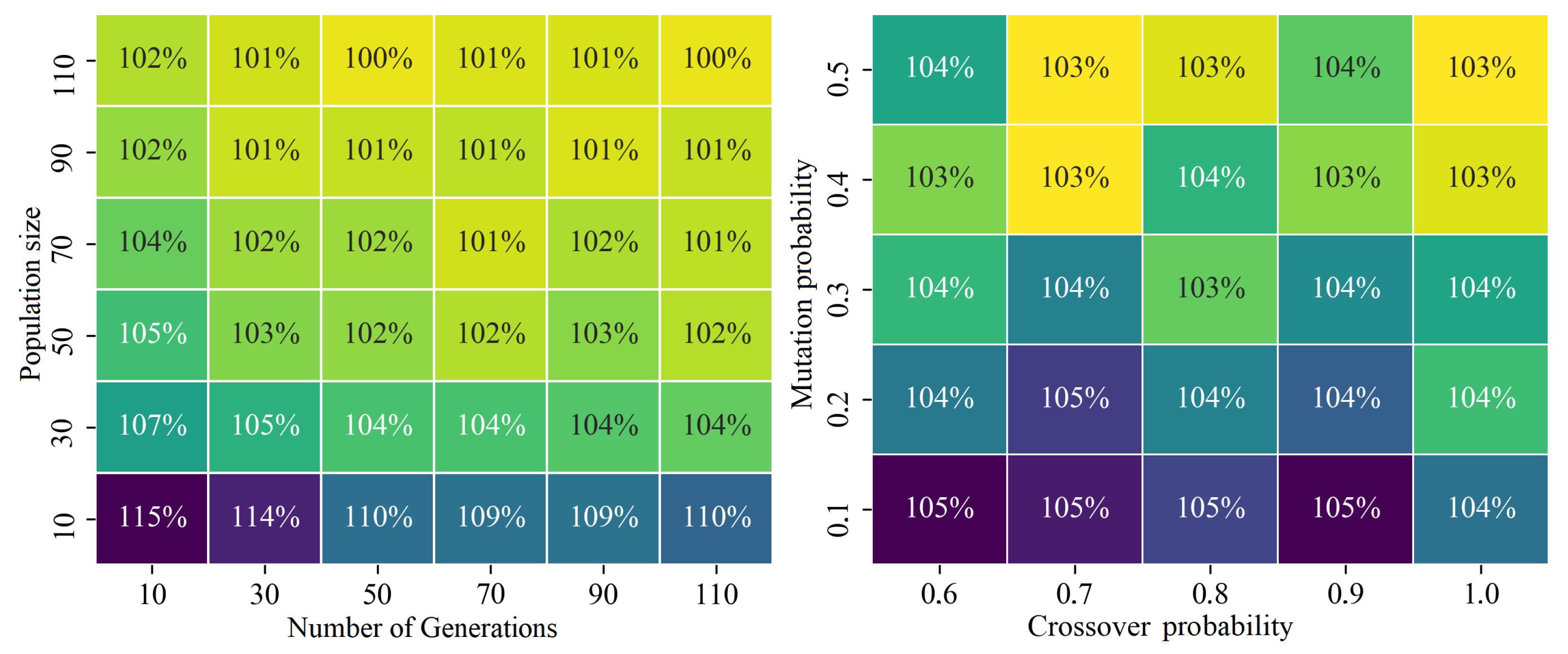
3.1. Optimal Parameters for Genetic Algorithms
- Number of generations: 30;
- Population size: 90;
- Two-point crossover; crossover probability: 1.0;
- Uniform mutation; mutation probability: 0.5;
- Competition selection; tournament size: 5.
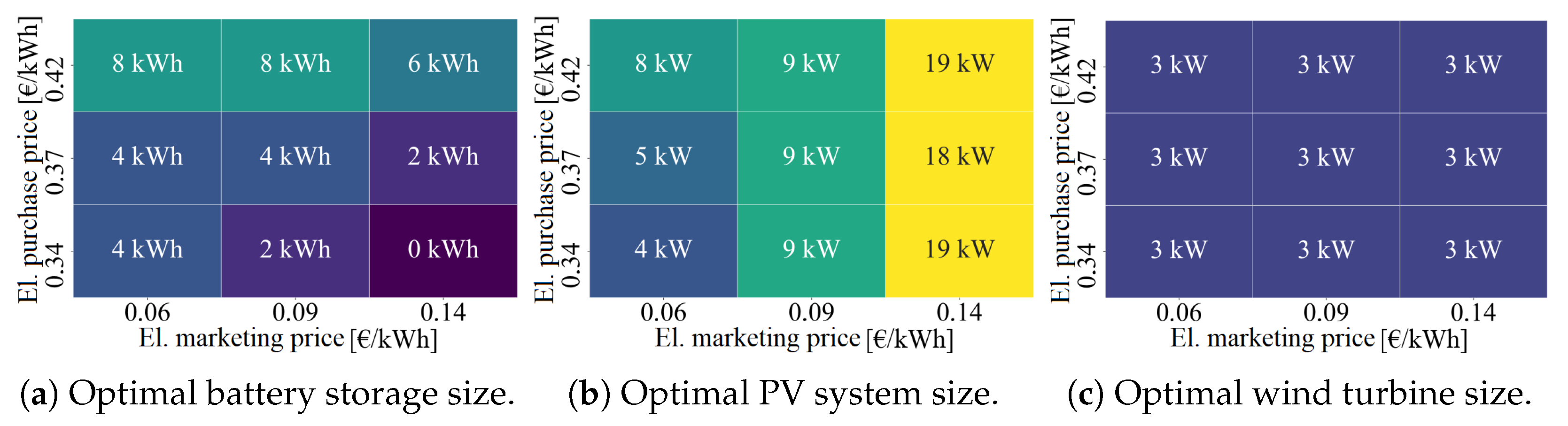
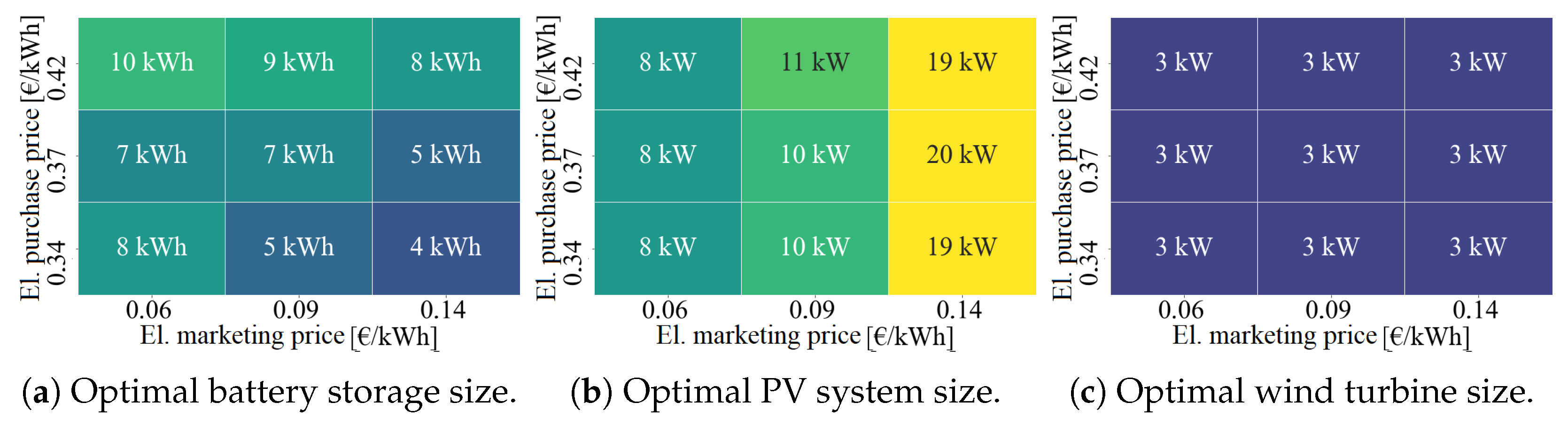
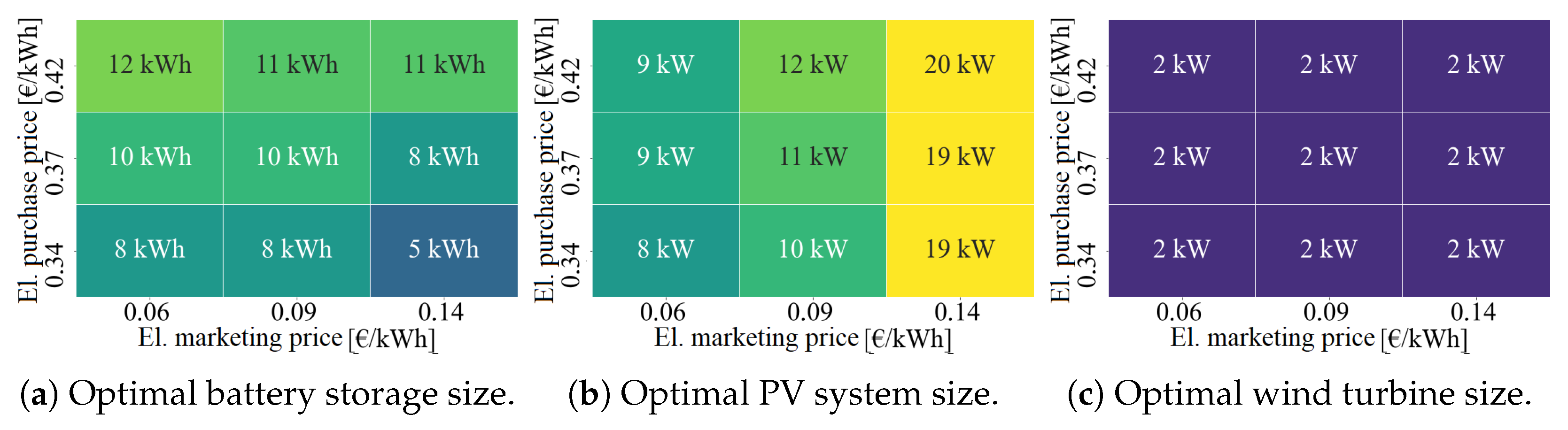
3.2. Current Framework Conditions
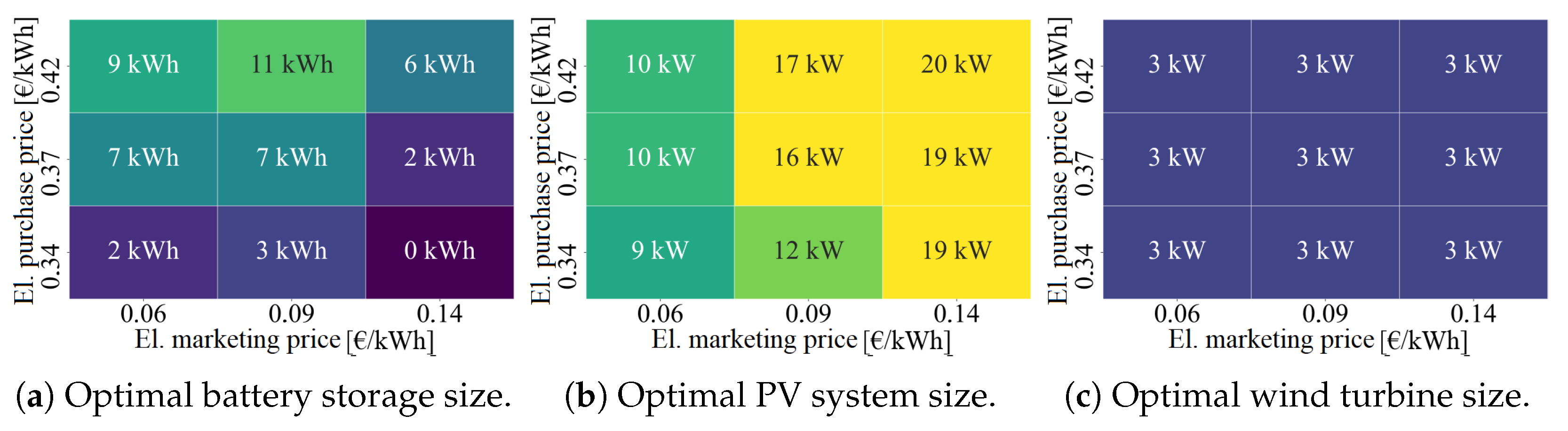
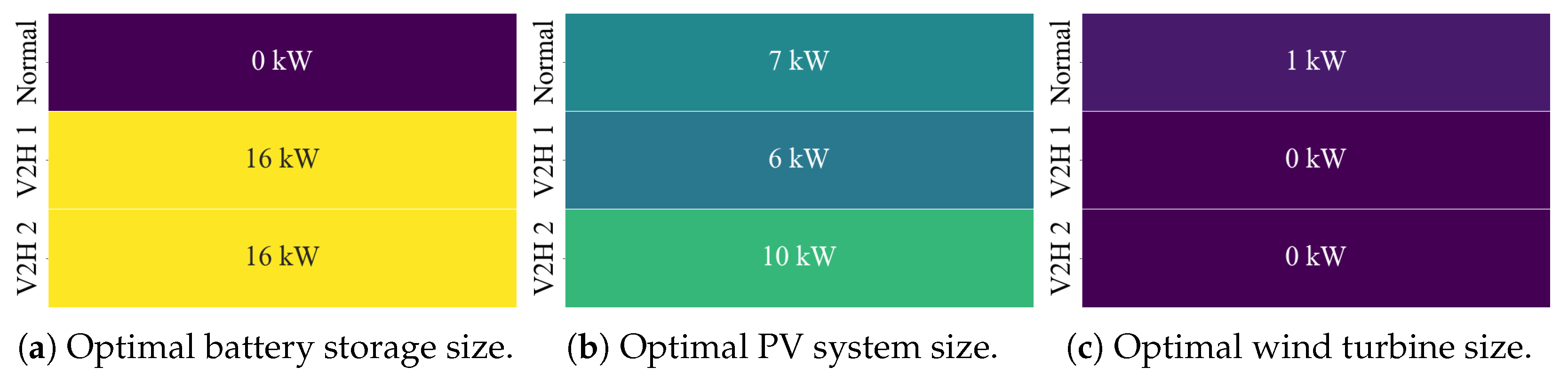
3.3. Current Framework Conditions with Vehicle-to-Home
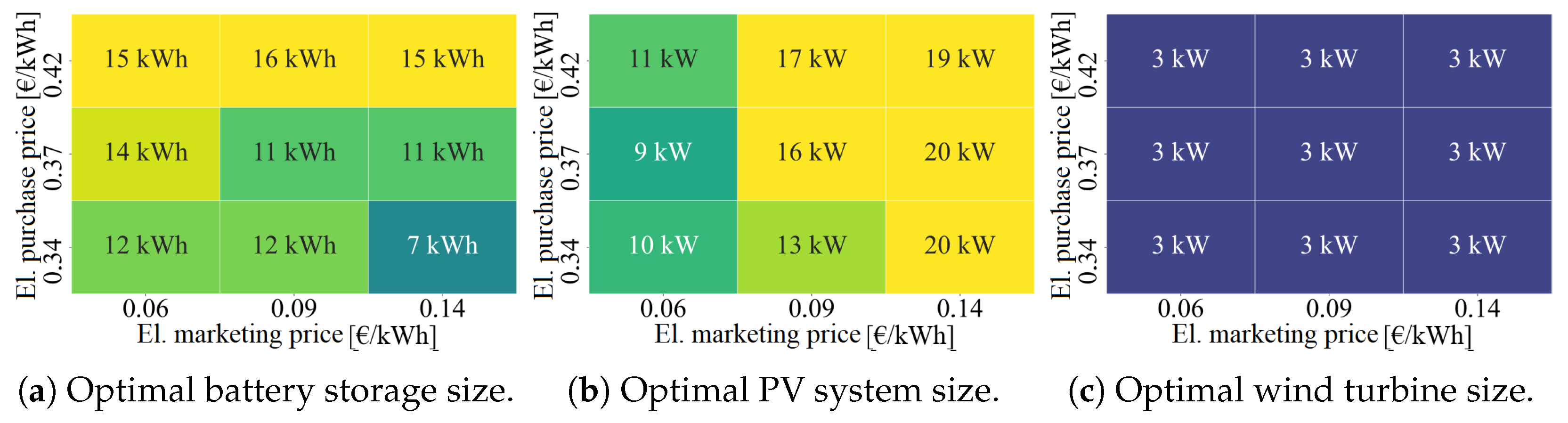
3.4. Future Framework Conditions
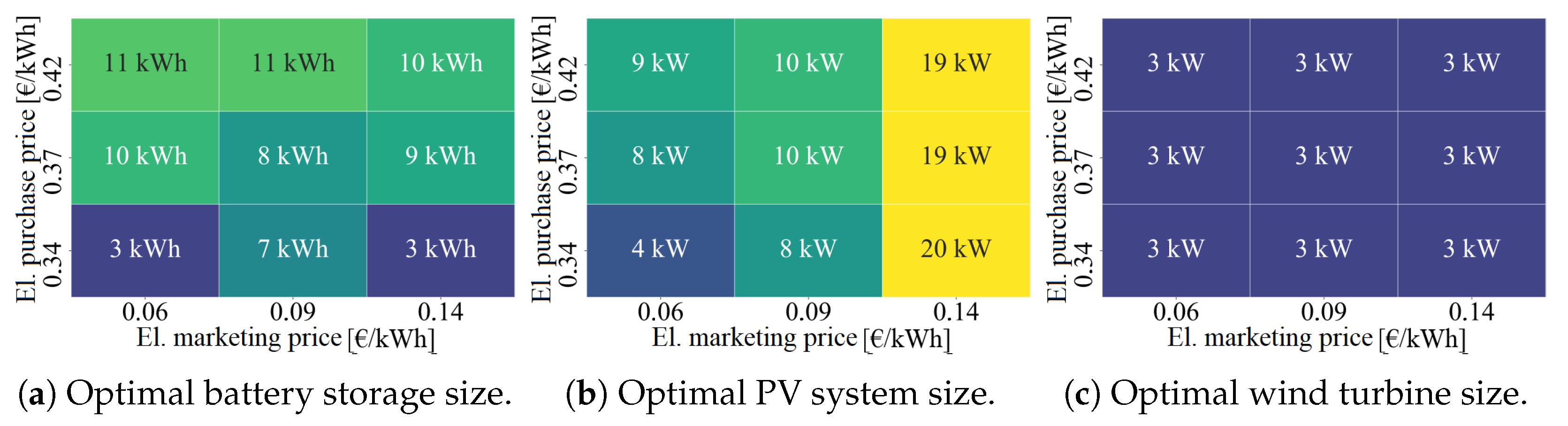
3.5. Aachen, Germany
3.6. Braunlage, Germany
3.7. Greifswald, Germany
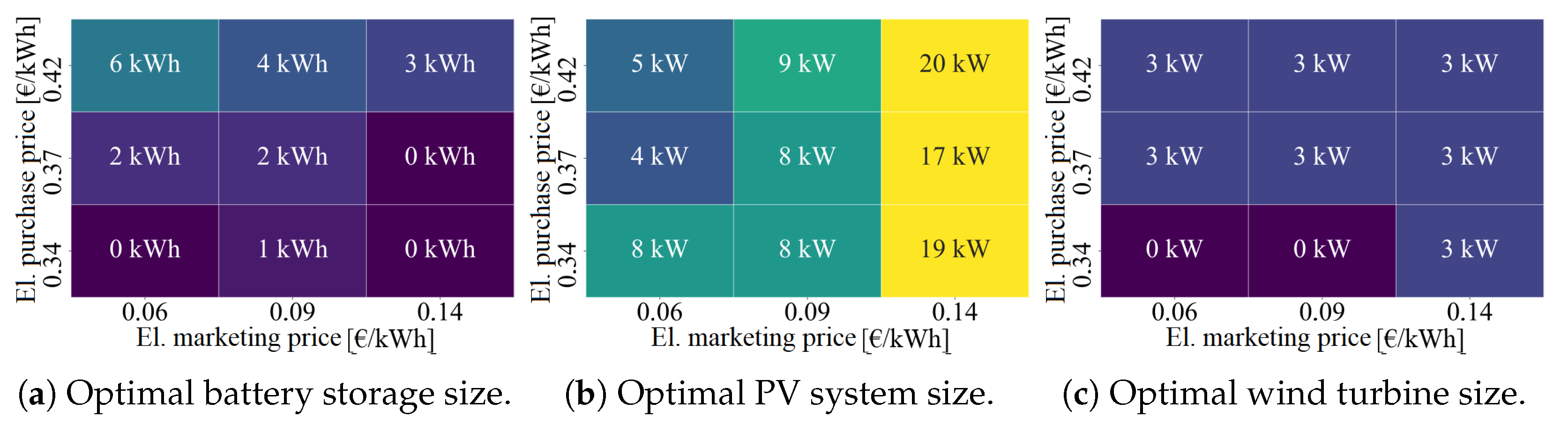
3.8. Potsdam, Germany
3.9. Stuttgart, Germany
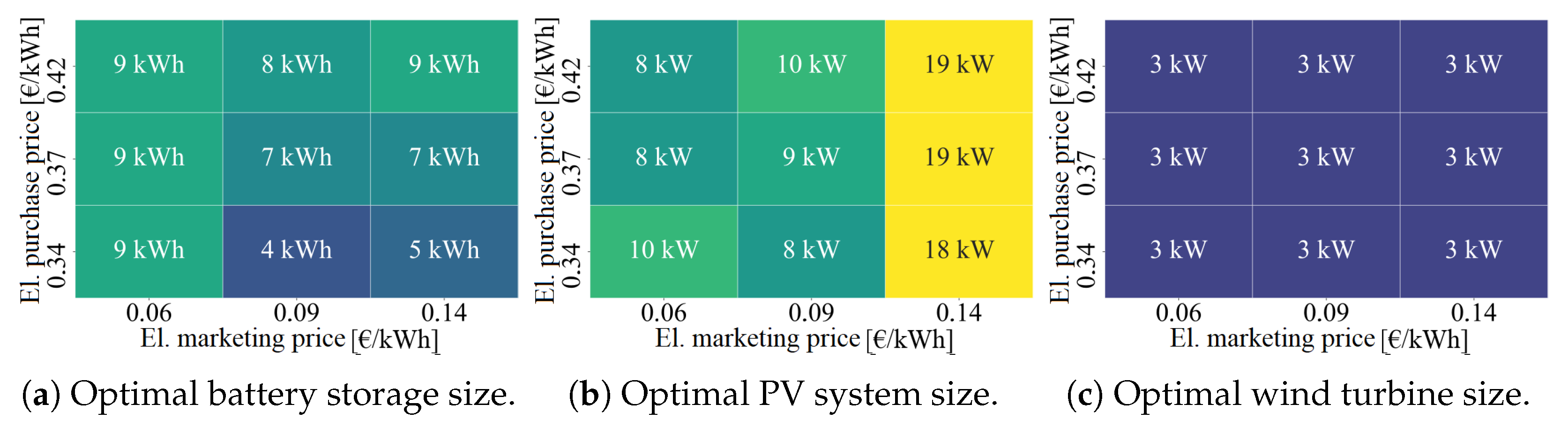
3.10. Wüstenrot, Germany
3.11. Montreal, Canada
4. Discussion
4.1. Current Framework Conditions
4.2. Future Framework Conditions
4.3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Battery Electric Vehicle | |
| Battery Capacity [kWh] | |
| Sum of electricity purchase or sale [€] | |
| Computational Fluid Dynamics | |
| Deutscher Wetterdienst (German Weather Service) | |
| Domestic Hot Water | |
| Evolutionary Algorithm | |
| Equivalent Annual Cost (economic evaluation) | |
| Environment and Climate Change Canada | |
| Genetic Algorithm | |
| Heat Pump | |
| Integrated Simulation Environment Language | |
| Estimated lifetime of the investment in years | |
| Operating and Maintenance Costs [€] | |
| P | Annualized Capital Cost [€] |
| Probability of crossover in genetic algorithms | |
| Electrical Power [kW] | |
| Probability of mutation in genetic algorithms | |
| Thermal Power [kW] | |
| Particle Swarm Optimization |
| Photovoltaic | |
| Present Value (for investment) [€] | |
| Amount of energy [kWh] | |
| Interest rate per period (e.g., annually) | |
| Renewable Energy | |
| Renewable Energy Source | |
| Simulated Annealing | |
| State of Charge | |
| Verein Deutscher Ingenieure (Association of German Engineers) | |
| Vehicle-to-Home |
Appendix A. Detailed Dimensioning Results
| Small Wind Turbine | |||
|---|---|---|---|
| System Size [kW] | Invest [EUR | Maintenance Cost | Life Span |
| 1 kW | 7254 | 3.0% | 20 years |
| 3 kW | 13,549 | ||
| 5 kW | 25,000 | ||
| 10 kW | 34,658 | ||
| 20 kW | 53,130 | ||
| PV system | |||
| System size [kW] | Invest [EUR | Maintenance cost | Life span |
| 4 | 6400 | 2.3% | 20 years |
| 6 | 9360 | ||
| 8 | 11,040 | ||
| 10 | 13,300 | ||
| 15 | 19,800 | ||
| 20 | 25,800 | ||
| Battery storage | |||
| System size [kW] | Invest [EUR | Maintenance cost | Life span |
| 0 | 1800 | 2.3% | 15 years |
| 5 | 5500 | ||
| 10 | 9000 | ||
| 15 | 12,000 | ||
| 20 | 15,000 | ||
| Heat pump | |||
| System size [kW] | Invest [EUR | Maintenance cost | Life span |
| 0 | 11,100 | 3.5% | 20 years |
| 4 | 11,100 | ||
| 10 | 12,500 | ||
| 15 | 14,500 | ||
| 20 | 16,000 | ||
| Thermal buffer storage | |||
| System size [Ł] | Invest [EUR | Maintenance cost | Life span |
| 200 | 1200 | 3.0% | 20 years |
| 500 | 1500 | ||
| 1000 | 2500 | ||
| 1500 | 2600 | ||
| 2000 | 2700 | ||
| 3000 | 3600 |
| Total Cost [EUR/a] | Energy Cost [EUR/a] | Invest./ Maintenance [EUR/a] | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | El. Marketing Price [EUR/kWh] | El. Purchase Price [EUR/kWh] |
|---|---|---|---|---|---|---|---|---|---|---|
| Investment Cost Reduction of Small Wind Turbine by 25%; Battery Storage by 25% | ||||||||||
| 6760 | 1669 | 5091 | 15 | 0.5 | 0.7 | 4 | 4 | 3 | 0.06 | 0.34 |
| 6805 | 1667 | 5138 | 15 | 0.5 | 0.7 | 4 | 5 | 3 | 0.06 | 0.37 |
| 6999 | 1372 | 5626 | 15 | 0.5 | 0.5 | 8 | 8 | 3 | 0.06 | 0.42 |
| 6643 | 1208 | 5435 | 15 | 0.9 | 0.6 | 2 | 9 | 3 | 0.09 | 0.34 |
| 6647 | 1161 | 5486 | 15 | 0.5 | 0.5 | 4 | 9 | 3 | 0.09 | 0.37 |
| 6868 | 1140 | 5728 | 15 | 0.5 | 0.5 | 8 | 9 | 3 | 0.09 | 0.42 |
| 6019 | −222 | 6241 | 15 | 0.5 | 0.5 | 0 | 19 | 3 | 0.14 | 0.34 |
| 6363 | −406 | 6768 | 15 | 0.5 | 0.5 | 2 | 18 | 4 | 0.14 | 0.37 |
| 6379 | −358 | 6737 | 15 | 0.5 | 0.5 | 6 | 19 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 25% | ||||||||||
| 6309 | 1708 | 4601 | 15 | 0.5 | 0.7 | 3 | 4 | 3 | 0.06 | 0.34 |
| 6558 | 1847 | 4710 | 15 | 0.5 | 0.5 | 5 | 3 | 3 | 0.06 | 0.37 |
| 6677 | 1324 | 5353 | 15 | 0.5 | 0.5 | 9 | 8 | 3 | 0.06 | 0.42 |
| 6301 | 1134 | 5167 | 15 | 0.8 | 0.5 | 4 | 8 | 3 | 0.09 | 0.34 |
| 6314 | 1259 | 5055 | 15 | 0.5 | 0.5 | 4 | 8 | 3 | 0.09 | 0.37 |
| 6548 | 1093 | 5455 | 15 | 0.5 | 0.5 | 9 | 9 | 3 | 0.09 | 0.42 |
| 5832 | −319 | 6150 | 15 | 0.6 | 0.7 | 0 | 20 | 3 | 0.14 | 0.34 |
| 5881 | −489 | 6371 | 15 | 0.6 | 0.7 | 3 | 20 | 3 | 0.14 | 0.37 |
| 6145 | −284 | 6430 | 15 | 0.8 | 0.7 | 4 | 19 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 25%; battery storage by 50% | ||||||||||
| 6513 | 1374 | 5140 | 15 | 0.5 | 0.7 | 7 | 5 | 3 | 0.06 | 0.34 |
| 6598 | 1486 | 5112 | 15 | 0.5 | 0.5 | 11 | 4 | 3 | 0.06 | 0.37 |
| 6863 | 1039 | 5824 | 15 | 0.5 | 0.8 | 12 | 10 | 3 | 0.06 | 0.42 |
| 6388 | 724 | 5664 | 15 | 0.5 | 0.5 | 12 | 9 | 3 | 0.09 | 0.34 |
| 6529 | 946 | 5584 | 15 | 0.6 | 0.7 | 8 | 9 | 3 | 0.09 | 0.37 |
| 6768 | 975 | 5793 | 15 | 0.8 | 0.7 | 13 | 9 | 3 | 0.09 | 0.42 |
| 5980 | −688 | 6668 | 15 | 0.8 | 0.5 | 7 | 19 | 3 | 0.14 | 0.34 |
| 6069 | −745 | 6813 | 15 | 0.8 | 0.5 | 8 | 20 | 3 | 0.14 | 0.37 |
| 6340 | −93 | 6433 | 15 | 0.5 | 0.7 | 8 | 16 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 50% | ||||||||||
| 6321 | 1486 | 4835 | 15 | 0.8 | 0.5 | 8 | 4 | 3 | 0.06 | 0.34 |
| 6260 | 1091 | 5169 | 15 | 0.5 | 0.5 | 10 | 8 | 3 | 0.06 | 0.37 |
| 6563 | 1360 | 5203 | 15 | 0.9 | 0.5 | 11 | 7 | 3 | 0.06 | 0.42 |
| 6107 | 880 | 5227 | 15 | 0.6 | 0.7 | 10 | 8 | 3 | 0.09 | 0.34 |
| 6135 | 1004 | 5131 | 15 | 0.5 | 0.5 | 9 | 8 | 3 | 0.09 | 0.37 |
| 6380 | 917 | 5463 | 15 | 0.6 | 0.7 | 11 | 10 | 3 | 0.09 | 0.42 |
| 5588 | −692 | 6280 | 15 | 0.5 | 0.5 | 7 | 19 | 3 | 0.14 | 0.34 |
| 5681 | −599 | 6280 | 15 | 0.5 | 0.5 | 7 | 19 | 3 | 0.14 | 0.37 |
| 5846 | −718 | 6564 | 15 | 0.5 | 0.5 | 12 | 20 | 3 | 0.14 | 0.42 |
| Total Cost [EUR/a] | Energy Cost [EUR/a] | Invest./ Maintenance [EUR/a] | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | El. Marketing Price [EUR/kWh] | El. Purchase Price [EUR/kWh] |
|---|---|---|---|---|---|---|---|---|---|---|
| Investment Cost Reduction of Small Wind Turbine by 25%; Battery Storage by 25% | ||||||||||
| 7812 | 4182 | 3631 | 15 | 0.5 | 0.6 | 0 | 4 | 0 | 0.06 | 0.34 |
| 8233 | 4106 | 4127 | 15 | 0.9 | 0.6 | 0 | 8 | 0 | 0.06 | 0.37 |
| 8720 | 4433 | 4287 | 15 | 0.5 | 0.7 | 2 | 8 | 0 | 0.06 | 0.42 |
| 7806 | 3596 | 4209 | 15 | 0.5 | 0.9 | 0 | 9 | 0 | 0.09 | 0.34 |
| 8104 | 3641 | 4463 | 15 | 0.5 | 0.7 | 3 | 9 | 0 | 0.09 | 0.37 |
| 8653 | 3359 | 5294 | 15 | 0.5 | 0.8 | 2 | 8 | 3 | 0.09 | 0.42 |
| 7454 | 2143 | 5311 | 15 | 0.5 | 0.8 | 0 | 19 | 0 | 0.14 | 0.34 |
| 7785 | 2221 | 5564 | 15 | 0.5 | 0.8 | 1 | 20 | 0 | 0.14 | 0.37 |
| 8265 | 1604 | 6661 | 15 | 0.5 | 0.6 | 3 | 20 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 25% | ||||||||||
| 7774 | 3075 | 4699 | 15 | 0.8 | 0.6 | 2 | 5 | 3 | 0.06 | 0.34 |
| 8005 | 3345 | 4659 | 15 | 0.7 | 0.8 | 3 | 4 | 3 | 0.06 | 0.37 |
| 8400 | 3665 | 4734 | 15 | 0.5 | 0.7 | 3 | 5 | 3 | 0.06 | 0.42 |
| 7648 | 2601 | 5047 | 15 | 0.6 | 0.6 | 2 | 9 | 3 | 0.09 | 0.34 |
| 7968 | 2843 | 5125 | 15 | 0.9 | 0.7 | 2 | 9 | 3 | 0.09 | 0.37 |
| 8305 | 3360 | 4945 | 15 | 0.5 | 0.7 | 2 | 8 | 3 | 0.09 | 0.42 |
| 7304 | 1353 | 5951 | 15 | 0.5 | 0.7 | 0 | 19 | 3 | 0.14 | 0.34 |
| 7508 | 1794 | 5715 | 15 | 0.5 | 0.6 | 0 | 17 | 3 | 0.14 | 0.37 |
| 8003 | 1613 | 6390 | 15 | 0.5 | 0.9 | 3 | 20 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 25%; battery storage by 50% | ||||||||||
| 7840 | 4025 | 3815 | 15 | 0.6 | 0.7 | 2 | 4 | 0 | 0.06 | 0.34 |
| 8062 | 3277 | 4785 | 15 | 0.5 | 0.7 | 11 | 10 | 0 | 0.06 | 0.37 |
| 8501 | 3703 | 4798 | 15 | 0.5 | 0.6 | 12 | 10 | 0 | 0.06 | 0.42 |
| 7768 | 3145 | 4623 | 15 | 0.6 | 0.7 | 6 | 10 | 0 | 0.09 | 0.34 |
| 7960 | 3339 | 4621 | 15 | 0.5 | 0.6 | 7 | 10 | 0 | 0.09 | 0.37 |
| 8469 | 2657 | 5812 | 15 | 0.6 | 0.8 | 11 | 10 | 3 | 0.09 | 0.42 |
| 7419 | 2109 | 5310 | 15 | 0.5 | 0.6 | 2 | 18 | 0 | 0.14 | 0.34 |
| 7746 | 1334 | 6412 | 15 | 0.5 | 0.6 | 7 | 17 | 3 | 0.14 | 0.37 |
| 8105 | 2224 | 5881 | 15 | 0.5 | 0.7 | 10 | 20 | 0 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 50% | ||||||||||
| 7597 | 3094 | 4503 | 15 | 0.5 | 0.7 | 3 | 4 | 3 | 0.06 | 0.34 |
| 7838 | 2611 | 5227 | 15 | 0.6 | 0.7 | 10 | 8 | 3 | 0.06 | 0.37 |
| 8152 | 2830 | 5322 | 15 | 0.5 | 0.6 | 11 | 9 | 3 | 0.06 | 0.42 |
| 7544 | 2448 | 5096 | 15 | 0.5 | 0.7 | 7 | 8 | 3 | 0.09 | 0.34 |
| 7761 | 2405 | 5356 | 15 | 0.7 | 0.6 | 8 | 10 | 3 | 0.09 | 0.37 |
| 8141 | 2659 | 5482 | 15 | 0.7 | 0.7 | 11 | 10 | 3 | 0.09 | 0.42 |
| 7291 | 1018 | 6273 | 15 | 0.5 | 0.8 | 3 | 20 | 3 | 0.14 | 0.34 |
| 7410 | 1036 | 6374 | 15 | 0.5 | 0.6 | 9 | 19 | 3 | 0.14 | 0.37 |
| 7777 | 1346 | 6431 | 15 | 0.5 | 0.7 | 10 | 19 | 3 | 0.14 | 0.42 |
| Total Cost [EUR/a] | Energy Cost [EUR/a] | Invest./ Maintenance [EUR/a] | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | El. Marketing Price [EUR/kWh] | El. Purchase Price [EUR/kWh] |
|---|---|---|---|---|---|---|---|---|---|---|
| Investment Cost Reduction of Small Wind Turbine by 25%; Battery Storage by 25% | ||||||||||
| 7457 | 3388 | 4069 | 15 | 0.5 | 0.7 | 0 | 8 | 0 | 0.06 | 0.34 |
| 7646 | 2770 | 4876 | 15 | 0.5 | 0.8 | 2 | 4 | 3 | 0.06 | 0.37 |
| 8034 | 2785 | 5248 | 15 | 0.5 | 0.6 | 6 | 5 | 3 | 0.06 | 0.42 |
| 7427 | 3175 | 4252 | 15 | 0.6 | 0.8 | 1 | 8 | 0 | 0.09 | 0.34 |
| 7508 | 2272 | 5236 | 15 | 0.5 | 0.5 | 2 | 8 | 3 | 0.09 | 0.37 |
| 7913 | 2407 | 5505 | 15 | 0.6 | 0.5 | 4 | 9 | 3 | 0.09 | 0.42 |
| 6872 | 631 | 6241 | 15 | 0.5 | 0.5 | 0 | 19 | 3 | 0.14 | 0.34 |
| 7081 | 1057 | 6024 | 15 | 0.5 | 0.5 | 0 | 17 | 3 | 0.14 | 0.37 |
| 7482 | 802 | 6680 | 15 | 0.5 | 0.7 | 3 | 20 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 25% | ||||||||||
| 7040 | 2552 | 4488 | 15 | 0.5 | 0.5 | 2 | 4 | 3 | 0.06 | 0.34 |
| 7352 | 2767 | 4585 | 15 | 0.5 | 1 | 2 | 4 | 3 | 0.06 | 0.37 |
| 7628 | 3140 | 4488 | 15 | 0.5 | 0.5 | 2 | 4 | 3 | 0.06 | 0.42 |
| 6979 | 2491 | 4488 | 15 | 0.5 | 0.5 | 2 | 4 | 3 | 0.09 | 0.34 |
| 7241 | 2585 | 4656 | 15 | 0.5 | 0.6 | 4 | 4 | 3 | 0.09 | 0.37 |
| 7580 | 2506 | 5074 | 15 | 0.6 | 0.5 | 4 | 8 | 3 | 0.09 | 0.42 |
| 6600 | 525 | 6075 | 15 | 0.5 | 0.6 | 1.0 | 19 | 3 | 0.14 | 0.34 |
| 6811 | 841 | 5970 | 15 | 0.5 | 0.8 | 0 | 19 | 3 | 0.14 | 0.37 |
| 7141 | 1100 | 6041 | 15 | 0.5 | 0.6 | 2 | 18 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 25%; battery storage by 50% | ||||||||||
| 7292 | 2324 | 4967 | 15 | 0.5 | 0.5 | 7 | 4 | 3 | 0.06 | 0.34 |
| 7467 | 2499 | 4967 | 15 | 0.5 | 0.5 | 7 | 4 | 3 | 0.06 | 0.37 |
| 7838 | 2395 | 5443 | 15 | 0.6 | 0.5 | 8 | 8 | 3 | 0.06 | 0.42 |
| 7255 | 1887 | 5368 | 15 | 0.5 | 0.6 | 6 | 8 | 3 | 0.09 | 0.34 |
| 7447 | 1781 | 5666 | 15 | 0.6 | 0.6 | 8 | 10 | 3 | 0.09 | 0.37 |
| 7751 | 2047 | 5703 | 15 | 0.6 | 0.6 | 9 | 10 | 3 | 0.09 | 0.42 |
| 6934 | 247 | 6687 | 15 | 0.8 | 0.6 | 7 | 19 | 3 | 0.14 | 0.34 |
| 6987 | 340 | 6647 | 15 | 0.5 | 0.5 | 8 | 19 | 3 | 0.14 | 0.37 |
| 7305 | 601 | 6703 | 15 | 0.6 | 0.5 | 9 | 19 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 50% | ||||||||||
| 7047 | 1711 | 5335 | 15 | 0.5 | 0.5 | 9 | 10 | 3 | 0.06 | 0.34 |
| 7225 | 2054 | 5170 | 15 | 0.7 | 0.5 | 9 | 8 | 3 | 0.06 | 0.37 |
| 7470 | 2338 | 5131 | 15 | 0.5 | 0.5 | 9 | 8 | 3 | 0.06 | 0.42 |
| 6932 | 1980 | 4952 | 15 | 0.6 | 0.5 | 4 | 8 | 3 | 0.09 | 0.34 |
| 7056 | 1897 | 5159 | 15 | 0.5 | 0.5 | 7 | 9 | 3 | 0.09 | 0.37 |
| 7364 | 2066 | 5298 | 15 | 0.5 | 0.5 | 8 | 10 | 3 | 0.09 | 0.42 |
| 6556 | 420 | 6136 | 15 | 0.5 | 0.7 | 5 | 18 | 3 | 0.14 | 0.34 |
| 6655 | 375 | 6280 | 15 | 0.5 | 0.5 | 7 | 19 | 3 | 0.14 | 0.37 |
| 7004 | 610 | 6394 | 15 | 0.6 | 0.6 | 9 | 19 | 3 | 0.14 | 0.42 |
| Total Cost [EUR/a] | Energy Cost [EUR/a] | Invest./ Maintenance [EUR/a] | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | El. Marketing Price [EUR/kWh] | El. Purchase Price [EUR/kWh] |
|---|---|---|---|---|---|---|---|---|---|---|
| Investment Cost Reduction of Small Wind Turbine by 25%; Battery Storage by 25% | ||||||||||
| 7349 | 3198 | 4151 | 15 | 0.5 | 0.6 | 0 | 9 | 0 | 0.06 | 0.34 |
| 7592 | 2169 | 5423 | 15 | 0.7 | 0.5 | 4 | 8 | 3 | 0.06 | 0.37 |
| 7932 | 2221 | 5711 | 15 | 0.6 | 0.6 | 7 | 9 | 3 | 0.06 | 0.42 |
| 7207 | 2954 | 4253 | 15 | 0.6 | 0.5 | 0 | 10 | 0 | 0.09 | 0.34 |
| 7419 | 2109 | 5310 | 15 | 0.5 | 0.5 | 3 | 8 | 3 | 0.09 | 0.37 |
| 7769 | 1975 | 5793 | 15 | 0.5 | 0.6 | 7 | 10 | 3 | 0.09 | 0.42 |
| 6705 | 1413 | 5292 | 15 | 0.7 | 0.5 | 0 | 19 | 0 | 0.14 | 0.34 |
| 6941 | 1776 | 5164 | 15 | 0.6 | 0.5 | 0 | 18 | 0 | 0.14 | 0.37 |
| 7335 | 541 | 6793 | 15 | 0.8 | 0.6 | 4 | 20 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 25% | ||||||||||
| 7035 | 2266 | 4770 | 15 | 0.5 | 0.5 | 4 | 5 | 3 | 0.06 | 0.34 |
| 7226 | 2511 | 4715 | 15 | 0.6 | 0.5 | 3 | 5 | 3 | 0.06 | 0.37 |
| 7533 | 2349 | 5185 | 15 | 0.5 | 0.5 | 6 | 8 | 3 | 0.06 | 0.42 |
| 6944 | 1740 | 5204 | 15 | 0.6 | 0.5 | 3 | 10 | 3 | 0.09 | 0.34 |
| 7086 | 2179 | 4907 | 15 | 0.5 | 0.5 | 2 | 8 | 3 | 0.09 | 0.37 |
| 7436 | 2028 | 5408 | 15 | 0.5 | 0.6 | 6 | 10 | 3 | 0.09 | 0.42 |
| 6597 | 352 | 6245 | 15 | 0.5 | 0.6 | 1 | 18 | 4 | 0.14 | 0.34 |
| 6596 | 556 | 6039 | 15 | 0.5 | 0.6 | 0 | 20 | 3 | 0.14 | 0.37 |
| 6971 | 694 | 6277 | 15 | 0.6 | 0.6 | 2 | 20 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 25%; battery storage by 50% | ||||||||||
| 7225 | 2594 | 4632 | 15 | 0.5 | 0.6 | 10 | 9 | 0 | 0.06 | 0.34 |
| 7405 | 2659 | 4746 | 15 | 0.5 | 0.5 | 11 | 10 | 0 | 0.06 | 0.37 |
| 7668 | 2245 | 5423 | 15 | 0.5 | 0.5 | 8 | 8 | 3 | 0.06 | 0.42 |
| 7127 | 2468 | 4659 | 15 | 0.5 | 0.6 | 8 | 10 | 0 | 0.09 | 0.34 |
| 7352 | 1713 | 5639 | 15 | 0.6 | 0.6 | 10 | 9 | 3 | 0.09 | 0.37 |
| 7644 | 1735 | 5910 | 15 | 0.8 | 0.5 | 11 | 11 | 3 | 0.09 | 0.42 |
| 6667 | 918 | 5749 | 15 | 0.6 | 0.5 | 7 | 20 | 0 | 0.14 | 0.34 |
| 6822 | 228 | 6593 | 15 | 0.5 | 0.5 | 4 | 20 | 3 | 0.14 | 0.37 |
| 7072 | 279 | 6792 | 15 | 0.5 | 0.5 | 9 | 20 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 50% | ||||||||||
| 6898 | 1804 | 5094 | 15 | 0.5 | 0.5 | 8 | 8 | 3 | 0.06 | 0.34 |
| 7073 | 1997 | 5076 | 15 | 0.6 | 0.5 | 7 | 8 | 3 | 0.06 | 0.37 |
| 7364 | 2176 | 5188 | 15 | 0.5 | 0.6 | 10 | 8 | 3 | 0.06 | 0.42 |
| 6813 | 1627 | 5186 | 15 | 0.5 | 0.5 | 5 | 10 | 3 | 0.09 | 0.34 |
| 6946 | 1685 | 5261 | 15 | 0.5 | 0.5 | 7 | 10 | 3 | 0.09 | 0.37 |
| 7257 | 1785 | 5472 | 15 | 0.5 | 0.6 | 9 | 11 | 3 | 0.09 | 0.42 |
| 6345 | 189 | 6156 | 15 | 0.5 | 0.5 | 4 | 19 | 3 | 0.14 | 0.34 |
| 6491 | 178 | 6314 | 15 | 0.5 | 0.5 | 5 | 20 | 3 | 0.14 | 0.37 |
| 6770 | 434 | 6337 | 15 | 0.6 | 0.5 | 8 | 19 | 3 | 0.14 | 0.42 |
| Total Cost [EUR/a] | Energy Cost [EUR/a] | Invest./ Maintenance [EUR/a] | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | El. Marketing Price [EUR/kWh] | El. Purchase Price [EUR/kWh] |
|---|---|---|---|---|---|---|---|---|---|---|
| Investment Cost Reduction of Small wind Turbine by 25%; Battery Storage by 25% | ||||||||||
| 6810 | 2386 | 4424 | 15 | 0.5 | 0.5 | 3 | 9 | 0 | 0.06 | 0.34 |
| 6992 | 2262 | 4730 | 15 | 0.5 | 0.5 | 6 | 10 | 0 | 0.06 | 0.37 |
| 7346 | 2255 | 5091 | 15 | 0.6 | 0.5 | 10 | 11 | 0 | 0.06 | 0.42 |
| 6728 | 1830 | 4897 | 15 | 0.6 | 0.5 | 3 | 13 | 0 | 0.09 | 0.34 |
| 6851 | 1314 | 5537 | 15 | 0.5 | 0.5 | 8 | 16 | 0 | 0.09 | 0.37 |
| 7176 | 1096 | 6080 | 15 | 0.5 | 0.8 | 11 | 19 | 0 | 0.09 | 0.42 |
| 5970 | 570 | 5400 | 15 | 0.6 | 0.6 | 0 | 20 | 0 | 0.14 | 0.34 |
| 6260 | 474 | 5786 | 15 | 0.8 | 0.6 | 3 | 20 | 0 | 0.14 | 0.37 |
| 6493 | 411 | 6082 | 15 | 0.5 | 0.5 | 10 | 20 | 0 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 25% | ||||||||||
| 6818 | 2542 | 4276 | 15 | 0.5 | 0.5 | 1 | 9 | 0 | 0.06 | 0.34 |
| 6990 | 2030 | 4959 | 15 | 0.5 | 0.5 | 8 | 11 | 0 | 0.06 | 0.37 |
| 7304 | 2067 | 5237 | 15 | 0.5 | 0.5 | 11 | 12 | 0 | 0.06 | 0.42 |
| 6710 | 2437 | 4273 | 15 | 0.6 | 0.6 | 0 | 10 | 0 | 0.09 | 0.34 |
| 6898 | 1511 | 5387 | 15 | 0.6 | 0.5 | 9 | 14 | 0 | 0.09 | 0.37 |
| 7171 | 1062 | 6109 | 15 | 0.5 | 0.7 | 12 | 19 | 0 | 0.09 | 0.42 |
| 5912 | 550 | 5361 | 15 | 0.5 | 0.5 | 0 | 20 | 0 | 0.14 | 0.34 |
| 6175 | 775 | 5400 | 15 | 0.7 | 0.5 | 0 | 20 | 0 | 0.14 | 0.37 |
| 6509 | 464 | 6045 | 15 | 0.5 | 0.6 | 9 | 20 | 0 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 25%; battery storage by 50% | ||||||||||
| 6620 | 1854 | 4766 | 15 | 0.5 | 0.6 | 11 | 10 | 0 | 0.06 | 0.34 |
| 6802 | 1965 | 4836 | 15 | 0.5 | 0.8 | 12 | 10 | 0 | 0.06 | 0.37 |
| 7074 | 1927 | 5148 | 15 | 0.5 | 0.7 | 15 | 12 | 0 | 0.06 | 0.42 |
| 6476 | 646 | 5830 | 15 | 0.5 | 0.5 | 13 | 19 | 0 | 0.09 | 0.34 |
| 6637 | 756 | 5881 | 15 | 0.6 | 0.5 | 14 | 19 | 0 | 0.09 | 0.37 |
| 6842 | 744 | 6098 | 15 | 0.5 | 0.5 | 18 | 20 | 0 | 0.09 | 0.42 |
| 6028 | 164 | 5865 | 15 | 1.1 | 0.5 | 11 | 19 | 0 | 0.14 | 0.34 |
| 5987 | 113 | 5874 | 15 | 0.5 | 0.5 | 11 | 20 | 0 | 0.14 | 0.37 |
| 6239 | 365 | 5874 | 15 | 0.5 | 0.5 | 11 | 20 | 0 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 50% | ||||||||||
| 6593 | 1815 | 4778 | 15 | 0.5 | 0.5 | 12 | 10 | 0 | 0.06 | 0.34 |
| 6752 | 1707 | 5045 | 15 | 0.5 | 0.5 | 13 | 12 | 0 | 0.06 | 0.37 |
| 7025 | 1949 | 5077 | 15 | 0.5 | 0.5 | 14 | 12 | 0 | 0.06 | 0.42 |
| 6488 | 863 | 5625 | 15 | 0.5 | 0.5 | 10 | 18 | 0 | 0.09 | 0.34 |
| 6601 | 599 | 6002 | 15 | 0.5 | 0.5 | 15 | 20 | 0 | 0.09 | 0.37 |
| 6835 | 769 | 6066 | 15 | 0.5 | 0.5 | 17 | 20 | 0 | 0.09 | 0.42 |
| 5861 | −13 | 5874 | 15 | 0.5 | 0.5 | 11 | 20 | 0 | 0.14 | 0.34 |
| 5987 | 113 | 5874 | 15 | 0.5 | 0.5 | 11 | 20 | 0 | 0.14 | 0.37 |
| 6248 | 259 | 5989 | 15 | 0.5 | 0.6 | 14 | 20 | 0 | 0.14 | 0.42 |
| Total Cost [EUR/a] | Energy Cost [EUR/a] | Invest./ Maintenance [EUR/a] | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | El. Marketing Price [EUR/kWh] | El. Purchase Price [EUR/kWh] |
|---|---|---|---|---|---|---|---|---|---|---|
| Investment Cost Reduction of Small Wind Turbine by 25%; Battery Storage by 25% | ||||||||||
| 7606 | 3355 | 4252 | 15 | 0.7 | 0.7 | 1 | 8 | 0 | 0.06 | 0.34 |
| 7931 | 3621 | 4310 | 15 | 0.8 | 0.9 | 1 | 8 | 0 | 0.06 | 0.37 |
| 8333 | 3898 | 4435 | 15 | 0.6 | 0.6 | 4 | 8 | 0 | 0.06 | 0.42 |
| 7369 | 3135 | 4234 | 15 | 0.5 | 0.5 | 0 | 10 | 0 | 0.09 | 0.34 |
| 7707 | 3396 | 4311 | 15 | 0.5 | 0.9 | 0 | 10 | 0 | 0.09 | 0.37 |
| 8251 | 3917 | 4334 | 15 | 0.6 | 0.7 | 1 | 9 | 0 | 0.09 | 0.42 |
| 7038 | 1494 | 5544 | 15 | 0.6 | 0.6 | 1 | 20 | 0 | 0.14 | 0.34 |
| 7174 | 1813 | 5361 | 15 | 0.5 | 0.5 | 0 | 20 | 0 | 0.14 | 0.37 |
| 7685 | 2432 | 5253 | 15 | 0.5 | 0.5 | 0 | 19 | 0 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 25% | ||||||||||
| 7455 | 3844 | 3611 | 15 | 0.5 | 0.5 | 0 | 4 | 0 | 0.06 | 0.34 |
| 7778 | 3428 | 4350 | 15 | 0.5 | 0.5 | 2 | 9 | 0 | 0.06 | 0.37 |
| 8304 | 3498 | 4806 | 15 | 0.6 | 0.5 | 7 | 10 | 0 | 0.06 | 0.42 |
| 7476 | 2986 | 4491 | 15 | 0.7 | 0.5 | 2 | 10 | 0 | 0.09 | 0.34 |
| 7680 | 3283 | 4397 | 15 | 0.5 | 0.6 | 1 | 10 | 0 | 0.09 | 0.37 |
| 8258 | 3947 | 4311 | 15 | 0.6 | 0.8 | 0 | 10 | 0 | 0.09 | 0.42 |
| 6962 | 1798 | 5164 | 15 | 0.6 | 0.5 | 0 | 18 | 0 | 0.14 | 0.34 |
| 7195 | 1922 | 5273 | 15 | 0.5 | 0.6 | 0 | 19 | 0 | 0.14 | 0.37 |
| 7698 | 2426 | 5273 | 15 | 0.5 | 0.6 | 0 | 19 | 0 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 25%; battery storage by 50% | ||||||||||
| 7390 | 2746 | 4644 | 15 | 0.5 | 0.5 | 11 | 9 | 0 | 0.06 | 0.34 |
| 7632 | 3071 | 4562 | 15 | 0.5 | 0.6 | 11 | 8 | 0 | 0.06 | 0.37 |
| 8060 | 3160 | 4901 | 15 | 0.5 | 0.8 | 14 | 10 | 0 | 0.06 | 0.42 |
| 7349 | 2520 | 4830 | 15 | 0.6 | 0.5 | 13 | 10 | 0 | 0.09 | 0.34 |
| 7542 | 2713 | 4830 | 15 | 0.5 | 0.6 | 13 | 10 | 0 | 0.09 | 0.37 |
| 7922 | 2995 | 4927 | 15 | 0.5 | 0.5 | 13 | 11 | 0 | 0.09 | 0.42 |
| 6981 | 1689 | 5292 | 15 | 0.7 | 0.5 | 0 | 19 | 0 | 0.14 | 0.34 |
| 7169 | 1363 | 5806 | 15 | 0.5 | 0.7 | 8 | 20 | 0 | 0.14 | 0.37 |
| 7517 | 1559 | 5957 | 15 | 0.5 | 0.6 | 13 | 20 | 0 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 50% | ||||||||||
| 7394 | 2782 | 4612 | 15 | 0.5 | 0.5 | 10 | 9 | 0 | 0.06 | 0.34 |
| 7682 | 2883 | 4799 | 15 | 0.6 | 0.7 | 14 | 9 | 0 | 0.06 | 0.37 |
| 8035 | 3142 | 4894 | 15 | 0.6 | 0.5 | 15 | 10 | 0 | 0.06 | 0.42 |
| 7371 | 2618 | 4753 | 15 | 0.7 | 0.5 | 10 | 10 | 0 | 0.09 | 0.34 |
| 7519 | 2741 | 4778 | 15 | 0.5 | 0.5 | 12 | 10 | 0 | 0.09 | 0.37 |
| 7973 | 3188 | 4785 | 15 | 0.5 | 0.7 | 11 | 10 | 0 | 0.09 | 0.42 |
| 7045 | 1435 | 5610 | 15 | 0.5 | 1.3 | 2 | 20 | 0 | 0.14 | 0.34 |
| 7142 | 1376 | 5766 | 15 | 0.5 | 0.5 | 11 | 19 | 0 | 0.14 | 0.37 |
| 7504 | 1630 | 5874 | 15 | 0.5 | 0.5 | 11 | 20 | 0 | 0.14 | 0.42 |
| Total Cost [EUR/a] | Energy Cost [EUR/a] | Invest./ Maintenance [EUR/a] | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | El. Marketing Price [EUR/kWh] | El. Purchase Price [EUR/kWh] |
|---|---|---|---|---|---|---|---|---|---|---|
| Investment Cost Reduction of Small Wind Turbine by 25%; Battery Storage by 25% | ||||||||||
| 7851 | 2493 | 5357 | 15 | 0.6 | 0.5 | 2 | 9 | 3 | 0.06 | 0.34 |
| 8015 | 2222 | 5793 | 15 | 0.5 | 0.6 | 7 | 10 | 3 | 0.06 | 0.37 |
| 8317 | 2430 | 5886 | 15 | 0.5 | 0.5 | 9 | 10 | 3 | 0.06 | 0.42 |
| 7577 | 1829 | 5748 | 15 | 0.5 | 0.5 | 3 | 12 | 3 | 0.09 | 0.34 |
| 7830 | 1342 | 6488 | 15 | 0.6 | 0.5 | 7 | 16 | 3 | 0.09 | 0.37 |
| 8103 | 1310 | 6793 | 15 | 0.5 | 0.5 | 11 | 17 | 3 | 0.09 | 0.42 |
| 6811 | 531 | 6280 | 15 | 0.5 | 0.7 | 0 | 19 | 3 | 0.14 | 0.34 |
| 7081 | 564 | 6518 | 15 | 0.6 | 0.7 | 2 | 19 | 3 | 0.14 | 0.37 |
| 7499 | 556 | 6943 | 15 | 0.8 | 0.7 | 6 | 20 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 25% | ||||||||||
| 7502 | 2298 | 5204 | 15 | 0.5 | 0.6 | 3 | 10 | 3 | 0.06 | 0.34 |
| 7703 | 2295 | 5408 | 15 | 0.6 | 0.5 | 6 | 10 | 3 | 0.06 | 0.37 |
| 8001 | 2175 | 5826 | 15 | 0.5 | 0.5 | 12 | 11 | 3 | 0.06 | 0.42 |
| 7253 | 1791 | 5462 | 15 | 0.5 | 0.5 | 2 | 13 | 3 | 0.09 | 0.34 |
| 7544 | 1689 | 5855 | 15 | 0.8 | 0.5 | 7 | 13 | 3 | 0.09 | 0.37 |
| 7841 | 1427 | 6414 | 15 | 0.5 | 0.8 | 11 | 16 | 3 | 0.09 | 0.42 |
| 6431 | 411 | 6020 | 15 | 0.5 | 0.5 | 0 | 20 | 3 | 0.14 | 0.34 |
| 6660 | 348 | 6312 | 15 | 0.5 | 0.5 | 3 | 20 | 3 | 0.14 | 0.37 |
| 7342 | 685 | 6657 | 16 | 0.5 | 0.5 | 6 | 19 | 3 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 25%; battery storage by 50% | ||||||||||
| 7621 | 1804 | 5818 | 15 | 0.6 | 0.5 | 13 | 10 | 3 | 0.06 | 0.34 |
| 7874 | 1861 | 6013 | 15 | 0.9 | 0.6 | 13 | 11 | 3 | 0.06 | 0.37 |
| 8141 | 2285 | 5856 | 15 | 0.6 | 0.7 | 13 | 10 | 3 | 0.06 | 0.42 |
| 7439 | 1153 | 6287 | 15 | 0.6 | 0.5 | 13 | 14 | 3 | 0.09 | 0.34 |
| 7539 | 982 | 6557 | 15 | 0.5 | 0.5 | 15 | 16 | 3 | 0.09 | 0.37 |
| 7813 | 1116 | 6697 | 15 | 0.5 | 0.5 | 16 | 17 | 3 | 0.09 | 0.42 |
| 6688 | −67 | 6755 | 15 | 0.5 | 0.5 | 8 | 20 | 3 | 0.14 | 0.34 |
| 6885 | −16 | 6901 | 15 | 0.5 | 0.7 | 11 | 20 | 3 | 0.14 | 0.37 |
| 8733 | 632 | 8101 | 18 | 0.5 | 0.6 | 6 | 17 | 7 | 0.14 | 0.42 |
| Investment cost reduction of small wind turbine by 50%; battery storage by 50% | ||||||||||
| 7242 | 1805 | 5437 | 15 | 0.5 | 0.5 | 12 | 10 | 3 | 0.06 | 0.34 |
| 7453 | 2034 | 5418 | 15 | 0.5 | 0.6 | 14 | 9 | 3 | 0.06 | 0.37 |
| 7713 | 2063 | 5650 | 15 | 0.5 | 0.5 | 15 | 11 | 3 | 0.06 | 0.42 |
| 7063 | 1275 | 5789 | 15 | 0.5 | 0.5 | 12 | 13 | 3 | 0.09 | 0.34 |
| 7216 | 1117 | 6099 | 15 | 0.5 | 0.5 | 11 | 16 | 3 | 0.09 | 0.37 |
| 7528 | 1141 | 6387 | 15 | 0.5 | 0.6 | 16 | 17 | 3 | 0.09 | 0.42 |
| 6397 | −10 | 6408 | 15 | 0.5 | 0.6 | 7 | 20 | 3 | 0.14 | 0.34 |
| 6511 | −21 | 6532 | 15 | 0.5 | 0.5 | 11 | 20 | 3 | 0.14 | 0.37 |
| 6803 | 251 | 6552 | 15 | 0.5 | 0.5 | 15 | 19 | 3 | 0.14 | 0.42 |
References
- Statistisches Bundesamt. Stromerzeugung 2022, 2023. Available online: https://www.destatis.de/DE/Presse/Pressemitteilungen/2023/03/PD23_090_43312.html (accessed on 27 June 2023).
- Bundesverband für WindEnergie BWE, e.V. Windenergie in Deutschland—Zahlen und Fakten. 2020. Available online: https://www.wind-energie.de/themen/zahlen-und-fakten/deutschland/ (accessed on 15 November 2023).
- Gehling, M. Installierte Leistung, Stromerzeugung und Marktentwicklung von Kleinwindanlagen in Deutschland; Technical Report; Ingenieurbüro für Erneuerbare Energien: Leipzig, Germany, 2019. [Google Scholar]
- Wagh, S.; Walke, T. Review on Wind-Solar Hybrid Power System. Int. J. Res. Sci. Eng. 2017, 3, 71–76. [Google Scholar]
- Acatech. Wie kann der Ausbau von Photovoltaik und Windenergie Beschleunigt Werden? Stellungnahme; Technical Report; Leopoldina Akademienunion: Schweinfurt, Germany, 2022. [Google Scholar]
- Brennenstuhl, M.; Lust, D.; Boch, P.; Yadack, M.; Eicker, U. The Potential of Small Wind Turbine Integration in Residential Buildings Complementing PV and Heat Pump Operation. ISEC Conf. Proc. Renew. Heat. Cool. Integr. Urban Ind. Energy Syst. 2018, 1, 331–339. [Google Scholar]
- Absatzzahlen und Marktanteile; Bundesverband WWärmepumpe (BWP) e. V.: Berlin, Germany, 2023.
- Anteil der Elektroautos am Bestand der Personenkraftwagen in Deutschland von 2018 bis 2020 und Prognose bis 2030; Statista GmbH: Hamburg, Germany, 2022.
- Ahmed, N.A.; Miyatake, M.; Al-Othman, A.K. Power fluctuations suppression of stand-alone hybrid generation combining solar photovoltaic/wind turbine and fuel cell systems. Energy Convers. Manag. 2008, 49, 2711–2719. [Google Scholar] [CrossRef]
- Mohammadi, S.; Soleymani, S.; Mozafari, B. Scenario-based stochastic operation management of MicroGrid including Wind, Photovoltaic, Micro-Turbine, Fuel Cell and Energy Storage Devices. Int. J. Electr. Power Energy Syst. 2014, 54, 525–535. [Google Scholar] [CrossRef]
- Niknam, T.; Golestaneh, F.; Shafiei, M. Probabilistic energy management of a renewable microgrid with hydrogen storage using self-adaptive charge search algorithm. Energy 2013, 49, 252–267. [Google Scholar] [CrossRef]
- Sichilalu, S.; Tazvinga, H.; Xia, X. Optimal control of a fuel cell/wind/PV/grid hybrid system with thermal heat pump load. Sol. Energy 2016, 135, 59–69. [Google Scholar] [CrossRef]
- Kaabeche, A.; Belhamel, M.; Ibtiouen, R. Techno-economic valuation and optimization of integrated photovoltaic/wind energy conversion system. Sol. Energy 2011, 85, 2407–2420. [Google Scholar] [CrossRef]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M.; Fadali, M.S.; Baghzouz, Y. Genetic-algorithm-based optimization approach for energy management. IEEE Trans. Power Deliv. 2013, 28, 162–170. [Google Scholar] [CrossRef]
- Mazzeo, D.; Matera, N.; De Luca, P.; Baglivo, C.; Congedo, P.M.; Oliveti, G. A literature review and statistical analysis of photovoltaic-wind hybrid renewable system research by considering the most relevant 550 articles: An upgradable matrix literature database. J. Clean. Prod. 2021, 295, 126070. [Google Scholar] [CrossRef]
- Grieser, B.; Sunak, Y.; Madlener, R. Economics of small wind turbines in urban settings: An empirical investigation for Germany. Renew. Energy 2015, 78, 334–350. [Google Scholar] [CrossRef]
- Rieck, J.; Taube, L.; Behrendt, F. Feasibility analysis of a heat pump powered by wind turbines and PV-Applications for detached houses in Germany. Renew. Energy 2020, 162, 1104–1112. [Google Scholar] [CrossRef]
- Weida, S.; Kumar, S.; Madlener, R. Financial viability of grid-connected solar PV and wind power systems in Germany. Energy Procedia 2016, 106, 35–45. [Google Scholar] [CrossRef]
- Weiler, V.; Lust, D.; Brennenstuhl, M.; Brassel, K.H.; Duminil, E.; Eicker, U. Automatic dimensioning of energy system components for building cluster simulation. Appl. Energy 2022, 313, 118651. [Google Scholar] [CrossRef]
- Mayer, M.J.; Szilágyi, A.; Gróf, G. Environmental and economic multi-objective optimization of a household level hybrid renewable energy system by genetic algorithm. Appl. Energy 2020, 269, 115058. [Google Scholar] [CrossRef]
- Ko, M.J.; Kim, Y.S.; Chung, M.H.; Jeon, H.C. Multi-objective optimization design for a hybrid energy system using the genetic algorithm. Energies 2015, 8, 2924–2949. [Google Scholar] [CrossRef]
- Koutroulis, E.; Kolokotsa, D.; Potirakis, A.; Kalaitzakis, K. Methodology for optimal sizing of stand-alone photovoltaic/wind-generator systems using genetic algorithms. Sol. Energy 2006, 80, 1072–1088. [Google Scholar] [CrossRef]
- Zhang, Y.; Lundblad, A.; Campana, P.E.; Yan, J. Comparative Study of Battery Storage and Hydrogen Storage to Increase Photovoltaic Self-sufficiency in a Residential Building of Sweden. Energy Procedia 2016, 103, 268–273. [Google Scholar] [CrossRef]
- Bee, E.; Prada, A.; Baggio, P. Optimization of Air Source Heat Pump Systems over the Heating Season through the Use of Renewable Energy Sources. In Proceedings of the International High Performance Buildings Conference Proceedings, West Lafayette, IN, USA, 11–14 July 2016. [Google Scholar]
- Bernal-Agustín, J.L.; Dufo-López, R. Efficient design of hybrid renewable energy systems using evolutionary algorithms. Energy Convers. Manag. 2009, 50, 479–489. [Google Scholar] [CrossRef]
- Xu, X.; Hu, W.; Cao, D.; Huang, Q.; Chen, C.; Chen, Z. Optimized sizing of a standalone PV-wind-hydropower station with pumped-storage installation hybrid energy system. Renew. Energy 2020, 147, 1418–1431. [Google Scholar] [CrossRef]
- Brennenstuhl, M.; Lust, D.; Pietruschka, D.; Schneider, D. Demand Side Management Based Power-to-Heat and Power-to-Gas Optimization Strategies for PV and Wind Self-Consumption in a Residential Building Cluster. Energies 2021, 14, 6712. [Google Scholar] [CrossRef]
- Rosa, M.D.; Brennenstuhl, M.; Cabrera, C.A.; Eicker, U.; Finn, D.P. An Iterative Methodology for Model Complexity Reduction in Residential Building Simulation. Energies 2019, 12, 2448. [Google Scholar] [CrossRef]
- Brennenstuhl, M.; Zeh, R.; Otto, R.; Pesch, R.; Stockinger, V.; Pietruschka, D. Report on a Plus-Energy District with Low- Temperature DHC Network, Novel Agrothermal Heat Source, and Applied Demand Response. Appl. Sci. 2019, 9, 5059. [Google Scholar] [CrossRef]
- Krien, U.; Schönfeldt, P.; Launer, J.; Hilpert, S.; Kaldemeyer, C.; Pleßmann, G. oemof.solph—A model generator for linear and mixed-integer linear optimisation of energy systems. Softw. Impacts 2020, 6, 100028. [Google Scholar] [CrossRef]
- Emmi, G.; Zarrella, A.; De Carli, M.; Galgaro, A. Solar assisted ground source heat pump in cold climates. Energy Procedia 2015, 82, 623–629. [Google Scholar] [CrossRef]
- Government of Canada. Residential Space Heating System Stock Share. 2021. Available online: https://oee.nrcan.gc.ca/corporate/statistics/neud/dpa/showTable.cfm?type=HB§or=res&juris=00&rn=13&year=2021&page=0#sources (accessed on 16 March 2025).
- DWD. Windkarten zur Mittleren Windgeschwindigkeit. 2024. Available online: https://www.dwd.de/DE/leistungen/windkarten/ (accessed on 22 November 2024).
- Deutsches Institut für Normung e.V. DIN EN 12831 Energetische Bewertung von Gebäuden—Verfahren zur Berechnung der Norm-Heizlast; Technical Report; DIN: Berlin, Germany, 2017. [Google Scholar]
- CEC. Climate Zones of North America. Available online: https://www.cec.org/mapmonday/climate-zones-in-north-america/ (accessed on 12 December 2024).
- DWD. Open-Data-Server des Deutschen Wetterdienstes. 2022. Available online: https://opendata.dwd.de/ (accessed on 22 October 2022).
- Brennenstuhl, M.; Harbola, S.; Koukofikis, A.; Padsala, R.; Schaaf, M.; Coors, V.; Voss, U. CFD Simulation and Visualization Based Investigation of Small Wind Turbine Potential: A Case Study “Neuer Stöckach” for Stuttgart. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 8, 17–24. [Google Scholar] [CrossRef]
- ECCC. Data Download for Montréal. 2022. Available online: https://montreal.weatherstats.ca/ (accessed on 22 January 2025).
- Jüttemann, P. Kleinwind-Marktreport Ausgabe 2020, 6th ed.; Patrick Jüttemann: Bad Honnef, Germany, 2019. [Google Scholar]
- Verein Deutscher Ingenieure. VDI 2067—Economic Efficiency of Building Installations: Fundamentals and Economic Calculation; Technical Report; Verein Deutscher Ingenieure e.V.: Harzgerode, Germany, 2012. [Google Scholar]
- Strom-Report. Strompreisentwicklung—Strompreise sinken 2023 wieder, 2023. Available online: https://strom-report.com/strompreise/strompreisentwicklung/ (accessed on 23 May 2023).
- Buttelmann, M.; Lohmann, B. Optimierung mit Genetischen Algorithmen und eine Anwendung zur Modellreduktion. At-Autom. 2004, 52, 151–163. [Google Scholar] [CrossRef]
- Kleine Büning, H.; Kramer, O.; Ting, C.; Aslan, D. Genetische Algorithmen; Technical Report; Universität Paderborn: Paderborn, Germany, 2007. [Google Scholar]
- Bundesministerium für Digitales und Verkehr. Deutsches Mobilitätspanel (MOP). 2021. Available online: https://bmdv.bund.de/SharedDocs/DE/Artikel/G/deutsches-mobilitaetspanel.html (accessed on 16 March 2023).
- Brennenstuhl, M.; Otto, R.; Elangovan, P.K.; Eicker, U. The Potential of Vehicle-to-Home Integration for Residential Prosumers: A Case Study. Smart Grids Sustain. Energy 2024, 9, 25. [Google Scholar] [CrossRef]
- Lehtola, T.A.; Zahedi, A. Electric Vehicle Battery Cell Cycle Aging in Vehicle to Grid Operations: A Review. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 423–437. [Google Scholar] [CrossRef]
- Rodrigues, A.; Machado, D.; Dentinho, T. Electrical Energy Storage Systems Feasibility; the Case of Terceira Island. Sustainability 2017, 9, 1276. [Google Scholar] [CrossRef]
- Fraunhofer ISE. Photovoltaics Report; Fraunhofer ISE: Freiburg, Germany, 2024. [Google Scholar]
- DNV. Energy Transition Outlook 2024: A Global and Regional Forecast to 2050; Technical Report; DNV: Bærum, Norway, 2024. [Google Scholar]
- Orangi, S.; Manjong, N.; Clos, D.P.; Usai, L.; Burheim, O.S.; Strømman, A.H. Historical and prospective lithium-ion battery cost trajectories from a bottom-up production modeling perspective. J. Energy Storage 2024, 76, 109800. [Google Scholar] [CrossRef]
- Renugen Limited. Renugen Limited Marketplace. 2022. Available online: https://www.renugen.co.uk/ (accessed on 11 April 2024).
- Scon-Marketing GmbH. Das sind die Kosten einer Photovoltaikanlage in 2022. 2022. Available online: https://www.solaranlagen-portal.de/photovoltaik/preis-solar-kosten.html/ (accessed on 11 April 2024).
- PV Magazine Group GmbH & Co. KG. PV Magazine: Speichermarkt in Deutschland auf Wachstumskurs bei Sinkenden Preisen. 2020. Available online: https://www.pv-magazine.de/2020/12/01/speichermarkt-in-deutschland-auf-wachstumskurs-bei-sinkenden-preisen/ (accessed on 11 March 2025).








2019 [m/s] | 2010–2020 [m/s] | 2019 [°C] | 2010–2020 [°C] | 2019 [W/m2] | 2010–2020 [W/m2] | |
|---|---|---|---|---|---|---|
| Aachen | 5.1 | 5.1 | 10.9 | 10.6 | 125.1 | 121.5 |
| Braunlage | 3.6 | 3.4 | 8.1 | 7.2 | 115.1 | 112.0 |
| Greifswald | 4.1 | 4.2 | 10.5 | 9.5 | 122.6 | 119.2 |
| Potsdam | 4.0 | 4.0 | 11.3 | 10.2 | 130.1 | 124.5 |
| Stuttgart | 1.5 | - | 12.8 | - | 124.8 | - |
| Wüstenrot | 2.3 | - | 9.2 | - | 126.2 | - |
| Montreal | 4.6 | 4.5 | 6.9 | 7.8 | 149.7 | 134.2 |
| Location | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | Total Costs [EUR/a] | EnergyCosts [EUR/a] | Invest. and Maintenance [EUR/a] |
|---|---|---|---|---|---|---|---|---|---|
| Aachen | 15 | 0.5 | 0.7 | 1 | 4 | 3 | 7084 | 1925 | 5159 |
| Braunlage | 15 | 0.5 | 0.8 | 0 | 9 | 0 | 7922 | 3732 | 4190 |
| Greifswald | 15 | 0.5 | 0.6 | 0 | 4 | 0 | 7430 | 3799 | 3631 |
| Potsdam | 15 | 0.7 | 0.6 | 0 | 5 | 0 | 7428 | 3625 | 3803 |
| Stuttgart | 15 | 0.6 | 0.5 | 0 | 8 | 0 | 6868 | 2819 | 4049 |
| Wüstenrot | 15 | 0.6 | 0.6 | 0 | 8 | 0 | 7541 | 3472 | 4069 |
| Montreal | 15 | 0.7 | 0.6 | 2 | 9 | 3 | 8316 | 2517 | 5798 |
| Location | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | Total Costs [EUR/a] | EnergyCosts [EUR/a] | Invest. and Maintenance [EUR/a] |
|---|---|---|---|---|---|---|---|---|---|
| Aachen | 15 | 0.5 | 0.5 | 16 | 0 | 3 | 7199 | 2847 | 4351 |
| Braunlage | 15 | 0.5 | 0.6 | 16 | 4 | 0 | 7912 | 4282 | 3631 |
| Greifswald | 15 | 0.5 | 0.5 | 16 | 4 | 0 | 7502 | 3891 | 3611 |
| Potsdam | 15 | 0.8 | 0.6 | 16 | 9 | 0 | 7490 | 3281 | 4210 |
| Stuttgart | 15 | 0.7 | 0.5 | 16 | 9 | 0 | 6995 | 2824 | 4171 |
| Wüstenrot | 15 | 0.6 | 0.5 | 16 | 4 | 0 | 7584 | 3953 | 3631 |
| Montreal | 15 | 0.7 | 0.7 | 16 | 10 | 0 | 8268 | 3957 | 4312 |
| Location | HP [kW] | DHW [m3] | Room [m3] | [kWh] | PV [kWp] | Wind [kW] | Total Costs [EUR/a] | EnergyCosts [EUR/a] | Invest. and Maintenance [EUR/a] |
|---|---|---|---|---|---|---|---|---|---|
| Aachen | 16 | 0.5 | 0.5 | 16 | 8 | 3 | 6856 | 1395 | 5462 |
| Braunlage | 15 | 0.6 | 0.7 | 16 | 9 | 0 | 7700 | 3510 | 4190 |
| Greifswald | 15 | 0.7 | 0.5 | 16 | 10 | 0 | 7261 | 2989 | 4273 |
| Potsdam | 15 | 0.7 | 0.5 | 16 | 8 | 0 | 7152 | 3084 | 4069 |
| Stuttgart | 15 | 0.5 | 0.5 | 16 | 11 | 0 | 6556 | 2205 | 4351 |
| Wüstenrot | 15 | 0.7 | 0.6 | 16 | 10 | 0 | 7367 | 3075 | 4292 |
| Montreal | 15 | 0.6 | 0.6 | 16 | 12 | 0 | 7889 | 3382 | 4507 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brennenstuhl, M.; Otto, R.; Pietruschka, D.; Schembera, B.; Eicker, U. Optimized Dimensioning and Economic Assessment of Decentralized Hybrid Small Wind and Photovoltaic Power Systems for Residential Buildings. Energies 2025, 18, 1811. https://doi.org/10.3390/en18071811
Brennenstuhl M, Otto R, Pietruschka D, Schembera B, Eicker U. Optimized Dimensioning and Economic Assessment of Decentralized Hybrid Small Wind and Photovoltaic Power Systems for Residential Buildings. Energies. 2025; 18(7):1811. https://doi.org/10.3390/en18071811
Chicago/Turabian StyleBrennenstuhl, Marcus, Robert Otto, Dirk Pietruschka, Björn Schembera, and Ursula Eicker. 2025. "Optimized Dimensioning and Economic Assessment of Decentralized Hybrid Small Wind and Photovoltaic Power Systems for Residential Buildings" Energies 18, no. 7: 1811. https://doi.org/10.3390/en18071811
APA StyleBrennenstuhl, M., Otto, R., Pietruschka, D., Schembera, B., & Eicker, U. (2025). Optimized Dimensioning and Economic Assessment of Decentralized Hybrid Small Wind and Photovoltaic Power Systems for Residential Buildings. Energies, 18(7), 1811. https://doi.org/10.3390/en18071811






