Prediction of Air-Conditioning Outlet Temperature in Data Centers Based on Graph Neural Networks
Abstract
1. Introduction
2. CFD Model and Simulation
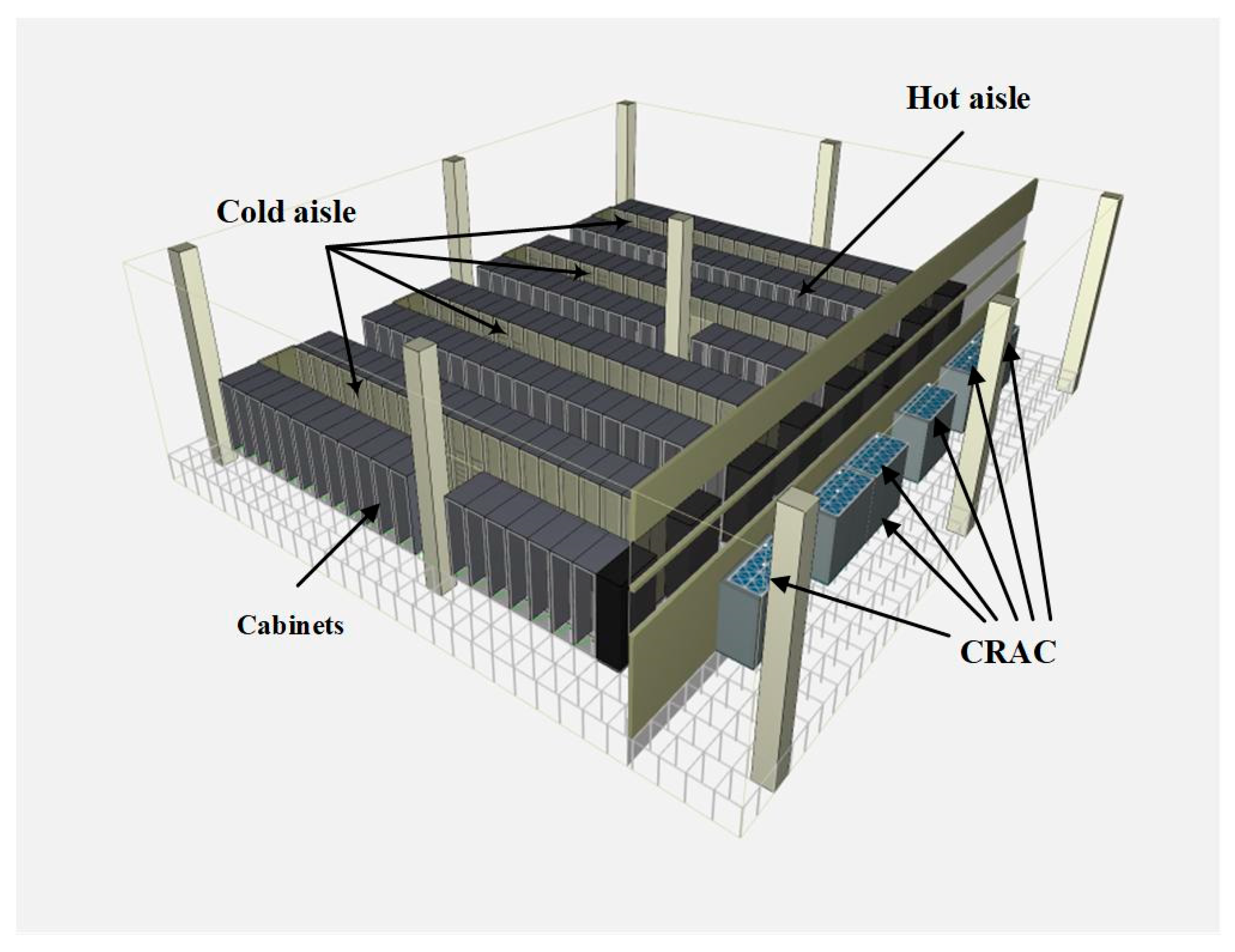
2.1. Server Room Layout and CFD Model
2.2. Governing Equation for the CFD Model
- (1)
- Mass Balance Equation
- (2)
- Momentum Balance Equation
- (3)
- Energy Balance Equation
- (4)
- Turbulence Model
- (5)
- Boundary Conditions
2.3. Target Cabinet Temperature Response Control Strategy
2.4. Simulation Results
3. Graph Neural Networks and Datasets
3.1. Artificial Neural Networks
3.2. Thermal Recirculation Phenomenon in Data Centers
3.3. Graph Neural Networks
3.4. Network Architecture Setup
3.5. Graph Model and Dataset
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jones, N. The information factories. Nature 2018, 561, 163–166. [Google Scholar] [CrossRef] [PubMed]
- Kleyko, D.; Osipov, E.; Patil, S.; Vyatkin, V.; Pang, Z. On methodology of implementing distributed function block applications using TinyOS WSN nodes. In Proceedings of the 2014 IEEE Emerging Technology and Factory Automation (ETFA), Barcelona, Spain, 16–19 September 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Zhou, H.; Li, Z.; Liu, Y.; Mei, L.; Lu, W.; Hu, J.; Cai, D. Air Conditioning System Design of Power Data Center Based on Automatic Control Technology. In Proceedings of the 2024 IEEE 2nd International Conference on Image Processing and Computer Applications (ICIPCA), Shenyang, China, 28–30 June 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Yuce, B.; Rezgui, Y. Computational intelligence techniques for HVAC systems: A review. Build. Simul. 2016, 9, 359–398. [Google Scholar] [CrossRef]
- Wu, Y.; Xue, X.; Le, L.; Ai, X.; Fang, J. Real-time Energy Management of Large-scale Data Centers: A Model Predictive Control Approach. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; pp. 2695–2701. [Google Scholar] [CrossRef]
- Kwon, Y.I. A study on the evaluation of ventilation system suitable for outside air cooling applied in large data center for energy conservation. J. Mech. Sci. Technol. 2016, 30, 2319–2324. [Google Scholar] [CrossRef]
- Yi, Y.; Zheng, A.; Shao, X.; Cui, G.; Wu, G.; Tong, G.; Gao, C. Joint Adjustment of Emergency Demand Response Considering Data Center and Air-Conditioning Load. In Proceedings of the 2018 IEEE International Conference on Energy Internet (ICEI), Beijing, China, 21–25 May 2018; pp. 72–76. [Google Scholar] [CrossRef]
- Su, Z. Optimization of an IDC Center Cooling System Based on PUE Analysis. Refrig. Air Cond. 2021, 35, 162–168. [Google Scholar]
- Ni, J.; Liu, S.Y.; Yuan, Z.Y.; Zhang, W.Q.; Gao, B. Optimization of Cooling System Performance of a Data Center in Sichuan Province. Refrig. Air Cond. 2023, 37, 410–416. [Google Scholar]
- Nada, S.A.; Said, M.A. Effect of CRAC units layout on thermal management of data center. Appl. Therm. Eng. 2017, 118, 339–344. [Google Scholar] [CrossRef]
- Available online: https://www.cadence.com/en_US/home/tools/reality-digital-twin.html#cadence-reality-dc-design (accessed on 14 September 2024).
- Tang, Q.; Gupta, S.K.S.; Stanzione, D.; Cayton, P. Thermal-Aware Task Scheduling to Minimize Energy Usage of Blade Server Based Datacenters. In Proceedings of the 2006 2nd IEEE International Symposium on Dependable, Autonomic and Secure Computing, Indianapolis, IN, USA, 29 September 2006–1 October 2006; pp. 195–202. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017; Available online: https://www.wiley.com/en-us/Design+and+Analysis+of+Experiments%2C+10th+Edition-p-9781119492443 (accessed on 14 September 2024).
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. arXiv 2018, arXiv:1710.10903. [Google Scholar]
- Athavale, J.; Joshi, Y.; Yoda, M. Artificial Neural Network Based Prediction of Temperature and Flow Profile in Data Centers. In Proceedings of the 2018 17th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), San Diego, CA, USA, 29 May 2018–1 June 2018; pp. 871–880. [Google Scholar] [CrossRef]
- ASHRAE Standard 90.1-2016; Energy Standard for Buildings Except Low-Rise Residential Buildings. ASHRAE: Peachtree Corners, GA, USA, 2016.













| CRAC Settings | |
|---|---|
| Cooling Method | Chilled Water Cooling |
| Fan Speed | 70% |
| Outlet Temperature Range | 13~25 °C |
| Rated Power Consumption | 8.1 kW |
| Maximum Sensible Cooling Capacity | 145 kW |
| Rated Airflow | 37,500 m3/h |
| Air Conditioner’s ID | Empirically Set Temperature (°C) | Experimentally Measured Temperature (°C) | Power Reduction (kW) |
|---|---|---|---|
| ACU1 | stopped | stopped | / |
| ACU2 | 20 | 24.4 | 1.782 |
| ACU3 | 20 | 21.9 | 0.770 |
| ACU4 | stopped | stopped | / |
| ACU5 | 22 | 23.1 | 0.446 |
| ACU6 | 22 | 23.3 | 0.527 |
| Mesh | Cell Numbers | Temperature of ACU2 (°C) | Percentage Difference (%) |
|---|---|---|---|
| Mesh-1 | 606302 | 24.3971 | / |
| Mesh-2 | 770784 | 24.5266 | 0.531 |
| Mesh-3 | 1030118 | 24.6321 | 0.430 |
| Mesh-4 | 1621540 | 24.9278 | 1.200 |
| Figure ID | Graph 2 | Graph 3 | Graph 5 | Graph 6 |
|---|---|---|---|---|
| Number of Nodes | 33 | 40 | 54 | 42 |
| Number of Edges | 63 | 92 | 128 | 101 |
| Feature of Edge | Undirected | Undirected | Undirected | Undirected |
| Number of Features | 330 | 440 | 540 | 420 |
| Label Rate | 100% | 100% | 100% | 100% |
| edge_index | [2,126] | [2,184] | [2,236] | [2,202] |
| Power x | Description of Feature Matrix |
|---|---|
| 400 | [x/2, x/2, 0, 0, 0, 0, 0, 0, 0, 0] |
| 400~800 | [x/4, x/4, x/4, x/4,0,0,0,0,0,0] |
| 800~1200 | [x/6, x/6, x/6, x/6, x/6, x/6, x/6,0,0,0,0] |
| 1200~1600 | [x/8, x/8, x/8, x/8, x/8, x/8, x/8, x/8,0,0] |
| 1600~2000 | [x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10] |
| 2000~2400 | [x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10] |
| 2400~2800 | [x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10] |
| 2800~3200 | [x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10] |
| 3200~3600 | [x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10] |
| 3600~4000 | [x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10, x/10] |
| Figure ID | Graph 2 | Graph 3 | Graph 5 | Graph 6 |
|---|---|---|---|---|
| GNNs | 0.02305 | 0.0366 | 0.1968 | 0.1301 |
| ANN | 0.2675 | 0.2372 | 0.6211 | 0.4070 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, Q.; Yang, J.; Shao, R.; Wang, Y. Prediction of Air-Conditioning Outlet Temperature in Data Centers Based on Graph Neural Networks. Energies 2025, 18, 1803. https://doi.org/10.3390/en18071803
Sha Q, Yang J, Shao R, Wang Y. Prediction of Air-Conditioning Outlet Temperature in Data Centers Based on Graph Neural Networks. Energies. 2025; 18(7):1803. https://doi.org/10.3390/en18071803
Chicago/Turabian StyleSha, Qilong, Jing Yang, Ruping Shao, and Yu Wang. 2025. "Prediction of Air-Conditioning Outlet Temperature in Data Centers Based on Graph Neural Networks" Energies 18, no. 7: 1803. https://doi.org/10.3390/en18071803
APA StyleSha, Q., Yang, J., Shao, R., & Wang, Y. (2025). Prediction of Air-Conditioning Outlet Temperature in Data Centers Based on Graph Neural Networks. Energies, 18(7), 1803. https://doi.org/10.3390/en18071803







