Energy Efficiency in Buildings: Smart Glass Technology Evaluation and Selection Model

Abstract

In the context of the architecture and construction industries implementing environmentally friendly sustainable solutions, smart glass is also designed using sustainable materials and sustainable operations, contributing to environmental protection efforts. The application of smart glass in large buildings optimizes the buildings’ operation, helping to reduce reliance on air conditioners that consume large amounts of electricity and emit significant amounts of CO₂ into the environment. Additionally, smart glass enhances energy-saving efficiency by intelligently regulating the indoor temperature and natural lighting, thereby reducing overall energy consumption and operational costs. In this study, the authors propose a fuzzy multi-criteria decision-making (MCDM) model to evaluate and select optimal sustainable smart glass technology based on technical, environmental, economic, and social criteria. The model integrates the fuzzy analytic hierarchy process (FAHP) to calculate the weights of the criteria and the Interactive and Multi-criteria Decision-Making in Portuguese Model (TODIM) to rank different smart glass technology alternatives. The findings highlight the most suitable smart glass technology, offering significant benefits in reducing energy consumption while ensuring aesthetic appeal and durability. This study provides a comprehensive approach to integrating sustainability into smart glass design, contributing to the development of green and energy-efficient buildings.

1. Introduction

The speed of urbanization and climate change is significantly influencing the overall development of countries in general and big cities in particular. The choice of materials in urban construction plays a decisive role in electricity consumption and the adoption of innovative technologies. With an increasing global emphasis on sustainability and energy efficiency, the demand for smart glass technology is growing, driven by advancements in materials science, automation, and Internet of Things (IoT) integration. Sustainable smart glass technologies are emerging as a key trend in construction due to their ability to enhance energy efficiency and reduce environmental impacts. Their sustainable features, thermal comfort, energy-saving properties, and convenience in adaptive shading and dynamic transparency control have contributed to their increasing popularity. Recent developments in electrochromic, suspended particle device, thermochromic, and photovoltaic smart glass have further expanded their potential applications, making them more viable for large-scale implementation in commercial and residential buildings. Additionally, as production costs decrease and market readiness improves, smart glass is expected to become more accessible and widely adopted across various industries. By reducing energy consumption, enhancing comfort, and providing privacy-on-demand solutions, smart glass is at the forefront of the sustainable building revolution, offering practical and scalable solutions for modern urban environments.

Choosing the right smart glass technology for sustainable construction is not a simple decision, as it requires careful consideration of both qualitative and quantitative factors. First, each smart glass technology offers different advantages and disadvantages regarding its energy-saving capacity, installation costs, and maintenance. Additionally, the climatic conditions of the construction area and the building’s purpose influence the choice of glass type. Therefore, selecting smart glass technology not only is a technical decision but also demands a comprehensive assessment of the building’s economic efficiency and long-term sustainability.

The multi-criteria decision-making (MCDM) model is useful for selecting smart glass for sustainable construction projects. With multiple criteria to consider, the MCDM model allows managers to evaluate and compare smart glass solutions comprehensively [1]. The MCDM model is an important method for assisting decision-makers in choosing between multiple alternatives based on various criteria. MCDM is not simply about selecting the best option; it is a complex process in which criteria may conflict, requiring a systematic approach to evaluate and compare options [2]. One of the prominent applications of MCDM is in sustainable development, where the assessment process enables decision-makers to consider various factors such as costs, benefits, and environmental impacts [3]. The general process of the MCDM model is shown in Figure 1.

In this research, the authors propose a fuzzy multi-criteria decision-making model (MCDM) to rank different smart glass technology alternatives. The FAHP model is applied in the first stage to calculate the weights of all criteria. In the second stage, the TODIM model is used to rank different smart glass technology alternatives. The TODIM is a decision-making method based on prospect theory, which considers the relative dominance of alternatives and incorporates decision-makers’ risk preferences. By integrating the FAHP for criterion weighting and the TODIM for ranking, this approach ensures a more comprehensive and rational evaluation of smart glass technologies. By assigning weights to important criteria, the model helps determine which glass technology is the most economically, technically, and environmentally efficient, thereby making the optimal decision for the project.

The primary goal of this study is to develop a fuzzy multi-criteria decision-making (fuzzy MCDM) model to provide an effective tool for evaluating and selecting the optimal sustainable smart glass technology, thereby promoting the integration of sustainability factors into the architecture and construction industry. The research focuses on using the FAHP model to analyze and determine the weights of criteria in four main areas—technical, environmental, economic, and social—ensuring that all important factors are comprehensively considered. Additionally, the TODIM model is applied to compare and rank smart glass technologies based on these criteria, enabling the selection of the most suitable technology. The research outcomes not only meet the requirements for technical performance and aesthetics but also effectively support energy consumption reduction and CO₂ emission mitigation, contributing to the development of green and sustainable buildings. This study is highly practical, offering a scientific and feasible solution for managers and designers in the architecture and construction industries to integrate sustainability factors into the process of selecting and applying smart glass technologies, minimizing negative environmental impacts, and fostering sustainable development.

The structure of this paper includes five sections: Section 1 presents the research problem, objectives, and main contributions of the study; Section 2 summarizes and analyzes previous related studies; Section 3 presents in detail the applied models and research processes. The authors illustrate the application of the method to real case studies and evaluate the results achieved in Section 4. Finally, the results and a discussion of limitations and suggestions for future research directions are presented in Section 5.

2. Literature Review

MCDM is an important tool in technology evaluation and selection, especially in smart glass design and construction. MCDM allows decision-makers to consider various factors, from technical to sustainability-related, to make optimal decisions in modern building projects. In the construction sector, the application of MCDM helps identify and prioritize technologies suitable for sustainability criteria. Many studies have shown that integrating economic, social, and environmental factors is necessary to develop sustainable smart cities [4]. MCDM helps evaluate new technologies but also assists in selecting smart glass design solutions, ensuring that they meet sustainability and energy efficiency standards [5,6]. Smart glass, with its ability to adjust its transparency and light reflectance, has become an important part of modern architectural design. Applying MCDM in selecting smart glass for buildings can include evaluating criteria such as energy efficiency, insulation, and environmental impact [7,8].

The selection of suppliers is a critical aspect of supply chain management, particularly in specialized fields such as smart glass technology for construction. The requirement to weigh several competing criteria adds to the complexity of this selection process, which is why multi-criteria decision-making (MCDM) techniques are so helpful. The results of several research studies investigating the use of MCDM approaches in supplier selection, with a particular emphasis on smart glass technology in the building industry, are summarized in this literature overview.

MCDM is a collection of approaches to help decision-makers assess and choose providers according to several factors. According to the published research, there is a growing trend in industries like construction and smart glass technology where sustainability and innovation are critical to using MCDM approaches when selecting suppliers [9,10,11]. A structured approach to decision-making is made possible by incorporating MCDM approaches, which enables organizations to efficiently evaluate qualitative and quantitative elements [12,13].

The importance of supplier selection in smart glass technology: Smart glass technology, which can manage light and heat transmission, is rapidly being used in construction projects. Supplier selection for smart glass is critical because it directly impacts project results in terms of energy efficiency, aesthetic appeal, and overall sustainability [14,15]. The literature emphasizes that when selecting suppliers in this context, the cost, technological capabilities, environmental impact, and reliability must be considered [16,17].

Several MCDM strategies have been used in the supplier selection process. The analytic hierarchy process (AHP) is a popular method that allows decision-makers to organize criteria hierarchically and assign weights accordingly [18,19]. The fuzzy AHP has also gained popularity, particularly in uncertain and ambiguous circumstances, such as evaluating supplier performance in the smart glass sector [20,21]. The TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) and VIKOR (VIsekriterijumska optimizacija i KOmpromisno Resenje) are widely used in conjunction with the AHP to improve decision-making accuracy [22].

Recent research has demonstrated the efficiency of hybrid MCDM systems, which integrate different methodologies to capitalize on their strengths. For example, integrating the fuzzy analytic hierarchy process (Fuzzy AHP) with the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) has improved supplier selection results by offering a more thorough evaluation framework [23]. Such hybrid models are especially useful in smart glass technology, where providers’ capabilities and offerings can differ greatly. These studies collectively explored sustainable supply chain management (SSCM) and multi-criteria decision-making (MCDM) methods, offering insights into how companies can integrate environmental, economic, and social criteria into their operations. Many researchers [24,25,26,27] presented frameworks for assessing supplier sustainability and supply chain performance using various MCDM approaches, emphasizing the triple bottom line and the importance of green supplier selection. Genovese et al. [28] demonstrated the role of analytics in enhancing supply chain sustainability, while Ahi and Searcy [29] analyzed metrics that measure SSCM effectiveness, pointing out gaps in current practices. Mardani et al. [30] provided a review of MCDM methods applied to renewable energy, reinforcing the importance of sustainability considerations. Additionally, Taticchi et al. [31] focused on SMEs, proposing performance metrics to help them achieve sustainability goals. Faisal and Talib [32] discussed green logistics practices in India, identifying barriers and motivators, and Rezaei and Ortt [33] examined MCDM’s role in production and logistics systems, offering a theoretical basis for complex decision-making in sustainable supply chains. Collectively, these works underscore the critical role of MCDM and robust metrics in advancing sustainable supply chain practices across various industries. The selection criteria for suppliers in the smart glass industry include technical standards, costs, delivery times, and sustainable practices. According to the research, environmental issues are becoming increasingly important in supplier selection, reflecting broader industry trends towards sustainability [34]. According to the literature, decision-makers should take a balanced approach when evaluating potential suppliers, considering standard performance measures and innovative skills [35].

Several case studies demonstrate the use of MCDM approaches in real-world supplier selection settings. For example, Wang et al. [36] used a hybrid MCDM model to pick suppliers for a biomass furnace, which had sustainability criteria similar to those for smart glass technology. Furthermore, research on the textile industry has shed light on adapting MCDM methodologies across several sectors, including construction. Despite the benefits of MCDM techniques, obstacles exist in their implementation. One major issue is the difficulty of accurately defining criterion weights and ratings, especially in dynamic situations like construction [37]. Furthermore, integrating qualitative and quantitative data adds complexity, demanding robust frameworks to support reliable decision-making [38]. The literature proposes various areas of future research in MCDM for supplier selection, notably in smart glass technologies. More empirical research is needed to investigate the efficiency of various MCDM strategies in varied circumstances and their adaptation to evolving technology [39]. Furthermore, advanced analytics and machine learning approaches could improve decision-making by offering more detailed insights into supplier performance and market trends [40].

To summarize, the use of MCDM approaches in supplier selection for smart glass technologies in buildings is a rapidly expanding topic. The combination of several MCDM methodologies provides a structured approach to navigating the intricacies of supplier evaluation, allowing decision-makers to make educated decisions aligned with their strategic goals. As the industry evolves, continuous research and practical implementations will be critical for refining these approaches and solving supplier selection issues.

3. Methodology

The evaluation and selection of optimal smart glass technology is a complex MCDM problem that encompasses both qualitative and quantitative factors. In this study, a novel fuzzy MCDM model was developed to support the selection process for smart glass technology by integrating the fuzzy analytical hierarchy process (Fuzzy AHP) and the Portuguese TODIM for interactive multi-criteria decision-making. The decision-making process consisted of three main steps:

Step 1, criterion identification: Through expert consultations and a comprehensive literature review, the criteria for evaluating and selecting the optimal smart glass technology were identified, ensuring a well-rounded assessment framework. This process not only was based on previous studies regarding the performance and applications of smart glass but also incorporated practical insights from experts in material technology, optics, and renewable energy. Defining these criteria ensures that the selected technology meets not only technical requirements but also economic and environmental considerations, promoting sustainability and high practical applicability.

Step 2, criterion weight determination: The importance of each criterion was determined using the FAHP model, allowing for the incorporation of expert judgment and the inherent uncertainty in decision-making.

Step 3, alternative ranking: The TODIM was applied to rank all potential smart glass technology alternatives based on the weighted criteria, leading to the selection of the most suitable option.

This approach ensures a systematic and robust evaluation process, addressing the complexities of sustainability and technological advancements in the smart glass domain.

3.1. Fuzzy Analytic Hierarchy Process

The fuzzy AHP model implementation is divided into four steps, which are as follows [41,42,43,44,45,46]:

Step 1, constructing the fuzzy AHP model: This involves defining the hierarchy of the decision-making problem, including the goal, criteria, sub-criteria, and alternatives, to set the model’s foundation.

Step 2, establishing the pairwise comparison matrix by employing fuzzy numbers, we create a matrix that compares the relative importance of criteria (and sub-criteria, if applicable). This matrix allows decision-makers to express preferences in a range (e.g., using triangular or trapezoidal fuzzy numbers), enabling the handling of uncertainty in judgments.

With fuzzy numbers, the pairwise comparison matrix is developed as follows:

$$\widetilde{M^k}=\left[\begin{array}{ccc}\widetilde{m_{11}^k}& \widetilde{m_{12}^k}& \cdots \\ \begin{array}{c}\widetilde{m_{21}^k}\\ \cdots \end{array}& \begin{array}{c}\widetilde{m_{22}^k}\\ \cdots \end{array}& \begin{array}{c}\cdots \\ \cdots \end{array}\\ \widetilde{m_{n1}^k}& \widetilde{m_{n2}^k}& \cdots \end{array} \begin{array}{c}\widetilde{m_{1n}^k}\\ \widetilde{m_{2n}^k}\\ \begin{array}{c}\cdots \\ \widetilde{m_{nn}^k}\end{array}\end{array}\right]$$

(1)

where

$\widetilde{M^k}$ is the pairwise comparison matrix for fuzzy elements;

$\widetilde{m_{nn}^k}$ is refer to the triangular fuzzy mean applied in comparing the priority levels of paired items.

To transform fuzzy numbers into real values, the triangular fuzzy trigonometric technique is utilized as follows [47]:

$$f_{\alpha ,\beta }\left({\overline{\alpha }}_{ij }\right)=\left[\beta .t_{\alpha }\left(L_{ij}\right)+\left(1-\beta \right).t_{\alpha }.\left(U_{ij}\right)\right]$$

(2)

with 0 $\le \beta \le 1,0\le \alpha \le 1$,

where

$$t_{\alpha }\left(L_{ij}\right)=\left(M_{ij}-L_{ij}\right).\alpha +L_{ij}$$

(3)

$$t_{\alpha }\left(U_{ij}\right)=U_{ij}-\left(U_{ij}-M_{ij}\right). \alpha$$

(4)

Once the diagonal matrix is matched, we obtain

$$f_{\alpha ,\beta }\left({\overline{\alpha }}_{ij }\right)={\displaystyle \frac{1}{t_{\alpha ,\beta }\left({\overline{\alpha }}_{ij }\right)}}$$

(5)

with 0 $\le \beta \le 1,0\le \alpha \le 1,i>j$.

After applying the conversion procedure to create the fuzzy comparison matrix, we obtain a comparison matrix with real-number components. This matrix contains m rows and n columns, where n is the number of indicators.

$$K={\left(k_{ij}\right)}_{m\times n}=\left[\begin{array}{cc}\begin{array}{cc}1& { k}_{12}\\ k_{21}& 1\end{array}& \begin{array}{cc}\dots & k_{1n}\\ \dots & k_{2n}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ k_{m1}& k_{m2}\end{array}& \begin{array}{cc}⋮& ⋮\\ \dots & 1\end{array}\end{array}\right]$$

(6)

The priority of the fuzzy analytic hierarchy process (FAHP) model is evaluated using Kuswandati’s fuzzy conversion scale [48].

Step 3: To find the greatest feasible individual value, Saaty’s lambda max approach is used [49]. Saaty’s lambda max (λmax) approach is a key concept in the analytic hierarchy process (AHP) used to check the consistency of a pairwise comparison matrix. It helps determine how consistently a decision-maker has assigned relative weights to criteria or alternatives. This method computes the greatest specified value for an indication, which aids in determining consistency within the comparison matrix. The formula for lambda max is

$$\left|K-{\mathsf{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}.I\right|=0$$

(7)

where

${\mathsf{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the matrix’s maximum value;

A is the matrix of pairwise comparisons;

I is the same level unit matrix as matrix K.

Step 4: To ensure consistency in the pairwise comparison matrix, Saaty introduced the Consistency Ratio (CR), which is calculated after determining the consistency index (CI). The CR measures how consistent the judgments are compared to random chance, balancing the reliability of the data with their inherent randomness. The formula for calculating the Consistency Ratio is

$$\mathrm{C}\mathrm{R}={\displaystyle \frac{\mathrm{C}\mathrm{I}}{\mathrm{R}\mathrm{I}}}$$

(8)

where CI represents the CI and RI (Random Index) is the average consistency index derived from many randomly generated matrices of the same order nn.

If CR ≤ 0.1, the level of inconsistency is acceptable. Otherwise, if CR > 0.1, the pairwise comparisons may need to be revised to improve consistency.

$$\mathrm{C}\mathrm{I}={\displaystyle \frac{{\mathsf{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{n}}{\mathrm{n}-1}}$$

(9)

Here,

${\mathsf{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the matrix’s maximum value;

n is the proportion of the number of indicators.

Saaty analyzed the creation of random matrices for each nn-level comparison matrix to determine the RI values. This RI represents the average consistency index for matrices of varying sizes, calculated from a large sample of randomly generated matrices. By establishing these RI values for different matrix sizes, Saaty provided a reference to assess the consistency of the pairwise comparison matrix in the analytic hierarchy process (AHP).

3.2. Interactive and Multi-Criteria Decision-Making in Portuguese Model

The TODIM methodology is a discrete multi-criteria method based on prospect theory, which was created in its current form at the start of the 1990s. The TODIM method’s main steps are the following [50,51,52,53,54,55]:

○

Step 1: Develop a decision-making matrix.

○

Step 2: The cumulative weights of all the criteria must equal one:

$$w_1+w_2+\cdots +w_j=1;j=\overline{1,n}$$

(10)

○

Step 3: To obtain comparable values, the quantitative criterion scales are standardized. To obtain comparable results, the estimates are normalized in the same way as the quantitative scales are. The collection of Equations (12)–(14) is used to maximize criteria, whereas Equation (11) is used to minimize them. Equation (12) is used to standardize data.

Equation (13) reduces the larger values to smaller ones, giving lower initial alternative estimates more weight. New values are normalized using Equation (19):

$${\overline{x}}_{ij}={\displaystyle \frac{{\overline{x}}_{ij}}{\sum _{i=1}^m{\overline{x}}_{ij}}}; i=\overline{1,m} ; j=\overline{1,n}$$

(11)

Each element ${\overline{x}}_{ij}$ is normalized by dividing it by the total sum of values in its category, allowing for a comparison on a consistent scale.

$${\overline{p}}_{ij}={\displaystyle \frac{{\overline{x}}_{ij}}{\sum _{i=1}^m{\overline{x}}_{ij}}}; i=\overline{1,m} ; j=\overline{1,n}$$

(12)

Like in the previous equation, each value ${\overline{x}}_{ij}$ is normalized, resulting in a standardized value ${\overline{p}}_{ij}$.

$${\overline{p}}_{ij}={\displaystyle \frac{{\overline{x}}_{ij}}{\sum _{i=1}^m{\overline{x}}_{ij}}}; i=\overline{1,m} ; j=\overline{1,n}$$

(13)

This formula scales down larger values by dividing each ${\overline{p}}_{ij}$ by the minimum value within the set, thereby giving more weight to smaller initial estimates.

$${\overline{x}}_{ij}={\displaystyle \frac{{\overline{p}}_{ij}^{\prime }}{\sum _{i=1}^m{\overline{p}}_{ij}^{\prime }}}; i=\overline{1,m} ; j=\overline{1,n}$$

(14)

In this step, each adjusted value ${\overline{p}}_{ij}^{\prime }$ is normalized again by dividing it by the sum of all adjusted values, producing a consistent scale across all elements.

○

Step 4: The criterion with the highest weight $q_c$ is selected to recalculate individual weights:

$$q_{jc}={\displaystyle \frac{q_j}{q_c}}; j=\overline{1,n}$$

(15)

where

$q_{jc}$ represents the adjusted weight of criterion j relative to the highest-weight criterion $q_c$.

○

Step 5: The “single-criterion dominance” is determined as follows for each criterion $j=\overline{1,n}$ and for two alternatives $s_i$ and $s_k$, $i,k=\overline{1,m}$:

$${\Phi }_i{s}_i,s_k=\left\{\begin{array}{c}-\sqrt{{\displaystyle \frac{\sum _{j=1}^n{q}_{jc}\left|{\overline{x}}_{ij}-{\overline{x}}_{kj}\right|}{q_{jc}}}, if {\overline{x}}_{ij}-{\overline{x}}_{kj}<0 }\\ 0, if {\overline{x}}_{ij}-{\overline{x}}_{kj}=0 \\ \sqrt{{\displaystyle \frac{q_{jc}=\left|{\overline{x}}_{ij}-{\overline{x}}_{kj}\right|}{\sum _{j=1}^n{q}_{jc}}}, if \left({\overline{x}}_{ij}-{\overline{x}}_{kj}\right)>0 }\end{array}\right.$$

(16)

i,k =$\overline{1,m}$, j =$\overline{1,n}$

○

Step 6: The “relative dominance” for each pair of alternatives $s_i$ and $s_k$ is calculated as follows:

$$\mathrm{\delta }\left(s_i, s_k\right)={\sum }_{j=1}^n{\Phi }_j\left(s_i,s_k\right);j=\overline{1,n}$$

(17)

○

Step 7: The “global overview” G($s_i$) of each alternative $s_i$ is calculated by summing the relative dominance over all other alternatives:

$$\left(s_i\right)={\sum }_{k=1}^m\mathrm{\delta }\left(s_i, s_k\right);k=\overline{1,m}$$

(18)

○

Step 8. The “global dominances” are normalized to obtain the “relative overall value” V($s_i$) of each alternative:

$$V\left(s_i\right)={\displaystyle \frac{\mathrm{G}\left(s_i\right)-{min}_i\mathrm{G}\left(s_i\right)}{{max}_i\mathrm{G}\left(s_i\right)-{min}_i\mathrm{G}\left(s_i\right)}} i=\overline{1,m}$$

(19)

This formula scales values between 0 and 1 from Equation (19) for easy comparisons of alternatives.

4. Case Study

In today’s rapidly developing era, environmental pollution has become a serious issue, directly impacting human health, ecosystems, and the global climate, requiring urgent action from governments, businesses, and communities. To address this issue, almost all nations and governments worldwide encourage production, construction, and development that is environmentally friendly, safe, and protective across various sectors, including the economy and society. Smart glass is an essential solution in sustainable construction, helping to reduce energy consumption and protect the environment. With its ability to adjust its transparency, smart glass optimizes natural light, minimizing the need for artificial lighting and air conditioning. This saves energy and creates comfortable, health-friendly living and working spaces. Thanks to this advanced feature, smart glass has become an indispensable part of modern buildings, promoting sustainable development in the construction industry.

Nowadays, many types of smart glass have been developed, and choosing the most suitable smart glass technology for each construction project is a difficult task. Decision-makers must consider multiple factors, including both qualitative and quantitative factors. In this study, expert surveys focused on quality over quantity, ensuring that the participants possessed deep domain knowledge and expertise relevant to the study [56,57]. These factors may range from energy efficiency, cost, and durability to aesthetic appeal and environmental impact, requiring a comprehensive evaluation to ensure that the selected technology aligns with the project’s sustainable goals and functionality. The authors propose a new FAHP-TODIM approach for selecting smart glass technology in this section. This research process includes two stages: calculating the weights of evaluation criteria by a fuzzy AHP (FAHP) and determining the ranking of smart glass technologies based on technical, environmental, economic, and social criteria through a TODIM method. The list of criteria is shown in

Table 1. List of criteria.

No.	Main Criteria	Sub-Criteria	Definition	Source
				References	Experts
1	Technical factors	SG01: Integration with Smart Systems	Assessment of compatibility with automated control systems or other high-tech systems in buildings.	[58]	X
		SG02: Transparency Adjustment Capability	Flexibility in changing transparency to optimize natural light.	[59,60]	X
		SG03: Durability and Lifespan	The glass’s resistance to environmental factors and its expected lifespan under usage conditions.	[61,62]	X
2	Environmental factors	SG04: Recyclability and Decomposition	The eco-friendliness of glass materials at the end of their life cycle.	[62]	X
		SG05: CO2 Emission Reduction	Measuring the level of CO2 reduction due to energy efficiency.	[60,63]	X
		SG06: Emissions during Production	The amount and type of gas or solid waste generated during glass production.	[63]	X
3	Economic factors	SG07: Energy-Saving Efficiency	Degree of reduction in electricity costs through insulation and light regulation.	[63]	X
		SG08: Initial Investment Cost	Total installation costs, including purchasing, transportation, and setup.	[63,64]	X
		SG09: Operational and Maintenance Costs	Costs incurred during usage, maintenance, repairs, or replacement.	[63,64]	X
4	Social factors	SG10: Aesthetic Appeal and Architectural Compatibility	Meeting aesthetic requirements and harmony with the overall architecture of the building.	[65]	X
		SG11: Health Impact and Comfort	The effect of the glass on users’ comfort, health, and working environment, such as reducing glare and regulating temperature.	[65]	X
		SG12: Safety and Security for Users	Protection for users from external impacts, such as UV rays or external visibility.	[65]	X

.

In the first stage, the model integrates the fuzzy analytic hierarchy process (FAHP) to calculate the criteria weights. The fuzzy AHP (FAHP) model is based on the fuzzy hierarchical analysis process, which combines elements of the AHP method with fuzzy theory to handle ambiguity and uncertainty in the decision-making process. Twelve experts participated in this study to ensure a well-rounded and comprehensive evaluation of the criterion selection and weighting process in the fuzzy analytic hierarchy process (FAHP). The expert panel was carefully selected to cover diverse areas relevant to smart glass technology and sustainable architecture, ensuring a balanced perspective across technical, environmental, economic, and practical aspects. The experts’ specializations is shown in

Table 2. Information on the experts.

No.	Area of Expertise	Quantity
1	Materials Science and Engineering	02
2	Sustainable Architecture and Building Design	02
3	Energy Efficiency and Green Building Standards	02
4	Smart Technology and Automation	02
5	Construction Project Management	02
6	Environmental Policy and Urban Planning	02

:

The pairwise comparison process was conducted in two phases to ensure a rigorous and well-balanced evaluation. In the first phase, all 12 experts participated in selecting and refining the evaluation criteria through expert consultations and a comprehensive literature review. In the second phase, each expert performed pairwise comparisons, providing judgments on the relative importance of the selected criteria. The collected responses were then aggregated using the FAHP to determine the final weights, ensuring consistency and minimizing bias in the decision-making process. This structured methodology guarantees a scientifically robust approach that incorporates diverse expert perspectives, ensuring that the criterion selection and weighting process aligns with real-world applications in sustainable architecture and smart glass technology. The weights of all criteria obtained by using Formulas (1)–(9) are shown in

Table 3. Weights of criteria.

No.	Criterion	Symbol	Weight
1	Integration with Smart Systems	SG01	0.0305
2	Transparency Adjustment Capability	SG02	0.0734
3	Durability and Lifespan	SG03	0.1160
4	Recyclability and Decomposition	SG04	0.0681
5	CO2 Emission Reduction	SG05	0.1179
6	Emissions during Production	SG06	0.0460
7	Energy-Saving Efficiency	SG07	0.0574
8	Initial Investment Cost	SG08	0.1080
9	Operational and Maintenance Costs	SG09	0.1064
10	Aesthetic Appeal and Architectural Compatibility	SG10	0.0899
11	Health Impact and Comfort	SG11	0.0799
12	Safety and Security for Users	SG12	0.1065

.

Based on the weight ranking results from the fuzzy AHP, we can interpret the findings as follows. The most important criteria identified are CO₂ Emission Reduction (SG05), Durability and Lifespan (SG03), Initial Investment Cost (SG08), Operational and Maintenance Costs (SG09), and Safety and Security for Users (SG12), each with relatively high weights. This indicates that environmental considerations, cost efficiency, product durability, and safety are prioritized in the selection process. Meanwhile, criteria such as Integration with Smart Systems (SG01), Transparency Adjustment Capability (SG02), Recyclability and Decomposition (SG04), and Emissions during Production (SG06) have lower weights, suggesting they are less critical but still relevant factors. Additionally, criteria like Aesthetic Appeal and Architectural Compatibility (SG10) and Health Impact and Comfort (SG11) hold moderate weights, showing that while these factors are valued, they play more of a supporting role. Overall, the results highlight that environmental impact, cost, and durability are primary concerns, while aesthetics and recyclability are secondary but still considered in the decision-making process.

The TODIM Model is a MCDM model developed by Gomes and Limato [51] that aids in decision-making that involves various criteria with different levels of importance. This model is based on prospect theory [52], which captures how people perceive gains and losses rather than absolute outcomes. The TODIM emphasizes the psychological behavior of decision-makers, particularly their risk aversion in gains and risk-seeking tendencies in losses [53,54,55]. With these ranked criteria from the fuzzy AHP as the input, we applied the TODIM method. This allowed us to account for decision-makers’ risk attitudes, as the TODIM considers both gains and losses relative to each criterion in the evaluation process. Four smart glass technologies (SMART01, SMART02, SMART03, and SMART04) were considered, and the TODIM was applied to rank different smart glass technology alternatives in the final stage. The normalized matrix and calculated single criterion dominances are presented in

Table 4. Normalized matrix.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12
A1	0.2069	0.2353	0.2069	0.1875	0.2424	0.2188	0.2647	0.2581	0.2581	0.2424	0.2424	0.2727
A2	0.3103	0.2353	0.2759	0.2500	0.2727	0.2500	0.2647	0.2581	0.2581	0.2727	0.2727	0.2424
A3	0.2759	0.2647	0.2759	0.2813	0.2424	0.2813	0.2353	0.2903	0.2903	0.2727	0.2424	0.2424
A4	0.2069	0.2647	0.2414	0.2813	0.2424	0.2500	0.2353	0.1935	0.1935	0.2121	0.2424	0.2424

and

Table 5. Sum of single criterion dominances.

	A1	A2	A3	A4
A1	0.0000	−6.0415	−6.8265	−2.8593
A2	−0.1235	0.0000	−3.0493	−0.8008
A3	−0.7641	−2.6538	0.0000	0.4245
A4	−3.1539	−6.5056	−5.5945	0.0000

.

The result of the TODIM is shown in

Table 6. Final ranking from TODIM.

Alternative	Relative Overall Value V(ai)	Ranking
A1	0	4
A2	0.9230	2
A3	1	1
A4	0.0372	3

.

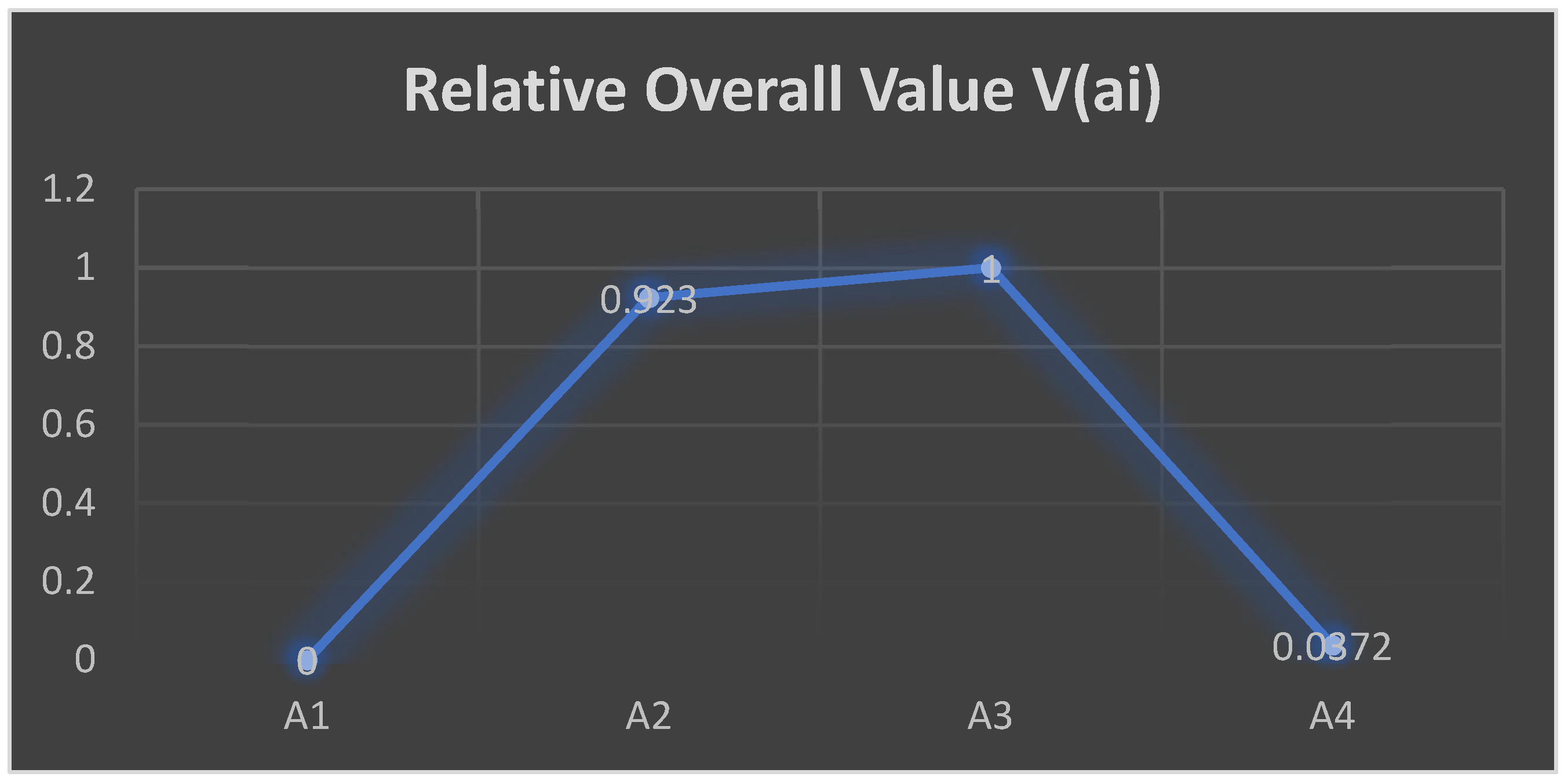
The TODIM was used in this stage to rank sustainable smart glass technology alternatives based on technical, environmental, economic, and social criteria. The results showed the superiority of some smart glass technologies in reducing energy consumption and CO₂ emissions while ensuring aesthetics and high durability for construction works.

These values, illustrated in Figure 2, provide a clear visual comparison of each alternative’s performance. The ranking outcomes underscore the strength of alternative A3 as the optimal choice based on the set criteria, aiding decision-makers in making a well-informed selection from among the alternatives. The calculation process of the TODIM clarified the differences between technology options based on the priority level of each criterion after applying the weights from the FAHP method. The smart glass technology with the highest score is the technology that meets the technical and economic criteria and is environmentally and socially sustainable.

To evaluate the robustness of the TODIM results for the multi-criteria decision-making problem, a sensitivity analysis was performed. This analysis examined the impact of excluding each criterion on the performance scores and rankings of the alternatives (A1, A2, A3, and A4). The criterion weights for all twelve scenarios, each representing the removal of one criterion, are presented in

Table 7. Criterion weights in all scenarios.

Criteria	Criterion Weights
	Original	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5	Scenario 6	Scenario 7	Scenario 8	Scenario 9	Scenario 10	Scenario 11	Scenario 12
VC01	0.0305		0.0329	0.0345	0.0327	0.0346	0.0320	0.0324	0.0342	0.0341	0.0335	0.0331	0.0341
VC02	0.0734	0.0757		0.0830	0.0788	0.0832	0.0769	0.0779	0.0823	0.0821	0.0807	0.0798	0.0821
VC03	0.1160	0.1196	0.1252		0.1245	0.1315	0.1216	0.1231	0.1300	0.1298	0.1275	0.1261	0.1298
VC04	0.0681	0.0702	0.0735	0.0770		0.0772	0.0714	0.0722	0.0763	0.0762	0.0748	0.0740	0.0762
VC05	0.1179	0.1216	0.1272	0.1334	0.1265		0.1236	0.1251	0.1322	0.1319	0.1295	0.1281	0.1320
VC06	0.0460	0.0474	0.0496	0.0520	0.0494	0.0521		0.0488	0.0516	0.0515	0.0505	0.0500	0.0515
VC07	0.0574	0.0592	0.0619	0.0649	0.0616	0.0651	0.0602		0.0643	0.0642	0.0631	0.0624	0.0642
VC08	0.1080	0.1114	0.1166	0.1222	0.1159	0.1224	0.1132	0.1146		0.1209	0.1187	0.1174	0.1209
VC09	0.1064	0.1097	0.1148	0.1204	0.1142	0.1206	0.1115	0.1129	0.1193		0.1169	0.1156	0.1191
VC10	0.0899	0.0927	0.0970	0.1017	0.0965	0.1019	0.0942	0.0954	0.1008	0.1006		0.0977	0.1006
VC11	0.0799	0.0824	0.0862	0.0904	0.0857	0.0906	0.0838	0.0848	0.0896	0.0894	0.0878		0.0894
VC12	0.1065	0.1099	0.1149	0.1205	0.1143	0.1207	0.1116	0.1130	0.1194	0.1192	0.1170	0.1157

.

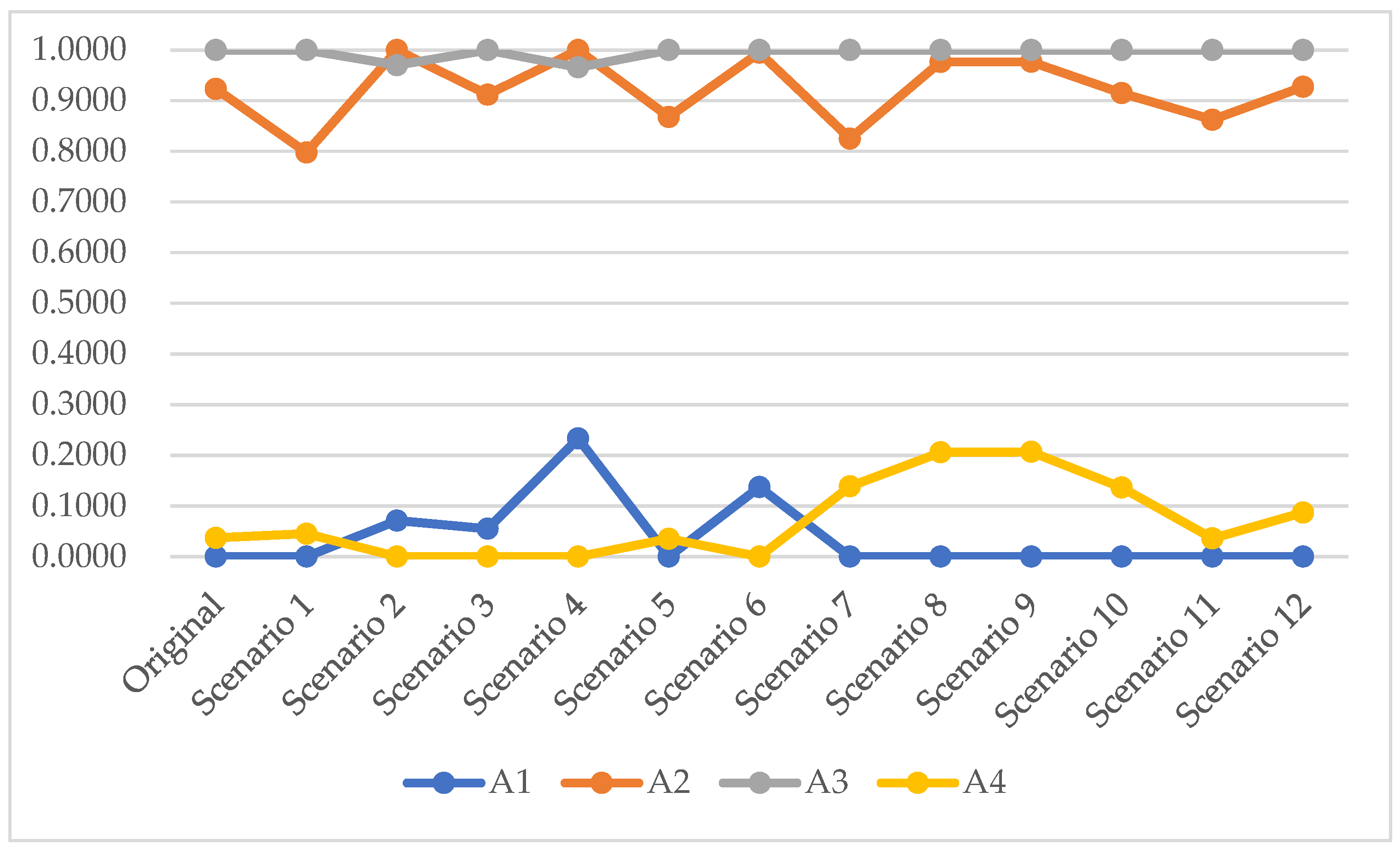
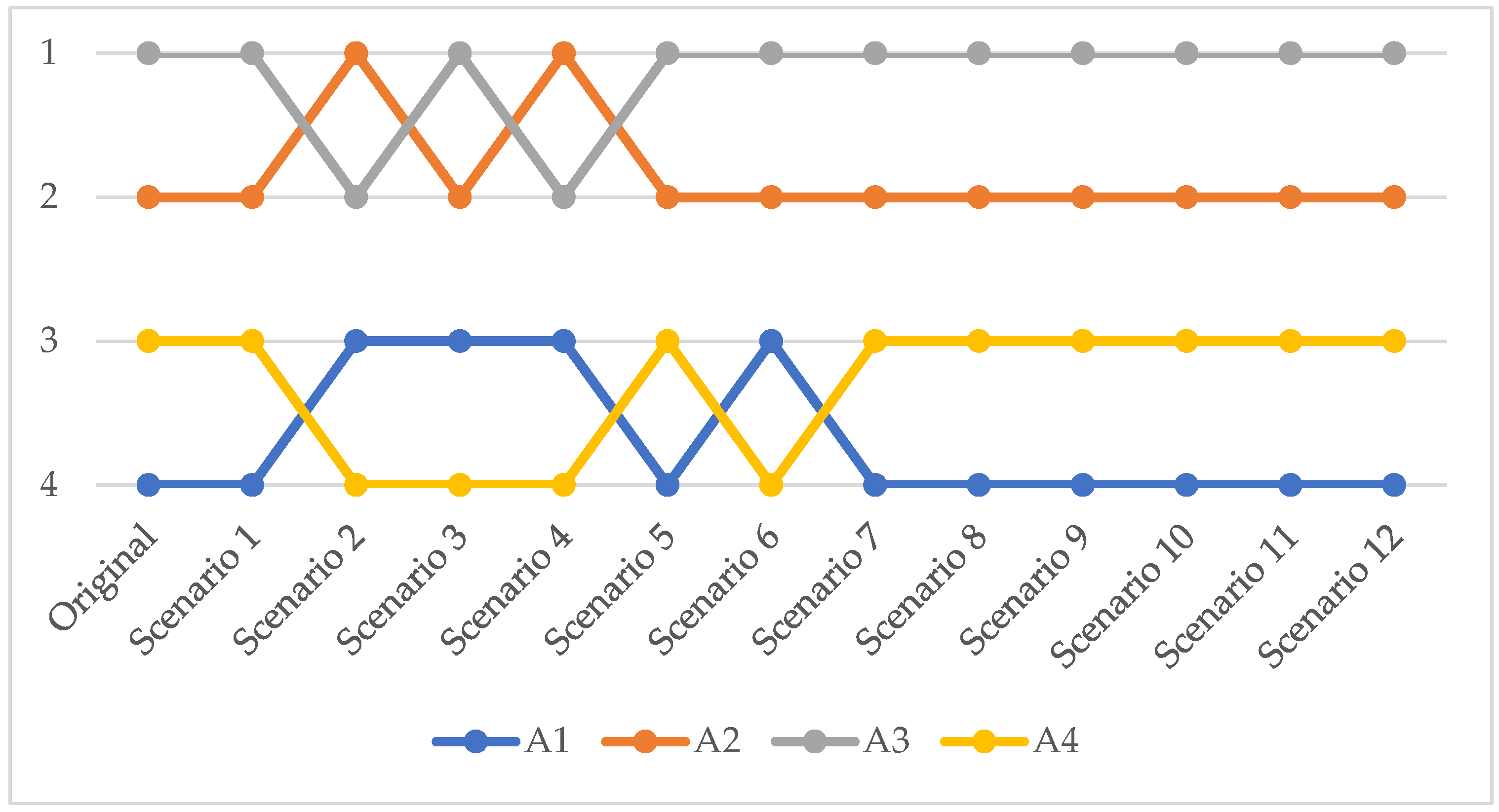
The findings displayed in

Table 8. Performance scores in all scenarios.

Alternatives	Performance Scores
	Original	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5	Scenario 6	Scenario 7	Scenario 8	Scenario 9	Scenario 10	Scenario 11	Scenario 12
A1	0.0000	0.0000	0.0712	0.0550	0.2334	0.0000	0.1374	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
A2	0.9230	0.7977	1.0000	0.9117	1.0000	0.8676	0.9945	0.8249	0.9763	0.9765	0.9147	0.8623	0.9271
A3	1.0000	1.0000	0.9700	1.0000	0.9658	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
A4	0.0372	0.0452	0.0000	0.0000	0.0000	0.0353	0.0000	0.1387	0.2059	0.2071	0.1365	0.0360	0.0871

and Figure 3 demonstrate that A3 consistently holds the highest rank across all scenarios, highlighting its dominance as the top-performing alternative. Its balanced performance across all criteria ensures that its ranking remains unaffected by the exclusion of any single criterion. Similarly, A2 maintains a stable second position throughout, reaffirming its reliability and robustness as a strong choice.

In contrast, A1 and A4 exhibit rank fluctuations in specific scenarios. For instance, A1 improves its ranking when VC03 is removed, suggesting a significant dependency on this criterion. The exclusion of VC03 also results in noticeable changes in the performance scores of A1 and A4, underscoring the critical role this criterion plays in differentiating these alternatives. Furthermore, the removal of VC08 or VC09 has a considerable effect on A4’s performance, emphasizing the importance of these criteria for this alternative.

The stability of A3’s performance across all scenarios (Figure 4) establishes it as a robust and reliable option with strong overall attributes. Meanwhile, the relatively consistent rankings of A3 and A2 bolster confidence in their positions as the top alternatives, making them dependable choices regardless of the scenario.

The sensitivity analysis highlights the impact of removing CO₂ Emission Reduction (SG05), Durability and Lifespan (SG03), and Initial Investment Cost (SG08) on alternative performance scores, underscoring their influence on the final rankings. These findings suggest that decision-makers in this case prioritize CO₂ reduction, durability, and cost efficiency, and they play a crucial role in technology selection. Additionally, manufacturers should focus on enhancing smart glass performance across these criteria to improve their competitiveness and alignment with sustainability and economic considerations in building projects.

5. Conclusions

In this study, the authors developed a fuzzy multi-criteria decision-making (MCDM) model to evaluate and select the optimal sustainable smart glass technology within the context of the architecture and construction industries’ efforts to implement environmentally friendly solutions. The model integrates the FAHP model to calculate the criteria weights and the TODIM model to rank various smart glass technology alternatives. As a result, the most suitable smart glass technology was identified, offering substantial benefits in reducing energy consumption while maintaining aesthetic appeal and durability. This study contributes to sustainable architecture by introducing a fuzzy multi-criteria decision-making (MCDM) model for selecting optimal smart glass technology—one of the few studies applying fuzzy logic in this field. Unlike traditional methods, this approach provides a comprehensive evaluation framework encompassing technical, environmental, economic, and social criteria, ensuring the selection of smart glass technology that enhances energy efficiency, reduces CO₂ emissions, and supports sustainable building operations. The findings offer practical guidance for architects, developers, and policymakers, reinforcing the role of smart glass in advancing green and energy-efficient buildings.

In the future, this study can be extended by adding additional criteria to enhance the model’s comprehensiveness and experimenting with other multi-criteria decision-making (MCDM) methods to improve its accuracy and applicability. Additionally, to strengthen the sensitivity analysis, future research could consider three weighting approaches for the experts: (i) equal weighting, (ii) experience-based weighting, and (iii) familiarity-based weighting. Furthermore, the model can be applied to other industries or regions with varying geographical and climatic characteristics to verify its feasibility and expand the application potential of sustainable smart glass technology.