Distributed Photovoltaic Short-Term Power Prediction Based on Personalized Federated Multi-Task Learning
Abstract
1. Introduction
- This paper introduces a framework for DPV power prediction, which is grounded in PFL. In this framework, local prediction models are trained at individual PV stations, and the model parameters are updated using federated learning algorithms on a cloud server. This enables secure information sharing and knowledge distillation among multiple PV stations.
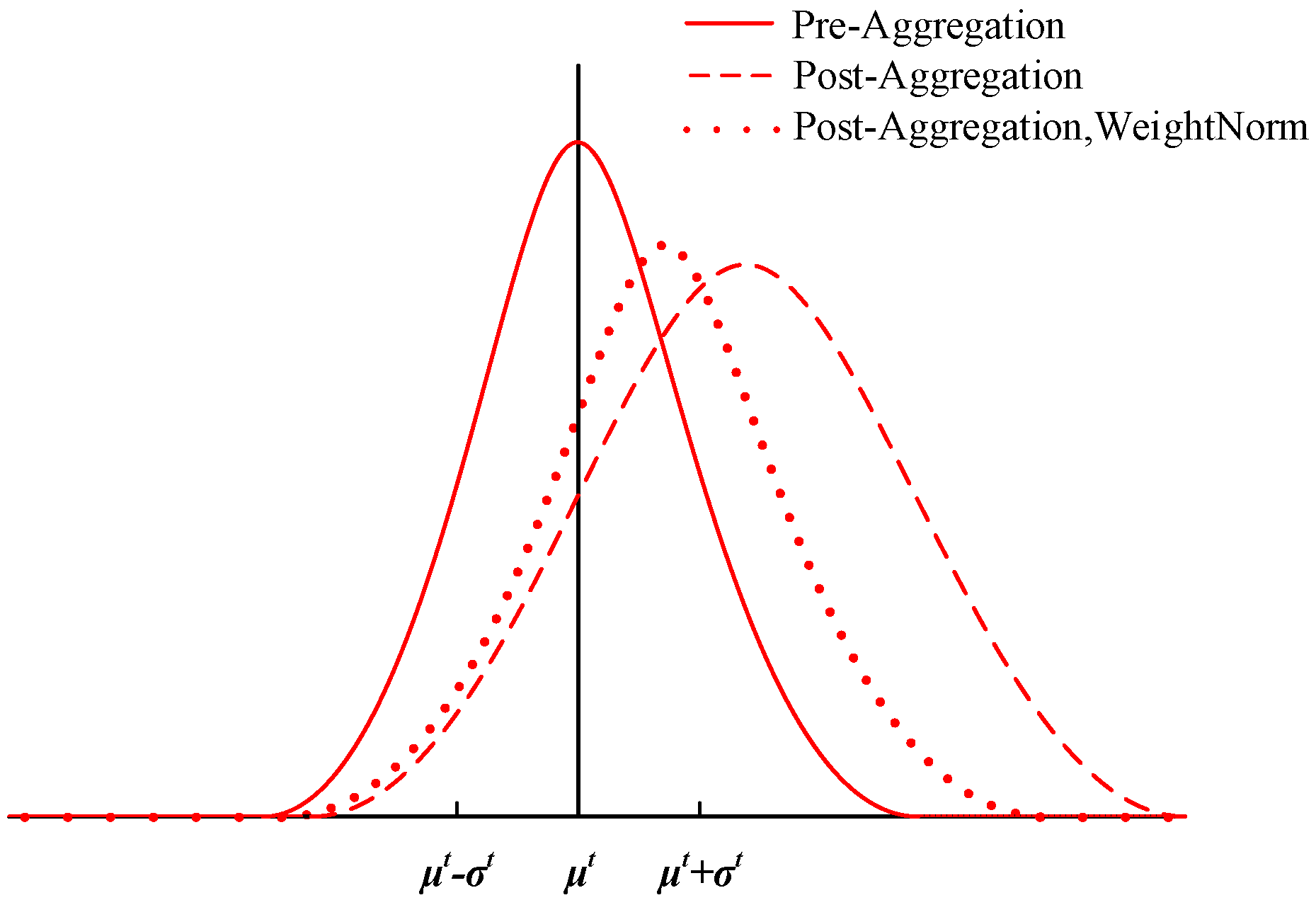
- In the process of Personalized Federated Multi-Task Learning (PFL), a multi-task training method is proposed. Clients have the capability to maintain the confidentiality of the Weight Normalization (WN) layer and develop distinct personalized models tailored to their unique data characteristics. This addresses the limitation of conventional federated learning (FL), wherein a unified global model fails to enhance prediction accuracy across all PV stations.
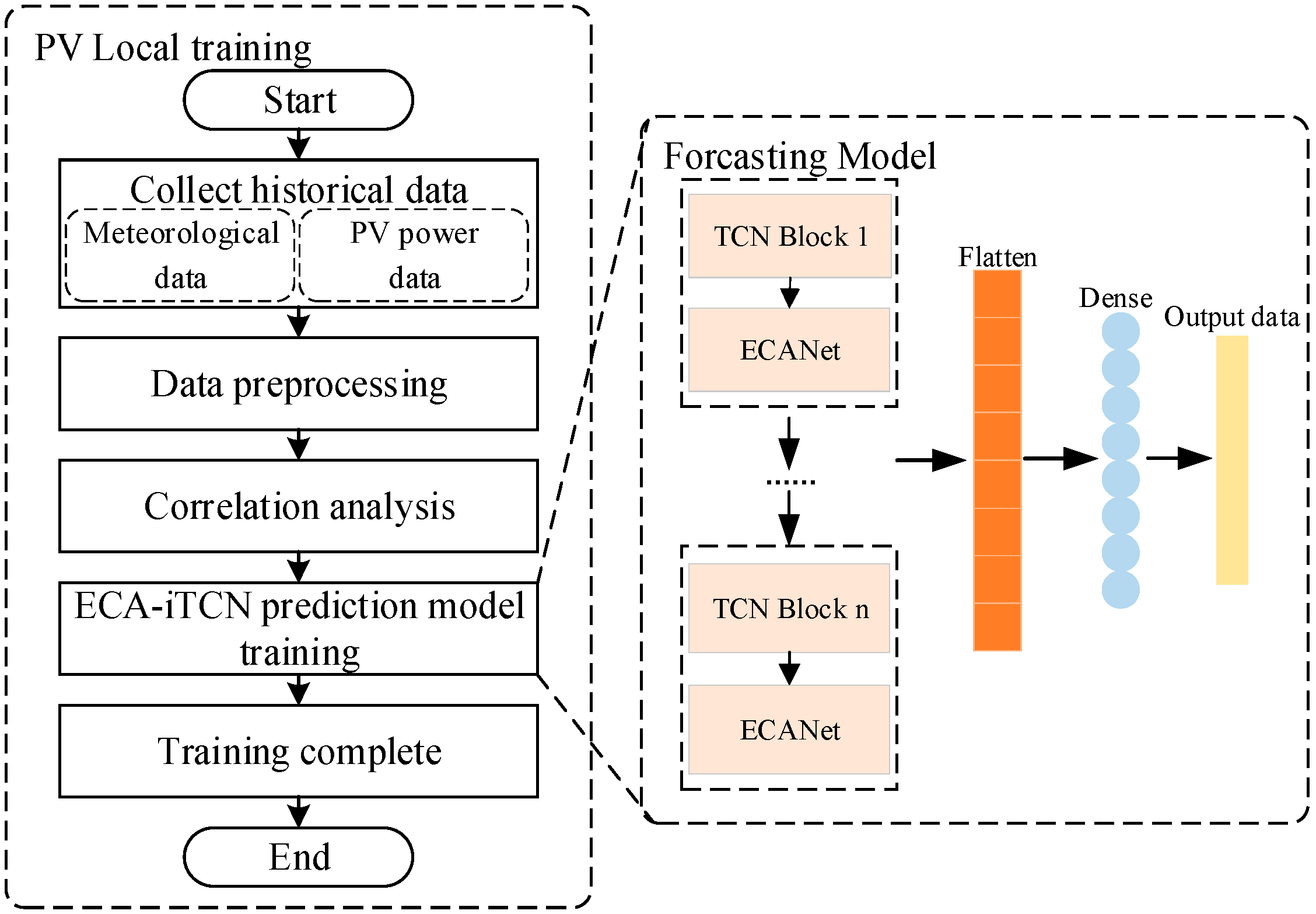
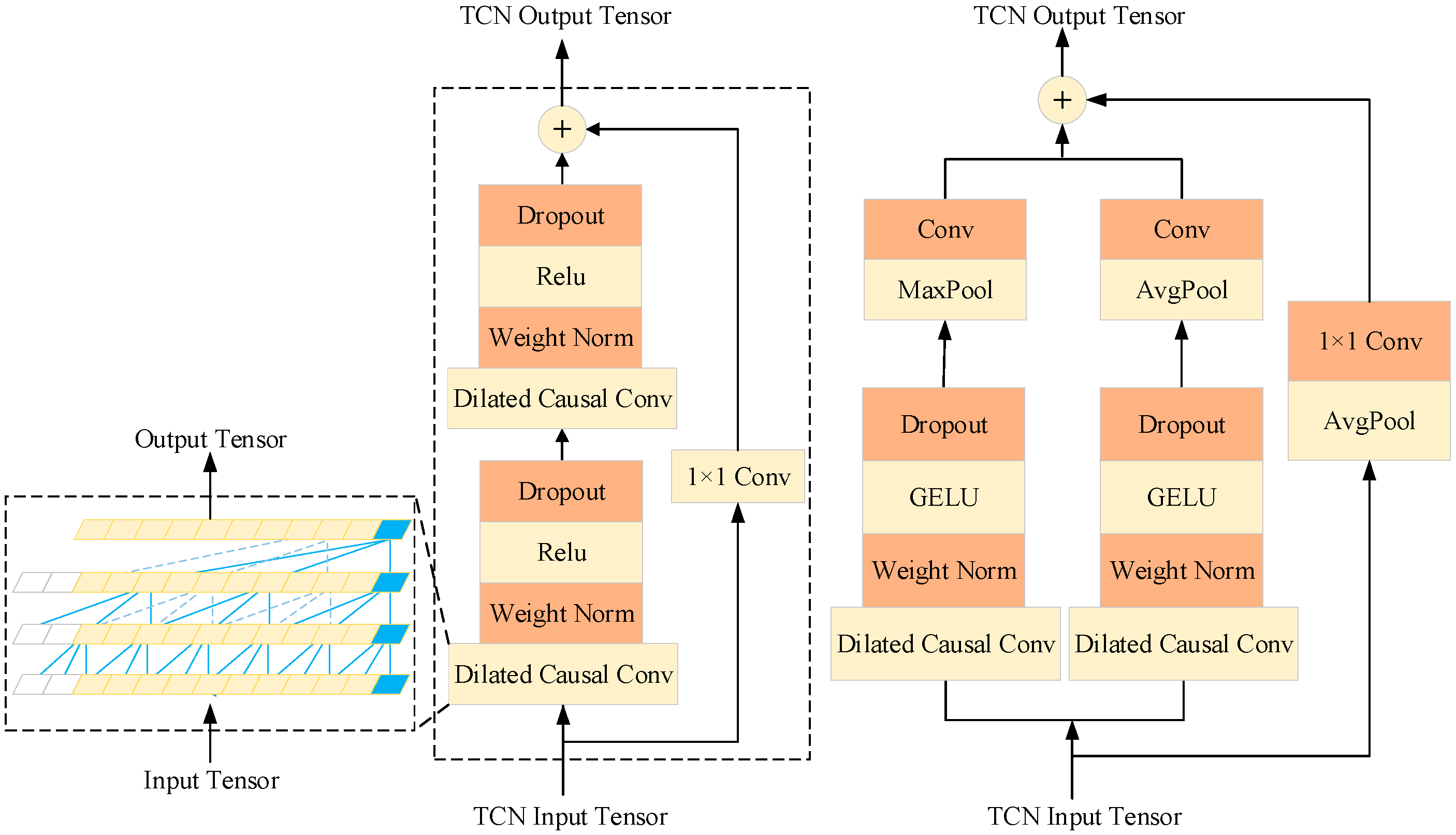
- An improved CBAM-iTCN PV power prediction model is proposed. The parallel pooling structure of the TCN is modified, and the attention mechanism CBAM net is added. By assigning different weights to different features extracted by the hidden layers of the TCN, key meteorological feature information is emphasized, enhancing the feature extraction capability for time series data in PV power prediction.
2. Related Works
2.1. Photovoltaic Power Prediction Based on Deep Learning
2.2. Federated Learning
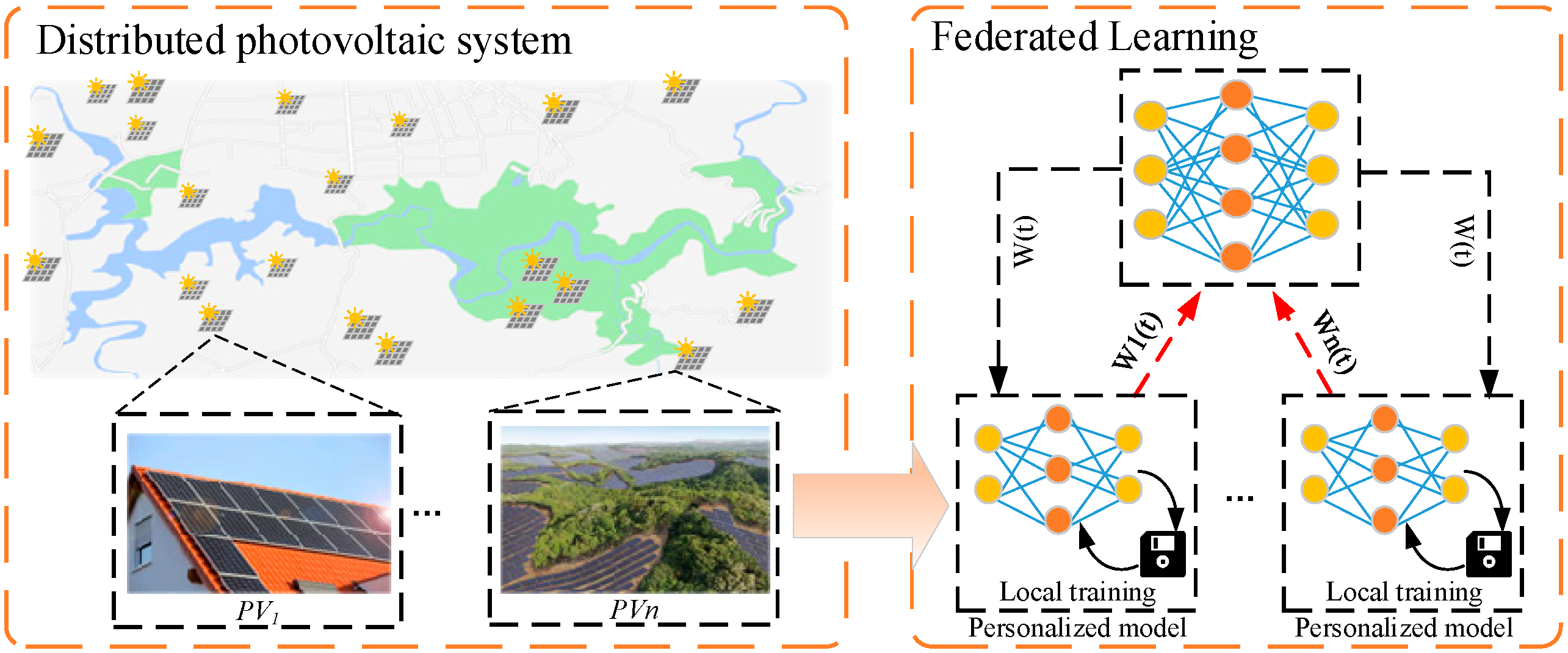
3. Overall Framework
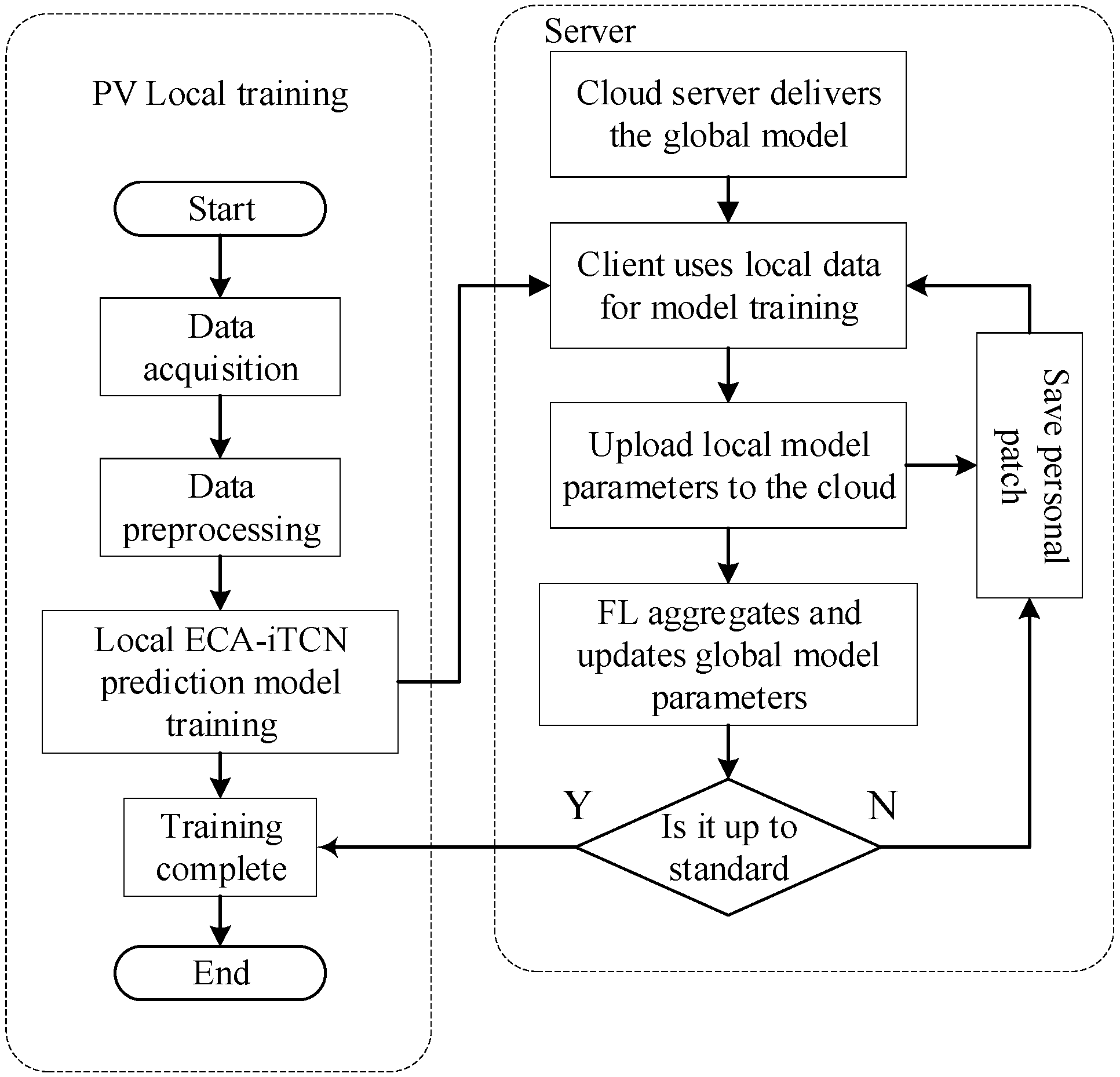
- For each photovoltaic power station, the local historical meteorological data and photovoltaic power data are preprocessed, including filling in missing data, abnormal data, and normalization.
- In response to task requests from the cloud server, each photovoltaic power station receives the global model parameters and utilizes its local historical photovoltaic and meteorological data to train the prediction model.
- Upon the completion of training, each photovoltaic power station will transmit its model parameters to the cloud server and retain its personalized update for the current round. The ECS then collects the received model parameters and updates the global model accordingly. If the accuracy threshold is satisfied, the FL training process is concluded, resulting in the final global model. The last round of private patches is pushed back to a personalized model to improve the prediction accuracy and model adaptability of photovoltaic power plants.
- If the accuracy of the aggregated global prediction model does not meet the standard, the global model will be re-distributed to each photovoltaic power station, and steps 2 and 3 will be repeated until it meets the standard.
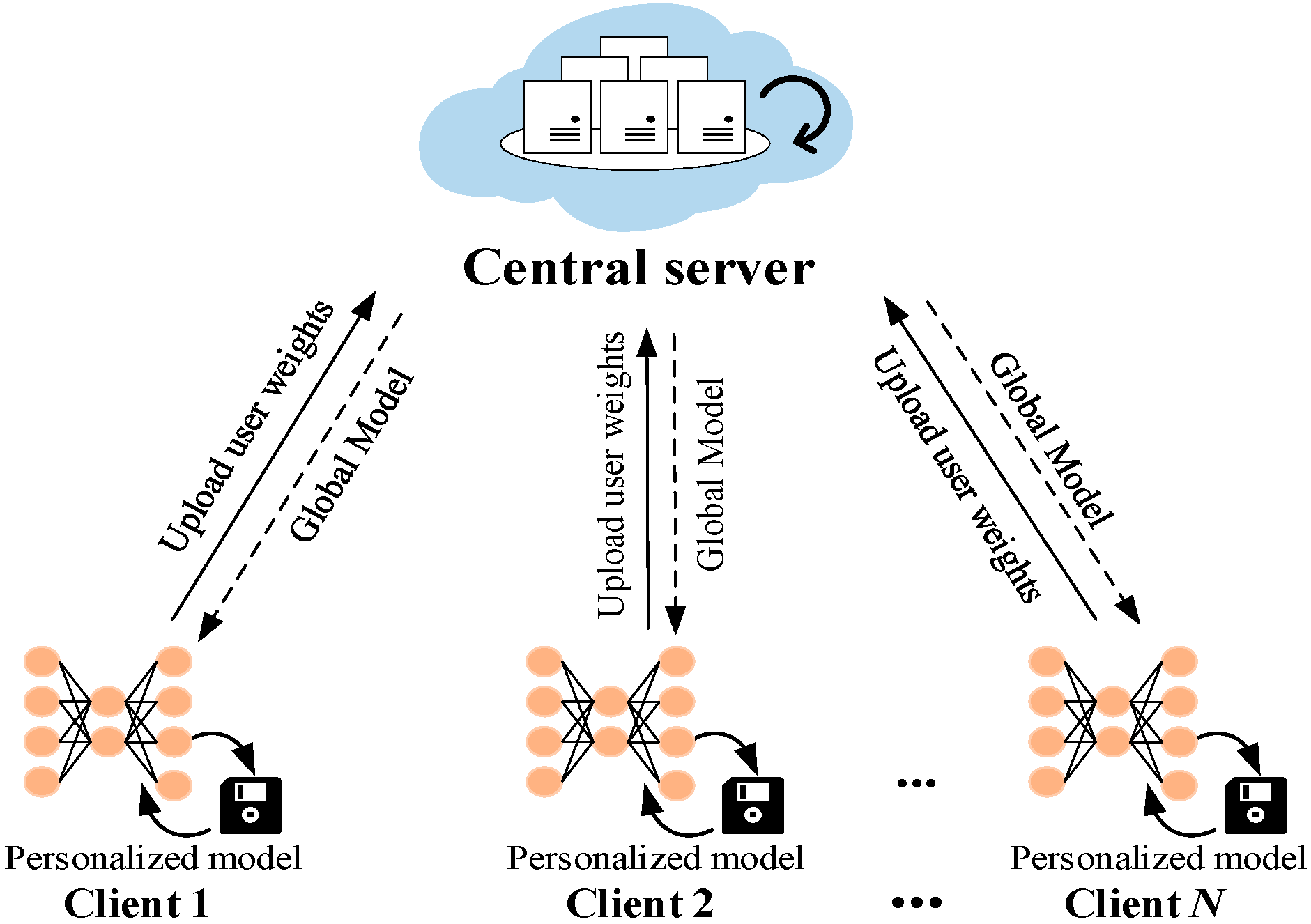
4. Personalized Federated Learning
4.1. Federated Learning
4.2. Personalized Federated Learning
5. Improved CBAM-iTCN
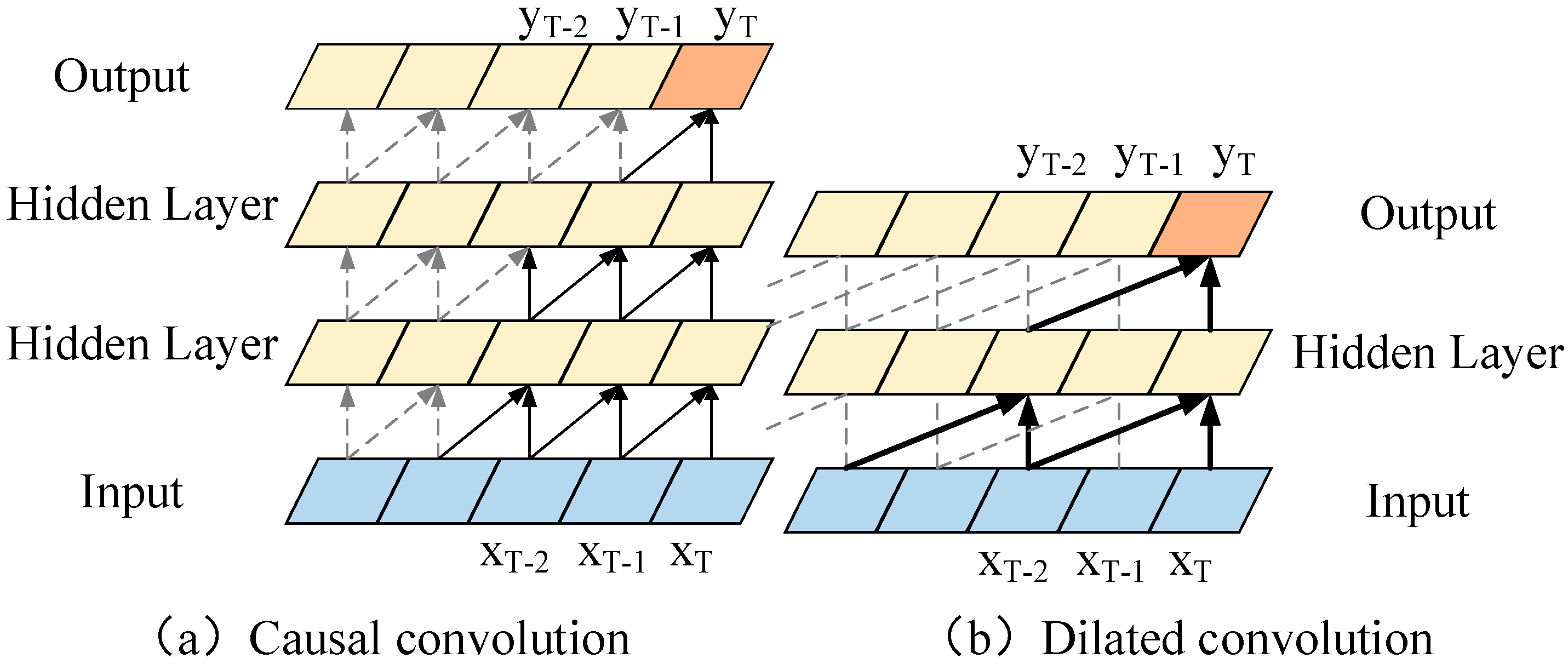
5.1. Temporal Convolutional Networks
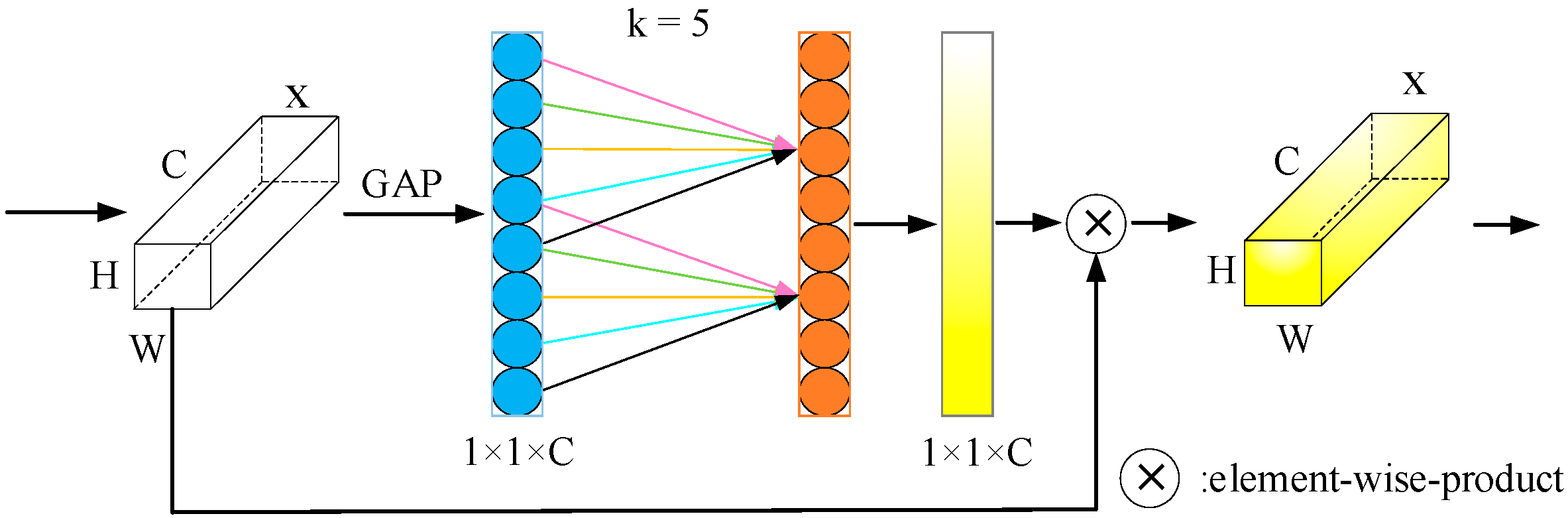
5.2. Attention Mechanism
6. Experimental Results and Analysis
6.1. Dateset
6.2. Evaluating Indicator
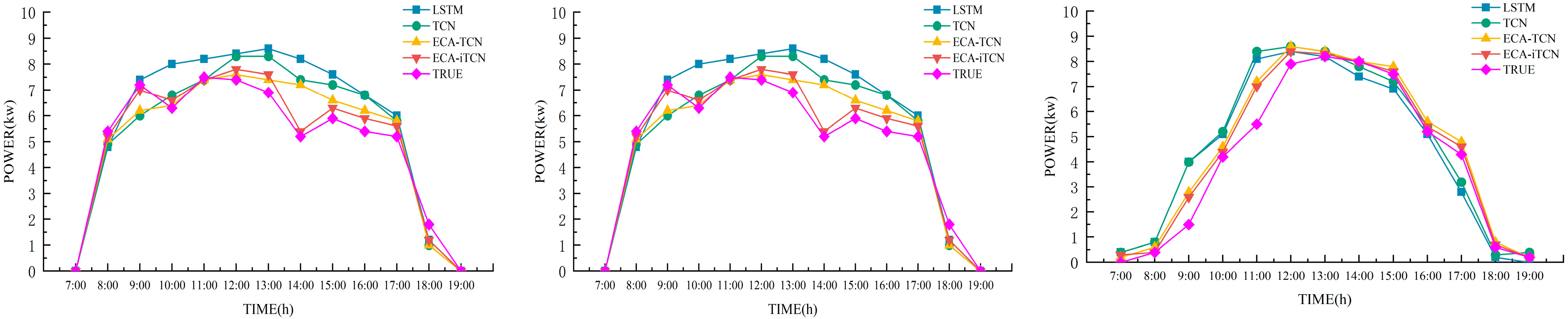
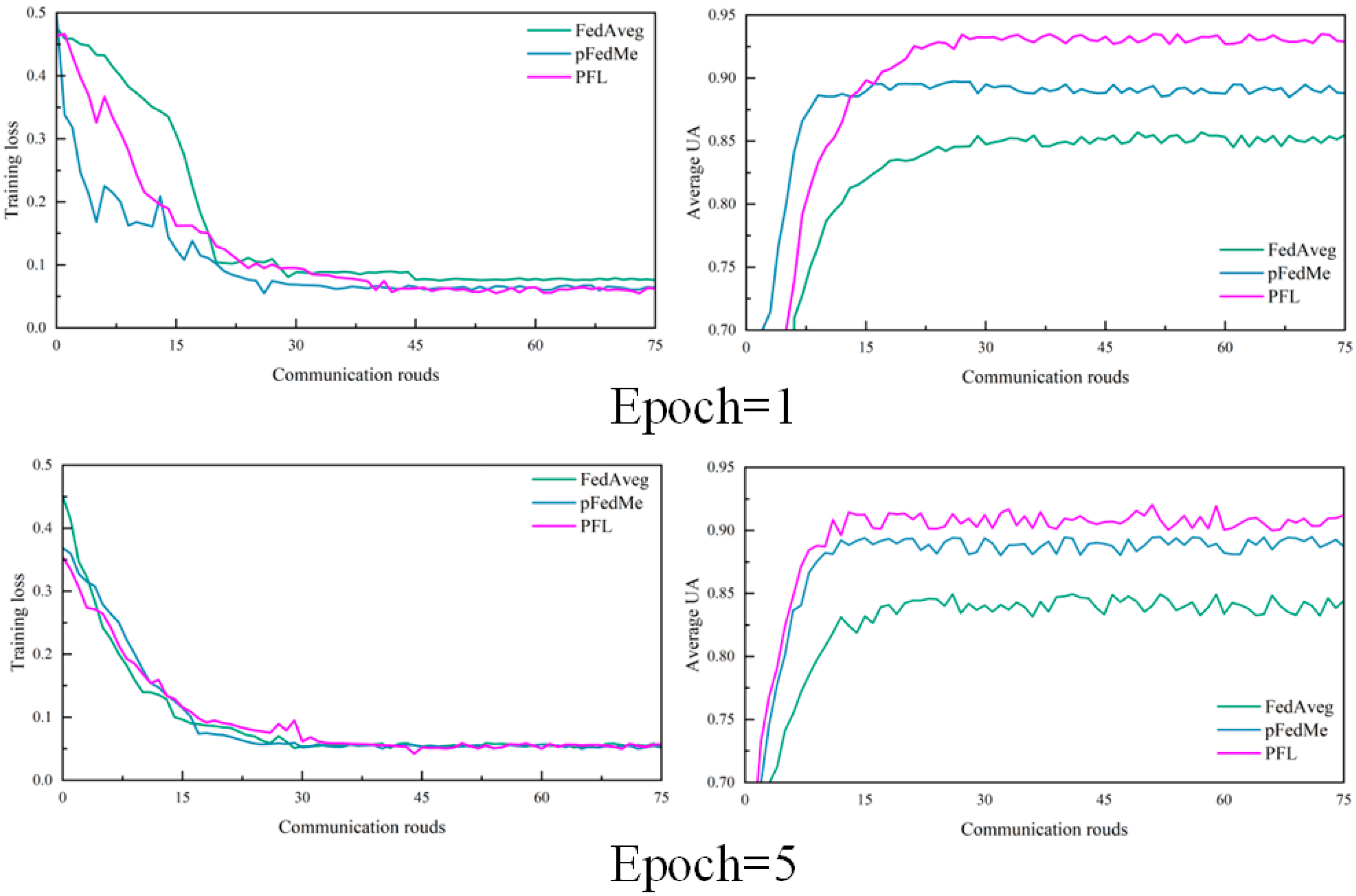
6.3. Model Training and Experimental Results
7. Conclusions
- (1)
- Improve the personalized federated learning algorithm to reduce computational cost;
- (2)
- Enhance the generalization ability of federated learning to highly heterogeneous environments or noise data;
- (3)
- Introduce continuous learning strategies and update model parameters regularly.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PFL | Personalized Federated Multi-Task Learning |
| iTCN | improved time series convolution network |
| TCN | time series convolution network |
| DPV | Distributed Photovoltaic |
| WN | Weight Normalization |
| FL | Federated Learning |
| CNN | Convolutional Neural Network |
| LSTM | long-term and short-term memory network |
| FedAvg | federal averaging |
| FML | Federated Meta-Learning |
| AFL | Adaptive Federated Learning |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Error Ratio |
| GRA | Grey Relational Analysis |
References
- United Nations. Department of Economic and Social Affairs. The Sustainable Development Goals: Report 2022; UN: New York, NY, USA, 2022. [Google Scholar]
- Dai, Q.; Huo, X.; Su, D.; Cui, Z. Photovoltaic power prediction based on sky images and tokens-to-token vision transformer. Int. J. Renew. Energy Dev. 2023, 12, 1104–1112. [Google Scholar] [CrossRef]
- Kim, G.G.; Choi, J.H.; Park, S.Y.; Bhang, B.G.; Nam, W.J.; Cha, H.L.; Park, N.; Ahn, H.K. Prediction model for PV performance with correlation analysis of environmental variables. IEEE J. Photovolt. 2019, 9, 832–841. [Google Scholar] [CrossRef]
- Nelega, R.; Greu, D.I.; Jecan, E.; Rednic, V.; Zamfirescu, C.; Puschita, E.; Turcu, R.V.F. Prediction of Power Generation of a Photovoltaic Power Plant Based on Neural Networks. IEEE Access 2023, 11, 20713–20724. [Google Scholar] [CrossRef]
- Ma, D.; Xie, R.; Pan, G.; Zuo, Z.; Chu, L.; Ouyang, J. Photovoltaic Power Output Prediction Based on TabNet for Regional Distributed Photovoltaic Stations Group. Energies 2023, 16, 5649. [Google Scholar] [CrossRef]
- Zhou, N.R.; Zhou, Y.; Gong, L.H.; Jiang, M.L. Accurate prediction of photovoltaic power power based on long short-term memory network. IET Optoelectron. 2020, 14, 399–405. [Google Scholar]
- Chen, J.; Li, J.; Huang, R.; Yue, K.; Chen, Z.; Li, W. Federated Transfer Learning for Bearing Fault Diagnosis with Discrepancy-Based Weighted Federated Averaging. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, K.; Lin, S. FedUR: Federated Learning Optimization Through Adaptive Centralized Learning Optimizers. IEEE Trans. Signal Process. 2023, 71, 2622–2637. [Google Scholar] [CrossRef]
- Abaoud, M.; Almuqrin, M.A.; Khan, M.F. Advancing Federated Learning Through Novel Mechanism for Privacy Preservation in Healthcare Applications. IEEE Access 2023, 11, 83562–83579. [Google Scholar] [CrossRef]
- Saraswat, R.; Jhanwar, D.; Gupta, M. Sky Image Classification Based Solar Power Prediction Using CNN. Trait. Signal 2023, 40, 1731–1738. [Google Scholar] [CrossRef]
- Jakoplić, A.; Franković, D.; Havelka, J.; Bulat, H. Short-Term Photovoltaic Power Plant Output Forecasting Using Sky Images and Deep Learning. Energies 2023, 16, 5428. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, F.; Li, D.; He, H.; Zhang, T.; Yang, S. Prediction of Photovoltaic Power by the Informer Model Based on Convolutional Neural Network. Sustainability 2022, 14, 13022. [Google Scholar] [CrossRef]
- Yuqi, F.; Hui, L.I.; Lijuan, L.I. Voltage trajectory prediction of photovoltaic power station based on CNN-GRU. Electr. Power 2022, 55, 163–171. [Google Scholar]
- He, Y.; Gao, Q.; Jin, Y.; Liu, F. Short-term photovoltaic power forecasting method based on convolutional neural network. Energy Rep. 2022, 8, 54–62. [Google Scholar] [CrossRef]
- Ahn, H.K.; Park, N. Deep RNN-based photovoltaic power short-term forecast using power IoT sensors. Energies 2021, 14, 436. [Google Scholar] [CrossRef]
- Succetti, F.; Rosato, A.; Araneo, R.; Panella, M. Deep Neural Networks for Multivariate Prediction of Photovoltaic Power Time Series. IEEE Access 2020, 8, 211490–211505. [Google Scholar] [CrossRef]
- Lin, W.; Zhang, B.; Li, H.; Lu, R. Multi-step prediction of photovoltaic power based on two-stage decomposition and BILSTM. Neurocomputing 2022, 504, 56–67. [Google Scholar] [CrossRef]
- Wang, S.; Ma, J. A novel GBDT-BiLSTM hybrid model on improving day-ahead photovoltaic prediction. Sci. Rep. 2023, 13, 15113. [Google Scholar] [CrossRef]
- Liu, L.; Sun, Q.; Wennersten, R.; Chen, Z. Day-Ahead Forecast of Photovoltaic Power Based on a Novel Stacking Ensemble Method. IEEE Access 2023, 11, 113593–113604. [Google Scholar] [CrossRef]
- Xiao, Z.; Huang, X.; Liu, J.; Li, C.; Tai, Y. A novel method based on time series ensemble model for hourly photovoltaic power prediction. Energy 2023, 276, 127542. [Google Scholar] [CrossRef]
- Cheng, L.; Zang, H.; Wei, Z.; Ding, T.; Sun, G. Solar Power Prediction Based on Satellite Measurements—A Graphical Learning Method for Tracking Cloud Motion. IEEE Trans. Power Syst. 2021, 37, 2335–2345. [Google Scholar] [CrossRef]
- Varma, R.K.; Akbari, M. Simultaneous Fast Frequency Control and Power Oscillation Damping by Utilizing PV Solar System as PV-STATCOM. IEEE Trans. Sustain. Energy 2019, 11, 415–425. [Google Scholar] [CrossRef]
- Asiri, E.C.; Chung, C.Y.; Liang, X. Day-Ahead Prediction of Distributed Regional-Scale Photovoltaic Power. IEEE Access 2023, 11, 27303–27316. [Google Scholar] [CrossRef]
- Nitisanon, S.; Hoonchareon, N. Solar power forecast with weather classification using self-organized map. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Pan, C.; Tan, J. Day-Ahead Hourly Forecasting of Solar Generation Based on Cluster Analysis and Ensemble Model. IEEE Access 2019, 7, 112921–112930. [Google Scholar] [CrossRef]
- Witt, L.; Heyer, M.; Toyoda, K.; Samek, W.; Li, D. Decentral and Incentivized Federated Learning Frameworks: A Systematic Literature Review. IEEE Internet Things J. 2022, 10, 3642–3663. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Aguera y Arcas, B. Communication-efficient learning of deep networks from decentralized data. Artificial intelligence and statistics. Proc. Mach. Learn. Res. 2017, 54, 1273–1282. [Google Scholar]
- Nishio, T.; Yonetani, R. Client selection for federated learning with heterogeneous resources in mobile edge. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–7. [Google Scholar]
- Deng, F.; Zeng, Z.; Mao, W.; Wei, B.; Li, Z. A Novel Transmission Line Defect Detection Method Based on Adaptive Federated Learning. IEEE Trans. Instrum. Meas. 2023, 72, 1–12. [Google Scholar] [CrossRef]
- Chen, B.; Chen, T.; Zeng, X.; Zhang, W.; Lu, Q.; Hou, Z.; Zhou, J.; Helal, S. DFML: Dynamic federated meta-learning for rare disease prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 21, 880–889. [Google Scholar]
- Zhang, P.; Sun, H.; Situ, J.; Jiang, C.; Xie, D. Federated Transfer Learning for IIoT Devices with Low Computing Power Based on Blockchain and Edge Computing. IEEE Access 2021, 9, 98630–98638. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, Y.B.; Ge, M.F.; Liu, J.; Wang, L. A Novel Bayesian-Optimization-Based Adversarial TCN for RUL Prediction of Bearings. IEEE Sens. J. 2022, 22, 20968–20977. [Google Scholar]
| Category | Edition |
|---|---|
| Operating system | Windows10 |
| CPU (Central server) | Intel Core i9-9900K Processor (Beijing, China) |
| CPU (Local server) | Intel Core i5-10200H Processor (Beijing, China) |
| GPU (Central server) | NVIDIA GeForce RTX 3080 Ti Graphics Card (Beijing, China) |
| GPU (Local server) | NVIDIA GeForce GTX 1660 Graphics Card (Beijing, China) |
| RAM | 32 Gb |
| Meteorological Factors | GRA Correlation |
|---|---|
| Active power | 1.000 |
| Solar radiation | 0.918 |
| Temperature | 0.56 |
| Wind speed | 0.056 |
| Relative humidity | −0.408 |
| Rainfall | −0.056 |
| Models | Spring | Summer | ||||||
|---|---|---|---|---|---|---|---|---|
| Sunny | Cloudy | Rain | Sunny | Cloudy | Rain | |||
| Centralized Learning | TCN | MAE | 0.7764 | 1.0652 | 1.1115 | 0.6352 | 0.8956 | 1.0325 |
| RMAE | 0.8756 | 1.5483 | 1.6168 | 0.7356 | 1.2497 | 1.4629 | ||
| LSTM | MAE | 0.3895 | 0.9546 | 1.2057 | 0.3036 | 0.7936 | 0.9832 | |
| RMAE | 0.4928 | 1.1719 | 1.4274 | 0.3982 | 1.0425 | 1.2952 | ||
| CBAM-TCN | MAE | 0.3255 | 0.8454 | 1.1456 | 0.2891 | 0.7052 | 0.9826 | |
| RMAE | 0.4565 | 0.9964 | 1.2564 | 0.4092 | 0.8925 | 1.1748 | ||
| Transformer | MAE | 0.2951 | 0.7562 | 0.9098 | 0.2581 | 0.6982 | 0.8791 | |
| RMAE | 0.3858 | 0.9076 | 1.2048 | 0.3287 | 0.8672 | 1.1349 | ||
| CBAM-iTCN | MAE | 0.2641 | 0.6423 | 0.7158 | 0.2273 | 0.6013 | 0.6891 | |
| RMAE | 0.3562 | 0.8547 | 1.1259 | 0.3159 | 0.7903 | 0.9864 | ||
| Federated Learning | FL-Transformer | MAE | 0.2731 | 0.6891 | 0.8314 | 0.2243 | 0.6142 | 0.8032 |
| RMAE | 0.3418 | 0.8158 | 1.0314 | 0.3014 | 0.7631 | 0.9868 | ||
| FL-CBAM-iTCN | MAE | 0.2519 | 0.5981 | 0.6482 | 0.2107 | 0.5572 | 0.6194 | |
| RMAE | 0.3215 | 0.7139 | 0.9381 | 0.2981 | 0.6739 | 0.8971 | ||
| PFL-CBAM-iTCN | MAE | 0.2117 | 0.5341 | 0.5982 | 0.1982 | 0.4832 | 0.5531 | |
| RMAE | 0.2971 | 0.6538 | 0.7891 | 0.2541 | 0.5936 | 0.7013 | ||
| Optimization Strategy | FedAvg | FedAdam | FedAvg-Adam | |||
|---|---|---|---|---|---|---|
| Epoch = 1 | Epoch = 5 | Epoch = 1 | Epoch = 5 | Epoch = 1 | Epoch = 5 | |
| FL | 256 | 171 | 124 | 73 | 22 | 18 |
| PFL | 53 | 48 | 31 | 24 | 12 | 9 |
| MAPE% | RASE/KW | |||
|---|---|---|---|---|
| Global Model | Personalized Model | Global Model | Personalized Model | |
| Client 1 | 7.82 | 5.79 | 8.81 | 2.55 |
| Client 2 | 19.13 | 6.08 | 9.75 | 2.67 |
| Client 3 | 11.87 | 5.84 | 9.58 | 2.62 |
| Client 4 | 24.47 | 6.41 | 10.61 | 2.68 |
| Average | 15.82 | 6.03 | 9.69 | 2.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, W.; Shen, Y.; Li, Z.; Deng, F. Distributed Photovoltaic Short-Term Power Prediction Based on Personalized Federated Multi-Task Learning. Energies 2025, 18, 1796. https://doi.org/10.3390/en18071796
Luo W, Shen Y, Li Z, Deng F. Distributed Photovoltaic Short-Term Power Prediction Based on Personalized Federated Multi-Task Learning. Energies. 2025; 18(7):1796. https://doi.org/10.3390/en18071796
Chicago/Turabian StyleLuo, Wenxiang, Yang Shen, Zewen Li, and Fangming Deng. 2025. "Distributed Photovoltaic Short-Term Power Prediction Based on Personalized Federated Multi-Task Learning" Energies 18, no. 7: 1796. https://doi.org/10.3390/en18071796
APA StyleLuo, W., Shen, Y., Li, Z., & Deng, F. (2025). Distributed Photovoltaic Short-Term Power Prediction Based on Personalized Federated Multi-Task Learning. Energies, 18(7), 1796. https://doi.org/10.3390/en18071796





