A Single-Phase Modular Multilevel Converter Based on a Battery Energy Storage System for Residential UPS with Two-Level Active Balancing Control
Abstract
:1. Introduction
2. Single-Phase MMC-BESS Configuration and Modeling
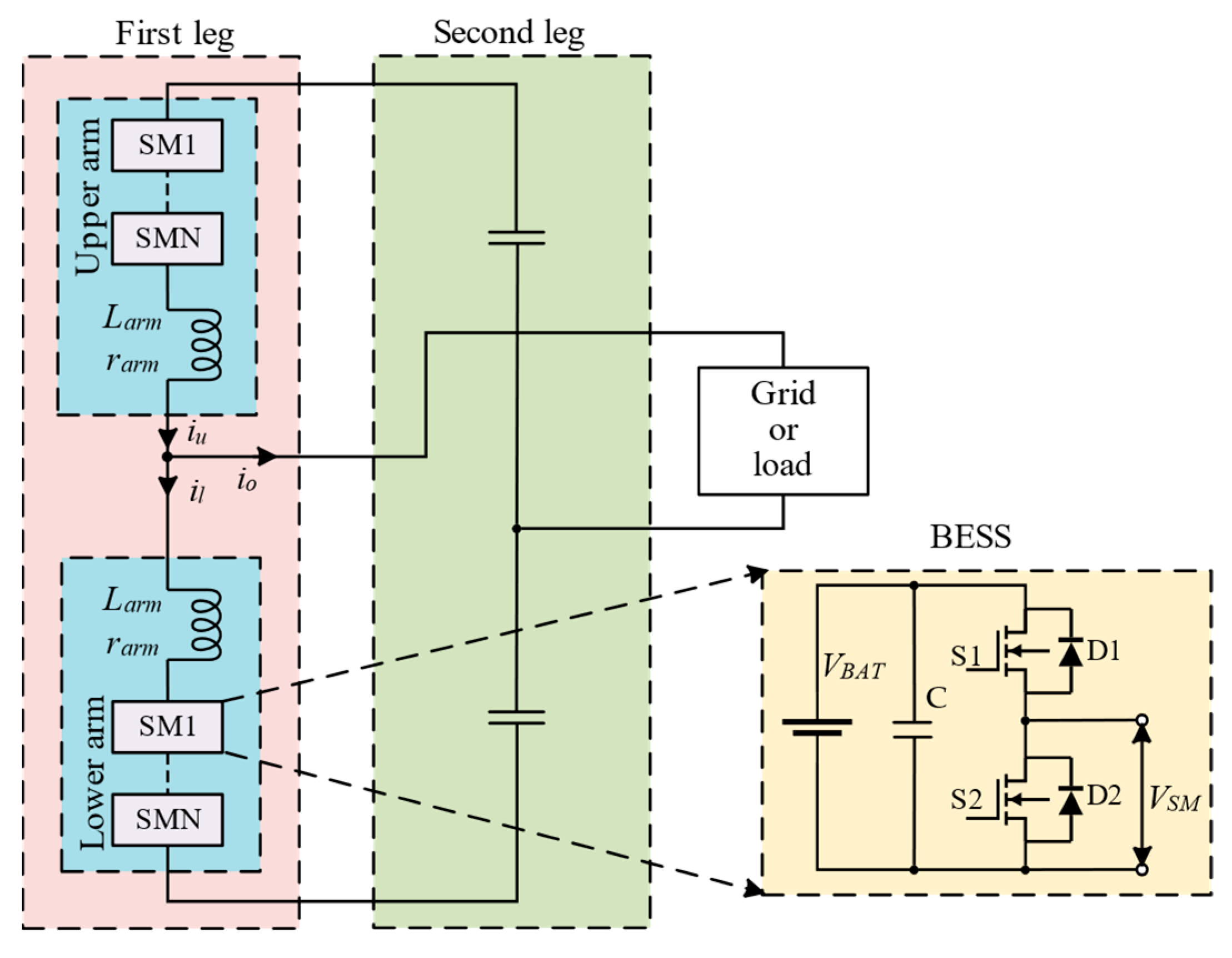
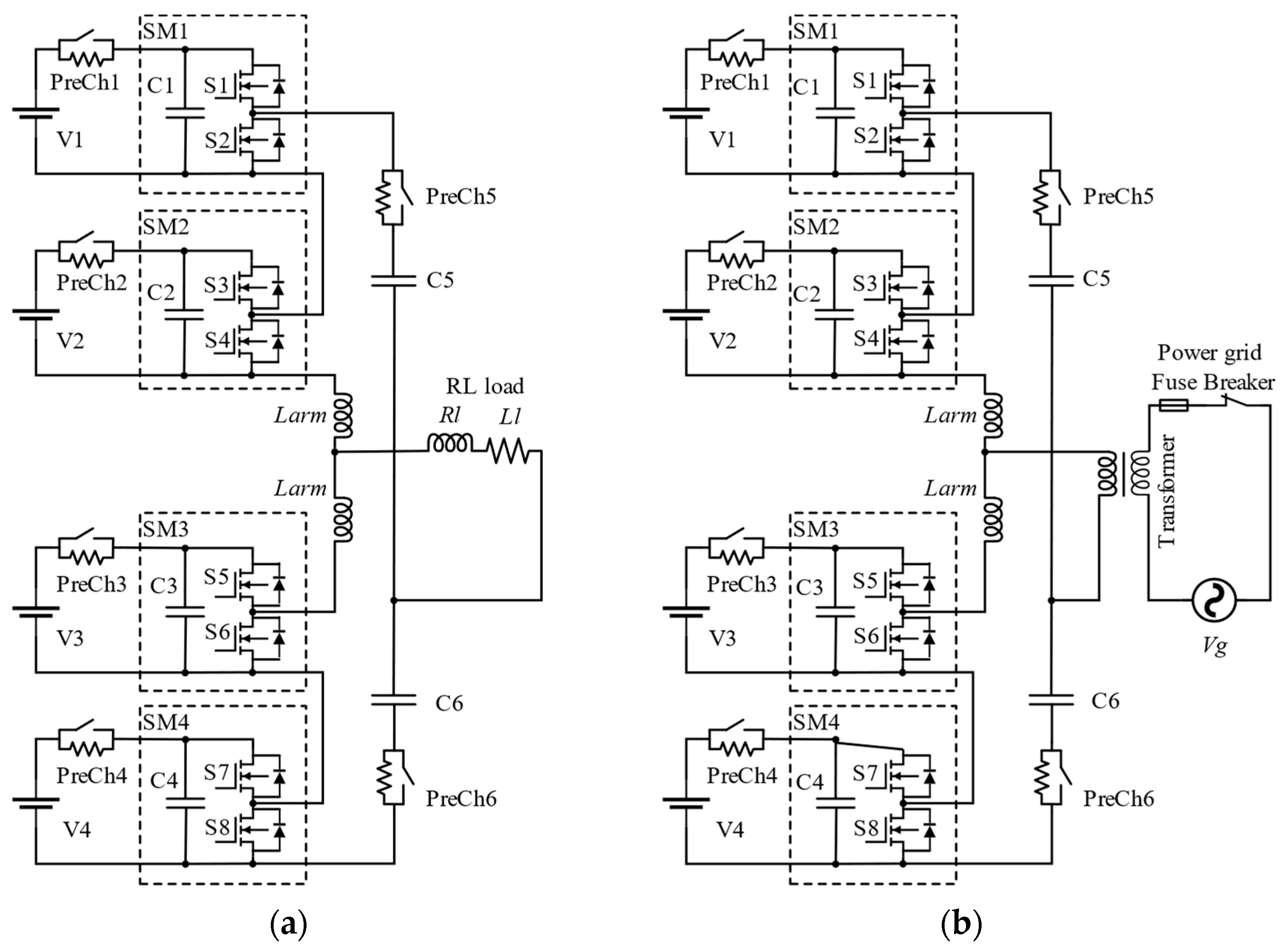
2.1. MMC-BESS Configuration
2.2. Mathematical Modeling
3. MMC-BESS Control Strategy
3.1. Dual-Loop Output Voltage and Current Control in Islanded Mode
3.2. Grid-Connected Control
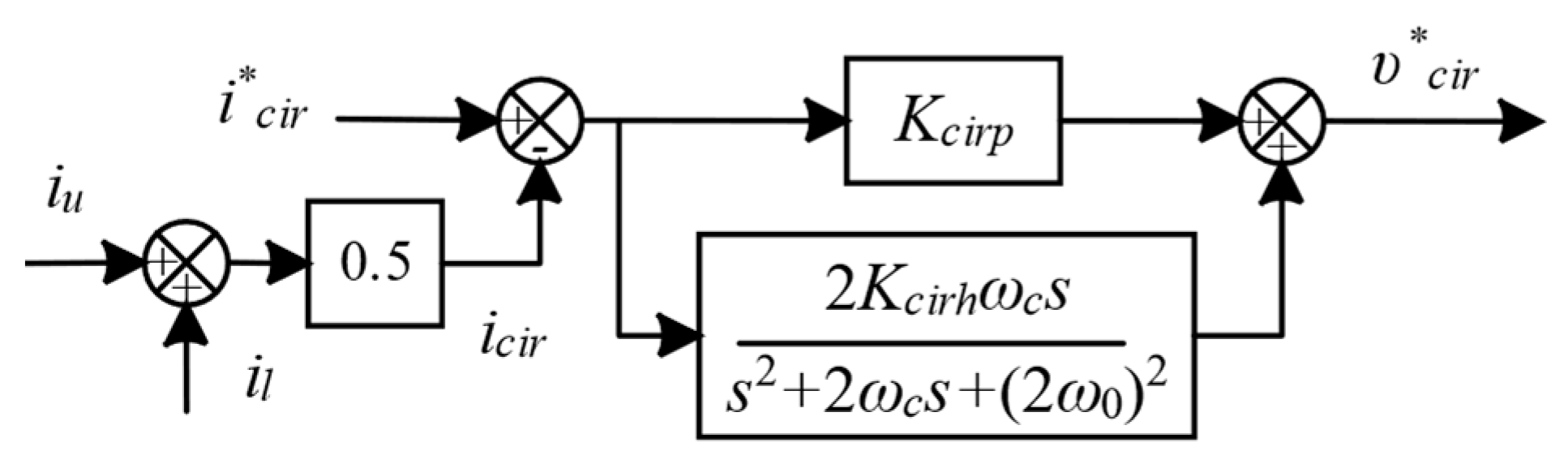
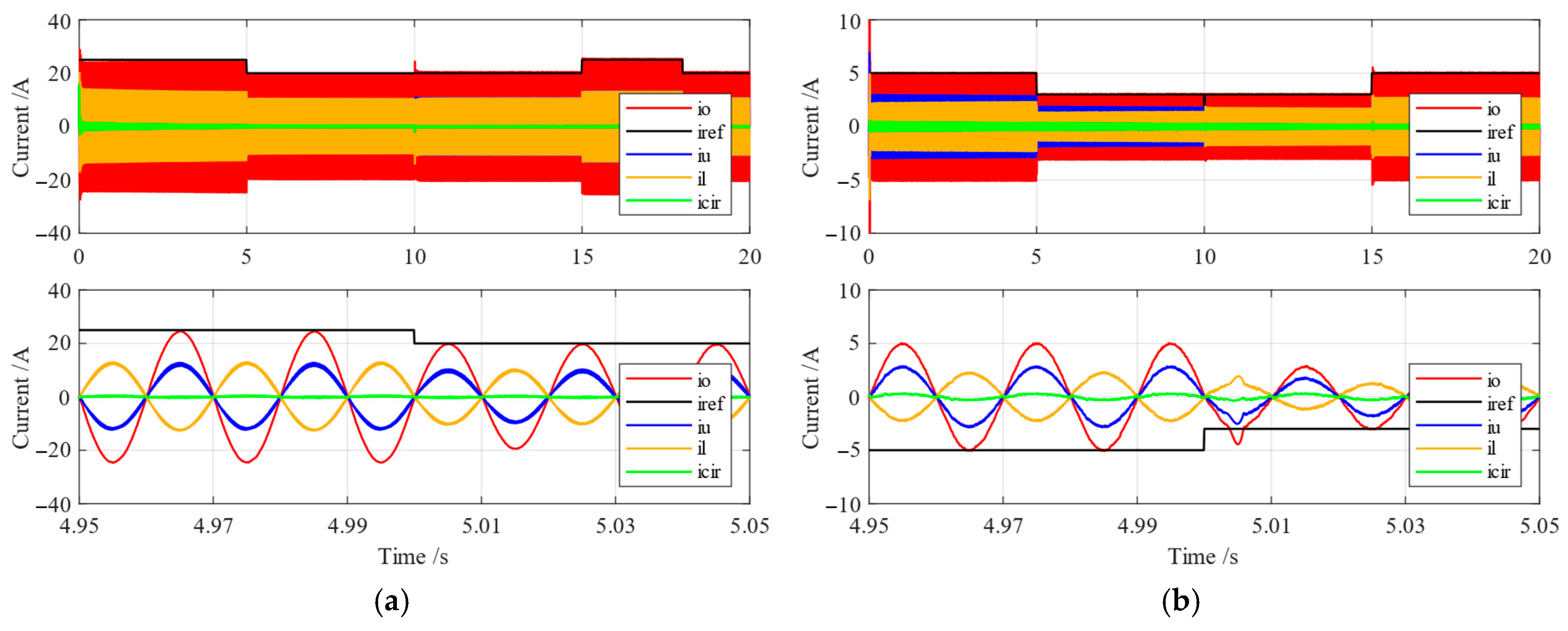
3.3. Circulating Current Control
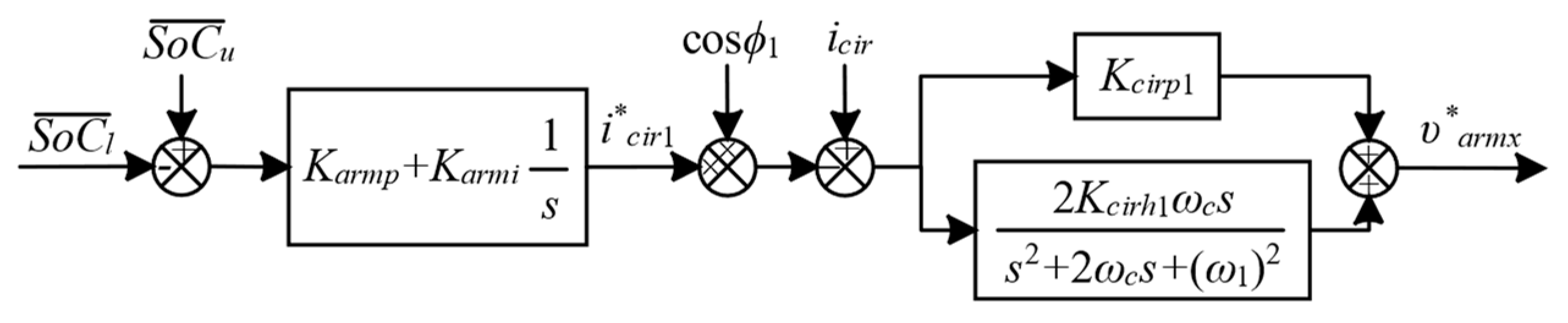
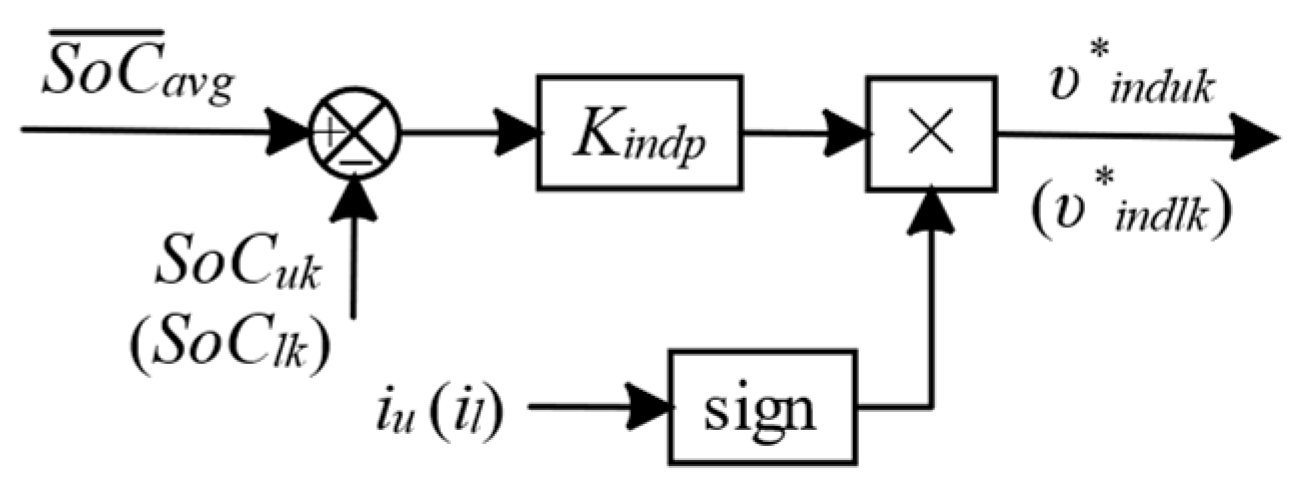
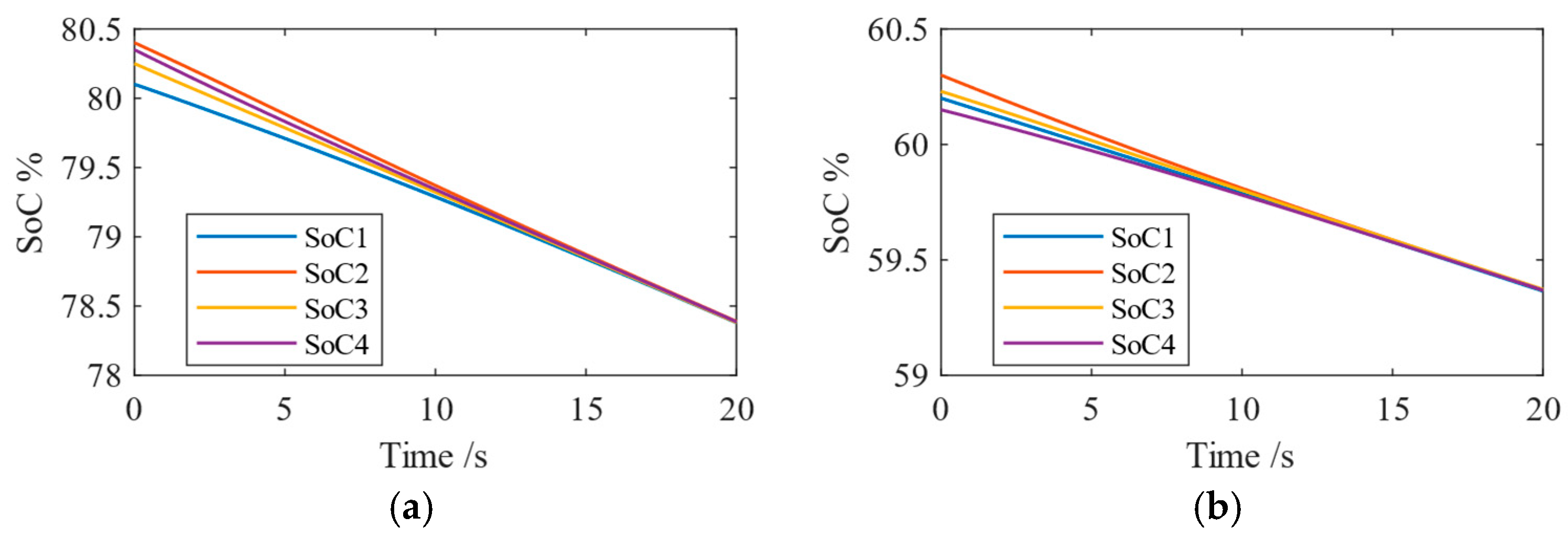
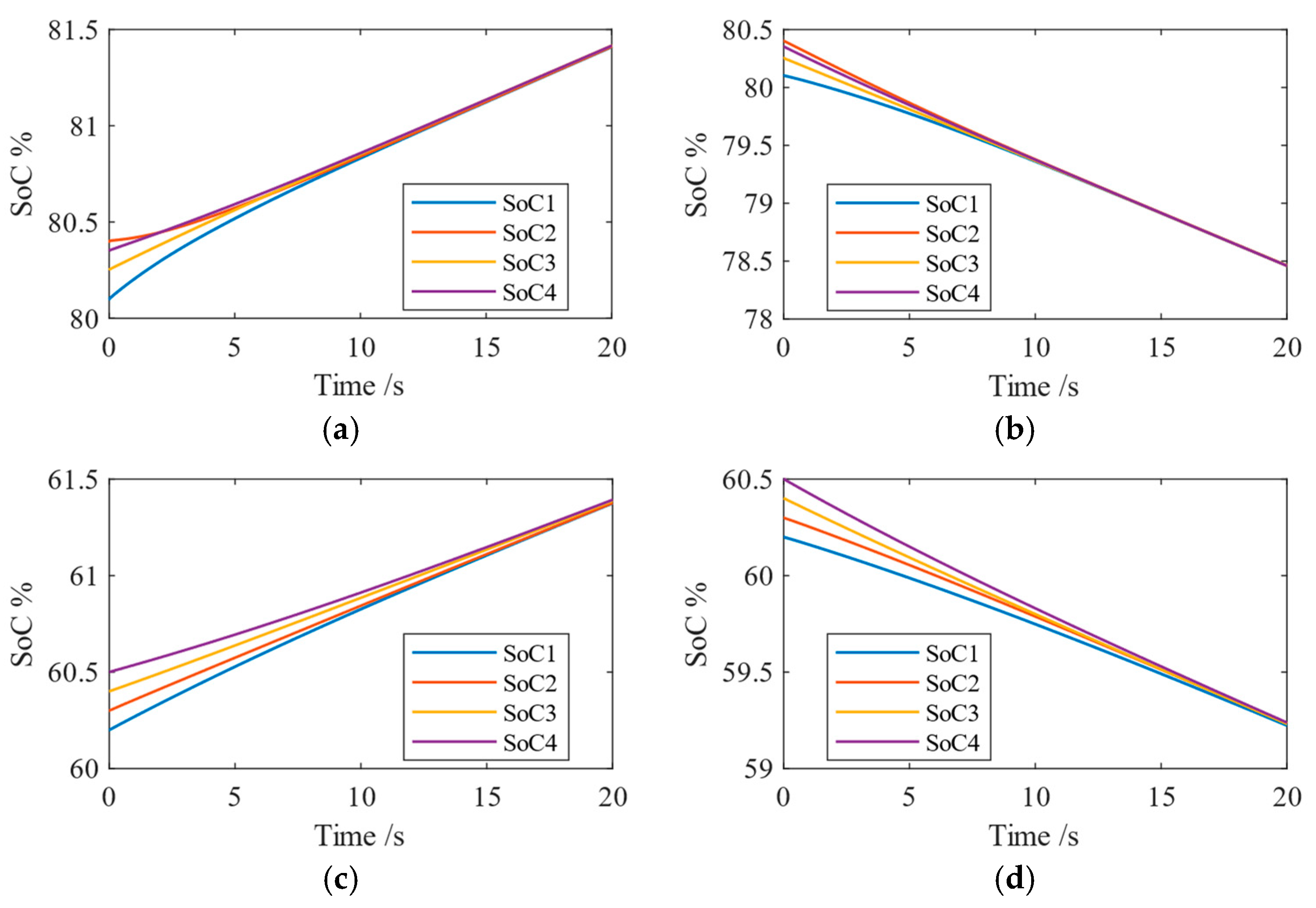
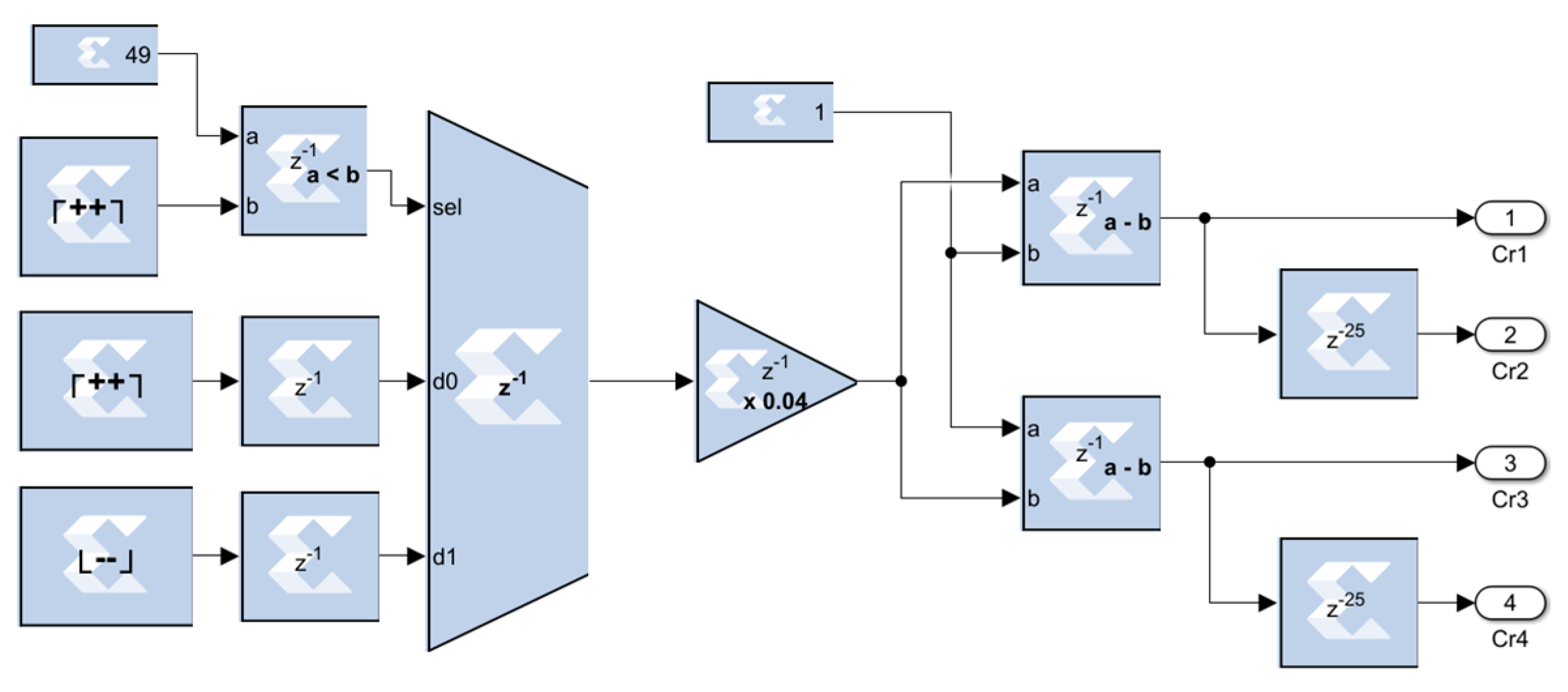
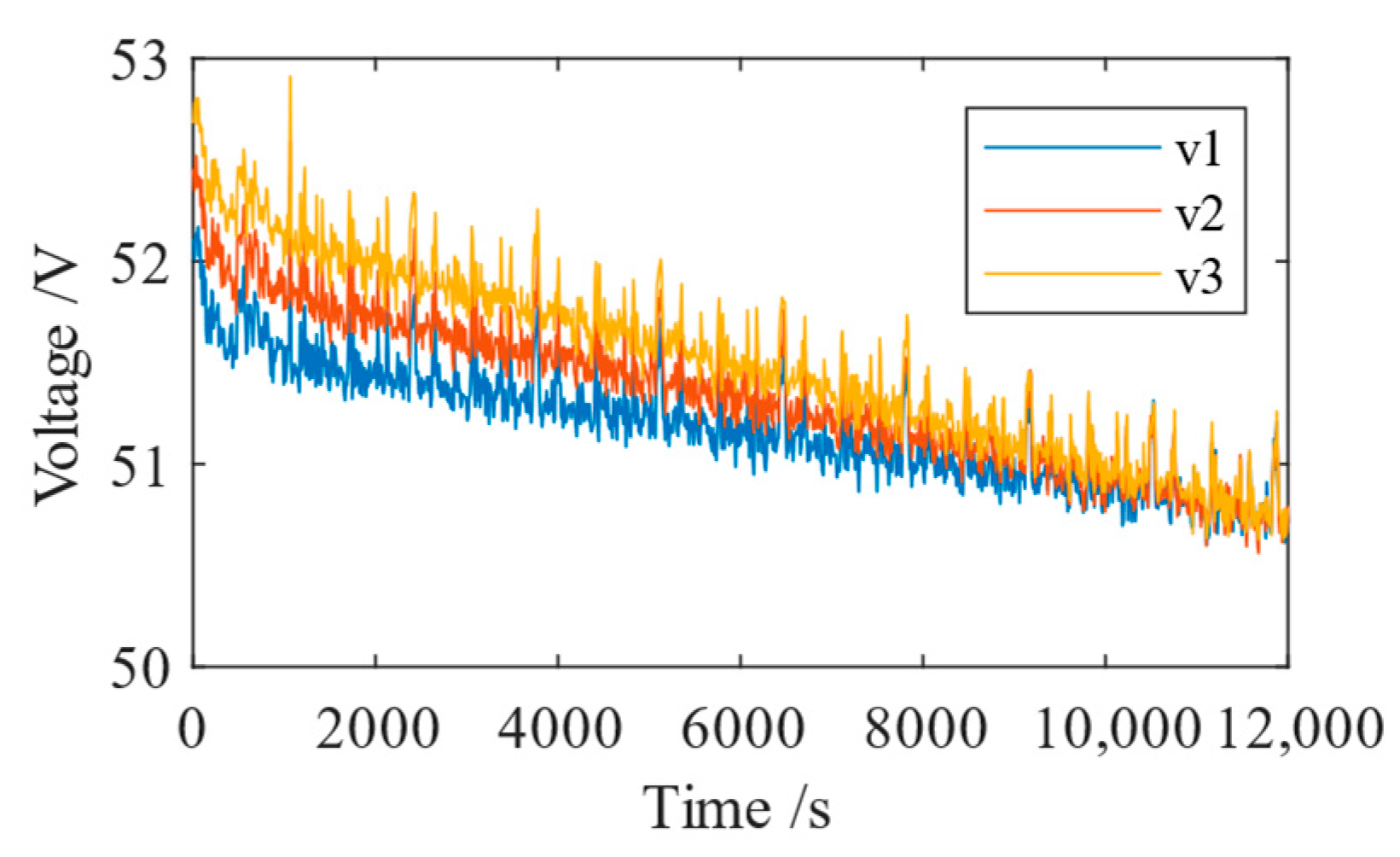
3.4. Two-Level Active SoC Balancing Control
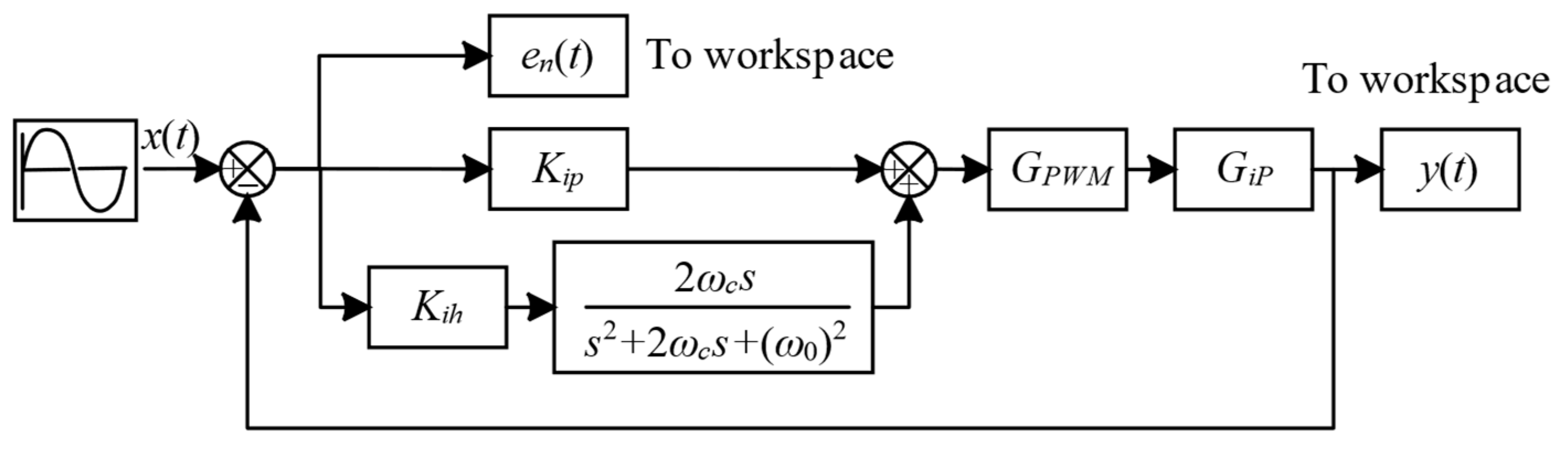
4. Design and Optimization of QPR Controller
4.1. Boundaries of Control Gains
4.2. Performance Evaluation of Sinusoidal Reference
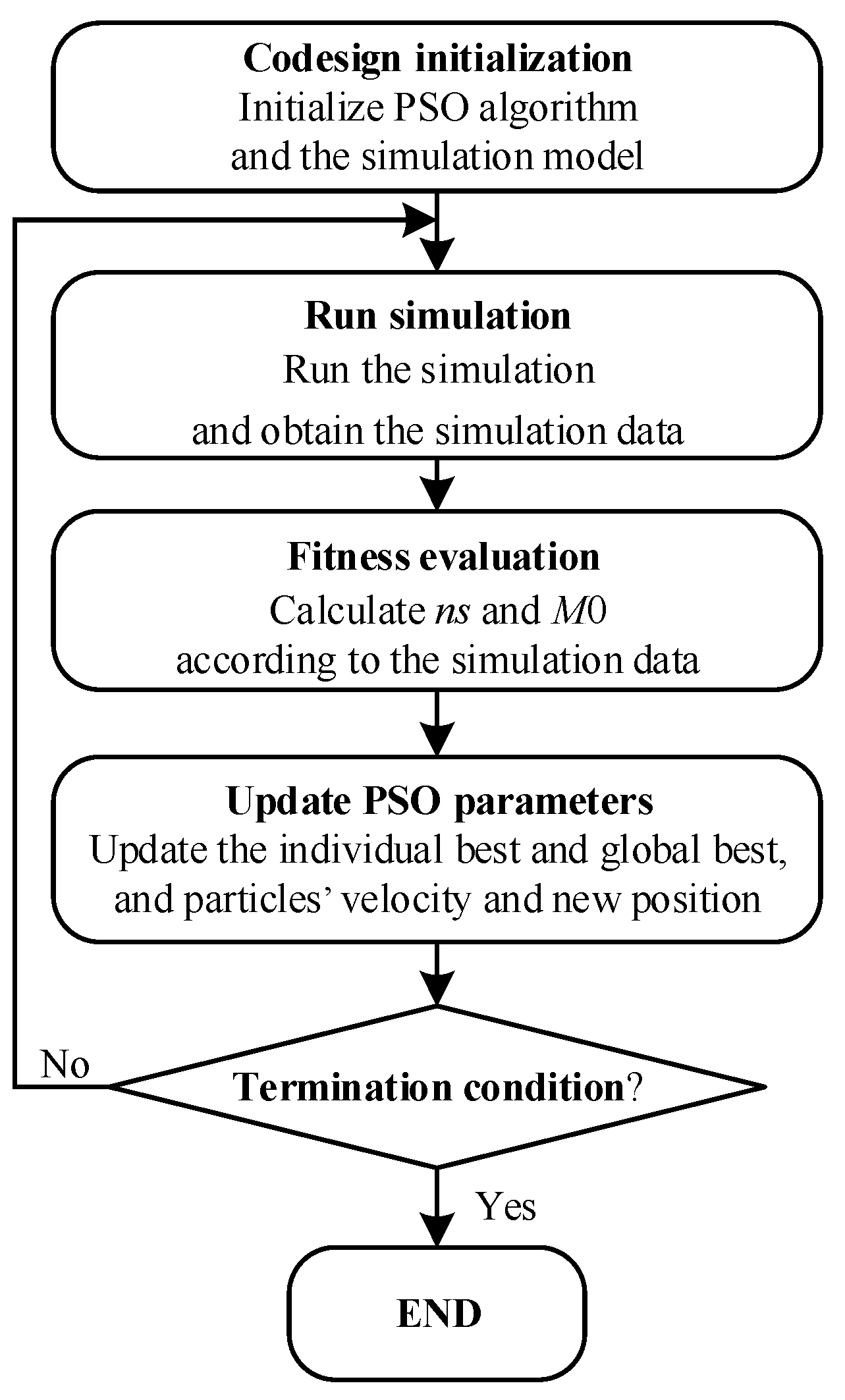
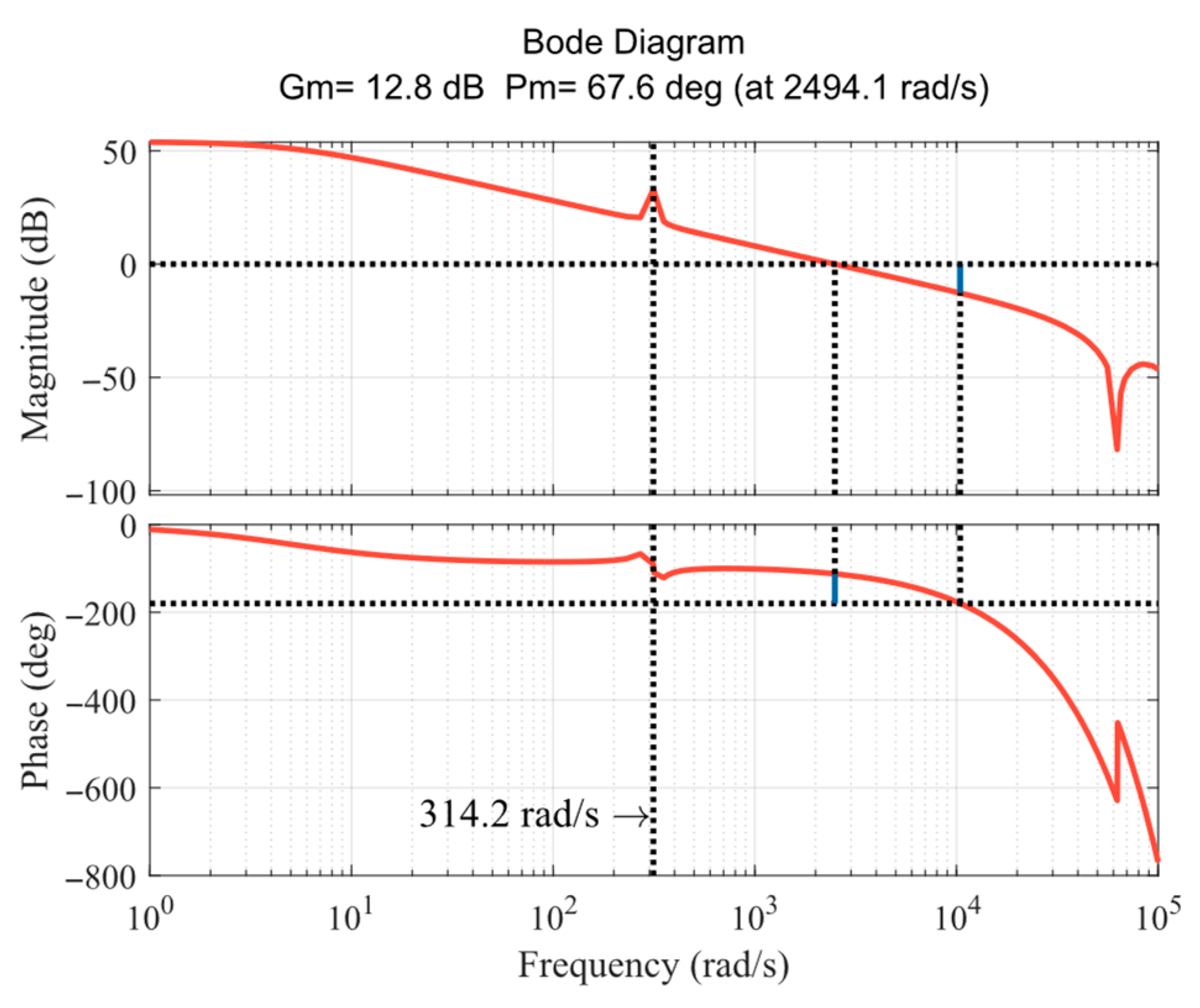
4.3. Optimization of QPR Controller
5. Simulation Results
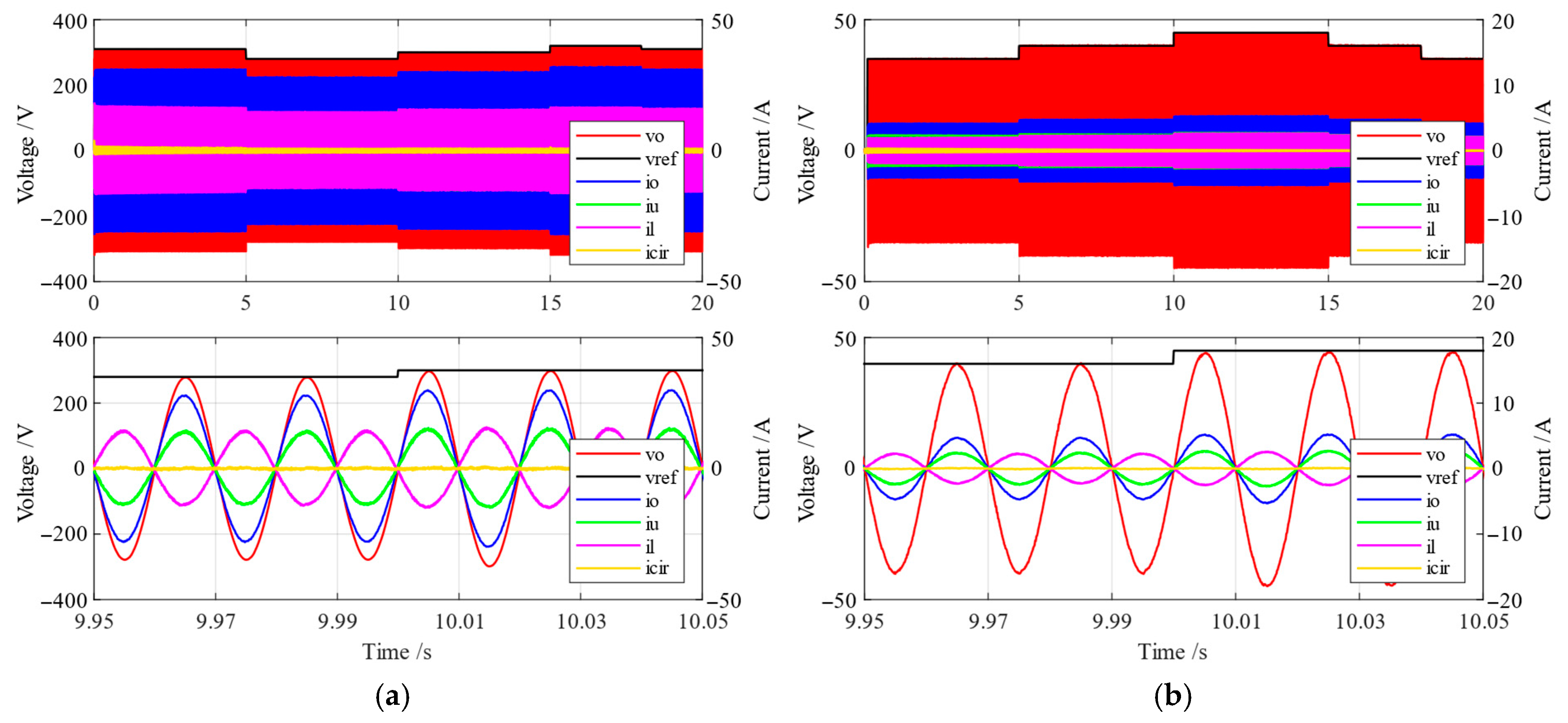
5.1. Simulation in Islanded Mode
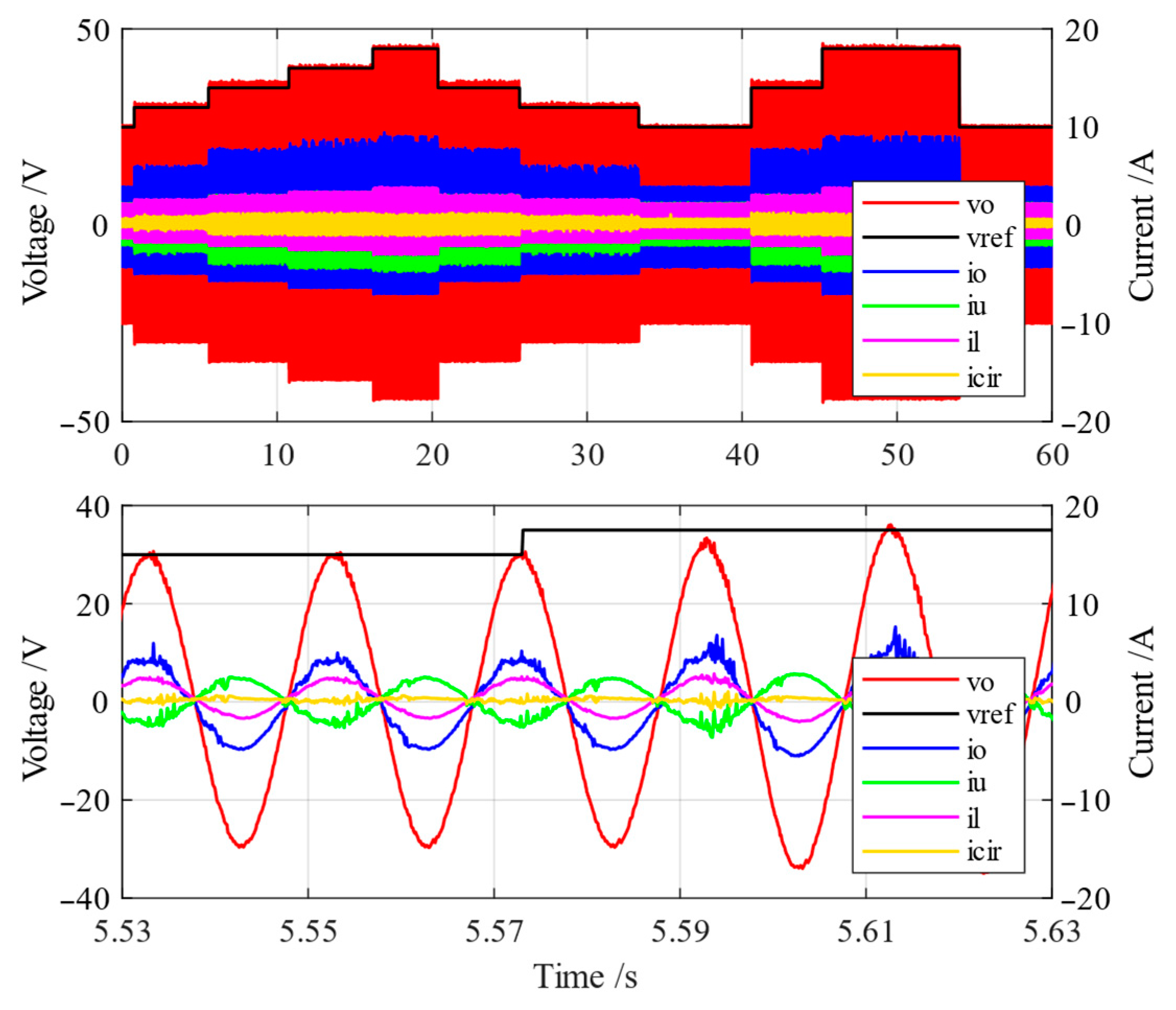
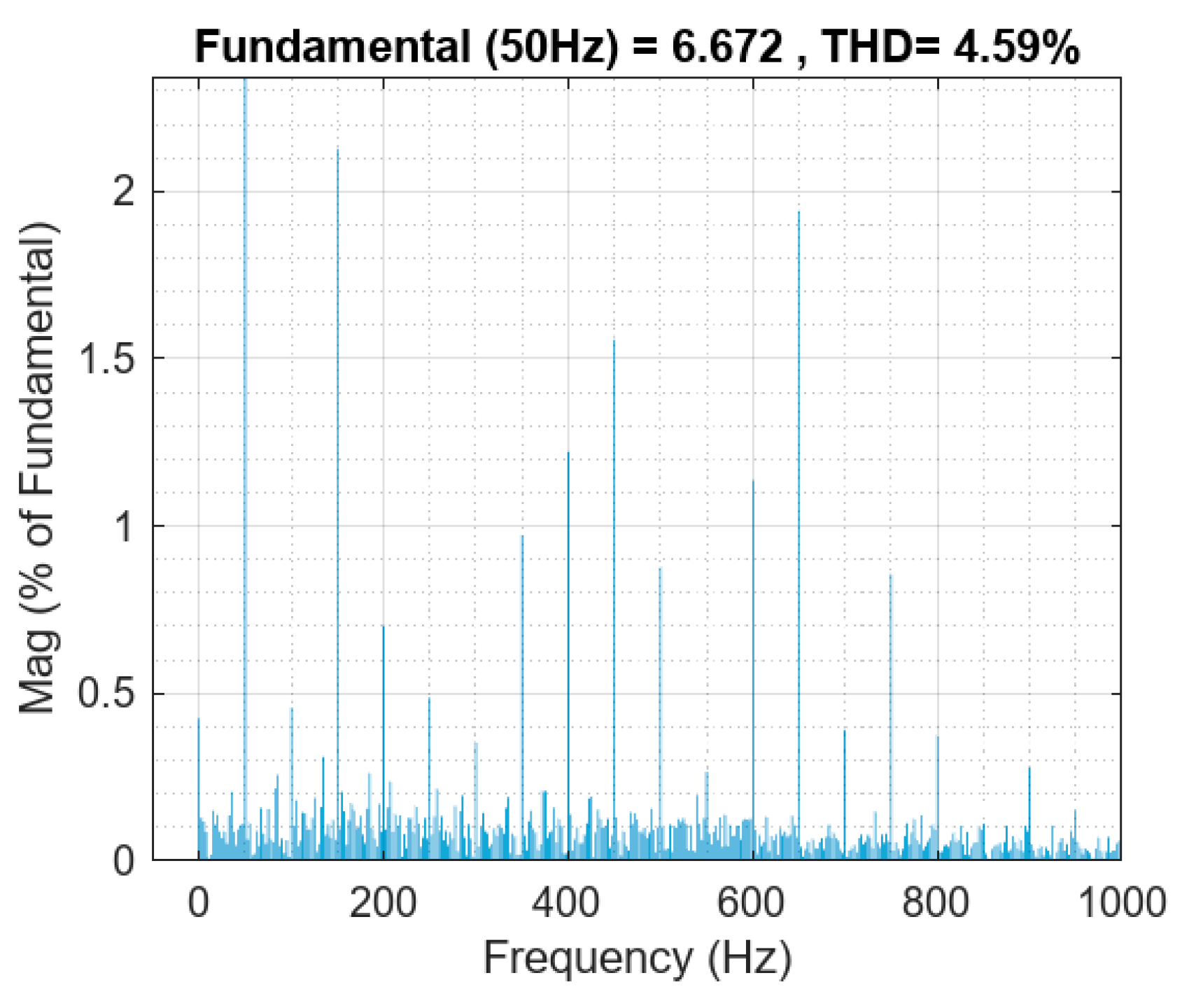
5.2. Simulation in Grid-Connected Mode
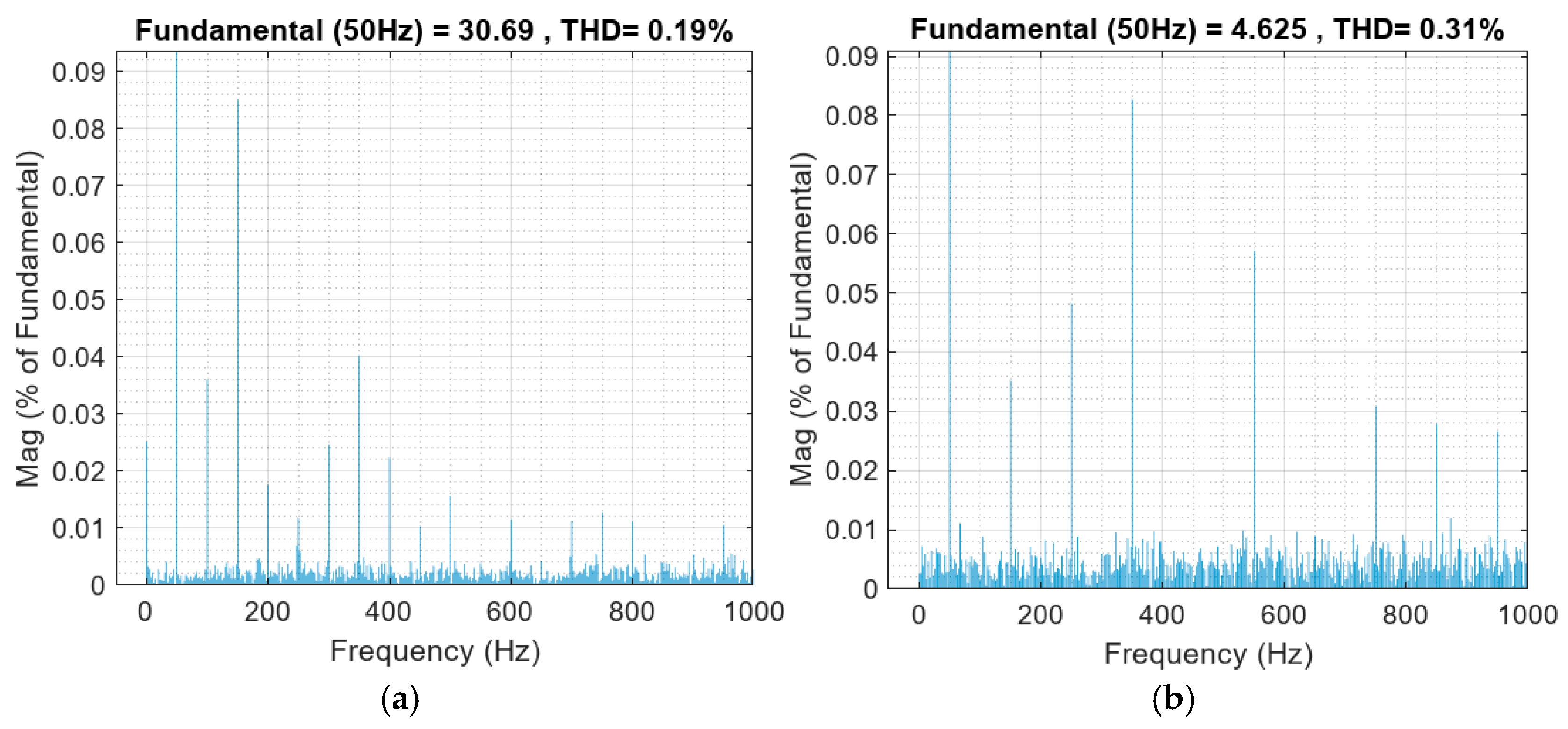
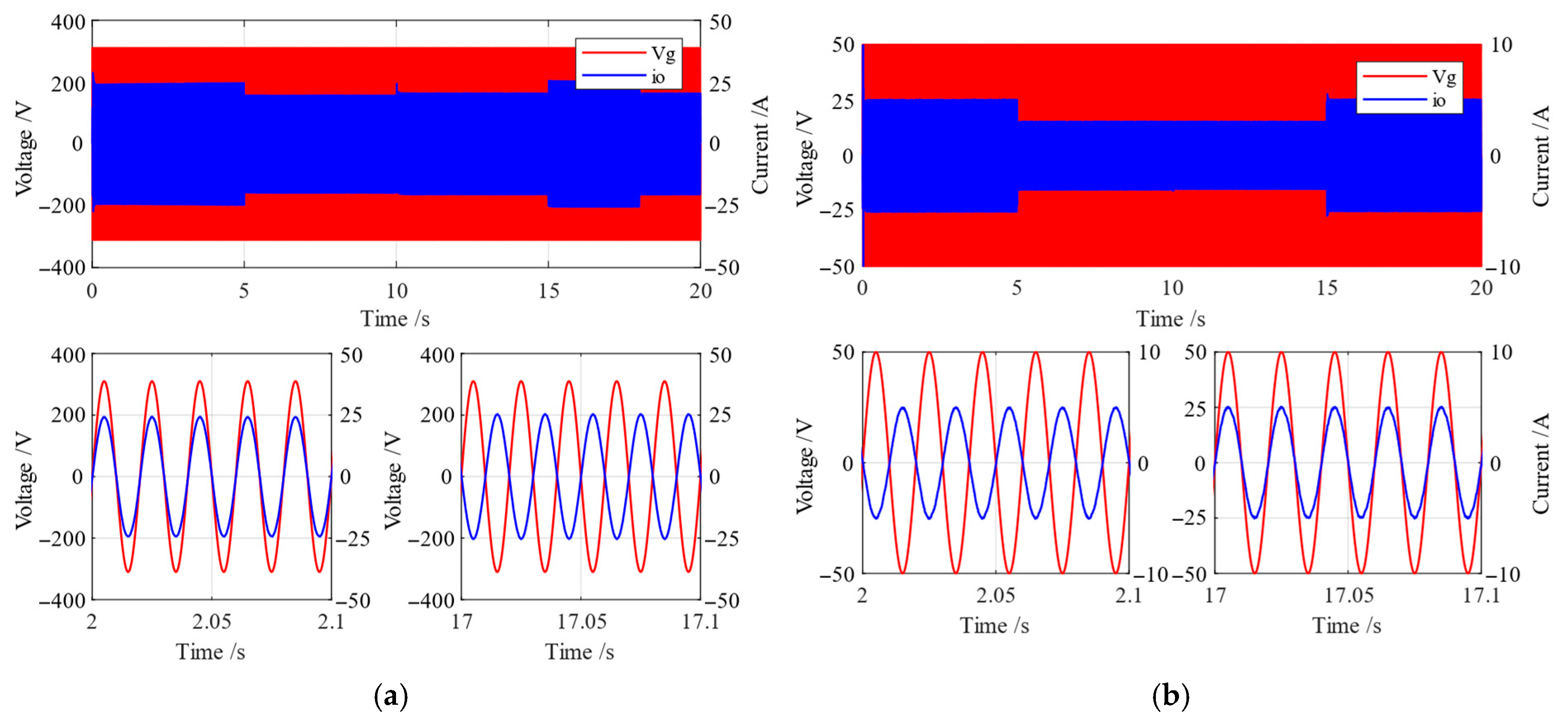
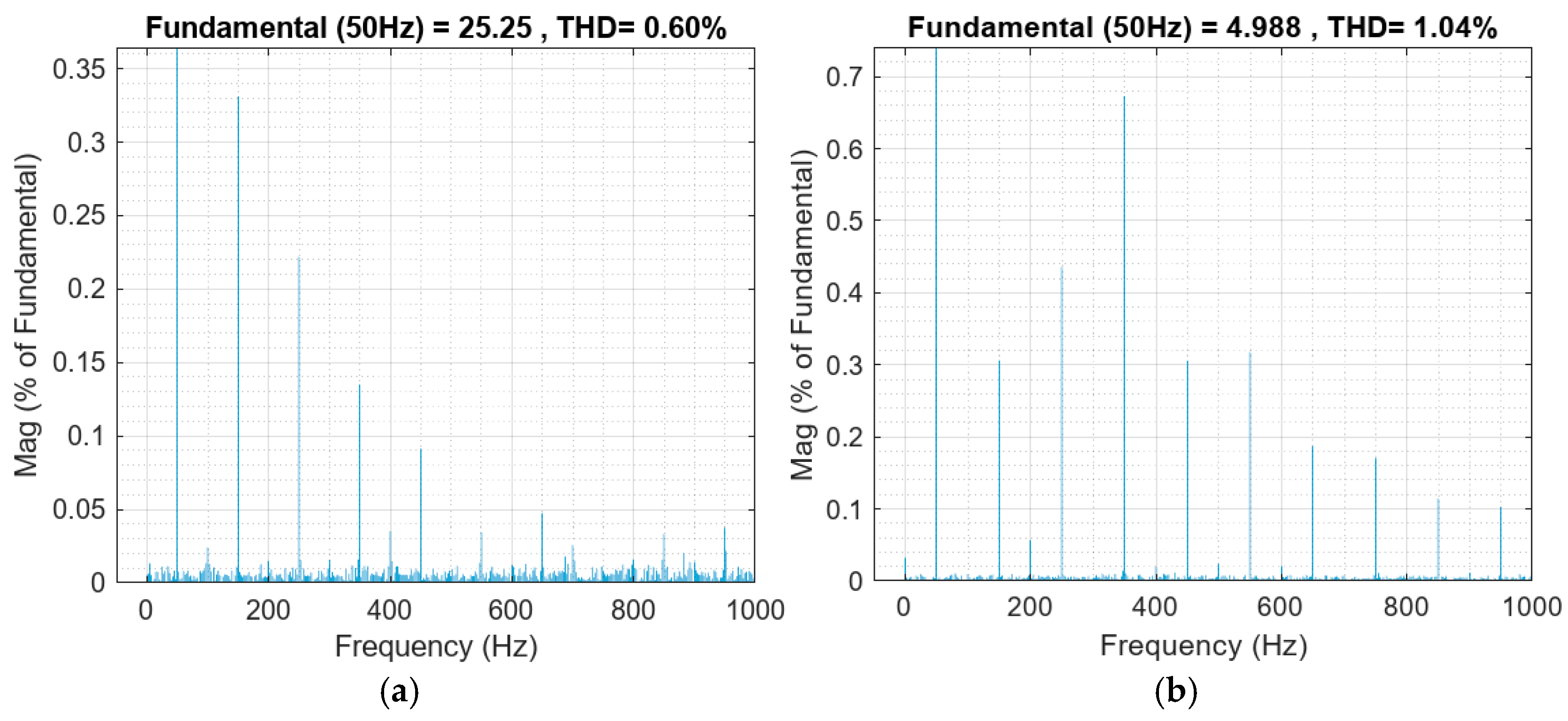
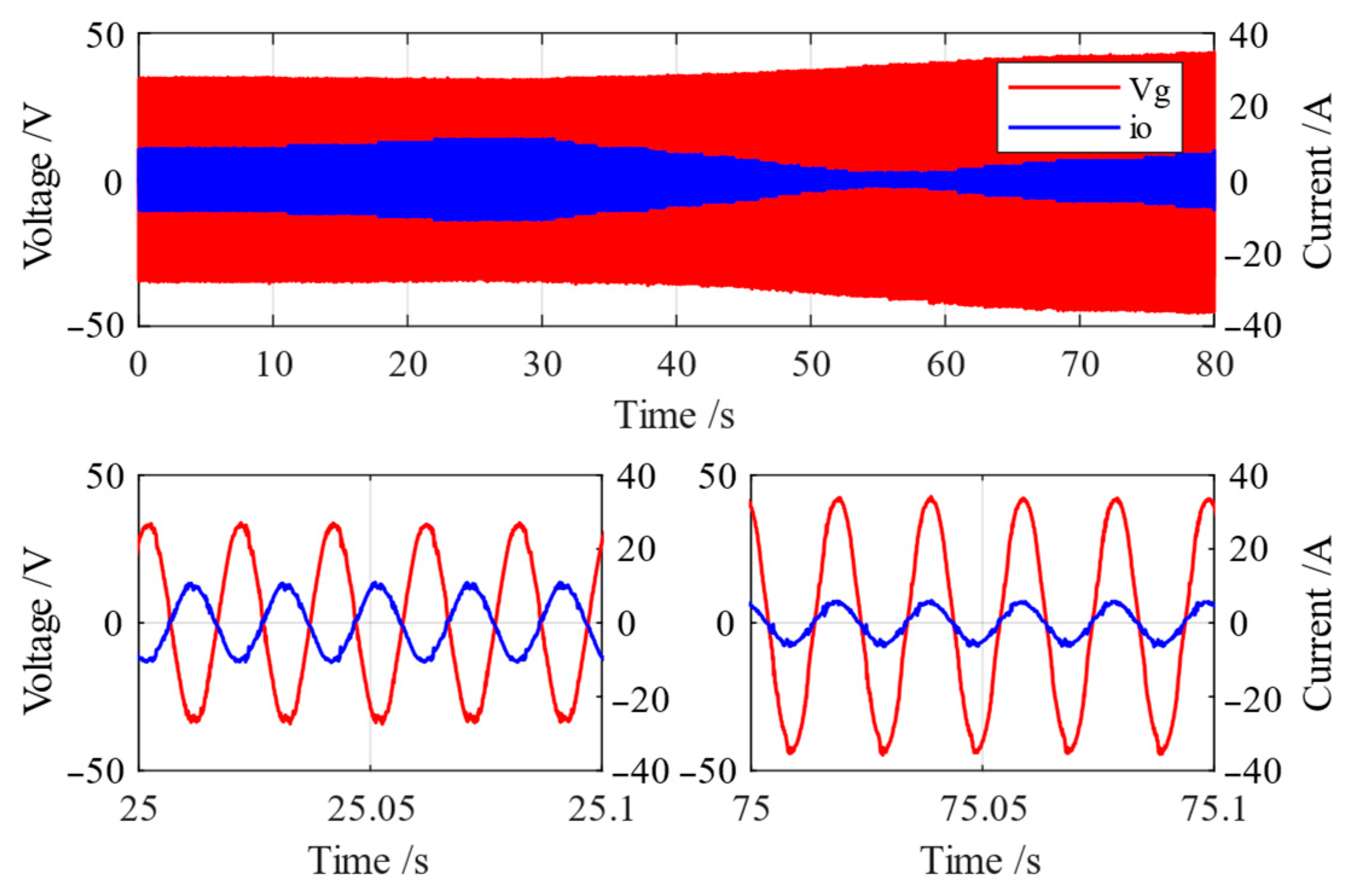
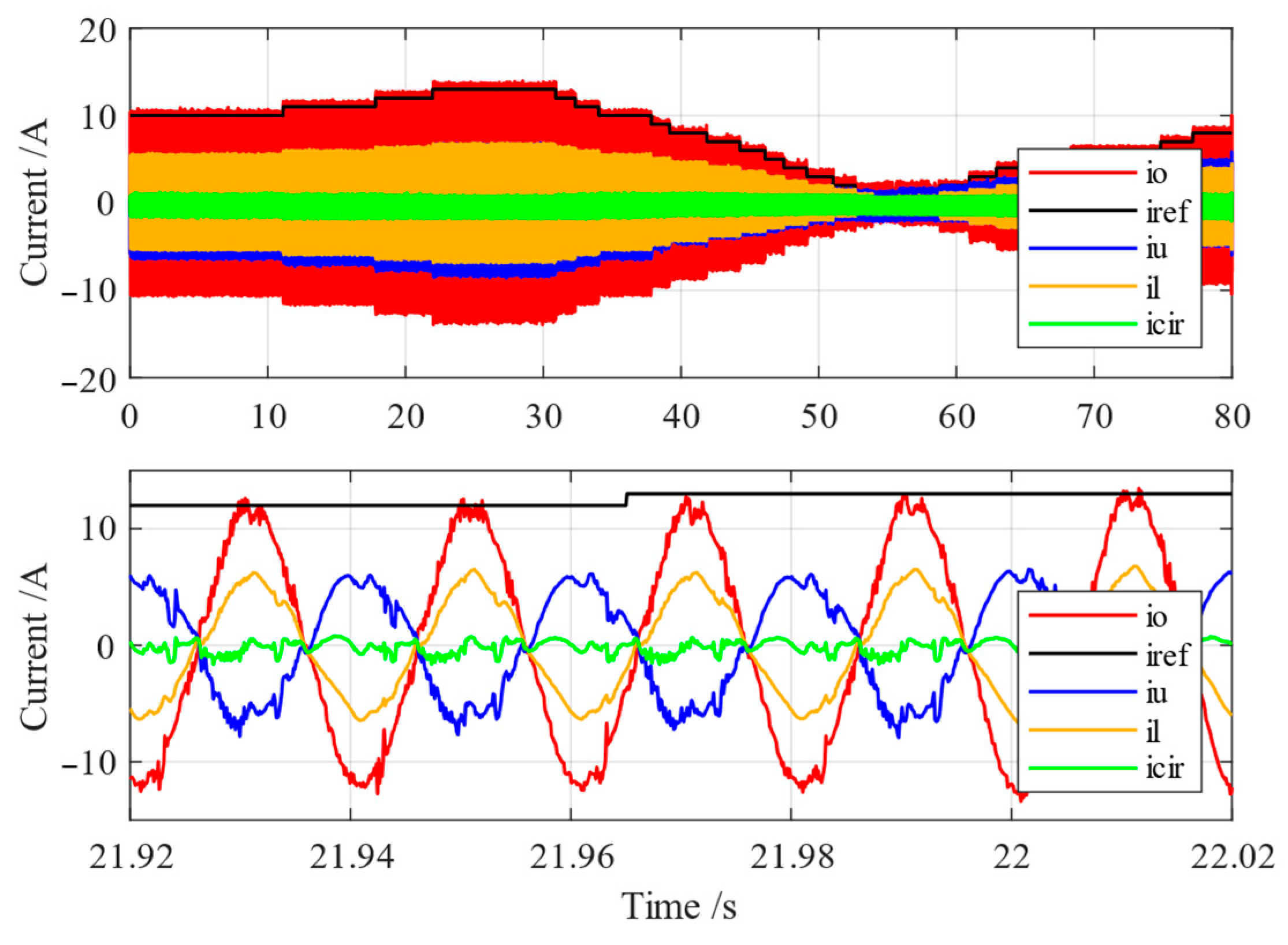
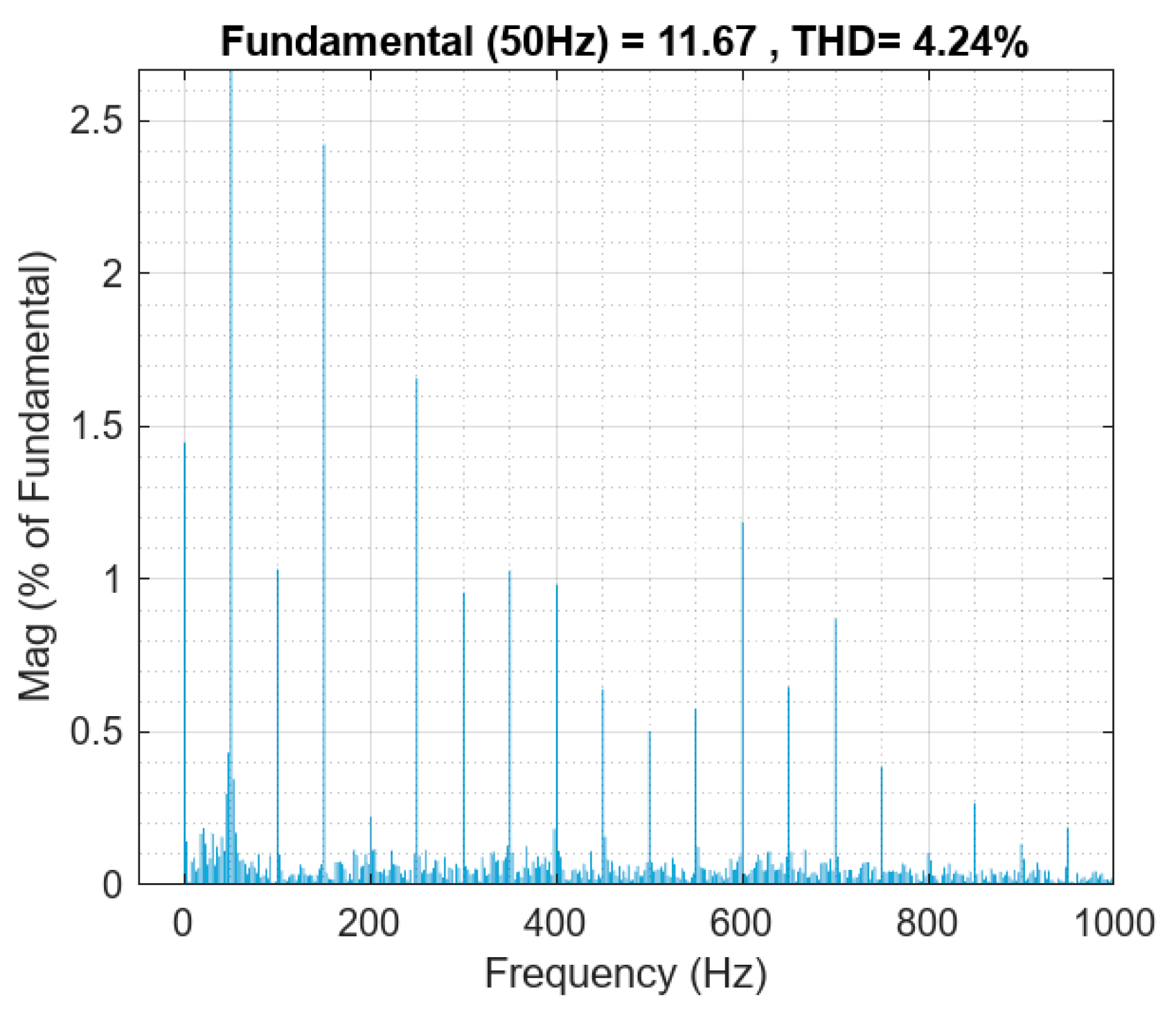
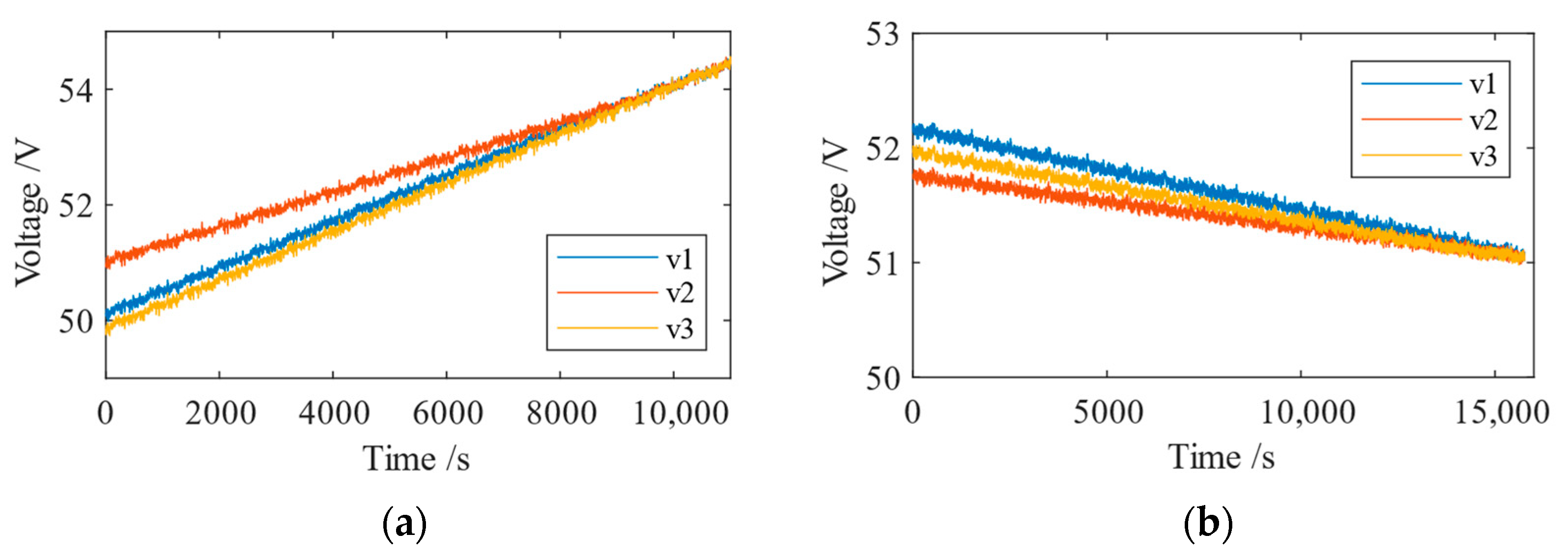
6. Experimental Results
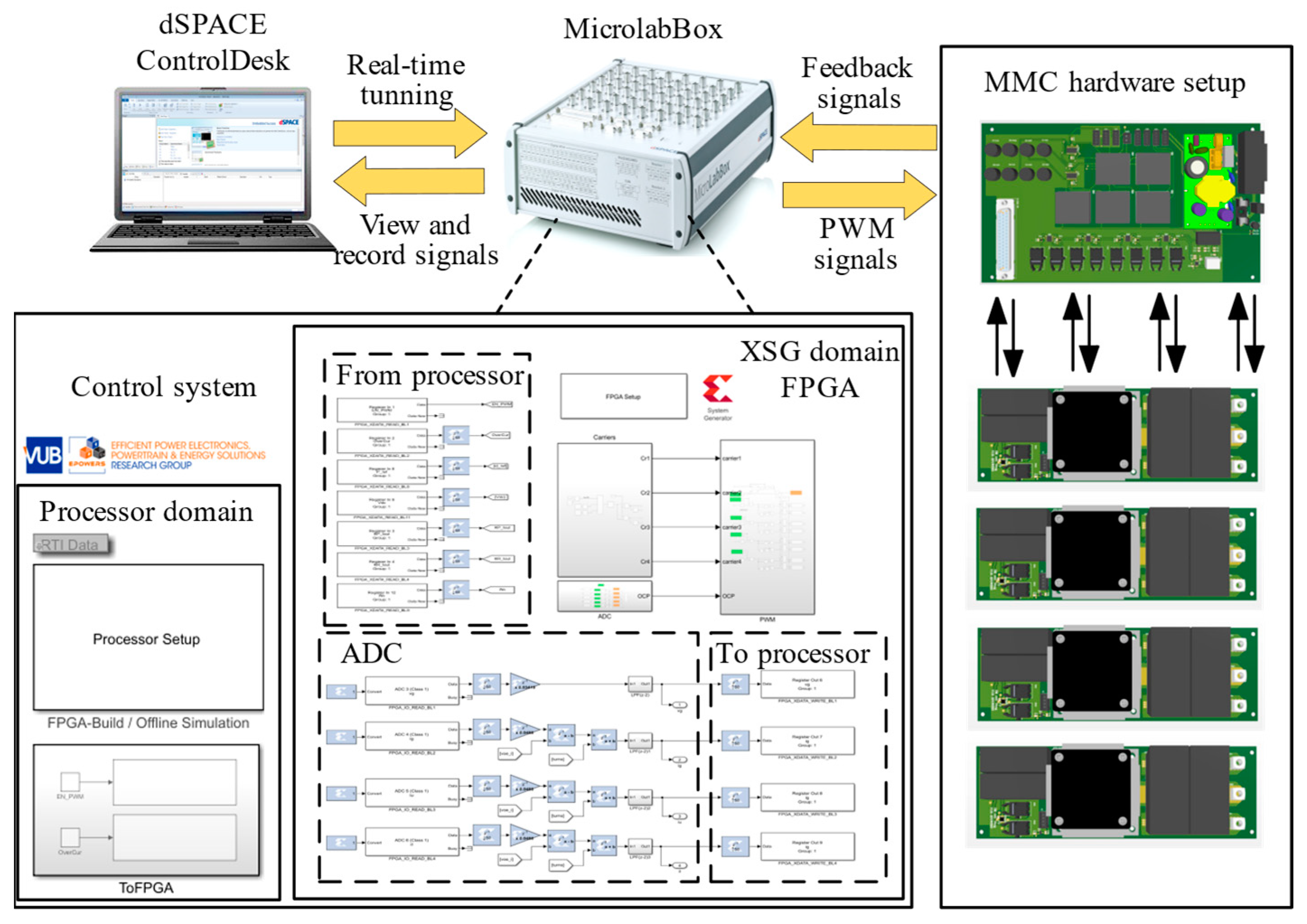
6.1. Experimental Prototype
6.2. Experiment in Islanded Mode
6.3. Experiment in Grid-Connected Mode
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yearly Electricity Data | Ember. Available online: https://ember-energy.org/data/yearly-electricity-data/ (accessed on 16 December 2024).
- Share of Electricity Production from Renewables. 2023. Available online: https://ourworldindata.org/grapher/share-electricity-renewables (accessed on 16 December 2024).
- Statistical Review of World Energy. Available online: https://www.energyinst.org/statistical-review (accessed on 16 December 2024).
- International Energy Agency. Batteries and Secure Energy Transitions. Available online: www.iea.org (accessed on 23 April 2024).
- Shamshuddin, M.A.; Kennel, R.M.; Verdugo, D. Nomenclature Overview and Beat Frequency in the Family of AC/AC Modular Multilevel Cascade Converters (MMCC). IEEE Access 2025, 13, 42064–42082. [Google Scholar] [CrossRef]
- Aslanian, M.; Neyshabouri, Y.; Raki, A.; Iman-Eini, H.; Liserre, M. A Fault-Tolerant Method Based on a Modified Selective Harmonic Mitigation Technique for Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2024, 71, 12890–12899. [Google Scholar] [CrossRef]
- Gao, X.; Tian, W.; Yang, Q.; Chai, N.; Rodriguez, J.; Kennel, R.; Heldwein, M.L. Model Predictive Control of a Modular Multilevel Converter Considering Control Input Constraints. IEEE Trans. Power Electron. 2024, 39, 636–648. [Google Scholar] [CrossRef]
- Salvadores, T.; Pereda, J.; Rojas, F. Power Imbalance Analysis of Modular Multilevel Converter with Distributed Energy Systems. IEEE Open J. Ind. Electron. Soc. 2024, 5, 109–121. [Google Scholar] [CrossRef]
- Wang, Y.; Chakraborty, S.; Geury, T.; Hegazy, O. Modeling and Control of a Modular Multilevel Converter Based on a Battery Energy Storage System with Soft Arm State-of-Charge Balancing Control. Energies 2024, 17, 740. [Google Scholar] [CrossRef]
- Soong, T.; Lehn, P.W. Evaluation of Emerging Modular Multilevel Converters for BESS Applications. IEEE Trans. Power Deliv. 2014, 29, 2086–2094. [Google Scholar] [CrossRef]
- de Lucena, M.P.; Gehrke, C.S.; da Silva, I.R.F. Modular Multilevel Converter for High-Performance UPS Systems. In Proceedings of the 2021 Brazilian Power Electronics Conference, COBEP 2021, João Pessoa, Brazil, 7–10 November 2021. [Google Scholar] [CrossRef]
- Mhiesan, H.; Al-Sarray, M.; Mackey, K.; McCann, R. High Step-Up/Down Ratio Isolated Modular Multilevel DC-DC Converter for Battery Energy Storage Systems on Microgrids. In Proceedings of the IEEE Green Technologies Conference, Kansas City, MO, USA, 6–8 April 2016; pp. 24–28. [Google Scholar] [CrossRef]
- Trusova, E.S.; Dobroskok, N.A.; Lavrinovskiy, V.S.; Simukhin, V.I. Comparison of Efficiencies of Modular Multilevel and Classic UPS Structures. In Proceedings of the 2022 Conference of Russian Young Researchers in Electrical and Electronic Engineering, Saint Petersburg, Russia, 25–28 January 2022; pp. 897–900. [Google Scholar] [CrossRef]
- Trusova, E.S.; Simukhin, V.I.; Lavrinovskiy, V.S.; Fedorkova, A.O. Determining the Reliability of a UPS Based on a Modular Multilevel Converter. In Proceedings of the Seminar on Electrical Engineering, Automation and Control Systems: Theory and Practical Applications, EEACS 2023, Saint Petersburg, Russia, 23–25 November 2023; pp. 319–321. [Google Scholar] [CrossRef]
- Wang, Y.; Aksoz, A.; Geury, T.; Ozturk, S.B.; Kivanc, O.C.; Hegazy, O. A review of modular multilevel converters for stationary applications. Appl. Sci. 2020, 10, 7719. [Google Scholar] [CrossRef]
- Du, S.; Dekka, A.; Wu, B.; Zargari, N. Modular Multilevel Converters: Analysis, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Quraan, M. Modular Multilevel Converter with Embedded Battery Cells for Traction Drives. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2016. [Google Scholar]
- Fan, S.; Zhang, K.; Xiong, J.; Xue, Y. An improved control system for modular multilevel converters featuring new modulation strategy and voltage balancing control. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, ECCE 2013, Denver, CO, USA, 15–19 September 2013; pp. 4000–4007. [Google Scholar] [CrossRef]
- Quraan, M.; Yeo, T.; Tricoli, P. Design and Control of Modular Multilevel Converters for Battery Electric Vehicles. IEEE Trans. Power Electron. 2015, 31, 507–517. [Google Scholar] [CrossRef]
- An, Q.; Zhang, J.; An, Q.; Shamekov, A. Quasi-Proportional-Resonant Controller Based Adaptive Position Observer for Sensorless Control of PMSM Drives Under Low Carrier Ratio. IEEE Trans. Ind. Electron. 2020, 67, 2564–2573. [Google Scholar] [CrossRef]
- Geng, S.; Gan, Y.; Li, Y.; Hang, L.; Li, G. Novel Method for Circulating Current Suppression in MMCs Based on Multiple Quasi-PR Controller. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 3560–3565. [Google Scholar] [CrossRef]
- Ye, T.; Dai, N.; Lam, C.S.; Wong, M.C.; Guerrero, J.M. Analysis, Design, and Implementation of a Quasi-Proportional-Resonant Controller for a Multifunctional Capacitive-Coupling Grid-Connected Inverter. IEEE Trans. Ind. Appl. 2016, 52, 4269–4280. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Iravani, M.R. A new phase-locked loop (PLL) system. In Proceedings of the 44th IEEE 2001 Midwest Symposium on Circuits and Systems. MWSCAS 2001, Dayton, OH, USA, 14–17 August 2001; pp. 421–424. [Google Scholar] [CrossRef]
- Wang, Y.; Chakraborty, S.; Geury, T.; Hegazy, O. Inductance and Power Losses Analysis of an Arm Inductor for a Modular Multilevel Converter. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Milan, Italy, 24–27 October 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Parikh, H.R.; Martin-Loeches, R.S. Control of Modular Multilevel Converter (MMC) based HVDC application under unbalanced conditions. In Master, Energy Technology; Aalborg University: Aalborg, Denmark, 2016. [Google Scholar]
- Holmes, D.G.; Lipo, T.A.; Mcgrath, B.P.; Kong, W.Y. Optimized Design of Stationary Frame Three Phase AC Current Regulators. IEEE Trans. Power Electron. 2009, 24, 2417–2426. [Google Scholar] [CrossRef]
- Pereira, L.F.A.; Bazanella, A.S. Tuning Rules for Proportional Resonant Controllers. IEEE Trans. Control. Syst. Technol. 2015, 23, 2010–2017. [Google Scholar] [CrossRef]
- Henz Mossmann, B.; Alves Pereira, L.F.; Gomes da Silva, J.M., Jr. Tuning of Proportional-Resonant Controllers Combined with Phase-Lead Compensators Based on the Frequency Response. J. Control. Autom. Electr. Syst. 2021, 32, 910–926. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| No. of SMs per arm | 2 |
| Nominal voltage of battery banks | 400 V/50 V |
| Battery capacity | 1 Ah |
| Rated power | 5 kW |
| Grid peak voltage | 311 V/50 V |
| Grid frequency | 50 Hz |
| Modulation technique | PSC-PWM |
| Carrier frequency | 20 kHz |
| SM capacitance | 100 μF |
| Arm capacitance | 480 μF |
| Arm inductance | 2.5 mH |
| Sampling time | 0.0001 s |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| No. of SM power units | 4 | Battery-rated capacity | 58 Ah |
| No. of interfacing board | 1 | Arm inductance | 2.5 mH |
| No. of battery modules | 3 | No. of buck capacitors | 6 |
| Battery chemistry | Li-ion NCA/NMC | Capacitance of buck capacitors | 160 μF |
| Battery nominal voltage | 50.4 V | Load inductance | 340 μH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Geury, T.; Hegazy, O. A Single-Phase Modular Multilevel Converter Based on a Battery Energy Storage System for Residential UPS with Two-Level Active Balancing Control. Energies 2025, 18, 1776. https://doi.org/10.3390/en18071776
Wang Y, Geury T, Hegazy O. A Single-Phase Modular Multilevel Converter Based on a Battery Energy Storage System for Residential UPS with Two-Level Active Balancing Control. Energies. 2025; 18(7):1776. https://doi.org/10.3390/en18071776
Chicago/Turabian StyleWang, Yang, Thomas Geury, and Omar Hegazy. 2025. "A Single-Phase Modular Multilevel Converter Based on a Battery Energy Storage System for Residential UPS with Two-Level Active Balancing Control" Energies 18, no. 7: 1776. https://doi.org/10.3390/en18071776
APA StyleWang, Y., Geury, T., & Hegazy, O. (2025). A Single-Phase Modular Multilevel Converter Based on a Battery Energy Storage System for Residential UPS with Two-Level Active Balancing Control. Energies, 18(7), 1776. https://doi.org/10.3390/en18071776








