Risk Assessment Model for Converter Transformers Based on Entropy-Weight Analytic Hierarchy Process
Abstract
1. Introduction
2. Model Development and Validation Framework
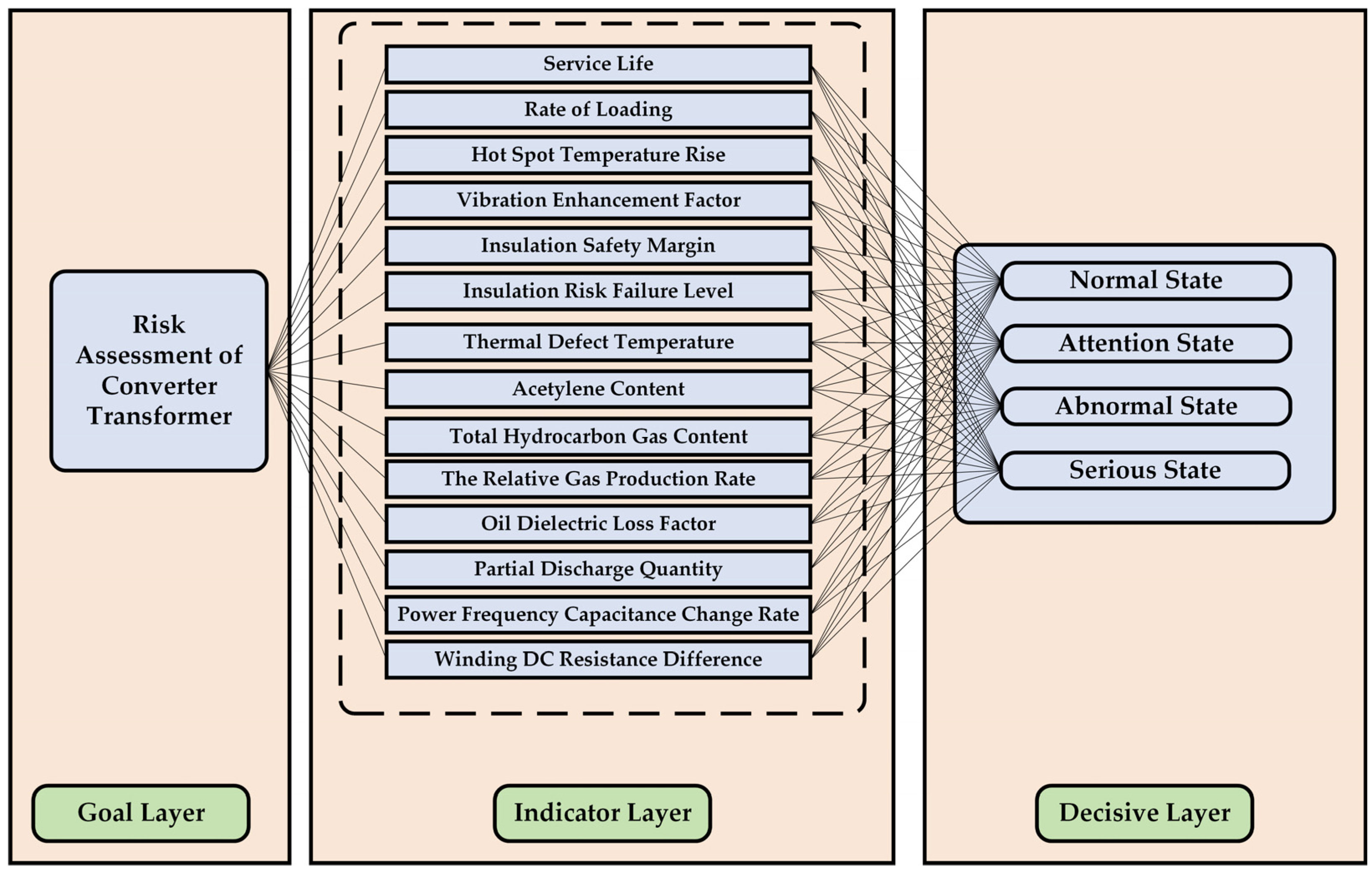
3. Selection of State Characteristic Parameters and Classification of Risk Grades
4. The Converter Transformer Risk Assessment Model Based on the Entropy-Weight AHP
4.1. Construction of Hierarchical Judgment Matrix Based on AHP
4.2. Construction of Risk Decision Matrix Based on Entropy-Weight Method
4.3. Comprehensive Weight Calculation Based on Subjective and Objective Fusion
5. Research on Risk Assessment of Converter Transformers
6. Verification of Risk Assessment Effects of Converter Transformers
7. Conclusions
- This paper selects 14 ‘electrical–thermal–mechanical’ multi-dimensional characteristic parameters, such as partial discharge, power frequency capacitance change rate, dissolved gas in oil, relative gas production rate, hot spot temperature rise, and thermal defect temperature, to comprehensively evaluate the risk state of the converter transformer, ensuring the comprehensiveness of the assessment model.
- By combining the subjective weighting method from the AHP with the objective weighting method from the entropy-weight method, the risk assessment model based on the entropy-weight AHP effectively addresses the issues of over-reliance on expert experience or statistical data in existing models, thereby enhancing the reliability and accuracy of the model, while simultaneously satisfying the requirements for both real-time online monitoring and continuous model updating.
- The effectiveness of the model risk assessment is validated using actual operational data from the converter transformer. The results indicate that the proposed risk assessment model can accurately assess the risk state of the transformer by providing comprehensive protection for HVDC systems, spanning from equipment-level anomaly detection to system-wide stability maintenance. The model exhibits particularly robust capabilities in predicting and preventing risks under complex operating conditions, such as commutation failures and harmonic resonance, enabling the proactive mitigation of potential failures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, W.; Zhang, Z.; Yang, Y.; Gao, J.; Pei, X.; Deng, J.; Pan, Z.; Lv, J.; Yao, H. Risk Assessment Study of Oil Flow Under Inrush Current on the Misoperation of Converter Transformer Gas Relay. Appl. Sci. 2025, 15, 2235. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Z.; He, W.; Chen, J.; Li, D. Simulation Analysis of Inrush Current and Electromagnetic-Force Characteristics of Converter Transformer During No-Load Closing. In Proceedings of the 2023 2nd International Conference on Power Systems and Electrical Technology (PSET), Milan, Italy, 25–27 August 2023; pp. 137–143. [Google Scholar]
- Liu, Z.; Yin, X.; Pan, Y.; Xi, W.; Yin, X.; Liu, B. Analysis of zero-mode inrush current characteristics of converter transformers. In Proceedings of the 2021 56th International Universities Power Engineering Conference (UPEC), Middlesbrough, UK, 31 August–3 September 2021; pp. 1–6. [Google Scholar]
- Li, X.; Chen, B.; Ma, Y.; Liu, J.; Yang, M. Differential analysis of gas generation between gas to liquid and mineral oil under electric-thermal combined fault based on molecular dynamics. In Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2025; pp. 1–9. [Google Scholar]
- Amalanathan, A.J.; Sarathi, R.; Zdanowski, M.; Vinu, R.; Nadolny, Z. Review on Gassing Tendency of Different Insulating Fluids Towards Transformer Applications. Energies 2023, 16, 488. [Google Scholar] [CrossRef]
- Manea, A.; Gorjanu, T.; Lazeanu, A.; Dumitran, L.M. Effect of Electrical Accelerated Aging on DC Resistivity of Mineral Oil Used in Power Transformers. Energies 2023, 16, 294. [Google Scholar]
- Zhang, S.; Zhou, H. Transformer Fault Diagnosis Based on Multi-Strategy Enhanced Dung Beetle Algorithm and Optimized SVM. Energies 2024, 17, 6296. [Google Scholar] [CrossRef]
- Saha, T.K. Review of modern diagnostic techniques for assessing insulation condition in aged transformers. IEEE Trans. Dielectr. Electr. Insul. 2003, 10, 903–917. [Google Scholar]
- Jin, L.; Kim, D.; Abu-Siada, A.; Kumar, S. Oil-Immersed Power Transformer Condition Monitoring Methodologies: A Review. Energies 2022, 15, 3379. [Google Scholar] [CrossRef]
- Manoj, T.; Ranga, C.; Abu-Siada, A.; Ghoneim, S.S.M. Analytic Hierarchy Processed Grey Relational Fuzzy Approach for Health Assessment of Power Transformers. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 1480–1489. [Google Scholar]
- Žarković, M.; Stojković, Z. Analysis of artificial intelligence expert systems for power transformer condition monitoring and diagnostics. Electr. Power Syst. Res. 2017, 149, 25–136. [Google Scholar]
- Yang, J.; Wu, H.; Yang, Y.; Zhao, X.; Xun, H.; Wei, X.; Guo, Z. A Transformer Maintenance Interval Optimization Method Considering Imperfect Maintenance and Dynamic Maintenance Costs. Appl. Sci. 2024, 14, 6845. [Google Scholar] [CrossRef]
- Luo, C.; Zhu, Y.; Li, Z.; Yu, P.; Zhou, Z.; Yang, X.; Liao, M. Diffusion Characteristics of Dissolved Gases in Oil Under Different Oil Flow Circulations. Energies 2025, 18, 432. [Google Scholar] [CrossRef]
- Zhang, C.; He, Y.; Du, B.; Li, B.; Jiang, S. Transformer fault diagnosis method using IoT based monitoring system and ensemble machine learning. Future Gener. Comput. Syst. 2020, 108, 533–545. [Google Scholar]
- Zhao, X.; Wu, G.; Yang, D.; Xu, G.; Xing, Y.; Yao, C.; Abu-Siada, A. Enhanced detection of power transformer winding faults through 3D FRA signatures and image processing techniques. Electr. Power Syst. Res. 2025, 242, 111433. [Google Scholar]
- Farhadian, A.H.; Mikhak-Beyranvand, M.; Fard, S.S.M. Aged Transformer Oil Analysis Through Laser-Induced Breakdown Spectroscopy. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 1988–1994. [Google Scholar]
- Velásquez, R.M.A.; Lara, J.V.M. Root cause analysis improved with machine learning for failure analysis in power transformers. Eng. Fail. Anal. 2020, 115, 104684. [Google Scholar]
- Jiang, T.; Yang, C.; Wang, J.; Huang, G.; Cao, L.; Shi, Y.; State Grid Shaanxi Electric Power Company; State Grid Shaanxi Electric Power Research Institute. Research on Insulation State Assessment Method of Power Transformer based on Health Index. High Volt. Appar. 2024, 60, 124–129. [Google Scholar]
- Zou, Y.; Lin, J.; Li, A.; Zhang, Y. Evaluation of Transformer Oil—Paper Insulation Status based on Grey Relational Analysis and a Cluster Cloud Model. Power Syst. Prot. Control 2023, 51, 35–43. [Google Scholar]
- Zhou, J. Transformer Fault Diagnosis and Condition Assessment Based on Neural Networks and Support Vector Machines; Kunming University of Science and Technology: Kunming, China, 2022. (In Chinese) [Google Scholar]
- Ming, T.; Zhang, L.; Wang, Q. Research on Transformer State Assessment based on Clustering and Time Series Analysis. Autom. Devices Equip. 2021, 43, 108–111. (In Chinese) [Google Scholar]
- Zhang, P.; Qi, B.; Shao, M.; Li, C.; Rong, Z.; Chen, J.; Wang, H. Optimal data selection rule mining for transformer condition assessment. IEEE Access 2021, 9, 156962–156972. [Google Scholar]
- Zeinoddini-Meymand, H.; Kamel, S.; Khan, B. An efficient approach with application of linear and nonlinear models for evaluation of power transformer health index. IEEE Access 2021, 9, 150172–150186. [Google Scholar]
- Sangwook, L. Determination of Priority Weights under Multiattribute Decision-Making Situations: AHP Versus Fuzzy AHP. J. Constr. Eng. Manag. 2015, 141, 05014015. [Google Scholar]
- Bidisha, B.; Mahapatro, J. Performance Evaluation of Priority-based Scheduling in Hybrid VANETs for Different Criteria Weights Using AHP-AHP and AHP-TOPSIS. IETE J. Res. 2024, 70, 5759–5770. [Google Scholar]
- Sui, L.; Huang, Q.; Liu, X. Research on safety investment decision evaluation and optimization of network booking taxi platform enterprise based on subjective-objective assessment method. Teh. Vjesn. 2023, 30, 1201–1208. [Google Scholar]
- Sun, D.; Hu, X.; Liu, B. Comprehensive evaluation for the sustainable development of fresh agricultural products logistics enterprises based on combination empowerment-TOPSIS method. PeerJ Comput. Sci. 2023, 9, 1719. [Google Scholar]
- Zhu, C. The Local Variational Principle of Weighted Entropy and Its Applications. J. Dyn. Differ. Equ. 2024, 36, 797–831. [Google Scholar]
- Wu, J.; Zhang, Q. Multicriteria decision making method based on intuitionistic fuzzy weighted entropy. Expert Syst. Appl. 2011, 38, 916–922. [Google Scholar]
- Xu, X. A note on the subjective and objective integrated approach to determine attribute weights. Eur. J. Oper. Res. 2004, 156, 530–532. [Google Scholar]
- Liu, H.; Hu, Y. An Evaluating Method with Combined Assigning-Weight Based on Maximizing Variance. Sci. Program. 2015, 1, 8. [Google Scholar]
- DL/T 1685-2017; Guideline for Condition Evaluation of Oil-Immersed Transformers (Reactors). China Electric Power Press: Beijing, China, 2017.
- DL/T 984-2018; Guideline for Judging Insulation Aging of Oil-Immersed Transformers. China Electricity Power Press: Beijing, China, 2018.
- DL/T 2002-2019; Converter Transformer Operation Procedure. China Electricity Power Press: Beijing, China, 2019.
- GB/T 1094.2-2013; Power Transformer Part 2: Temperature Rise of Liquid-Immersed Transformer. China Standards Press: Beijing, China, 2013.
- IEC 60076-7-2018; Power Transformers-Part 7: Loading Guide for Mineral-Oil-Immersed Power Transformers. Multiple. Distributed through American National Standards Institute (ANSI): New York, NY, USA, 2018.
- IEEE C57.91-2011; IEEE Guide for Loading Mineral-Oil-Immersed Transformers and Step-Voltage Regulators. IEEE: New York, NY, USA, 2011.
- IEC 60599-2022; Mineral Oil-Filled Electrical Equipment in Service-Guidance on the Interpretation of Dissolved and Free Gases Analysis. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- Franek, J.; Kresta, A. Judgment Scales and Consistency Measure in AHP. Procedia Econ. Financ. 2014, 12, 164–173. [Google Scholar]

| Characteristic Parameter Index | Normal State | Attention State | Abnormal State | Serious State |
|---|---|---|---|---|
| Service Life K1 | 700 | 500 | 250 | 150 |
| Rate of Loading K2 | 1 | 1.1 | 1.3 | 1.5 |
| Hot Spot Temperature Rise K3/K | 60 | 68 | 78 | 90 |
| Vibration Enhancement Factor K4 | 1 | 1.2 | 1.4 | 1.5 |
| Insulation Safety Margin K5 | 0.8 | 0.7 | 0.6 | 0.5 |
| Insulation Risk Failure Level K6 | 1 | 2 | 3 | 4 |
| Thermal Defect Temperature K7/°C | 150 | 300 | 500 | 700 |
| Acetylene Content K8/μL/L | 2 | 5 | 20 | 50 |
| Total Hydrocarbon Gas Content K9/μL/L | 100 | 150 | 350 | 500 |
| The Relative Gas Production Rate K10/%/month | 7 | 10 | 20 | 30 |
| Partial Discharge Quantity K11/pC | 100 | 250 | 700 | 1000 |
| Oil Dielectric Loss Factor tanδ K12/% | 0.5 | 2 | 3 | 4 |
| Power Frequency Capacitance Change Rate K13/% | 2 | 3 | 4 | 5 |
| Winding DC Resistance Difference K14/% | 1 | 2 | 4 | 5 |
| Scale | Implication |
|---|---|
| 1 | The two feature vectors have the same importance |
| 2 | The ith row feature vector is more important than the jth column feature vector |
| 3 | The ith row feature vector is much more important than the jth column feature vector |
| 4 | The ith row feature vector is extremely important compared to the jth column feature vector |
| 5 | The ith row feature vector is the most important compared to the jth column feature vector |
| 1/aij | The feature vector of column j is more important than the feature vector of row i |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| RI | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.24 | 1.36 | 1.41 | 1.46 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 |
| Parameter | Transformer A | Transformer B | Transformer C | Transformer D |
|---|---|---|---|---|
| K1 | 800 | 667 | 476 | 118 |
| K2 | 1 | 1 | 1.2 | 1.5 |
| K3 | 53 | 62 | 75 | 98 |
| K4 | 1 | 1 | 1.1 | 1.3 |
| K5 | 0.80 | 0.78 | 0.63 | 0.47 |
| K6 | 1 | 1 | 2 | 4 |
| K7 | 0 | 87 | 462 | 885 |
| K8 | 0.53 | 1.38 | 15.26 | 187.05 |
| K9 | 87.04 | 134.20 | 267.42 | 961.99 |
| K10 | 4 | 6 | 13 | 45 |
| K11 | 27.47 | 74.88 | 296.57 | 1332.45 |
| K12 | 0.5 | 0.5 | 2 | 3 |
| K13 | 2 | 2 | 3 | 5 |
| K14 | 1 | 1 | 2 | 5 |
| Parameter | Transformer A | Transformer B | Transformer C | Transformer D |
|---|---|---|---|---|
| K1 | 1 | 0.9524 | 0.6803 | 0.1681 |
| K2 | 1 | 1 | 0.8333 | 0.6667 |
| K3 | 1 | 0.9677 | 0.8333 | 0.6122 |
| K4 | 1 | 1 | 0.9091 | 0.7692 |
| K5 | 1 | 0.9690 | 0.7911 | 0.5952 |
| K6 | 1 | 1 | 0.5000 | 0.2500 |
| K7 | 1 | 0.58 | 0.3247 | 0.1695 |
| K8 | 1 | 1 | 0.1311 | 0.0107 |
| K9 | 1 | 0.7452 | 0.3739 | 0.1040 |
| K10 | 1 | 1 | 0.5385 | 0.1556 |
| K11 | 1 | 1 | 0.3372 | 0.0750 |
| K12 | 1 | 1 | 0.2500 | 0.1667 |
| K13 | 1 | 1 | 0.6667 | 0.4000 |
| K14 | 1 | 1 | 0.5000 | 0.2000 |
| Transformer Type | Transformer A | Transformer B | Transformer C | Transformer D |
| Comprehensive score | 1 | 0.8986 | 0.3953 | 0.1717 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, G.; Dai, W.; Zou, D.; Sun, H.; Zhang, H.; Hao, J. Risk Assessment Model for Converter Transformers Based on Entropy-Weight Analytic Hierarchy Process. Energies 2025, 18, 1757. https://doi.org/10.3390/en18071757
Qian G, Dai W, Zou D, Sun H, Zhang H, Hao J. Risk Assessment Model for Converter Transformers Based on Entropy-Weight Analytic Hierarchy Process. Energies. 2025; 18(7):1757. https://doi.org/10.3390/en18071757
Chicago/Turabian StyleQian, Guochao, Weiju Dai, Dexu Zou, Haoruo Sun, Hanting Zhang, and Jian Hao. 2025. "Risk Assessment Model for Converter Transformers Based on Entropy-Weight Analytic Hierarchy Process" Energies 18, no. 7: 1757. https://doi.org/10.3390/en18071757
APA StyleQian, G., Dai, W., Zou, D., Sun, H., Zhang, H., & Hao, J. (2025). Risk Assessment Model for Converter Transformers Based on Entropy-Weight Analytic Hierarchy Process. Energies, 18(7), 1757. https://doi.org/10.3390/en18071757







