Modeling of Exhaust Gas Temperature at the Turbine Outlet Using Neural Networks and a Physical Expansion Model

Abstract

The accurate estimation of exhaust gas temperature across the turbine is always more important for the optimization of engine performance, ensuring durability of the turbine impeller and catalyst, and reducing and calculating emissions concentration. Traditional physical modeling approaches, based on thermodynamic and fluid dynamics features of gas expansion, can be used for this purpose. However, recent advancements in machine learning, particularly neural networks, offer a data-driven alternative that may enhance prediction accuracy and computational efficiency. This study presents a methodology that integrates a semi-physical turbine model for estimating the exhaust gas temperature at the turbine outlet with a neural network-based approach for predicting the pressure at the turbine inlet. The model utilizes the exhaust gas temperature upstream of the turbine, a model for which was developed in a previous work of the authors. The models are calibrated with steady-state data and then evaluated based on accuracy and robustness under transient operating conditions on six driving cycles with different features. In this way, robust and reliable validation of the models is presented, since the testing is performed on various conditions not used for model development and calibration. Results show an average root mean square error of 14%, including the initial portions of driving cycles performed with a cold engine. Thus, the developed approach that includes multiple modeling methods shows a good predictivity, which is the main objective of this research activity.

1. Introduction

The exhaust gas temperature (EGT) across the turbine outlet is a critical parameter in internal combustion engines, influencing combustion efficiency, emission conversion efficiency, and turbine and after-treatment (AT) integrity and reliability. In the last decades, the automotive sector has been driven by regulations to control with increasing accuracy both the efficiency of the overall energy conversion process (to reduce CO₂ emissions, i.e., brake-specific fuel consumption) and the reliability of the AT system, reducing the emission concentration [1,2].

As is well known, the EGT represents a key parameter to be managed in modern engine control, even if it is not directly measured on final production applications [3]. For this reason, the physical dependence of the EGT on other engine parameters has been widely investigated [4], such as for different, on-board compatible methods for the estimation of the temperature. Indeed, there are in the literature several works describing the indirect measurement of the exhaust gas temperature with an universal exhaust gas oxygen (UEGO) probe [5] or methodologies for direct modelling, which can be grouped as follows:

• Mean value models for EGT estimation [6,7,8];
• Data-driven approaches [9,10,11];
• 0-D physical and semi-physical methods grounded in thermodynamics and heat transfer equations [12,13,14];
• 1-D EGT modeling [15,16,17].

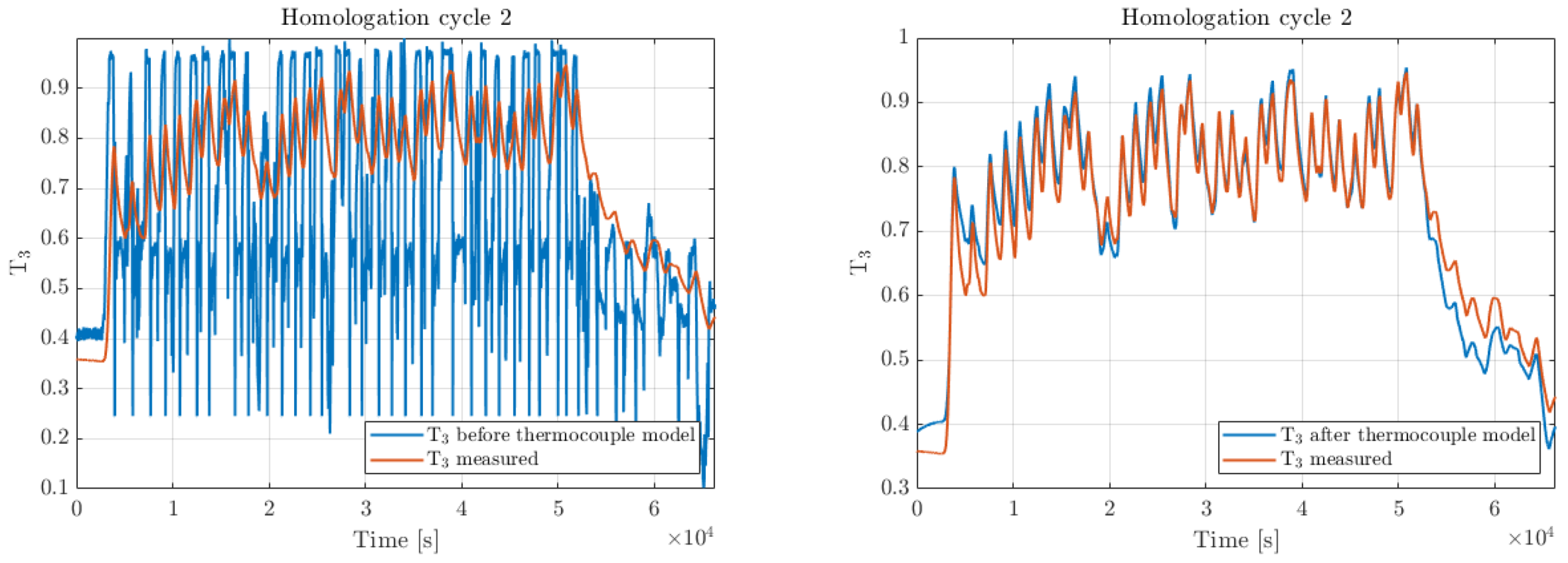
The raw EGT measurement available at the engine test cell is typically performed with thermocouple (TC), and physical or semi-physical models could include the sensor effect for the final temperature estimation [18]. A TC introduces both a delay in the temperature sensing that has an effect, especially under transient conditions, and an offset with respect to the temperature measured with other sensors [19]. This second aspect is typically not fully considered, since a TC is often used to evaluate the temperature limits too (for example temperature limitation at the turbine inlet in turbocharged engine and gas turbines). This means the TC measurement becomes a reference and the temperature delta between the measurement and the gas temperature can be neglected. On the other hand, the delay introduced by TC dynamics can be well represented by a first-order system, where the time constant τ can be calibrated for the particular features of the used sensor (i.e., the sensing tip size and type of thermocouple).

One of the main limitations of pure data-driven methods is the extrapolation capability, even with important differences between various algorithms [20,21]. Generally speaking, machine learning models typically need wide databases for training and they cannot guarantee a high accuracy when inputs assume values outside the range considered for algorithm training [22]. For both these reasons, authors have already effectively developed and implemented hybrid approaches where a machine learning algorithm is mainly used to include the effect of input features that do not vary outside the range assumed in the training database, while analytical functions are instead used to describe the physical relationship between inputs that could change significantly and the output [23]. Thus, this hybrid approach can be considered halfway between methods 2 and 3 listed above.

The literature is not so populated in the field of hybrid modeling approaches, and in particular the application of such methods for the estimation of the EGT at the turbine outlet can be considered as a quite innovative contribution in this field. In fact, the majority of recent works that describe data driven-based exhaust gas temperature models [24,25] are focused on the procedures for the hyperparameters’ optimization and input features’ selection. The comparison between different machine learning approaches is another widely presented topic, as described in [26]. On the contrary, the present work deals with the development of a viable strategy to enhance the extrapolation capability of pure data-driven approaches and to extend their applicability to conditions unseen during the training phase. The innovative contribution of the research is thus the simplification of a complicated phenomenon into simpler sub-problems, on the base of the physics of the system, and the application of most appropriate modeling approach to each. The application of a hybrid approach to engine modeling demonstrates that integrated models, which blend analytical functions with artificial neural networks (ANNs), achieve superior predictive accuracy and generalization performance compared to models relying solely on ANNs. This type of modeling approach is based on the effects of superposition principle [27], and this means each input variable brings a specific contribution to the physical process [28,29]. With a hybrid approach, it is possible to improve the accuracy of each method (pure data-driven and pure analytical) when used as the main approach, maintaining a low computational effort for the complete algorithm. Developing models requiring low computational power to be executed is important for deploying them in real-time (RT) devices. Authors typically deal with the development of innovative sensors [30] and control-oriented engine and combustion models compatible with RT execution and their implementation in RT control strategies [31]. This objective is maintained also for the EGT modeling activity.

In this work, the aforementioned hybrid approach is applied to model the EGT at the turbine outlet, starting from the estimation of the temperature at the turbine inlet, which serves as an input for modeling the expansion across the turbine impeller. Expansion modeling is approached with equations of the physical process. This study aims to assess the advantages and limitations of this approach in terms of its accuracy and adaptability to varying operational conditions. The results provide valuable insights into the reliability of hybrid models, where ANNs and physical 0-D functions work together to improve the reliability of the overall model in terms of extrapolation capability.

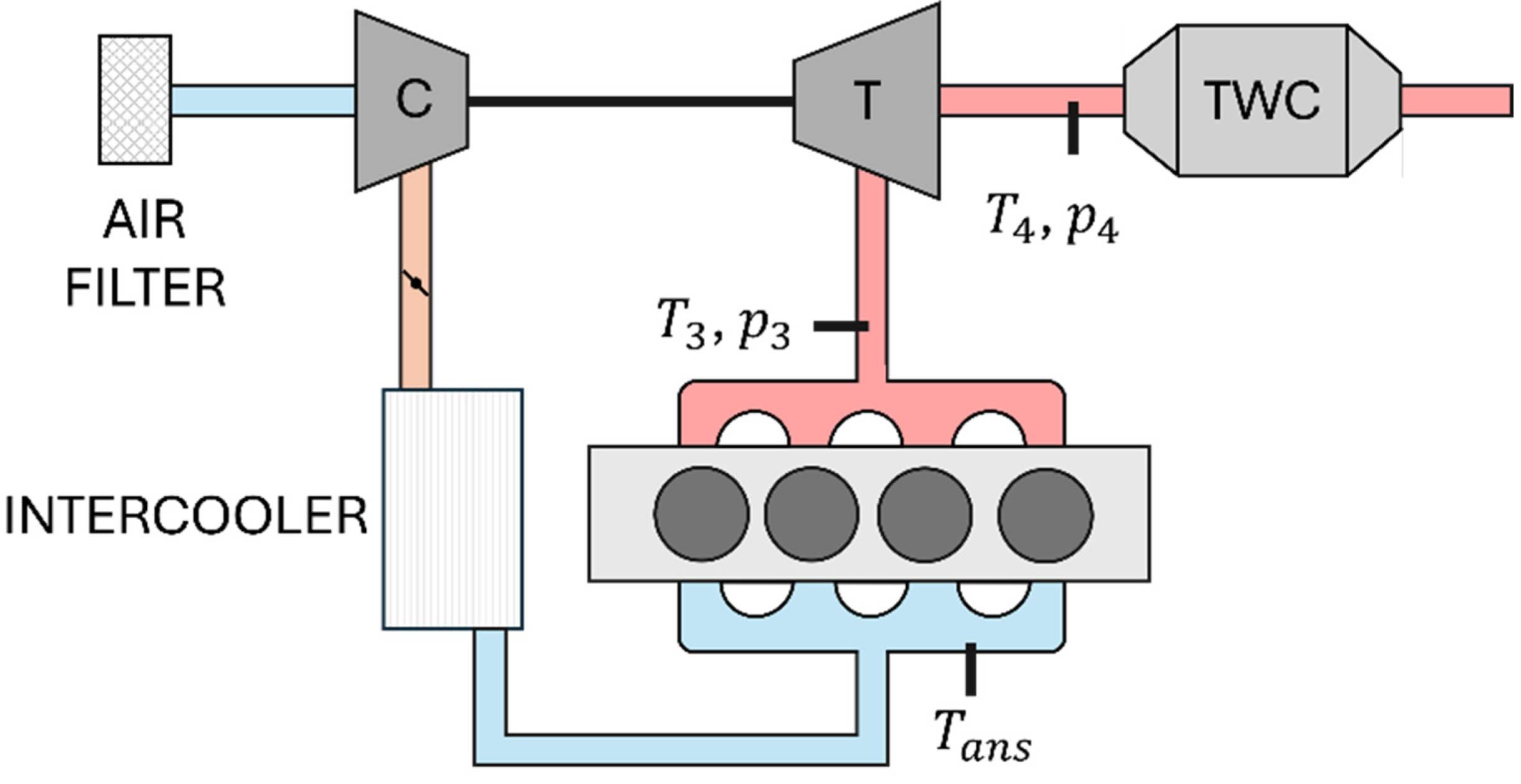
In the first part, the experimental setup used to collect experimental datasets for the model development and validation is presented and the type of tests carried out at the test rig for data collection are described. Both steady states and transient states are recorded, because the model is developed with steady-state data only and validated under transient conditions. The engine is a turbocharged, gasoline direct injection (GDI), V8 engine and the model developed in this work refers to a single engine bank.

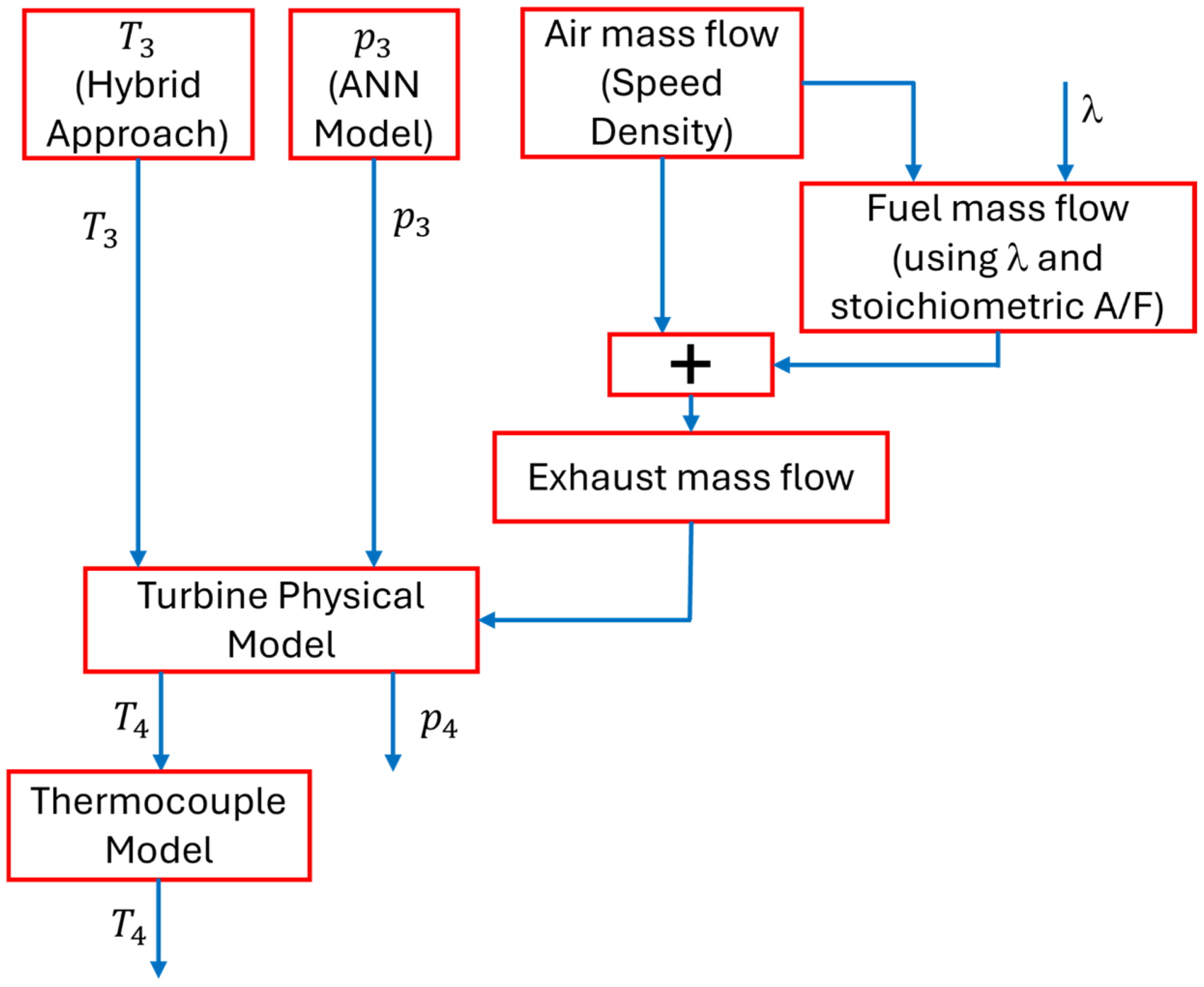
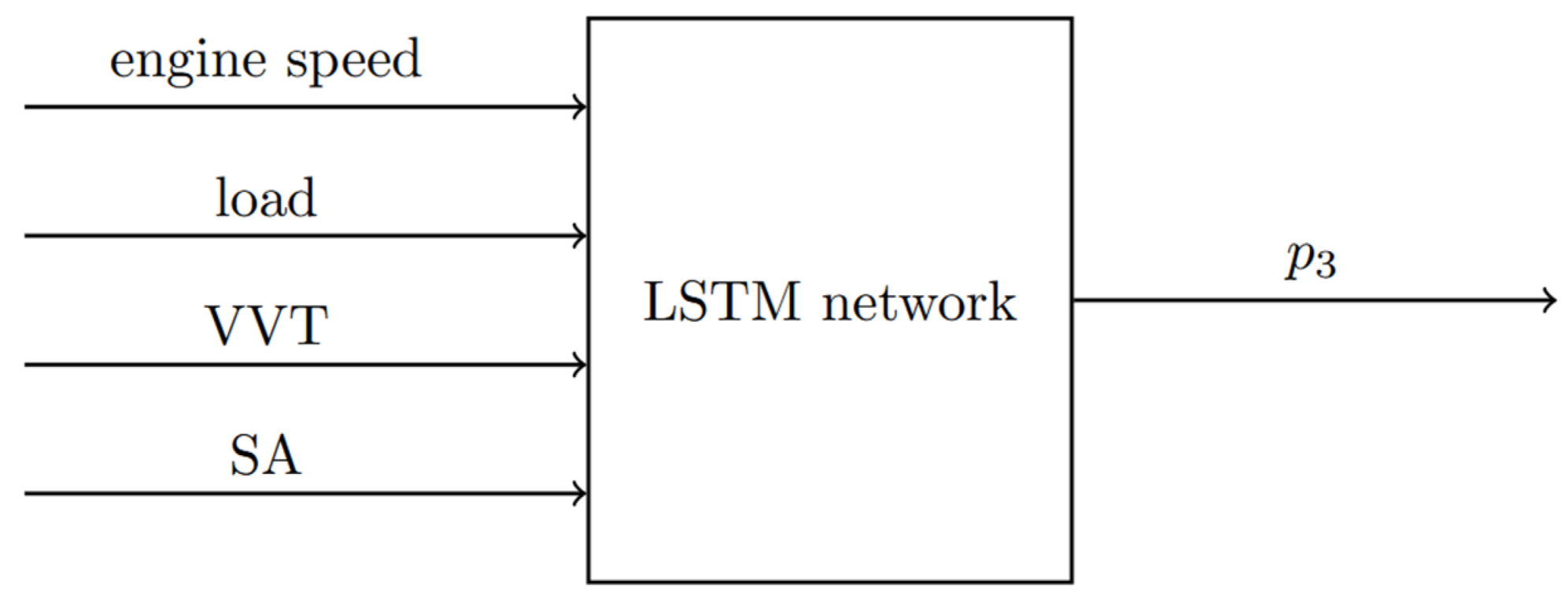
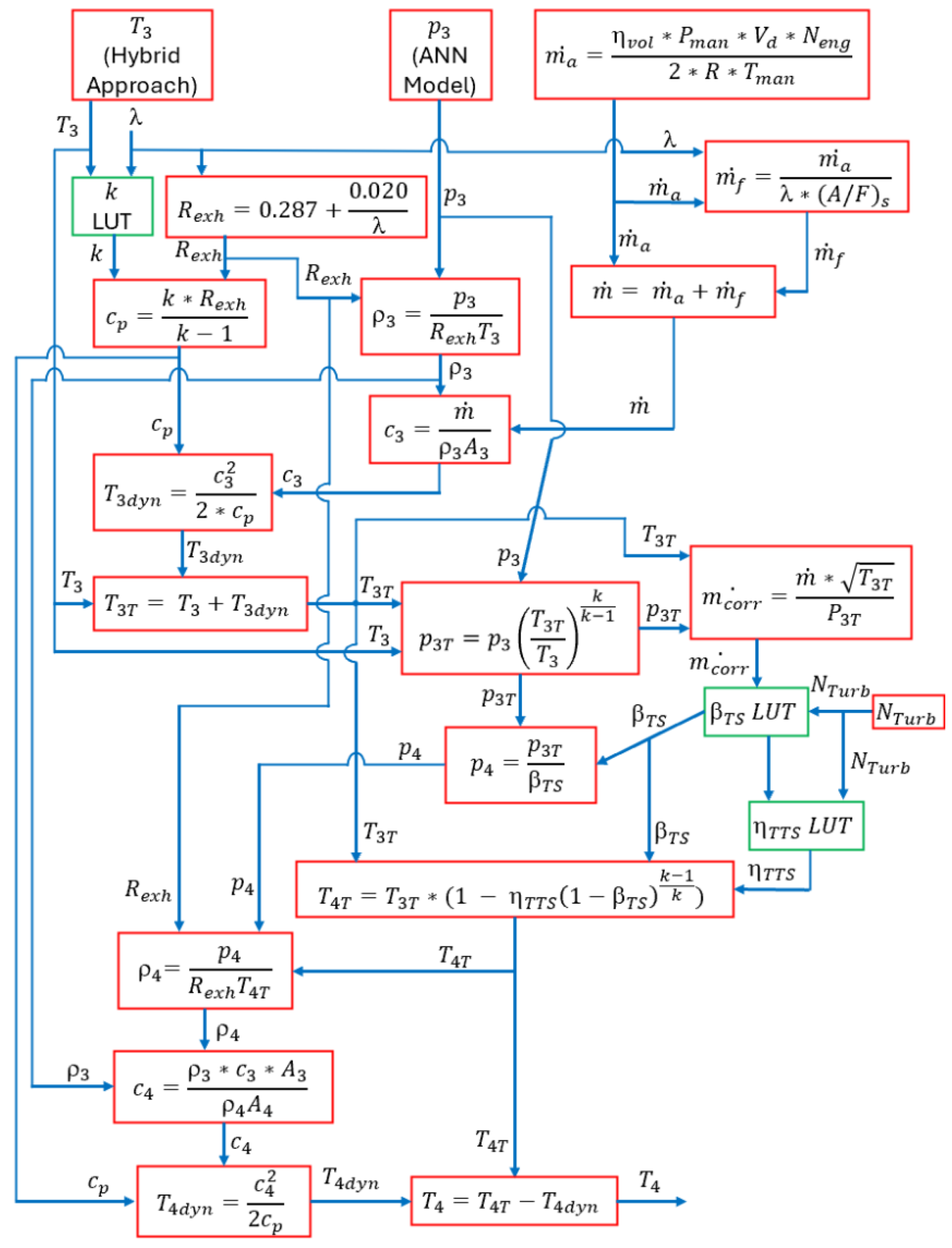
The modeling approach is then presented in Section 3, highlighting the part of the model in which ANNs, analytical functions, and physical equations are implemented. In this section, the complete calculation chain for the estimation of the exhaust gas temperature at the turbine outlet. The EGT before the turbine impeller (T₃) and the pressure in the same position of the exhaust line ($p_3$) are the two main inputs for the calculation of the EGT at the turbine outlet (T₄). 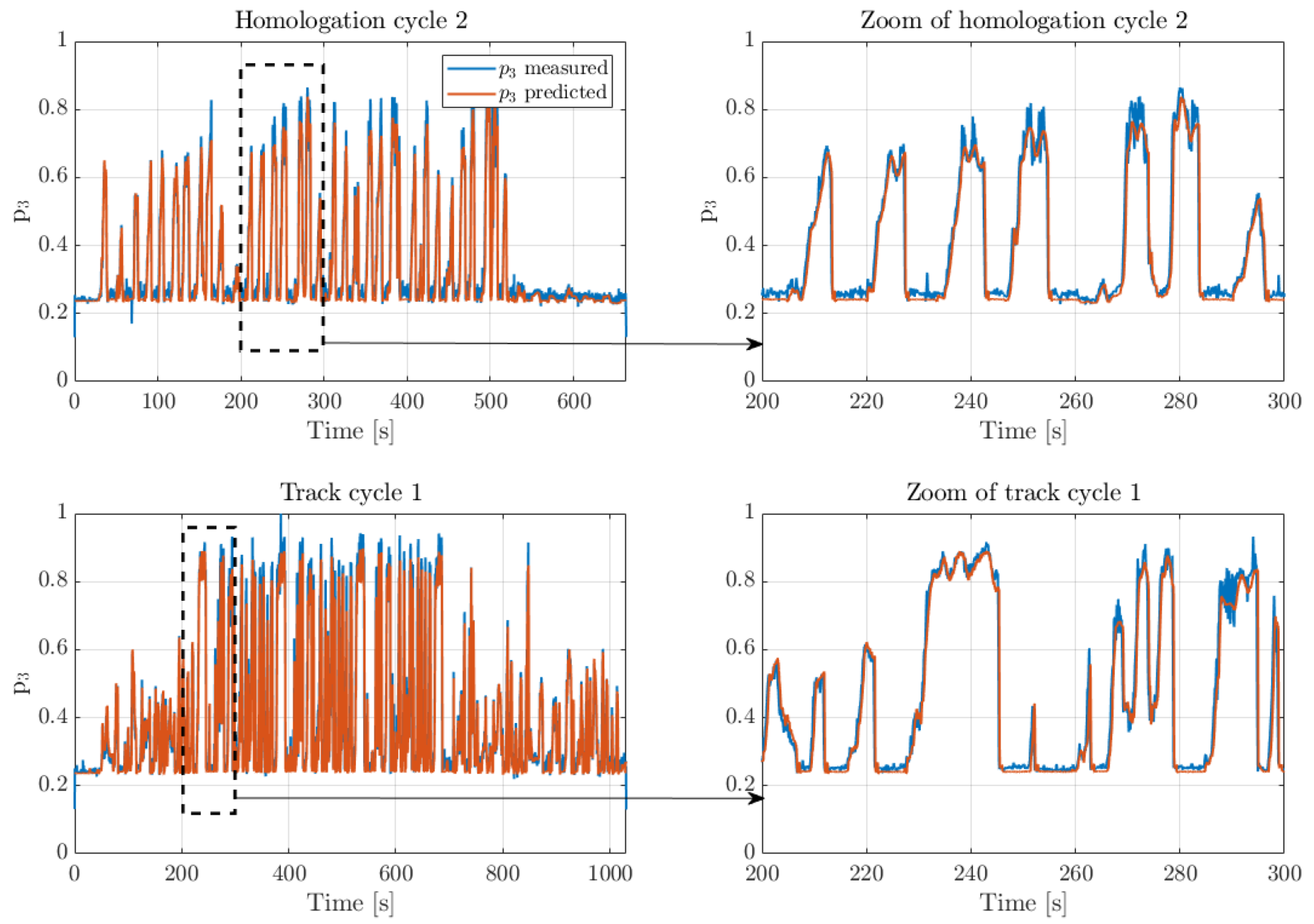The T₃ is modelled with the hybrid approach previously described by the authors in [32] while $p_3$ is modelled with an ANN in Section 3.1. Section 3.2 deals with the description of the expansion equations used to calculate the T₄ value [33]. 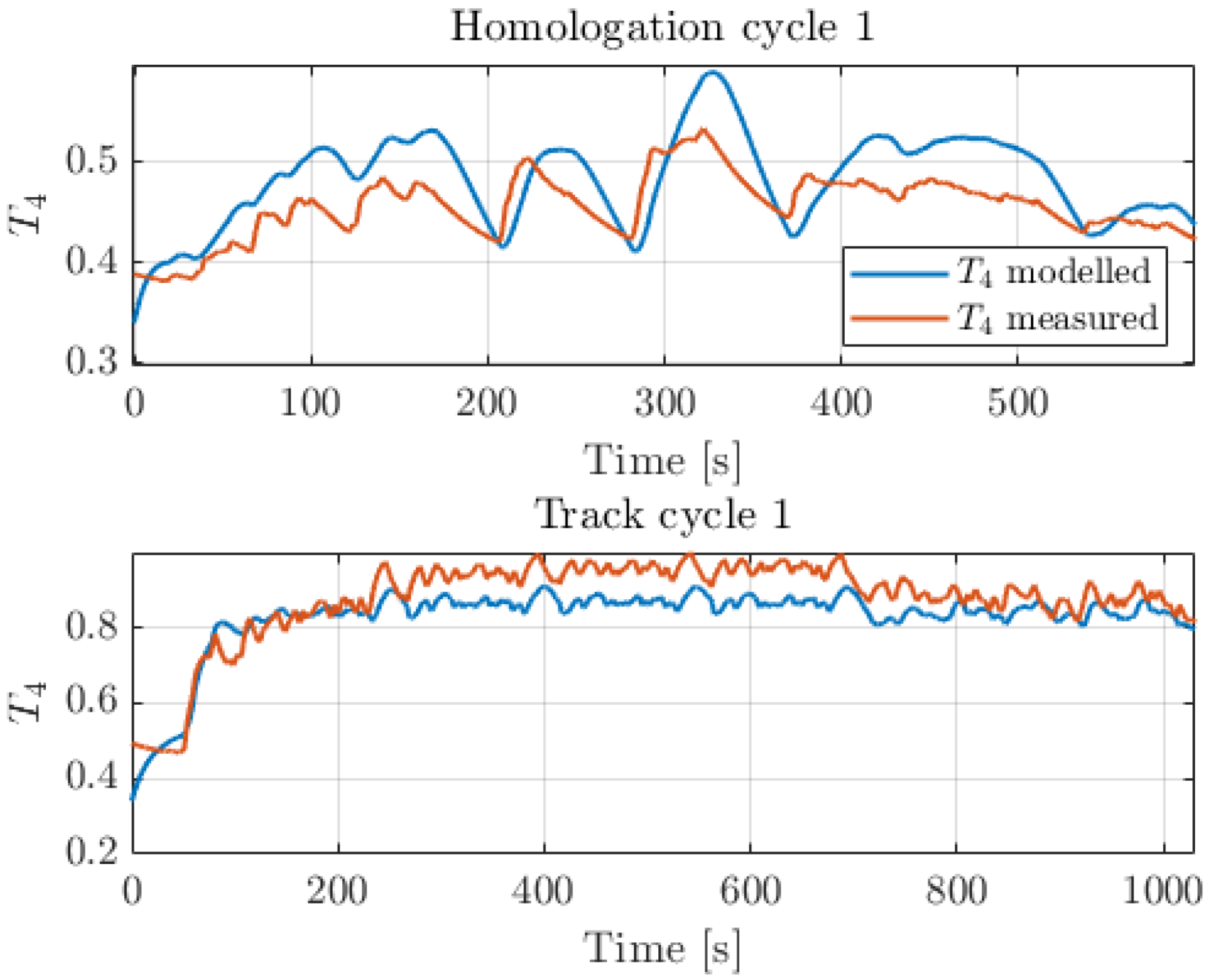The output of the T₄ model is the EGT at the turbine outlet for steady-state conditions, because all the models are calibrated with steady-state data. The T₄ value determined in this way cannot be directly compared with the T₄ measured at the bench under transient conditions, because of the TC dynamics. The TC effect is included as a first-order system, where the time constant is calibrated to minimize the error between the experimental and the calculated T₄ trace under transient conditions. The layout of the overall calculation chain is shown in Figure 1.

In Section 4, the validation process for both new models introduced with the present work is shown by evaluating the root mean square error (RMSE) between calculated and measured values under transient conditions for both $p_3$ and T₄ estimations. Indeed, the simulation of real driving cycles represents the conditions for the final application of the T₄ model. The estimation of the complete calculation chain (composed by the T₃ model, $p_3$ model, turbine model, and TC model) is directly compared with the experimental trace. The results demonstrate for six different tests that the RMSE is small and constant. This second aspect is particularly important for evaluating the extrapolation reliability of the complete simulator. Indeed, this observation suggests that similar results can be expected in further simulations.

2. Experimental Framework

2.1. Experimental Setup and Instrumentation

The experimental campaign was conducted on a high-performance V8 gasoline direct injection (GDI) turbocharged engine coupled with an eddy current brake from Borghi and Saveri. The detailed specifications of the engine are presented in

Table 1. Eight-cylinder engine characteristics.

Engine Characteristics
Displaced volume [cc]	3990
Number of cylinders [#]	8
Stroke [mm]	82
Bore [mm]	88
Connecting Rod [mm]	143
Compression ratio [-]	9.5:1
Number of valves per cylinder [#]	4
Combustion system	Spark-ignited Gasoline Direct Injection
Charging system	Single turbocharger for each bank

. Throughout the experimental activity, gasoline with a Research Octane Number (RON) of 98 was used as fuel.

To measure the pressure and temperature at various points along the intake and exhaust lines, piezoresistive transducers and thermocouples were employed, respectively. The piezoresistive sensors have an accuracy of ±0.5% of the full-scale output (defined by Best Fit Straight Line, BFSL) and the thermocouples have an accuracy of ±2.2 °C. The specifications for the transducers are detailed in

Table 2. Piezoresistive pressure transducer characteristics.

Pressure Range [Bar]	0 to 4
Accuracy (BFSL)	±0.5% of full-scale output
Operating temperature range [°C]	−30 to 100

, while the thermocouples’ characteristics are listed in

Table 3. Thermocouple characteristics.

Type	K
Diameter [mm]	3.3
Accuracy [°C]	±2.2

.

The data acquisition system comprises a National Instruments Compact-Rio 9024 integrated with the 9213 module, which operates at a sampling frequency of 100 Hz. For each steady-state operating point, temperature data were collected after the transient phase stabilized, ensuring an accurate representation of the equilibrium temperature under the given working conditions. Main measurements for pressure and temperature at the turbine inlet and outlet were performed with the thermocouples and pressure transducers mentioned above. Figure 2 reports a scheme of one engine bank with the indication of main measurement points and nomenclature of signals used in the following.

2.2. Experimental Campaign

The experimental tests were designed to construct a consistent dataset for the training and validation of the ANNs. In this study, all the tests are divided between steady-state data for model calibration and dynamic recordings for validation.

Steady-state tests involved performing sweep tests for a fixed engine speed and load in which each independent variable, including the spark advance (SA), lambda (λ), variable valve timing (VVT), and intake manifold temperature (Tans), was varied individually while the others were kept constant. These variables were selected due to their influence on combustion behavior and, consequently, on the parameters being modeled in this study: $p_3$ and T₄. To minimize extrapolation risks during model inference and to ensure robust interpolation within the domain, sweep tests were conducted over both wide and narrow engine operating fields. Only this dataset was used to train neural networks and develop the expansion model. Figure 3 illustrates the engine operating points tested for each sweep, represented in terms of the engine load and speed. The values for the engine load and speed were normalized relative to their maximum values and expressed as percentages, a normalization method consistently applied throughout this paper.

Transient tests were conducted at the test bench by reproducing a variety of driving cycles, encompassing both pedal and engine speed profiles from homologation cycles and on-track trajectories. These profiles included a wide range of maneuvers, from slow transients to aggressive transients, and included scenarios with standard calibrations as well as various control strategies affecting the aforementioned variables. Such variations ensured that the models were tested and validated across a broad spectrum of operating conditions. At the same time, EGT measurement under transient conditions is affected by the TC dynamics, as described in the introductive section of this paper. This means that for a direct comparison between calculated and experimental values, the modelled EGT for steady-state conditions had to be adjusted with the TC model mentioned above. The TC and the effect of heat exchanges were modelled as a first-order system. Figure 4 illustrates examples of the tested cycles: the left displays a homologation cycle, while the right depicts an on-track maneuver.

3. Model Formulation

The two important indexes required to evaluate the temperature T₄ are T₃ and $p_3$. As mentioned earlier, the T₃ model was developed in previous work of the authors. Instead, the $p_3$ and T₄ models were developed as explained below. For this study, the following assumptions were considered:

• The exhaust gases behave as an isentropic fluid;
• The exhaust gases behave as an ideal gas.

3.1. p₃ Model

The prediction of $p_3$ was carried out using a Long Short-Term Memory (LSTM) network, with inputs consisting of ECU variables, namely the engine speed, load, VVT and SA. Figure 5 represents the block diagram of the calculation chain for $p_3$. The model was trained using steady-state data (as described in Section 2.2) and validated using transient data from the same section.

As reported in the literature [34], Bayesian optimization is preferred over the grid search algorithm for hyperparameter optimization due to its capability to achieve better results with fewer evaluations. Consequently, this approach was adopted, and the optimization results are presented in

Table 4. $p_3$ LSTM configuration.

Number of hidden units in the LSTM layer	84
Number of FC layer	1
Number of neurons in the FC layer	99
Number of Epochs	4921
Validation frequency	62
Mini-batch size	133
Dropout probability	0.5
Solver	Adam
Training data percentage	70%

. Furthermore, since the signals recorded at the test bench were noisy, the network’s output also exhibited undesirable oscillations, leading to higher errors. To address this issue, a low-pass filter was applied to the network’s output, effectively smoothing the oscillations while preserving the essential content of the signal.

3.2. T₄ Model

The T₄ model was formulated based on the theory of the turbomachines, specifically addressing the gas expansion process within turbines. The following paragraph reports the equations from turbine theory used for the evaluation of the temperature.

The exhaust gas mass flow $\dot{m}$ is calculated as the sum of the air mass flow rate (evaluated with the speed–density model) and of the fuel flow rate which can be evaluated starting from the stoichiometric air–fuel ratio (A/F) and the measured λ, as reported in Equation (1).

$${\dot{m}}_f={\displaystyle \frac{{\dot{m}}_a}{\lambda {(A/F)}_s}}$$

(1)

The temperature T₃ has been modelled with a hybrid approach. The total temperature $T_{3T}$ has been calculated as the sum of T₃ and of the dynamic temperature $T_{3dyn}$. This $T_{3dyn}$ is as represented in Equation (2).

$$T_{3dyn}={\displaystyle \frac{c_3^2}{2c_p}}$$

(2)

where $c_3$ is calculated from the definition of mass flow rate and $c_p$, the specific heat at constant pressure, is a function of the gas constant $R_{exh}$ and of the ratio of the specific heat k. As described by Krieger et al. [35], the gas constant R for temperatures below 1450 K can be defined as represented in Equation (3).

$$R_{exh}=0.287+{\displaystyle \frac{0.020}{\lambda }}$$

(3)

The specific heat ratio k has been evaluated from a Look-Up Table (LUT) which is a function of T₃ and λ, as described in [36].

The total pressure $p_{3T}$ is a function of $p_3$, $T_{3T}$, $T_3$, and k which is as described in Equation (4).

$$p_{3T}=p_3{\left({\displaystyle \frac{T_{3T}}{T_3}}\right)}^{{\displaystyle \frac{k}{k-1}}}$$

(4)

The reduced mass flow rate (${\dot{m}}_{corr}$) has been defined as the product of mass flow rate and square root of the total turbine inlet temperature $T_{3T}$ divided by the total pressure at the turbine inlet $p_{3T}$, as demonstrated by Equation (5).

$${\dot{m}}_{corr}={\displaystyle \frac{\dot{m}\sqrt{T_{3T}}}{p_{3T}}}$$

(5)

Given the values of ${\dot{m}}_{corr}$ and the turbine rotational speed (N), the value of ${\beta }_{TTS}$ has been evaluated from the ${\beta }_{TTS}-{\dot{m}}_{corr}$ map provided by the turbocharger manufacturer. The LUT is shown in Figure 6, with each curve corresponding to a different value of N. Punctual values of the speed cannot be disclosed for confidentiality reasons.

The total-to-static isentropic efficiency ${\eta }_{TTS}$ has been interpolated from the ${\beta }_{TS}-{\eta }_{TTS}$ map given by the manufacturer, since the expansion ratio ${\beta }_{TS}$ and the turbine speed are known. This LUT is shown in Figure 7.

Starting from the ${\eta }_{TTS}$ equation, the temperature $T_{4T}$ has been evaluated following Equation (6).

$$T_{4T}=T_{3T}\left(1-{\eta }_{TTS}\left(1-{({\beta }_{TS})}^{{\displaystyle \frac{k-1}{k}}}\right)\right)$$

(6)

The temperature $T_{4dyn}$ has been defined as the ratio between the flow speed ($c_4$) and the specific heat at constant pressure ($c_p$) following Equation (7).

$$T_{4dyn}={\displaystyle \frac{c_4^2}{2c_p}}$$

(7)

where $c_4$ is calculated under the assumption of equal mass flow at the inlet and the outlet of the turbine as evaluated by Equation (8).

$$c_4={\displaystyle \frac{{\rho }_3{c}_3{A}_3}{{\rho }_4{A}_4}}$$

(8)

Here, $A_3$ represents the inlet area, $A_4$ represents the exducer area, and the densities ${\rho }_3$and ${\rho }_4$ are calculated from the ideal gas law.

Finally, the temperature T₄ is defined as the difference between the total temperature $T_{4T}$ and the dynamic temperature $T_{4dyn}$, as represented in Equation (9).

$$T_4=T_{4T}-T_{4dyn}$$

(9)

Figure 8 shows a clear representation of the complete calculation chain, reporting all the steps for the estimation of T₄.

This calculation is valid under steady-state conditions; however, under transient conditions, the dynamic response of the thermocouple must also be considered. The model of a thermocouple previously developed by the authors [32] is represented as a first-order system characterized by a time constant τ. This τ was calibrated using a custom optimization algorithm designed to determine the optimal value across various driving cycles and transient tests. Figure 9 shows the comparison between the temperature signal calculated before and after the integration of the thermocouple model. The TC model filters the steady state EGT value, introducing the effect of heat exchanges between the sensor and the environment, the exhaust runner walls, and the irradiation.

4. Simulations and Results

4.1. p₃ Model

The data-driven model developed for $p_3$ estimation, described in the previous paragraphs, has been validated under transient conditions. The simulations were done in the MATLAB environment, in particular with version R2022b.

The tests results presented in

Table 5. $p_3$ LSTM configuration.

Type of Test	RMSE [Bar]
Steady-state tests	0.3057
Homologation cycle 1	0.0255
Homologation cycle_2	0.1798
Homologation cycle 3	0.1650
Track cycle 1	0.2546
Track cycle 2	0.2351
Track cycle 3	0.0706

demonstrate a high level of accuracy in predicting the signal, confirming the reliability of the data-driven model. The predicted values are closely aligned with the actual signal data (as shown in Figure 10), indicating strong model performance. The RMSE remained within acceptable limits, and the lower values for homologation cycle 1 and track cycle 3 are due to the limited $p_3$ reached during the cycles. Overall, the model responded well across different test scenarios, maintaining consistency and stability. The RMSE reported below actually corresponds to a relative error of only 4–5%.

4.2. T₄ Model

The semi-physical model for T₄ estimation, described in the previous section, has been validated under transient conditions. The simulations were done in the MATLAB environment.

Table 6. Results for T₄.

Type of Test	Modeling Approach RMSE [°K]
Steady-state tests	72.79
Homologation cycle 1	41.07
Homologation cycle_2	50.88
Homologation cycle 3	56.56
Track cycle 1	70.35
Track cycle 2	69.81
Track cycle 3	64.84

 displays the results obtained for the T₄ evaluation, indicating a mean percentage error of 14%. Such an error is evaluated as the mean percentage value between all the tests reported in the table below. In particular, the driving cycles recorded at the test bench start with a cold engine, and this demonstrates the variety of operating and environmental conditions used for the validation of the model. Moreover, it can be stated that the error remains quite constant between all the six dynamic tests, and this means the complete model works well in terms of predictivity also outside those conditions available in the data used for model development and calibration. This is the main objective of this model, since it has to be coupled with combustion models described in [28] and applied to predict the engine behavior under new driving cycles.

Figure 11 shows the visual representation of the result of homologation cycle 1 and track cycle 1. The predicted data follow the trend of the measured data, showing a similar overall pattern that confirms the validity of the calculations.

The model overestimates the T₄ value at a low engine speed and low load, while it underestimates T₄ at a high engine speed and high load. This suggests potential inaccuracies in the thermodynamic modeling (i.e., heat transfer to catalyst), especially at a low speed and load.

The overall computational efficiency of a pure data-driven model is maintained also for the complete, semi-physical T₄ model. The speed of the execution is evaluated as the ratio between the time of the simulation duration and the time of the simulated driving cycle. The average value of all driving cycles is 0.003. Simulations are performed on a laptop with Intel Core i7 CPU and 8 GB of RAM. This means that the execution is about 33 times faster than the RT.

5. Conclusions and Future Works

This study presents an innovative methodology that integrates a semi-physical turbine model for the estimation of the exhaust gas temperature at the turbine outlet using a neural network-based approach for predicting the pressure at the turbine inlet. The hybrid approach developed in this work combines the precision and robustness of physical models with the adaptability and learning capabilities of artificial neural networks. By incorporating physical models instead of relying solely on a purely data-driven, black-box approach, this methodology helps mitigate common limitations of machine learning-based models, such as poor feature extrapolation and the inability to capture physical dynamics effectively. The presented approach ensures robust and reliable model validation by testing under six different driving cycles, reproduced at the engine test cell, not used for model development or calibration. The results indicate an average root mean square error of 14%, including the initial phases of driving cycles conducted with a cold engine. Therefore, the proposed method, which integrates multiple modeling techniques, demonstrates strong predictive capability, which represents the primary objective of this research.

The results demonstrate that this methodology maintains consistency with experimental datasets and aligns with physical trends, even under operating conditions that deviate significantly from the training data. This capability is crucial for ensuring robustness and reliability of this model in real-world scenarios, including anomalous engine operations such as misfires and fuel cut-offs. These outcomes demonstrate that this new methodology can be successfully employed to estimate the exhaust gas temperature downstream the turbine, together with the implementation of a semi-physical thermocouple model.

Future developments of this work will focus on further enhancing the model’s accuracy and robustness, with a more in-depth investigation of thermal exchanges in the exhaust runner and turbine. Additionally, the exhaust gas temperature model at the turbine outlet, coupled with the previously developed engine simulator, will be extended to estimate the temperatures of various aftertreatment system components. The complete engine simulator will also be integrated with a physical catalyst model to simulate its exothermic and heat exchange reactions, enabling the prediction of exhaust gas temperatures at the catalyst inlet and outlet.