Numerical Simulation Study on the Feasibility of Cyclone PIV Tracer Particle Seeder in Microgravity
Abstract
1. Introduction
- Contrasting design objectives: The cyclone separator separates particles from the gas flow to obtain a clean gas phase, whereas the cyclone particle seeder generates and delivers aerosols, ensuring a well-mixed gas-particle flow;
- Different inlet flow compositions: The cyclone separator involves gas–solid two-phase flow at the inlet, whereas the cyclone particle seeder only has one fluid phase at the inlet;
- Different structural features: The cyclone separator typically includes a dust hopper for collecting solid particles carried by the fluid, while the cyclone particle seeder does not include a dust hopper.
2. Physical and Mathematical Model
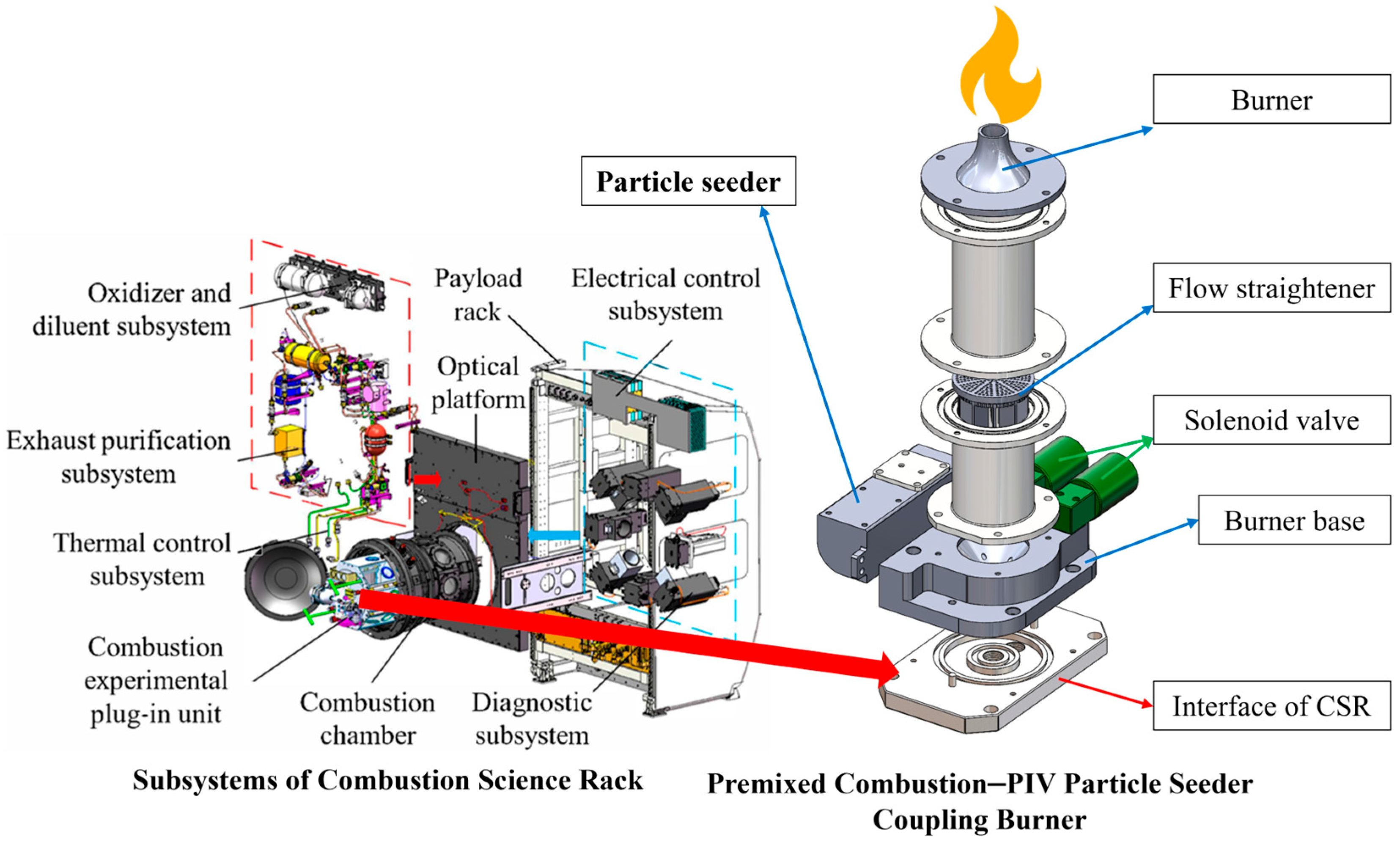
2.1. Structure and Working Principle of the PIV Particle Seeder–Premixed Combustion Coupling Burner
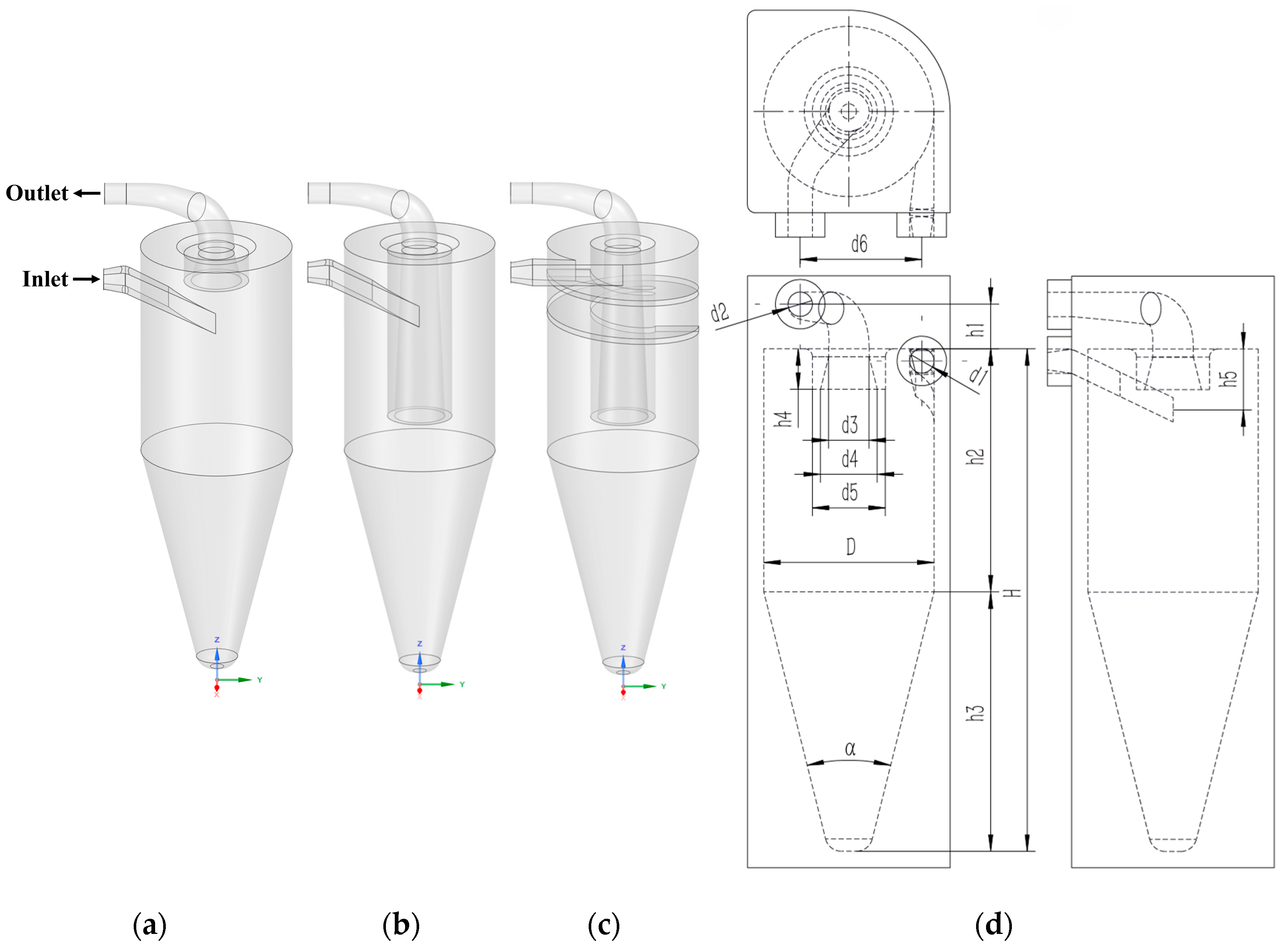
2.2. The Geometrical Model
2.3. Gas Phase Turbulence Model
2.4. The Two-Phase Simulation Model
3. The Computational Domain Model
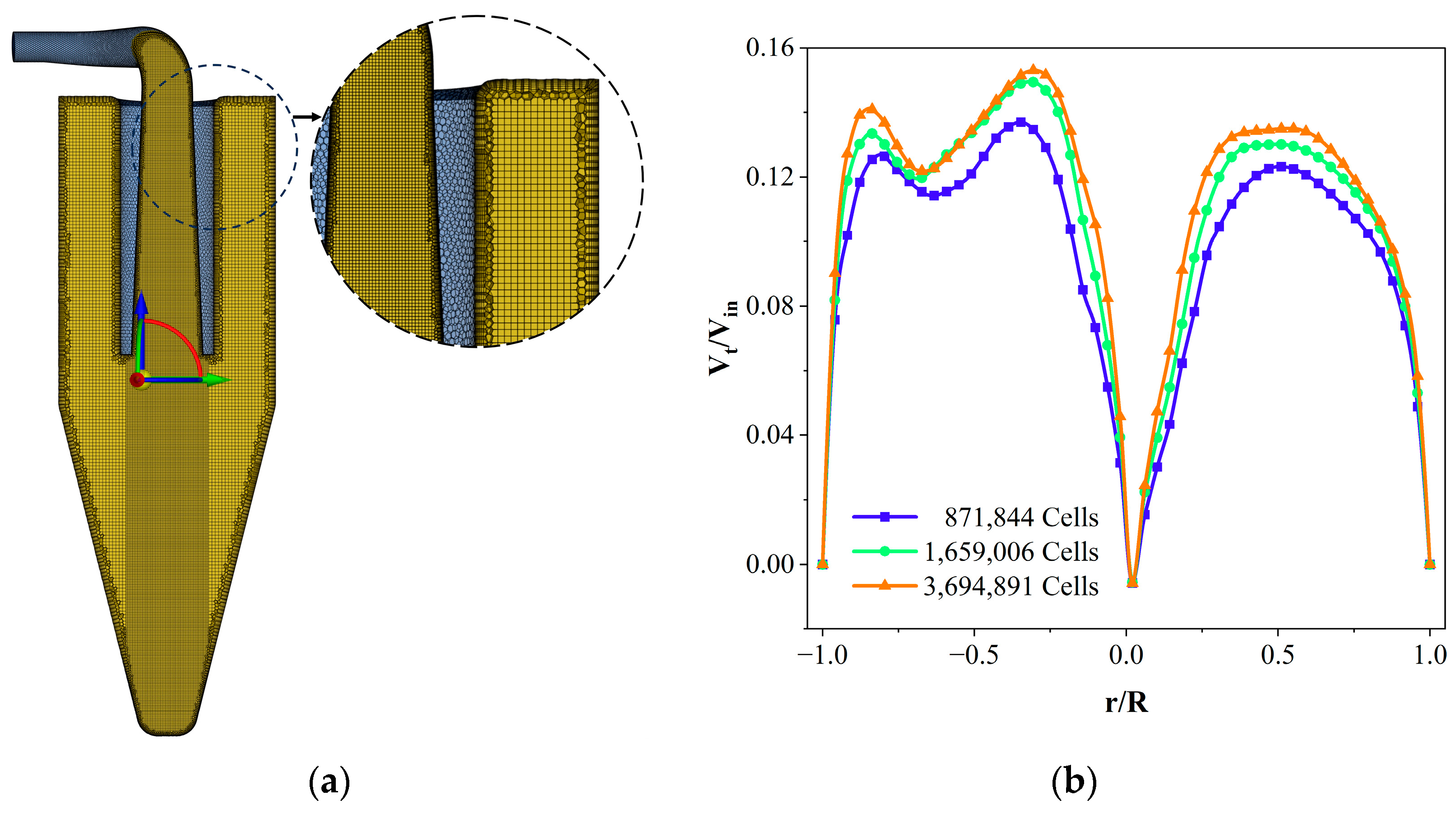
3.1. Grid Partition and Independence Check
3.2. Boundary Conditions and Solving Methods
3.3. Validation of the Computational Model
4. Experiment Setup
5. Results and Discussion
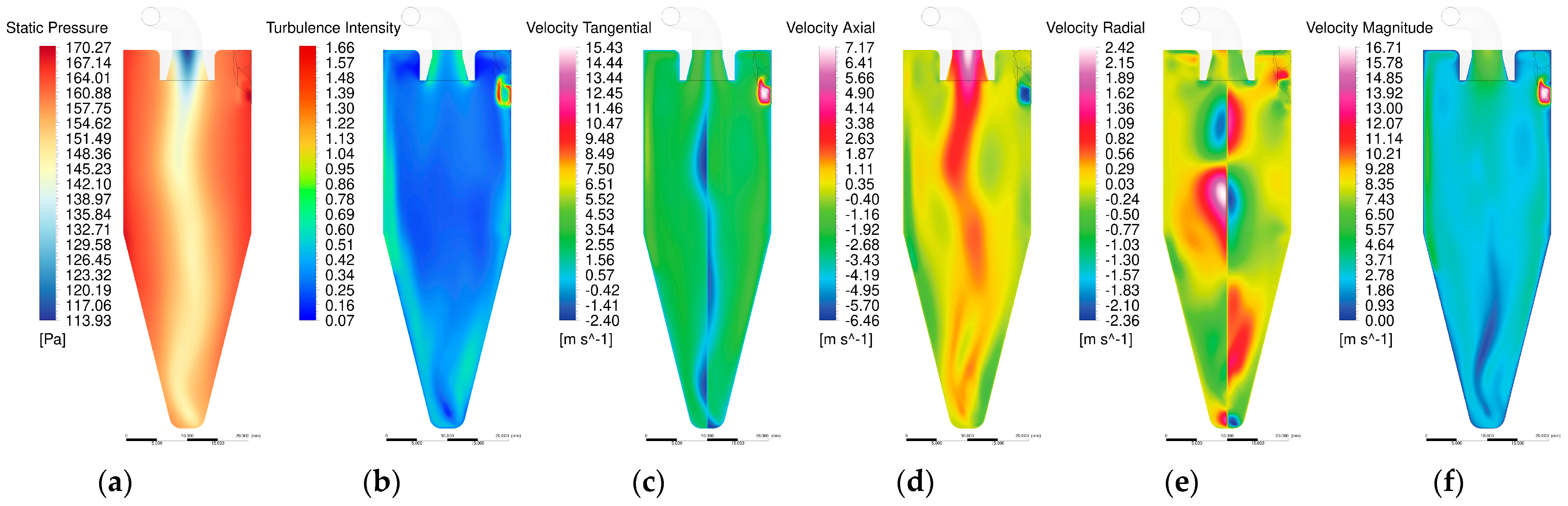
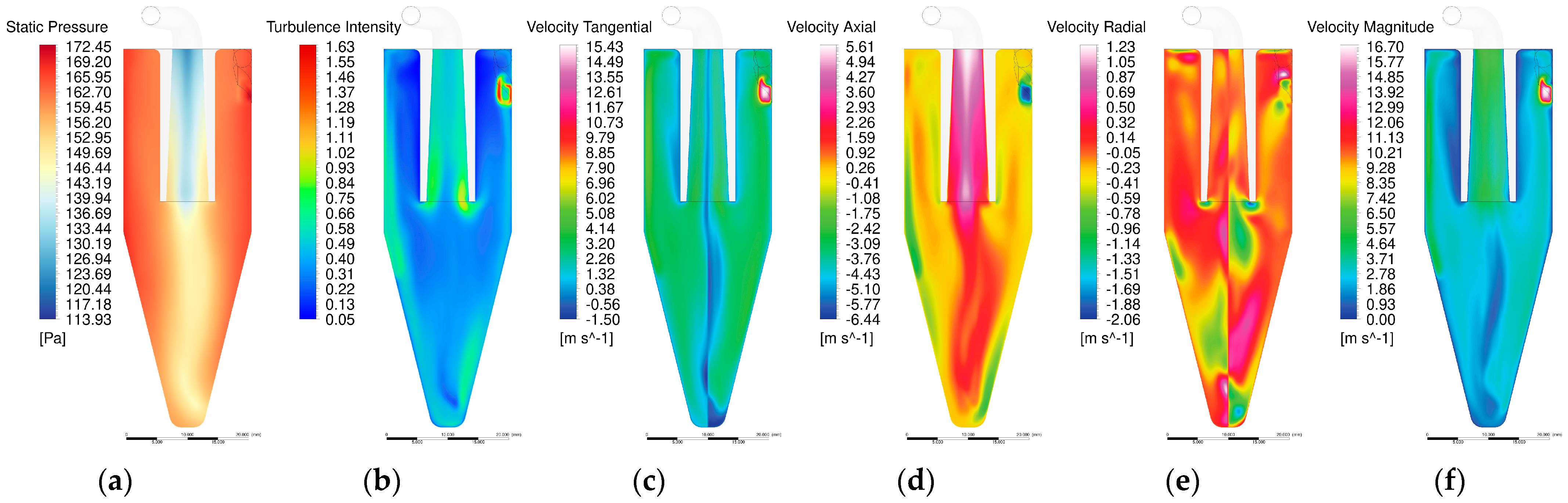
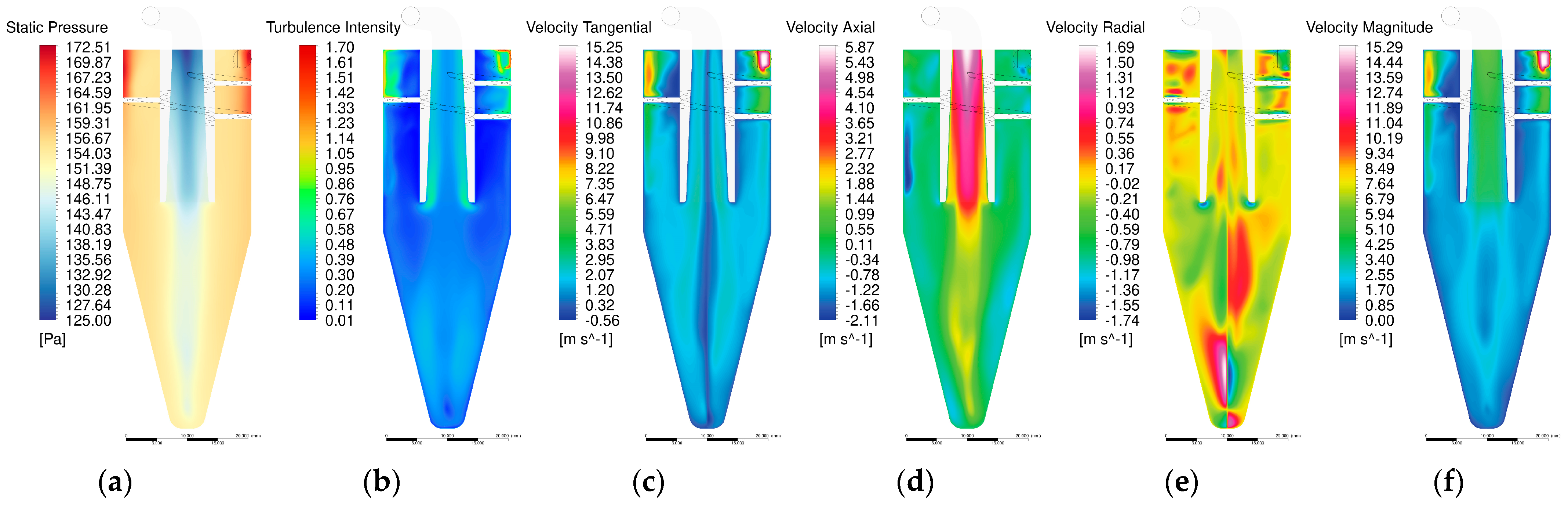
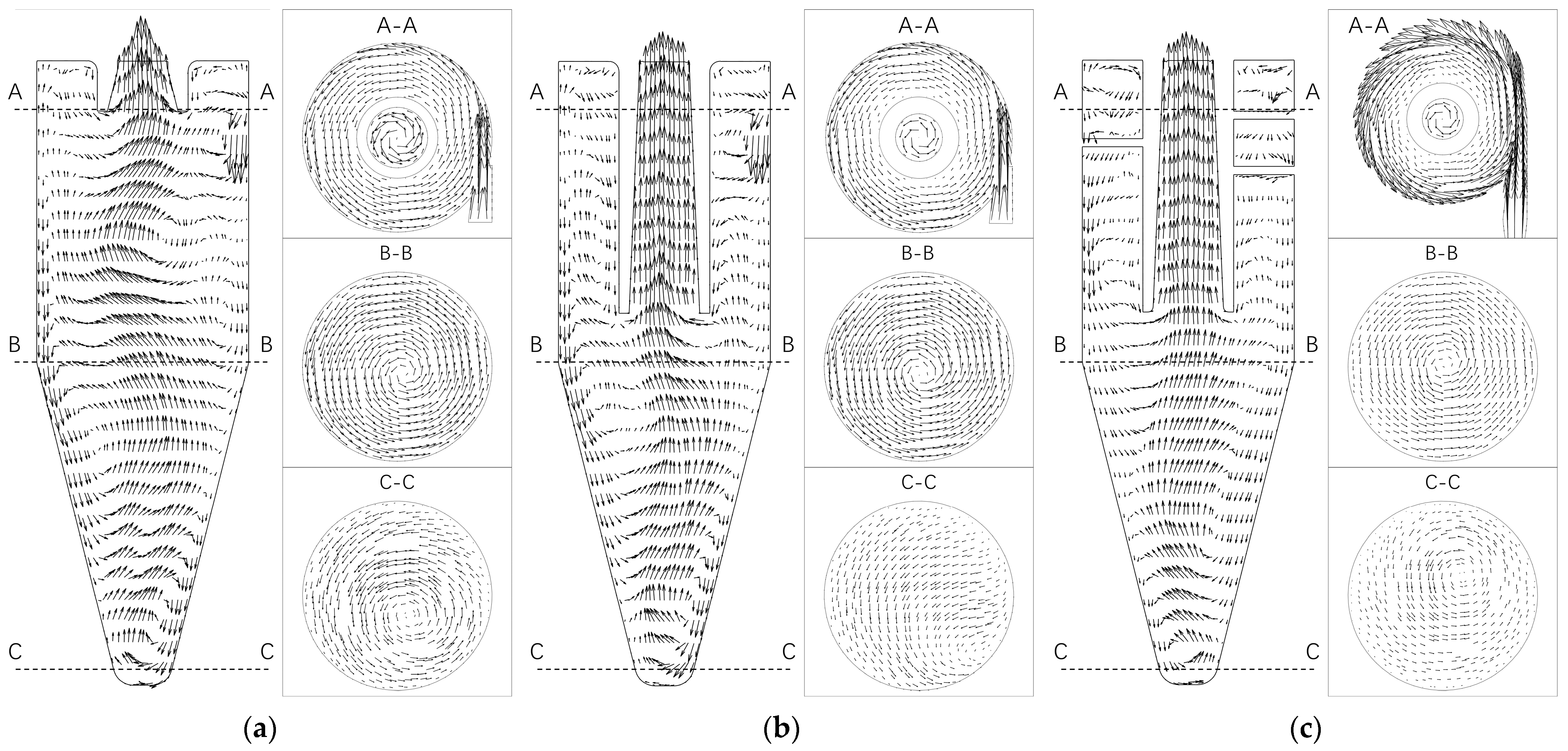
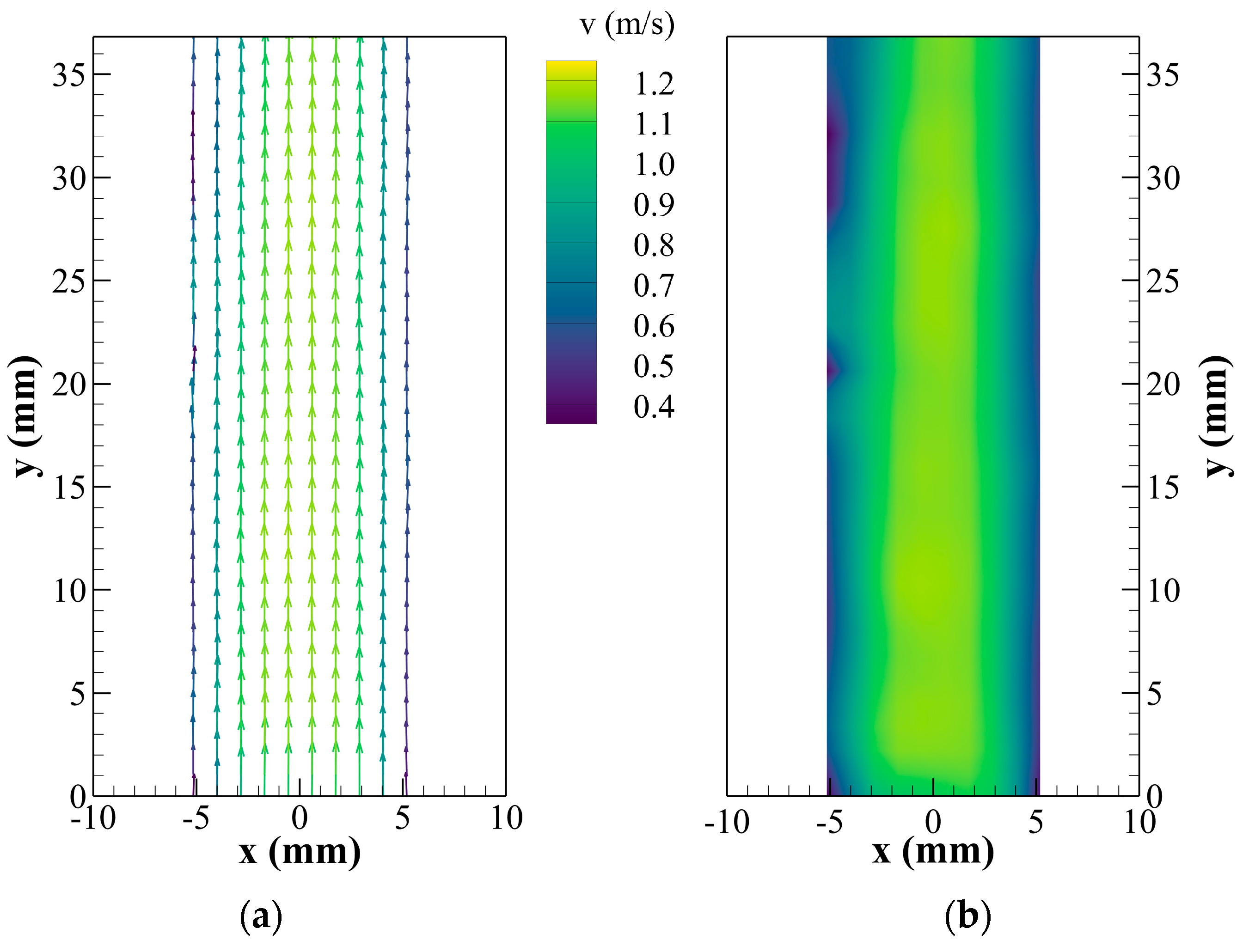
5.1. Steady Flow Field in Different Seeder Geometries
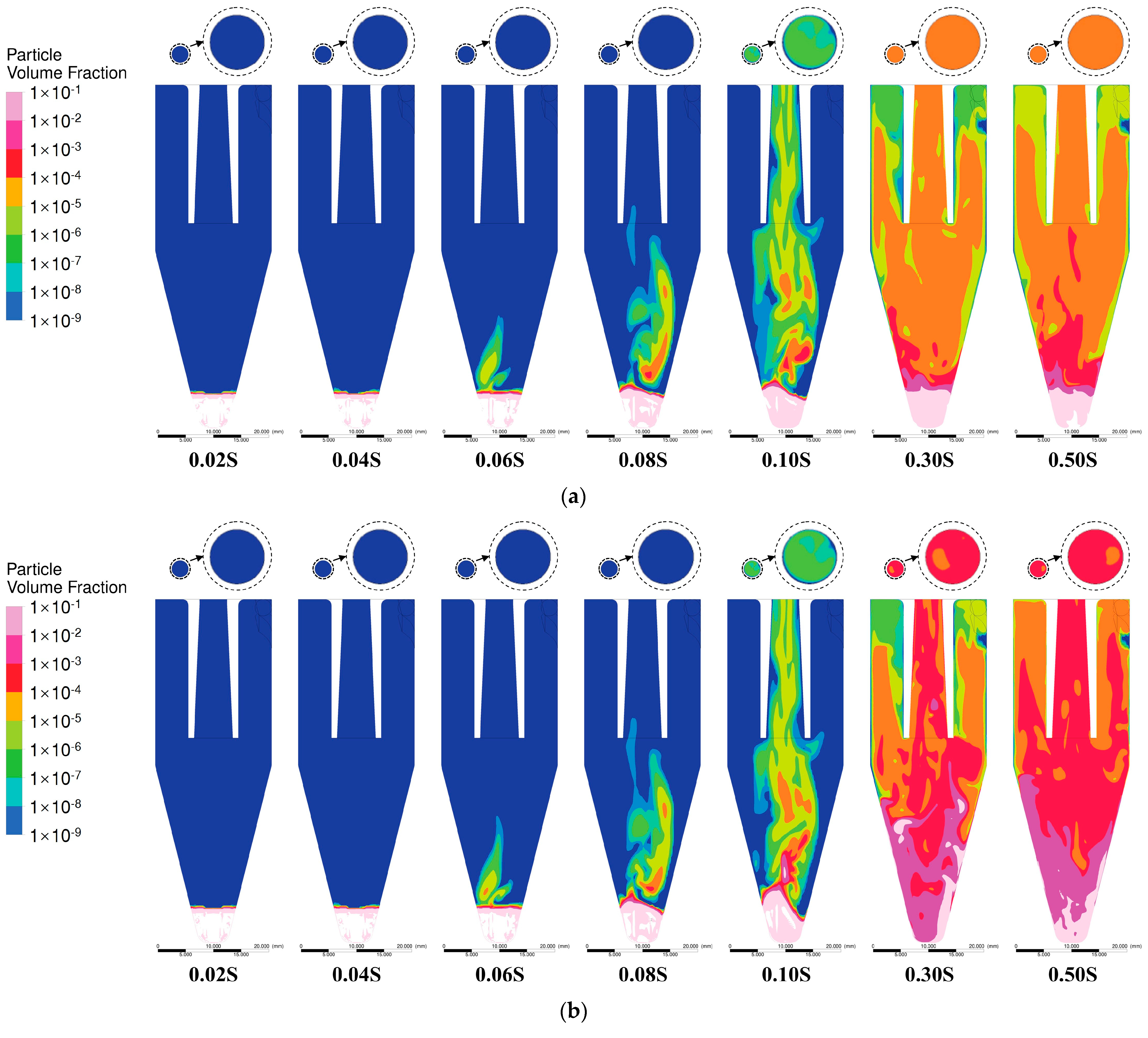
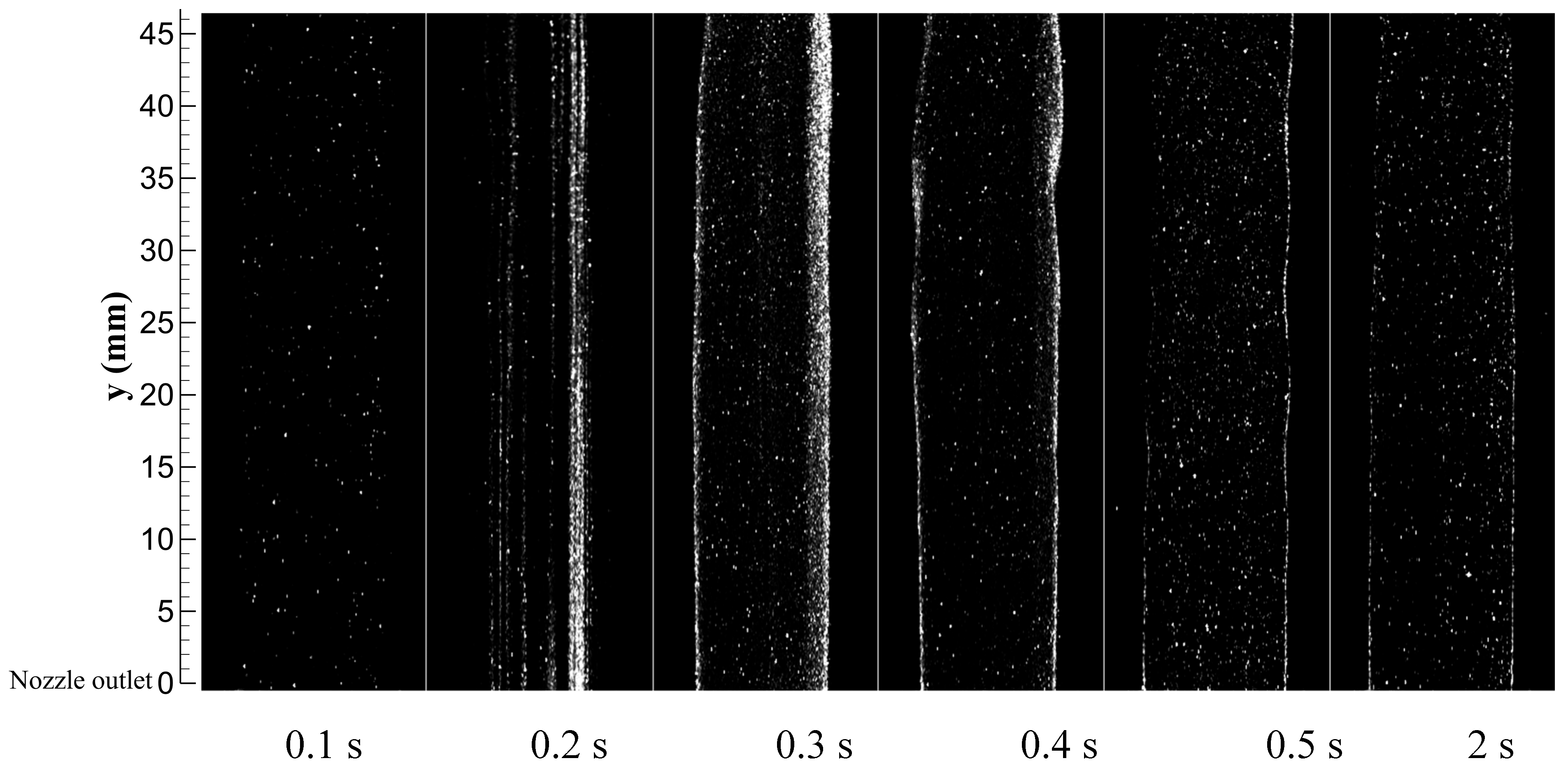
5.2. Spatiotemporal Evolution of Particle Distribution in Unsteady Flow
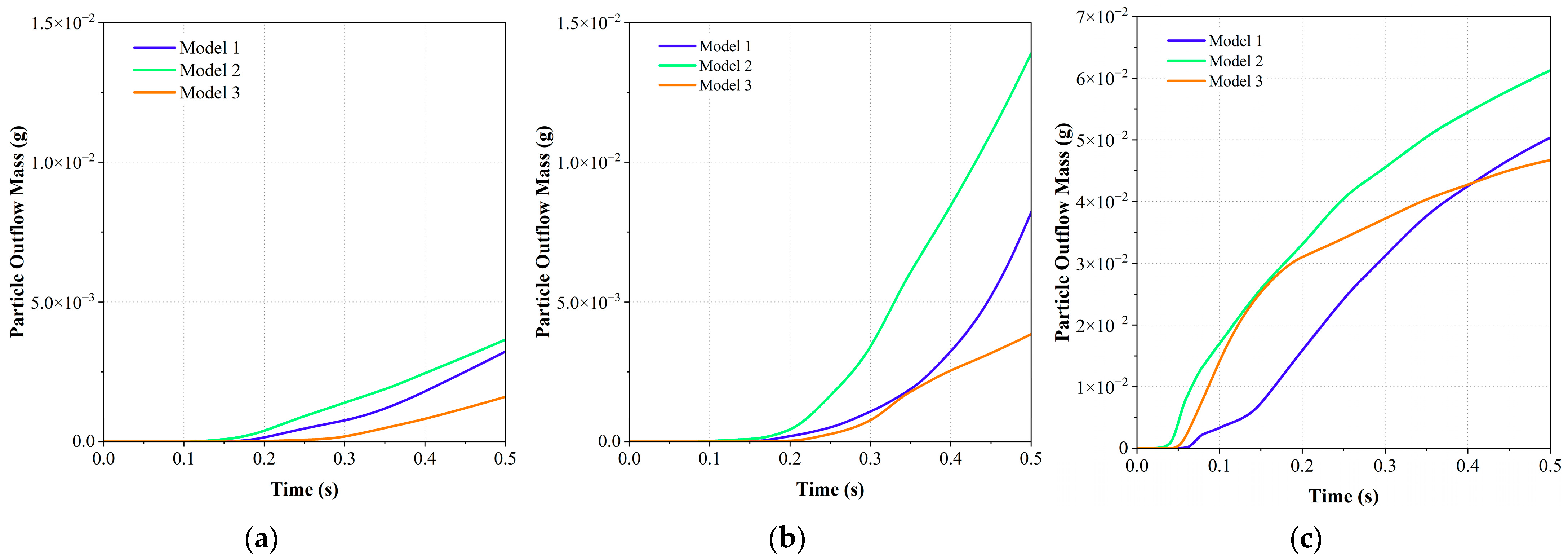
5.3. Particle Outflow in Different Gravity and Seeder Geometries
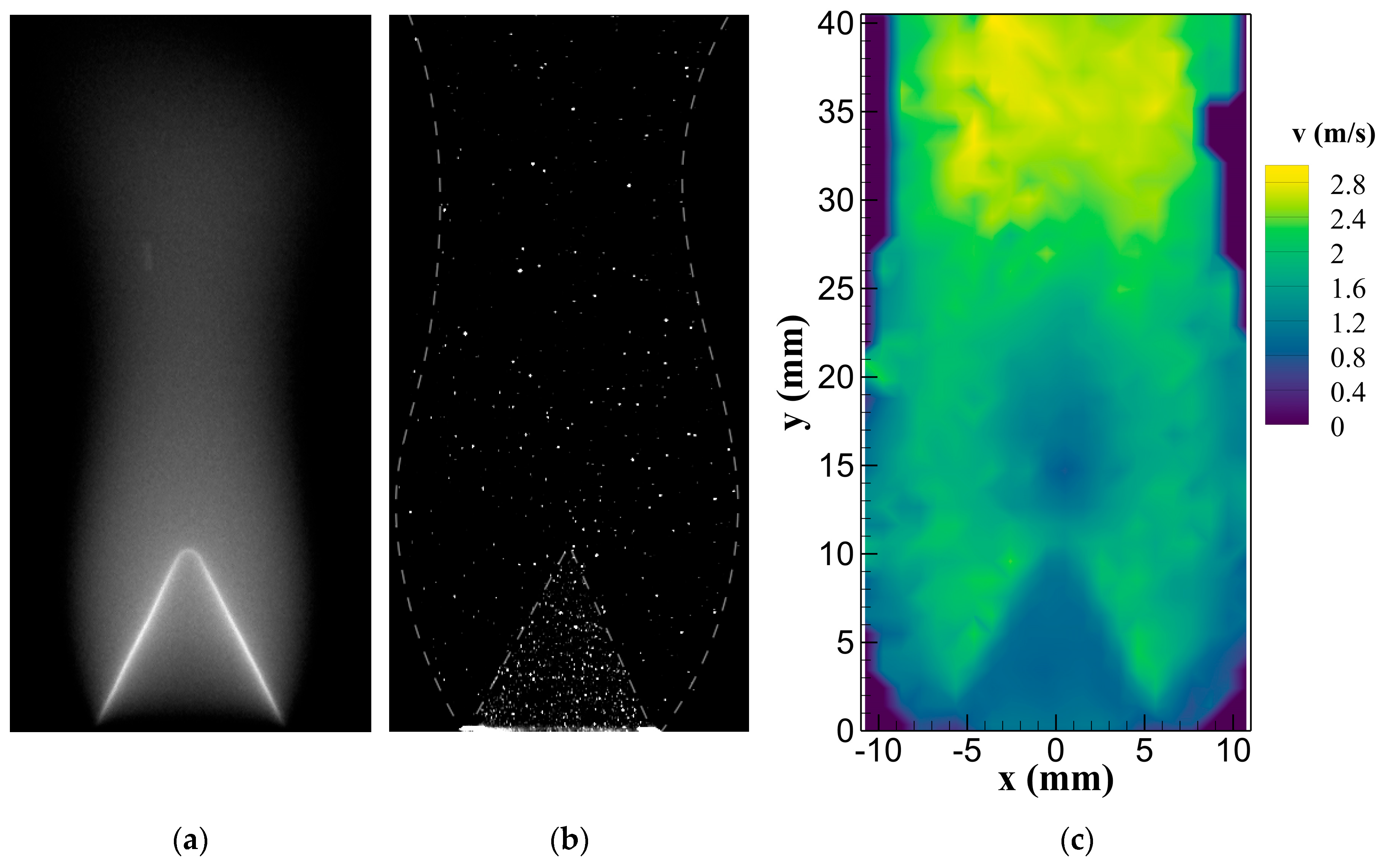
5.4. Ground-Based PIV Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Kong, W.; Zhang, H. Design of combustion science experimental system for China Space Station. Chin. J. Space Sci. 2020, 40, 72. [Google Scholar]
- Wen, Y.; Li, L.; Li, X.; Luo, L.; Chen, T.; Zhang, W.; Zhou, H.; Chen, S.; Sun, Y.; Shi, J. Extinction of microgravity partially premixed flame aboard the Chinese Space Station. Proc. Combust. Inst. 2024, 40, 105574. [Google Scholar]
- Li, Y.; Guibaud, A.; Citerne, J.-M.; Consalvi, J.-L.; Coimbra, A.; Sarazin, J.; Bourbigot, S.; Torero, J.; Legros, G. Effects of flame retardants on extinction limits, spread rate, and smoke release in opposed-flow flame spread over thin cylindrical polyethylene samples in microgravity. Proc. Combust. Inst. 2023, 39, 3919–3928. [Google Scholar]
- Li, D.; Wen, Y.; Liu, Y.C.; Wang, S. On the transition modes and mechanisms for laminar to turbulent lifted jet diffusion flames at normal-and micro-gravity. Combust. Flame 2024, 260, 113269. [Google Scholar]
- Law, C. Combustion in microgravity-Opportunities, challenges, and progress. In Proceedings of the 28th Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 1990; p. 120. [Google Scholar]
- Su, Y.; Zhang, B.; Chen, Y.; Sui, C.; Chen, W. 3D velocity and temperature distribution measurement and characteristic analysis of swirling combustion. Measurement 2022, 193, 110949. [Google Scholar]
- Turns, S.R. Introduction to Combustion; McGraw-Hill Companies: New York, NY, USA, 1996; Volume 287. [Google Scholar]
- He, L.; Zheng, H.; Wang, X.; Yang, X.; Zhang, X. Ground Experiment Investigation of PIV Unit for Combustion Science Experimental System of China Space Station. Chin. J. Space Sci. 2022, 42, 1152. [Google Scholar]
- Greenberg, P.S.; Wernet, M.P.; Yanis, W.; Urban, D.L.; Sunderland, P.B. Development of PIV for microgravity diffusion flames. In Proceedings of the 7th International Workshop on Microgravity Combustion and Chemically Reacting Systems, Cleveland, OH, USA, 3–6 June 2003. [Google Scholar]
- Kato, H.; Kunieda, S.; Enomoto, H. Effects of Co-flowing Air on Behavior of Gas jet Diffusion flames under Normal-and Micro-gravity Fields. Space Forum 2000, 6, 269–276. [Google Scholar]
- Most, J.M.; Most, A.; Susset, A.; Baillargeat, J.; Joulain, P. Flame characterization by PIV in microgravity conditions. In Proceedings of the 10th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 10–13 July 2001. [Google Scholar]
- Boxx, I.G.; Idicheria, C.A.; Clemens, N.T. Kilohertz PIV/PLMS of low-gravity turbulent flames in a drop tower. In Proceedings of the 12th International Symposium on Application of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 12–15 July 2004. [Google Scholar]
- Wernet, M.P.; Greenberg, P.S.; Sunderland, P.B.; Yanis, W. A PIV investigation of weakly buoyant laminar jet diffusion flames. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000; p. 694. [Google Scholar]
- Albrecht, H.-E.; Damaschke, N.; Borys, M.; Tropea, C. Laser Doppler and Phase Doppler Measurement Techniques; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Glass, M.; Kennedy, I. An improved seeding method for high temperature laser Doppler velocimetry. Combust. Flame 1977, 29, 333–335. [Google Scholar]
- Scheel, F. PIV Measurement of a 3-Dimensional Reacting Flow in a Scramjet Combustion Chamber. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar]
- Chen, F.; Liu, H.; Yang, Z.; Hu, H. Tracking characteristics of tracer particles for PIV measurements in supersonic flows. Chin. J. Aeronaut. 2017, 30, 577–585. [Google Scholar]
- Anderson, D.; Greated, C.; Jones, J.; Nimmo, G.; Wiseall, S. Fibre optic PIV studies in an industrial combustor. In Proceedings of the 8th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 8–11 July 1996. [Google Scholar]
- Hoekstra, A.J. Gas Flow Field and Collection Efficiency of Cyclone Separators. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2000. [Google Scholar]
- Liang, Y.; Cheng, T.; Li, Q.; Liu, J.; Li, Q.; Li, J.; Ma, S.; Jiang, X.; Wang, H.; Fu, P. CFD-DEM simulation of cyclone self-rotation drying: Particle high-speed self-rotation and heat transfer. Energy 2024, 290, 130277. [Google Scholar] [CrossRef]
- Matsuzaki, K.; Ushijima, H.; Munekata, M.; Ohba, H. Numerical study on particle motions in swirling flows in a cyclone separator. J. Therm. Sci. 2006, 15, 181–185. [Google Scholar]
- Cokljat, D.; Slack, M.; Vasquez, S.; Bakker, A.; Montante, G. Reynolds-stress model for Eulerian multiphase. Prog. Comput. Fluid Dyn. Int. J. 2006, 6, 168–178. [Google Scholar]
- Ma, L.; Ingham, D.; Wen, X. Numerical modelling of the fluid and particle penetration through small sampling cyclones. J. Aerosol Sci. 2000, 31, 1097–1119. [Google Scholar]
- Meier, H.; Mori, M. Gas-solid flow in cyclones: The Eulerian-Eulerian approach. Comput. Chem. Eng. 1998, 22, S641–S644. [Google Scholar]
- Li, Q.-P.; Xu, Y.-J.; Du, L.-H.; Xie, J.; Cheng, J.-W.; Wang, Y. Numerical simulation of JLX cyclone separator with guiding vane. Chem. Engineeing 2015, 43, 37–41. [Google Scholar]
- Kitamura, O.; Yamamoto, M. Proposal of a Reynolds Stress Model for Gas-Particle Turbulent Flows and its Application to Cylone Separators. In Engineering Turbulence Modelling and Experiments 4; Elsevier: Amsterdam, The Netherlands, 1999; pp. 893–902. [Google Scholar]
- Argyropoulos, C.D.; Markatos, N. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Safikhani, H. Modeling and multi-objective Pareto optimization of new cyclone separators using CFD, ANNs and NSGA II algorithm. Adv. Powder Technol. 2016, 27, 2277–2284. [Google Scholar]
- Mao, Y.; Chen, J.-l.; Chen, Z.-b.; Liu, N.; Lyu, Y.-l. Comparative Study on Cyclone Gas-Solid Two-phase Flow Using Lagrange Method and Euler Method. Bull. Chin. Ceram. Soc. 2017, 36, 459–465. [Google Scholar]
- Song, C.; Pei, B.; Jiang, M.; Wang, B.; Xu, D.; Chen, Y. Numerical analysis of forces exerted on particles in cyclone separators. Powder Technol. 2016, 294, 437–448. [Google Scholar]
- Fan, L.-S.; Zhu, C. Principles of Gas-Solid Flows, 1st ed.; Cambridge University Press: Cambridge, UK, 1998; pp. 87–101. [Google Scholar]
- Wen, C.Y. Mechanics of fluidization. Fluid Part. Technol. Chem. Eng. Progress. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Upadhyay, M.; Kim, A.; Kim, H.; Lim, D.; Lim, H. An assessment of drag models in eulerian–eulerian cfd simulation of gas–solid flow hydrodynamics in circulating fluidized bed riser. ChemEngineering 2020, 4, 37. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; MacGraw Hill: New York, NY, USA, 1979. [Google Scholar]
- Zhu, Z.; Na, Y.; Lu, Q. Pressure drop in cyclone separator at high pressure. J. Therm. Sci. 2008, 17, 275–280. [Google Scholar] [CrossRef]
- Wang, B.; Xu, D.; Chu, K.; Yu, A. Numerical study of gas–solid flow in a cyclone separator. Appl. Math. Model. 2006, 30, 1326–1342. [Google Scholar] [CrossRef]
- Ling, Z.; Deng, X. Study of a novel rotary cyclone gas-solid separator. J. Therm. Sci. 2003, 12, 275–278. [Google Scholar] [CrossRef]
- Ter Linden, A. Investigations into cyclone dust collectors. Proc. Inst. Mech. Eng. 1949, 160, 233–251. [Google Scholar] [CrossRef]
- Thielicke, W.; Sonntag, R. Particle Image Velocimetry for MATLAB: Accuracy and enhanced algorithms in PIVlab. J. Open Res. Softw. 2021, 9, 12. [Google Scholar] [CrossRef]



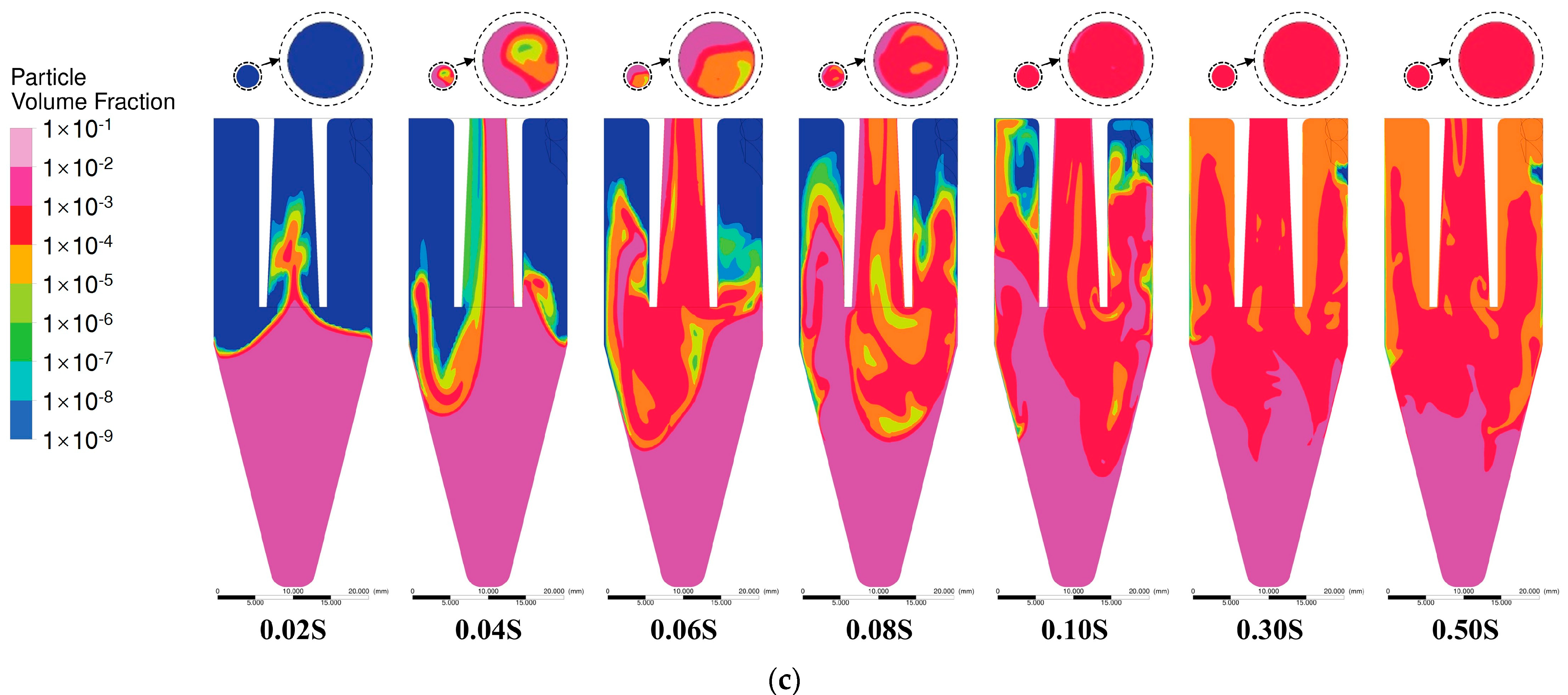
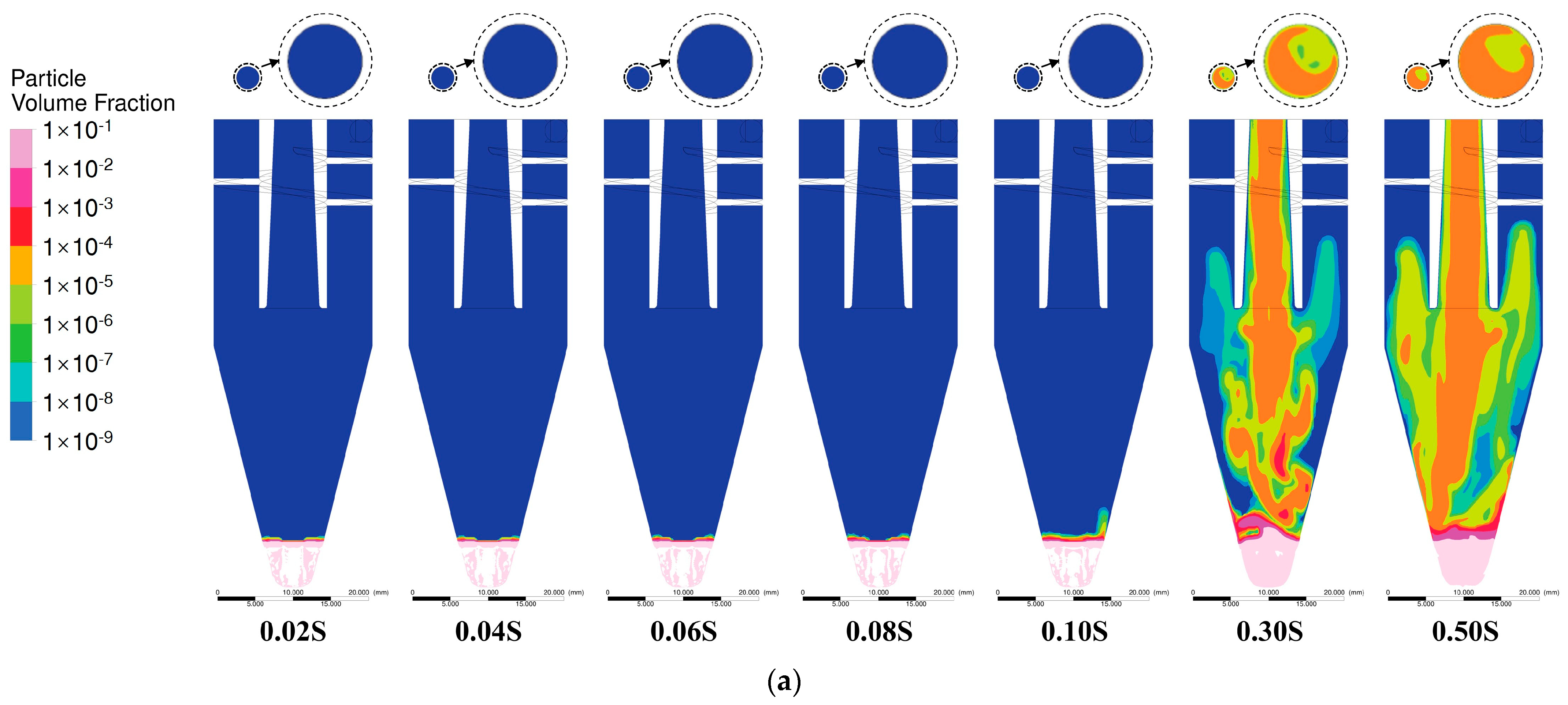
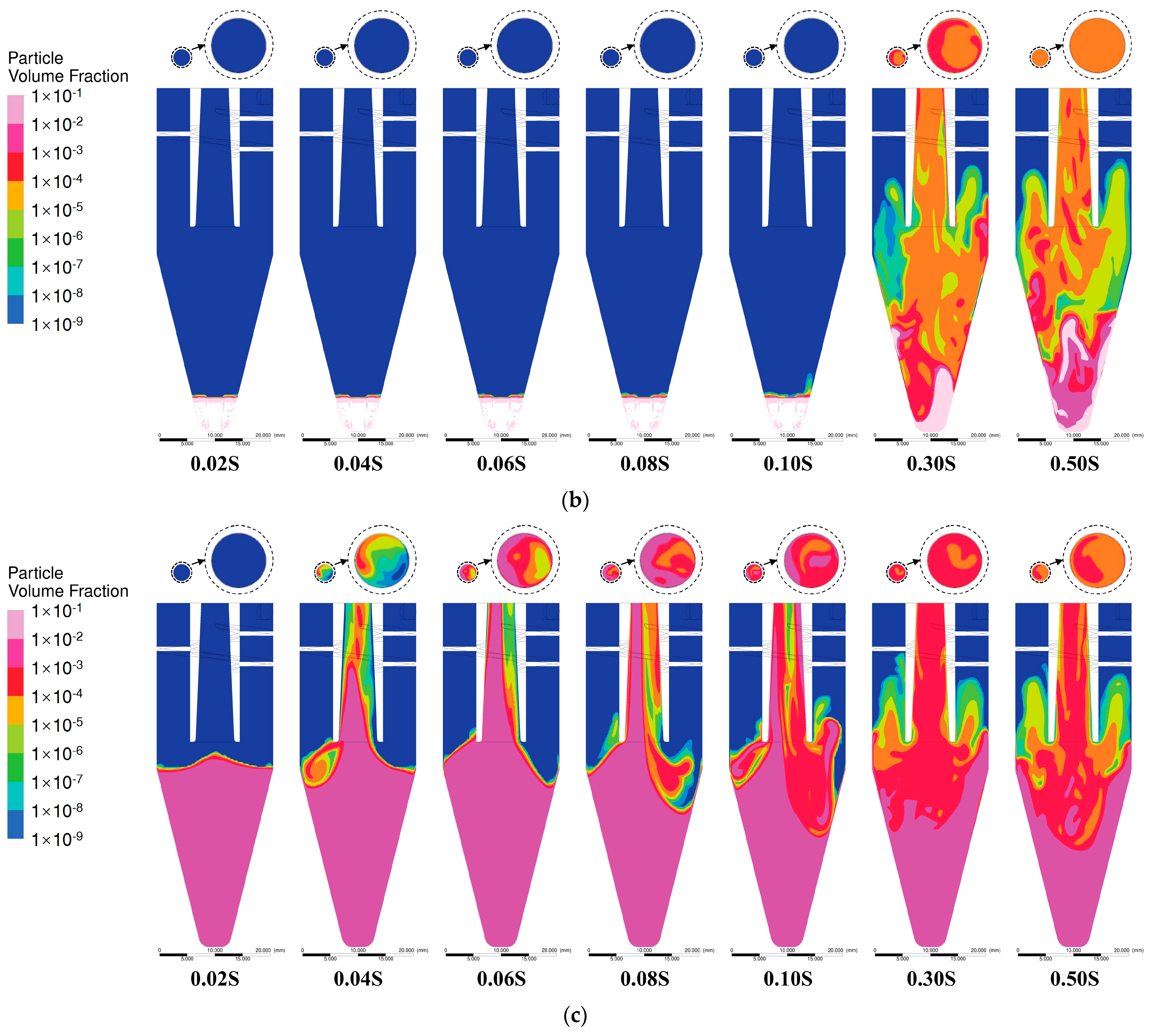
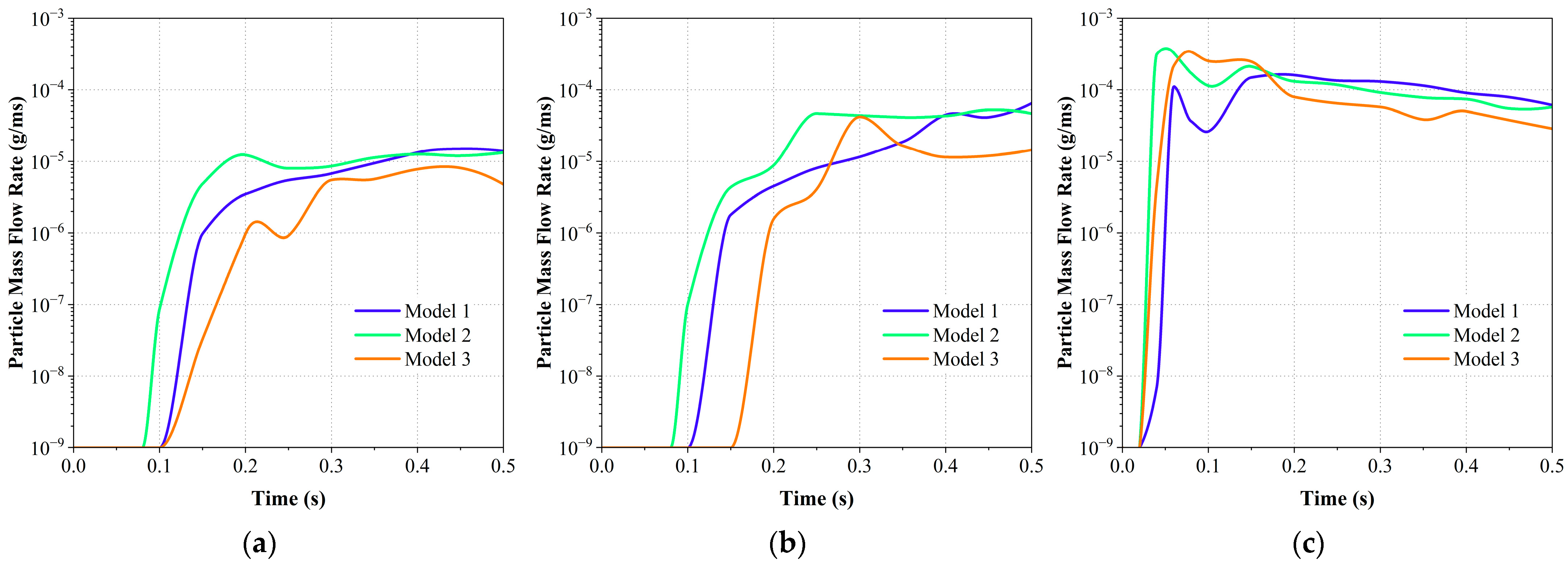
| Property | Scen 1 | Scen 2 | Scen 3 |
|---|---|---|---|
| Gravity | 1 G | 0 G | 0 G |
| Particle total mass | 8.29 × 10−4 kg | 8.29 × 10−4 kg | 8.29 × 10−4 kg |
| Particle bulk volume | 196 mm3 | 196 mm3 | 4777 mm3 |
| Particle bulk fraction | 0.1 | 0.1 | 0.004 |
| Facility | Item | Operating Parameter |
|---|---|---|
| CW Laser | Power | 10 W |
| Wave length | 532 nm | |
| Camera (Photron fastcam mini ax100) | Resolution | 1024 × 880 |
| Frame rate | 5000 | |
| Exposure time | 40 μs | |
| Lens (Tamron macro 100 mm) | Focal length | 100 mm |
| Aperture | F 2.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Zheng, H.; Fang, Y.; Lan, X.; Yang, X.; Zhang, X. Numerical Simulation Study on the Feasibility of Cyclone PIV Tracer Particle Seeder in Microgravity. Energies 2025, 18, 1700. https://doi.org/10.3390/en18071700
Peng X, Zheng H, Fang Y, Lan X, Yang X, Zhang X. Numerical Simulation Study on the Feasibility of Cyclone PIV Tracer Particle Seeder in Microgravity. Energies. 2025; 18(7):1700. https://doi.org/10.3390/en18071700
Chicago/Turabian StylePeng, Xianzhang, Huilong Zheng, Yu Fang, Xiaoyang Lan, Xiaofang Yang, and Xiaowu Zhang. 2025. "Numerical Simulation Study on the Feasibility of Cyclone PIV Tracer Particle Seeder in Microgravity" Energies 18, no. 7: 1700. https://doi.org/10.3390/en18071700
APA StylePeng, X., Zheng, H., Fang, Y., Lan, X., Yang, X., & Zhang, X. (2025). Numerical Simulation Study on the Feasibility of Cyclone PIV Tracer Particle Seeder in Microgravity. Energies, 18(7), 1700. https://doi.org/10.3390/en18071700





