Study on the Influence of Split Blades on the Force Characteristics and Fluid–Structure Coupling Characteristics of Pumps as Turbines
Abstract
1. Introduction
2. Model Parameter
2.1. Original Hydraulic Turbine Parameters
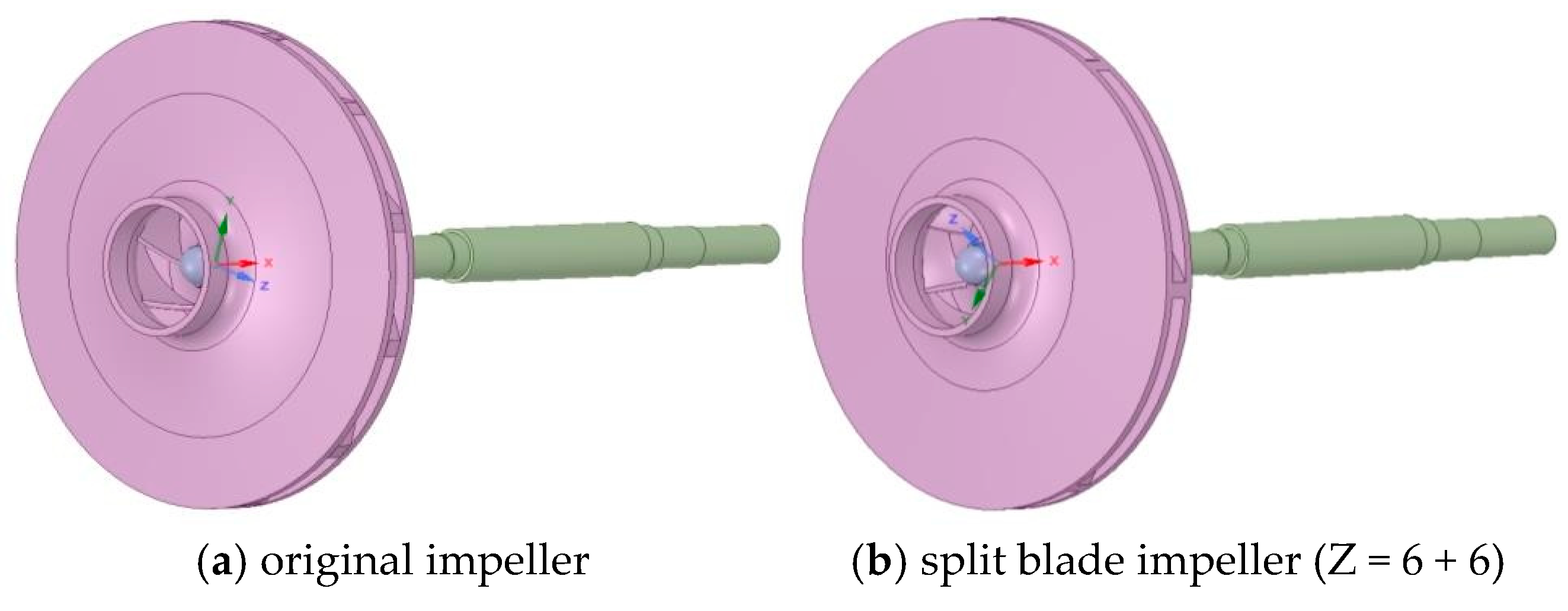
2.2. Optimization and Improvement of the Pump-Turbine Model
3. Numerical Calculation Model
3.1. Three-Dimensional Modeling and Mesh Division
3.2. Numerical Simulation Methods
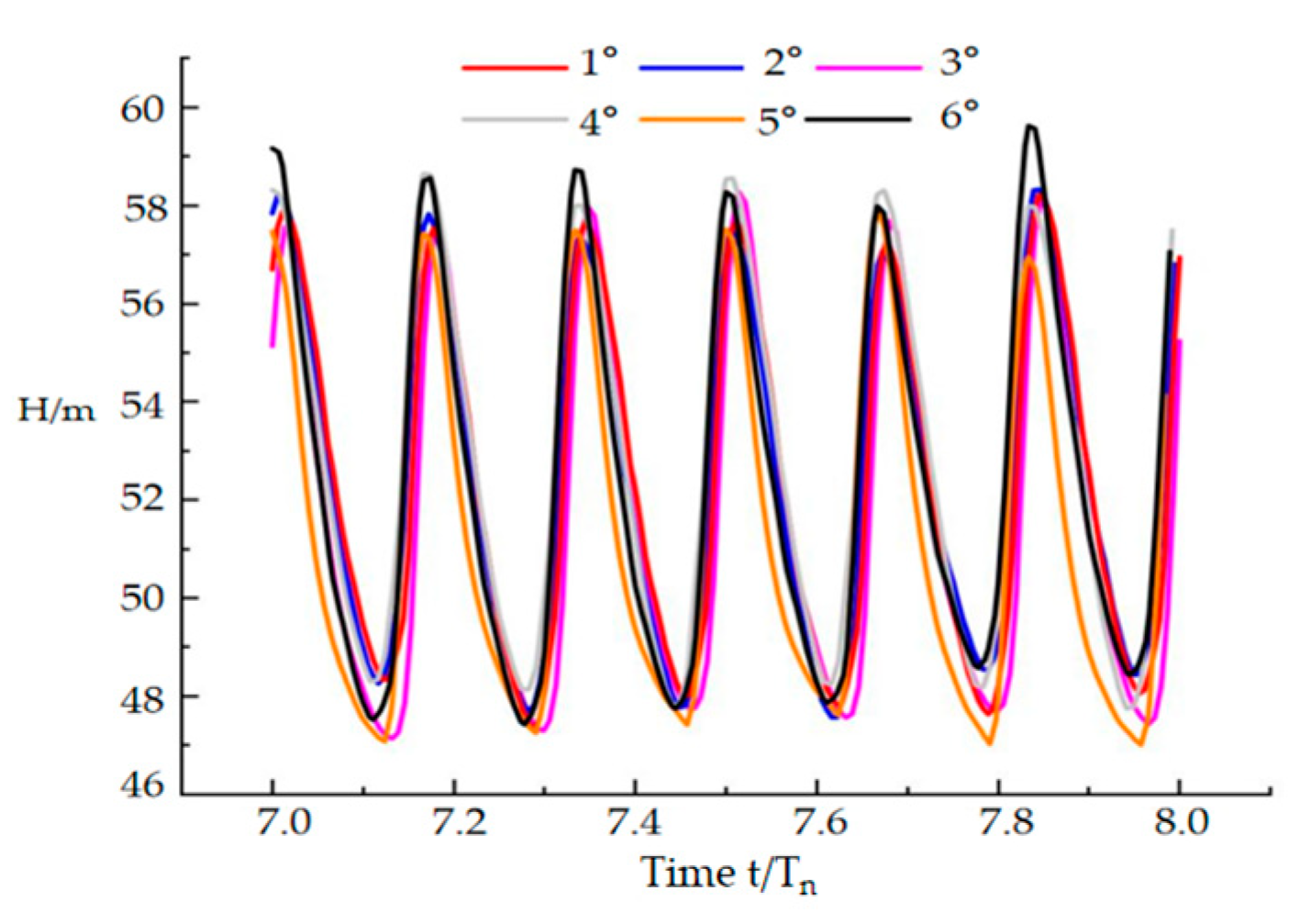
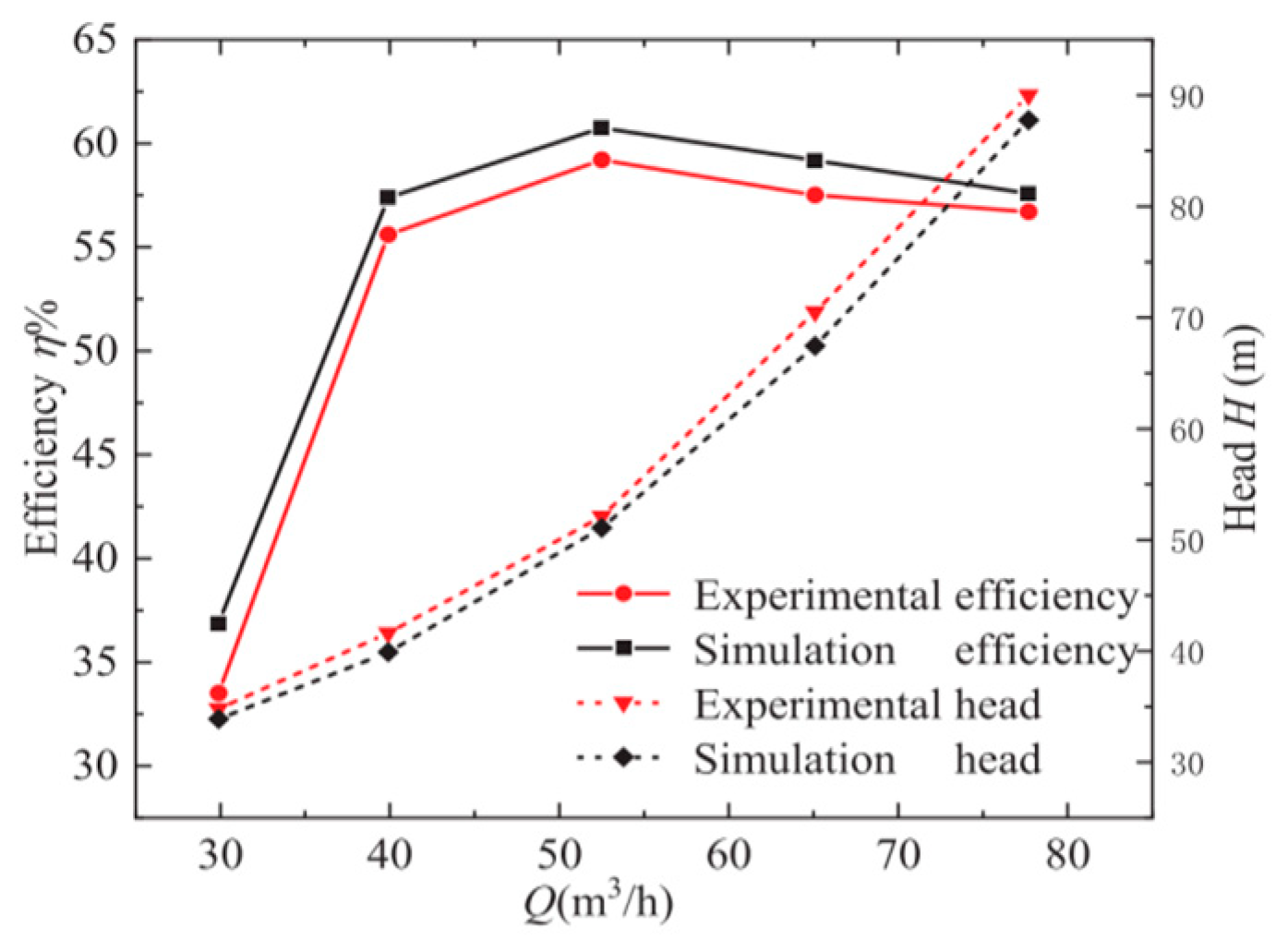
3.3. Verification of Numerical Calculation Accuracy
4. Result and Analysis
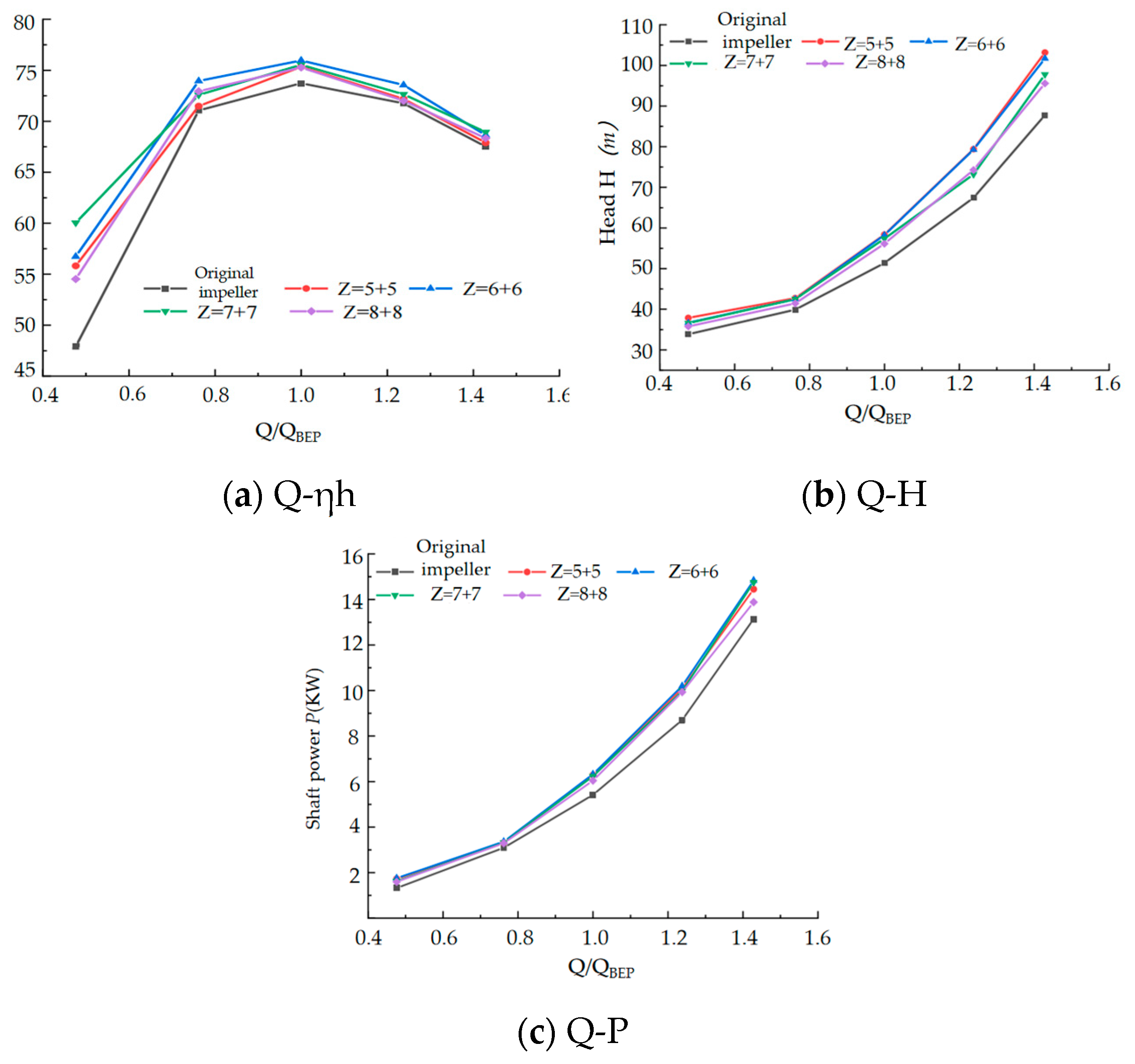
4.1. External Characteristic Analysis
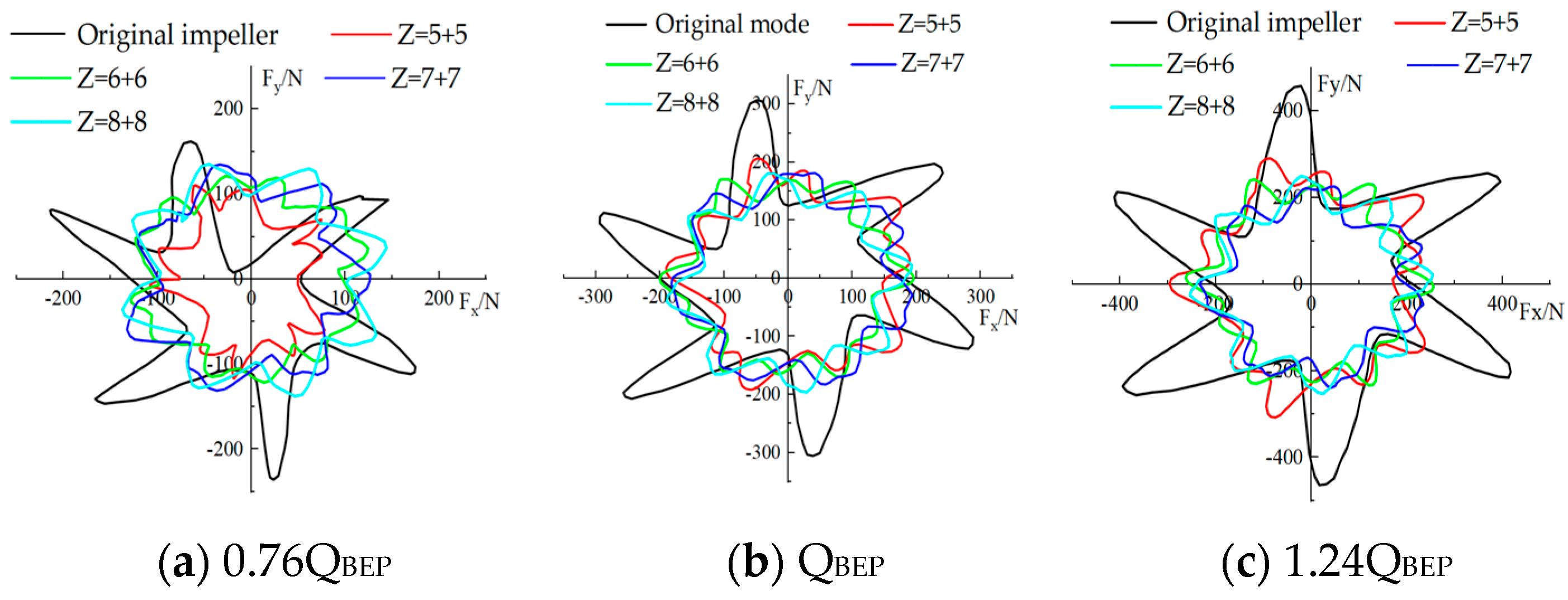
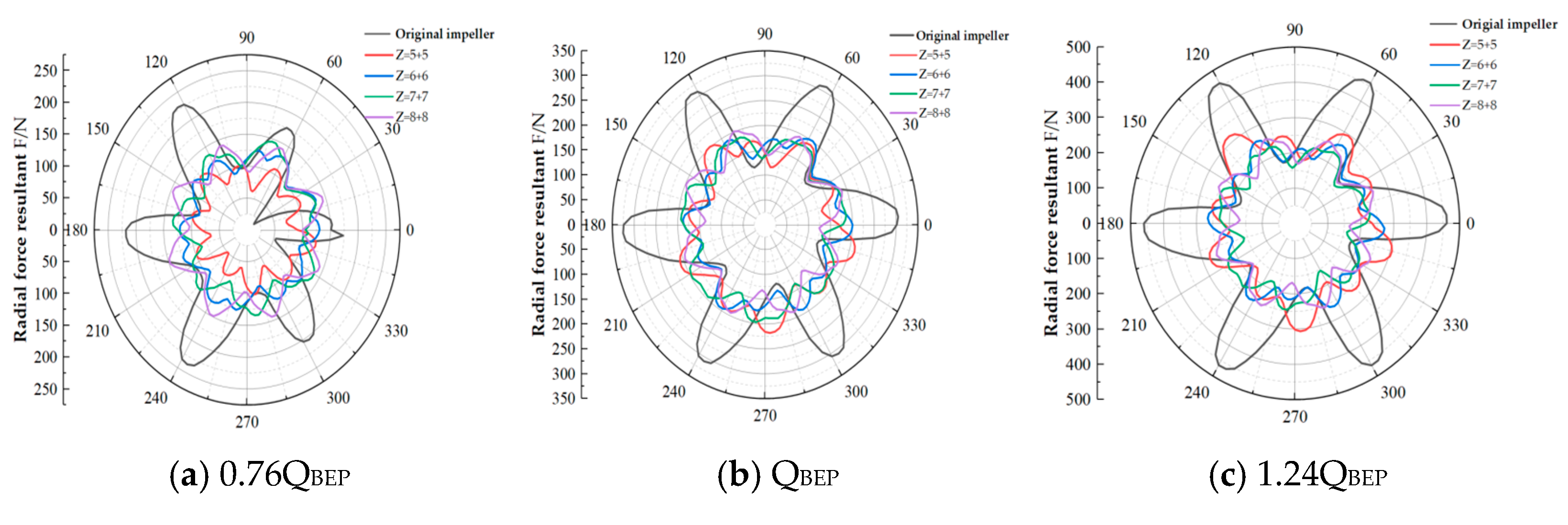
4.2. Transient Radial Force Analysis
4.3. Transient Axial Force Analysis
5. Analysis of the Fluid–Structure Coupling Characteristics of the Rotor System
5.1. Computation Model
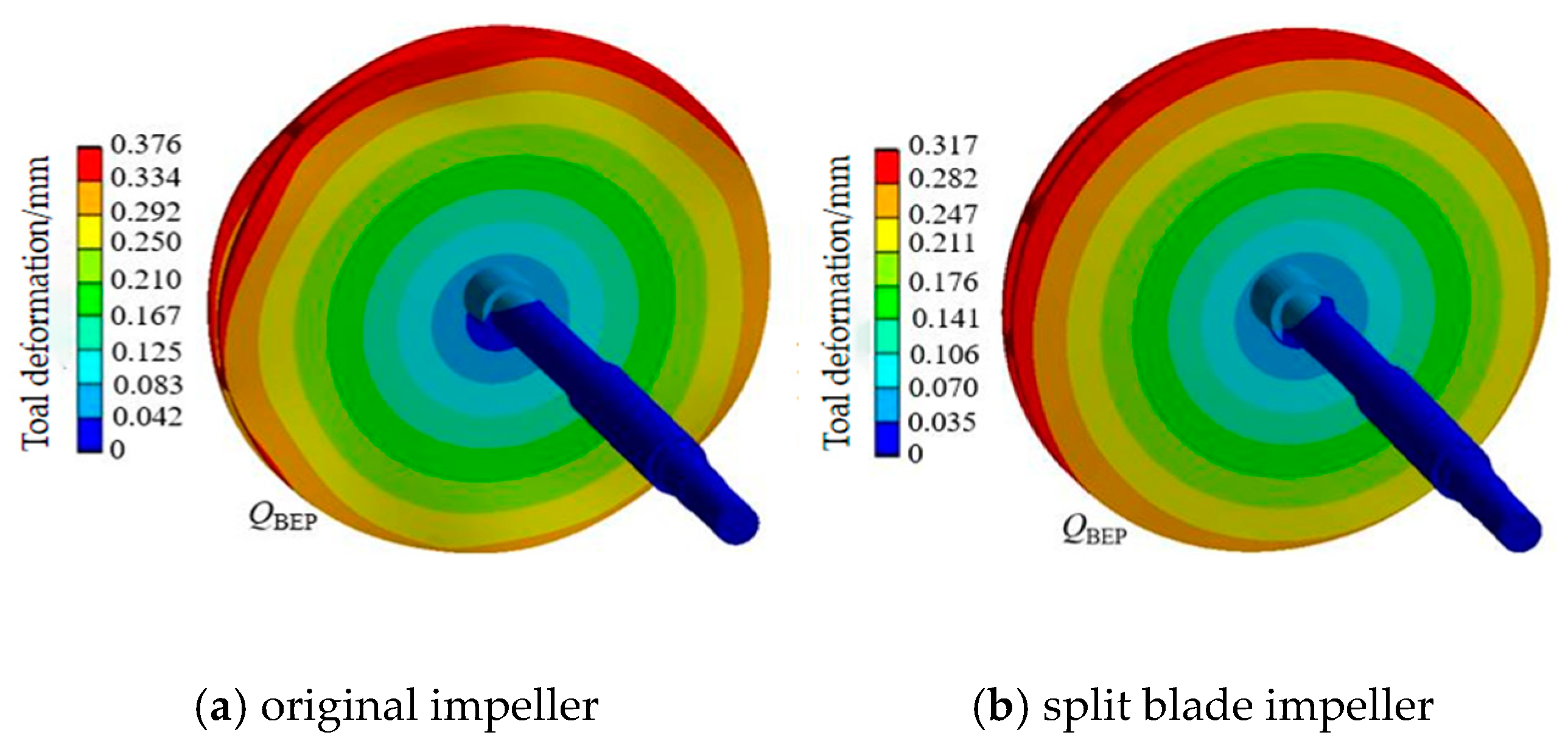
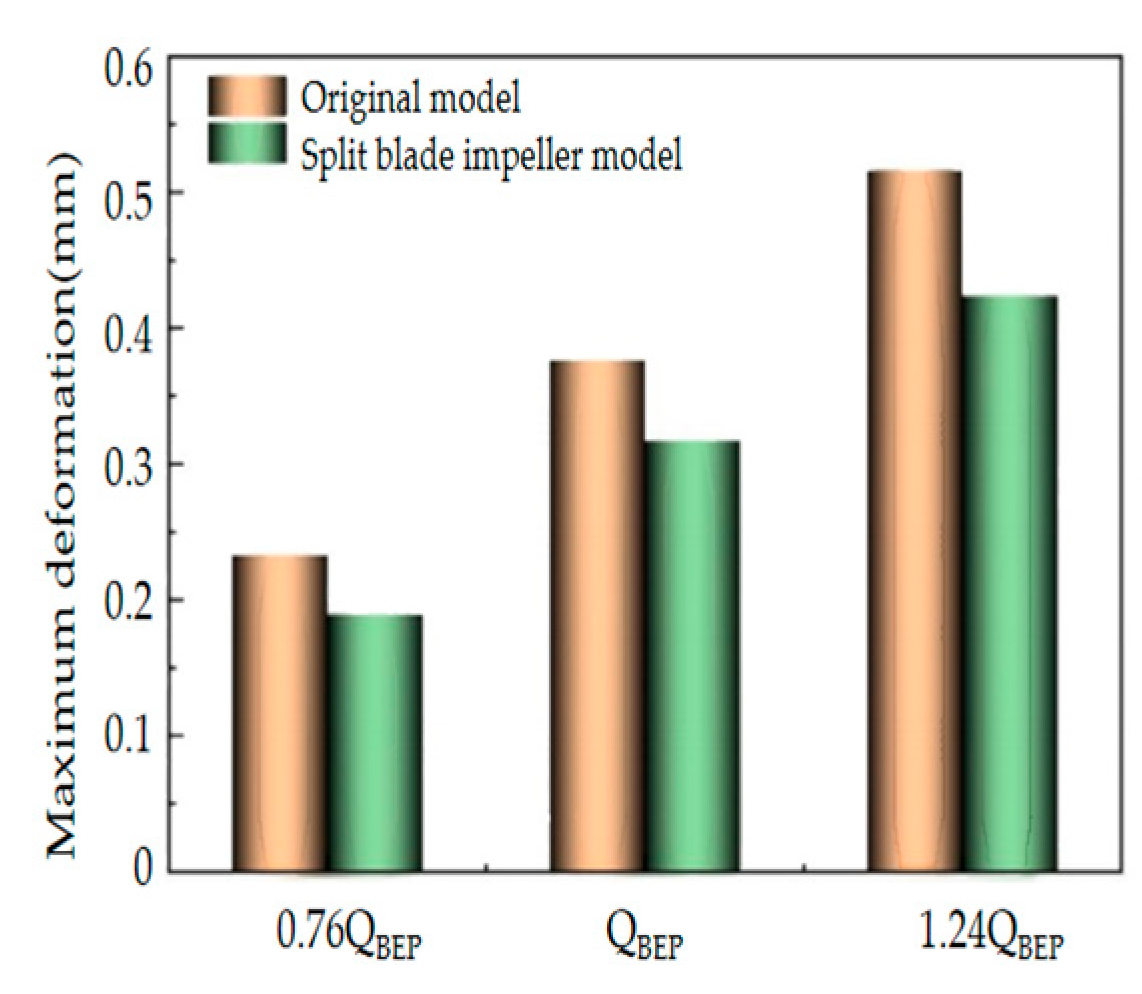
5.2. Deformation Analysis of the Rotor System
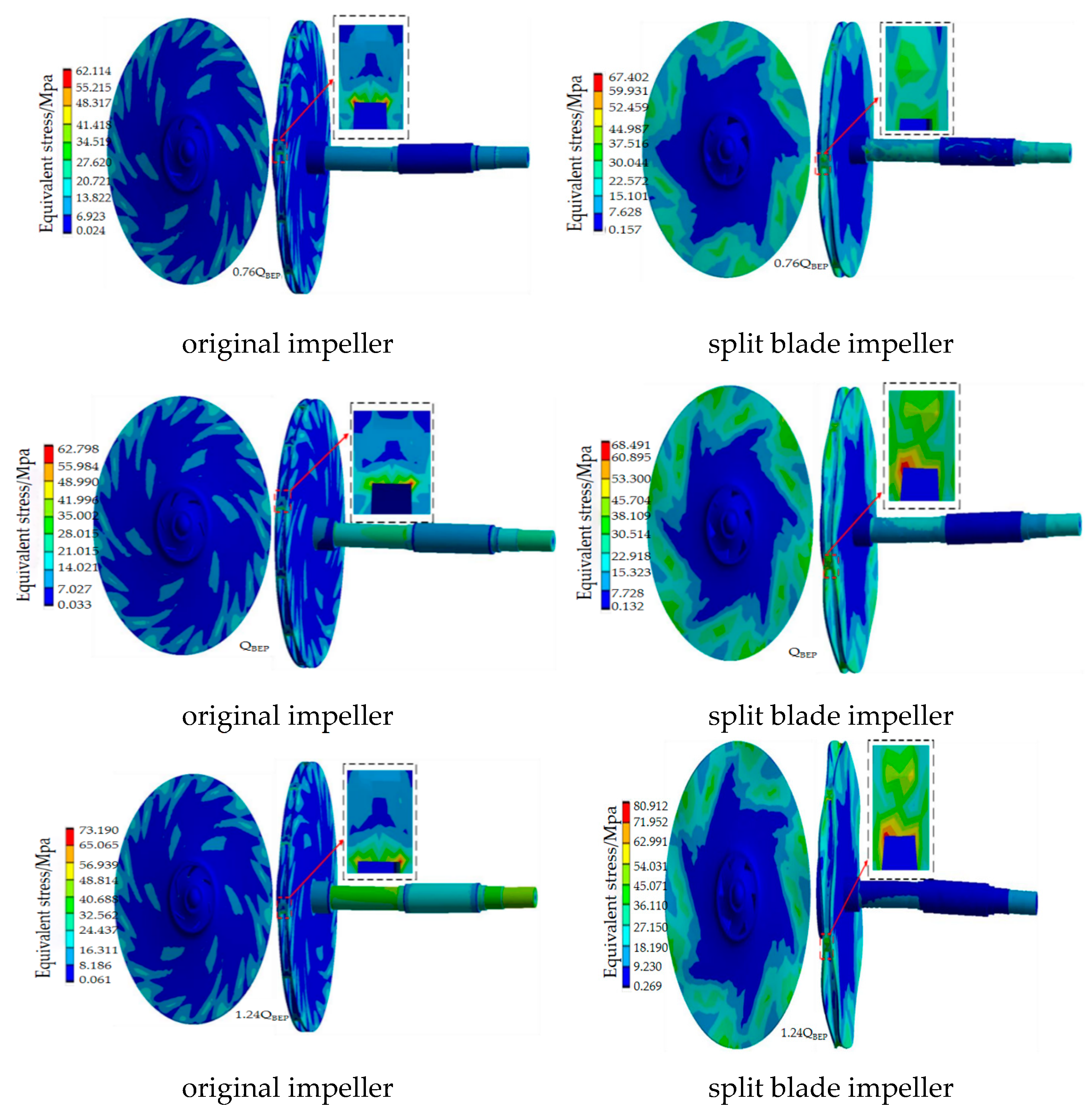
5.3. Equivalent Stress Analysis of the Rotor System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Z.; Xiao, Y.; Wang, C.P.; Zhu, Y.L.; Liu, S.H.; Cui, Y.K.; Yin, X.L. Numerical Analysis of Hydraulic Characteristics of Turbine Type Energy Recovery Integrated Machine. J. Hydroelectr. Eng. 2021, 40, 131–140. [Google Scholar]
- Barbarelli, S.; Amelio, M.; Florio, G. Predictive Model Estimating the Performances of Centrifugal Pumps Used as Turbines. Energy 2016, 107, 103–121. [Google Scholar]
- Zhang, D.; Qi, B.; Zhao, R.; Zhang, Q. Optimization Design of a Hydraulic Model for Energy Recovery Turbine in Seawater Desalination. J. Irrig. Drain. Eng. 2021, 39, 649–654. [Google Scholar]
- Williams, A. Pumps as Turbines Used with Induction Generations of Stand-Alone Micro-Hydroelectric Power Plants. Ph.D. Thesis, Nottingham Polytechnic, Nottingham, UK, 1992. [Google Scholar]
- Yang, H.; He, Q.; Huang, X.; Yang, M.; Bi, H.; Wang, Z. Experimental and Numerical Investigation of Rotor–Stator Interaction in a Large Prototype Pump–Turbine in Turbine Mode. Energies 2022, 15, 5523. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L.; Yin, G. Numerical Investigation of the FSI Characteristics in a Tubular Pump. Math. Probl. Eng. 2017, 2, 7897614. [Google Scholar]
- Li, Y.; Guo, D.; Fan, Z.; Du, J. Effects of Different Blade Numbers on Radial Exciting Force of Lobe Pump Rotor. Int. J. Fluid Mach. Syst. 2020, 13, 281–291. [Google Scholar]
- Yu, H.; Wang, T.; Dong, Y.; Gou, Q.; Lei, L.; Liu, Y. Numerical Investigation of splitter Blades on the Performance of a Forward-Curved Impeller Used in a Pump as Turbine. Ocean Eng. 2023, 281, 114721. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, Z.; He, X.; Zeng, W.; Yang, J. Design Techniques for Improving Energy Performance and S-Shaped Characteristics of a Pump-Turbine with split Blades. Renew. Energy 2023, 212, 333–349. [Google Scholar]
- Benra, F.; Dohmen, H.; Wan, B. Determination of Pump Impeller Deflections: Comparison of FSI-Simulation Measurements. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, Miami, FL, USA, 17–20 July 2006; ASME: New York, NY, USA, 2006. [Google Scholar]
- Kobayashi, K.; Ono, S.; Harada, I.; Chiba, Y. Numerical Analysis of Stress on Pump Blade by One-Way Coupled Fluid-Structure Simulation. J. Fluid Sci. Technol. 2010, 5, 219–234. [Google Scholar]
- Benra, F.K.; Dohmen, H.J.; Pei, J.; Schuster, S.; Wan, B. A Comparison of One-Way and Two-Way Coupling Methods for Numerical Analysis of Fluid-Structure Interactions. J. Appl. Math. 2011, 2011, 853560. [Google Scholar]
- Adkins, D.R.; Brennen, C.E. Analyses of Hydrodynamic Radial Forces on Centrifugal Pump Impellers. J. Fluids Eng. 1988, 110, 20–28. [Google Scholar]
- Barrio, R.; Fernández, J.; Blanco, E.; Parrondo, J. Estimation of Radial Load in Centrifugal Pumps Using Computational Fluid Dynamics. Eur. J. Mech. B Fluids 2011, 30, 316–324. [Google Scholar]
- Yang, S.S.; Kong, F.Y.; Qu, X.Y.; Jiang, W.M. Influence of Blade Number on the Performance and Pressure Pulsations in a Pump Used as a Turbine. J. Fluids Eng. 2012, 134, 12–23. [Google Scholar]
- Harano, M.; Tani, K.; Nomoto, S. Practical Application of High-Performance Francis-Turbine Runner Fitted with split Blades at Ontake and Shinkurobegawa No.3 Power Stations of the Kansai Electric Power Co., Inc. Eng. Appl. Sci. 2006, 55, 109–113. [Google Scholar]
- Gölcü, M.; Pancar, Y.; Sekmen, Y. Energy Saving in a Deep Well Pump with split Blade. Energy Convers. Manag. 2006, 47, 638–651. [Google Scholar]
- Solano, J.P.; Pinilla, V.; Paniagua, G.; Lavagnoli, S.; Yasa, T. Aero-Thermal Investigation of a Multi-split Axial Turbine. Int. J. Heat Fluid Flow 2011, 32, 1036–1046. [Google Scholar] [CrossRef]
- Adu, D.; Du, J.; Darko, R.O.; Ofosu Antwi, E.; Khan, M.A.S. Numerical and Experimental Characterization of split Blade Impact on Pump as Turbine Performance. Sci. Prog. 2021, 104, 36850421993247. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, Z.; Ran, J.; Li, H. Multi-Objective Parameter Optimization of Turbine Impeller Based on RBF Neural Network and NSGA-II Genetic Algorithm. Energy Rep. 2021, 7, 584–593. [Google Scholar]
- Liu, H.; Xu, H.; Ellison, P.J.; Jin, Z. Application of Computational Fluid Dynamics and Fluid–Structure Interaction Method to the Lubrication Study of a Rotor–Bearing System. Tribol. Lett. 2010, 38, 325–336. [Google Scholar]
- Cai, J.-C.; Chen, H.-J.; Brazhenko, V.; Gu, Y.-H. Study of the Hydrodynamic Unsteady Flow Inside a Centrifugal Fan and Its Downstream Pipe Using Detached Eddy Simulation. Sustainability 2021, 13, 5113. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S.L.; Pan, X.H.; Zheng, S.Y. A New Method for Studying the 3D Transient Flow of Misaligned Journal Bearings in Flexible Rotor-Bearing Systems. J. Zhejiang Univ. Sci. A 2012, 13, 293–310. [Google Scholar] [CrossRef]
- Al-Hussain, K.M. Dynamic Stability of Two Rigid Rotors Connected by a Flexible Coupling with Angular Misalignment. J. Sound Vib. 2003, 266, 217–234. [Google Scholar] [CrossRef]
- Sinha, J.K.; Lees, A.W.; Friswell, M.I. Estimating Unbalance and Misalignment of a Flexible Rotating Machine from a Single Run-Down. J. Sound Vib. 2004, 272, 967–989. [Google Scholar] [CrossRef]
- Nasir, A.; Dribssa, E.; Girma, M. The Pump as a Turbine: A Review on Performance Prediction, Performance Improvement, and Economic Analysis. Heliyon 2024, 10, e26084. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.H.; Yang, J.H.; Guo, Y.L.; Xia, Z.T.; Miao, S.C. Mechanism of Velocity Slip in Reversible Pump-Turbine. Chin. J. Mech. Eng. 2018, 54, 189–196. [Google Scholar] [CrossRef]
- Assefa, E.Y.; Tesfay, A.H. Effect of Blade Number on Internal Flow and Performance Characteristics in Low-Head Cross-Flow Turbines. Energies 2025, 18, 318. [Google Scholar] [CrossRef]
- Sakran, H.K.; Abdul Aziz, M.S.; Abdullah, M.Z.; Khor, C.Y. Effects of Blade Number on the Centrifugal Pump Performance: A Review. Arab. J. Sci. Eng. 2022, 47, 7945–7961. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar]
- Sakran, H.K.; Abdul Aziz, M.S.; Khor, C.Y. Effect of Blade Number on the Energy Dissipation and Centrifugal Pump Performance Based on the Entropy Generation Theory and Fluid–Structure Interaction. Arab. J. Sci. Eng. 2024, 49, 11031–11052. [Google Scholar] [CrossRef]
- Chai, B.D.; Yang, J.H.; Wang, X.H. Transient Characteristic Analysis of Centrifugal Pump during Turbine Start-Up Process. J. Vib. Shock 2021, 40, 38–43+57. [Google Scholar]

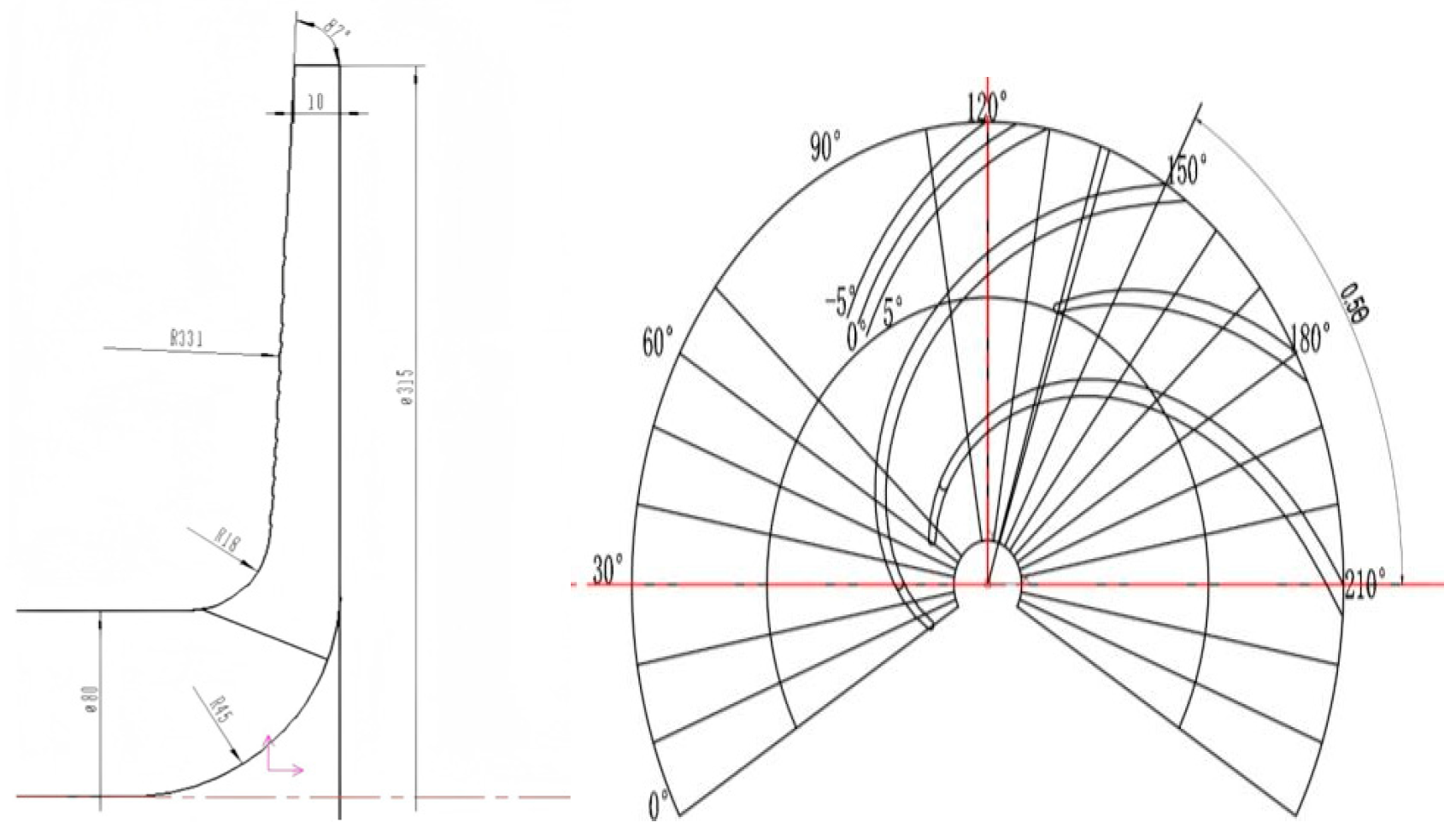





| Parameter | Numerical Value |
|---|---|
| Impeller inlet diameter | 315 |
| Impeller diameter at the outlet | 80 |
| Impeller width at the outlet | 10 |
| Blade wrap angle (°) | 150 |
| Blade inlet angle (°) | 32 |
| number of blades | 6 |
| Volute base circle diameter | 320 |
| Spiral shell outlet width | 24 |
| Volute inlet diameter | 50 |
| Numerical Solution Type | Numerical Solution φ1 | Numerical Solution φ2 | Numerical Solution φ3 | Safety Factor Fs | Convergence Accuracy p | Grid Convergence Index (GCI) |
|---|---|---|---|---|---|---|
| Head | 50.45 | 51.48 | 52.69 | 1.25 | 2.52 | 0.42 |
| Efficiency | 74.02 | 73.75 | 73.14 | 1.25 | 1.42 | 0.67 |
| Impeller Model | Minimum Radial Force Resultant Force (N) | Maximum Radial Force Resultant Force (N) | Average Value | Error1 (%) | Error2 (%) |
|---|---|---|---|---|---|
| Original Impeller | 137.96 | 325.67 | 209.95 | 34.29 | 55.11 |
| Z = (5 + 5) | 165.34 | 218.13 | 170.16 | 2.82 | 28.19 |
| Z = (6 + 6) | 134.09 | 200.51 | 166.69 | 19.56 | 20.28 |
| Z = (7 + 7) | 136.67 | 207.03 | 171.54 | 20.33 | 20.69 |
| Z = (8 + 8) | 124.05 | 201.79 | 165.48 | 25.04 | 21.94 |
| Type of Impeller | Maximum Deformation (mm) | Mean Strain (%) | Ratio of Strain (ɛmax/ɛavg) |
|---|---|---|---|
| Original Impeller | 0.376 | 0.18 | 2.09 |
| Z = 6 + 6 | 0.317 | 0.16 | 1.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, F.; Zong, X.; Zhao, G.; Zhang, D.; Wang, P.; Zhan, H. Study on the Influence of Split Blades on the Force Characteristics and Fluid–Structure Coupling Characteristics of Pumps as Turbines. Energies 2025, 18, 1642. https://doi.org/10.3390/en18071642
Shi F, Zong X, Zhao G, Zhang D, Wang P, Zhan H. Study on the Influence of Split Blades on the Force Characteristics and Fluid–Structure Coupling Characteristics of Pumps as Turbines. Energies. 2025; 18(7):1642. https://doi.org/10.3390/en18071642
Chicago/Turabian StyleShi, Fengxia, Xuexue Zong, Guangbiao Zhao, Denghui Zhang, Pengcheng Wang, and Haonan Zhan. 2025. "Study on the Influence of Split Blades on the Force Characteristics and Fluid–Structure Coupling Characteristics of Pumps as Turbines" Energies 18, no. 7: 1642. https://doi.org/10.3390/en18071642
APA StyleShi, F., Zong, X., Zhao, G., Zhang, D., Wang, P., & Zhan, H. (2025). Study on the Influence of Split Blades on the Force Characteristics and Fluid–Structure Coupling Characteristics of Pumps as Turbines. Energies, 18(7), 1642. https://doi.org/10.3390/en18071642





