Axial Flux Electromagnetic Energy Harvester Driven by a Stirling Engine for Waste Heat Recovery
Abstract
1. Introduction
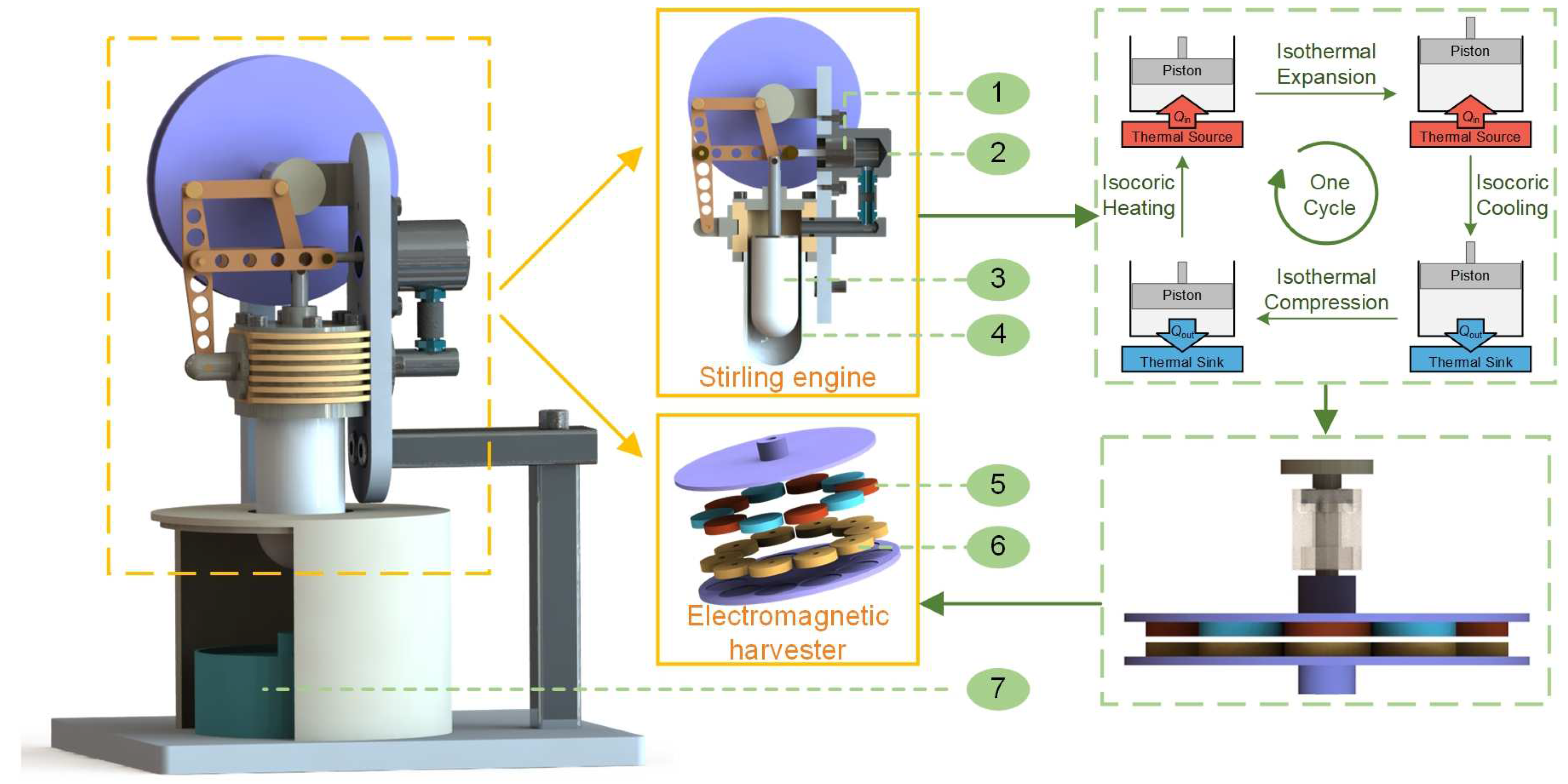
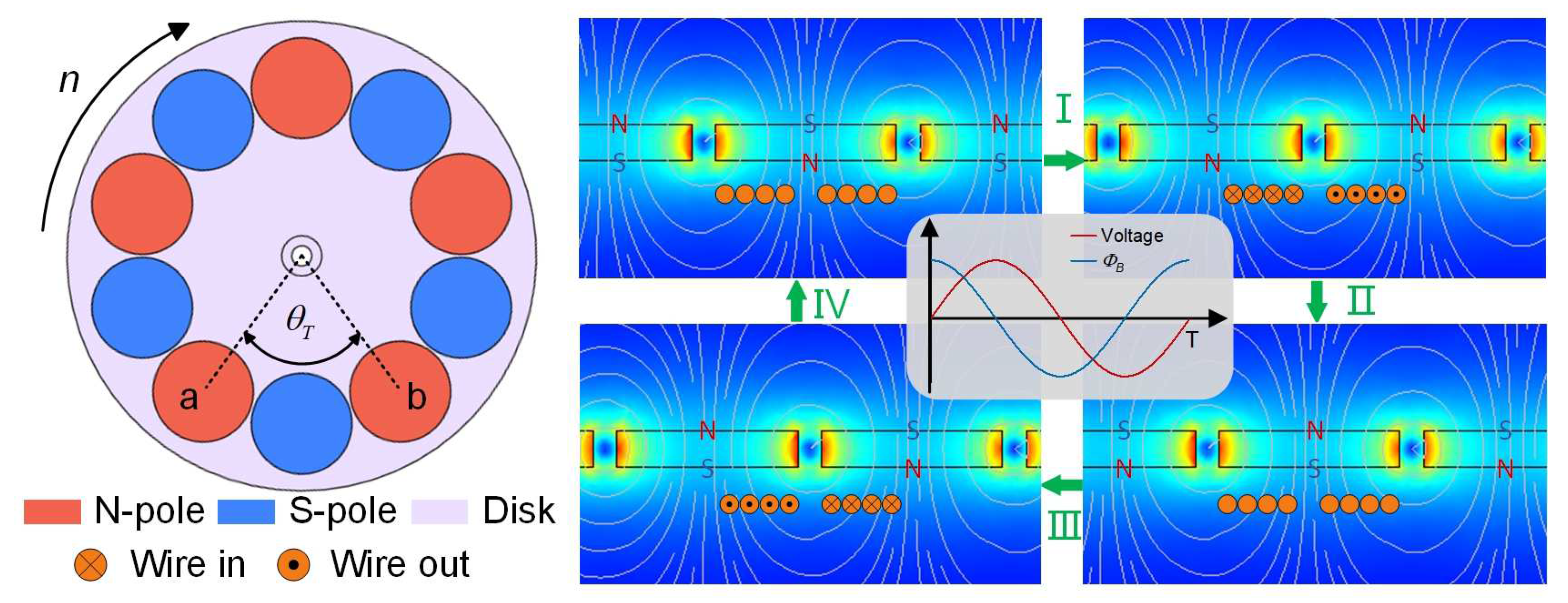
2. Design and Working Principle
3. Results and Discussion
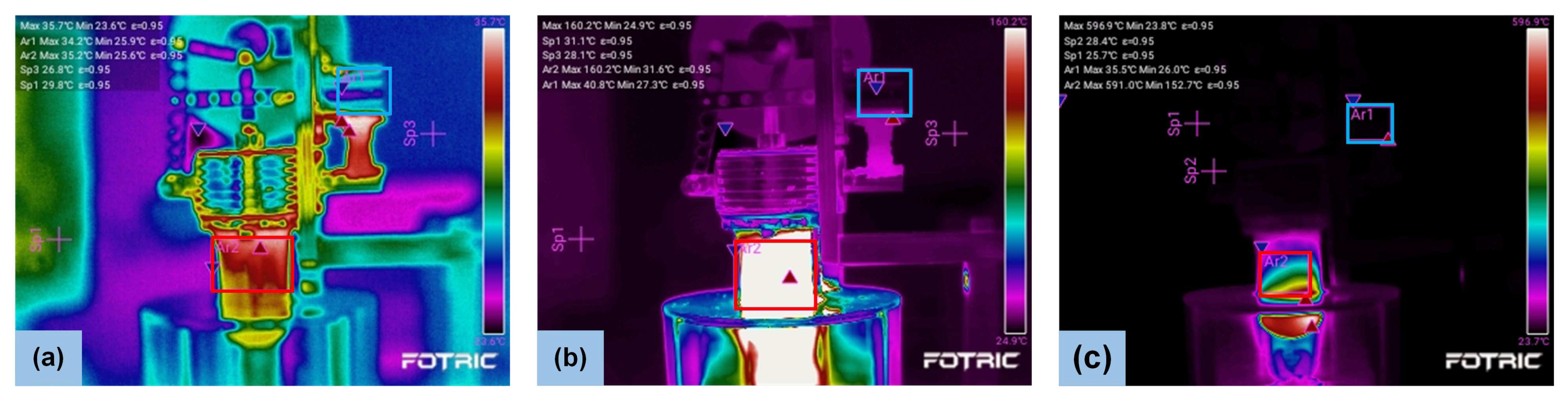
3.1. Experimental Setup and Prototype
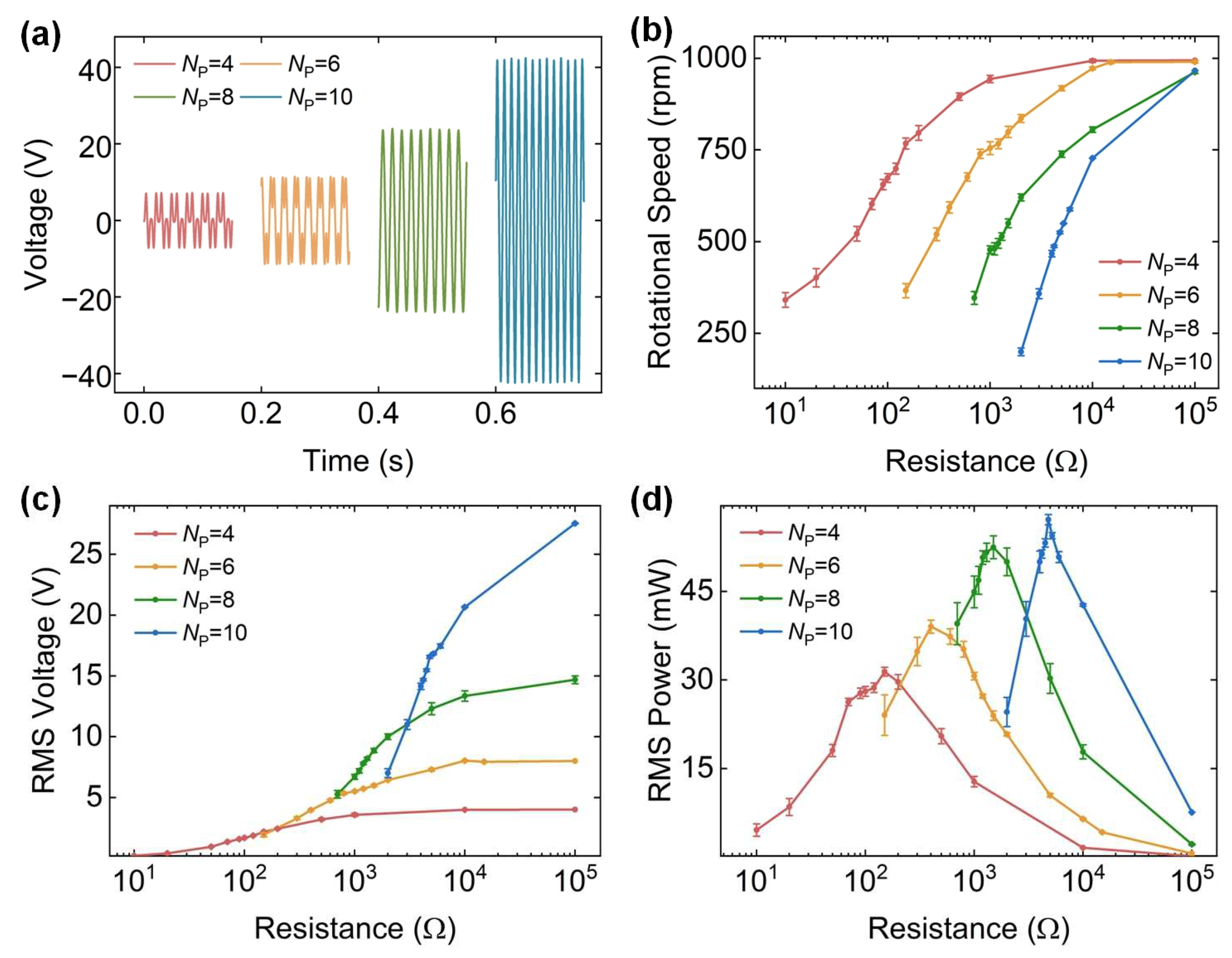
3.2. Rotational Speed for Different Magnet Arrays
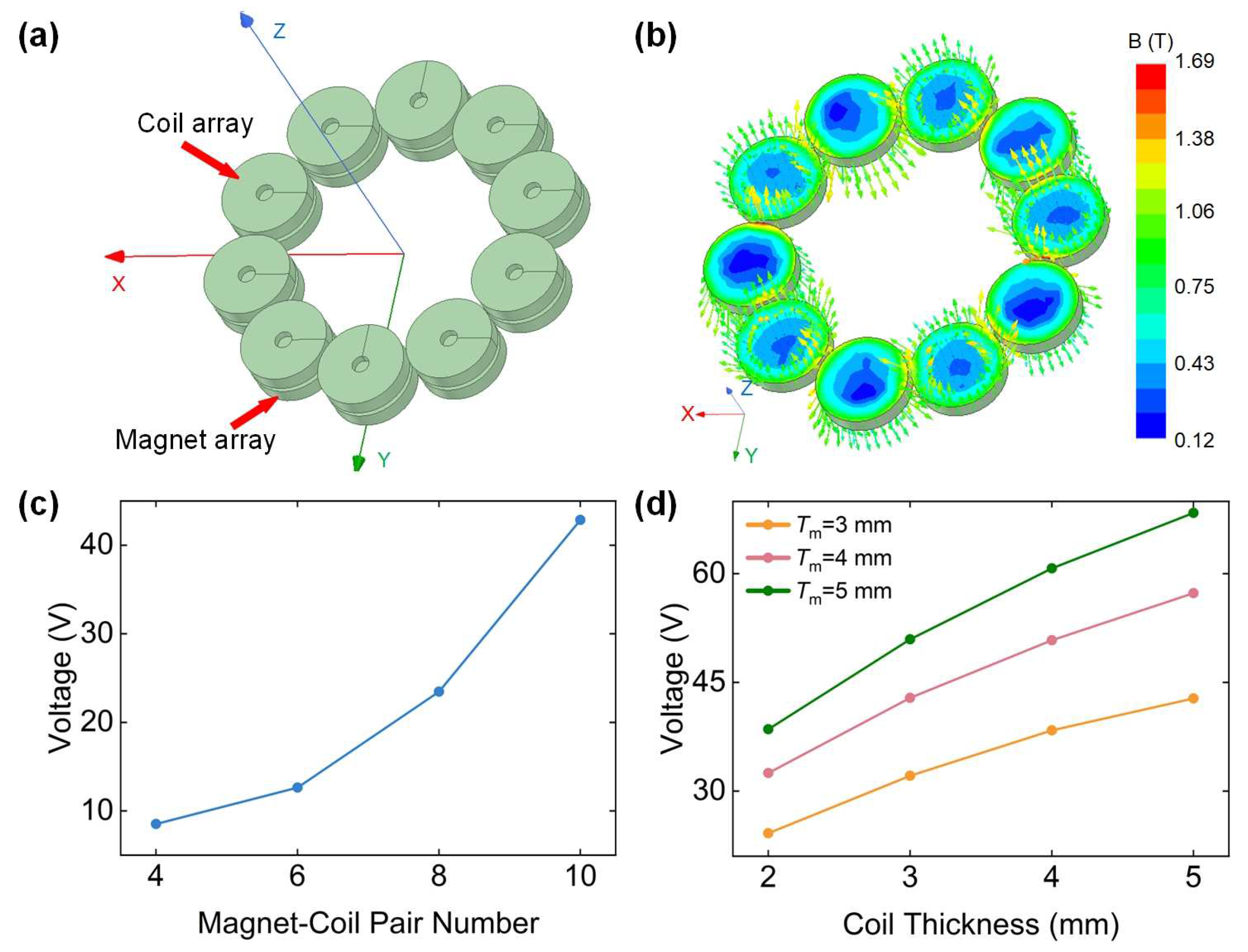
3.3. Simulation of Open-Circuit Voltage
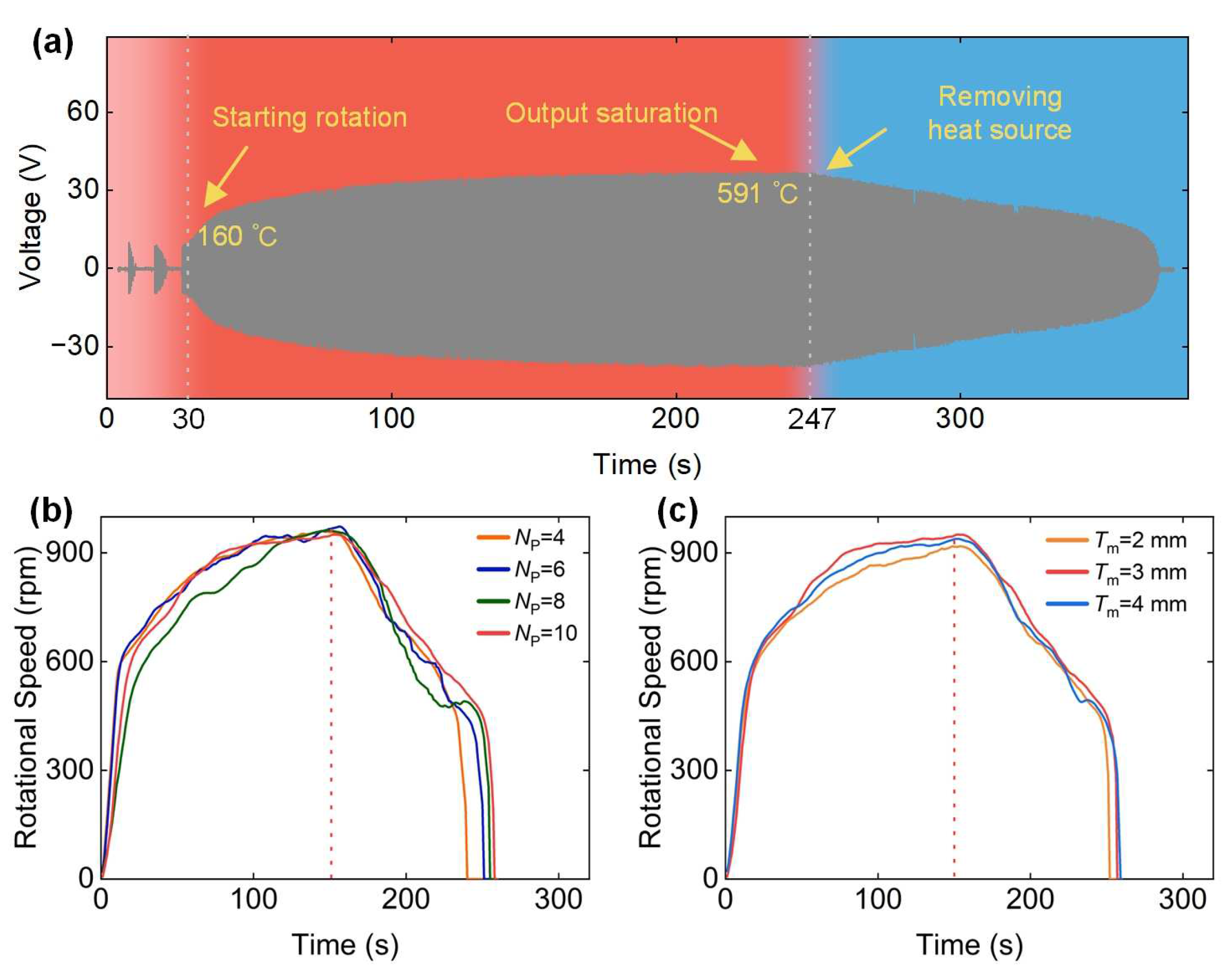
3.4. Comparisons of Experimental Results
3.4.1. Prototype Performance for Different Numbers of Magnet-Coil Pairs
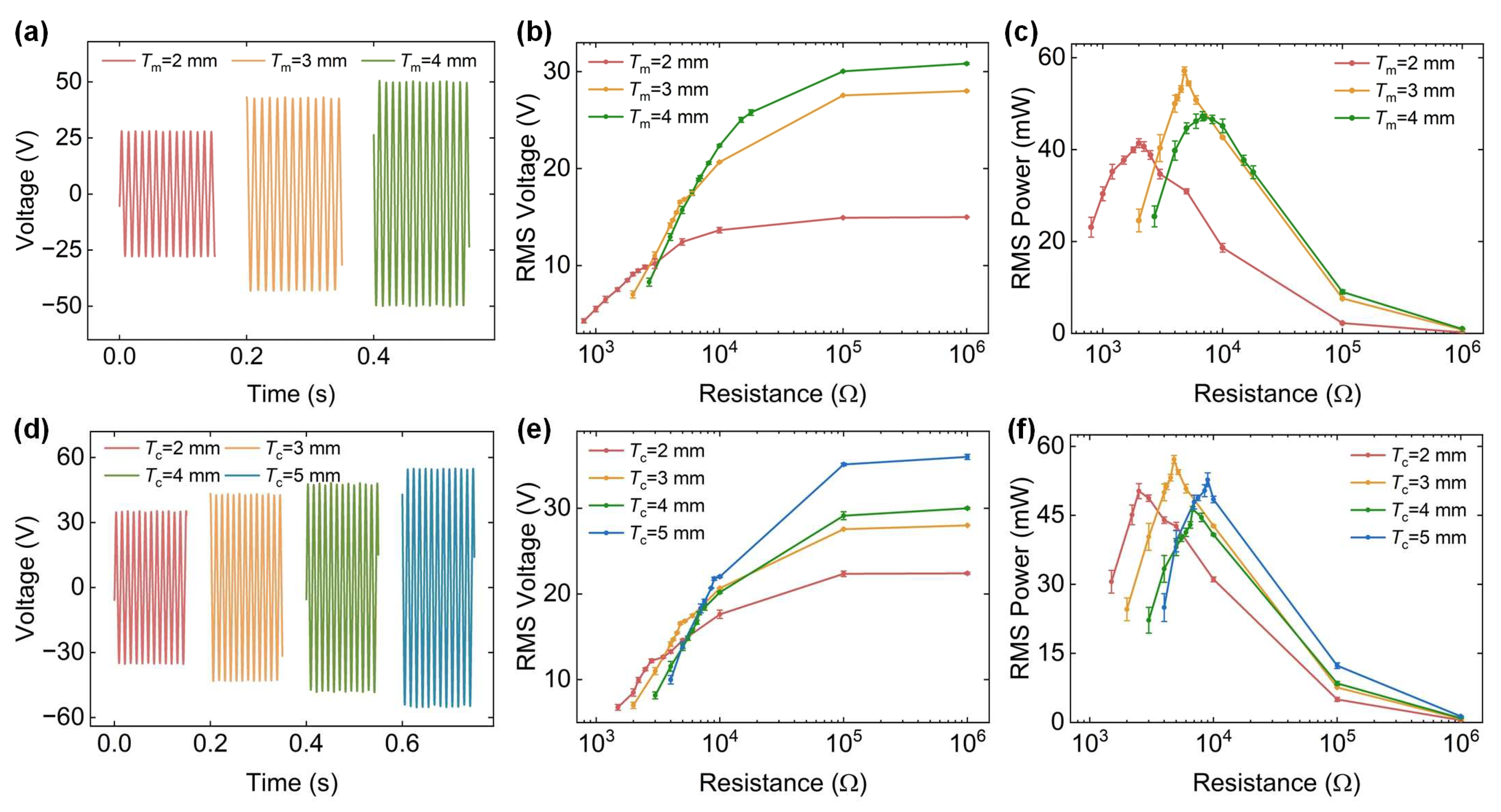
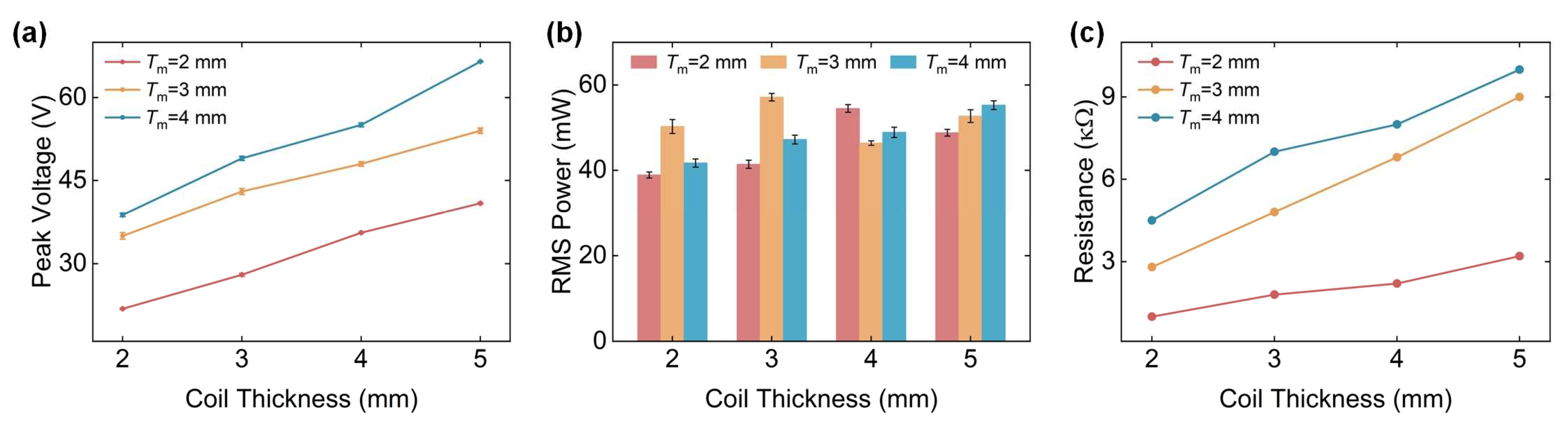
3.4.2. Prototype Performance for Different Thicknesses of Magnets and Coils
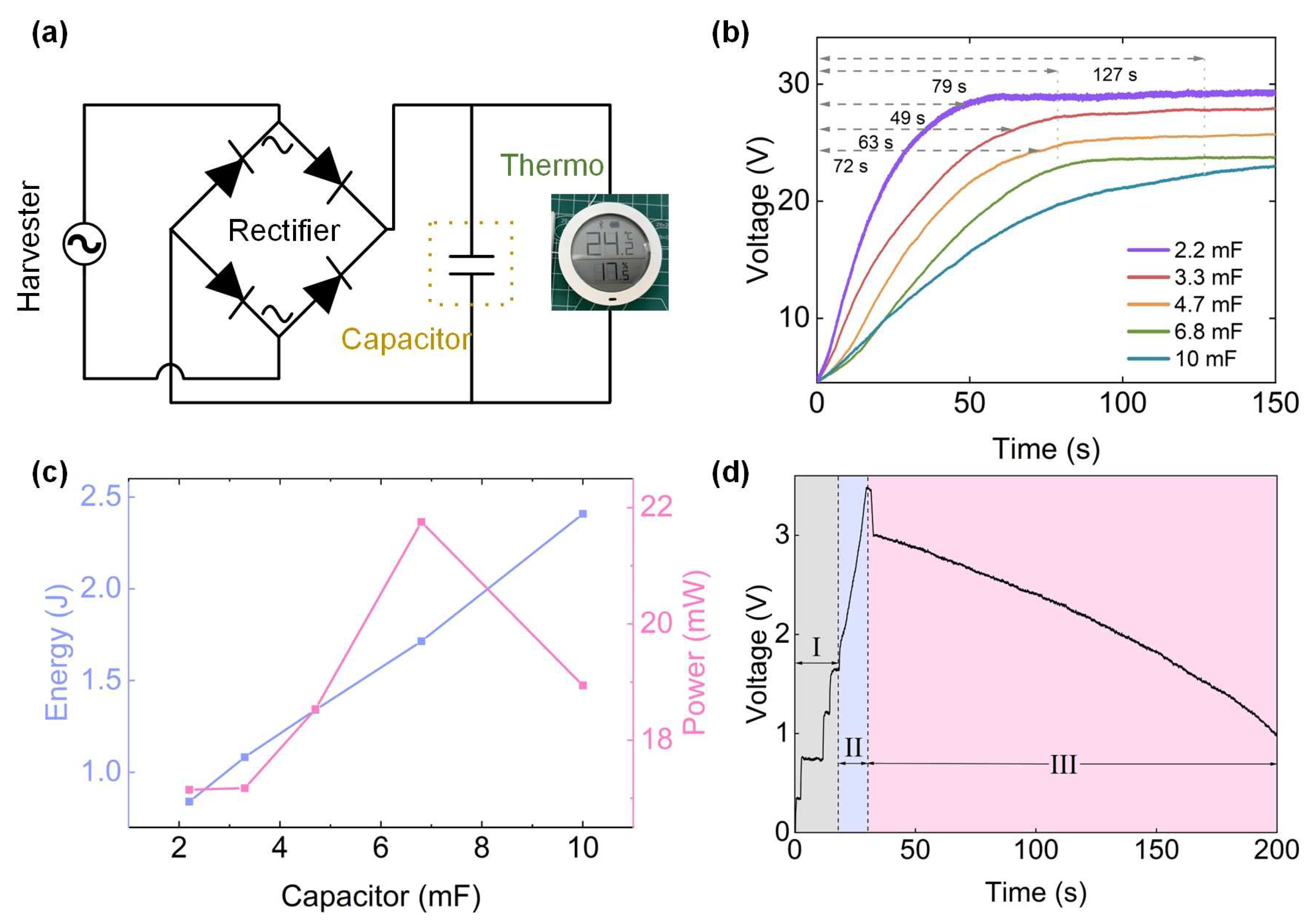
3.5. Performance for Capacitor Charging
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFEEH-SE | Axial flux electromagnetic energy harvester driven by a Stirling engine |
| PZTs | Piezoelectric nanogenerators |
| EMEHs | Electromagnetic energy harvesters |
| TENGs | Triboelectric nanogenerators |
| MFD | Magnetic flux density |
References
- Jouhara, H.; Żabnieńska-Góra, A.; Khordehgah, N.; Ahmad, D.; Lipinski, T. Latent thermal energy storage technologies and applications: A review. Int. J. Thermofluids 2020, 5, 100039. [Google Scholar] [CrossRef]
- Sadeghi, G. Energy storage on demand: Thermal energy storage development, materials, design, and integration challenges. Energy Storage Mater. 2022, 46, 192–222. [Google Scholar] [CrossRef]
- Wu, M.; Wu, S.; Cai, Y.; Wang, R.; Li, T. Form-stable phase change composites: Preparation, performance, and applications for thermal energy conversion, storage and management. Energy Storage Mater. 2021, 42, 380–417. [Google Scholar] [CrossRef]
- Zuo, L.; Tang, X. Large-scale vibration energy harvesting. J. Intell. Mater. Syst. Struct. 2013, 24, 1405–1430. [Google Scholar] [CrossRef]
- Miraglia, M.; Tannous, M.; Inglese, F.; Brämer, B.; Milazzo, M.; Stefanini, C. Energy recovery from shock absorbers through a novel compact electro-hydraulic system architecture. Mechatronics 2022, 81, 102701. [Google Scholar] [CrossRef]
- Liu, H.; Lim, C.W.; Gao, S.; Zhao, J. Effects analysis of bias and excitation conditions on power output of an environmental vibration energy harvesting device using Fe-Ga slice. Mechatronics 2019, 57, 20–28. [Google Scholar] [CrossRef]
- Kan, J.; Lin, S.; Wang, J.; Wang, K.; Gu, Y.; Wang, S.; Meng, F.; Zhang, Z. Design, fabrication and characterization of a wind-isolated galloping energy harvester via an embedded piezoelectric transducer. Mechatronics 2024, 99, 103147. [Google Scholar] [CrossRef]
- Shi, B.; Wang, Q.; Su, H.; Li, J.; Xie, B.; Wang, P.; Qiu, J.; Wu, C.; Zhang, Y.; Zhou, X. Progress in recent research on the design and use of triboelectric nanogenerators for harvesting wind energy. Nano Energy 2023, 116, 108789. [Google Scholar] [CrossRef]
- Liu, F.R.; Zhao, L.C.; Yan, G.; Zhang, W.M.; Wu, Z.Y.; Zhang, X.L. Performing Magnetic Boundary Modulation to Broaden the Operational Wind Speed Range of a Piezoelectric Cantilever-Type Wind Energy Harvester. Micromachines 2024, 15, 1286. [Google Scholar] [CrossRef]
- Lin, Y.; Chong, C.H.; Ma, L.; Li, Z.; Ni, W. Quantification of waste heat potential in China: A top-down Societal Waste Heat Accounting Model. Energy 2022, 261, 125194. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, Y.; Wang, J.; Liu, W.; Wan, F. Research on the Robustness of the Roots Waste Heat Power Generation System. IEEE Access 2021, 9, 155103–155112. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Wang, R.Z.; Yang, C. Perspectives for low-temperature waste heat recovery. Energy 2019, 176, 1037–1043. [Google Scholar] [CrossRef]
- Shchegolkov, A.; Komarov, F.; Lipkin, M.; Milchanin, O.; Parfimovich, I.; Shchegolkov, A.; Semenkova, A.; Velichko, A.; Chebotov, K.; Nokhaeva, V. Synthesis and study of cathode materials based on carbon nanotubes for lithium-ion batteries. Inorg. Mater. Appl. Res. 2021, 12, 1281–1287. [Google Scholar]
- Gong, S.; Li, X.; Sheng, M.; Liu, S.; Zheng, Y.; Wu, H.; Lu, X.; Qu, J. High thermal conductivity and mechanical strength phase change composite with double supporting skeletons for industrial waste heat recovery. ACS Appl. Mater. Interfaces 2021, 13, 47174–47184. [Google Scholar]
- Michel, B.; Dufour, N.; Börtlein, C.; Zoude, C.; Prud’Homme, E.; Gremillard, L.; Clausse, M. First experimental characterization of CaCl2 coated heat exchanger for thermochemical heat transformer applications in industrial waste heat recovery. Appl. Therm. Eng. 2023, 227, 120400. [Google Scholar]
- Kim, Y.; Mehmood, M.U.; Han, H.J.; Kim, Y.J.; Oh, S.J.; Lim, S.-H. Reclaiming Power Potential from Low Temperature Waste Heat by Thermomagnetic Heat Engines. Energies 2022, 15, 2817. [Google Scholar] [CrossRef]
- Thombare, D.; Verma, S. Technological development in the Stirling cycle engines. Renew. Sustain. Energy Rev. 2008, 12, 1–38. [Google Scholar]
- Zare, S.; Tavakolpour-Saleh, A. Free piston Stirling engines: A review. Int. J. Energy Res. 2020, 44, 5039–5070. [Google Scholar]
- Walker, G.; Fauvel, R.; Gustafson, R.; Van Bentham, J. Stirling engine heat pumps. Int. J. Refrig. 1982, 5, 91–97. [Google Scholar]
- Ahmed, F.; Huang, H.; Ahmed, S.; Wang, X. A comprehensive review on modeling and performance optimization of Stirling engine. Int. J. Energy Res. 2020, 44, 6098–6127. [Google Scholar]
- Arif, H.; Shah, A.; Ratlamwala, T.A.H.; Kamal, K.; Khan, M.A. Effect of material change on Stirnol engine: A combination of NiTiNOL (shape memory alloy) and gamma Stirling engine. Materials 2023, 16, 3257. [Google Scholar] [CrossRef] [PubMed]
- Li, J.Q.; Wang, F.P. Numerical investigations on the Stirling engine power and the efficiency of Stirling engine generator. Adv. Mech. Eng. 2022, 14, 16878132221117017. [Google Scholar] [CrossRef]
- Yu, X.; She, C.; Gholizadeh, F.; Xu, Y.-P. Numerical investigation of a new combined energy cycle based on Miller cycle, Organic Rankine cycle, Stirling engine and alkaline fuel cell. Energy Rep. 2021, 7, 5406–5419. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Pourfayaz, F.; Hosseinzade, H.; Acıkkalp, E.; Tlili, I.; Feidt, M. Designing a powered combined Otto and Stirling cycle power plant through multi-objective optimization approach. Renew. Sustain. Energy Rev. 2016, 62, 585–595. [Google Scholar] [CrossRef]
- Entezari, A.; Manizadeh, A.; Ahmadi, R. Energetical, exergetical and economical optimization analysis of combined power generation system of gas turbine and Stirling engine. Energ Convers Manag. 2018, 159, 189–203. [Google Scholar] [CrossRef]
- Chapman, J.W.; Simon, D.L.; McNichols, E. An Analysis of the Strayton Engine, a Brayton and Stirling Cycle Recuperating Engine. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar]
- Tavares, R.; Ruderman, M. Energy harvesting using piezoelectric transducers for suspension systems. Mechatronics 2020, 65, 102294. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Wu, Z.H.; Chen, I.M.; Xu, Q.S. Recent Advances in Piezoelectric Compliant Devices for Ultrahigh-Precision Engineering. Micromachines 2024, 15, 1456. [Google Scholar] [CrossRef]
- Pasharavesh, A.; Moheimani, R.; Dalir, H. Performance Analysis of an Electromagnetically Coupled Piezoelectric Energy Scavenger. Energies 2020, 13, 845. [Google Scholar] [CrossRef]
- Miao, G.; Fang, S.; Wang, S.; Zhou, S. A low-frequency rotational electromagnetic energy harvester using a magnetic plucking mechanism. Appl. Energy 2022, 305, 117838. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, G.; Zhou, S.; Peng, Y.; Xie, S.; Li, Z. Magnetic coupling and amplitude truncation based bistable energy harvester. Int. J. Mech. Sci. 2024, 273, 109228. [Google Scholar] [CrossRef]
- Soares, I.N.; Altafim, R.A.C.; Altafim, R.A.P.; Moreira, M.d.M.A.C.; Sousa, F.S.I.d.; Afonso, J.A.; Carmo, J.P.; Flauzino, R.d.A. Investigation of a Magnetic Levitation Architecture with a Ferrite Core for Energy Harvesting. Energies 2024, 17, 5315. [Google Scholar] [CrossRef]
- Jiao, P.; Wang, Z.L.; Alavi, A.H. Maximizing Triboelectric Nanogenerators by Physics-Informed AI Inverse Design. Adv. Mater. 2024, 36, e2308505. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Liu, H.; Guo, H.; Gong, Y.; Shen, F.; Zhang, Q.; Li, Z. Toward Highly Sensitive Ocean-Wave Monitoring With Sliding-Triboelectric Effect: Modeling, Experimental Validation, and Demonstration. IEEE/ASME Trans. Mechatron. 2024, 29, 4630–4639. [Google Scholar] [CrossRef]
- Zheng, Q.; Xin, L.; Zhang, Q.; Shen, F.; Lu, X.; Cao, C.; Xin, C.; Zhao, Y.; Liu, H.; Peng, Y. Leech-Inspired Amphibious Soft Robot Driven by High-Voltage Triboelectricity. Adv. Mater. 2025, 37, 2417380. [Google Scholar]
- Formosa, F.; Badel, A.; Arroyo, E. Electromagnetic generator design for membrane micro Stirling engine. Power MEMS 2010 2010, 1–4. Available online: https://www.researchgate.net/publication/267687913 (accessed on 18 March 2025).
- Yun, J.; Kim, I.; Kim, D. Hybrid energy harvesting system based on Stirling engine towards next-generation heat recovery system in industrial fields. Nano Energy 2021, 90, 106508. [Google Scholar] [CrossRef]
- Shaislamov, U.; Kim, Y.; Kim, W.S.; Jeong, H.; Lee, H.J.; Chun, W. Hybrid operation of triboelectric nanogenerator for electricity generation by a low-temperature differential heat engine. Int. J. Energy Res. 2017, 41, 1412–1421. [Google Scholar]
- Panigrahi, B.K.; Ahmed, R.; Mehmood, M.U.; Park, J.C.; Kim, Y.; Chun, W. Operation of a low-temperature differential heat engine for power generation via hybrid nanogenerators. Appl. Energy 2021, 285, 116385. [Google Scholar]
- Stolyarov, S.P.; Stolayrov, A.S. Stirling Generators: Challenges and Opportunities. Russ. Electr. Eng. 2018, 88, 778–782. [Google Scholar] [CrossRef]
- Zhang, Q.; Kim, E.S. Vibration energy harvesting based on magnet and coil arrays for watt-level handheld power source. Proc. IEEE 2014, 102, 1747–1761. [Google Scholar]
- Hou, G.; Gao, L.; Qin, Y. Two-Temperature Approximation Analyzing the Combustion Characteristics of Premixed Gas-Air Mixture in Inert Porous Media. In Proceedings of the 2010 The Second China Energy Scientist Forum, Xuzhou, China, 18–19 October 2010. [Google Scholar]
- Zeeshan, A.R.; Chun, W.; Oh, S.; Kim, Y. Power generation from a hybrid generator (teng-emg) run by a thermomagnetic engine harnessing low temperature waste heat. Energies 2019, 12, 1774. [Google Scholar] [CrossRef]

| Description | Value | |
|---|---|---|
| The Stirling engine | Hot chamber bore (mm) | 25 |
| Hot chamber length (mm) | 47.5 | |
| Gas distribution piston bore (mm) | 19 | |
| Gas distribution piston length (mm) | 40.5 | |
| Cold chamber bore (mm) | 12 | |
| Cold chamber length (mm) | 25 | |
| Power piston bore (mm) | 12 | |
| Power piston length (mm) | 12 | |
| Weight of the Stirling engine (g) | 419.62 | |
| Magnets | Number | 4, 6, 8, 10 |
| Diameter (mm) | 15 | |
| Thickness (mm) | 2, 3, 4 | |
| Pitch diameter (mm) | 50 | |
| Coils | Inner diameter (mm) | 3 |
| Outer diameter (mm) | 15 | |
| Thickness (mm) | 2, 3, 4, 5 | |
| Wire gauge (mm) | 0.15 | |
| Number of turns | 360 (Tc = 2), 540 (Tc = 3), 720 (Tc = 4), 900 (Tc = 5) | |
| Heat source | Materials | mineral oil |
| Container volume (mL) | 50 |
| Refs. | Driver | Conversion Mechanism | Operating Temp (°C) | Speed (rpm) | Voltage (V) | Power (mW) |
|---|---|---|---|---|---|---|
| [37] | Stirling engine | TENG-EMEH hybrid | <100 | - | - | 0.0014 |
| [38] | Stirling engine | TENG | <100 | 250 | 105 | - |
| [39] | Stirling engine | TENG-PZT hybrid | <100 | 244 | 40 | 0.041 |
| [43] | Thermomagnetic engine | TENG-EMEH hybrid | <100 | 251 | 5 | 0.75 |
| This work | Stirling engine | EMEH | >200 | 950 | 42.8 | 57.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhou, L.; Gong, Y.; Shen, F.; Peng, Y.; Wu, H. Axial Flux Electromagnetic Energy Harvester Driven by a Stirling Engine for Waste Heat Recovery. Energies 2025, 18, 1620. https://doi.org/10.3390/en18071620
Li Z, Zhou L, Gong Y, Shen F, Peng Y, Wu H. Axial Flux Electromagnetic Energy Harvester Driven by a Stirling Engine for Waste Heat Recovery. Energies. 2025; 18(7):1620. https://doi.org/10.3390/en18071620
Chicago/Turabian StyleLi, Zhongjie, Limeng Zhou, Ying Gong, Fan Shen, Yan Peng, and Hao Wu. 2025. "Axial Flux Electromagnetic Energy Harvester Driven by a Stirling Engine for Waste Heat Recovery" Energies 18, no. 7: 1620. https://doi.org/10.3390/en18071620
APA StyleLi, Z., Zhou, L., Gong, Y., Shen, F., Peng, Y., & Wu, H. (2025). Axial Flux Electromagnetic Energy Harvester Driven by a Stirling Engine for Waste Heat Recovery. Energies, 18(7), 1620. https://doi.org/10.3390/en18071620






