Transmission and Generation Expansion Planning Considering Virtual Power Lines/Plants, Distributed Energy Injection and Demand Response Flexibility from TSO-DSO Interface
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contributions
- Battery energy storage modeling for implementation of virtual power lines, in generation and transmission expansion planning;
- Modeling of virtual power plants providing aggregated energy and power capacity to transmission nodes;
- Modeling of the distributed energy resources services at the TSO-DSO interconnection as demand response flexibility, providing energy and capacity reserve to the transmission system;
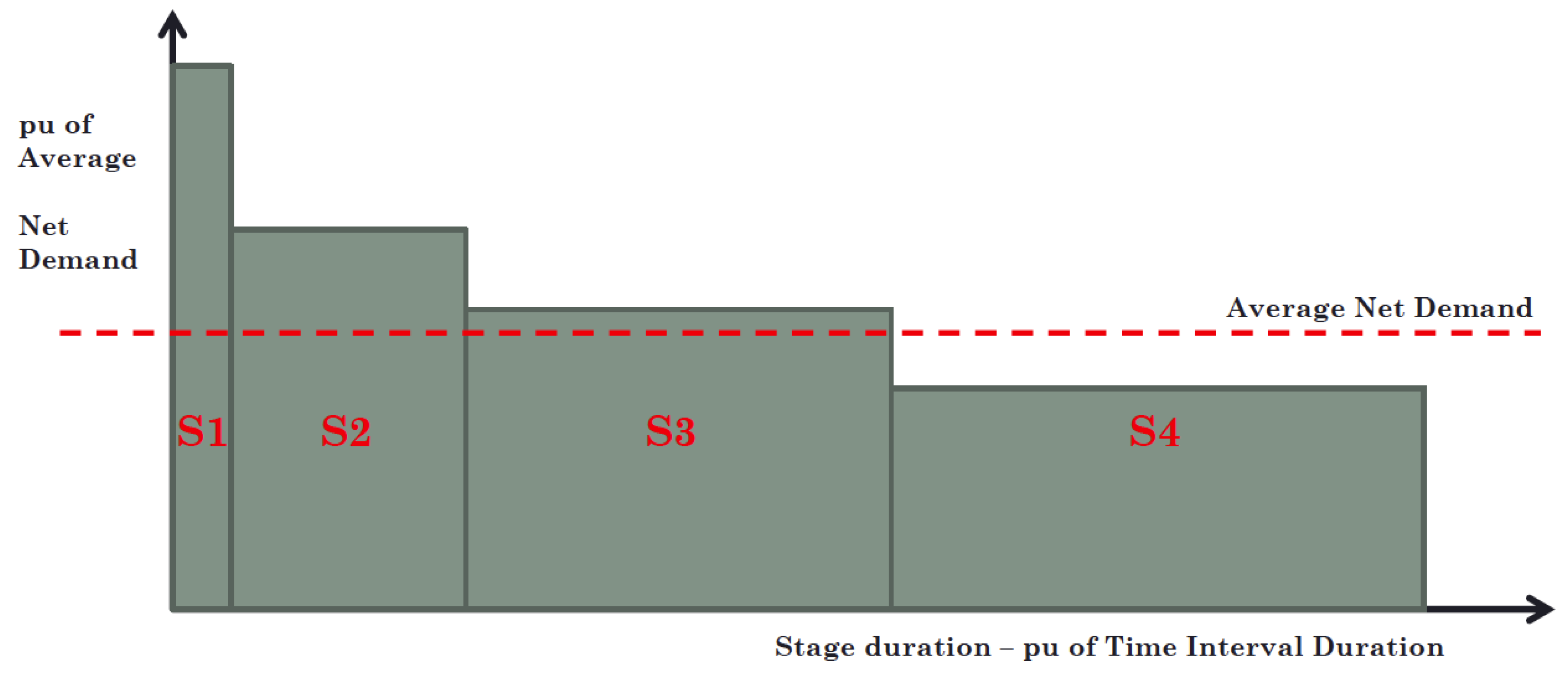
- Implementation of a net demand model associated with load duration curve stages to deal with the use of variable renewable energy.
2. Problem Formulation—Deterministic Model
2.1. Net Demand Model
2.2. Flexibility
2.3. Virtual Power Lines
2.4. Virtual Power Plants
2.5. Objective Function
2.6. Power Balance Constraints
2.7. Demand Response Constraints
2.8. Reference Bar and Voltage Constraints
2.9. Transmission Line Circuits Constraints
2.10. Transmission Line Circuits Constraints AC Linearized
2.11. Transmission Line Circuits Constraints AC—Second-Order Cone Constraint
2.12. Energy Storage System Constraints
2.13. Virtual Power Line Constraints
2.14. Flexibility Constraints
2.15. Virtual Power Plants Constraints
2.16. Power Limits Constraints
3. Problem Formulation—Modeling Uncertainties
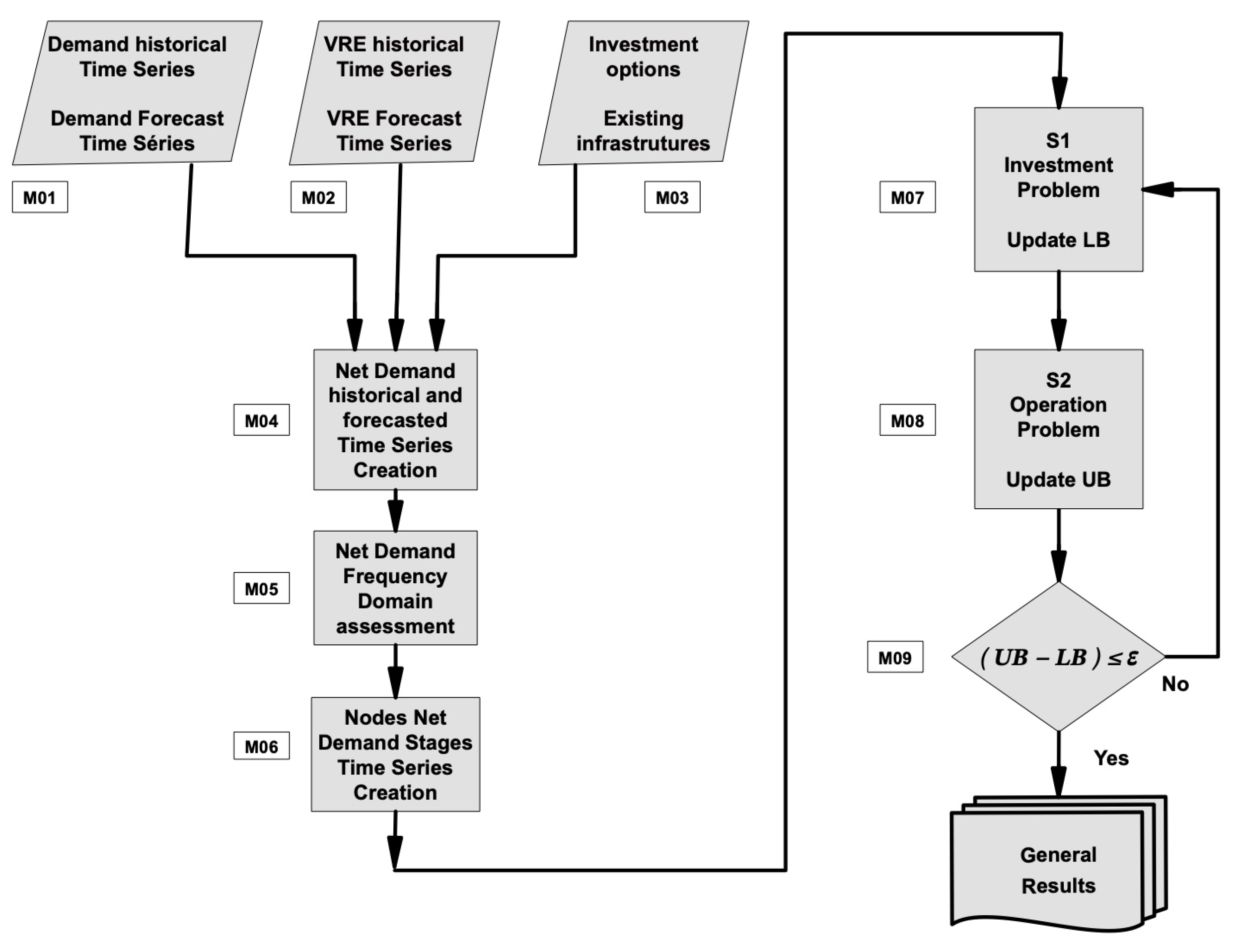
4. Solution Procedure
4.1. Deterministic Procedure
- Set , , k = 0 and
- Solve the following master problem:s.t.Solution:
- Update
- Solve the following slave problem:s.t.
- Update [ ]
- If return and finish
- Create variables
- Add the following constraints to the master problem:
- Update k = k + 1 and go to Step 2
4.2. Procedure Considering Uncertainties
4.2.1. Ambiguity Set
4.2.2. Duality-Free Approach
5. Case Studies
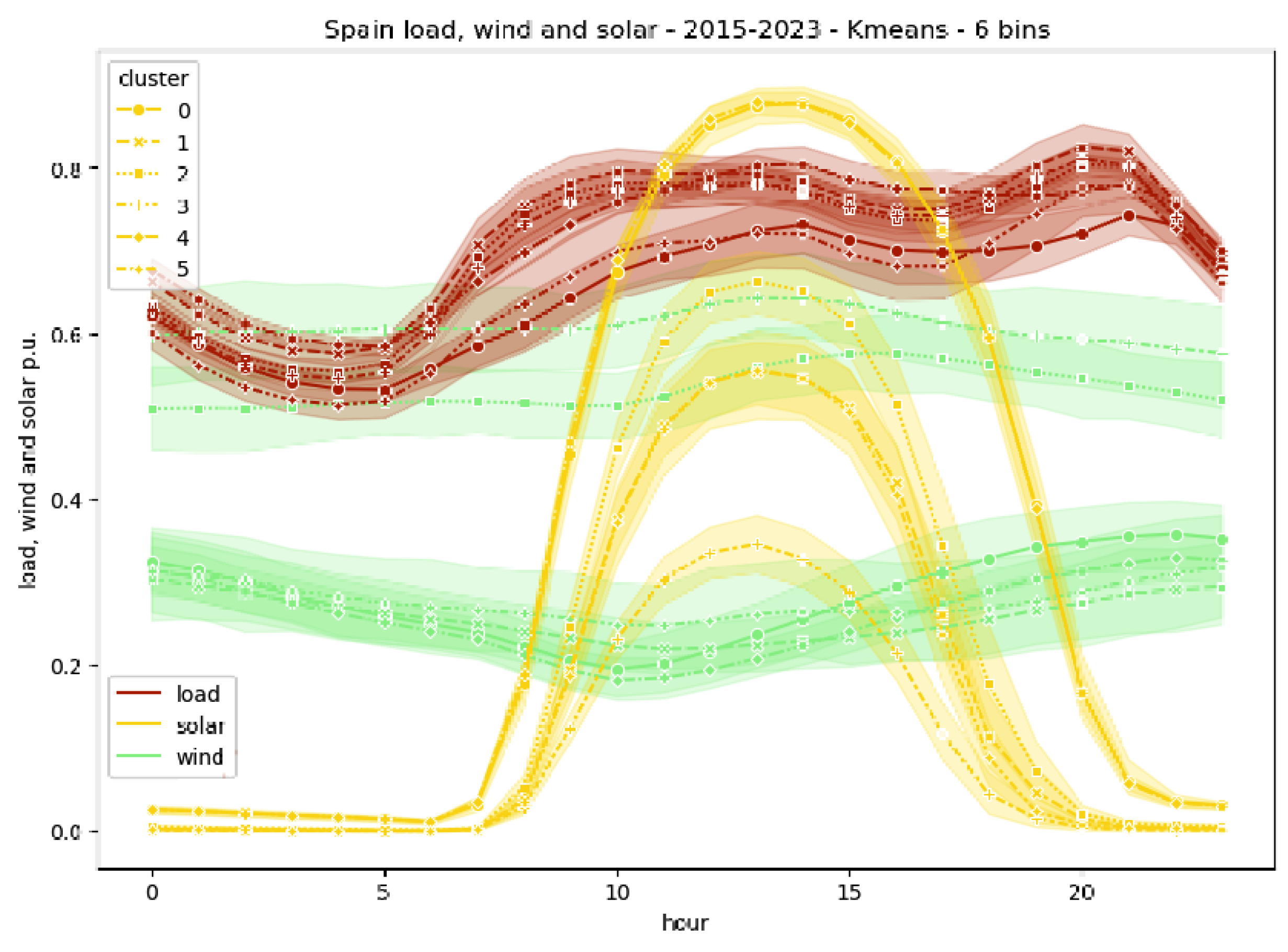
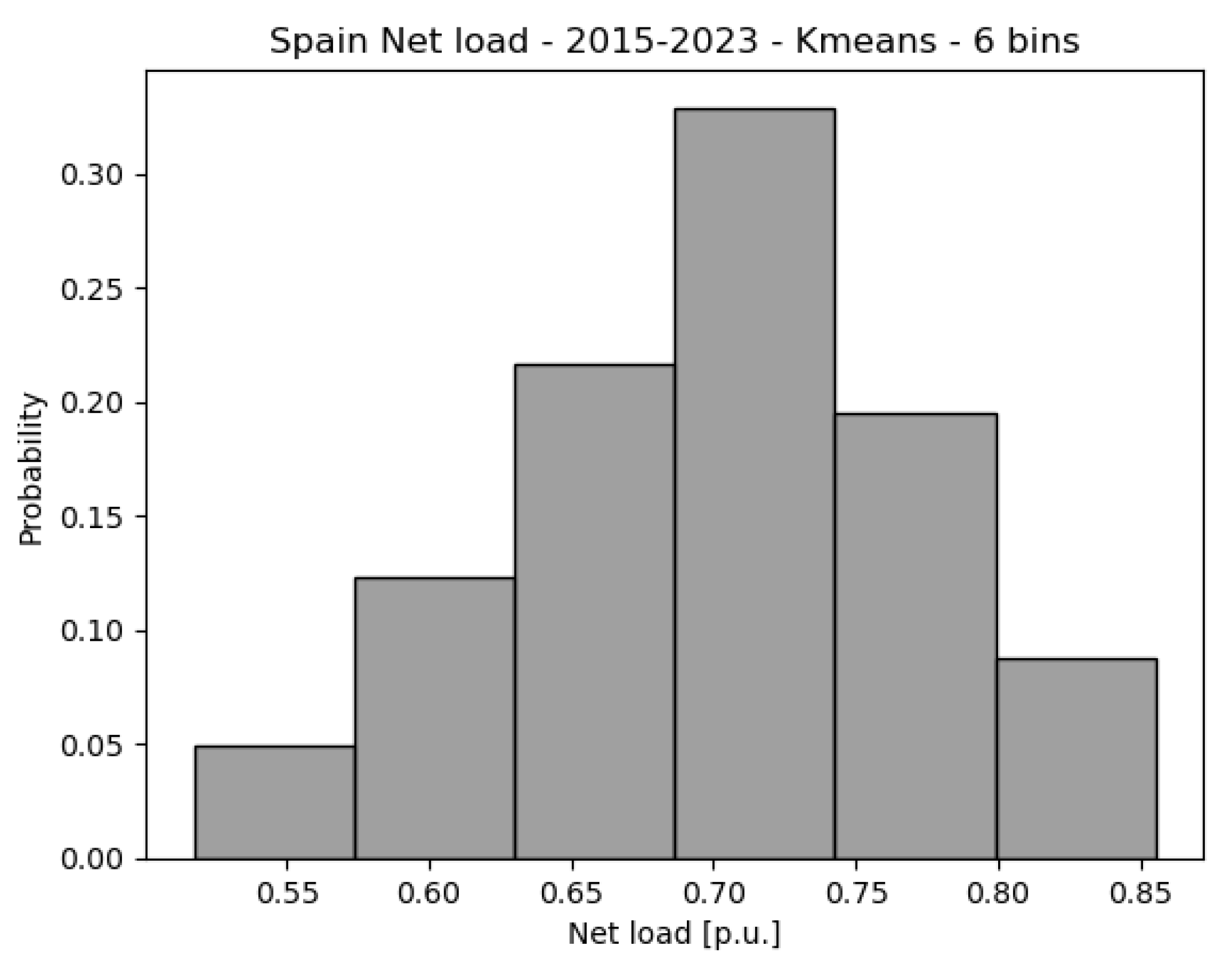
5.1. Cluster of Data Bins
5.2. Presentation of Case Studies Results
5.3. Garver 6-Node Network
5.3.1. Garver 6-Node Network—Scenario S1.1
5.3.2. Garver 6-Node Network—Scenario S1.2
5.3.3. Garver 6-Node Network—Scenario S1.3
5.4. IEEE RTS-GMLC
5.4.1. IEEE RTS-GMLC—Scenario S2.1
5.4.2. IEEE RTS-GMLC—Scenario S2.2
5.4.3. IEEE RTS-GMLC—Scenario S2.3
5.4.4. IEEE RTS-GMLC—Scenario S2.4
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sets | |
| Dispatchable generation units | |
| Candidate dispatchable generation units | |
| Non-dispatchable generation units | |
| Candidate non-dispatchable generation units | |
| VPP dispatchable generation units | |
| VPP non-dispatchable generation units | |
| Battery storage units | |
| Virtual power lines | |
| Virtual power plants | |
| Demand stages | |
| Candidate storage units | |
| Set of nodes in the power transmission network | |
| Set of lines in the power transmission network, | |
| Set of circuits in the power transmission network line | |
| Set of scenarios | |
| DDDRO ambiguity set | |
| Indices | |
| Node, | |
| Line dircuit, | |
| Candidate dispatchable generation, | |
| Candidate non-dispatchable generation, | |
| Battery storage unit, | |
| Line, | |
| Stage, | |
| Time step, | |
| Virtual power line, | |
| Virtual power plant, | |
| Scenario, | |
| Input Data and Operators | |
| Time horizon of the problem | |
| Area | |
| Susceptance [p.u.] of line | |
| Discount rate | |
| Conductance (p.u.) of line | |
| Maximum number of circuits of line | |
| Active power capacity of circuit of line | |
| Apparent power capacity of circuit of line | |
| Investment cost of additional line circuit at corridor l in time period t [$/circuit] | |
| Investment cost of additional dispatchable generation at node b in time period t [$/] | |
| Investment cost of additional non-dispatchable generation at node b in time period t [$/] | |
| Investment cost of battery storage in time period t [$/] | |
| Investment cost of VPL in time period t [$/] | |
| Variable cost of existing dispatchable generation at node b in time period t [$/] | |
| Variable cost of candidate dispatchable generation at node b in time period t [$/] | |
| Variable cost of upward flexibility at node b in time period t [$/] | |
| Variable cost of downward flexibility at node b in time period t [$/] | |
| Variable cost of demand response upward flexibility at node b in time period t [$/] | |
| Variable cost of demand response downward flexibility at node b in time period t [$/] | |
| Variable cost of storage h in time period t [$/] | |
| Variable cost of P2P active power contracted at node b in time period t [$/] | |
| Variable cost of P2P active generation contracted at node b in time period t [$/] | |
| Variable cost of load curtailment at node b in time period t [$/] | |
| Variable cost of non-dispatchable generation curtailment at node b in time period t [$/] | |
| Variable cost of congestion in time period t [$/] | |
| Probability of scenario | |
| Probability of scenario from data | |
| Active power of demand response, bus , time period , demand stage [] | |
| Reactive power of demand response, bus , time period , demand stage [] | |
| Demand response available flexibility band, bus , time period , demand stage [] | |
| Active power of net demand, bus , time period , demand stage , scenario [] | |
| Reactive power of net demand, bus , time period , demand stage , scenario [] | |
| Active power of candidate non-dispatchable generation units, bus , time period , demand stage , scenario [] | |
| Reactive power of candidate non-dispatchable generation units, bus , time period , demand stage , scenario [] | |
| Active power of VPP contracted in the P2P market, vpp , bus , time period [] | |
| Reactive power of VPP contracted in the P2P market, vpp , bus , time period [] | |
| Active power available as downward flexibility at bus , time period [] | |
| Active power available as upward flexibility at bus , time period [] | |
| Energy capacity of battery storage , time period [] | |
| Maximum power of battery storage [] | |
| Maximum active power of existing dispatchable generation units, bus [] | |
| Maximum reactive power of existing dispatchable generation units, bus [] | |
| Maximum active power of VPP dispatchable generation, vpp [] | |
| Maximum reactive power of VPP dispatchable generation, vpp [] | |
| Maximum active power of VPP dispatchable generation, vpp [] | |
| Maximum reactive power of VPP dispatchable generation, vpp [] | |
| Maximum active power of candidate dispatchable generation, bus [] | |
| Maximum reactive power of candidate dispatchable generation, bus [] | |
| Maximum active power of upward flexibility, bus [] | |
| Maximum active power of downward flexibility, bus [] | |
| Reference bar for voltage angle | |
| Large power value [p.u.] | |
| Decision Variables | |
| Active power flow of line , time period , demand stage , scenario [] | |
| Signed active power flow of origin side of line , time period , demand stage , scenario [] | |
| Signed active power flow of destination side of line , time period , demand stage , scenario [] | |
| Reactive power flow of line , time period , demand stage , scenario [] | |
| Active power of VPP demanded from reserve market, vpp , bus , time period , demand stage , scenario [] | |
| Reactive power of VPP demanded from reserve market, vpp , bus , time period , demand stage , scenario [] | |
| Active power of VPP dispatchable generation, vpp , bus , time period , demand stage , scenario [] | |
| Reactive power of VPP dispatchable generation, vpp , bus , time period , demand stage, scenario [] | |
| Active power of existing dispatchable generation units, bus , time period , demand stage , scenario [] | |
| Reactive power of existing dispatchable generation units, bus , time period , demand stage , scenario [] | |
| Active power of candidate dispatchable generation units, bus , time period , demand stage , scenario [] | |
| Reactive power of candidate dispatchable generation units, bus , time period , demand stage , scenario [] | |
| Active power of existing non-dispatchable generation units, bus , time period , demand stage , scenario [] | |
| Reactive power of existing non-dispatchable generation units, bus , time period , demand stage , scenario [] | |
| Active power of VPP non-dispatchable generation, vpp , bus , time period , demand stage [] | |
| Reactive power of VPP non-dispatchable generation, vpp , bus , time period , demand stage [] | |
| Active power of curtailed non-dispatchable generation units, bus , time period , demand stage , scenario [] | |
| Active power of upward flexibility, bus , time period , demand stage , scenario [] | |
| Active power of downward flexibility, bus , time period , demand stage , scenario [] | |
| Active power of procured demand response upward flexibility, bus , time period , demand stage , scenario [] | |
| Active power of procured demand response downward flexibility, bus , time period , demand stage , scenario [] | |
| Active power of curtailed demand, bus , time period , demand stage , scenario [] | |
| Storage active power discharge of storage , time period , demand stage , scenario [] | |
| Storage active power charge of storage , time period , demand stage , scenario [] | |
| Time duration of demand stage [pu] | |
| Voltage (p.u.) at bus at time , demand stage , scenario | |
| Voltage (p.u.) at bus at time , demand stage , scenario | |
| Voltage phase angle between nodes and at time , demand stage , scenario | |
| State-of-charge (), storage , at time , demand stage , scenario | |
| Energy available at storage device h in time period , scenario [] | |
| Admittance of line –real part | |
| Admittance of line –imaginary part | |
| Binary variable indicating if downward flexibility is considered at bus , during demand stage [0,1] | |
| Binary variable indicating if upward flexibility is considered at bus , during demand stage [0,1] | |
| Binary variable indicating the presence of a circuit , in corridor , time period [0,1] | |
| Binary variable indicating the presence of storage , time period [0,1] | |
| Binary variable indicating the presence of VPL , time period [0,1] | |
| Binary variable indicating the presence of candidate dispatchable generation , bus , time period [0,1] | |
| Binary variable indicating the presence of candidate non-dispatchable generation , bus , time period [0,1] | |
| Binary variable indicating the charge/discharge status of battery storage unit , time period , stage [0,1] | |
| Binary variable indicating the flow status of VPL line from side, time period , stage [0,1] | |
| Binary variable indicating the flow status of VPL line to side, time period , stage [0,1] | |
| Binary variable indicating the charge/discharge status of VPL Battery storage unit 1 of line , time period , stage [0,1] | |
| Binary variable indicating the charge/discharge status of VPL Battery storage unit 2 of line , time period , stage [0,1] | |
| Vector Notation | |
| Set of network variables: [, , , ] . | |
| Set of network variables: [, , , , , , , , , , , , , , , , , , , , , , , , , , , ] . |
References
- Matevosyan, J.; Huang, S.H.; Du, P.; Mago, N.; Guiyab, R. Operational Security: The Case of Texas. IEEE Power Energy Mag. 2021, 19, 18–27. [Google Scholar] [CrossRef]
- Spyrou, E.; Ho, J.L.; Hobbs, B.F.; Johnson, R.M.; McCalley, J.D. What are the Benefits of Co-Optimizing Transmission and Generation Investment? Eastern Interconnection Case Study. IEEE Trans. Power Syst. 2017, 32, 4265–4277. [Google Scholar] [CrossRef]
- Latorre, G.; Cruz, R.D.; Areiza, J.M.; Villegas, A. Classification of publications and models on transmission expansion planning. IEEE Trans. Power Syst. 2003, 18, 938–946. [Google Scholar] [CrossRef]
- Hemmati, R.; Hooshmand, R.; Khodabakhshian, A. Comprehensive review of generation and transmission expansion planning. IET Gener. Transm. Distrib. 2013, 7, 955–964. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sabillon Antunez, C.; Ajalli, M.; Romero, R. Transmission Expansion Planning: Literature Review and Classification. IEEE Syst. J. 2019, 13, 3129–3140. [Google Scholar] [CrossRef]
- El-Meligy, M.A.; Sharaf, M.; Soliman, A.T. A coordinated scheme for transmission and distribution expansion planning: A Tri-level approach. Electr. Power Syst. Res. 2021, 196, 107274. [Google Scholar] [CrossRef]
- Ranjbar, H.; Hosseini, S.H.; Zareipour, H. A robust optimization method for co-planning of transmission systems and merchant distributed energy resources. Int. J. Electr. Power Energy Syst. 2020, 118, 105845. [Google Scholar] [CrossRef]
- Abushamah, H.A.S.; Haghifam, M.; Bolandi, T.G. A novel approach for distributed generation expansion planning considering its added value compared with centralized generation expansion. Sustain. Energy Grids Netw. 2021, 25, 100417. [Google Scholar] [CrossRef]
- Ranjbar, H.; Hosseini, S.H.; Zareipour, H. Resiliency-Oriented Planning of Transmission Systems and Distributed Energy Resources. IEEE Trans. Power Syst. 2021, 36, 4114–4125. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, L.; Cheng, H.; Liu, D.; Zhang, J.; Li, G. Data-driven distributionally robust transmission expansion planning considering contingency-constrained generation reserve optimization. Int. J. Electr. Power Energy Syst. 2021, 131, 106973. [Google Scholar] [CrossRef]
- Mohanapriya, T.; Manikandan, T.R. Congestion management of deregulated electricity market using locational marginal pricing. In Proceedings of the 2014 IEEE International Conference on Computational Intelligence and Computing Research, Bhopal, India, 14–16 November 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Benders, J.F. Partitioning Procedures for Solving Mixed-variables Programming Problems. Numer. Math. 1962, 4, 238–252. [Google Scholar] [CrossRef]
- Conejo, A.J.; Mínguez, R.; Castillo, E.; García-Bertrand, R. Decomposition Techniques in Mathematical Programming, 1st ed.; Springer: Cham, Switzerland, 2006. [Google Scholar]
- Romero, R.; Monticelli, A. A hierarchical decomposition approach for transmission network expansion planning. IEEE Trans. Power Syst. 1994, 9, 373–380. [Google Scholar] [CrossRef]
- Haffner, S.L. O Planejamento da Expansão dos Sistemas Elétricos no Contexto de um Ambiente Competitivo. Ph.D. Thesis, Universidade Estadual de Campinas, Campinas, Brazil, 2000. [Google Scholar]
- Jabr, R.A. Robust Transmission Network Expansion Planning with Uncertain Renewable Generation and Loads. IEEE Trans. Power Syst. 2013, 28, 4558–4567. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Wang, L.; He, Y.; Wang, Z. Robust Optimization for Transmission Expansion Planning: Minimax Cost vs. Minimax Regret. IEEE Trans. Power Syst. 2014, 29, 3069–3077. [Google Scholar] [CrossRef]
- Ruiz, C.; Conejo, A. Robust transmission expansion planning. Eur. J. Oper. Res. 2015, 242, 390–401. [Google Scholar] [CrossRef]
- Xing, T.; Caijuan, Q.; Liang, Z.; Pengjiang, G.; Jianfeng, G.; Panlong, J. A comprehensive flexibility optimization strategy on power system with high-percentage renewable energy. In Proceedings of the 2017 2nd International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 20–23 September 2017; pp. 553–558. [Google Scholar] [CrossRef]
- Alvarez, E.F.; Olmos, L.; Ramos, A.; Antoniadou-Plytaria, K.; Steen, D.; Tuan, L.A. Values and impacts of incorporating local flexibility services in transmission expansion planning. Electr. Power Syst. Res. 2022, 212, 108480. [Google Scholar] [CrossRef]
- Ding, Z.; Hu, Z.; Wu, J.; Peng, Q.; Zhao, H.; Huang, X. Optimal Transmission Expansion Planning Considering Demand Response Characteristics of Load Duration Curve. In Proceedings of the 2022 7th Asia Conference on Power and Electrical Engineering (ACPEE), Virtual Conference, 16–17 April 2022; pp. 40–44. [Google Scholar] [CrossRef]
- Kristiansen, M.; Korpås, M.; Farahmand, H.; Graabak, I.; Härtel, P. Introducing system flexibility to a multinational transmission expansion planning model. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Tejada-Arango, D.A.; Morales-España, G.; Wogrin, S.; Centeno, E. Power-Based Generation Expansion Planning for Flexibility Requirements. IEEE Trans. Power Syst. 2020, 35, 2012–2023. [Google Scholar] [CrossRef]
- Dehghan, S.; Amjady, N.; Conejo, A.J. A Multistage Robust Transmission Expansion Planning Model Based on Mixed Binary Linear Decision Rules—Part I. IEEE Trans. Power Syst. 2018, 33, 5341–5350. [Google Scholar] [CrossRef]
- Zhang, H.; Heydt, G.T.; Vittal, V.; Quintero, J. An Improved Network Model for Transmission Expansion Planning Considering Reactive Power and Network Losses. IEEE Trans. Power Syst. 2013, 28, 3471–3479. [Google Scholar] [CrossRef]
- Liu, J.; Bynum, M.; Castillo, A.; Watson, J.P.; Laird, C.D. A multitree approach for global solution of ACOPF problems using piecewise outer approximations. Comput. Chem. Eng. 2018, 114, 145–157. [Google Scholar] [CrossRef]
- Bynum, M.; Castillo, A.; Watson, J.P.; Laird, C.D. Tightening McCormick Relaxations Toward Global Solution of the ACOPF Problem. IEEE Trans. Power Syst. 2019, 34, 814–817. [Google Scholar] [CrossRef]
- Ghaddar, B.; Jabr, R.A. Power transmission network expansion planning: A semidefinite programming branch-and-bound approach. Eur. J. Oper. Res. 2019, 274, 837–844. [Google Scholar] [CrossRef]
- Mehrtash, M.; Cao, Y. A New Global Solver for Transmission Expansion Planning with AC Network Model. IEEE Trans. Power Syst. 2022, 37, 282–293. [Google Scholar] [CrossRef]
- Mehrtash, M.; Hobbs, B.F.; Mahroo, R.; Cao, Y. Does Choice of Power Flow Representation Matter in Transmission Expansion Optimization? A Quantitative Comparison for a Large-Scale Test System. IEEE Trans. Ind. Appl. 2024, 60, 1433–1441. [Google Scholar] [CrossRef]
- Palmintier, B.S.; Webster, M.D. Impact of Operational Flexibility on Electricity Generation Planning with Renewable and Carbon Targets. IEEE Trans. Sustain. Energy 2016, 7, 672–684. [Google Scholar] [CrossRef]
- Chen, X.; Lv, J.; McElroy, M.B.; Han, X.; Nielsen, C.P.; Wen, J. Power System Capacity Expansion Under Higher Penetration of Renewables Considering Flexibility Constraints and Low Carbon Policies. IEEE Trans. Power Syst. 2018, 33, 6240–6253. [Google Scholar] [CrossRef]
- Wendelborg, M.A.; Backe, S.; del Granado, P.C.; Seifert, P.E. Consequences of Uncertainty from Intraday Operations to a Capacity Expansion Model of the European Power System. In Proceedings of the 2023 19th International Conference on the European Energy Market (EEM), Lappeenranta, Finland, 6–8 June 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Ramos, A.; Alvarez, E.F.; Lumbreras, S. OpenTEPES: Open-source Transmission and Generation Expansion Planning. SoftwareX 2022, 18, 101070. [Google Scholar] [CrossRef]
- Domínguez, R.; Conejo, A.J.; Carrión, M. Toward Fully Renewable Electric Energy Systems. IEEE Trans. Power Syst. 2015, 30, 316–326. [Google Scholar] [CrossRef]
- Baringo, L.; Baringo, A. A Stochastic Adaptive Robust Optimization Approach for the Generation and Transmission Expansion Planning. IEEE Trans. Power Syst. 2018, 33, 792–802. [Google Scholar] [CrossRef]
- Moreira, A.; Pozo, D.; Street, A.; Sauma, E. Reliable Renewable Generation and Transmission Expansion Planning: Co-Optimizing System’s Resources for Meeting Renewable Targets. IEEE Trans. Power Syst. 2017, 32, 3246–3257. [Google Scholar] [CrossRef]
- Ahmadi, S.; Mavalizadeh, H.; Ghadimi, A.A.; Miveh, M.R.; Ahmadi, A. Dynamic robust generation–transmission expansion planning in the presence of wind farms under long- and short-term uncertainties. IET Gener. Transm. Distrib. 2020, 14, 5418–5427. [Google Scholar] [CrossRef]
- Moreira, A.; Pozo, D.; Street, A.; Sauma, E.; Strbac, G. Climate-aware generation and transmission expansion planning: A three-stage robust optimization approach. Eur. J. Oper. Res. 2021, 295, 1099–1118. [Google Scholar] [CrossRef]
- Backe, S.; Ahang, M.; Tomasgard, A. Stable stochastic capacity expansion with variable renewables: Comparing moment matching and stratified scenario generation sampling. Appl. Energy 2021, 302, 117538. [Google Scholar] [CrossRef]
- Curty, M.G.; Borges, C.L.; Saboia, C.H.; Lisboa, M.L.; Berizzi, A. A soft-linking approach to include hourly scheduling of intermittent resources into hydrothermal generation expansion planning. Renew. Sustain. Energy Rev. 2023, 188, 113838. [Google Scholar] [CrossRef]
- Toolabi Moghadam, A.; Bahramian, B.; Shahbaazy, F.; Paeizi, A.; Senjyu, T. Stochastic Flexible Power System Expansion Planning, Based on the Demand Response Considering Consumption and Generation Uncertainties. Sustainability 2023, 15, 1099. [Google Scholar] [CrossRef]
- García-Bertrand, R.; Mínguez, R. Dynamic Robust Transmission Expansion Planning. IEEE Trans. Power Syst. 2017, 32, 2618–2628. [Google Scholar] [CrossRef]
- Roldán, C.; Mínguez, R.; García-Bertrand, R.; Arroyo, J.M. Robust Transmission Network Expansion Planning Under Correlated Uncertainty. IEEE Trans. Power Syst. 2019, 34, 2071–2082. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, H.; Chen, S.; Wang, Y.; Zhang, C.; Kang, C. Robust Transmission Expansion Planning Based on Adaptive Uncertainty Set Optimization Under High-Penetration Wind Power Generation. IEEE Trans. Power Syst. 2021, 36, 2798–2814. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, H.; Chen, S.; Lin, Z.; Kang, C. Probability-driven transmission expansion planning with high-penetration renewable power generation: A case study in northwestern China. Appl. Energy 2019, 255, 113610. [Google Scholar] [CrossRef]
- Yin, X.; Chen, H.; Liang, Z.; Zeng, X.; Zhu, Y.; Chen, J. Robust transmission network expansion planning based on a data-driven uncertainty set considering spatio-temporal correlation. Sustain. Energy Grids Netw. 2023, 33, 100965. [Google Scholar] [CrossRef]
- Garcia-Cerezo, A.; Baringo, L.; Garcia-Bertrand, R. Dynamic Robust Transmission Network Expansion Planning in Renewable Dominated Power Systems Considering Inter-Temporal and Non-Convex Operational Constraints. In Proceedings of the 2022 International Conference on Smart Energy Systems and Technologies (SEST), Eindhoven, The Netherlands, 5–7 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Garcia-Cerezo, A.; Baringo, L.; Garcia-Bertrand, R. Expansion planning of the transmission network with high penetration of renewable generation: A multi-year two-stage adaptive robust optimization approach. Appl. Energy 2023, 349, 121653. [Google Scholar] [CrossRef]
- Zhang, X.; Conejo, A.J. Coordinated Investment in Transmission and Storage Systems Representing Long- and Short-Term Uncertainty. IEEE Trans. Power Syst. 2018, 33, 7143–7151. [Google Scholar] [CrossRef]
- Verastegui, F.; Lorca, A.; Olivares, D.E.; Negrete-Pincetic, M.; Gazmuri, P. An Adaptive Robust Optimization Model for Power Systems Planning with Operational Uncertainty. IEEE Trans. Power Syst. 2019, 34, 4606–4616. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Liu, F.; Ye, H.; Zhang, X.; Mei, S.; Chang, N. Robust Coordinated Transmission and Generation Expansion Planning Considering Ramping Requirements and Construction Periods. IEEE Trans. Power Syst. 2018, 33, 268–280. [Google Scholar] [CrossRef]
- Yin, X.; Chen, H.; Liang, Z.; Zhu, Y. A Flexibility-oriented robust transmission expansion planning approach under high renewable energy resource penetration. Appl. Energy 2023, 351, 121786. [Google Scholar] [CrossRef]
- Ni, F.; Nijhuis, M.; Nguyen, P.H.; Cobben, J.F.G. Variance-Based Global Sensitivity Analysis for Power Systems. IEEE Trans. Power Syst. 2018, 33, 1670–1682. [Google Scholar] [CrossRef]
- Fonseca, N.; Neyestani, N.; Soares, F.; Iria, J.; Lopes, M.; Antunes, C.H.; Pinto, D.; Jorge, H. Bottom-up approach to compute der flexibility in the transmission-distribution networks boundary. In Proceedings of the Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2018), Dubrovnik, Croatia, 12–15 November 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Byrne, R.H. Evaluation of Energy Storage Providing Virtual Transmission Capacity. In Proceedings of the 2021 IEEE Power and Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
- IRENA. Virtual Power Lines—Innovation Landscape Brief; IRENA International Renewable Energy: Masdar City, United Arab Emirates, 2020. [Google Scholar]
- Baringo, A.; Baringo, L.; Arroyo, J.M. Holistic planning of a virtual power plant with a nonconvex operational model: A risk-constrained stochastic approach. Int. J. Electr. Power Energy Syst. 2021, 132, 107081. [Google Scholar] [CrossRef]
- Ferreira, T.; Machado, G.; Rego, E.; Esteves, H.; Carvalho, A. Manual de Utilização do Modelo de Otimização da Expansão da Oferta de Energia Elétrica—Modelo PLANEL. 2022. Available online: https://www.epe.gov.br/sites-pt/publicacoes-dados-abertos/publicacoes/PublicacoesArquivos/publicacao-227/topico-563/NT_PR_004.22_Manual%20PLANEL.pdf (accessed on 29 January 2025).
- Ding, T.; Yang, Q.; Liu, X.; Huang, C.; Yang, Y.; Wang, M.; Blaabjerg, F. Duality-Free Decomposition Based Data-Driven Stochastic Security-Constrained Unit Commitment. IEEE Trans. Sustain. Energy 2019, 10, 82–93. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, C.; Gong, K.; Si, R.; Shao, H.; Liu, W. Data-driven distributionally robust economic dispatch for distribution network with multiple microgrids. IET Gener. Transm. Distrib. 2020, 14, 5712–5719. [Google Scholar] [CrossRef]
- Zeng, B.; Zhao, L. Solving two-stage robust optimization problems using a column-and-constraint generation method. Oper. Res. Lett. 2013, 41, 457–461. [Google Scholar] [CrossRef]
- Erseghe, T. Distributed Optimal Power Flow Using ADMM. IEEE Trans. Power Syst. 2014, 29, 2370–2380. [Google Scholar] [CrossRef]
- Kar, R.S.; Miao, Z.; Zhang, M.; Fan, L. ADMM for nonconvex AC optimal power flow. In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, X.; Conejo, A.J. Robust Transmission Expansion Planning Representing Long- and Short-Term Uncertainty. IEEE Trans. Power Syst. 2018, 33, 1329–1338. [Google Scholar] [CrossRef]
- Zhao, L.; Zeng, B. Robust unit commitment problem with demand response and wind energy. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Mahroo, R.; Kargarian, A.; Mehrtash, M.; Conejo, A.J. Robust Dynamic TEP with an Security Criterion: A Computationally Efficient Model. IEEE Trans. Power Syst. 2023, 38, 912–920. [Google Scholar] [CrossRef]
- Zhao, C.; Guan, Y. Data-Driven Stochastic Unit Commitment for Integrating Wind Generation. IEEE Trans. Power Syst. 2016, 31, 2587–2596. [Google Scholar] [CrossRef]
- Bagheri, A.; Wang, J.; Zhao, C. Data-Driven Stochastic Transmission Expansion Planning. IEEE Trans. Power Syst. 2017, 32, 3461–3470. [Google Scholar] [CrossRef]
- ENTSOE. Electricity Generation, Transportation and Consumption Data and Information for the Pan-European Market. 2024. Available online: https://transparency.entsoe.eu/dashboard/show (accessed on 29 January 2025).
- Ferreira, F. UFPR—Data Repository. 2022. Available online: https://github.com/Falferreira/Phd_Files.git (accessed on 29 January 2025).
- Rider, M.J. Planejamento da Expansão de Sistemas de Transmissão Usando os Modelos CC—CA e Técnicas de Programação Não—Linear. Ph.D. Thesis, University of Campinas, São Paulo, Brazil, 2006. [Google Scholar]
- Barrows, C.; Bloom, A.; Ehlen, A.; Ikäheimo, J.; Jorgenson, J.; Krishnamurthy, D.; Lau, J.; McBennett, B.; O’Connell, M.; Preston, E.; et al. The IEEE Reliability Test System: A Proposed 2019 Update. IEEE Trans. Power Syst. 2020, 35, 119–127. [Google Scholar] [CrossRef]
- Goerigk, M.; Khosravi, M. Optimal scenario reduction for one- and two-stage robust optimization with discrete uncertainty in the objective. Eur. J. Oper. Res. 2023, 310, 529–551. [Google Scholar] [CrossRef]
- Ayres, D.; Zamora, L. Renewable Power Generation Costs in 2023; IRENA: Masdar City, United Arab Emirates, 2024; p. 211. [Google Scholar]
- Zobaa, A.F.; Ribeiro, P.F.; Aleem, S.H.A.; Afifi, S.N. Energy Storage at Different Voltage Levels: Technology, Integration, and Market Aspects; Institution of Engineering and Technology: London, UK, 2018; Volume 111. [Google Scholar]
| Ref 1 | GEP 2 | TEP 3 | UC 4 | VPP 5 | VPL 6 | Flx 7 | Gen Flx 8 | DR E Flx 9 | DR C Flx 10 | T Scale 11 | VRE 12 | Cong 13 | AC 14 | DC 15 | Sen 16 | Static 17 | Dynamic 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [23] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||||
| [24] | ✔ | ✔ | ✔ | ✔ | |||||||||||||
| [25] | ✔ | ✔ | ✔ | ||||||||||||||
| [26] | ✔ | ||||||||||||||||
| [27] | ✔ | ||||||||||||||||
| [28] | ✔ | ✔ | ✔ | ||||||||||||||
| [29] | ✔ | ✔ | ✔ | ||||||||||||||
| [30] | ✔ | ✔ | ✔ | ||||||||||||||
| [31] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||
| [32] | ✔ | ✔ | ✔ | ✔ | |||||||||||||
| [33] | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||||
| [34] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||
| [35] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||
| [36] | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||||
| [37] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||||
| [7] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||||
| [10] | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||||
| [9] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||||
| [8] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||
| [38] | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||||
| [39] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||||
| [40] | ✔ | ✔ | |||||||||||||||
| [6] | ✔ | ✔ | ✔ | ||||||||||||||
| [41] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||||
| [29] | ✔ | ✔ | ✔ | ||||||||||||||
| [42] | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||
| [43] | ✔ | ✔ | ✔ | ✔ | |||||||||||||
| [44] | ✔ | ✔ | ✔ | ✔ | |||||||||||||
| [45] | ✔ | ✔ | ✔ | ||||||||||||||
| [46] | ✔ | ✔ | ✔ | ✔ | |||||||||||||
| [47] | ✔ | ✔ | ✔ | ||||||||||||||
| [48] | ✔ | ✔ | ✔ | ✔ | |||||||||||||
| [49] | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||||
| [50] | ✔ | ✔ | ✔ | ✔ | |||||||||||||
| [51] | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||||
| [52] | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||||
| [53] | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||||
| [54] | ✔ | ||||||||||||||||
| Proposed model | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ |
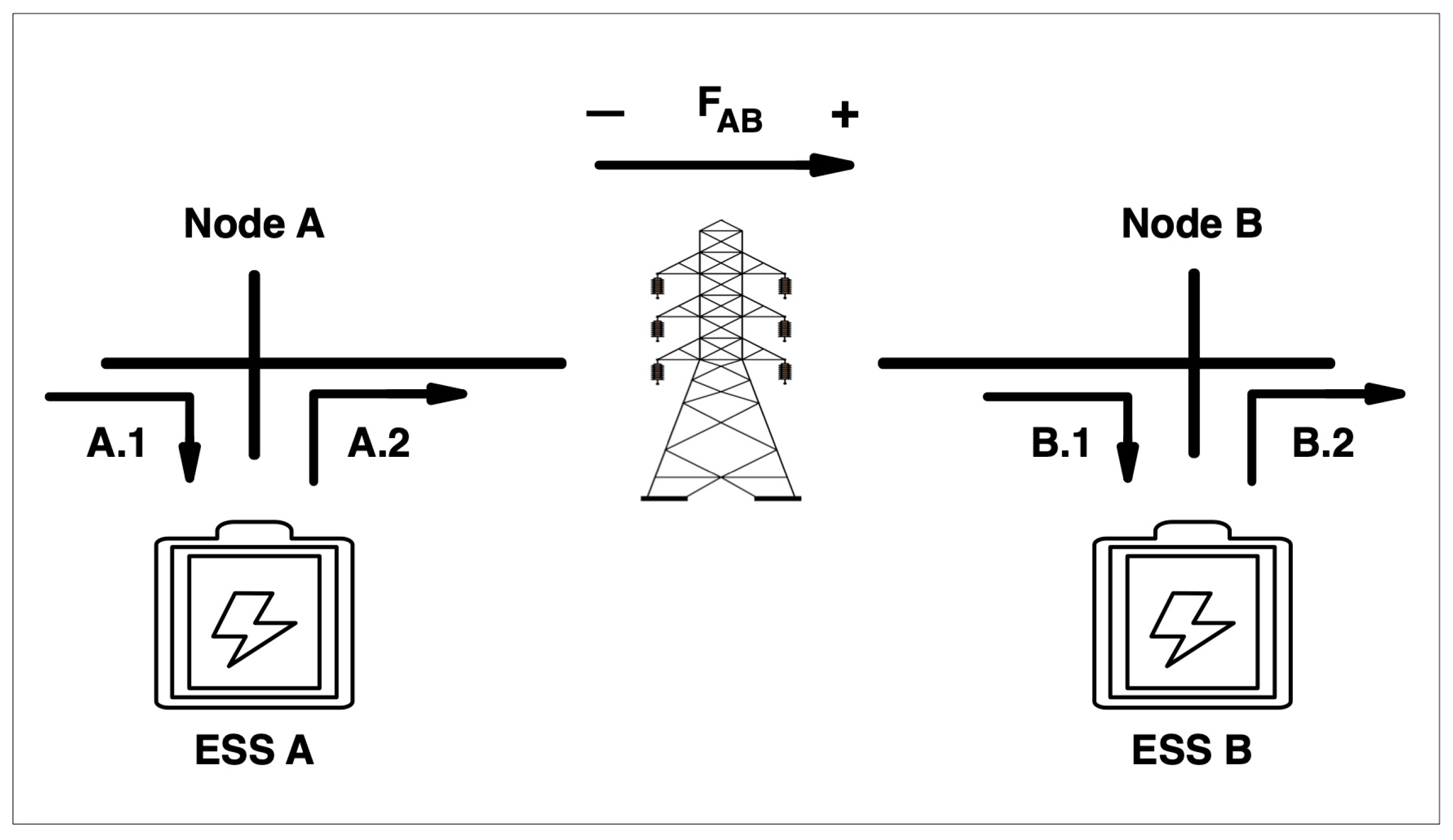
| Demand Side Fij (+) | Supply Side Fij (−) | |
|---|---|---|
| High grid usage | Discharge | Charge |
| Low grid usage | Charge | Discharge |
| Scenario S1.1 | ||||||
|---|---|---|---|---|---|---|
| New Circuits | VPL | Disp Gen [GW] | Ndisp Gen [GW] | Dem Response [GW] | DSO Flex [GW] | Cost [M$] |
| 2–6 | - | - | - | - | - | 30 |
| 2–6 | - | - | - | - | - | 30 |
| 3–5 | - | - | - | - | - | 20 |
| 4–6 | - | - | - | - | - | 30 |
| - | - | 0.68 | - | - | - | 28.2 |
| Total | 138.2 | |||||
| Scenario S1.2 | ||||||
|---|---|---|---|---|---|---|
| New Circuits | VPL | Disp Gen [GW] | Ndisp Gen [GW] | Dem Response [GW] | DSO Flex [GW] | Cost [M$] |
| 2–6 | - | - | - | - | - | 30 |
| - | 2–6 | - | - | - | - | 27.5 |
| 3–5 | - | - | - | - | - | 20 |
| - | 4–6 | - | - | - | - | 27.5 |
| - | - | 0.68 | - | - | - | 28.2 |
| Total | 133.2 | |||||
| Scenario S1.3 | ||||||
|---|---|---|---|---|---|---|
| New Circuits | VPL | Disp Gen [GW] | Ndisp Gen [GW] | Dem Response [GW] | DSO Flex [GW] | Cost [M$] |
| 2–6 | - | - | - | - | - | 30 |
| - | 2–6 | - | - | - | - | 18.75 |
| - | 3–5 | - | - | - | - | 18.75 |
| - | 4–6 | - | - | - | - | 18.75 |
| - | - | 0.68 | - | - | - | 28.2 |
| Total | 114.45 | |||||
| Scenario S2.1 | ||||||
|---|---|---|---|---|---|---|
| New Circuits | VPL | Disp Gen [GW] | Ndisp Gen [GW] | Dem Response [GW] | DSO Flex [GW] | Cost [M$] |
| 15–24 | - | - | - | - | - | 99.8 |
| 55–56 | - | - | - | - | - | 39.3 |
| 59–61 | - | - | - | - | - | 24.9 |
| 58–60 | - | - | - | - | - | 14.7 |
| - | - | 8.2 | - | - | - | 348 |
| Total | 526.7 | |||||
| Scenario S2.2 | ||||||
|---|---|---|---|---|---|---|
| New Circuits | VPL | Disp Gen [GW] | Ndisp Gen [GW] | Dem Response [GW] | DSO Flex [GW] | Cost [M$] |
| - | 15–24 | - | - | - | - | 37.5 |
| - | 55–56 | - | - | - | - | 37.5 |
| 59–61 | - | - | - | - | - | 24.9 |
| 58–60 | - | - | - | - | - | 14.7 |
| - | - | 8.2 | - | - | - | 348 |
| Total | 462.6 | |||||
| Scenario S2.3 | ||||||
|---|---|---|---|---|---|---|
| New Circuits | VPL | Disp Gen [GW] | Ndisp Gen [GW] | Dem Response [GW] | DSO Flex [GW] | Cost [M$] |
| - | 15–24 | - | - | - | - | 22.5 |
| - | 55–56 | - | - | - | - | 22.5 |
| - | 59–61 | - | - | - | - | 22.5 |
| 58–60 | - | - | - | - | - | 14.7 |
| - | - | 8.2 | - | - | - | 338 |
| Total | 420.2 | |||||
| Scenario S2.4 | ||||||
|---|---|---|---|---|---|---|
| New Circuits | VPL | Disp Gen [GW] | Ndisp Gen [GW] | Dem Response [GW] | DSO Flex [GW] | Cost [M$] |
| - | 15–24 | - | - | - | - | 37.5 |
| - | 55–56 | - | - | - | - | 37.5 |
| 59–61 | - | - | - | - | - | 24.9 |
| 58–60 | - | - | - | - | - | 14.7 |
| - | - | 5.05 | 1.1 | 2.05 | 0.615 | 282.76 |
| Total | 397.36 | |||||
| Scenario | Average Line Usage [p.u.] | Line Losses [p.u. h] | LMP Average [$] |
|---|---|---|---|
| S2.1 | 0.968 | 450.3 | 1001.3 |
| S2.2 | 1.167 | 447.4 | 981.1 |
| S2.3 | 1.185 | 443.0 | 731.5 |
| S2.4 | 1.196 | 440.5 | 66.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, F.A.L.; Unsihuay-Vila, C.; Núñez-Rodríguez, R.A. Transmission and Generation Expansion Planning Considering Virtual Power Lines/Plants, Distributed Energy Injection and Demand Response Flexibility from TSO-DSO Interface. Energies 2025, 18, 1602. https://doi.org/10.3390/en18071602
Ferreira FAL, Unsihuay-Vila C, Núñez-Rodríguez RA. Transmission and Generation Expansion Planning Considering Virtual Power Lines/Plants, Distributed Energy Injection and Demand Response Flexibility from TSO-DSO Interface. Energies. 2025; 18(7):1602. https://doi.org/10.3390/en18071602
Chicago/Turabian StyleFerreira, Flávio Arthur Leal, Clodomiro Unsihuay-Vila, and Rafael A. Núñez-Rodríguez. 2025. "Transmission and Generation Expansion Planning Considering Virtual Power Lines/Plants, Distributed Energy Injection and Demand Response Flexibility from TSO-DSO Interface" Energies 18, no. 7: 1602. https://doi.org/10.3390/en18071602
APA StyleFerreira, F. A. L., Unsihuay-Vila, C., & Núñez-Rodríguez, R. A. (2025). Transmission and Generation Expansion Planning Considering Virtual Power Lines/Plants, Distributed Energy Injection and Demand Response Flexibility from TSO-DSO Interface. Energies, 18(7), 1602. https://doi.org/10.3390/en18071602






