Optimal Protection Coordination for Grid-Connected and Islanded Microgrids Assisted by the Crow Search Algorithm: Application of Dual-Setting Overcurrent Relays and Fault Current Limiters
Abstract
1. Introduction
- How can a comprehensive two-stage framework improve both the planning and protection coordination of microgrids to enhance reliability and efficiency?
- What advantages do advanced optimization techniques, such as the Crow Search Algorithm, offer in improving protection schemes for both grid-connected and islanded microgrid operations?
- How does the proposed framework compare to conventional methods in terms of relay operation time, energy loss reduction, and voltage stability under varying operating conditions?
2. Literature Review
- Development of a stochastic OPC approach for grid-connected and islanded MGs, incorporating the use of DSORs and FCLs for optimal protection coordination.
- Establishment of a reliable islanded MG through the optimal expansion planning of DGs and ESSs, with the careful consideration of energy demand, operational limits, and cost minimization.
- Implementation of a robust and secure solver for large-scale optimization problems, ensuring minimal standard deviation in the results and improving the reliability of the system.
- Enhancement of OPC for DSORs by incorporating real-time daily data on load, generation, and storage parameters, allowing for dynamic adjustments that reflect the actual operational conditions of the MG.
- Evaluation of OPC strategies that account for DGs and ESSs with optimal locations and sizes, addressing a key limitation in prior research that often relied on fixed sizes and locations for these components.
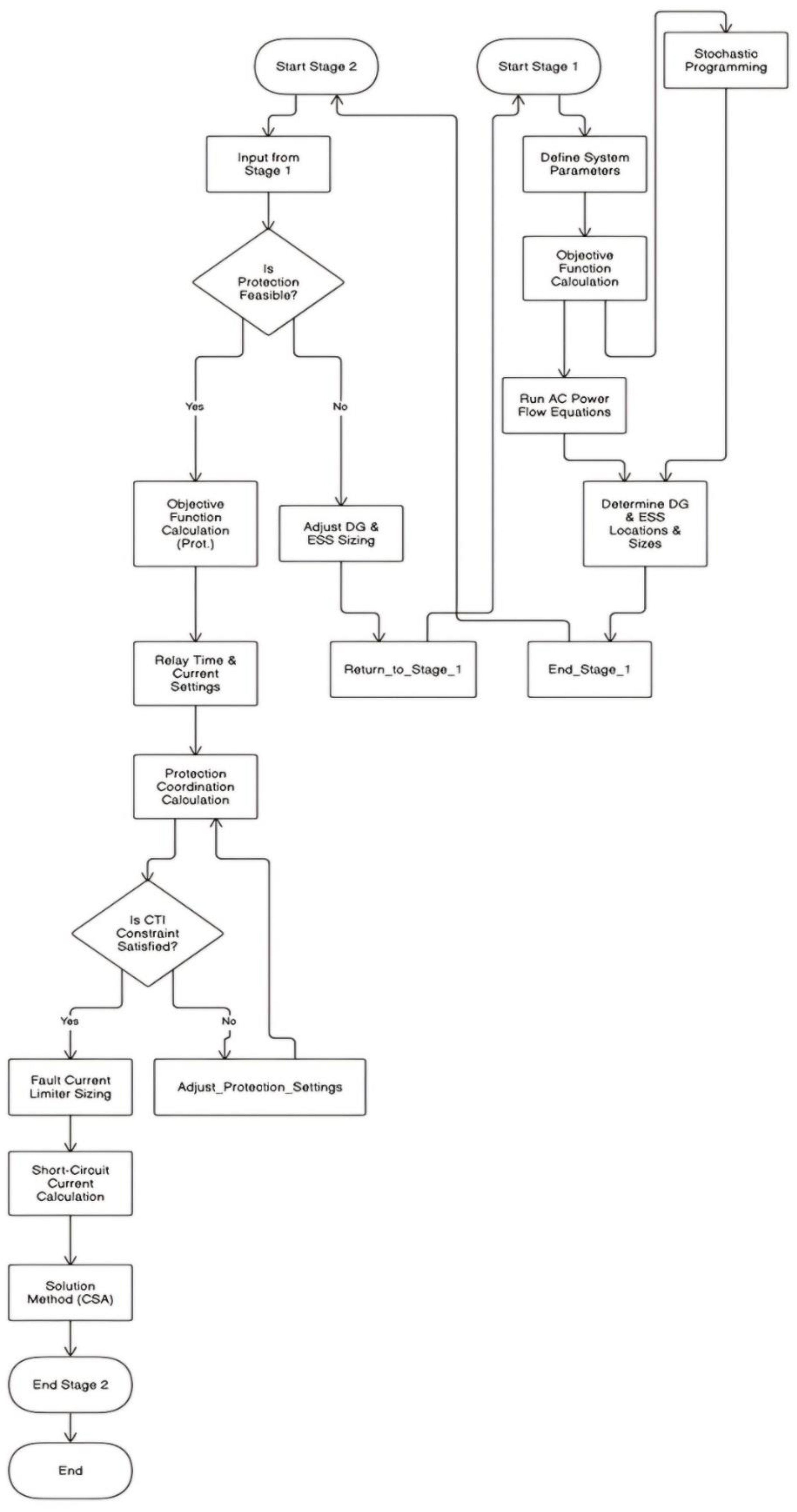
3. Proposed Problem Model
- How can a comprehensive two-stage framework improve both the planning and protection coordination of microgrids to enhance reliability and efficiency?
- What advantages do advanced optimization techniques, such as the Crow Search Algorithm, offer in improving protection schemes for both grid-connected and islanded microgrid operations?
- How does the proposed framework compare to conventional methods in terms of relay operation time, energy loss reduction, and voltage stability under varying operating conditions?
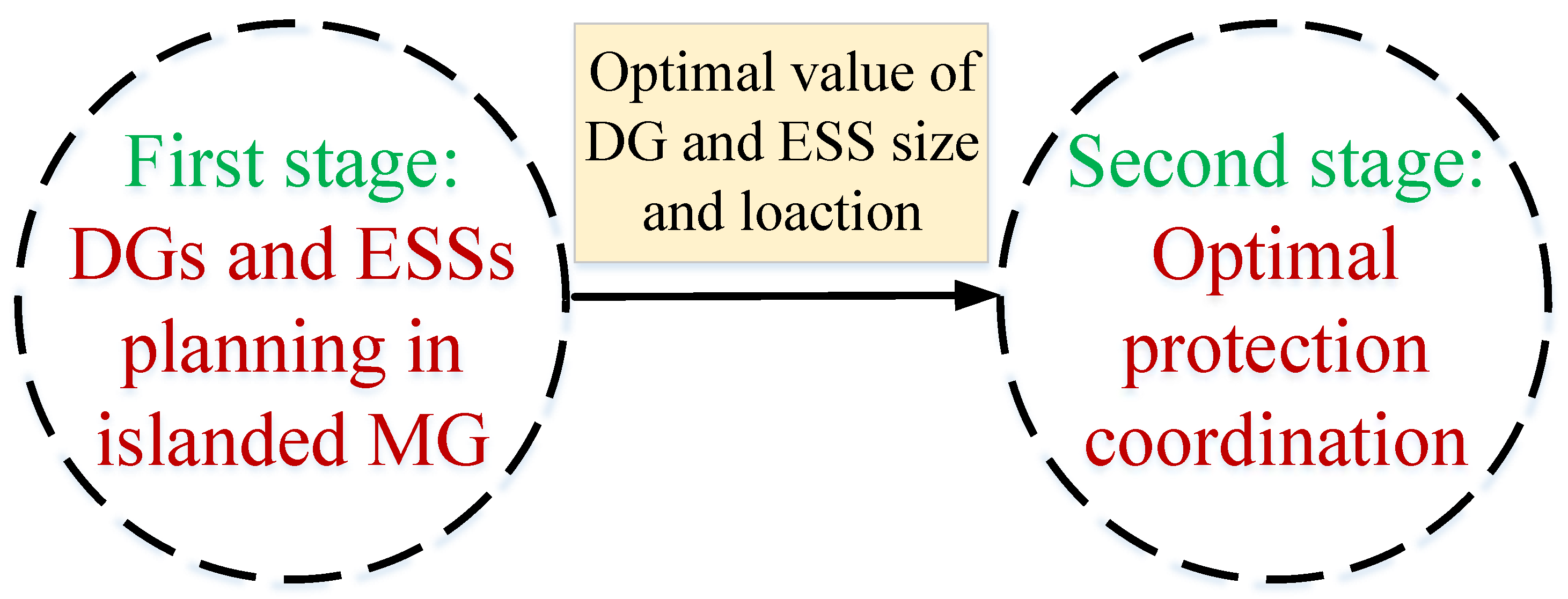
3.1. Optimal Location and Sizing of the Islanded MG Power Sources (First Stage)
3.1.1. Objective Function
3.1.2. Islanded MG Constraints
3.1.3. DG Constraints
3.1.4. ESS Constraints
3.1.5. Stochastic Programming
3.2. Optimal Protection Coordination (Second Stage)
| Algorithm 1 Short-circuit current calculation |
|
4. Solution Method
| Algorithm 2 Crow Search Algorithm (CSA) |
for i = 1: N Select one of the crow as random (such as j). Define the random value between 0 and 1 for crow-j, i.e. rj. if rj ≥ AP position(i, iteration + 1) = position(i, iteration) + rj × fl × {memory(i, iteration)-position(i, iteration)} Check of the feasibility of position of all crows. else position(i, iteration + 1) = a random value for position between its minimum and maximum values. End end Evaluate the objective function value based on the date of new position. Update the memory of crows. if fitness(position(i, iteration + 1)) is better than fitness(position(i, iteration)) memory(i, iteration + 1) = position(i, iteration + 1) else memory(i, iteration + 1) = memory(i, iteration) end end |
4.1. Initialization
4.2. Fitness Evaluation
4.3. Leader and Personal Best Update
4.4. Position Update (Exploration and Exploitation)
4.5. Boundary Check
4.6. Leader Update
4.7. Stopping Criterion
- Stage One: In the first stage, CSA helped determine the optimal locations and sizes for DGs and ESSs. The algorithm explored different configurations, balancing investment costs with operational expenses and ensuring that the system operates efficiently even under varying load and generation conditions. Using stochastic programming, CSA handled the uncertainties in load demand and DG power generation by considering different possible scenarios.
- Stage Two: In the second stage, CSA focused on optimizing protection coordination. This involves fine-tuning the settings for DSORs and FCLs to minimize the operating time of these devices while ensuring that the system met critical coordination and protection constraints. The algorithm seeks the optimal balance between quick fault detection and system stability, updating the positions of crows to reflect the most efficient protection settings.
5. Numerical Results
- Fault currents: Larger systems might have more dispersed fault currents, requiring different relay settings.
- Relay coordination: More relays in a complex network might lead to longer computation times and stricter coordination constraints.
- Energy loss and voltage profile: Larger networks may experience higher losses and more voltage variations, influencing optimal DG and ESS placement.
5.1. 9-Bus Radial MG
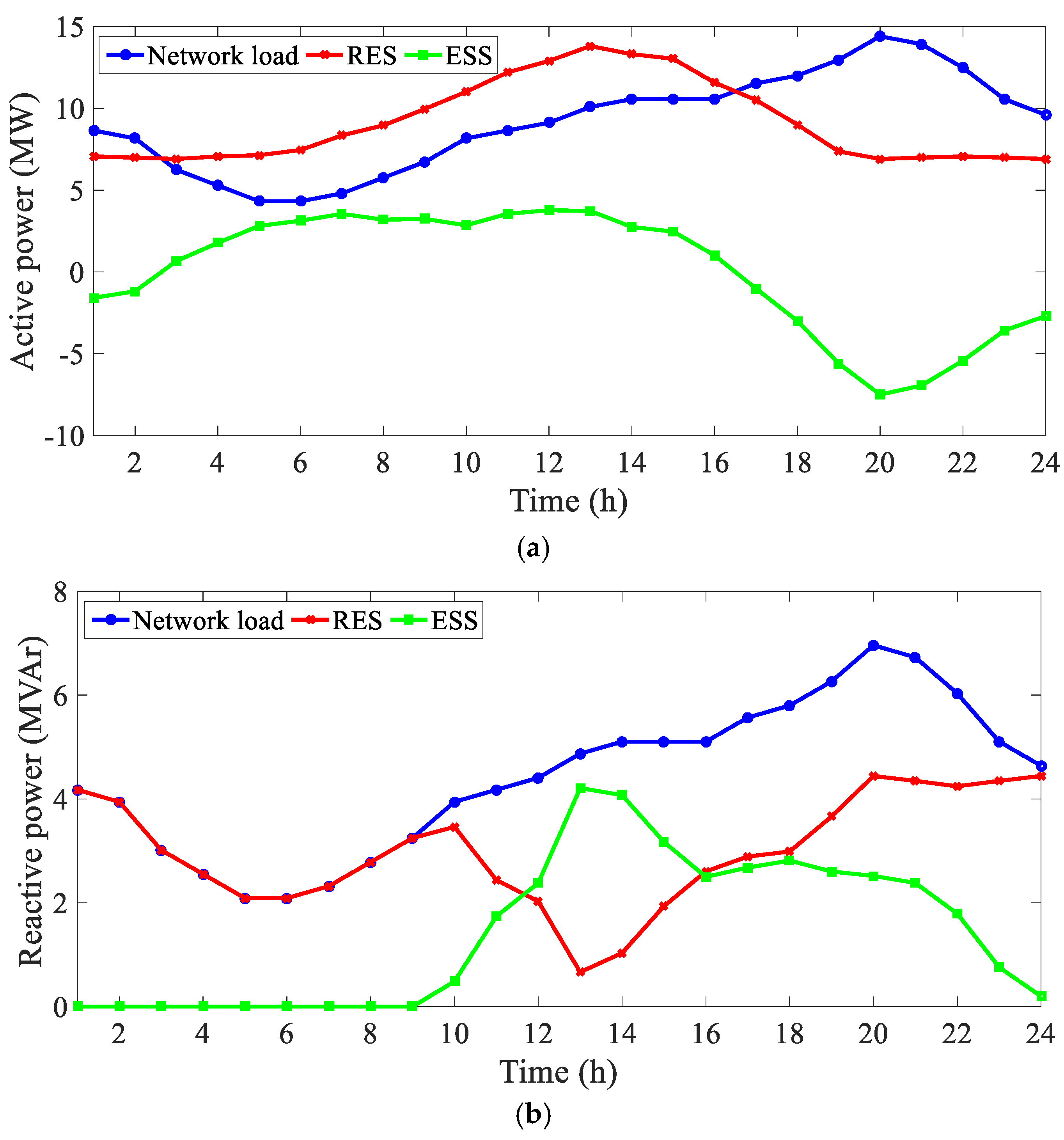
5.1.1. DG and ESS Planning in the Islanded MG
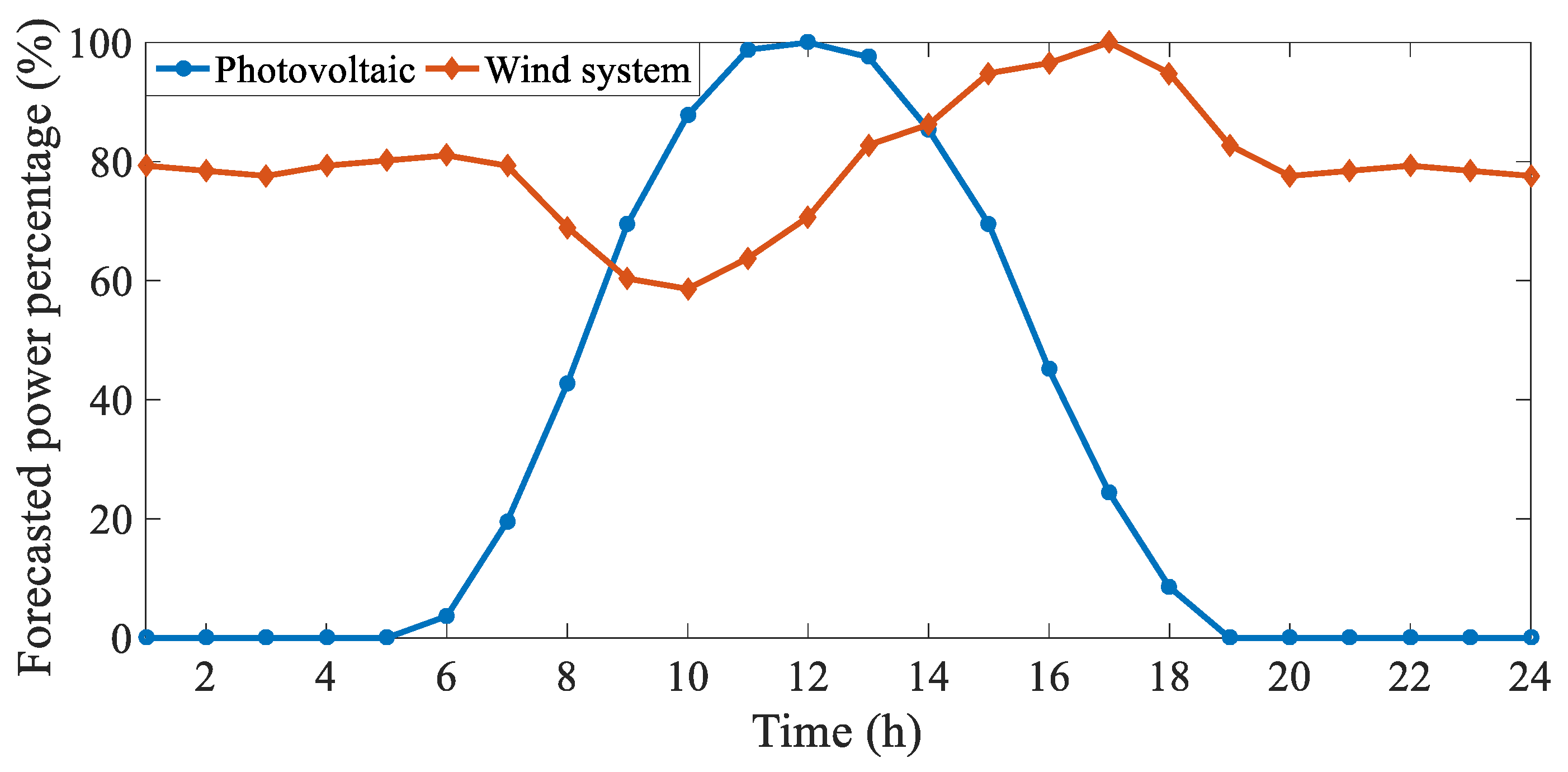
- Historical data: The forecasted power output of PV and wind turbines was derived from real-world data sources referenced in the study of [15].
- Seasonal variations: The profiles account for daily fluctuations in solar irradiation and wind speeds, ensuring a realistic energy generation pattern.
- Load matching: The profiles were adjusted to match the MG’s expected daily load demand and minimize surplus energy waste.
- Stochastic modeling: The uncertainty in renewable energy generation was modeled using the scenario-based stochastic programming (SBSP) approach, ensuring that forecast variations were accurately represented.
5.1.2. Optimal Protection Coordination
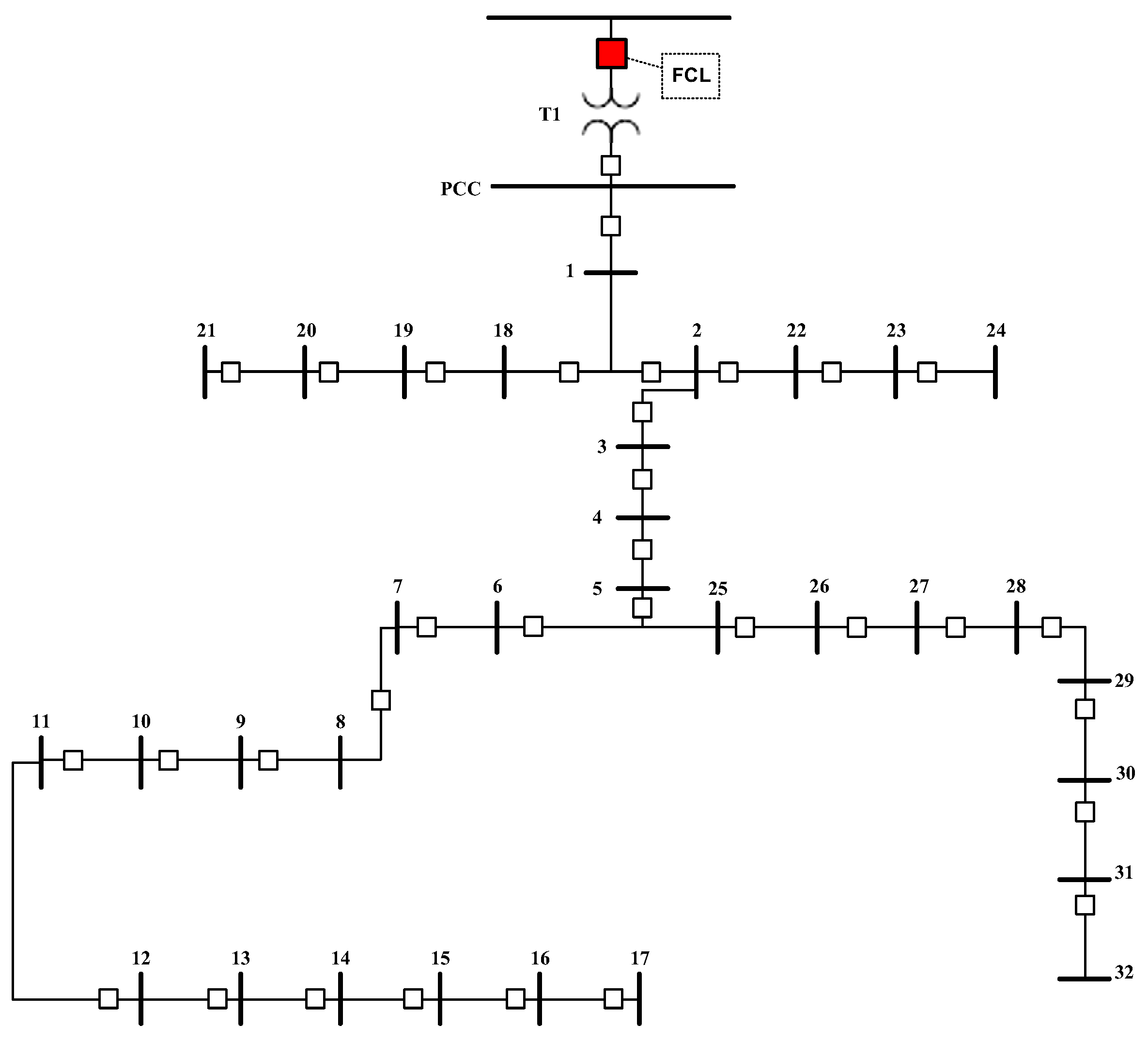
5.2. 32-Bus Radial MG
6. Discussion
- MG reliability: Similar studies on industrial MGs have shown that integrating FCLs enhances network protection by limiting short-circuit currents, consistent with the findings in this study.
- Operational efficiency: The reduction in total relay operating time aligns with practical MG setups where optimized relay coordination reduces unnecessary tripping and enhances system stability.
- Scalability considerations: Larger MGs, such as those deployed in smart industrial parks or university campuses, may require additional computational effort due to increased relay and DG complexity.
7. Conclusions
Future Studies
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Symbols
| c, C | Index and set of MG operating mode, i.e., grid-connected and islanded |
| i, I | Index and set of the DSOR |
| j, J | Index and set of the fault location |
| k, K | Index and set of the backup protection of the DSOR |
| n, l, N, NRES | Index of the bus and line, set of the bus and RES location |
| n (j) | The virtual bus corresponding to the fault location j |
| t, ST | Index and set of the simulation time |
| w, S | Index and set of the scenario sample |
| CDG, CES | Optimal DG and ESS capacity size (p.u) |
| Cost | Summation of the annual investment and operation cost (USD) |
| E | The stored energy of the ESS (p.u) |
| IP_fw, IP_rv | Forward and reverse pickup current setting of the DSOR (p.u) |
| Isc | Short-circuit current (p.u) |
| PDG, QDG | Active and reactive power of DG (p.u) |
| PESch, PESdch, QES | Charging and discharging active power and reactive power of the ESS (p.u) |
| PL, QL | Active and reactive power flow of the line (p.u) |
| PS, QS | Active and reactive power of the MG station (upstream network) (p.u) |
| ZDG | The impedance of the DG (p.u.) |
| Z | Impedance matrices of the network |
| κ | Impedance–capacity curve factor of the SDG |
| V, θ | Voltage magnitude (p.u) and voltage angles (rad) |
| T | Total operating time of all DSORs (s) |
| TDSfw, TDSrv | Forward and reverse time dial setting of DSORs (s) |
| tB_re | Operating time of the DSOR in reverse setting when it acts in backup protection (s) |
| tP_fw | Operating time of the DSOR in forward setting when it acts in primary protection (s) |
| XFCL | Optimal reactance size of the FCL (p.u) |
| AL | Incidence matrix of bus line based on the current direction |
| , | Maximum capacity size of DG and the ESS (p.u) |
| CTI | Coordination time interval |
| g, b | Conductance and susceptance of a line (p.u) |
| ICDG, ICES | Annual investment cost of the DG and ESS (USD/p.u/year) |
| , | Minimum and maximum value of pickup current setting of the DSOR (p.u) |
| PD, QD | Active and reactive load (p.u) |
| Maximum RES active power (p.u) | |
| SLmax | Maximum capacity of a line (p.u) |
| , | Minimum and maximum time dial setting of the DSOR (s) |
| Vmin, Vmax | Minimum and maximum voltage magnitude (p.u) |
| Maximum reactance size of the FCL | |
| α | Rate between the minimum energy of ESS and CES |
| β | Rate between ESS charger capacity and CES |
| ε | Rate of islanded MG overloading providing by DG and ESS |
| ηch, ηdch | Charging and discharging efficiency of the ESS without unit |
| λ | Operation price of DG (USD/p.u) |
| π | Probability of the scenario |
| ρch, ρdch | Charging and discharging operation cost of the ESS (USD/p.u) |
| τ | Time charging of the ESS (hour) |
References
- Tejeswini, M.V.; Raglend, I.J.; Yuvaraja, T.; Radha, B.N. An advanced protection coordination technique for solar in-feed distribution systems. Ain Shams Eng. J. 2019, 10, 379–388. [Google Scholar]
- Chabanloo, R.M.; Maleki, M.G.; Agah, S.M.M.; Habashi, E.M. Comprehensive coordination of radial distribution network protection in the presence of synchronous distributed generation using fault current limiter. Int. J. Electr. Power Energy Syst. 2018, 99, 214–224. [Google Scholar]
- Bukar, A.L.; Tan, C.W. A review on stand-alone photovoltaic-wind energy system with fuel cell: System optimization and energy management strategy. J. Clean. Prod. 2019, 221, 73–88. [Google Scholar] [CrossRef]
- Sharaf, H.M.; Zeineldin, H.H.; El-Saadany, E. Protection Coordination for Microgrids with Grid-Connected and Islanded Capabilities Using Communication Assisted Dual Setting Directional Overcurrent Relays. IEEE Trans. Smart Grid 2018, 9, 143–151. [Google Scholar]
- Aghdam, T.S.; Karegar, H.K.; Zeineldin, H.H. Optimal Coordination of Double-Inverse Overcurrent Relays for Stable Operation of DGs. IEEE Trans. Ind. Inform. 2019, 15, 183–192. [Google Scholar]
- Shad, H.; Gandomkar, M.; Nikoukar, J. Analysis the securable operation and protection coordination indices on multi-objective sitting and sizing of synchronous distributed generations on distribution networks. IET Gener. Transm. Distrib. 2022, 17, 2169–2181. [Google Scholar]
- Aghdam, T.S.; Karegar, H.K.; Zeineldin, H.H. Transient Stability Constrained Protection Coordination for Distribution Systems with DG. IEEE Trans. Smart Grid 2018, 9, 5733–5741. [Google Scholar]
- Najy, W.K.A.; Zeineldin, H.H.; Woon, W.L. Optimal Protection Coordination for Microgrids with Grid-Connected and Islanded Capability. IEEE Trans. Ind. Electron. 2013, 60, 1668–1677. [Google Scholar]
- Alkaran, D.S.; Vatani, M.R.; Sanjari, M.J.; Gharehpetian, G.B.; Naderi, M.S. Optimal Overcurrent Relay Coordination in Interconnected Networks by Using Fuzzy-Based GA Method. IEEE Trans. Smart Grid 2018, 9, 3091–3101. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. MOPSO/FDMT-based Pareto-optimal solution for coordination of overcurrent relays in interconnected networks and multi-DER microgrids. IET Gener. Transm. Distrib. 2018, 12, 2871–2886. [Google Scholar]
- Zhang, C.; Xu, Y.; Dong, Z.Y. Probability-Weighted Robust Optimization for Distributed Generation Planning in Microgrids. IEEE Trans. Power Syst. 2018, 33, 7042–7051. [Google Scholar] [CrossRef]
- Khanavandi, H.A.; Gandomkar, M.; Nikoukar, J. Resiliency planning of distribution network using of active distribution network partitioning. Heliyon. 2024, 10, e36422. [Google Scholar] [CrossRef] [PubMed]
- Khanavandi, H.A.; Gandomkar, M.; Nikoukar, J. Optimal planning and partitioning of multiple distribution Micro-Grids based on reliability evaluation. PLoS ONE 2014, 19, e0305745. [Google Scholar] [CrossRef] [PubMed]
- Tanha, M.H.; Gandomkar, M.; Nikoukar, J. Coordination of protection and operation in micro-grids with inverter based distributed generation using SAOA. PLoS ONE 2024, 19, e0311584. [Google Scholar] [CrossRef]
- Maleki, A.; Askarzadeh, A. Optimal sizing of a PV/wind/diesel system with battery storage for electrification to an off-grid remote region: A case study of Rafsanjan, Iran. Sustain. Energy Technol. Assess. 2014, 7, 147–153. [Google Scholar]
- Arya, Y. Impact of ultra-capacitor on automatic generation control of electric energy systems using an optimal FFOID controller. Int. J. Energy Res. 2019, 43, 8765–8778. [Google Scholar] [CrossRef]
- Ozbak, M.; Ghazizadeh-Ahsaee, M.; Ahrari, M.; Jahantigh, M.; Mirshekar, S.; Mirmozaffari, M.; Aranizadeh, A. Improving power output wind turbine in micro-grids assisted virtual wind speed prediction. Sustain. Oper. Comput. 2024, 5, 119–130. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Byrne, A.; Nichol, B. A community-centred approach to global health security: Implementation experience of community-based surveillance (CBS) for epidemic preparedness. Glob. Secur. Health Sci. Policy 2020, 5, 71–84. [Google Scholar] [CrossRef]
- Abbasghorbani, M.; Mashhadi, H.R.; Damchi, Y. Reliability-centred maintenance for circuit breakers in transmission networks. IET Gener. Transm. Distrib. 2014, 8, 1583–1590. [Google Scholar] [CrossRef]
- Adewumi, O.B.; Fotis, G.; Vita, V.; Nankoo, D.; Ekonomou, L. The Impact of Distributed Energy Storage on Distribution and Transmission Networks’ Power Quality. Appl. Sci. 2022, 12, 6466. [Google Scholar] [CrossRef]
- Shahbazi, A.; Aghaei, J.; Pirouzi, S.; Niknam, T.; Shafie-khah, M.; Catalão, J.P. Effects of resilience-oriented design on distribution networks operation planning. Electr. Power Syst. Res. 2021, 191, 106902. [Google Scholar] [CrossRef]
- Shahbazi, A.; Aghaei, J.; Pirouzi, S.; Shafie-khah, M.; Catalão, J.P. Hybrid stochastic/robust optimization model for resilient architecture of distribution networks against extreme weather conditions. Int. J. Electr. Power Energy Syst. 2021, 126, 106576. [Google Scholar] [CrossRef]
- Asl, S.A.F.; Gandomkar, M.; Nikoukar, J. Optimal protection coordination in the micro-grid including inverter-based distributed generations and energy storage system with considering grid-connected and islanded modes. Electr. Power Syst. Res. 2020, 184, 106317. [Google Scholar] [CrossRef]
- Ghobadpour, S.; Gandomkar, M.; Nikoukar, J. Determining Optimal Size of Superconducting Fault Current Limiters to Achieve Protection Coordination of Fuse-Recloser in Radial Distribution Networks with Synchronous DGs. Electr. Power Syst. Res. 2020, 185, 106357. [Google Scholar] [CrossRef]
- Elmitwally, A.; Kandil, M.S.; Gouda, E.; Amer, A. Mitigation of DGs Impact on Variable-Topology Meshed Network Protection System by Optimal Fault Current Limiters Considering Overcurrent Relay Coordination. Electr. Power Syst. Res. 2020, 186, 106417. [Google Scholar] [CrossRef]
- Farzinfar, M.; Jazaeri, M. A novel methodology in optimal setting of directional fault current limiter and protection of the MG. Int. J. Electr. Power Energy Syst. 2020, 116, 105564. [Google Scholar] [CrossRef]
- Pirouzi, S.; Aghaei, J.; Vahidinasab, V.; Niknam, T.; Khodaei, A. Robust linear architecture for active/reactive power scheduling of EV integrated smart distribution networks. Electr. Power Syst. Res. 2018, 155, 8–20. [Google Scholar] [CrossRef]
- Pirouzi, S.; Aghaei, J. Mathematical Modeling of Electric Vehicles Contributions in Voltage Security of Smart Distribution Networks. Simul. Trans. Soc. Model. Simul. Int. 2018, 95, 429–439. [Google Scholar]
- Pirouzi, S.; Aghaei, J.; Shafie-khah, M.; Osório, G.J.; Catalão, J.P.S. Evaluating the security of electrical energy distribution networks in the presence of electric vehicles. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Hamidpour, H.; Aghaei, J.; Dehghan, S.; Pirouzi, S.; Niknam, T. Integrated resource expansion planning of wind integrated power systems considering demand response programmes. IET Renew. Power Gener. 2018, 13, 519–529. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Khodaei, A. Efficient integration of plug-in electric vehicles via reconfigurable microgrids. Energy 2016, 111, 653–663. [Google Scholar] [CrossRef]
- Aghaei, J.; Barani, M.; Shafie-khah, M.; AASdl, N.; Catalão, J.P.S. Risk-constrained offering strategy for aggregated hybrid power plant including wind power producer and demand response provider. IEEE Trans. Sustain. Energy 2016, 7, 513–525. [Google Scholar] [CrossRef]
- Sheta, A.N.; Sedhom, B.E.; Eladl, A.A. Comparative framework for AC-microgrid protection schemes: Challenges, solutions, real applications, and future trends. Prot. Control Mod. Power Syst. 2023, 8, 1–40. [Google Scholar] [CrossRef]
- Aranizadeh, A.; Mirmozaffari, M.; Farahani, B.K. Maximizing Wind Turbine Power Generation Through Adaptive Fuzzy Logic Control for Optimal Efficiency and Performance. Wind 2025, 5, 4. [Google Scholar] [CrossRef]

| No. | Aspect | [6] | [12] | [13] | [14] | [22] | [23] | [24] | [25] | [26] | [27] | PS |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Opt. Algorithm | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| 2 | Protection | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| 3 | MG Clustering | ✓ | ✓ | |||||||||
| 4 | MMG | ✓ | ✓ | |||||||||
| 5 | Reliability | ✓ | ||||||||||
| 6 | DG Planning | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| 7 | FCL Planning | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| 8 | Economic | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| 9 | Operation | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| 10 | Security | ✓ | ✓ |
| Parameter | Value |
|---|---|
| Load power (MVA) at peak load time | 2 |
| Load power factor | 0.9 |
| Forecasted load profile (percentage) | Hourly pattern for one day based on [28] |
| Line length (m) | 500 |
| Resistance of line (Ω/km) | 0.1529 |
| Reactance of line (Ω/km) | 0.1406 |
| Transformer characterize | 20 MVA, 115 kV/12.47 kV |
| Maximum reactance size of FCL (Ω) | 6 |
| Minimum and maximum voltage (p.u) | 0.9 and 1.05 [29] |
| Maximum capacity size of DG and ESS (p.u) | 4 MVA and 25 MWh |
| Annual investment cost of DG and ESS ($/p.u/year) | 5000 and 1000 |
| Horizon planning | 5 years |
| Charging and discharging efficiency of ESS | 0.88 |
| α, β, τ, ε | 0.1, 0.5, 2.5 h, 0.1 |
| ρch, ρdch ($/MWh) | 1, 1.5 |
| Device | Location (Bus) | Capacity | Relay Number | Investment Cost (USD) | Expected Operation Cost (USD) |
|---|---|---|---|---|---|
| PV1 | 3 | 3 MVA | R18 | 75,000 | 0 |
| PV2 | 7 | 3 MVA | R19 | 75,000 | 0 |
| WS1 | 3 | 4 MVA | R20 | 100,000 | 0 |
| WS2 | 7 | 4 MVA | R21 | 100,000 | 0 |
| ESS1 | 3 | 21 MWh | R22 | 105,000 | 87,816 |
| ESS2 | 7 | 21 MWh | R23 | 105,000 | 87,816 |
| Total cost (USD) | 560,000 | 175,632 | |||
| Grid-Connected Mode | Islanded Mode | ||
|---|---|---|---|
| Variable | Value | Variable | Value |
| Maximum voltage deviation (p.u) | 0.0073 | Maximum voltage deviation (p.u) | 0.0038 |
| Expected daily energy loss (MWh) | 1.0114 | Expected daily energy loss (MWh) | 0.9435 |
| Fault Location | The Operation Mode of Relays, P: Primary, B: Backup | |||
|---|---|---|---|---|
| P1 | B | P2 | B | |
| F10 | R1 | R10, R17 | R2 | R4 |
| F11 | R3 | R1 | R4 | R6, R18, R20, R22 |
| F12 | R5 | R3, R18, R20, R22 | R6 | R8 |
| F13 | R7 | R5 | R8 | |
| F14 | R9 | R2, R17 | R10 | R12 |
| F15 | R11 | R9 | R12 | R14, R19, R21, R23 |
| F16 | R13 | R11, R19, R21, R23 | R14 | R16 |
| F17 | R15 | R13 | R16 | |
| Relay | TDSfw (s) | TDSrv (s) | IP_fw (p.u) | IP_rv (p.u) |
|---|---|---|---|---|
| R1 | 0.1 | 0.2135 | 0.4648 | 0.4648 |
| R2 | 0.1 | 0.1888 | 0.5155 | 0.5248 |
| R3 | 0.1 | 0.5000 | 0.2597 | 0.2597 |
| R4 | 0.1 | 0.4782 | 0.5350 | 0.5350 |
| R5 | 0.1 | 0.1200 | 0.2058 | 0.2058 |
| R6 | 0.1 | 0.4519 | 0.6783 | 0.6783 |
| R7 | 0.1 | 0.3402 | 0.1000 | 0.1000 |
| R8 | 0.1 | 0.1 | 0.9998 | 0.9998 |
| R9 | 0.1 | 0.4179 | 0.3107 | 0.3107 |
| R10 | 0.1 | 0.2966 | 0.5816 | 0.5816 |
| R11 | 0.1 | 0.1 | 0.4878 | 0.4878 |
| R12 | 0.1 | 0.4959 | 0.3988 | 0.3988 |
| R13 | 0.1 | 0.1 | 0.3057 | 0.3057 |
| R14 | 0.1 | 0.1200 | 0.7129 | 0.7129 |
| R15 | 0.1 | 0.1 | 0.1000 | 0.1000 |
| R16 | 0.1 | 0.3366 | 0.7273 | 0.7273 |
| R17 | 0.1 | 0.3028 | 0.6747 | 0.6747 |
| R18 | 0.1 | 0.4530 | 0.7891 | 0.8561 |
| R19 | 0.1 | 0.3116 | 0.9780 | 0.9780 |
| R20 | 0.1 | 0.4997 | 0.6674 | 0.6674 |
| R21 | 0.1 | 0.4835 | 0.7891 | 0.7891 |
| R22 | 0.1 | 0.3223 | 0.9780 | 0.9780 |
| R23 | 0.1 | 0.1 | 0.6674 | 0.6674 |
| ze of FCL (XFCL) | 1.5212 p.u | |||
| MG Operation Mode | Grid-Connected Mode | Islanded Mode | Both Modes of Operation |
|---|---|---|---|
| Expected total daily relay operation time (s) | 510 | 531.36 | 1041.36 |
| Expected total hourly relay operation time (s) | 21.25 | 22.14 | 43.39 |
| Minimum operation time (s) | 0.1835 | 0.1924 | 0.1835 |
| maximum operation time (s) | 1.9541 | 2.01836 | 2.01836 |
| Device | Bus | Capacity | Relay Number |
|---|---|---|---|
| WS1, ESS1 | 18 | 0.45 MVA, 1.8 MWh | R33, R34 |
| WS2, ESS2 | 22 | 1.1 MVA, 4.8 MWh | R35, R36 |
| WS3, ESS3 | 25 | 0.6 MVA, 2.5 MWh | R37, R38 |
| WS4, ESS4 | 30 | 0.6 MVA, 2.5 MWh | R39, R40 |
| WS5, ESS5 | 6 | 0.7 MVA, 2.8 MWh | R41, R42 |
| WS6, ESS6 | 13 | 0.7 MVA, 2.8 MWh | R43, R44 |
| Total investment cost = USD 194,750. Expected operation cost = USD 56,583. | |||
| MG Operation Mode | Grid-Connected Mode | Islanded Mode | Both Modes of Operation |
|---|---|---|---|
| Expected total daily relay operation time (s) | 578.4 | 652.32 | 1282 |
| Expected total hourly relay operation time (s) | 24.10 | 27.18 | 51.28 |
| Minimum operation time (s) | 0.1336 | 0.1411 | 0.1336 |
| maximum operation time (s) | 1.5372 | 1.6422 | 1.6422 |
| Size of FCL (XFCL) = 1.8735 p.u | |||
| Parameter | Stage 1 | ||
| CSA | GA | PSO | |
| Minimum of the objective function | 226,331 | 257,302 | 249,463 |
| Maximum of the objective function | 226,342 | 257,518 | 249,685 |
| Mean of the objective function | 226,336 | 257,422 | 249,574 |
| Median of the objective function | 226,335 | 257,404 | 249,564 |
| Mode of the objective function | 226,336 | 257,445 | 249,588 |
| Standard deviation the of objective function | 1.13% | 5.33% | 3.74% |
| Parameter | Stage 2 | ||
| CSA | CSA | CSA | |
| Minimum of the objective function | 1280.34 | 1280.34 | 1280.34 |
| Maximum of the objective function | 1285.23 | 1285.23 | 1285.23 |
| Mean of the objective function | 1282.11 | 1282.11 | 1282.11 |
| Median of the objective function | 1281.96 | 1281.96 | 1281.96 |
| Mode of the objective function | 1282.11 | 1282.11 | 1282.11 |
| Standard deviation the of objective function | 1.21% | 1.21% | 1.21% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shad, H.; Amini Khanavandi, H.; Abrisham Foroushan Asl, S.; Aranizadeh, A.; Vahidi, B.; Mirmozaffari, M. Optimal Protection Coordination for Grid-Connected and Islanded Microgrids Assisted by the Crow Search Algorithm: Application of Dual-Setting Overcurrent Relays and Fault Current Limiters. Energies 2025, 18, 1601. https://doi.org/10.3390/en18071601
Shad H, Amini Khanavandi H, Abrisham Foroushan Asl S, Aranizadeh A, Vahidi B, Mirmozaffari M. Optimal Protection Coordination for Grid-Connected and Islanded Microgrids Assisted by the Crow Search Algorithm: Application of Dual-Setting Overcurrent Relays and Fault Current Limiters. Energies. 2025; 18(7):1601. https://doi.org/10.3390/en18071601
Chicago/Turabian StyleShad, Hossien, Hamid Amini Khanavandi, Saeed Abrisham Foroushan Asl, Ali Aranizadeh, Behrooz Vahidi, and Mirpouya Mirmozaffari. 2025. "Optimal Protection Coordination for Grid-Connected and Islanded Microgrids Assisted by the Crow Search Algorithm: Application of Dual-Setting Overcurrent Relays and Fault Current Limiters" Energies 18, no. 7: 1601. https://doi.org/10.3390/en18071601
APA StyleShad, H., Amini Khanavandi, H., Abrisham Foroushan Asl, S., Aranizadeh, A., Vahidi, B., & Mirmozaffari, M. (2025). Optimal Protection Coordination for Grid-Connected and Islanded Microgrids Assisted by the Crow Search Algorithm: Application of Dual-Setting Overcurrent Relays and Fault Current Limiters. Energies, 18(7), 1601. https://doi.org/10.3390/en18071601







