A Dynamic Power Flow Calculation Method for the “Renewable Energy–Power Grid–Transportation Network” Coupling System
Abstract
1. Introduction
- Utilizing the asymmetric characteristics of traction transformers, a dynamic asymmetric nodal admittance matrix for the “renewable energy–power grid–transportation network” coupled system is established.
- A three-phase power balance strategy that considers the single-phase loads of the traction load units and the output of renewable energy sources is proposed.
- The dynamic power flow characteristics of the “renewable energy–power grid–transportation network” coupled system and the mutual influence between the renewable energy sources and traction load units are analyzed.
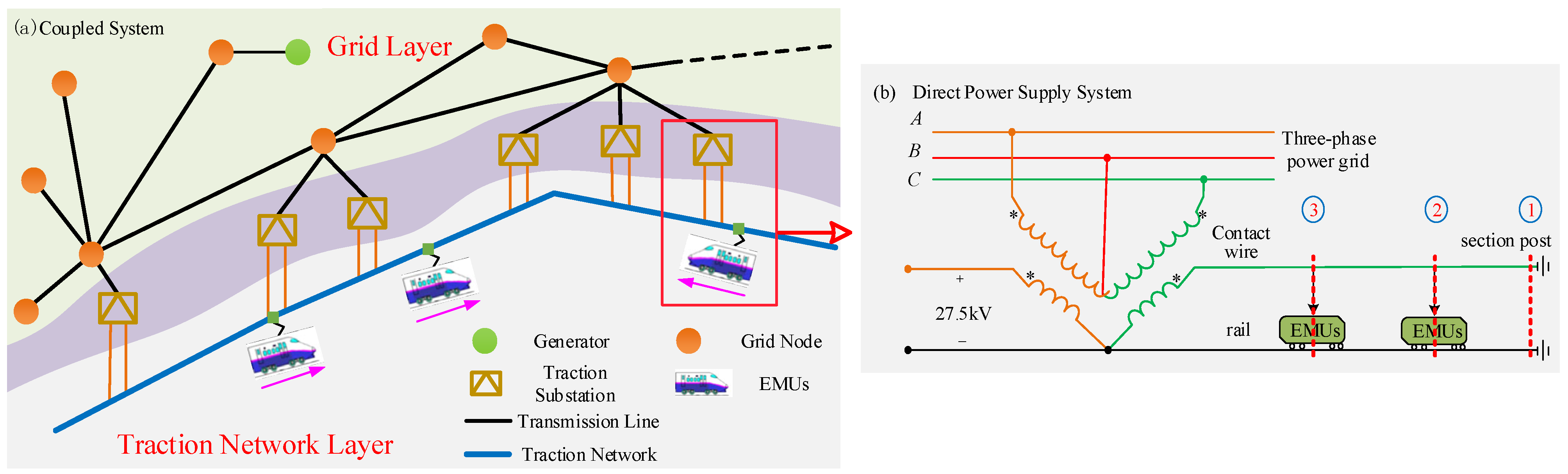
2. Construction of Dynamic Admittance Matrix for the “Renewable Energy–Power Grid–Transportation Network” Coupled System
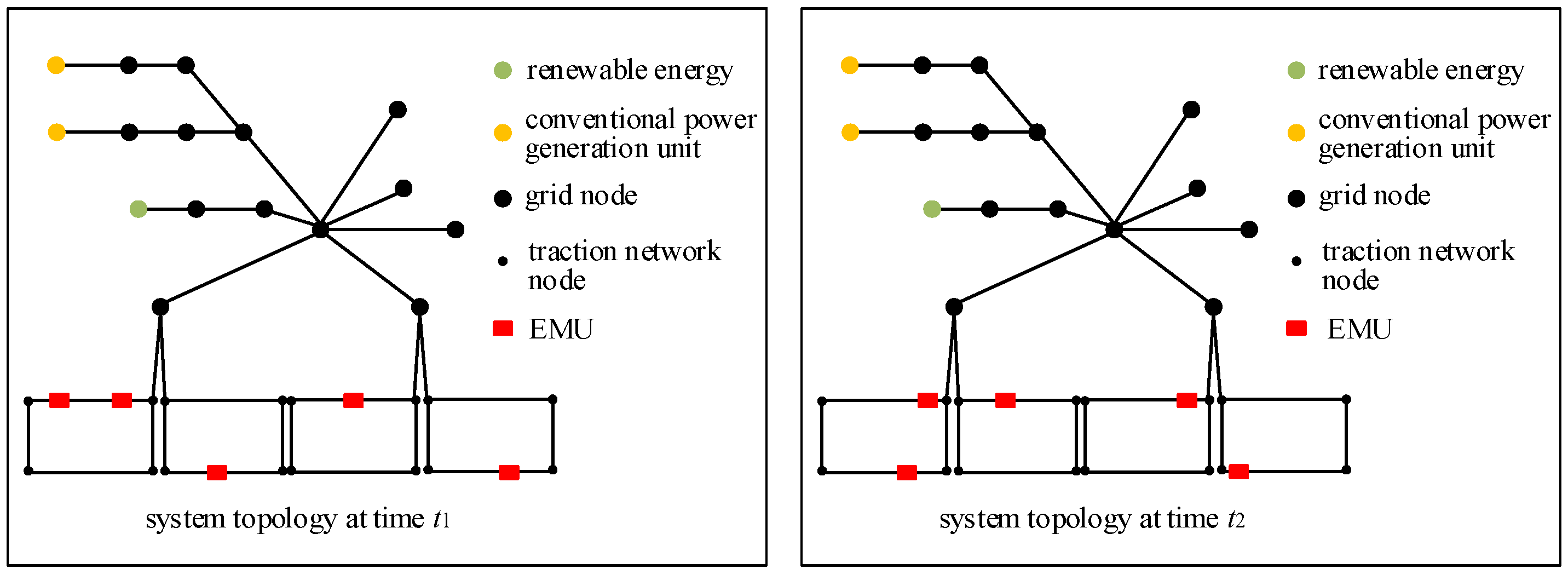
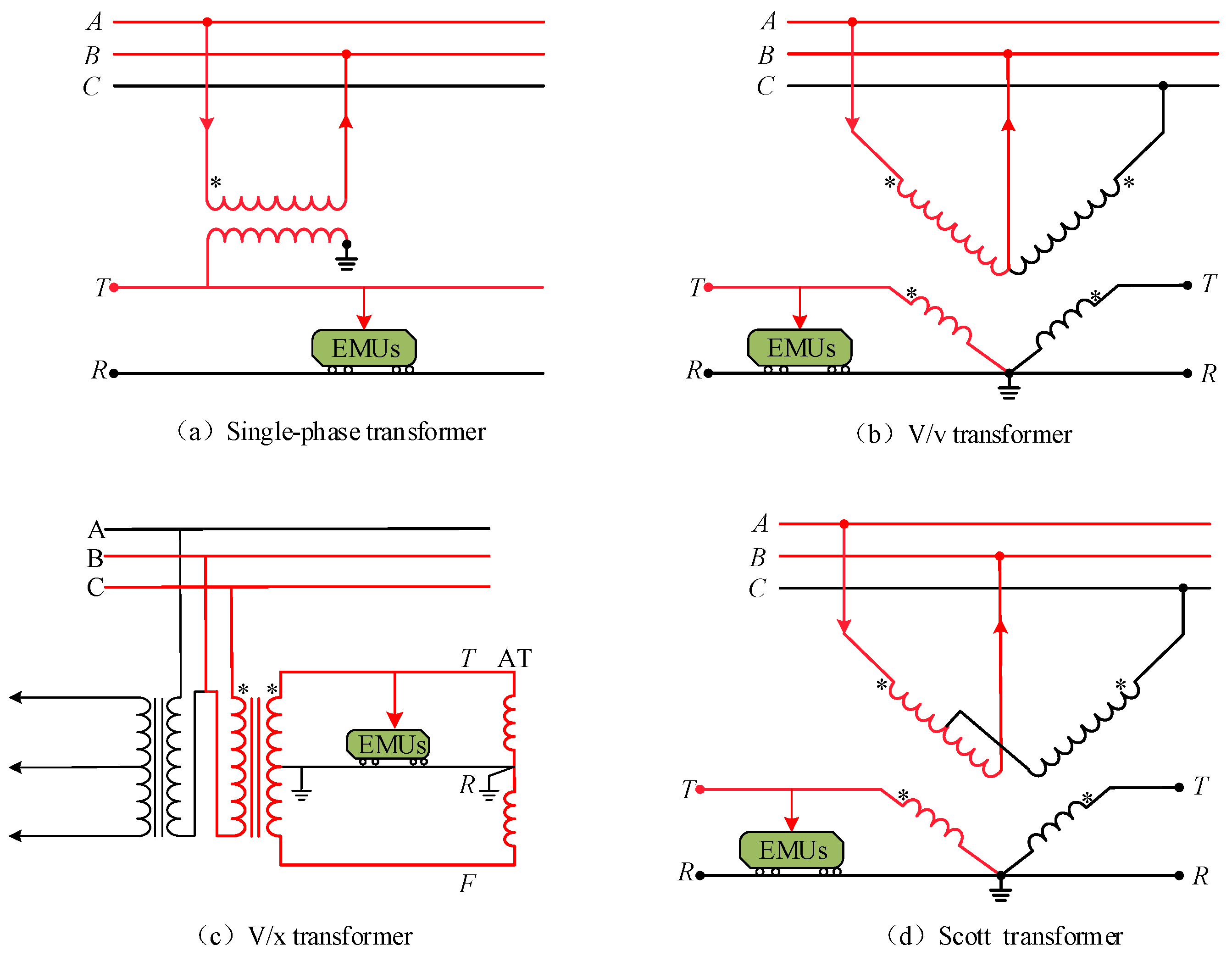
2.1. Construction of Dynamic Topological Structure for the Coupled System
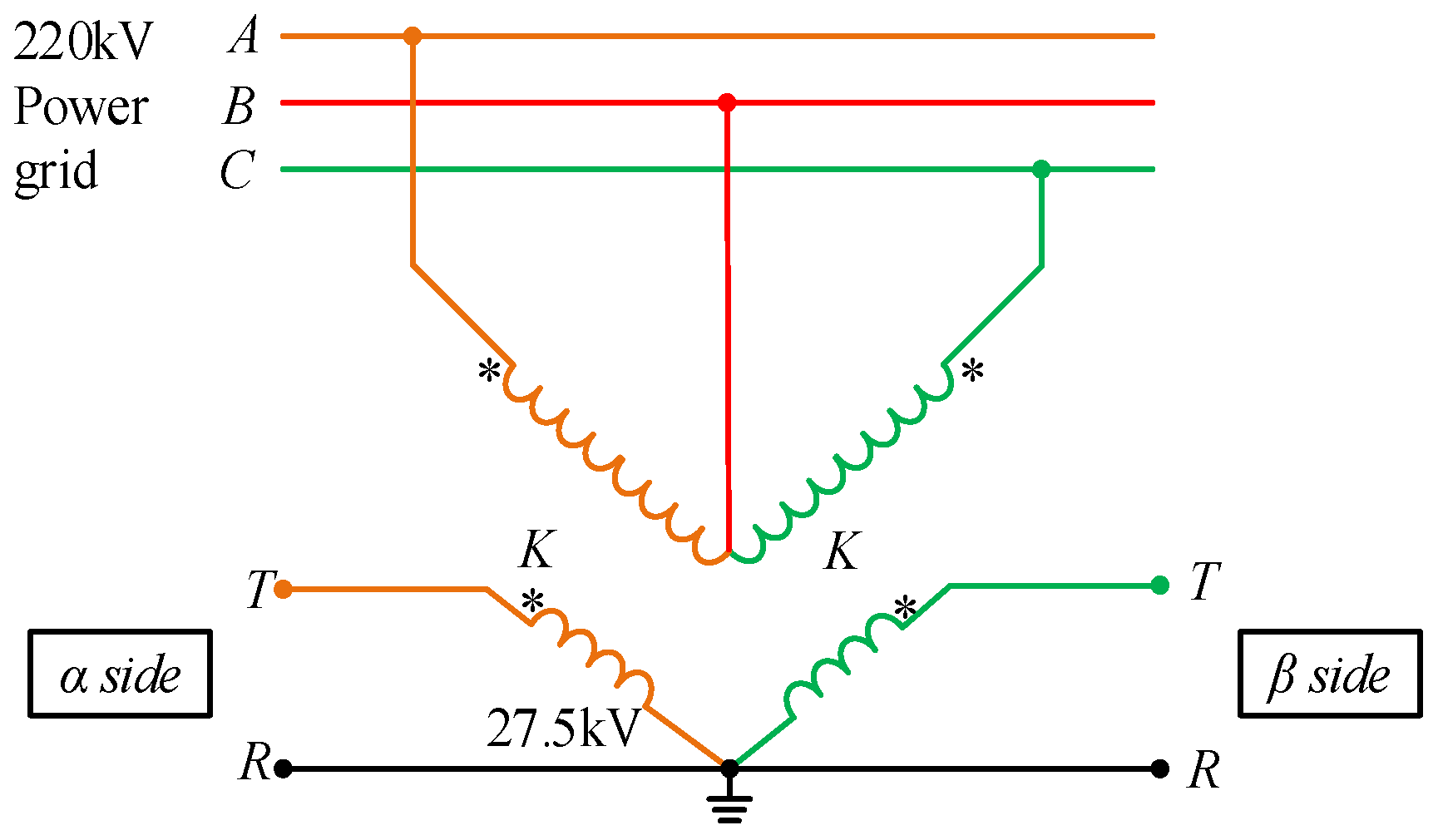
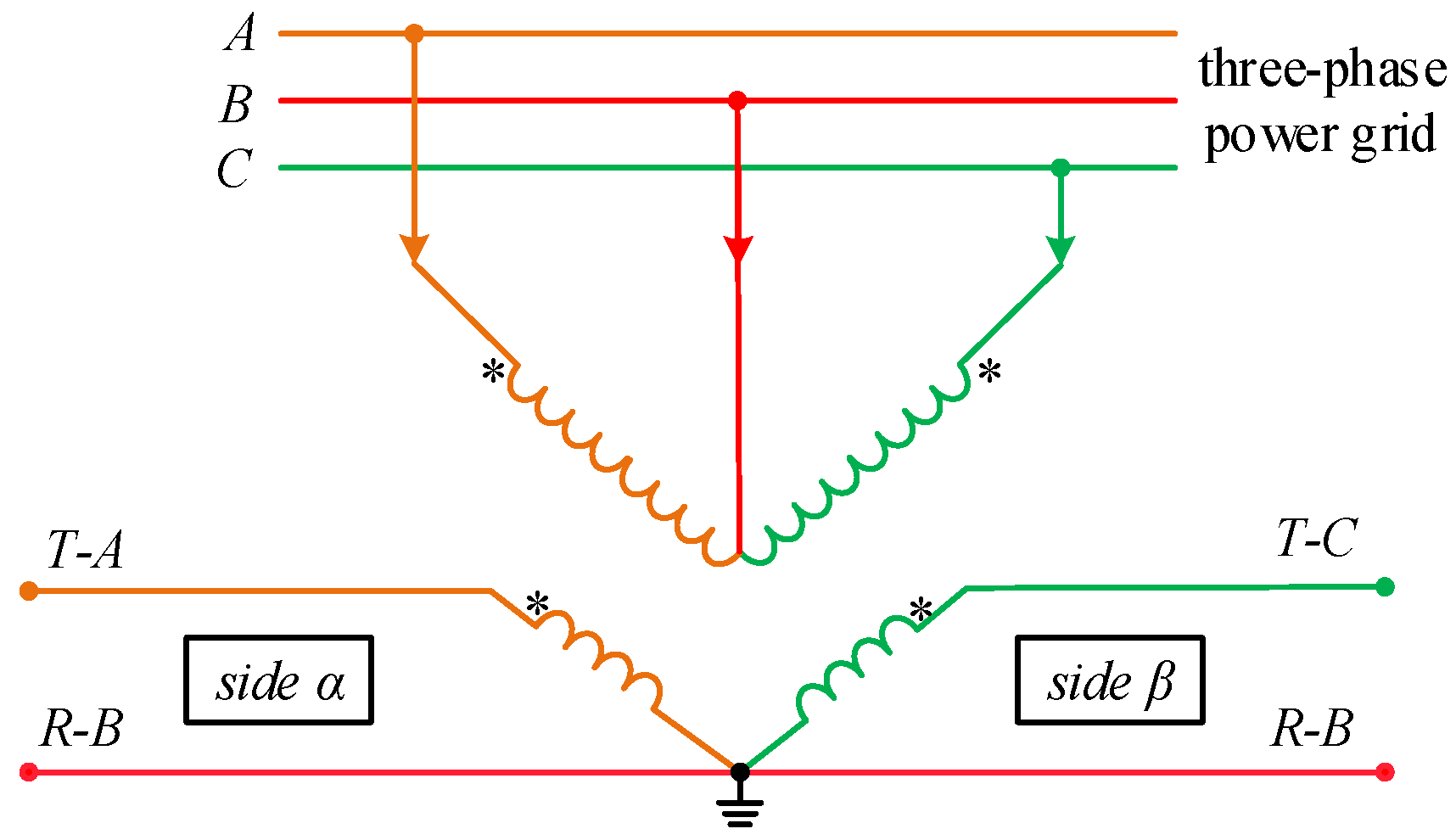
2.2. V/v Traction Transformer Branch Admittance Modeling
2.3. Construction of Dynamic Nodal Admittance Matrix for Coupled Systems
3. Dynamic Power Flow Calculation for the Hybrid Asymmetric System of the “Renewable Energy–Power Grid–Transportation Network”
3.1. The Construction of Hybrid Power Flow Equations for the Coupled System of Power Grid and Transportation Network
3.2. A Three-Phase Power Balance Strategy Considering Renewable Energy and Traction Loads
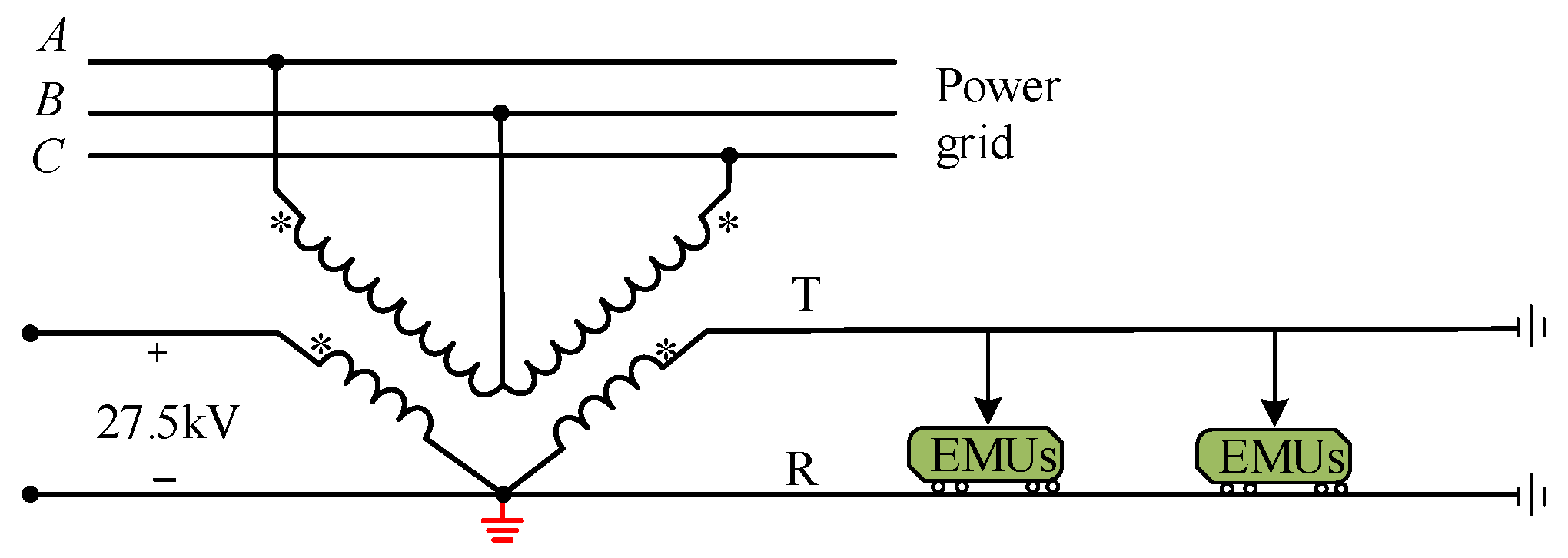
3.2.1. The Conversion Relationship Between the Power of the EMUs and the Three-Phase Power at the High-Voltage Side of the Traction Transformer
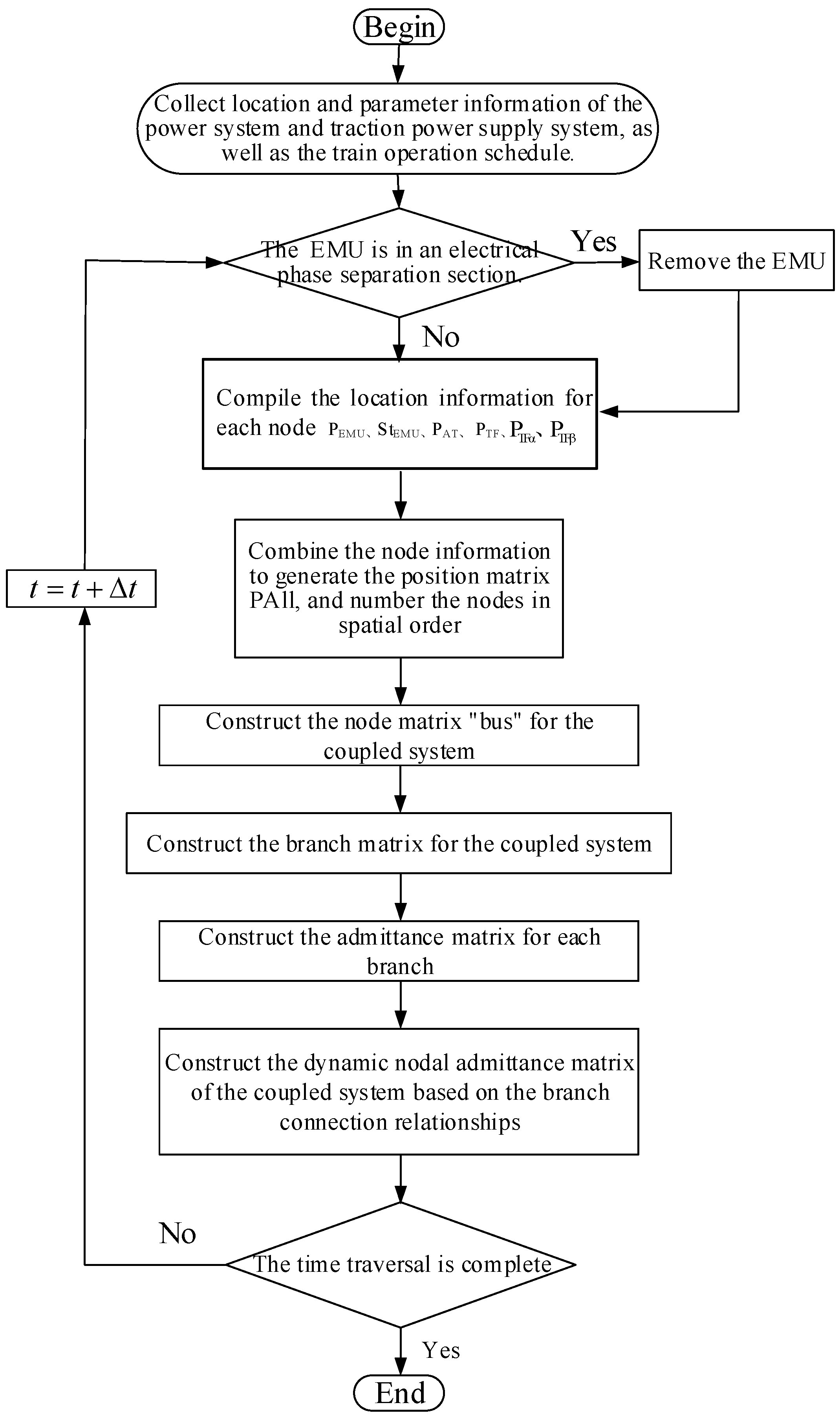
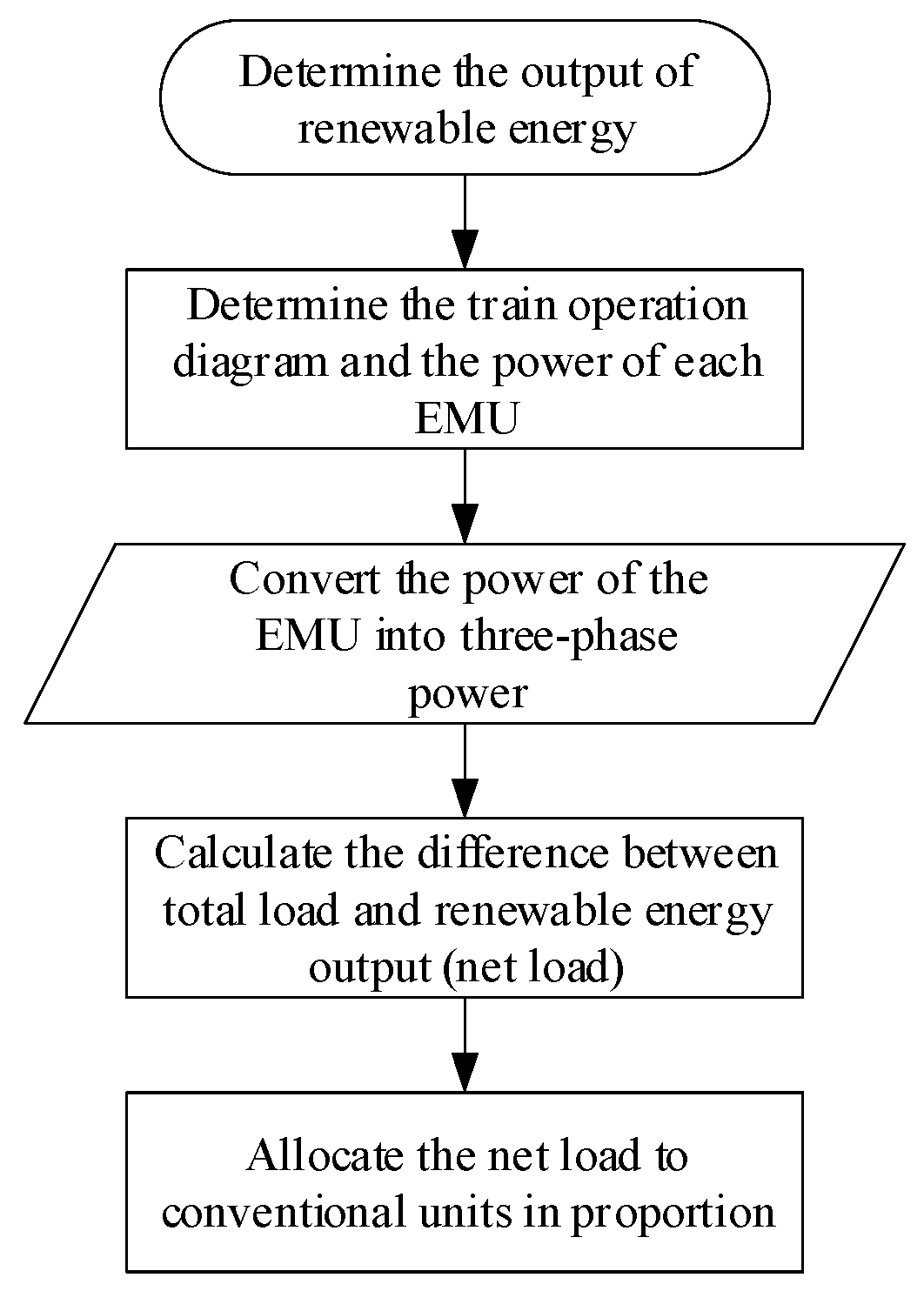
3.2.2. The Strategy Process for Power Balance Considering Renewable Energy and Traction Load
3.3. Solving the Nonlinear Equations for Hybrid Power Flow in a Coupled System
3.3.1. Matrix Partitioning
3.3.2. Handling of Boundary Conditions for the Traction Power Supply System
3.3.3. Handling of Boundary Conditions on the Power Grid Side
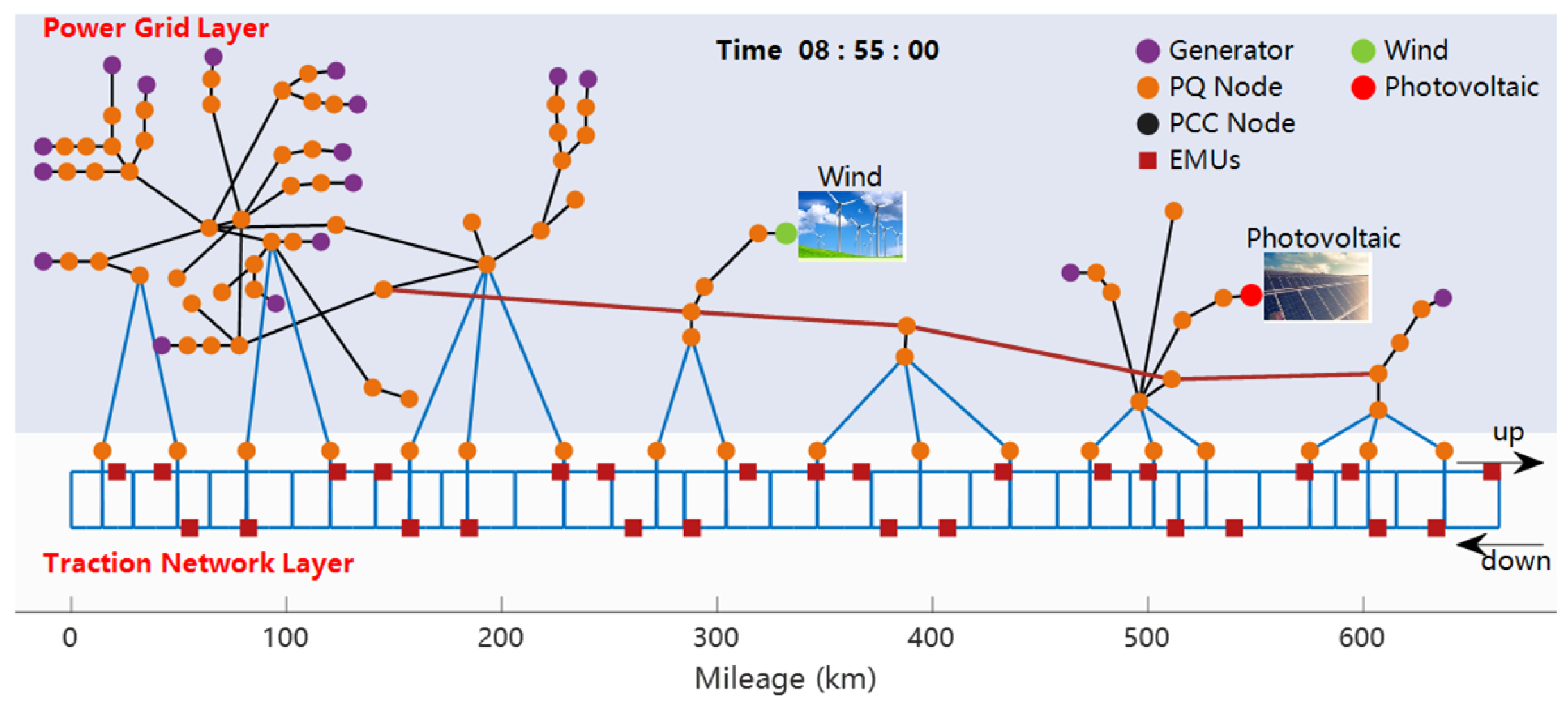
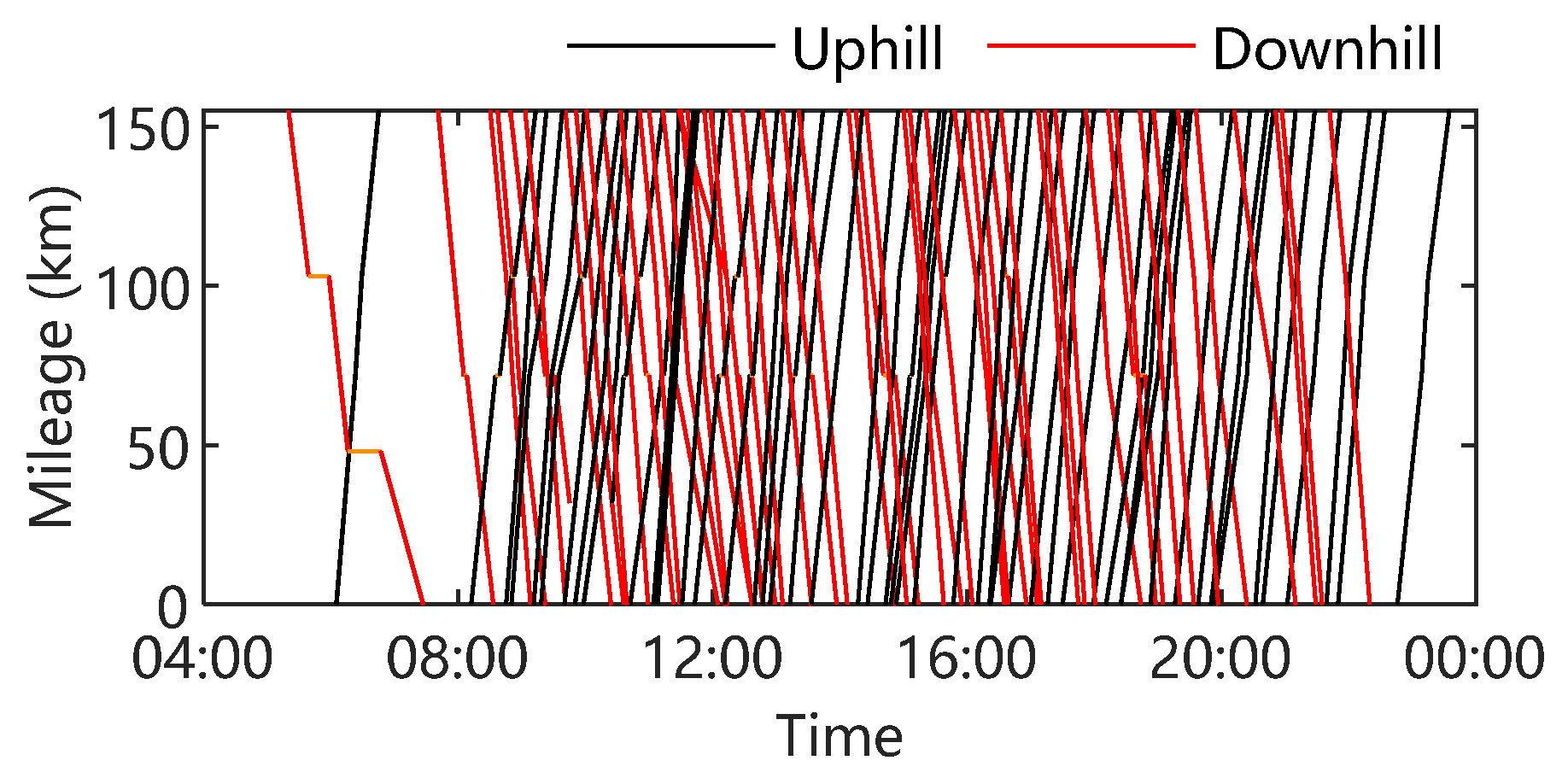
4. Case Study Analysis
4.1. Analysis of Multi-Vehicle Single-Time Section Results
4.2. Analysis of Continuous Operation Conditions for Single Vehicles
4.3. Analysis of System Operation Results
5. Conclusions
- In light of the severe fluctuations of high-speed railway loads in mountainous regions, the three-phase power balance strategy proposed in this study, which considers both renewable energy and traction loads, effectively regulates the power in such asymmetric coupling systems.
- Due to the structural influence of the traction transformer, there is a significant difference in the average phase values between the three phases on the grid side and the alpha and beta phases on the traction side.
- Under braking conditions, the pantograph voltage is significantly higher than that in traction mode compared to the regenerative power feedback from the locomotive, which manifests a distinct voltage elevation effect in the traction power supply system. At both sides of each neutral section, the phase angle exhibits jumps influenced by the different phase-sequence power supply from the grid.
Author Contributions
Funding
Conflicts of Interest
References
- Trias, A. The Holomorphic Embedding Load Flow method. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Subramanian, M.K.; Feng, Y.; Tylavsky, D. PV bus modeling in a holomorphically embedded power-flow formulation. In Proceedings of the 2013 North American Power Symposium (NAPS), Manhattan, KS, USA, 22–24 September 2013; pp. 1–6. [Google Scholar]
- Rao, S.; Feng, Y.; Tylavsky, D.J.; Subramanian, M.K. The Holomorphic Embedding Method Applied to the Power-Flow Problem. IEEE Trans. Power Syst. 2016, 31, 3816–3828. [Google Scholar] [CrossRef]
- Chiang, H.D.; Wang, T.; Sheng, H. A Novel Fast and Flexible Holomorphic Embedding Power Flow Method. IEEE Trans. Power Syst. 2018, 33, 2551–2562. [Google Scholar] [CrossRef]
- Goodman, C.J.; Kulworawanichpong, T. Sequential linear power flow solution for AC electric railway power supply systems. WIT Trans. Built Environ. 2002, 61, 10. [Google Scholar]
- Goodman, C.J.; Kulworawanichpong, T. Sequential Linear Power Flow Solution for AC Electric Railway Power Supply Systems; WIT Press: Southampton, UK, 2002; pp. 531–540. [Google Scholar]
- Zhang, W.; Yang, S.; Zhang, J.; Ye, J.; Wu, M. A two-phase power flow algorithm of traction power supply system based on traction substation-network decoupling. Int. J. Electr. Power Energy Syst. 2023, 152, 109252. [Google Scholar] [CrossRef]
- He, J.W.; Li, Q.Z.; Liu, W.; Zhou, X.H. General mathematical model for simulation of AC traction power supply system and its application. Power Syst. Technol. 2010, 34, 25–29. [Google Scholar]
- Hongwei, C.; Guangchao, G.; Quanyuan, J. Power flow algorithm for traction power supply system of electric railway based on locomotive and network coupling. Autom. Electr. Power Syst. 2012, 36, 76–80+110. [Google Scholar]
- Fang, W.; Xiaoru, W. A power flow analysis method of traction power supply system based on constant-power load. Proc. CSU-EPSA 2015, 27, 59–64. [Google Scholar]
- Wan, Q.; Wu, M.; Chen, J.; Wang, Z.; Liu, X. Simulating calculation of traction substation’s feeder current based on traction calculation. Trans. China Electrotech. Soc. 2007, 22, 108–113. [Google Scholar]
- Xiaoqin, L.; Xiaoru, W. State-space model of high-speed railway traction power-supply system. Proc. CSEE 2017, 37, 857–868. [Google Scholar]
- Junqi, Z.; Mingli, W. Power flow algorithm for electric railway traction network based on multiple load port equivalence. Trans. China Electrotech. Soc. 2018, 33, 2479–2485. [Google Scholar]
- Mongkoldee, K.; Kulworawanichpong, T. Current-based Newton-Raphson power flow calculation for AT-fed railway power supply systems. Int. J. Electr. Power Energy Syst. 2018, 98, 11–22. [Google Scholar]
- Hui, W.; Wei, L.; Qunzhan, L.; Qing, M.; Tongtong, L. Dynamic power flow calculation of AC electrified railway based on unified chain circuit of source-network-load. J. China Electrotech. Soc. 2022, 42, 3936–3953. [Google Scholar]
- Hu, H.; He, Z.; Li, X.; Wang, K.; Gao, S. Power-Quality Impact Assessment for High-Speed Railway Associated with High-Speed Trains Using Train Timetable-Part I: Methodology and Modeling. IEEE Trans. Power Deliv. 2016, 31, 693–703. [Google Scholar] [CrossRef]
- Hu, H.; He, Z.; Wang, K.; Ma, X.; Gao, S. Power-Quality Impact Assessment for High-Speed Railway Associated with High-Speed Trains Using Train Timetable—Part II: Verifications, Estimations and Applications. IEEE Trans. Power Deliv. 2016, 31, 1482–1492. [Google Scholar] [CrossRef]
- Hu, H.; He, Z.; Wang, J.; Gao, S.; Qian, Q. Power Flow Calculation of High-speed Railway Traction Network Based on Train-network Coupling Systems. Proc. CSEE 2012, 32, 101–108. [Google Scholar]
- He, Z.; Hu, H.; Zhang, Y.; Gao, S. Harmonic Resonance Assessment to Traction Power-Supply System Considering Train Model in China High-Speed Railway. IEEE Trans. Power Deliv. 2014, 29, 1735–1743. [Google Scholar] [CrossRef]
- Mohamed, B.; Arboleya, P.; El-Sayed, I.; González-Morán, C. High-speed 2 × 25 kV traction system model and solver for extensive network simulations. IEEE Trans. Power Syst. 2019, 34, 3837–3847. [Google Scholar] [CrossRef]



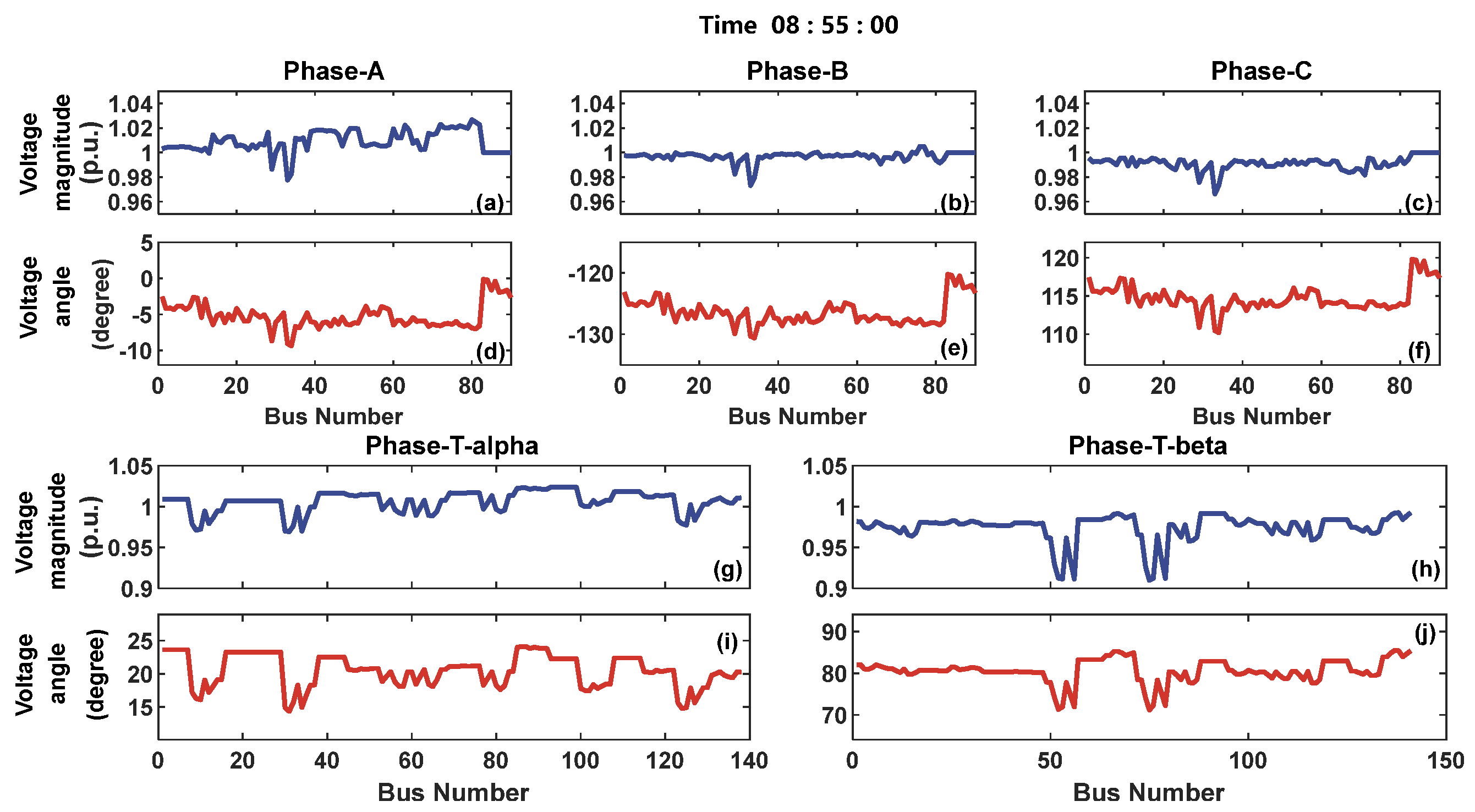


| Phases | A | B | C | |
|---|---|---|---|---|
| Average Phase Angle (°) | −4.9439 | −126.095 | 115.0173 | |
| Phases | alpha | beta | ||
| Average Phase Angle (°) | 20.44 | 80.5516 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Liu, J.; Su, Y.; Zhang, Q.; Zhang, D.; Liu, Z. A Dynamic Power Flow Calculation Method for the “Renewable Energy–Power Grid–Transportation Network” Coupling System. Energies 2025, 18, 1567. https://doi.org/10.3390/en18071567
Li B, Liu J, Su Y, Zhang Q, Zhang D, Liu Z. A Dynamic Power Flow Calculation Method for the “Renewable Energy–Power Grid–Transportation Network” Coupling System. Energies. 2025; 18(7):1567. https://doi.org/10.3390/en18071567
Chicago/Turabian StyleLi, Bo, Jiawei Liu, Yunche Su, Qiao Zhang, Deyuan Zhang, and Zhigang Liu. 2025. "A Dynamic Power Flow Calculation Method for the “Renewable Energy–Power Grid–Transportation Network” Coupling System" Energies 18, no. 7: 1567. https://doi.org/10.3390/en18071567
APA StyleLi, B., Liu, J., Su, Y., Zhang, Q., Zhang, D., & Liu, Z. (2025). A Dynamic Power Flow Calculation Method for the “Renewable Energy–Power Grid–Transportation Network” Coupling System. Energies, 18(7), 1567. https://doi.org/10.3390/en18071567






