A Novel Water-Flooding Characteristic Curve Based on Fractal Theory and Its Application
Abstract
1. Introduction
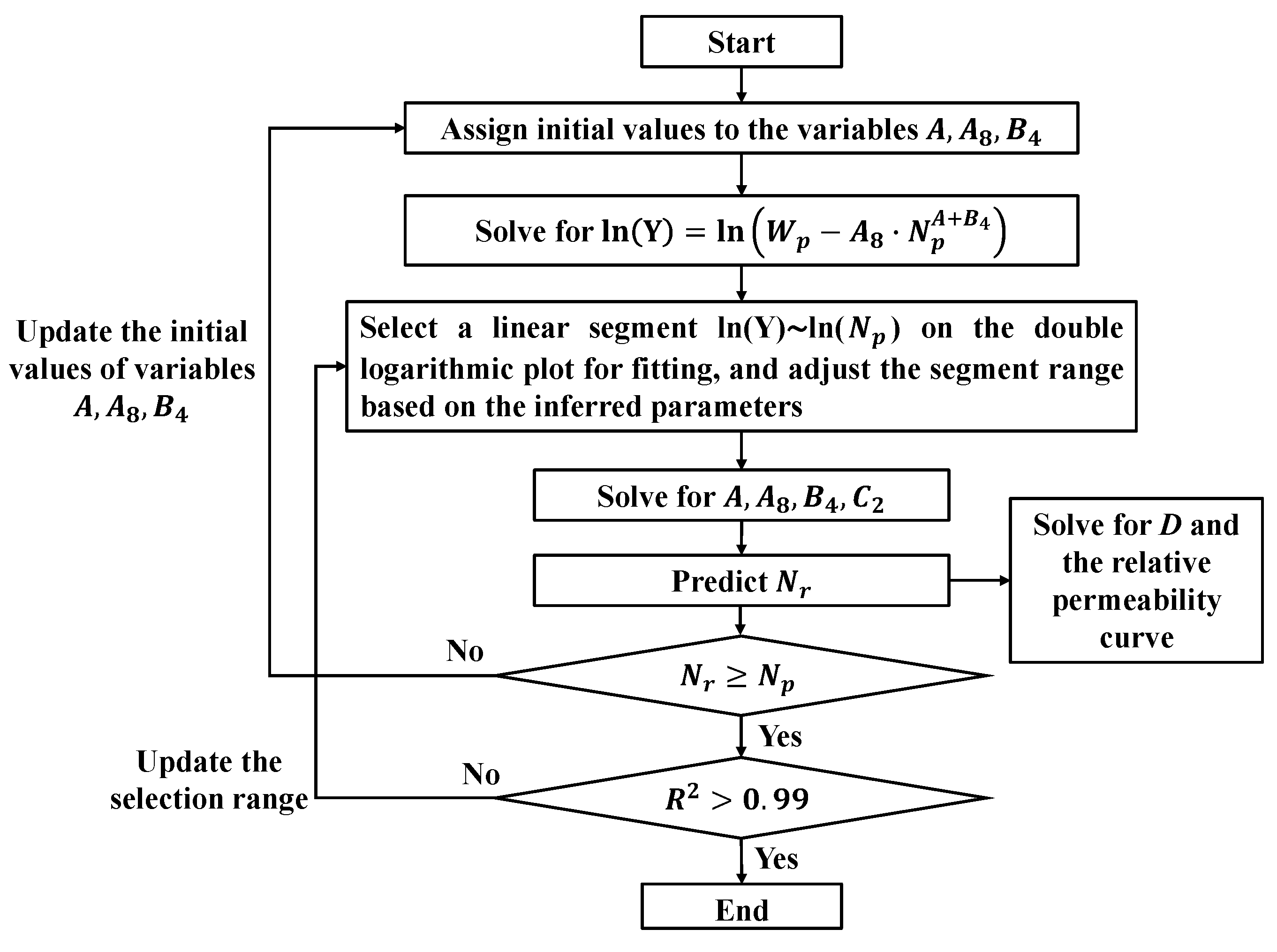
2. Establishment of the Mathematical Model
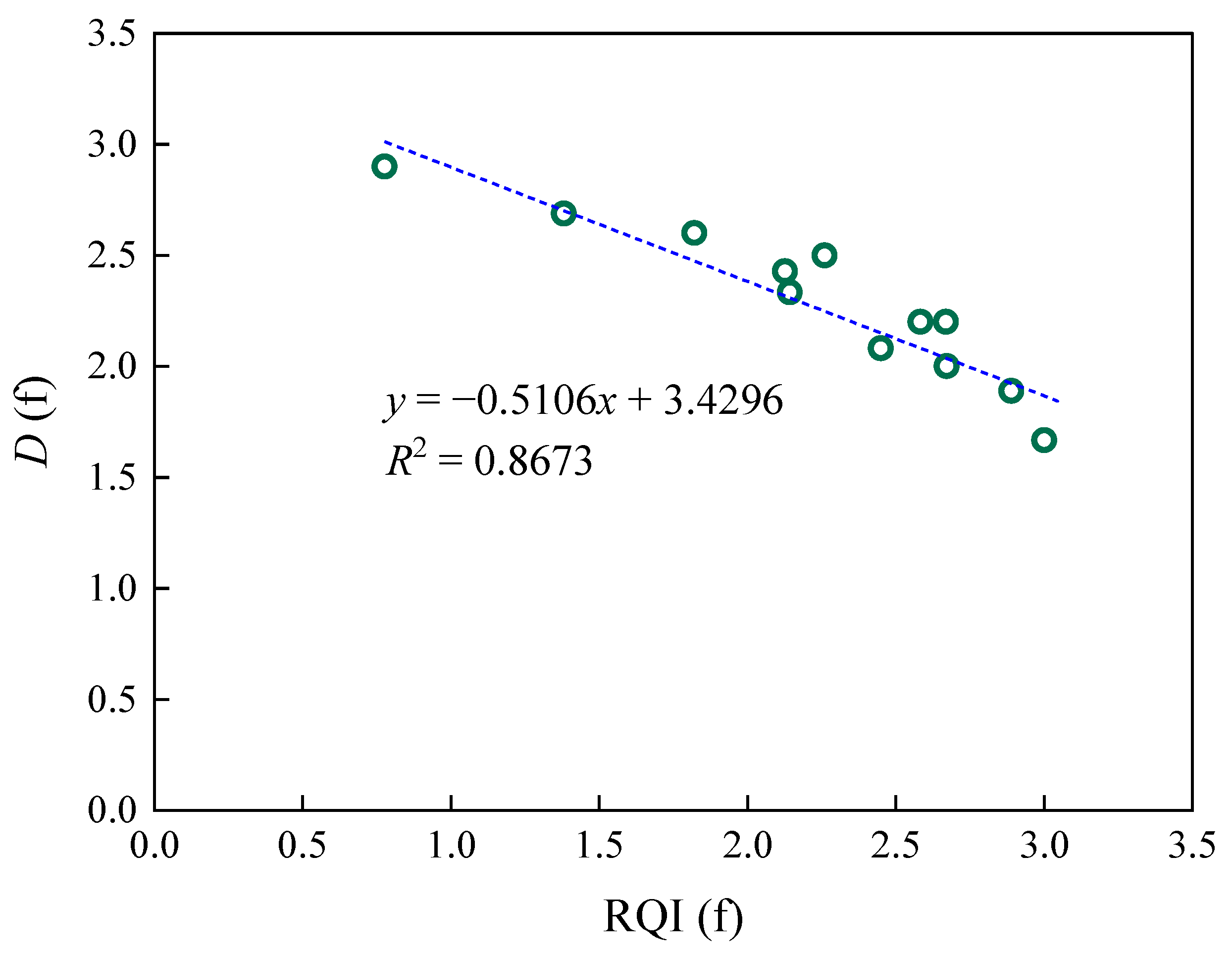
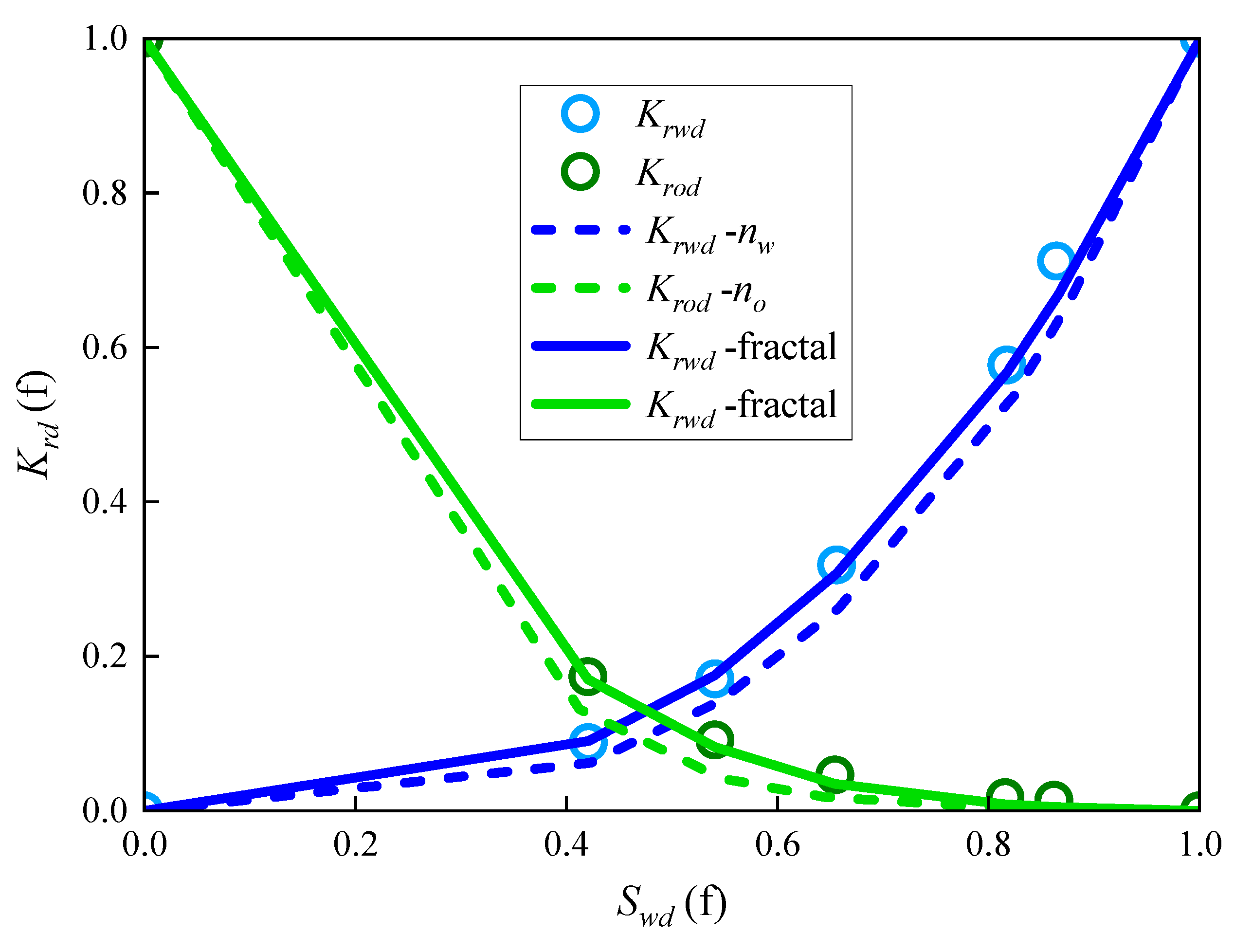
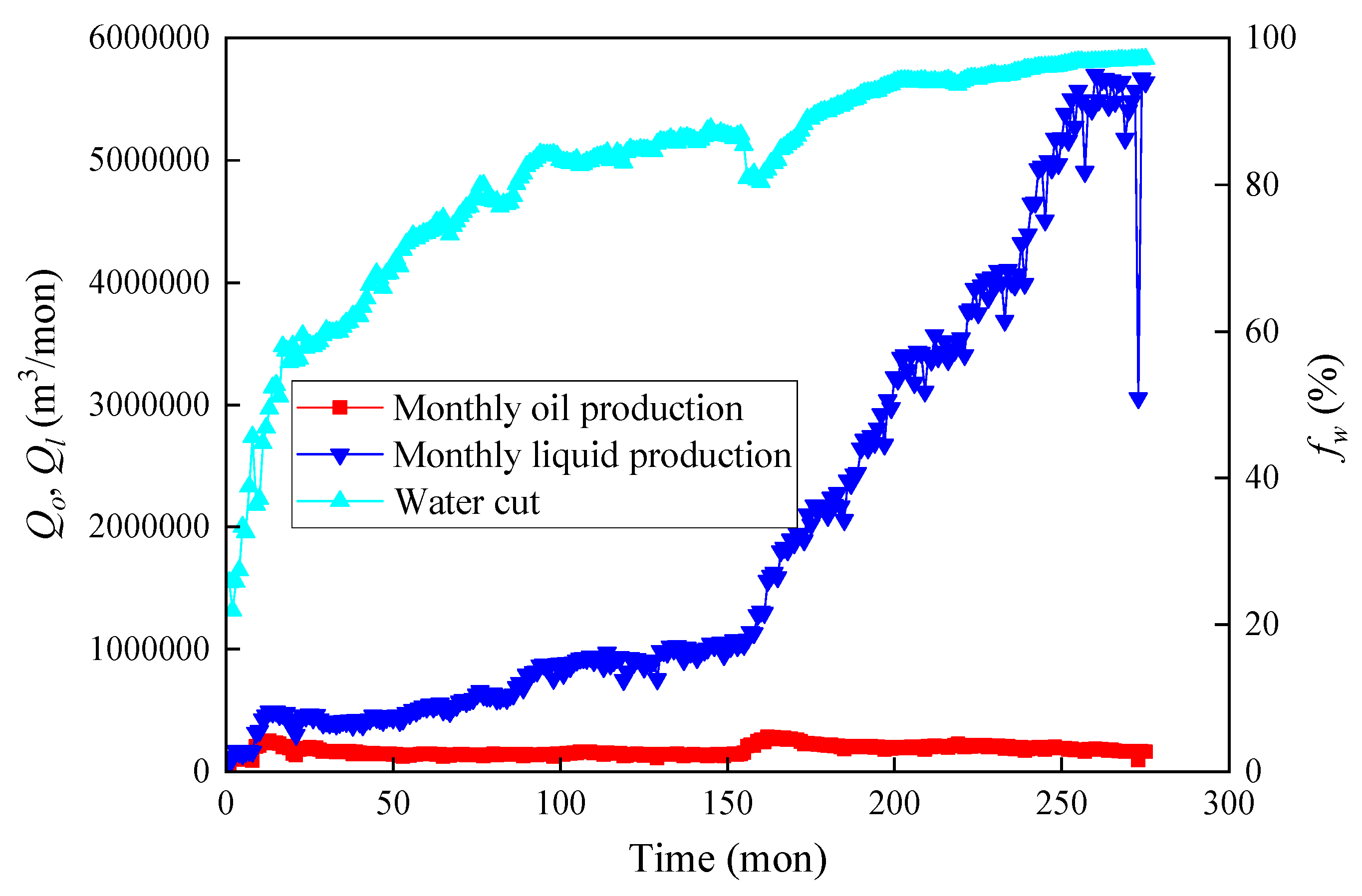
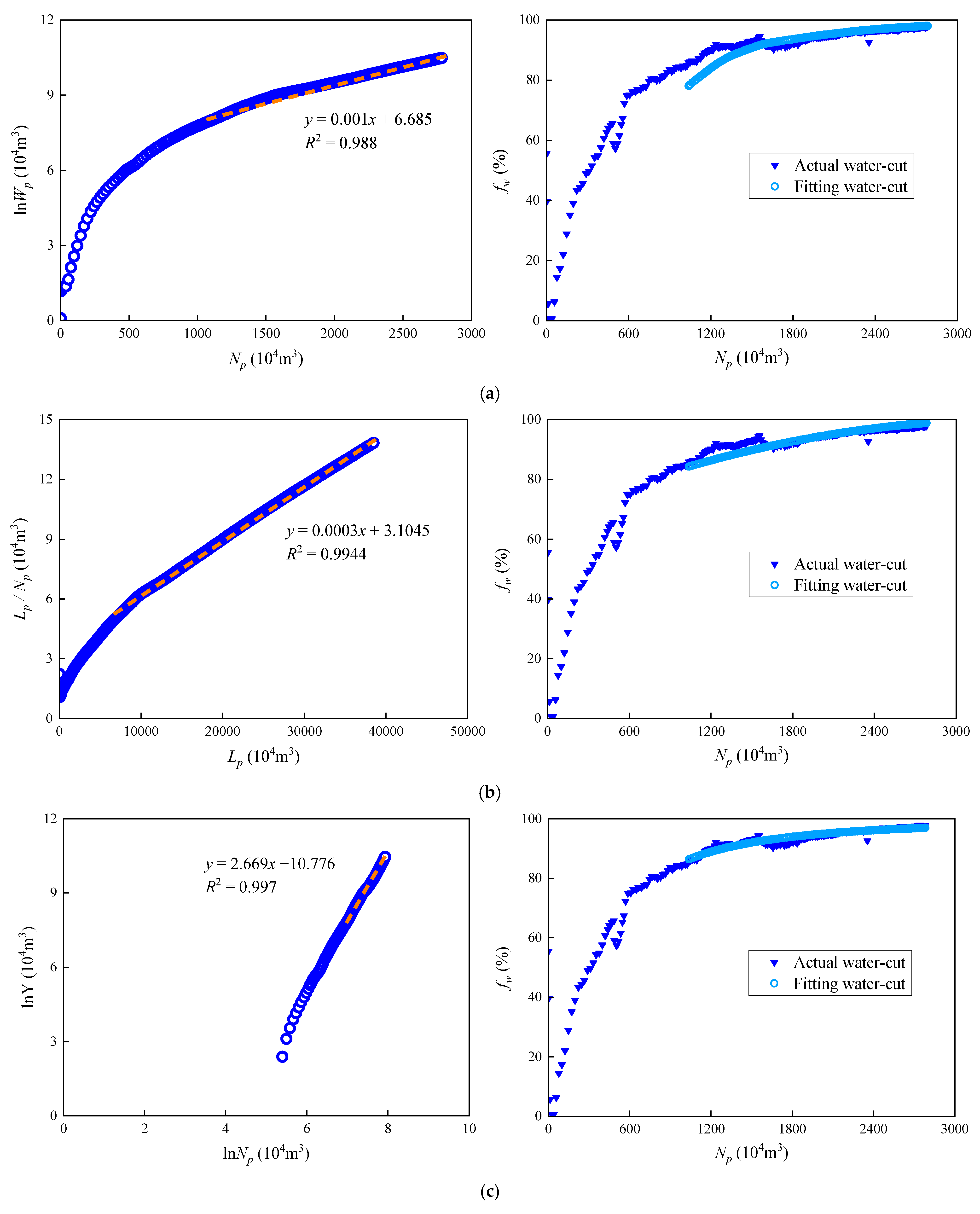
3. Case Study Analysis and Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| normalized oil-phase relative permeability | normalized oil saturation | ||
| normalized water-phase relative permeability | normalized water saturation | ||
| fractal dimension | oil-phase relative permeability | ||
| water-phase relative permeability | irreducible water saturation | ||
| residual oil saturation | water-phase index | ||
| oil-phase index | water production rate | ||
| oil production rate | water-phase viscosity | ||
| oil-phase viscosity | water-phase volume factor | ||
| oil-phase volume factor | geological reserves of crude oil | ||
| water saturation at the outlet | time | ||
| cumulative water production | cumulative oil production | ||
| movable oil volume | water cut | ||
| water-phase relative permeability at the residual oil endpoint | |||
| recoverable oil reserves extraction degree | |||
| intermediate variables in the formula, | |||
| fitting coefficients in the empirical formulas and have different values in different formulas | |||
| the undetermined coefficients in the formula | |||
| the undetermined coefficients in the formula | |||
| the undetermined coefficients in the formula | |||
| constant | |||
References
- Amrouche, F.; Blunt, M.; Iglauer, S.; Short, M.; Aiouache, F. Electrical heating impacts on wetting properties in electrical enhanced oil recovery (EEOR). In Proceedings of the Third EAGE Workshop on EOR, Buenos Aires, Argentina, 3–4 October 2024. [Google Scholar]
- Amrouche, F.; Blunt, M.J.; Iglauer, S.; Aiouache, F.; Short, M. A novel hybrid enhanced oil recovery technique to enhance oil production from oil-wet carbonate reservoirs by combining electrical heating with nanofluid flooding. Mater. Today Sustain. 2024, 27, 100915. [Google Scholar]
- Dou, H.; Zhang, H.; Shen, S. Correct understanding and application of waterflooding characteristic curve. Pet. Explor. Dev. 2019, 46, 755–762. [Google Scholar]
- Zhang, J.; Yang, R. Proposing of theoretical waterflooding curve and discussion on the relationships between theoretical waterflooding curve and production decline curve. China Offshore Oil Gas 2018, 30, 86–92. [Google Scholar]
- Gao, W.; Yin, R.; Yang, J. Establishment and theoretical basis of the new water-flooding characteristic curve. Acta Pet. Sin. 2020, 41, 342–347. [Google Scholar]
- Gao, W.; Xu, J. Theoretical study on common water-drive characteristic curves. Acta Pet. Sin. 2007, 28, 89–92. [Google Scholar]
- Gao, W.; Liu, Y.; Wang, Z.; Liu, Y. Establishment and study on transitional water displacement curve. Xinjiang Pet. Geol. 2001, 22, 247–250. [Google Scholar]
- Wang, Y.; Shi, C.; Wang, J. New equations for characterizing water flooding in ultra-high water-cut oilfields. Oil Gas Geol. 2020, 41, 1282–1287. [Google Scholar]
- Zhu, M.; Shi, L.; Xue, Y.; Wen, J.; Li, S.; Liu, M.; Xin, C. Study and application of new water drive characteristic curve. Unconv. Oil Gas 2022, 9, 65–70. [Google Scholar]
- Gu, J.; Ren, Y.; Zhang, Y.; Cui, W. Research and application of an improved Type-B water-flooding characteristic curve. Spec. Oil Gas Reserv. 2020, 27, 102–107. [Google Scholar]
- Zhang, X. The laboratorial measurement of relative permeability curve of oil and water. Oil Drill. Prod. Technol. 1994, 16, 87–90. [Google Scholar]
- Zhang, B.; Pu, C.; Zhu, J.; Yu, H.; Zeng, X. Effect of temperature on the oil/water relative permeability of heavy oil of different viscosity. J. Xi’an Shiyou Univ. (Nat. Sci. Ed.) 2013, 28, 61–63. [Google Scholar]
- Guo, P.; Zhang, T.; Zhu, Z.; Du, J.; Wu, G. Study on oil-water relative permeability experiments of fractured-porous reservoirs. Reserv. Eval. Dev. 2013, 3, 19–22. [Google Scholar]
- Gao, H.; Jiang, H.; Chen, M. Simulation study on the effect of the microscopic parameters of reservoir pore structure on oil-water relative permeability. J. Xi’an Shiyou Univ. (Nat. Sci. Ed.) 2007, 22, 56–59. [Google Scholar]
- Chen, Y.; Du, X. A comparison between the different forms of displacement characteristic curves and the criterion for the appearance of straight line section. Pet. Explor. Dev. 1986, 6, 55–63. [Google Scholar]
- Chen, Y. Derivation of water drive curve at high water-cut stage and its analysis of up warding problem. Fault Block Oil Gas Field 1997, 4, 19–24. [Google Scholar]
- Huang, Y. Waterflooding performance of oil reservoir in ultra-high water-cut stage. Spec. Oil Gas Reserv. 2018, 25, 95–99. [Google Scholar]
- Li, Z.; Sun, L.; Deng, H.; Zhang, J.; Li, Y. The research of suitable conditions to water drive characteristic curve. Comput. Tech. Geophys. Geochem. Explor. 2012, 34, 143–146. [Google Scholar]
- Yu, Q. How to study and apply the water displacement curves correctly. Pet. Explor. Dev. 2000, 27, 122–126. [Google Scholar]
- Li, L.; Han, J.; Chen, J. Optimization of predicted recoverable reserves by using water drive type curves. Xinjiang Pet. Geol. 2017, 38, 719–722. [Google Scholar]
- Li, J.; Liu, F.; Liu, C.; Li, K.; Yang, R.; Tang, S.; Yang, L.; Zhang, Y.; Pei-wen, W. Comparisons of fractal normalized relative permeability models and its application in P oilfields, China. In Proceedings of the International Field Exploration and Development Conference, Wuhan, Hubei, China, 20–22 September 2023. [Google Scholar]
- Li, K. More general capillary pressure and relative permeability models from fractal geometry. J. Contam. Hydrol. 2010, 111, 13–24. [Google Scholar] [CrossRef]
- Li, K. Analytical derivation of Brooks–Corey type capillary pressure models using fractal geometry and evaluation of rock heterogeneity. J. Pet. Sci. Eng. 2010, 73, 20–26. [Google Scholar]
- Li, K.; Horne, R.N. Experimental verification of methods to calculate relative permeability using capillary pressure data. In Proceedings of the SPE Western Regional/AAPG Pacific Section Joint Meeting, Anchorage, AK, USA, 20–22 May 2002. [Google Scholar]
- Chen, Y. Derivation of relationships of water drive curves. Acta Pet. Sin. 1985, 6, 69–78. [Google Scholar]
- Ahmed, T. Reservoir Engineering Handbook; Petroleum Industry Press: Beijing, China, 2009; pp. 288–330. [Google Scholar]
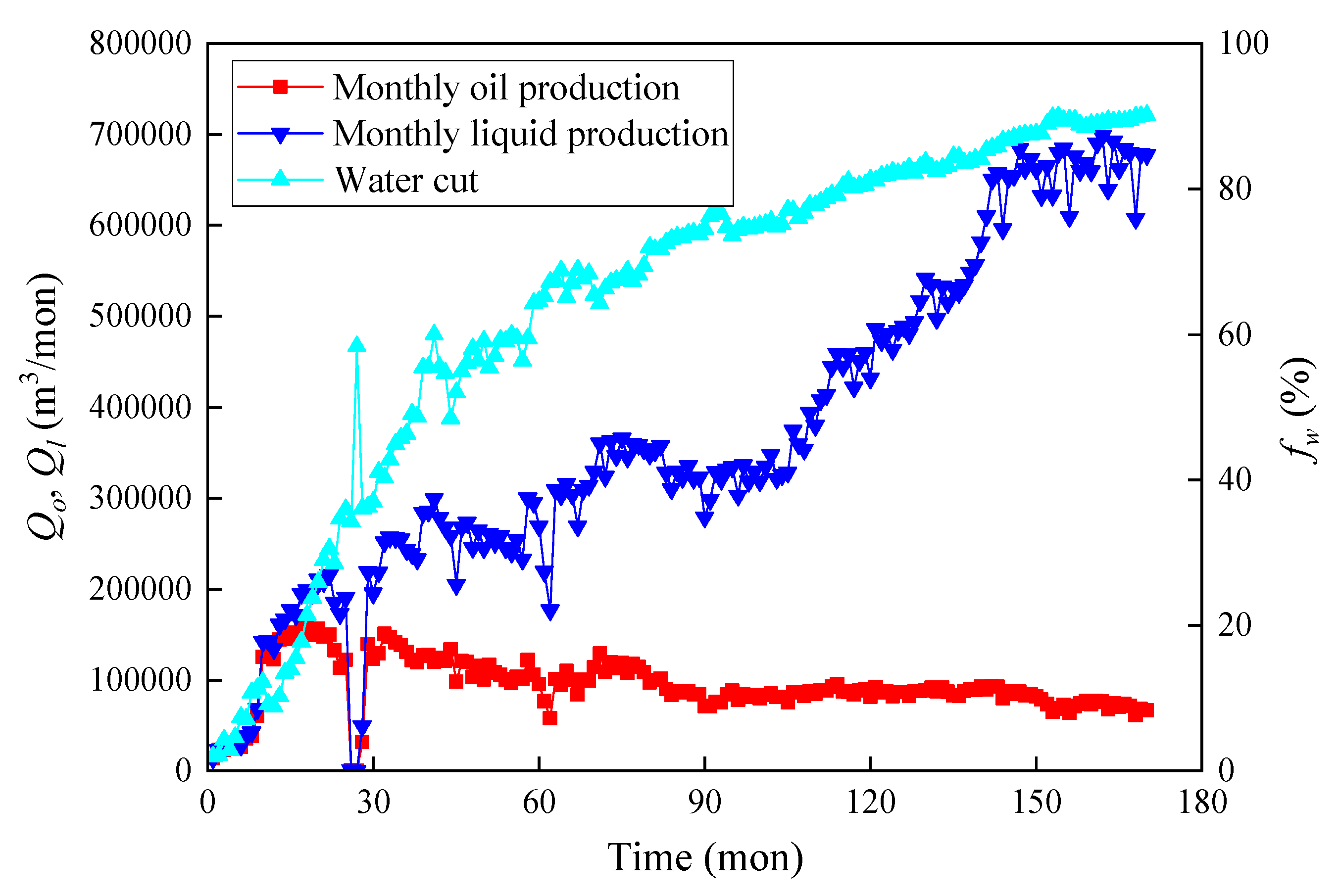
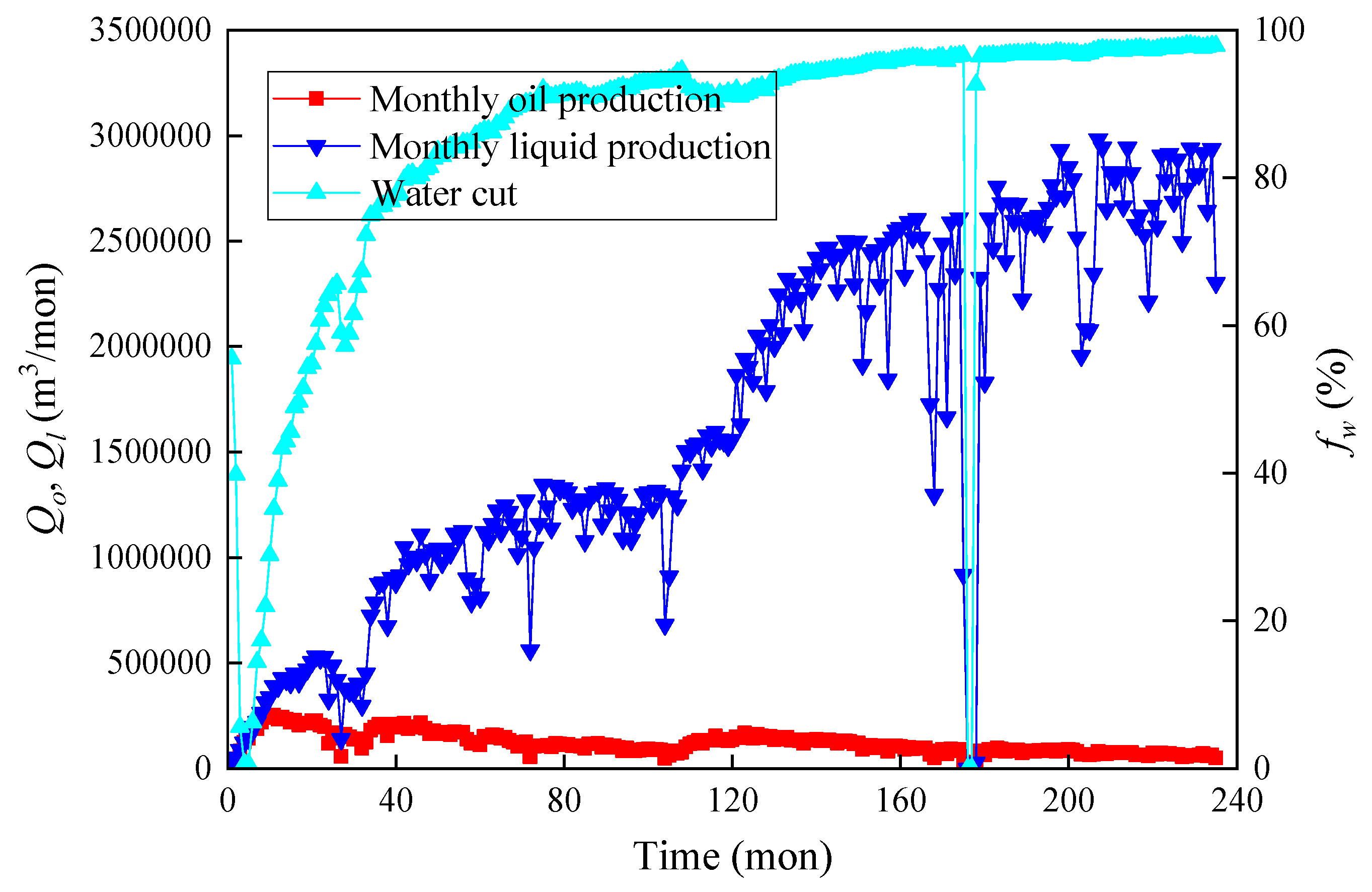
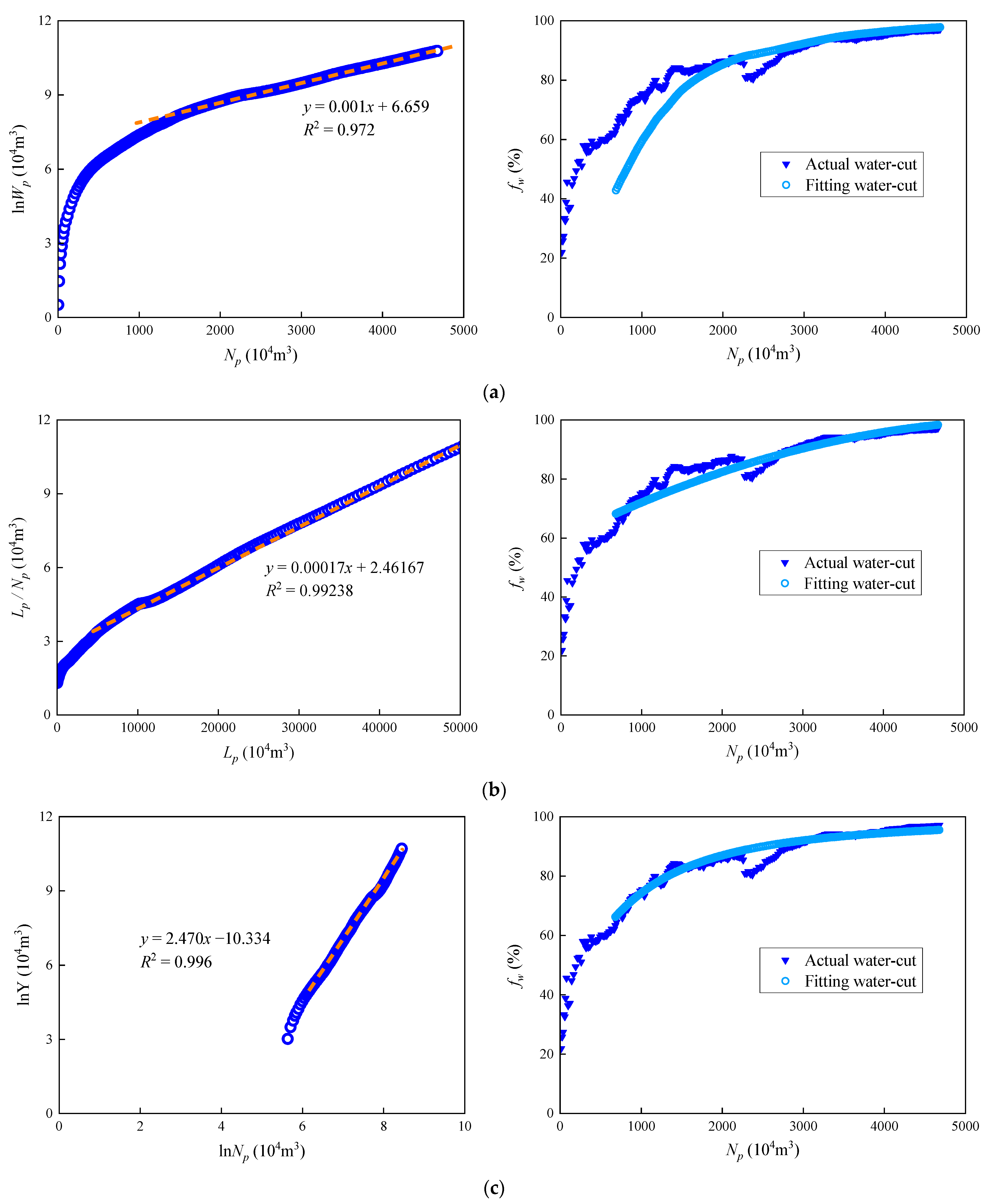
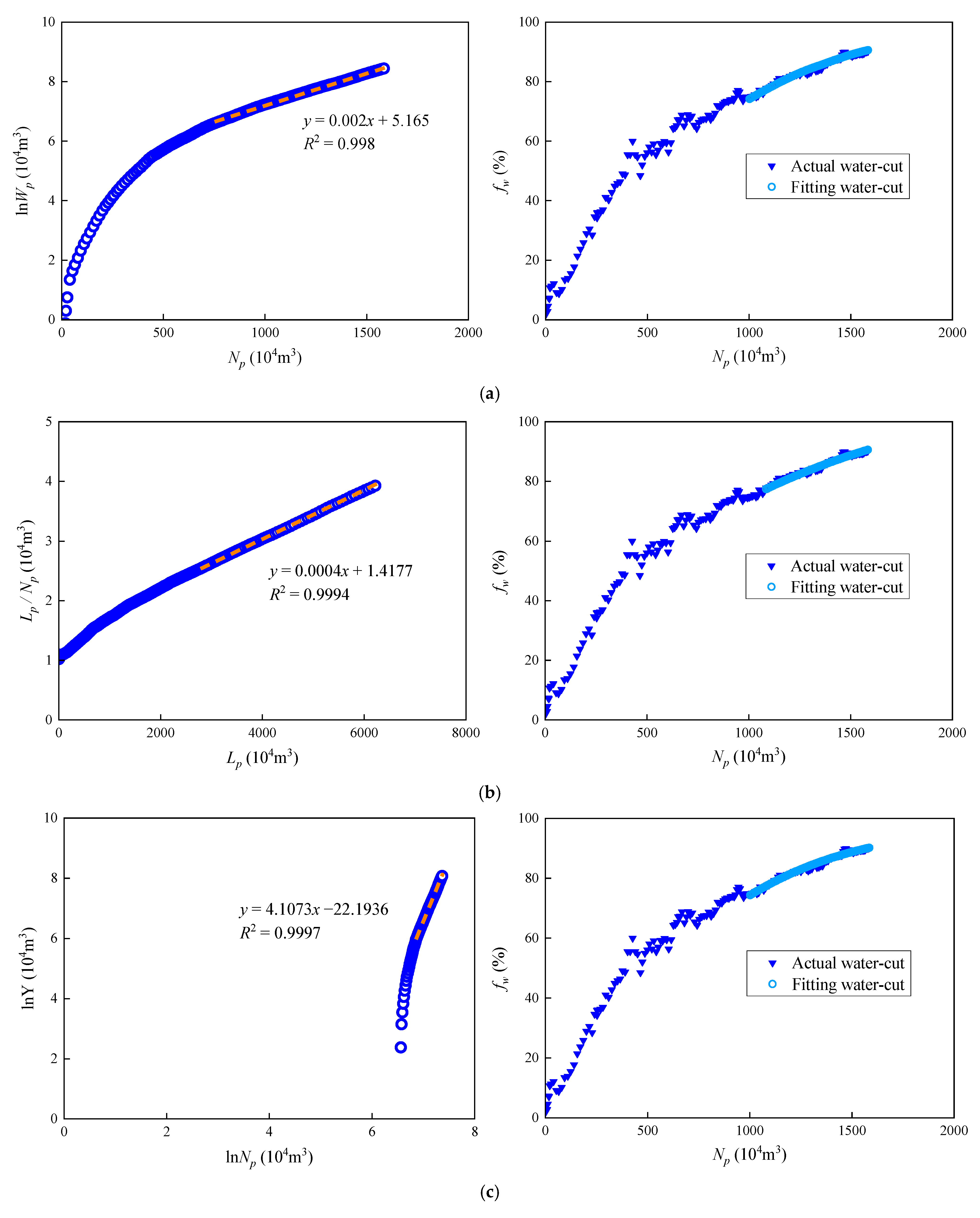
| Oilfield (Reservoir) | Current Monthly Oil Production | Current Water Cut | The M-T Water-Flooding Curve | The Type C Water-Flooding Curve | The Novel Water-Flooding Curve | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fitting Correlation Coefficient | The Sum of Squared Residuals of fw~Np | Predicted Recoverable Reserves | Fitting Correlation Coefficient | The Sum of Squared Residuals of fw~Np | Predicted Recoverable Reserves | Fitting Correlation Coefficient | The Sum of Squared Residuals of fw~Np | Predicted Recoverable Reserves | |||
| 104 m3 | % | f | f | 104 m3 | f | f | 104 m3 | f | f | 104 m3 | |
| Q oilfield | 16.0 | 97.2 | 0.972 | 13,870.0 | 4591.4 | 0.992 | 2179.2 | 4577.1 | 0.996 | 1091.9 | 8333.2 |
| Q1 reservoir | 0.8 | 94.8 | 0.940 | 8925.0 | 149.9 | 0.980 | 1835.7 | 152.4 | 0.997 | 429.4 | 195.7 |
| Q2 reservoir | 2.1 | 97.7 | 0.959 | 1299.4 | 181.3 | 0.974 | 464.4 | 184.5 | 0.998 | 172.7 | 240.5 |
| B oilfield | 6.7 | 90.2 | 0.999 | 35.5 | 2370.8 | 0.999 | 37.1 | 2079 | 0.999 | 35.5 | 2791.1 |
| B1 reservoir | 0.8 | 72.5 | 0.992 | 1133.5 | 95.6 | 0.991 | 706.4 | 141.1 | 0.995 | 544.0 | 209.8 |
| B2 reservoir | 0.4 | 89.3 | 0.964 | 2459.7 | 91.8 | 0.984 | 1739.2 | 93.3 | 0.994 | 752.2 | 178.7 |
| P oilfield | 1.9 | 97.6 | 0.988 | 1142.3 | 2723.3 | 0.994 | 624.6 | 2589.7 | 0.997 | 173.1 | 3628.4 |
| P1 reservoir | 0.1 | 97.2 | 0.919 | 1969.7 | 11.7 | 0.988 | 9308.8 | 12.5 | 0.994 | 506.2 | 14.8 |
| P2 reservoir | 0.6 | 97.6 | 0.994 | 186.1 | 121.2 | 0.997 | 82.7 | 122.4 | 0.999 | 72.4 | 137.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Du, X.; Li, J.; Jiang, J.; Cai, S. A Novel Water-Flooding Characteristic Curve Based on Fractal Theory and Its Application. Energies 2025, 18, 1555. https://doi.org/10.3390/en18061555
Li K, Du X, Li J, Jiang J, Cai S. A Novel Water-Flooding Characteristic Curve Based on Fractal Theory and Its Application. Energies. 2025; 18(6):1555. https://doi.org/10.3390/en18061555
Chicago/Turabian StyleLi, Ke, Xulin Du, Jing Li, Junzhe Jiang, and Shaobin Cai. 2025. "A Novel Water-Flooding Characteristic Curve Based on Fractal Theory and Its Application" Energies 18, no. 6: 1555. https://doi.org/10.3390/en18061555
APA StyleLi, K., Du, X., Li, J., Jiang, J., & Cai, S. (2025). A Novel Water-Flooding Characteristic Curve Based on Fractal Theory and Its Application. Energies, 18(6), 1555. https://doi.org/10.3390/en18061555






