Development of WHED Method to Study Operational Stability of Typical Transitions in a Hydropower Plant and a Pumped Storage Plant
Abstract
1. Introduction
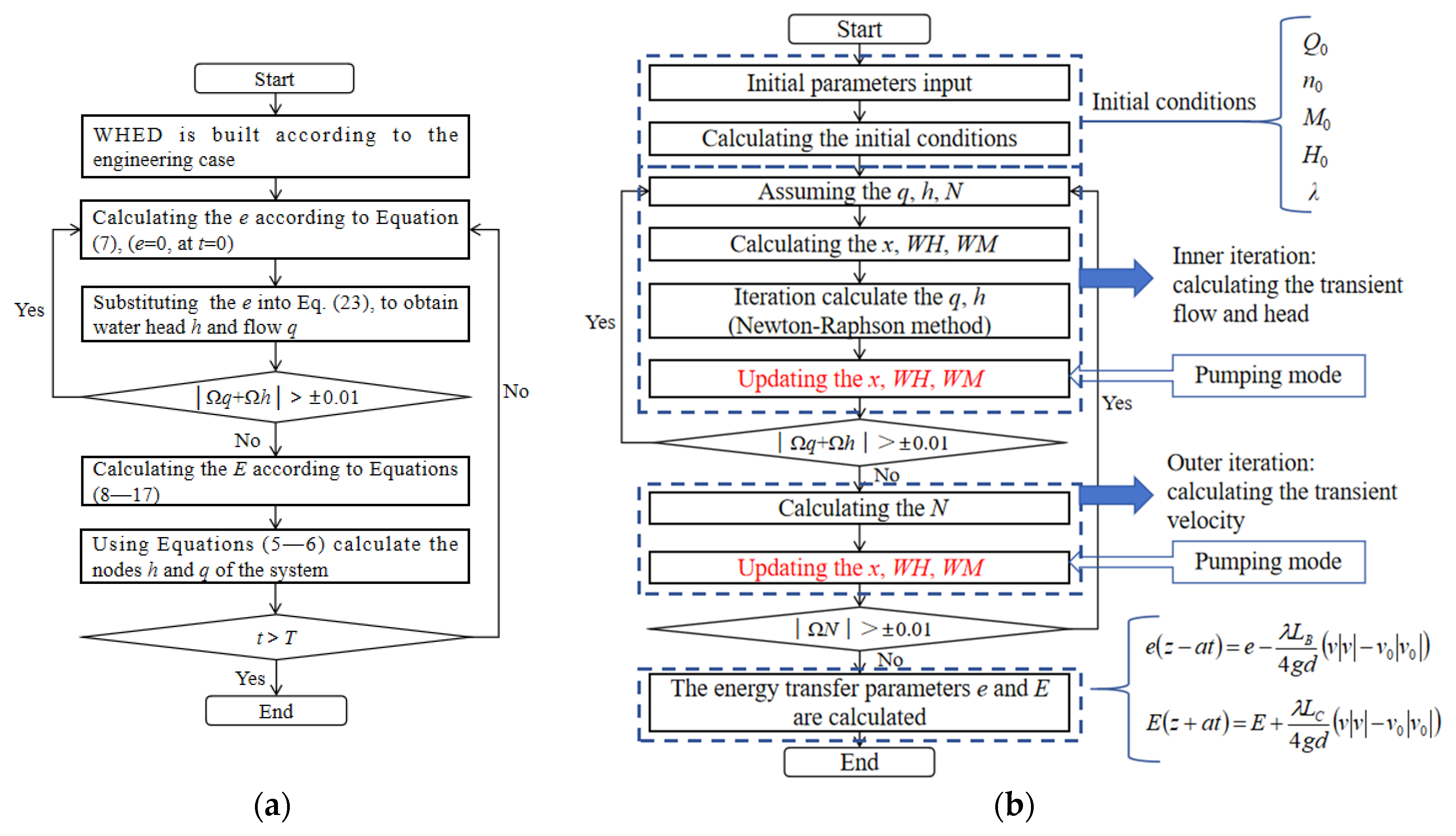
2. Method of Water Hammer Energy Difference (WHED)
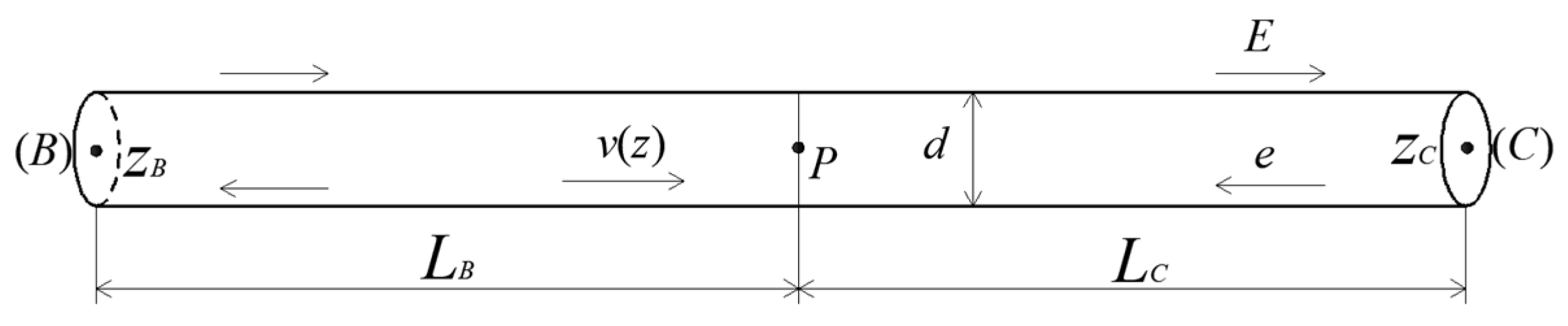
2.1. Fundamental Theory of WHED
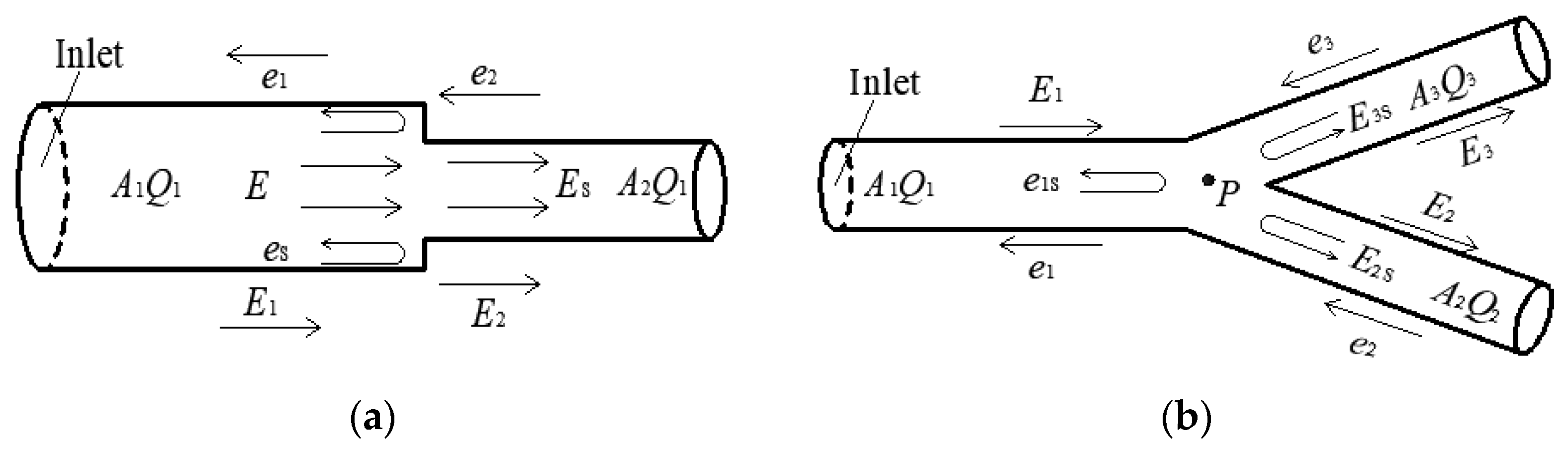
2.2. Pipeline with Varying Diameter and Bifurcated Conduit
2.3. Boundary Conditions of Pump Turbine
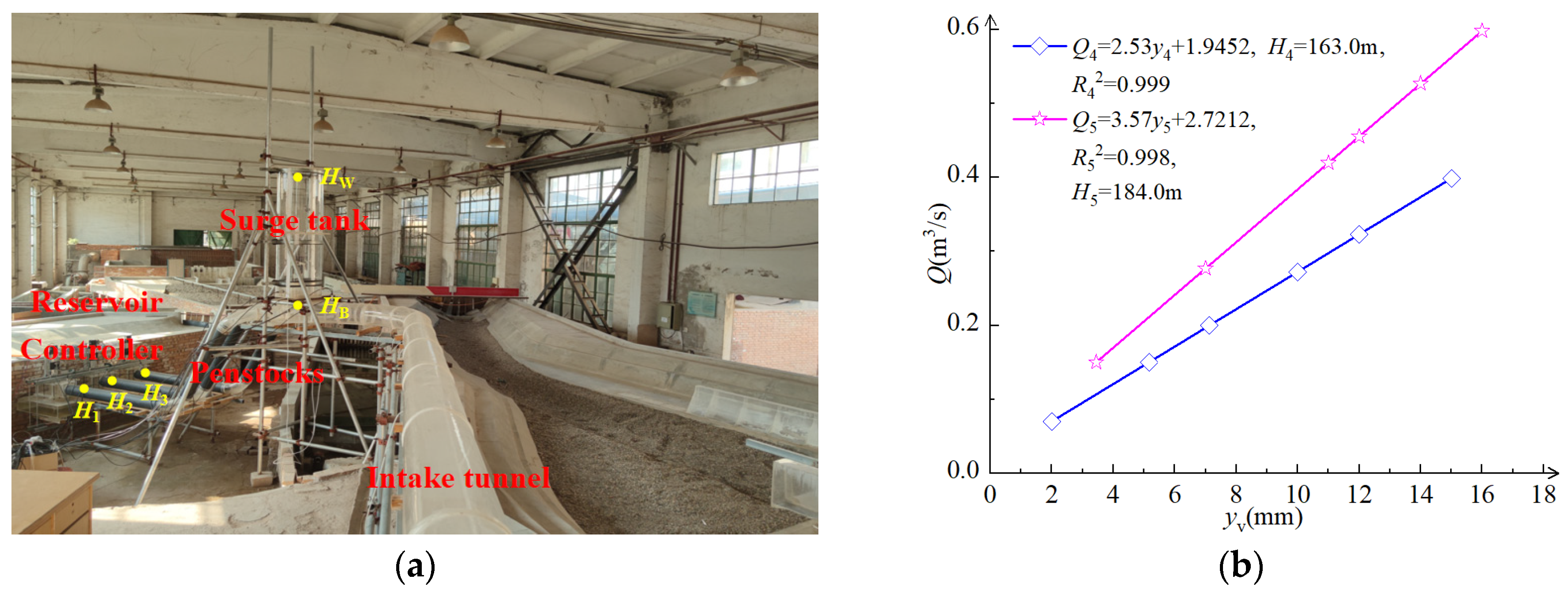
3. Validation of WHED in an HP
- (1)
- The overflow weir regulates the water level in the upper reservoir, and the flow rate is determined by the gauging weir in conjunction with the regulating valve.
- (2)
- A high-speed camera records the changes in waves within the surge tank.
- (3)
- The signal acquisition system monitors from 0 to 350 s.
- (4)
- The wave velocity a is measured by quickly cutting off the water flow using a gate to produce water hammer waves. The pressure sensors at both ends of the pipe record the first wave time t1, which is used to calculate the water hammer wave velocity (a = l/t1).
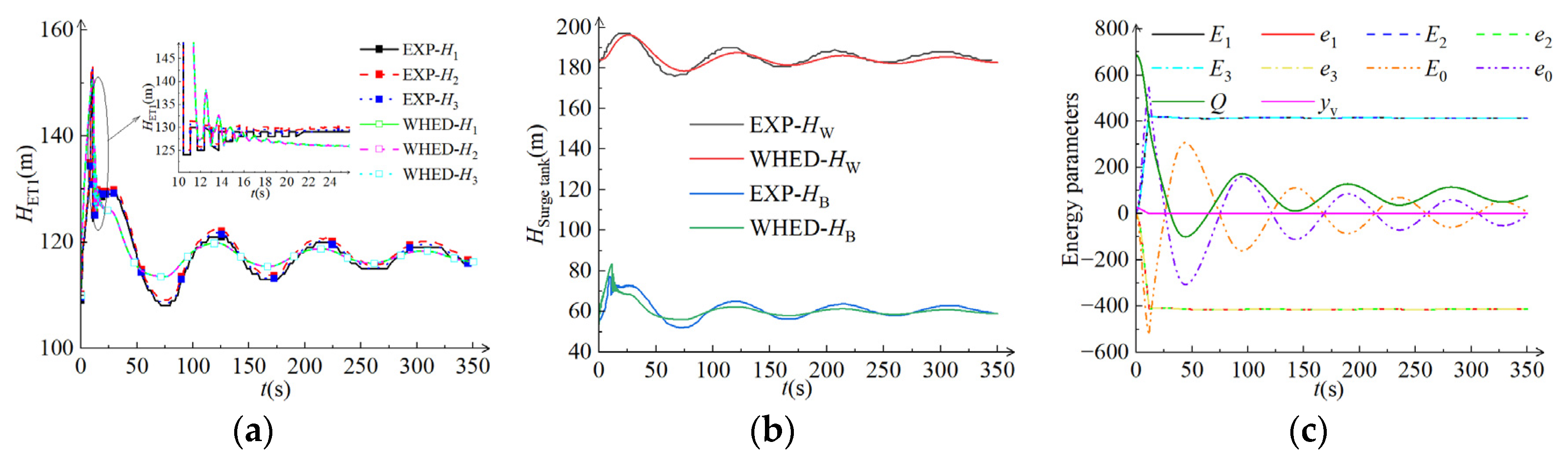
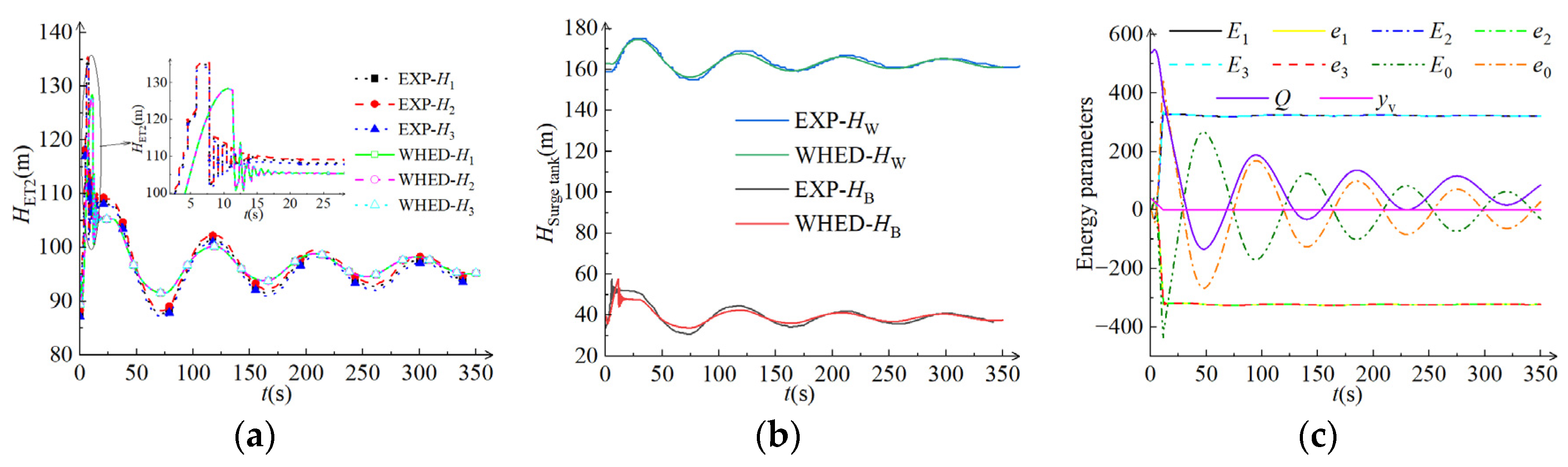
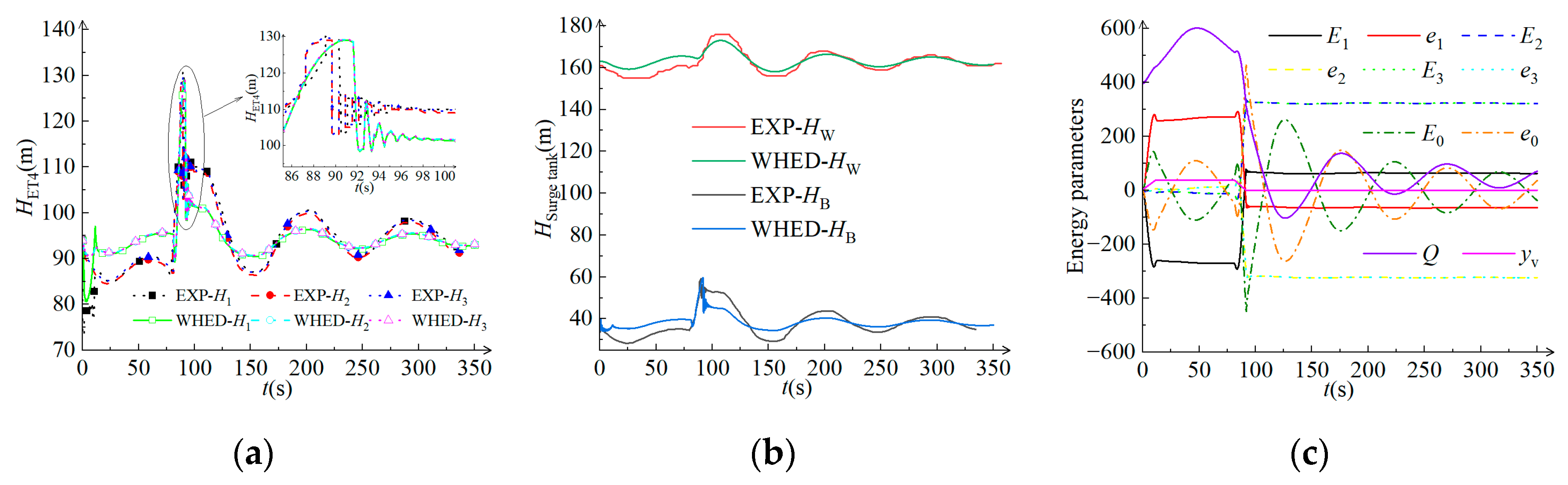
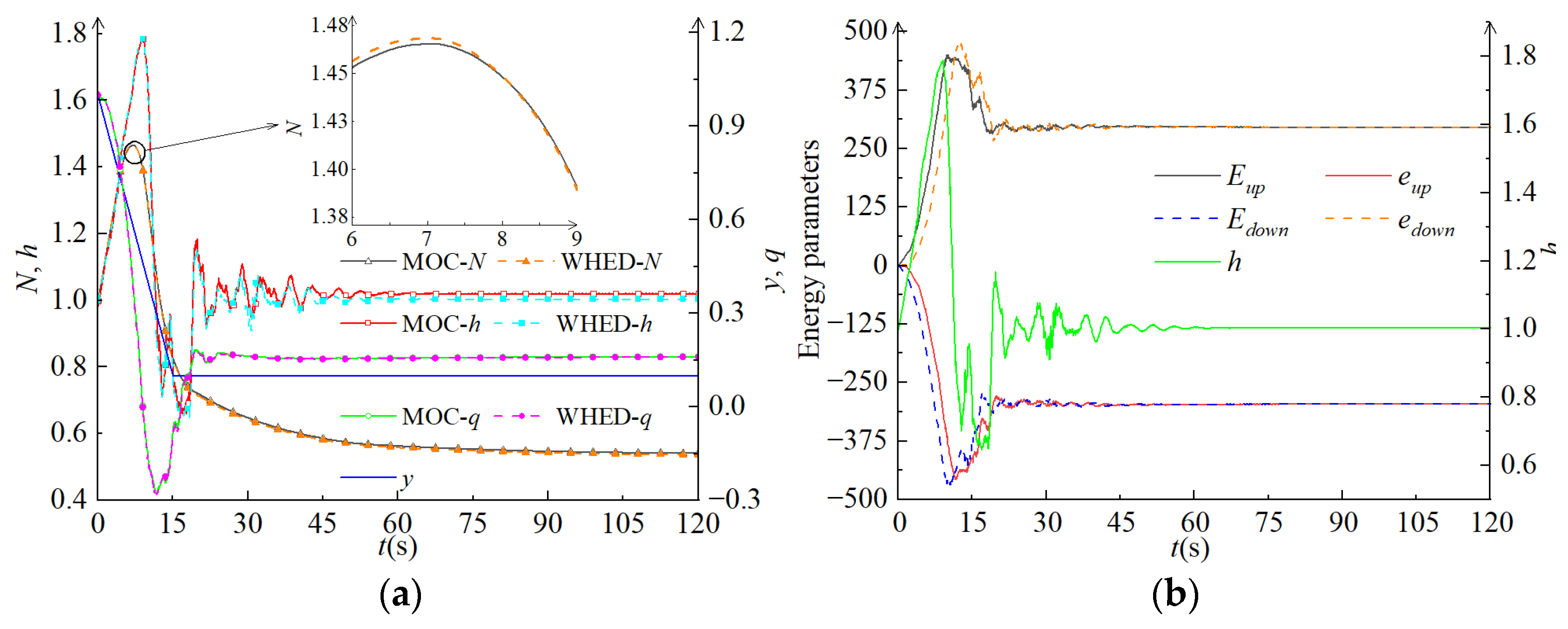
3.1. Comparative Analysis of Numerical and Experimental Results
3.2. Stability Analysis of Pressure Parameters in WDS of HP
3.3. Coupled Computation of 1D WHED with 3D Numerical Simulation
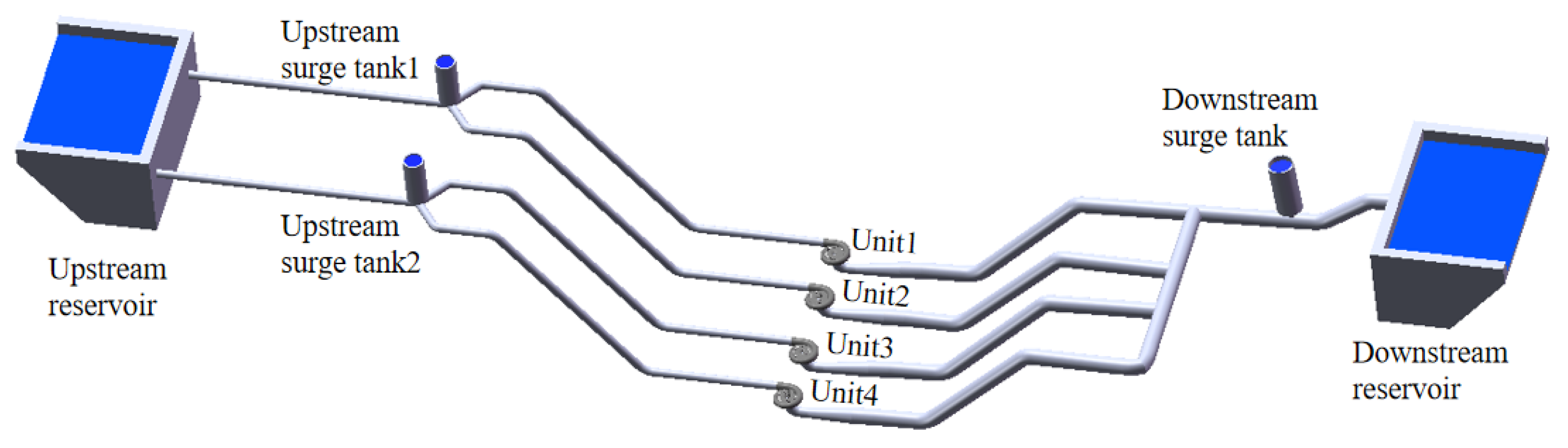
4. Validation and Application of WHED in a Pumped Storage Plant
4.1. Validation of Dangerous Working Conditions
- (1)
- WHED adopts energy transfer parameters from the initial and calculating time, using Equations (3)–(8) to derive boundary equations that solve the system. However, MOC uses two adjacent nodes at the previous moment to build the characteristic functions for the calculating moment. The functions constructed by each pair of nodes are generally different, making MOC more complicated than WHED.
- (2)
- WHED has better timeliness because it only needs to calculate the boundary conditions of the two endpoints of the target segment. By dynamically considering the wave propagation time, WHED allows for a larger time step, significantly improving computational efficiency. Conversely, MOC requires dividing the pipeline into multiple sections and constructing equations with adjacent nodes, requiring a smaller time step and the processing of a large amount of unnecessary nodes.
- (3)
- WHED provides a clear physical interpretation by analyzing changes in energy transfer parameters to explain pressure changes under transient conditions. However, MOC relies on characteristic equations based on the finite difference method, which do not directly characterize the causes of changes in the system’s flow regimes.
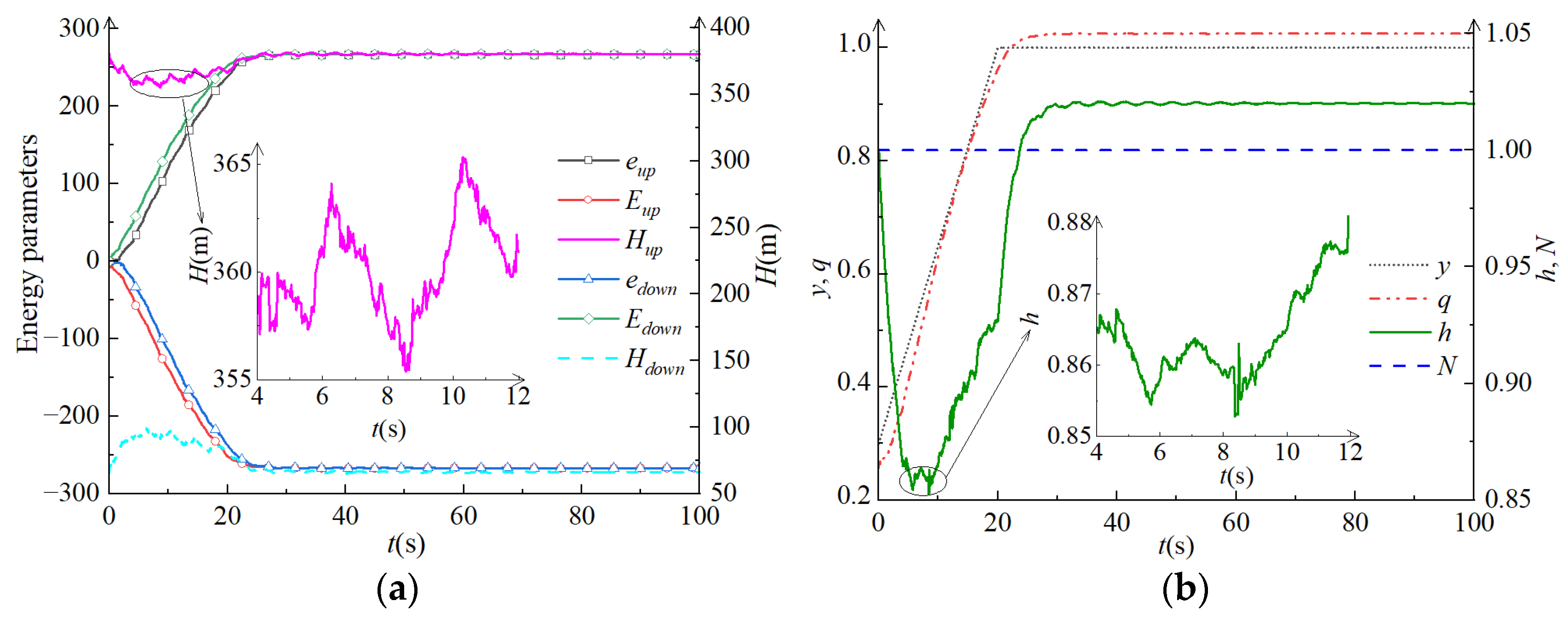
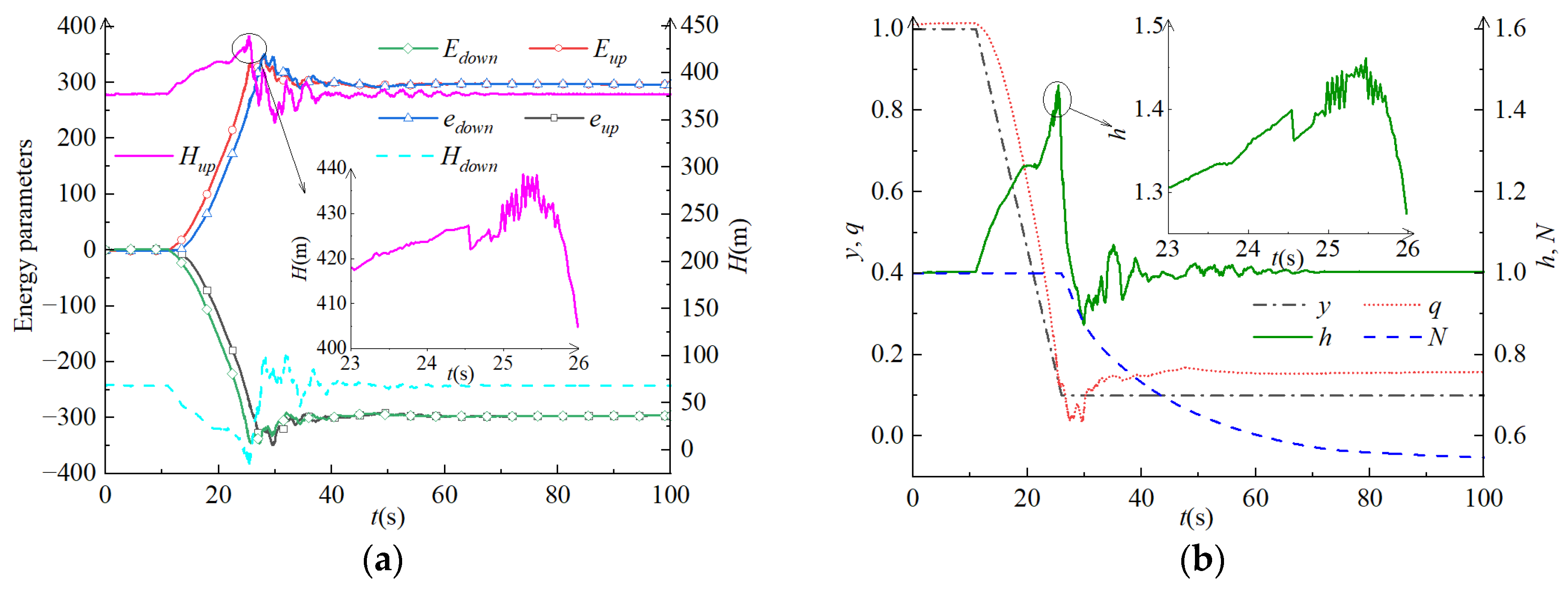
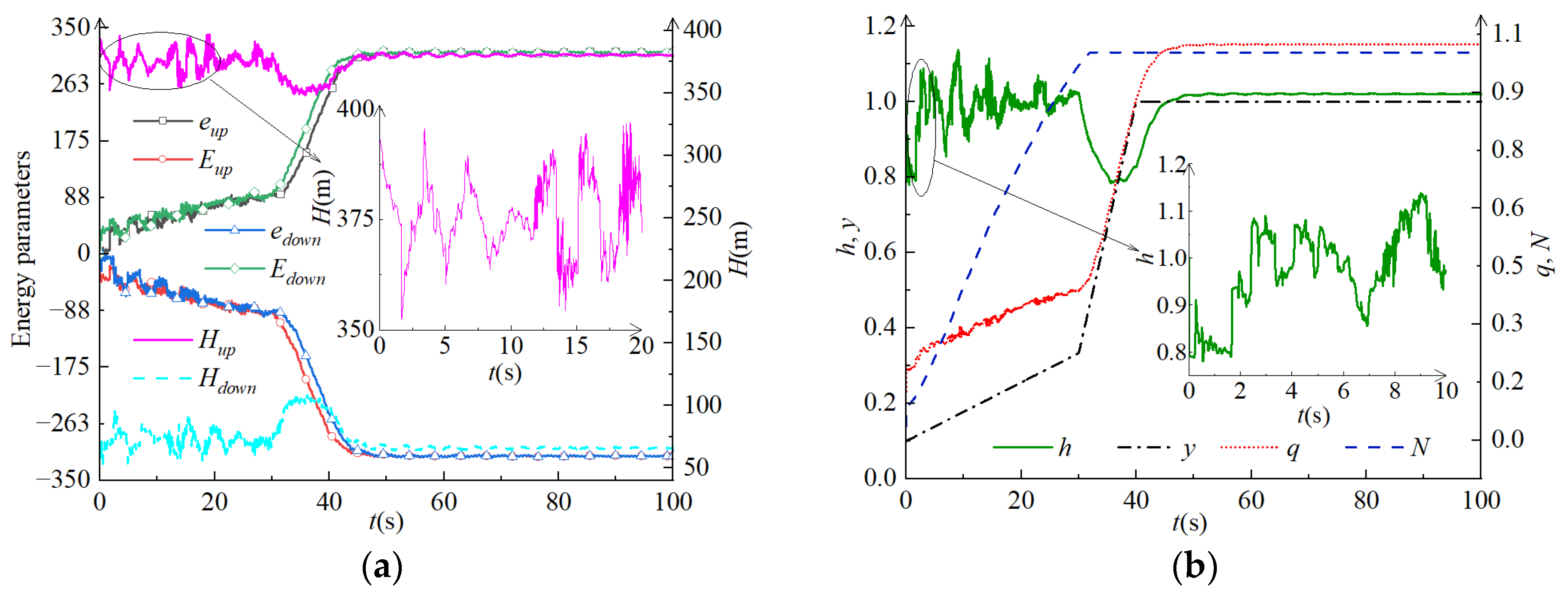
4.2. Calculation and Analysis of Generation Conditions
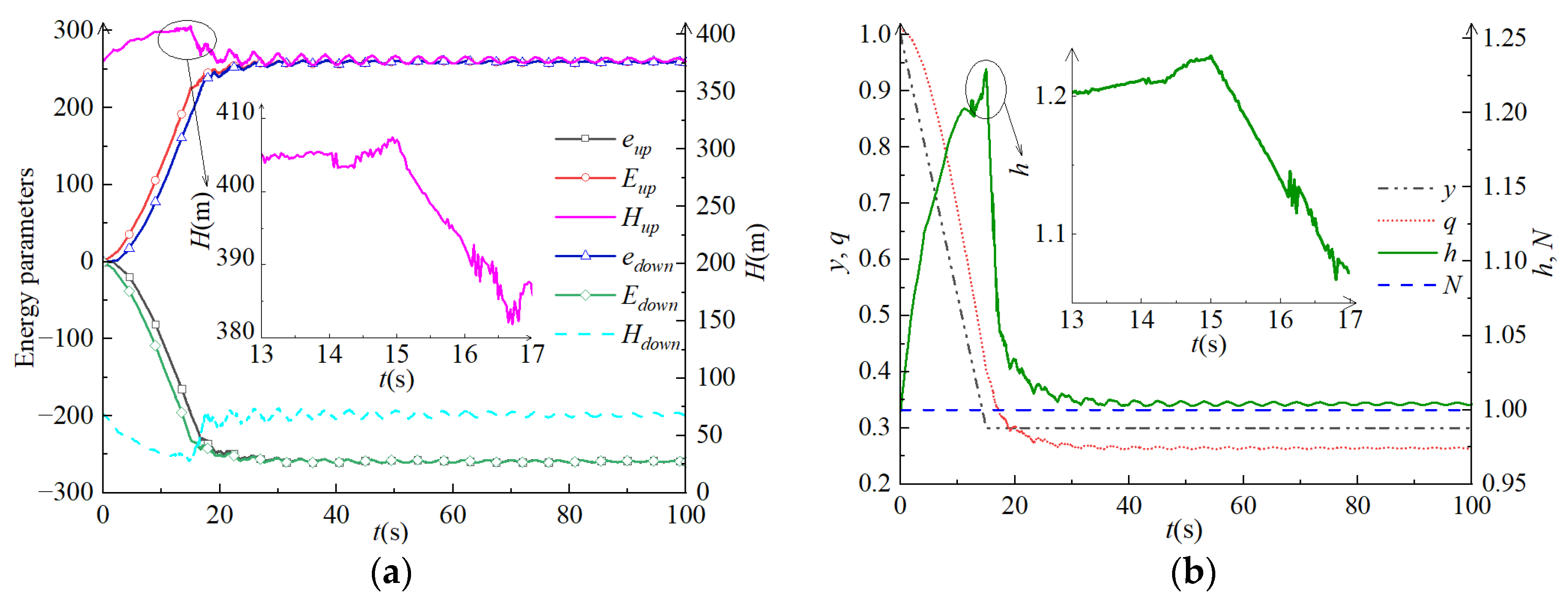
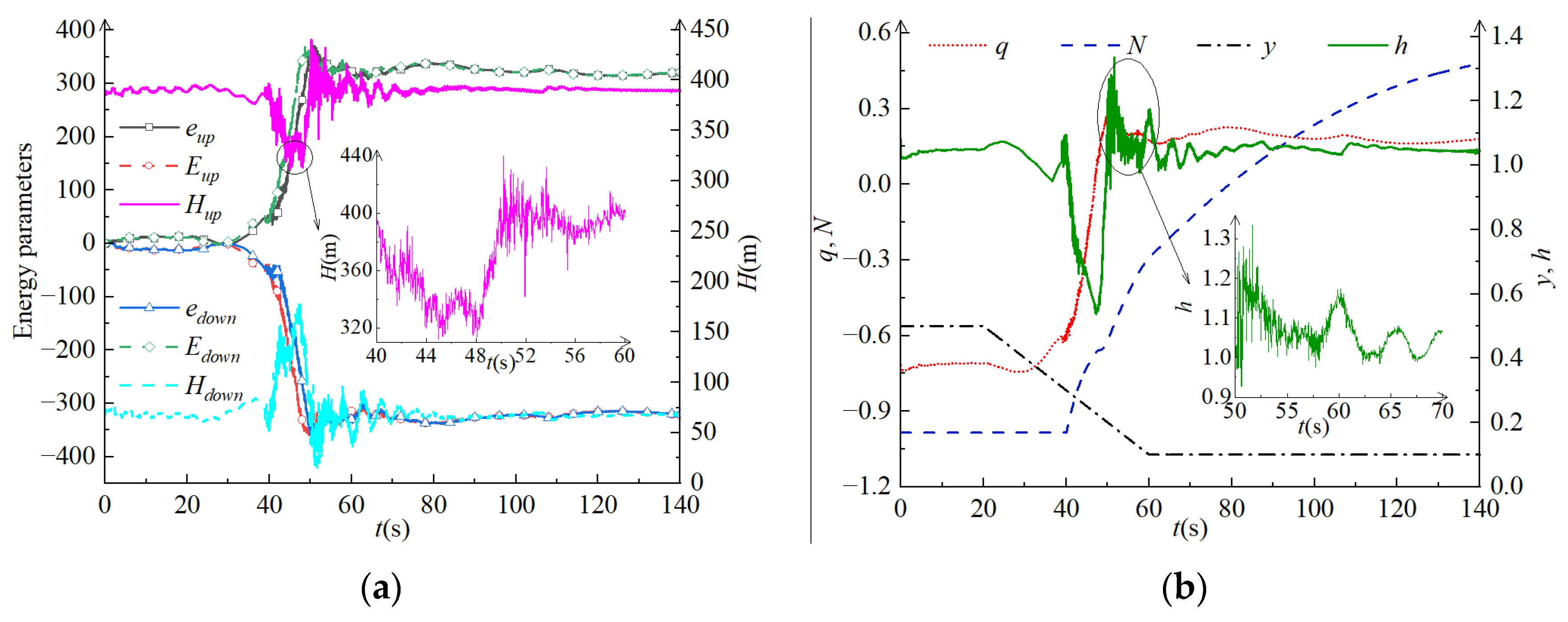
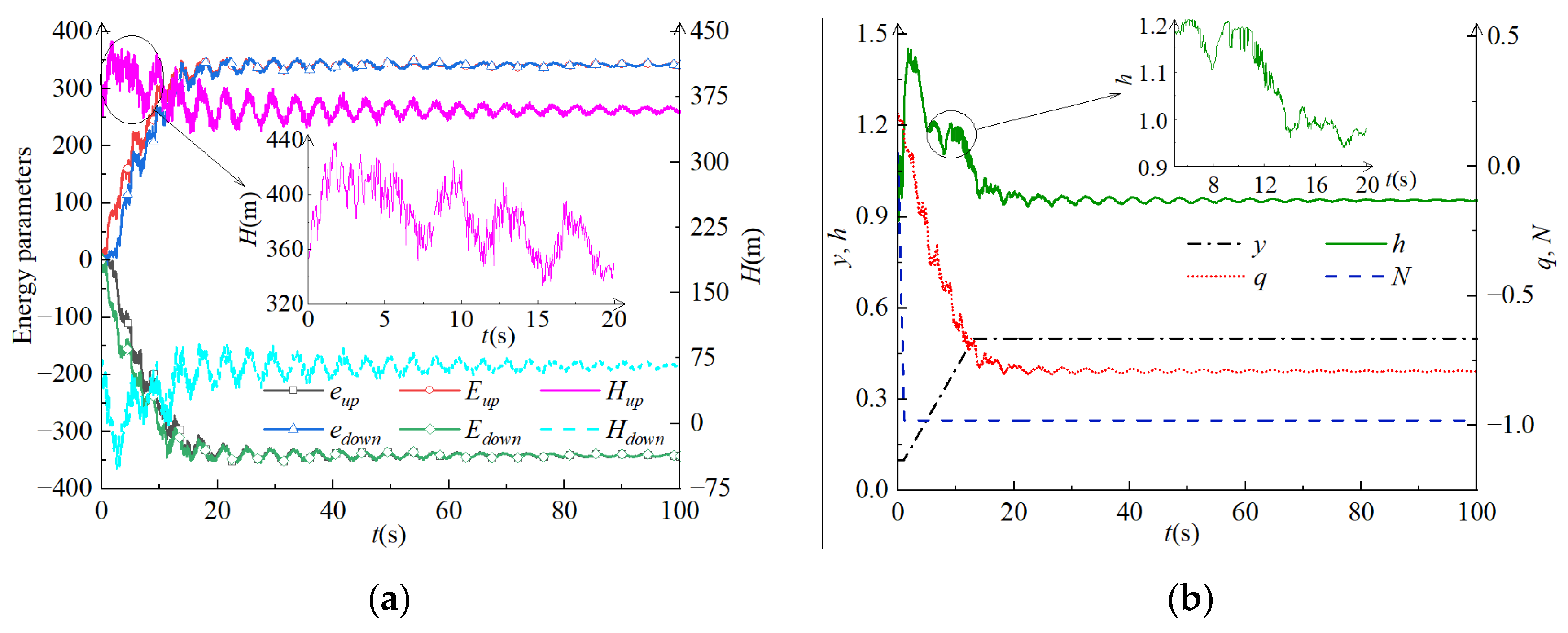
4.3. Calculation and Analysis of Pumping Conditions
4.4. Stability Analysis of Parameters (Pressure, Flow Rate, and Rotating Speed)
5. Conclusions
- (1)
- A key contribution of this paper is the proposal of WHED: WHED employs energy transfer parameters to characterize system stability, which makes it possible to explain the operations of HPs and PSPs from a physical point of view, and it further breaks the limitation of MOC being limited to mathematical analyses. Thus WHED does not need to take into account the Courant condition in its calculation. Also, WHED can be used with a large time step condition so that it can directly calculate the transient parameters of the target node, improving calculation speed by about 4 times compared with MOC.
- (2)
- The behavior of core parameters in WHED: Negative energy waves are always reflected from positive energy waves, meaning that the negative energy transfer parameter appears later than the positive energy transfer parameter. The energy transfer parameter reflects the energy variation in the system, and the pattern of energy transfer on the upstream side is opposite to that on the downstream side. The regulating well can effectively reduce water hammer pressure, so the energy transfer parameter in the regulating well changes in the opposite direction to that in the pipeline. Larger load adjustments correspond to greater changes in energy transfer parameters and increased system instability. The positive and negative values of the energy transfer parameters indicate different types of water hammer, with positive values corresponding to positive water hammer as pressure increases. The system is stable when the sum of the positive and negative energy transfer parameters equals zero.
- (3)
- This paper verifies the accuracy of WHED by comparing it with model tests and MOC. Due to limitations of the test bench, the wave speed used in the model experiment differs from that in the calculation, resulting in a larger discrepancy in the model test compared to the calculation verification. The smallest error occurs in the TC0 condition, demonstrating that the water hammer energy difference calculation method is highly reliable based on the comparison of results. Additionally, the one-dimensional and three-dimensional coupled calculations highlight the broad applicability of WHED in scientific research. The coupling performance is well validated through comparison with experimental results, and CFD simulations of TKE distribution in the regulating well show that turbulence is more intense in the low-water-level transition condition.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations and Symbols
| Abbreviations | Q11 | Unit flow rate, m3/s | |
| WDS | Water diversion system | Qr | Rated flow rate, m3/s |
| WHED | Water hammer energy difference | Hr | Rated water head, m |
| PSP | Pumped storage plant | H11 | Unit water head, m |
| HP | Hydropower plant | nr | Rated rotation speed, r/min |
| MOC | Method of characteristics | n11 | Unit rotation speed, r/min |
| 1D | One-dimensional | Mr | Rated torque, kN·m |
| 3D | Three-dimensional | t | Time, s |
| MDS | Multidimensional scale | y | Relative opening of guide vane, - |
| EXP | Experiment | yv | Relative opening of guide valve, - |
| SSR | Sum of squares of residuals | HR | Reservoir level, m |
| TSS | Total sum of squares | R2 | Linearly dependent coefficient, - |
| Symbols | Hw | Water level of surge tank, m | |
| v | Flow velocity of pipe cross-section, m/s | HB | Bottom pressure of surge tank, m |
| h | Water head, m | Δ | Maximum fault tolerance, - |
| l | Length of pipe, m | u1 | Amplitude of parameter, - |
| d | Diameter of pipe, m | u2 | Change rate of parameter, - |
| a | Wave velocity of water hammer, m/s | u | Stability coefficient, - |
| λ | Head loss coefficient, - | The weighted average, - | |
| H0 | Initial water head, m | c | Sum of , - |
| v0 | Initial flow velocity, m/s | δc | Velocity scale |
| E | Transfer parameters of positive energy, - | δl | Geometric scale |
| e | Transfer parameters of negative energy, - | Ω | Differences between predicted and calculated values, - |
| A | Sectional area of pipe, m3 | ||
| n | Rotation speed, r/min | WH, WM | Flow rate and torque coefficient after Suter transformation, - |
| M | Torque, kN·m | ||
| Q | Flow rate, m3/s | ||
References
- Liu, X.; Ni, Y.; Sun, Y.; Wang, J.; Wang, R.; Sun, Q. Multi-VPPs power-carbon joint trading optimization considering low-carbon operation mode. J. Energy Storage 2024, 83, 110786. [Google Scholar]
- Ma, X.; Zhai, Y.; Zhang, T.; Yao, X.; Hong, J. What changes can solar and wind power bring to the electrification of China compared with coal electricity: From a cost-oriented life cycle impact perspective. Energy Convers. Manag. 2023, 289, 117162. [Google Scholar] [CrossRef]
- Morabito, A.; Hendrick, P. Pump as turbine applied to micro energy storage and smart water grids: A case study. Appl. Energy 2019, 241, 567–597. [Google Scholar]
- Ali, M.; Ahmad, M.; Koondhar, M.A.; Akram, M.S.; Verma, A.; Khan, B. Maximum power point tracking for grid-connected photovoltaic system using adaptive fuzzy logic controller. Comput. Electr. Eng. 2023, 110, 108879. [Google Scholar] [CrossRef]
- Oskouei, M.Z.; Yazdankhah, A.S. Scenario-based stochastic optimal operation of wind, photovoltaic, pump-storage hybrid system in frequency-based pricing. Energy Convers. Manag. 2015, 105, 1105–1114. [Google Scholar] [CrossRef]
- Fang, G.; Chen, G.; Yang, K.; Yin, W.; Tian, L. How does green fiscal expenditure promote green total factor energy efficiency?-Evidence from Chinese 254 cities. Appl. Energy 2024, 353, 122098. [Google Scholar] [CrossRef]
- Luo, X.Q.; Zhu, G.J.; Feng, J.J. The technology progress and development trend of hydraulic turbine. J. Hydroelectr. Eng. 2020, 39, 1–18. (In Chinese) [Google Scholar]
- Chen, Y.; Deng, C.; Wu, H.; Li, D.; Chen, M.; Peng, P.; Zhao, Y. Multi-stage Soft Coordinated Control of Variable Speed Pumped Storage Unit in the Process of Mode Conversion Under the Generation Condition. Proc. CSEE 2021, 41, 5258–5274. (In Chinese) [Google Scholar]
- Hu, J.; Yang, J.; He, X.; Zhao, Z.; Yang, J. Transient analysis of a hydropower plant with a super-long headrace tunnel during load acceptance: Instability mechanism and measurement verification. Energy 2023, 263, 125671. [Google Scholar] [CrossRef]
- Zhao, H.J.; Liu, S.B.; Zhang, Y.H. Study on reservoir ice regime of Pushihe pumped-storage power station. Water Power 2019, 45, 90–94. (In Chinese) [Google Scholar]
- Yuan, B.; Li, C.; Feng, Y. Partition of operating regions in turbine mode for No.4 unit of Pushihe pumped storage power station. Water Resour. Power 2017, 35, 153–157. (In Chinese) [Google Scholar]
- Lu, J.; Wu, G.; Zhou, L.; Wu, J. Finite Volume method for modeling the load-rejection process of a hydropower plant with an air cushion surge chamber. Water 2023, 15, 682. [Google Scholar] [CrossRef]
- Ma, Z.; Zhu, B. Pressure fluctuations in vaneless space of pump-turbines with large blade lean runners in the S-shaped region. Renew. Energy 2020, 153, 1283–1295. [Google Scholar] [CrossRef]
- Nasir, J.; Javed, A.; Ali, M.; Ullah, K.; Kazmi, S.A.A. Capacity optimization of pumped storage hydropower and its impact on an integrated conventional hydropower plant operation. Appl. Energy 2022, 323, 119651. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Z.; Cheng, Y.; Zhang, X.; Liu, K.; Xia, L. Differences of Flow Patterns and Pressure Pulsations in Four Prototype Pump-Turbines during Runaway Transient Processes. Energies 2020, 13, 5296. [Google Scholar] [CrossRef]
- Li, Z.; Bi, H.; Karney, B.; Wang, Z.; Yao, Z. Three-dimensional transient simulation of a prototype pump-turbine during normal turbine shutdown. J. Hydraul. Res. 2017, 55, 520–537. [Google Scholar] [CrossRef]
- Su, W.-T.; Li, X.-B.; Xia, Y.-X.; Liu, Q.-Z.; Binama, M.; Zhang, Y.-N. Pressure fluctuation characteristics of a model pump-turbine during runaway transient. Renew. Energy 2021, 163, 517–529. [Google Scholar] [CrossRef]
- Henclik, S. Analytical solution and numerical study on water hammer in a pipeline closed with an elastically attached valve. J. Sound Vib. 2018, 417, 245–259. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Bergant, A.; Stosiak, M.; Deptuła, A.; Karpenko, M.; Kubrak, M.; Kodura, A. Water Hammer Simulation Using Simplified Convolution-Based Unsteady Friction Model. Water 2022, 14, 3151. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, Y.; Xia, L.; Meng, W.; Liu, K.; Zhang, X. Evolutions of flow patterns and pressure fluctuations in a prototype pump-turbine during the runaway transient process after pump-trip. Renew. Energy 2020, 152, 149–1159. [Google Scholar] [CrossRef]
- Hou, J.; Li, G.H.; Li, X.X.; Wu, X.M.; Chen, Y.M. Transient Process of Complex Hydraulic System; China & Water Power Press: Beijing, China, 2019. (In Chinese) [Google Scholar]
- Zhang, L.; Wu, Q.; Ma, Z.; Wang, X. Transient vibration analysis of unit-plant structure for hydropower station in sudden load increasing process. Mech. Syst. Signal Process. 2019, 120, 486–504. [Google Scholar] [CrossRef]
- Telikani, A.; Rossi, M.; Khajehali, N.; Renzi, M. Pumps-as-Turbines (PaTs) performance prediction improvement using evolutionary artificial neural networks. Appl. Energy 2023, 330, 120316. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Zheng, Y.; Rodriguez, E.F.; Liu, H.; Feng, J. Analysis on Guide Vane Closure Schemes of High-Head Pumped Storage Unit during Pump Outage Condition. Math. Probl. Eng. 2019, 2019, 8262074. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, J.; Zhou, L. Hydraulic Transients in the Long Diversion-Type Hydropower Station with a Complex Differential Surge Tank. Sci. World J. 2014, 2014, 241868. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wan, Z.; Huang, W.; Zeng, M.; Fang, J.; Xie, J. Robust comprehensive evaluation of guide vane closure law in hydraulic turbines in moderately-high head hydropower plants. J. Tsinghua Univ. (Sci. Technol.) 2023, 63, 125–133. (In Chinese) [Google Scholar]
- Wang, Y.; Zhang, J.; Xu, T.; Liu, Y.; Yao, T.; Wang, K.; Zhang, M. Air valve arrangement criteria for preventing secondary pipe bursts in long-distance gravitational water supply systems. Aqua-Water Infrastruct. Ecosyst. Soc. 2023, 72, 1566–1581. [Google Scholar] [CrossRef]
- Trivedi, C.; Gandhi, B.K.; Cervantes, M.J.; Dahlhaug, O.G. Experimental investigations of a model Francis turbine during shutdown at synchronous speed. Renew. Energy 2015, 83, 828–836. [Google Scholar] [CrossRef]
- Ye, J.; Do, N.C.; Zeng, W.; Lambert, M. Physics-informed neural networks for hydraulic transient analysis in pipeline systems. Water Res. 2022, 211, 118828. [Google Scholar] [CrossRef]
- Chen, S.; Wang, J.; Zhang, J.; Yu, X.; He, W. Transient behavior of two-stage load rejection for multiple units system in pumped storage plants. Renew. Energy 2020, 169, 1012–1022. [Google Scholar] [CrossRef]
- Mao, X.; Zhong, P.; Wang, Y.; Tan, Q.; Cui, Q. Study on the evolution of transient flow field in WDS based on numerical and experimental methods. J. Energy Storage 2023, 73, 108996. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, J.; Wang, P.; Wang, Y. Study on similitude method for turbine considering working fluid physical properties variation. Appl. Energy 2023, 338, 120930. [Google Scholar] [CrossRef]
- Zhang, P.; Cheng, Y.; Xue, S.; Hu, Z.; Tang, M.; Chen, X. 1D-3D coupled simulation method of hydraulic transients in ultra-long hydraulic systems based on OpenFOAM. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2229889. [Google Scholar] [CrossRef]
- Bi, H.; Chen, F.; Wang, C.; Wang, Z.; Fan, H.; Luo, Y. Analysis of dynamic performance in a pump-turbine during the successive load rejection. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012152. [Google Scholar] [CrossRef]
- Cherny, S.; Chirkov, D.; Bannikov, D.; Lapin, V.; Skorospelov, V.; Eshkunova, I.; Avdushenko, A. 3D numerical simulation of transient processes in hydraulic turbines. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012071. [Google Scholar] [CrossRef]
- Zhang, X.-X.; Cheng, Y.-G.; Yang, J.-D.; Xia, L.-S.; Lai, X. Simulation of the load rejection transient process of a francis turbine by using a 1D-3D coupling approach. J. Hydrodyn. 2014, 26, 715–724. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Zhang, J.B.; Chen, G.; Zhang, D. Automatic Regulation of Water Turbine; China Water & Power Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Zheng, Y.; Zhang, J. Hydro Unit Transition Process; Peking University Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Mao, X.L.; Wen, G.Q. Pumped Storage Power Station Power Generation Mode Full Load Condition and Pumping Mode Power Off Condition Transition Process Calculation Software, version 2023SR1542053; Northwest A & F University: Xianyang, China, 2023. (In Chinese)

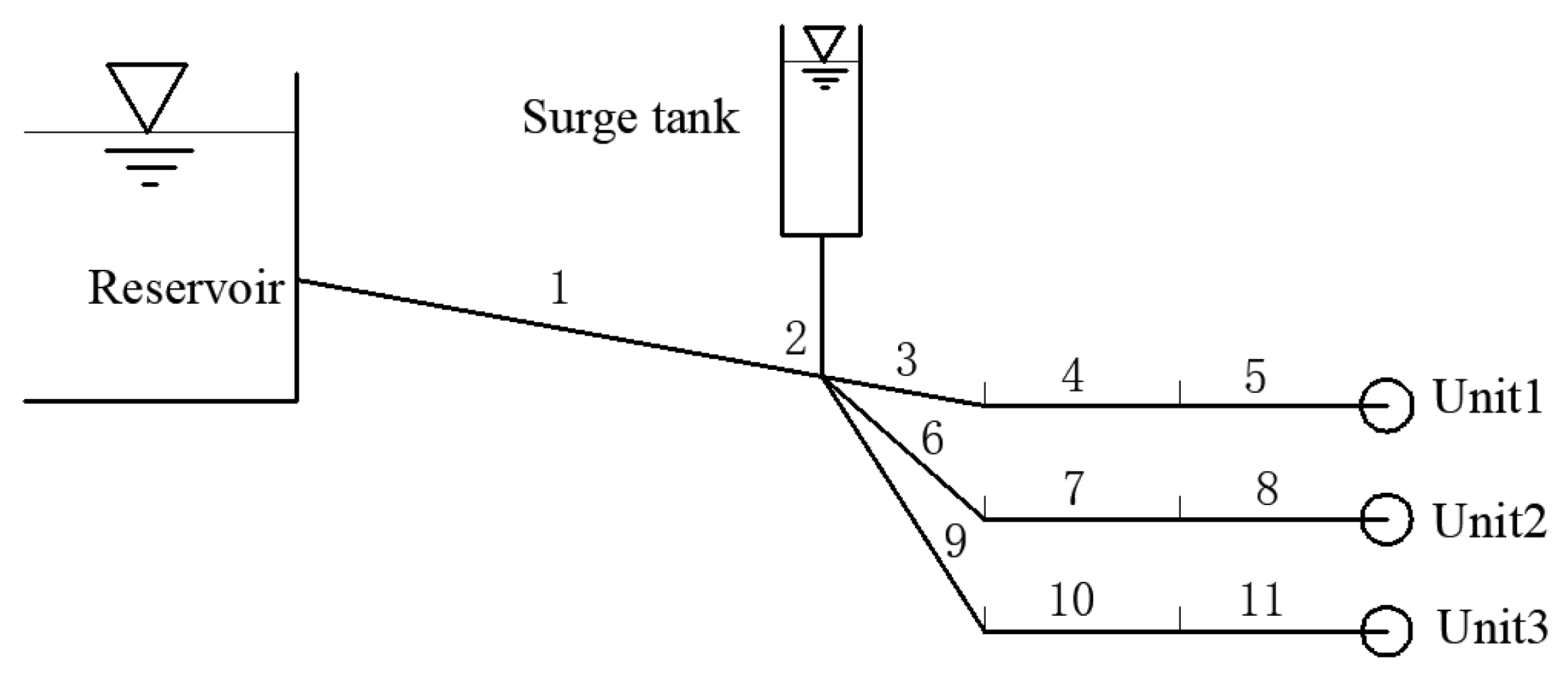





| Number | Length (m) | Pipe Diameter (m) | Area (m2) | Wave Velocity (m/s) | Roughness |
|---|---|---|---|---|---|
| 1 | 493.42 | 11 | 94.99 | 1319 | 0.015 |
| 2 | 7.8 | 11 | 94.99 | 1319 | 0.015 |
| 3 | 19.3 | 6.35 | 31.65 | 1157.66 | 0.012 |
| 4 | 65.55 | 6.35 | 31.65 | 1157.66 | 0.012 |
| 5 | 53.20 | 6.35 | 31.65 | 1157.66 | 0.012 |
| 6 | 19.3 | 6.35 | 31.65 | 1157.66 | 0.012 |
| 7 | 65.55 | 6.35 | 31.65 | 1157.66 | 0.012 |
| 8 | 53.20 | 6.35 | 31.65 | 1157.66 | 0.012 |
| 9 | 19.3 | 6.35 | 31.65 | 1157.66 | 0.012 |
| 10 | 65.55 | 6.35 | 31.65 | 1157.66 | 0.012 |
| 11 | 53.20 | 6.35 | 31.65 | 1157.66 | 0.012 |
| Conditions | Description |
|---|---|
| ET1 | Upstream reservoir—184 m, three units rejecting loads at the same time |
| ET2 | Upstream reservoir—163 m, three units rejecting loads at the same time |
| ET3 | Upstream reservoir—184 m, two units operating at full load, one unit increasing to full load, and then three units rejecting loads at the same time |
| ET4 | Upstream reservoir—163 m, two units operating at full load, one unit increasing to full load, and then three units rejecting loads at the same time |
| Conditions | H1 | H2 (H3) | Hw | ||||||
|---|---|---|---|---|---|---|---|---|---|
| u1 | u2 | u | u1 | u2 | u | u1 | u2 | u | |
| ET1 | 19.51 | 3.71 | 17.14 | 19.61 | 3.71 | 16.91 | 8.82 | 0.49 | 8.49 |
| ET2 | 19.65 | 3.56 | 17.24 | 19.05 | 3.56 | 16.42 | 9.09 | 0.42 | 8.74 |
| ET3 | 19.92 | 3.88 | 17.51 | 15.84 | 3.83 | 13.79 | 7.17 | 0.12 | 6.89 |
| ET4 | 22.06 | 3.65 | 19.29 | 18.92 | 3.72 | 16.34 | 6.84 | 0.17 | 6.57 |
| Conditions | ||||
|---|---|---|---|---|
| ET1 | 7.34 | 6.60 | 1.53 | 15.47 |
| ET2 | 7.13 | 6.40 | 1.52 | 15.05 |
| ET3 | 7.46 | 5.38 | 1.26 | 14.10 |
| ET4 | 8.22 | 6.37 | 1.18 | 15.77 |
| Designation | Transitions | Description |
|---|---|---|
| TC0 | Load rejection (Generation mode) | Upstream reservoir—normal water level Initial state—the rated condition Load rejection—guide vanes spend 15 s from 100% to 10% opening |
| TC1 | Load increment (Generation mode) | Upstream reservoir—normal water level Initial state—generating mode with 30% load Load increment—guide vanes spend 20 s from 30% to 100% opening |
| TC2 | Load reduction (Generation mode) | Upstream reservoir—normal water level Initial state—the rated condition Load reduction—guide vanes spend 15 s from 100% to 30% opening |
| TC3 | Shutdown (Generation mode) | Upstream reservoir—normal water level Initial state—the rated condition Shutdown—guide vanes spend 15 s from 100% to 10% opening |
| TC4 | Startup (Generation mode) | Upstream reservoir—normal water level Initial state—shutdown Shutdown—guide vanes spend 20 s from 10% to 100% opening |
| PC0 | Power outage (Pumping mode) | Downstream reservoir—normal water level Initial state—the rated condition Shutdown—guide vanes spend 15 s from 50% to 10% opening |
| PC1 | Shutdown (Pumping mode) | Downstream reservoir—normal water level Initial state—the rated condition Shutdown—guide vanes spend 40 s from 50% to 10% opening |
| PC2 | Startup (Pumping mode) | Downstream reservoir—normal water level Initial state—shutdown Shutdown—guide vanes spend 12 s from 10% to 50% opening |
| Nmax | Nmin | hmax | hmin | qmax | qmin | ||
|---|---|---|---|---|---|---|---|
| WHED | 1.469 | 0.541 | 1.796 | 0.673 | 1.010 | −0.277 | |
| TC0 | MOC | 1.465 | 0.537 | 1.794 | 0.659 | 1.000 | −0.285 |
| Δ2 | 0.2% | 0.7% | 0.1% | 1.9% | 1.0% | 2.8% | |
| WHED | 0.560 | −0.957 | 1.305 | 0.543 | 0.301 | −0.709 | |
| PC0 | MOC | 0.557 | −0.956 | 1.297 | 0.533 | 0.298 | −0.717 |
| Δ2 | 0.5% | 0.1% | 0.6% | 1.8% | 1.0% | 1.1% |
| TC1 | Emax | emax | Hest (m) | T (s) |
|---|---|---|---|---|
| Upstream side | −265.8 | 265.7 | 355.6 | 8.6 |
| Downstream side | 265.7 | −265.2 | 99.1 | 9.3 |
| TC2 | Emax | emax | Hest (m) | T (s) |
|---|---|---|---|---|
| Upstream side | 258.27 | −258.69 | 407.08 | 15.1 |
| Downstream side | −257.46 | 257.63 | 28.06 | 15.2 |
| TC3 | Emax | emax | Hest (m) | T (s) |
|---|---|---|---|---|
| Upstream side | 347.86 | −348.22 | 438.73 | 25.24 |
| Downstream side | −349.21 | 350.68 | −17.46 | 25.47 |
| TC4 | Emax | emax | Hest (m) | T (s) |
|---|---|---|---|---|
| Upstream side | −308.49 | 309.35 | 348.6 | 35.87 |
| Downstream side | 307.37 | −307.57 | 36.81 | 36.09 |
| PC1 | Emax | emax | Hest (m) | T (s) |
|---|---|---|---|---|
| Upstream side | −370.59 | 370.05 | 311.73 | 44.97 |
| Downstream side | 369.64 | −370.45 | 159.29 | 42.63 |
| PC2 | Emax | emax | Hest (m) | T (s) |
|---|---|---|---|---|
| Upstream side | 348.77 | −348.17 | 438.58 | 1.83 |
| Downstream side | −344.34 | 344.12 | −50.14 | 2.58 |
| Conditions | q | h | N | ||||||
|---|---|---|---|---|---|---|---|---|---|
| u1 | u2 | u | u1 | u2 | u | u1 | u2 | u | |
| TC0 | 0.64 | 0.11 | 0.587 | 0.57 | 0.09 | 0.498 | 0.47 | 0.07 | 0.418 |
| TC1 | 0.39 | 0.03 | 0.345 | 0.08 | 0.02 | 0.071 | 0.00 | 0.00 | 0.000 |
| TC2 | 0.36 | 0.03 | 0.327 | 0.11 | 0.02 | 0.097 | 0.00 | 0.00 | 0.000 |
| TC3 | 0.39 | 0.06 | 0.357 | 0.30 | 0.03 | 0.260 | 0.23 | 0.01 | 0.201 |
| TC4 | 0.38 | 0.01 | 0.343 | 0.17 | 0.07 | 0.155 | 0.42 | 0.03 | 0.369 |
| PC0 | 0.50 | 0.10 | 0.460 | 0.39 | 0.06 | 0.341 | 0.29 | 0.01 | 0.254 |
| PC1 | 0.49 | 0.04 | 0.445 | 0.37 | 0.03 | 0.319 | 0.24 | 0.01 | 0.210 |
| PC2 | 0.49 | 0.04 | 0.445 | 0.24 | 0.04 | 0.210 | 0.50 | 0.20 | 0.461 |
| Conditions | ||||
|---|---|---|---|---|
| TC0 | 0.27 | 0.13 | 0.11 | 0.51 |
| TC1 | 0.16 | 0.02 | 0.00 | 0.18 |
| TC2 | 0.15 | 0.03 | 0.00 | 0.18 |
| TC3 | 0.16 | 0.07 | 0.05 | 0.28 |
| TC4 | 0.16 | 0.04 | 0.10 | 0.30 |
| PC0 | 0.21 | 0.09 | 0.07 | 0.37 |
| PC1 | 0.20 | 0.09 | 0.06 | 0.35 |
| PC2 | 0.20 | 0.06 | 0.12 | 0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, X.; Wen, G.; Wang, Y.; Hu, J.; Gan, X.; Zhong, P. Development of WHED Method to Study Operational Stability of Typical Transitions in a Hydropower Plant and a Pumped Storage Plant. Energies 2025, 18, 1549. https://doi.org/10.3390/en18061549
Mao X, Wen G, Wang Y, Hu J, Gan X, Zhong P. Development of WHED Method to Study Operational Stability of Typical Transitions in a Hydropower Plant and a Pumped Storage Plant. Energies. 2025; 18(6):1549. https://doi.org/10.3390/en18061549
Chicago/Turabian StyleMao, Xiuli, Guoqing Wen, Yuchuan Wang, Jiaren Hu, Xuetao Gan, and Pengju Zhong. 2025. "Development of WHED Method to Study Operational Stability of Typical Transitions in a Hydropower Plant and a Pumped Storage Plant" Energies 18, no. 6: 1549. https://doi.org/10.3390/en18061549
APA StyleMao, X., Wen, G., Wang, Y., Hu, J., Gan, X., & Zhong, P. (2025). Development of WHED Method to Study Operational Stability of Typical Transitions in a Hydropower Plant and a Pumped Storage Plant. Energies, 18(6), 1549. https://doi.org/10.3390/en18061549







