Day-Ahead Net Load Forecasting for Renewable Integrated Buildings Using XGBoost
Abstract
1. Introduction
- Demonstrating a weighted average function to blend historical load and PV trends with forecasted predictions, maximizing accuracy in day-ahead net load forecasting.
- Utilizing relevant training and validation data from a mixed-use university building.
- Implementing XGBoost as the forecasting framework, in contrast to other popular techniques such as LSTM and SVM.
- Expanding research on day-ahead net load forecasting rather than focusing solely on short-term or singular-interval forecasting.
2. Background
2.1. Building Load and PV Data
2.2. Open-Meteo Historical Weather Database
2.3. XGboost
2.4. Weighted-Average Function
2.5. Evaluation
3. Experiment and Results
3.1. Training Hyperparameters and Dataset
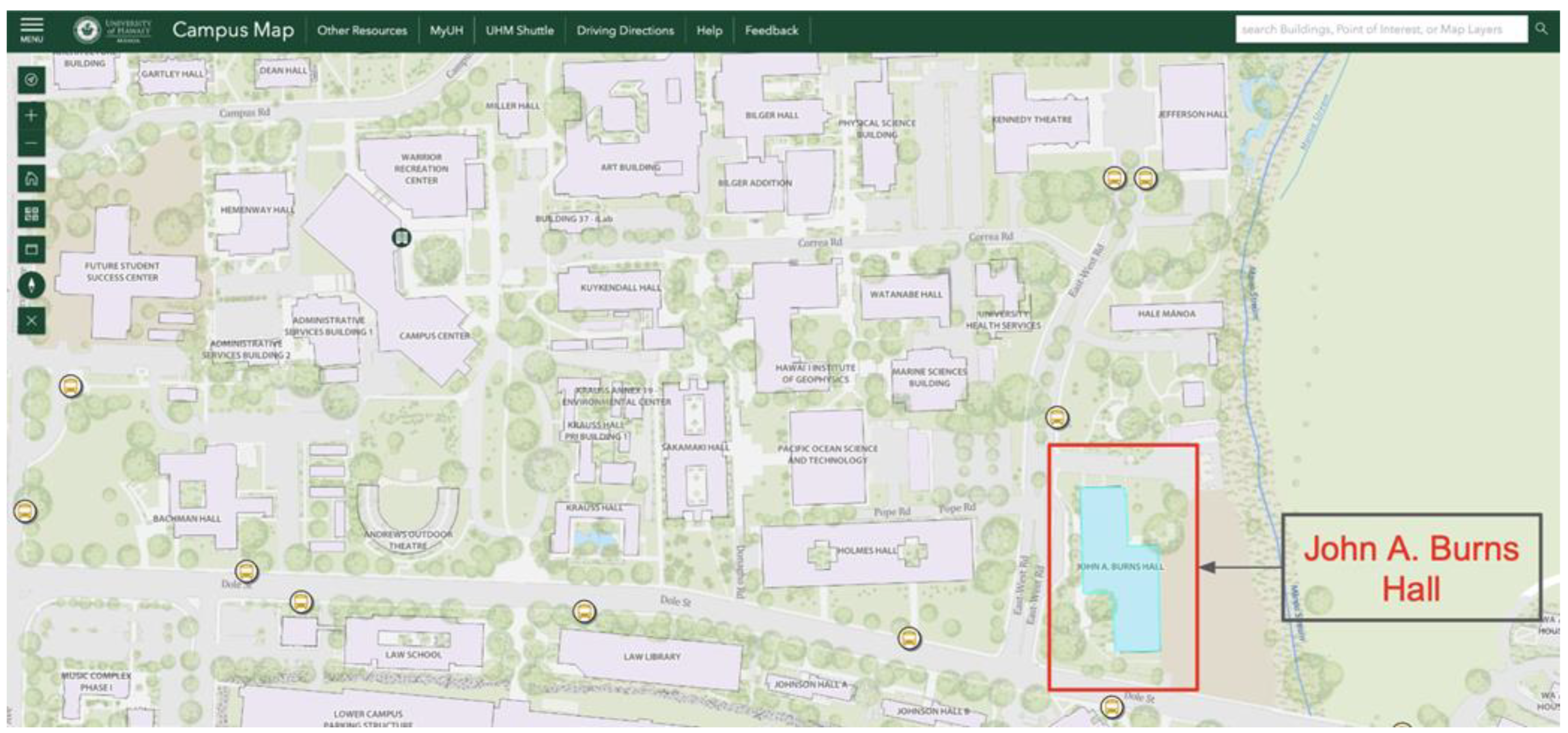
3.2. Case Study
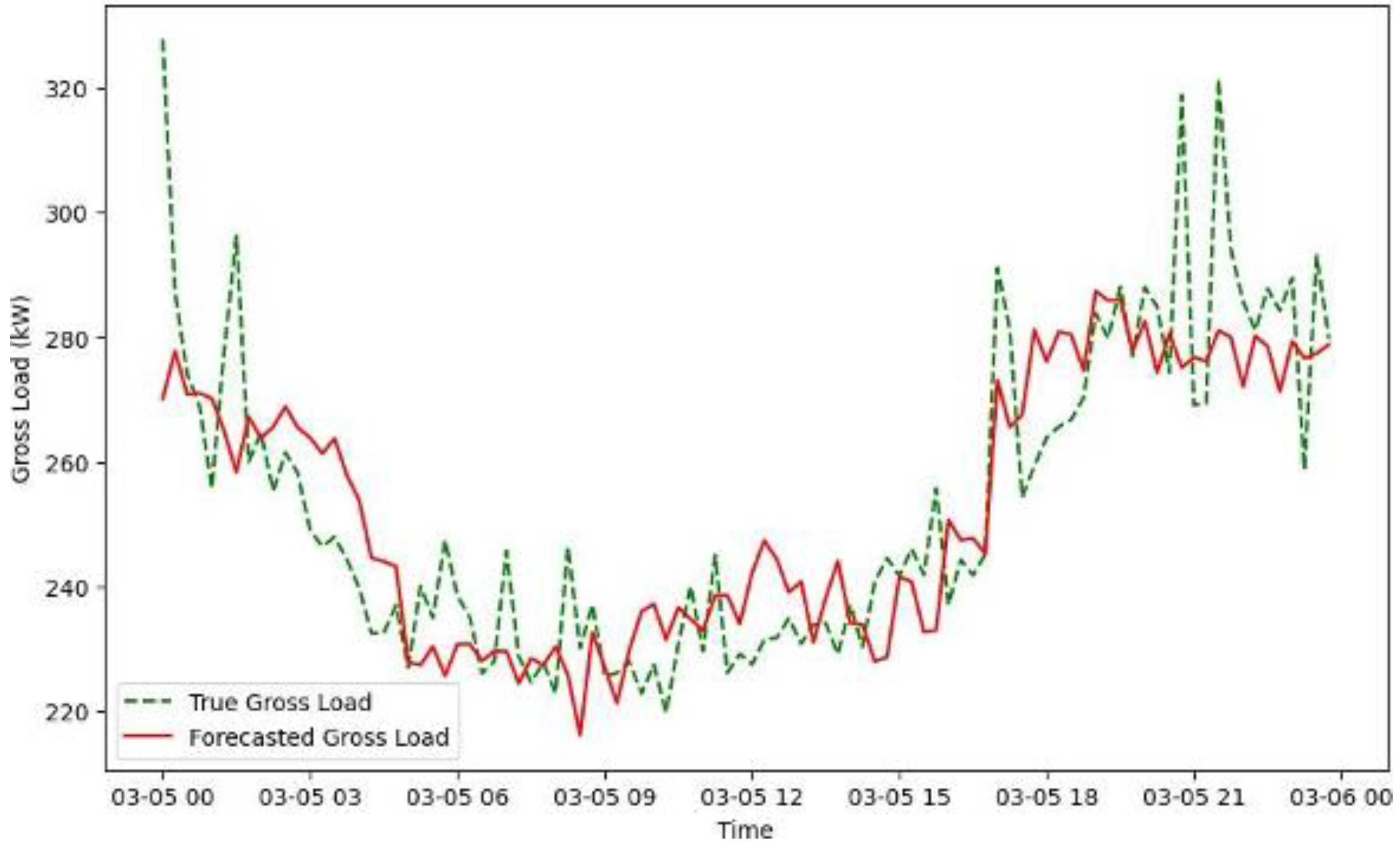
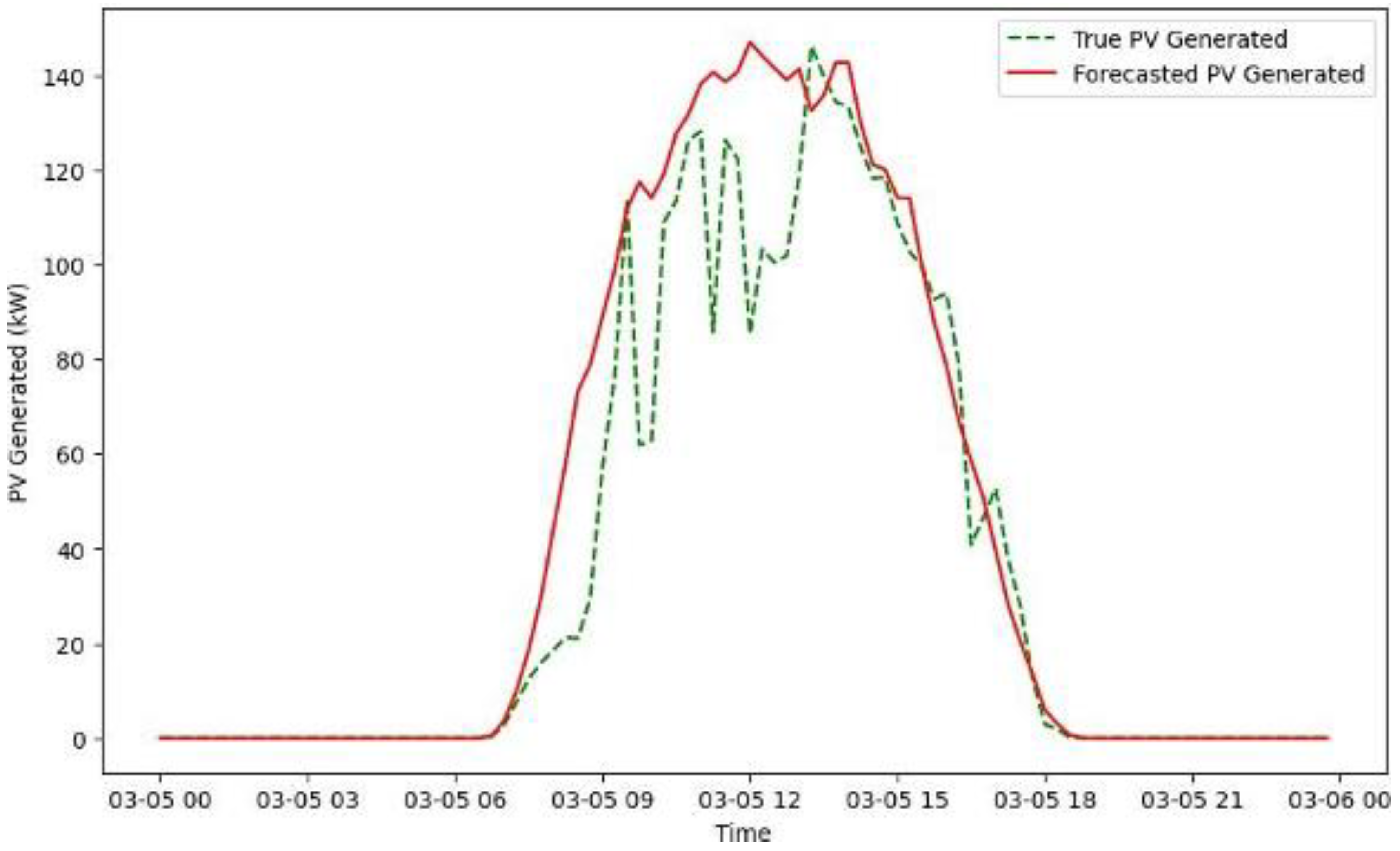
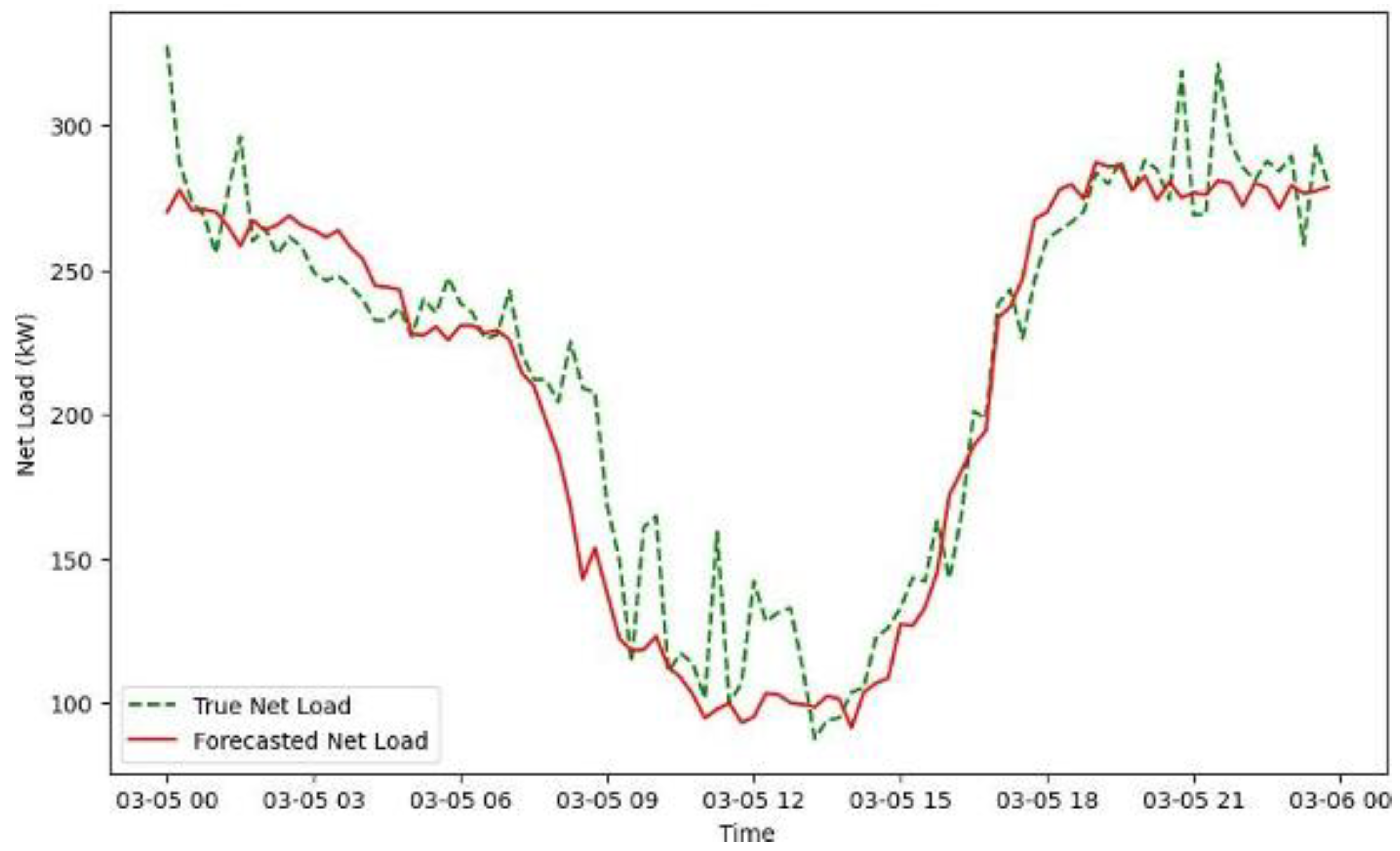
3.3. Results and Analysis
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Drevers, H. At a Glance: How Renewable Energy Is Transforming the Global Electricity Supply. National Renewable Energy Laboratory. 2023. Available online: https://www.nrel.gov/news/program/2023/how-renewable-energy-is-transforming-the-global-electricity-supply.html (accessed on 1 March 2025).
- News Release: Next Decade Decisive for PV Growth on the Path to 2050. National Renewable Energy Laboratory. 2023. Available online: https://www.nrel.gov/news/press/2023/news-release-next-decade-decisive-for-pv-growth-on-the-path-to-2050.html (accessed on 1 March 2025).
- Renewable Power Generation Costs in 2020. International Renewable Energy Agency. 2021. Available online: https://www.irena.org/publications/2021/Jun/Renewable-Power-Costs-in-2020 (accessed on 1 March 2025).
- State Renewable Portfolio Standards and Goals. National Conference of State Legislatures. 2021. Available online: https://www.ncsl.org/energy/state-renewable-portfolio-standards-and-goals (accessed on 1 March 2025).
- Mamun, A.A.; Sohel, M.; Mohammad, N.; Haque Sunny, M.S.; Dipta, D.R.; Hossain, E. A Comprehensive Review of the Load Forecasting Techniques Using Single and Hybrid Predictive Models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Barhmi, K.; Heynen, C.; Golroodbari, S.; van Sark, W. A Review of Solar Forecasting Techniques and the Role of Artificial Intelligence. Solar 2024, 4, 99–135. [Google Scholar] [CrossRef]
- Hong, T.; Wang, P. Artificial Intelligence for Load Forecasting: History, Illusions, and Opportunities. IEEE Power Energy Mag. 2022, 20, 14–23. [Google Scholar] [CrossRef]
- Kagade, R.B.; Vijayaraj, N. Intrusion detection via optimal tuned LSTM model with trust and risk level evaluation. Int. J. Bio-Inspired Comput. 2024, 23, 39–52. [Google Scholar] [CrossRef]
- Dai, Y.; Zhao, P. A Hybrid Load Forecasting Model Based on Support Vector Machine with Intelligent Methods for Feature Selection and Parameter Optimization. Appl. Energy 2020, 279, 115332. [Google Scholar] [CrossRef]
- Montoya, A.Y.; Mandal, P. Day-Ahead and Week-Ahead Solar PV Power Forecasting Using Deep Learning Neural Networks. In Proceedings of the 2022 North American Power Symposium (NAPS), Salt Lake City, UT, USA, 9–11 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Bui Duy, L.; Nguyen Quang, N.; Doan Van, B.; Riva Sanseverino, E.; Tran Thi Tu, Q.; Le Thi Thuy, H.; Le Quang, S.; Le Cong, T.; Cu Thi Thanh, H. Refining Long Short-Term Memory Neural Network Input Parameters for Enhanced Solar Power Forecasting. Energies 2024, 17, 4174. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Li, X.; Chen, J.; Liu, H.; Zhao, Q.; Xu, Z. Long-Term Energy and Peak Power Demand Forecasting Based on Sequential-XGBoost. IEEE Trans. Power Syst. 2024, 39, 3088–3104. [Google Scholar] [CrossRef]
- Sebi, N.P. Intelligent MPPT for photovoltaic panels on grid-connected inverter system using hybrid meta-heuristic algorithm. Int. J. Bio-Inspired Comput. 2024, 23, 245–256. [Google Scholar] [CrossRef]
- Tziolis, G.; Livera, A.; Montes-Romero, J.; Theocharides, S.; Makrides, G.; Georghiou, G.E. Direct Short-Term Net Load Forecasting Based on Machine Learning Principles for Solar-Integrated Microgrids. IEEE Access 2023, 11, 102038–102049. [Google Scholar] [CrossRef]
- Mokarram, M.J.; Rashiditabar, R.; Gitizadeh, M.; Aghaei, J. Net Load Forecasting of Renewable Energy Systems Using Multi-Input LSTM Fuzzy and Discrete Wavelet Transform. Energy 2023, 275, 127425. [Google Scholar] [CrossRef]
- XGBoost Documentation—Xgboost 2.1.3 Documentation. Available online: https://xgboost.readthedocs.io/en/stable/ (accessed on 14 March 2025).
- Zippenfenig, P. Open-Meteo.com Weather API [Computer Software]. Zenodo 2023. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1940 to Present [Data Set]. ECMWF 2023. [Google Scholar] [CrossRef]
- Muñoz Sabater, J. ERA5-Land Hourly Data from 2001 to Present [Data Set]. ECMWF 2019. [Google Scholar] [CrossRef]
- Schimanke, S.; Ridal, M.; Le Moigne, P.; Berggren, L.; Undén, P.; Randriamampianina, R.; Andrea, U.; Bazile, E.; Bertelsen, A.; Brousseau, P.; et al. CERRA Subdaily Regional Reanalysis Data for Europe on Single Levels from 1984 to Present [Data Set]. ECMWF 2021. [Google Scholar] [CrossRef]
- Dairu, X.; Shilong, Z. Machine Learning Model for Sales Forecasting by Using XGBoost. In Proceedings of the 2021 IEEE International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 15–17 January 2021; pp. 480–483. [Google Scholar] [CrossRef]
- Zhai, N.; Yao, P.; Zhou, X. Multivariate Time Series Forecast in Industrial Process Based on XGBoost and GRU. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; pp. 1397–1400. [Google Scholar] [CrossRef]
- Dong, D.; Wen, F.; Zhang, Y.; Qiu, W. Application of XGBoost in Electricity Consumption Prediction. In Proceedings of the 2023 IEEE 3rd International Conference on Electronic Technology, Communication and Information (ICETCI), Changchun, China, 26–28 May 2023; pp. 1260–1264. [Google Scholar] [CrossRef]
- Pramanik, A.S.; Sepasi, S.; Nguyen, T.L.; Roose, L. An Ensemble-Based Approach for Short-Term Load Forecasting for Buildings with High Proportion of Renewable Energy Sources. Energy Build. 2024, 308, 113996. [Google Scholar] [CrossRef]
- Sepasi, S.; Reihani, E.; Howlader, A.M.; Roose, L.R.; Matsuura, M.M. Very Short-Term Load Forecasting of a Distribution System with High PV Penetration. Renew. Energy 2017, 106, 142–148. [Google Scholar] [CrossRef]


| Hyperparameter | Gross Load Forecast | PV Forecast |
|---|---|---|
| Estimators | 200 | 250 |
| Learning Rate | 0.25 | 0.5 |
| Max Depth | 6 | 6 |
| Metric | RMSE [kW] | MAE [kW] | MAPE |
|---|---|---|---|
| Gross Load Forecast | 13.93 | 10.40 | 0.04 |
| PV Forecast | 25.80 | 18.80 | 0.39 |
| Net Load Forecast | 21.13 | 15.24 | 0.09 |
| Metric | RMSE [kW] | MAE [kW] | MAPE |
|---|---|---|---|
| Gross Load Forecast | 10.63 | 8.41 | 0.04 |
| PV Forecast | 34.31 | 27.00 | 0.94 |
| Net Load Forecast | 23.57 | 16.54 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kerkau, S.; Sepasi, S.; Howlader, H.O.R.; Roose, L. Day-Ahead Net Load Forecasting for Renewable Integrated Buildings Using XGBoost. Energies 2025, 18, 1518. https://doi.org/10.3390/en18061518
Kerkau S, Sepasi S, Howlader HOR, Roose L. Day-Ahead Net Load Forecasting for Renewable Integrated Buildings Using XGBoost. Energies. 2025; 18(6):1518. https://doi.org/10.3390/en18061518
Chicago/Turabian StyleKerkau, Spencer, Saeed Sepasi, Harun Or Rashid Howlader, and Leon Roose. 2025. "Day-Ahead Net Load Forecasting for Renewable Integrated Buildings Using XGBoost" Energies 18, no. 6: 1518. https://doi.org/10.3390/en18061518
APA StyleKerkau, S., Sepasi, S., Howlader, H. O. R., & Roose, L. (2025). Day-Ahead Net Load Forecasting for Renewable Integrated Buildings Using XGBoost. Energies, 18(6), 1518. https://doi.org/10.3390/en18061518








