A Multi-Variable Coupled Control Strategy Based on a Deep Deterministic Policy Gradient Reinforcement Learning Algorithm for a Small Pressurized Water Reactor
Abstract
1. Introduction
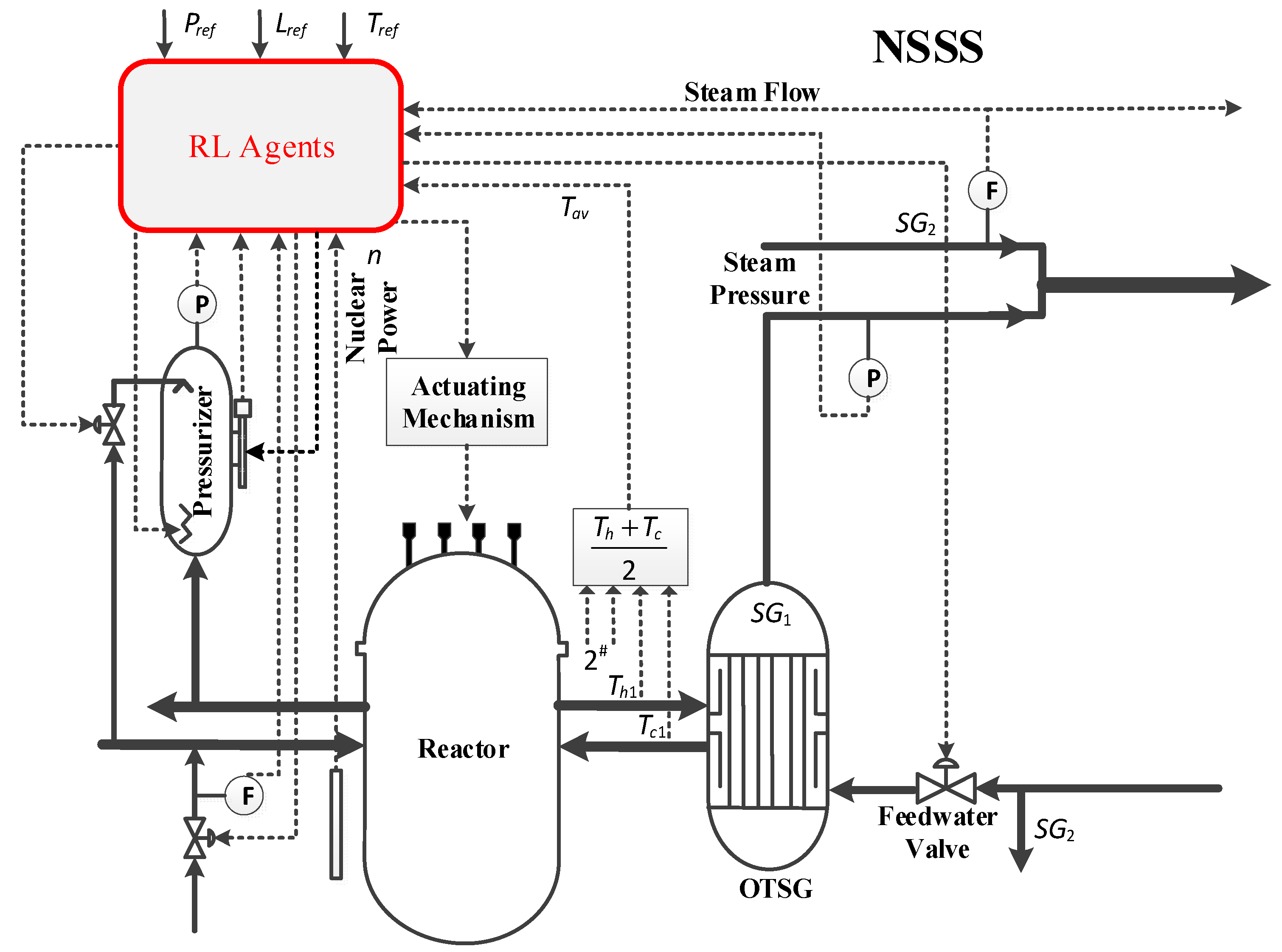
2. Modeling of Nuclear Steam Supply System
2.1. Core Modeling
2.2. OTSG Modeling
- (1)
- Identical flow rates and heat transfer capacities for all spiral tubes;
- (2)
- Fluid dynamics are modeled one-dimensionally along the main flow direction, with radial secondary flow effects incorporated through correction coefficients for heat transfer and pressure drop calculations;
- (3)
- The axial thermal conductivity of the working material and tube walls on both primary and secondary sides is neglected, along with external heat dissipation from the steam generator;
- (4)
- The primary-side fluid is treated as the average heat transfer channel, consistent across all spiral tubes, with the assumption of incompressibility and uniform pressure throughout;
- (5)
- Thermodynamic equilibrium is always maintained between the vapor and liquid phases in the two-phase region, ignoring the phenomenon of subcooling and boiling.
2.3. Pressurizer Modeling
- (1)
- At the same moment, the three zones have the same pressure;
- (2)
- The vapor and liquid phases are completely distinct, yet their thermodynamic state parameters remain identical simultaneously;
- (3)
- The vapor phase can only be saturated or superheated, and the liquid phase can only be saturated or supercooled;
- (4)
- The mass exchange at the interface of the two phases of the vapor and liquid phases is performed instantaneously;
- (5)
- The non-condensable gas in the vessel is neglected;
- (6)
- The spray water is saturated before leaving the vapor zone;
- (7)
- The spray condensation process is completed instantaneously;
- (8)
- The bubble rise flow in the liquid-phase zone and the vapor condensation flow in the vapor-phase zone are generated instantaneously;
- (9)
- The fluctuating liquid-phase zone acts as a buffer zone, assuming no mass or energy exchange with the main-phase zone.
2.4. Traditional PID Control System Modeling
3. RL-Based Control System
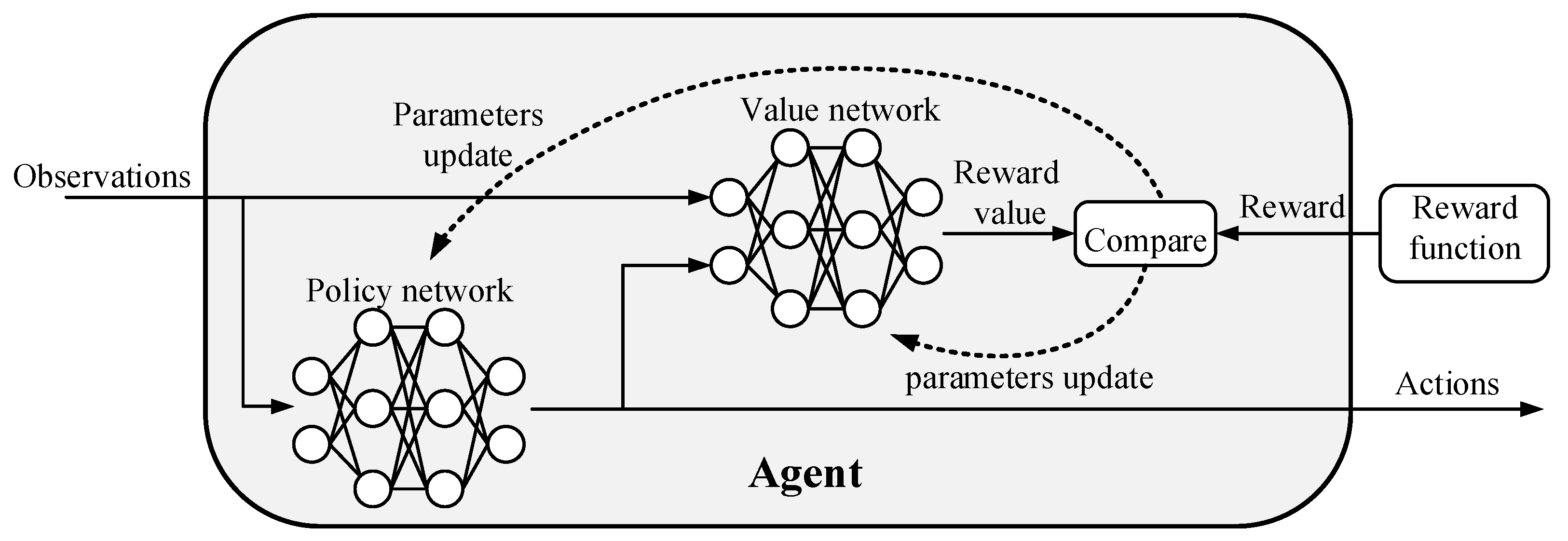
3.1. RL-Based Reactor Control System Structure and Principles
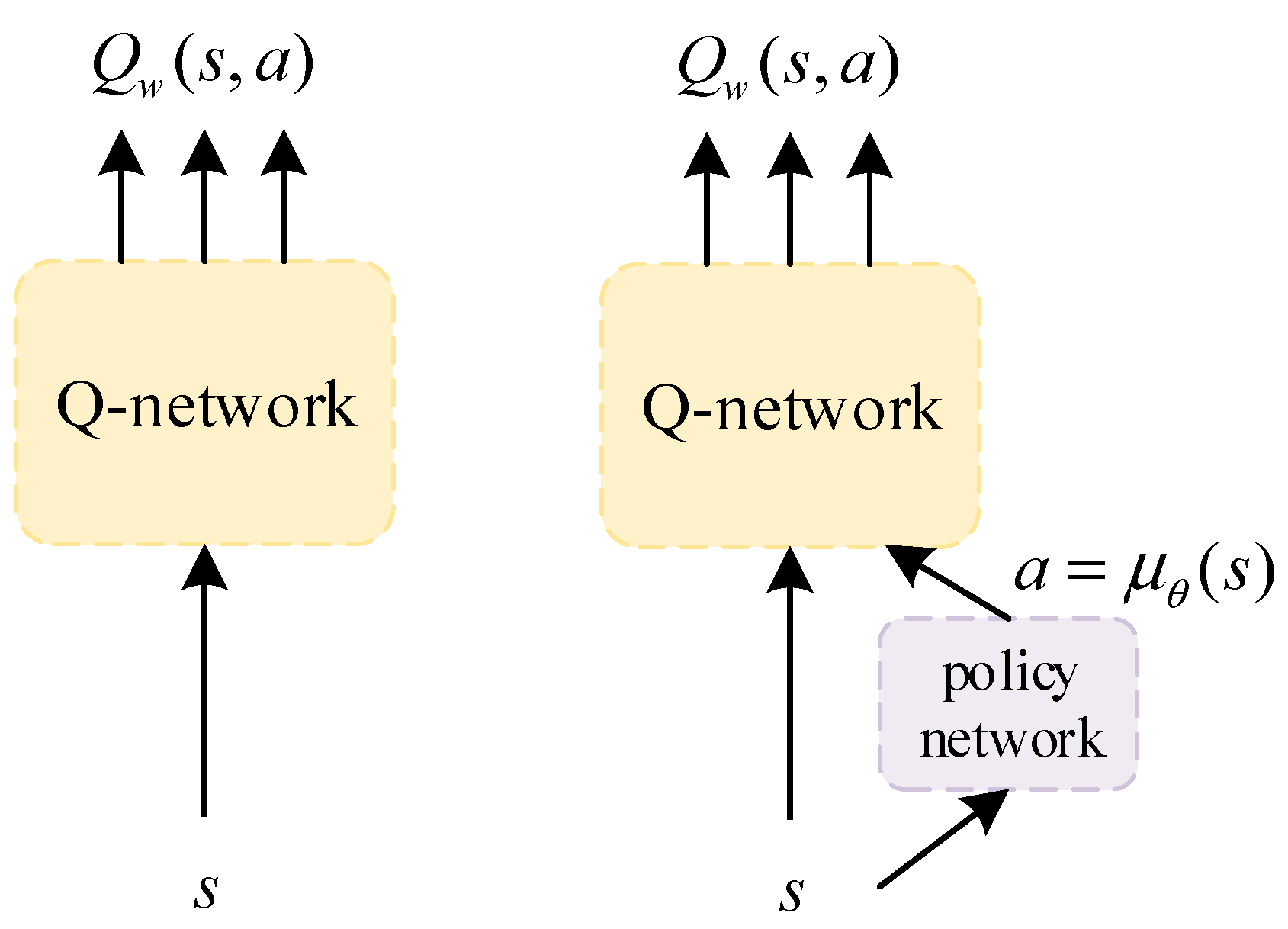
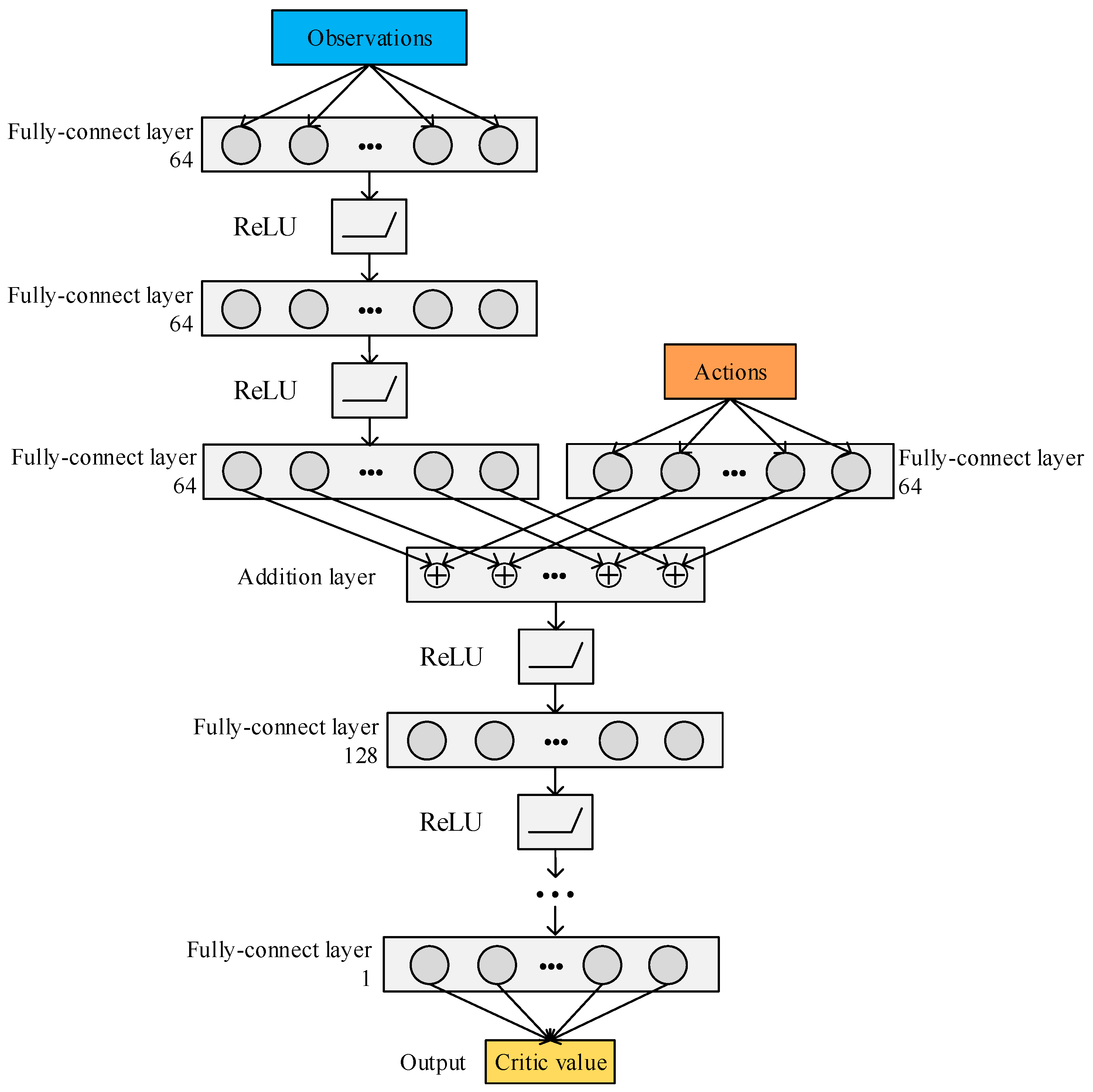
3.2. DDPG Reinforcement Learning Algorithm
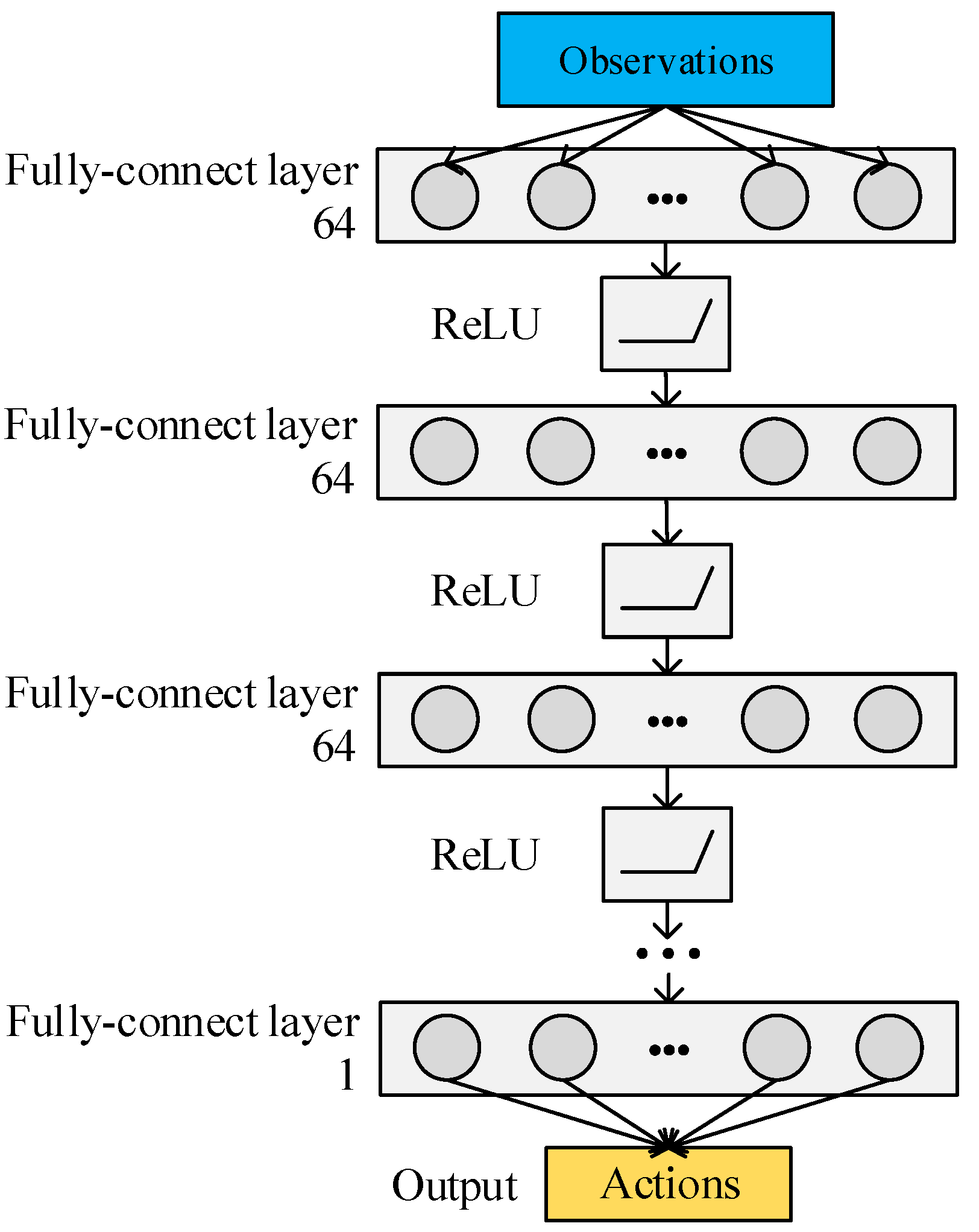
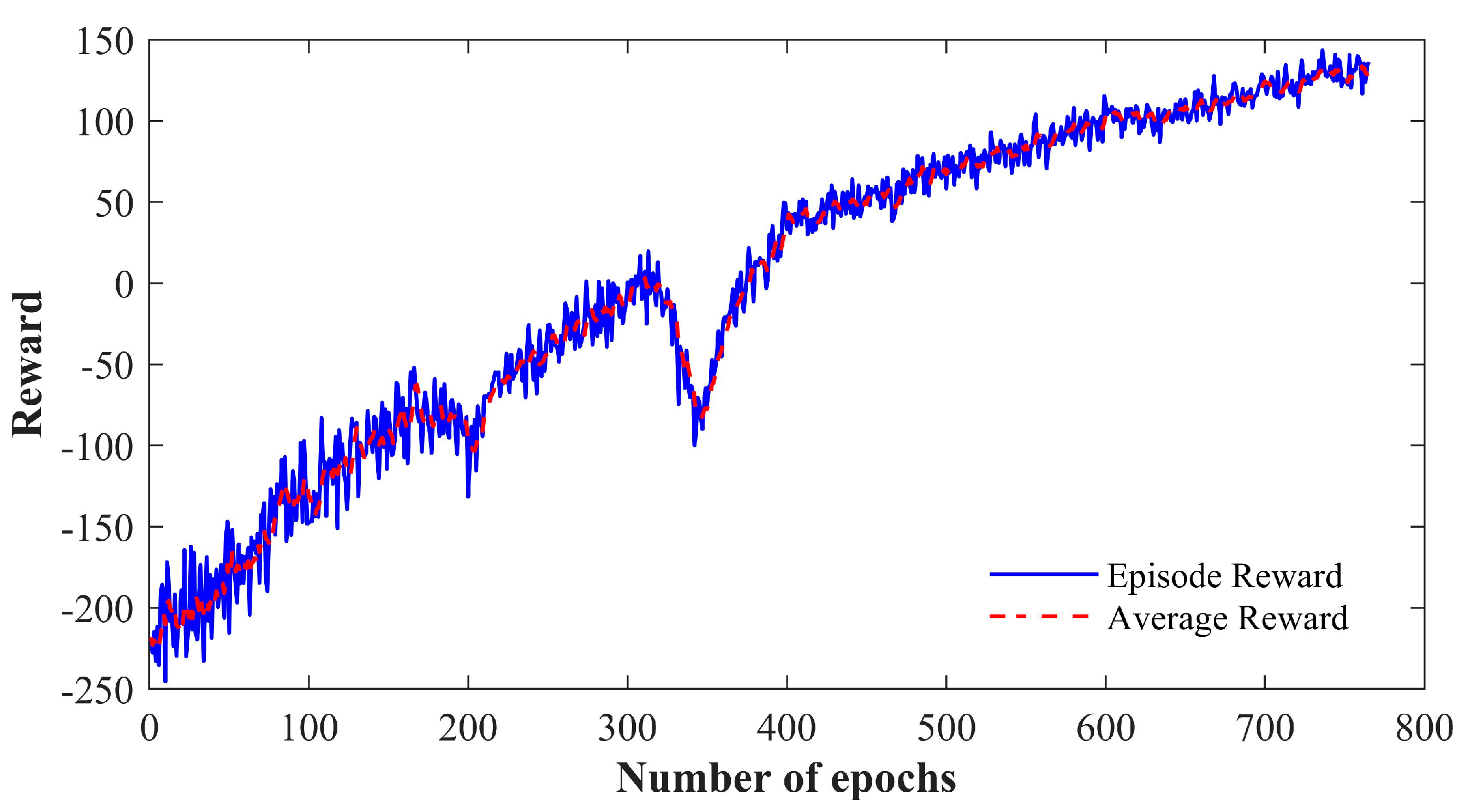
3.3. RL Agents’ Design and Training
4. Simulations and Analyses
4.1. The ±10% FP Step Load Change Transients
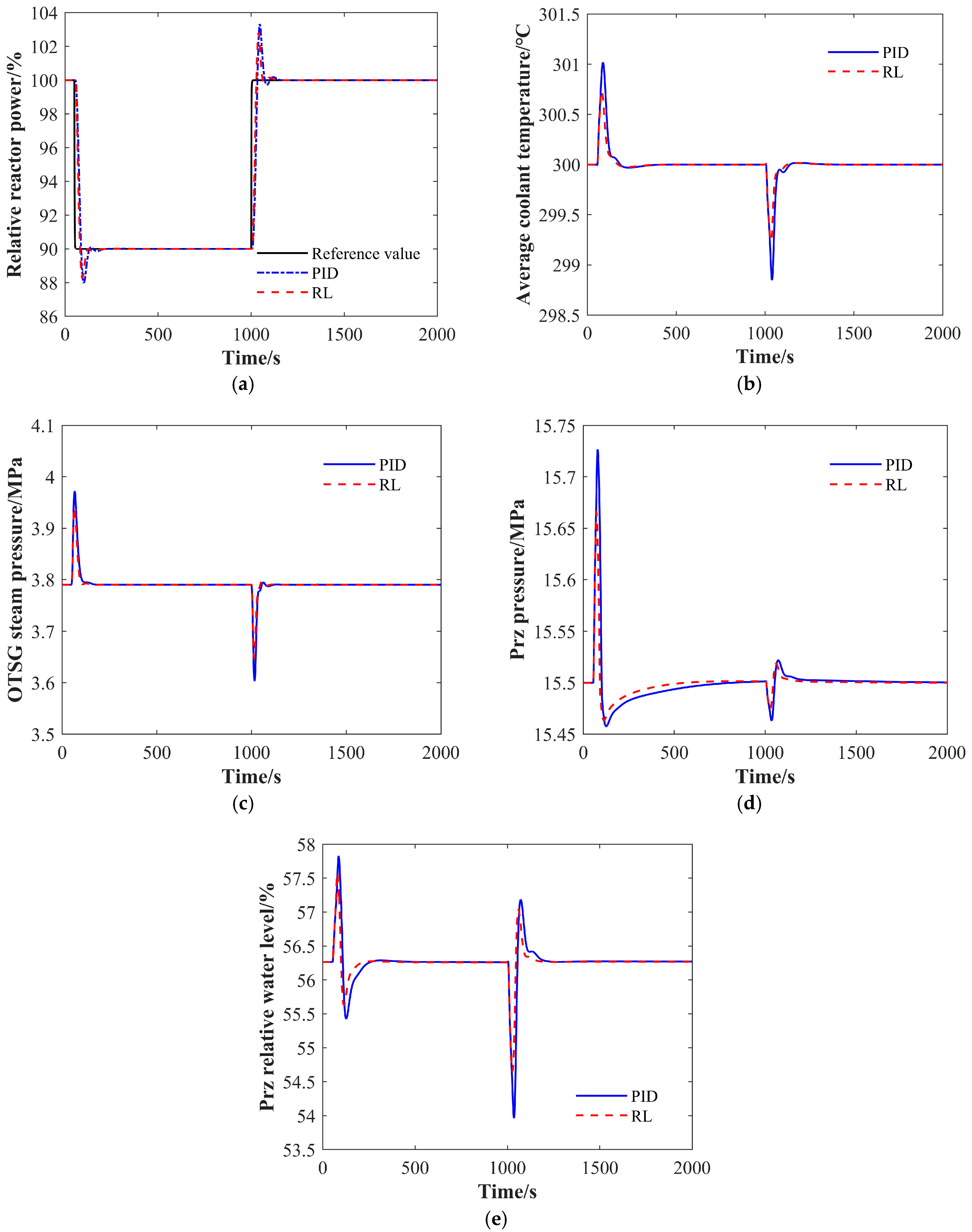
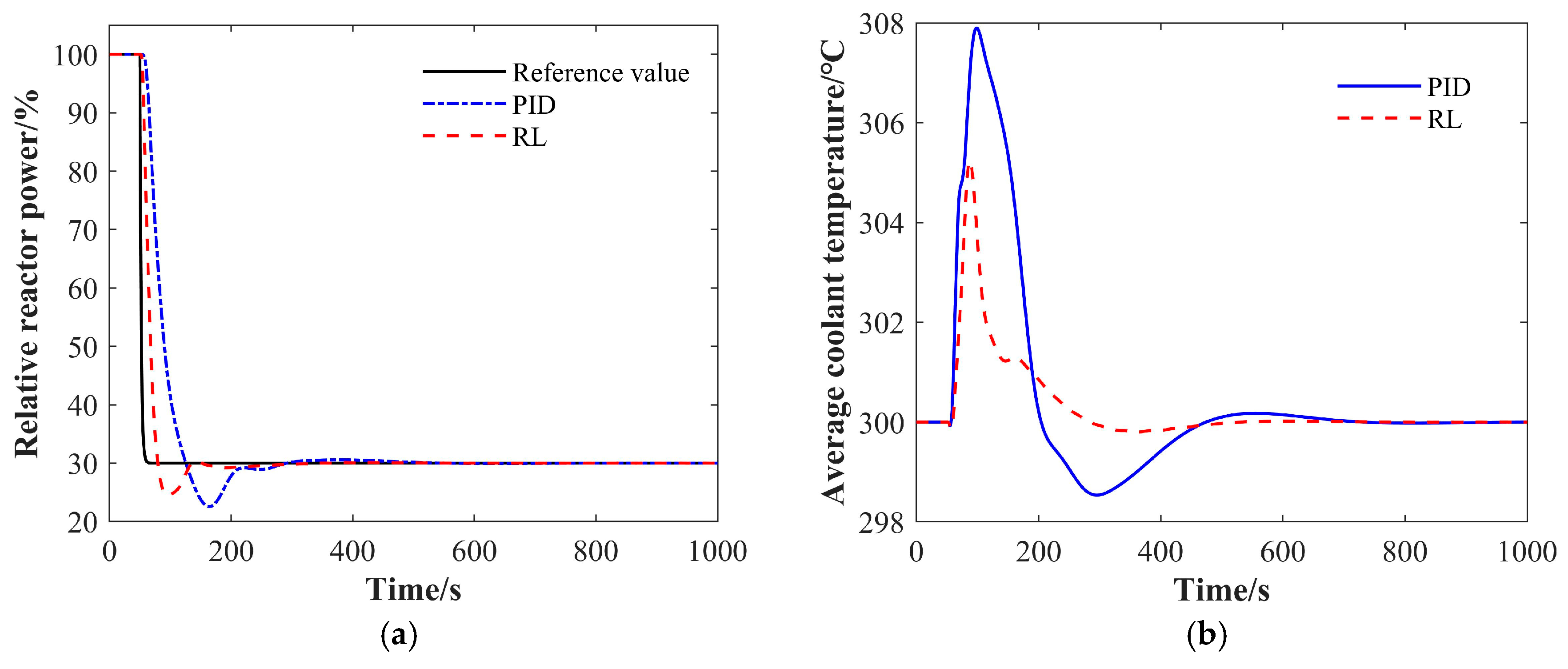
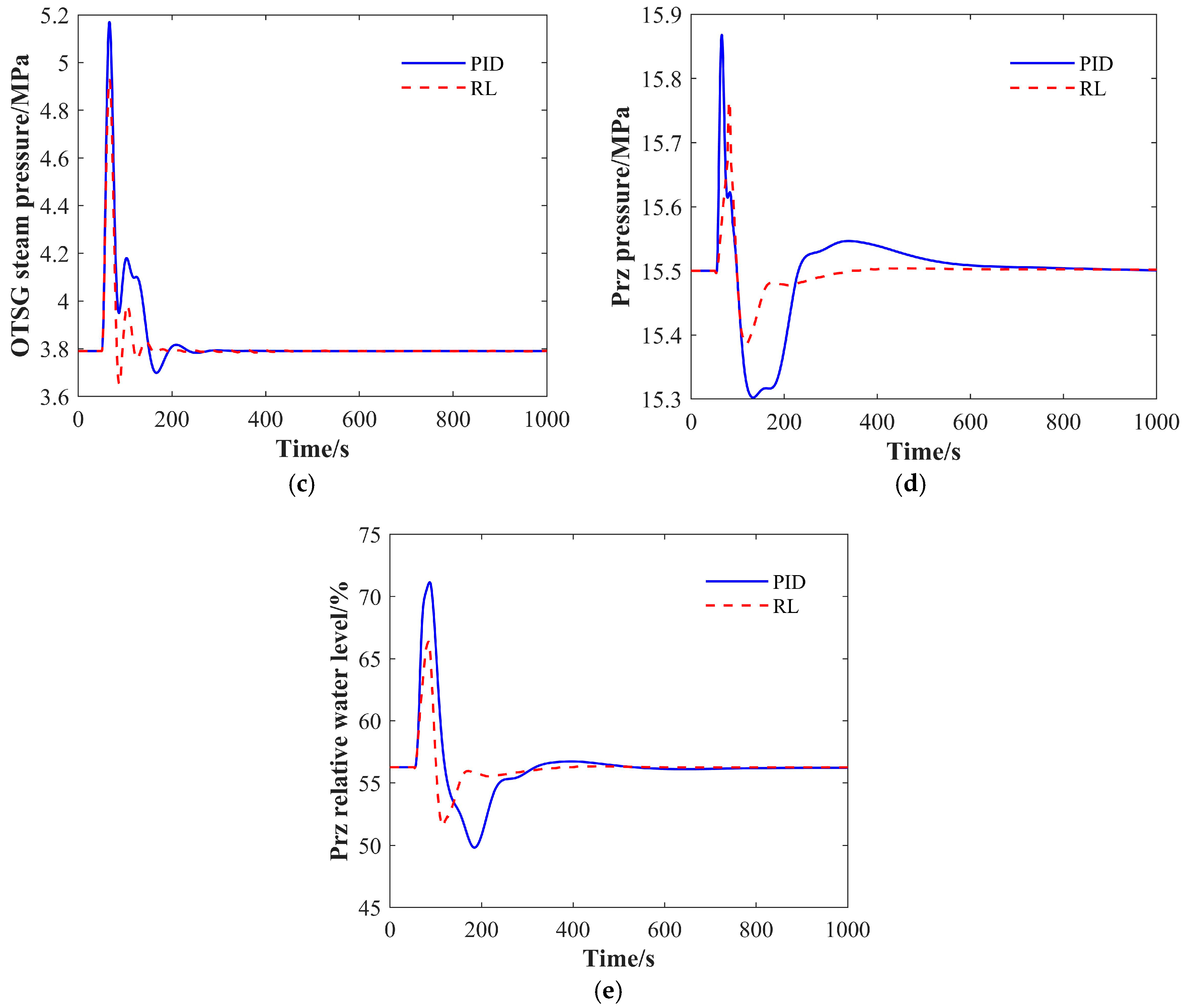
4.1.1. The 100% FP-90% FP-100% FP Condition
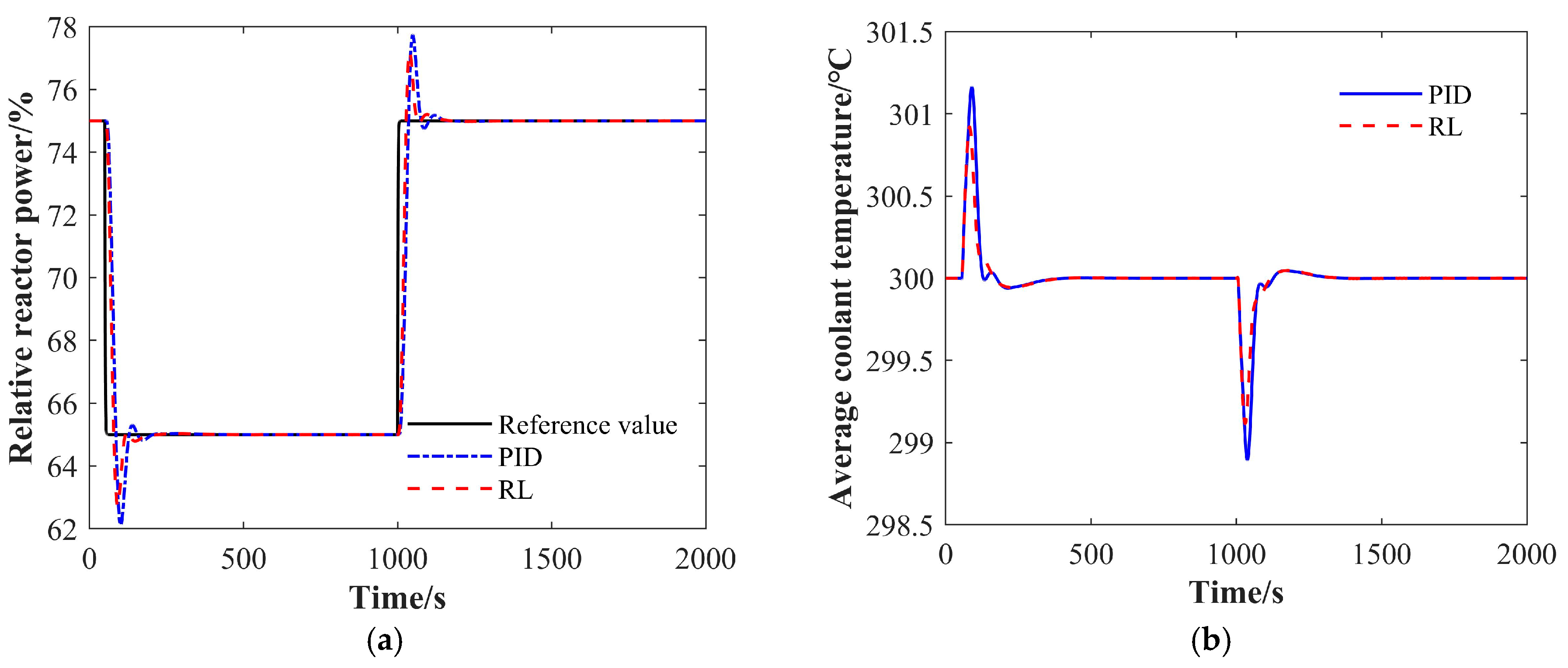
4.1.2. The 75% FP-65% FP-75% FP Condition
4.1.3. The 50% FP-40% FP-50% FP Condition
4.1.4. The 30% FP-20% FP-30% FP Condition
4.2. Ramp Load Change Transients
4.2.1. The ±10% FP/min Ramp Load Change Transient
4.2.2. The ±1% FP/s Ramp Load Change Transient
4.3. Load Rejection Transient
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| n | the neutron density |
| ρ | the total reactivity |
| the total share of delayed neutrons | |
| the average fuel temperature | |
| the core outlet coolant temperature | |
| the full power value of the reactor | |
| the total heat capacity of the core coolant | |
| the heat transfer coefficient between the fuel and coolant | |
| the constant-pressure specific heat capacity | |
| the total reactivity | |
| the fuel reactivity temperature coefficient | |
| the initial temperature of | |
| the initial temperature of | |
| ρh | the density of the main steam |
| Ph | the pressure of the main steam |
| WD | the side exhaust steam flow |
| hs1 | the specific enthalpy of the steam on the secondary side of the SG |
| kf | the equivalent resistance coefficient |
| vF, vG | the liquid-phase region and the vapor-phase region of the mass specific volume |
| hf, hg | the saturated water and saturated steam specific enthalpy |
| Wsp | the spray flow rate, given by the pressurizer pressure control system of the spray valve |
| C | the precursor nucleus density |
| Λ | the neutron generation time |
| λ | the one-group delayed neutron decay constant |
| the average core coolant temperature | |
| the core inlet coolant temperature | |
| the total heat capacity of the core fuel | |
| the share of heat generated in the fuel in total power | |
| the core coolant flow rate | |
| the constant-pressure specific heat capacity of the core coolant | |
| the reactivity introduced by the control rods | |
| the coolant reactivity temperature coefficient | |
| the initial temperature of | |
| Vh | the total volume of the main steam system |
| hh | the specific enthalpy of the main steam |
| WT | the turbine inlet steam flow |
| Ws1 | the steam flow on the secondary side of the SG |
| ∆Hh | the outlet of the steam generator is the height difference from the steam nozzle to the main steam bus |
| MF, MG | the liquid-phase region and vapor-phase region of the mass of the mass |
| hF, hG | the liquid-phase region and the vapor-phase region of the mass specific enthalpy |
| Wsu | the fluctuations in the flow rate caused by the first back to the thermal expansion and upward and downward drainage flow |
| Wbe, Wbc | the liquid-phase region of the bubble rising flow and the vapor-phase steam self-condensation flow rate |
References
- Zhou, G.; Tan, D. Review of nuclear power plant control research: Neural network-based methods. Ann. Nuclear Energy 2023, 181, 109513. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and fractional-order controllers. Inst. Exp. Phys. Slovak. Acad. Sci. Kosice 1994, 12, 1–18. [Google Scholar]
- Gupta, D.; Goyal, V.; Kumar, J. Design of fractional-order NPID controller for the NPK model of advanced nuclear reactor. Prog. Nucl. Energy 2022, 150, 104319. [Google Scholar] [CrossRef]
- Zeng, W.; Jiang, Q.; Liu, Y.; Yan, S.; Zhang, G.; Yu, T.; Xie, J. Core power control of a space nuclear reactor based on a nonlinear model and fuzzy-PID controller. Prog. Nucl. Energy 2021, 132, 103564. [Google Scholar] [CrossRef]
- Torabi, K.; Safarzadeh, O.; Rahimi-Moghaddam, A. Robust Control of the PWR Core Power Using Quantitative Feedback Theory. IEEE Trans. Nucl. Sci. 2011, 58, 258–266. [Google Scholar] [CrossRef]
- Abdulraheem, K.K.; Korolev, S.A. Robust optimal-integral sliding mode control for a pressurized water nuclear reactor in load following mode of operation. Ann. Nucl. Energy 2021, 158, 108288. [Google Scholar] [CrossRef]
- Li, G.; Liang, B.; Wang, X.; Li, X.; Xia, B. Application of H-Infinity Output Feedback Control with Analysis of Weight Functions and LMI to Nonlinear Nuclear Reactor Cores; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 457–468. [Google Scholar]
- Li, G.; Zhao, F. Flexibility control and simulation with multimodel and LQG/LTR design for PWR core load following operation. Ann. Nucl. Energy 2013, 56, 179–188. [Google Scholar] [CrossRef]
- Li, G. Modeling and LQG/LTR control for power and axial power difference of load-follow PWR core. Ann. Nucl. Energy 2014, 68, 193–203. [Google Scholar] [CrossRef]
- Fu, J.; Jin, Z.; Dai, Z.; Su, G.H.; Wang, C.; Tian, W.; Qiu, S. Model predictive control for automatic operation of space nuclear reactors: Design, simulation, and performance evaluation. Ann. Nucl. Energy 2024, 199, 110321. [Google Scholar] [CrossRef]
- Wang, G.; Wu, J.; Zeng, B.; Xu, Z.; Wu, W.; Ma, X. Design of a model predictive control method for load tracking in nuclear power plants. Prog. Nucl. Energy 2017, 101, 260–269. [Google Scholar] [CrossRef]
- Naimi, A.; Deng, J.; Vajpayee, V.; Becerra, V.; Shimjith, S.R.; Arul, A.J. Nonlinear Model Predictive Control Using Feedback Linearization for a Pressurized Water Nuclear Power Plant. IEEE Access 2022, 10, 16544–16555. [Google Scholar] [CrossRef]
- Khansari, M.E.; Sharifian, S. A deep reinforcement learning approach towards distributed Function as a Service (FaaS) based edge application orchestration in cloud-edge continuum. J. Netw. Comput. Appl. 2025, 233, 104042. [Google Scholar] [CrossRef]
- Wang, J.; Liang, S.; Guo, M.; Wang, H.; Zhang, H. Adaptive multimodal control of trans-media vehicle based on deep reinforcement learning. Eng. Appl. Artif. Intell. 2025, 139, 109524. [Google Scholar] [CrossRef]
- Gong, A.; Chen, Y.; Zhang, J.; Li, X. Possibilities of reinforcement learning for nuclear power plants: Evidence on current applications and beyond. Nucl. Eng. Technol. 2024, 56, 1959–1974. [Google Scholar] [CrossRef]
- Dong, Z.; Huang, X.; Dong, Y.; Zhang, Z. Multilayer perception based reinforcement learning supervisory control of energy systems with application to a nuclear steam supply system. Appl. Energy 2020, 259, 114193. [Google Scholar] [CrossRef]
- Yi, Z.; Luo, Y.; Westover, T.; Katikaneni, S.; Ponkiya, B.; Sah, S.; Khanna, R. Deep reinforcement learning based optimization for a tightly coupled nuclear renewable integrated energy system. Appl. Energy 2022, 328, 120113. [Google Scholar] [CrossRef]
- Zhang, T.; Dong, Z.; Huang, X. Multi-objective optimization of thermal power and outlet steam temperature for a nuclear steam supply system with deep reinforcement learning. Energy 2024, 286, 129526. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Qing, X.; Xiao, K.; Zhang, Y.; Yang, P.; Yang, Y.M. The application of Deep Reinforcement Learning in Coordinated Control of Nuclear Reactors. J. Phys. Conf. Ser. 2021, 2113, 012030. [Google Scholar] [CrossRef]
- Cao, D.H.; Pham, T.N.; Hoang, T.H.; Nguyen, V.H. Preliminary study of thermal hydraulics system for small modular reactor type pressurized water reactor used for floating nuclear power plant. In Proceedings of the Vietnam Conference on Nuclear Science and Technology VINANST-14 Agenda and Abstracts, Nha Trang City, Vietnam, 9–11 August 2023; p. 246. [Google Scholar]
- Phu, T.V.; Nam, T.H.; Khanh, H.V. Application of Evolutionary Simulated Annealing Method to Design a Small 200 MWt Reactor Core. Nucl. Sci. Technol. 2020, 10, 16–23. [Google Scholar] [CrossRef]
- Hoang, V.K.; Tran, V.P.; Cao, D.H. Study on fuel design for the long-life core of ACPR50S nuclear reactor. In VINATOM-AR—20; Trang, P.T.T., Ed.; International Atomic Energy Agency (IAEA): Vienna, Austria, 2021; pp. 57–59. [Google Scholar]
- Wang, X.; Wang, M. Development of Advanced Small Modular Reactors in CHINA. Nucl. Esp. 2017, 380, 34–37. [Google Scholar]
- China General Nuclear Power Corporation (CGN). Design, Applications and Siting Requirements of CGNACPR50(S); China General Nuclear Power Corporation (CGN): Shenzhen, China, 2017. [Google Scholar]
- Kerlin, T.W.; Katz, E.M.; Thakkar, J.G.; Strange, J.E. Theoretical and experimental dynamic analysis of the HB Robinson nuclear plant. Nucl. Technol. 1976, 30, 299–316. [Google Scholar] [CrossRef]
- Nuerlan, A.; Wang, P.; Wan, J.; Zhao, F. Decoupling header steam pressure control strategy in multi-reactor and multi-load nuclear power plant. Prog. Nucl. Energy 2020, 118, 103073. [Google Scholar] [CrossRef]
- Wang, P.; He, J.; Wei, X.; Zhao, F. Mathematical modeling of a pressurizer in a pressurized water reactor for control design. Appl. Math. Model. 2019, 65, 187–206. [Google Scholar] [CrossRef]
- Wan, J.; Wang, P.; Wu, S.; Zhao, F. Conventional controller design for the reactor power control system of the advanced small pressurized water reactor. Nucl. Technol. 2017, 198, 26–42. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, Q.; Zhang, J.; Wan, J.; Wu, S. A fuzzy fault accommodation method for nuclear power plants under actuator stuck faults. Ann. Nucl. Energy 2021, 165, 108674. [Google Scholar] [CrossRef]
- Tan, H. Reinforcement Learning with Deep Deterministic Policy Gradient. In Proceedings of the 2021 International Conference on Artificial Intelligence, Big Data and Algorithms (CAIBDA), Xi’an, China, 28–30 May 2021; pp. 82–85. [Google Scholar]



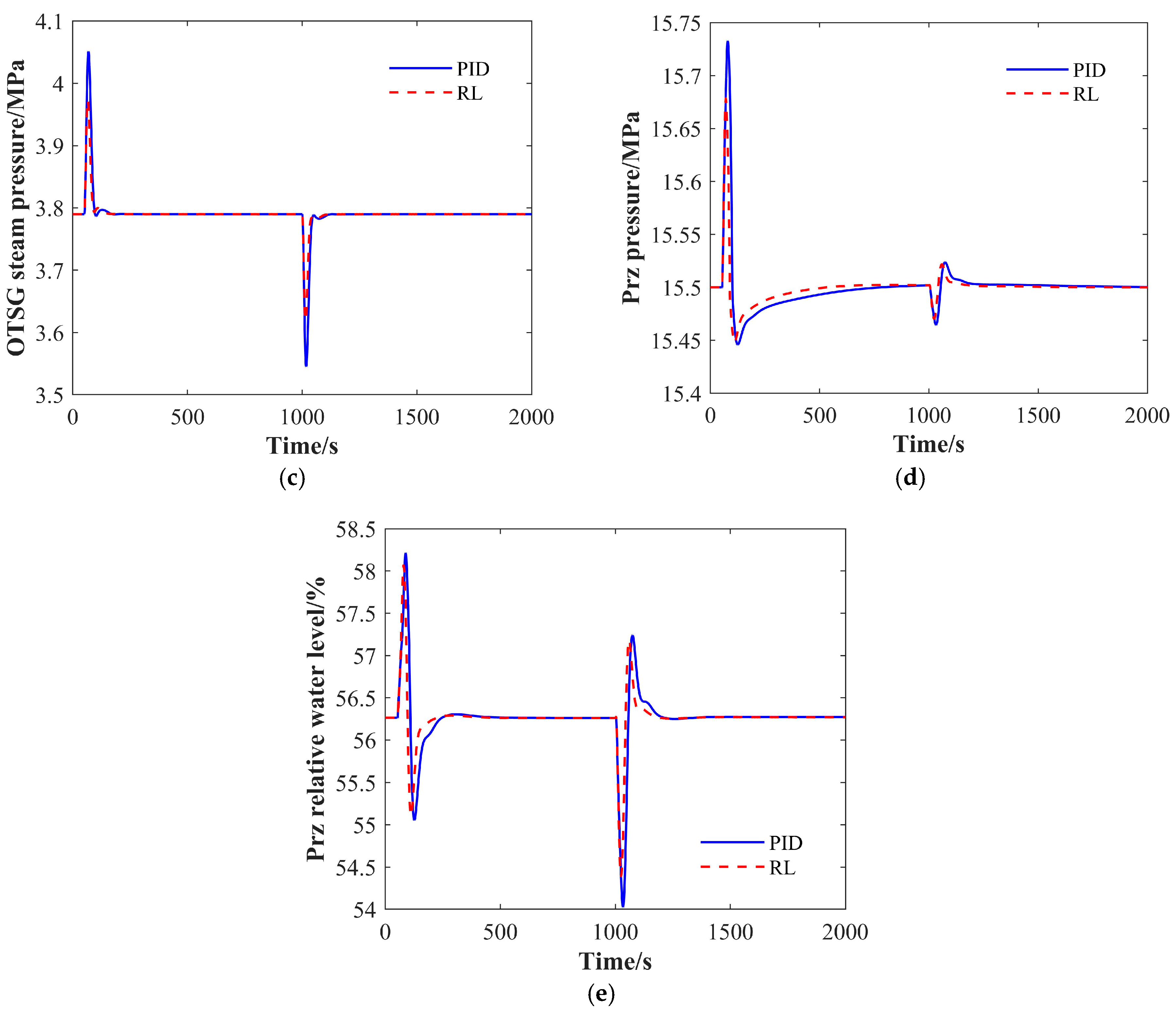

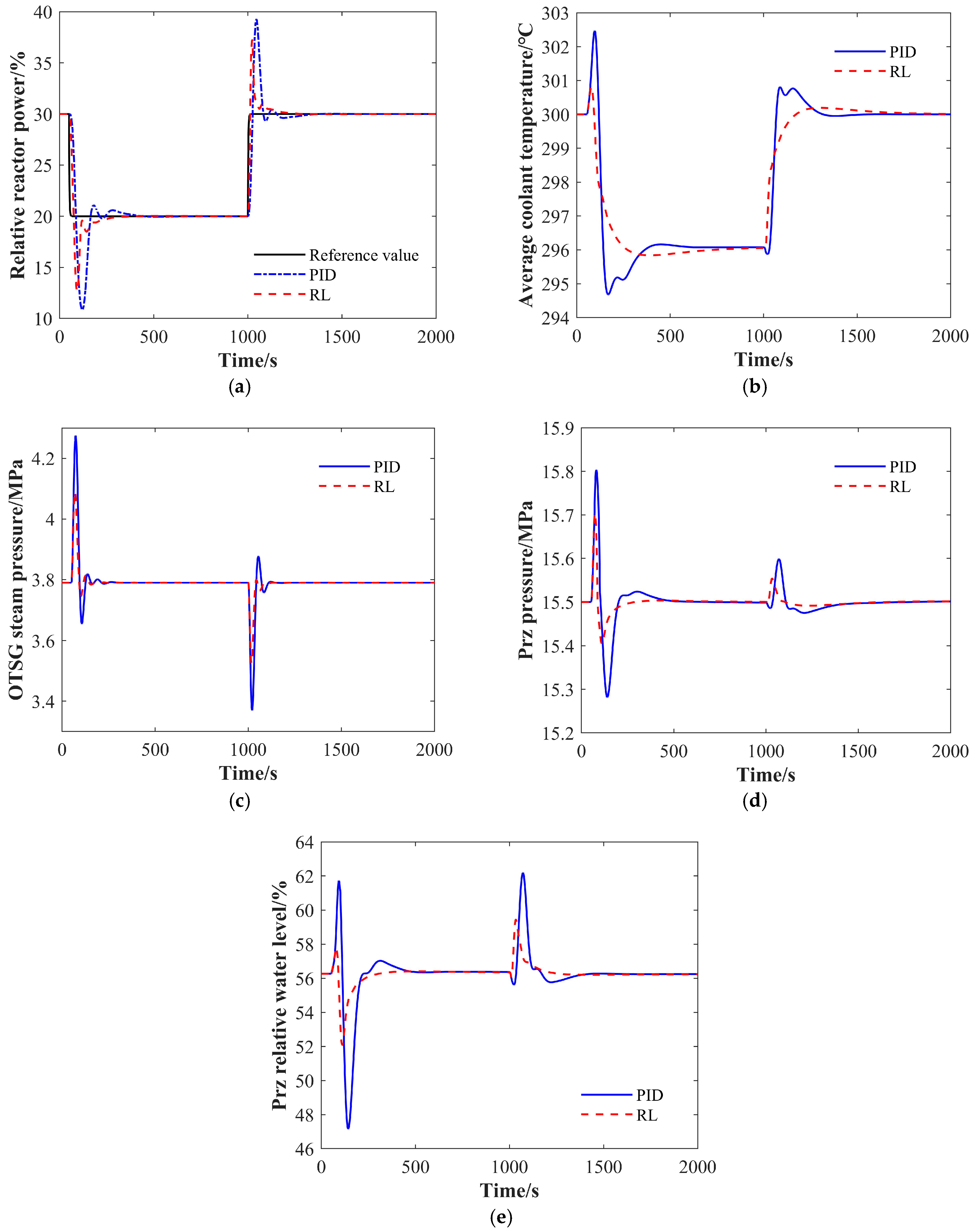

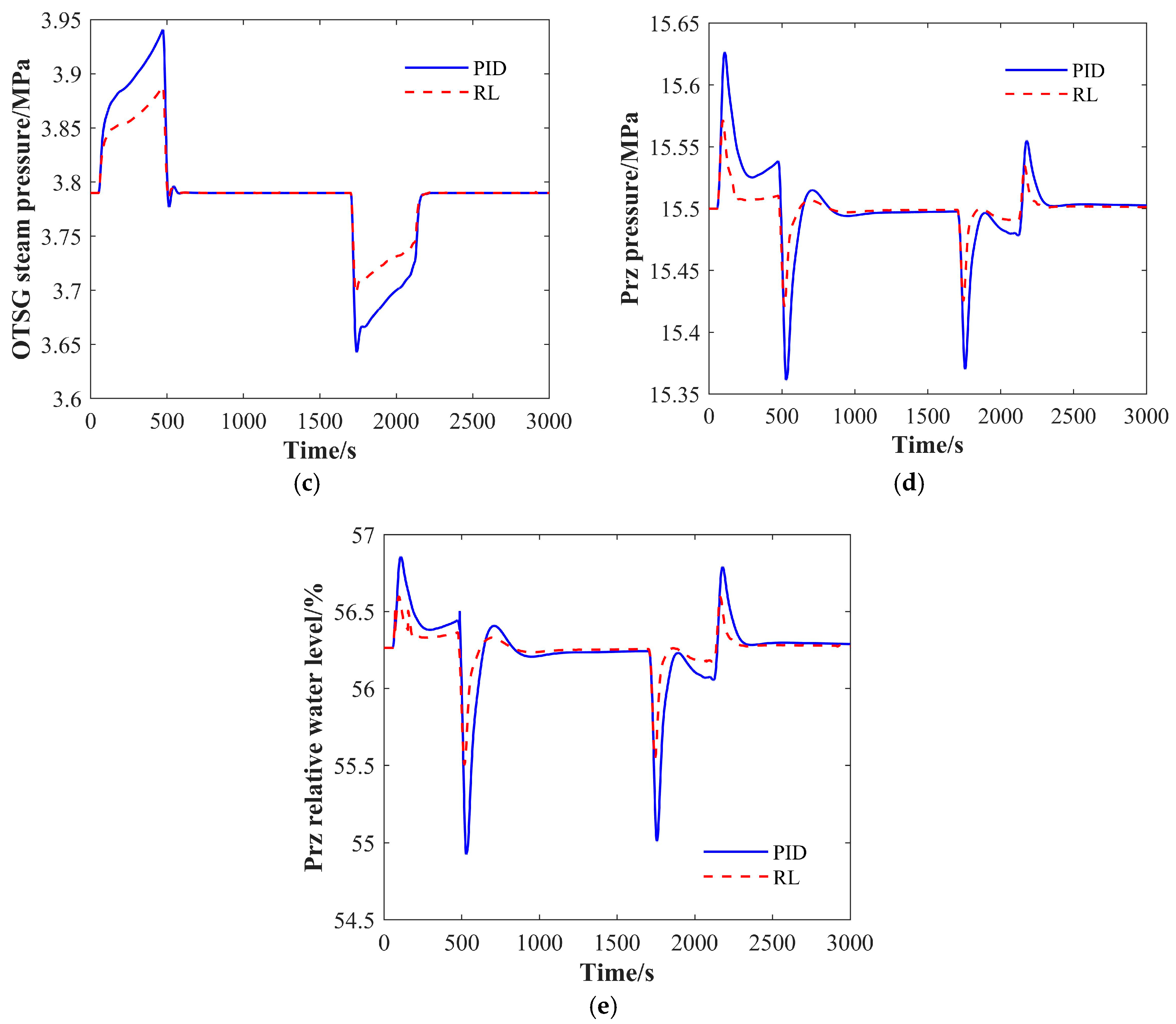
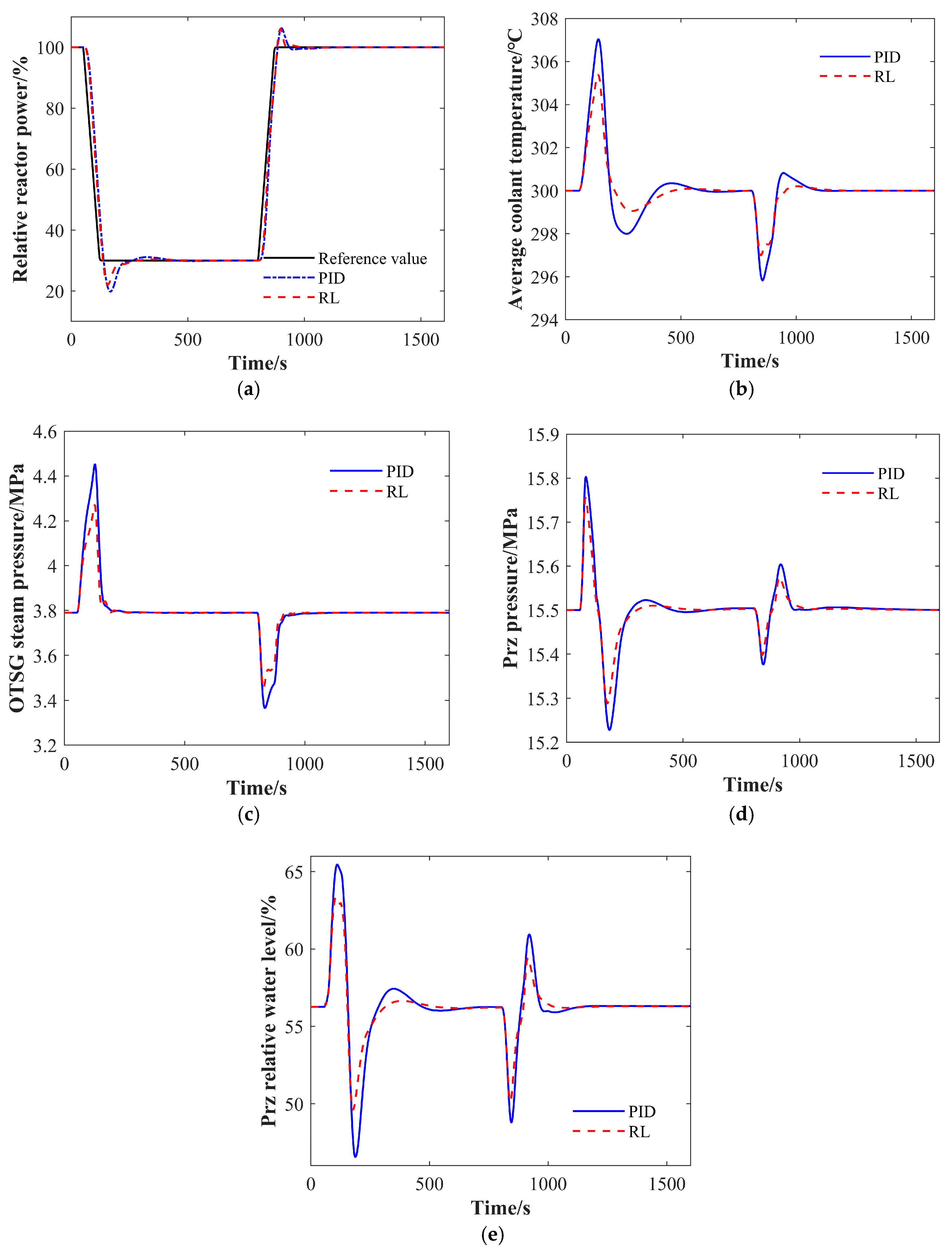
| Observed Variables and Control Variables | |
|---|---|
| Observations | Reactor Power/% |
| Deviation of Reactor Power from Initial Power/% | |
| Deviation of Reactor Power from Setpoint Power/% | |
| Deviation of Average Coolant Temperature/°C | |
| Deviation of Steam Pressure/MPa | |
| Deviation of Pressurizer Pressure/MPa | |
| Deviation of Pressurizer Relative Water Level/% | |
| Actions | Control Rod Position/step |
| Feedwater Valve Opening/% | |
| Electric Heater Power/kW | |
| Spray Valve Opening/% | |
| Charging Valve Opening/% |
| Power | Tavg | Ph | Prz | PrzL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ/% | ts/s | ∆/°C | ts/s | ∆/MPa | ts/s | ∆/MPa | ts/s | ∆/% | ts/s | |
| PID | 3.32 | 71 | 1.15 | 116 | 0.19 | 47 | 0.23 | 312 | 2.30 | 159 |
| RL | 2.80 | 60 | 0.76 | 93 | 0.14 | 37 | 0.17 | 202 | 1.60 | 112 |
| Optimization Improvement/% | 15.8 | 15.5 | 33.9 | 19.0 | 23.8 | 21.3 | 26.8 | 35.3 | 30.2 | 29.6 |
| Power | Tavg | Ph | Prz | PrzL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ/% | ts/s | ∆/°C | ts/s | ∆/MPa | ts/s | ∆/MPa | ts/s | ∆/% | ts/s | |
| PID | 4.44 | 73 | 1.16 | 175 | 0.26 | 42 | 0.23 | 329 | 2.24 | 161 |
| RL | 3.48 | 59 | 0.92 | 50 | 0.18 | 35 | 0.18 | 209 | 1.87 | 110 |
| Optimization Improvement/% | 21.6 | 19.2 | 20.9 | 71.4 | 30.2 | 16.7 | 23.4 | 36.5 | 16.5 | 31.7 |
| Power | Tavg | Ph | Prz | PrzL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ/% | ts/s | ∆/°C | ts/s | ∆/MPa | ts/s | ∆/MPa | ts/s | ∆/% | ts/s | |
| PID | 10.7 | 100 | 1.66 | 203 | 0.35 | 63 | 0.26 | 344 | 3.33 | 160 |
| RL | 8.53 | 63 | 1.24 | 95 | 0.24 | 37 | 0.20 | 229 | 2.78 | 125 |
| Optimization Improvement/% | 20.6 | 37.0 | 25.5 | 53.2 | 31.6 | 41.3 | 25.1 | 33.4 | 16.5 | 21.9 |
| Power | Tavg | Ph | Prz | PrzL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ/% | ts/s | ∆/°C | ts/s | ∆/MPa | ts/s | ∆/MPa | ts/s | ∆/% | ts/s | |
| PID | 45.9 | 253 | 2.47 | 279 | 0.48 | 92 | 0.30 | 312 | 9.10 | 331 |
| RL | 36.6 | 156 | 0.81 | 163 | 0.30 | 67 | 0.20 | 138 | 4.17 | 155 |
| Optimization Improvement/% | 20.2 | 38.3 | 67.2 | 41.6 | 38.3 | 27.2 | 33.2 | 55.8 | 54.2 | 53.2 |
| Power | Tavg | Ph | Prz | PrzL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ/% | ts/s | ∆/°C | ts/s | ∆/MPa | ts/s | ∆/MPa | ts/s | ∆/% | ts/s | |
| PID | 7.41 | 62 | 0.97 | 164 | 0.15 | 52 | 0.14 | 312 | 1.34 | 312 |
| RL | 5.46 | 51 | 0.67 | 73 | 0.10 | 29 | 0.08 | 124 | 0.76 | 124 |
| Optimization Improvement/% | 26.4 | 17.7 | 30.6 | 55.5 | 34.8 | 44.2 | 43.2 | 60.3 | 43.4 | 60.3 |
| Power | Tavg | Ph | Prz | PrzL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ/% | ts/s | ∆/°C | ts/s | ∆/MPa | ts/s | ∆/MPa | ts/s | ∆/% | ts/s | |
| PID | 33.9 | 272 | 7.03 | 148 | 0.66 | 39 | 0.30 | 269 | 9.71 | 304 |
| RL | 26.3 | 132 | 5.38 | 51 | 0.48 | 20 | 0.26 | 148 | 6.65 | 164 |
| Optimization Improvement/% | 22.6 | 51.5 | 23.5 | 65.5 | 27.5 | 48.7 | 15.8 | 45.0 | 31.5 | 46.1 |
| Power | Tavg | Ph | Prz | PrzL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ/% | ts/s | ∆/°C | ts/s | ∆/MPa | ts/s | ∆/MPa | ts/s | ∆/% | ts/s | |
| PID | 24.9 | 222 | 7.90 | 369 | 1.38 | 126 | 0.37 | 452 | 14.9 | 233 |
| RL | 18.4 | 178 | 5.23 | 187 | 1.14 | 65 | 0.26 | 183 | 10.1 | 165 |
| Optimization Improvement/% | 26.0 | 19.8 | 33.7 | 49.3 | 17.6 | 48.4 | 28.2 | 59.5 | 32.1 | 29.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Xiao, K.; Huang, K.; Yang, Z.; Chu, Q.; Jiang, G. A Multi-Variable Coupled Control Strategy Based on a Deep Deterministic Policy Gradient Reinforcement Learning Algorithm for a Small Pressurized Water Reactor. Energies 2025, 18, 1517. https://doi.org/10.3390/en18061517
Chen J, Xiao K, Huang K, Yang Z, Chu Q, Jiang G. A Multi-Variable Coupled Control Strategy Based on a Deep Deterministic Policy Gradient Reinforcement Learning Algorithm for a Small Pressurized Water Reactor. Energies. 2025; 18(6):1517. https://doi.org/10.3390/en18061517
Chicago/Turabian StyleChen, Jie, Kai Xiao, Ke Huang, Zhen Yang, Qing Chu, and Guanfu Jiang. 2025. "A Multi-Variable Coupled Control Strategy Based on a Deep Deterministic Policy Gradient Reinforcement Learning Algorithm for a Small Pressurized Water Reactor" Energies 18, no. 6: 1517. https://doi.org/10.3390/en18061517
APA StyleChen, J., Xiao, K., Huang, K., Yang, Z., Chu, Q., & Jiang, G. (2025). A Multi-Variable Coupled Control Strategy Based on a Deep Deterministic Policy Gradient Reinforcement Learning Algorithm for a Small Pressurized Water Reactor. Energies, 18(6), 1517. https://doi.org/10.3390/en18061517






