CFD-DEM Modeling and Experimental Verification of Heat Transfer Behaviors of Cylindrical Biomass Particles with Super-Ellipsoid Model
Abstract
1. Introduction
2. Mathematical Model
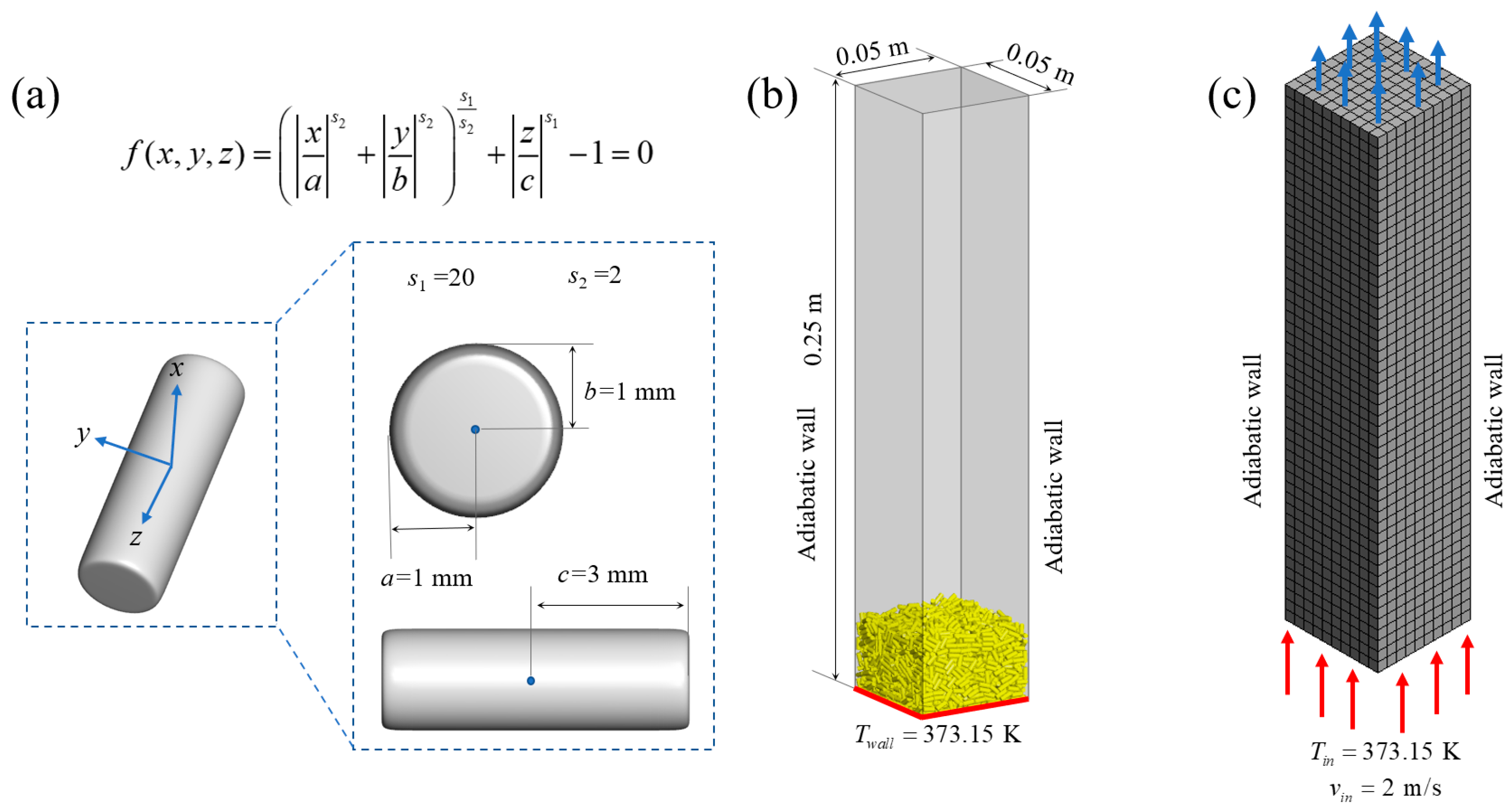
2.1. Particle Geometry Governing Equation
2.2. Governing Equations of Particles
2.3. Governing Equations of Fluid
2.4. Interphase Force Model
2.5. Heat Transfer Model
3. Model Validation
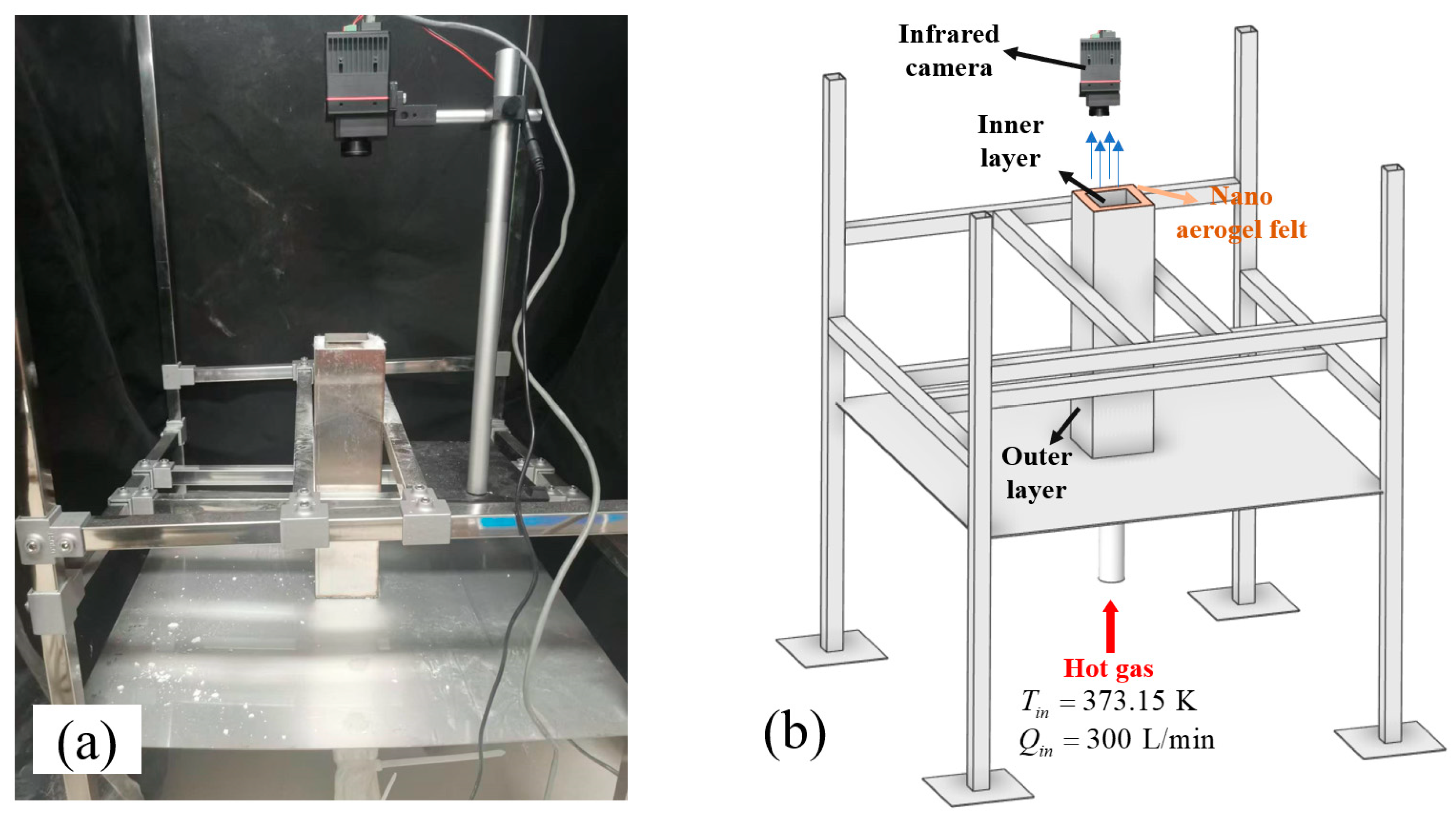
3.1. Experiment Settings
3.2. Simulation Settings
3.3. Comparison of Numerical Results with Experiments
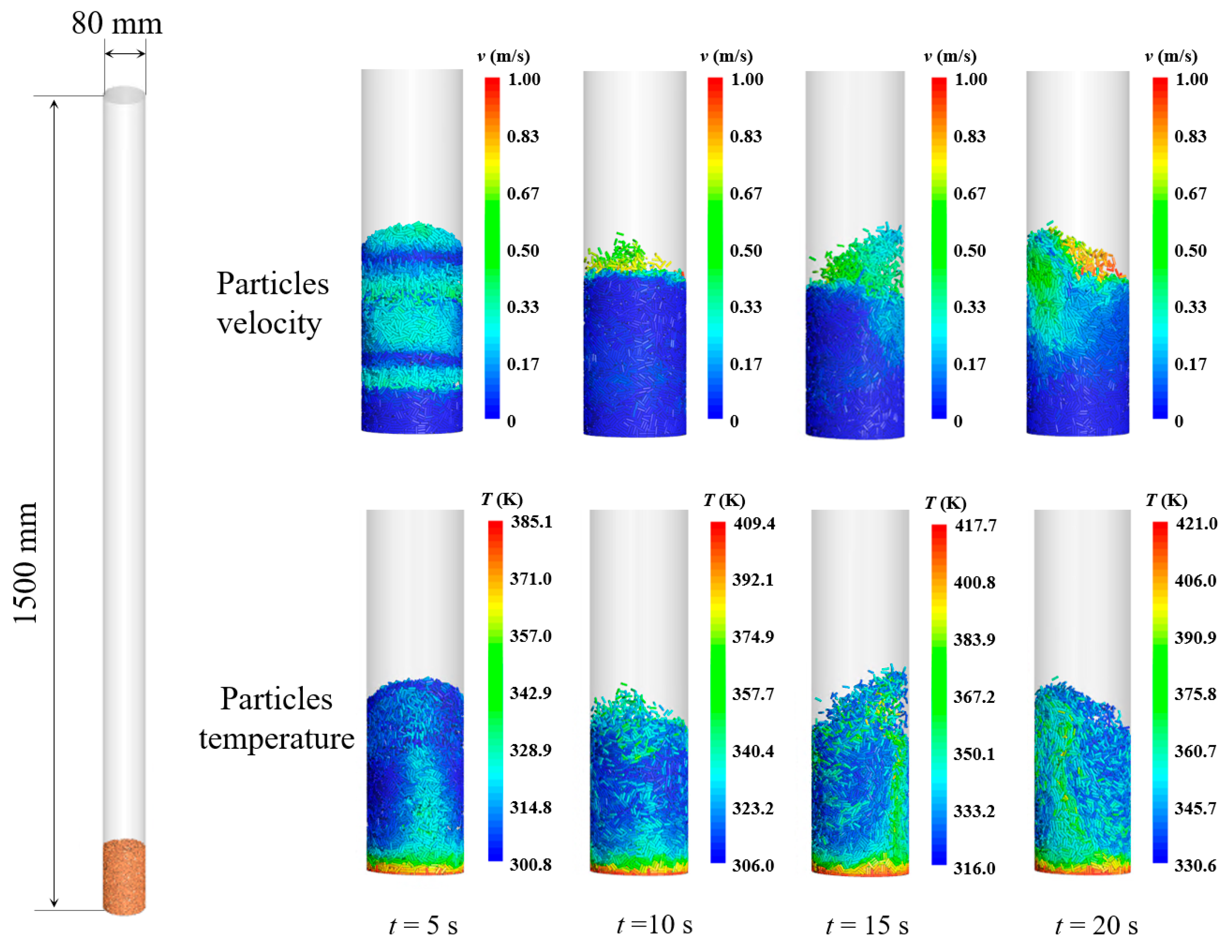
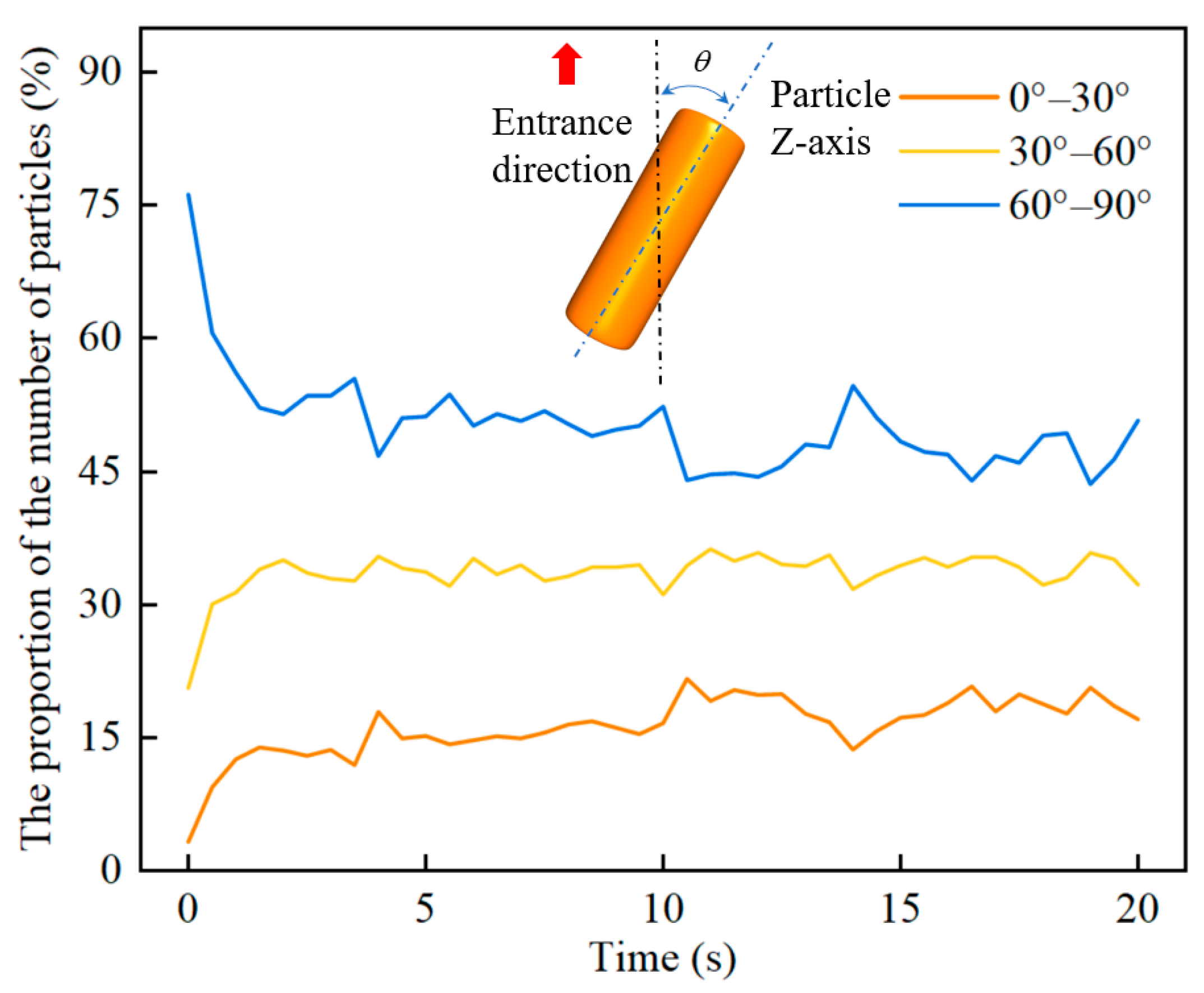
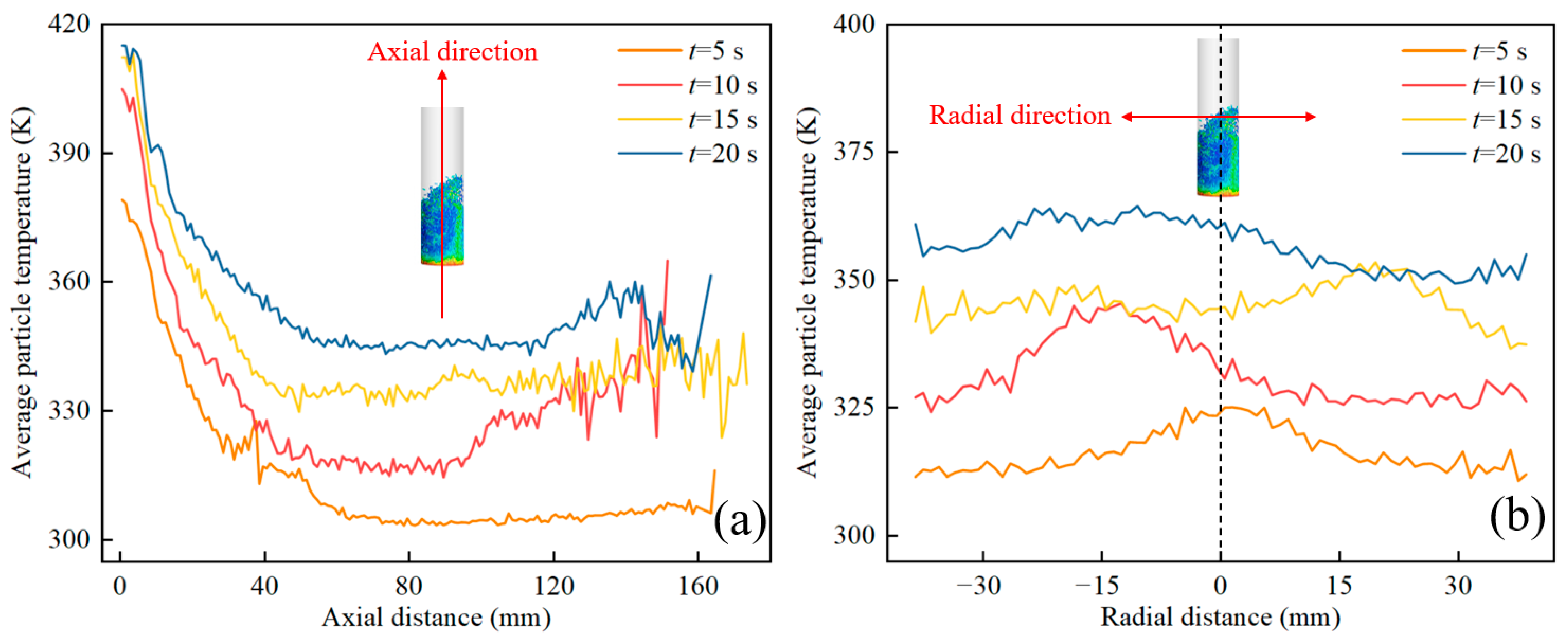
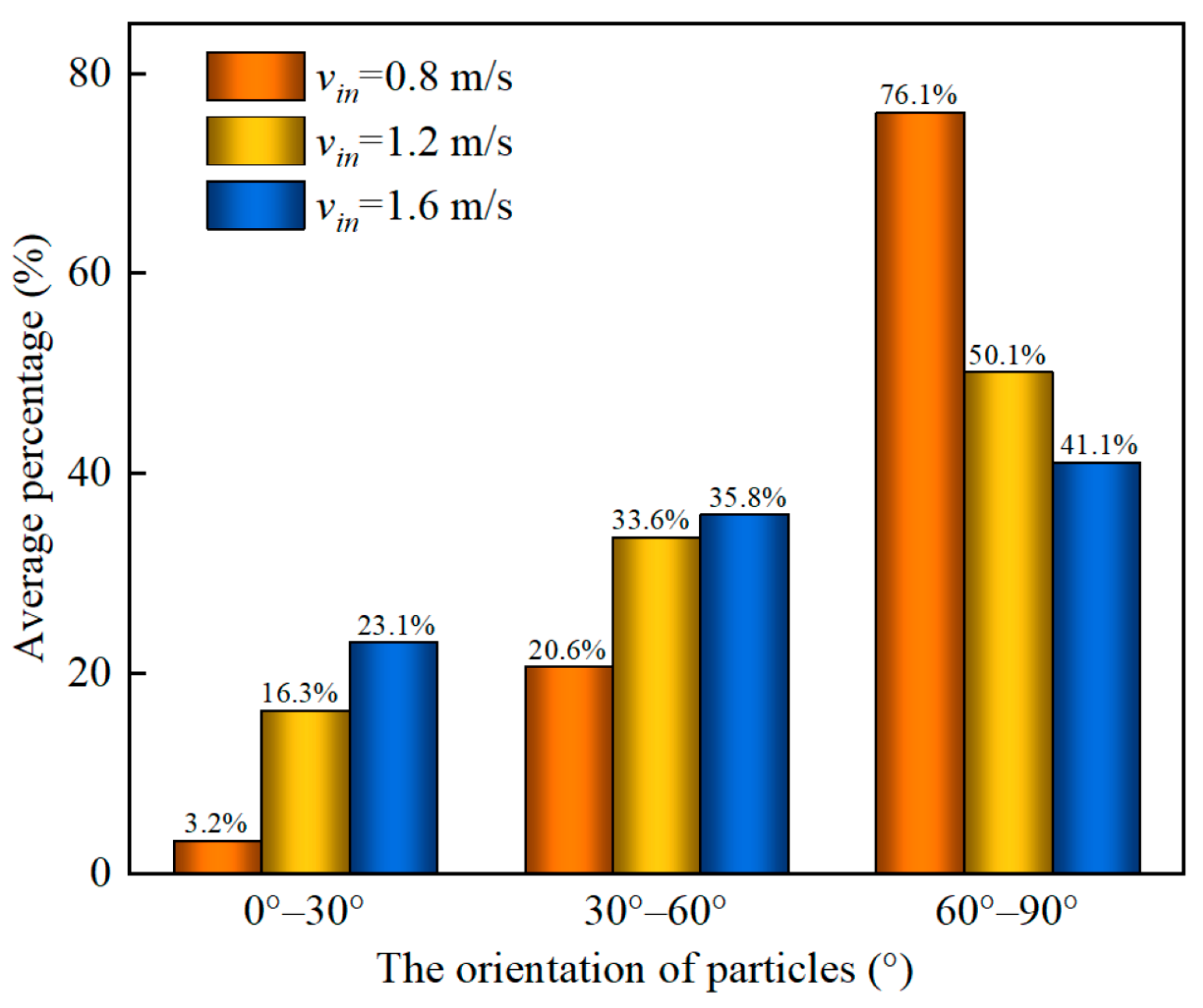
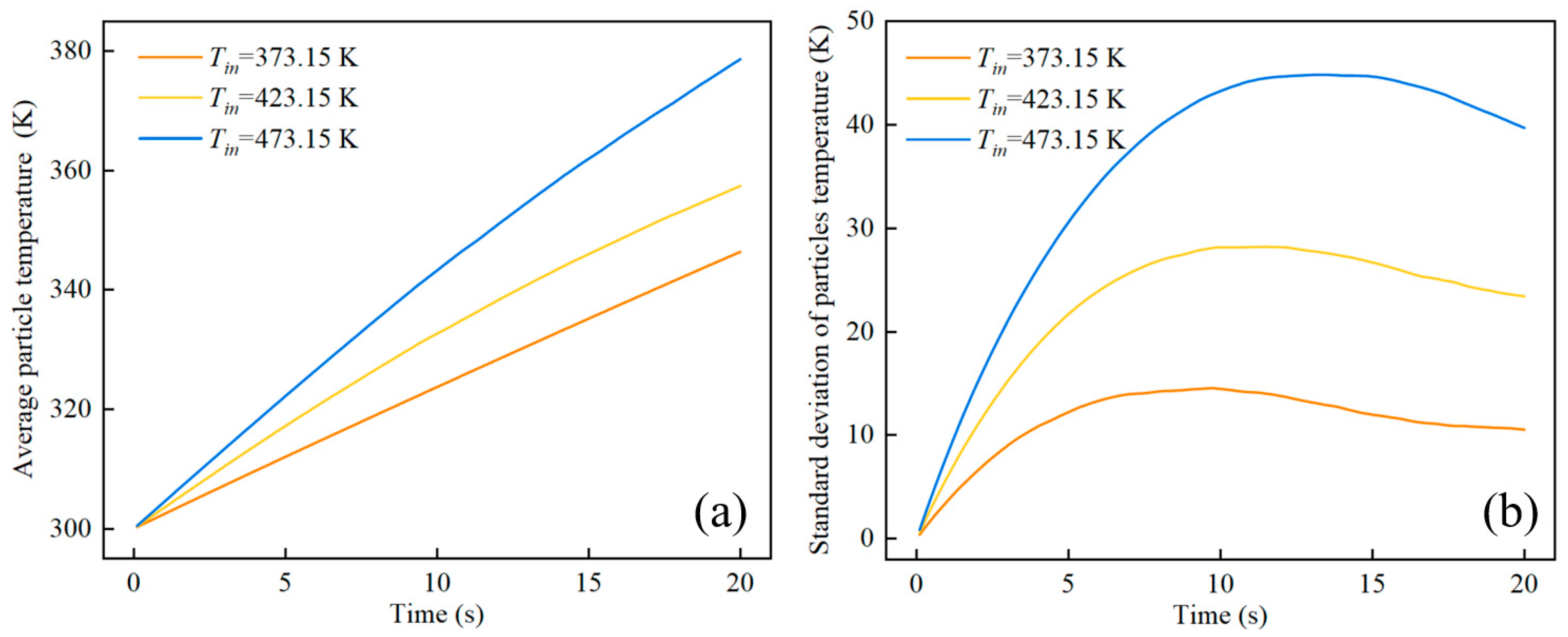
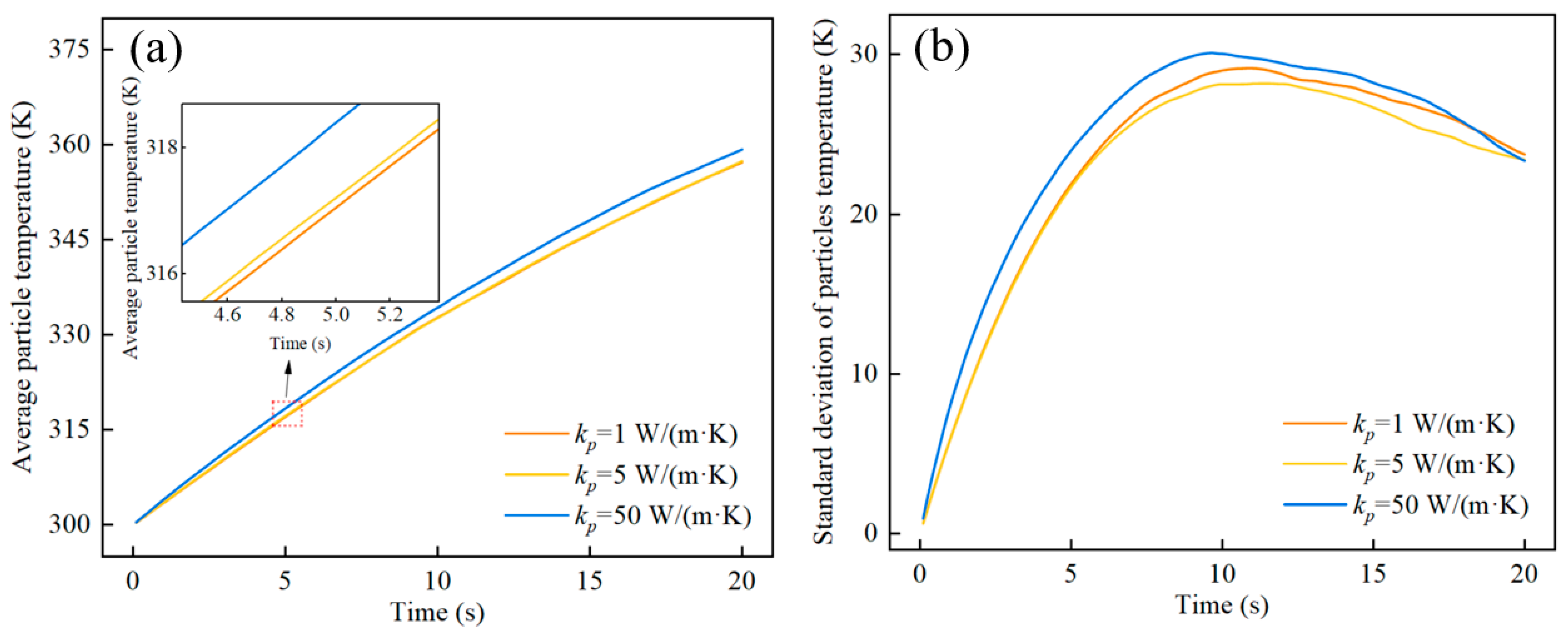
4. Results and Discussion
4.1. The Effect of Gas Velocity
4.2. The Effect of Inlet Temperature
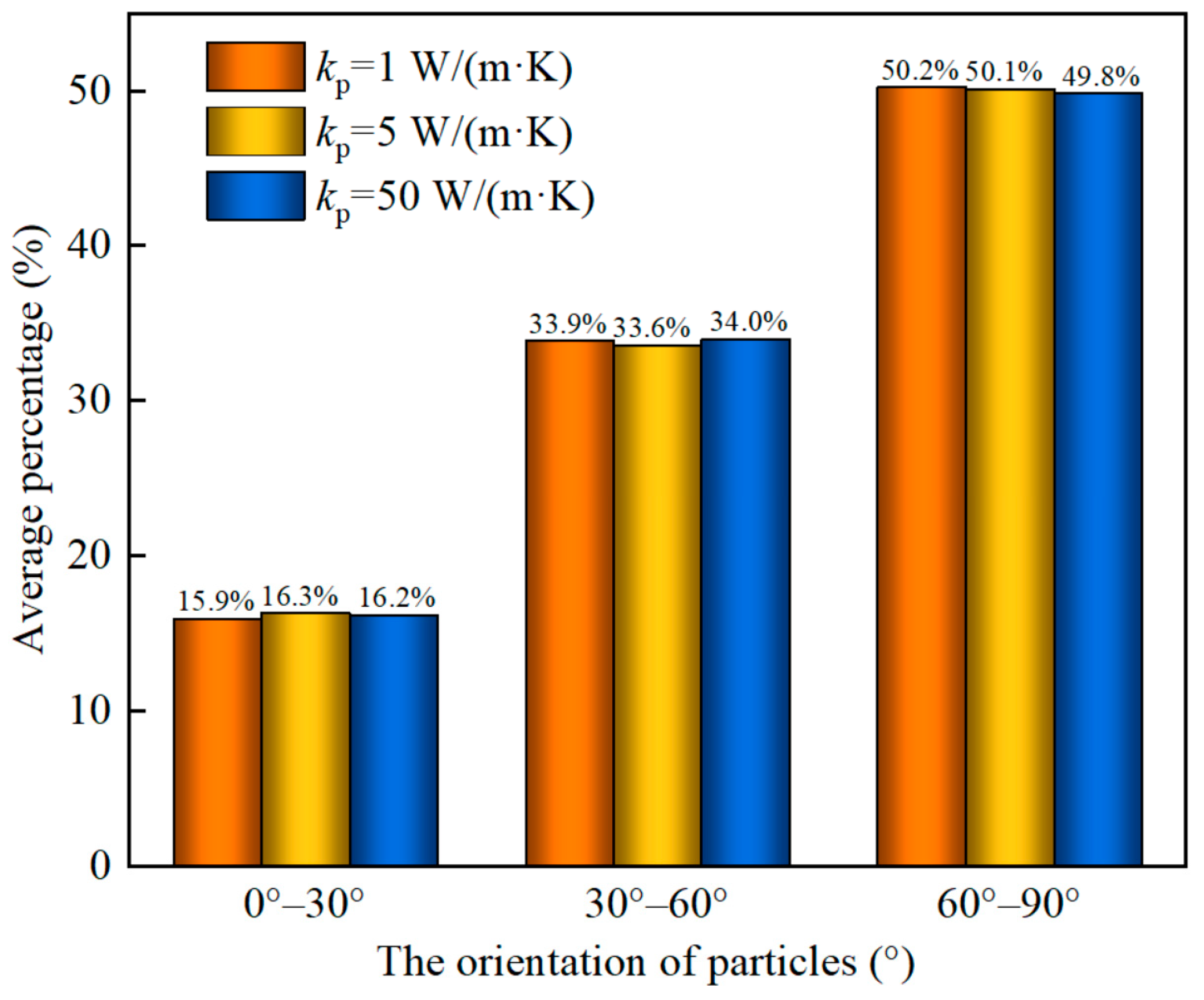
4.3. The Effect of the Thermal Conductivity of Particles
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, L.; Ma, H.; Liu, Z.; Zhao, Y. Development and verification of coarse-grain CFD-DEM for nonspherical particles in a gas–solid fluidized bed. AIChE J. 2022, 68, e17876. [Google Scholar] [CrossRef]
- Kong, D.; Luo, K.; Wang, S.; Yu, J.; Fan, J. Particle behaviours of biomass gasification in a bubbling fluidized bed. Chem. Eng. J. 2022, 428, 131847. [Google Scholar] [CrossRef]
- Hou, Q.F.; Zhou, Z.Y.; Yu, A.B. Gas–solid flow and heat transfer in fluidized beds with tubes: Effects of material properties and tube array settings. Powder Technol. 2016, 296, 59–71. [Google Scholar] [CrossRef]
- Boer, L.; Buist, K.A.; Deen, N.G.; Padding, J.T.; Kuipers, J.A.M. Experimental study on orientation and de-mixing phenomena of elongated particles in gas-fluidized beds. Powder Technol. 2018, 329, 332–344. [Google Scholar] [CrossRef]
- Wu, K.; Dai, L.; Li, B.; Gu, C.; Yuan, Z.; Luo, D. Study on flow characteristics of dilute phase flexible ribbon particles in a fluidised bed riser using particle tracking velocimetry. Chem. Eng. Res. Des. 2019, 152, 254–268. [Google Scholar] [CrossRef]
- Buist, K.A.; Jayaprakash, P.; Kuipers, J.A.M.; Deen, N.G.; Padding, J.T. Magnetic particle tracking for nonspherical particles in a cylindrical fluidized bed. AIChE J. 2017, 63, 5335–5342. [Google Scholar] [CrossRef]
- Li, Z.; Janssen, T.C.E.; Buist, K.A.; Deen, N.G.; van Sint Annaland, M.; Kuipers, J.A.M. Experimental and simulation study of heat transfer in fluidized beds with heat production. Chem. Eng. J. 2017, 317, 242–257. [Google Scholar] [CrossRef]
- Patil, A.V.; Peters, E.A.J.F.; Kuipers, J.A.M. Comparison of CFD-DEM heat transfer simulations with infrared/visual measurements. Chem. Eng. J. 2015, 277, 388–401. [Google Scholar] [CrossRef]
- Yu, Y.; Lu, F.; Bai, H.; Wei, F.; Zhang, C. Effect of fines addition on heat transfer performance in gas-solid fluidized bed: An integrated experimental, simulation, and theoretical study. Chem. Eng. J. 2023, 476, 146806. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Kang, Z.; Su, F.; Fang, L.; Zhu, H. DEM-CFD coupled simulation of limestone calcination and fuel combustion in beam type lime shaft kiln. Appl. Therm. Eng. 2023, 231, 120935. [Google Scholar] [CrossRef]
- Kong, R.; Bi, D.; Yao, D.; Zhang, Y.; He, J.; Liu, J. CFD-DEM study of a V-shaped Down-tube pyrolysis Reactor: Flow and heat transfer between heat carrier and biomass. Appl. Therm. Eng. 2022, 207, 118179. [Google Scholar] [CrossRef]
- Lu, W.; Ma, C.; Liu, D.; Zhao, Y.; Ke, X.; Zhou, T. A comprehensive heat transfer prediction model for tubular moving bed heat exchangers using CFD-DEM: Validation and sensitivity analysis. Appl. Therm. Eng. 2024, 247, 123072. [Google Scholar] [CrossRef]
- Oyedeji, O.A.; Pecha, M.B.; Finney, C.E.A.; Peterson, C.A.; Smith, R.G.; Mills, Z.G.; Gao, X.; Shahnam, M.; Rogers, W.A.; Ciesielski, P.N.; et al. CFD–DEM modeling of autothermal pyrolysis of corn stover with a coupled particle- and reactor-scale framework. Chem. Eng. J. 2022, 446, 136920. [Google Scholar] [CrossRef]
- Wang, S.; Luo, K.; Fan, J. CFD-DEM coupled with thermochemical sub-models for biomass gasification: Validation and sensitivity analysis. Chem. Eng. Sci. 2020, 217, 115550. [Google Scholar] [CrossRef]
- Ostermeier, P.; Fischer, F.; Fendt, S.; DeYoung, S.; Spliethoff, H. Coarse-grained CFD-DEM simulation of biomass gasification in a fluidized bed reactor. Fuel 2019, 255, 115790. [Google Scholar] [CrossRef]
- Wang, S.; Shen, Y. CFD-DEM study of biomass gasification in a fluidized bed reactor: Effects of key operating parameters. Renew. Energy 2020, 159, 1146–1164. [Google Scholar] [CrossRef]
- Lian, G.; Zhong, W. Coupling CFD-DEM with cohesive force and chemical reaction sub-models for biomass combustion in a fluidized bed. Fuel 2023, 350, 128858. [Google Scholar] [CrossRef]
- Mohseni, M.; Peters, B.; Baniasadi, M. Conversion analysis of a cylindrical biomass particle with a DEM-CFD coupling approach. Case Stud. Therm. Eng. 2017, 10, 343–356. [Google Scholar] [CrossRef]
- Lu, L.; Gao, X.; Shahnam, M.; Rogers, W.A. Simulations of biomass pyrolysis using glued-sphere CFD-DEM with 3-D intra-particle models. Chem. Eng. J. 2021, 419, 129564. [Google Scholar] [CrossRef]
- Prakotmak, P.; Wangchai, S. CFD-DEM simulation of fluidization of multi sphere-modeled corn particles. Part. Sci. Technol. 2022, 40, 752–761. [Google Scholar] [CrossRef]
- Zhang, R.; Ku, X.; Yang, S. Study of air-steam gasification of spherocylindrical biomass particles in a fluidized bed by using CFD-DEM coupling with the multi-sphere model. Energy Convers. Manag. 2023, 276, 116561. [Google Scholar] [CrossRef]
- Tsuji, T.; Sakamoto, Y.; Harada, S.; Uemoto, K.; Oshitani, J.; Washino, K.; Tanaka, T.; Kajiwara, H.; Matsuoka, K. FPM-SE: A numerical model for dense gas–solid flows with large non-spherical object. Chem. Eng. Sci. 2022, 264, 118149. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, S.; Zhou, X. DEM investigation of angle of repose for super-ellipsoidal particles. Particuology 2020, 50, 53–66. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, H.; Zhou, L.; Xu, C.; Zhang, X.; Zhao, Y. DEM-DDM investigation of the intra-tablet coating uniformity for tablets with different shapes. Powder Technol. 2024, 438, 119666. [Google Scholar] [CrossRef]
- You, Y.; Zhao, Y. Discrete element modelling of ellipsoidal particles using super-ellipsoids and multi-spheres: A comparative study. Powder Technol. 2018, 331, 179–191. [Google Scholar] [CrossRef]
- Barr. Superquadrics and Angle-Preserving Transformations. IEEE Comput. Graph. Appl. 1981, 1, 11–23. [Google Scholar] [CrossRef]
- Ma, H.; Xu, L.; Zhao, Y. CFD-DEM simulation of fluidization of rod-like particles in a fluidized bed. Powder Technol. 2017, 314, 355–366. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, H.; Wang, B.; Yu, C.; Fan, X. Experimental and numerical analysis of oil shale drying in fluidized bed. Dry. Technol. 2017, 35, 802–814. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Gao, X.; Yu, J.; Lu, L.; Li, C.; Rogers, W.A. Development and validation of SuperDEM-CFD coupled model for simulating non-spherical particles hydrodynamics in fluidized beds. Chem. Eng. J. 2021, 420, 127654. [Google Scholar] [CrossRef]
- Richter, A.; Nikrityuk, P.A. Drag forces and heat transfer coefficients for spherical, cuboidal and ellipsoidal particles in cross flow at sub-critical Reynolds numbers. Int. J. Heat Mass Transf. 2012, 55, 1343–1354. [Google Scholar] [CrossRef]
- Brazhenko, V.; Mochalin, I. Terminal velocity and drag coefficient of a smooth steel sphere moving in the water-filled vertical and inclined glass pipe (Newton regime). Powder Technol. 2024, 446, 120120. [Google Scholar] [CrossRef]
- Hölzer, A.; Sommerfeld, M. New simple correlation formula for the drag coefficient of non-spherical particles. Powder Technol. 2008, 184, 361–365. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, M.; Liu, Y.; Zheng, J. Particle-scale simulation of the flow and heat transfer behaviors in fluidized bed with immersed tube. AIChE J. 2009, 55, 3109–3124. [Google Scholar] [CrossRef]
- Shen, Y.; Zheng, B.; Sun, P.; Qi, C.; Wang, M.; Dong, Y.; Wang, Y.; Lv, J.; Wang, Y. Effects of ellipsoidal and regular hexahedral particles on the performance of the waste heat recovery equipment in a methanol reforming hydrogen production system. Int. J. Hydrogen Energy 2023, 48, 11141–11152. [Google Scholar] [CrossRef]
- Korkerd, K.; Zhou, Z.; Zou, R.; Piumsomboon, P.; Chalermsinsuwan, B. Effect of immersed tubes configurations on mixing and heat transfer of mixed biomass and silica sand in a bubbling fluidized bed using CFD-DEM and statistical experimental design analysis. Powder Technol. 2024, 437, 119542. [Google Scholar] [CrossRef]
- Handayani, S.U.; Wahyudi, H.; Agustina, S.; Yulianto, M.E.; Aryanto, H.D. CFD-DEM Study of heat and mass transfer of ellipsoidal particles in fluidized bed dryers. Powder Technol. 2023, 425, 118535. [Google Scholar] [CrossRef]
- Gan, J.; Zhou, Z.; Yu, A. Particle scale study of heat transfer in packed and fluidized beds of ellipsoidal particles. Chem. Eng. Sci. 2016, 144, 201–215. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Zhou, L.; Song, T.; Yang, J.; Zou, G.; Ma, H.; Zhao, Y. An improved model for predicting the erosion within the DEM framework. Powder Technol. 2023, 428, 118786. [Google Scholar] [CrossRef]
- Barton, I.E. Comparison of simple- and piso-type algorithms for transient flows. Int. J. Numer. Methods Fluids 1998, 26, 459–483. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Camb. Philos. Soc. 1947, 43, 50–67. [Google Scholar] [CrossRef]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]







| Properties and Parameters | Value |
|---|---|
| Particle size, a × b × c (mm × mm × mm) | 1 × 1 × 3 |
| Particle number | 3000 |
| Particle density (kg/m3) | 7874 |
| Elastic modulus of particle (GPa) | 194.02 |
| Poisson ratio of particle | 0.3 |
| Specific heat capacity of particle (J/(kg·K)) | 500 |
| Thermal conductivity of particle (W/(m·K)) | 16.3 |
| Initial particle temperature (K) | 298.15 |
| Emissivity of particle | 0.7 |
| Ambient temperature (K) | 298.15 |
| Gas flow rate (L/min) | 300 |
| Inlet gas temperature (K) | 373.15 |
| Parameters | Value |
|---|---|
| Particle size, a × b × c (mm × mm × mm) | 1 × 1 × 3 |
| Particle number | 3000 |
| Particle density (kg/m3) | 7874 |
| Elastic modulus of particle (GPa) | 194.02 |
| Poisson ratio of particle | 0.3 |
| Specific heat capacity of particle (J/(kg·K)) | 500 |
| Thermal conductivity of particle (W/(m·K)) | 16.3 |
| Initial particle temperature (K) | 298.15 |
| Normal spring stiffness (N/m) | 7000 |
| Tangential spring stiffness (N/m) | 2000 |
| Restitution coefficient | 0.9 |
| Friction coefficient | 0.3 |
| Grid size, x × y × z (mm × mm × mm) | 5 × 5 × 5 |
| Inlet gas velocity (m/s) | 2 |
| Inlet gas temperature (K) | 373.15 |
| DEM time step (s) | 2 × 10−5 |
| CFD time step (s) | 1 × 10−4 |
| Total simulation time (s) | 60 |
| Parameters | Value |
|---|---|
| CBP, a × b × c (mm × mm × mm) | 1 × 1 × 3 |
| CBP number | 18,000 |
| CBP density (kg/m3) | 700 |
| Elastic modulus of CBP (GPa) | 10 |
| Poisson ratio of CBP | 0.2 |
| Specific heat capacity of CBP (J/(kg·K)) | 1800 |
| Thermal conductivity of CBP (W/(m·K)) | 5 |
| Initial CBP temperature (K) | 300 |
| Normal spring stiffness (N/m) | 700 |
| Tangential spring stiffness (N/m) | 200 |
| Restitution coefficient | 0.9 |
| Friction coefficient | 0.3 |
| Inlet gas velocity (m/s) | 1.2 |
| Inlet gas temperature (K) | 423.15 |
| DEM time step (s) | 4 × 10−5 |
| CFD time step (s) | 2 × 10−4 |
| Total simulation time (s) | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Chen, L.; Liu, Z.; Ma, H.; Zhou, L.; Zhao, Y. CFD-DEM Modeling and Experimental Verification of Heat Transfer Behaviors of Cylindrical Biomass Particles with Super-Ellipsoid Model. Energies 2025, 18, 1504. https://doi.org/10.3390/en18061504
Hu Y, Chen L, Liu Z, Ma H, Zhou L, Zhao Y. CFD-DEM Modeling and Experimental Verification of Heat Transfer Behaviors of Cylindrical Biomass Particles with Super-Ellipsoid Model. Energies. 2025; 18(6):1504. https://doi.org/10.3390/en18061504
Chicago/Turabian StyleHu, Yuhao, Likuan Chen, Zihan Liu, Huaqing Ma, Lianyong Zhou, and Yongzhi Zhao. 2025. "CFD-DEM Modeling and Experimental Verification of Heat Transfer Behaviors of Cylindrical Biomass Particles with Super-Ellipsoid Model" Energies 18, no. 6: 1504. https://doi.org/10.3390/en18061504
APA StyleHu, Y., Chen, L., Liu, Z., Ma, H., Zhou, L., & Zhao, Y. (2025). CFD-DEM Modeling and Experimental Verification of Heat Transfer Behaviors of Cylindrical Biomass Particles with Super-Ellipsoid Model. Energies, 18(6), 1504. https://doi.org/10.3390/en18061504






