Modeling and Analysis of Wind Turbine Wake Vortex Evolution Due to Time-Constant Spatial Variations in Atmospheric Flow
Abstract
1. Introduction
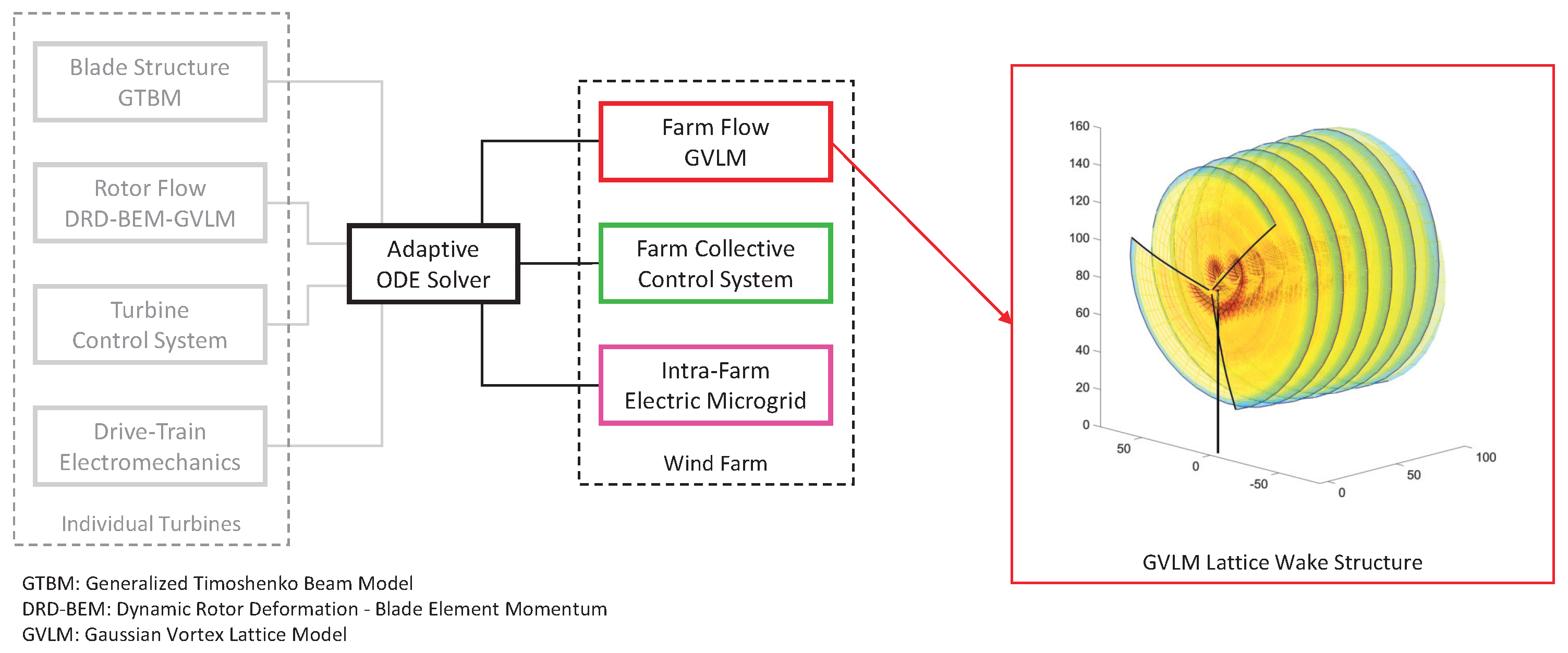
2. The CODEF Modeling Suite and the Methodology of Analysis
2.1. Model for Turbine Blade Structure and Aeroelastic Response
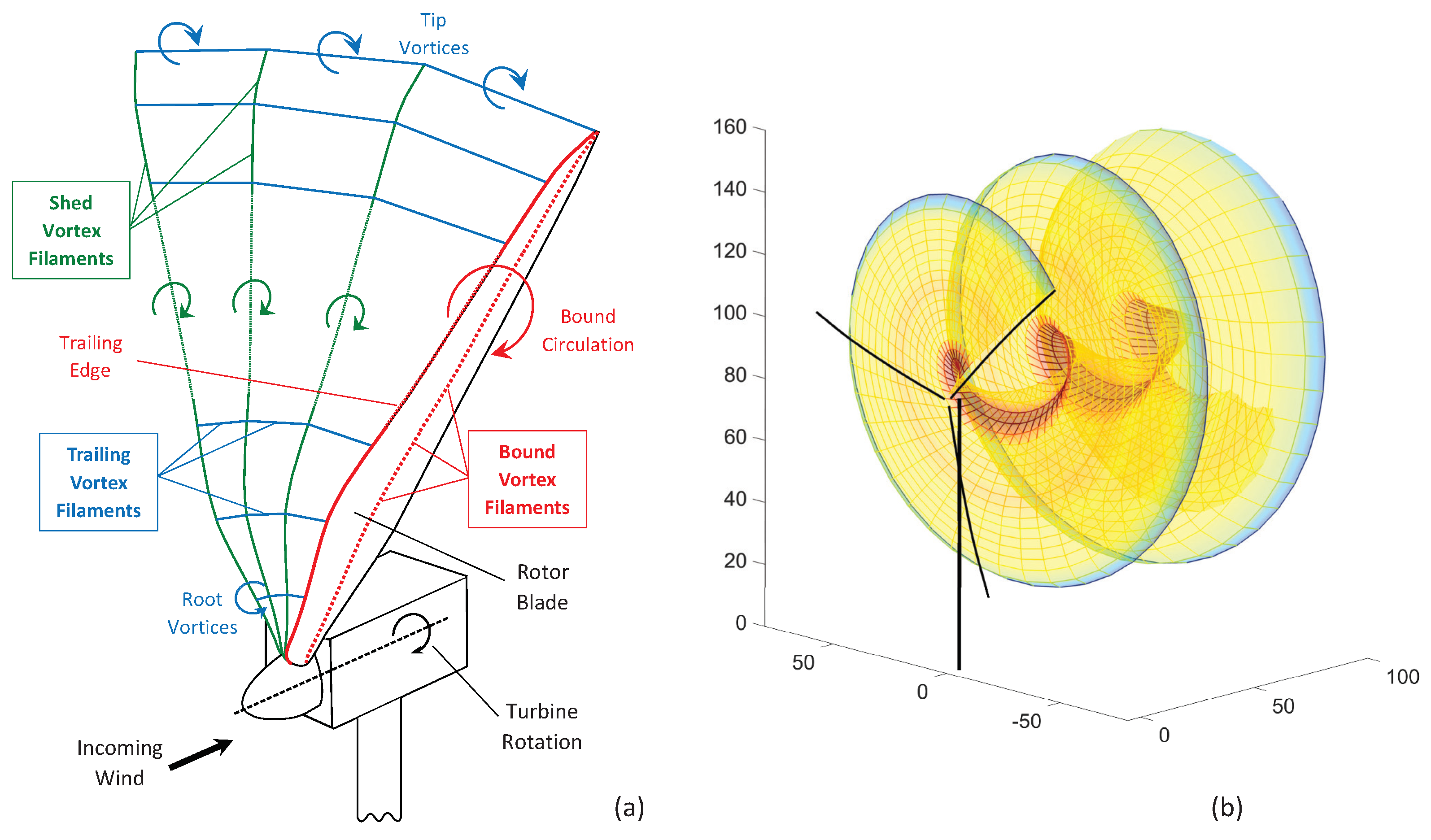
2.2. Turbine Wake Flow Model
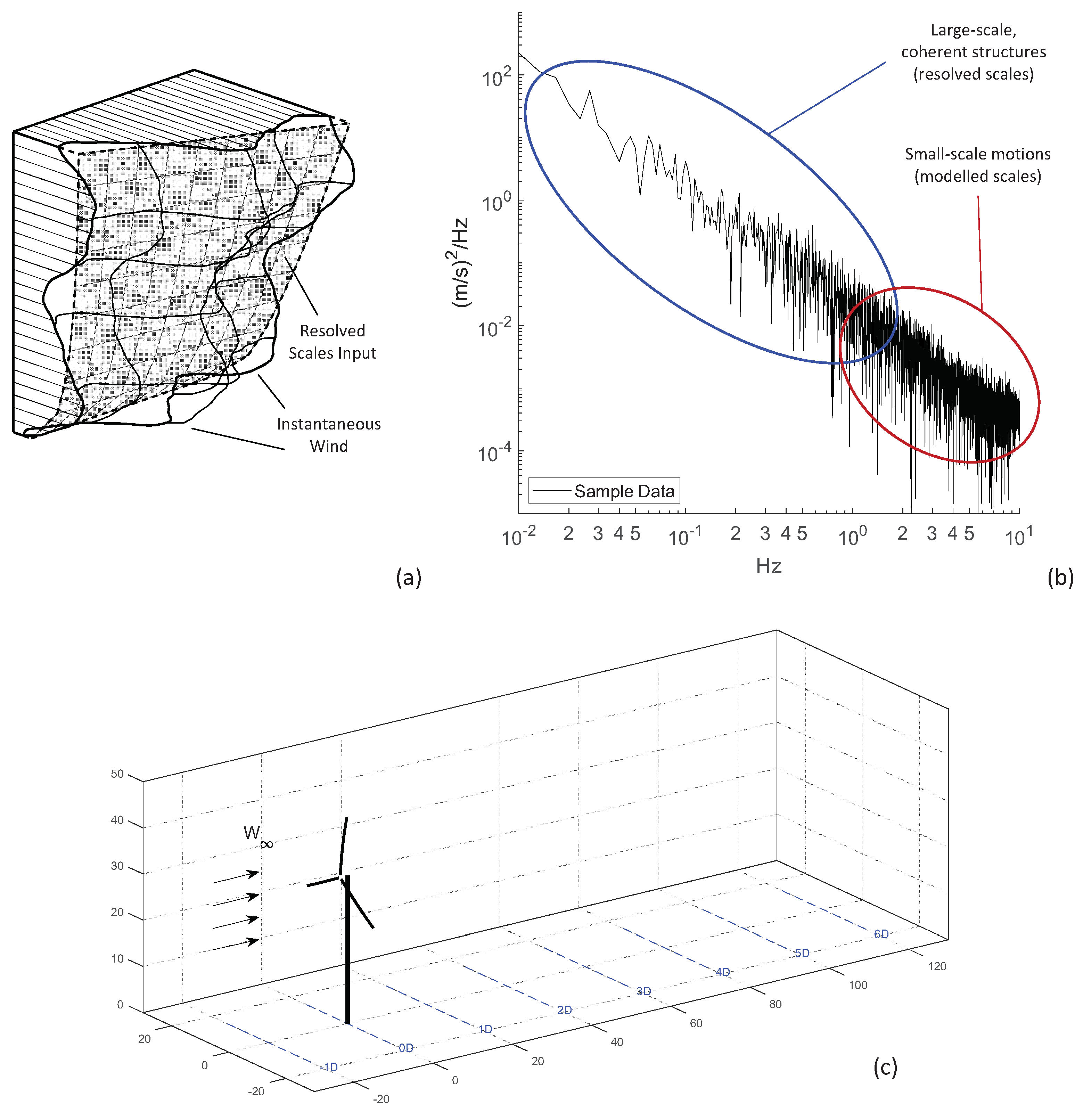
2.3. Atmospheric Flow Characterization
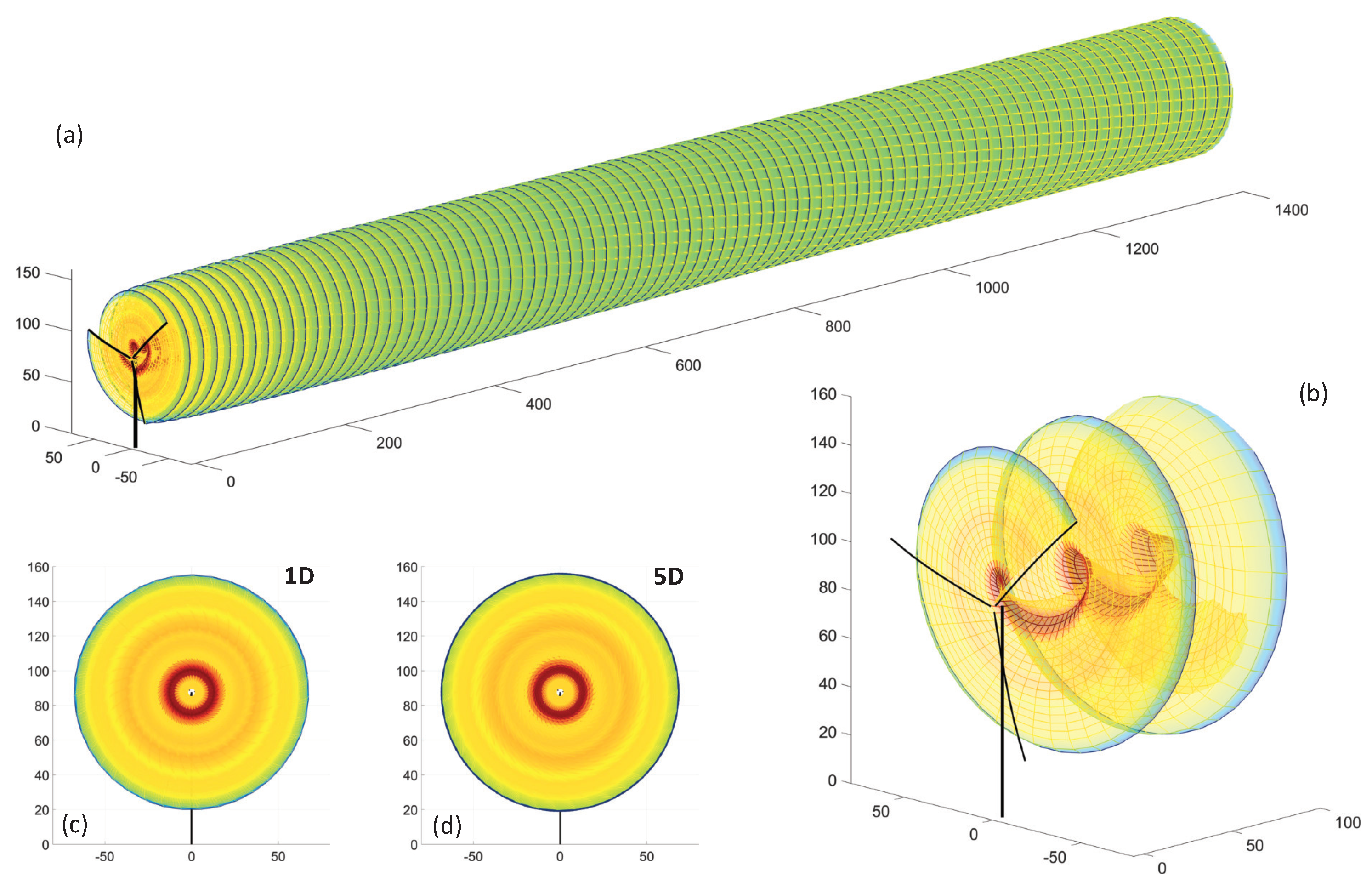
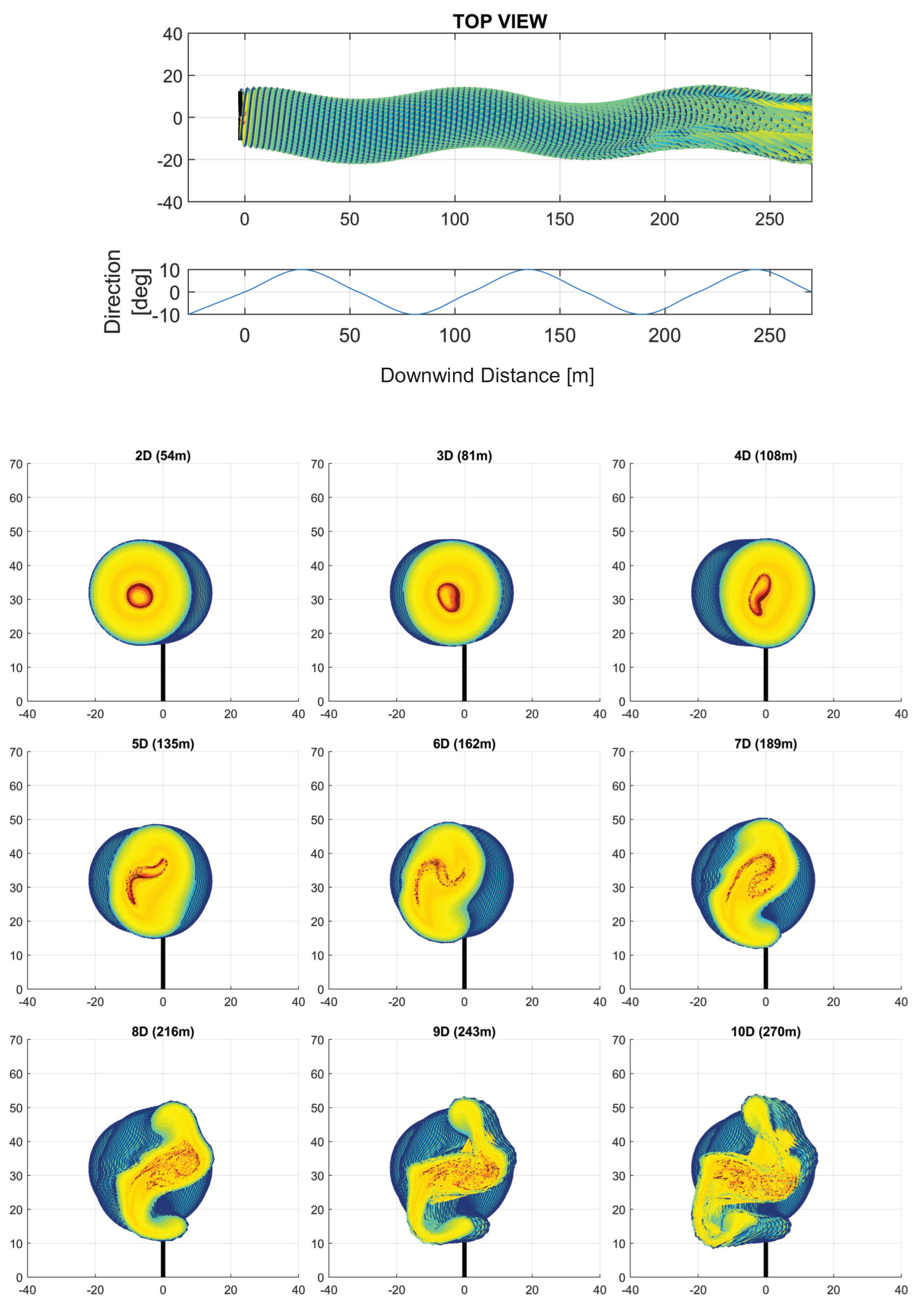
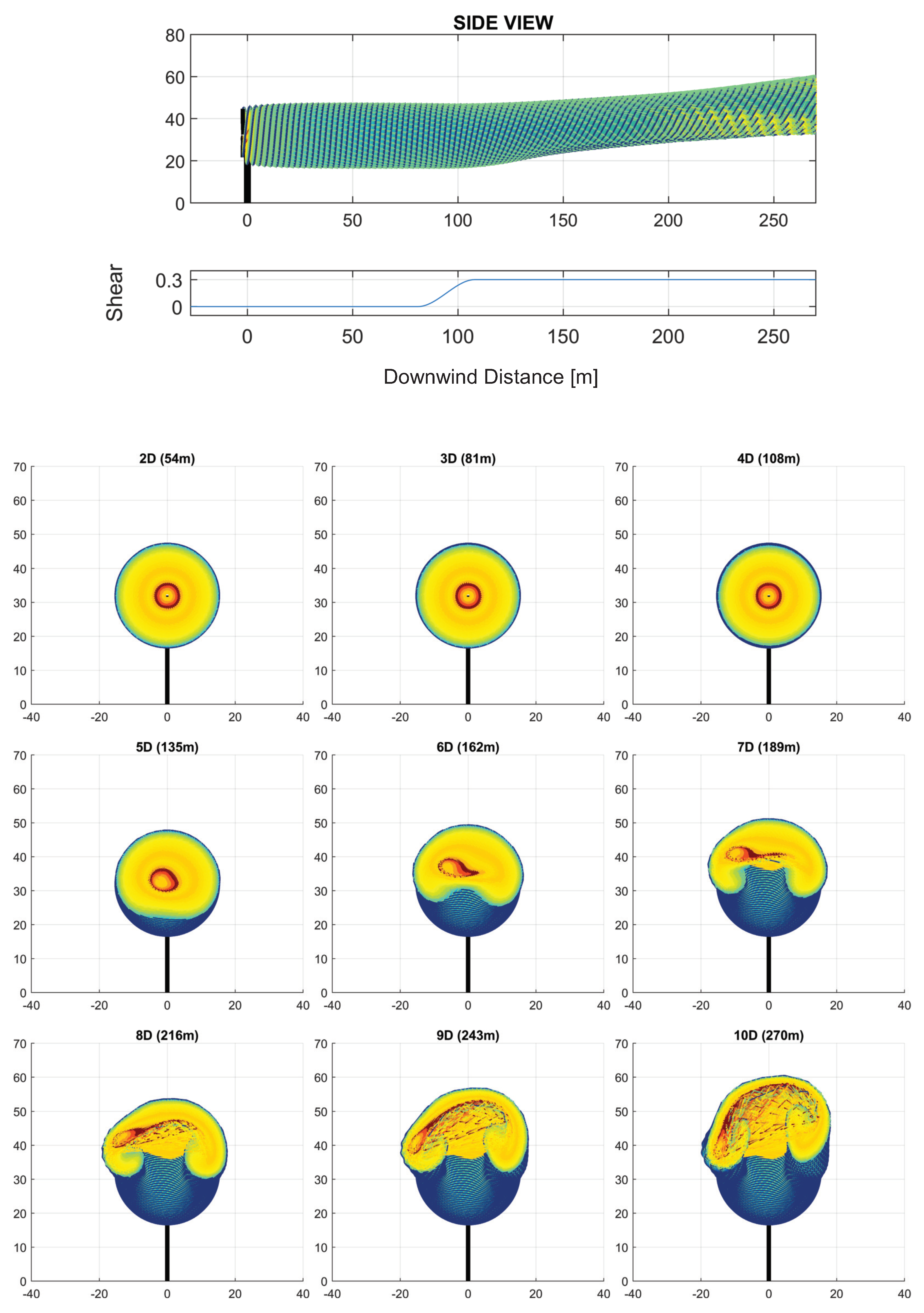
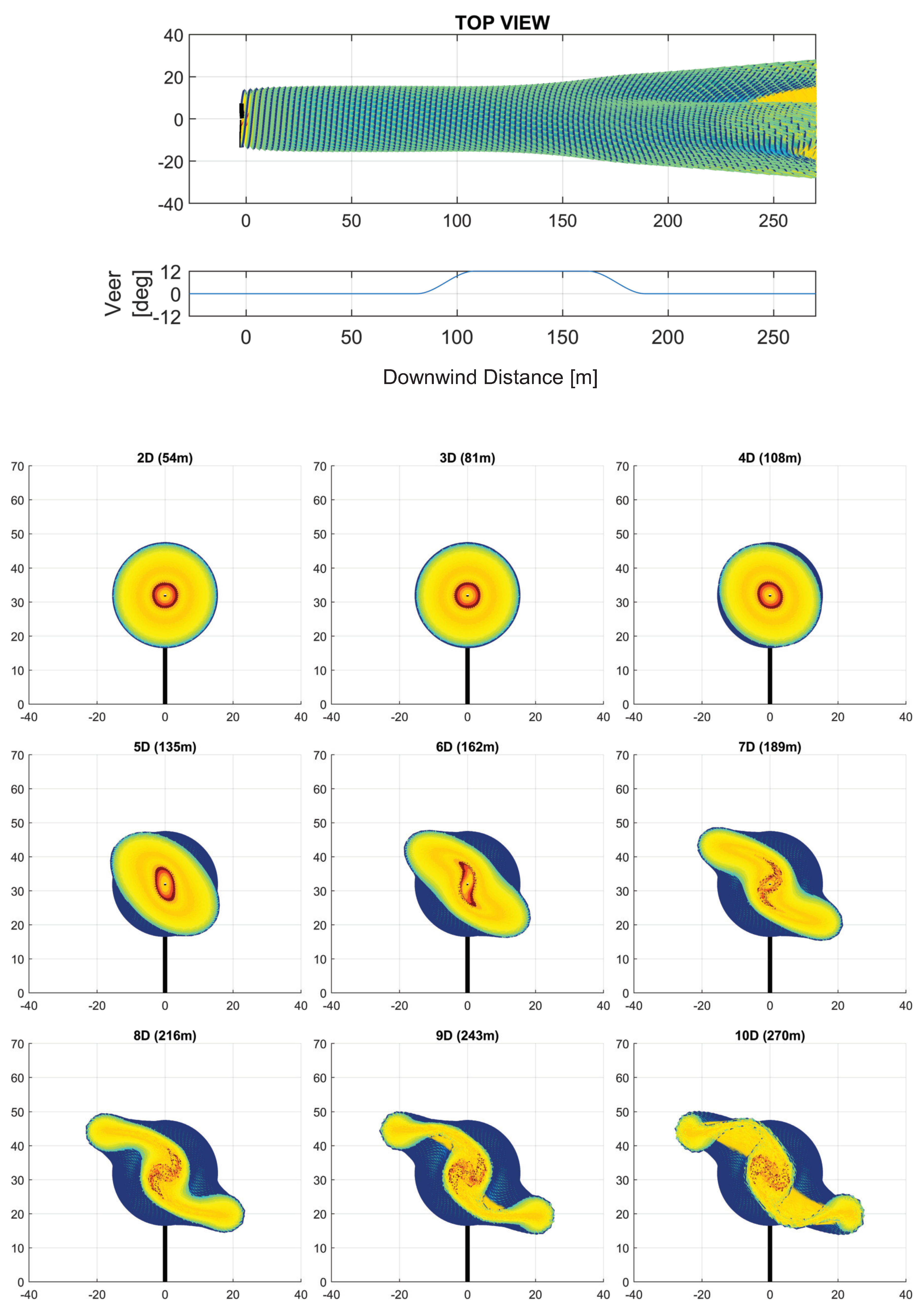
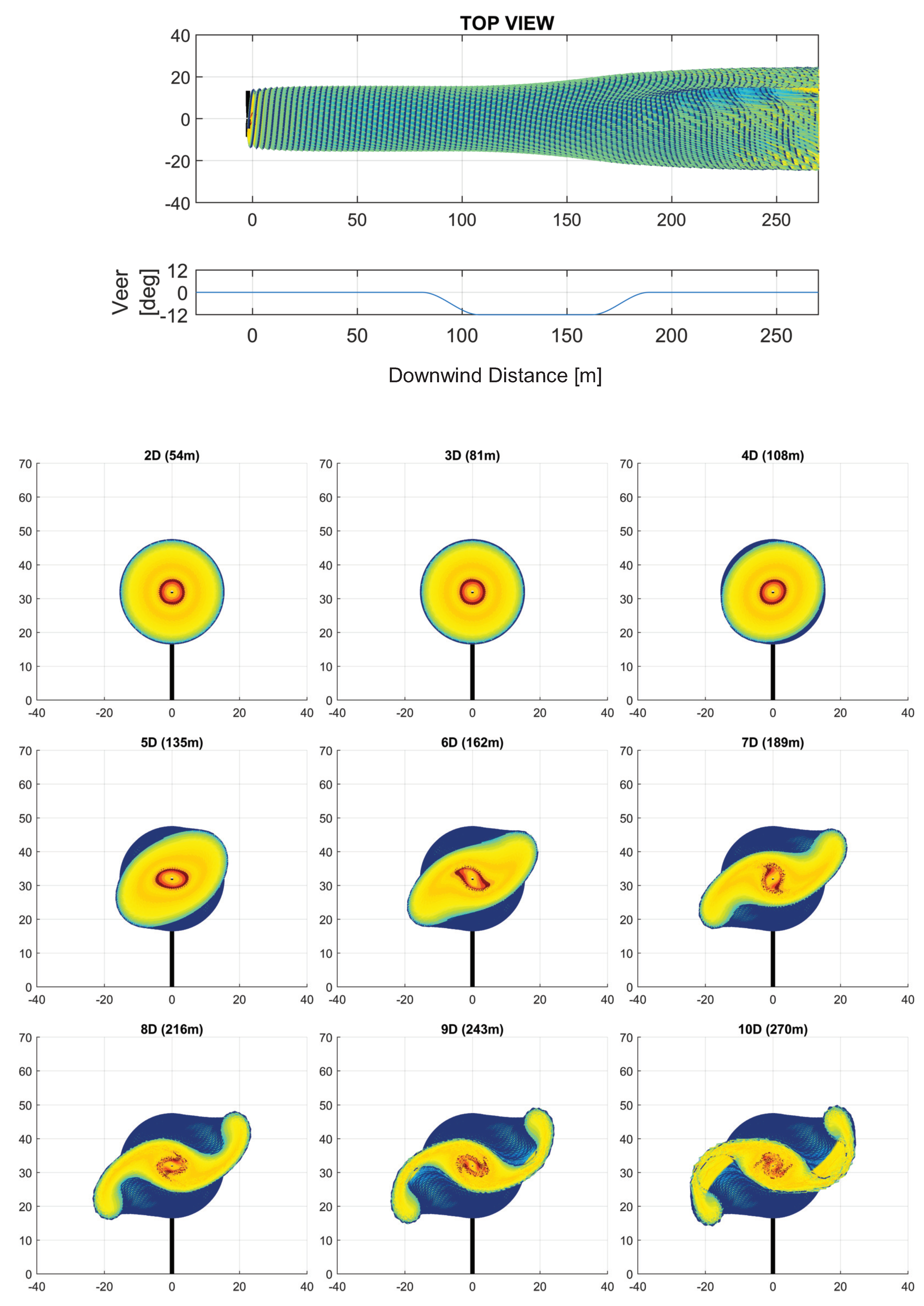
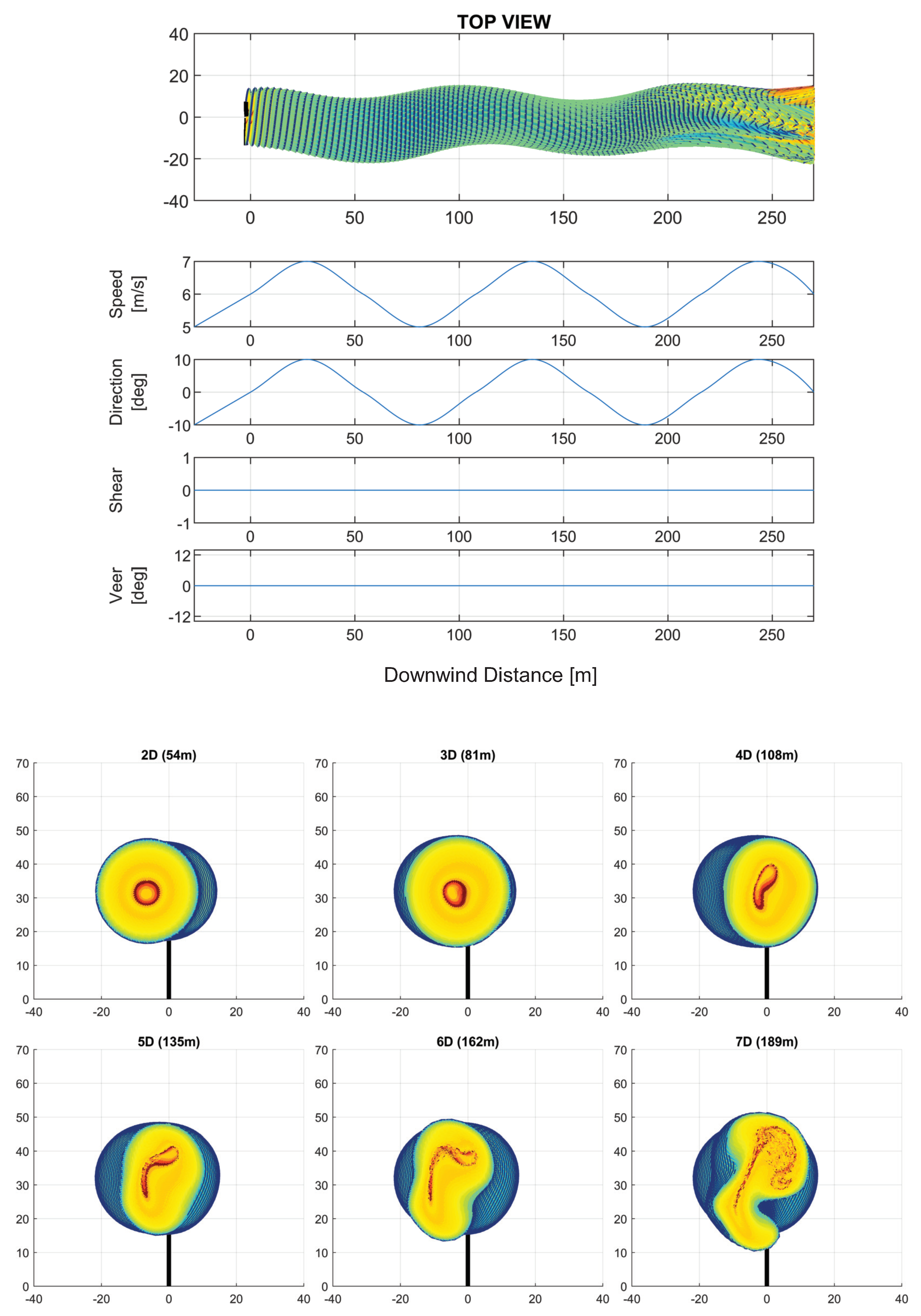
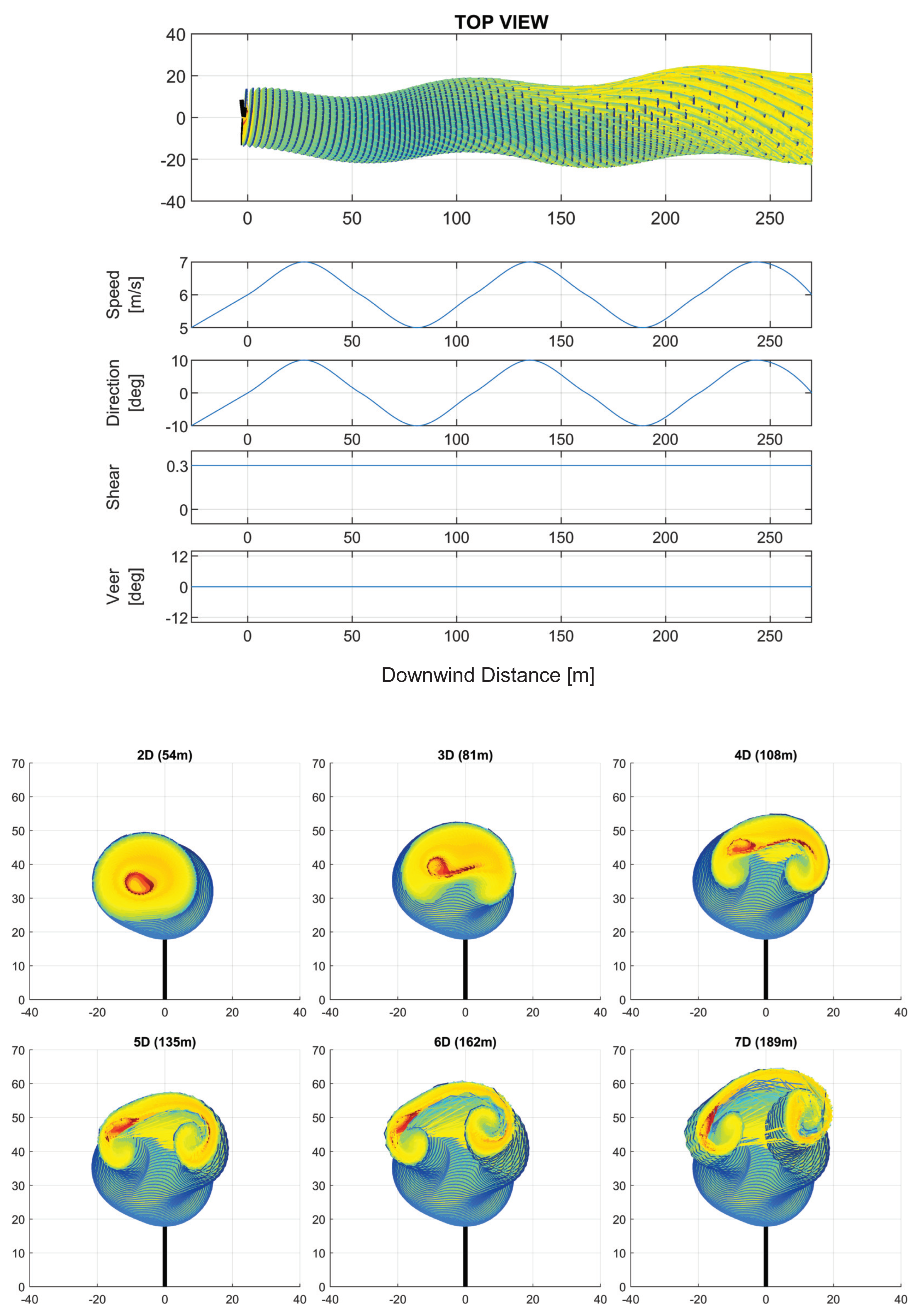
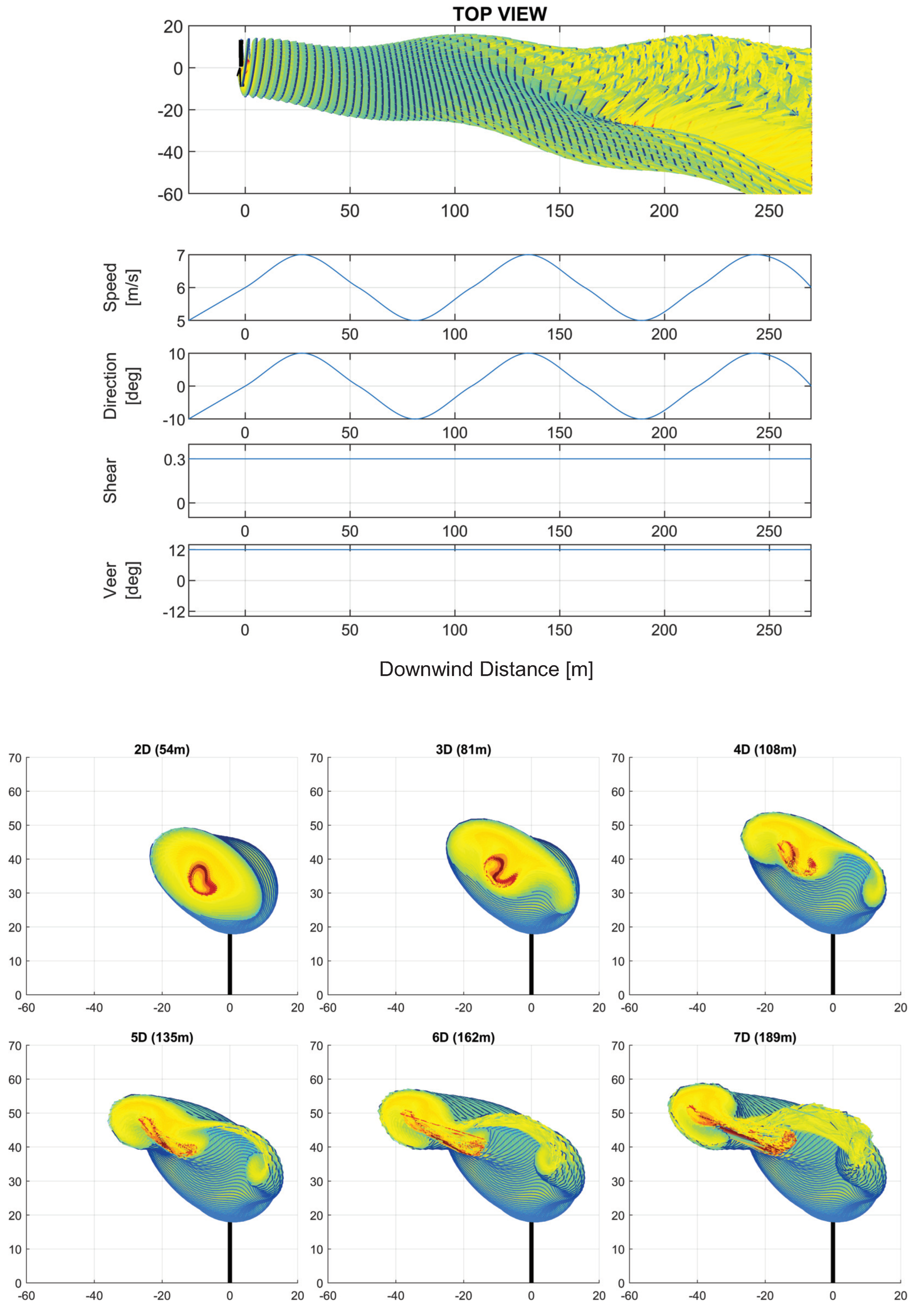
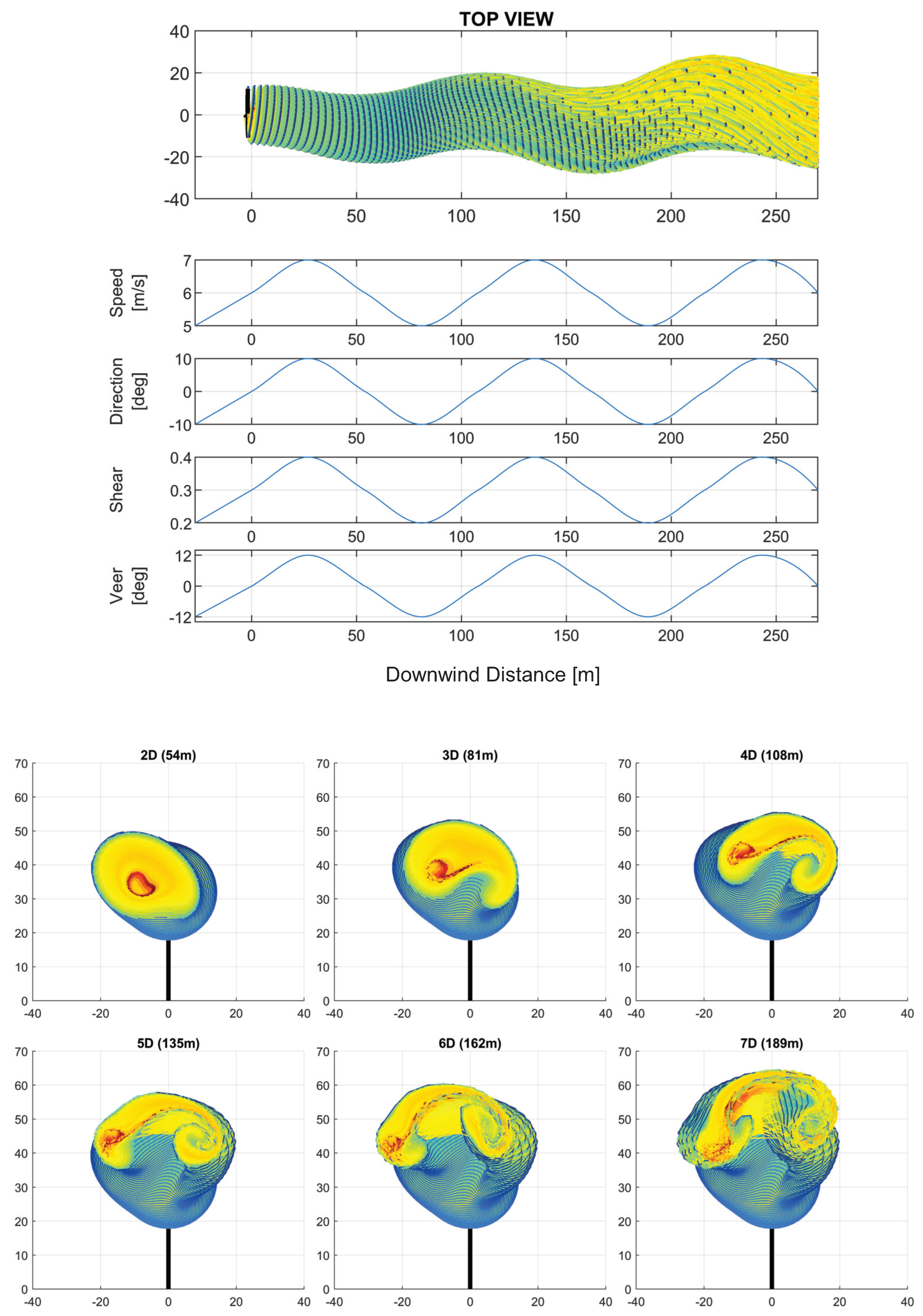
3. Analysis of the Effects of Downwind Variation in Wind Parameters on the Wake Structure
3.1. Combined Effects of Wind Parameter Spatial Variation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dykes, K.L.; Veers, P.S.; Lantz, E.J.; Holttinen, H.; Carlson, O.; Tuohy, A.; Sempreviva, A.M.; Clifton, A.; Rodrigo, J.S.; Berry, D.S.; et al. IEA Wind TCP: Results of IEA Wind TCP Workshop on a Grand Vision for Wind Energy Technology; Technical Report NREL/TP-5000-72437; National Renewable Energy Laboratory: Golden, CO, USA, 2019.
- IRENA. Global Energy Transformation: A Roadmap to 2050 (2019 Edition); Technical Report; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- TPI Composites Inc. Parametric Study for Large Wind Turbine Blades; Report SAND2002-2519; Sandia National Laboratories: Albuquerque, NM, USA, 2002.
- Griffin, D.A. Blade System Design Studies Volume I: Composite Technologies for Large Wind Turbine Blades; Report SAND2002-1879; Sandia National Laboratories: Albuquerque, NM, USA, 2002.
- Kong, C.; Bang, J.; Sugiyama, Y. Structural investigation of composite wind turbine blade considering various load cases and fatigue life. Energy 2005, 30, 2101–2114. [Google Scholar] [CrossRef]
- Stiesdal, H. Rotor loadings on the Bonus 450 kW turbine. J. Wind Eng. Ind. Aerodyn. 1992, 39, 303–315. [Google Scholar] [CrossRef]
- Veers, P.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Clifton, A.; Green, J.; Green, P.; Holttinen, H.; et al. Grand challenges in the science of wind energy. Science 2019, 366, eaau2027. [Google Scholar] [CrossRef]
- Veers, P.; Dykes, K.; Basu, S.; Bianchini, A.; Clifton, A.; Green, P.; Holttinen, H.; Kitzing, L.; Kosovic, B.; Lundquist, J.K.; et al. Grand Challenges: Wind energy research needs for a global energy transition. Wind Energy Sci. 2022, 7, 2491–2496. [Google Scholar] [CrossRef]
- Loth, E.; Fingersh, L.; Griffith, D.; Kaminski, M.; Qin, C. Gravo-aeroelastically scaling for extreme-scale wind turbines. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Tabor, A. Testing on the Ground Before You Fly: Wind Tunnels at NASA Ames. 2020. Available online: https://www.nasa.gov/centers-and-facilities/ames/testing-on-the-ground-before-you-fly-wind-tunnels-at-nasa-ames/ (accessed on 20 January 2024).
- Van Bussel, G.J. The Aerodynamics of Horizontal Axis Wind Turbine Rotors Explored with Asymptotic Expansion Methods. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1995. [Google Scholar]
- Ekaterinaris, J.A. Numerical simulation of incompressible two-blade rotor flowfields. J. Propuls. Power 1998, 14, 367–374. [Google Scholar] [CrossRef]
- Duque, E.; Van Dam, C.; Hughes, S. Navier-Stokes simulations of the NREL combined experiment phase II rotor. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999; p. 37. [Google Scholar]
- Sorensen, N. Aerodynamic predictions for the unsteady aerodynamics experiment phase-II rotor at the National Renewable Energy Laboratory. In Proceedings of the 2000 ASME Wind Energy Symposium, Reno, NV, USA, 14–17 January 2002; p. 37. [Google Scholar]
- Sprague, M.A.; Geers, T.L. Legendre spectral finite elements for structural dynamics analysis. Commun. Numer. Methods Eng. 2007, 24, 1953–1965. [Google Scholar] [CrossRef]
- Hansen, M.; Sorensen, J.; Michelsen, J.; Sorensen, N.; Hansen, M.; Sorensen, J.; Michelsen, J.; Sorensen, N. A global Navier-Stokes rotor prediction model. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–10 January 1997; p. 970. [Google Scholar]
- Maronga, B.; Gryschka, M.; Heinze, R.; Hoffmann, F.; Kanani-Sühring, F.; Keck, M.; Ketelsen, K.; Letzel, M.O.; Sühring, M.; Raasch, S. The Parallelized Large-Eddy Simulation Model (PALM) version 4.0 for atmospheric and oceanic flows: Model formulation, recent developments, and future perspectives. Geosci. Model Dev. 2015, 8, 2515–2551. [Google Scholar] [CrossRef]
- Churchfield, M.; Lee, S.; Moriarty, P.; Martinez, L.; Leonardi, S.; Vijayakumar, G.; Brasseur, J. A large-eddy simulation of wind-plant aerodynamics. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA 9–12 January 2012; p. 537. [Google Scholar]
- Domino, S. Sierra Low Mach Module: Nalu Theory Manual 1.0; Sandia National Laboratories: Albuquerque NM, USA, 2015.
- Doubrawa, P.; Quon, E.W.; Martinez-Tossas, L.A.; Shaler, K.; Debnath, M.; Hamilton, N.; Herges, T.G.; Maniaci, D.; Kelley, C.L.; Hsieh, A.S.; et al. Multimodel validation of single wakes in neutral and stratified atmospheric conditions. Wind Energy 2020, 23, 2027–2055. [Google Scholar] [CrossRef]
- Lignarolo, L.E.; Mehta, D.; Stevens, R.J.; Yilmaz, A.E.; van Kuik, G.; Andersen, S.J.; Meneveau, C.; Ferreira, C.J.; Ragni, D.; Meyers, J.; et al. Validation of four LES and a vortex model against stereo-PIV measurements in the near wake of an actuator disc and a wind turbine. Renew Energy 2016, 94, 510–523. [Google Scholar] [CrossRef]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; Wiley: Chichester, UK, 2001. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; Wiley: Chichester, UK, 2009. [Google Scholar]
- Ponta, F.L.; Otero, A.D.; Lago, L.I.; Rajan, A. Effects of rotor deformation in wind-turbine performance: The Dynamic Rotor Deformation Blade Element Momentum model (DRD–BEM). Renew Energy 2016, 92, 157–170. [Google Scholar] [CrossRef]
- Kelley, C.L.; Ennis, B.L. SWiFT Site Atmospheric Characterization; Technical Report SAND2016-0216; Sandia National Lab: Albuquerque, NM, USA, 2016.
- Berg, J.; Bryant, J.; LeBlanc, B.; Maniaci, D.C.; Naughton, B.; Paquette, J.A.; Resor, B.R.; White, J.; Kroeker, D. Scaled wind farm technology facility overview. In Proceedings of the 32nd ASME Wind Energy Symposium, National Harbor, MD, USA, 13–17 January 2014; p. 1088. [Google Scholar]
- Barone, M.F.; White, J. DOE/SNL-TTU Scaled Wind Farm Technology Facility; Technical Report SAND2011-6522; Sandia National Lab: Albuquerque, NM, USA, 2011.
- Kelley, C.L. Aerodynamic Design of the National Rotor Testbed; Technical Report SAND2015-8989; Sandia National Lab: Albuquerque, NM, USA, 2015.
- Karpenko, M.; Nugaras, J. Vibration damping characteristics of the cork-based composite material in line to frequency analysis. J. Theor. Appl. Mech. 2022, 60, 593–602. [Google Scholar] [CrossRef] [PubMed]
- Karpenko, M.; Stosiak, M.; Deptuła, A.; Urbanowicz, K.; Nugaras, J.; Królczyk, G.; Żak, K. Performance evaluation of extruded polystyrene foam for aerospace engineering applications using frequency analyses. Int. J. Adv. Manuf. Technol. 2023, 126, 5515–5526. [Google Scholar] [CrossRef]
- Otero, A.D.; Ponta, F.L. Structural Analysis of Wind-Turbine Blades by a Generalized Timoshenko Beam Model. J. Sol. Energy Eng. 2010, 132, 011015. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- Xudong, W.; Shen, W.Z.; Zhu, W.J.; Sorensen, J.; Jin, C. Shape optimization of wind turbine blades. Wind Energy 2009, 12, 781–803. [Google Scholar] [CrossRef]
- Otero, A.D.; Ponta, F.L. On the sources of cyclic loads in horizontal-axis wind turbines: The role of blade-section misalignment. Renew Energy 2018, 117, 275–286. [Google Scholar] [CrossRef]
- Jalal, S.; Ponta, F.; Baruah, A.; Rajan, A. Dynamic Aeroelastic Response of Stall-Controlled Wind Turbine Rotors in Turbulent Wind Conditions. Appl. Sci. 2021, 11, 6886. [Google Scholar] [CrossRef]
- Menon, M.; Ponta, F. Aeroelastic Response of Wind Turbine Rotors under Rapid Actuation of Flap-Based Flow Control Devices. Fluids 2022, 7, 129. [Google Scholar] [CrossRef]
- Rajan, A.; Ponta, F.L. A Novel Correlation Model for Horizontal Axis Wind Turbines Operating at High-Interference Flow Regimes. Energies 2019, 12, 1148. [Google Scholar] [CrossRef]
- Baruah, A.; Ponta, F. Analysis of Wind Turbine Wake Dynamics by a Gaussian-Core Vortex Lattice Technique. Dynamics 2024, 4, 97–118. [Google Scholar] [CrossRef]
- Herges, T.; Maniaci, D.C.; Naughton, B.T.; Mikkelsen, T.; Sjöholm, M. High resolution wind turbine wake measurements with a scanning lidar. J. Phys. Conf. Ser. 2017, 854, 012021. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ponta, F.L.; Jacovkis, P.M. A vortex model for Darrieus turbine using finite element techniques. Renew Energy 2001, 24, 1–18. [Google Scholar] [CrossRef]
- Strickland, J.H.; Webster, B.T.; Nguyen, T. A Vortex Model of the Darrieus Turbine: An Analytical and Experimental Study. J. Fluids Eng. 1979, 101, 500–505. [Google Scholar] [CrossRef]
- Ponta, F.L. Vortex decay in the Kármán eddy street. Phys. Fluids 2010, 22, 093601. [Google Scholar] [CrossRef]
- Flór, J.B.; van Heijst, G.J.F. An experimental study of dipolar structures in a stratified fluid. J. Fluid Mech. 1994, 279, 101–133. [Google Scholar] [CrossRef]
- Trieling, R.R.; van Wesenbeeck, J.M.A.; van Heijst, G.J.F. Dipolar vortices in a strain flow. Phys. Fluids 1998, 10, 144–159. [Google Scholar] [CrossRef]
- Hooker, S.G. On the action of viscosity in increasing the spacing ration of a vortex street. Proc. R. Soc. 1936, A154, 67–89. [Google Scholar]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Cottet, G.H.; Koumoutsakos, P.D. Vortex Methods: Theory and Practice; Cambridge University Press: London, UK, 2000. [Google Scholar]
- Karamcheti, K. Principles of Ideal-Fluid Aerodynamics; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Hau, E. Wind Turbines: Fundamentals, Technologies, Application, Economics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Trudnowski, D.; LeMieux, D. Independent pitch control using rotor position feedback for wind-shear and gravity fatigue reduction in a wind turbine. In Proceedings of the 2002 American Control Conference (IEEE Cat. No. CH37301), Anchorage, AK, USA, 8–10 May 2002; Volume 6, pp. 4335–4340. [Google Scholar]
- EWEA. Upwind: Design Limits and Solutions for Very Large Wind Turbines; Sixth Framework Programme; European Wind Energy Association: Brussels, Belgium, 2011. [Google Scholar]
- Kelley, C.; Naughton, B. Surface Meteorological Station—SWiFT Southwest—METa1—Reviewed Data. 2021. Available online: https://www.osti.gov/biblio/1349888 (accessed on 20 December 2023).
- Kelley, C.; Naughton, B. Lidar—DTU SpinnerLidar—Reviewed Data. 2021. Available online: https://www.osti.gov/biblio/1349890 (accessed on 20 December 2023).
- Englberger, A.; Lundquist, J.K.; Dörnbrack, A. Changing the rotational direction of a wind turbine under veering inflow: A parameter study. Wind Energy Sci. 2020, 5, 1623–1644. [Google Scholar] [CrossRef]
- Abkar, M.; Sørensen, J.N.; Porté-Agel, F. An Analytical Model for the Effect of Vertical Wind Veer on Wind Turbine Wakes. Energies 2018, 11, 1838. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-Turbine and Wind-Farm Flows: A Review. Bound.-Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef]
- Zong, H.; Porté-Agel, F. Experimental investigation and analytical modelling of active yaw control for wind farm power optimization. Renew Energy 2021, 170, 1228–1244. [Google Scholar] [CrossRef]
- Su, K.; Bliss, D. A numerical study of tilt-based wake steering using a hybrid free-wake method. Wind Energy 2020, 23, 258–273. [Google Scholar] [CrossRef]
- Uchida, T. Effects of Inflow Shear on Wake Characteristics of Wind-Turbines over Flat Terrain. Energies 2020, 13, 3745. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Prasad, A. A new mechanism for oblique wave resonance in the natural far wake. J. Fluid Mech. 1993, 256, 269–313. [Google Scholar] [CrossRef]
- Cimbala, J.M.; Nagib, H.M.; Roshko, A. Large structure in the far wakes of two-dimensional bluff bodies. J. Fluid Mech. 1988, 190, 265–298. [Google Scholar] [CrossRef]
- Taneda, S. Downstream development of the wakes behind cylinders. J. Phys. Soc. Jpn. 1959, 14, 843–848. [Google Scholar] [CrossRef]
- Meneghini, J.R.; Bearman, P.W. Numerical simulation of high amplitude oscillatory flow about a circular cylinder. J. Fluids Struct. 1995, 9, 435–455. [Google Scholar] [CrossRef]
- Inoue, O.; Yamazaki, T. Secondary vortex streets in Two-dimensional cylinder wakes. Fluid Dyn. Res. 1999, 25, 1–18. [Google Scholar] [CrossRef]
- Aref, H.; Siggia, E. Evolution and breakdown of a vortex street in two dimensions. J. Fluid Mech. 1981, 109, 435–463. [Google Scholar] [CrossRef]
- Ponta, F.L.; Aref, H. Numerical experiments on vortex shedding from an oscillating cylinder. J. Fluids Struct. 2006, 22, 327–344. [Google Scholar] [CrossRef]
- Matsui, T.; Okude, M. Formation of the secondary vortex street in the wake of a circular cylinder. In Proceedings of the IUTAM Symposium on Structures of Compressible Turbulent Shear Flows, Symposium, Marseille, France, 31 August–3 September 1982; Springer: Berlin/Heidelberg, Germany, 1983; pp. 156–164. [Google Scholar]
- Meiburg, E. On the role of subharmonic perturbations in the far wake. J. Fluid Mech. 1987, 177, 83–107. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Roshko, A. Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 1988, 2, 355–381. [Google Scholar] [CrossRef]
- Ponta, F.L.; Aref, H. Vortex synchronization regions in shedding from an oscillating cylinder. Phys. Fluids 2005, 17, 011703. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C.H.K. Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 2000, 420, 85–130. [Google Scholar] [CrossRef]
- Griffin, O.M.; Ramberg, S.E. The vortex street wakes of vibrating cylinders. J. Fluid Mech. 1974, 66, 553–576. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farrell, A.; Ponta, F.; Yates, N. Modeling and Analysis of Wind Turbine Wake Vortex Evolution Due to Time-Constant Spatial Variations in Atmospheric Flow. Energies 2025, 18, 1499. https://doi.org/10.3390/en18061499
Farrell A, Ponta F, Yates N. Modeling and Analysis of Wind Turbine Wake Vortex Evolution Due to Time-Constant Spatial Variations in Atmospheric Flow. Energies. 2025; 18(6):1499. https://doi.org/10.3390/en18061499
Chicago/Turabian StyleFarrell, Alayna, Fernando Ponta, and North Yates. 2025. "Modeling and Analysis of Wind Turbine Wake Vortex Evolution Due to Time-Constant Spatial Variations in Atmospheric Flow" Energies 18, no. 6: 1499. https://doi.org/10.3390/en18061499
APA StyleFarrell, A., Ponta, F., & Yates, N. (2025). Modeling and Analysis of Wind Turbine Wake Vortex Evolution Due to Time-Constant Spatial Variations in Atmospheric Flow. Energies, 18(6), 1499. https://doi.org/10.3390/en18061499





