Mathematical Formulation of Intelligent Management Algorithms for Isolated Microgrids: A Pareto-Based Critical Approach
Abstract
1. Introduction
1.1. Literature Review
1.2. Motivation and Research Gap
1.3. Contributions and Scope
- Demonstrate that few studies in the literature focus on testing MGs with a single pollutant-based generator;
- Identify inaccuracies in the existing mathematical modeling of isolated MGs in this specific case;
- Propose a simplified cost formulation that eliminates unnecessary calculations during the optimization process;
- Develop a novel cost–emission modeling approach for systems with a single pollutant-based generator, ensuring a true conflict between objectives;
- Introduce a single-objective formulation for the cost–emission optimization problem, reducing the number of objectives and enhancing the model’s robustness and effectiveness.
2. Materials and Methods
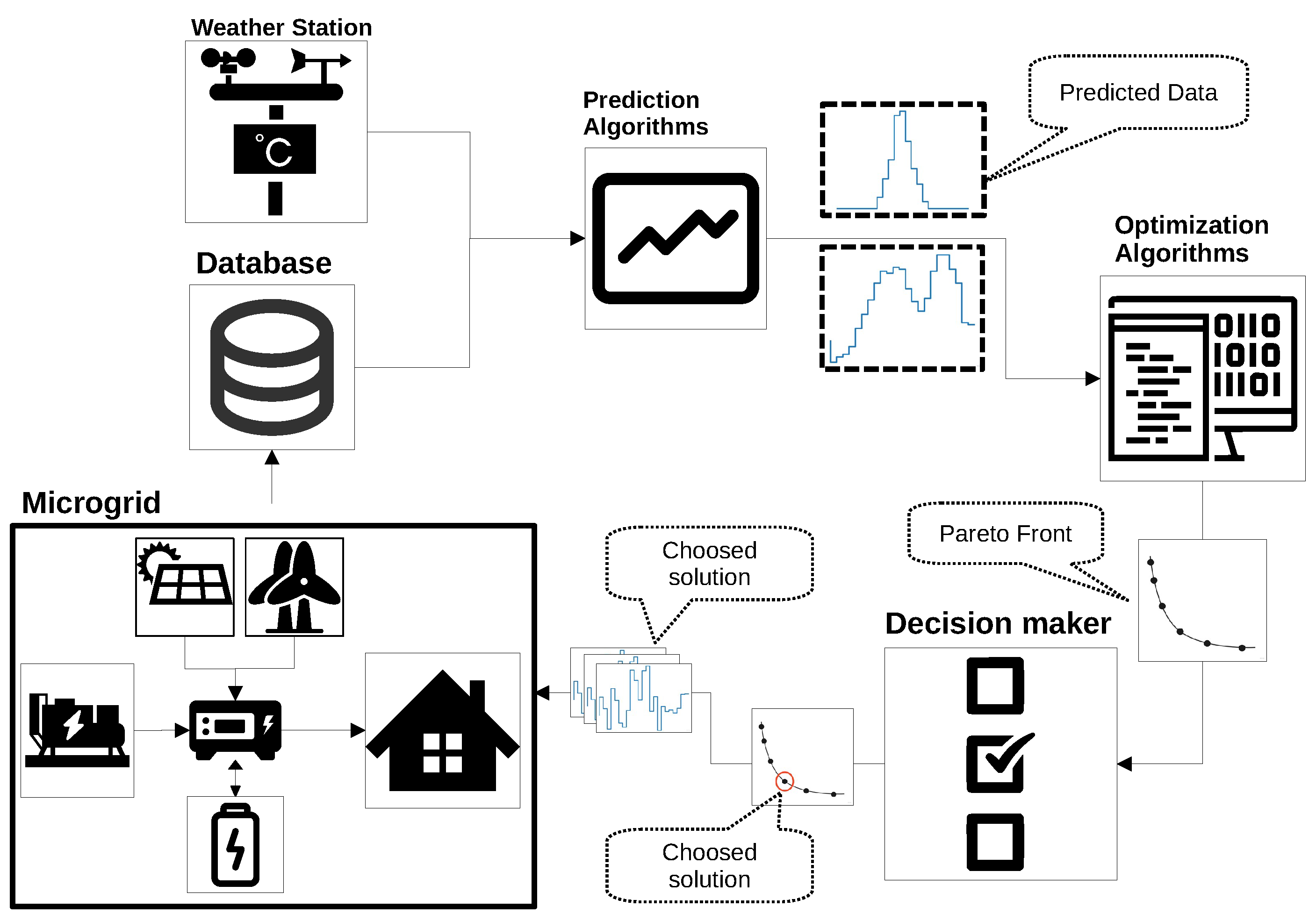
2.1. MG Management
2.2. Mathematical Formulation
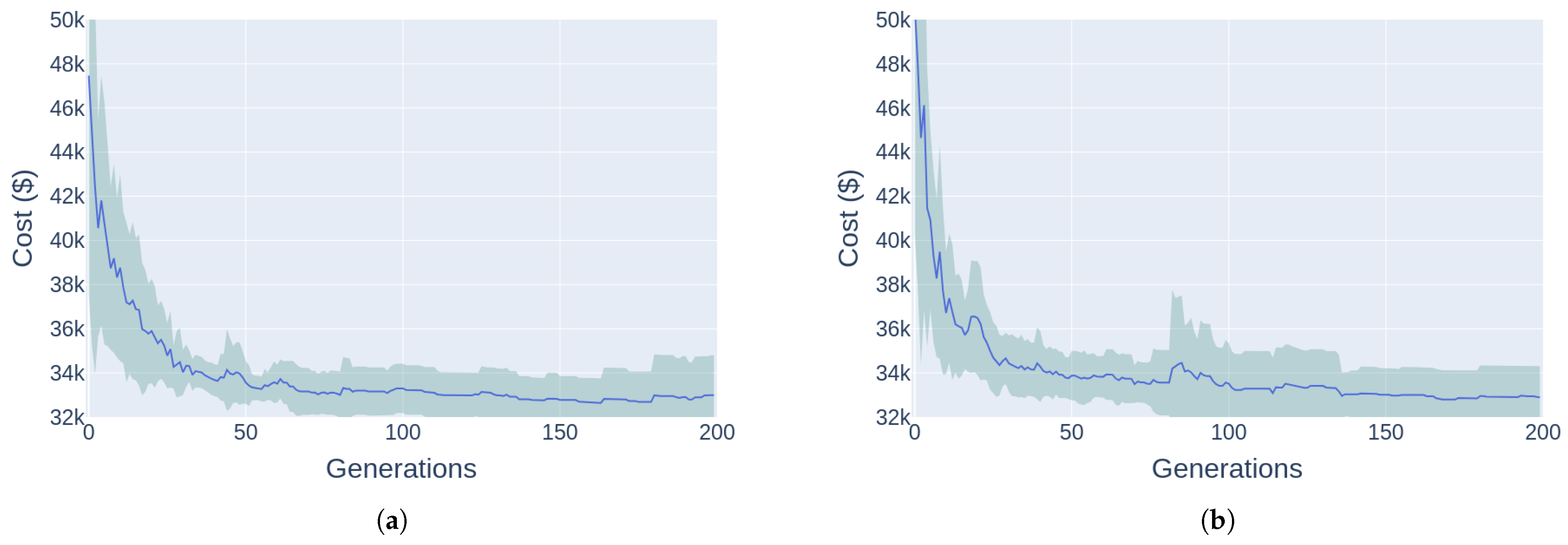
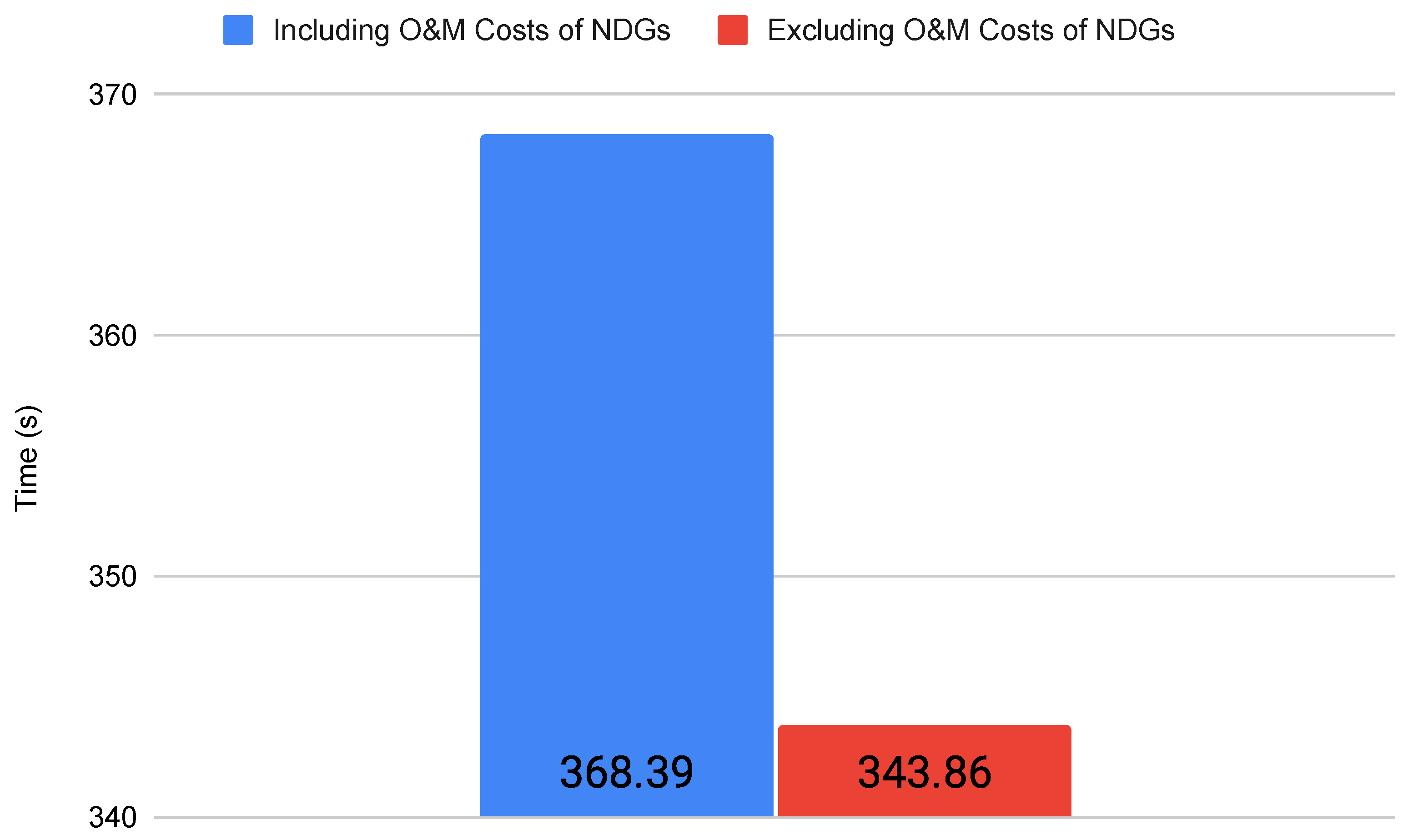
2.3. Analyzing the Influence of Including O&M Costs
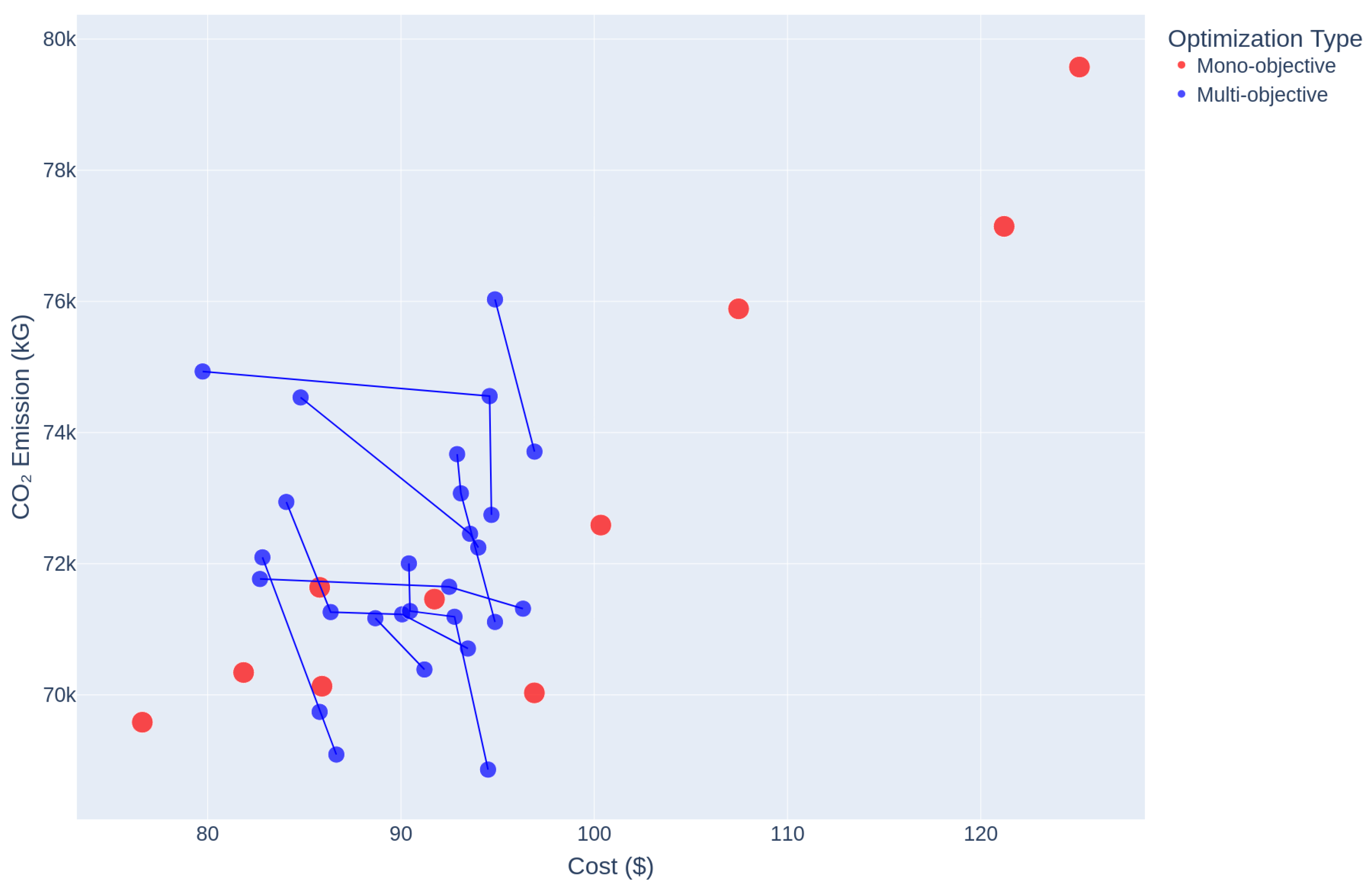
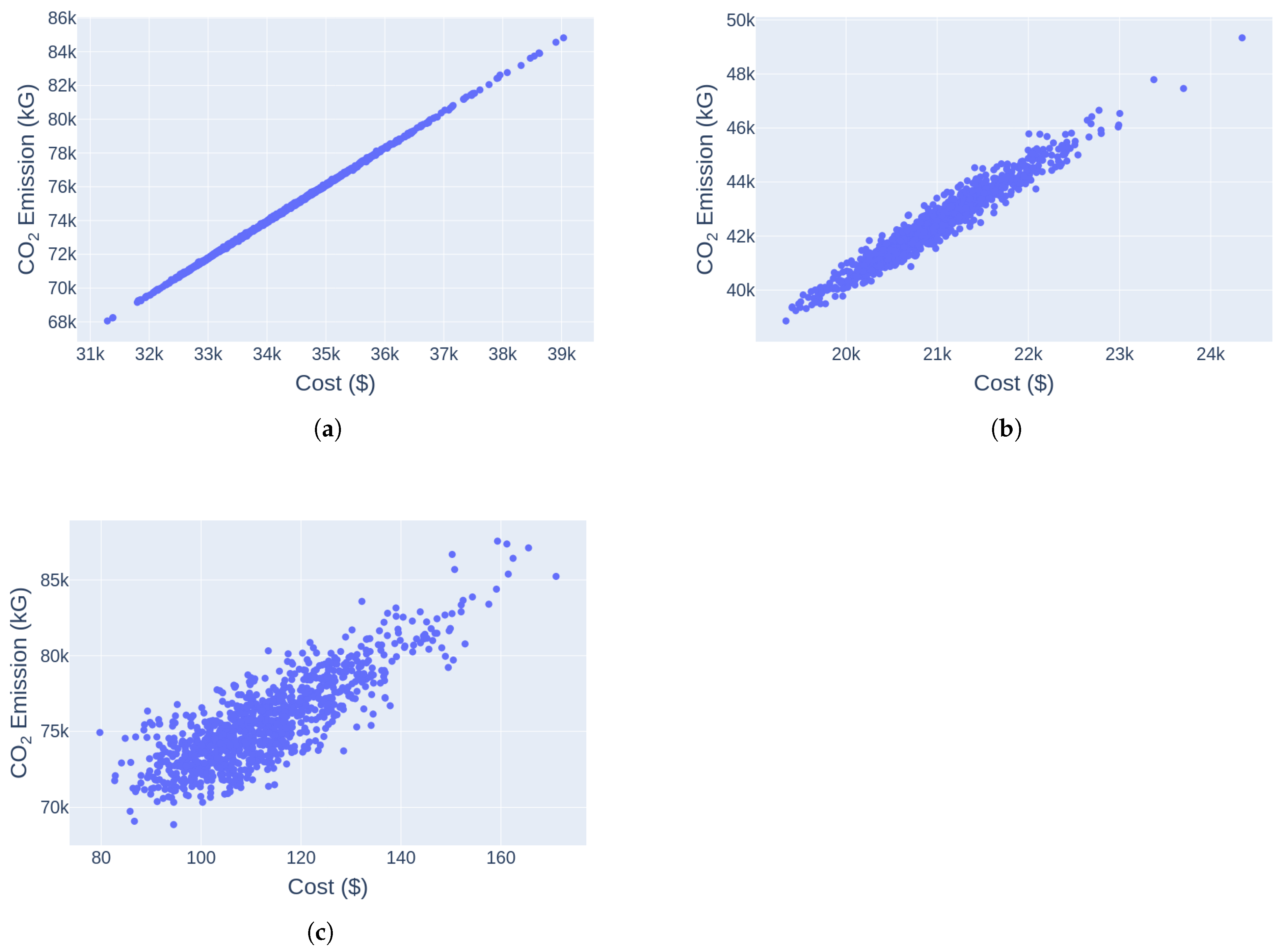
2.4. Analyzing the Relationship Between Costs and Emissions
2.5. Testing and Validation Procedures
3. Results
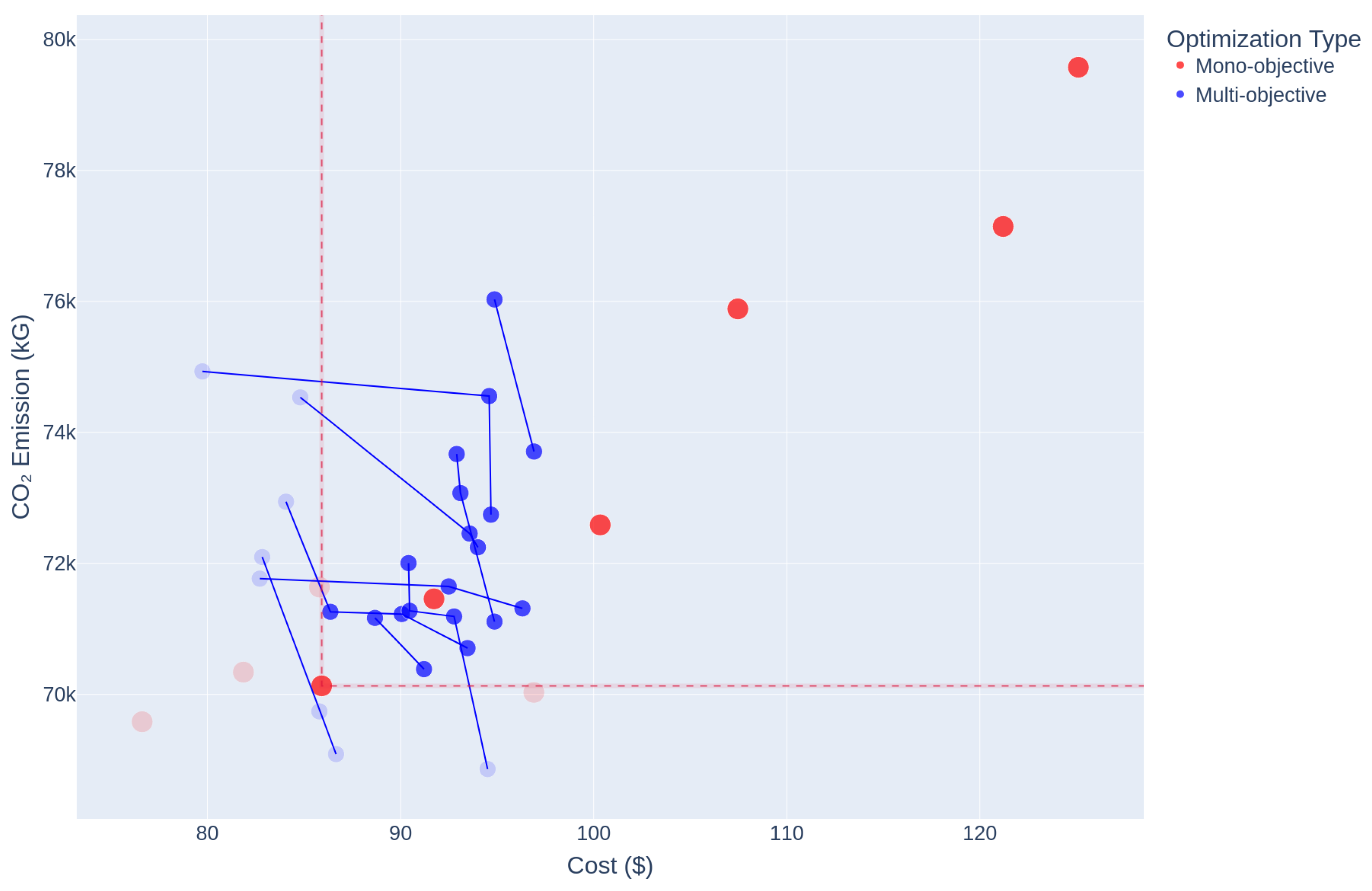
3.1. Comparing the Mathematical Formulation Regarding the O&M Costs
3.2. Comparing the Cost vs. Emissions Relation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MG | Microgrid |
| MPC | Model Predictive Control |
| O&M | Operation and Maintenance |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| GA | Genetic Algorithm |
| DG | Dispatchable Generator |
| NDG | Non-Dispatchable Generator |
References
- Agüera-Pérez, A.; Palomares-Salas, J.C.; de la Rosa, J.J.G.; Florencias-Oliveros, O. Weather forecasts for microgrid energy management: Review, discussion and recommendations. Appl. Energy 2018, 228, 265–278. [Google Scholar] [CrossRef]
- Vera, Y.E.; Dufo-López, R.; Bernal-Agustín, J.L. Energy management in microgrids with renewable energy sources: A literature review. Appl. Sci. 2019, 9, 3854. [Google Scholar] [CrossRef]
- Kavitha, V.; Malathi, V.; Guerrero, J.M.; Bazmohammadi, N. Energy management system using Mimosa Pudica optimization technique for microgrid applications. Energy 2021, 244, 122605. [Google Scholar] [CrossRef]
- Raghav, L.P.; Kumar, R.S.; Raju, D.K.; Singh, A.R. Optimal Energy Management of Microgrids Using Quantum Teaching Learning Based Algorithm. IEEE Trans. Smart Grid 2021, 12, 4834–4842. [Google Scholar] [CrossRef]
- Ahmad, S.; Shafiullah, M.; Ahmed, C.B.; Alowaifeer, M. A Review of Microgrid Energy Management and Control Strategies. IEEE Access 2023, 11, 21729–21757. [Google Scholar] [CrossRef]
- Zubaran, T.K. A Study on Shop Scheduling Problems. Ph.D. Thesis, Federal University of Rio Grande do Sul, Porto Alegre, Brazil, 2018. [Google Scholar]
- Leonori, S.; Martino, A.; Mascioli, F.M.F.; Rizzi, A. Microgrid Energy Management Systems Design by Computational Intelligence Techniques. Appl. Energy 2020, 277, 115524. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics from Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009; p. 593. [Google Scholar] [CrossRef]
- Thirunavukkarasu, G.S.; Seyedmahmoudian, M.; Jamei, E.; Horan, B.; Mekhilef, S.; Stojcevski, A. Role of optimization techniques in microgrid energy management systems—A review. Energy Strategy Rev. 2022, 43, 100899. [Google Scholar] [CrossRef]
- Arunkumar, A.P.; Kuppusamy, S.; Muthusamy, S.; Pandiyan, S.; Panchal, H.; Nagaiyan, P. An extensive review on energy management system for microgrids. Energy Sources Part A Recover. Util. Environ. Eff. 2022, 44, 4203–4228. [Google Scholar] [CrossRef]
- Akter, A.; Zafir, E.I.; Dana, N.H.; Joysoyal, R.; Sarker, S.K.; Li, L.; Muyeen, S.M.; Das, S.K.; Kamwa, I. A review on microgrid optimization with meta-heuristic techniques: Scopes, trends and recommendation. Energy Strategy Rev. 2024, 51, 101298. [Google Scholar] [CrossRef]
- Elsakaan, A.A.; El-Sehiemy, R.A.; Kaddah, S.S.; Elsaid, M.I. Optimal economic–emission power scheduling of RERs in MGs with uncertainty. IET Gener. Transm. Distrib. 2020, 14, 37–52. [Google Scholar] [CrossRef]
- Roslan, M.F.; Hannan, M.A.; Ker, P.J.; Begum, R.A.; Mahlia, T.M.I.; Dong, Z.Y. Scheduling controller for microgrids energy management system using optimization algorithm in achieving cost saving and emission reduction. Appl. Energy 2021, 292, 116883. [Google Scholar] [CrossRef]
- Maulik, A.; Das, D. Optimal Operation of Droop-Controlled Islanded Microgrids. IEEE Trans. Sustain. Energy 2018, 9, 1337–1348. [Google Scholar] [CrossRef]
- Shezan, S.A.; Ishraque, M.F.; Shafiullah, G.M.; Kamwa, I.; Paul, L.C.; Muyeen, S.M.; NSS, R.; Saleheen, M.Z.; Kumar, P.P. Optimization and control of solar-wind islanded hybrid microgrid by using heuristic and deterministic optimization algorithms and fuzzy logic controller. Energy Rep. 2023, 10, 3272–3288. [Google Scholar] [CrossRef]
- Ibrahim, M.M.; Hasanien, H.M.; Farag, H.E.; Omran, W.A. Energy Management of Multi-Area Islanded Hybrid Microgrids: A Stochastic Approach. IEEE Access 2023, 11, 101409–101424. [Google Scholar] [CrossRef]
- Suresh, V.; Janik, P.; Jasinski, M.; Guerrero, J.M.; Leonowicz, Z. Microgrid energy management using metaheuristic optimization algorithms. Appl. Soft Comput. 2023, 134, 109981. [Google Scholar] [CrossRef]
- Wu, D.; Wu, L.; Wen, T.; Li, L. Microgrid Operation Optimization Method Considering Power-to-Gas Equipment: An Improved Gazelle Optimization Algorithm. Symmetry 2024, 16, 83. [Google Scholar] [CrossRef]
- Wang, S.; Tan, Q.; Ding, X.; Li, J. Efficient microgrid energy management with neural-fuzzy optimization. Int. J. Hydrogen Energy 2024, 64, 269–281. [Google Scholar] [CrossRef]
- Majeed, M.A.; Phichisawat, S.; Asghar, F.; Hussan, U. Optimal Energy Management System for Grid-Tied Microgrid: An Improved Adaptive Genetic Algorithm. IEEE Access 2023, 11, 117351–117361. [Google Scholar] [CrossRef]
- Abo-Elyousr, F.K.; Elnozahy, A. Bi-objective economic feasibility of hybrid micro-grid systems with multiple fuel options for islanded areas in Egypt. Renew. Energy 2018, 128, 37–56. [Google Scholar] [CrossRef]
- Maulik, A.; Das, D. Optimal power dispatch considering load and renewable generation uncertainties in an AC–DC hybrid microgrid. IET Gener. Transm. Distrib. 2019, 13, 1164–1176. [Google Scholar] [CrossRef]
- Li, Y.; Wang, P.; Gooi, H.B.; Ye, J.; Wu, L. Multi-objective optimal dispatch of microgrid under uncertainties via interval optimization. IEEE Trans. Smart Grid 2019, 10, 2046–2058. [Google Scholar] [CrossRef]
- Tan, B.; Chen, H. Multi-objective energy management of multiple microgrids under random electric vehicle charging. Energy 2020, 208, 118360. [Google Scholar] [CrossRef]
- Elkholy, M.H.; Senjyu, T.; Elymany, M.; Gamil, M.M.; Talaat, M.; Masrur, H.; Ueda, S.; Lotfy, M.E. Optimal resilient operation and sustainable power management within an autonomous residential microgrid using African vultures optimization algorithm. Renew. Energy 2024, 224, 120247. [Google Scholar] [CrossRef]
- Taabodi, M.H.; Niknam, T.; Sharifhosseini, S.M.; Aghajari, H.A.; Bornapour, S.M.; Sheybani, E.; Javidi, G. Optimizing Rural MG’s Performance: A Scenario-Based Approach Using an Improved Multi-Objective Crow Search Algorithm Considering Uncertainty. Energies 2025, 18, 294. [Google Scholar] [CrossRef]
- Aldosary, A. Optimizing Economic Dispatch with Renewable Energy and Natural Gas Using Fractional-Order Fish Migration Algorithm. Fractal Fract. 2024, 8, 350. [Google Scholar] [CrossRef]
- Labra-Cáceres, N.I.; Grisales-Noreña, L.F.; Bolaños, R.I.; Guzmán-Henao, J.A.; Montoya, O.D. Energy management system for PV-based distributed generators in AC microgrids using an adapted JAYA optimizer to minimize operational costs, energy losses, and CO2 emissions. Results Eng. 2025, 25, 104397. [Google Scholar] [CrossRef]
- Alam, M.N.; Chakrabarti, S.; Liang, X. A Benchmark Test System for Networked Microgrids. IEEE Trans. Ind. Inform. 2020, 16, 6217–6230. [Google Scholar] [CrossRef]
- Savier, j.; Das, D. Impact of Network Reconfiguration on Loss Allocation of Radial Distribution Systems. Power Deliv. IEEE Trans. 2007, 22, 2473–2480. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Thurner, L.; Scheidler, A.; Schäfer, F.; Menke, J.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. pandapower—An Open-Source Python Tool for Convenient Modeling, Analysis, and Optimization of Electric Power Systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef]

| Device | O&M | Emission |
|---|---|---|
| Batteries | 5 | N/A |
| Photovoltaic | 5 | N/A |
| Wind Generator | 12 | N/A |
| Diesel Generator | 20 | 0.8 |
| Biomass | 20 | 0.072 |
| Natural Gas | 4 | 0.5 |
| Parameters | GA/NSGA-II |
|---|---|
| Number of Generations | 200 |
| Population Size | 100 |
| Crossover Rate (%) | 0.1 |
| Mutation Rate (%) | 0.7 |
| Number of Parents for Crossover | 2 |
| Number of Offspring after Crossover | 2 |
| Current Methodology (Equation (2)) | Average | Proposed Methodology (Equation (3)) | Average | |
|---|---|---|---|---|
| 1 | $33,719.08 | $32,311.52 | $31,791.52 | $32,229.64 |
| 2 | $32,052.54 | $32,374.59 | ||
| 3 | $32,311.52 | $32,158.35 | ||
| 4 | $34,926.78 | $33,006.85 | ||
| 5 | $32,692.05 | $31,843.69 | ||
| 6 | $31,978.37 | $35,063.20 | ||
| 7 | $36,772.56 | $32,198.60 | ||
| 8 | $31,997.99 | $32,556.67 | ||
| 9 | $30,776.29 | $32,229.64 | ||
| 10 | $36,274.52 | $35,596.39 | ||
| 11 | $34,191.52 | $32,076.50 | ||
| 12 | $31,423.62 | $35,233.22 | ||
| 13 | $32,687.50 | $34,070.44 | ||
| 14 | $31,615.55 | $31,126.25 | ||
| 15 | $31,397.64 | $32,156.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batista, V.d.S.; Soares, T.M.; Tostes, M.E.d.L.; Bezerra, U.H.; Lott, H.G. Mathematical Formulation of Intelligent Management Algorithms for Isolated Microgrids: A Pareto-Based Critical Approach. Energies 2025, 18, 1487. https://doi.org/10.3390/en18061487
Batista VdS, Soares TM, Tostes MEdL, Bezerra UH, Lott HG. Mathematical Formulation of Intelligent Management Algorithms for Isolated Microgrids: A Pareto-Based Critical Approach. Energies. 2025; 18(6):1487. https://doi.org/10.3390/en18061487
Chicago/Turabian StyleBatista, Vitor dos Santos, Thiago Mota Soares, Maria Emília de Lima Tostes, Ubiratan Holanda Bezerra, and Hugo Gonçalves Lott. 2025. "Mathematical Formulation of Intelligent Management Algorithms for Isolated Microgrids: A Pareto-Based Critical Approach" Energies 18, no. 6: 1487. https://doi.org/10.3390/en18061487
APA StyleBatista, V. d. S., Soares, T. M., Tostes, M. E. d. L., Bezerra, U. H., & Lott, H. G. (2025). Mathematical Formulation of Intelligent Management Algorithms for Isolated Microgrids: A Pareto-Based Critical Approach. Energies, 18(6), 1487. https://doi.org/10.3390/en18061487