Comparative Analysis of Catenary and TLP Mooring Systems on the Wave Power Efficiency for a Dual-Chamber OWC Wave Energy Converter
Abstract
1. Introduction
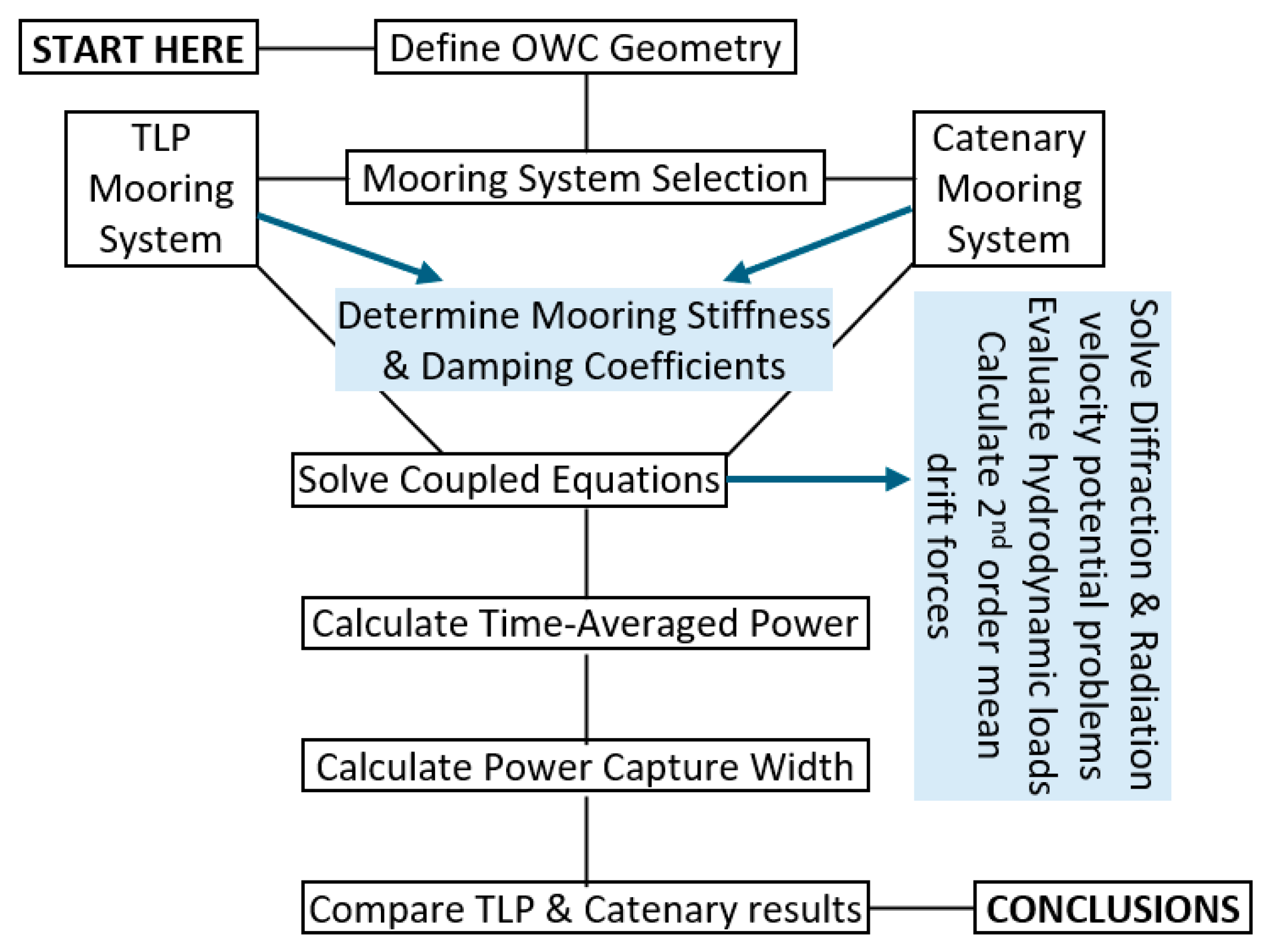
2. Methods and Materials
2.1. Hydrodynamic Analysis
2.1.1. Description of the OWC Converter
2.1.2. Air Volume Flow
2.1.3. Hydrodynamic Forces
2.1.4. Equilibrium Equations—Absorbed Wave Power
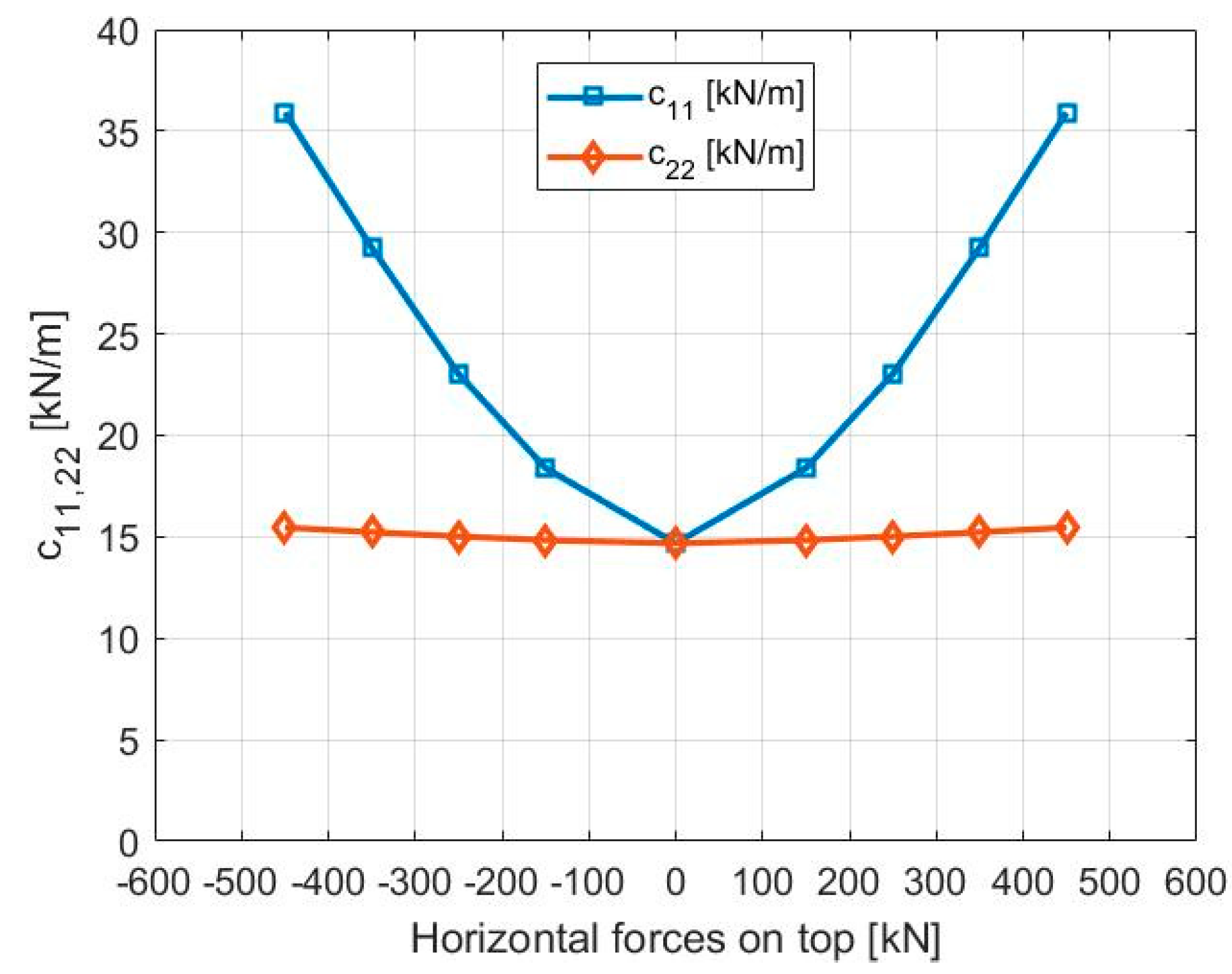
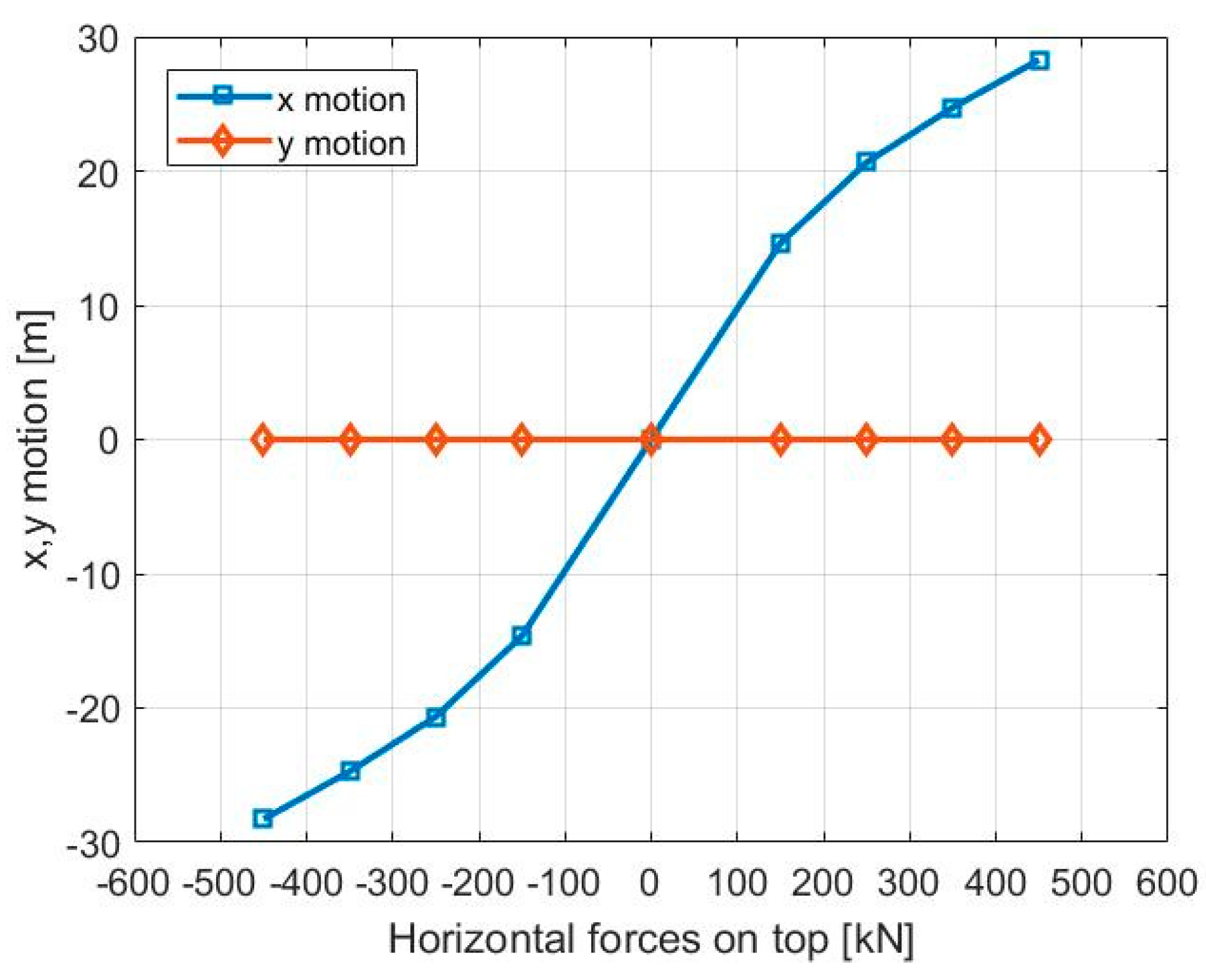
2.2. Mooring Coefficients
2.2.1. Tension-Leg Mooring System
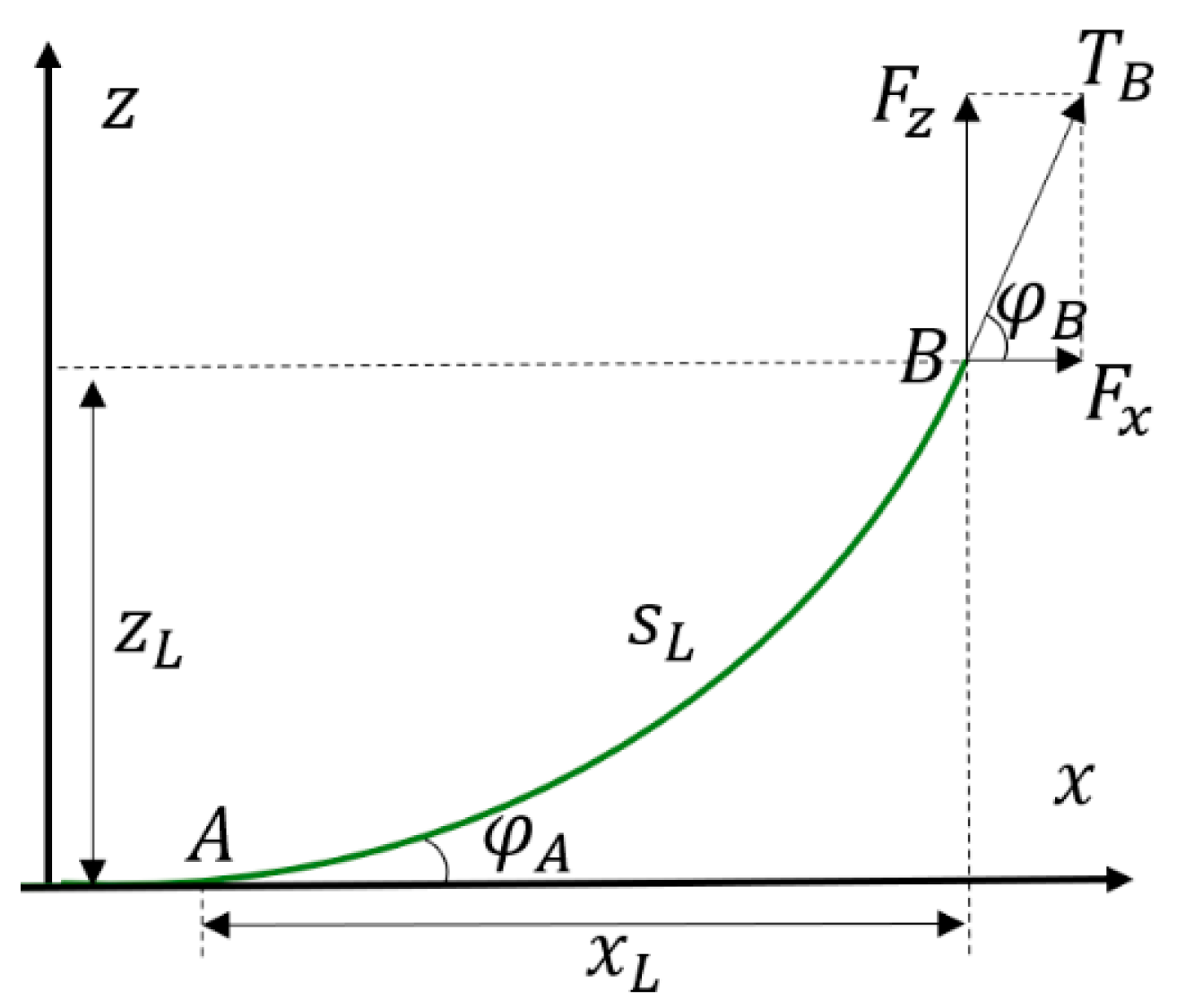
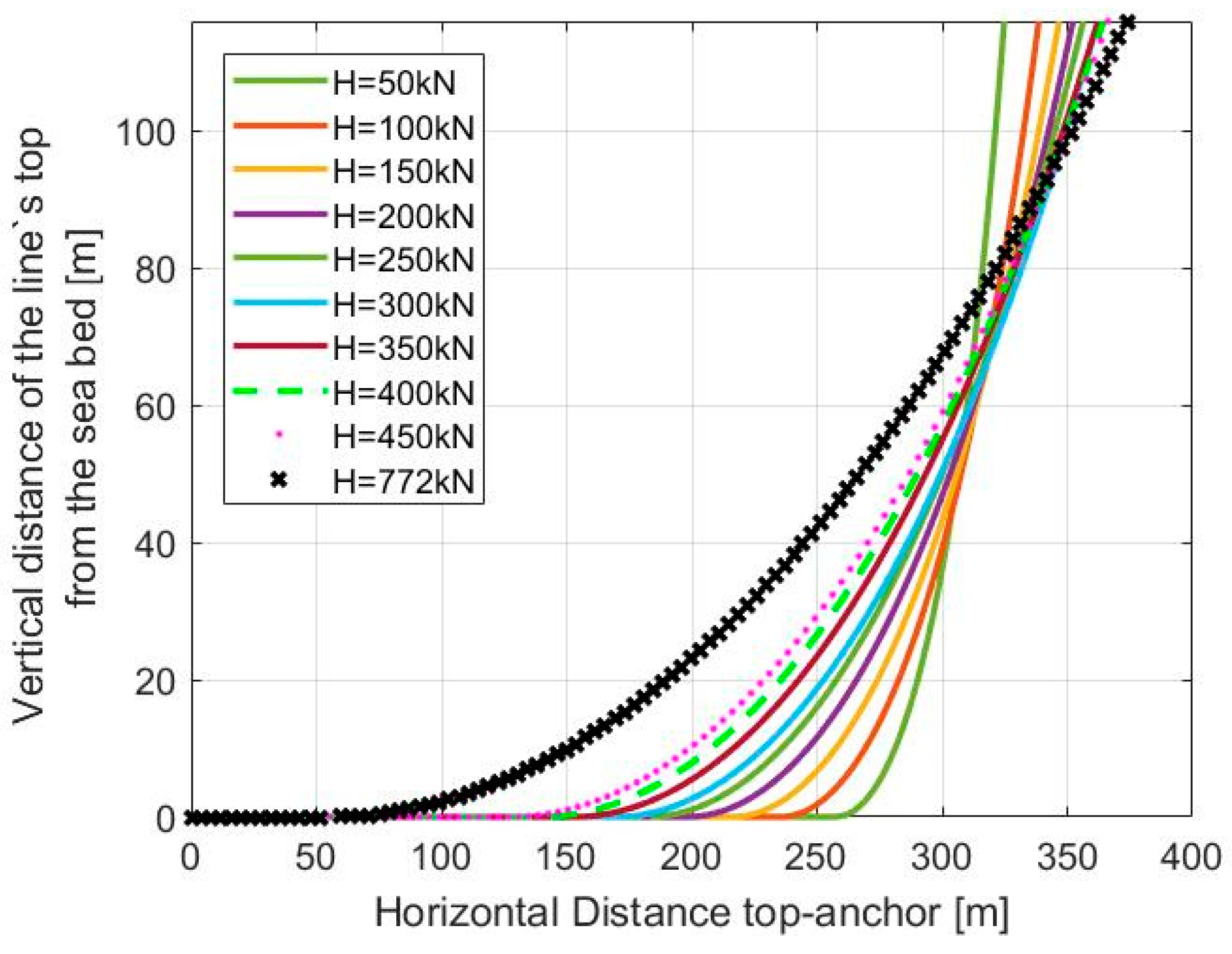
2.2.2. Catenary Mooring System
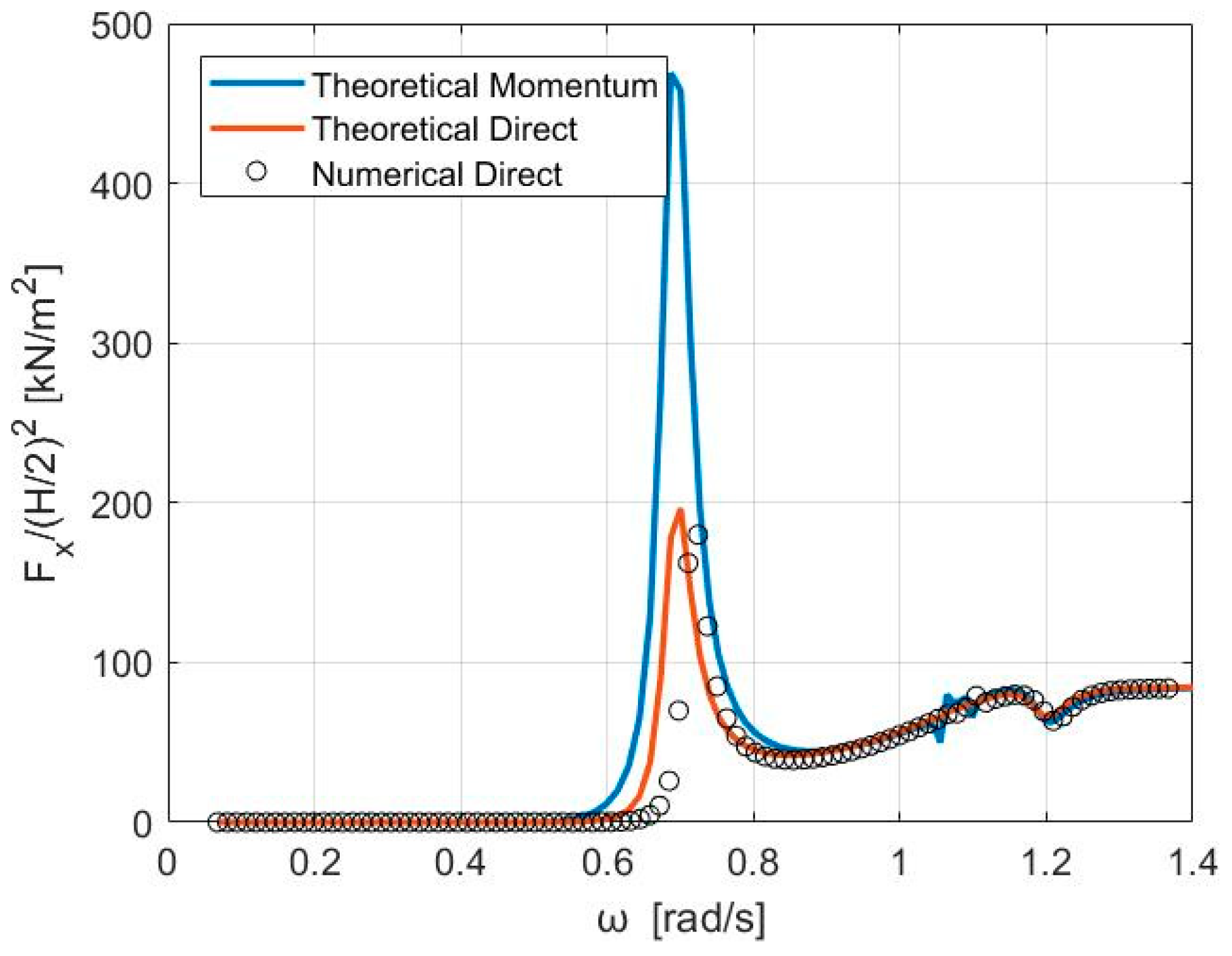
3. Results Validation
4. Numerical Simulations
4.1. Mooring Case: Catenary
4.2. Mooring Case: TLP
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- State of the Energy Union Report 2024 Shows EU Progress to Ensure Secure, Competitive and Affordable Energy for All. Available online: https://ec.europa.eu/commission/presscorner/api/files/document/print/en/ip_24_4581/IP_24_4581_EN.pdf (accessed on 1 March 2025).
- Collombert, R.; Cagney, D. Last Stop to 2025. A 2022 Action Plan to deliver on the Offshore Strategy’s Ocean Energy Target. 2022 Ocean Energy Europe. Available online: https://www.etipocean.eu/knowledge_hub/last-stop-to-2025-a-2022-action-plan-to-deliver-on-the-offshore-strategys-ocean-energy-target/ (accessed on 1 March 2025).
- IRENA. Innovation Outlook: Ocean Energy Technologies; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020. [Google Scholar]
- Ding, J.; Pang, S.; Chen, Z. Optimization of the chamber of OWC to improve hydrodynamic performance. Ocean Eng. 2023, 287, 115782. [Google Scholar] [CrossRef]
- Heath, T.V. A review of oscillating water columns. Philos. Trans. R. Soc. 2012, 370, 235–245. [Google Scholar] [CrossRef]
- Davidson, J.; Ringwood, J.V. Mathematical Modelling of Mooring Systems for Wave Energy Converters—A Review. Energies 2017, 10, 666. [Google Scholar] [CrossRef]
- Kisacik, D.; Stratigaki, V.; Wu, M.; Cappietti, L.; Simonetti, I.; Troch, P.; Crespo, A.; Altomare, C.; Domínguez, J.; Hall, M.; et al. Efficiency and Survivability of a Floating Oscillating Water Column Wave Energy Converter Moored to the Seabed: An Overview of the EsflOWC MaRINET2 Database. Water 2020, 12, 992. [Google Scholar] [CrossRef]
- Harris, R.E.; Johanning, L.; Wolfram, J. Mooring systems for wave energy converters: A review of design issues and choices. In Proceedings of the 3rd International Conference on Marine Renewable Energy, Blyth, UK, 7–9 July 2004; pp. 180–189. [Google Scholar]
- Johanning, L.; Smith, G.H.; Wolfram, J. Towards design standards for WEC moorings. In Proceedings of the 6th European Wave and Tidal Energy Conference, EWTEC, Glasgow, UK, 29 August–2 September 2005. [Google Scholar]
- Johanning, L.; Wolfram, J. Challenging tasks on moorings for floating WECs. In Proceedings of the International Symposium on Fluid Machinery for Wave and Tidal Energy: State of the Art and New Developments, IMechE 2005, London, UK, 19 October 2005. [Google Scholar]
- Johanning, L.; Smith, G.H.; Wolfram, J. Measurements of static and dynamic mooring line damping and their importance for floating WEC devices. Ocean Eng. 2007, 34, 1918–1934. [Google Scholar] [CrossRef]
- Vijayakrishna Rapaka, E.; Natarajan, R.; Neelamani, S. Experimental investigation on the dynamic response of a moored wave energy device under regular sea waves. Ocean Eng. 2004, 31, 725–743. [Google Scholar] [CrossRef]
- Elwood, D.; Yim, S.C.; Prudell, J.; Stillinger, C.; Jouanne, A.; Brekken, T.; Brown, A.; Paasch, R. Design, construction, and ocean testing of a taut-moored dual-body wave energy converter with a linear generator power take-off. Renew. Energy 2010, 35, 348–354. [Google Scholar] [CrossRef]
- Xu, S.; Wang, S.; Guedes Soares, C. Review of mooring design for floating wave energy converters. Renew. Sustain. Energy Rev. 2019, 111, 595–621. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Z.; Peng, G.; Xiao, Y.; Zhai, L.; Liu, X.; Zhang, Q. Numerical simulation of a heave-only floating OWC (oscillating water column) device. Energy 2014, 76, 799–806. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Deng, Z. Hydrodynamic performance of a heaving oscillating water column device restrained by a spring-damper system. Renew. Energy 2022, 187, 331–346. [Google Scholar] [CrossRef]
- Imai, Y.; Toyota, K.; Nagata, S.; Setoguchi, T.; Takao, M. An experimental study on generating efficicncy of a wave energy converter “Backward Bent Duct Buoy”. In Proceedings of the 9th European Wave and Tidal Energy Conference, EWTEC, Southampton, UK, 5–9 September 2011. [Google Scholar]
- Guo, P.; Zhang, Y.; Chen, W.; Wang, C. Fully coupled simulation of dynamic characteristics of a backward bent duct buoy oscillating water column wave energy converter. Energy 2024, 294, 130870. [Google Scholar] [CrossRef]
- Cerveira, F.; Fonseca, N.; Pascoal, R. Mooring system influence on the efficiency of wave energy converters. Int. J. Mar. Energy 2013, 3–4, 65–81. [Google Scholar] [CrossRef]
- Krivtsov, V.; Linfoot, B. Basin testing of wave energy converters in Trondheim: Investigation of mooring loads and implications for wider research. J. Mar. Sci. Eng. 2014, 2, 326–335. [Google Scholar] [CrossRef]
- Fong Lee, C.; Fjermedal, S.; Chen Ong, M. Design and analysis of taut mooring systems for a combined floating offshore wind and wave energy system at intermediate water depth. Ocean Eng. 2024, 312, 119174. [Google Scholar]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Experimental and numerical investigations on the hydrodynamic performance of a floating-moored oscillating water column wave energy converter. Appl. Energy 2017, 205, 369–390. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Experimental and numerical investigations on the intact and damage survivability of a floating-moored oscillating water column device. Appl. Ocean Res. 2017, 68, 276–292. [Google Scholar] [CrossRef]
- Singh, U.; Abdussamie, N.; Hore, J. Hydrodynamic performance of a floating offshore OWC wave energy converter: An experimental study. Renew. Sustain. Energy Rev. 2020, 117, 109501. [Google Scholar] [CrossRef]
- Wu, M.; Stratigaki, V.; Troch, P.; Altomare, C.; Verbrugghe, T.; Crespo, A.; Cappietti, L.; Hall, M.; Gomez-Gesteira, M. Experimental study of a moored floating oscillating water column wave-energy converter and of a moored cubic box. Energies 2019, 12, 1834. [Google Scholar] [CrossRef]
- Mia, R.M.; Zhao, M.; Wu, H.; Dhamelia, V.; Hu, P. Hydrodynamic performance of a floating offshore oscillating water column wave energy converter. J. Mar. Sci. Eng. 2022, 10, 1551. [Google Scholar] [CrossRef]
- Correia da Fonseca, F.X.; Gomes, R.P.F.; Henriques, J.C.C.; Gato, L.M.C.; Falcao, A.F.O. Model testing of an oscillating water column spar-buoy wave energy converter isolated and in array: Motions and mooring forces. Energy 2016, 112, 1207–1218. [Google Scholar] [CrossRef]
- Giorgi, G.; Gomes, R.P.F.; Bracco, G.; Mattiazzo, G. The effect of mooring line parameters in inducing parametric resonance on the Spar-Buoy oscillating water column wave energy converter. J. Mar. Sci. Eng. 2020, 8, 29. [Google Scholar] [CrossRef]
- Gomes, R.P.F.; Henriques, J.C.C.; Gato, L.M.C.; Falcao, A.F.O. Wave power extraction of a heaving floating oscillating water column in a wave channel. Renew. Energy 2016, 99, 1262–1275. [Google Scholar] [CrossRef]
- Gomes, R.P.F.; Henriques, J.C.C.; Gato, L.M.C.; Falcao, A.F.O. Time-domain simulation of a slack-moored floating oscillating water column and validation with physical model tests. Renew. Energy 2020, 149, 165–180. [Google Scholar] [CrossRef]
- Oikonomou, C.L.G.; Gomes, R.P.F.; Gato, L.M.C.; Falcao, A.F.O. On the dynamics of an array of spar-buoy oscillating water column devices with inter-body mooring connections. Renew. Energy 2020, 148, 309–325. [Google Scholar] [CrossRef]
- Touzon, I.; Nava, V.; Gao, Z.; Petuya, V. Frequency domain modelling of a coupled system of floating structure and mooring lines: An application to a wave energy converter. Ocean Eng. 2021, 220, 108498. [Google Scholar] [CrossRef]
- Howey, B.; Collins, K.; Hann, M.; Iglesias, G.; Gomes, R.; Henriques, J.; Gato, L.M.C.; Greaves, D. Compact floating wave energy converter arrays: Inter-device mooring connectivity and performance. Appl. Ocean Res. 2021, 115, 102820. [Google Scholar] [CrossRef]
- Pols, A.; Gubesch, E.; Abdussamie, N.; Penesis, I.; Chin, C. Mooring analysis of a floating OWC wave energy converter. J. Mar. Sci. Eng. 2021, 9, 228. [Google Scholar] [CrossRef]
- Gubesch, E.; Abdussamie, N.; Penesis, I.; Chin, C. Effects of mooring configurations on the hydrodynamic performance of a floating offshore oscillating water column wave energy converter. Renew. Sustain. Energy Rev. 2022, 166, 112643. [Google Scholar] [CrossRef]
- Xu, S.; Rezanejad, K.; Gadelho, J.F.M.; Wang, S.; Guedes Soares, C. Experimental investigation on a dual chamber floating oscillating water column moored by flexible mooring systems. Ocean Eng. 2020, 216, 108083. [Google Scholar] [CrossRef]
- Gadelho, J.; Rezanejad, K.; Xu, S.; Hinostroza, M.; Guedes Soares, C. Experimental study on the motions of a dual chamber floating oscillating water column device. Renew. Energy 2021, 170, 1257–1274. [Google Scholar] [CrossRef]
- Xu, S.; Rezanejad, K.; Gadelho, J.F.M.; Guedes Soares, C. Influence of the power take-off damping of a dual chamber floating oscillating water column on the mooring fatigue damage. Ocean Eng. 2022, 249, 110832. [Google Scholar] [CrossRef]
- Konispoliatis, D.N. Hydrodynamic analysis of a dual chamber floating oscillating water column device. Appl. Ocean Res. 2025, 154, 104340. [Google Scholar] [CrossRef]
- Mavrakos, A.S.; Konispoliatis, D.N.; Ntouras, D.G.; Papadakis, G.P.; Mavrakos, S.A. Hydrodynamics of moonpool-type floaters: A theoretical and a CFD formulation. Energies 2022, 15, 570. [Google Scholar] [CrossRef]
- Mavrakos, A.S.; Konispoliatis, D.N.; Ntouras, D.G.; Papadakis, G.P.; Mavrakos, S.A. Hydrodynamic coefficients in heave of a moonpool-type floater using theoretical, numerical and CFD methodologies. Ocean Eng. 2023, 279, 114519. [Google Scholar] [CrossRef]
- Kokkinowrachos, K.; Thanos, I.; Zibell, H.G. Hydrodynamic analysis of some wave energy conversion systems. In Proceedings of the OCEANS’87 Conference, Halifax, NS, Canada, 28 September–1 October 1987; pp. 566–574. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Evans, D.V.; Porter, R. Efficient calculator of hydrodynamic properties of OWC-type devices. J. Offshore Mech. Arct. Eng. 1997, 119, 210–218. [Google Scholar] [CrossRef]
- Mavrakos, A.S.; Konispoliatis, D.N.; Mavrakos, S.A. Hydrodynamic analysis of two coaxial moonpool floaters using theoretical methodologies. J. Mar. Sci. Eng. 2023, 11, 99. [Google Scholar] [CrossRef]
- Falcao, A.F.O. Stohastic modelling of OWC wave power plant performance. Appl. Ocean Res. 2002, 24, 59–71. [Google Scholar] [CrossRef]
- Mavrakos, S. The vertical drift force and pitch moment on axisymmetric bodies in regular waves. Appl. Ocean Res. 1988, 10, 207–218. [Google Scholar] [CrossRef]
- Sclavounos, P.D. The vertical wave drift force on floating bodies. In Proceedings of the 2nd International Workshop on Water Waves and Floating Bodies, Bristol, UK, 16–19 March 1987. [Google Scholar]
- Molin, B. On second-order motion and vertical drift forces for three-dimensional bodies in regular waves. In Proceedings of the International Workshop on Ship and Platform Motion, Berkeley, CA, USA, 26–28 October 1983. [Google Scholar]
- Papanikolaou, A.; Zaraphonitis, G. On the improved method for the evaluation of second-order motions and loads on 3D floating bodies in waves. J. Schiffstechnik 1987, 34, 170–211. [Google Scholar]
- Shao, Y.L. Numerical analysis of second-order mean wave forces by a stabilized higher order boundary element method. In Proceedings of the 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 July 2018. [Google Scholar]
- Konispoliatis, D.N.; Mavrakos, S.A. Mean drift wave forces on arrays of bodies surrounded by thin porous surfaces. J. Mar. Sci. Eng. 2023, 11, 1269. [Google Scholar] [CrossRef]
- Martins-Rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column at the tip of a breakwater. J. Fluid Mech. 2009, 626, 395–414. [Google Scholar] [CrossRef]
- Senjanovic, I.; Hadzic, N.; Tomic, M. On the linear stiffness of tension leg platforms. Sustain. Marit. Transp. Exploit. Sea Resour. 2011, 108, 1081–1088. [Google Scholar]
- Loukogeorgaki, E.; Angelidis, D. Stiffness of mooring lines and performance of floating breakwater in three dimensions. Appl. Ocean Res. 2005, 27, 187–208. [Google Scholar] [CrossRef]
- ANSYS AQWA Theory Manual; ANSYS Inc.: Canonsburg, PA, USA,, 2015.
- Bachynski, E.E.; Moan, T. Design considerations for tension leg platform wind turbines. Mar. Struct. 2012, 29, 89–114. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Katsaounis, G.M.; Manolas, D.I.; Soukissian, T.H.; Polyzos, S.; Mazarakos, T.P.; Voutsinas, S.G.; Mavrakos, S.A. REFOS: A renewable energy multi-purpose floating offshore system. Energies 2021, 14, 3126. [Google Scholar] [CrossRef]
- DNVGL-OS-E301; Position Mooring. Det Norske Veritas: Høvik, Norway, 2018.
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Pinkster, J.A. Low-frequency phenomena associated with vessels moored at sea. Soc. Pet. Eng. 1975, 15, 487–494. [Google Scholar] [CrossRef]
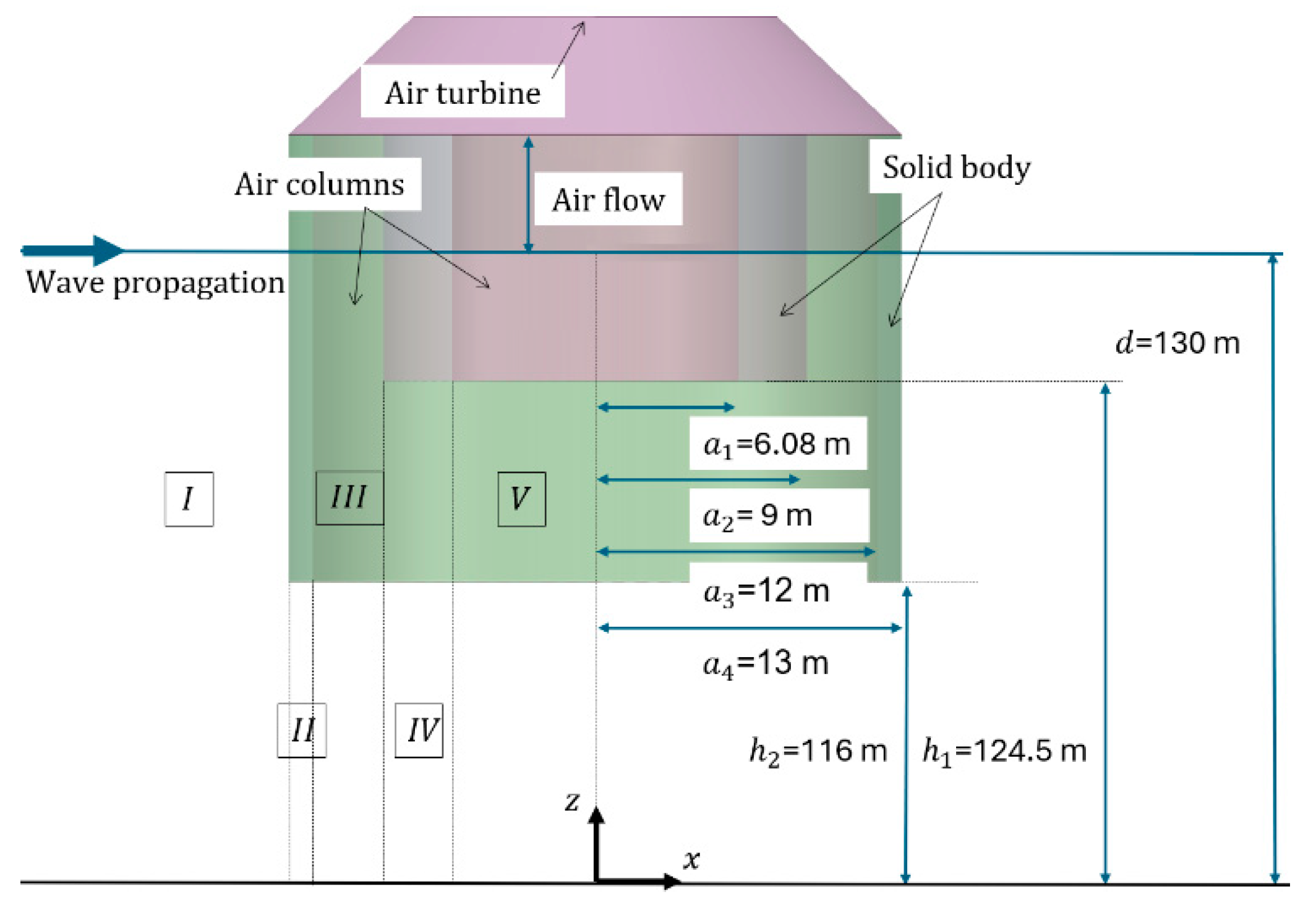

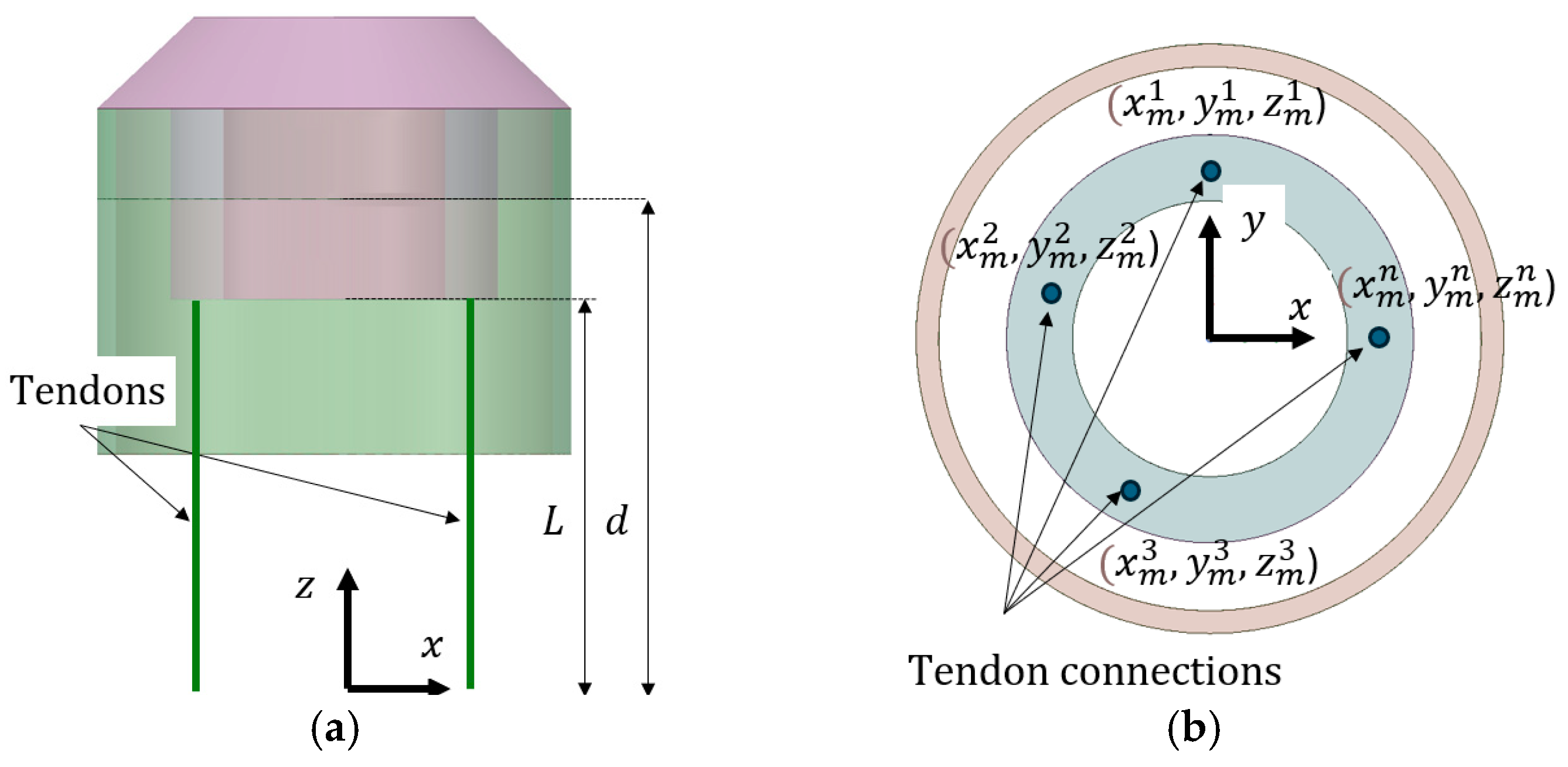





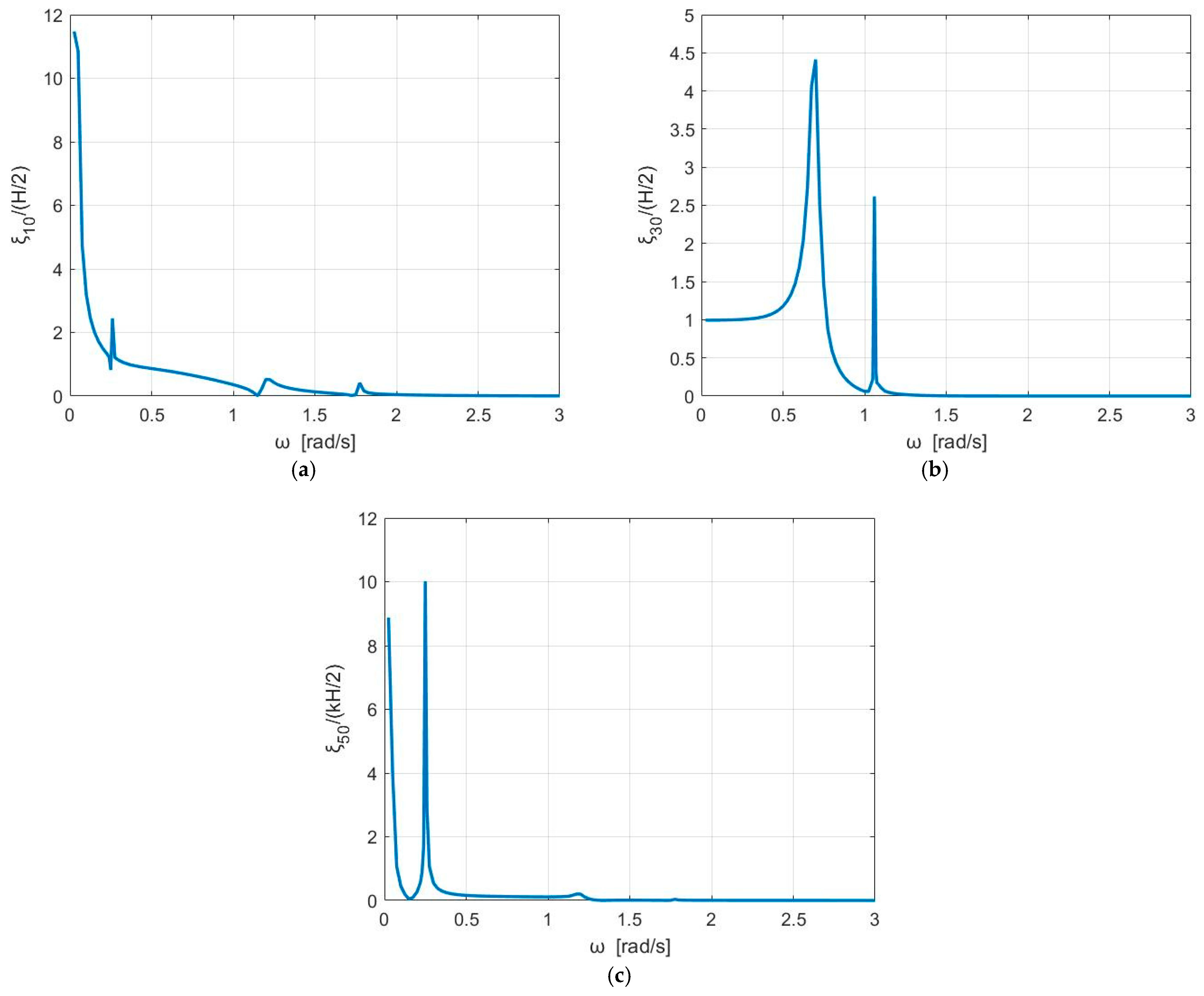






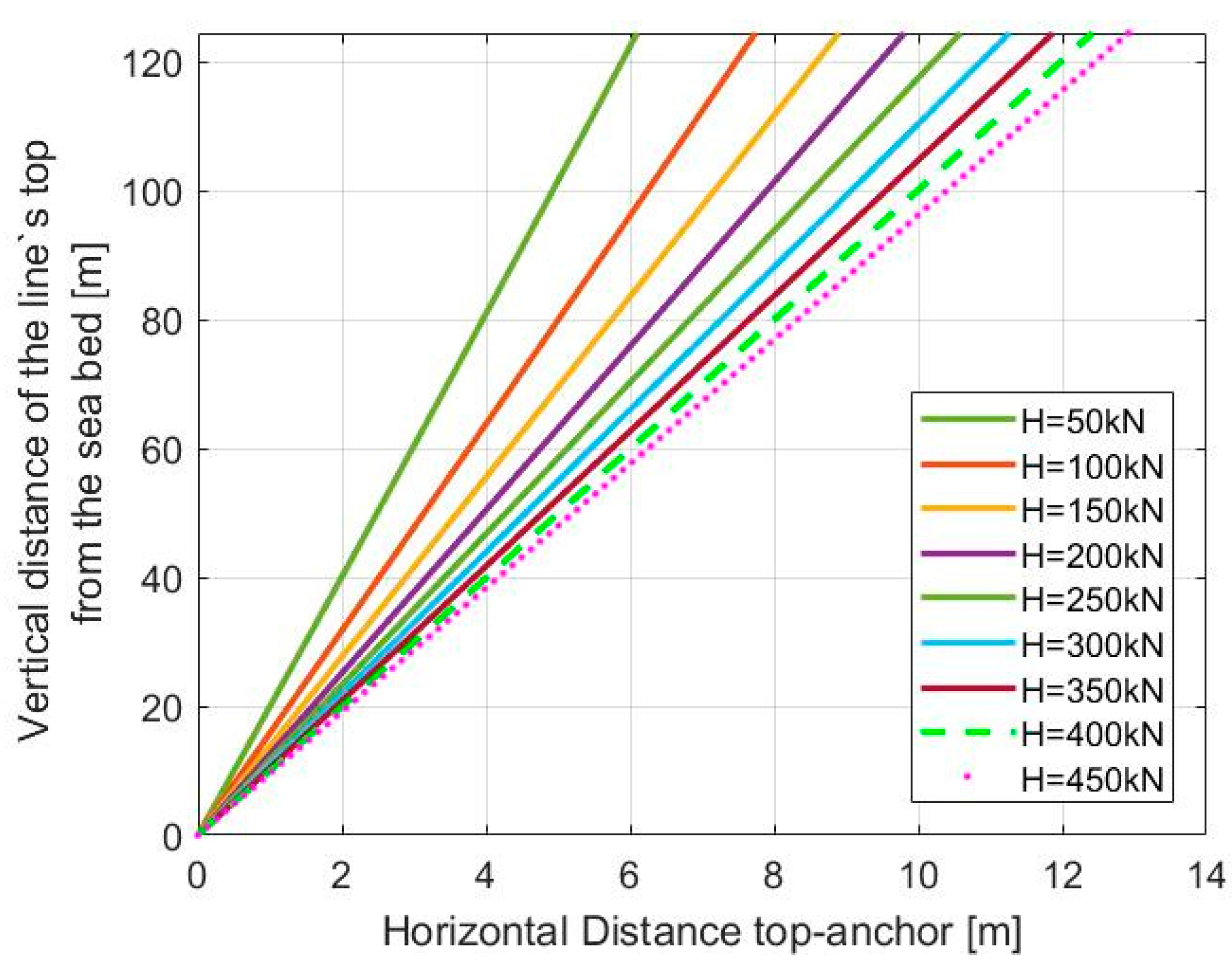

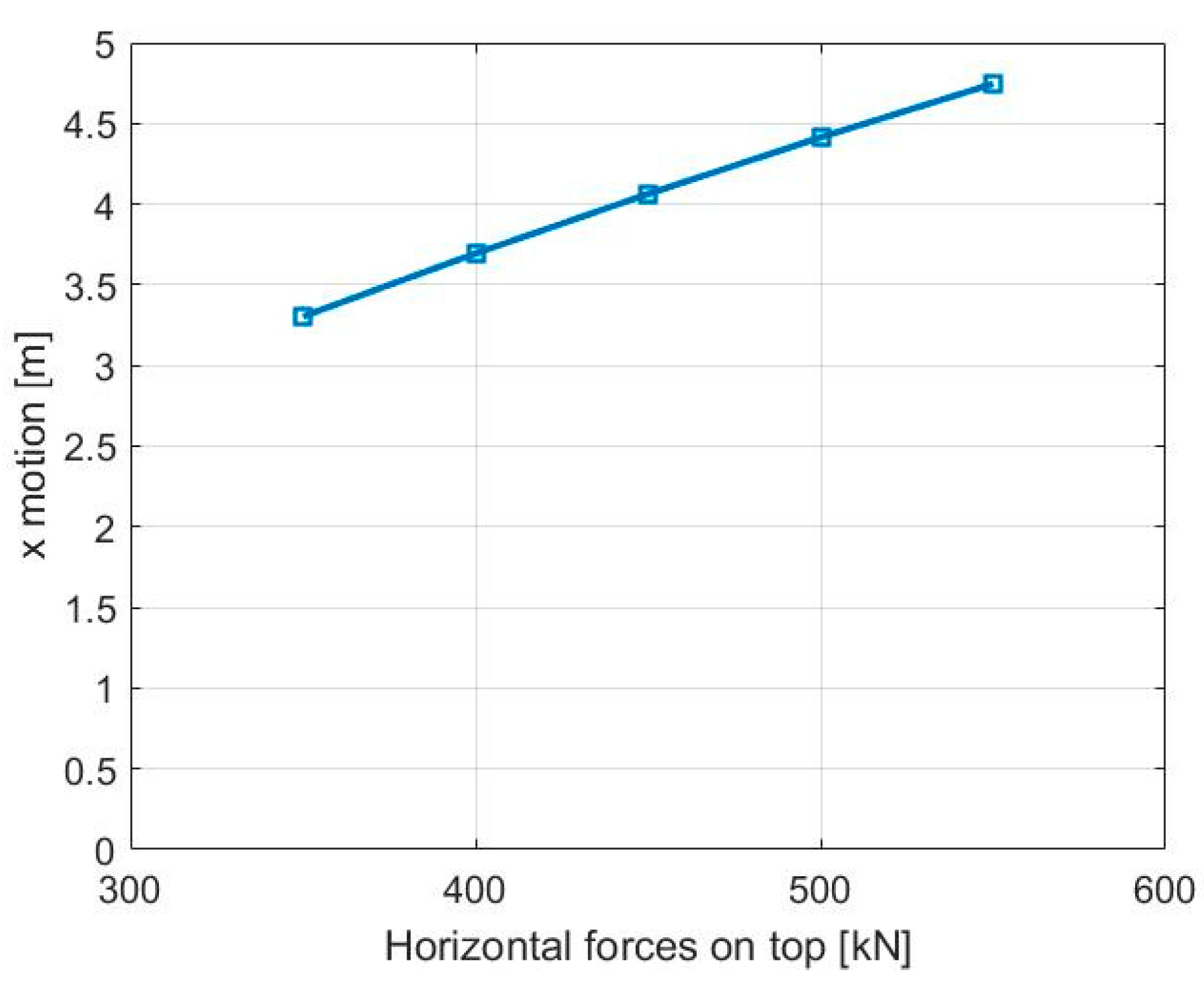




| Depth of the outer pontoon below seawater level (SWL) | 14 m |
| Depth of the inner pontoon below SWL | 5.5 m |
| Elevation of the oscillating chamber above SWL | 5 m |
| Outer radius of outer pontoon | 13 m |
| Inner radius of outer pontoon | 12 m |
| Outer radius of inner pontoon | 9 m |
| Inner radius of inner pontoon | 6.08 m |
| Water depth | 130 m |
| Mass in air per line | 199.0 kg/m |
| Mass in water per line | 173.0 kg/m |
| Axial stiffness per line | 854.0 MN |
| Minimum breaking load per line | 8028 kN |
| Nominal diameter | 100 mm |
| Unstretched length per line | 400 m |
| Pretension at the top of the line | 297 kN |
| Maximum horizontal design load | 450 kN |
| Mass in air per line | 48.8 kg/m |
| Mass in water per line | 42.3 kg/m |
| Axial stiffness per line | 8.02E8 N |
| Minimum breaking load per line | 9147 kN |
| Nominal diameter | 0.1 m |
| Unstretched length per line | 124.5 m |
| Pretension at the top of the line | 3006 kN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konispoliatis, D.N.; Mavrakos, A.S. Comparative Analysis of Catenary and TLP Mooring Systems on the Wave Power Efficiency for a Dual-Chamber OWC Wave Energy Converter. Energies 2025, 18, 1473. https://doi.org/10.3390/en18061473
Konispoliatis DN, Mavrakos AS. Comparative Analysis of Catenary and TLP Mooring Systems on the Wave Power Efficiency for a Dual-Chamber OWC Wave Energy Converter. Energies. 2025; 18(6):1473. https://doi.org/10.3390/en18061473
Chicago/Turabian StyleKonispoliatis, Dimitrios N., and Anargyros S. Mavrakos. 2025. "Comparative Analysis of Catenary and TLP Mooring Systems on the Wave Power Efficiency for a Dual-Chamber OWC Wave Energy Converter" Energies 18, no. 6: 1473. https://doi.org/10.3390/en18061473
APA StyleKonispoliatis, D. N., & Mavrakos, A. S. (2025). Comparative Analysis of Catenary and TLP Mooring Systems on the Wave Power Efficiency for a Dual-Chamber OWC Wave Energy Converter. Energies, 18(6), 1473. https://doi.org/10.3390/en18061473







