Experimental Study on the Organic Rankine Cycle for the Recovery of the Periodic Waste Heat Source
Abstract
1. Introduction
2. Testing of Experimental Prototype
2.1. Experimental System
2.2. Experiment Measuring Process
3. Computational Model and Data Processing
3.1. Physical Properties of Hydraulic Oil and Air
3.2. System Performance
3.3. Data Processing
3.3.1. Steady-State Data Processing
3.3.2. Dynamic Data Processing
4. Results and Discussion
4.1. Steady-State Experiment
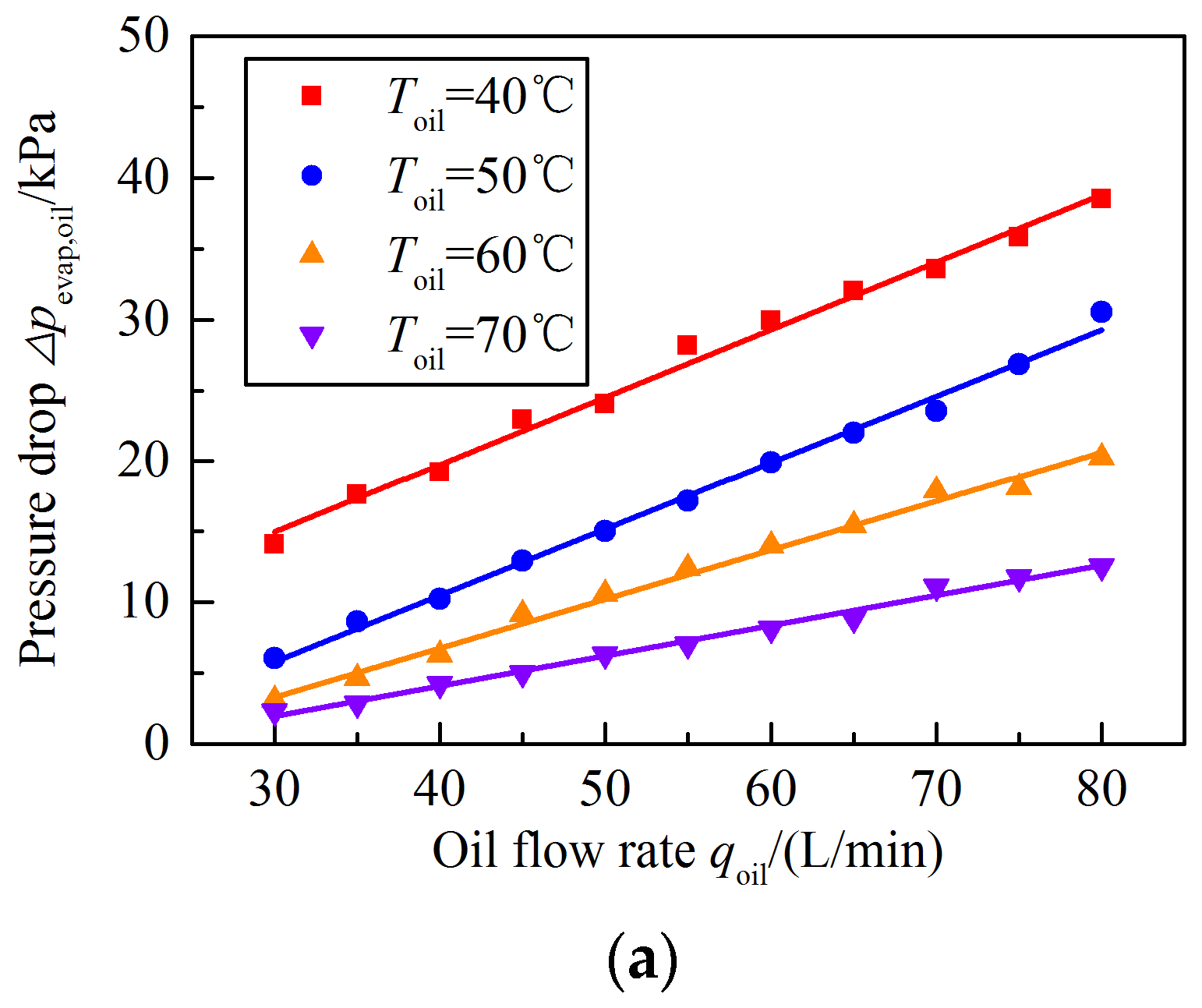
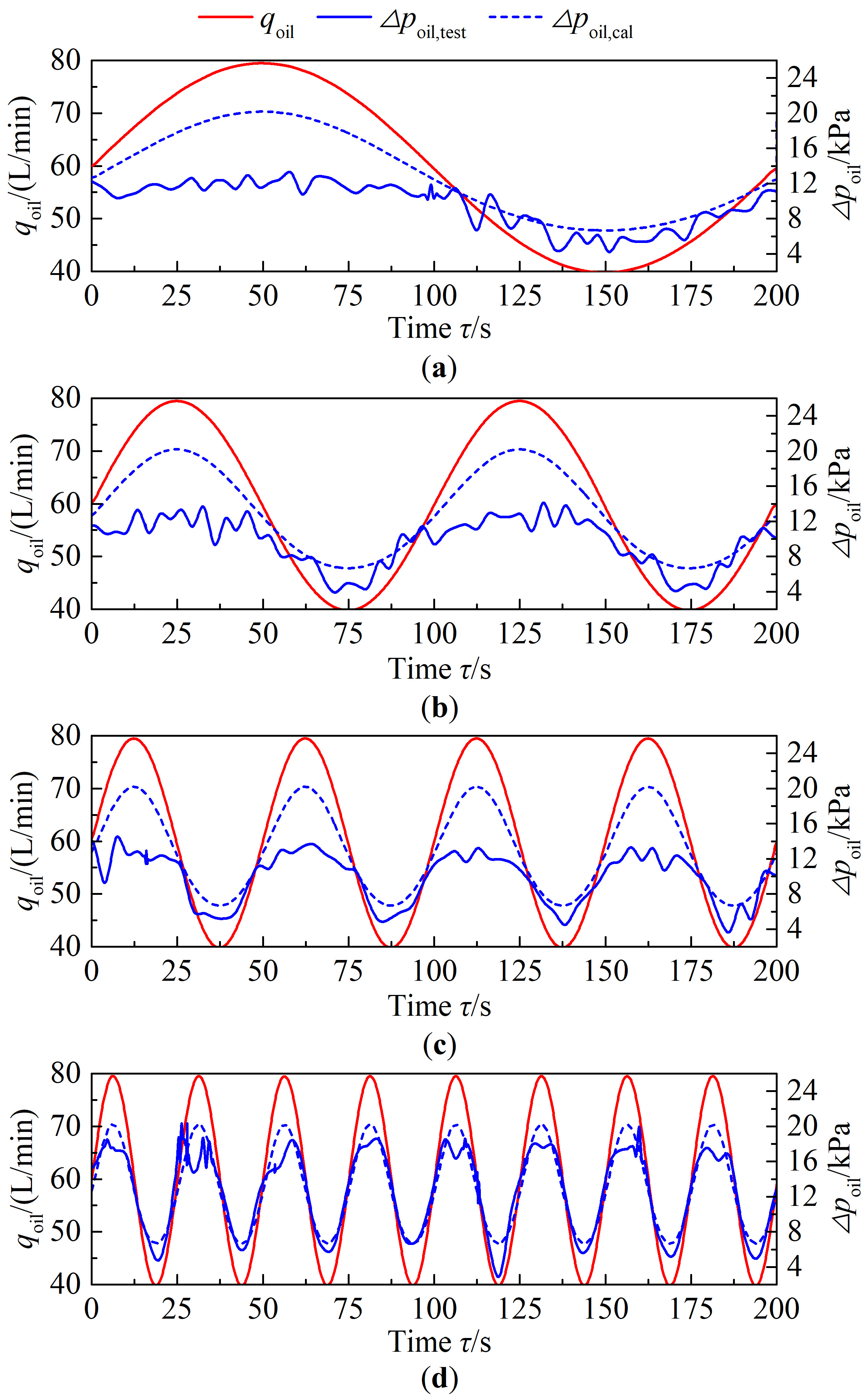
4.1.1. Pressure Drop Characteristics
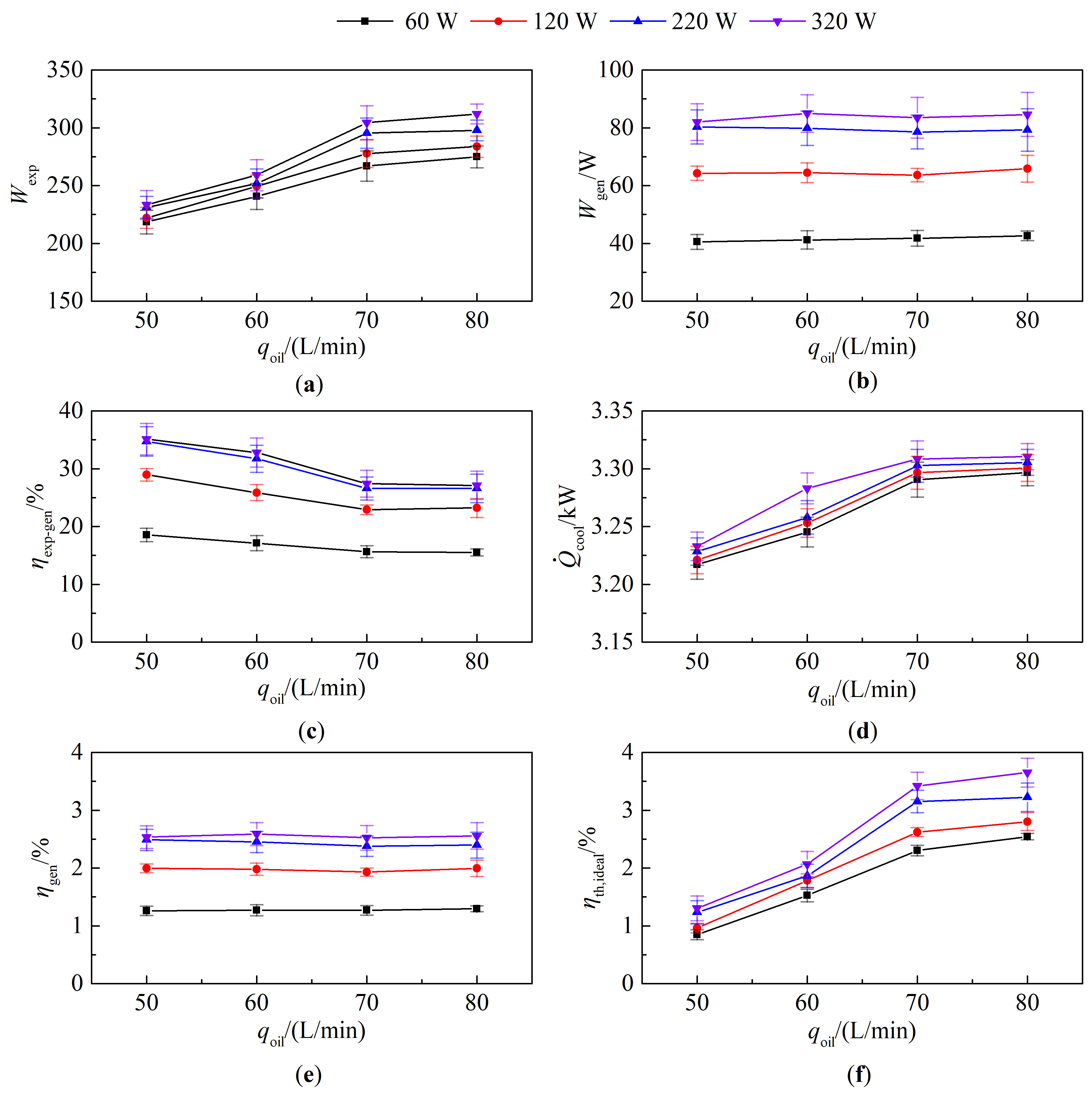
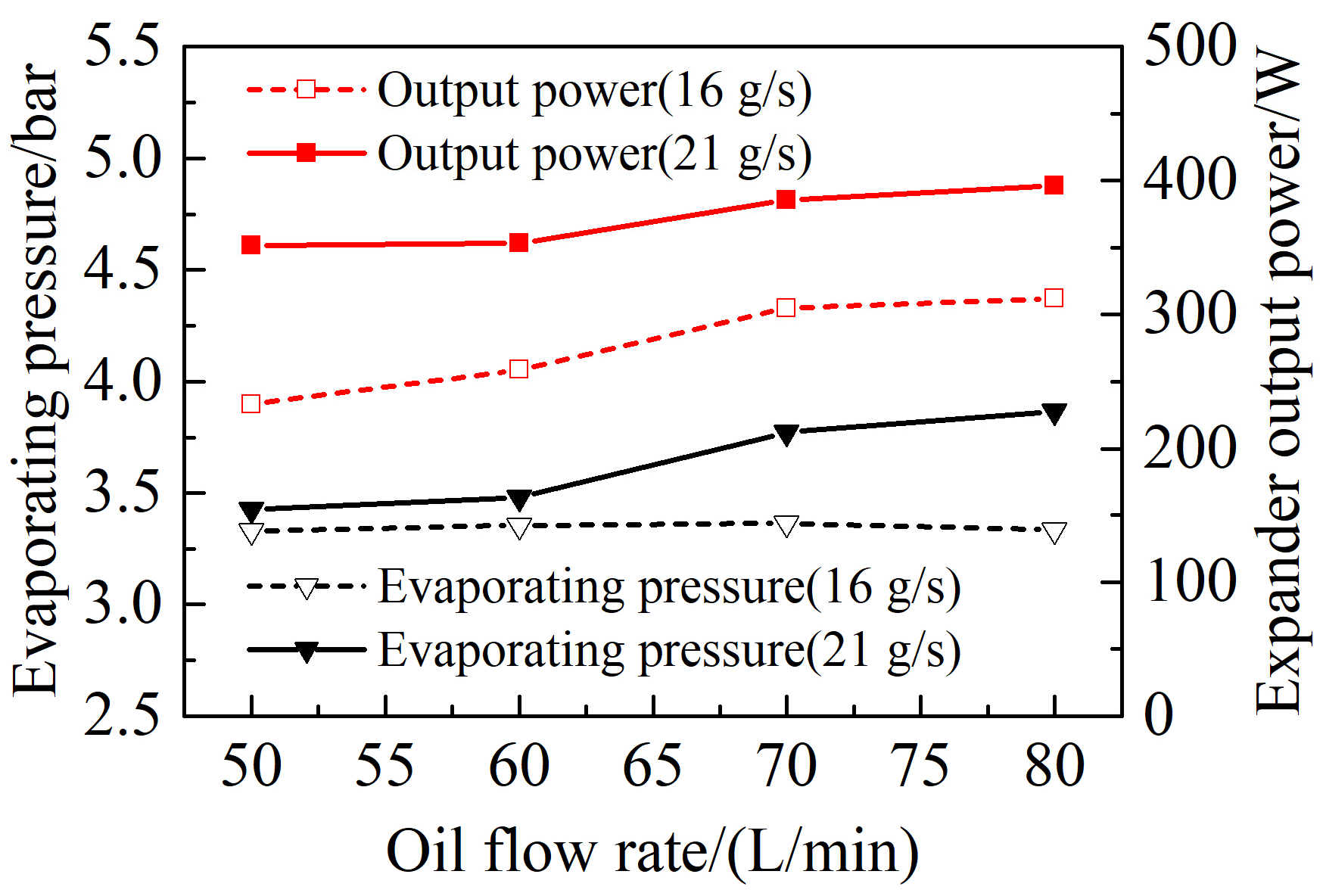
4.1.2. Steady-State Performance of ORC
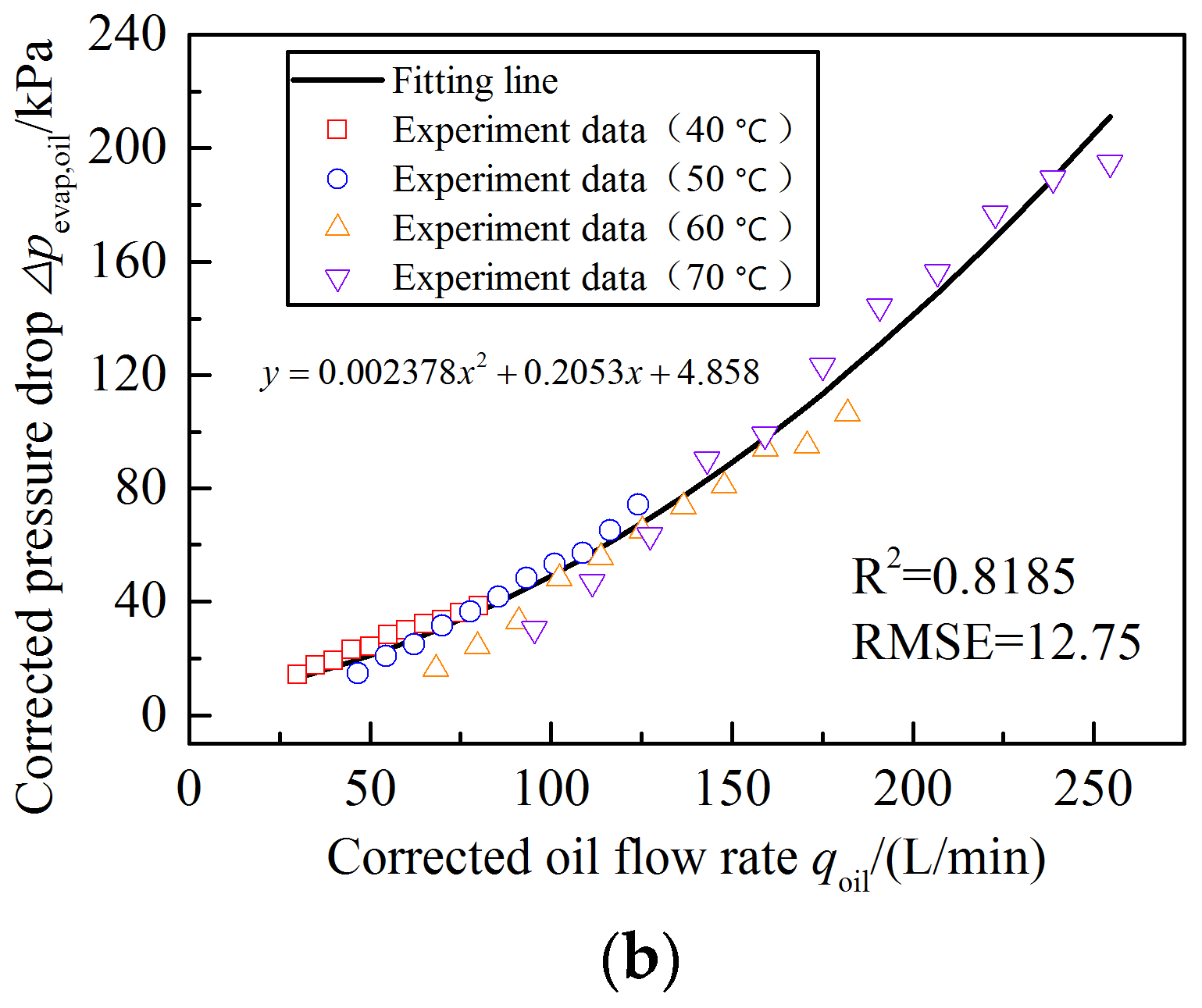
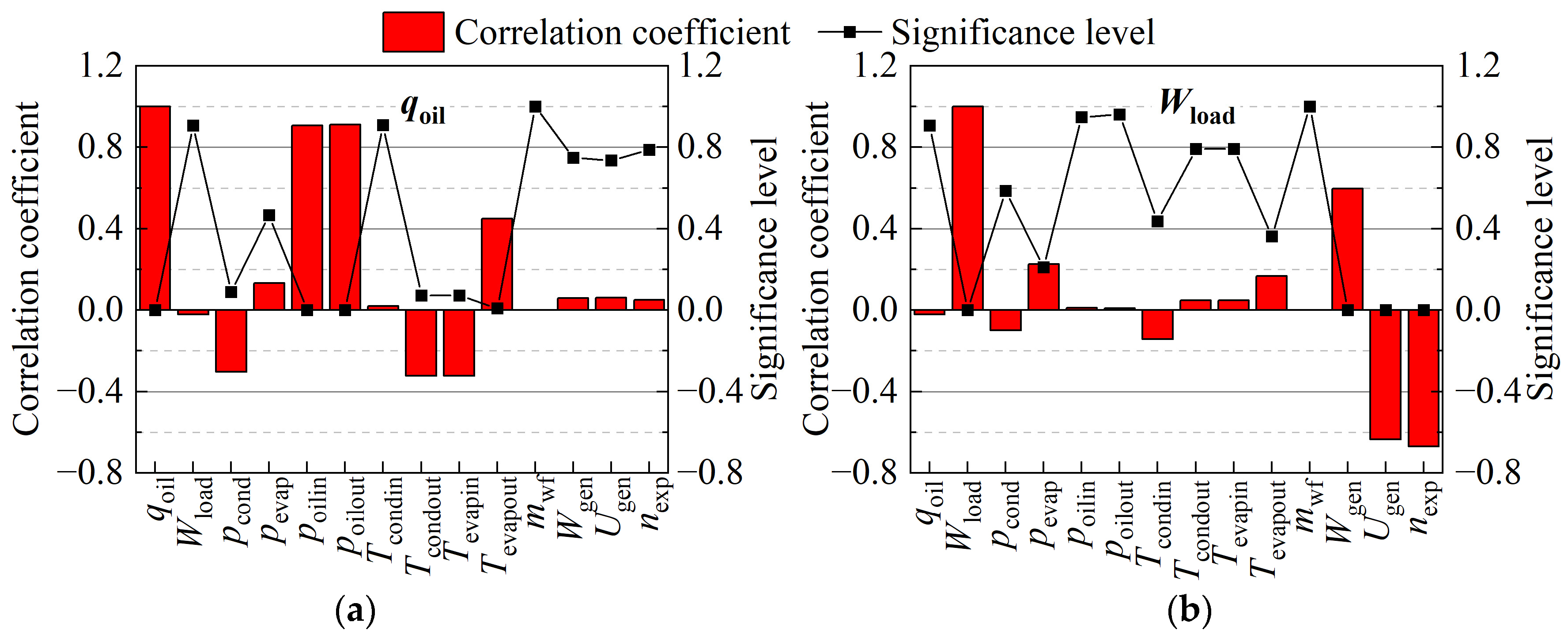
4.1.3. Correlation Analysis
4.2. Dynamic Experiment
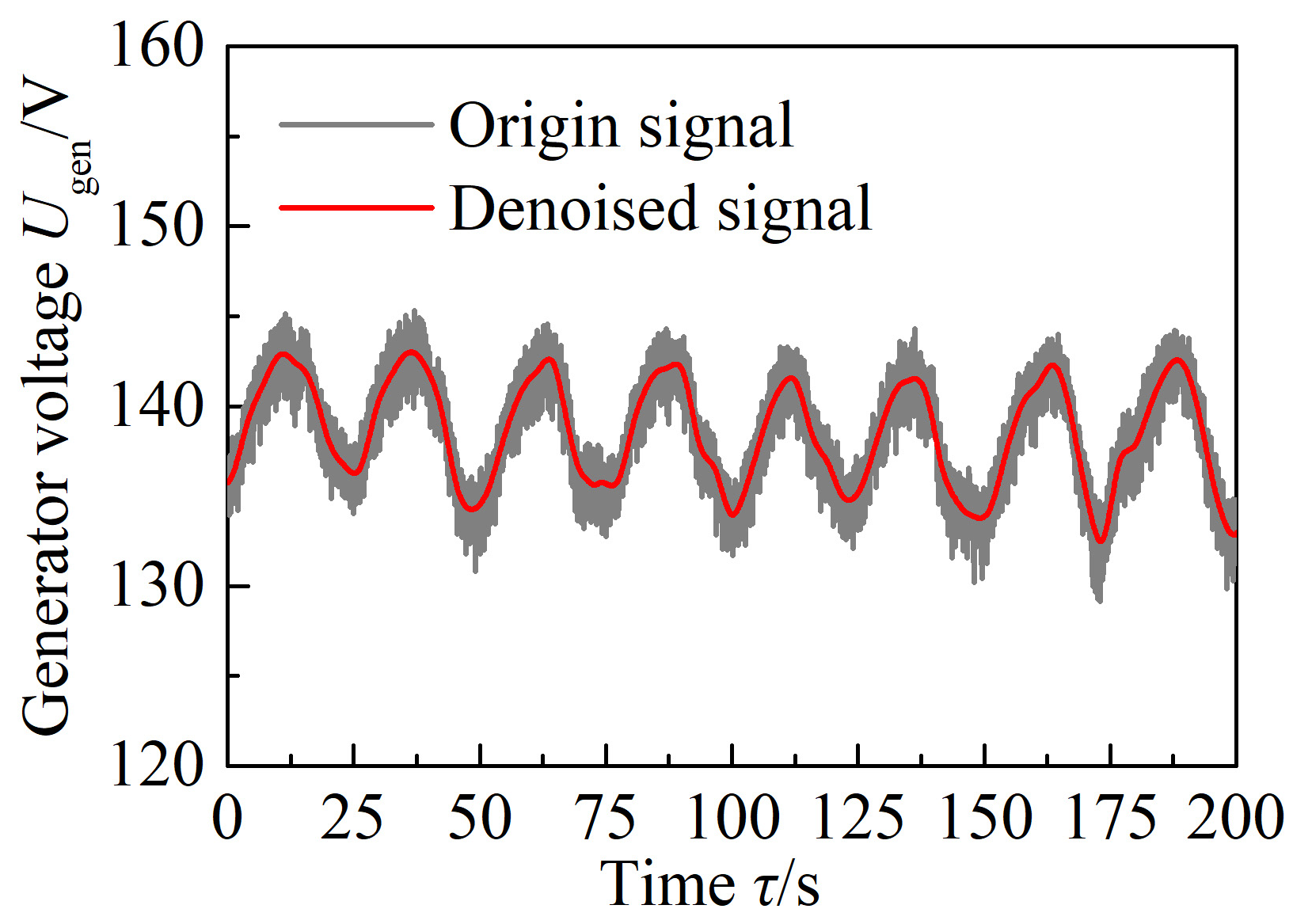
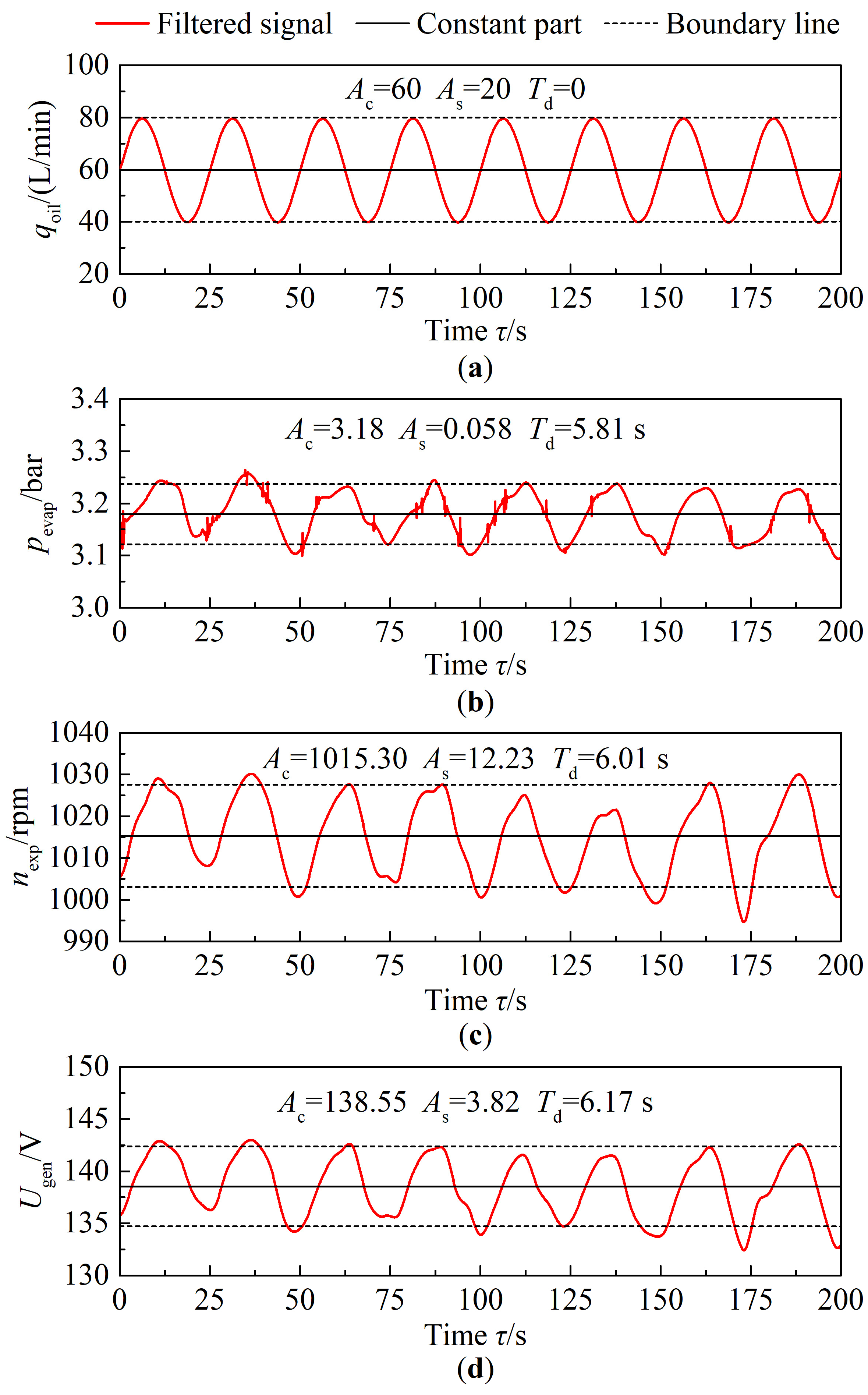
4.2.1. Signal Processing Results
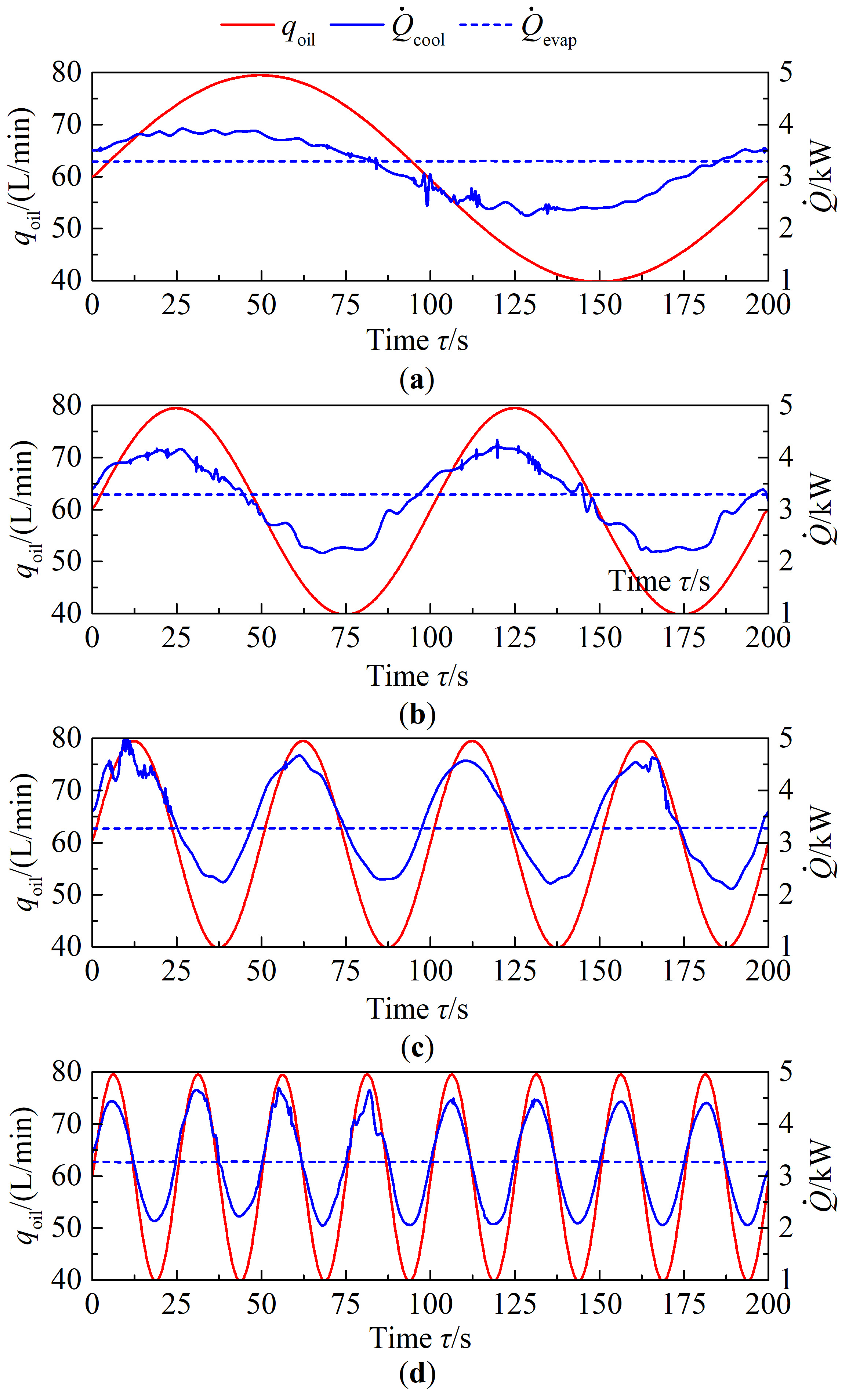
4.2.2. Effect on the Evaporator
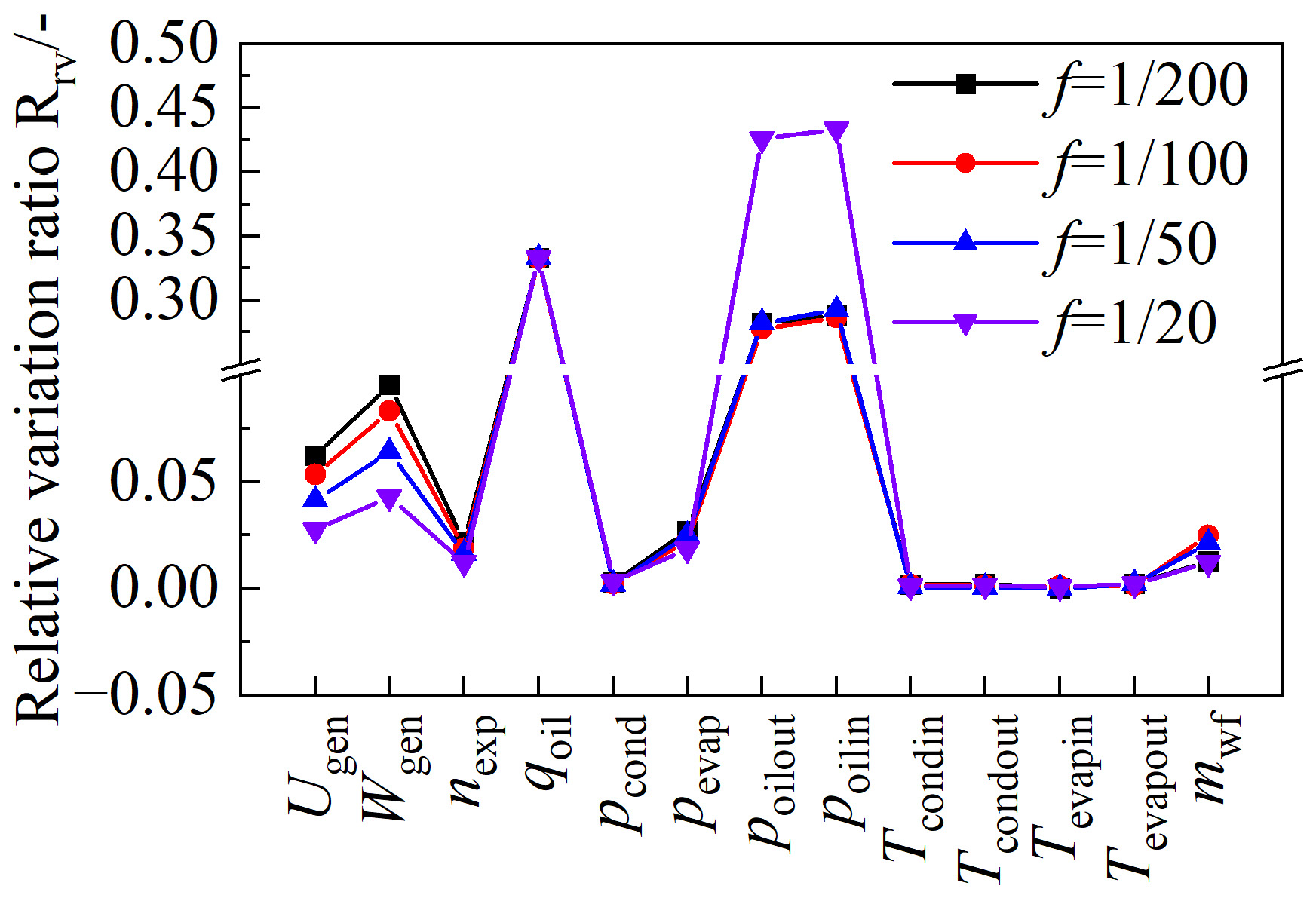
4.2.3. Response of the Operating Parameters
5. Conclusions
- The influence of hydraulic oil flow rate and connected load on the performance of the ORC system is studied through qualitative and quantitative analysis. When the connected load is improved from 60 W to 320 W, the generator output power raises from nearly 42 W to 85 W, and the expander power raises from 218 W to 312 W.
- Based on the correlation analysis, the Wgen (ρcor = 0.59), Ugen (ρcor = 0.64), and nexp (ρcor = 0.67) are strongly correlated with the connected load.
- Through the dynamic experiment, the variation rule of the operating parameters when the oil flow rate changes periodically. As the oil flow rate changes in the range of 40~80 L/min, the oil pressure drop in the evaporator varies on a scale of 3.6~18.6 kPa, and the evaporator heat transfer rate changes between about 2~5 kW.
- When the change frequency of the oil flow rate is 1/25 Hz, the ratios of relative variation of evaporating pressure, expander revolution speed, and generator voltage are 1.82% (0.058 bar), 1.20% (12.23 rpm), and 2.76% (3.82 V), respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |
| ρ | density (kg/m3) |
| T | temperature (°C, K) |
| cp | isobaric specific heat capacity (J/kg·K) |
| heat transfer rate (W) | |
| q | flow rate (m3/s) |
| W | power produced or consumed (W) |
| h | specific enthalpy (kJ/kg) |
| m | mass flow rate (kg/s) |
| p | pressure (Pa) |
| ΔT | temperature difference (K) |
| η | efficiency (-) |
| U | voltage (V) |
| n | revolution speed (rpm) |
| τ | time (s) |
| A | amplitude |
| f | frequency (Hz) |
| R | ratio (-) |
| Subscript | |
| oil | hydraulic oil |
| in | input |
| out | output |
| cool | cooling for hydraulic system |
| cond | condenser |
| air | ambient air |
| exp | expander |
| wp | working fluid pump |
| th | thermal |
| cor | correlation |
| gen | generator |
| rv | ratio of the relative amplitude |
| oilin | oil at the input |
| oilout | oil at the output |
| cal | calculation |
| Acronyms | |
| ORC | organic Rankine cycle |
| SNR | signal-to-noise ratio |
| RMSE | root mean square error |
| FFT | Fast Fourier Transform |
| DFT | Discrete Fourier Transform |
References
- An, K.; Kang, H.; An, Y.; Park, J.; Lee, J. Methodology of Excavator System Energy Flow-Down. Energies 2020, 13, 951. [Google Scholar] [CrossRef]
- Moradi, R.; Cioccolanti, L. Modelling Approaches of Micro and Small-Scale Organic Rankine Cycle Systems: A Critical Review. Appl. Therm. Eng. 2024, 236, 121505. [Google Scholar] [CrossRef]
- Kondratiev, V.V.; Sysoev, I.A.; Kolosov, A.D.; Galishnikova, V.V.; Gladkikh, V.A.; Karlina, A.I.; Karlina, Y.I. Development and Testing of the Thermoelectric Thermal Energy Conversion Device in the Conditions of Existing Aluminum Production. Materials 2022, 15, 8526. [Google Scholar] [CrossRef]
- Meftahpour, H.; Saray, R.K.; Aghaei, A.T.; Bahlouli, K. Comprehensive Analysis of Energy, Exergy, Economic, and Environmental Aspects in Implementing the Kalina Cycle for Waste Heat Recovery from a Gas Turbine Cycle Coupled with a Steam Generator. Energy 2024, 290, 130094. [Google Scholar] [CrossRef]
- Gu, Z.; Zhang, X.; Dong, Z.; Quan, L. A Solution to the Cooling and Preheating of Hydraulic System by Organic Rankine Cycle with Heat Pump. Energy Convers. Manag. 2019, 180, 94–105. [Google Scholar] [CrossRef]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N.; Mirhadizadeh, S.A. Review of Organic Rankine Cycle for Small-Scale Applications. Energy Convers. Manag. 2017, 134, 135–155. [Google Scholar] [CrossRef]
- Maksimov, I.; Kindra, V.; Vegera, A.; Rogalev, A.; Rogalev, N. Thermodynamic Analysis and Optimization of Power Cycles for Waste Heat Recovery. Energies 2024, 17, 6375. [Google Scholar] [CrossRef]
- Daniarta, S.; Nemś, M.; Kolasiński, P. A Review on Thermal Energy Storage Applicable for Low- and Medium-Temperature Organic Rankine Cycle. Energy 2023, 278, 127931. [Google Scholar] [CrossRef]
- Valencia-Ochoa, G.; Duarte-Forero, J.; Mendoza-Casseres, D. Multi-Objective Optimization of the Energy, Exergy, and Environmental Performance of a Hybrid Solar–Biomass Combined Brayton/Organic Rankine Cycle. Energies 2025, 18, 203. [Google Scholar] [CrossRef]
- Hu, Z.; Wu, W.; Si, Y. Optimization of Organic Rankine Cycle for Hot Dry Rock Power System: A Stackelberg Game Approach. Energies 2024, 17, 5151. [Google Scholar] [CrossRef]
- Wilberforce, T.; Muhammad, I. Dynamic Modelling and Analysis of Organic Rankine Cycle Power Units for the Recovery of Waste Heat from 110kW Proton Exchange Membrane Fuel Cell System. Int. J. Thermofluids 2023, 17, 100280. [Google Scholar] [CrossRef]
- Ling, J.; Chen, X. Energy and Economic Analysis of a New Combination Cascade Waste Heat Recovery System of a Waste-to-Energy Plant. Energies 2024, 17, 5196. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, H.; Song, S.; Tian, Y.; Yang, Y.; Liu, Y. Integrated Simulation and Control Strategy of the Diesel Engine–Organic Rankine Cycle (ORC) Combined System. Energy Convers. Manag. 2018, 156, 639–654. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Cheng, Z.; Sun, Q.; Zhao, P.; Dai, Y. Dynamic Performance of an Organic Rankine Cycle System with a Dynamic Turbine Model: A Comparison Study. Appl. Therm. Eng. 2020, 181, 115940. [Google Scholar] [CrossRef]
- Xu, B.; Rathod, D.; Kulkarni, S.; Yebi, A.; Filipi, Z.; Onori, S.; Hoffman, M. Transient Dynamic Modeling and Validation of an Organic Rankine Cycle Waste Heat Recovery System for Heavy Duty Diesel Engine Applications. Appl. Energy 2017, 205, 260–279. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, S.; Xia, X.; Zhao, Y.; Yi, Q.; Zhang, X. Experimental Study on Dynamic Characteristics of Organic Rankine Cycle Coupled Vapor Compression Refrigeration System with a Zeotropic Mixture. Energy 2024, 307, 132736. [Google Scholar] [CrossRef]
- Wu, J.; Liang, Y.; Sun, Z.; Zhu, Y.; Ye, J.; Lu, J. Dynamic Analysis and Control Strategy of ORC Coupled Ejector Expansion Refrigeration Cycle Driven by Geothermal Water. J. Clean. Prod. 2024, 445, 141309. [Google Scholar] [CrossRef]
- Zhang, H.-H.; Xi, H.; He, Y.-L.; Zhang, Y.-W.; Ning, B. Experimental Study of the Organic Rankine Cycle under Different Heat and Cooling Conditions. Energy 2019, 180, 678–688. [Google Scholar] [CrossRef]
- Shao, L.; Zhu, J.; Meng, X.; Wei, X.; Ma, X. Experimental Study of an Organic Rankine Cycle System with Radial Inflow Turbine and R123. Appl. Therm. Eng. 2017, 124, 940–947. [Google Scholar] [CrossRef]
- Muhammad, U.; Imran, M.; Lee, D.H.; Park, B.S. Design and Experimental Investigation of a 1kW Organic Rankine Cycle System Using R245fa as Working Fluid for Low-Grade Waste Heat Recovery from Steam. Energy Convers. Manag. 2015, 103, 1089–1100. [Google Scholar] [CrossRef]
- Pesyridis, A.; Asif, M.S.; Mehranfar, S.; Mahmoudzadeh Andwari, A.; Gharehghani, A.; Megaritis, T. Design of the Organic Rankine Cycle for High-Efficiency Diesel Engines in Marine Applications. Energies 2023, 16, 4374. [Google Scholar] [CrossRef]
- Bai, M.; Zhang, Y.; Deng, S.; Zhao, L.; Zhao, R.; Lu, Y. An Experimental Study on Operation Characteristics of the Organic Rankine Cycle System under the Single-and Multiple-Variables Regulation. Sustain. Energy Technol. Assess. 2020, 41, 100785. [Google Scholar] [CrossRef]
- Ni, J.; Zhao, L.; Zhang, Z.; Zhang, Y.; Zhang, J.; Deng, S.; Ma, M. Dynamic Performance Investigation of Organic Rankine Cycle Driven by Solar Energy under Cloudy Condition. Energy 2018, 147, 122–141. [Google Scholar] [CrossRef]
- Li, S.; Ma, H.; Li, W. Dynamic Performance Analysis of Solar Organic Rankine Cycle with Thermal Energy Storage. Appl. Therm. Eng. 2018, 129, 155–164. [Google Scholar] [CrossRef]
- Fu, B.-R.; Lee, Y.-R.; Hsieh, J.-C. Design, Construction, and Preliminary Results of a 250-kW Organic Rankine Cycle System. Appl. Therm. Eng. 2015, 80, 339–346. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, Y.-Q.; Xu, K.-J.; Liang, H.-J.; Liu, Z.-N.; Zhao, C.-Y.; Wang, Y.-Z.; Sapin, P.; Markides, C.N. Dynamic Behaviour and Performance Evaluation of a Biomass-Fired Organic Rankine Cycle Combined Heat and Power (ORC-CHP) System under Different Control Strategies. Appl. Therm. Eng. 2024, 248, 123236. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, E.; Meng, F.; Zhang, F.; Zhao, C. Closed-Loop PI Control of an Organic Rankine Cycle for Engine Exhaust Heat Recovery. Energies 2020, 13, 3817. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, Y.; Zuo, T.; Chen, R.; Xu, Y. Experimental Study and Energy Loss Analysis of an R245fa Organic Rankine Cycle Prototype System with a Radial Piston Expander. Appl. Therm. Eng. 2020, 169, 114939. [Google Scholar] [CrossRef]
- Zhang, Y.; Tsai, Y.-C.; Ren, X.; Tuo, Z.; Wang, W.; Gong, L.; Hung, T.-C. Experimental Study of the External Load Characteristics on a Micro-Scale Organic Rankine Cycle System. Energy 2024, 306, 132453. [Google Scholar] [CrossRef]
- Liu, C.; Wang, S.; Zhang, C.; Li, Q.; Xu, X.; Huo, E. Experimental Study of Micro-Scale Organic Rankine Cycle System Based on Scroll Expander. Energy 2019, 188, 115930. [Google Scholar] [CrossRef]
- Cao, S.; Xu, J.; Miao, Z.; Liu, X.; Zhang, M.; Xie, X.; Li, Z.; Zhao, X.; Tang, G. Steady and Transient Operation of an Organic Rankine Cycle Power System. Renew. Energy 2019, 133, 284–294. [Google Scholar] [CrossRef]
- Xu, B.; Rathod, D.; Yebi, A.; Filipi, Z.; Onori, S.; Hoffman, M. A Comprehensive Review of Organic Rankine Cycle Waste Heat Recovery Systems in Heavy-Duty Diesel Engine Applications. Renew. Sustain. Energy Rev. 2019, 107, 145–170. [Google Scholar] [CrossRef]
- Wang, C.; Yang, F.; Zhang, H.; Zhao, R.; Xu, Y. Energy Recovery Efficiency Analysis of Organic Rankine Cycle System in Vehicle Engine under Different Road Conditions. Energy Convers. Manag. 2020, 223, 113317. [Google Scholar] [CrossRef]
- Ashwni; Sherwani, A.F.; Tiwari, D.; Kumar, A. Sensitivity Analysis and Multi-Objective Optimization of Organic Rankine Cycle Integrated with Vapor Compression Refrigeration System. Energy Sources Recovery Util. Environ. Eff. 2021, 43, 1–13. [Google Scholar] [CrossRef]
- Dang, H.; Han, Y.; Liu, J.; Tan, M.; Wang, X. Feasibility Analysis and Performance Characteristic Investigation of Thermal Energy Storage System Based on Organic Rankine Cycle for Engine Exhaust Temperature Modulation. Energy Sources Recovery Util. Environ. Eff. 2024, 46, 53–74. [Google Scholar] [CrossRef]
- Ping, X.; Yang, F.; Zhang, H.; Xing, C.; Wang, C.; Zhang, W.; Wang, Y. Energy, Economic and Environmental Dynamic Response Characteristics of Organic Rankine Cycle (ORC) System under Different Driving Cycles. Energy 2022, 246, 123438. [Google Scholar] [CrossRef]

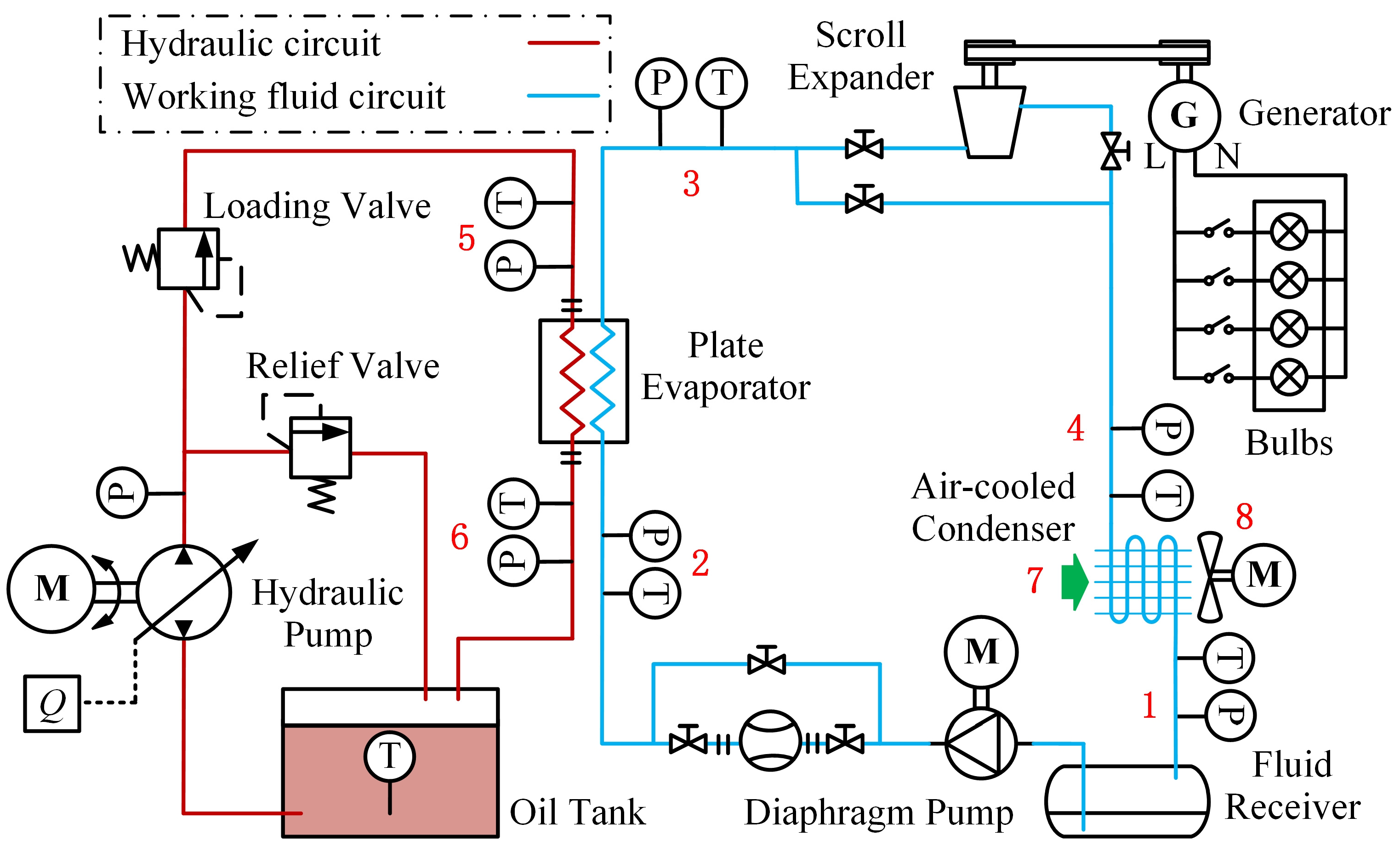

| Component | Parameters | Structure |
|---|---|---|
| Hydraulic pump | Displacement 71 mL/r, pressure 280 bar | Axial piston pump |
| Loading valve | Flow rate 200 L/min, pressure 250 bar | Overflow valve |
| Evaporator | Counterflow, area 3 m2 | Plate type |
| Condenser | Crossflow, area 120 m2 | Tub-finned |
| Working fluid pump | Flow rate 800 L/h, pressure 18 bar | Diaphragm metering pump |
| Expander | Sweeping displacement 106 mL/r | Scroll type |
| Parameters | Type of Sensors | Manufacturer | Range | Accuracy |
|---|---|---|---|---|
| Working fluid temperature | T type thermocouple | OMEGA (Norwalk, CT, USA) | −20~150 °C | 0.4% |
| Hydraulic oil temperature | PT100 | HYDAC (Hamburg, Germany) | −25~100 °C | 0.8% |
| Hydraulic oil pressure | Relative pressure | HYDAC (Hamburg, Germany) | 0~10 bar | 0.25% |
| Working fluid pressure | Absolute pressure | HYDAC(Hamburg, Germany) | 0~30 bar/0~16 bar | 0.25% |
| Working fluid mass flow rate | Coriolis sensor | Xi’an Dongfeng (Xi’an, China) | 0.04~0.4 t/h | 0.15% |
| Electric power | Power meter | YOKOGAWA (Tokyo, Japan) | 0~3000 W | 0.02% |
| Air velocity | Air flowmeter | UNI-T (Dongguan, China) | 0.3~45 m/s | 3% |
| Rotational speed | Photoelectric tachometer | UNI-T (Dongguan, China) | 10~99,999 rpm | 0.4% |
| τd | f = 1/200 Hz | f = 1/100 Hz | f = 1/50 Hz | f = 1/25 Hz |
|---|---|---|---|---|
| pevap | 8.34 | 6.85 | 7.03 | 5.81 |
| nexp | 14.11 | 10.7 | 8.44 | 6.01 |
| Ugen | 18.22 | 12.21 | 9.05 | 6.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Z.; Shi, Y.; Wu, P. Experimental Study on the Organic Rankine Cycle for the Recovery of the Periodic Waste Heat Source. Energies 2025, 18, 1458. https://doi.org/10.3390/en18061458
Gu Z, Shi Y, Wu P. Experimental Study on the Organic Rankine Cycle for the Recovery of the Periodic Waste Heat Source. Energies. 2025; 18(6):1458. https://doi.org/10.3390/en18061458
Chicago/Turabian StyleGu, Zhengzhao, Yan Shi, and Pu Wu. 2025. "Experimental Study on the Organic Rankine Cycle for the Recovery of the Periodic Waste Heat Source" Energies 18, no. 6: 1458. https://doi.org/10.3390/en18061458
APA StyleGu, Z., Shi, Y., & Wu, P. (2025). Experimental Study on the Organic Rankine Cycle for the Recovery of the Periodic Waste Heat Source. Energies, 18(6), 1458. https://doi.org/10.3390/en18061458





