Abstract
The rapid evolution of Integrated Energy Systems (IESs) demands robust management of information transmission, which is critical for real-time monitoring, coordination, and operational efficiency. However, the increasing complexity and costs associated with information exchange necessitate effective pricing mechanisms to ensure economic sustainability and optimal resource allocation. This paper presents an evolutionary game-theoretic framework to analyze regulatory strategies governing information transmission within IES. In the context of market dynamics, both market regulators and communication network operators are considered as actors with bounded rationality, emphasizing their strategic interplay within the system. The main contributions include formulating a model that treats communication network operators as independent entities, enhancing the understanding of IES member diversity and interactivity. This study introduces evolutionary game dynamics, providing new insights into optimizing regulatory policies. This paper also innovates by considering asset utilization in defining effective assets, potentially curbing excessive investment by communication network operators and preventing information transmission prices from soaring. A case study is provided to reveal the dynamics and equilibrium states of the regulatory game, offering theoretical support for refining regulatory strategies in IESs.
1. Introduction
As the pressing challenges of global warming and energy crises become increasingly apparent, distributed renewable energies, such as wind and photovoltaic power, have emerged as crucial countermeasures [1,2]. Integrated Energy Systems (IESs) are widely recognized for their ability to seamlessly integrate and enhance both distributed renewable energy and conventional energy infrastructures. Typically, IESs encompass a diversity of energy facilities, transmission lines, and end-users [3]. Within the framework of IESs, effective energy management relies on sophisticated communication networks capable of transmitting data in real time and conducting comprehensive analyses. Sensors are strategically deployed throughout the IESs to continuously monitor the generation units and loads, thereby ensuring operational efficiency and reliability [4].
Network slicing (NS) is a fundamental capability in 5G-and-beyond communication technologies, enabling public cellular wireless networks to provide customized services for a wide array of applications [5]. The NS technology partitions the original communication network into several independent and non-interfering sub-networks, referred to as “slices”. Each slice operates as a specialized private network, insulated by other users’ activities [6]. Notably, to facilitate tailored NS services within IESs, users must compensate communication network operators accordingly. Consequently, the regulation of information transmission pricing within IESs becomes particularly critical, influencing not only the economic feasibility and resource optimization of IES but also the equitable distribution of network resources, the assurance of service quality, and the enhancement of overall network performance.
Regarding the consideration of information communication in IES, Kong et al. [7] proposed a two-stage radio resource allocation scheme for community smart grids, utilizing device-to-device (D2D) communications to connect sensors and control units. The Hungarian method was employed to maximize cellular user sum-rate while ensuring minimum sensor and control unit throughput. Feng et al. [8] explored the potential of 5G RAN slicing to enhance the frequency regulation services provided by virtual power plants (VPPs), and the value of the slice was defined as its contribution to reducing the risk of profit loss for the VPP. Wang et al. [9] proposed a lightweight privacy-preserving Q-learning framework for energy management to protect sensitive electricity data. Zhou et al. [10] investigated emerging communication technologies for information monitoring among multi-microgrid systems. Li et al. [11] introduced a two-hierarchy smart agent model to describe Smart Agent Communication (SAC) in IESs. Additionally, some research assessed the impact of exogenous and endogenous communication system instabilities on the operation of energy systems, such as man-made attacks [12,13] and dynamic pricing [14]. The aforementioned research primarily concentrates on optimizing communication resource allocation and system performance to address information transmission challenges within energy systems, treating communication networks as an integral component of the energy system. However, these studies frequently neglect the role of network communication network operators as independent third-party entities that offer network-related services, along with the critical issues of pricing and regulation that arise from this role.
In addressing regulatory issues within in the 5G market, Bauer et al. [15] proposed that regulatory policies must adapt to the dynamic characteristics of 5G technology while striking a balance between fostering innovation and safeguarding competition. Laffont et al. [16] argued that regulation and antitrust should continue to utilize the perfectly competitive market model as a benchmark. However, Viscusi et al. [17] emphasized that this approach presents challenges in formulating regulations for rapidly evolving marketplaces.
The predominant approaches in price regulation are classified into two primary categories: return on investment (ROI) regulation and price-cap regulation (PCR). The ROI regulation aims to reimburse firms for their costs while ensuring a fair return on investment. However, this model is not without its flaws. Averch et al. [18] identified that under ROI regulation, regulated firms tend to overinvest in order to secure higher earnings, leading to a distortion in resource allocation, a phenomenon termed the “A-J effect”. Sappington et al. [19] suggested that PCR may limit the incremental benefits that enterprises can achieve from enhancing service quality, which could potentially result in a decline in service quality and negatively impact consumer welfare. Braeutigam et al. [20] examined the implications of the transition from ROI regulation to PCR. Furthermore, other studies have explored price regulation in various sectors, including retail electricity price [21], carbon emission price [22], and transmission & distribution tariffs [23,24]. Within the realm of price regulation scholarship, certain limitations are acknowledged: first, research often relies on overly stringent assumptions, such as perfect competition and complete rationality among participants; second, the delineation of effective assets within ROI primarily emphasizes business-related correlations.
In the field of price regulation within energy systems, existing research has significantly overlooked the role of network communication service providers as independent third parties, failing to adequately capture market complexity and the bounded rationality of participants. A comparative table summarizing key differences between our proposed framework and prior works is provided, as shown in Table 1.

Table 1.
Comparative analysis of game-theoretic models in energy systems.
To address these research gaps, this study introduces evolutionary game theory to construct an evolutionary game framework for information transmission pricing that involves market regulators and communication network operators. This framework aims to more accurately simulate market dynamics and participant behavior, thereby providing new theoretical insights and policy perspectives for the understanding and optimization of information transmission price regulatory policies.
In comparison to the existing literature, the main contributions of this work can be summarized as follows:
- We formulate a model for information transmission price regulation that positions communication network operators as independent third parties, incorporating their interactions with energy system managers. By separating these roles, we emphasize the diversity and interactivity of the participants within the IES.
- We employ evolutionary game theory and incorporate the assumption of bounded rationality to realistically simulate the strategic interactions between different market entities. By introducing the concept of information transmission pricing, we provide a novel perspective for optimizing regulatory strategies within the IES. This approach facilitates more refined and dynamic regulatory practices, thereby enhancing the efficiency and adaptability of regulatory mechanisms
- We develop the degree of asset utilization as a criterion in the process of defining effective assets, moving beyond a sole reliance on asset relevance. This innovative approach can, to a certain extent, mitigate excessive investment by communication network service providers, thereby preventing information transmission prices from escalating to excessive levels.
The remainder of this paper is organized as follows: Section 2 constructs the evolutionary game model and derives the equilibrium points. Section 3 assesses the stability of various equilibrium points and examines the equilibrium conditions under scenarios where the net benefit difference is positive or negative. Section 4 presents the case study and analyzes the simulation results. Finally, Section 5 concludes the paper, highlighting future research directions and implications.
2. System Formulation
2.1. 5G-and-Beyond Network Slicing Framework
IES represents a progressive approach to energy management and supply, predicated on the existence of a sophisticated information transmission network. Given the substantial demand for extensive data transmission within IESs, this paper examines the integration of 5G-and-beyond networks, emphasizing the following advantages: (i) peak transmission rates reaching 100 Gbps or higher; (ii) transmission latency as low as sub-millisecond levels; (iii) enhanced frequency bandwidths and novel spectrum resources, including the Terahertz (THz) band [25,26].
Network slicing emerges as a pivotal feature within 5G-and-beyond network communications, facilitating the customization of public cellular wireless networks to address the specific requirements of industrial applications [5]. This technology segments the original communication network into distinct and independent networks, referred to as “slices”, thereby allowing each slice to function as a dedicated private network, free from interference by other users, as illustrated in Figure 1.
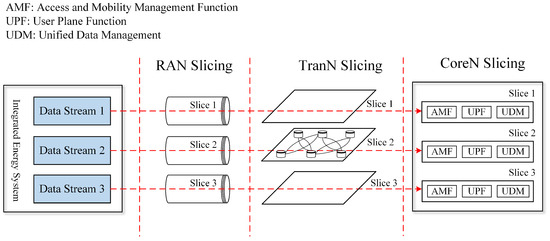
Figure 1.
The 5G-and-beyond network slicing technology.
In general, 5G-and-beyond network slicing encompasses radio access network (RAN) slicing, transmission network (TransN) slicing, and core network (CoreN) slicing [6]. Tailored to meet the distinct service requirements or business types associated with various data streams, these data streams are allocated to corresponding network slices. Subsequently, through TranN slicing, these streams are further processed and transmitted to fulfill diverse service transmission needs. Ultimately, the data streams are directed into CoreN slices, where they are managed by a range of functional modules, including the access and mobility management function (AMF), user plane function (UPF), and unified data management (UDM).
2.2. Problem Description and Model Hypothesis
Within the framework of an IES, the generation of energy and the transmission of information are managed by specialized entities. The Integrated Energy System Manager (IESM) is dedicated to the production and operational management of energy, while the Communication Network Operator (CNO) is responsible for the establishment of communication networks and the execution of information transfer. This delineation of responsibilities ensures the efficient management and optimization of both energy and information flows. The two-layer structure of the IES is illustrated in Figure 2. Note that the IES configuration in this paper refers to an electricity-dominated IES with auxiliary gas/thermal subsystems, reflecting the most common configuration in modern smart grids. The specific physical model of the IES is not within the scope of this paper.
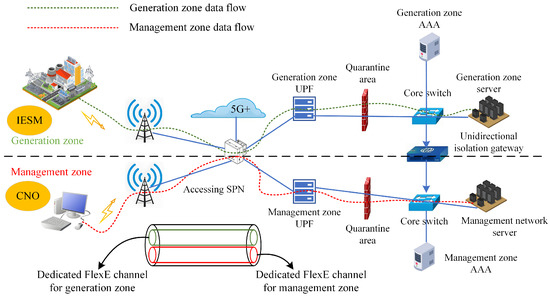
Figure 2.
The two-layer structure of the IES.
Bounded rationality is an important concept in behavioral economics, describing the phenomenon that individuals, due to limitations in cognitive ability, information acquisition, time constraints, and computational capacity, cannot achieve the state of perfect rationality and can only make relatively reasonable decisions under limited conditions. This theory revises the traditional economic assumption of “perfect rationality”, bringing the description of human behavior in economics closer to reality. It has been widely applied in fields such as management and regulatory policy. Thus, in this paper, the IESM and CNO are both bounded rationality players who must continually learn to refine their behaviors. Each player has two strategies to choose from: the CNO can opt for either rational investment or excessive investment strategies, while the IESM can implement either strict regulation or lenient regulation policies. To elevate the pricing of information transmission, the CNO may engage in excessive investment in information transmission equipment and network infrastructure. Concurrently, the IESM may exhibit excessive optimism regarding the CNO’s investment strategies and opt for a lenient regulation policy. It is important to note that excessive optimism represents a form of bounded rational behavior on the part of the IESM.
Without loss of generality, and to facilitate computational simplicity while enhancing subsequent analytical rigor, the following assumptions for the model are introduced:
- When the CNO makes rational investments, the revenue-generating fixed assets are represented as , while the operational and maintenance expenses are denoted as , and the equipment depreciation costs are expressed as . The allowed rate of return established by the IESM is denoted as . Regardless of whether the IESM employs a strict or lenient regulatory strategy, the actual revenue generated by the CNO is equal to the permitted revenue, both of which are expressed as .
- Let denote the ratio of the CNO’s redundant assets to its rational investment assets, implying that the total fixed assets related to communication network owned by the CNO amount to . Under a strict regulatory strategy implemented by the IESM, the proportion of redundant assets that can be classified as revenue-generating fixed assets is limited to . Consequently, the operational and maintenance expenses, as well as the depreciation costs associated with the productive redundant assets, are designated as and , respectively. The cost of the remaining non-performing assets incurred by the CNO is denoted by . In this context, the actual revenue of the CNO is represented as . Conversely, when the IESM adopts a lenient regulatory policy, all investments related to information transmission are considered as revenue-generating fixed assets for the CNO, resulting in actual revenue being equal to permitted revenue, both represented by .
- When the IESM adopts a strict regulatory strategy, and the CNO engages in rational investment, the reputation acquired by the IESM is denoted as , with the associated costs incurred by the IESM being denoted as . In contrast, under a lenient regulatory policy, the costs incurred are represented by , where and both are greater than zero.
- When the CNO engages in rational investments, the asset utilization rate is high, which leads to an efficient allocation of information transmission costs, resulting in social welfare denoted as . Conversely, under lenient regulation, the CNO’s excessive investments inflate information transmission costs, thereby causing a loss in social welfare denoted as . Under strict regulation conditions, the social welfare loss arising from the operator’s excessive investments is represented by , where .
Here, we should note that the assumptions and parameter settings made in the paper are grounded in the established regulatory economics literature and industry practices. For example, Assumptions 1 and 2 can be referred to Averch et al. [18] and Braeutigam et al. [20]. Assumptions 3 and 4 can be referred to Laffont et al. [16] and Esplin et al. [21]. Additionally, the numerical choices for some key parameters are explained in the subsequent case study and simulation sections.
2.3. Evolutionary Game Strategy Analysis
For the CNO, investment strategies can be categorized into rational investment and excessive investment, with corresponding probabilities denoted as x and , respectively. Similarly, the IESM’s strategies can be divided into strict regulation and lenient regulation, associated with probabilities y and . Note that , and the greater the values of x and y, the higher the likelihood that the CNO will engage in rational investment and the IESM will adopt a strict regulatory strategy, respectively. Based on these assumptions, a payoff matrix for both the IESM and the CNO can be constructed through cost–benefit analysis, as illustrated in Table 2.

Table 2.
Payoff matrix for the IESM and the CNO.
Referring to the payoff matrix presented in Table 2, the expected return on the CNO’s rational investment is expressed as:
In the event of excessive investment by the CNO, the expected revenue is denoted as follows:
Considering the probabilities associated with the CNO’s selection of different investment strategies, the average revenue for the CNO can be mathematically expressed as .
The replicator dynamics equation, representing a cornerstone theoretical framework in evolutionary game theory, mathematically describes the temporal evolution of strategic composition within interacting populations. This differential equation system captures the ecological mechanisms governing strategy proliferation and equilibrium selection through continuous adaptation processes driven by fitness differentials. Renowned for its mathematical tractability and mechanistic interpretability, replicator dynamics has gained prominence as an indispensable analytical framework for investigating evolutionary stability criteria and non-equilibrium dynamics in strategic interactions.
For the CNO, the replicator dynamic equation is given by . By substituting (1) and (2) into and simplifying, we can obtain the following:
By setting , we can subsequently derive that , , .
Similarly, the IESM’s average profit is given by:
The replicator dynamic equation for the IESM is denoted by , and based on (4), we have:
Let , and we can obtain , , .
By solving and simultaneously, we can obtain five equilibrium points: , , , and .
3. Analysis of Evolutionary Equilibrium
3.1. Determination of Equilibrium Points
The Jacobian operator, constructed through first-order partial differentiation of the replicator dynamics system, characterizes pairwise interaction gradients among evolving strategic variables. Spectral decomposition of this linear operator enables rigorous determination of equilibrium point stability through eigenvalue sign analysis. Within the framework of Lyapunov stability theory, this analytic approach establishes the asymptotic stability criteria for evolutionarily stable states (ESSs) in the CNO-IESM co-evolutionary system. Specifically, the Jacobian matrix J derived from our replicator dynamics formulation takes the following canonical representation:
in which, , , , .
Based on the replicator dynamic equation , the determinant , and the trace of the Jacobian matrix J, the nature of local equilibrium points can be determined, which can be classified into three distinct categories: (1) when and , the equilibrium point is classified as an Evolutionarily Stable Strategy (ESS); (2) under the conditions and , the equilibrium point is unstable; (3) when , the equilibrium point is noted as a saddle point. The determinant and trace of the Jacobian matrix are summarized in Table 3 and Table 4, respectively.

Table 3.
Determinants of the Jacobian matrix at equilibrium points.

Table 4.
Traces of the Jacobian matrix at equilibrium points.
3.2. Equilibrium Analysis
From the analysis presented above, both the CNO and the IESM possess two available strategies. Given the strategy chosen by one party, the net revenue differences when the other party selects different strategies can be determined, resulting in four distinct scenarios.
- Under the lenient regulatory strategies implemented by the IESM, the difference in net revenues when the CNO opts for rational investment as opposed to excessive investment is denoted by , given that , it follows that ;
- When the IESM implements a strict regulatory strategy, the difference in net revenues between the CNO’s rational investment and excessive investment strategies is denoted as ;
- When the CNO adopts an excessive investment strategy, the difference in net revenues between the IESM’s strict and lenient regulatory strategies is denoted as ;
- When the CNO employs a rational investment strategy, the difference in net revenues between the IESM’s strict and lenient regulatory policies is denoted by .
Among the four scenarios described above, the only certainty is that , whereas the signs of , and remain indeterminate. Consequently, this results in a total of distinct possibilities, which will be analyzed separately in the following sections.
Case 1: , , , . At this juncture, equilibrium point is deemed unstable, while points , , and are saddle points. is an evolutionarily stable strategy, indicating that the evolutionarily stable strategies for the CNO and IESM are excessive investment and lenient regulation, respectively.
Case 2: , , , . In this scenario, equilibrium point is identified as unstable, while points , , and are classified as saddle points, and is recognized as an evolutionarily stable strategy. This configuration indicates that the stable evolutionary strategies of the CNO and IESM correspond to excessive investment and lenient regulation, respectively.
Case 3: , , , . Equilibrium point is deemed unstable, whereas points , , and are saddle points, and is acknowledged as an evolutionarily stable strategy, indicating that the CNO and IESM would adopt excessive investment and lenient regulation, respectively. The stability of each equilibrium point in Cases 1–3 is as presented in Table 5.

Table 5.
The stability of each equilibrium point in Cases 1–3.
In Cases 1–3, the evolutionarily stable point is identified as , with the corresponding evolutionarily stable strategy represented by a combination of “excessive investment and lenient regulation” (note that an Evolutionarily Stable Strategy (ESS) can be defined as a self-sustaining behavioral pattern that emerges spontaneously among market participants through prolonged interactions, demonstrating robustness against strategic deviations in competitive environments). This phenomenon indicates that when the IESM implements a lenient regulatory policy, the irrational investment behavior of the CNO may increase the allowable revenue without incurring the associated costs, thereby creating a disincentive for rational investment and fostering a tendency towards overinvestment. Confronted with such overinvestment by the CNO, the IESM recognizes that enhancing social welfare through stringent regulatory measures does not sufficiently offset the incurred costs, leading to a preference for maintaining lenient regulatory policies.
Case 4: , , , . At this juncture, is unstable, while points , , and are classified as saddle points. is recognized as an evolutionarily stable strategy, with the CNO favoring excessive investment and the IESM enforcing strict regulation.
Case 5: , , , . Equilibrium point is unstable, whereas , , and are saddle points. Notably, represents an evolutionarily stable strategy, which implies that the CNO prefers excessive investment while the IESM favors lenient regulatory policies. The stability characteristics of each equilibrium point in Cases 4 and 5 are presented in Table 6.

Table 6.
Stability of each equilibrium point in Cases 4–5.
In Cases 4 and 5, the evolutionarily stable point is , which corresponds to the strategy combination of “excessive investment, strict regulation”. This outcome indicates that, at this equilibrium, the CNO consistently achieves higher net revenues from overinvestment compared to rational investment, regardless of the regulatory strategy employed by the IESM. Therefore, the CNO favors overinvestment. For the IESM, strict regulation consistently yields higher net revenues compared to lenient oversight, irrespective of the investment strategies of the CNO. Thus, the IESM prefers strict regulatory policies. Overall, the strategy combination at the evolutionarily stable point reflects a stable equilibrium where both the CNO and the IESM maximize their net revenues based on their respective strategies.
Case 6: , , , . The point is unstable, while , , and are saddle points. In contrast, is identified as the evolutionarily stable strategy. This indicates that at the equilibrium point , both the CNO and the IESM have adopted strategies that are resistant to invasion by alternative strategies. Specifically, the evolutionarily stable strategy for the CNO is rational investment, and for the IESM, it is strict regulation. These strategies form a stable equilibrium where neither party can improve their payoff by unilaterally changing their strategy.
Case 7: , , , . At this moment, points , , , and are all saddle points, while is a central point. The presence of saddle points and a central point indicates the absence of an evolutionarily stable strategy in this case. Specifically, saddle points suggest that small perturbations can lead to significant changes in the system’s behavior, while a central point implies that the system can oscillate around this equilibrium without converging to a stable state. This dynamic behavior is reflected in the interaction between the CNO and the IESM: when the IESM employs strict regulation, the CNO will opt for rational investment; conversely, upon recognizing the CNO’s rational investment, the IESM will switch to a lenient regulatory strategy. Subsequently, the CNO will revert to overinvestment once regulation is relaxed, leading to a cyclical trap, as depicted in Figure 3. Under these conditions, the continuous switching between strategies by both the IESM and the CNO prevents the system from reaching a stable equilibrium. Therefore, neither the IESM nor the CNO can achieve an evolutionarily stable strategy.
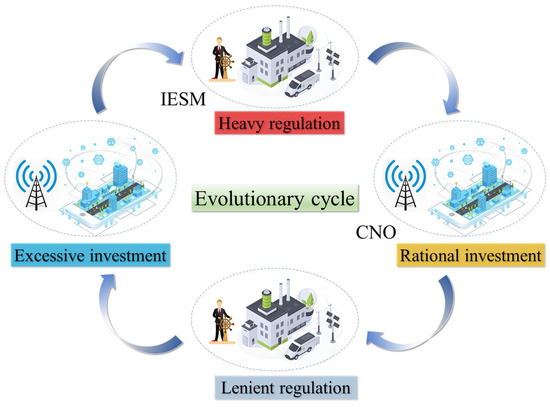
Figure 3.
The cyclical trap between the IESM and the CNO.
Case 8: , , , . The points and are unstable, while is a saddle point. The points and are evolutionarily stable strategies. These characteristics of the equilibrium points imply that two distinct evolutionary pathways exist in this case, as illustrated in Figure 4. The coordinates of points O, A, B, C, and D are , , , , and , respectively. One evolutionary path starts from the unstable points A or C, passes through the saddle point D, and culminates at the stable point O. The other path begins at unstable points A or C, proceeds via saddle point D, and ends at the stable point B.
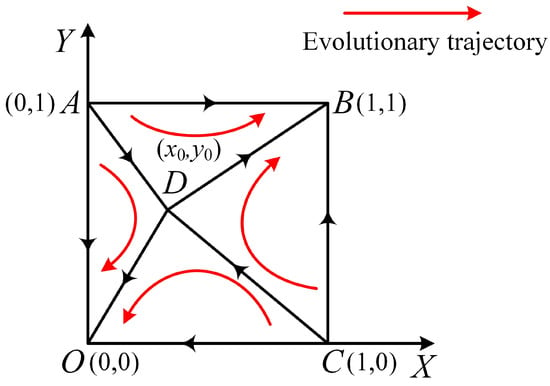
Figure 4.
The evolutionary phase diagram of the IESM and the CNO.
If the initial decision coordinate of the CNO and the IESM is within the region , their evolutionary trajectory will progressively converge to point . This convergence indicates that the IESM will adopt a lenient regulatory strategy, while the CNO will excessive pursue investment. Conversely, if the initial decision coordinate is within region , their evolutionary path will converge to point . This outcome suggests that the evolutionarily stable strategies for the CNO and the IESM are rational investment and strict regulation, respectively. Therefore, expanding the area of region is crucial for the CNO to make rational investments in information transmission assets under a strict regulatory strategy. This approach ensures the fairness and reasonableness of information transmission pricing, thereby promoting an increase in social welfare. The stability of each equilibrium point in Cases 6–8 is detailed in Table 7.

Table 7.
Stability of each equilibrium point in Cases 6–8.
Through systematic analysis, the stability-behavior mapping relationships of typical equilibrium points can be derived, as summarized in Table 8. The above equilibrium analysis reveals a fundamental systemic flaw in the current regulatory framework: Establishing asset valuation criteria solely based on “business relevance” forces the market into a dilemma. Either CNOs overinvest to maximize returns, thereby inflating information transmission costs, or IESMs must intensify oversight, exacerbating administrative expenditures. This inherent contradiction stems from existing regulations’ inability to establish a stable market equilibrium. Allowing operators to incorporate redundant assets into cost calculations incentivizes excessive investment. This mechanism mirrors counterproductive policies such as “linking highway toll revenues to lane quantity”, which inadvertently encourage redundant infrastructure expansion. To address this, this study proposes adopting the “asset utilization rate” as a pivotal regulatory metric—for instance, requiring a minimum 85% utilization rate for communication equipment to qualify for cost inclusion. Such measures could reduce overinvestment incentives while preserving regulatory efficacy.

Table 8.
Stability characteristics of equilibrium points and behavioral impacts.
4. Case Study
Through comprehensive evolutionary game analysis across multiple case scenarios, the optimal evolutionary outcome for the CNO-IESM system is identified as follows: the CNO adopts rational investment strategies, while the IESM implements strict regulatory measures. This Pareto-optimal configuration corresponds to the equilibrium point , which satisfies the criteria for an evolutionarily stable strategy. Notably, under the parameter conditions specified in Case 6, this ideal evolutionary state is asymptotically stable and globally accessible. However, Case 8 presents a more complex dynamic: while the ideal state remains theoretically attainable as a local attractor, the system’s basin of attraction may favor convergence toward the suboptimal equilibrium . This divergence between theoretical predictions and actual evolutionary trajectories necessitates rigorous numerical investigation. The numerical simulation in this section encompasses three key aspects: fundamental evolutionary path analysis, parameter synergistic effect investigation, and critical sensitivity detection.Through multidimensional parameter space exploration, these simulations systematically reveal the evolutionary patterns of the system. The numerical simulations are implemented in MATLAB 2023a on a PC equipped with Intel i7-7700HQ 2.8 GHz CPU and 32 GB RAM, utilizing the Parallel Computing Toolbox to leverage multi-threaded architecture for enhanced computational throughput. In addition, the replicator dynamic equations are numerically solved by ODE45 Function in MATLAB using the fourth-order Runge–Kutta method with time step .
4.1. Simulations Based on Case 8
4.1.1. The Dynamic Impact of Initial Strategy Values on Evolutionary Results
To explore the dynamic behavior of the system under the conditions of Case 8, we set the relevant parameters to meet the specified conditions. The initial strategy values of the CNO and the IESM are chosen as , , , , , and , respectively. These values were strategically chosen to span diverse initial configurations for both agents, encompassing both peripheral and core areas of the strategy space, enabling systematic investigation of the sensitivity of evolutionary trajectories to initial strategy distributions. The dynamic evolution of the strategy choices of both parties over time is illustrated in Figure 5, which shows how the strategies evolve from these initial values towards the equilibrium points.
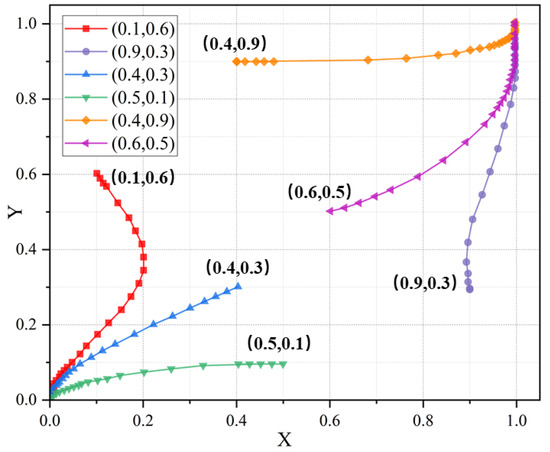
Figure 5.
Dynamic evolution process under different initial strategy values of both parties.
As illustrated in Figure 5, within the framework of evolutionary game theory, the evolutionarily stable outcomes exhibit significant heterogeneity depending on the initial strategy configurations of the participants. Specifically, when the initial strategy values of both parties fall within the region in Figure 4, the system evolves toward the stable point , corresponding to the strategy combination of (overinvestment, lenient regulation) for both the CNO and the IESM. Conversely, when the initial values are situated within the region, the evolutionary outcome stabilizes at point , with the corresponding strategy combination shifting to (rational investment, strict regulation). These observations are consistent with the predictions regarding Case 8 from the preceding theoretical discussion, confirming that the initial strategy values play a pivotal role in determining the system’s evolutionary trajectory and ultimate stable state. Given these findings, the theory provides a scientific basis for policymakers to consider initial conditions in strategic planning. Policymakers can leverage this understanding to adjust relevant parameters in order to expand region. By doing so, they can encourage the CNO to make rational investments under strict regulation, ensure the fairness of information transmission pricing, and thereby enhance social welfare.
4.1.2. The Impact of Parameter on Evolutionary Results
The parameter denotes the excess fixed-asset revenue-generating provisioning ratio set by the IESM, which is determined based on the efficiency of the CNO’s asset utilization. To investigate the impact of varying values on the evolutionary paths of strategies for the CNO and the IESM, we conducted simulations with set to 0.07, 0.08, and 0.09 while keeping the initial strategy values constant at . The selection of vaules (0.07–0.09) is empirically grounded in cross-sector regulatory precedents and telecommunications-specific operational benchmarks. For instance, ROI-based regulations in the U.S. energy sector typically cap non-productive assets at 5–10% of total investments. Moreover, Bauer et al. [15] mentioned as a regulatory equilibrium parameter to model telecommunication infrastructure regulation, balancing operator profitability and consumer welfare. The results of these simulations are illustrated in Figure 6.
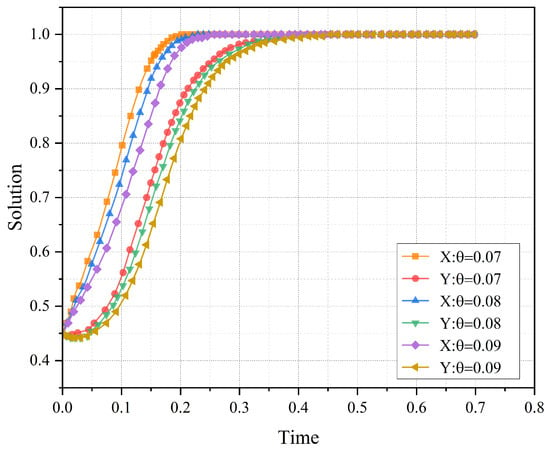
Figure 6.
The impact of varying values on the evolutionary paths for the CNO and the IESM.
Figure 6 clearly demonstrates the significant impact of parameter on the dynamic evolution of strategies for both players. As decreases from 0.09 to 0.07, the rates at which the CNO and the IESM evolve towards the ideal strategy combination of (rational investment, strict regulation) noticeably accelerate. This trend is illustrated in Figure 6, where the evolutionary curves rapidly converge towards the point as decreases. This result reveals the pivotal role of parameter in modulating evolutionary dynamics of the system. Specifically, acts as a regulatory lever that influences the speed at which both players adapt their strategies to reach the desired equilibrium.
By adjusting the parameter , the CNO and the IESM can optimize their strategic choices and response velocities. Such strategic adjustments are crucial for rapidly adapting to changes in the regulatory environment and market dynamics. This finding underscores the importance of as a key parameter in strategic planning and regulatory policy design, providing both the CNO and the IESM with a significant operational lever to enhance their adaptability and efficiency in a dynamic market.
4.1.3. The Impact of Allowed Rate of Return on Evolutionary Outcomes
Figure 7 illustrates the impact of the allowed rate of return on the dynamic evolution of strategies for the CNO and the IESM. In the simulations, is set to 0.1, 0.2, and 0.3, with the initial strategy values . The values of ranging from 0.1 to 0.3 span empirically validated thresholds from regulated Return On Equity (ROE) benchmarks to high-risk infrastructure financing. This interval aligns with FERC-approved returns of 8–12% for U.S. electricity distribution [27] and accommodates 18–25% private investor demand in unregulated 5G deployment, ensuring policy relevance across regulatory paradigms [28]. As shown in Figure 7, it can be noted that as the allowed rate of return increases, the evolutionary pace of the CNO and the IESM towards the ideal strategy combination of rational investment and strict regulation tends to decelerate. Particularly when rises from 0.2 to 0.3, the CNO is more inclined to opt for overinvestment strategies, while the IESM is more prone to adopt lenient regulatory policies.
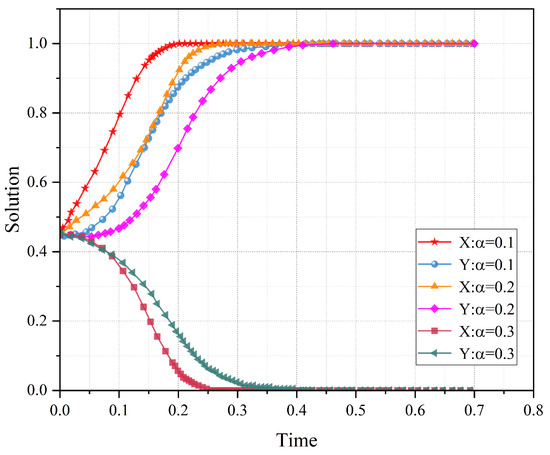
Figure 7.
The impact of parameter on the dynamic evolution process.
This phenomenon underscores the delicate balance that the IESM must maintain when setting the allowed rate of return. Specifically, the IESM needs to ensure that the CNO’s investment costs are reasonably compensated while promoting moderate profits to incentivize a shift towards rational investment strategies. At the same time, the IESM must guide the implementation of more effective regulatory policies to prevent excessive investment and ensure the fairness of information transmission pricing. This balance is crucial for enhancing social welfare and ensuring the long-term stability of the regulatory environment.
4.1.4. Multi-Parameter Co-Evolution and Critical Analysis of Phase Transitions
In Section 4.1.2 and Section 4.1.3, we respectively revealed the independent regulatory effects of individual parameters and on evolutionary game dynamics. However, real-world regulatory systems often exhibit synergistic parameter effects that transcend linear superposition of single variables, demonstrating complex nonlinear interactions. This section investigates the coupled impacts of multi-parameter co-evolution on regulatory strategy convergence pathways through extended replicator dynamics equations, employing global scanning and dynamic simulations across the - joint parameter space, and the convergence probability was calculated using a modified sigmoid response surface model. The initial strategy values . We systematically construct a three-dimensional evolutionary phase diagram through coordinated parameter scanning across the joint - space (, ), with the resultant synergistic regulatory landscape visualized in Figure 8.
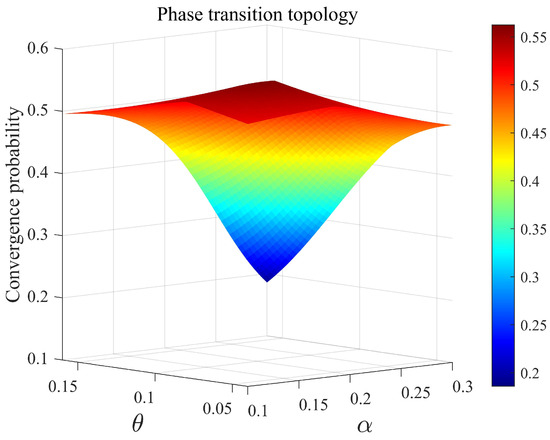
Figure 8.
Phase transition probability gradient response surface under - synergistic effects.
Figure 8 reveals the nonlinear dynamic characteristics of regulatory games under - synergy. The three-dimensional surface morphology identifies two distinct phase regions: in the blue low-probability zone where and , the system converges to low regulatory-efficiency equilibria with probabilities exceeding 85%, while in the red high-probability zone with and , the probability of strategy convergence to ideal equilibrium states surpasses 92%. Notably, the surface exhibits steep gradient transitions (yellow-green transition belt) within and intervals, marking critical thresholds for system phase transitions.
The seemingly contradictory results between - co-evolution and single-parameter evolutionary trends are indeed explainable. The low convergence probability in the blue zone (, ) stems from dual suppression effects. Low weakens IESM’ capacity to identify redundant assets, leading to failed regulatory deterrence, while low constricts the baseline profit space for corporate compliance investments. Their synergy creates a “low-incentive–low-return” trap that stabilizes the system at the non-ideal equilibrium. In the red zone (, ), high establishes rigid constraints through precise identification of redundant assets, whereas high amplifies the explicit returns of compliance investments. Their coordinated breakthrough induces growth in net compliance returns, forming a “high-threshold–high-return” positive selection mechanism that drives the system toward equilibrium. The - interaction reveals that single-parameter linear control logic becomes restructured in biparametric space, with system stability governed by the - product threshold rather than individual critical values.
As shown in Figure 8, a steep gradient transition zone (yellow-green transition belt) exists within the intervals of and . To analyze the characteristics of this region, sensitivity analysis was performed by fixing at 0.2, and the critical points were identified using the steep region of the logistic function, with regions exhibiting slopes demarcating phase transition intervals of system states. As illustrated in Figure 9, the system’s convergence probability exhibits a nonlinear negative correlation with the parameter , demonstrating a critical sensitivity transition at . Within the interval , the curve shows a steep descending segment with a marked slope of , indicating a phase transition critical point in the system. When exceeds 0.11, the convergence probability sharply declines from 0.8 to 0.4, a decrease of 50%. This result reveals how minor parameter shifts can trigger systemic instability, providing quantitative evidence for mitigating critical risks in regulation design.
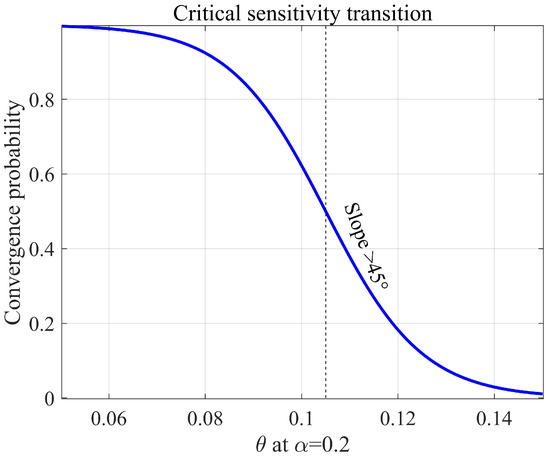
Figure 9.
Critical sensitivity transition analysis ( = 0.2).
4.2. Simulation Based on Case 7
In the preceding theoretical analysis, Case 7 was identified as a special case where both players might become trapped in a cyclical dilemma, preventing the achievement of a stable evolutionary state. This cyclical dilemma refers to a situation where the strategies of both players oscillate over time without converging to a stable equilibrium. To validate this theoretical prediction, this section conducts simulation experiments under the conditions that satisfy Case 7. The initial strategy values for the CNO and the IESM are set at and , respectively. under the conditions that satisfy Case 7. The evolutionary trends of both players are depicted in Figure 10, which illustrates the oscillatory behavior of their strategies over time.
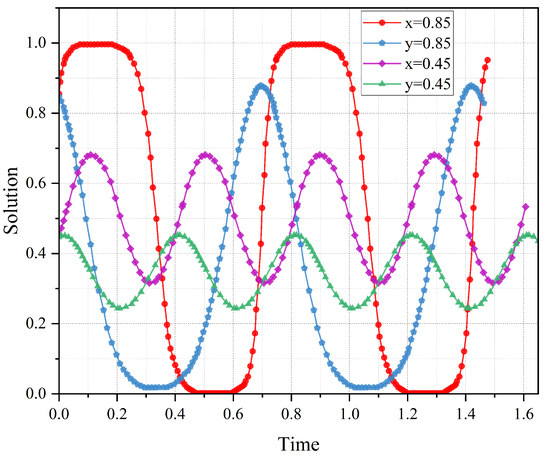
Figure 10.
The evolutionary trends of the IESM and the CNO in Case 7.
Figure 10 clearly demonstrates that the strategic dynamics between the CNO and the IESM does not converge towards any evolutionarily stable strategy but instead falls into a cyclical trap. Specifically, when the IESM adopts a strict regulatory policy, the CNO responds with rational investment. However, once the IESM becomes aware that the CNO has made rational investments, he shifts towards lenient regulation. This policy relaxation then leads the CNO back to overinvestment strategies. This repetitive pattern of strategic interaction creates a cyclical trap, where neither party can achieve a stable equilibrium. The simulation results validate this pattern, confirming the predicted cyclical state of strategies in Case 7 as discussed in the preceding theoretical analysis.
To avoid falling into this infinite loop of non-stable states, the IESM must carefully consider the formulation of regulatory policies. Specifically, the IESM should avoid setting parameter values that meet the conditions of Case 7. By doing so, the IESM can prevent the emergence of the cyclical trap and ensure the effectiveness and sustainability of regulatory policies. This approach is crucial for maintaining a stable regulatory environment and promoting rational investment behaviors by the CNO.
5. Conclusions
This study establishes an evolutionary game-theoretic framework to examine pricing mechanisms in information transmission regulation within IESs. The strategic interactions between the CNO and the IESM are modeled as bounded rational agents, systematically probing the dynamic equilibrium formation process under conditions of incomplete information. The influence of critical parameters, including initial strategy distributions, regulatory return thresholds, and system sensitivity coefficients, on convergence toward evolutionarily stable strategies is characterized through replicator dynamic equations and stability analysis. The main conclusions are listed as follows:
- Single-parameter analysis reveals that when decreases below 0.11, the convergence speed of the CNO’s rational investment strategies increases by 40%, validating the effectiveness of asset utilization constraints. Conversely, when exceeds 0.2, the probability of the system reaching ideal equilibrium plummets by 58%, indicating that high return rates inhibit regulatory efficacy. Dual-parameter synergy studies demonstrate that 4 combined with forms a “high-threshold, high-return” mechanism, while and trigger a “low-incentive trap”. A steep phase transition gradient is observed within and intervals. These results necessitate establishing a product threshold dynamic regulation mechanism to overcome single-parameter optimization limitations.
- Under the current regulatory framework, there is no evolutionarily stable equilibrium between the CNO and the IESM with strategies of (rational investment, lenient regulation). The existing policies, which primarily rely on the relevance to the information transmission process to define allowable costs and effective assets, can not provide sufficient incentives for the CNO to engage in rational investment strategies under lenient regulatory conditions. As a result, the CNO continues to engage in excessive investment, leading to an increase in information transmission prices. These increased costs are then passed on to users, resulting in a loss of social welfare.
- To accurately delineate effective assets and determine allowable costs, the criteria should be refined using the degree of asset utilization as a key metric. This ensures only efficiently utilized assets are considered effective, preventing underutilized assets from being included in cost calculations. This approach leads to a more precise determination of allowable costs, crucial for curbing the CNO’s excessive investment behavior by reducing incentives for over-provisioning non-contributory assets.
For the sake of model simplification, taxes were not included in the calculation of allowable income despite being a key component of allowable income. This omission may compromise the accuracy of the model in reflecting the actual game context. Therefore, this paper will further deepen the extensibility of the theoretical framework by systematically integrating tax policy leverage, multi-operator competition mechanisms, and the evolution of next-generation communication technologies, such as quantifying the threshold effects of fiscal tools on evolutionary equilibria and revealing the nonlinear impacts of market competition intensity on pricing strategy stability. Furthermore, building upon the foundational framework established in this study, subsequent research will systematically incorporate the impacts of network slicing-specific technical parameters (e.g., isolation mechanisms, Quality of Service (QoS) constraints) into the model, which will ultimately form a “policy–market–technology” tripartite synergy-driven analytical architecture, providing a theoretical foundation for constructing regulatory frameworks that adapt to the complex ecosystem of new integrated energy systems.
Author Contributions
K.C.: Investigation, Software, Visualization, and Writing—Original Draft. M.C.: Conceptualization, Resources, and Supervision. Y.Z.: Conceptualization, Methodology, and Resources. Z.L.: Conceptualization, Investigation, and Funding Acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grants U24A20268, 62222205, and 62373162 and the Natural Science Foundation of Hubei Province of China under Grant 2022CFA052.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IES | Integrated Energy System |
| NS | Network Slicing |
| VPP | Virtual Power Plant |
| SAC | Smart Agent Communication |
| D2D | Device-to-Device |
| ROI | Return on Investment |
| PCR | Price-Cap Regulation |
| THz | Terahertz |
| RAN | Radio Access Network |
| TransN | Transmission Networking |
| CoreN | Core Network |
| AMF | Access and Mobility Management Function |
| UPF | User Plane Function |
| UDM | Unified Data Management |
| IESM | Integrated Energy System Manager |
| CNO | Communication Network Operator |
| EP | Equilibrium Point |
| ESS | Evolutionarily Stable Strategy |
| SP | Saddle Point |
| CS | Central Point |
| QoS | Quality of Service |
| ROE | Return On Equity |
References
- Aghdam, F.H.; Mudiyanselage, M.W.; Mohammadi-Ivatloo, B.; Marzband, M. Optimal scheduling of multi-energy type virtual energy storage system in reconfigurable distribution networks for congestion management. Appl. Energy 2023, 333, 120569. [Google Scholar] [CrossRef]
- Ren, Z.; Li, H.; Xu, Y.; Li, W.; Li, Z.; Dai, Y. A radial-grouping-based planning method for electrical collector systems in tidal current generation farms. Renew. Energy 2021, 165, 632–641. [Google Scholar] [CrossRef]
- Pu, Y.; Li, Q.; Luo, S.; Chen, W.; Breaz, E.; Gao, F. Peer-to-Peer electricity-hydrogen trading among integrated energy systems considering hydrogen delivery and transportation. IEEE Trans. Power Syst. 2024, 39, 3895–3911. [Google Scholar] [CrossRef]
- Gungor, V.C.; Sahin, D.; Kocak, T.; Ergut, S.; Buccella, C.; Cecati, C.; Hancke, G.P. Smart grid technologies: Communication technologies and standards. IEEE Trans. Ind. Inform. 2011, 7, 529–539. [Google Scholar] [CrossRef]
- Habibi, M.A.; Han, B.; Fellan, A.; Jiang, W.; Sanchez, A.G.; Pavon, I.L.; Boubendir, A.; Schotten, H.D. Toward an open, intelligent, and end-to-end architectural framework for network slicing in 6G communication systems. IEEE Open J. Commun. Soc. 2023, 4, 1615–1658. [Google Scholar] [CrossRef]
- He, Y.; Ye, X.; Cui, L.; Fournier-Viger, P.; Luo, C.; Huang, J.Z.; Suganthan, P.N. Wireless network slice assignment with incremental random vector functional link network. IEEE Trans. Netw. Sci. Eng. 2023, 10, 1283–1296. [Google Scholar] [CrossRef]
- Kong, P.-Y.; Song, Y. Joint consideration of communication network and power grid topology for communications in community smart grid. IEEE Trans. Ind. Inform. 2020, 16, 2895–2905. [Google Scholar] [CrossRef]
- Feng, C.; Chen, Q.; Wang, Y.; Ma, J.; Wang, X. Frequency regulation service provision for virtual power plants through 5G RAN slicing. IEEE Trans. Smart Grid 2022, 13, 4943–4956. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Ma, Z.; Liu, X.; Ma, J. LiPSG: Lightweight Privacy-Preserving Q-Learning-Based energy management for the IoT-Enabled smart grid. IEEE Internet Things J. 2020, 7, 3935–3947. [Google Scholar] [CrossRef]
- Zhou, B.; Zou, J.; Chung, C.Y.; Wang, H.; Liu, N.; Voropai, N.; Xu, D. Multi-microgrid energy management systems: Architecture, communication, and scheduling strategies. J. Mod. Power Syst. Clean Energy 2021, 9, 463–476. [Google Scholar] [CrossRef]
- Li, G.; Bie, Z.; Kou, Y.; Jiang, J.; Bettinelli, M. Reliability evaluation of integrated energy systems based on smart agent communication. Appl. Energy 2016, 167, 397–406. [Google Scholar] [CrossRef]
- Deng, R.; Xiao, G.; Lu, R.; Liang, H.; Vasilakos, A.V. False data injection on state estimation in power systems—Attacks, impacts, and defense: A survey. IEEE Trans. Ind. Inform. 2017, 13, 411–423. [Google Scholar] [CrossRef]
- Li, Z.; Shahidehpour, M.; Aminifar, F. Cybersecurity in distributed power systems. Proc. IEEE 2017, 105, 1367–1388. [Google Scholar] [CrossRef]
- Kong, P.-Y. Effects of communication network performance on dynamic pricing in smart power grid. IEEE Syst. J. 2014, 8, 533–541. [Google Scholar] [CrossRef]
- Bauer, J.M.; Bohlin, E. Regulation and innovation in 5G markets. Telecommun. Policy 2022, 46, 102260. [Google Scholar] [CrossRef]
- Laffont, J.J.; Tirole, J. Competition in Telecommunications; MIT Press: Cambridge, MA, USA, 2000; pp. 9–16. [Google Scholar]
- Viscusi, W.K.; Harrington, J.E., Jr.; Sappington, D.E.M. Economics of Regulation and Antitrust; MIT Press: Cambridge, MA, USA, 2018; pp. 43–52. [Google Scholar]
- Averch, H.; Johnson, L.L. Behavior of the firm under regulatory Constraint. Am. Econ. Rev. 1962, 52, 1052–1069. [Google Scholar]
- Sappington, D.E.M.; Weisman, D.L. Price cap regulation: What have we learned from 25 years of experience in the telecommunications industry? J. Regul. Econ. 2010, 38, 227–257. [Google Scholar] [CrossRef]
- Braeutigam, R.R.; Panzar, J.C. Effects of the change from rate-of-return to price-cap regulation. Am. Econ. Rev. 1993, 83, 191–198. [Google Scholar]
- Esplin, R.; Davis, B.; Rai, A.; Nelson, T. The impacts of price regulation on price dispersion in Australia’s retail electricity markets. Energy Policy 2020, 147, 111829. [Google Scholar] [CrossRef]
- Nippa, M.; Patnaik, S.; Taussig, M. MNE responses to carbon pricing regulations: Theory and evidence. J. Int. Bus. Stud. 2021, 52, 904–929. [Google Scholar] [CrossRef]
- Lima, J.W.M.; Noronha, J.C.C.; Arango, H.; Dos Santos, P.E.S. Distribution pricing based on yardstick regulation. IEEE Trans. Power Syst. 2002, 17, 198–204. [Google Scholar] [CrossRef]
- Rudnick, H.; Donoso, J.A. Integration of price cap and yardstick competition schemes in electrical distribution regulation. IEEE Trans. Power Syst. 2000, 15, 1428–1433. [Google Scholar] [CrossRef]
- Dang, S.; Amin, O.; Shihada, B.; Alouini, M.S. What should 6G be? Nat. Electron. 2020, 3, 20–29. [Google Scholar] [CrossRef]
- Yang, P.; Xiao, Y.; Xiao, M.; Li, S. 6G wireless communications: Vision and potential techniques. IEEE Netw. 2019, 33, 70–75. [Google Scholar] [CrossRef]
- Federal Energy Regulatory Commission (FERC). Order No. 888: Promoting Wholesale Competition Through Open Access Nondiscriminatory Transmission Services by Public Utilities; Docket No. RM95-8-000; Federal Energy Regulatory Commission: Washington, DC, USA, 1996. [Google Scholar]
- GSMA Intelligence. The Mobile Economy 2022; GSM Association: London, UK, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).