Electrochemical Analysis of Carbon-Based Supercapacitors Using Finite Element Modeling and Impedance Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Cell Manufacturing
2.2. Experimental Setups
2.3. Finite Element Model (FEM)
3. Results and Discussion
3.1. Experimental Results
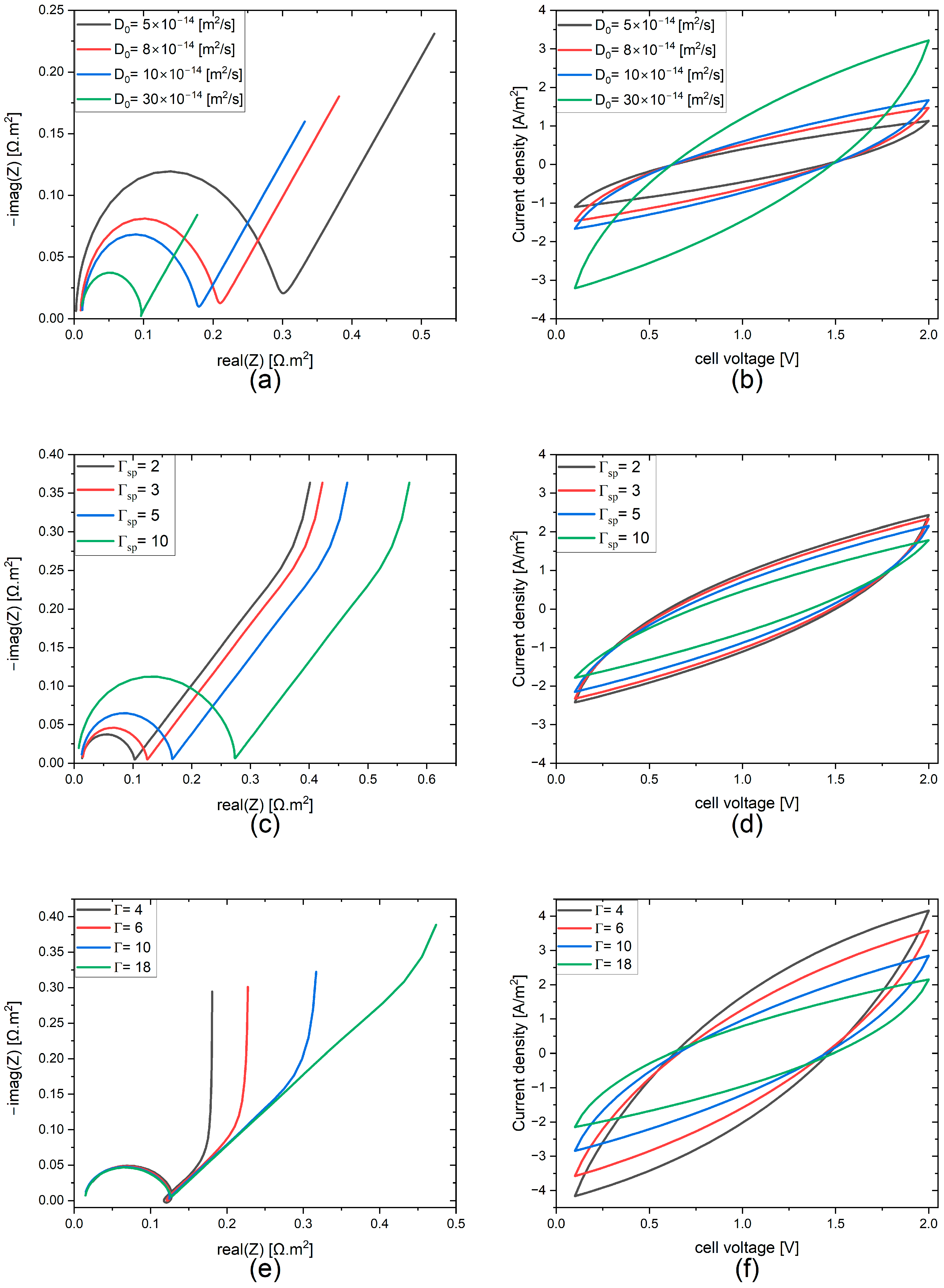
3.2. FEM Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Activated Carbon |
| CNTs | Carbon Nanotubes |
| CV | Cyclic Voltammetry |
| EC | Equivalent Circuit |
| EDL | Electric Double Layer |
| EDLC | Electric Double Layer Capacitor |
| EIS | Impedance Spectroscopy |
| EV | Electric Vehicle |
| FEM | Finite Element Modeling |
| G | Graphite |
| HESS | Hybrid Energy Storage System |
| IL | Ionic Liquid |
| LIB | Lithium-Ion Battery |
| MD | Molecular Dynamics |
| MPNP | Modified Poisson–Nernst–Planck |
| OCV | Open Circuit Voltage |
| PDE | Partial Differential Equations |
| PNP | Poisson–Nernst–Planck |
| SSA | Specific Surface Area |
| SC | Supercapacitor |
References
- Chen, N.; Zhang, H.; Li, L.; Chen, R.; Guo, S. Ionogel Electrolytes for High-Performance Lithium Batteries: A Review. Adv. Energy Mater. 2018, 8, 1702675. [Google Scholar] [CrossRef]
- Chen, G.Z. Supercapacitor and supercapattery as emerging electrochemical energy stores. Int. Mater. Rev. 2017, 62, 173–202. [Google Scholar] [CrossRef]
- Dutta, S.; Bhaumik, A.; Wu, K.C.-W. Hierarchically porous carbon derived from polymers and biomass: Effect of interconnected pores on energy applications. Energy Environ. Sci. 2014, 7, 3574–3592. [Google Scholar] [CrossRef]
- Patel, M.R.; Beik, O. Wind and Solar Power Systems: Design, Analysis, and Operation, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2021; ISBN 9780367476939. [Google Scholar]
- Liu, Y.; Fan, L.-Z.; Jiao, L. Graphene intercalated in graphene-like MoS2: A promising cathode for rechargeable Mg batteries. J. Power Sources 2017, 340, 104–110. [Google Scholar] [CrossRef]
- Burke, A. Ultracapacitors: Why, how, and where is the technology. J. Power Sources 2000, 91, 37–50. [Google Scholar] [CrossRef]
- Brodd, R.J.; Bullock, K.R.; Leising, R.A.; Middaugh, R.L.; Miller, J.R.; Takeuchi, E. Batteries, 1977 to 2002. J. Electrochem. Soc. 2004, 151, K1. [Google Scholar] [CrossRef]
- Kötz, R.; Carlen, M. Principles and applications of electrochemical capacitors. Electrochim. Acta 2000, 45, 2483–2498. [Google Scholar] [CrossRef]
- Ahsan, M.B.F.; Mekhilef, S.; Soon, T.K.; Mubin, M.B.; Shrivastava, P.; Seyedmahmoudian, M. Lithium-ion battery and supercapacitor-based hybrid energy storage system for electric vehicle applications: A review. Int. J. Energy Res. 2022, 46, 19826–19854. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, N. Supercapacitors Performance Evaluation. Adv. Energy Mater. 2015, 5, 1401401. [Google Scholar] [CrossRef]
- Bokhari, S.W.; Siddique, A.H.; Sherrell, P.C.; Yue, X.; Karumbaiah, K.M.; Wei, S.; Ellis, A.V.; Gao, W. Advances in graphene-based supercapacitor electrodes. Energy Rep. 2020, 6, 2768–2784. [Google Scholar] [CrossRef]
- Shchegolkov, A.V.; Lipkin, M.S.; Semenkova, A. Application of carbon nanotubes produced by CVD-method for supercapacitor with LiPF6-based electrolyte. Vopr. Materialoved. 2022, 64–76. [Google Scholar] [CrossRef]
- Zhang, P.; Fan, J.; Wang, Y.; Dang, Y.; Heumann, S.; Ding, Y. Insights into the role of defects on the Raman spectroscopy of carbon nanotube and biomass-derived carbon. Carbon 2024, 222, 118998. [Google Scholar] [CrossRef]
- Elmouwahidi, A.; Bailón-García, E.; Romero-Cano, L.A.; Zárate-Guzmán, A.I.; Pérez-Cadenas, A.F.; Carrasco-Marín, F. Influence of Surface Chemistry on the Electrochemical Performance of Biomass-Derived Carbon Electrodes for its Use as Supercapacitors. Materials 2019, 12, 2458. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.S.; Abbas, M.A.; Kang, M.S.; Kyung, H.; Bang, J.H.; Yoo, W.C. Study of the structure-properties relations of carbon spheres affecting electrochemical performances of EDLCs. Electrochim. Acta 2019, 304, 210–220. [Google Scholar] [CrossRef]
- Zhang, K.; Sun, J.; E, L.; Ma, C.; Luo, S.; Wu, Z.; Li, W.; Liu, S. Effects of the Pore Structure of Commercial Activated Carbon on the Electrochemical Performance of Supercapacitors. J. Energy Storage 2022, 45, 103457. [Google Scholar] [CrossRef]
- Epstein, N. On tortuosity and the tortuosity factor in flow and diffusion through porous media. Chem. Eng. Sci. 1989, 44, 777–779. [Google Scholar] [CrossRef]
- Nemani, V.P.; Harris, S.J.; Smith, K.C. Design of Bi-Tortuous, Anisotropic Graphite Anodes for Fast Ion-Transport in Li-Ion Batteries. J. Electrochem. Soc. 2015, 162, A1415–A1423. [Google Scholar] [CrossRef]
- Suthar, B.; Landesfeind, J.; Eldiven, A.; Gasteiger, H.A. Method to Determine the In-Plane Tortuosity of Porous Electrodes. J. Electrochem. Soc. 2018, 165, A2008–A2018. [Google Scholar] [CrossRef]
- Leyva-García, S.; Lozano-Castelló, D.; Morallón, E.; Vogl, T.; Schütter, C.; Passerini, S.; Balducci, A.; Cazorla-Amorós, D. Electrochemical performance of a superporous activated carbon in ionic liquid-based electrolytes. J. Power Sources 2016, 336, 419–426. [Google Scholar] [CrossRef]
- Tsai, W.-Y.; Lin, R.; Murali, S.; Li Zhang, L.; McDonough, J.K.; Ruoff, R.S.; Taberna, P.-L.; Gogotsi, Y.; Simon, P. Outstanding performance of activated graphene based supercapacitors in ionic liquid electrolyte from −50 to 80 °C. Nano Energy 2013, 2, 403–411. [Google Scholar] [CrossRef]
- Sato, T.; Masuda, G.; Takagi, K. Electrochemical properties of novel ionic liquids for electric double layer capacitor applications. Electrochim. Acta 2004, 49, 3603–3611. [Google Scholar] [CrossRef]
- Xu, N.; Klein, J.M.; Huang, P.; Alwusaydi, H.A.; Mann, E.K.; Gurkan, B.E. Improved accessibility of porous carbon electrodes with surfactant ionic liquids for supercapacitors. J. Appl. Electrochem. 2019, 49, 151–162. [Google Scholar] [CrossRef]
- Perdana, M.Y.; Johan, B.A.; Abdallah, M.; Hossain, M.E.; Aziz, M.A.; Baroud, T.N.; Drmosh, Q.A. Understanding the Behavior of Supercapacitor Materials via Electrochemical Impedance Spectroscopy: A Review. Chem. Rec. 2024, 24, e202400007. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.S.; Dickinson, E.J.; Heins, T.P.; Park, J.; Gaberšček, M.; Lee, Y.Y.; Heinrich, M.; Ruiz, V.; Napolitano, E.; Kauranen, P.; et al. Comparison of methodologies to estimate state-of-health of commercial Li-ion cells from electrochemical frequency response data. J. Power Sources 2022, 542, 231814. [Google Scholar] [CrossRef]
- Al-Zubaidi R-Smith, N.; Leitner, M.; Alic, I.; Toth, D.; Kasper, M.; Romio, M.; Surace, Y.; Jahn, M.; Kienberger, F.; Ebner, A.; et al. Assessment of lithium ion battery ageing by combined impedance spectroscopy, functional microscopy and finite element modelling. J. Power Sources 2021, 512, 230459. [Google Scholar] [CrossRef]
- Sánchez-Romate, X.F.; Del Bosque, A.; Artigas-Arnaudas, J.; Muñoz, B.K.; Sánchez, M.; Ureña, A. A proof of concept of a structural supercapacitor made of graphene coated woven carbon fibers: EIS study and mechanical performance. Electrochim. Acta 2021, 370, 137746. [Google Scholar] [CrossRef]
- Catelani, M.; Ciani, L.; Corti, F.; Laschi, M.; Patrizi, G.; Reatti, A.; Vangi, D. Experimental Characterization of Hybrid Supercapacitor Under Different Operating Conditions Using EIS Measurements. IEEE Trans. Instrum. Meas. 2024, 73, 1–10. [Google Scholar] [CrossRef]
- Kötz, R.; Hahn, M.; Gallay, R. Temperature behavior and impedance fundamentals of supercapacitors. J. Power Sources 2006, 154, 550–555. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.-S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- Kasper, M.; Leike, A.; Thielmann, J.; Winkler, C.; Al-Zubaidi R-Smith, N.; Kienberger, F. Electrochemical impedance spectroscopy error analysis and round robin on dummy cells and lithium-ion-batteries. J. Power Sources 2022, 536, 231407. [Google Scholar] [CrossRef]
- Burt, R.; Birkett, G.; Zhao, X.S. A review of molecular modelling of electric double layer capacitors. Phys. Chem. Chem. Phys. 2014, 16, 6519–6538. [Google Scholar] [CrossRef] [PubMed]
- Georgi, N.; Kornyshev, A.A.; Fedorov, M.V. The anatomy of the double layer and capacitance in ionic liquids with anisotropic ions: Electrostriction vs. lattice saturation. J. Electroanal. Chem. 2010, 649, 261–267. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, J.; Zhao, H.; Sumpter, B.G.; Qiao, R. Dynamics of electrical double layer formation in room-temperature ionic liquids under constant-current charging conditions. J. Phys. Condens. Matter 2014, 26, 284109. [Google Scholar] [CrossRef]
- Merlet, C.; Rotenberg, B.; Madden, P.A.; Taberna, P.-L.; Simon, P.; Gogotsi, Y.; Salanne, M. On the molecular origin of supercapacitance in nanoporous carbon electrodes. Nat. Mater. 2012, 11, 306–310. [Google Scholar] [CrossRef] [PubMed]
- Højgaard Olesen, L.; Bazant, M.Z.; Bruus, H. Strongly nonlinear dynamics of electrolytes in large ac voltages. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010, 82, 11501. [Google Scholar] [CrossRef] [PubMed]
- Pilon, L.; Wang, H.; d’Entremont, A. Recent Advances in Continuum Modeling of Interfacial and Transport Phenomena in Electric Double Layer Capacitors. J. Electrochem. Soc. 2015, 162, A5158–A5178. [Google Scholar] [CrossRef]
- Satpathy, S.; Misra, N.K.; Shukla, D.k.; Goyal, V.; Bhattacharyya, B.K.; Yadav, C.S. An in-depth study of the electrical characterization of supercapacitors for recent trends in energy storage system. J. Energy Storage 2023, 57, 106198. [Google Scholar] [CrossRef]
- Maria Lozito, G.; Intravaia, M.; Corti, F.; Patrizi, G.; Laschi, M.; Ciani, L.; Vangi, D.; Reatti, A. Equivalent Circuit Modelling of Hybrid Supercapacitors Through Experimental Spectroscopic Measurements. IEEE Access 2024, 12, 78449–78462. [Google Scholar] [CrossRef]
- Wang, H.; Pilon, L. Intrinsic limitations of impedance measurements in determining electric double layer capacitances. Electrochim. Acta 2012, 63, 55–63. [Google Scholar] [CrossRef]
- Lian, C.; Jiang, D.; Liu, H.; Wu, J. A Generic Model for Electric Double Layers in Porous Electrodes. J. Phys. Chem. C 2016, 120, 8704–8710. [Google Scholar] [CrossRef]
- Mei, B.-A.; Munteshari, O.; Lau, J.; Dunn, B.; Pilon, L. Physical Interpretations of Nyquist Plots for EDLC Electrodes and Devices. J. Phys. Chem. C 2018, 122, 194–206. [Google Scholar] [CrossRef]
- Aderyani, S.; Flouda, P.; Shah, S.A.; Green, M.J.; Lutkenhaus, J.L.; Ardebili, H. Simulation of cyclic voltammetry in structural supercapacitors with pseudocapacitance behavior. Electrochim. Acta 2021, 390, 138822. [Google Scholar] [CrossRef]
- Mei, B.-A.; Lau, J.; Lin, T.; Tolbert, S.H.; Dunn, B.S.; Pilon, L. Physical Interpretations of Electrochemical Impedance Spectroscopy of Redox Active Electrodes for Electrical Energy Storage. J. Phys. Chem. C 2018, 122, 24499–24511. [Google Scholar] [CrossRef]
- Verbrugge, M.W.; Liu, P. Microstructural Analysis and Mathematical Modeling of Electric Double-Layer Supercapacitors. J. Electrochem. Soc. 2005, 152, D79. [Google Scholar] [CrossRef]
- Allu, S.; Velamur Asokan, B.; Shelton, W.A.; Philip, B.; Pannala, S. A generalized multi-dimensional mathematical model for charging and discharging processes in a supercapacitor. J. Power Sources 2014, 256, 369–382. [Google Scholar] [CrossRef]
- Kroupa, M.; Offer, G.J.; Kosek, J. Modelling of Supercapacitors: Factors Influencing Performance. J. Electrochem. Soc. 2016, 163, A2475–A2487. [Google Scholar] [CrossRef]
- Al-Zubaidi R-Smith, N.; Kasper, M.; Kumar, P.; Nilsson, D.; Mårlid, B.; Kienberger, F. Advanced Electrochemical Impedance Spectroscopy of Industrial Ni-Cd Batteries. Batteries 2022, 8, 50. [Google Scholar] [CrossRef]
- Drummond, R.; Howey, D.A.; Duncan, S.R. Low-order mathematical modelling of electric double layer supercapacitors using spectral methods. J. Power Sources 2015, 277, 317–328. [Google Scholar] [CrossRef]
- Béguin, F.; Frąckowiak, E. (Eds.) Supercapacitors: Materials, Systems, and Applications; Wiley-VCH: Weinheim, Germany, 2013; ISBN 9783527646661. [Google Scholar]
- Wang, H.; Pilon, L. Physical interpretation of cyclic voltammetry for measuring electric double layer capacitances. Electrochim. Acta 2012, 64, 130–139. [Google Scholar] [CrossRef]
- Rahim, A.H.A.; Ramli, N.; Nordin, A.N.; Wahab, M.F.A. Supercapacitor performance with activated carbon and graphene nanoplatelets composite electrodes, and insights from the equivalent circuit model. Carbon Trends 2021, 5, 100101. [Google Scholar] [CrossRef]
- Lehtimäki, S.; Suominen, M.; Damlin, P.; Tuukkanen, S.; Kvarnström, C.; Lupo, D. Preparation of Supercapacitors on Flexible Substrates with Electrodeposited PEDOT/Graphene Composites. ACS Appl. Mater. Interfaces 2015, 7, 22137–22147. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Chen, G.Z. Ionic Liquid-Based Electrolytes for Supercapacitor and Supercapattery. Front. Chem. 2019, 7, 272. [Google Scholar] [CrossRef] [PubMed]
- Tõnurist, K.; Thomberg, T.; Jänes, A.; Romann, T.; Sammelselg, V.; Lust, E. Influence of separator properties on electrochemical performance of electrical double-layer capacitors. J. Electroanal. Chem. 2013, 689, 8–20. [Google Scholar] [CrossRef]
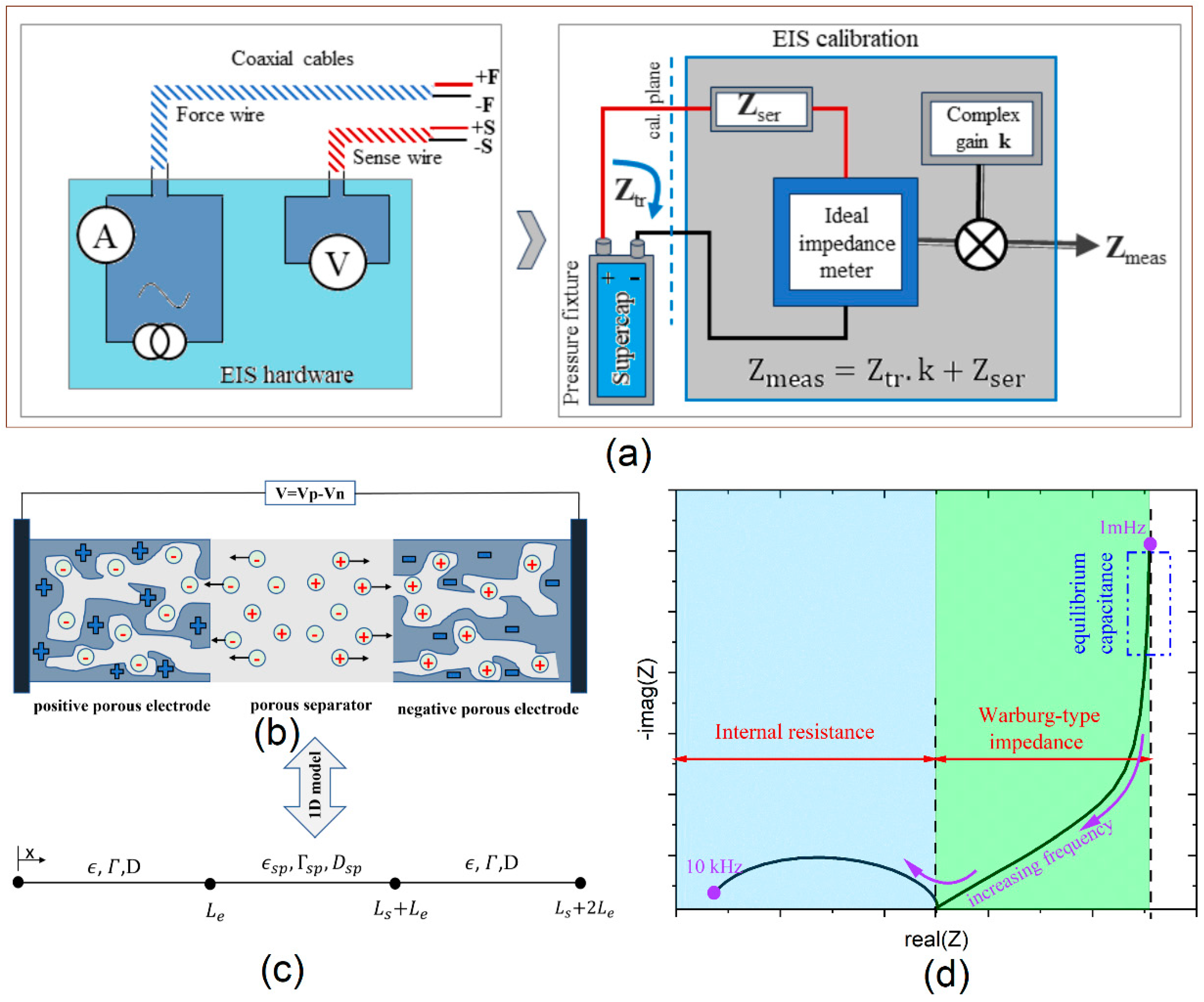
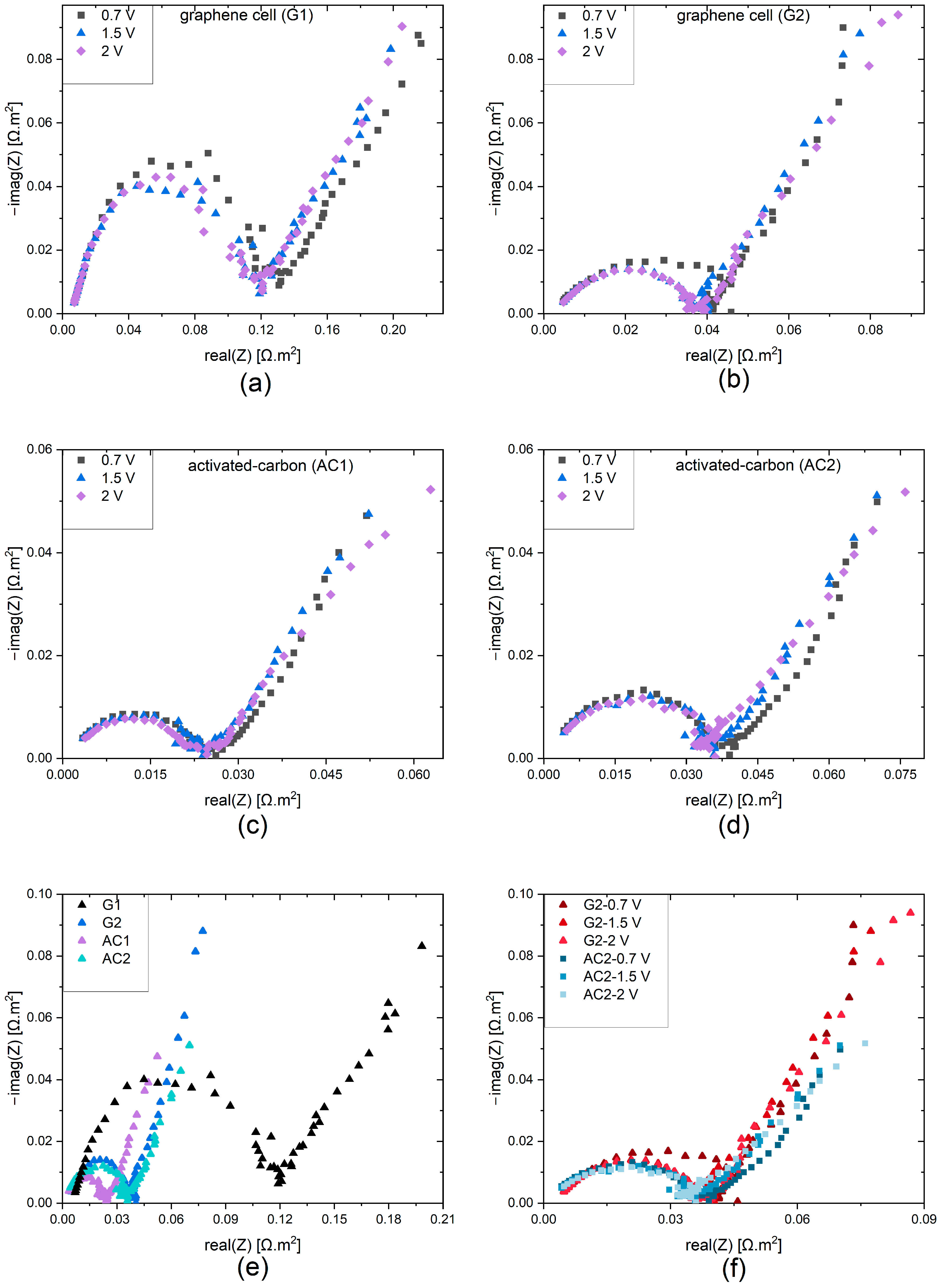
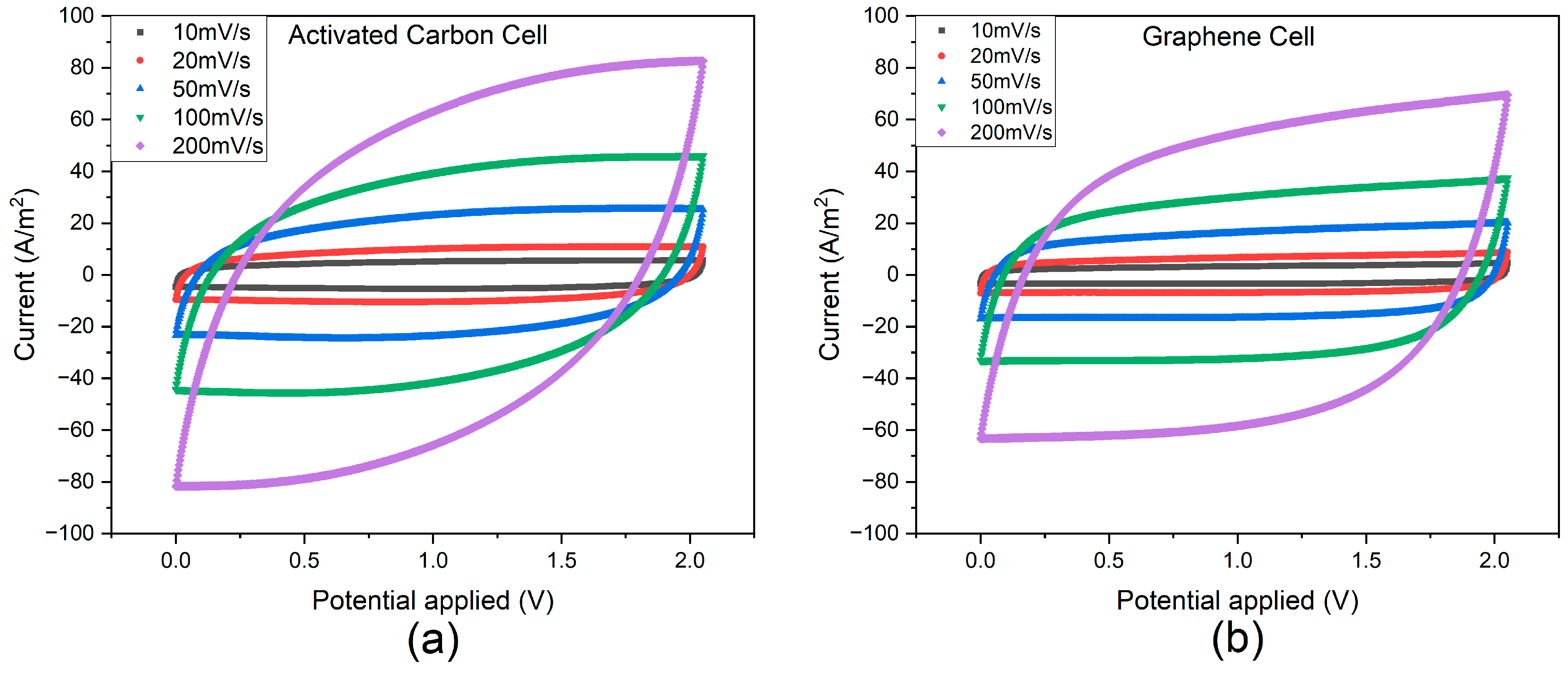
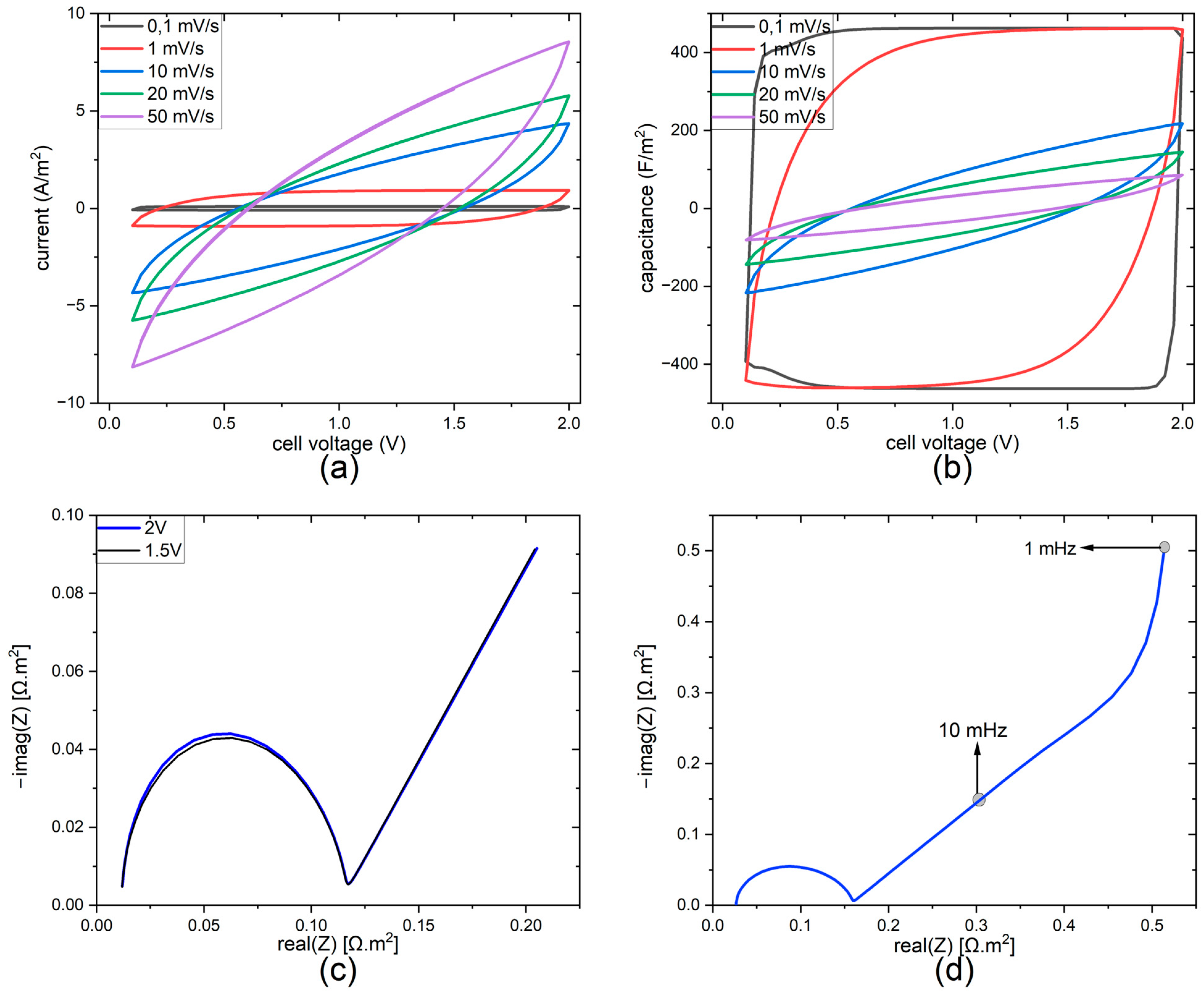

| Parameter | Symbol | Unit | Value | Reference |
|---|---|---|---|---|
| Separator thickness | Ls | µm | 50 | |
| Electrode thickness | Le | µm | 95 | |
| Electrode nominal surface | S | m2 | 0.06–0.2 | |
| Electrode porosity | ε | - | 0.67 | |
| Electrode tortuosity | ᴦe | - | 1–20 | |
| Separator porosity | εsp | - | 0.7 | |
| Separator tortuosity | ᴦsp | - | 1–10 | |
| Specific surface area | a | 1/m | 1–10 × 107 | |
| Stern layer thickness | λs | Nm | 0.4 | [54] |
| Relative permittivity | ϵr | 36 | [47] | |
| Initial electrolyte concentration | c(0,x) | mol/m3 | 3000 | |
| Electrode conductivity | σ | S/m | 0.001–1 | [47,49] |
| Bulk diffusion coefficient | D0 | m2/s | 10−13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azizpour, A.; Bagovic, N.; Ploumis, N.; Mylonas, K.; Hoxha, D.; Kienberger, F.; Al-Zubaidi-R-Smith, N.; Gramse, G. Electrochemical Analysis of Carbon-Based Supercapacitors Using Finite Element Modeling and Impedance Spectroscopy. Energies 2025, 18, 1450. https://doi.org/10.3390/en18061450
Azizpour A, Bagovic N, Ploumis N, Mylonas K, Hoxha D, Kienberger F, Al-Zubaidi-R-Smith N, Gramse G. Electrochemical Analysis of Carbon-Based Supercapacitors Using Finite Element Modeling and Impedance Spectroscopy. Energies. 2025; 18(6):1450. https://doi.org/10.3390/en18061450
Chicago/Turabian StyleAzizpour, Ahmad, Niko Bagovic, Nikolaos Ploumis, Konstantinos Mylonas, Dorela Hoxha, Ferry Kienberger, Nawfal Al-Zubaidi-R-Smith, and Georg Gramse. 2025. "Electrochemical Analysis of Carbon-Based Supercapacitors Using Finite Element Modeling and Impedance Spectroscopy" Energies 18, no. 6: 1450. https://doi.org/10.3390/en18061450
APA StyleAzizpour, A., Bagovic, N., Ploumis, N., Mylonas, K., Hoxha, D., Kienberger, F., Al-Zubaidi-R-Smith, N., & Gramse, G. (2025). Electrochemical Analysis of Carbon-Based Supercapacitors Using Finite Element Modeling and Impedance Spectroscopy. Energies, 18(6), 1450. https://doi.org/10.3390/en18061450







