Analysis of Methods for Intensifying Heat and Mass Transfer in Liquid Media
Abstract
1. Introduction
2. Methods of Intensification
2.1. The Local Intensification of Mass Transfer Processes Is a Key Consideration, as Is the Mechanical Energy Supply
2.2. Unproductive Energy Consumption Associated with the Intensification of Technological Processes
2.3. Main Factors Determining the Intensification of Processes
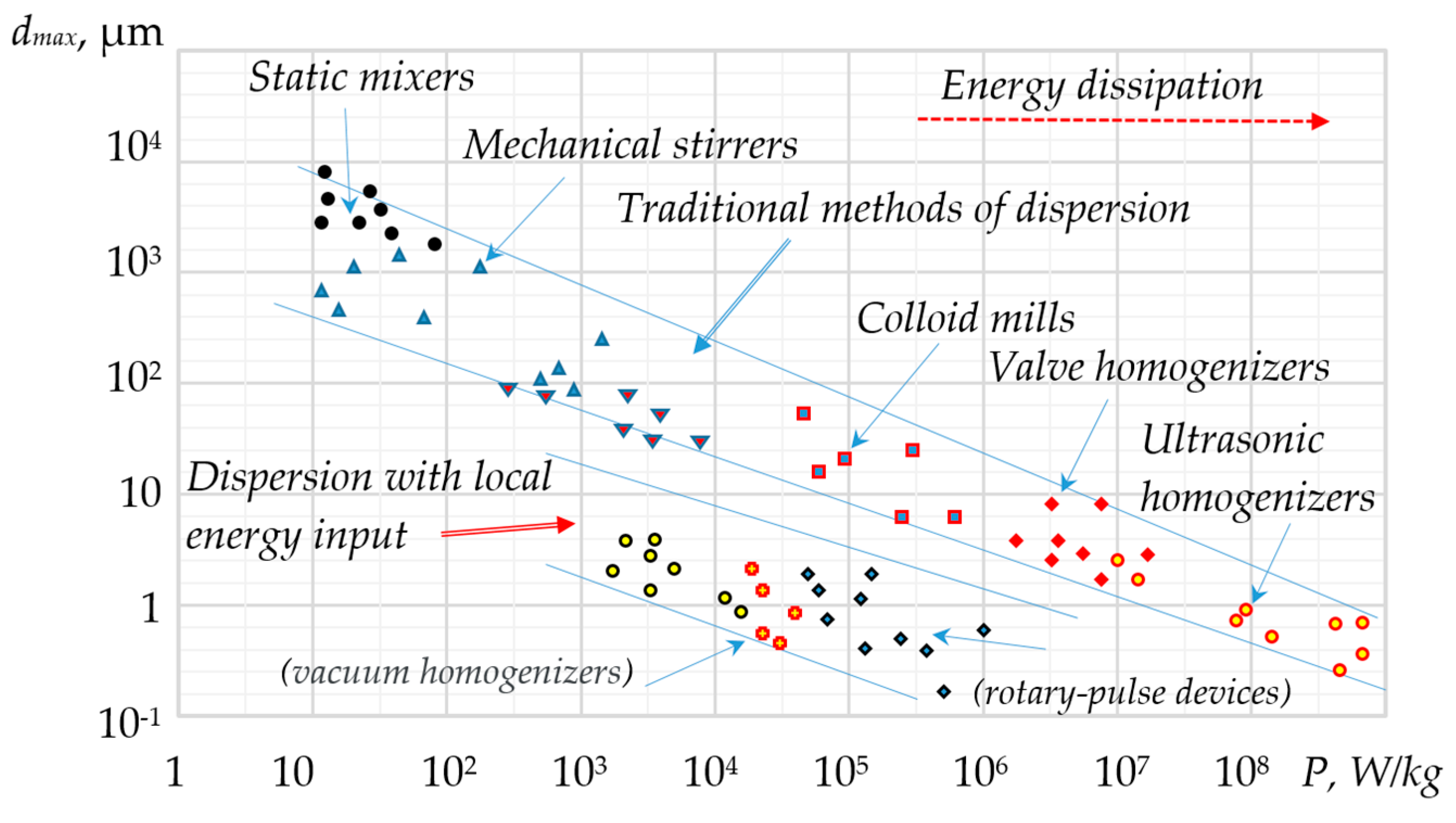
3. Intensification of Heat and Mass Transfer Processes in Localised Volumes
4. Alternative Approaches to the Intensification of Processes in Dispersed Media
4.1. Local Isotropic Turbulence
4.2. Local Energy Input
5. Processes Contributing to Localised Energy Input
5.1. Action of Shear Stress
5.2. Cavitation Processes
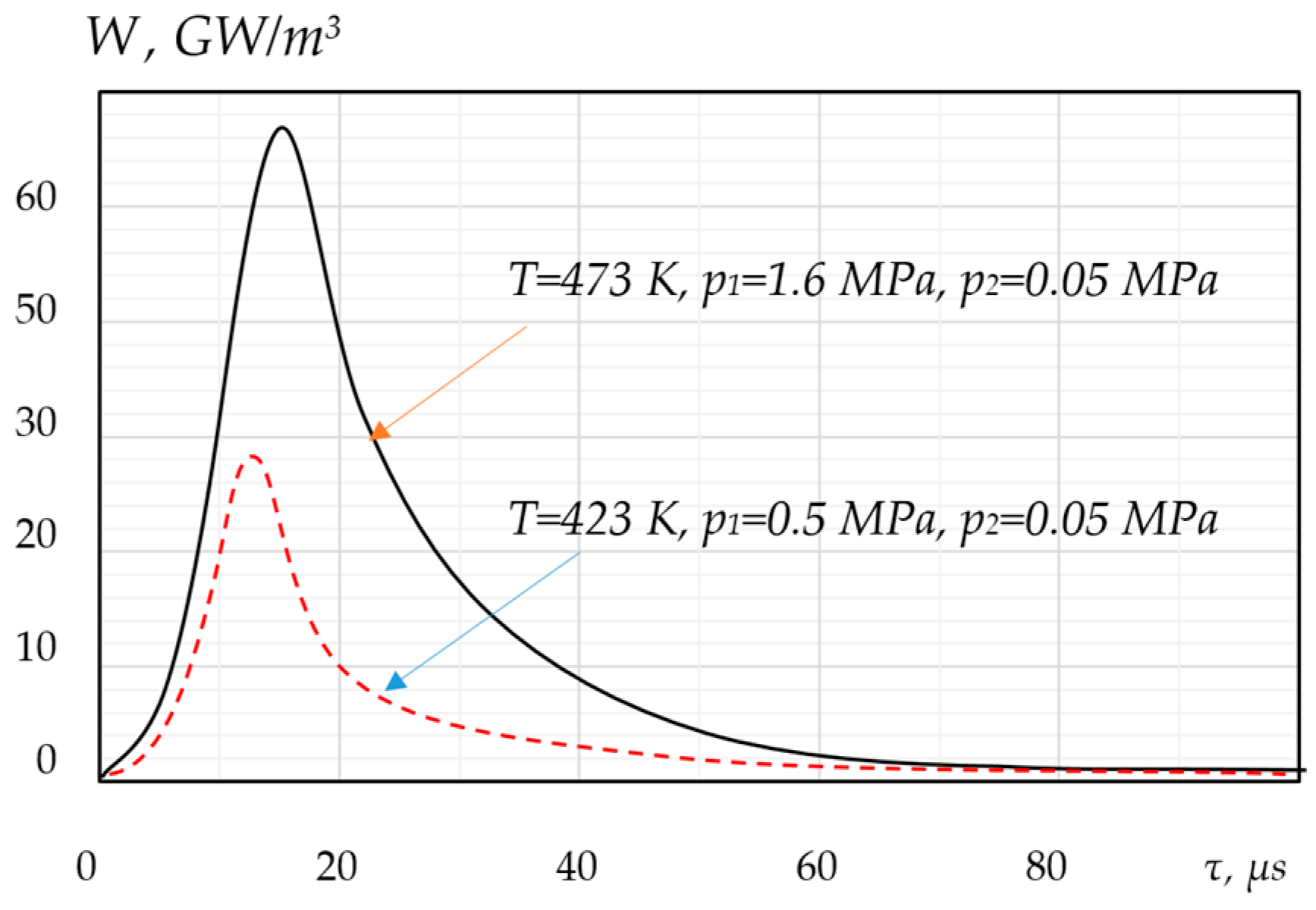
5.3. Explosive Boiling
5.4. Collective Effects in Bubble Clusters
5.5. An Example of the Implementation of a Method for the Local Input and Transformation of Energy in Liquid Media
5.5.1. Sudden Increase in External Pressure
5.5.2. Sharp Decrease in Fluid Pressure
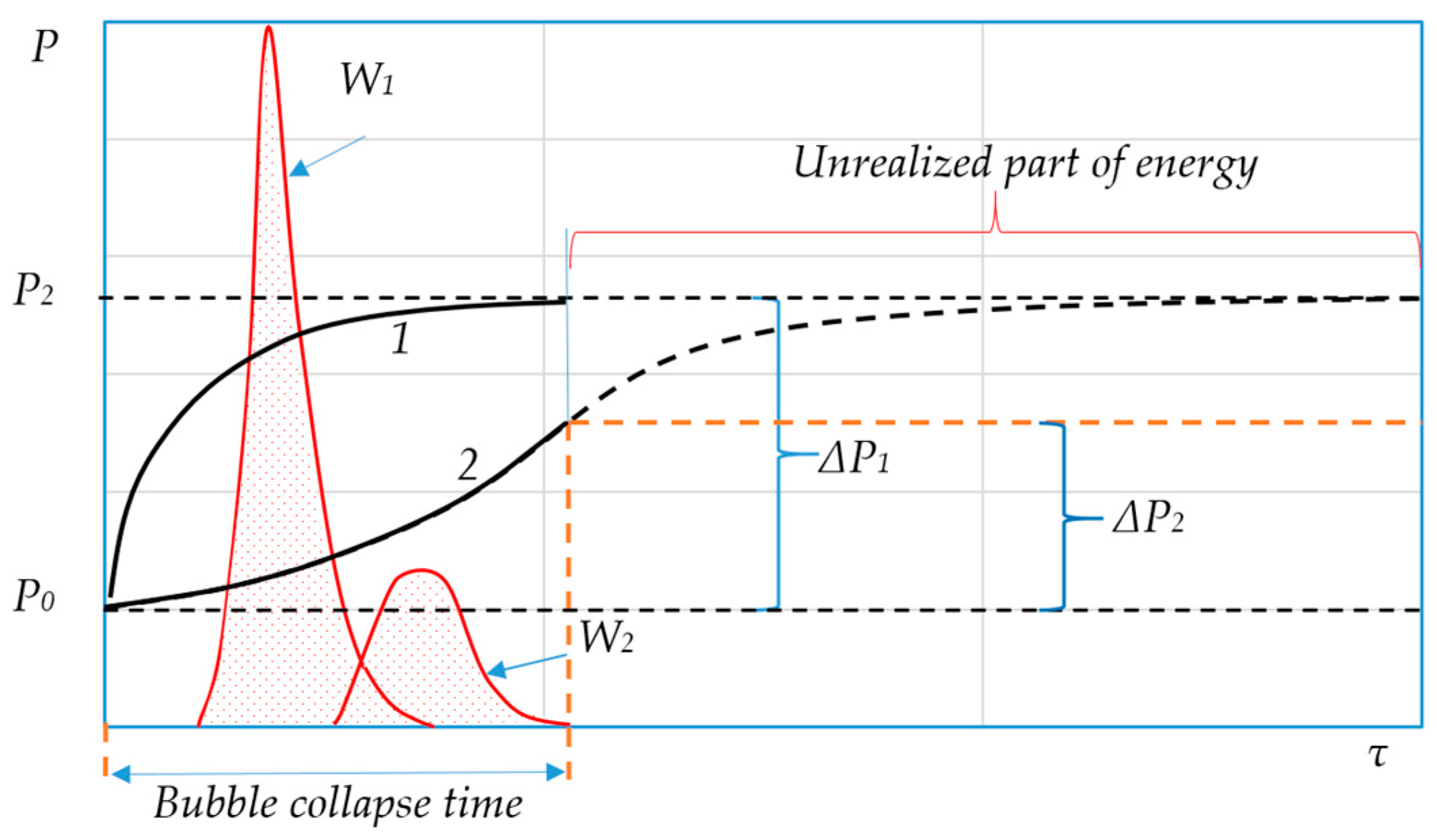
6. Efficiency Criteria for Local Energy Input Mechanisms
- (1)
- The rate of potential energy accumulation should exceed the rate of its subsequent conversion into kinetic energy. When using bubbles as energy transformers, this condition is reduced to the requirement to ensure the maximum pressure difference between the phases in the shortest possible time and can be written in the following form:
- (2)
- The duration of the energy transformation should be extremely short since the useful power released as a pulse is directly proportional to the value of the stored energy and inversely proportional to the transformation time. This condition boils down to the requirement to achieve extremely high values for the velocity and acceleration of the radial motion of the fluid:
- (3)
- Energy in the form of a pulse must be released simultaneously in a large number of small local zones, evenly located throughout the working volume of the apparatus.
7. Advantages of Localised Energy Input in Terms of Energy Savings
8. Conclusions
Funding
Conflicts of Interest
References
- Fatras, N.; Ma, Z.; Jorgensen, B.N. Process-to-market matrix mapping: A multi-criteria evaluation framework for industrial processes’ electricity market participation feasibility. Appl. Energy 2022, 313, 118829. [Google Scholar] [CrossRef]
- Yan, C.; Geng, X.; Bie, Z.; Xiec, L. Two-stage robust energy storage planning with probabilistic guarantees: A data-driven approach. Appl. Energy 2022, 313, 118623. [Google Scholar] [CrossRef]
- Ostergaard, J.; Ziras, C.; Bindner, H.W.; Kazempour, J.; Marinelli, M.; Markussen, P.; Rosted, S.H.; Christensen, J.S. Energy Security Through Demand-Side Flexibility: The Case of Denmark. IEEE Power Energy Mag. 2021, 19, 46–55. [Google Scholar] [CrossRef]
- Hongbo, C.; Kaile, Z. Industrial power load scheduling considering demand response. J. Clean. Prod. 2018, 204, 447–460. [Google Scholar]
- Gils, H.C. Assessment of the theoretical demand response potential in Europe. Energy 2014, 67, 1–18. [Google Scholar] [CrossRef]
- Moritz, P.; Frieder, F. The potential of demand-side management in energy-intensive industries for electricity markets in Germany. Appl. Energy 2011, 88, 432–441. [Google Scholar]
- Sklabinsky, V.; Pavlenko, I. Intensification of mass transfer processes through the impact of the velocity gradient on hydrodynamics and stability of liquid droplets in a gas flow. Chem. Eng. Sci. 2021, 235, 116470. [Google Scholar] [CrossRef]
- Sharma, A.K.; Bhandari, R.; Pinca-Bretotean, C.; Sharma, C.; Dhakad, S.K.; Mathur, A. A study of trends and industrial prospects of Industry 4.0. Mater. Today Proc. 2021, 47, 2364–2369. [Google Scholar] [CrossRef]
- Mohan, S.; Katakojwala, R. The circular chemistry conceptual framework: A way forward to sustainability in industry 4.0. Curr. Opin. Green Sustain. Chem. 2021, 28, 100434. [Google Scholar] [CrossRef]
- Hofmann, M.; Bayles, A.V.; Vermant, J. Stretch, fold, and break: Intensification of emulsification of high viscosity ratio systems by fractal mixers. AIChE J. 2021, 67, e17192. [Google Scholar] [CrossRef]
- López-Guajardo, E.A.; Delgado-Licona, F.; Álvarez, A.J.; Nigam, K.D.; Montesinos-Castellanos, A.; Morales-Menendez, R. Process intensification 4.0: A new approach for attaining new, sustainable and circular processes enabled by machine learning. Chem. Eng. Process.-Process Intensif. 2022, 180, 108671. [Google Scholar] [CrossRef]
- Volk, A.A.; Epps, R.W.; Abolhasani, M. Accelerated development of colloidal nanomaterials enabled by modular microfluidic reactors: Toward autonomous robotic experimentation. Adv. Mater. 2021, 33, 2004495. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Karadaghi, L.R.; Brutchey, R.L.; Malmstadt, N. Self-optimizing parallel millifluidic reactor for scaling nanoparticle synthesis. Chem. Commun. 2020, 56, 3745–3748. [Google Scholar] [CrossRef]
- Kleiner, J.; Hinrichsen, O. Epoxidation of methyl oleate in a rotor-stator spinning disc reactor. Chem. Eng. Process.-Process Intensif. 2019, 136, 152–162. [Google Scholar] [CrossRef]
- Manzano Martínez, A.N.; van Eeten, K.M.; Schouten, J.C.; van der Schaaf, J. Micromixing in a rotor–stator spinning disc reactor. Ind. Eng. Chem. Res. 2017, 56, 13454–13460. [Google Scholar] [CrossRef]
- Toma, H.; Nishino, K. Convective mixing of miscible liquids in a rotor-stator spinning disk reactor. Chem. Eng. J. 2017, 346, 329–339. [Google Scholar] [CrossRef]
- Ferrouillat, S.; Tochon, P.; Garnier, C.; Peerhossaini, H. Intensification of heat-transfer and mixing in multifunctional heat exchangers by artificially generated streamwise vorticity. Appl. Therm. Eng. 2006, 26, 1820–1829. [Google Scholar] [CrossRef]
- Keil, F.J. Process intensification. Rev. Chem. Eng. 2017, 34, 135–200. [Google Scholar] [CrossRef]
- Ohmura, N.; Masuda, H.; Wang, S. Intensification of Mixing Processes with Complex Fluids. J. Chem. Eng. Jpn. 2018, 51, 129–135. [Google Scholar] [CrossRef]
- Elayarani, M.; Shanmugapriya, M.; Senthil Kumar, P. Intensification of heat and mass transfer process in MHD carreau nanofluid flow containing gyrotactic microorganisms. Chem. Eng. Process.-Process Intensif. 2021, 160, 108299. [Google Scholar] [CrossRef]
- Law, R.; Ramshaw, C.; Reay, D. Process intensification—Overcoming impediments to heat and mass transfer enhancement when solids are present, via the IbD project. Therm. Sci. Eng. Prog. 2017, 1, 53–58. [Google Scholar] [CrossRef]
- Jin, Y.; Zhao, W.; Li, Z. Effect of Gas-Liquid Contact Intensification on Heat and Mass Transfer in Deflector and Rod Bank Desulfurization Spray Tower. Processes 2021, 9, 1269. [Google Scholar] [CrossRef]
- Wang, P.; Dai, G. Field Synergy of the Rod Bank on the Enhancement of Mass Transfer in a Spray Column. Ind. Eng. Chem. Res. 2018, 57, 12531–12542. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, T.; Liu, Z.; Wang, S.; Gao, Y.; Wu, M. Mass Transfer in a Rotating Packed Bed: A Critical Review. Chem. Eng. Process.-Process Intensif. 2019, 139, 78–94. [Google Scholar] [CrossRef]
- Bangerth, S.; Tiwari, R.; Shooshtari, A.; Ohadi, M. Process intensification in a spinning disk absorber for absorption heat pumps. Appl. Therm. Eng. 2019, 162, 114179. [Google Scholar] [CrossRef]
- Boodhoo, K.V.K.; Jachuck, R.J. Process intensification: Spinning disk reactor for styrene polymerisation. Appl. Therm. Eng. 2000, 20, 1127–1146. [Google Scholar] [CrossRef]
- Basok, B.; Davydenko, B.; Pavlenko, A.M. Numerical Network Modeling of Heat and Moisture Transfer through Capillary-Porous Building Materials. Materials 2021, 14, 1819. [Google Scholar] [CrossRef]
- Pavlenko, A. Energy conversion in heat and mass transfer processes in boiling emulsions. Therm. Sci. Eng. Prog. 2020, 15, 100439. [Google Scholar] [CrossRef]
- Adibi, O.; Rashidi, S.; Abolfazli Esfahani, J. Effects of perforated anchors on heat transfer intensification of turbulence nanofluid flow in a pipe. J. Therm. Anal. Calorim. 2020, 141, 2047–2059. [Google Scholar] [CrossRef]
- De Beer, M.M.; Loane, L.P.M.; Keurentjes, J.T.F.; Schouten, J.C.; van der Schaaf, J. Single phase fluid-stator heat transfer in a rotor–stator spinning disc reactor. Chem. Eng. Sci. 2014, 119, 88–98. [Google Scholar] [CrossRef]
- Haseidl, F.; Pottbäcker, J.; Hinrichsen, O. Gas–Liquid mass transfer in a rotor–stator spinning disc reactor: Experimental study and correlation. Chem. Eng. Process. Process Intensif. 2016, 104, 181–189. [Google Scholar] [CrossRef]
- Zhang, J.; Teixeira, A.R.; Zhang, H.; Jensen, K.F. Determination of fast gas–liquid reaction kinetics in flow. React. Chem. Eng. 2020, 5, 51–57. [Google Scholar] [CrossRef]
- Hu, B.; Li, X.; Fu, Y.; Zhang, F.; Gu, C.; Ren, X.; Wang, C. Experimental investigation on the flow and flow-rotor heat transfer in a rotor-stator spinning disk reactor. Appl. Therm. Eng. 2019, 162, 114316. [Google Scholar] [CrossRef]
- De Beer, M.M.; Keurentjes, J.T.; Schouten, J.C.; van der Schaaf, J. Intensification of convective heat transfer in a stator–rotor–stator spinning disc reactor. AIChE J. 2015, 61, 2307–2318. [Google Scholar] [CrossRef]
- Yang, P.; Li, X.; Li, H.; Cong, H.; Kiss, A.A.; Gao, X. Unraveling the influence of residence time distribution on the performance of reactive distillation–Process optimization and experimental validation. Chem. Eng. Sci. 2021, 237, 116559. [Google Scholar] [CrossRef]
- Pavlenko, A.M.; Basok, B.I.; Avramenko, A.A. Heat conduction of a multi-layer disperse particle of emulsion. Heat Transf. Res. 2005, 36, 55–61. [Google Scholar] [CrossRef]
- Lloyd, D.M.; Norton, I.T.; Spyropoulos, F. Process optimisation of rotating membrane emulsification through the study of surfactant dispersions. J. Food Eng. 2015, 166, 316–324. [Google Scholar] [CrossRef]
- Atkins, M.D.; Kienhöfer, F.W.; Kang, K.; Lu, T.J.; Kim, T. Cooling Mechanisms in a Rotating Brake Disc with a Wire-Woven-Bulk Diamond Cellular Core. ASME. J. Thermal Sci. Eng. Appl. 2021, 13, 041006. [Google Scholar] [CrossRef]
- Atkins, M.D.; Kienhöfer, F.W.; Lu, T.J.; Kim, T. Local Heat Transfer Distributions Within a Rotating Pin-Finned Brake Disk, ASME. J. Heat Transf. 2020, 142, 112101. [Google Scholar] [CrossRef]
- Steurer, A.; Poser, R.; von Wolfersdorf, J.; Retzko, S. Application of the Transient Heat Transfer Measurement Technique Using Thermochromic Liquid Crystals in a Network Configuration with Intersecting Circular Passages, ASME. J. Turbomach. 2019, 141, 051010. [Google Scholar] [CrossRef]
- Mitkowski, P.T.; Szaferski, W. Production of emulsion in tank mixer with sieve bottom. Chem. Eng. Res. Des. 2016, 109, 618–627. [Google Scholar] [CrossRef]
- Jadhav, A.J.; Ferraro, G.; Barigou, M. Generation of Bulk Nanobubbles Using a High-Shear Rotor–Stator Device. Ind. Eng. Chem. Res. 2021, 60, 8597–8606. [Google Scholar] [CrossRef]
- Li, W.; Xia, F.; Zhao, S.; Guo, J.; Zhang, M.; Li, W.; Zhang, J. Mixing Performance of an Inline High-Shear Mixer with a Novel Pore-Array Liquid Distributor. Ind. Eng. Chem. Res. 2019, 58, 20213–20225. [Google Scholar] [CrossRef]
- Kwon, C.; Pak, U.S.; Kim, C.M.; Paek, C.H. CFD analysis of flow field and power consumption of in-line high shear mixers with different stator structures. J. Indian Chem. Soc. 2021, 98, 100159. [Google Scholar] [CrossRef]
- Li, X.; Yang, L.; Guo, J.; Li, W.; Zhou, M.; Zhang, J. Micromixing performance of the teethed high shear mixer under semi-batch operation. Front. Chem. Sci. Eng. 2021, 16, 546–559. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, J.; Li, W.; Li, W.; Zhang, J. Investigation of gas-liquid mass transfer and power consumption characteristics in jet-flow high shear mixers. Chem. Eng. J. 2021, 411, 128580. [Google Scholar] [CrossRef]
- Yang, L.; Li, W.; Guo, J.; Li, W.; Wang, B.; Zhang, M.; Zhang, J. Effects of rotor and stator geometry on dissolution process and power consumption in jet-flow high shear mixers. Front. Chem. Sci. Eng. 2021, 15, 384–398. [Google Scholar] [CrossRef]
- Vashisth, V.; Nigam, K.; Kumar, V. Design and development of high shear mixers: Fundamentals, applications and recent progress. Chem. Eng. Sci. 2021, 232, 116296. [Google Scholar] [CrossRef]
- Kwon, C.; Song, U.; Pak, U.; Kim, C.; Kim, K.-C. Effect of structural parameters on the flow field and power consumption of in-line high shear mixer. J. Indian Chem. Soc. 2021, 98, 100042. [Google Scholar] [CrossRef]
- Kwon, C.; Kim, K.; Pak, U. Effect of the stator tooth thickness on flow characteristics of high shear mixer. J. Phys. Conf. Ser. 2021, 1750, 012026. [Google Scholar] [CrossRef]
- Espinoza, C.J.U.; Alberini, F.; Mihailova, O.; Kowalski, A.J.; Simmons, M.J.H. Flow, turbulence and potential droplet break up mechanisms in an in-line Silverson 150/250 high shear mixer. Chem. Eng. Sci. X 2020, 6, 100055. [Google Scholar] [CrossRef]
- Lv, Y.; Ye, C.; Zhang, J.; Guo, C. Rapid and efficient synthesis of highly crystalline SSZ-13 zeolite by applying high shear mixing in the aging process. Microporous Mesoporous Mater. 2020, 293, 109812. [Google Scholar] [CrossRef]
- Municchi, F.; Nagrani, P.P.; Christov, I.C. A two-fluid model for numerical simulation of shear-dominated suspension flows. Int. J. Multiph. Flow 2019, 120, 103079. [Google Scholar] [CrossRef]
- Snider, R.F. Irreversible thermodynamics of multicomponent fluids and its statistical mechanics basis. Phys. Rev. 2021, 103, 032121. [Google Scholar] [CrossRef] [PubMed]
- Beris, A.N.; Jariwala, S.; Wagner, N.J. Flux-based modeling of heat and mass transfer in multicomponent systems. Phys. Fluids 2022, 34, 033113. [Google Scholar] [CrossRef]
- Gondrexon, N.; Cheze, L.; Jin, Y.; Legay, M.; Tissot, Q.; Hengl, N.; Baup, S.; Boldo, P.; Pignon, F.; Talansier, E. Intensification of heat and mass transfer by ultrasound: Application to heat exchangers and membrane separation processes. Ultrason. Sonochem. 2015, 25, 40–50. [Google Scholar] [CrossRef]
- Chen, B.; Wan, Z.; Chen, G.; Zhong, G.; Tang, Y. Improvement of ultrasonic heat transfer enhancement using acoustical focusing and resonance properties. Int. Commun. Heat Mass Transf. 2019, 104, 60–69. [Google Scholar] [CrossRef]
- Peñas, P.; Soto, Á.M.; Lohse, D.; Lajoinie, G.; van der Meer, D. Ultrasound-enhanced mass transfer during the growth and dissolution of surface gas bubbles. Int. J. Heat Mass Transf. 2021, 174, 121069. [Google Scholar] [CrossRef]
- Pavlenko, A.; Koshlak, H. Application of Thermal and Cavitation Effects for Heat and Mass Transfer Process Intensification in Multicomponent Liquid Media. Energies 2021, 14, 7996. [Google Scholar] [CrossRef]
- Mao, Y.; Robinson, J.; Binner, E. Understanding heat and mass transfer processes during microwave-assisted and conventional solvent extraction. Chem. Eng. Sci. 2021, 233, 116418. [Google Scholar] [CrossRef]
- Lee, C.S.; Binner, E.; Winkworth-Smith, C.; John, R.; Gomes, R.; Robinson, J. Enhancing natural product extraction and mass transfer using selective microwave heating. Chem. Eng. Sci. 2016, 149, 97–103. [Google Scholar] [CrossRef]
- Foukrach, M.; Bouzit, M.; Ameur, K.Y. Effect of Agitator’s Types on the Hydrodynamic Flow in an Agitated Tank. Chin. J. Mech. Eng. 2020, 33, 37. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, G.-H.; Duan, J.-H.; Wang, W.-W. Mixing characteristics in a vessel equipped with cylindrical stirrer. Results Phys. 2018, 10, 699–705. [Google Scholar] [CrossRef]
- Feng, X.; Cheng, J.; Li, X.; Yang, C.; Mao, Z.S. Numerical simulation of turbulent flow in a baffled stirred tank with an explicit algebraic stress model. Chem. Eng. Sci. 2012, 69, 30–44. [Google Scholar] [CrossRef]
- Kamla, Y.; Bouzit, M.; Hadjeb, A.; Arab, I.M.; Beloudane, M. CFD study of the effect of Baffles on the energy consumption and the flow structure in a vessel stirred by a Rushton turbine. Mechanika 2016, 22, 190–197. [Google Scholar] [CrossRef]
- Ascanio, G. Mixing time in stirred vessels: A review of experimental techniques. Chin. J. Chem. Eng. 2015, 23, 1065–1076. [Google Scholar] [CrossRef]
- Ameur, H. Mixing of complex fluids with flat and pitched bladed impellers: Effect of blade attack angle and shear-thinning behavior. Food Bioprod. Process. 2016, 99, 71–77. [Google Scholar] [CrossRef]
- Heyter, A.; Wollny, S. Influence of different baffle variations on the effectiveness of multi-stage agitated vessels. Chem. Ing. Tech. 2017, 89, 416–423. [Google Scholar] [CrossRef]
- Hu, L.; Zhu, H.; Hua, J. DEM simulation of energy transitions in a hammer mill: Effect of impeller configurations, agitation speed, and fill level. Powder Technol. 2021, 394, 1077–1093. [Google Scholar] [CrossRef]
- Pang, H.; Ngaile, G. Modeling of a valve-type low-pressure homogenizer for oil-in-water emulsions. Chem. Eng. Process.-Process Intensif. 2021, 160, 108249. [Google Scholar] [CrossRef]
- Yadav, K.S.; Kale, K. High Pressure Homogenizer in Pharmaceuticals: Understanding Its Critical Processing Parameters and Applications. J. Pharm. Innov. 2020, 15, 690–701. [Google Scholar] [CrossRef]
- Taghinia, J.; Rahman, M.; Tse, T.K.; Siikonen, T. CFD modeling of homogenizer valve: A comparative study. Chem. Eng. Res. Des. 2016, 106, 327–336. [Google Scholar] [CrossRef]
- Pang, H.; Ngaile, G. Utilization of Secondary Jet in Cavitation Peening and Cavitation Abrasive Jet Polishing. Micromachines 2022, 13, 86. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.-X.; Linz, N.; Freidank, S.; Paltauf, G.; Vogel, A. Comprehensive analysis of spherical bubble oscillations and shock wave emission in laser-induced cavitation. J. Fluid Mech. 2022, 940, A5. [Google Scholar] [CrossRef]
- Ho, D.S.; Scialabba, D.; Terry, R.S.; Ma, X.; Chen, J.; Sankin, G.N.; Xiang, G.; Qi, R.; Preminger, G.M.; Lipkin, M.E.; et al. The Role of Cavitation in Energy Delivery and Stone Damage During Laser Lithotripsy. J. Endourol. 2021, 35, 860–870. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Wang, D.; Bi, Y. Investigation of the influence of different liquid temperatures on the dynamics of long-pulse laser-induced cavitation bubbles. AIP Adv. 2024, 14, 025013. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, S.; Wang, P.; Qiu, W.; Zhang, G. Progress in applications of laser induced cavitation on surface processing. Opt. Laser Technol. 2024, 170, 110212. [Google Scholar] [CrossRef]
- Schoppink, J.J.; Krizek, J.; Moser, C.; Rivas, D.F. Cavitation induced by pulsed and continuous-wave fiber lasers in confinement. Exp. Therm. Fluid Sci. 2023, 146, 110926. [Google Scholar] [CrossRef]
- Tiang, S.S.L.; Low, L.E.; Ali, I.; Zhou, L.; Goh, B.-H.; Gew, L.T.; Tang, S.Y. Recent advances in ultrasonic cavitation technologies for emulsion preparation: A mini review. Curr. Opin. Chem. Eng. 2024, 45, 101046. [Google Scholar] [CrossRef]
- Tiong, T.; Chu, J.K.; Tan, K.W. Advancements in Acoustic Cavitation Modelling: Progress, Challenges, and Future Directions in Sonochemical Reactor Design. Ultrason. Sonochem. 2025, 112, 107163. [Google Scholar] [CrossRef]
- Guo, D.-S.; Li, X.-B.; Zhang, H.-N.; Li, F.-C.; Ming, P.-J.; Oishi, M.; Oshima, M. Experimental study on the characteristics of temperature dependent surface/interfacial properties of a non-ionic surfactant aqueous solution at quasi-thermal equilibrium condition. Int. J. Heat Mass Transf. 2022, 182, 122003. [Google Scholar] [CrossRef]
- Wang, J.; Li, F.-C.; Li, X.-B. On the mechanism of boiling heat transfer enhancement by surfactant addition. Int. J. Heat Mass Transf. 2016, 101, 800–806. [Google Scholar] [CrossRef]
- Takeyama, M.; Zupančič, M.; Kunugi, T. Influence of hydrodynamic interactions among multiple bubbles on convective heat transfer in nucleate boiling. Exp. Therm. Fluid Sci. 2021, 128, 110449. [Google Scholar] [CrossRef]
- Sergi, D.; Scocchi, G.; Ortona, A. Molecular dynamics simulations of the contact angle between water droplets and graphite surfaces. Fluid Phase Equilibria 2012, 332, 173–177. [Google Scholar] [CrossRef]
- Feraco, F.; Marino, R.; Primavera, L.; Pumir, A.; Mininni, P.D.; Rosenberg, D.; Pouquet, A.; Foldes, R.; Lévêque, E.; Camporeale, E.; et al. Connecting Large-Scale Velocity and Temperature Bursts with Small-Scale Intermittency in Stratified Turbulence. EPL 2021, 135, 14001. [Google Scholar] [CrossRef]
- Brůha, T.; Procházka, P.; Uruba, V. Investigation of Low-Frequency Phenomena within Flow Pattern in Standard Mixing Vessel Induced by Pitched Blade Impeller. Processes 2021, 9, 545. [Google Scholar] [CrossRef]
- Pozorski, J.; Wacławczyk, M. Mixing in Turbulent Flows: An Overview of Physics and Modelling. Processes 2020, 8, 1379. [Google Scholar] [CrossRef]
- Gomaa, H.G.; Taweel, A.M.A. Intensification of inter-phase mass transfer: The combined effect of oscillatory motion and turbulence promoters. Heat Mass Transf. 2007, 43, 371. [Google Scholar] [CrossRef]
- Zaki, M.; Abdel-Aziz, M.H.; Nirdosh, I.; Sedahmed, G.H. Intensification of the rate of heat and mass transfer in a batch and continuous parallel plate contactor by pulsed flow. Chem. Eng. J. 2020, 398, 125589. [Google Scholar] [CrossRef]
- He, F.; Dong, W.; Wang, J. Modeling and Numerical Investigation of Transient Two-Phase Flow with Liquid Phase Change in Porous Media. Nanomaterials 2021, 11, 183. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Dissipation of Energy in the Locally Isotropic Turbulence. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1991, 434, 15–17. [Google Scholar] [CrossRef]
- McComb, W.D. A local energy-transfer theory of isotropic turbulence. J. Phys. A Math. Nucl. Gen. 2001, 7, 632. [Google Scholar] [CrossRef]
- Osawa, K.; Naka, Y.; Fukushima, N.; Shimura, M.; Tanahashi, M.; Miyauchi, T. Effect of Flow Structures on Turbulence Statistics of Taylor-Couette Flow in the Torque Transition State. Flow Turbul. Combust 2016, 97, 973–986. [Google Scholar] [CrossRef]
- Takaoka, M.; Yokoyama, N.; Sasaki, E. Local-flux vectors of conserved quantities in wavenumber space: Anisotropic structures in Charney–Hasegawa–Mima turbulence. Phys. Rev. Fluids 2022, 7, L012601. [Google Scholar] [CrossRef]
- Dodd, M.S.; Jofre, L. Small-scale flow topologies in decaying isotropic turbulence laden with finite-size droplets. Phys. Rev. Fluids 2019, 4, 064303. [Google Scholar] [CrossRef]
- Portwood, G.; Kops, S.d.B.; Caulfield, C. Implications of inertial subrange scaling for stably stratified mixing. J. Fluid Mech. 2022, 939, A10. [Google Scholar] [CrossRef]
- Lang, C.J.; Waite, M.L. Scale-dependent anisotropy in forced stratified turbulence. Phys. Rev. Fluids 2019, 4, 044801. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H.; Zhang, X.; Li, Q.; Cai, X.; Song, Y.; Kang, L.; Zhu, T. Temporal and spatial characteristics of turbulent transfer and diffusion coefficient of PM2. 5. Sci. Total Environ. 2021, 782, 146804. [Google Scholar] [CrossRef]
- Ohsawa, A.; Murata, A.; Iwamoto, K. Contribution of advetion, turbulent transport and diffusion terms to Nusselt number and torque coefficient in Taylor-Couette flow. J. Therm. Sci. Technol. 2016, 11, JTST0027. [Google Scholar] [CrossRef]
- Brouwers, J.J.H. Statistical Model of Turbulent Dispersion Recapitulated. Fluids 2021, 6, 190. [Google Scholar] [CrossRef]
- Nouri, L.; Abouda, L.; Legrand, J. Estimation of the micromixing time in the torus reactor by the application of the incorporation model. Chem. Eng. Process. Process Intensif. 2014, 78, 37–43. [Google Scholar] [CrossRef]
- Ouyang, Y.; Manzano, M.N.; Wetzels, R.; Chen, S.; Lang, X.; Heynderickx, G.J.; Van Geem, K.M. Liquid hydrodynamics in a gas-liquid vortex reactor. Chem. Eng. Sci. 2021, 246, 116970. [Google Scholar] [CrossRef]
- Martínez, A.N.M.; Jansen, R.; Walker, K.; Assirelli, M.; van der Schaaf, J. Experimental and modeling study on meso- and micromixing in the rotor–stator spinning disk reactor. Chem. Eng. Res. Des. 2021, 173, 279–288. [Google Scholar] [CrossRef]
- Tao, R.; Wang, Z. Comparative numerical studies for the flow energy dissipation features in a pump-turbine in pump mode and turbine mode. J. Energy Storage 2021, 41, 102835. [Google Scholar] [CrossRef]
- Lu, Z.; Xiao, R.; Tao, R.; Li, P.; Liu, W. Influence of guide vane profile on the flow energy dissipation in a reversible pump-turbine at pump mode. J. Energy Storage 2022, 49, 104161. [Google Scholar] [CrossRef]
- De Beer, M.M.; Keurentjes, J.T.F.; Schouten, J.C.; Van der Schaaf, J. Bubble formation in co-fed gas–liquid flows in a rotor-stator spinning disc reactor. Int. J. Multiph. Flow 2016, 83, 142–152. [Google Scholar] [CrossRef]
- Manzano Martinez, A.N.; Chaudhuri, A.; Besten, M.; Assirelli, M.; van der Schaaf, J. Micromixing Efficiency in the Presence of an Inert Gas in a Rotor–Stator Spinning Disk Reactor. Ind. Eng. Chem. Res. 2021, 60, 8677–8686. [Google Scholar] [CrossRef]
- Hinze, J.O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1955, 1, 289–295. [Google Scholar] [CrossRef]
- Foronda-Trillo, F.; Rodríguez-Rodríguez, J.; Gutiérrez-Montes, C.; Martínez-Bazán, C. Deformation and breakup of bubbles interacting with single vortex rings. Int. J. Multiph. Flow 2021, 142, 103734. [Google Scholar] [CrossRef]
- Hasan, B.O.; Hamad, M.F.; Majdi, H.S.; Hathal, M.M. Experimental characterization of dynamic behavior of single bubble breakage in an agitated tank. Eur. J. Mech.-B/Fluids 2021, 85, 430–443. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Sayyar, A.; Wang, T. Experimental study on breakup of a single bubble in a stirred tank: Effect of gas density and liquid properties. AIChE J. 2021, 69, e17511. [Google Scholar] [CrossRef]
- Mutsch, B.; Preiss, F.J.; Dagenbach, T.; Karbstein, H.P.; Kähler, C.J. Scaling of Droplet Breakup in High-Pressure Homogenizer Orifices. Part II: Visualization of the Turbulent Droplet Breakup. Chem. Eng. 2021, 5, 31. [Google Scholar] [CrossRef]
- Wang, Z.; Hopfes, T.; Giglmaier, M.; Adams, N.A. Experimental investigation of shock-induced tandem droplet breakup. Phys. Fluids 2021, 33, 012113. [Google Scholar] [CrossRef]
- Zhou, H.; Yu, X.; Wang, B.; Jing, S.; Lan, W.; Li, S. Breakup model of oscillating drops in turbulent flow field. Chem. Eng. Sci. 2021, 247, 117036. [Google Scholar] [CrossRef]
- Rosti, M.; Ge, Z.; Jain, S.; Dodd, M.; Brandt, L. Droplets in homogeneous shear turbulence. J. Fluid Mech. 2019, 876, 962–984. [Google Scholar] [CrossRef]
- Gallassi, M.; Gonçalves, G.F.; Botti, T.C.; Moura, M.J.; Carneiro, J.N.; Carvalho, M.S. Numerical and experimental evaluation of droplet breakage of O/W emulsions in rotor-stator mixers. Chem. Eng. Sci. 2019, 204, 270–286. [Google Scholar] [CrossRef]
- Soligo, G.; Roccon, A.; Soldati, A. Turbulent Flows with Drops and Bubbles: What Numerical Simulations Can Tell Us—Freeman Scholar Lecture. J. Fluids Eng. 2021, 143, 080801. [Google Scholar] [CrossRef]
- Crialesi-Esposito, M.; Rosti, M.; Chibbaro, S.; Brandt, L. Modulation of homogeneous and isotropic turbulence in emulsions. J. Fluid Mech. 2022, 940, A19. [Google Scholar] [CrossRef]
- Podgórska, W. The Influence of Internal Intermittency, Large Scale Inhomogeneity, and Impeller Type on Drop Size Distribution in Turbulent Liquid-Liquid Dispersions. Entropy 2019, 21, 340. [Google Scholar] [CrossRef]
- Han, L.; Gong, S.; Li, Y.; Gao, N.; Fu, J.; Luo, H.; Liu, Z. Influence of energy spectrum distribution on drop breakage in turbulent flows. Chem. Eng. Sci. 2014, 117, 55–70. [Google Scholar] [CrossRef]
- Philip, R.M.; Hewitt, I.J.; Howell, P.D. Modeling the Effect of Surfactant on Droplet Breakup in a Turbulent Flow. J. Appl. Math. 2021, 81, 129–152. [Google Scholar] [CrossRef]
- Zhou, H.; Tang, X.; Zhu, Z.; Li, S. 0D Homogeneous Simulation of Droplet Size Evolution in a Turbulent Stirred Tank. Ind. Eng. Chem. Res. 2022, 61, 5632–5641. [Google Scholar] [CrossRef]
- Eskin, D.; Vikhansky, A.; Mohammadzadeh, O.; Ma, S. A model of droplet breakup in a turbulent flow for a high dispersed phase holdup. Chem. Eng. Sci. 2021, 232, 116350. [Google Scholar] [CrossRef]
- Maxey, M. Droplets in turbulence: A new perspective. J. Fluid Mech. 2017, 816, 1–4. [Google Scholar] [CrossRef]
- Basok, B.; Davydenko, B.; Koshlak, H.; Novikov, V. Free Convection and Heat Transfer in Porous Ground Massif during Ground Heat Exchanger Operation. Materials 2022, 15, 4843. [Google Scholar] [CrossRef]
- Wang, D.; Wang, N.; Liu, H. Droplet deformation and breakup in shear-thinning viscoelastic fluid under simple shear flow. J. Rheol. 2022, 66, 585. [Google Scholar] [CrossRef]
- Peng, K.; Qin, F.G.; Jiang, R.; Kang, S. Interpreting the influence of liquid temperature on cavitation collapse intensity through bubble dynamic analysis. Ultrason. Sonochem. 2020, 69, 105253. [Google Scholar] [CrossRef]
- Qin, Z.; Alehossein, H. Heat transfer during cavitation bubble collapse. Appl. Therm. Eng. 2016, 105, 1067–1075. [Google Scholar] [CrossRef]
- Phan, T.-H.; Nguyen, V.-T.; Duy, T.-N.; Kim, D.-H.; Park, W.-G. Influence of phase-change on the collapse and rebound stages of a single spark-generated cavitation bubble. Int. J. Heat Mass Transf. 2022, 184, 122270. [Google Scholar] [CrossRef]
- Phan, T.-H.; Kadivar, E.; Nguyen, V.-T.; el Moctar, O.; Park, W.-G. Thermodynamic effects on single cavitation bubble dynamics under various ambient temperature conditions. Phys. Fluids 2022, 34, 023318. [Google Scholar] [CrossRef]
- Yu, Q.; Ma, X.; Xu, Z.; Zhao, J.; Wang, D.; Huang, Z. Thermodynamic effect of single bubble near a rigid wall. Ultrason. Sonochem. 2021, 71, 105396. [Google Scholar] [CrossRef]
- Pavlenko, A.; Szkarowski, A.; Janta-Lipińska, S. Research on Burning of Water Black Oil Emulsions. Rocz. Ochr. Sr. 2014, 16, 376–385. [Google Scholar]
- Pavlenko, A.M. Dispersed phase breakup in boiling of emulsion. Heat Transf. Res. 2018, 49, 633–641. [Google Scholar] [CrossRef]
- Pavlenko, A.M.; Koshlak, H. Intensification of Gas Hydrate Formation Processes by Renewal of Interfacial Area between Phases. Energies 2021, 14, 5912. [Google Scholar] [CrossRef]
- Pavlenko, A.M. Change of emulsion structure during heating and boiling. Int. J. Energy A Clean Environ. 2019, 20, 291–302. [Google Scholar] [CrossRef]
- Nigmatulin, R.I.; Taleyarkhan, R.P.; Lahey, R.T. Evidence for nuclear emissions during acoustic cavitation revisited. Proc. Inst. Mech. Eng. Part A J. Power Energy 2004, 218, 345–364. [Google Scholar] [CrossRef]
- Pavlenko, A. Numerical Modeling of the Behavior of Bubble Clusters in Cavitation Processes. Energies 2024, 17, 1741. [Google Scholar] [CrossRef]
- Tinguely, M.; Ohtani, K.; Farhat, M.; Sato, T. Observation of the Formation of Multiple Shock Waves at the Collapse of Cavitation Bubbles for Improvement of Energy Convergence. Energies 2022, 15, 2305. [Google Scholar] [CrossRef]
- Gonzalez-Avila, S.R.; Denner, F.; Ohl, C.-D. The acoustic pressure generated by the cavitation bubble expansion and collapse near a rigid wall. Phys. Fluids 2021, 33, 032118. [Google Scholar] [CrossRef]
- Kozubková, M.; Jablonská, J.; Bojko, M.; Pochylý, F.; Fialová, S. Multiphase Flow in the Gap Between Two Rotating Cylinders. MATEC Web Conf. 2020, 328, 02017. [Google Scholar] [CrossRef]
- Naseem, U.; Awan, M.B.; Saeed, B.; Abbas, N.; Nawaz, S.; Hussain, M. Experimental investigation of flow instabilities in a wide gap turbulent rotating Taylor-Couette flow. Case Stud. Therm. Eng. 2019, 14, 100449. [Google Scholar] [CrossRef]
- Ekanem, E.E.; Wilson, A.; Scott, J.L.; Edler, K.J.; Mattia, D. Continuous rotary membrane emulsification for the production of sustainable Pickering emulsions. Chem. Eng. Sci. 2022, 249, 117328. [Google Scholar] [CrossRef]
- Van der Schaaf, U.S.; Karbstein, H.P. Chapter 6—Fabrication of Nanoemulsions by Rotor-Stator Emulsification. In Nanoemulsions—Formulation, Applications, and Characterization; Academic Press: Cambridge, MA, USA, 2018; pp. 141–174. [Google Scholar] [CrossRef]
- Pavlenko, A.; Melnyk, V. Destruction of the Structure of Boiling Emulsions. Rocz. Ochr. Sr. 2020, 22, 70–81. [Google Scholar]
- Gazolu-Rusanova, D.; Lesov, I.; Tcholakova, S.; Denkov, N.; Ahtchi, B. Food grade nanoemulsions preparation by rotor-stator homogenization. Food Hydrocoll. 2020, 102, 105579. [Google Scholar] [CrossRef]
- Sneha, K.; Kumar, A. Nanoemulsions: Techniques for the preparation and the recent advances in their food applications. Innov. Food Sci. Emerg. Technol. 2022, 76, 102914. [Google Scholar] [CrossRef]
- Li, Y.; Mei, R.A.; Yang, Z. A facile method for preparation of emulsion using the high gravity technique. J. Colloid Interface Sci. 2017, 506, 120–125. [Google Scholar] [CrossRef]
- Huang, T.; Gong, S. Preparation of Emulsifier-Free Styrene–Acrylic Emulsion via Reverse Iodine Transfer Polymerization. Polymers 2021, 13, 3348. [Google Scholar] [CrossRef]
- Rajamanickam, P.; Weiss, A.D. Steady axisymmetric vortices in radial stagnation flows. Q. J. Mech. Appl. Math. 2021, 74, 367–378. [Google Scholar] [CrossRef]
- Adebayo, D.; Al-Ameri, J.; Tyukin, I.; Rona, A. Linear stability analysis of the flow between rotating cylinders of wide gap. Eur. J. Mech.-B/Fluids 2018, 72, 567–575. [Google Scholar] [CrossRef]
- Lee, H.-I. Shears and vortices of rotational couette flow in a cylindrical gap with radial injection and suction. Appl. Eng. Sci. 2021, 8, 100071. [Google Scholar] [CrossRef]
- Feng, J.; Muradoglu, M.; Kim, H.; Ault, J.; Stone, H. Dynamics of a bubble bouncing at a liquid/liquid/gas interface. J. Fluid Mech. 2016, 807, 324–352. [Google Scholar] [CrossRef]
- Zhang, H.; Li, C.; Zhao, M.; Zhu, Y.; Wang, W. Influence of interface wettability on explosive boiling of ultra-thin liquid films on a heated substrate using molecular dynamics simulations. In Proceedings of the 2017 IEEE 12th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Los Angeles, CA, USA, 9–12 April 2017; pp. 742–745. [Google Scholar] [CrossRef]
- Bai, L.; Yan, J.; Zeng, Z.; Ma, Y. Cavitation in thin liquid layer: A review. Ultrason. Sonochem. 2020, 66, 105092. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, W.; Shen, Y.; Wu, Y.; Zhao, G. The nonlinear characteristics of the pulsations, translations and the secondary Bjerknes force. Chaos Solitons Fractals 2021, 152, 111322. [Google Scholar] [CrossRef]
- Reuter, F.; Ohl, C.-D. Chapter 2—Nonspherical Collapse of Single Bubbles Near Boundaries and in Confined Spaces. In Cavitation and Bubble Dynamics—Fundamentals and Applications; Academic Press: Cambridge, MA, USA, 2021; pp. 37–72. [Google Scholar] [CrossRef]
- Lyu, X.; Zhu, Y.; Zhang, C.; Hu, X.; Adams, N.A. Modeling of Cavitation Bubble Cloud with Discrete Lagrangian Tracking. Water 2021, 13, 2684. [Google Scholar] [CrossRef]
- Reinke, P.; Ahlrichs, J.; Beckmann, T.; Schmidt, M. Bubble Dynamics in a Narrow Gap Flow under the Influence of Pressure Gradient and Shear Flow. Fluids 2020, 5, 208. [Google Scholar] [CrossRef]
- Li, G.; Chen, F.; Bie, W.; Zhao, B.; Fu, Z.; Wang, X. Cavitation Effect in Ultrasonic-Assisted Electrolytic In-Process Dressing Grinding of Nanocomposite Ceramics. Materials 2021, 14, 5611. [Google Scholar] [CrossRef]
- Du, J.; Chen, F. Cavitation dynamics and flow aggressiveness in ultrasonic cavitation erosion. Int. J. Mech. Sci. 2021, 204, 106545. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, G.; Petkovšek, M.; Long, K.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean. Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Radchenko, M.; Radchenko, A.; Trushliakov, E.; Pavlenko, A.; Radchenko, R. Advanced Method of Variable Refrigerant Flow (VRF) System Design to Forecast on Site Operation—Part 3: Optimal Solutions to Minimize Sizes. Energies 2023, 16, 2417. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, Y.; Lu, L.; Shi, C.; Huang, Y.; Mao, Z.; Duan, C.; Ren, X.; Guo, Y.; Huang, C. Hydrodynamic cavitation: A feasible approach to intensify the emulsion cross-linking process for chitosan nanoparticle synthesis. Ultrason. Sonochem. 2021, 74, 105551. [Google Scholar] [CrossRef]
- Brijkishore; Khare, R.; Prasad, V. Prediction of cavitation and its mitigation techniques in hydraulic turbines—A review. Ocean Eng. 2021, 221, 108512. [Google Scholar] [CrossRef]
- Zhang, B.; Banks, D.; Robles, V.; Cruz, L.F.D.; Aguilar, G. High Resolution Optical Investigation of Intensity and Solution Temperature Effects on Thermocavitation. Exp. Therm. Fluid Sci. 2022, 136, 110683. [Google Scholar] [CrossRef]
- Han, R.; Zhang, A.-M.; Tan, S.; Li, S. Interaction of cavitation bubbles with the interface of two immiscible fluids on multiple time scales. J. Fluid Mech. 2022, 932, A8. [Google Scholar] [CrossRef]
- Li, T.; Zhang, A.M.; Wang, S.P.; Li, S.; Liu, W.T. Bubble interactions and bursting behaviors near a free surface. Phys. Fluids 2019, 31, 042104. [Google Scholar] [CrossRef]
- Ren, J.; Zhao, B.; Wang, C.; Bi, M. Experimental study on the characteristics of the strong boiling induced by pressure relief at the top of vertical vessels. J. Loss Prev. Process Ind. 2020, 67, 104181. [Google Scholar] [CrossRef]
- Gao, W.; Qi, J.; Zhang, J.; Chen, G.; Wu, D. An experimental study on explosive boiling of superheated droplets in vacuum spray flash evaporation. Int. J. Heat Mass Transf. 2019, 144, 118552. [Google Scholar] [CrossRef]
- Sen, U.; Roy, T.; Ganguly, R.; Angeloni, L.A.; Schroeder, W.A.; Megaridis, C.M. Explosive behavior during binary-droplet impact on superheated substrates. Int. J. Heat Mass Transf. 2020, 154, 119658. [Google Scholar] [CrossRef]
- Chen, A.; Lin, T.F.; Ali, H.M.; Yan, W.M. Experimental study on bubble characteristics of time periodic subcooled flow boiling in annular ducts due to wall heat flux oscillation. Int. J. Heat Mass Transf. 2020, 157, 119974. [Google Scholar] [CrossRef]
- Desheng, C.; Man, Q.; Zhe, L.; Qi, L.; Guang, Z.; Zuchao, Z. Experimental study on the interaction of a cavitation bubble flanked by two particles. Acta Mech. 2021, 232, 4801–4810. [Google Scholar] [CrossRef]
- Liu, F.; Li, Z.; Wang, Z.; Dai, X.; Lee, C.F. Dynamics and primary breakup of cavitation bubbles under throttling conditions. Appl. Therm. Eng. 2019, 149, 678–687. [Google Scholar] [CrossRef]
- Sarkar, P.; Ghigliotti, G.; Franc, J.-P.; Fivel, M. Mechanism of material deformation during cavitation bubble collapse. J. Fluids Struct. 2021, 105, 103327. [Google Scholar] [CrossRef]
- Duan, H.; Chen, L.; Liang, X. Numerical Study of the Emission of Acoustic Energy of Single Collapsing Vapor Bubble Near a Rigid Wall. Water 2022, 14, 455. [Google Scholar] [CrossRef]
- Trummler, T.; Schmidt, S.J.; Adams, N.A. Effect of stand-off distance and spatial resolution on the pressure impact of near-wall vapor bubble collapses. Int. J. Multiph. Flow 2021, 141, 103618. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, Y.; Zhu, J.; Lv, L.; Tian, L. An experimental and numerical study on the dynamical behaviors of the rebound cavitation bubble near the solid wall. Int. J. Heat Mass Transf. 2021, 177, 121525. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Deng, J. Numerical Study of the Collapse of Multiple Bubbles and the Energy Conversion during Bubble Collapse. Water 2019, 11, 247. [Google Scholar] [CrossRef]
- Tang, J.; Yan, C.; Sun, L.; Li, Y.; Wang, K. Effect of liquid subcooling on acoustic characteristics during the condensation process of vapor bubbles in a subcooled pool. Nucl. Eng. Des. 2015, 293, 492–502. [Google Scholar] [CrossRef]
- Kobayashi, H.; Hayashi, M.; Kurose, K.; Ueno, I. On homogeneity of vapor bubbles’ oscillation and corresponding heat transfer characteristics and boiling sound in microbubble emission boiling (MEB). Int. J. Heat Mass Transf. 2022, 188, 122564. [Google Scholar] [CrossRef]
- Sinha, K.N.R.; Kumar, V.; Kumar, N.; Thakur, A.; Raj, R. Deep learning the sound of boiling for advance prediction of boiling crisis. Cell Rep. Phys. Sci. 2021, 2, 100382. [Google Scholar] [CrossRef]
- Shokrollahi, F.; Lau, K.K.; Tay, W.H. Performance comparison of ultrasonic-assisted and magnetic stirred absorption methods for CO2 separation. SN Appl. Sci. 2020, 2, 1217. [Google Scholar] [CrossRef]
- Leong, T.; Yasui, K.; Kato, K.; Harvie, D.; Ashokkumar, M.; Kentish, S. Effect of surfactants on single bubble sonoluminescence behavior and bubble surface stability. Phys. Rev. E 2014, 89, 043007. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S. A General Approach for Rectified Mass Diffusion of Gas Bubbles in Liquids Under Acoustic Excitation. ASME J. Heat Transf. 2014, 136, 042001. [Google Scholar] [CrossRef]
- Wang, H.; Yang, W.; Yan, X.; Wang, L.; Wang, Y.; Zhang, H. Regulation of bubble size in flotation: A review. J. Environ. Chem. Eng. 2020, 8, 104070. [Google Scholar] [CrossRef]
- Angulo, A.; van der Linde, P.; Gardeniers, H.; Modestino, M.; Rivas, D.F. Influence of Bubbles on the Energy Conversion Efficiency of Electrochemical Reactor. Joule 2020, 4, 555–579. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Hu, L. Jet formation and breakup inside highly deformed bubbles. Int. J. Heat Mass Transf. 2020, 163, 120507. [Google Scholar] [CrossRef]
- Radchenko, M.; Radchenko, A.; Trushliakov, E.; Pavlenko, A.; Radchenko, R. Advanced Method of Variable Refrigerant Flow (VRF) Systems Designing to Forecast On-Site Operation—Part 1: General Approaches and Criteria. Energies 2023, 16, 1381. [Google Scholar] [CrossRef]
- Pavlenko, A.; Koshlak, H. Study of the Dynamics of a Single Bubble. Energies 2024, 17, 4236. [Google Scholar] [CrossRef]
- Saito, T.; Toriu, M. Effects of a bubble and the surrounding liquid motions on the instantaneous mass transfer across the gas–liquid interface. Chem. Eng. J. 2015, 265, 164–175. [Google Scholar] [CrossRef]
- Bao, Y.; Jia, J.; Tong, S.; Gao, Z.; Cai, Z. A review on single bubble gas–liquid mass transfer. Chin. J. Chem. Eng. 2020, 28, 2707–2722. [Google Scholar] [CrossRef]
- Kazemi, K.; Vernet, A.; Grau, F.X.; Cito, S.; Fabregat, A. Passive scalar transfer rate at bubble interface in Carreau liquid in a transition regime. Int. J. Multiph. Flow 2022, 150, 104000. [Google Scholar] [CrossRef]
- Park, H.J.; Tasaka, Y.; Murai, Y. Spatial development of single void pulse in a horizontal turbulent bubbly channel flow investigated by a time-resolved two-laser measurement. Int. J. Multiph. Flow 2022, 146, 103867. [Google Scholar] [CrossRef]
- Kováts, P.; Thévenin, D.; Zähringer, K. Influence of viscosity and surface tension on bubble dynamics and mass transfer in a model bubble column. Int. J. Multiph. Flow 2020, 123, 103174. [Google Scholar] [CrossRef]
- Valdés, J.P.; Kahouadji, L.; Matar, O.K. Current advances in liquid–liquid mixing in static mixers: A review. Chem. Eng. Res. Des. 2022, 177, 694–731. [Google Scholar] [CrossRef]
- Farzi, G.A.; Rezazadeh, N.; Nejad, A.P. Homogenization efficiency of two immiscible fluids in static mixer using droplet tracking technique. J. Dispers. Sci. Technol. 2016, 37, 1486–1493. [Google Scholar] [CrossRef]
- Haddadi, M.M.; Hosseini, S.H.; Rashtchian, D.; Olazar, M. Comparative analysis of different static mixers performance by CFD technique: An innovative mixer. Chin. J. Chem. Eng. 2020, 28, 672–684. [Google Scholar] [CrossRef]
- Marcos, S.; Meinecke, M.; Kilzer, A.; Petermann, M. Study of L–L water-in-oil dispersions generated in SMX-Plus static mixers with dissolved CO2 under high pressure. J. Supercrit. Fluids 2018, 132, 24–32. [Google Scholar] [CrossRef]
- Valdés, J.P.; Asuaje, M.; Ratkovich, N. Study of an ESP’s performance handling liquid-liquid flow and unstable O-W emulsions Part I: Experimental. Chem. Eng. Sci. 2020, 223, 115726. [Google Scholar] [CrossRef]
- Koshlak, H. Synthesis of Zeolites from Coal Fly Ash Using Alkaline Fusion and Its Applications in Removing Heavy Metals. Materials 2023, 16, 4837. [Google Scholar] [CrossRef]
- Häfeli, R.; Rüegg, O.; Altheimer, M.; von Rohr, P.R. Investigation of emulsification in static mixers by optical measurement techniques using refractive index matching. Chem. Eng. Sci. 2016, 143, 86–98. [Google Scholar] [CrossRef]
- Pavlenko, A.; Koshlak, H. Heat and Mass Transfer During Phase Transitions in Liquid Mixtures. Rocz. Ochr. Sr. 2019, 21, 234–249. [Google Scholar]
- Vashisth, V.; Nigam, K.; Kumar, V. Nanoparticle de-agglomeration in viscous fluids using different high shear mixer geometries. Chem. Eng. Sci. 2022, 248, 117132. [Google Scholar] [CrossRef]
- Maindarkar, S.; Dubbelboer, A.; Meuldijk, J.; Hoogland, H.; Henson, M. Prediction of emulsion drop size distributions in colloid mills. Chem. Eng. Sci. 2014, 118, 114–125. [Google Scholar] [CrossRef]
- Gall, V.; Runde, M.; Schuchmann, H.P. Extending Applications of High-Pressure Homogenization by Using Simultaneous Emulsification and Mixing (SEM)—An Overview. Processes 2016, 4, 46. [Google Scholar] [CrossRef]
- Baudron, V.; Taboada, M.; Gurikov, P.; Smirnova, I.; Whitehouse, S. Production of starch aerogel in form of monoliths and microparticles. Colloid Polym. Sci. 2020, 298, 477–494. [Google Scholar] [CrossRef]
- Ryan, D.J.; Baker, M.R.; Kowalski, A.J.; Simmons, M.J. Emulsification using a “Sonolator” liquid whistle: A new correlation for droplet size from pilot-scale experiments. Chem. Eng. Sci. 2018, 189, 369–379. [Google Scholar] [CrossRef]
- Yamamoto, T.; Matsutaka, R.; Komarov, S.V. High-speed imaging of ultrasonic emulsification using a water-gallium system. Ultrason. Sonochem. 2021, 71, 105387. [Google Scholar] [CrossRef]
- Radchenko, A.; Radchenko, M.; Koshlak, H.; Radchenko, R.; Forduy, S. Enhancing the Efficiency of Integrated Energy Systems by the Redistribution of Heat Based on Monitoring Data. Energies 2022, 15, 8774. [Google Scholar] [CrossRef]
- Liu, L.; Niu, J.; Wu, J.-Y. Preparation of Stable Phase Change Material Emulsions for Thermal Energy Storage and Thermal Management Applications: A Review. Materials 2022, 15, 121. [Google Scholar] [CrossRef]
- Felix, M.; Guerrero, A.; Carrera-Sánchez, C. Optimization of Multiple W1/O/W2 Emulsions Processing for Suitable Stability and Encapsulation Efficiency. Foods 2022, 11, 1367. [Google Scholar] [CrossRef]
- Taha, A.; Ahmed, E.; Ismaiel, A.; Ashokkumar, M.; Xu, X.; Pan, S.; Hu, H. Ultrasonic emulsification: An overview on the preparation of different emulsifiers-stabilized emulsions. Trends Food Sci. Technol. 2020, 105, 363–377. [Google Scholar] [CrossRef]
- Gheisari, S.M.M.M.; Gavagsaz-Ghoachani, R.; Malaki, M.; Safarpour, P.; Zandi, M. Ultrasonic nano-emulsification—A review. Ultrason. Sonochem. 2019, 52, 88–105. [Google Scholar] [CrossRef]
- Sarangapany, A.K.; Murugesan, A.; Annamalai, A.S.; Balasubramanian, A.; Shanmugam, A. An overview on ultrasonically treated plant-based milk and its properties—A Review. Appl. Food Res. 2022, 2, 100130. [Google Scholar] [CrossRef]
- Jun, S.-H.; Kim, H.; Lee, H.; Song, J.E.; Park, S.G.; Kang, N.-G. Synthesis of Retinol-Loaded Lipid Nanocarrier via Vacuum Emulsification to Improve Topical Skin Delivery. Polymers 2021, 13, 826. [Google Scholar] [CrossRef]
- Norcino, L.B.; Mendes, J.F.; Figueiredo, J.d.A.; Oliveira, N.L.; Botrel, D.A.; Mattoso, L.H.C. Development of alginate/pectin microcapsules by a dual process combining emulsification and ultrasonic gelation for encapsulation and controlled release of anthocyanins from grapes (Vitis labrusca L.). Food Chem. 2022, 391, 133256. [Google Scholar] [CrossRef]
- Tan, C.; McClements, D.J. Application of Advanced Emulsion Technology in the Food Industry: A Review and Critical Evaluation. Foods 2021, 10, 812. [Google Scholar] [CrossRef]
- Davies, J.T. A physical interpretation of drop sizes in homogenizers and agitated tanks, including the dispersion of viscous oils. Chem. Eng. Sci. 1987, 42, 1671–1676. [Google Scholar] [CrossRef]
- Pavlenko, A.M.; Basok, B.I. Kinetics of water evaporation from emulsions. Heat Transf. Res. 2005, 36, 425–430. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlenko, A. Analysis of Methods for Intensifying Heat and Mass Transfer in Liquid Media. Energies 2025, 18, 1419. https://doi.org/10.3390/en18061419
Pavlenko A. Analysis of Methods for Intensifying Heat and Mass Transfer in Liquid Media. Energies. 2025; 18(6):1419. https://doi.org/10.3390/en18061419
Chicago/Turabian StylePavlenko, Anatoliy. 2025. "Analysis of Methods for Intensifying Heat and Mass Transfer in Liquid Media" Energies 18, no. 6: 1419. https://doi.org/10.3390/en18061419
APA StylePavlenko, A. (2025). Analysis of Methods for Intensifying Heat and Mass Transfer in Liquid Media. Energies, 18(6), 1419. https://doi.org/10.3390/en18061419