Abstract
With advancements in cable manufacturing processes, the physical parameters of certain cable conductors fall outside of the scope specified by the IEC60287-1-1 standard, and the alternating current (AC) resistance calculated using the IEC standard may lead to reliability issues in the thermal evaluation of cable lines. Therefore, conducting an AC resistance test on cable conductors becomes critical for the thermal evaluation of cable lines. The source of error in the existing AC resistance test was analyzed first. It was found that the characteristics of the source used in the test lead to an error between the test value and the actual value of AC resistance. Moreover, an optimized AC resistance testing method based on active power was proposed to decrease the error. The accuracy of the method was also demonstrated. Finally, AC resistance tests were conducted on cable conductors with different cross-sectional areas, segmental methods, and oxidation methods by using the proposed method. The test results are also thoroughly discussed.
1. Introduction
As a kind of compact and reliable transmission equipment, power cables are widely used in the construction and renovation of urban power grids [1,2,3,4,5]. However, due to the contradiction between the rapid growth of the demand for electrical energy and the increasing challenges of establishing new transmission corridors, it is critical to focus on enhancing the ampacity of existing transmission lines [6,7,8,9]. Since the ampacity of a cable is determined by its maximum operating temperature, the thermal evaluation result of a cable is the basis for load scheduling. Currently, the thermal evaluation of a cable is mainly carried out based on the IEC standards, which utilize the load, the physical parameters of the cable, and environmental parameters to perform a thermal evaluation, as shown in Figure 1 [10,11,12,13,14].
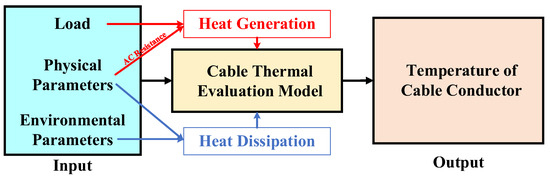
Figure 1.
Cable thermal evaluation model in IEC standard.
The alternating current (AC) resistance of a cable conductor is directly correlated with the cable’s heat generation within the physical parameters of the cable. Therefore, advanced conductor manufacturing techniques have been implemented to decrease the heat generation of the cable, such as stranded conductors and segmental conductors. The value of the reference parameter of these conductors is specified by the IEC standard, which is applied to the conductors with a cross-sectional area of 1600 mm2 or less [15,16,17]. However, the scope of application specified by the IEC standard is not suitable to new cable conductors, such as conductors with large cross-sections (>1600 mm2) and oxidation [18], resulting in reliability issues in the thermal evaluation of cable lines [19,20,21]. Therefore, testing AC resistance is essential to conduct a thermal evaluation of cable lines. The methods of measuring conductor AC resistance are mainly divided into the thermal measurement method and electrical measurement method [22,23]. The thermal measurement method derives the AC resistance from the heat generated by the conductor and the material parameters of each layer. However, due to the long preparation time and large errors faced with this method, its application is limited. In contrast, the voltage–current phase difference method calculates AC resistance by measuring the voltage and current at both ends of the cable conductor and the phase difference between the two, which has the advantages of simple operation and high accuracy, so it is widely used. Research on the calculation and experimental measurement methods of the alternating current (AC) equivalent resistance of cable conductors has not yet established any industry standards, nor have widely adopted methods and measurement devices been developed. Analyzing the existing measurement methods and equipment has revealed that each method has its own limitations, making it difficult to meet large-scale testing demands in future engineering applications. Further research and explorations of new measurement methods and devices are still required to improve the accuracy and reliability of AC equivalent resistance measurements [24,25]. Therefore, an error analysis of existing AC resistance electrical measurement methods was conducted in this paper. The results show that the error between the test value and the actual value of AC resistance is inevitable due to the characteristics of the source used in the test. Secondly, an optimized AC resistance testing method based on active power was proposed. Thirdly, AC resistance tests were carried out on cable conductors with different cross-sectional areas, segmental methods, and oxidation methods. Finally, the influence of these three physical parameters on the AC resistance of cable conductors was discussed, as well as the limitations of the IEC standard based on the test results.
2. Theory of the Optimized Method
2.1. Error Analysis of AC Resistance Test Results for Cable Conductors
Currently, the current amplitude I0, the voltage amplitude U0 across the cable conductor, and the phase difference θ between the current and voltage are measured to derive the test value of the cable conductor’s AC resistance, as Equation (1) shows:
Clearly, since the derivation of Equation (1) is based on the phasor, it requires both the voltage and current to have sinusoidal waves of the same frequency. The AC resistance testing circuit is recommended by the report of CIGRE TB 894 [24], as shown in Figure 2.
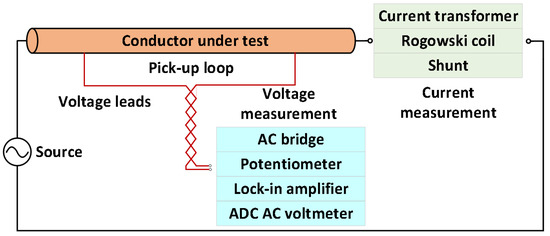
Figure 2.
Wiring method for AC resistance testing circuit in CIGRE TB 894.
Currently, the combination of a voltage regulator and a transformer is typically used for the source of the testing circuit shown above. There are mainly two types of voltage regulators; one type is the auto-transformer, which adjusts the voltage by altering the positions of the electric brushes. However, issues such as brush wear, aging, and poor contact arise over time, resulting in the distortion of the output voltage. Figure 3 illustrates the output voltage from a source using an auto-transformer. It was found that the voltage deviates from the ideal sinusoidal waveform.
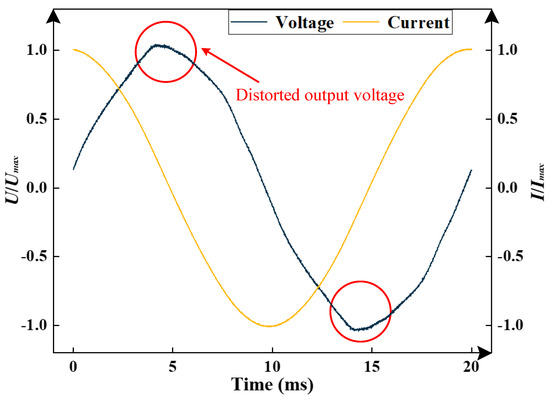
Figure 3.
Output voltage of auto-transformer voltage regulator.
The other type is the power electronic voltage regulator, which adjusts the voltage by altering the waveform of the input voltage. Obviously, distortion is bound to be introduced into the source [26].
Therefore, it is necessary to analyze the error between the test values and actual values of AC resistance under the distorted voltage and current. Suppose a voltage U contains up to the m-th harmonic; the expression of U is given by the following:
where Ak is the amplitude of the k-th voltage harmonic; Ω is the angular frequency of the power frequency.
When U is treated as a sinusoidal wave U*, the expression of U* is given by Equation (3):
where A is the maximum value of U. When t = 0, Equation (4) is deduced:
Similarly, for a current I containing up to the n-th harmonic,
where Bk is the amplitude of the k-th current harmonic; B is the amplitude of I. Therefore, according to the superposition theorem, the test value R* and the actual value R can be determined using Equations (8) and (9), respectively:
It is clear that R* is not equal to R. In other words, there are errors between the test value and the actual value of AC resistance under the distorted voltage and current. The reason for the errors is that only the maximum values of the voltage and current are used for the derivation of AC resistance. Therefore, it is necessary to propose a new testing method for AC resistance based on the measured data.
2.2. Optimized Method of AC Resistance Test Based on Active Power
To decrease the error between the test value and the actual value of AC resistance under the distorted voltage and current, an optimized method based on active power is proposed in this paper [27,28]. For voltage data points u(tk) and current data points i(tk), at the sampling time tk, the active power can be calculated using Equation (10):
where p(tk) is the active power of the cable conductor at tk; n is the number of data points. The total active power P is calculated by the Simpson interpolation method, as shown in Equation (11):
where Δt is the sample interval of the measured data. Next, the root mean square (RMS) value of the current I can be calculated using Equation (12):
The value of AC resistance per unit length of the conductor RAC is given by Equation (13):
where L is the length of the tested cable conductor.
The optimized method utilizes all measured data of the voltage and current, which take into account the distortion of the voltage and current when testing AC resistance. It is worth noting that if the waveform is different for each test, then the calculated value of the AC resistance of the cable should also be different. Subsequently, an AC resistance testing system is established to validate the optimized method’s results.
3. Design and Verification of AC Resistance Testing System
In this section, an AC resistance testing system is established first. And an accuracy verification test of the optimized method is then performed using the testing system, which provides the experimental foundation for subsequent AC resistance tests of different cable conductors.
3.1. The Design of the AC Resistance Testing System
The structure of the cable conductor’s AC resistance testing system consists of four main components, the source, the testing circuit, the sample cable, and the data processing unit, as shown in Figure 4. The experimental platform is shown in Figure 5.
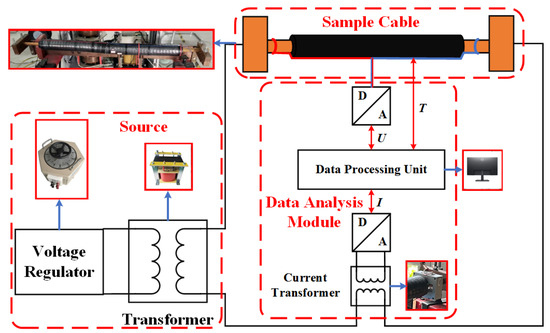
Figure 4.
Testing system of cable conductor’s AC resistance.

Figure 5.
The actual installation of the experimental platform.
The source of the testing system consists of a voltage regulator and a transformer. During testing, the output voltage of the voltage regulator can be adjusted to control the current passing through the sample cable. Firstly, the sample cable is stripped to expose the conductor. Meanwhile, clamps with a fastening structure are used to connect the conductor and the testing circuit. Secondly, to decrease the influence of the external electromagnetic wave during the test, the voltage measurement leads are securely attached to the surface of the cable. Additionally, the ends of the voltage leads are spirally wound before being connected to the measurement module. Thirdly, temperature sensors are installed on the conductor of the sample cable by perforation, as shown in Figure 6. Therefore, real-time monitoring of the conductor temperature is applied for the test to ensure the sample cable has a stable temperature. Finally, the voltage and current data can be stored and exported through the data processing unit.
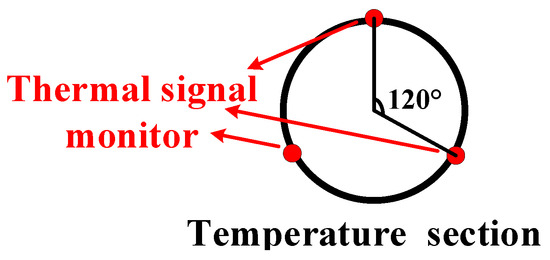
Figure 6.
Installation method for thermal signal monitor.
3.2. Steps of AC Resistance Test
As shown in Figure 7, the AC resistance test of the cable conductors follows the steps below:
- (1)
- Installing the Sample Cable: Choose clamps to match the cross-sectional area of the sample cable conductor. Then, connect and fasten the sample cable to the clamps. Meanwhile, install thermal signal monitors on the sample cable.
- (2)
- Connecting the Testing Circuit: Connect the source, the testing circuit, the sample cable, and the data processing unit, as shown in Figure 4.
- (3)
- Conducting the Test: Applying the specified current to the sample cable causes the cable to heat up. If the temperature variation ΔT1h of the cable conductor remains within ±1 °C for one hour near the target temperature, the cable conductor’s temperature is considered to be stable. After this, multiple sets of voltage and current data should be recorded. Repeat the test by varying the current through the cable conductor and set the conductor temperature to the recommended temperatures of 40 °C, 50 °C, 60 °C, 70 °C, and 80 °C. Ensure that the temperature points of these settings are all traversed.
- (4)
- Deriving AC Resistance at Different Temperatures: Export the measured voltage and current data of the sample cable. Then, for each temperature of the sample cable, calculate the AC resistance of the conductor using Equations (10)–(13). Then, calculate the average value as the AC resistance of the cable conductor for each temperature to obtain a set of AC resistance data at different temperatures.
- (5)
- Deriving AC Resistance at 20 °C: Perform linear fit of the AC resistance–temperature curve R(T) by using the AC resistance–temperature data obtained in step (4). Then, obtain the AC resistance of the sample cable conductor at 20 °C based on R(T).
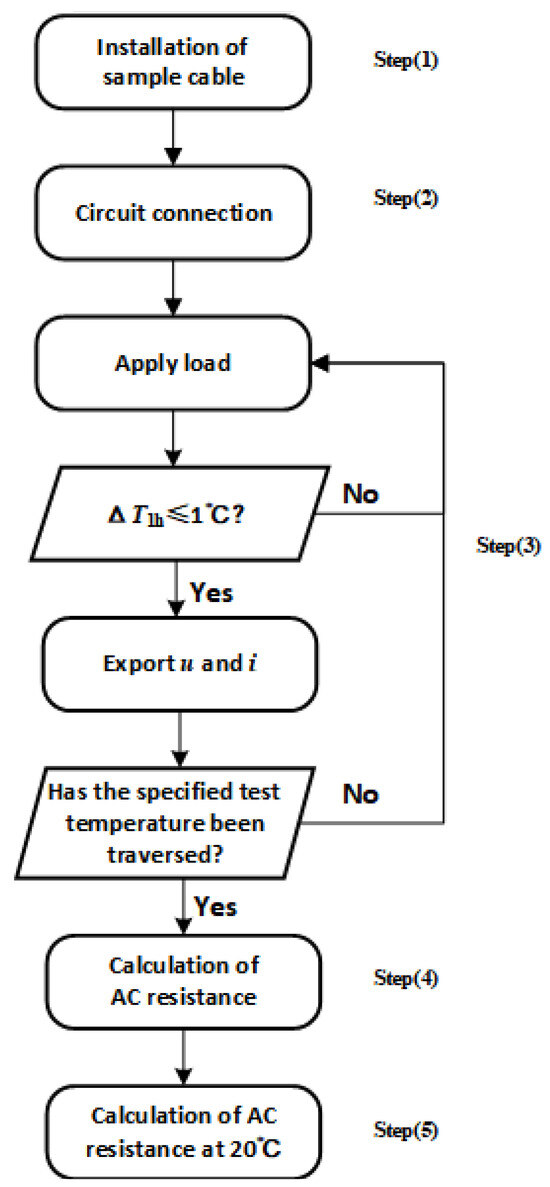
Figure 7.
Procedure for testing AC resistance.
3.3. Accuracy Verification of the Optimized Method
It is necessary to define a standard value before performing an accuracy verification test of the optimized method. The calculating model of the solid copper conductor is established in the report of CIGRE TB 272, as shown in Figure 8. The Maxwell’s Equations (14)–(16) and the equation of Joule losses WJ (17) are presented to describe the electromagnetism thermal field in the conductor [29,30,31].
where ρ represents the radial distance in the polar coordinates; Ez is the electric field component in the z direction; Ω is the angular frequency of the electromagnetic wave; Hρ is the component of the magnetic field along the polar angle (ρ); j is an imaginary number unit, which represents a complex number; Hθ is the component of the magnetic field in the polar angle direction (θ); and WJ is the energy density. Finally, the calculation method for the AC resistance of cable conductors Rac0 in the IEC standard is derived from the perspective of AC losses [15]:
where Rdc is the direct current (DC) resistance of the conductor; μ is the magnetic permeability of the conductor; and f is the power frequency. Therefore, it is accurate to calculate the AC resistance of the solid conductors using the IEC standard.
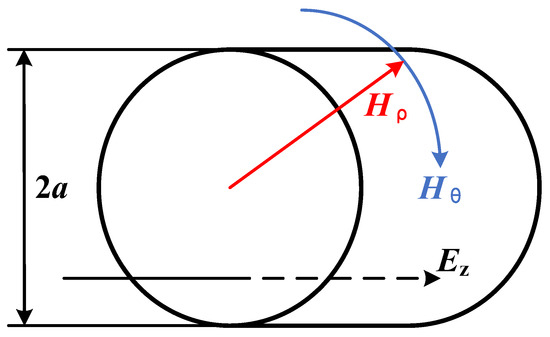
Figure 8.
Calculating model of solid copper conductor.
In the accuracy verification test, a solid copper conductor with a cross-sectional area of 2000 mm2 was selected as the sample. The AC resistance of the sample conductor Ract was tested at different temperatures following the steps in Section 2.2. The test value was then compared with the AC resistance value obtained from the IEC standard Rac0, as shown in Figure 9.
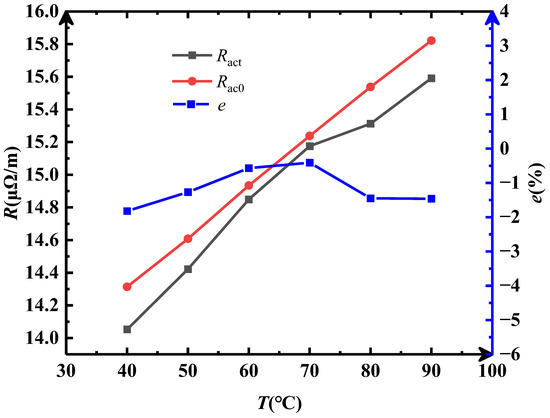
Figure 9.
The results of the accuracy verification test for the optimized method.
It was found that the error between Ract and Rac0 is less than 2% at the temperatures of 40 °C, 50 °C, 60 °C, 70 °C, 80 °C, and 90 °C, which means the test value of the optimized method is faithful for an AC resistance test of a cable conductor. Additionally, the error of the AC resistance is the smallest within temperatures between 60 and 70 °C. Therefore, it is recommended to choose data at this temperature range for the derivation of AC resistance at 20 °C.
3.4. An Error Analysis of the AC Resistance Testing System
The formula for the cable’s AC resistance is as follows:
The formula considering errors is as follows:
where u is the instantaneous value of voltage measurement, i is the instantaneous value of current measurement, t is the sampling time, L is the measurement length, ui is the voltage drop across the sampling resistor, r is the sampling resistor value, and NT is the CT ratio.
Due to the time base error of 25 ppm in the measuring instrument used for voltage measurement (for intervals greater than 1 ms), and with the measurement time being the duration of 10 power frequency cycles, the maximum error in time measurement is 200 × ±25 × 10−6 = ±0.005 ms. Since the error of 25 ppm is very small, it can be neglected in the calculations. The voltage measurement accuracy can be estimated as the vertical range × ±3%. The vertical range when measuring the cable voltage at both ends is 2 V, so the maximum error is ±0.06 V.
The primary side current measurement component used is a 5000:5 0.2 S class CT for measuring the cable current, and thus, the maximum error in the CT measurement is ±2 A. The accuracy of the secondary side measurement loop’s sampling resistor is 0.01 Ω ± 5%, which results in a maximum error of ±0.0005 Ω. The voltage measurement accuracy can also be estimated as the vertical range × ±3%. When measuring the voltage across the sampling resistor, the vertical range is 0.5 V, so the maximum error is ±0.015 V. When steel tape is used for measurement, the error is estimated at ±1%.
Considering the errors in the parameters involved in the calculation using Equation (21), namely Δu, Δui, Δr, ΔNT, and ΔL, which follow a normal distribution N(μ,σ), and if a confidence level of 99.7% is selected, then σ = Emax/3, and the true value range of the parameters is μ + σ/3 × randn (where randn is a standard normal distribution random value). Here, μ is the measured or nominal value of the parameter, and Emax is the maximum error of the parameter. By applying the Monte Carlo method, the error estimation of the calculation results can be performed using Equation (21).
For a 2000 mm2 solid copper conductor measurement, an average of three tests is calculated. The AC resistance of the cable sample at 90 °C is 15.5912 × 10−6 ± 3.39% (Ω/m). As long as the true value of the calculation parameters falls within the range specified in Equation (21), the maximum error of the calculation result is within ±3.5% with a 95% confidence level.
A further analysis of the contribution of calculation parameter errors to the calculation result error reveals (by calculating the partial derivative of the result with respect to each parameter) that the accuracy of the sampling resistor has the largest effect on the test result accuracy. When the maximum error of the sampling resistor is reduced from ±5% to ±2%, the maximum error of the test result can be reduced to approximately ±1.54%.
4. Preparation of Test Samples
To investigate the influence of different cross-sectional areas on the AC resistance of cable conductors, the cables shown in Table 1 are used for the samples.

Table 1.
Sample cables with different cross-sectional areas.
To investigate the influence of different segmentation conductors on the AC resistance of cable conductors, the cables shown in Table 2 are used for the samples. Schematic diagrams of the four segmental methods described in Table 2 are shown in Figure 10. It can be seen that the degree of segmentation on the sample conductors increases from XLPE-S1 to XLPE-S4.

Table 2.
Sample cables with different segmental conductors.
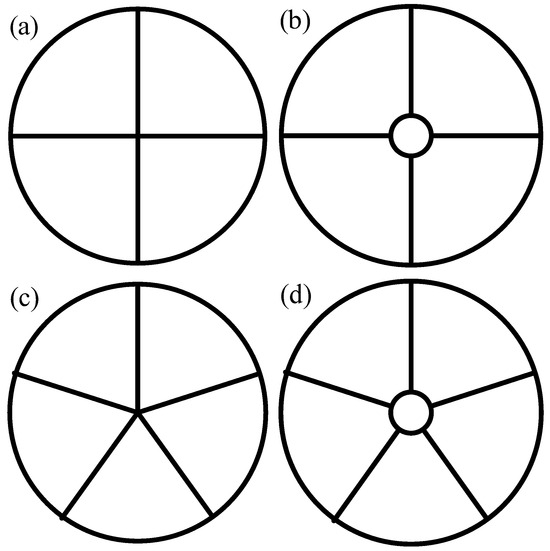
Figure 10.
Schematic diagram of different segmental sample cables: (a) 4 + 0; (b) 4 + 1; (c) 5 + 0; and (d) 5 + 1.
To investigate the influence of different oxidative conductors on the AC resistance of cable conductors, the cables shown in Table 3 are used for the samples. Schematic diagrams of different oxidized cable conductors are shown in Figure 11.

Table 3.
Different oxidation methods of sample cables.
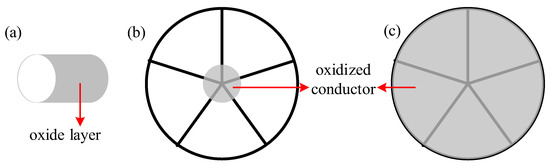
Figure 11.
Schematic diagram of different oxidative cable conductor (a) oxidation methods of copper wire: (b) partial oxidation; (c) entire oxidation.
5. Results and Discussion
Based on the optimized method proposed, the influence of different cross-sectional area conductors, segmental conductors, and oxidized conductors on AC resistance is investigated in this section. Furthermore, the test values are compared with the calculated values derived from the IEC standard.
A comparison of the test value and the IEC standard value of AC resistance from XLPE-C1 to XLPE-C5 at 20 °C is presented in Figure 12. It was found that the IEC standard values are larger than the test values when the cross-sectional area of the conductor is smaller than 2000 mm2. Therefore, it can be considered that the IEC standard provides a conservative estimate of AC resistance when cable conductors have smaller cross-sectional areas, ensuring reliable results in the evaluation of line design.
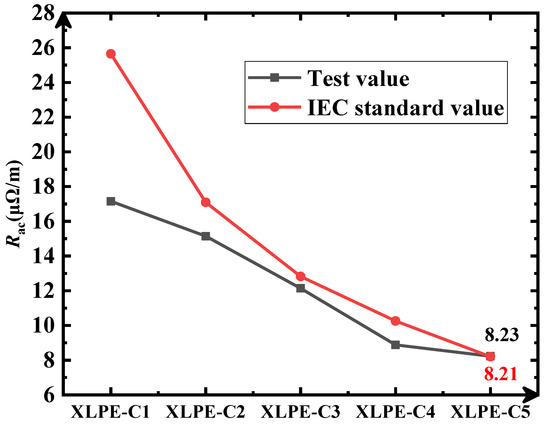
Figure 12.
Comparison between test and IEC standard values (800–2000 mm2 cable conductor).
However, the IEC standard value is smaller than the test value for the conductor with a cross-sectional area of 2000 mm2. It can be considered that the conservatism of the IEC standard is lost on this kind of conductor. A comparison of the test value and the IEC standard value of AC resistance from XLPE-C6 to XLPE-C8 at 20 °C is presented in Figure 13. It is obvious that the IEC standard values are consistently lower than the test values for cables with cross-sectional areas over 2000 mm2. Moreover, the error between the IEC standard and the test values has a positive correlation with the cross-sectional area of the conductor. Therefore, it is not suggested to apply the IEC standard to the evaluation for load scheduling because it could potentially lead to overheating during the actual operation of the cable lines.
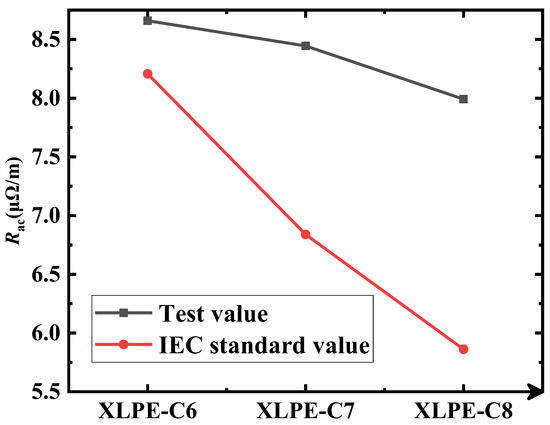
Figure 13.
Comparison of test and IEC standard values (2500–3500 mm2 cable conductor).
A comparison of the test value and the IEC standard value of AC resistance from XLPE-S1 to XLPE-S4 at 20 °C is presented in Figure 14. Since the IEC standard does not specify the relevant calculation parameter values on the cable with 4 + 1 and 5 + 1 segmental conductors, the AC resistance values of 4 + 0 and 5 + 0 segmental conductors were used as references. It was found that the IEC standard value is larger than the test value of AC resistance due to the samples having a cross-sectional area of 800 mm2. Moreover, as the degree of splitting increases, the test value of AC resistance has a negative correlation with the degree of segmentation on the sample conductors, with a maximum error of 20.15%.
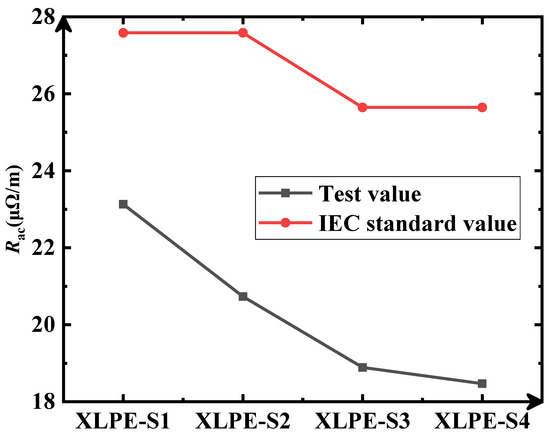
Figure 14.
Comparison of test and IEC standard values (different segmental conductors).
A comparison of the test value and the IEC standard value of AC resistance from XLPE-O1 to XLPE-O3 at 20 °C is presented in Figure 15. Since the IEC standard does not specify the relevant calculation parameter values on the cable with oxidation, the AC resistance values of a 5 + 0 segmental conductor without oxidation were used as references. It was found that the degree of oxidation has a negative correlation with the AC resistance of the conductor based on the test results, with a maximum reduction of 5.70%.
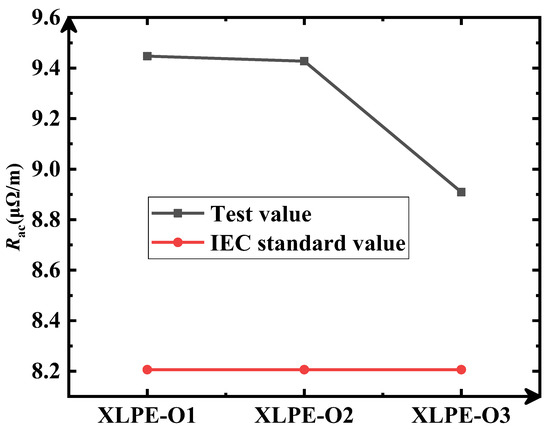
Figure 15.
Comparison of test and IEC standard values (different oxidated cable conductors).
6. Conclusions
This paper presented the limitations of AC resistance calculations of the IEC standard. These calculations are critical to conduct an AC resistance test on the cable conductor. Moreover, the error between the test value and the actual value of AC resistance was analyzed. Afterwards, an optimized AC resistance testing method based on the active power for AC resistance was proposed to decrease the error. Finally, AC resistance tests were conducted on different cable conductors after verifying the accuracy of the proposed testing method. The main conclusions of this study are as follows:
- (1)
- Waveform distortion is a common issue in the existing AC resistance test, which leads to an error between the test value and the actual value of AC resistance when using the testing method recommended by CIGRE TB 894.
- (2)
- An optimized AC resistance testing method based on active power is proposed. The results of the accuracy verification test of the testing method show that the AC resistance measuring error of the testing method does not exceed 2%.
- (3)
- The conservatism of the AC resistance evaluation of the IEC standard is negatively correlated with the cross-sectional area of the cable conductor. Furthermore, the conservatism is lost when the cross-sectional area of the cable conductor exceeds 2000 mm2.
- (4)
- The AC resistance of cable conductors is negatively correlated with both the degree of segmentation and the number of oxidized copper wires in the conductor. Therefore, increasing the degree of segmentation and the number of oxidized copper wires in production can effectively reduce the AC resistance of cable conductors.
Author Contributions
Conceptualization, G.Y.; Methodology, G.Y.; Software, G.Y. and H.C.; Validation, Y.Z., X.X. and X.L.; Formal analysis, H.C.; Resources, X.X., X.L., D.D. and G.L.; Data curation, Y.Z.; Writing—original draft, G.Y. and Y.Z.; Writing—review & editing, G.L.; Supervision, D.D.; Funding acquisition, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Xiaofeng Xu was employed by the company Shanghai Electric Cable Research Institute Co., Ltd., and author Xiaodong Liu was employed by the company Guangzhou Nanyang Cable Group Co., Ltd., The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| I0 | current amplitude |
| U0 | voltage amplitude |
| Θ | phase difference |
| Ak | amplitude of k-th voltage harmonic |
| Ω | angular frequency of power frequency |
| Bk | amplitude of k-th current harmonic |
| u(tk) | voltage data points |
| i(tk) | current data points |
| Tk | sampling time |
| p(tk) | active power |
| n | number of data points |
| RAC | AC resistance |
| ρ | radial distance |
| Ez | electric field component in z direction |
| Hρ | component of magnetic field along polar angle (ρ) |
| j | imaginary number unit |
| Hθ | component of magnetic field in polar angle direction (θ) |
| WJ | energy density |
| μ | magnetic permeability |
| f | power frequency |
References
- Zeng, T.; Yang, G.; Yuan, M.; Chen, Y.; Fang, F.; Xu, X. Theoretical modeling and experimental verification of AC resistance in large cross-section XLPE single-core cables. In Proceedings of the 2024 9th International Conference on Power and Renewable Energy (ICPRE), Guangzhou, China, 20–23 September 2024; pp. 77–82. [Google Scholar]
- Li, L. Design and selection of conductor structure for large cross-section high-voltage cable. Wire Cable 2021, 64, 41–43+46. [Google Scholar]
- Zhang, H.; Zhang, J.; Duan, L.; Xie, S.; Xue, J. Application status of XLPE insulated submarine cable used in offshore wind farm in China. J. Eng. 2017, 13, 702–707. [Google Scholar] [CrossRef]
- Lin, R.; Huang, Y.; Lu, Y.; Li, Q.; Liu, S.; Luo, G. Research on optimal selection of submarine cable cross-section considering ampacity matching in all laying scenarios. In Proceedings of the 2024 4th Power System and Green Energy Conference (PSGEC), Shanghai, China, 22–24 August 2024; pp. 604–611. [Google Scholar]
- Song, Y.; Chen, W.; Wan, F.; Zhang, Z.; Du, L.; Wang, P.; Li, J.; Wu, Z.; Huang, H. Online multi-parameter sensing and condition assessment technology for power cables: A review. Electr. Power Syst. Res. 2022, 210, 108140. [Google Scholar] [CrossRef]
- Wang, J.; Li, W.; Zhang, W.; Wan, B.; Zha, J. Aging and life control of cross-linked polyethylene as cable insulation material. Acta Phys. Sin. 2024, 73, 078801. [Google Scholar] [CrossRef]
- Zhu, X.; Yin, Y.; Wu, J.; Wang, X. Study on aging characteristics of XLPE cable insulation based on quantum chemical calculation. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1942–1950. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, T.; Lin, W.; Wu, S.; Feng, Y.; Zuo, X.; Zhang, Y. Electrical resistance performance of cable accessory interface considering thermal effects. Materials 2023, 16, 4122. [Google Scholar] [CrossRef] [PubMed]
- Nie, Y.; Zhao, X.P.; Li, S.T. Research progress in condition monitoring and insulation diagnosis of XLPE cable. High Volt. Eng. 2020, 46, 1361–1371. [Google Scholar]
- Zhao, Y.; Xie, Y.; Zhao, Y.; Huang, J.; Fan, X.; Nie, Y.; Liu, G. Dynamic ageing research of cross-linked polyethylene cable insulation based on temporal-spatial dimension under combined electro-thermal effect. High Volt. 2023, 8, 1067–1081. [Google Scholar] [CrossRef]
- Cabral, S.H.L.; Bertoli, S.L.; Medeiros, A.; Hillesheim, C.R.; De Souza, C.K.; Stefenon, S.F. Practical aspects of the skin effect in low frequencies in rectangular conductors. IEEE Access 2021, 9, 49424–49433. [Google Scholar] [CrossRef]
- Jabłoński, P.; Kusiak, D.; Szczegielniak, T.; Piątek, Z. The proximity effect in twin line with round conductors placed in conductive medium. Energies 2020, 13, 6087. [Google Scholar] [CrossRef]
- Raicevic, N.B.; Aleksic, S.R.; Iatcheva, I.; Barukcic, M. Enhanced method for pulse skin effect calculation of cylindrical conductors. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2020, 39, 623–635. [Google Scholar] [CrossRef]
- Tabei, B.; Ametani, A.; Gole, A.M.; Kordi, B. Study of skin and proximity effects of conductors for MTL-based modeling of power transformers using FEM. In Proceedings of the IEEE Power Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- GB/T 3048.4-2007; Performance Test Methods for Wires and Cables—Part 4: DC Resistance Test of Conductors. Standardization Administration of China: Beijing, China, 2007.
- IEC 60228-2004; Conductors of Insulated Cables. International Electrotechnical Commission: Geneva, Switzerland, 2004.
- IEC 60287-1-1-2014; Electrical Cables—Calculation of the Current Rating Part 1-1: Current Rating Equations (100% Load Factor) and Calculation of Losses General. International Electrotechnical Commission: Geneva, Switzerland, 2014.
- Deng, X.; Ouyang, B.; Kong, X. Optimization of AC resistance in large cross-section high-voltage cable conductors. High Volt. Eng. 2016, 42, 522–527. [Google Scholar]
- Jabłoński, P.; Szczegielniak, T.; Kusiak, D.; Piątek, Z. Analytical–numerical solution for the skin and proximity effects in two parallel round conductors. Energies 2019, 12, 3584. [Google Scholar] [CrossRef]
- Wu, W.; Qu, X. Measurement of the AC resistance of power cable with large cross-section conductor. In Proceedings of the 16th Annual Conference of China Electrotechnical Society, Proceedings of the 16th Annual Conference of China Electrotechnical Society, Beijing, China, 24–26 September 2021; Yang, Q., Liang, X., Li, Y., He, J., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2022; Volume 889, pp. 415–419. [Google Scholar]
- Xie, D.; Qin, Z.; Xie, S.; Jiang, J.; Bai, F.; Li, J.; He, G. Research on the measurement of AC resistance of overhead transmission lines considering actual operating conditions. Energies 2024, 17, 6336. [Google Scholar] [CrossRef]
- Suzuki, H.; Kanaoka, M. Theoretical investigation on skin effect factor of conductor in power cables. Electr. Eng. Jpn. 2008, 165, 18–34. [Google Scholar] [CrossRef]
- Qin, S.; Xu, Q.; Wang, Q.; Zhang, J.; Ju, Z.; Hou, Z.; Lian, H.; Wu, T.; Zhang, J. Study on temperature rise characteristics of 110 kV XLPE cable under different service years considering dielectric loss. Energy Rep. 2022, 8 (Suppl. S8), 493–501. [Google Scholar] [CrossRef]
- Domae, A.; Kumagai, M.; Zama, M.; Abe, T.; Oe, T.; Kaneko, N.H. AC characterization of a 1-kΩ metal-foil resistor. in Precision Electromagnetic Measurements. IEEE Trans. Power Electron. 2014, 6, 24–31. [Google Scholar]
- Niroumand, F.J.; Nymand, M. A new method for measuring winding AC resistance of high efficiency power inductors. IEEE Trans. Power Electron. 2018, 33, 10736–10747. [Google Scholar]
- Zhao, E.; Han, Y.; Lin, X.; Liu, E.; Yang, P.; Zalhaf, A.S. Harmonic characteristics and control strategies of grid-connected photovoltaic inverters under weak grid conditions. Int. J. Electr. Power Energy Syst. 2022, 142, 108280. [Google Scholar] [CrossRef]
- Richman, P.; Walker, N. A new fast computing RMS-to-DC conversion. IEEE Trans. Instrum. Meas. 1971, 20, 313–319. [Google Scholar] [CrossRef]
- Liu, P.; Wang, W.; Zhou, L.; Zhao, M.; Wu, C.; He, L.; Liu, H. Development of a zero-flux Hall current sensor dedicated for large-current measurement of superconducting cable. IEEE Trans. Appl. Supercond. 2025, 35, 9000205. [Google Scholar] [CrossRef]
- Riba, J.-R. The role of AC resistance of bare stranded conductors for developing dynamic line rating approaches. Appl. Sci. 2024, 14, 8982. [Google Scholar] [CrossRef]
- Du, G.; Li, N.; Ye, W.; Cui, C.; Jiang, R. Effect of harmonics on AC losses and temperature of round-wire and form-wound windings for HSPMMs. IEEE Trans. Transp. Electrif. 2024, 10, 6115–6128. [Google Scholar] [CrossRef]
- Tang, B.; Yang, S.; Wang, D.; Xie, B.; Li, S.; Jiang, S. A numerical method coupling the T-A formulation for dynamic resistance computation in HTS coated conductors. IEEE Trans. Appl. Supercond. 2024, 34, 8200205. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).