Multi-Frequency Time-Sharing Strategy to Achieve Independent Power Regulation for Multi-Receiver ICPT System
Abstract
1. Introduction
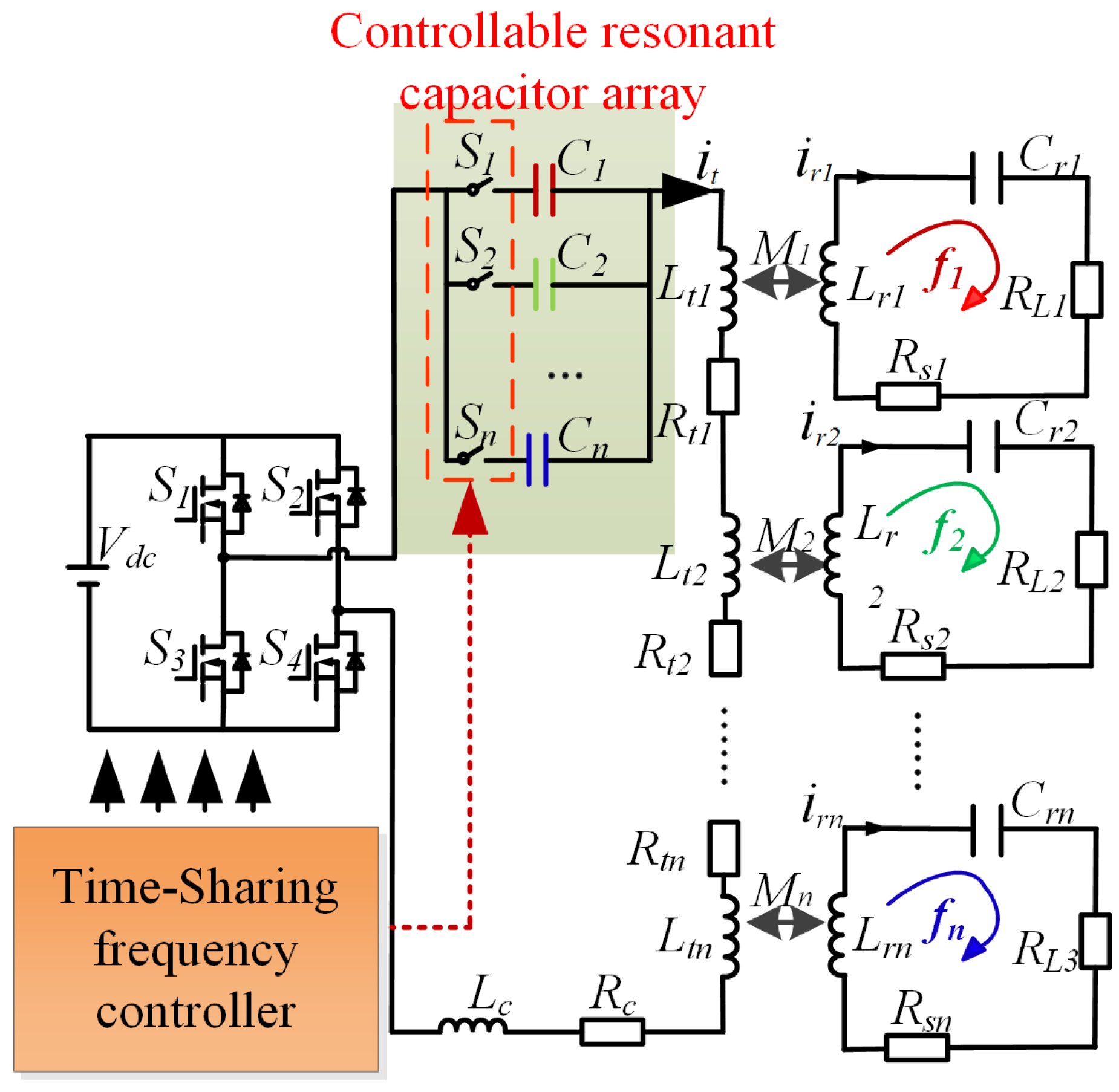
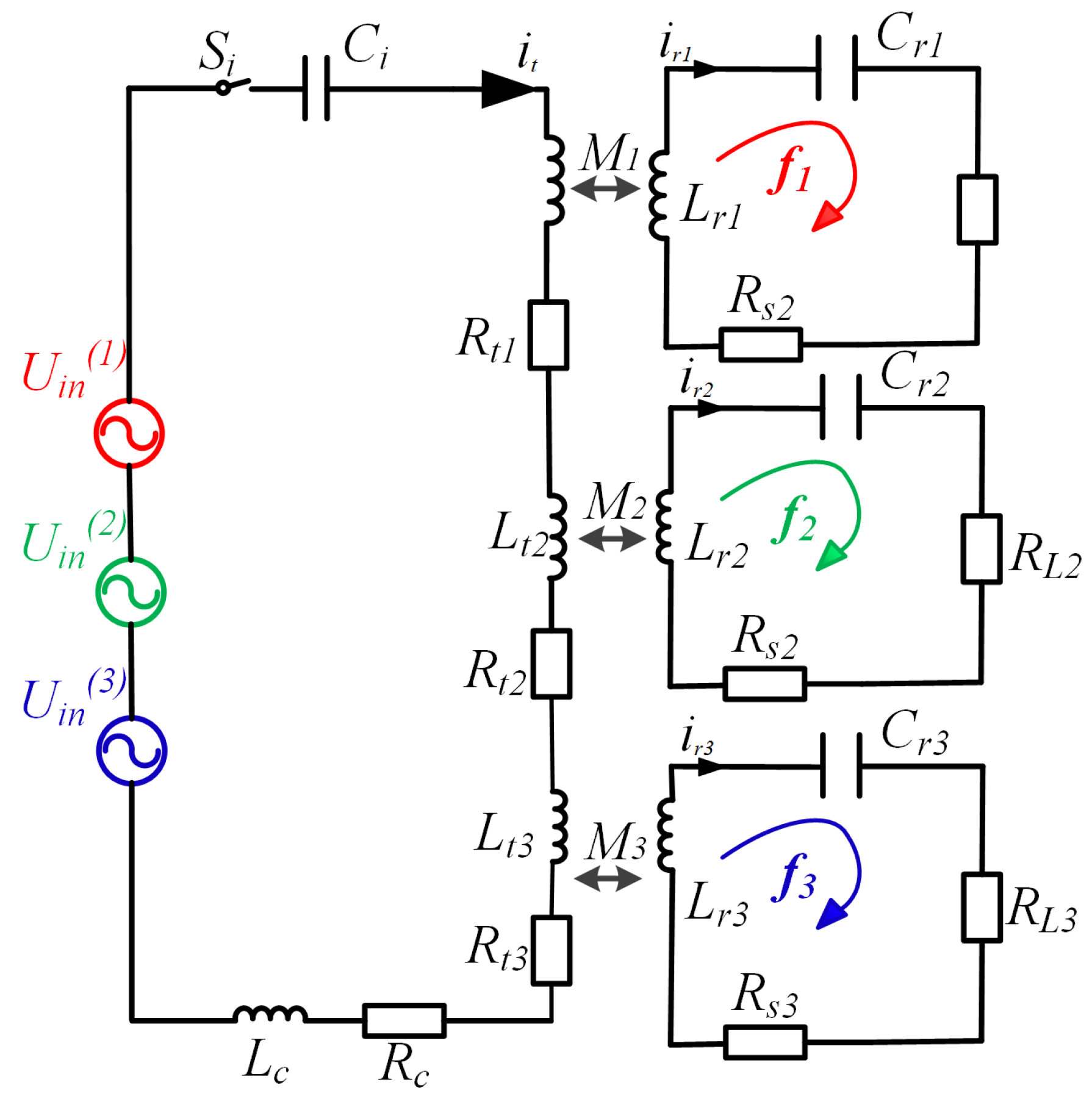
2. Circuit Model and Analysis
3. Analysis of Time-Sharing MFMR-ICPT System
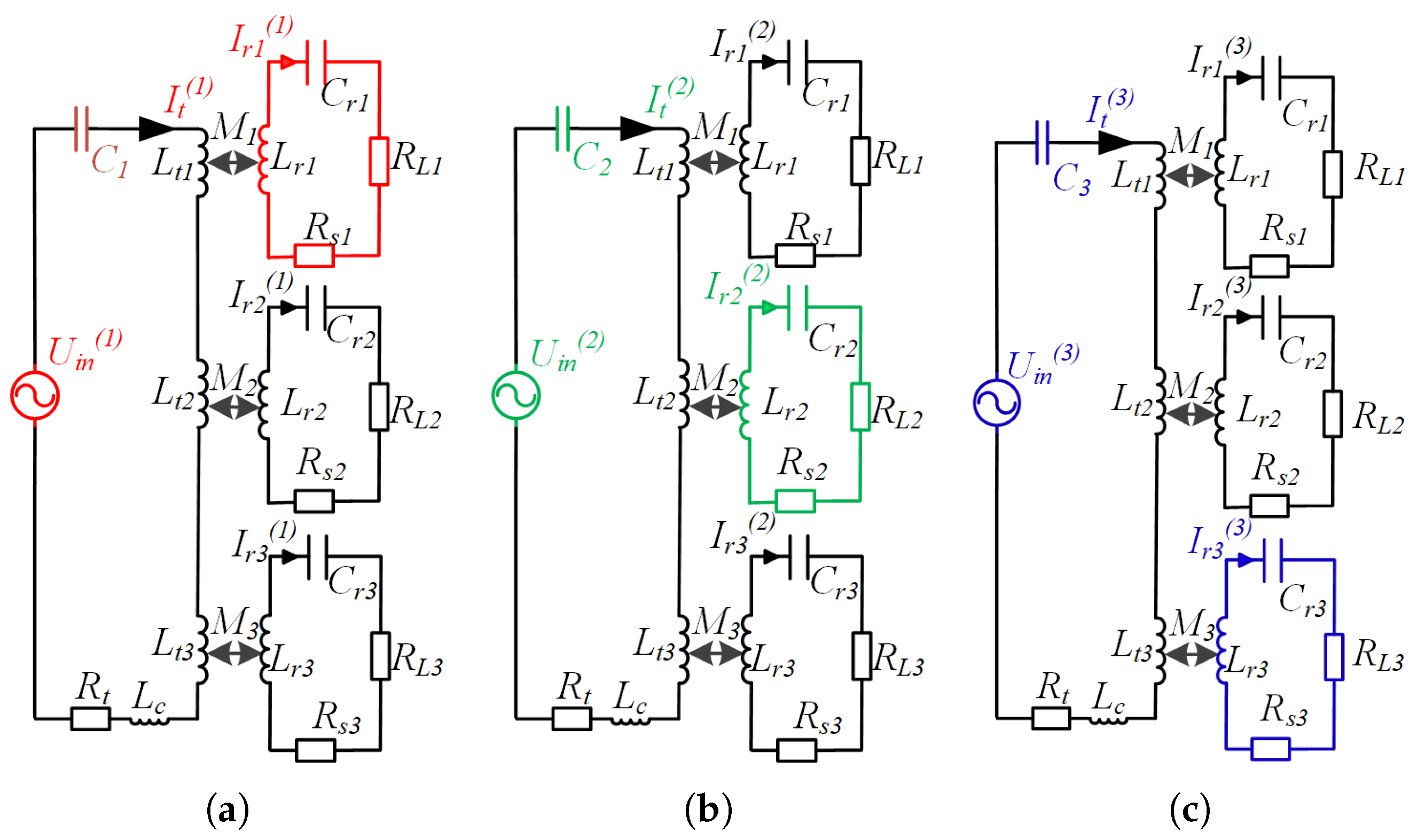
3.1. Analysis of Power Decoupling Transmission
- (1)
- , acting alone
- (2)
- , acting alone
- (3)
- , acting aloneThe current of the primary side can be expressed asThe interference current of receiving circuit 1 is
3.2. Time-Sharing Control Strategy
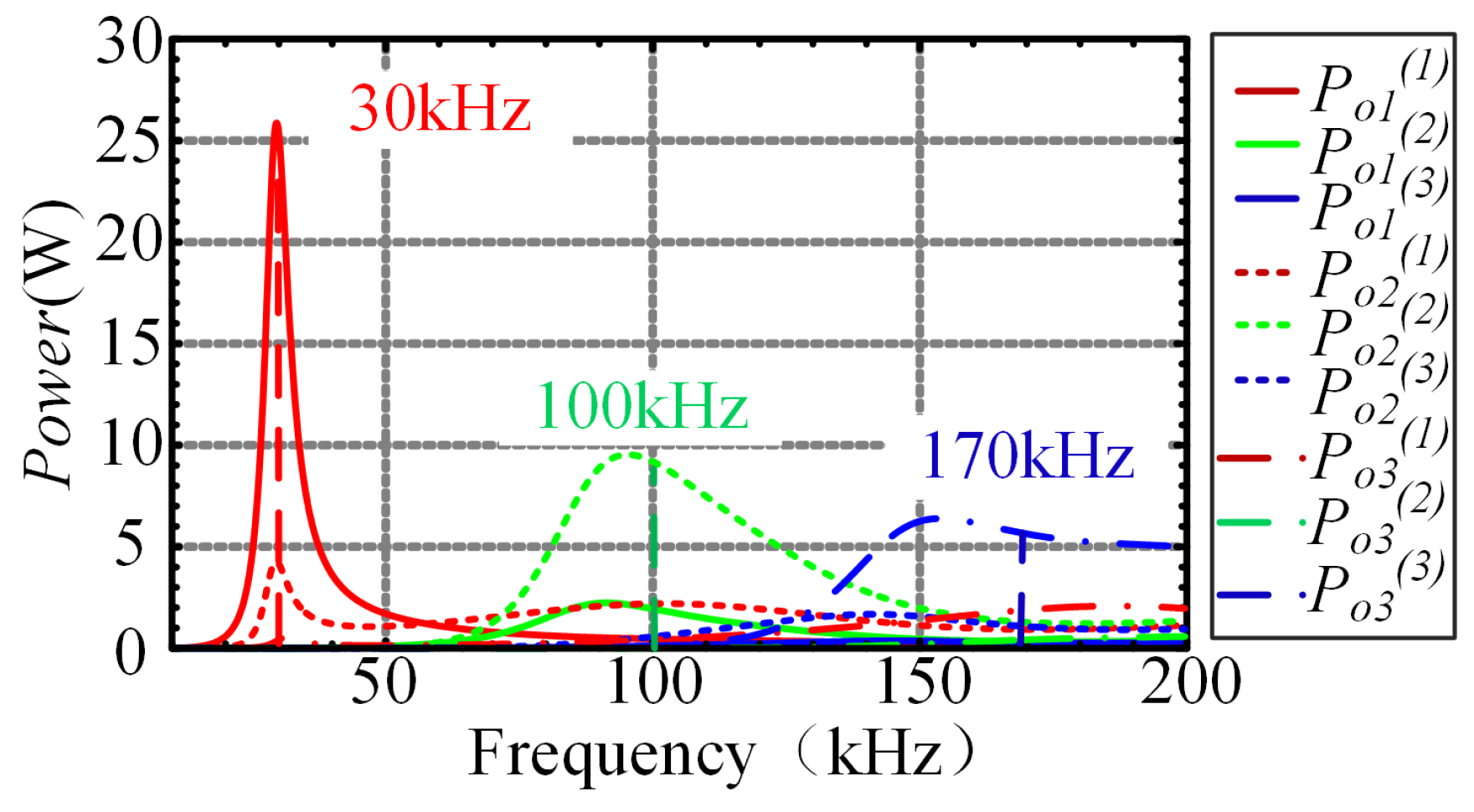
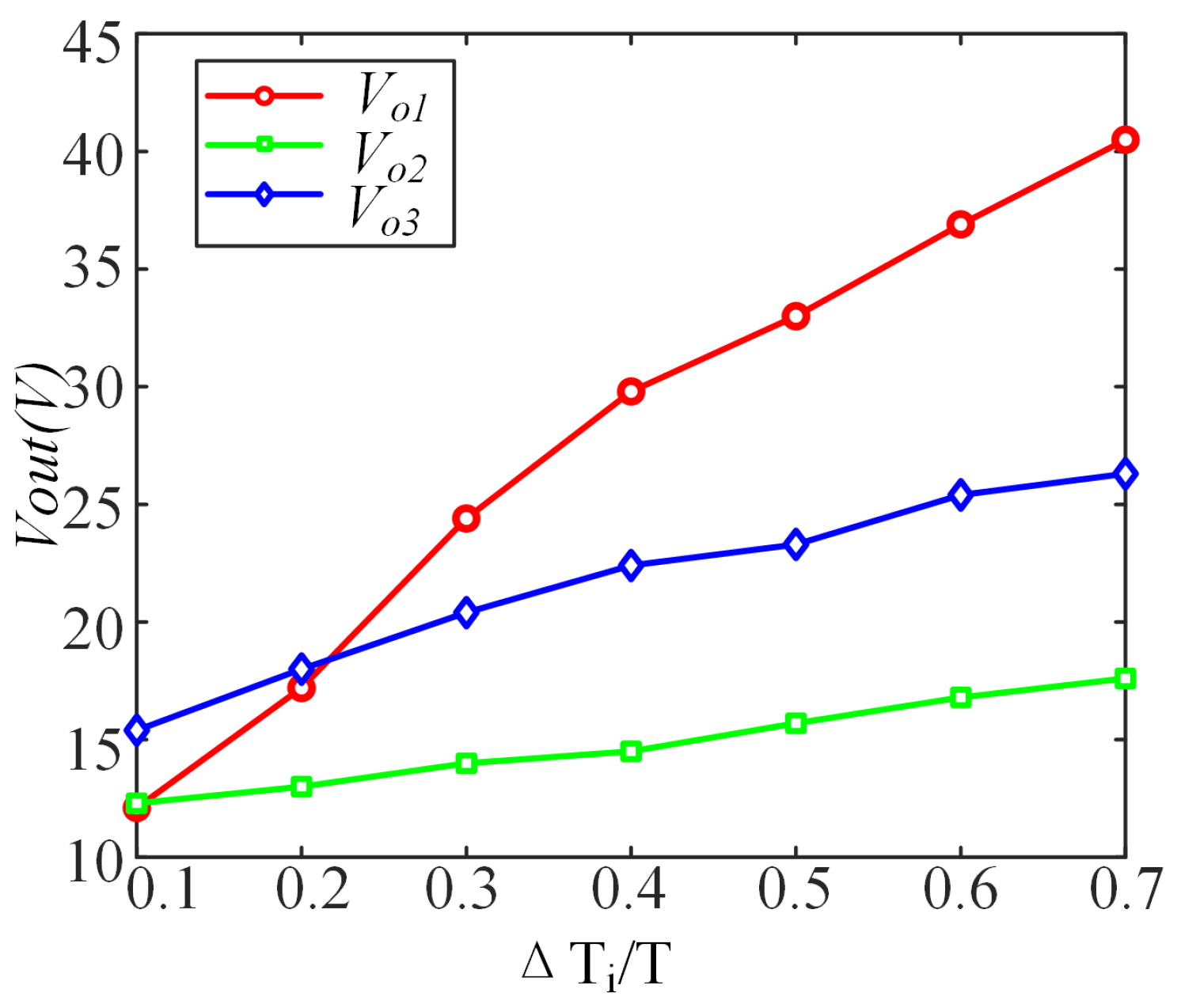
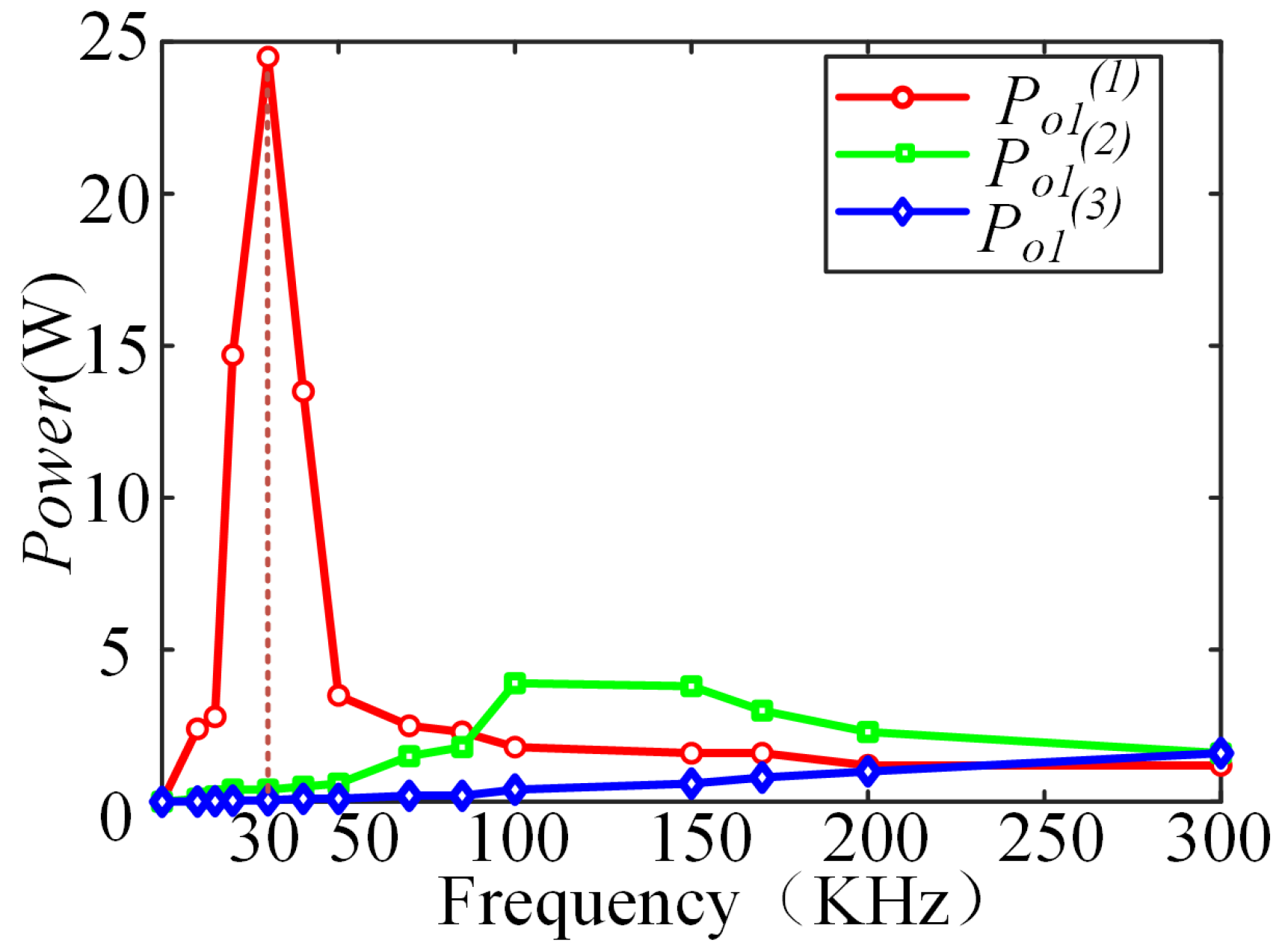
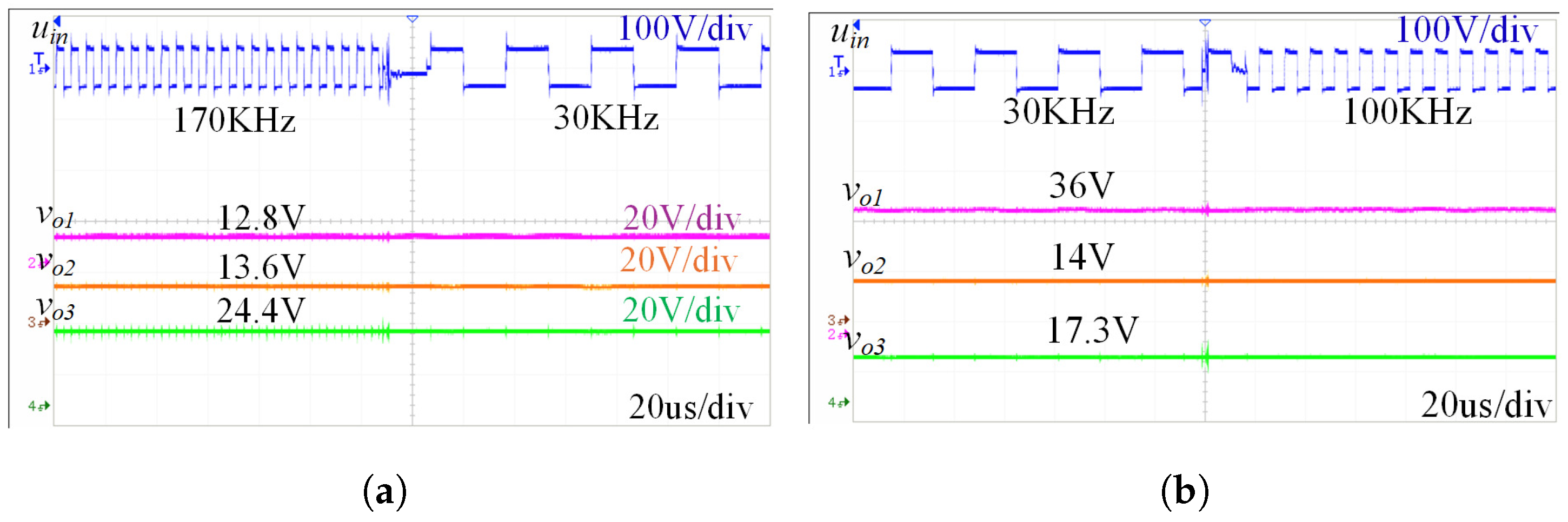
4. Experimental Verification
4.1. Experimental System Structure
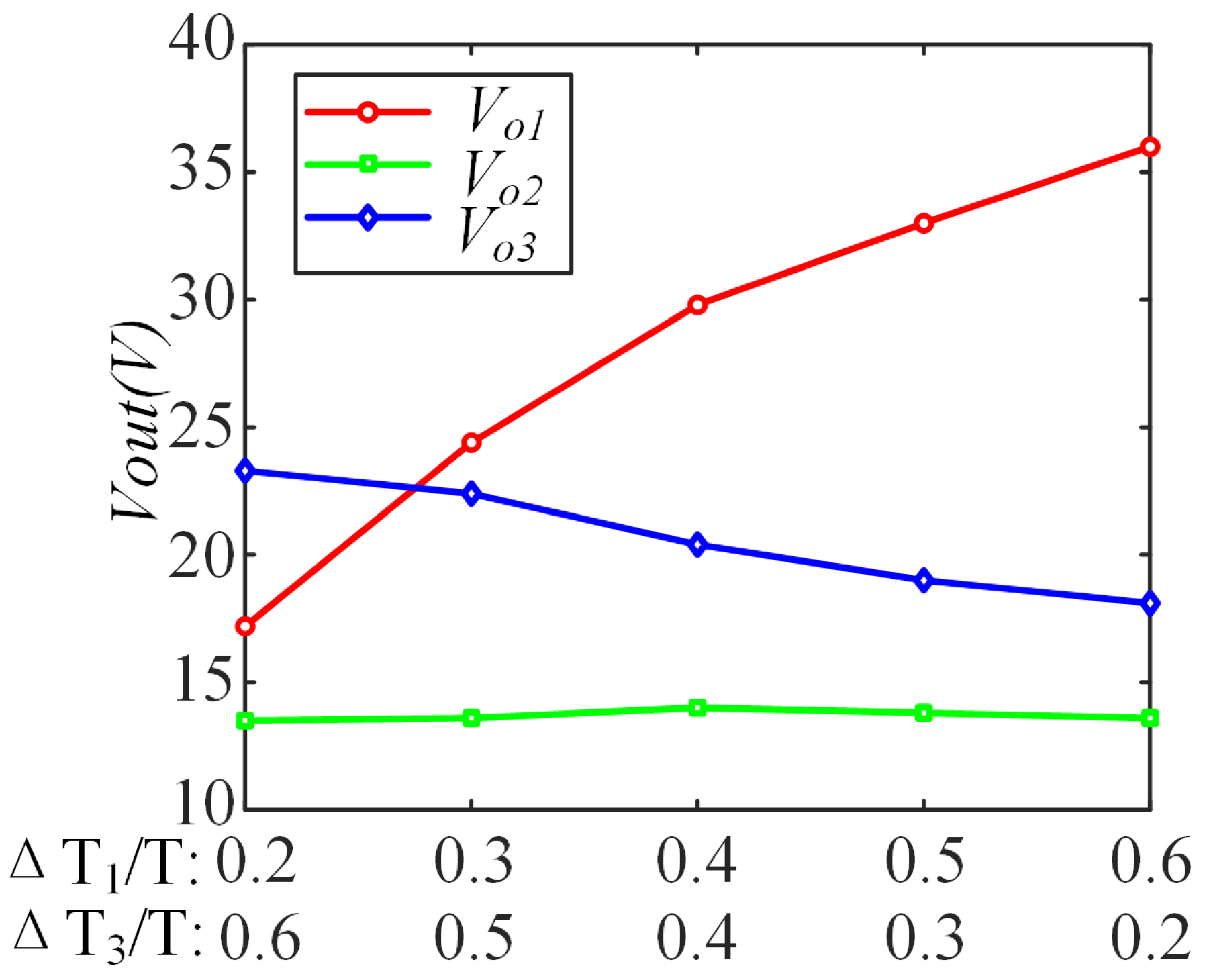
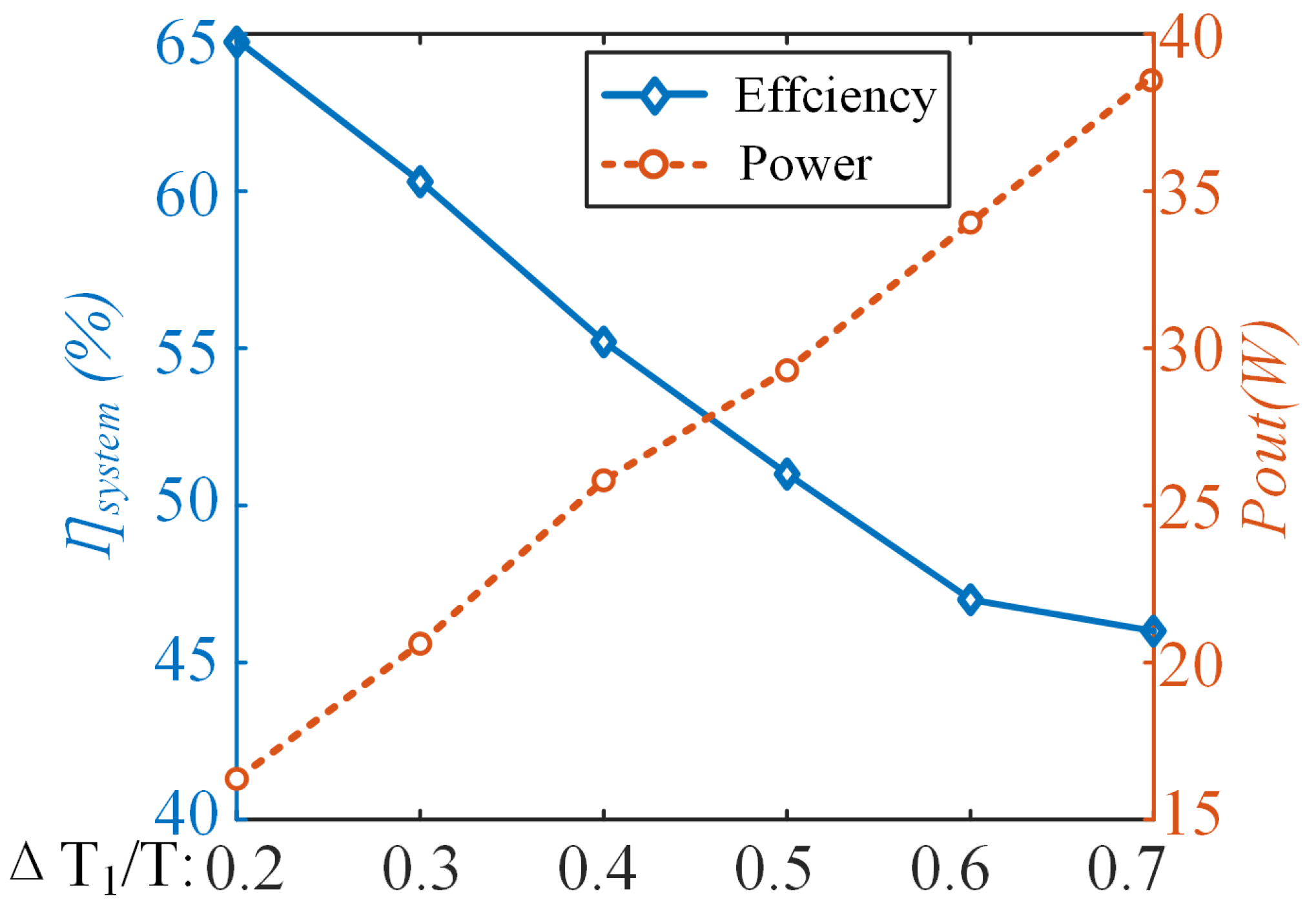
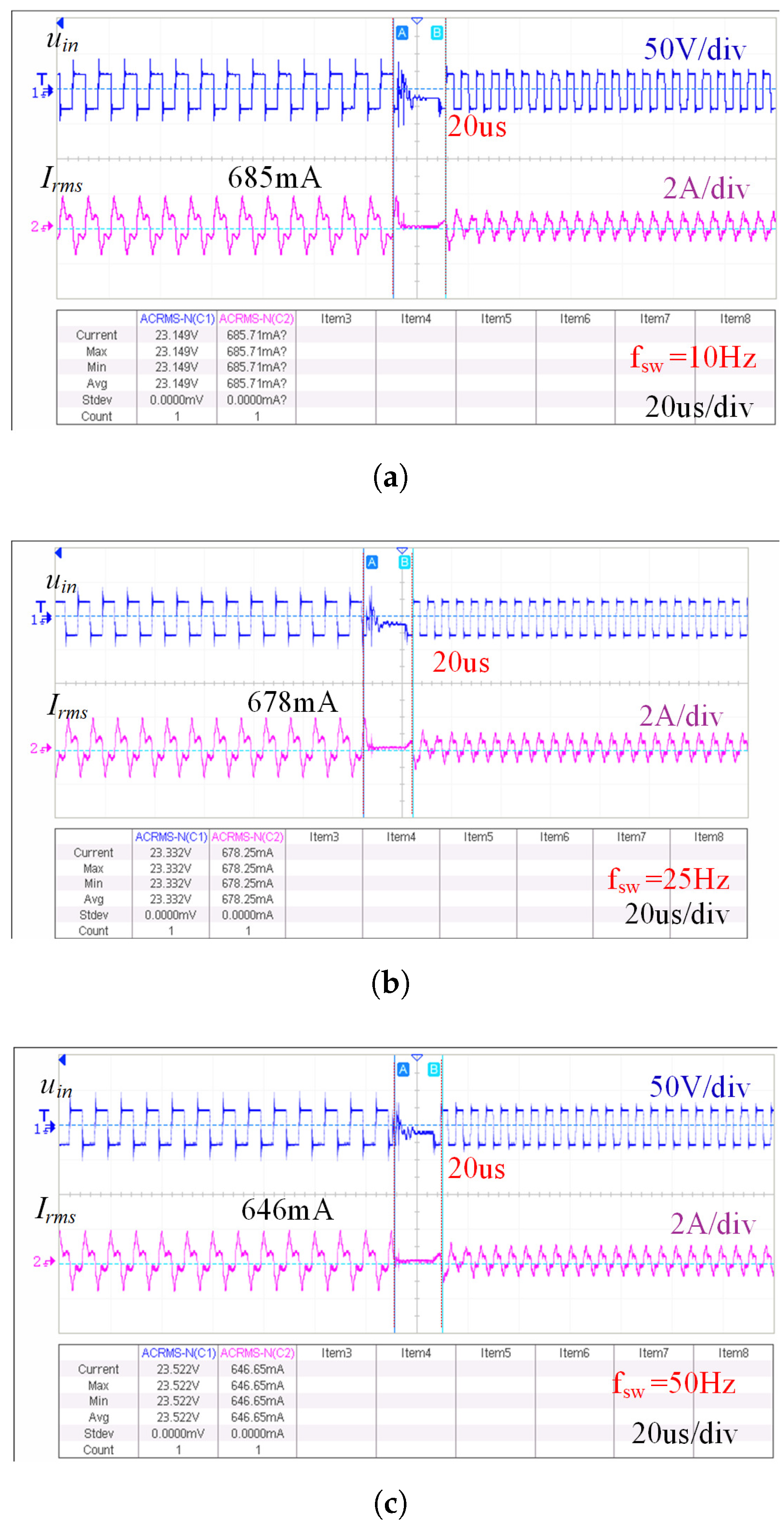
4.2. Experimental Results of Power Regulation in MFMR-ICPT Systems
4.3. Comparison with References
5. Conclusions
- (1)
- The efficiency of the cable-based MFMR-ICPT system is lower compared to the other ICPT systems, at 64.8%. On the one hand, the parasitic resistance of the tethered cable itself affects the system efficiency due to the specificity of the cable structure; on the other hand, with the power transfer using the TSFC strategy, the system’s controllable resonant capacitor arrays have to maintain high switching frequencies, which increases the switching losses. Therefore, the resonance compensation topology should be optimized for the particularities of the tethered cable structure, and methods to reduce the switching losses should be investigated to further improve the efficiency of the system. A longer-term plan is to design a real-time power distribution control strategy for the MFMR-ICPT and a closed-loop control method to increase the robustness of the system.
- (2)
- The MFMR-ICPT system, which employs the TSFC strategy, also exhibits certain deficiencies in a practical application. In accordance with the time-sharing strategy, it is not possible for the system to charge multiple loads concurrently, despite the fact that the switching speed is very fast. Furthermore, switching delays and losses are still present. So, the switching speed should be studied for the TSFC strategy to dynamically meet the needs of loads in the future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Guo, X.; Zhao, Q.; Zhao, Z.; Kang, S. Research status and thinking of atmospheric duct. Chin. J. Radio Sci. 2020, 35, 813–831. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, D.; Huang, S.; Huang, K.; Chen, J. Statistical estimations of atmospheric duct over the South China Sea and the tropical eastern Indian Ocean. Chin. Sci. Bull. 2013, 58, 2794–2797. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Q.; Wang, S.; Yang, K.; Yang, Y.; Yan, X.; Ma, Y. A comprehensive study on maximum wavelength of electromagnetic propagation in different evaporation ducts. IEEE Access 2019, 7, 82308–82319. [Google Scholar] [CrossRef]
- Zhang, Z.; Pang, H.; Georgiadis, A.; Cecati, C. Wireless power transfer—An overview. IEEE Trans. Ind. Electron. 2018, 66, 1044–1058. [Google Scholar] [CrossRef]
- Zhang, Z.; Ai, W.; Liang, Z.; Wang, J. Topology-reconfigurable capacitor matrix for encrypted dynamic wireless charging of electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 9284–9293. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Liu, S.; Hu, J.; He, Z. A Wide Output Voltage Range and High Efficiency Dual-Channel WPT System Employing Multimode Control Strategy. IEEE Trans. Ind. Electron. 2024, 71, 12075–12085. [Google Scholar] [CrossRef]
- Ahn, D.; Hong, S. Wireless power transmission with self-regulated output voltage for biomedical implant. IEEE Trans. Ind. Electron. 2013, 61, 2225–2235. [Google Scholar] [CrossRef]
- Yan, Z.; Song, B.; Zhang, Y.; Zhang, K.; Mao, Z.; Hu, Y. A rotation-free wireless power transfer system with stable output power and efficiency for autonomous underwater vehicles. IEEE Trans. Power Electron. 2018, 34, 4005–4008. [Google Scholar] [CrossRef]
- Cui, S.; Zhang, J.; Bie, Z.; Song, K.; Zhu, C. A novel arc-shaped lightweight magnetic coupler for AUV wireless power transfer. IEEE Trans. Ind. Appl. 2021, 58, 1315–1329. [Google Scholar]
- Gu, Y.; Wang, J.; Liang, Z.; Wu, Y.; Cecati, C.; Zhang, Z. Single-transmitter multiple-pickup wireless power transfer: Advantages, challenges, and corresponding technical solutions. IEEE Ind. Electron. Mag. 2020, 14, 123–135. [Google Scholar] [CrossRef]
- Xu, J.; Li, X.; Xie, Z.; Fu, C.; Du, R. Design and Analysis of Inductively Coupled Power Transfer System on Mooring Buoy With Double Ultracapacitor Chargers Using Indirect Control. IEEE Trans. Ind. Electron. 2020, 67, 4836–4845. [Google Scholar] [CrossRef]
- Xu, J.; Li, X.; Xie, Z.; Zhang, H.; Wu, T.; Fang, C. Research on a Multiple-Receiver Inductively Coupled Power Transfer System for Mooring Buoy Applications. Energies 2017, 10, 519. [Google Scholar] [CrossRef]
- Cui, X.; Xu, J.; Pang, S.; Li, X.; Li, H. Design and Implementation of Inductively Coupled Power and Data Transmission for Buoy Systems. Energies 2023, 16, 4417. [Google Scholar] [CrossRef]
- Qi, C.; Miao, H.; Lang, Z.; Chen, X. A generalized methodology to generate, amplify and compensate multi-frequency power for a single-inverter-based MF-MR-S-WPT system. IEEE Access 2020, 8, 181513–181525. [Google Scholar] [CrossRef]
- De Souza, W.G.; Gomes, L.C.; Lannes, L.R.; Andrade, D.A. Analysis and modeling of a wireless power transmission system for multiple receivers. IEEE Lat. Am. Trans. 2021, 19, 1987–1994. [Google Scholar] [CrossRef]
- Fu, M.; Zhang, T.; Ma, C.; Zhu, X. Efficiency and optimal loads analysis for multiple-receiver wireless power transfer systems. IEEE Trans. Microw. Theory Tech. 2015, 63, 801–812. [Google Scholar] [CrossRef]
- Xie, X.; Xie, C.; Wang, J.; Li, Y.; Du, Y.; Li, L. Constant Current Output Control Based on Cross-Coupling Compensation in Multireceiver WPT System Using Active Rectifier. IEEE Trans. Transp. Electrif. 2023, 9, 1960–1972. [Google Scholar] [CrossRef]
- Ahn, D.; Mercier, P.P. Wireless power transfer with concurrent 200-kHz and 6.78-MHz operation in a single-transmitter device. IEEE Trans. Power Electron. 2015, 31, 5018–5029. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Y.; Ding, Z.; Chen, X.; Kennel, R.M. A multifrequency superposition methodology to achieve high efficiency and targeted power distribution for a multiload MCR WPT system. IEEE Trans. Power Electron. 2017, 33, 9005–9016. [Google Scholar] [CrossRef]
- Pantic, Z.; Lee, K.; Lukic, S.M. Receivers for multifrequency wireless power transfer: Design for minimum interference. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 3, 234–241. [Google Scholar] [CrossRef]
- Xia, C.; Wei, N.; Zhang, H.; Zhao, S.; Li, Z.; Liao, Z. Multifrequency and multiload MCR-WPT system using hybrid modulation waves SPWM control method. IEEE Trans. Power Electron. 2021, 36, 12400–12412. [Google Scholar] [CrossRef]
- Qi, C.; Huang, S.; Chen, X.; Wang, P. Multifrequency modulation to achieve an individual and continuous power distribution for simultaneous MR-WPT system with an inverter. IEEE Trans. Power Electron. 2021, 36, 12440–12455. [Google Scholar] [CrossRef]
- Pang, S.; Xu, J.; Li, H.; Ma, Q.; Li, X. Dual-frequency modulation to achieve power independent regulation for dual-load underwater wireless power connector. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 11, 2377–2389. [Google Scholar] [CrossRef]
- Kim, Y.J.; Ha, D.; Chappell, W.J.; Irazoqui, P.P. Selective wireless power transfer for smart power distribution in a miniature-sized multiple-receiver system. IEEE Trans. Ind. Electron. 2015, 63, 1853–1862. [Google Scholar] [CrossRef]
- Luo, C.; Qiu, D.; Gu, W.; Zhang, B.; Chen, Y.; Xiao, W. Multiload wireless power transfer system with constant output power and efficiency. IEEE Trans. Ind. Appl. 2021, 58, 1101–1114. [Google Scholar] [CrossRef]
- Sun, A.; Xia, C.; Chen, Y.; Liu, Y.; Yang, Z.; Zhao, S.; Yang, Z. Multifrequency and Multiload MCR-WPT System Based on Hysteresis Current Control. IEEE Trans. Power Electron. 2024, 39, 10532–10545. [Google Scholar] [CrossRef]
- Wang, C.; Li, F.; Cao, Y. Dual-Frequency Dual-Type-Output Wireless Power Transfer System with Independent Adjustable Outputs. IEEE J. Emerg. Sel. Top. Power Electron. 2025. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, Z.; Chang, S. Single-Transmitter-Controlled Multiple-Channel Constant Current Outputs for In-Flight Wireless Charging of Drones. IEEE Trans. Ind. Electron. 2024, 71, 3606–3616. [Google Scholar] [CrossRef]
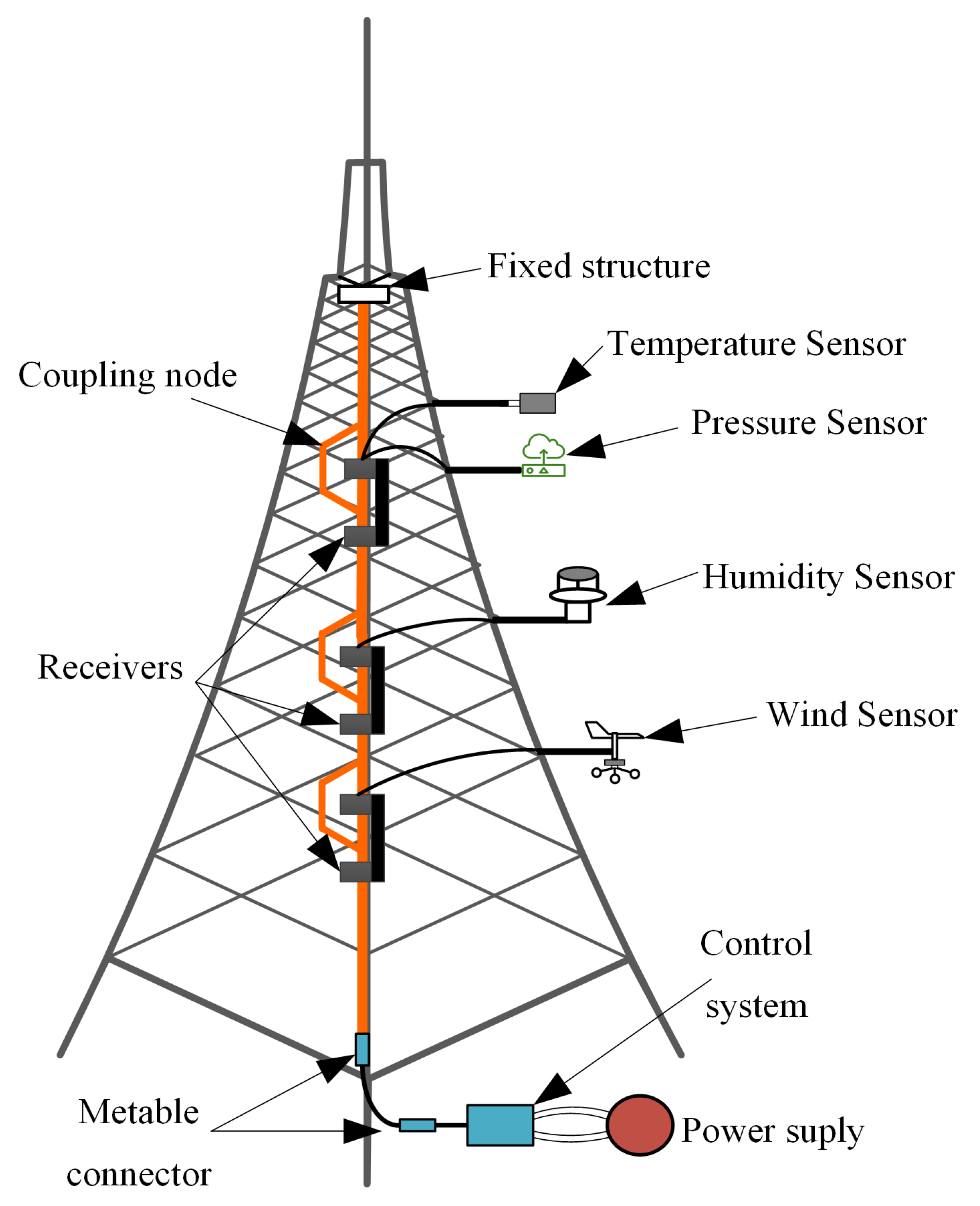




| Sensor | Input Voltage | Power Consumption |
|---|---|---|
| Temperature Sensor | 5 V | 0.5 W |
| 3D Sonic Anemometer Sensor | 9–30 V | 1.0 W |
| Atmospheric Pressure Sensor | 10–35 V | 8.0 W |
| Infrared Gas Analyzer | 10–30 V | 10.0 W |
| Parameter | Experiment Value | Unit | |
|---|---|---|---|
| DC supply | 36 | V | |
| Frequency | 30/100/170 | kHz | |
| Transmitting coil | 14.8/15.6/13.2 0.01/0.09/0.1 | H | |
| Compensation | (i = 1, 2, 3) | 500/44.9/15.5 | nF |
| Mooring cable | 12.7 1.2 | H | |
| Receiving coil | 92/94.5/80.7 0.1/0.6/1.2 | H | |
| Mutual inductance | (i = 1, 2, 3) | 36/36.25/30.75 | H |
| Compensation | (i = 1, 2, 3) | 306/26.8/10.85 | nF |
| Loads | (i = 1, 2, 3) | 50/50/100 |
| Load Value | Output Voltage | Output Power |
|---|---|---|
| , , | V V V | W W W |
| , , | V V V | W W W |
| , , | V V V | W W W |
| , , | V V V | W W W |
| , , | V V V | W W W |
| , , | V V V | W W W |
| , , | V V V | W W W |
| 10 Hz | 25 Hz | 50 Hz | |
| 95.1% | 94.1% | 92.3% |
| Reference | Number of Inverters | Multi-Frequency Current Generation | Cross-Interference | Power Distribution | Efficiency (%) |
|---|---|---|---|---|---|
| [19] | Several | Multiple inverters and transformers | Exist(large) | Uncontrollable | 85 |
| [20] | One | Fundamental and harmonic | Minimum | Uncontrollable | n/a (Not applicable) |
| [21] | One | HSPWM (with high carrier frequency) | Minimum | Controllable | 6570 |
| [22] | One | Delta–sigma modulation (with complex calculation) | Minimum | Controllable | 84 |
| [25] | One | Time sharing | Exist | Controllable | 80 |
| This work | One | Time sharing | Almost eliminated | Controllable | 64.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Pang, S.; Xu, J.; Pan, J.; Li, H.; Liu, Y.; Yang, Y. Multi-Frequency Time-Sharing Strategy to Achieve Independent Power Regulation for Multi-Receiver ICPT System. Energies 2025, 18, 1389. https://doi.org/10.3390/en18061389
Wang G, Pang S, Xu J, Pan J, Li H, Liu Y, Yang Y. Multi-Frequency Time-Sharing Strategy to Achieve Independent Power Regulation for Multi-Receiver ICPT System. Energies. 2025; 18(6):1389. https://doi.org/10.3390/en18061389
Chicago/Turabian StyleWang, Guanwen, Shui Pang, Jiayi Xu, Jianguo Pan, Hongyu Li, Yu Liu, and Yuhang Yang. 2025. "Multi-Frequency Time-Sharing Strategy to Achieve Independent Power Regulation for Multi-Receiver ICPT System" Energies 18, no. 6: 1389. https://doi.org/10.3390/en18061389
APA StyleWang, G., Pang, S., Xu, J., Pan, J., Li, H., Liu, Y., & Yang, Y. (2025). Multi-Frequency Time-Sharing Strategy to Achieve Independent Power Regulation for Multi-Receiver ICPT System. Energies, 18(6), 1389. https://doi.org/10.3390/en18061389







