Machine Learning-Based Evaluation of Solar Photovoltaic Panel Exergy and Efficiency Under Real Climate Conditions
Abstract
1. Introduction
2. Material and Methods
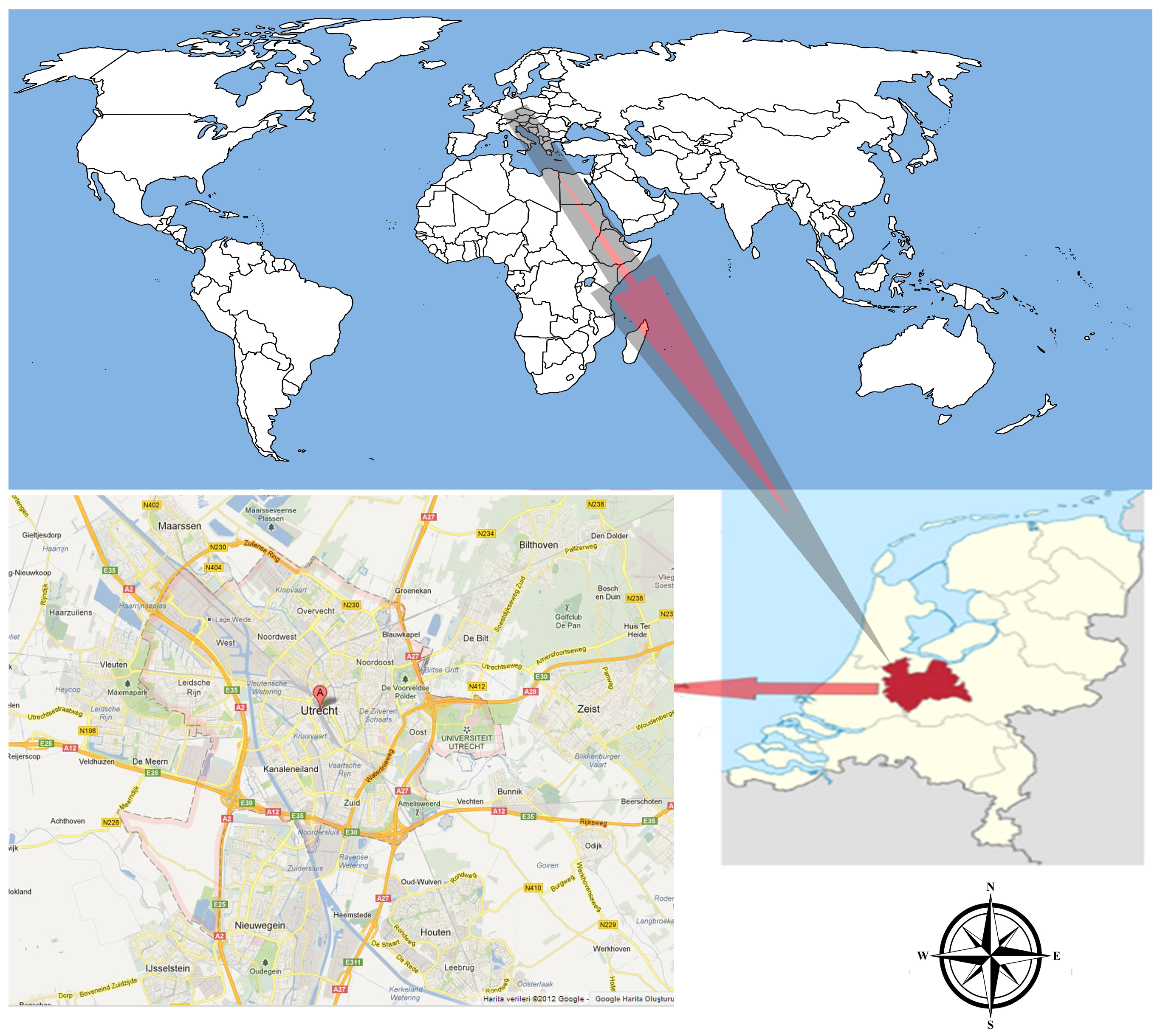
2.1. Study Area
2.2. Parameters Used in PV Solar Power Plant Efficiency
2.3. Multiple Linear Regression
2.4. Account Methods
2.4.1. Exergy Efficiency Calculation in Solar Panel
2.4.2. Exergy Efficiency and Temperature in Photovoltaic Systems
3. Results and Discussion
3.1. Applying Multiple Linear Regression
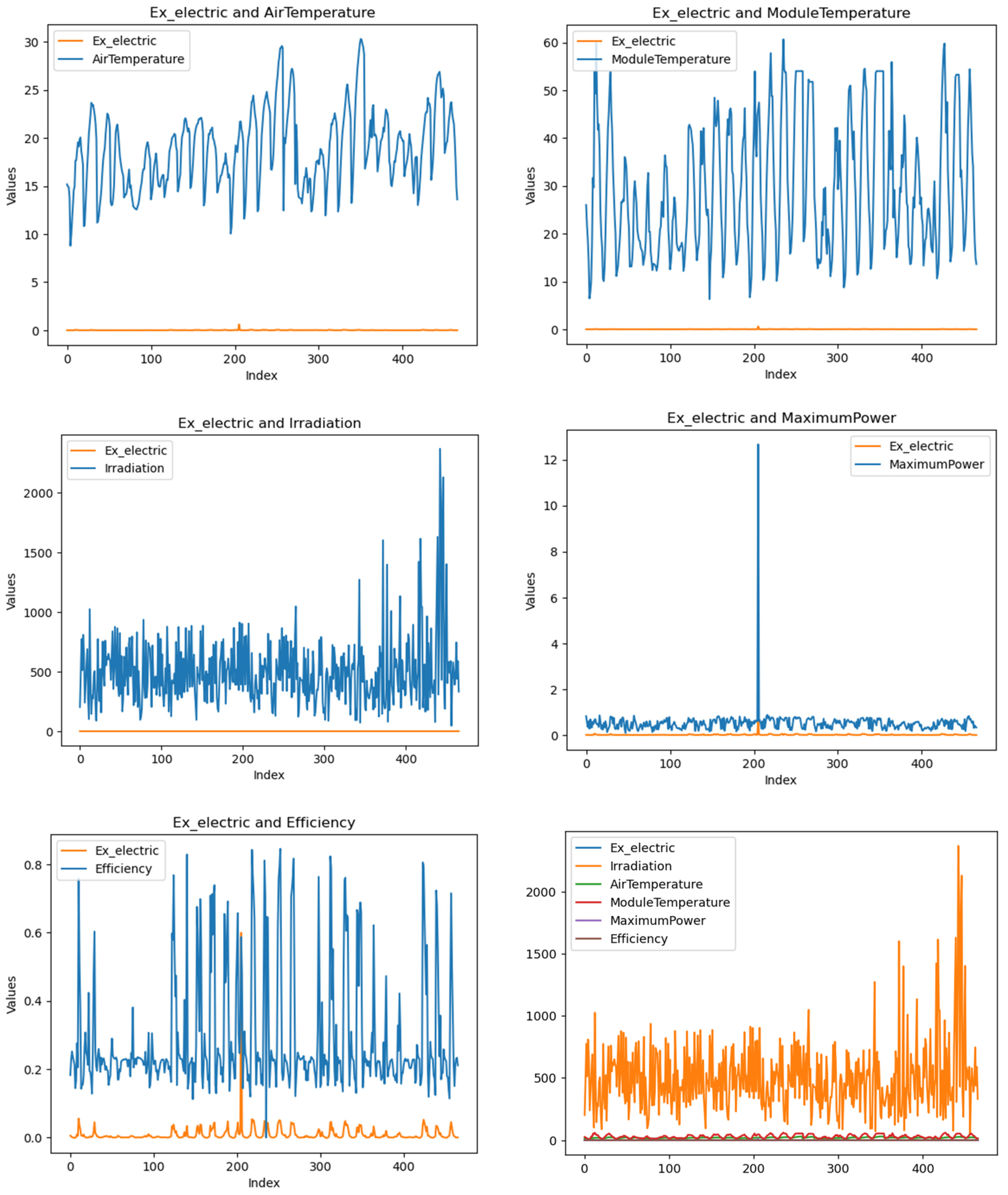
3.2. Applying Exergy Solar, Exergy Electric and Exergy Efficiency
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Çengel, Y.A.; Boles, M.A. Mühendislik Yaklaşımıyla Termodinamik, 7th ed.; Palme Publishing: Ankara, Turkey, 2008. [Google Scholar]
- El-Emam, R.S.; Dincer, I. Exergy and exergoeconomic analyses and optimization of geothermal organic Rankine cycle. Appl. Therm. Eng. 2013, 59, 435–444. [Google Scholar] [CrossRef]
- Bayrak, F.; Ertürk, G.; Oztop, H.F. Effects of partial shading on energy and exergy efficiencies for photovoltaic panels. J. Clean. Prod. 2017, 164, 58–69. [Google Scholar] [CrossRef]
- Nami, H.; Mahmoudi, S.M.S.; Nemati, A. Exergy, economic and environmental impact assessment and optimization of a novel cogeneration system including a gas turbine, a supercritical CO2 and an Organic Rankine Cycle (GT-HRSG/SCO2). Appl. Therm. Eng. 2017, 110, 1315–1330. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Tabatabaei, M.; Mohammadi, P.; Pourvosoughi, N.; Nikbakht, A.M.; Goli, S.A.H. Improving exergetic and sustainability parameters of a DI diesel engine using polymer waste dissolved in biodiesel as a novel diesel additive. Energy Convers. Manag. 2015, 105, 328–337. [Google Scholar] [CrossRef]
- Tsatsaronis, G. Definition and nomenclature in exergy analysis and exergoeconomics. Energy 2007, 32, 249–253. [Google Scholar] [CrossRef]
- Pathak, M.J.M.; Sanders, P.G.; Pearce, J.M. Optimizing limited solar roof access by exergy analysis of solar thermal, photovoltaic, and hybrid photovoltaic thermal systems. Appl. Energy 2014, 120, 115–124. [Google Scholar] [CrossRef]
- Sudhakar, K.; Srivastava, T. Energy and exergy analysis of 36 W solar photovoltaic module. Int. J. Ambient. Energy 2014, 35, 51–57. [Google Scholar] [CrossRef]
- Sahin, A.D.; Dincer, I.; Rosen, M.A. Thermodynamic analysis of solar photovoltaic cell systems. Sol. Energy Mater. Sol. Cells 2007, 91, 153–159. [Google Scholar] [CrossRef]
- Joshi, A.S.; Dincer, I.; Reddy, B.V. Performance analysis of photovoltaic systems: A review. Renew. Sustain. Energy Rev. 2009, 13, 1884–1897. [Google Scholar] [CrossRef]
- Saloux, E.; Teyssedou, A.; Sorin, M. Analysis of photovoltaic (PV) and photovoltaic/thermal (PV/T) systems using the exergy method. Energy Build. 2013, 67, 275–285. [Google Scholar] [CrossRef]
- Izgi, E.; Akkaya, Y.E. Exergoeconomic analysis of a solar photovoltaic system in Istanbul, Turkey. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 350–359. [Google Scholar]
- Pandey, A.K.; Tyagi, V.V.; Tyagi, S.K. Exergetic analysis and parametric study of multi-crystalline solar photovoltaic system at a typical climatic zone. Clean Technol. Environ. Policy 2013, 15, 333–343. [Google Scholar] [CrossRef]
- Aoun, N.; Nahman, B.; Chenni, R. Study of Experimental Energy and Exergy of mono-crystalline PV Panel in Adrar Region, Algeria. Int. J. Sci. Eng. Res. 2014, 5, 585–589. [Google Scholar]
- Sebbagh, T.; Kelaiaia, R.; Zaatri, A.; Bechara, T.; Abdelouahed, L. Exergetic Efficiency Evaluation of a So Lar Photovoltaic Energy Converter, CIMSI2017; University of Skikda: Skikda, Algeria, 2017. [Google Scholar]
- Gaur, A.; Tiwari, G.N. Exergoeconomic and enviroeconomic analysis of photovoltaic modules of different solar cells. J. Sol. Energy 2014, 2014, 719424. [Google Scholar] [CrossRef]
- Pandey, A.K.; Pant, P.C.; Sastry, O.S.; Kumar, A.; Tyagi, S.K. Energy and exergy performance evaluation of a typical solar photovoltaic module. Therm. Sci. 2015, 19 (Suppl. S2), 625–636. [Google Scholar] [CrossRef]
- Bayrak, F.; Abu-Hamdeh, N.; Alnefaie, K.A.; Öztop, H.F. A review on exergy analysis of solar electricity production. Renew. Sustain. Energy Rev. 2017, 74, 755–770. [Google Scholar] [CrossRef]
- Bayrak, F.; Oztop, H.F.; Selimefendigil, F. Effects of different fin parameters on temperature and efficiency for cooling of photovoltaic panels under natural convection. Sol. Energy 2019, 188, 484–494. [Google Scholar] [CrossRef]
- Sukumaran, S.; Sudhakar, K. Performance analysis of solar powered airport based on energy and exergy analysis. Energy 2018, 149, 1000–1009. [Google Scholar] [CrossRef]
- Bayat, M.; Ozalp, M. Energy, Exergy and Exergoeconomic Analysis of a solar Photovoltaic Module. In Exergetic, Energetic and Environmental Dimensions; Dincer, İ., Ozgur Colpan, C., Kizilkan, O., Eds.; Academic Press: Cambridge, UK, 2018; pp. 383–402. [Google Scholar]
- Kumar, M.; Chandel, S.S.; Kumar, A. Performance analysis of a 10 MWp utility scale grid-connected canal-top photovoltaic power plant under Indian climatic conditions. Energy 2020, 204, 117903. [Google Scholar] [CrossRef]
- Sreenath, S.; Sudhakar, K.; Yusop, A.F. Energy-exergy-economic environmental-energo-exergo-enviroecono (7E) analysis of solar photovoltaic power plant: A case study of 7 airport sites in India. Sustain. Energy Technol. Assess. 2021, 47, 101352. [Google Scholar] [CrossRef]
- Manjunath, C.; Reddy, J.; Reddy KS, R.; Kumar, I.G.; Sanketh, S. Energy, exergy performance and analysis of 50w solar photovoltaic module. Mater. Today Proc. 2022, 54, 531–536. [Google Scholar] [CrossRef]
- Kuczynski, W.; Chliszcz, K. Energy and exergy analysis of photovoltaic panels in northern Poland. Renew. Sustain. Energy Rev. 2023, 174, 113138. [Google Scholar] [CrossRef]
- Khandakar, A.; Chowdhury, M.E.H.; Khoda Kazi, M.-; Benhmed, K.; Touati, F.; Al-Hitmi, M.; Gonzales, A.S.P., Jr. Machine learning based photovoltaics (PV) power prediction using different environmental parameters of Qatar. Energies 2019, 12, 2782. [Google Scholar] [CrossRef]
- Kaya, F.; Sahin, G.; Alma, M.H. Investigation effects of environmental and operating factors on PV panel efficiency using by multivariate linear regression. Int. J. Energy Res. 2021, 45, 554–567. [Google Scholar] [CrossRef]
- Sahin, G.; Isik, G.; van Sark, W.G. Predictive modeling of PV solar power plant efficiency considering weather conditions: A comparative analysis of artificial neural networks and multiple linear regression. Energy Rep. 2023, 10, 2837–2849. [Google Scholar] [CrossRef]
- Michaelides, E. Exergy Analysis for Energy Conversion Systems; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Bagdanavicius, A. Energy and Exergy Analysis of Renewable Energy Conversion Systems. Energies 2022, 15, 5528. [Google Scholar] [CrossRef]
- Almarshoud, A.F.; Abdel-halim, M.A.; Almasri, R.A.; Alshwairekh, A.M. Exergy and Energy Analysis of Bifacial PV Module Performance on a Cloudy Day in Saudi Arabia. Sustainability 2024, 16, 7428. [Google Scholar] [CrossRef]
- Ganesan, K.; Winston, D.P.; Sugumar, S.; Prasath, T.H. Performance Investigation of n-type PERT Bifacial Solar Photovoltaic Module Installed at Different Elevations. Renew. Energy 2024, 227, 120526. [Google Scholar] [CrossRef]
- Raina, G.; Sinha, S. A simulation study to evaluate and compare monofacial Vs bifacial PERC PV cells and the effect of albedo on bifacial performance. Mater. Today Proc. 2021, 46, 5242–5247. [Google Scholar] [CrossRef]
- Michaelides, E.E.S. Alternative Energy Sources, Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Khosravi, A.; Koury, R.N.N.; Machado, L.; Pabon, J.J.G. Energy, exergy and economic analysis of a hybrid renewable energy with hydrogen storage system. Energy 2018, 148, 1087–1102. [Google Scholar] [CrossRef]
- Rosen, M.A. The Development and Application of a Process Analysis Methodology and Code Based on Exergy, Cost, Energy and Mass. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1986. [Google Scholar]
- Gundersen, T. An Introduction to the Concept of Exergy and Energy Quality, 4th ed.; Department of Energy and Process Engineering, Norwegian University of Science and Technology: Trondheim, Norway, 2011. [Google Scholar]
- Cengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach, 4th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Bejan, A. Advanced Engineering Thermodynamics, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Kalogirou, S.A.; Karellas, S.; Badescu, V.; Braimakis, K. Exergy analysis on solar thermal systems: A better understanding of their sustainability. Renew. Energy 2016, 85, 1328–1333. [Google Scholar] [CrossRef]
- Baghel, N.S.; Chander, N. Performance comparison of mono and polycrystalline silicon solar photovoltaic modules under tropical wet and dry climatic conditions in east-central India. Clean Energy 2022, 6, 165–177. [Google Scholar] [CrossRef]

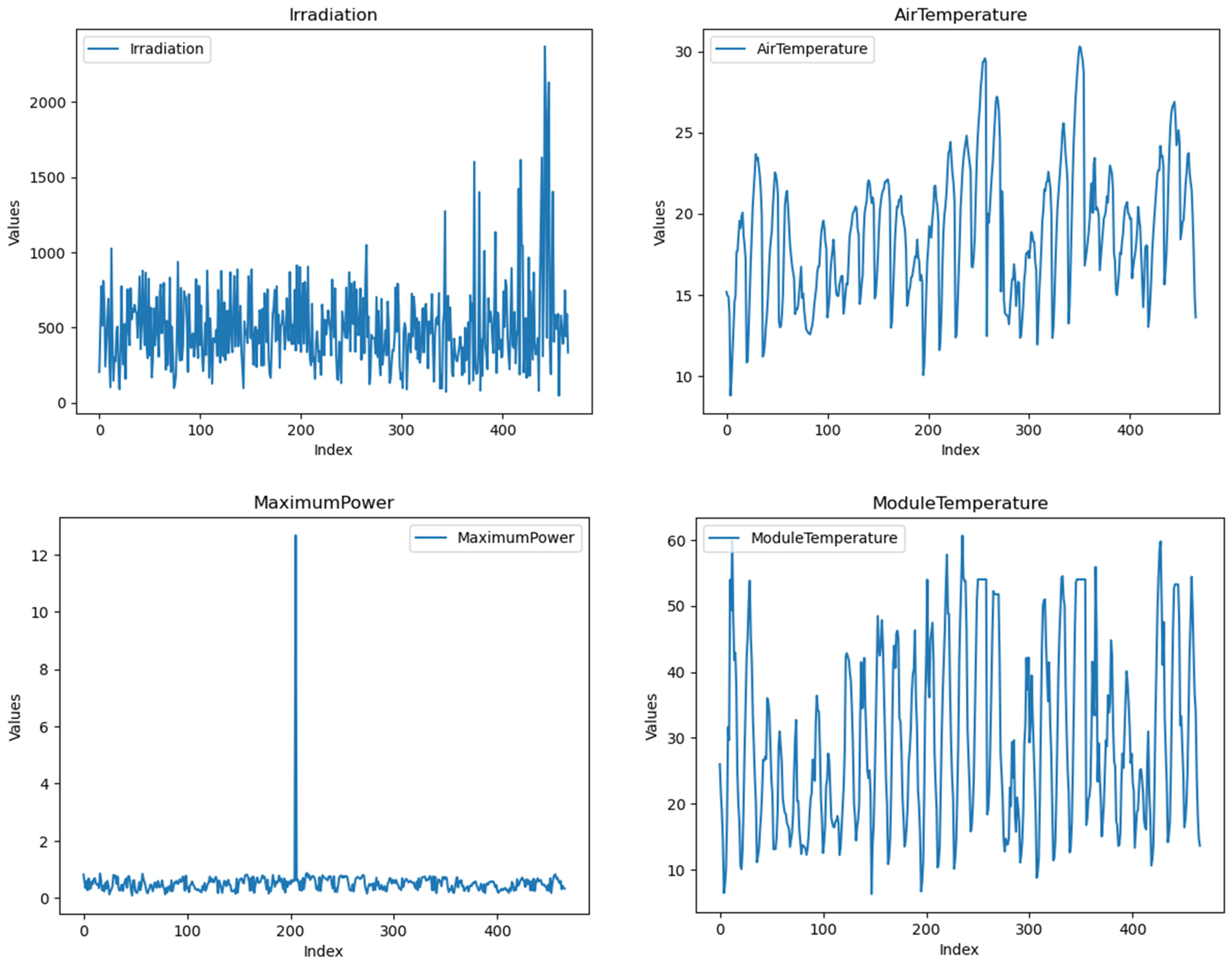
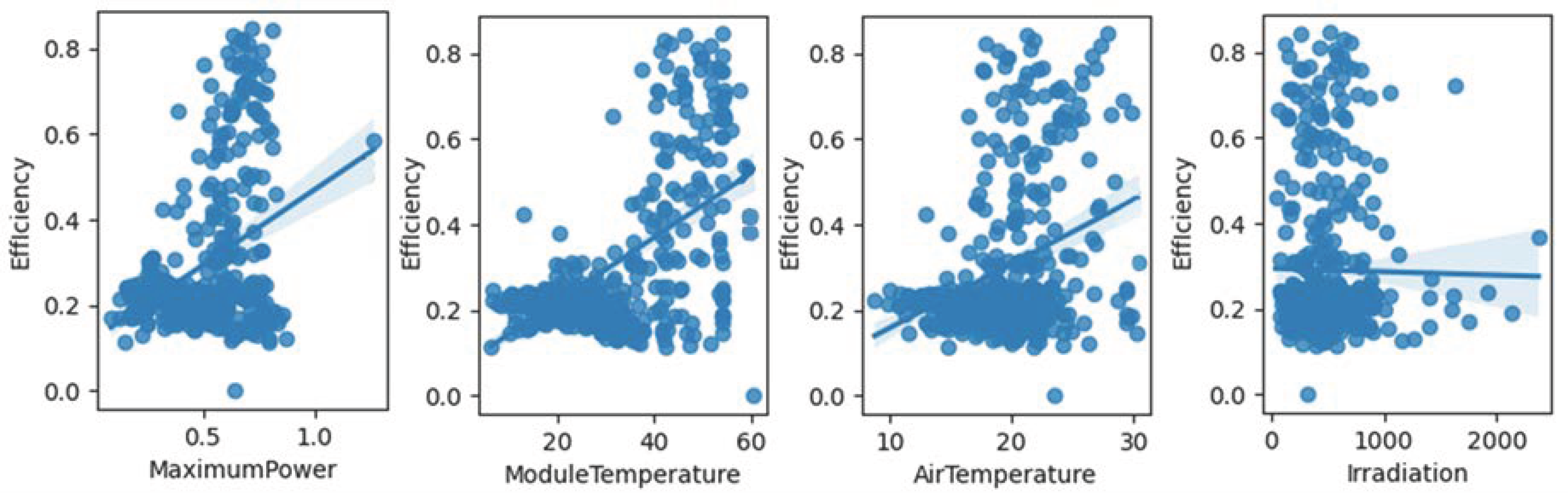
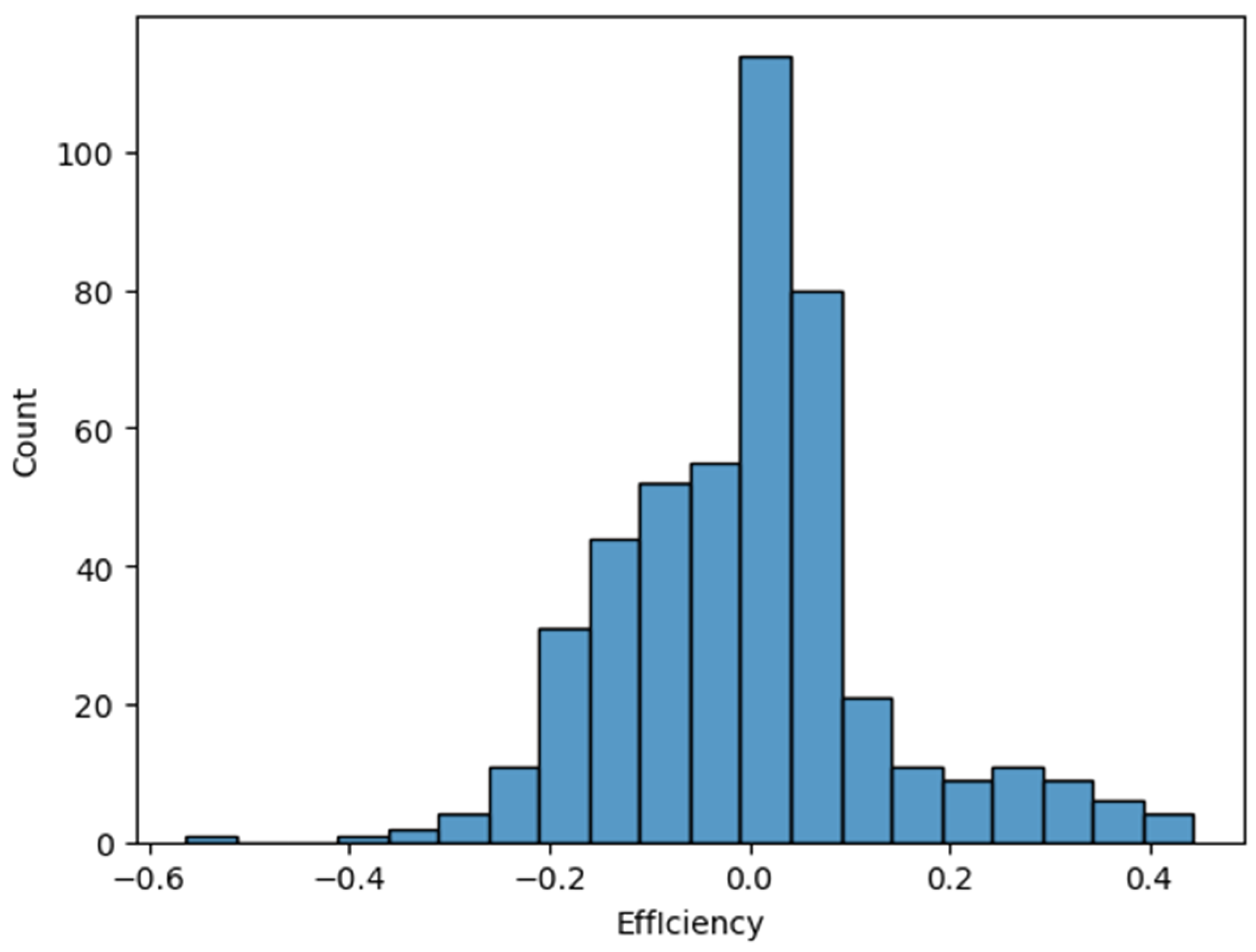
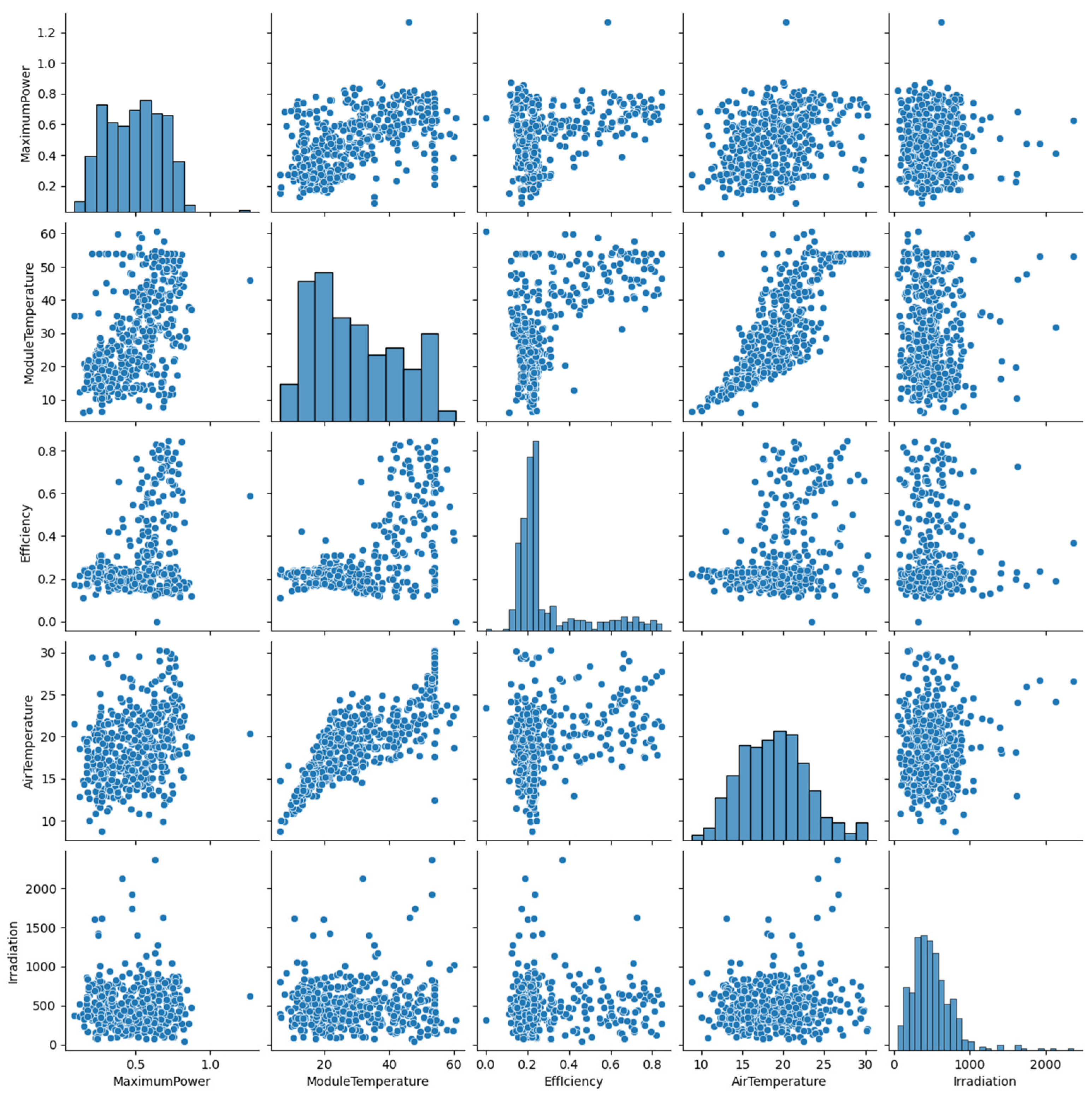
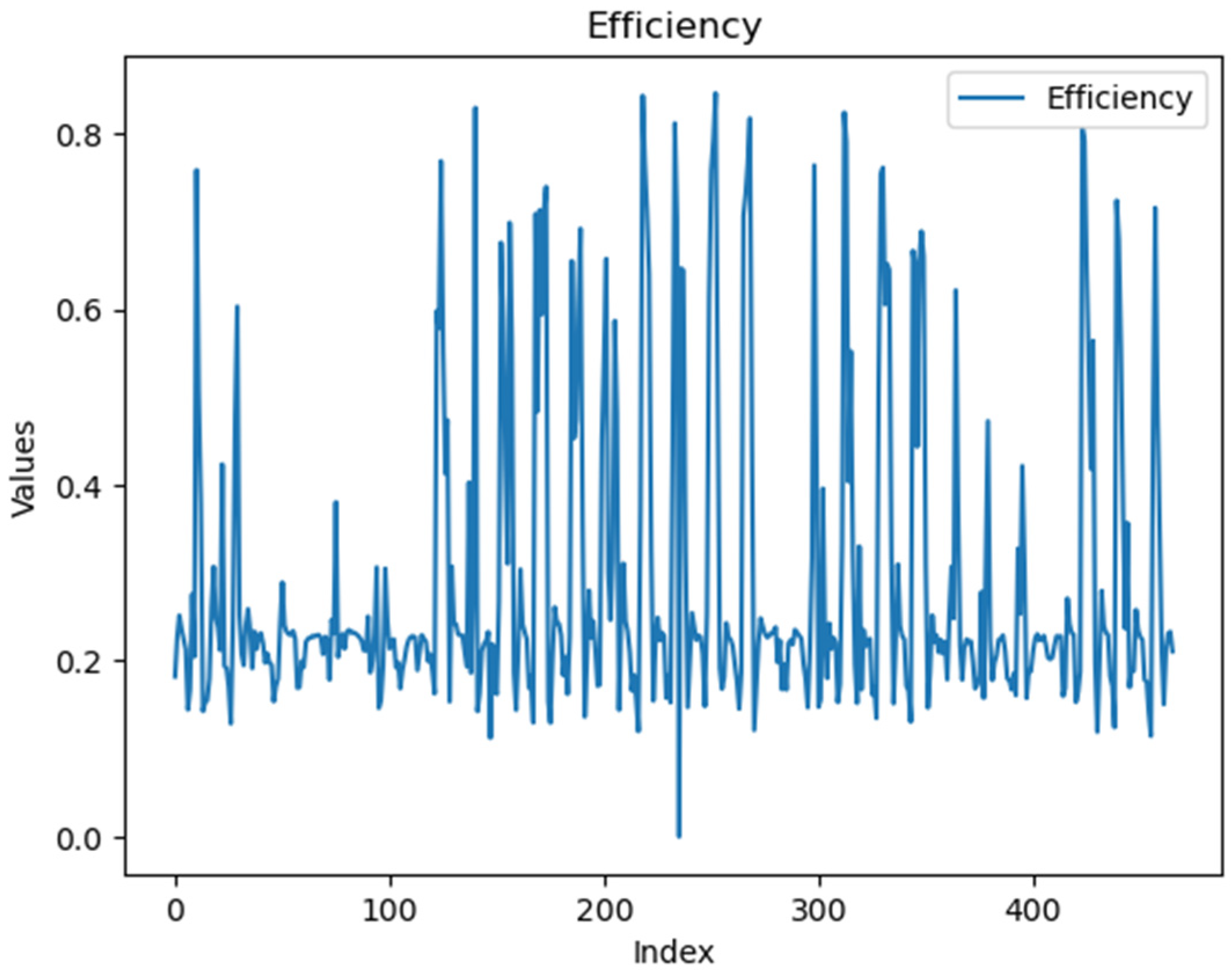
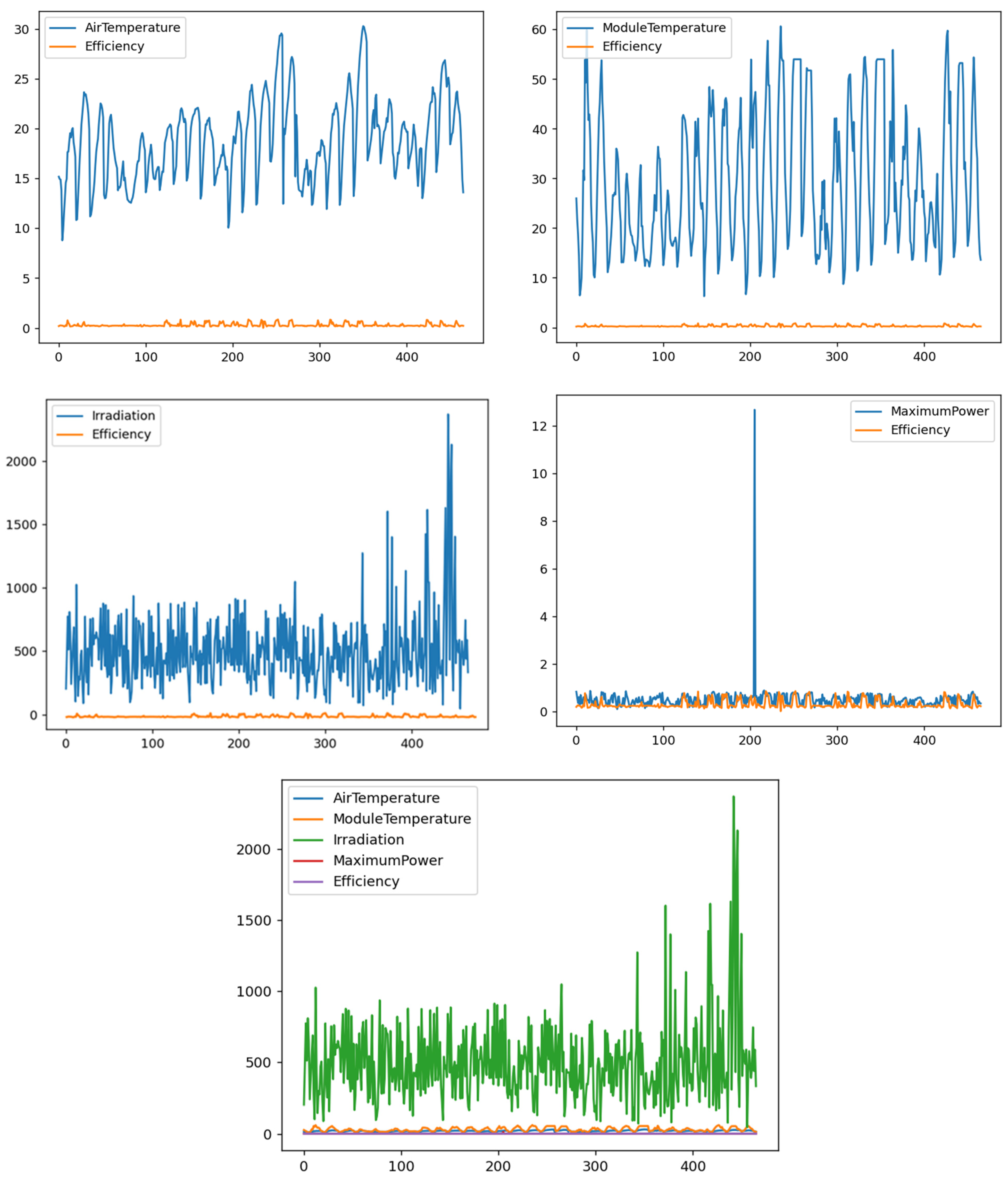
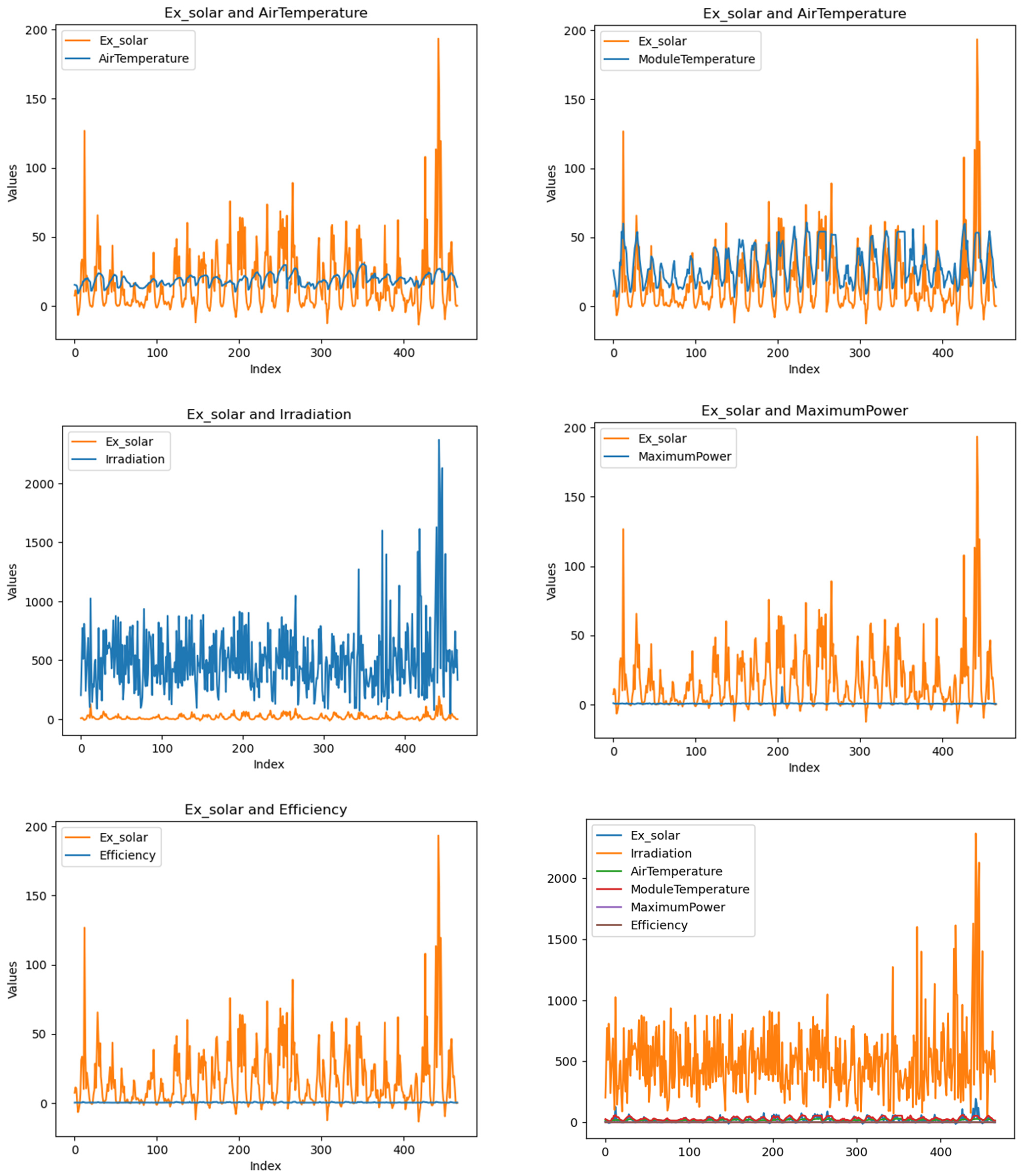
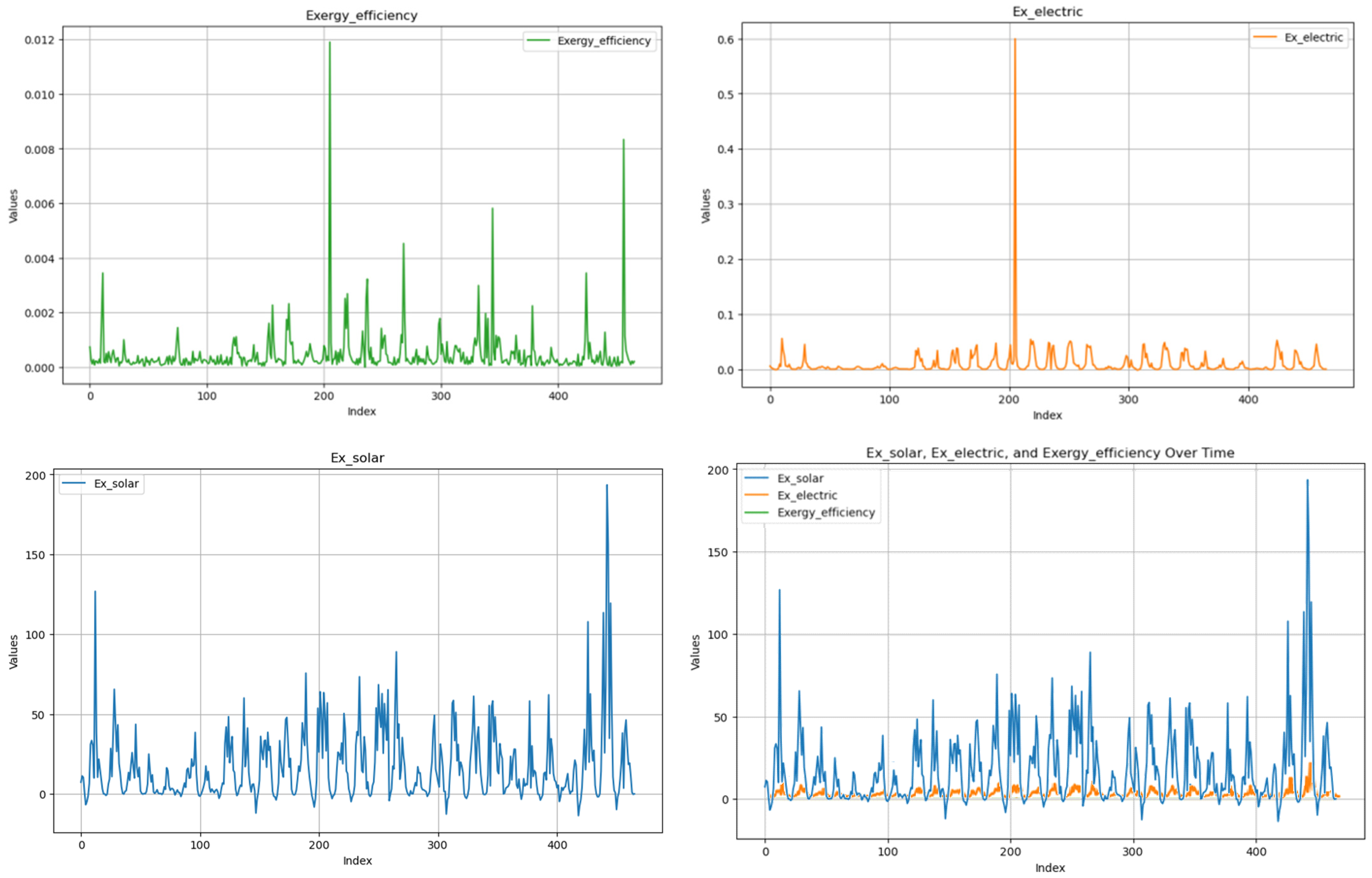

| Feature | Values Between |
|---|---|
| Open Circuit Voltage (Voc) [Volt] | 30–36 |
| Short Circuit Current (Isc) [A] | 6–8 |
| Maximum Power (Pmpp) [W] | 0.08–1.26 |
| Solar Irradiation Spread [m2] | 0.000516–0.007284 |
| Maximum Voltage (Vmpp) [V] | 15.18–29.34 |
| Maximum Current (Impp) [A] | 0.13–0.54 |
| FillFactor (FF) [%] | 50–75 |
| Parallel Resistance (Rp) [Ohm] | 0.18–1.20 |
| Series Resistance (Rs) [Ohm] | 0.18–0.97 |
| Module Temperature [°C] | 7.72–59.89 |
| Efficiency [%] | 5–20 |
| Model | R2 | RMSE | MAE |
|---|---|---|---|
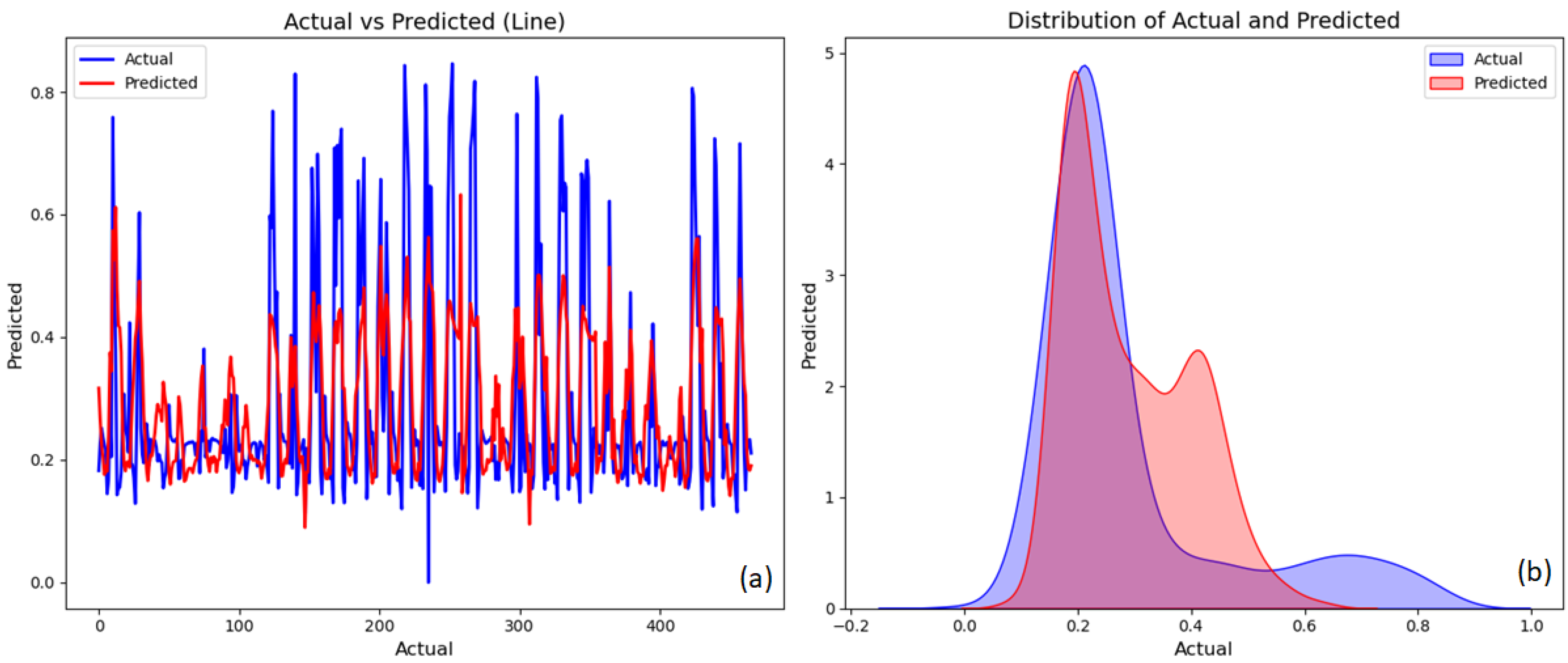
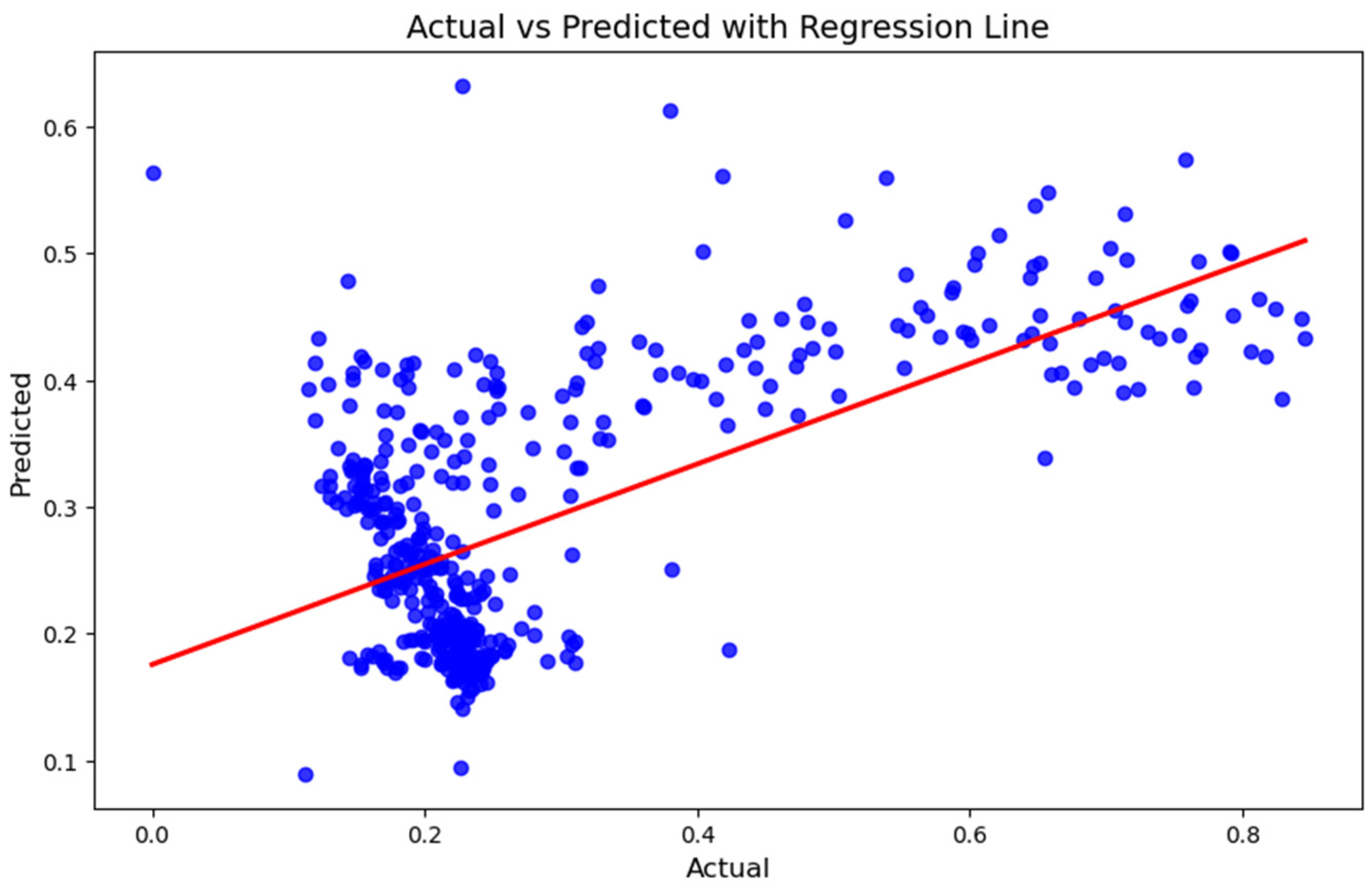
| RF | 0.94889 | 0.0180499 | 0.0983381 |
| Input Internal Parameters | PV Solar Power Efficiency |
|---|---|
| Maximum Power | +0.314 |
| Module Temperature | +0.106 |
| Air Temperature | +0.980 |
| Irradiation | +0.318 |
| Maximum Power | Module Temperature | Efficiency | Air Temperature | Irradiation | |
|---|---|---|---|---|---|
| Maximum Power | 1 | ||||
| Module Temperature | 0.553477 | 1 | |||
| Efficiency | 0.377574 | 0.593858 | 1 | ||
| Air Temperature | 0.367222 | 0.800951 | 0.354029 | 1 | |
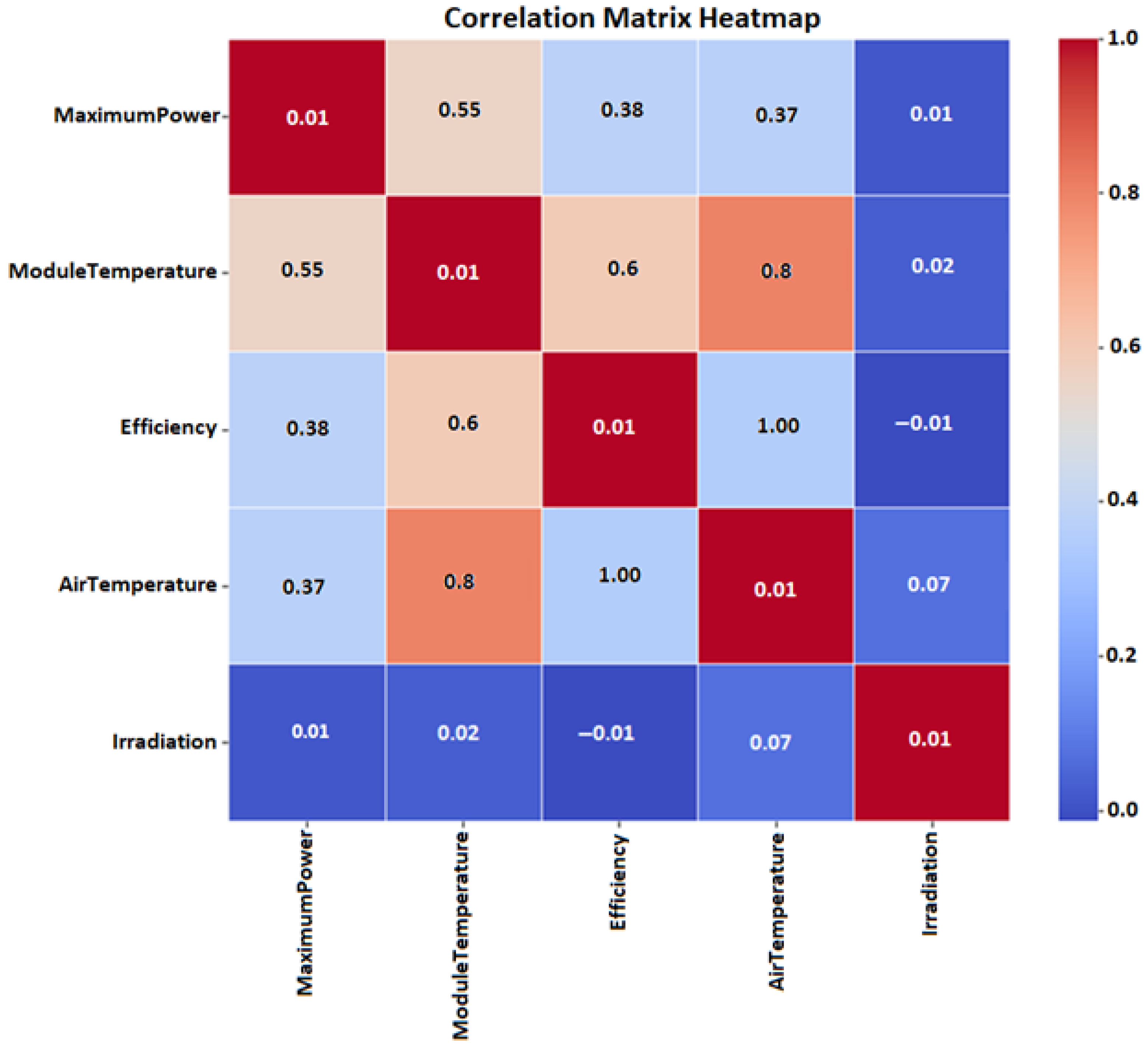
| Irradiation | 0.013694 | 0.028378 | −0.013180 | 0.073490 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şahin, G.; van Sark, W.G.J.H.M. Machine Learning-Based Evaluation of Solar Photovoltaic Panel Exergy and Efficiency Under Real Climate Conditions. Energies 2025, 18, 1318. https://doi.org/10.3390/en18061318
Şahin G, van Sark WGJHM. Machine Learning-Based Evaluation of Solar Photovoltaic Panel Exergy and Efficiency Under Real Climate Conditions. Energies. 2025; 18(6):1318. https://doi.org/10.3390/en18061318
Chicago/Turabian StyleŞahin, Gökhan, and Wilfried G. J. H. M. van Sark. 2025. "Machine Learning-Based Evaluation of Solar Photovoltaic Panel Exergy and Efficiency Under Real Climate Conditions" Energies 18, no. 6: 1318. https://doi.org/10.3390/en18061318
APA StyleŞahin, G., & van Sark, W. G. J. H. M. (2025). Machine Learning-Based Evaluation of Solar Photovoltaic Panel Exergy and Efficiency Under Real Climate Conditions. Energies, 18(6), 1318. https://doi.org/10.3390/en18061318







