Enhanced Models for Wind, Solar Power Generation, and Battery Energy Storage Systems Considering Power Electronic Converter Precise Efficiency Behavior
Abstract
1. Introduction
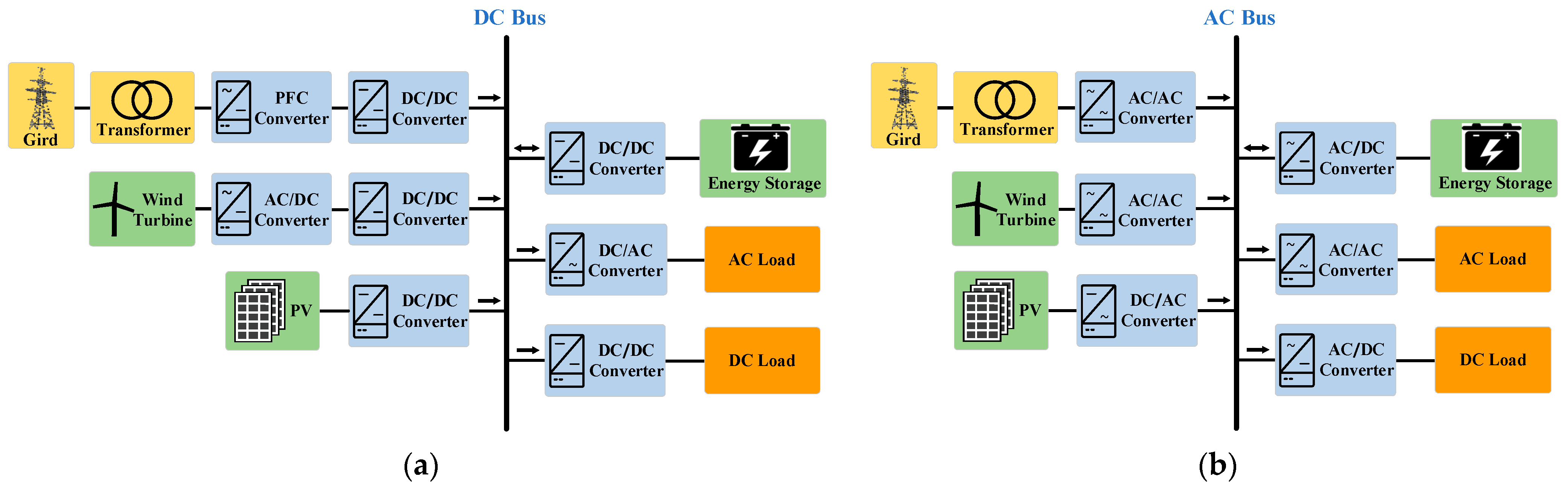
2. AC/DC Power System Structures and Efficiency Model of PECs
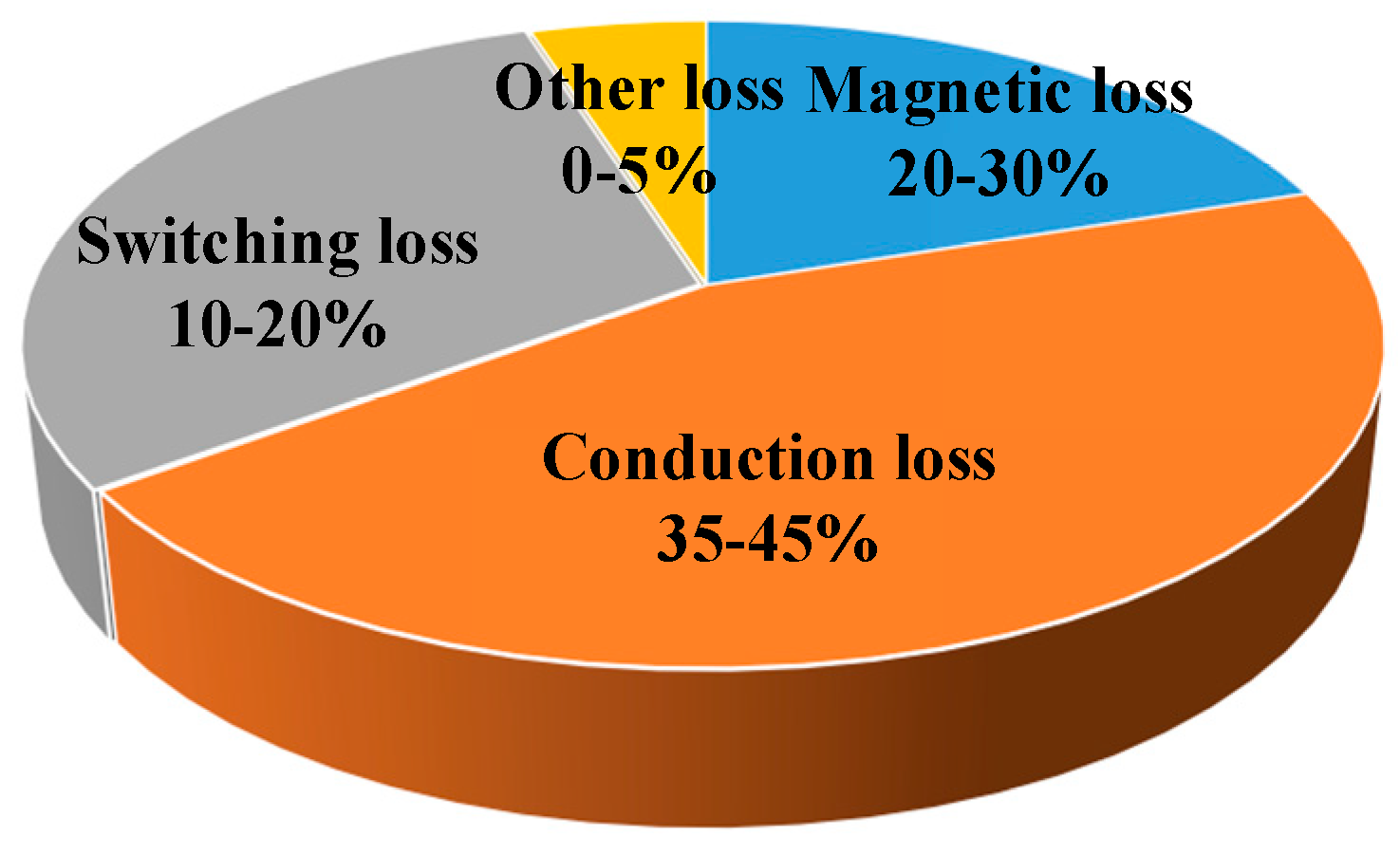
2.1. Converter Loss Analysis
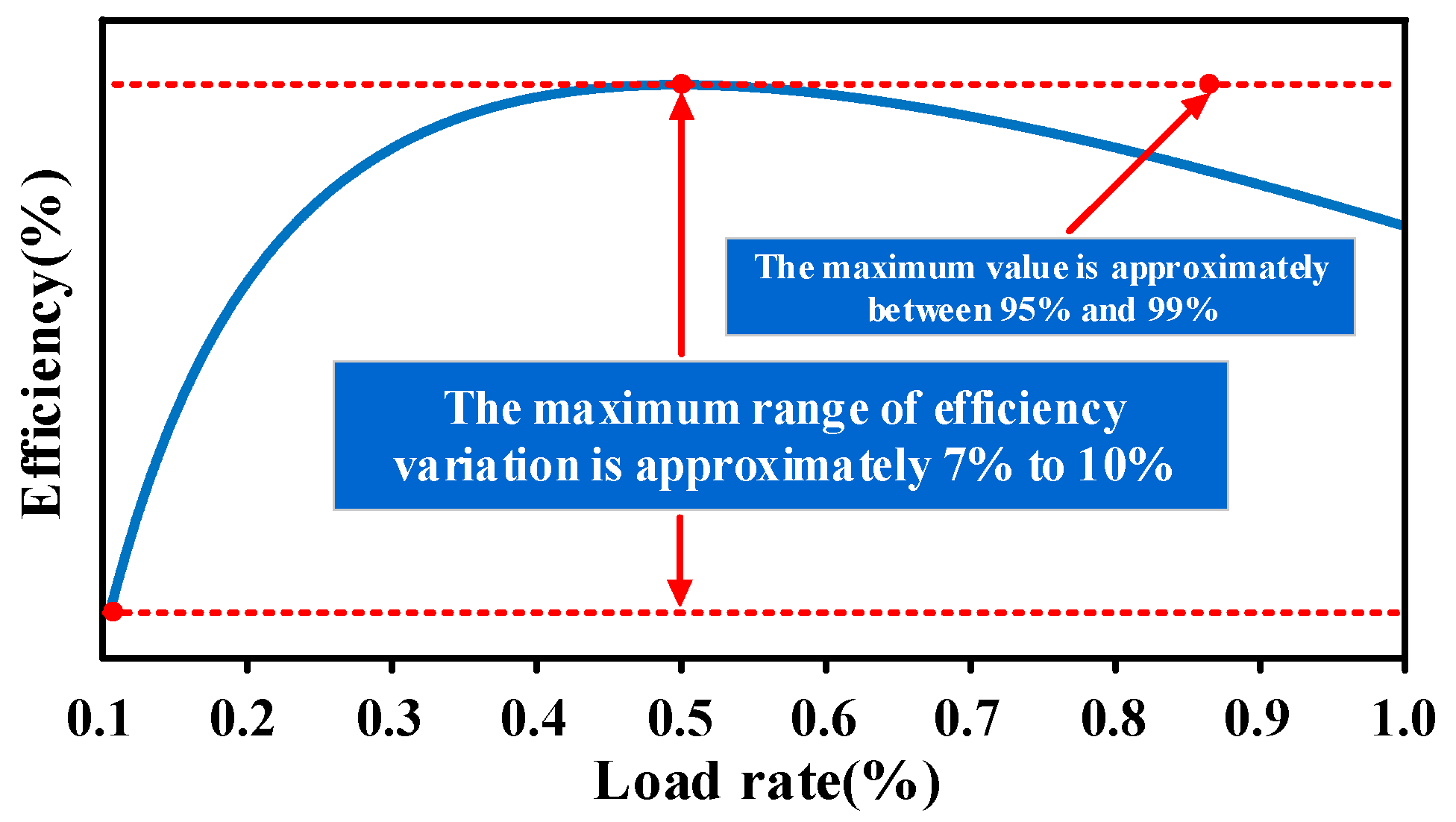
2.2. Converter Efficiency Model
3. Enhanced AC/DC Power System Models
3.1. Wind Turbine Model
3.2. Photovoltaic System Model
3.3. Load Model
3.4. Battery Energy Storage System Model
3.5. Power Grid Supply Model
4. Capacity Configuration Optimization
4.1. Objective Function
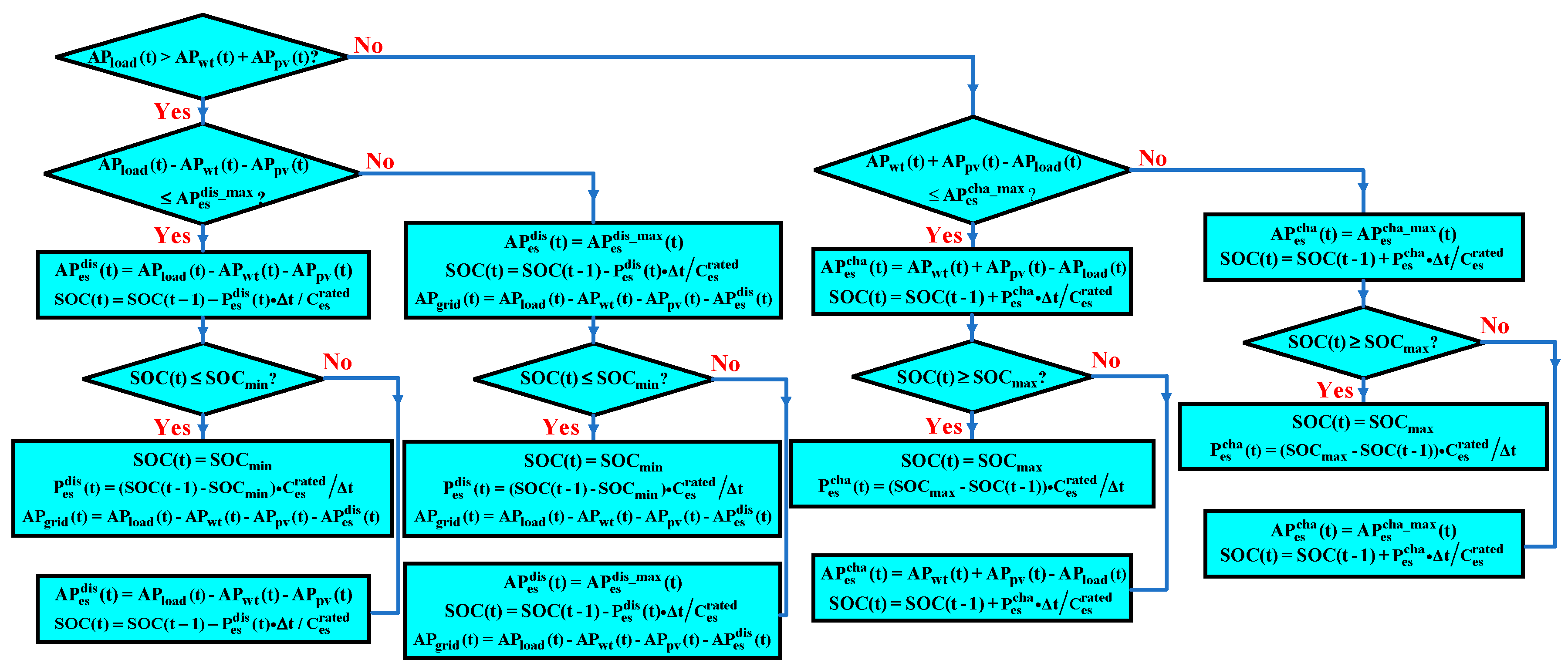
4.2. Power Output Strategy
4.3. Optimization Algorithm
5. Example Analysis
5.1. Example 1: DC Power System
5.2. Example 2: AC Power System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anoune, K.; Bouya, M.; Astito, A.; Abdellah, A.B. Sizing methods and optimization techniques for PV-wind based hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2018, 93, 652–673. [Google Scholar] [CrossRef]
- Han, Z.; Li, Z.; Wang, W.; Liu, W.; Ma, Q.; Sun, S.; Liu, H.; Zhang, Q.; Cao, Y. Multi-Time Optimization Scheduling Strategy for Integrated Energy Systems Considering Multiple Controllable Loads and Carbon Capture Plants. Energies 2024, 17, 5995. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J. Revolution in renewables: Integration of green hydrogen for a sustainable future. Energies 2024, 17, 4148. [Google Scholar] [CrossRef]
- Zhang, Y.; Hua, Q.S.; Sun, L.; Liu, Q. Life cycle optimization of renewable energy systems configuration with hybrid battery/hydrogen storage: A comparative study. J. Energy Storage 2020, 30, 101470. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Z.; Duan, Y. Optimal capacity and operation strategy of a solar-wind hybrid renewable energy system. Energy Convers. Manag. 2021, 244, 114519. [Google Scholar] [CrossRef]
- Xiao, Y.; Zou, C.; Dong, M.; Chi, H.; Yan, Y.; Jiang, S. Feasibility study: Economic and technical analysis of optimal configuration and operation of a hybrid CSP/PV/wind power cogeneration system with energy storage. Renew. Energy 2024, 225, 120273. [Google Scholar] [CrossRef]
- Emad, D.; El-Hameed, M.A.; El-Fergany, A.A. Optimal techno-economic design of hybrid PV/wind system comprising battery energy storage: Case study for a remote area. Energy Convers. Manag. 2021, 249, 114847. [Google Scholar] [CrossRef]
- Megaptche, C.A.M.; Musau, P.M.; Tjahè, A.V.; Kim, H.; Waita, S.; Aduda, B.O. Demand response-fuzzy inference system controller in the multi-objective optimization design of a photovoltaic/wind turbine/battery/supercapacitor and diesel system: Case of healthcare facility. Energy Convers. Manag. 2023, 291, 117245. [Google Scholar] [CrossRef]
- Javed, M.S.; Song, A.; Ma, T. Techno-economic assessment of a stand-alone hybrid solar-wind-battery system for a remote island using genetic algorithm. Energy 2019, 176, 704–717. [Google Scholar] [CrossRef]
- Arabi-Nowdeh, S.; Nasri, S.; Saftjani, P.B.; Naderipour, A.; Abdul-Malek, Z.; Kamyab, H.; Jafar-Nowdeh, A. Multi-criteria optimal design of hybrid clean energy system with battery storage considering off-and on-grid application. J. Clean. Prod. 2021, 290, 125808. [Google Scholar] [CrossRef]
- Naderipour, A.; Ramtin, A.R.; Abdullah, A.; Marzbali, M.H.; Nowdeh, S.A.; Kamyab, H. Hybrid energy system optimization with battery storage for remote area application considering loss of energy probability and economic analysis. Energy 2022, 239, 122303. [Google Scholar] [CrossRef]
- Tebibel, H. Methodology for multi-objective optimization of wind turbine/battery/electrolyzer system for decentralized clean hydrogen production using an adapted power management strategy for low wind speed conditions. Energy Convers. Manag. 2021, 238, 114125. [Google Scholar] [CrossRef]
- Nyeche, E.N.; Diemuodeke, E.O. Modelling and optimisation of a hybrid PV-wind turbine-pumped hydro storage energy system for mini-grid application in coastline communities. J. Clean. Prod. 2020, 250, 119578. [Google Scholar] [CrossRef]
- Al-Ghussain, L.; Samu, R.; Taylan, O.; Fahrioglu, M. Sizing renewable energy systems with energy storage systems in microgrids for maximum cost-efficient utilization of renewable energy resources. Sustain. Cities Soc. 2020, 55, 102059. [Google Scholar] [CrossRef]
- Medghalchi, Z.; Taylan, O. A novel hybrid optimization framework for sizing renewable energy systems integrated with energy storage systems with solar photovoltaics, wind, battery and electrolyzer-fuel cell. Energy Convers. Manag. 2023, 294, 117594. [Google Scholar] [CrossRef]
- Xu, X.; Hu, W.; Cao, D.; Huang, Q.; Chen, C.; Chen, Z. Optimized sizing of a standalone PV-wind-hydropower station with pumped-storage installation hybrid energy system. Renew. Energy 2020, 147, 1418–1431. [Google Scholar] [CrossRef]
- Jamshidi, M.; Askarzadeh, A. Techno-economic analysis and size optimization of an off-grid hybrid photovoltaic, fuel cell and diesel generator system. Sustain. Cities Soc. 2019, 44, 310–320. [Google Scholar] [CrossRef]
- Hou, H.; Xu, T.; Wu, X.; Wang, H.; Tang, A.; Chen, Y. Optimal capacity configuration of the wind-photovoltaic-storage hybrid power system based on gravity energy storage system. Appl. Energy 2020, 271, 115052. [Google Scholar] [CrossRef]
- Emrani, A.; Berrada, A.; Arechkik, A.; Bakhouya, M. Improved techno-economic optimization of an off-grid hybrid solar/wind/gravity energy storage system based on performance indicators. J. Energy Storage 2022, 49, 104163. [Google Scholar] [CrossRef]
- Iqbal, R.; Liu, Y.; Zeng, Y.; Zhang, Q.; Zeeshan, M. Comparative study based on techno-economics analysis of different shipboard microgrid systems comprising PV/wind/fuel cell/battery/diesel generator with two battery technologies: A step toward green maritime transportation. Renew. Energy 2024, 221, 119670. [Google Scholar] [CrossRef]
- Ren, Y.; Jin, K.; Gong, C.; Hu, J.; Liu, D.; Jing, X.; Zhang, K. Modelling and capacity allocation optimization of a combined pumped storage/wind/photovoltaic/hydrogen production system based on the consumption of surplus wind and photovoltaics and reduction of hydrogen production cost. Energy Convers. Manag. 2023, 296, 117662. [Google Scholar] [CrossRef]
- Alshammari, N.; Asumadu, J. Optimum unit sizing of hybrid renewable energy system utilizing harmony search, Jaya and particle swarm optimization algorithms. Sustain. Cities Soc. 2020, 60, 102255. [Google Scholar] [CrossRef]
- Arasteh, A.; Alemi, P.; Beiraghi, M. Optimal allocation of photovoltaic/wind energy system in distribution network using meta-heuristic algorithm. Appl. Soft Comput. 2021, 109, 107594. [Google Scholar] [CrossRef]
- Abdel-Mawgoud, H.; Ali, A.; Kamel, S.; Rahmann, C.; Abdel-Moamen, M.A. A modified manta ray foraging optimizer for planning inverter-based photovoltaic with battery energy storage system and wind turbine in distribution networks. IEEE Access 2021, 9, 91062–91079. [Google Scholar] [CrossRef]
- Alzahrani, A.; Hayat, M.A.; Khan, A.; Hafeez, G.; Khan, F.A.; Khan, M.I.; Ali, S. Optimum sizing of stand-alone microgrids: Wind turbine, solar photovoltaic, and energy storage system. J. Energy Storage 2023, 73, 108611. [Google Scholar] [CrossRef]
- Chen, X.; Dong, W.; Yang, Q. Robust optimal capacity planning of grid-connected microgrid considering energy management under multi-dimensional uncertainties. Appl. Energy 2022, 323, 119642. [Google Scholar] [CrossRef]
- Sahoo, B.; Routray, S.K.; Rout, P.K. AC, DC, and hybrid control strategies for smart microgrid application: A review. Int. Trans. Electr. Energy Syst. 2021, 31, e12683. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, H.; Vilathgamuwa, D.M. Single-switch high step-up boost converter based on a novel voltage multiplier. IET Power Electron. 2019, 12, 3732–3738. [Google Scholar] [CrossRef]
- Zhu, B.; Yang, Y.; Wang, K.; Liu, J.; Vilathgamuwa, D.M. High transformer utilization ratio and high voltage conversion gain flyback converter for photovoltaic application. IEEE Trans. Ind. Appl. 2024, 60, 2840–2851. [Google Scholar] [CrossRef]
- Shahin, A.; Payman, A.; Martin, J.P.; Pierfederici, S.; Meibody-Tabar, F. Approximate novel loss formulae estimation for optimization of power controller of DC/DC converter. In Proceedings of the IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; IEEE: New York, NY, USA, 2010; pp. 373–378. [Google Scholar]
- Zhu, B.; Liu, Y.; Zhi, S.; Wang, K.; Liu, J. A family of bipolar high step-up zeta–buck–boost converter based on “coat circuit”. IEEE Trans. Power Electron. 2023, 38, 3328–3339. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, H.; Zhang, Y.; Chen, S. Buck-based active-clamp circuit for current-fed isolated DC–DC converters. IEEE Trans. Power Electron. 2022, 37, 4337–4345. [Google Scholar] [CrossRef]
- Kasprzyk, L.; Tomczewski, A.; Pietracho, R.; Mielcarek, A.; Nadolny, Z.; Tomczewski, K.; Trzmiel, G.; Alemany, J. Optimization of a PV-Wind hybrid power supply structure with electrochemical storage intended for supplying a load with known characteristics. Energies 2020, 13, 6143. [Google Scholar] [CrossRef]
- Geng, C.; Shi, Z.; Chen, X.; Sun, Z.; Jin, Y.; Shi, T.; Wu, X. Stochastic Capacity Optimization of an Integrated BFGCC–MSHS–Wind–Solar Energy System for the Decarbonization of a Steelmaking Plant. Energies 2024, 17, 2994. [Google Scholar] [CrossRef]
- Al Shereiqi, A.; Al-Hinai, A.; Albadi, M.; Al-Abri, R. Optimal sizing of a hybrid wind-photovoltaic-battery plant to mitigate output fluctuations in a grid-connected system. Energies 2020, 13, 3015. [Google Scholar] [CrossRef]
- Zhong, X.; Sun, X.; Wu, Y. A capacity optimization method for a hybrid energy storage microgrid system based on an augmented ε-constraint method. Energies 2022, 15, 7593. [Google Scholar] [CrossRef]
- Weng, Z.; Zhou, J.; Zhan, Z. Reliability evaluation of standalone microgrid based on sequential Monte Carlo simulation method. Energies 2022, 15, 6706. [Google Scholar] [CrossRef]
- Dong, J.; Dou, Z.; Si, S.; Wang, Z.; Liu, L. Optimization of capacity configuration of wind–solar–diesel–storage using improved sparrow search algorithm. J. Electr. Eng. Technol. 2022, 17, 1–14. [Google Scholar] [CrossRef]
- He, Y.; Guo, S.; Zhou, J.; Wu, F.; Huang, J.; Pei, H. The quantitative techno-economic comparisons and multi-objective capacity optimization of wind-photovoltaic hybrid power system considering different energy storage technologies. Energy Convers. Manag. 2021, 229, 113779. [Google Scholar] [CrossRef]
- Wang, J.; Deng, H.; Qi, X. Cost-based site and capacity optimization of multi-energy storage system in the regional integrated energy networks. Energy 2022, 261, 125240. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Z.; Duan, Y. Capacity optimization and feasibility assessment of solar-wind hybrid renewable energy systems in China. J. Clean. Prod. 2022, 368, 133139. [Google Scholar] [CrossRef]
- Yi, T.; Ye, H.; Li, Q.; Zhang, C.; Ren, W.; Tao, Z. Energy storage capacity optimization of wind-energy storage hybrid power plant based on dynamic control strategy. J. Energy Storage 2022, 55, 105372. [Google Scholar] [CrossRef]
- Taha, H.A.; Alham, M.H.; Youssef, H.K.M. Multi-objective optimization for optimal allocation and coordination of wind and solar DGs, BESSs and capacitors in presence of demand response. IEEE Access 2022, 10, 16225–16241. [Google Scholar] [CrossRef]
- Chennaif, M.; Zahboune, H.; Elhafyani, M.; Zouggar, S. Electric System Cascade Extended Analysis for optimal sizing of an autonomous hybrid CSP/PV/wind system with Battery Energy Storage System and thermal energy storage. Energy 2021, 227, 120444. [Google Scholar] [CrossRef]

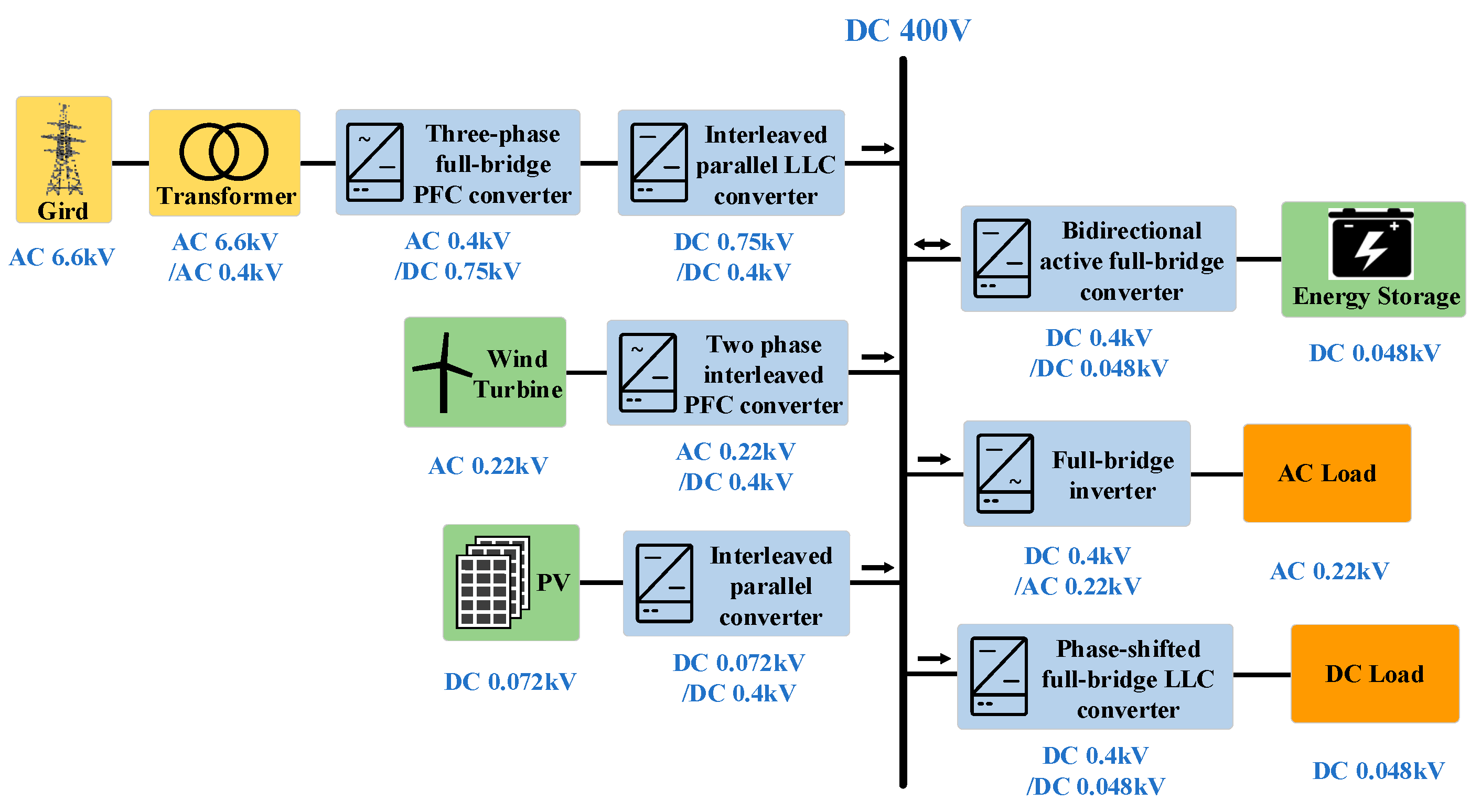
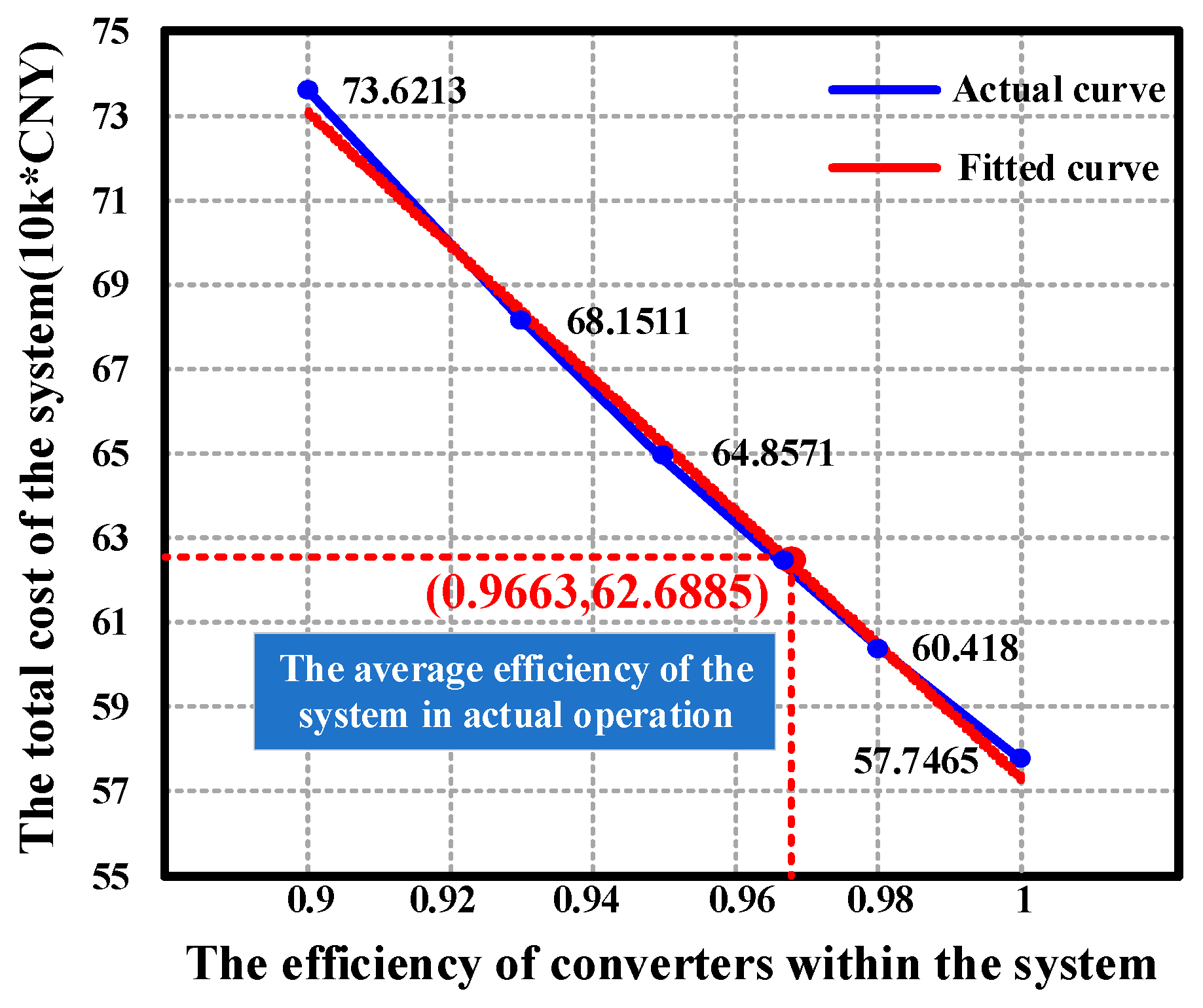
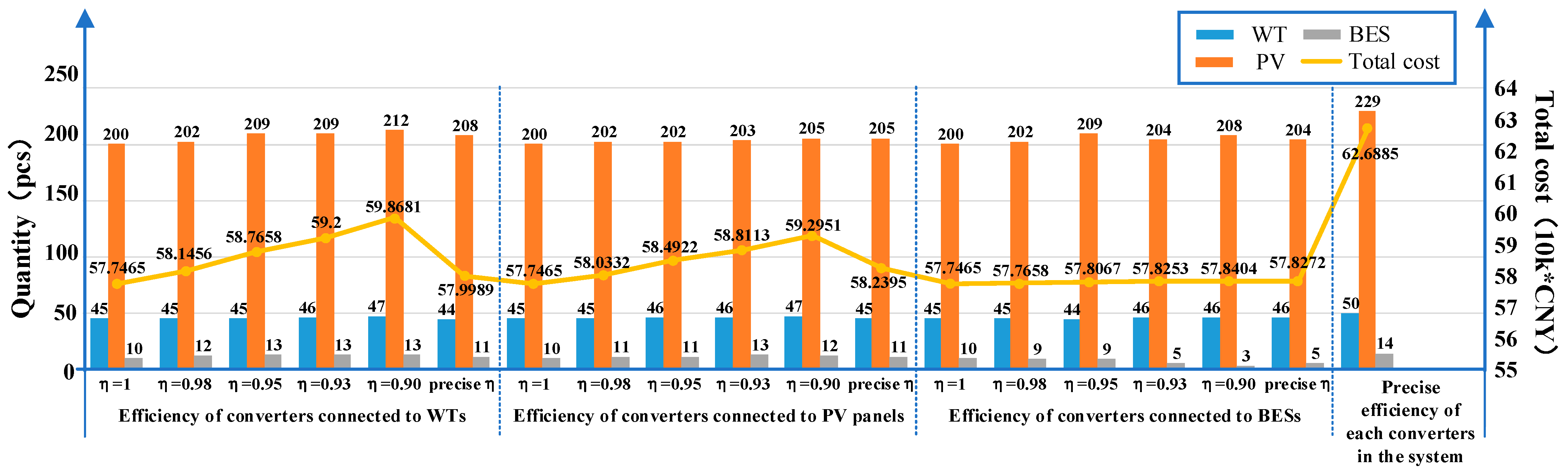
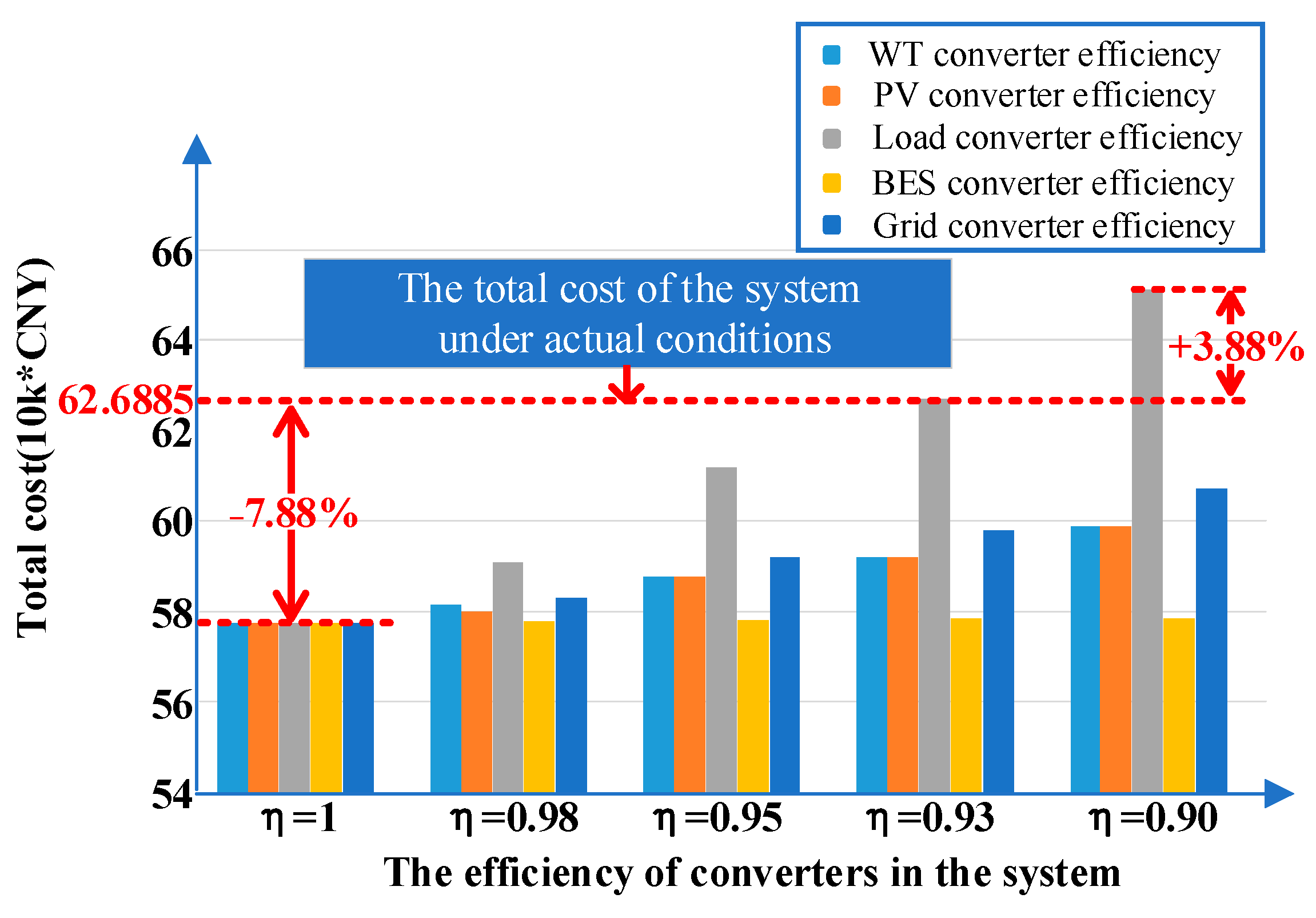


| Component | Parameter | Value | Parameter | Value |
|---|---|---|---|---|
| WT [41,43] | The rated power (kW/pcs) | 10 | Cut-in wind speed (m/s) | 3 |
| The rated wind speed (m/s) | 11 | Cut-out wind speed (m/s) | 25 | |
| Unit purchase price | 3.86 | Unit installation price | 0.15 | |
| Unit maintenance price | 0.1 | Lifespan (years) | 20 | |
| PV [39,43] | The rated power (kW/pcs) | 2 | Unit purchase price | 0.8 |
| Standard solar radiation intensity (kW/m2) | 1 | Unit installation price | 0.03 | |
| Coefficient of environmental temperature | 4.7 × 10−3 | Unit maintenance price | 0.002 | |
| Standard environmental temperature (°C) | 25 | Lifespan (years) | 20 | |
| BES [44] | Battery charging efficiency | 0.85 | Unit purchase price | 0.16 |
| Battery discharging efficiency | 0.85 | Unit installation price | 0.005 | |
| Maximum SOC | 0.9 | Unit maintenance price | 0.002 | |
| Minimum SOC | 0.2 | Lifespan (years) | 1.36 | |
| The rated capacity | 6 | |||
| Grid | Low purchase unit price | 5.5 × 10−5 | Medium purchase unit price | 6.0 × 10−5 |
| High purchase unit price | 8.5 × 10−5 | |||
| Other | Discount rate (%) | 4.75 | The standard power waste penalty fee (10k*CNY) | 1 |
| Time interval (h) | 1 | The standard penalty coefficient | 0.2 |
| Component | Parameter | Value | Parameter | Value |
|---|---|---|---|---|
| Coefficient of the efficiency curve | for WT converters | 6.12 × 10−2 | for grid converters | −2.28 × 10−4 |
| for WT converters | −5.50 × 10−1 | for grid converters | −9.426 | |
| for WT converters | 98.64 | for grid converters | 98.02 | |
| for PV converters | −2.588 | for AC load converters | −7.39 × 10−1 | |
| for PV converters | −9.02×10−1 | for AC load converters | −10.71 | |
| for PV converters | 100.4 | for AC load converters | 99.52 | |
| for BESS converters | −2.56×10−1 | for DC load converters | −2.14 × 10−1 | |
| for BESS converters | −7.025 | for DC load converters | −4.86 × 10−1 | |
| for BESS converters | 99.82 | for DC load converters | 98.97 | |
| Unit price | Purchase of WT converter | 0.2 | Installing of grid converter | 0.02 |
| Installing of WT converter | 0.03 | Purchase of AC load converter | 0.07 | |
| Purchase of PV converter | 0.02 | Purchase of DC load converter | 0.04 | |
| Installing of PV converter | 0.01 | Installing of AC load converter | 0.01 | |
| Purchase of BES converter | 0.05 | Installing of DC load converter | 0.01 | |
| Installing of BES converter | 0.01 | Maintenance of converter | 0.001 | |
| Purchase of grid converter | 0.1 | |||
| Rated power | Grid converter (kW) | 10 | DC load converter (kW) | 2 |
| AC load converter (kW) | 5 | |||
| Lifespan | Various types of converters (years) | 10 |
| The Efficiency of Each Converter in the System | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 45 | 200 | 10 | 31.2712 | 1.8819 | 19.1365 | 0.3269 | 5.1300 | 57.7465 |
| 0.98 | 46 | 223 | 14 | 33.6512 | 2.0067 | 19.1516 | 0.3245 | 5.2840 | 60.4180 |
| 0.95 | 50 | 244 | 22 | 37.4272 | 2.1953 | 19.1513 | 0.3413 | 5.7420 | 64.8571 |
| 0.93 | 53 | 265 | 25 | 40.2083 | 2.3398 | 19.1490 | 0.3640 | 6.0900 | 68.1511 |
| 0.90 | 59 | 280 | 37 | 44.7811 | 2.5603 | 19.1496 | 0.3863 | 6.7440 | 73.6213 |
| Precise efficiency model proposed in this paper | 50 | 229 | 14 | 35.3677 | 2.0928 | 19.1406 | 0.3914 | 5.6960 | 62.6885 |
| Component | Parameter | Value | Parameter | Value |
|---|---|---|---|---|
| WT [41,43] | The rated power (kW/pcs) | 5 | Cut-in wind speed (m/s) | 3 |
| The rated wind speed (m/s) | 11 | Cut-out wind speed (m/s) | 25 | |
| Unit purchase price | 3.86 | Unit installation price | 0.15 | |
| Unit maintenance price | 0.1 | Lifespan (years) | 20 | |
| PV [39,43] | The rated power (kW/pcs) | 1 | Unit purchase price | 0.8 |
| Standard solar radiation intensity (kW/m2) | 1 | Unit installation price | 0.03 | |
| Coefficient of environmental temperature | 4.7 × 10−3 | Unit maintenance price | 0.002 | |
| Standard environmental temperature (°C) | 25 | Lifespan (years) | 20 | |
| BES [44] | Battery charging efficiency | 0.85 | Unit purchase price | 0.16 |
| Battery discharging efficiency | 0.85 | Unit installation price | 0.005 | |
| Maximum SOC | 0.9 | Unit maintenance price | 0.002 | |
| Minimum SOC | 0.2 | Lifespan (years) | 1.36 | |
| The rated capacity | 2 | |||
| Grid | Low purchase unit price | 5.5 × 10−5 | Medium purchase unit price | 6.0 × 10−5 |
| High purchase unit price | 8.5 × 10−5 | |||
| Other | Discount rate (%) | 4.75 | The standard power waste penalty fee (10k*CNY) | 1 |
| Time interval (h) | 1 | The standard penalty coefficient | 0.2 |
| Component | Parameter | Value | Parameter | Value |
|---|---|---|---|---|
| Coefficient of the efficiency curve | for PV converters | −5.16 | for BESS converters | 97.8 |
| for PV converters | −4.56 × 10−1 | for DC load converters | −2.14 × 10−1 | |
| for PV converters | 100.5 | for DC load converters | −4.86 × 10−1 | |
| for BESS converters | 3.11 × 10−1 | for DC load converters | 98.97 | |
| for BESS converters | −2.406 |
| The Efficiency of Each Converter in the System | |||||||||
|---|---|---|---|---|---|---|---|---|---|
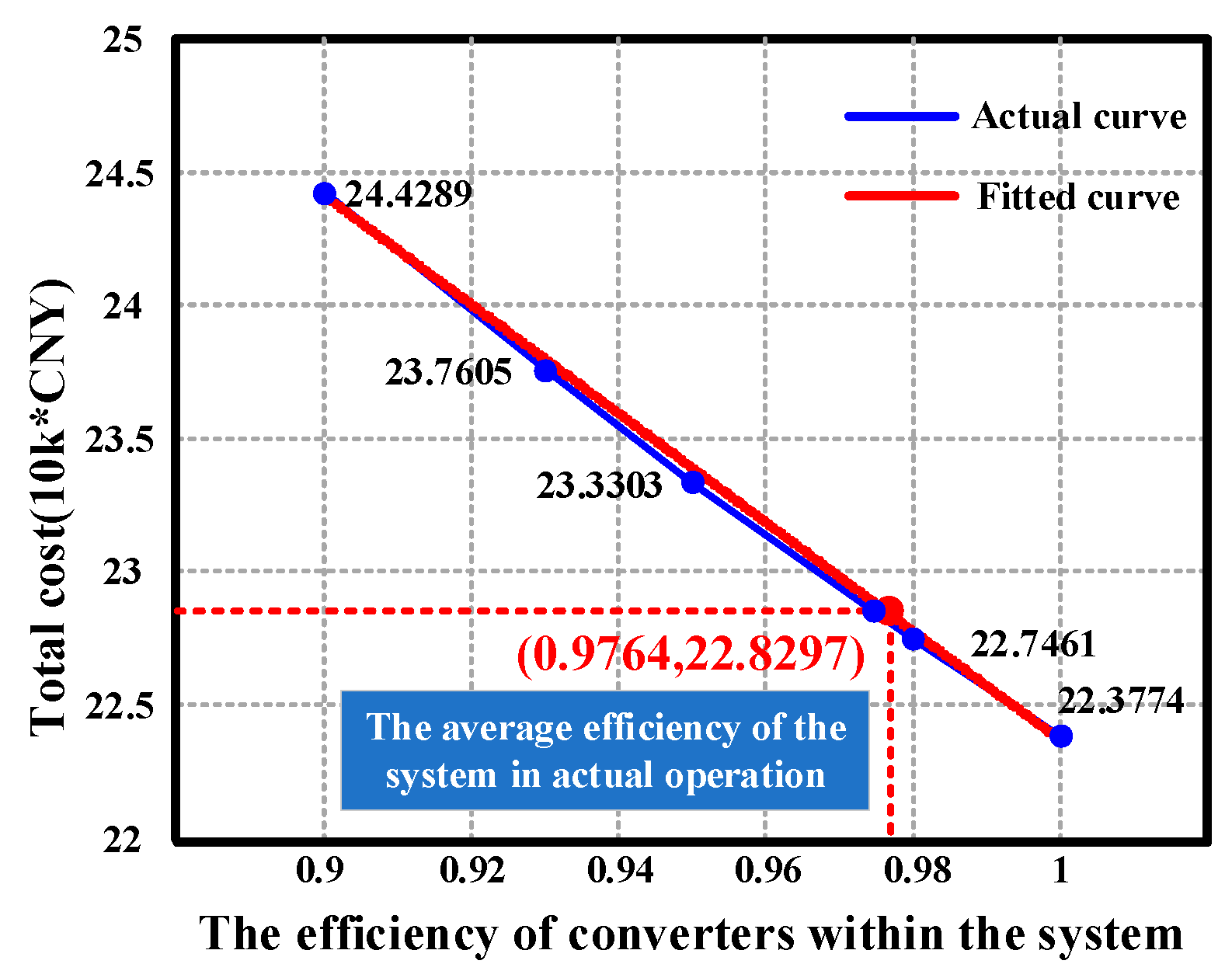
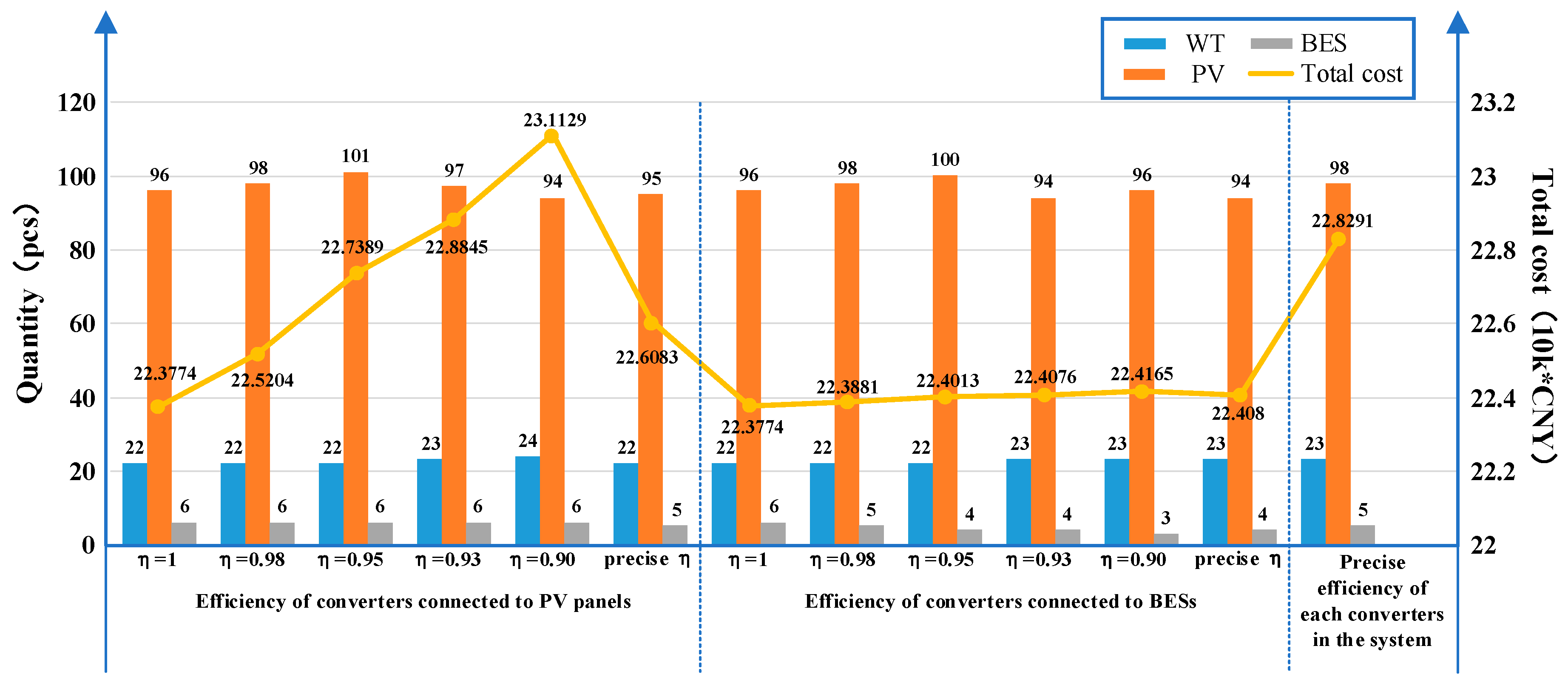
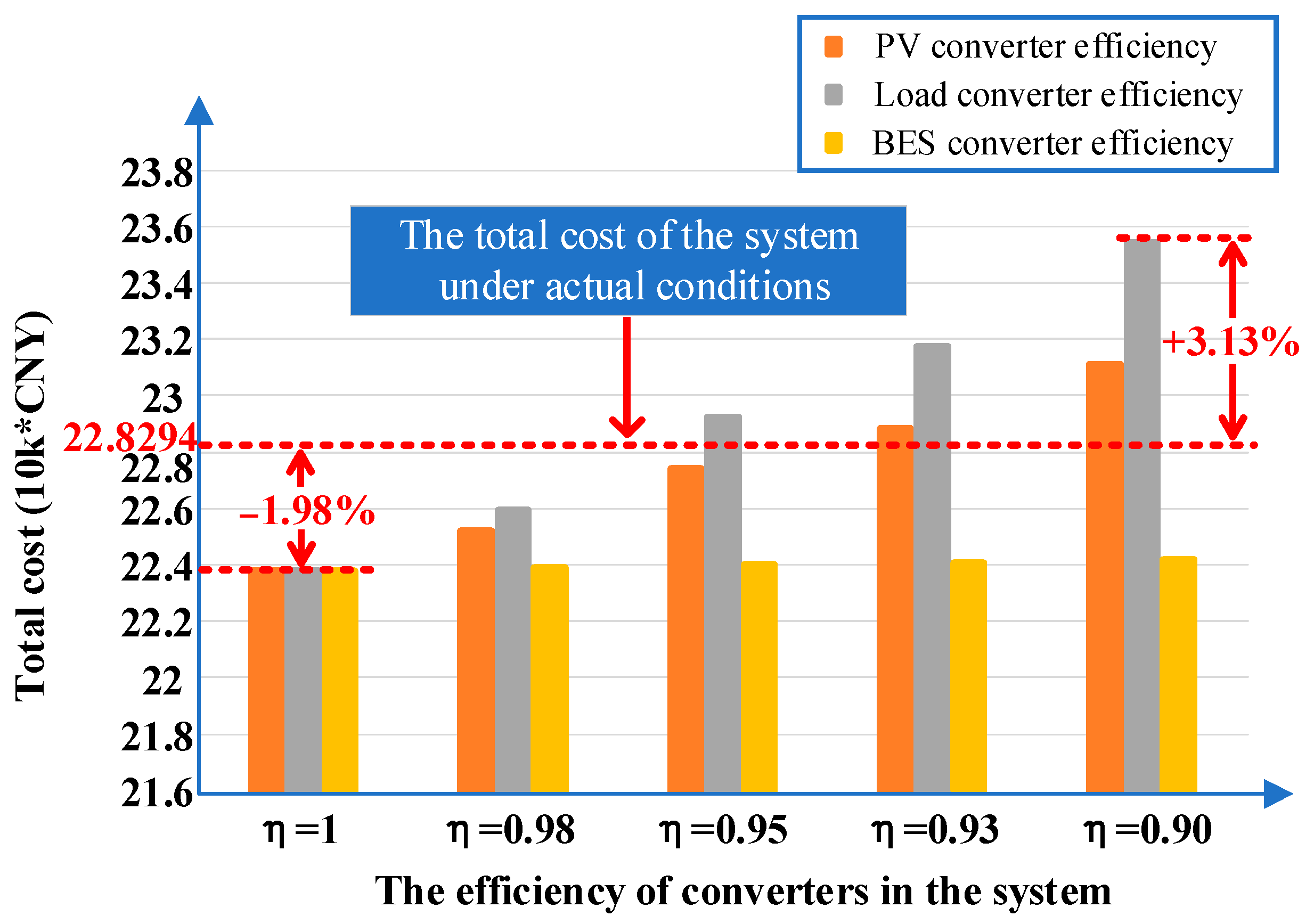
| 1 | 22 | 96 | 6 | 13.8863 | 0.6776 | 4.9229 | 0.2957 | 2.5949 | 22.3774 |
| 0.98 | 23 | 95 | 6 | 14.1241 | 0.6858 | 4.9211 | 0.3221 | 2.6930 | 22.7461 |
| 0.95 | 23 | 103 | 6 | 14.6473 | 0.7149 | 4.9237 | 0.3273 | 2.7171 | 23.3303 |
| 0.93 | 24 | 101 | 7 | 14.9503 | 0.7245 | 4.9218 | 0.3486 | 2.8153 | 23.7605 |
| 0.90 | 24 | 112 | 6 | 15.5391 | 0.7594 | 4.9244 | 0.3606 | 2.8454 | 24.4289 |
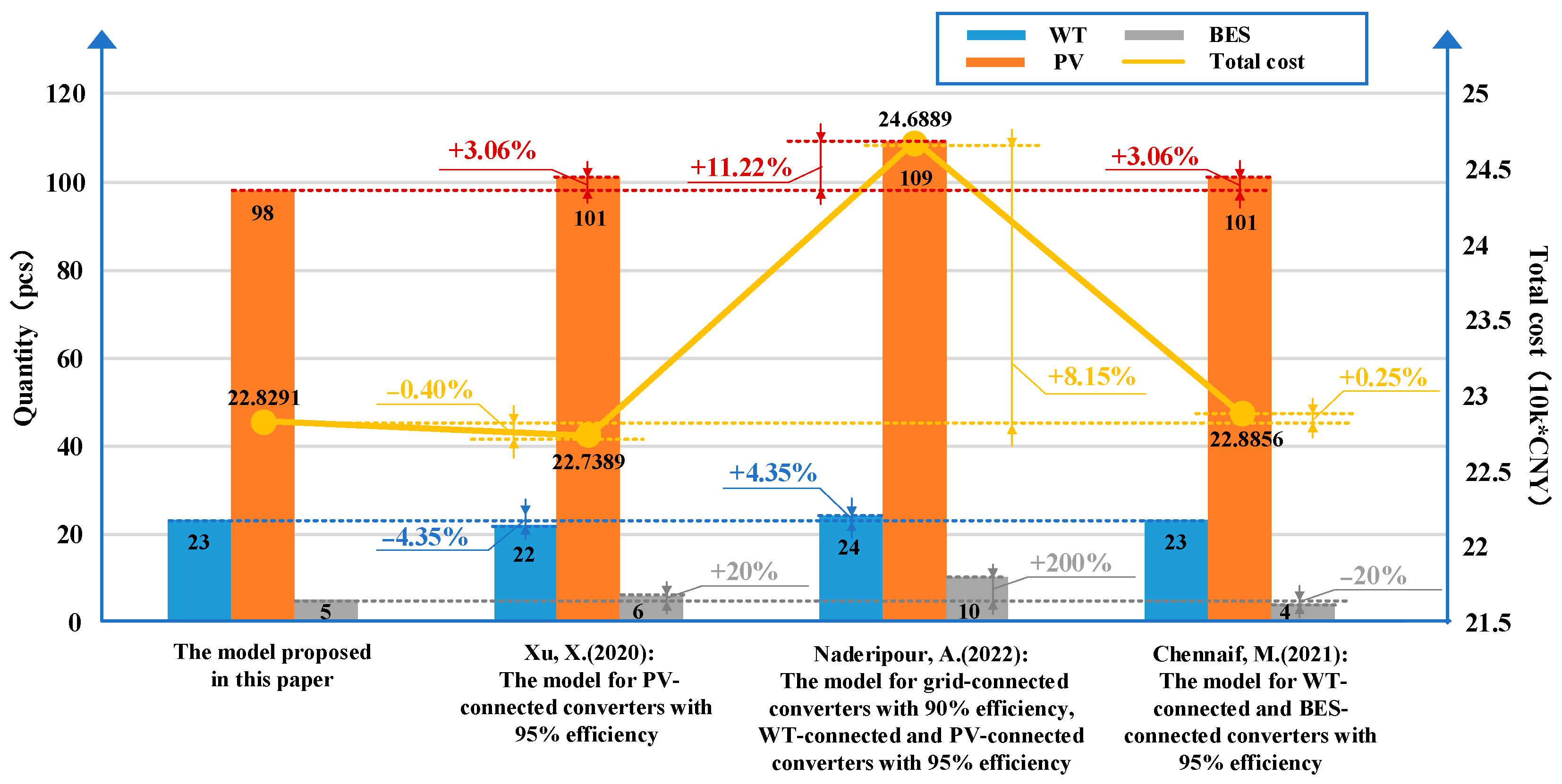
| Precise efficiency model proposed in this paper | 23 | 98 | 5 | 14.1896 | 0.6915 | 4.9215 | 0.3275 | 2.6990 | 22.8291 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, B.; Liu, J.; Wang, S.; Li, Z. Enhanced Models for Wind, Solar Power Generation, and Battery Energy Storage Systems Considering Power Electronic Converter Precise Efficiency Behavior. Energies 2025, 18, 1320. https://doi.org/10.3390/en18061320
Zhu B, Liu J, Wang S, Li Z. Enhanced Models for Wind, Solar Power Generation, and Battery Energy Storage Systems Considering Power Electronic Converter Precise Efficiency Behavior. Energies. 2025; 18(6):1320. https://doi.org/10.3390/en18061320
Chicago/Turabian StyleZhu, Binxin, Junliang Liu, Shusheng Wang, and Zhe Li. 2025. "Enhanced Models for Wind, Solar Power Generation, and Battery Energy Storage Systems Considering Power Electronic Converter Precise Efficiency Behavior" Energies 18, no. 6: 1320. https://doi.org/10.3390/en18061320
APA StyleZhu, B., Liu, J., Wang, S., & Li, Z. (2025). Enhanced Models for Wind, Solar Power Generation, and Battery Energy Storage Systems Considering Power Electronic Converter Precise Efficiency Behavior. Energies, 18(6), 1320. https://doi.org/10.3390/en18061320





