Analysis and Control Parameters Optimization of Wind Turbines Participating in Power System Primary Frequency Regulation with the Consideration of Secondary Frequency Drop
Abstract
1. Introduction
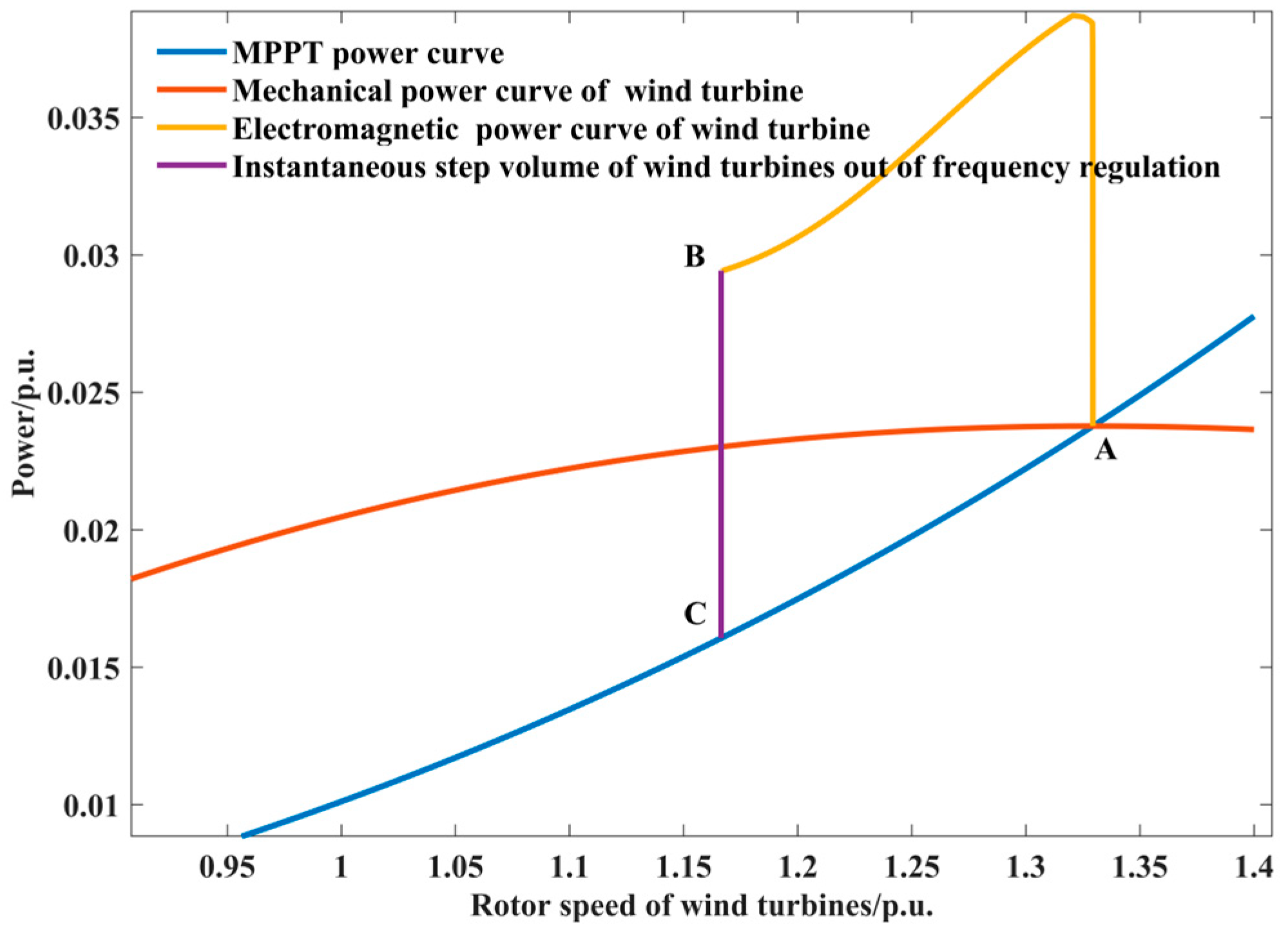
2. Analysis of the Influence of the Wind Turbine Rotor Speed on Mechanical Power
3. Analysis of Wind Turbine Rotor Motion Status When Participating in Frequency Regulation
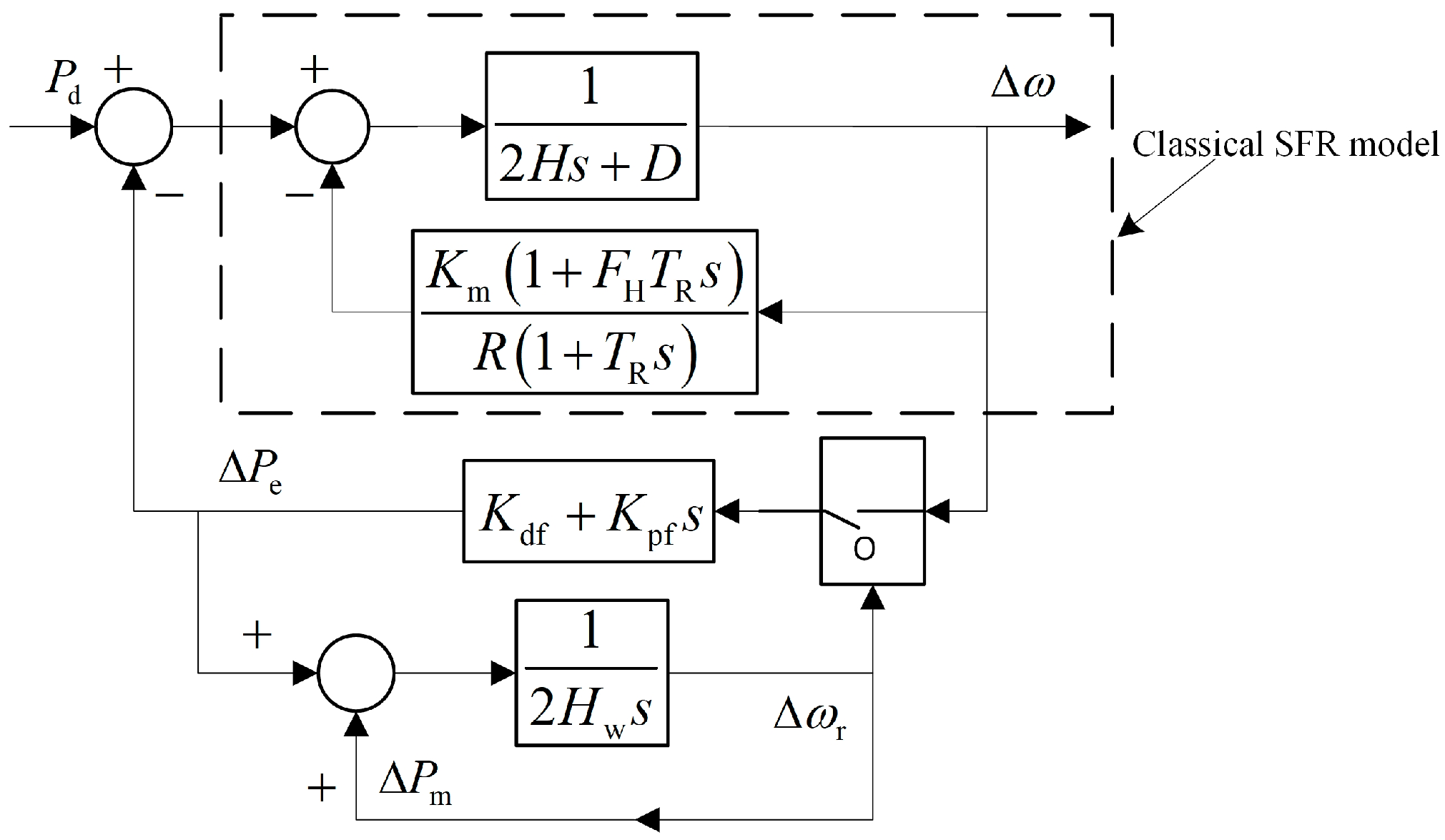
4. Dynamic Frequency Calculation Considering Wind Turbines Participating in Primary Frequency Regulation
4.1. Calculation of the Primary Frequency Drop and Its Minimum Value
4.2. Calculation of the Secondary Frequency Drop and Its Minimum Value
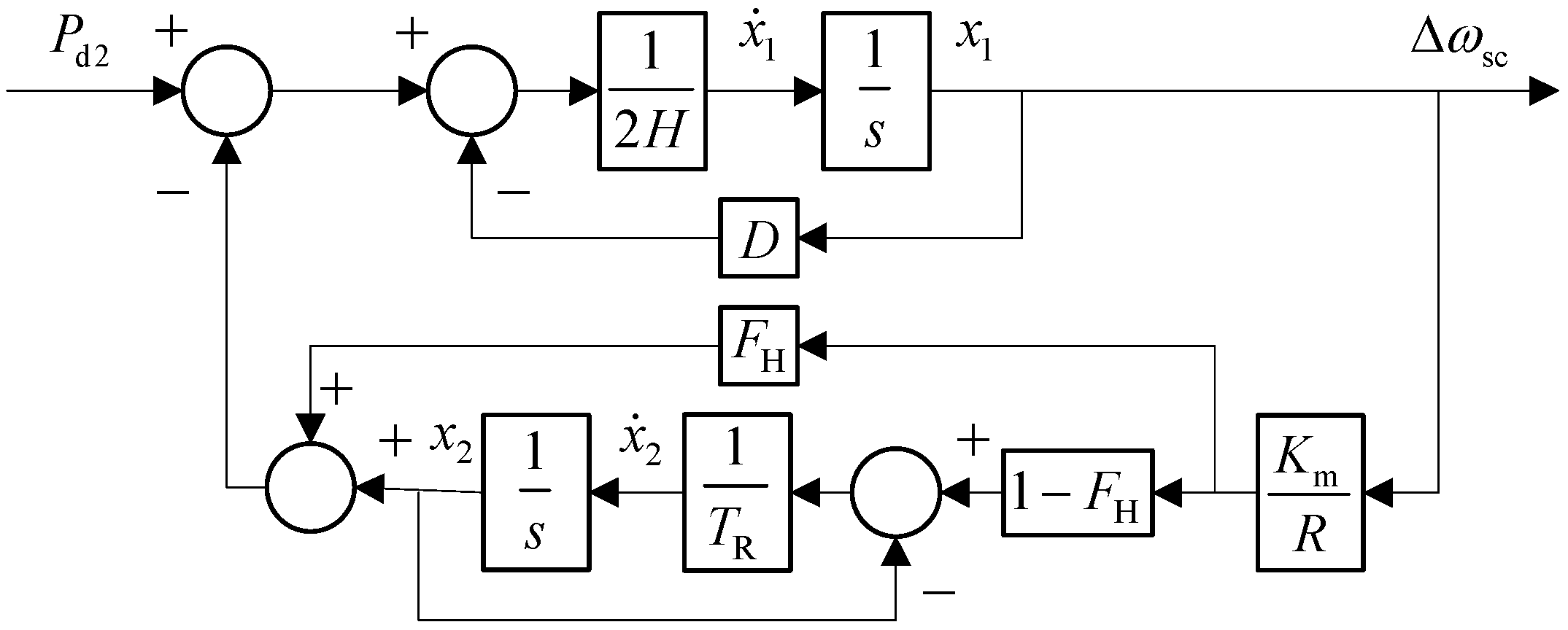
4.3. State Variable Initial Values Calculation
5. Parameters Optimization of the Wind Turbine Participating in Primary Frequency Regulation
5.1. Optimization Objective and Solution Vector
5.2. Constraint Conditions
6. Case Study
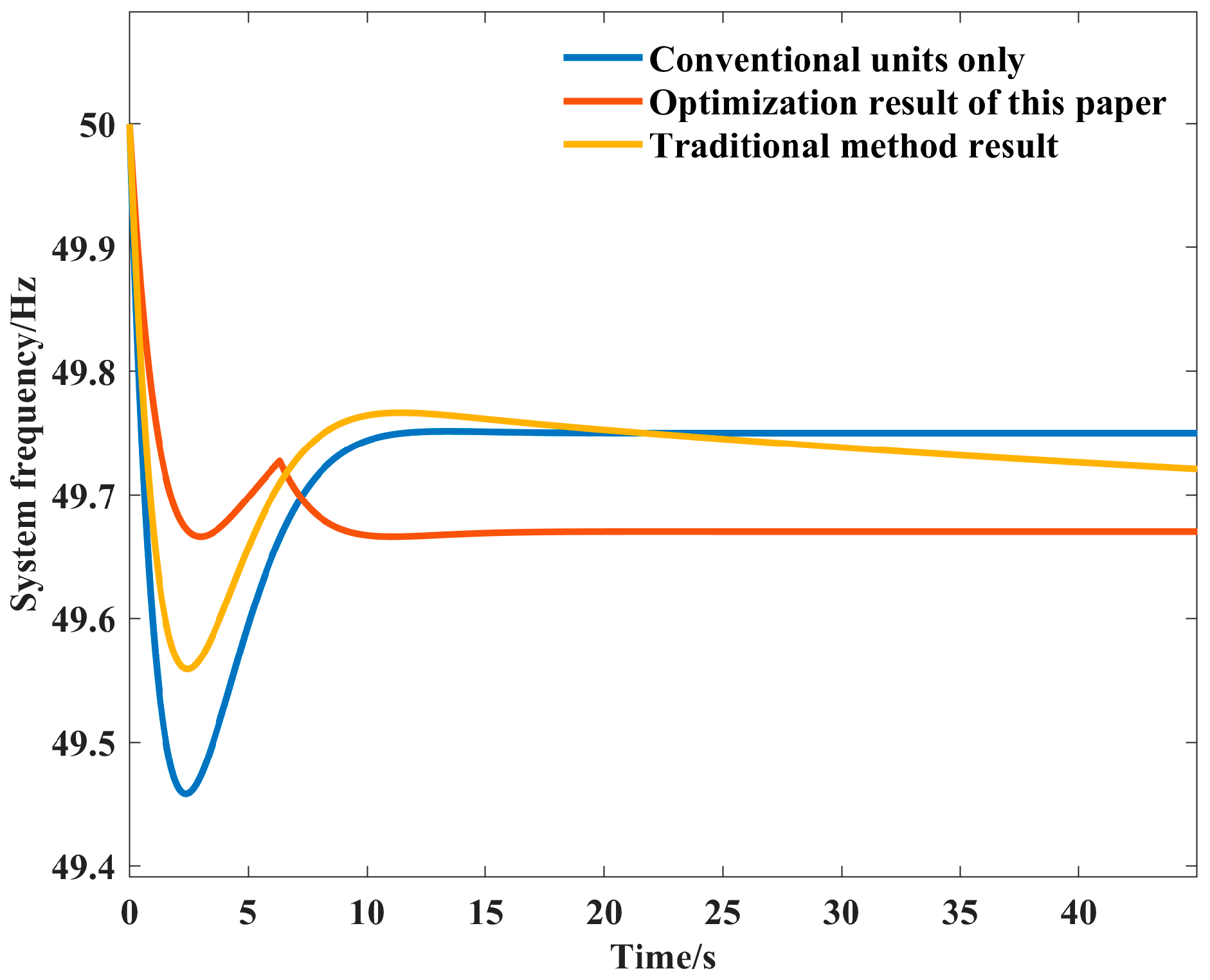
6.1. The Primary Frequency Regulation Effects of the Method Proposed in This Paper
6.2. Comparison of Frequency Regulation Effects with Different Control Parameters and Strategies
7. Conclusions
- (1)
- The optimization of wind turbine primary frequency regulation control parameters necessitates a precise understanding of the correlation between these parameters and the power system dynamic frequency characteristics. Furthermore, it is essential to consider the interdependent relationship between primary and secondary frequency drops within the power system. Case study analysis demonstrates that the implementation of control parameters which holistically address both primary and secondary frequency drops can substantially enhance the power system dynamic frequency performance.
- (2)
- The optimization results demonstrate that the power system frequency exhibits optimal dynamic characteristics when the minimum values of primary and secondary frequency drops are equivalent. This finding reveals the existence of a game-theoretic relationship between primary and secondary frequency drops.
- (3)
- The optimal configuration of wind turbine primary frequency regulation control parameters is inherently dynamic rather than static. These parameters require coordinated tuning and real-time adjustment in response to both the magnitude of power system disturbances and the operational status of wind turbines.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Wang, R.; Qin, S.; Bao, W.; Hou, A.; Ying, Y.; Ding, L. Configuration and control strategy for an integrated system of wind turbine generator and supercapacitor to provide frequency support. Int. J. Electr. Power Energy Syst. 2023, 154, 109456. [Google Scholar] [CrossRef]
- Messasma, C.; Barakat, A.; Chouaba, S.E.; Sari, B. PV system frequency regulation employing a new power reserve control approach and a hybrid inertial response. Electr. Power Syst. Res. 2023, 223, 109556. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability—Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar]
- Morren, J.; Haan, S.W.H.D.; Kling, W.L.; Ferreira, J.A. Wind turbines emulating inertia and supporting primary frequency control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Chen, C.; Su, Y.; Yang, T.; Huang, Z. Virtual inertia coordination control strategy of DFIG-based wind turbine for improved grid frequency response ability. Electr. Power Syst. Res. 2023, 216, 109076. [Google Scholar] [CrossRef]
- Boyle, J.; Littler, T.; Muyeen, S.M.; Foley, A.M. An alternative frequency-droop scheme for wind turbines that provide primary frequency regulation via rotor speed control. Int. J. Electr. Power Energy Syst. 2021, 133, 107219. [Google Scholar] [CrossRef]
- Wang, S.; Tomsovic, K. A Novel Active Power Control Framework for Wind Turbine Generators to Improve Frequency Response. IEEE Trans. Power Syst. 2018, 33, 6579–6589. [Google Scholar] [CrossRef]
- Morren, J.; Pierik, J.; de Haan, S.W.H. Inertial response of variable speed wind turbines. Electr. Power Syst. Res. 2006, 76, 980–987. [Google Scholar] [CrossRef]
- Bao, W.; Ding, L.; Liu, Z.; Zhu, G.; Kheshti, M.; Wu, Q.; Terzija, V. Analytically derived fixed termination time for stepwise inertial control of wind turbines—Part I: Analytical derivation. Int. J. Electr. Power Energy Syst. 2020, 121, 106120. [Google Scholar] [CrossRef]
- Kang, M.; Muljadi, E.; Hur, K.; Kang, Y.C. Stable Adaptive Inertial Control of a Doubly-Fed Induction Generator. IEEE Trans. Smart Grid 2016, 7, 2971–2979. [Google Scholar] [CrossRef]
- Kang, M.; Kim, K.; Muljadi, E.; Park, J.W.; Kang, Y.C. Frequency Control Support of a Doubly-Fed Induction Generator Based on the Torque Limit. IEEE Trans. Power Syst. 2016, 31, 4575–4583. [Google Scholar] [CrossRef]
- Sun, M.; Min, Y.; Xiong, X.; Chen, L.; Zhao, L.; Feng, Y.; Wang, B. Practical Realization of Optimal Auxiliary Frequency Control Strategy of Wind Turbine Generator. J. Mod. Power Syst. Clean Energy 2022, 10, 617–626. [Google Scholar] [CrossRef]
- Meng, L.; Qin, C.; Zeng, Y.; Sun, B.; Chen, Q.; Chen, W. A two-stage frequency response method for DFIGs under variable wind speeds. Electr. Power Syst. Res. 2023, 225, 109813. [Google Scholar] [CrossRef]
- Wu, Y.K.; Yang, W.H.; Hu, Y.L.; Dzung, P.Q. Frequency Regulation at a Wind Farm Using Time-Varying Inertia and Droop Controls. IEEE Trans. Ind. Appl. 2019, 55, 213–224. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, F.; Ding, L.; Cornélusse, B.; Zhang, G.; Salimu, A. Multi-segment droop control and optimal parameter setting strategy of wind turbine for frequency regulation. Int. J. Electr. Power Energy Syst. 2024, 158, 109968. [Google Scholar] [CrossRef]
- Nie, Y.; Liu, J.; Gao, L.; Wu, Y.; Li, Z. Nonlinear rotor kinetic energy control strategy of DFIG-based wind turbine participating in grid frequency regulation. Electr. Power Syst. Res. 2023, 223, 109678. [Google Scholar] [CrossRef]
- Sun, M.; Min, Y.; Chen, L.; Hou, K.; Xia, D.; Mao, H. Optimal auxiliary frequency control of wind turbine generators and coordination with synchronous generators. CSEE J. Power Energy Syst. 2021, 7, 78–85. [Google Scholar]
- Lin, C.H.; Wu, Y.K. Coordinated Frequency Control Strategy for VSC-HVDC-Connected Wind Farm and Battery Energy Storage System. IEEE Trans. Ind. Appl. 2023, 59, 5314–5328. [Google Scholar] [CrossRef]
- Xiong, L.; Yang, S.; Huang, S.; He, D.; Li, P.; Khan, M.W.; Wang, J. Optimal Allocation of Energy Storage System in DFIG Wind Farms for Frequency Support Considering Wake Effect. IEEE Trans. Power Syst. 2022, 37, 2097–2112. [Google Scholar] [CrossRef]
- Rahimi, T.; Ding, L.; Kheshti, M.; Faraji, R.; Guerrero, J.M.; Tinajero, G.D.A. Inertia Response Coordination Strategy of Wind Generators and Hybrid Energy Storage and Operation Cost-Based Multi-Objective Optimizing of Frequency Control Parameters. IEEE Access 2021, 9, 74684–74702. [Google Scholar] [CrossRef]
- Xia, Y.; Ahmed, K.H.; Williams, B.W. Wind Turbine Power Coefficient Analysis of a New Maximum Power Point Tracking Technique. IEEE Trans. Ind. Electron. 2013, 60, 1122–1132. [Google Scholar] [CrossRef]
- Anderson, P.M.; Mirheydar, M. A low-order system frequency response model. IEEE Trans. Power Syst. 1990, 5, 720–729. [Google Scholar] [CrossRef]
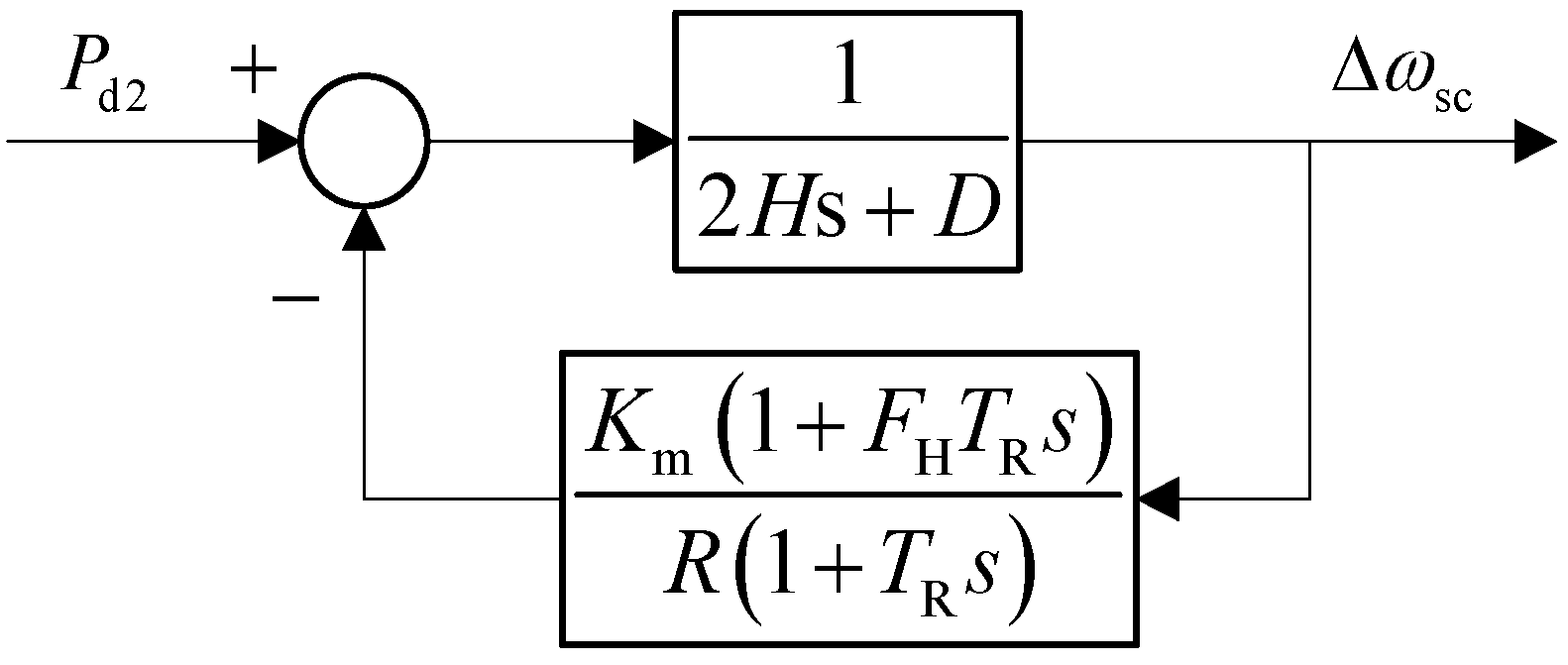
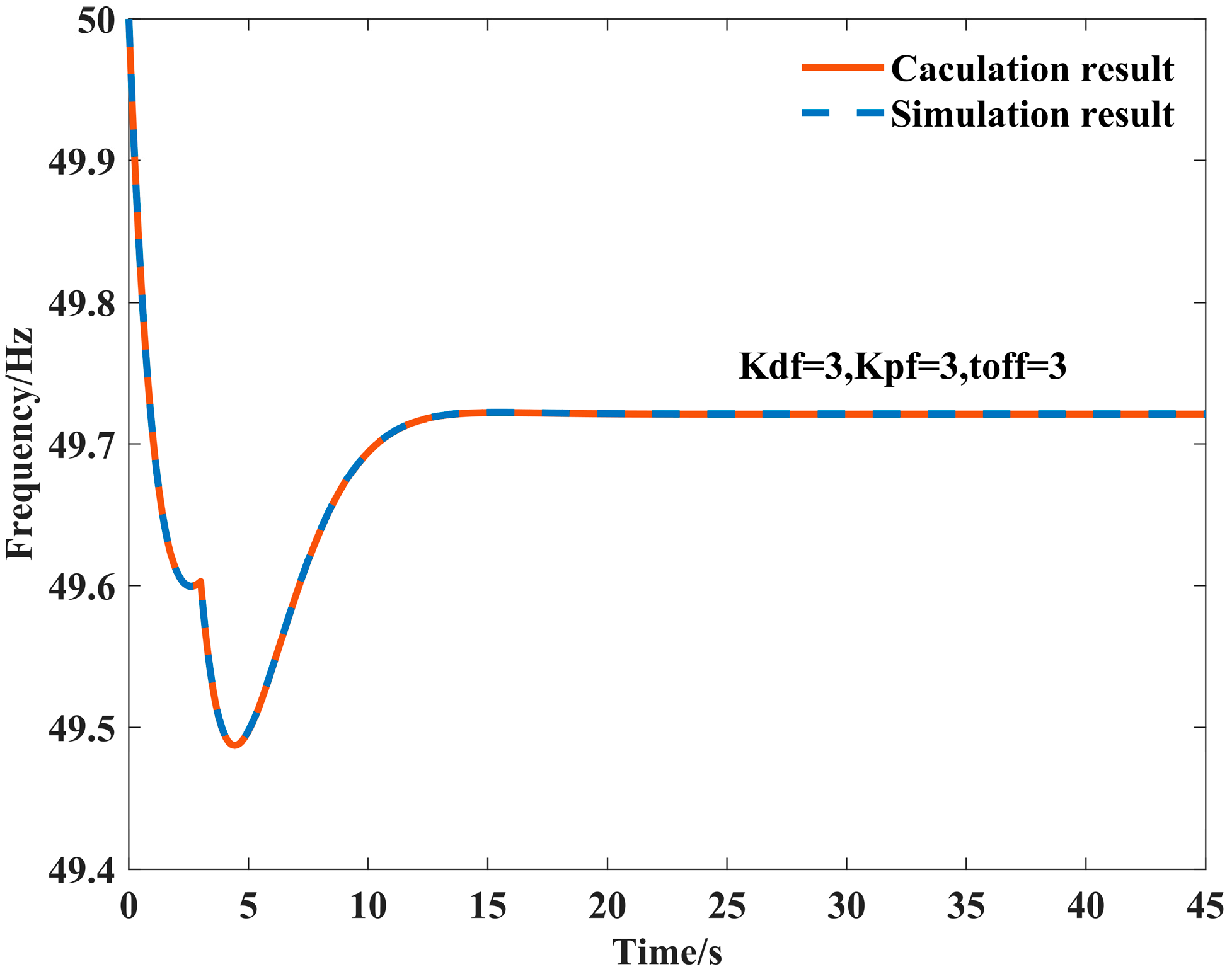

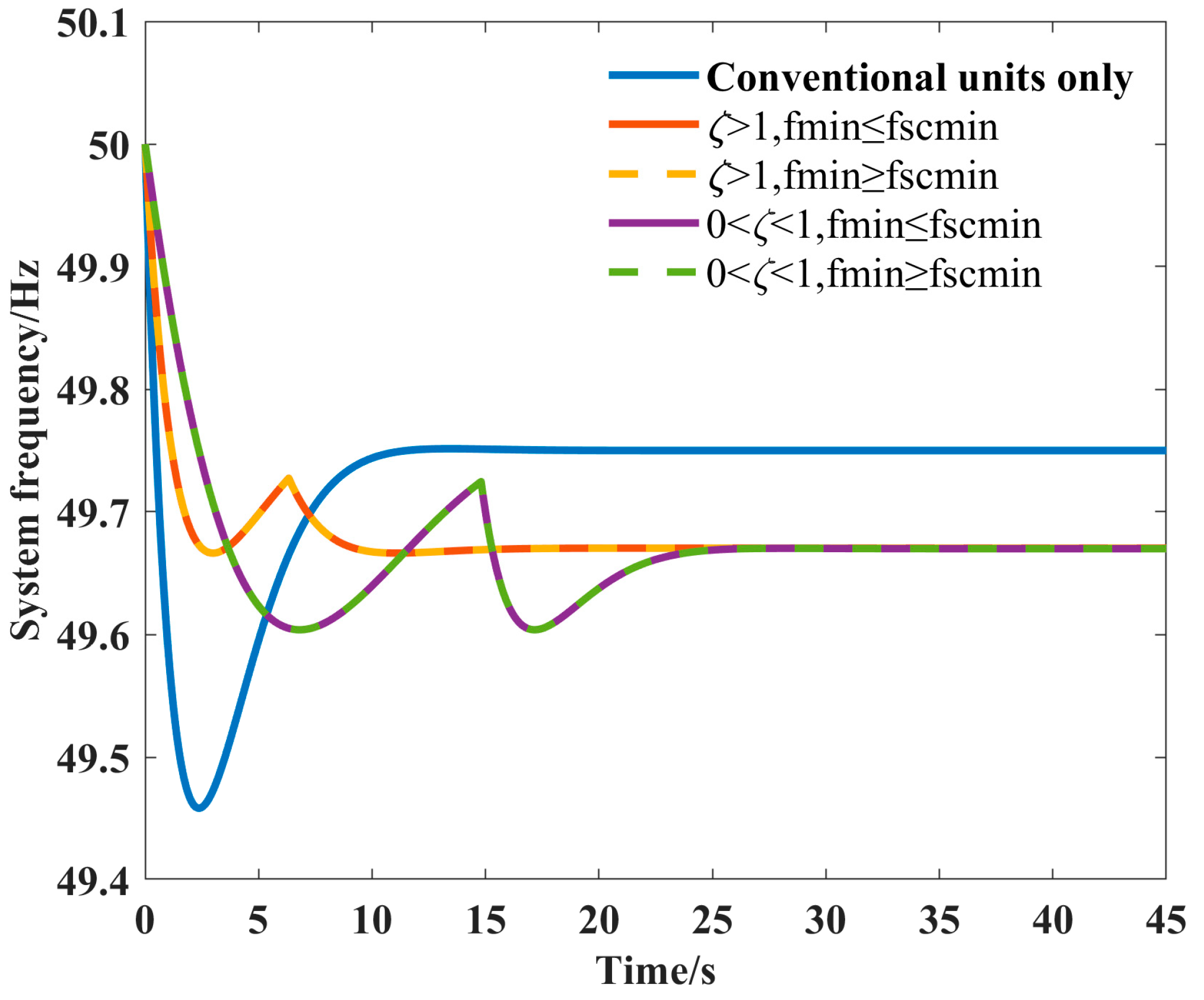
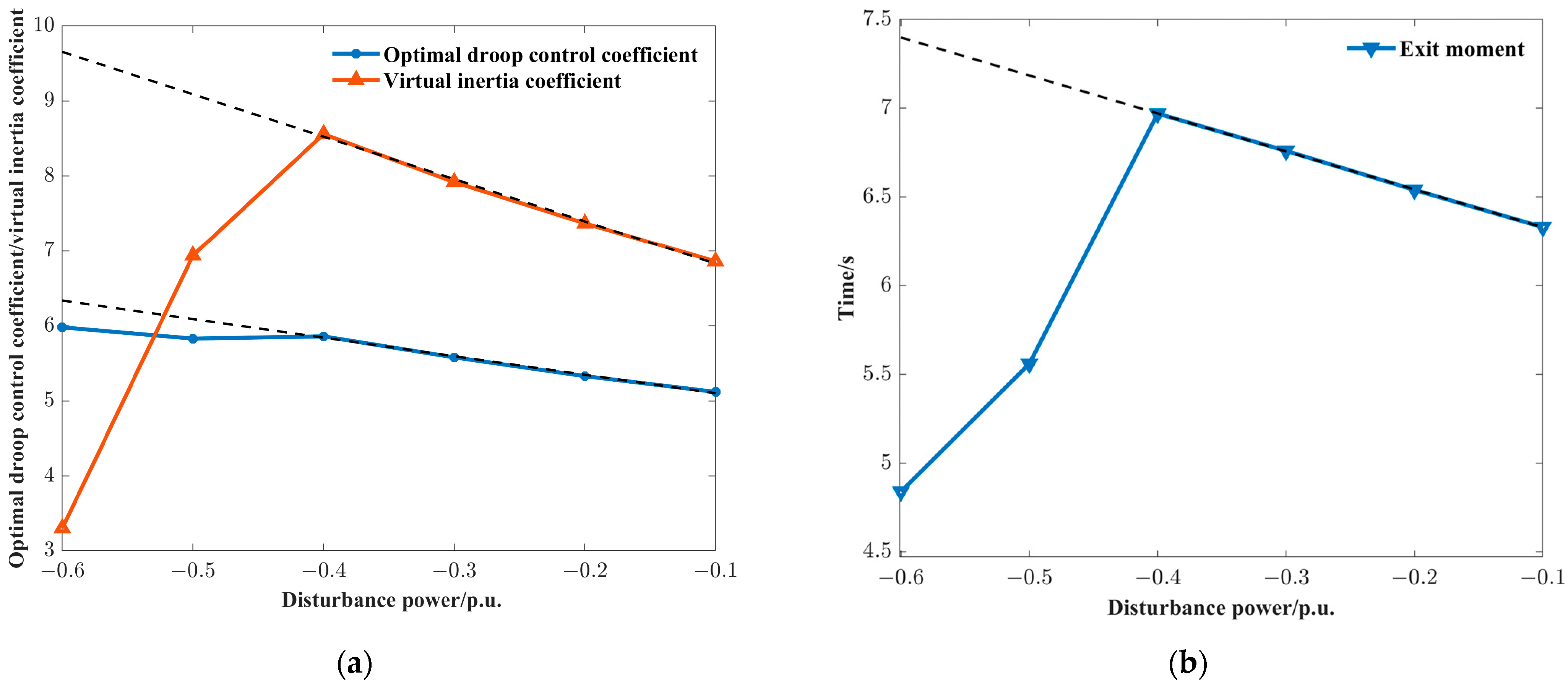
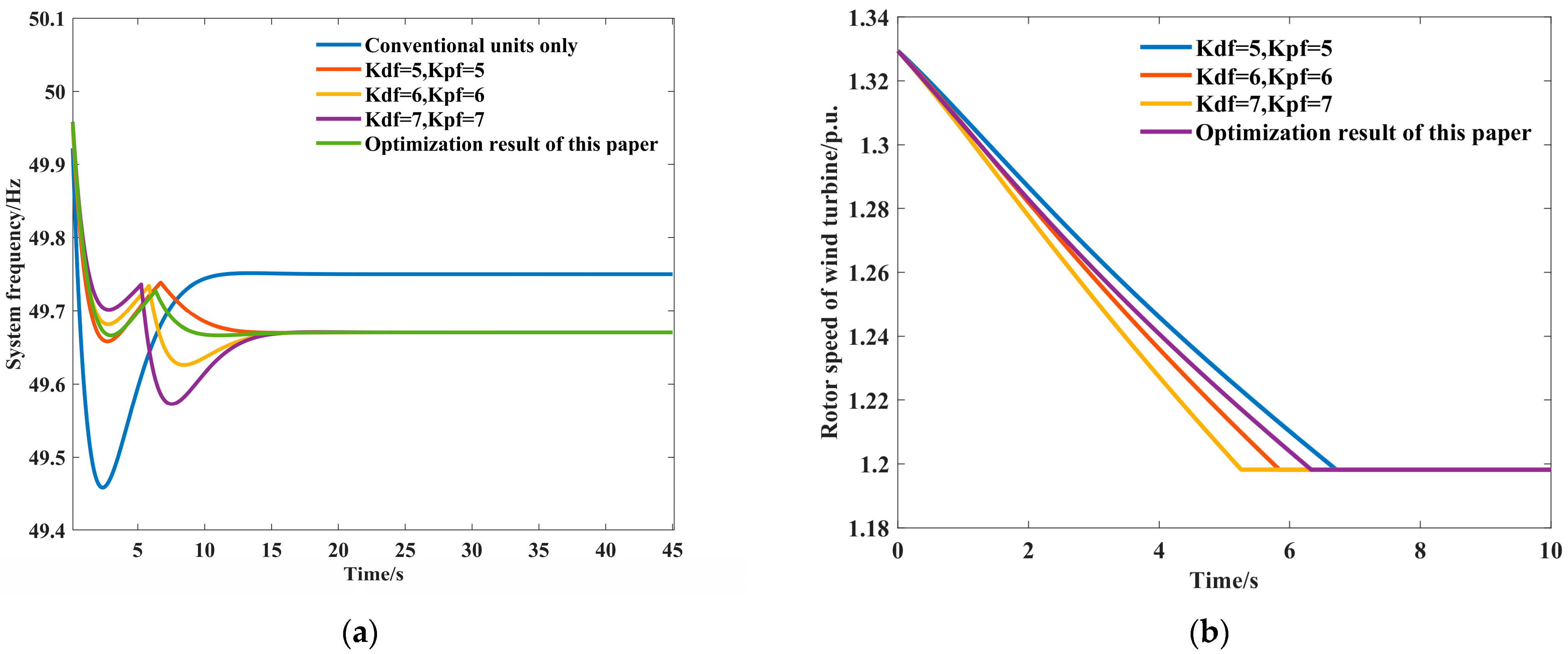

| Minimum Frequency/Hz | Droop Control Coefficient | Virtual Inertia Coefficient | Exit Time/s | |
|---|---|---|---|---|
| When 0 < ζ < 1 | 49.61 | 0.10 | 28.89 | 14.80 |
| When ζ > 1 | 49.67 | 5.12 | 6.86 | 6.33 |
| Only conventional units involved | 49.46 | / | / | / |
| Value of Primary Frequency Drop/Hz | Value of Secondary Frequency Drop/Hz | Exiting Time/s | Percentage of Maximum Frequency Drop | |
|---|---|---|---|---|
| Kdf = 5, Kpf = 5 | 49.66 | 49.67 | 6.71 | 0.68% |
| Kdf = 6, Kpf = 6 | 49.68 | 47.63 | 5.84 | 0.74% |
| Kdf = 7, Kpf = 7 | 49.70 | 49.57 | 5.26 | 0.86% |
| Conventional units only | 49.46 | / | / | 1.08% |
| The method in this paper | 49.67 | 49.67 | 6.33 | 0.66% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Chen, Z.; Li, X.; Gao, Y. Analysis and Control Parameters Optimization of Wind Turbines Participating in Power System Primary Frequency Regulation with the Consideration of Secondary Frequency Drop. Energies 2025, 18, 1317. https://doi.org/10.3390/en18061317
Liu K, Chen Z, Li X, Gao Y. Analysis and Control Parameters Optimization of Wind Turbines Participating in Power System Primary Frequency Regulation with the Consideration of Secondary Frequency Drop. Energies. 2025; 18(6):1317. https://doi.org/10.3390/en18061317
Chicago/Turabian StyleLiu, Ketian, Zhengxi Chen, Xiang Li, and Yi Gao. 2025. "Analysis and Control Parameters Optimization of Wind Turbines Participating in Power System Primary Frequency Regulation with the Consideration of Secondary Frequency Drop" Energies 18, no. 6: 1317. https://doi.org/10.3390/en18061317
APA StyleLiu, K., Chen, Z., Li, X., & Gao, Y. (2025). Analysis and Control Parameters Optimization of Wind Turbines Participating in Power System Primary Frequency Regulation with the Consideration of Secondary Frequency Drop. Energies, 18(6), 1317. https://doi.org/10.3390/en18061317





