An Innovative Cryogenic Heat Exchanger Design for Sustainable Aviation

Abstract

Aviation is one of the most important industries in the current global scenario, but it has a significant impact on climate change due to the large quantities of carbon dioxide emitted daily from the use of fossil kerosene-based fuels (jet fuels). Although technological advancements in aircraft design have enhanced efficiency and reduced emissions over the years, the rapid growth of the aviation industry presents challenges in meeting the environmental targets outlined in the “Flightpath 2050” report. This highlights the urgent need for effective decarbonisation strategies. Hydrogen propulsion, via fuel cells or combustion, offers a promising solution, with the combustion route currently being more practical for a wider range of aircraft due to the limited power density of fuel cells. In this context, this paper designs and models a nitrogen–hydrogen heat exchanger architecture for use in an innovative hydrogen-propelled aircraft fuel system, where the layout was recently proposed by the same authors to advance sustainable aviation. This system stores hydrogen in liquid form and injects it into the combustion chamber as a gas, making the cryogenic heat exchanger essential for its operation. In particular, the heat exchanger enables the vaporisation and superheating of liquid hydrogen by recovering heat from turbine exhaust gases and utilising nitrogen as a carrier fluid. A pipe-in-pipe design is employed for this purpose, which, to the authors’ knowledge, is not yet available on the market. Specifically, the paper first introduces the proposed heat exchanger architecture, then evaluates its feasibility with a detailed thermodynamic model, and finally presents the calculation results. By addressing challenges in hydrogen storage and usage, this work contributes to advancing sustainable aviation technologies and reducing the environmental footprint of air travel.

1. Introduction

Aviation plays a crucial role in modern life, connecting people, businesses, and families worldwide while boosting economic growth. In 2016 alone, the aviation sector generated USD 2.7 trillion in economic activity and supported 65.5 million jobs, representing 3.6% of global gross domestic product [1]. Despite these benefits, conventional aircraft propulsion systems, which depend on fossil kerosene-based fuels (jet fuels), significantly contribute to global warming [2]. The combustion of these fuels releases large amounts of carbon emissions into the atmosphere daily. This problem has been exacerbated by the rapid growth of air travel in recent years, leading to annual carbon dioxide (CO₂) emissions exceeding 900 million tons [3]. In addition to CO₂, the aviation industry is also responsible for non-CO₂ emissions, including nitrogen oxides (NO_x), sulphur oxides (SO_x), hydrocarbons (HC), black carbon (soot), and water vapour [4]. These pollutants have severe consequences for the environment, contributing to the formation of contrails and cirrus clouds [5,6].

To maintain the benefits aviation provides while addressing environmental challenges, the Advisory Council for Aeronautics Research in Europe (ACARE) introduced the “Flight Path 2050” report [7,8]. This report sets ambitious environmental goals for the aviation industry by 2050, aiming to reduce CO₂ emissions, NO_x, and noise per passenger kilometre by 75%, 90%, and 60%, respectively, compared to the levels from the year 2000. However, with air travel projected to triple by 2050, meeting these targets through incremental technological improvements alone, such as new composite materials, aerodynamic refinements, and improved aircraft designs, seems unlikely [9]. Despite modern aircraft being up to 80% more fuel-efficient than those from 60 years ago [10], further substantial reductions in emissions are becoming increasingly difficult to achieve.

As a result, finding effective solutions to decarbonize the aviation sector and address its energy needs is crucial. Fully electric aircraft have been proposed as one potential solution to reduce aviation’s environmental impact. However, this approach faces limitations for general aviation due to the current constraints of battery technology, which restricts flying time due to the limited specific energy of today’s batteries [11].

Sustainable aviation fuels (SAFs), which include biofuels, used cooking oil, and other waste materials, i.e., fuels that are made from sustainable sources, offer a viable alternative to conventional jet fuels. These hydrocarbon fuels have reduced lifecycle emissions compared to fossil fuels, releasing only as much CO₂ as was absorbed during their production [12]. SAFs can directly replace kerosene, allowing existing aircraft to operate with minimal or no modifications. However, SAFs are more expensive than conventional jet fuels, which increases airline operating costs [13]. While they can potentially reduce the climate impact of flying by up to 60% [14], they are unlikely to achieve net-zero lifecycle emissions, as they emit NO_x emissions comparable to conventional jet fuels [15].

To meet the previous mentioned ambitious targets of the “Flight Path 2050” report, the most promising and cost-effective solution for sustainable aviation may be using fuels that do not emit carbon emissions during use [16]. Hydrogen (H₂), which does not contain carbon and thus does not produce CO₂ when used, is one such option. Being the most abundant element in the universe, H₂ can be produced using renewable electricity through electrolysis, creating green H₂, which serves as a clean, zero-emission fuel [17].

Hydrogen propulsion systems can be implemented in two ways, either by using H₂ in fuel cells to generate electrical power or burning it directly in aircraft engines [18]. Currently, the combustion route is considered more practical for a broader range of aircraft, as hydrogen fuel cells do not yet offer sufficient power density [3,19].

Hydrogen combustion aircraft eliminate CO₂ emissions and significantly reduce other pollutants. However, burning H₂ in aircraft engines produces large quantities of water vapour—about three times more than with conventional jet fuels [20]. Although water vapour is a greenhouse gas like CO₂ and contributes to contrail formation, its impact on climate is still under investigation [20,21]. Additionally, it is known that water vapour remains in the upper atmosphere for a much shorter period than CO₂ [22,23].

Using H₂ as a fuel poses design challenges and constraints compared to conventional kerosene-powered aircraft. These challenges arise from hydrogen’s higher specific energy (energy per mass unit) and lower energy density (energy per unit volume), requiring it to be stored as either a compressed gas or cryogenic liquid to obtain practical energy densities [24].

Table 1. Properties of Jet A-1, LH₂ and GH₂ [14,25].

Property [Unit]	Jet A-1	LH2	GH2 (350 [bar])	GH2 (700 [bar])
Specific energy [MJ/kg]	43.2	120	120	120
Energy density [MJ/L]	34.9	8.5	2.9	4.8
Storage temperature [K]	Ambient	20	Ambient	Ambient
Storage pressure [bar]	Ambient	~2	350	700
Storage density [kg/m3]	804	71.4	23.3	39.2

compares the specific energy and energy densities of kerosene (Jet A-1), cryogenic liquid hydrogen (LH₂), and gaseous hydrogen (GH₂) at two different pressures, along with the corresponding storage thermodynamic properties required for each fuel type [14,25].

Cryogenic LH₂ storage is the most viable solution for aviation, offering significant advantages over compressed GH₂ storage. Firstly, LH₂ can be stored at pressures close to atmospheric levels, eliminating the need for high-pressure tanks. Additionally, LH₂ enhances hydrogen’s density by two to three times over GH₂. Despite this increase, LH₂ remains approximately 11 times less dense than kerosene. Consequently, although LH₂ has a specific energy nearly three times greater than kerosene, LH₂ tanks need about four times the volumetric capacity to store the same amount of energy. The main challenge with LH₂ is maintaining its cryogenic temperature, as it boils at 20 K under atmospheric pressure. This necessitates boil-off management, tank venting, and extensive insulation [26,27]. However, the cryogenic temperature and high specific heat capacity of LH₂ also make it an excellent coolant, offering potential use as a heat sink for components close to the engine [28,29,30].

According to the ZEROe project of Airbus, using LH₂ as fuel for modified gas turbine engines, along with hydrogen fuel cells for generating electrical power, is considered the right green solution for next-generation aircraft [31].

In a recent research study, a potential architecture for an innovative aircraft fuel system using H₂ as fuel was proposed [32,33]. This system, which was developed based on conventional layouts [34], is illustrated in Figure 1.

A significant modification involves adapting the system to handle LH₂ instead of kerosene. In conventional aircraft fuel systems, tank-mounted boost pumps are used to transfer fuel to the engines and slightly increase its pressure. For hydrogen aircraft fuel system, a similar setup can be employed, potentially using slightly pressurized tanks with inert gases (0). Shut-off valves (1), as in conventional aircraft fuel systems, can be used to stop LH₂ flow for safety. While positive displacement pumps are suitable for kerosene handling, they are not appropriate for LH₂. The literature suggests that centrifugal pumps are better suited for handling LH₂, which is why the main fuel pump in this innovative system is an electrically driven (2) two-stage centrifugal pump (3). This design allows for greater control flexibility, as the pump’s speed can be independently regulated, unlike conventional systems where the main fuel pump is driven through the engine’s accessory gearbox [34].

Maintaining cryogenic conditions along the supply line poses a challenge in controlling the flow of LH₂. This challenge is addressed by vaporising the LH₂ upstream of the metering system using a heat exchanger (4) that recovers heat from exhaust gases exiting the turbine. Thus, after the main fuel pump, H₂ is vaporised and heated to an optimal temperature for combustion in the engine. The downstream components involved in fuel metering are then adapted to handle GH₂. Specifically, while a conventional engine’s fuel metering unit (FMU) includes components such as a fuel metering servovalve, bypass valve, actuator valve, pressurising valve, and shut-off valve to control the flow of liquid kerosene delivered for combustion and for adjusting the position of compressor inlet guide vanes [34], this innovative system uses a cutting-edge metering valve (5) for handling GH₂. The novel metering valve is a convergent–divergent nozzle that precisely controls the flow of GH₂ into the combustion chamber by adjusting the throat area. Additionally, an external hydraulic unit with conventional two-stage servovalves is used for primary and secondary flight controls. It is important to note that, despite their high complexity and high internal leakage issues, which can be addressed with piezoelectric actuators [35,36], two-stage servovalves are preferred over single-stage proportional solenoid valves in aeronautical applications due to their better response time and advantages in compactness and lightweight [37].

One of the key components of this innovative aircraft fuel system, which operates initially with LH₂ and then with GH₂, is the heat exchanger. This component marks a significant difference between kerosene and hydrogen fuel systems. Although conventional aircraft fuel systems also use heat exchangers to raise the fuel temperature to the ideal range for combustion before it reaches the FMU, the heat exchanger plays a more crucial role in hydrogen-powered aircraft fuel systems because H₂ requires a phase change from cryogenic liquid to gas for the metering process.

To the authors’ knowledge, there are only a few studies in the literature focusing on the design of cryogenic heat exchangers for hydrogen-powered aircraft engines [38,39,40]. In particular, one such study [40], examined the use of compact, engine-integrated heat exchangers for intercooling and recuperation systems in hydrogen-fuelled turbofan engines for short-to-medium range aircraft. The authors specifically evaluated the impact of these heat exchangers on fuel consumption and emissions, discovering that an intercooled-recuperated engine could reduce specific fuel consumption at take-off by up to 7.7%, while an intercooled engine achieved a 4% improvement compared to a baseline uncooled engine.

In this context, this paper extends the work presented in [41] by designing and modelling a novel cryogenic heat exchanger for the innovative fuel system illustrated in Figure 1, with the goal of advancing sustainable aviation. Indeed, in previous studies [32,33] the heat exchanger (4) was modelled by means of Matlab/Simulink 2023b as a “black box” to facilitate the phase change from LH₂ to GH₂ using exhaust gas thermal energy. This paper expands on that work by proposing and modelling a feasible heat exchanger architecture based on the take-off phase. Specifically, the pipe-in-pipe technology is used, which, to the authors’ knowledge, is not yet available on the market. The paper starts by presenting the proposed heat exchanger architecture in Section 2. Section 3 then investigates the feasibility of the proposed configuration using a detailed thermodynamic model based on well-established equations. Finally, Section 4 provides the results of the calculations, focusing on minimising the key performance parameters of the heat exchanger architecture, including mass, length, and volume.

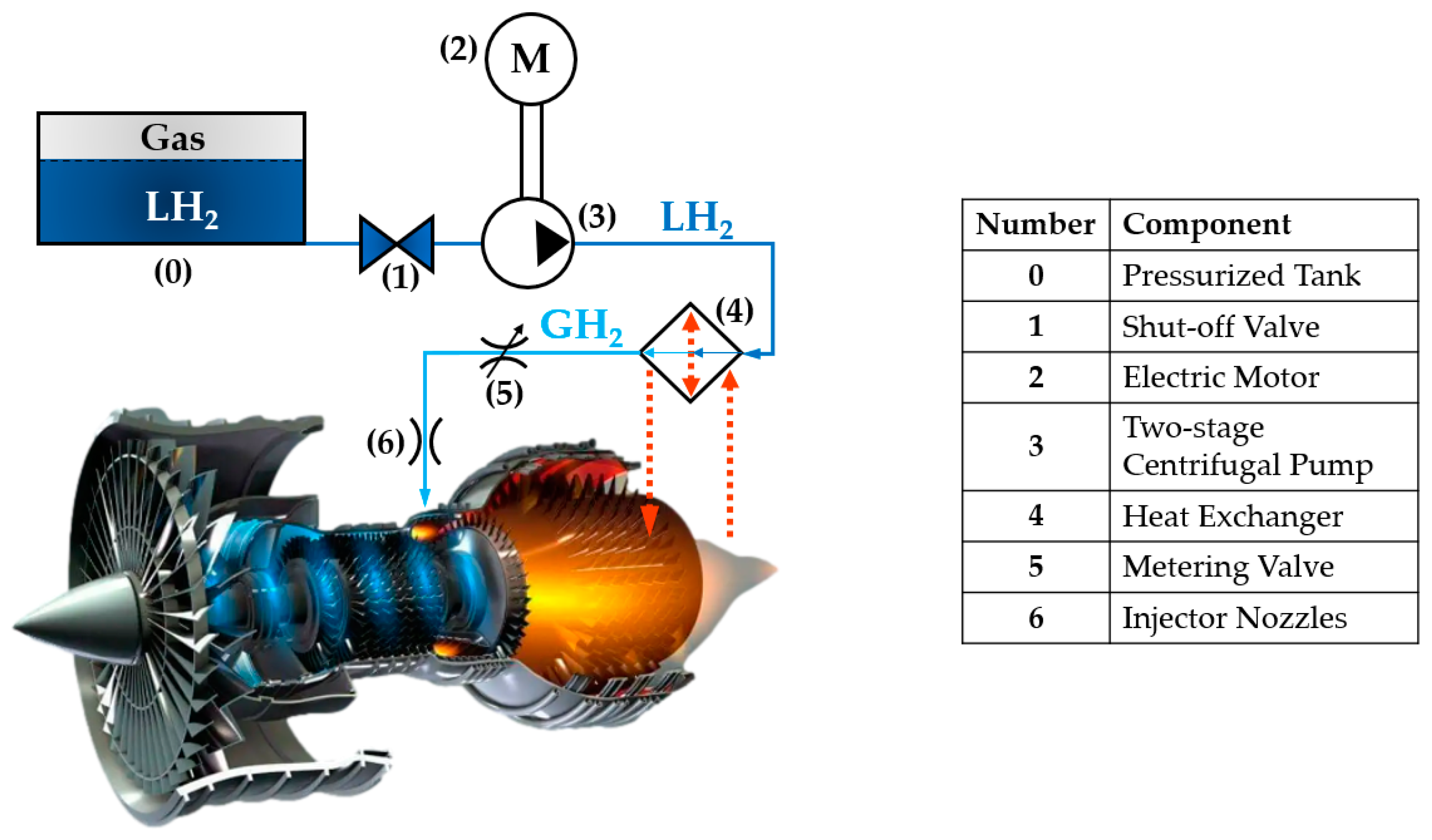
2. Heat Exchanger Layout

As shown in Figure 1, LH₂ vaporises upstream of the metering system via a heat exchanger (4), which uses heat from the exhaust gases exiting the turbine to convert H₂ from its liquid form (LH₂) to a gaseous form (GH₂).

The proposed heat exchanger design, depicted in Figure 2, consists of three subunits (recovery heater, main heater, and pre-heater) and incorporates two separate fluid circuits: nitrogen (N₂) and hydrogen (H₂) circuit. The following concern the fluid circuits:

⮚

N₂ circuit: N₂, a safe and inert gas with excellent thermophysical properties, is widely used in high-performance heat exchangers [42,43]. Specifically, N₂ is particularly suitable for use with H₂ under supercritical conditions, as its critical temperature is moderately higher than that of H₂ and, for both fluids, slightly supercritical operative pressures are employed. This aspect makes N₂ a suitable carrier fluid, favoured over commonly used alternatives like water, ethylene, and glycol, as their critical temperatures are excessively higher compared to that of H₂, thus not allowing a correct heat exchange between the fluids in the exchanger. In this system, N₂ operates within a closed-loop circuit as follows:

• It absorbs heat from the turbine’s exhaust gases (EGs), raising its temperature;
• This energy is then transferred to the H₂ circuit to heat GH₂ to high temperatures;
• After completing the heat exchange, N₂ is recirculated and reheated by the EGs, enabling continuous operation.

⮚

H₂ circuit: This circuit ensures the complete phase change of H₂ from liquid form (LH₂) to gaseous form (GH₂) while achieving the desired thermodynamic conditions for metering. Key processes include the following:

• Pre–Heating: LH₂ is initially vaporised using a portion of the heat from high-temperature GH₂;
• Main Heating: The resulting GH₂ is further heated through energy transfer from the N₂ circuit;
• Final Cooling: A portion of the high-temperature GH₂’s energy is used to vaporise incoming LH₂. After this step, the GH₂ exits the heat exchanger at the precise thermodynamic conditions required for metering.

The three subunits of the heat exchanger are detailed below:

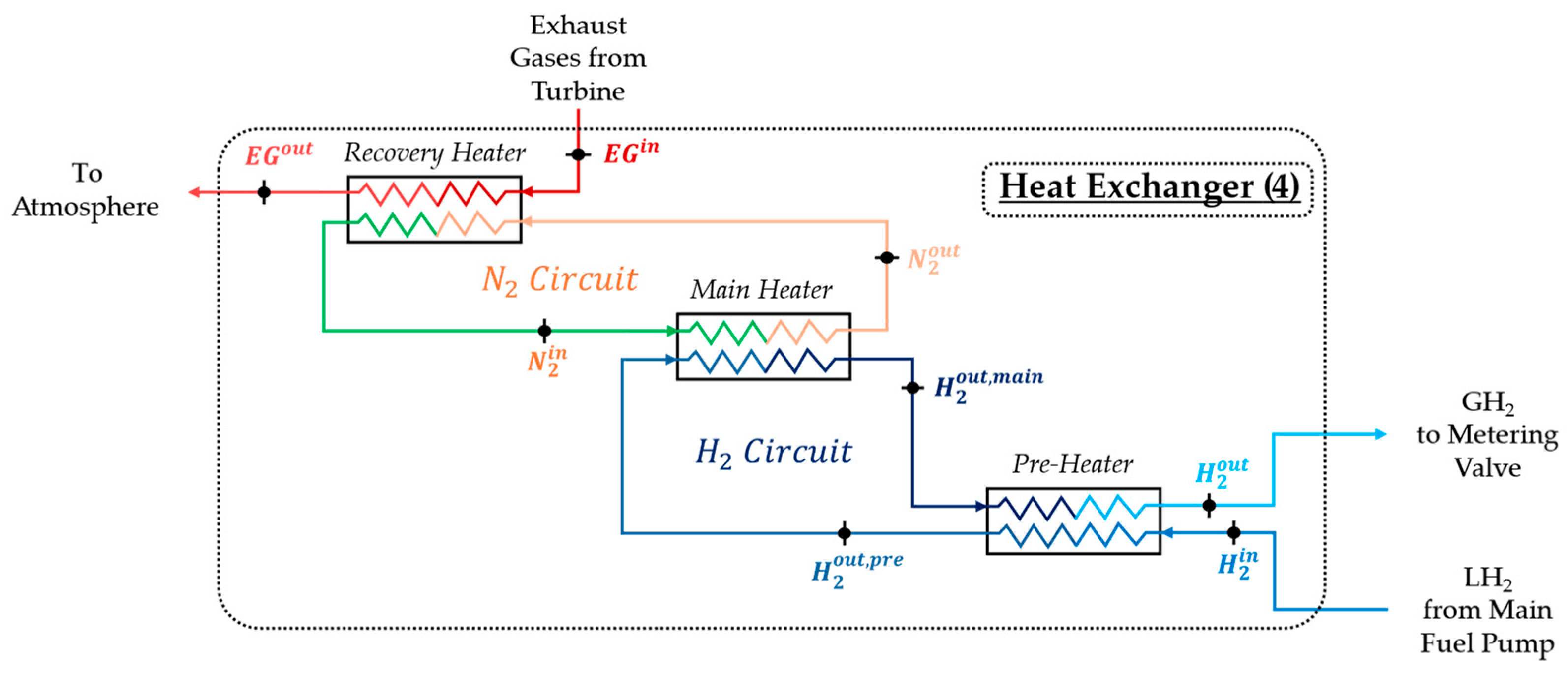
• Recovery Heater: The first subunit, the recovery heater, captures thermal energy from the EGs leaving the turbine ($\mathrm{E}{\mathrm{G}}^{\mathrm{in}}$), which retain significant heat. The hot EGs transfer this heat to N₂, increasing its temperature (${\mathrm{N}}_2^{\mathrm{in}}$). After the heat exchange, the EGs are discharged into the atmosphere ($\mathrm{E}{\mathrm{G}}^{\mathrm{out}})$;
• Main Heater: The high-temperature N₂ exiting the recovery heater (${\mathrm{N}}_2^{\mathrm{in}}$) flows into the second subunit, called the main heater, where it transfers heat to the H₂. This H₂, already in gaseous form due to vaporisation by the third subunit (the pre-heater) in the H₂ circuit (${\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}$), receives additional heat from the N₂, further increasing its temperature (${\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}$). Since the N₂ circuit is closed, the cooled nitrogen (${\mathrm{N}}_2^{\mathrm{out}}$) exits the main heater and is recirculated back to the inlet of the recovery heater for reheating;
• Pre-Heater: LH₂ from the main fuel pump enters the heat exchanger $({\mathrm{H}}_2^{\mathrm{in}}$) and flows into the third subunit, the pre-heater. Within this subunit, high-temperature GH₂ from the main heater (${\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}$) transfers a part of heat to the incoming LH₂, causing its vaporisation. After this process, the GH₂ from the main heater exits the pre-heater at a slightly reduced temperature (${\mathrm{H}}_2^{\mathrm{out}}$) and is ready to flow toward the metering system under the required thermodynamic conditions.

It is important to note that numerical modelling has been conducted only for the pre-heater and main heater subunits, assuming negligible pressure losses. As a result, the pressure of H₂ in the H₂ circuit and N₂ in the N₂ circuit can be considered constant. This reasonable assumption ensures that pump power consumption remains within acceptable limits, preventing it from rising too high. In this way, the overall system efficiency is not compromised.

For the recovery heater subunit, a possible design is presented in Figure 3. This configuration is included for illustrative purposes only and will neither be designed nor modelled in this preliminary analysis. In this concept, the high-temperature EGs exiting the turbine ($\mathrm{E}{\mathrm{G}}^{\mathrm{in}}$) transfer heat to N₂ flowing through a serpentine tubular pipe. This pipe, integrated into the structure of the outlet nozzle, acts as the recovery heater subunit. After transferring their heat to the N₂, the EGs are discharged into the atmosphere ($\mathrm{E}{\mathrm{G}}^{\mathrm{out}})$.

3. Heat Exchanger Numerical Model

This section details the numerical model of the heat exchanger architecture, as previously shown in Figure 2. It provides a comprehensive characterisation of the system, excluding the recovery heater, which is included only for illustrative purposes. The analysis addresses the input variables, input thermodynamic and geometric parameters, and output variables that define the system’s performance.

The thermodynamic model leverages the CoolProp libraries [44] for its calculations. In this model, the two heat exchanger subunits are assumed to be adiabatic to the environment, a valid assumption given that these devices must be effectively insulated using vacuum systems.

The model is structured into three main parts: first, the temperature calculations are detailed (Section 3.1); second, the heat transfer coefficients are described (Section 3.2); and finally, the heat exchanger key performance parameters are characterised (Section 3.3). A schematic representation at the end of this section summarises the flow of calculations and parameter interrelations.

3.1. Calculation of the Temperatures

Since the recovery heater subunit is included solely to illustrate the heat recovery mechanism from EGs, this study will focus on modelling the remaining two heat exchanger subunits. Each subunit will be represented with four ports, and the corresponding thermodynamic states will be considered.

All thermodynamic calculations are performed using the CoolProp thermodynamic libraries, which are open-source and widely used due to their thorough validation, as shown in [44]. These libraries have the capability to model over 120 fluids with real gas state equations, including HEOS, PR, and SRK [44].

It is important to note that, when referring to H₂, parahydrogen has been considered for these calculations. This choice is driven by the fact that LH₂ storage requires the fuel to withstand boil-off, a condition that only parahydrogen can meet [45]. Moreover, at 20 K, parahydrogen concentration exceeds 98%, making the presence of orthohydrogen (around 2%) negligible [46]. However, the spontaneous conversion from ortho to para form occurs very slowly, making catalytic conversion unavoidable in hydrogen liquefaction processes [47].

Another key point of this analysis to highlight is that the operating pressures of both fluids in this study considered in the study (N₂ and H₂) are maintained above the critical limit (supercritical conditions) to prevent any two-phase behaviour during the heat exchange process.

The inputs for the calculation are as follows: for the H₂ circuit, the required thermodynamic parameters are the hydrogen mass flow rate (${\dot{\mathrm{m}}}_{{\mathrm{H}}_2}$), the inlet and outlet temperatures of hydrogen at the heat exchanger (${\mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{in}}},{\mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{out}}}$) and the hydrogen pressure (${\mathrm{p}}_{{\mathrm{H}}_2}$) [32,33]. For the N₂ circuit, the input thermodynamic parameters include the inlet and outlet temperatures of nitrogen at the main heater subunit (${\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}},{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{out}}}$) and the nitrogen pressure (${\mathrm{p}}_{{\mathrm{N}}_2}$). Additionally, the temperature difference between the inlet temperature of nitrogen and the hydrogen outlet temperature at the main heater subunit ($\mathsf{\Delta }{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$) is required.

Using these inputs, the nitrogen mass flow rate (${\dot{\mathrm{m}}}_{{\mathrm{N}}_2}$), the main heater hydrogen outlet enthalpy (${\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$) and the pre-heater hydrogen outlet enthalpy (${\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}}$) can be evaluated from the following equations, which describe the power balance for the main heater subunit (1), the pre-heater subunit (2), and the temperature difference between the inlet temperature of nitrogen and the hydrogen outlet temperature at the main heater (3).

$${\dot{\mathrm{m}}}_{{\mathrm{N}}_2}\cdot \left({\mathrm{h}}_{{\mathrm{N}}_2^{\mathrm{in}}}-{\mathrm{h}}_{{\mathrm{N}}_2^{\mathrm{out}}}\right)={\dot{\mathrm{m}}}_{{\mathrm{H}}_2}\cdot \left({\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}-{\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}}\right),$$

(1)

$${\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}-{\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out}}}={\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}}-{\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{in}}},$$

(2)

$$\mathsf{\Delta }{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}={\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}}-{\mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}},$$

(3)

where

• ${\mathrm{h}}_{{\mathrm{N}}_2^{\mathrm{in}}}$ and ${\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{in}}}$ are the enthalpies for N₂ at the inlet of the main heater subunit and for H₂ at inlet of the heat exchanger, respectively;
• ${\mathrm{h}}_{{\mathrm{N}}_2^{\mathrm{out}}}$ and ${\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out}}}$ are the enthalpies for N₂ at the outlet of the main heater subunit and for H₂ at the outlet of the heat exchanger, respectively;
• ${\mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$ is the temperature associated with ${\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$.

Specifically, to solve these equations, the CoolProp libraries are used to calculate the enthalpies required for Equations (1) and (2). Once the enthalpies are obtained $({\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$, ${\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}}$), CoolProp is used again to calculate the associated temperatures (${\mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$, ${\mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}}$), which are then used to determine the temperature profile inside the pipes (for both subunits). Figure 4 illustrates qualitatively the heat exchange process occurring in the pre-heater and main heater subunits.

The technology at the core of this study is the pipe-in-pipe technology, where the internal pipes are enclosed within the external ones. In both heat exchanger subunits, the hot fluid flows inside the internal pipe, while the cold fluid circulates in the space between the internal and external pipes. This configuration offers advantages in terms of compactness and reduced system weight. The system geometry is shown in Figure 5 where ${\mathrm{d}}_{\mathrm{i},\mathrm{i}}$ represents the internal diameter of the internal pipe, ${\mathrm{d}}_{\mathrm{e},\mathrm{i}}$ represents the external diameter of the internal pipe, ${\mathrm{d}}_{\mathrm{i},\mathrm{e}}$ represents the internal diameter of the external pipe and ${\mathrm{d}}_{\mathrm{e},\mathrm{e}}$ represents the external diameter of the external pipe. The authors are unaware of any previous market applications of this technology, making it a novel proposal. The number of pipes (${\mathrm{n}}_{\mathrm{t}}$) is the same for both the main heater and pre-heater subunits.

All considerations regarding the thermodynamic states must align with the material strength of the pipes (for both subunits). The pipes need to withstand the pressure imposed by the system to prevent any potential breakdowns. To ensure that the chosen material can handle the required pressure, a law governing the minimum required thickness for a pressurised vessel is applied, specifically the Mariotte’s law which is shown in the following equation:

$$\mathrm{t} \ge {\displaystyle \frac{\mathrm{p}\cdot {\mathrm{d}}_{\mathrm{i}}}{2{\mathsf{\sigma }}_{\mathrm{yield}}}}\cdot \mathsf{\alpha },$$

(4)

where $\mathrm{t}$ is the minimum thickness required for the generic tube, $\mathrm{p}$ is the pressure acting on the pipe walls, ${\mathrm{d}}_{\mathrm{i}}$ is the internal diameter of the generic pipe, ${\mathsf{\sigma }}_{\mathrm{yield}}$ is the yield stress of the material and $\mathsf{\alpha }$ is the Mariotte safety coefficient.

Since the two heat exchanger subunits (namely, the pre-heater and the main heater) use the pipe-in-pipe technology for their pipe configuration, it is important to specify the hot and cold fluids in each subunit. For this reason,

Table 2. Specification of cold fluid and hot fluid for both heat exchanger subunits.

	Cold Fluid (c)	Hot Fluid (h)
Pre-heater	${\mathrm{H}}_2^{\mathrm{in}}$	${\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}$
Main heater	${\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}$	${\mathrm{N}}_2^{\mathrm{in}}$

below details, for each subunit, the hot fluid (denoted by the subscript “h”) and the cold fluid (denoted by the subscript “c”).

The flow area for both the cold fluid and the hot fluid can be calculated as:

$${\mathrm{A}}_{\mathrm{h}}={\displaystyle \frac{\mathsf{\pi }\cdot {\mathrm{d}}_{\mathrm{i},\mathrm{i}}^2}{4}},$$

(5)

$${\mathrm{A}}_{\mathrm{c}}={\displaystyle \frac{\mathsf{\pi }\cdot \left({\mathrm{d}}_{\mathrm{i},\mathrm{e}}^2-{\mathrm{d}}_{\mathrm{e},\mathrm{i}}^2\right)}{4}},$$

(6)

where $A_h$ represents the flow area for the hot fluid, while $A_c$ represents the flow area for the cold fluid. By means of Equations (5) and (6), the hydraulic diameter for the hot fluid ${\left({\mathrm{d}}_{\mathrm{h}}\right)}_{\mathrm{h}}$ and the hydraulic diameter for the cold fluid ${\left({\mathrm{d}}_{\mathrm{h}}\right)}_{\mathrm{c}}$ can be obtained as follows:

$${\left({\mathrm{d}}_{\mathrm{h}}\right)}_{\mathrm{h}}={\displaystyle \frac{4\cdot {\mathrm{A}}_{\mathrm{h}}}{\mathsf{\pi }\cdot {\mathrm{d}}_{\mathrm{i},\mathrm{i}}}},$$

(7)

$${\left({\mathrm{d}}_{\mathrm{h}}\right)}_{\mathrm{c}}={\displaystyle \frac{4\cdot {\mathrm{A}}_{\mathrm{c}}}{\mathsf{\pi }\cdot ({\mathrm{d}}_{\mathrm{i},\mathrm{e}}+{\mathrm{d}}_{\mathrm{e},\mathrm{i}})}},$$

(8)

In order to trace the temperature profile along the pipes, they can be ideally divided into modules, with constant properties assumed for each module. In this analysis, the number of modules is imposed to be $\mathrm{n}=50$ for both subunits. In each module, the cold fluid undergoes a temperature variation given by:

$$\mathsf{\Delta }{\mathrm{T}}_{\mathrm{c}}={\displaystyle \frac{{\mathrm{T}}_{\mathrm{c}}^{\mathrm{out}}-{\mathrm{T}}_{\mathrm{c}}^{\mathrm{in}}}{\mathrm{n}}},$$

(9)

where ${\mathrm{T}}_{\mathrm{c}}^{\mathrm{out}}$ and ${\mathrm{T}}_{\mathrm{c}}^{\mathrm{in}}$ represent the outlet temperature and the inlet temperature of the generic cold fluid. A single module can be schematically represented in Figure 6, where ${\left({\mathrm{T}}_{\mathrm{in},\mathrm{h}}\right)}_{\mathrm{i}}$, ${\left({\mathrm{T}}_{\mathrm{out},\mathrm{h}}\right)}_{\mathrm{i}}$, ${\left({\mathrm{T}}_{\mathrm{in},\mathrm{c}}\right)}_{\mathrm{i}}$, ${\left({\mathrm{T}}_{\mathrm{out},\mathrm{c}}\right)}_{\mathrm{i}}$ and ${(\mathsf{\Delta }\mathrm{x}(}_{\mathrm{i}}$ are the input and output temperature for the hot fluid, the input and output temperature for the cold fluid, and the length of the i-th module, respectively.

The outlet temperature of the cold fluid in each module i (i = 1, …, n) is calculated as follows:

$${\left({\mathrm{T}}_{\mathrm{out},\mathrm{c}}\right)}_{\mathrm{i}}={\left({\mathrm{T}}_{\mathrm{in},\mathrm{c}}\right)}_{\mathrm{i}}+\mathsf{\Delta }{\mathrm{T}}_{\mathrm{c}},$$

(10)

$${\left({\mathrm{T}}_{\mathrm{in},\mathrm{c}}\right)}_{\mathrm{i}}={\left({\mathrm{T}}_{\mathrm{out},\mathrm{c}}\right)}_{\mathrm{i}-1},$$

(11)

where ${\left({\mathrm{T}}_{\mathrm{in},\mathrm{c}}\right)}_1\equiv {\mathrm{T}}_{\mathrm{c}}^{\mathrm{in}}$ and ${\left({\mathrm{T}}_{\mathrm{out},\mathrm{c}}\right)}_{\mathrm{n}}\equiv {\mathrm{T}}_{\mathrm{c}}^{\mathrm{out}}$. For the pre-heater ${\mathrm{T}}_{\mathrm{c}}^{\mathrm{in}}\equiv {\mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{in}}}$, while for the main heater ${\mathrm{T}}_{\mathrm{c}}^{\mathrm{in}}\equiv {\mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}}$. Similarly, for the pre-heater ${\mathrm{T}}_{\mathrm{c}}^{\mathrm{out}}\equiv {\mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}},$ while for the main heater ${\mathrm{T}}_{\mathrm{c}}^{\mathrm{out}}{\equiv \mathrm{T}}_{{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$. Once ${\left({\mathrm{T}}_{\mathrm{in},\mathrm{c}}\right)}_{\mathrm{i}}$ and ${\left({\mathrm{T}}_{\mathrm{out},\mathrm{c}}\right)}_{\mathrm{i}}$ are known, CoolProp libraries can be used to calculate the corresponding enthalpies ${\left({\mathrm{h}}_{\mathrm{in},\mathrm{c}}\right)}_{\mathrm{i}}$ and ${\left({\mathrm{h}}_{\mathrm{out},\mathrm{c}}\right)}_{\mathrm{i}}$. The values of the latter can be used to calculate the thermal power absorbed by the cold fluid in a single module:

$${\left({\dot{\mathrm{Q}}}_{\mathrm{exc}}\right)}_{\mathrm{i}}={\dot{\mathrm{m}}}_{\mathrm{c}}\cdot \left[{\left({\mathrm{h}}_{\mathrm{out},\mathrm{c}}\right)}_{\mathrm{i}}-{\left({\mathrm{h}}_{\mathrm{in},\mathrm{c}}\right)}_{\mathrm{i}}\right],$$

(12)

where ${\dot{m}}_c$ represents the mass flow rate of the generic cold fluid. Since the thermal power absorbed by the cold fluid is equal to the thermal power provided by the hot fluid, the inlet enthalpy and the outlet enthalpy of the hot fluid can be calculated for each module (i) as follows:

$${\left({\mathrm{h}}_{\mathrm{in},\mathrm{h}}\right)}_{\mathrm{i}}={\left({\mathrm{h}}_{\mathrm{out},\mathrm{h}}\right)}_{\mathrm{i}}+{\displaystyle \frac{{\left({\dot{\mathrm{Q}}}_{\mathrm{exc}}\right)}_{\mathrm{i}}}{{\dot{\mathrm{m}}}_{\mathrm{h}}}},$$

(13)

$${\left({\mathrm{h}}_{\mathrm{out},\mathrm{h}}\right)}_{\mathrm{i}}={\left({\mathrm{h}}_{\mathrm{in},\mathrm{h}}\right)}_{\mathrm{i}-1},$$

(14)

where ${\dot{\mathrm{m}}}_{\mathrm{h}}$ represents the mass flow rate for the hot fluid. Similarly to the cold fluid, when $\mathrm{i}=1$, ${\left({\mathrm{h}}_{\mathrm{out},\mathrm{h}}\right)}_1\equiv {\mathrm{h}}_{\mathrm{h}}^{\mathrm{out}}$, where ${\mathrm{h}}_{\mathrm{h}}^{\mathrm{out}}$ is the outlet enthalpy for the generic hot fluid. For the pre-heater ${\mathrm{h}}_{\mathrm{h}}^{\mathrm{out}}\equiv {\mathrm{h}}_{{\mathrm{H}}_2^{\mathrm{out}}}$, while for the main heater ${\mathrm{h}}_{\mathrm{h}}^{\mathrm{out}}\equiv {\mathrm{h}}_{{\mathrm{N}}_2^{\mathrm{out}}}$. Consequently, once ${\left({\mathrm{h}}_{\mathrm{out},\mathrm{h}}\right)}_{\mathrm{i}}$ and ${\left({\mathrm{h}}_{\mathrm{in},\mathrm{h}}\right)}_{\mathrm{i}}$ have been determined in each module (i), the temperatures of the hot fluid ${{(\mathrm{T}}_{\mathrm{out},\mathrm{h}})}_{\mathrm{i}}$ and ${{(\mathrm{T}}_{\mathrm{in},\mathrm{h}})}_{\mathrm{i}}$ can be calculated in each module (i), by using the libraries of CoolProp, as a function of pressure and enthalpy.

3.2. Calculation of the Heat Transfer Coefficients

After the temperature profile along the pipes is traced, it is possible to calculate the heat transfer coefficients, with reference to the average fluid properties of each module (i), which are defined for cold fluid ${\left(\overline{{\mathrm{T}}_{\mathrm{c}}}\right)}_{\mathrm{i}}$ and hot fluid ${\left(\overline{{\mathrm{T}}_{\mathrm{h}}}\right)}_{\mathrm{i}}$ as follows:

$${\left(\overline{{\mathrm{T}}_{\mathrm{h}}}\right)}_{\mathrm{i}}={\displaystyle \frac{{{(\mathrm{T}}_{\mathrm{in},\mathrm{h}})}_{\mathrm{i}}+{{(\mathrm{T}}_{\mathrm{out},\mathrm{h}})}_{\mathrm{i}}}{2}}{;(\overline{{\mathrm{T}}_{\mathrm{c}}})}_{\mathrm{i}}={\displaystyle \frac{{{(\mathrm{T}}_{\mathrm{in},\mathrm{c}})}_{\mathrm{i}}+{{(\mathrm{T}}_{\mathrm{out},\mathrm{c}})}_{\mathrm{i}}}{2}},$$

(15)

Once again, by means of CoolProp libraries, once the average temperatures are obtained for each module (i), it is also possible to calculate the following:

• The average densities of the hot and cold fluids (${\left(\overline{{\mathsf{\rho }}_{\mathrm{h}}}\right)}_{\mathrm{i}}$, ${\left(\overline{{\mathsf{\rho }}_{\mathrm{c}}}\right)}_{\mathrm{i}})$;
• The average thermal conductivities of the hot and cold fluids $({\left(\overline{{\mathsf{\lambda }}_{\mathrm{h}}}\right)}_{\mathrm{i}}$, ${\left(\overline{{\mathsf{\lambda }}_{\mathrm{c}}}\right)}_{\mathrm{i}})$;
• The average viscosities of the hot and cold fluids ${\left(\right(\overline{{\mathsf{\mu }}_{\mathrm{h}}})}_{\mathrm{i}}$, ${\left(\overline{{\mathsf{\mu }}_{\mathrm{c}}}\right)}_{\mathrm{i}})$;
• The average specific heats of the hot and cold fluids $({\left(\overline{{\mathrm{cp}}_{\mathrm{h}}}\right)}_{\mathrm{i}}$, ${\left(\overline{{\mathrm{cp}}_{\mathrm{c}}}\right)}_{\mathrm{i}})$.

Another property to be calculated in each module (i) is the average velocity for both the hot fluid and the cold fluid:

$${{\left(\overline{{\mathrm{V}}_{\mathrm{x}}}\right)}_{\mathrm{i}}={\displaystyle \frac{{\dot{\mathrm{m}}}_{\mathrm{x}}}{{\mathrm{n}}_{\mathrm{t}}·{\left(\overline{{\mathsf{\rho }}_{\mathrm{x}}}\right)}_{\mathrm{i}}·\mathrm{A}}}}_{\mathrm{x}},$$

(16)

where either x = h (hot fluid) or x = c (cold fluid).

Along these average thermodynamic and cinematic parameters, also the average Reynolds number and the average Prandtl number of the hot and cold fluids can be calculated in each module (i) as:

$${\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}={\displaystyle \frac{{\left(\overline{{\mathrm{V}}_{\mathrm{x}}}\right)}_{\mathrm{i}}{·(\overline{{\mathsf{\rho }}_{\mathrm{x}}})}_{\mathrm{i}}{·\mathrm{d}}_{\mathrm{h},\mathrm{x}}}{{\left(\overline{{\mathsf{\mu }}_{\mathrm{x}}}\right)}_{\mathrm{i}}}},$$

(17)

$${\left(\overline{{\mathrm{Pr}}_{\mathrm{x}}}\right)}_{\mathrm{i}}={\displaystyle \frac{{\left(\overline{{\mathsf{\mu }}_{\mathrm{x}}}\right)}_{\mathrm{i}}·{\left(\overline{{\mathrm{cp}}_{\mathrm{x}}}\right)}_{\mathrm{i}}}{{\left(\overline{{\mathsf{\lambda }}_{\mathrm{x}}}\right)}_{\mathrm{i}}}},$$

(18)

The Average Nusselt number in each module (i) is expressed as a function of the average Reynolds number as:

• when ${\left(\overline{{Re}_x}\right)}_i<2300$ ${\left(\overline{{Nu}_x}\right)}_i=4.36$
• when $2300<{\left(\overline{{Re}_x}\right)}_i<{10}^6$, the Gnielinski correlation can be used
• when ${\left(\overline{{Re}_x}\right)}_i>{10}^6$, the Chilton–Coulburn correlation can be used.

The following Equation (19) encloses all the cases described above:

$${\left(\overline{{\mathrm{Nu}}_{\mathrm{x}}}\right)}_{\mathrm{i}}=\left\{\begin{array}{l} 4.36, \mathrm{i}\mathrm{f} {\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}<2300\\ {\displaystyle \frac{\frac{{(\mathsf{\xi })}_{\mathrm{i}}}{8}·({\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}-1000)·{\left(\overline{{\mathrm{Pr}}_{\mathrm{x}}}\right)}_{\mathrm{i}})}{1+12.7{\left(\frac{{(\mathsf{\xi })}_{\mathrm{i}}}{8}\right)}^{0.5}·\left({{\left(\overline{{\mathrm{Pr}}_{\mathrm{x}}}\right)}_{\mathrm{i}}}^{2/3}-1\right)}}, \mathrm{i}\mathrm{f} 2300<{\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}<{10}^6\\ 0.023·{{\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}}^{0.8}{{·(\overline{{\mathrm{Pr}}_{\mathrm{x}}})}_{\mathrm{i}}}^{1/3}, {\mathrm{if}\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}>{10}^6\end{array}\right.$$

(19)

where ${\left(\mathsf{\xi }\right)}_{\mathrm{i}}$ represents the friction factor in each module (i), which can be calculated as:

$${\left(\mathsf{\xi }\right)}_{\mathrm{i}}={(1.82·\log {\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}-1.64)}^{-2}$$

(20)

Equations (19) and (20) are well established and widely used in the literature [48,49]; therefore, they are to be considered reliable for fully developed (hydrodynamically and thermally) flow.

Finally, once all these average quantities are available, the convective heat exchange coefficients in each module (i), for the hot fluid ${\left(\overline{{\mathrm{h}}_{\mathrm{h}}}\right)}_{\mathrm{i}}$ and cold fluid ${\left(\overline{{\mathrm{h}}_{\mathrm{c}}}\right)}_{\mathrm{i}}$, can be obtained as:

$${\left(\overline{{\mathrm{h}}_{\mathrm{h}}}\right)}_{\mathrm{i}}={\displaystyle \frac{{\left(\overline{{\mathrm{Nu}}_{\mathrm{h}}}\right)}_{\mathrm{i}}·{\left(\overline{{\mathsf{\lambda }}_{\mathrm{h}}}\right)}_{\mathrm{i}}}{{\mathrm{d}}_{\mathrm{h},\mathrm{h}}}};{\left(\overline{{\mathrm{h}}_{\mathrm{c}}}\right)}_{\mathrm{i}}={\displaystyle \frac{{\left(\overline{{\mathrm{Nu}}_{\mathrm{c}}}\right)}_{\mathrm{i}}·{\left(\overline{{\mathsf{\lambda }}_{\mathrm{c}}}\right)}_{\mathrm{i}}}{{\mathrm{d}}_{\mathrm{h},\mathrm{c}}}}$$

(21)

3.3. Calculation of the Performance Parameters

The knowledge of the convective heat exchange coefficients and the temperatures of the hot and cold fluids allows for the determination of the mean heat transfer coefficient ${\left(\mathrm{U}\right)}_{\mathrm{i}}$ and the logarithmic mean temperature difference ${(\stackrel{-}{\mathsf{\Delta }\mathrm{T}})}_{\mathrm{i}}$ in each module (i) with the following equations:

$${\left(\mathrm{U}\right)}_{\mathrm{i}}={\displaystyle \frac{1}{\frac{1}{{\left(\overline{{\mathrm{h}}_{\mathrm{c}}}\right)}_{\mathrm{i}}}+\frac{1}{{\left(\overline{{\mathrm{h}}_{\mathrm{h}}}\right)}_{\mathrm{i}}·\frac{{\mathrm{d}}_{\mathrm{i},\mathrm{i}}}{{\mathrm{d}}_{\mathrm{e},\mathrm{i}}}}+\frac{{\mathrm{d}}_{\mathrm{e},\mathrm{i}}\cdot \ln \frac{{\mathrm{d}}_{\mathrm{e},\mathrm{i}}}{{\mathrm{d}}_{\mathrm{i},\mathrm{i}}}}{2\cdot \mathsf{\lambda }}}}$$

(22)

$${(\stackrel{-}{\mathsf{\Delta }\mathrm{T}})}_{\mathrm{i}}={\displaystyle \frac{\left[{{(\mathrm{T}}_{\mathrm{in},\mathrm{h}})}_{\mathrm{i}}-{{(\mathrm{T}}_{\mathrm{out},\mathrm{c}})}_{\mathrm{i}}\right]-\left[{{(\mathrm{T}}_{\mathrm{out},\mathrm{h}})}_{\mathrm{i}}-{{(\mathrm{T}}_{\mathrm{in},\mathrm{c}})}_{\mathrm{i}}\right]}{\ln \left(\frac{{{(\mathrm{T}}_{\mathrm{in},\mathrm{h}})}_{\mathrm{i}}-{{(\mathrm{T}}_{\mathrm{out},\mathrm{c}})}_{\mathrm{i}}}{{{(\mathrm{T}}_{\mathrm{out},\mathrm{h}})}_{\mathrm{i}}-{{(\mathrm{T}}_{\mathrm{in},\mathrm{c}})}_{\mathrm{i}}}\right)}}$$

(23)

where λ is the thermal conductivity of the material constituting the pipes. In this way, it is possible to determine the length of each module ($\mathsf{\Delta }{\mathrm{x}}_{\mathrm{i}}$), and thus the overall length of both heat exchanger subunits (pre-heater and main heater):

$${\mathsf{\Delta }\mathrm{x}}_{\mathrm{i}}={\displaystyle \frac{({{\dot{\mathrm{Q}}}_{\mathrm{exc}})}_{\mathrm{i}}}{\mathsf{\pi }·{\mathrm{d}}_{\mathrm{e},\mathrm{i}}{·\mathrm{n}}_{\mathrm{t}}·{\mathrm{U}}_{\mathrm{i}}{·(\stackrel{-}{\mathsf{\Delta }\mathrm{T}})}_{\mathrm{i}}}}$$

(24)

$${\mathrm{L}}_{\mathrm{y}}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathsf{\Delta }\mathrm{x}}_{\mathrm{i}}$$

(25)

where “y” is a generic subscript indicating the pre-heater when y = pre and the main heater when y = main. To represent the total length of the pipes, considering the lengths of both subunits, it is defined as: ${\mathrm{L}}_{\mathrm{tot}}={\mathrm{L}}_{\mathrm{pre}}+{\mathrm{L}}_{\mathrm{main}}$.

The pressure drop is calculated using the Darcy formula for both the hot ($\mathsf{\Delta }{\mathrm{p}}_{\mathrm{h}}$) and cold ($\mathsf{\Delta }{\mathrm{p}}_{\mathrm{c}}$) fluids (for both subunits), based on the average properties of the fluids, as follows:

$${\mathsf{\Delta }\mathrm{p}}_{\mathrm{h}}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\displaystyle \frac{1}{2}}{{{{·(\mathrm{f}}_{\mathrm{h}})}_{\mathrm{i}}·(\overline{{\mathrm{V}}_{\mathrm{h}}})}_{\mathrm{i}}}^2{·(\overline{{\mathsf{\rho }}_{\mathrm{h}}})}_{\mathrm{i}}·{\displaystyle \frac{{\mathsf{\Delta }\mathrm{x}}_{\mathrm{i}}}{{\mathrm{d}}_{\mathrm{h},\mathrm{h}}}}$$

(26)

$${\mathsf{\Delta }\mathrm{p}}_{\mathrm{c}}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\displaystyle \frac{1}{2}}{{{{·(\mathrm{f}}_{\mathrm{c}})}_{\mathrm{i}}·(\overline{{\mathrm{V}}_{\mathrm{c}}})}_{\mathrm{i}}}^2{·(\overline{{\mathsf{\rho }}_{\mathrm{c}}})}_{\mathrm{i}}·{\displaystyle \frac{{\mathsf{\Delta }\mathrm{x}}_{\mathrm{i}}}{{\mathrm{d}}_{\mathrm{h},\mathrm{c}}}}$$

(27)

where ${\left({\mathrm{f}}_{\mathrm{h}}\right)}_{\mathrm{i}}$ and ${\left({\mathrm{f}}_{\mathrm{c}}\right)}_{\mathrm{i}}$ are the friction factors in rough pipes for the hot and cold fluids, respectively, calculated based on the value of the average Reynold number in each module (i):

$${\left({\mathrm{f}}_{\mathrm{x}}\right)}_{\mathrm{i}}=\left\{\begin{array}{l}{\displaystyle \frac{64}{{\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}}}, \mathrm{i}\mathrm{f} {\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}<2300\\ {\displaystyle \frac{1}{{\left[-1.8·\log {\left(\frac{\text{Ɛ}}{{\mathrm{d}}_{\mathrm{h},\mathrm{x}}3.7}\right)}^{1.11}+\frac{6.9}{{\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}}\right]}^2}}, \mathrm{i}\mathrm{f} {\left(\overline{{\mathrm{Re}}_{\mathrm{x}}}\right)}_{\mathrm{i}}\ge 2300\end{array}\right.$$

(28)

where the first expression represents laminar flow condition, while the second expression (also known as Haaland formula) is representative of turbulent flow and ε is the roughness of the tubes.

In order to calculate the mass of both the heat exchanger subunits, the following equation is applied:

$${\mathrm{m}}_{\mathrm{y}}={\mathrm{V}}_{\mathrm{y}}\cdot {\mathsf{\rho }}_{\mathrm{mat}}$$

(29)

where ${\mathsf{\rho }}_{\mathrm{mat}}$ is the density of the selected material and ${\mathrm{V}}_{\mathrm{y}}$ indicates the volume of the pipes, which is evaluated as:

$${\mathrm{V}}_{\mathrm{y}}=\mathsf{\pi }\cdot \left[{\displaystyle \frac{\left({\mathrm{d}}_{\mathrm{e},\mathrm{e}}^2-{\mathrm{d}}_{\mathrm{i},\mathrm{e}}^2\right)+\left({\mathrm{d}}_{\mathrm{e},\mathrm{i}}^2-{\mathrm{d}}_{\mathrm{i},\mathrm{i}}^2\right)}{4}}\right]\cdot {\mathrm{L}}_{\mathrm{y}}$$

(30)

Similarly to the comprehensive length of the pipes, the total mass of the latter can be indicated as: ${\mathrm{m}}_{\mathrm{tot}}={\mathrm{m}}_{\mathrm{pre}}+{\mathrm{m}}_{\mathrm{main}}$, while the total volume of the pipes: ${\mathrm{V}}_{\mathrm{tot}}={\mathrm{V}}_{\mathrm{pre}}+{\mathrm{V}}_{\mathrm{main}}$.

Figure 7 provides a simplified algorithm flow diagram to represent the flow of calculations.

4. Results

This section evaluates the feasibility of the proposed heat exchanger architecture using the thermodynamic model described earlier. In the calculation, the pre-heater is divided into 50 modules, as is the main heater.

Table 3. H₂ thermodynamic parameters used as inputs in the calculation [32,33,50].

	Parameter	Symbol	Take-Off Value [Unit]
${\mathbf{H}}_{\mathbf{2}}$  Circuit	Mass flow rate	${\dot{\mathrm{m}}}_{{\mathrm{H}}_2}$	0.411 [kg/s]
	LH2 inlet heat exchanger temperature (from main fuel pump)	${\mathrm{T}}_{{\mathrm{H}}_2}^{\mathrm{in}}$	29.9 [K]
	GH2 outlet heat exchanger temperature (to metering valve)	${\mathrm{T}}_{{\mathrm{H}}_2}^{\mathrm{out}}$	353 [K]
	Pressure	${\mathrm{p}}_{{\mathrm{H}}_2}$	51.55 [bar]

summarises the input parameters for the H₂ circuit, including the inlet LH₂ temperature to the heat exchanger, the outlet GH₂ temperature from the heat exchanger, as well as the H₂ circuit pressure and mass flow rate. These parameters are derived from [32,33], which introduced and modelled the innovative hydrogen-fuelled aircraft system depicted in Figure 1 using Matlab/Simulink. The numerical model in these studies was validated by comparing simulated operating conditions with data from the literature [50], focusing on the take-off phase.

Building on this foundation, the current study aims to design the heat exchanger architecture, previously illustrated in Figure 2 (taking into account only the pre-heater and main heater subunits), suitable for integration into the innovative hydrogen-fuelled aircraft system, with particular attention to the take-off phase. This phase is identified as the most critical for optimising the dimensions and performance parameters of the heat exchanger [50].

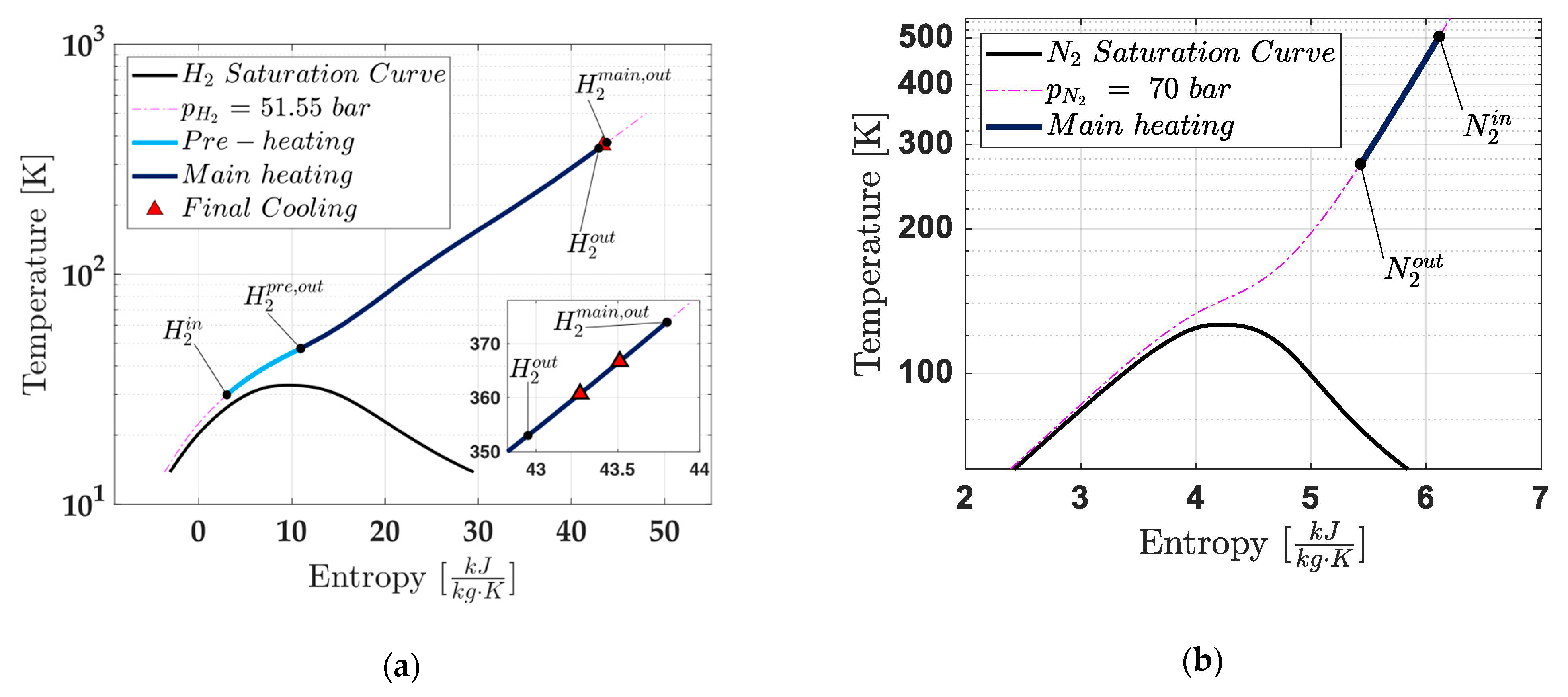
Specific assumptions were made to define the operating thermodynamic conditions of the N₂ circuit as follows:

• The N₂ inlet temperature to the main heater, ${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{in}}$, was set to 504 K. This value represents the temperature achieved by N₂ after heat exchange with the EGs in the recovery heater;
• The pressure in the N₂ circuit was set to 70 bar.

These N₂ input thermodynamic parameters, summarised in

Table 4. N₂ thermodynamic parameters used as inputs in the calculation.

	Parameter	Symbol	Value [Unit]
${\mathbf{N}}_{\mathbf{2}}$  Circuit	N2 inlet main heater temperature	${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{in}}$	504 [K]
	Pressure	${\mathrm{p}}_{{\mathrm{N}}_2}$	70 [bar]

, were chosen to ensure N₂ in a supercritical gaseous state at high temperature, optimising its thermophysical properties for effective heat transfer.

To comply with the temperature limits outlined in ASME B31.12 (Standard on Hydrogen Piping and Pipelines), austenitic stainless steels (300 series) are recommended for piping in both GH₂ and LH₂ systems, rather than other materials like aluminium, which, despite having better thermal conductivity, offers lower corrosion resistance and mechanical strength [51]. Among the various stainless steel grades, 316/316 L is preferred due to its superior stability and resistance to H₂ embrittlement, especially under high-pressure and temperature H₂ exposure [52]. This balance of thermal performance and structural reliability makes it the ideal choice for this application.

For the pre-heater and main heater subunits, piping made from stainless steel 316 was chosen. Using its material properties, along with the pipe key geometric parameters provided as model inputs, the minimum pipe thickness was calculated based on the Mariotte formula (outlined earlier in Section 3.1, Equation (4)).

It is important to remember that in the pipes of the pre-heater subunit, the hot fluid (h) is the high-temperature GH₂ exiting the main heater subunit (${\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}$), while the cold fluid (c) is the LH₂ supplied from the main fuel pump (${\mathrm{H}}_2^{\mathrm{in}}$). Conversely, in the pipes of the main heater subunit, the cold fluid (c) is the vaporised H₂ leaving the pre-heater subunit (${\mathrm{H}}_2^{\mathrm{out},\mathrm{pre}}$), and the hot fluid (h) is the high-temperature N₂ from the recovery heater subunit (${\mathrm{N}}_2^{\mathrm{in}}$), where it absorbs heat from EGs.

The material properties of stainless steel 316/316L are detailed in

Table 5. Stainless steel 316 properties.

	Propriety	Symbol	Value [Unit]
Stainless Steel 316	Density	${\mathsf{\rho }}_{\mathrm{mat}}$	8060 [kg/m3]
	Tensile Strength, Yield	${\mathsf{\sigma }}_{\mathrm{yield}}$	200 [MPa]
	Tensile Strength, Max	${\mathsf{\sigma }}_{\max }$	550 [MPa]
	Young Modulus	${\mathrm{E}}_{\mathrm{mat}}$	193 [GPa]
	Specific Heat Capacity	${\mathrm{c}}_{\mathrm{mat}}$	500 [J/(kg∙K)]
	Thermal Conductivity	${\mathsf{\lambda }}_{\mathrm{mat}}$	16 [W/(m∙K)]

, while the considered geometric parameters of the pipes and the calculated minimum pipe thickness are summarised in

Table 6. Key geometric parameters and calculated minimum thickness of the pipes (pre-heater and main heater subunits).

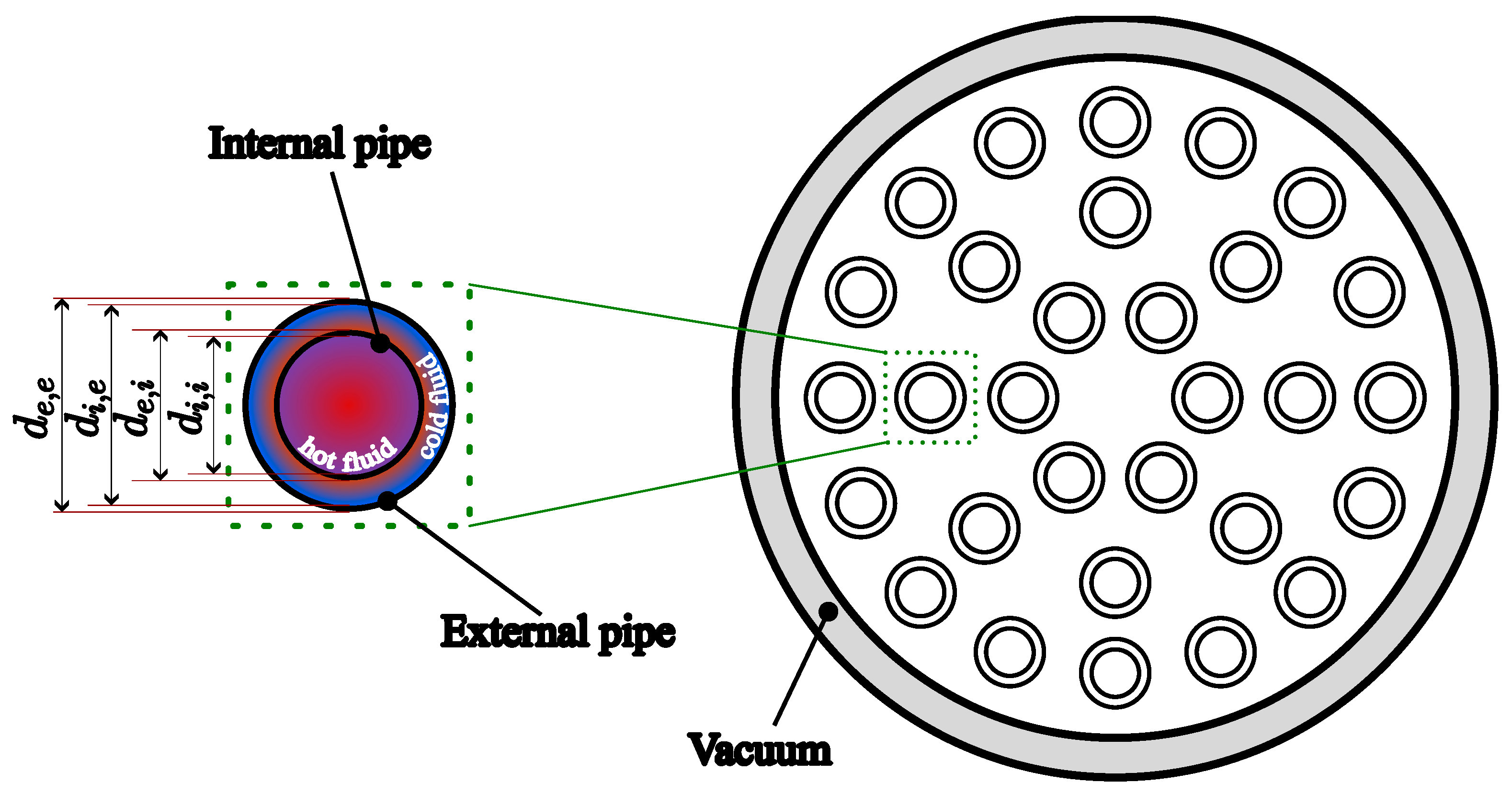
		Internal Tube		External Tube
	Parameter	Symbol	Value [Unit]	Symbol	Value [Unit]
Geometry of Pipes (both Subunits)	Internal Diameter	${\mathrm{d}}_{\mathrm{i},\mathrm{i}}$	20 [mm]	${\mathrm{d}}_{\mathrm{i},\mathrm{e}}$	25 [mm]
	External Diameter	${\mathrm{d}}_{\mathrm{e},\mathrm{i}}$	20.8 [mm]	${\mathrm{d}}_{\mathrm{e},\mathrm{e}}$	26 [mm]
	Roughness	${\mathsf{\epsilon }}_{\mathrm{i}}$	0.2 [mm]	${\mathsf{\epsilon }}_e$	0.2 [mm]
	Safety factor for Mariotte’s law	${\mathsf{\alpha }}_{\mathrm{i}}$	1.5 [-]	${\mathsf{\alpha }}_e$	1.5 [-]
	Calculated Minimum Thickness	${\mathrm{t}}_{\mathrm{i}}$	0.22 [mm]	${\mathrm{t}}_e$	0.48 [mm]
	Actual Thickness	${\mathrm{t}}_{\mathrm{i},\mathrm{t}}$	0.8 [mm]	${\mathrm{t}}_{e,\mathrm{t}}$	1 [mm]

.

To identify the optimal design point for the heat exchanger, minimising its performance parameters, namely the total pipes length (${\mathrm{L}}_{\mathrm{tot}}={\mathrm{L}}_{\mathrm{pre}}+{\mathrm{L}}_{\mathrm{main}}$) and mass (${\mathrm{m}}_{\mathrm{tot}}={\mathrm{m}}_{\mathrm{pre}}+{\mathrm{m}}_{\mathrm{main}}$), three key input parameters of the thermodynamic model were varied:

• The outlet N₂ temperature from the main heater (${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{out}}$).
• The temperature difference between the inlet N₂ temperature to the main heater and the outlet H₂ temperature from the main heater ($\mathsf{\Delta }{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$).
• The number of pipes in both the pre-heater and main heater subunits (${\mathrm{n}}_{\mathrm{t}}$).

The process was conducted using Esteco modeFRONTIER 2019 software [53], with a constraint that the pressure drops across the pipes remain below Δp ≤ 0.1 bar. This applied to both the cold fluids (denoted as “c”) and hot fluids (denoted as “h”) in the respective subunits, ensuring that the heat exchange process in both subunits could be treated as isobaric.

Table 7. Input thermodynamic and geometric variables: range values, step size, and number of points.

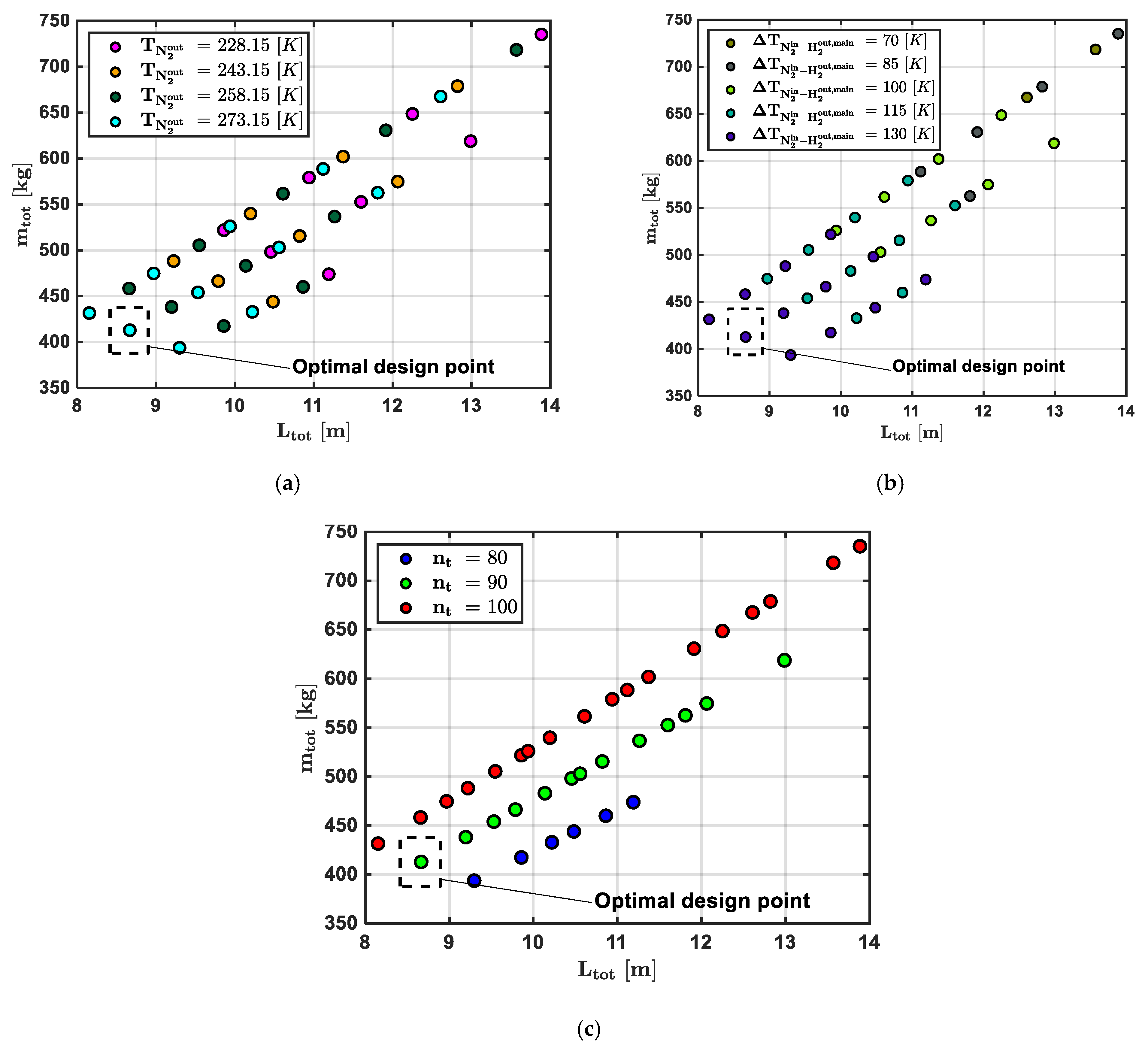
	Parameter	Symbol	Range Values [Unit]	Step Size [Unit]	Number of Points
Input Thermodynamic Variables	N2 outlet main heater temperature	${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{out}}$	(228.15–273.15) [K]	15 [K]	4
	Temperature difference between N2 entering and H2 exiting the main heater	$\mathsf{\Delta }{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$	(70–130) [K]	15 [K]	5
Input Geometric Variables	Number of pipes (both subunits)	${\mathrm{n}}_{\mathrm{t}}$	(80–100) [-]	10 [-]	3

provides a summary of the input variables involved in the calculation, including their value ranges, variation steps and number of points considered. The constraints applied during the process are outlined in

Table 8. Constraints considered in the calculation process.

	Propriety	Symbol	Objective [Unit]
Constraints	Pressure drops across pipes (both subunits)	$\mathsf{\Delta }\mathrm{p}$	$\text{≤}0.1$ [bar]

. A total of 60 design points were generated, which can be easily obtained by multiplying the individual number of points for each input variable.

The results, showing the influence of these input variables (${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{out}}$, $\mathsf{\Delta }{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$) and (${\mathrm{n}}_{\mathrm{t}}$) on the performance parameters (${\mathrm{L}}_{\mathrm{tot}}$ and ${\mathrm{m}}_{\mathrm{tot}}$) are presented in Figure 8, which highlights the selected optimal design point. The analysis reveals that higher values of the thermodynamic variables (${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{out}}$ and $\mathsf{\Delta }{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$) combined with intermediate values of the geometric variable (${\mathrm{n}}_{\mathrm{t}}$) effectively minimise both the total length (${\mathrm{L}}_{\mathrm{tot}}$) and mass (${\mathrm{m}}_{\mathrm{tot}}$) of the heat exchanger. Based on this, the optimal design point has been selected with ${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{out}}$ = 273.15 K, ${\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$ = 130 K and ${\mathrm{n}}_{\mathrm{t}}$ = 90.

Table 9. Values of thermodynamic and geometric input variables for the selected design point.

	Parameter	Symbol	Design Point Value [Unit]
Input Thermodynamic Variables	N2 outlet main heater temperature	${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{o}\mathrm{u}\mathrm{t}}$	273.15 [K]
	Temperature difference between N2 entering and H2 exiting the main heater	$\mathsf{\Delta }{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$	130 [K]
Input Geometric Variables	Number of pipes (both subunits)	${\mathrm{n}}_{\mathrm{t}}$	90 [-]

specifies the thermodynamic and geometric input variable values corresponding to the optimal design point.

Considering the thermodynamic input values for N₂ corresponding to the optimal design point from Table 9 and the assumed values from Table 4, along with the input values for H₂ provided in Table 3 (to meet the take-off phase requirements), the corresponding enthalpies for the H₂ and N₂ circuits, as calculated by the thermodynamic model using CoolProp, are presented in

Table 10. Enthalpies for the input thermodynamical values of H₂ and N₂.

	Parameter	Symbol	Value [Unit]
H2 circuit	LH2 inlet enthalpy (from main fuel pump)	${\mathrm{h}}_{{\mathrm{H}}_2}^{\mathrm{in}}$	148.7 [kJ/kg]
	GH2 outlet enthalpy (to metering valve)	${\mathrm{h}}_{{\mathrm{H}}_2}^{\mathrm{out}}$	5264 [kJ/kg]
N2 circuit	N2 inlet enthalpy (to main heater)	${\mathrm{h}}_{{\mathrm{N}}_2}^{\mathrm{in}}$	522.5 [kJ/kg]
	N2 outlet enthalpy (from main heater)	${\mathrm{h}}_{{\mathrm{N}}_2}^{\mathrm{out}}$	265.8 [kJ/kg]

. It is important to note that the thermodynamic model also incorporates the input geometric parameters of the pipes (for both subunits) from Table 6, considers the properties of stainless steel 316 for the pipes (for both subunits) from Table 5, and uses the optimal number of pipes (for both subunits), as previously obtained and specified in Table 9.

Additionally, the results from solving Equations (1)–(3), as described earlier in Section 3.1, are presented in

Table 11. Heat exchange calculations for the pre-heater and main heater subunits.

	Parameter	Symbol	Value [Unit]
H2 circuit	Vaporised H2 outlet temperature (from pre-heater)	${\mathrm{T}}_{{\mathrm{H}}_2}^{\mathrm{out},\mathrm{pre}}$	47.6 [K]
	Vaporised H2 outlet enthalpy (from pre-heater)	${\mathrm{h}}_{{\mathrm{H}}_2}^{\mathrm{out},\mathrm{pre}}$	457.14 [kJ/kg]
	Thermal Power absorbed by LH2 (in the pre-heater)	${\dot{\mathrm{Q}}}_{{\mathrm{LH}}_2}^{\mathrm{pre}}$	126.75 [kW]
	GH2 outlet temperature (from main heater)	${\mathrm{T}}_{{\mathrm{H}}_2}^{\mathrm{out},\mathrm{main}}$	374 [K]
	GH2 outlet enthalpy (from main heater)	${\mathrm{h}}_{{\mathrm{H}}_2}^{\mathrm{out},\mathrm{main}}$	5572.5 [kJ/kg]
	Thermal Power absorbed by GH2 (in the main heater)	${\dot{\mathrm{Q}}}_{{\mathrm{GH}}_2}^{\mathrm{main}}$	2102.4 [kW]
	Thermal Power released by GH2 (in the pre-heater)	${\dot{\mathrm{Q}}}_{{\mathrm{GH}}_2}^{\mathrm{pre}}$	−126.75 [kW]
N2 circuit	N2 mass flow rate (in the main heater)	${\dot{\mathrm{m}}}_{{\mathrm{N}}_2}$	8.19 [kg/s]
	Thermal Power released by N2 (in the main heater)	${\dot{\mathrm{Q}}}_{{\mathrm{N}}_2}^{\mathrm{main}}$	−2102.4 [kW]

. These outcomes, which are detailed below, also include the thermal powers absorbed/released by the cold/hot fluids in both subunits:

• The temperatures and enthalpies of H₂ at the outlets of the pre-heater and main heater subunits.
• The required mass flow rate of N₂ in the main heater subunit.
• The thermal power is absorbed by LH₂ and released by GH₂ in the pre-heater subunit.
• The thermal power is absorbed by GH₂ and released by N₂ in the main heater subunit.

These data provide a comprehensive evaluation of the heat exchange process.

With the thermodynamic data for the heat exchange in both subunits fully determined, the trends of the thermodynamic states of H₂ and N₂ throughout the pre-heater and main heater subunits can be analysed. Figure 9 illustrates these thermodynamic transformations for both fluids on a temperature–entropy (T-s) diagram, with Figure 9a detailing the transformations for H₂ and Figure 9b for N₂. It is evident that no two-phase or cyclic behaviours occur during heat exchange, as both fluids are handled at supercritical pressure values.

Furthermore, Figure 10 illustrates the temperature–thermal power plots for both the pre-heater (Figure 10a) and the main heater (Figure 10b), based on the identified optimal design point. It is evident that this depiction, which includes the calculated data (quantitative graphs), is analogous to Figure 4, which instead presents a qualitative graph.

In conclusion,

Table 12. Key performance parameters and pressure drops across the pipes (for both subunits) calculated at the optimal design point.

	Parameter	Symbol	Value [Unit]
Pre-heater	Length	${\mathrm{L}}_{\mathrm{pre}}$	0.141 [m]
	Mass	${\mathrm{m}}_{\mathrm{pre}}$	6.711 [kg]
	Volume	${\mathrm{V}}_{\mathrm{pre}}$	9.25$\times {10}^{-6}$ [m3]
	Pressure drops hot fluid (GH2)	${\mathsf{\Delta }\mathrm{p}}_{\mathrm{h}}^{\mathrm{pre}}$	5.74 $\times {10}^{-5}$ [bar]
	Pressure drops cold fluid (LH2)	${\mathsf{\Delta }\mathrm{p}}_{\mathrm{c}}^{\mathrm{pre}}$	1.02$\times {10}^{-4}$ [bar]
Main heater	Length	${\mathrm{L}}_{\mathrm{main}}$	8.525 [m]
	Mass	${\mathrm{m}}_{\mathrm{main}}$	406.2 [kJ/kg]
	Volume	${\mathrm{V}}_{\mathrm{main}}$	5.60$\times {10}^{-4}$ [m3]
	Pressure drops hot fluid (N2)	${\mathsf{\Delta }\mathrm{p}}_{\mathrm{h}}^{\mathrm{main}}$	0.064 [bar]
	Pressure drops cold fluid (GH2)	${\mathsf{\Delta }\mathrm{p}}_{\mathrm{c}}^{\mathrm{main}}$	0.059 [bar]

summarises the key performance parameters of the heat exchanger for both the pre-heater and main heater subunits, along with the pressure drop across the pipes for both the hot and cold fluids.

The length of the pre-heater is smaller (0.141 m) because the temperature difference between the two fluids is larger in the main heater. In both subunits, the pressure drops are negligible, as the optimal design point analysis was constrained to ensure a pressure drop of Δp ≤ 0.1 bar for the hot and cold fluid.

Based on the values in Table 12, the total length, mass, and volume of the heat exchanger pipes are ${\mathrm{L}}_{\mathrm{tot}}=8.666\mathrm{m}$, ${\mathrm{m}}_{\mathrm{tot}}=412.9\mathrm{kg}$ and ${\mathrm{V}}_{\mathrm{tot}}=5.69\times {10}^{-4}{\mathrm{m}}^3$, respectively. These performance parameters are suitable for a fuel system application.

Moreover, with the heat exchanger’s thermal power requirement at approximately 2 MW [34] and the theoretical power generated by fuel combustion at around 48 MW, it is possible to conclude that the system is feasible. Specifically, the novel cryogenic heat exchanger operates with a negligible cost for energy use, as it only needs 4% of the thermal power generated by the engine. This is particularly efficient when considering that the overall efficiency of an aircraft engine is around 40%.

5. Conclusions

This paper proposed a nitrogen–hydrogen heat exchanger, which can be employed in an innovative hydrogen-propelled aircraft fuel system recently proposed by the authors. The novel cryogenic heat exchanger is designed to vaporise and superheat LH₂ using heat recovered from the turbine EGs of an aircraft. Specifically, the study focused on the design of the heat exchanger architecture, modelling the pre-heater and main heater subunits, with particular attention to the performance requirements for the critical take-off phase. The system employed a pipe-in-pipe architecture and was modelled using a comprehensive thermodynamic model. The latter incorporated rigorously validated equations and utilised the CoolProp libraries for accurate thermodynamic calculations.

Austenitic stainless steel 316 was selected for the piping of both heat exchanger subunits due to their resistance to H₂ embrittlement and stability under high pressure.

The heat exchanger design was optimised by varying three key input parameters: the outlet N₂ temperature from the main heater (${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{out}}$), the temperature difference between the inlet N₂ and outlet H₂ temperatures at the main heater ($\mathsf{\Delta }{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}$), and the number of pipes in both the pre-heater and main heater subunits (${\mathrm{n}}_{\mathrm{t}}$). The process was conducted using Esteco modeFRONTIER 2019 software, with a constraint that pressure drops across the pipes remained below Δp ≤ 0.1 bar for both cold and hot fluids. This ensured that the heat exchange process in both subunits could be treated as isobaric.

The results of calculations showed that for the optimal design point (${\mathrm{T}}_{{\mathrm{N}}_2}^{\mathrm{out}}=273.15\mathrm{K}$, $\mathsf{\Delta }{\mathrm{T}}_{{\mathrm{N}}_2^{\mathrm{in}}-{\mathrm{H}}_2^{\mathrm{out},\mathrm{main}}}=130\mathrm{K}$ and ${\mathrm{n}}_{\mathrm{t}}=90$) the performance parameters were ${\mathrm{L}}_{\mathrm{tot}}=8.666\mathrm{m}$, ${\mathrm{m}}_{\mathrm{tot}}=412.9\mathrm{kg}$ and ${\mathrm{V}}_{\mathrm{tot}}=5.69\times {10}^{-4}{\mathrm{m}}^3$, respectively, which demonstrated the plant’s feasibility for aircraft fuel system applications. Additionally, the system feasibility is also supported by the fact that the heat exchanger requires approximately 2 MW of thermal power, which is well within the available 48 MW generated by fuel combustion.

In conclusion, this work provides a robust foundation for future advancements in sustainable aviation, as it provides the design of one of the key components of the next hydrogen-propelled aircraft. Further studies will include a thermal stress analysis to assess the impact of temperature gradients on the strength and lifespan of pipeline materials (for both subunits) during the heat exchange process.