Numerical Simulation of Convective Heat Transfer in Gyroid, Diamond, and Primitive Microstructures Using Water as the Working Fluid
Abstract
1. Introduction
2. Function Representation of TPMS
3. Physical Control Equations
4. Numerical Analysis for Microstructure
4.1. Controllability Construction of TPMS
4.2. The Construction Method of Fluid Heat Transfer Model for TPMS Microstructure
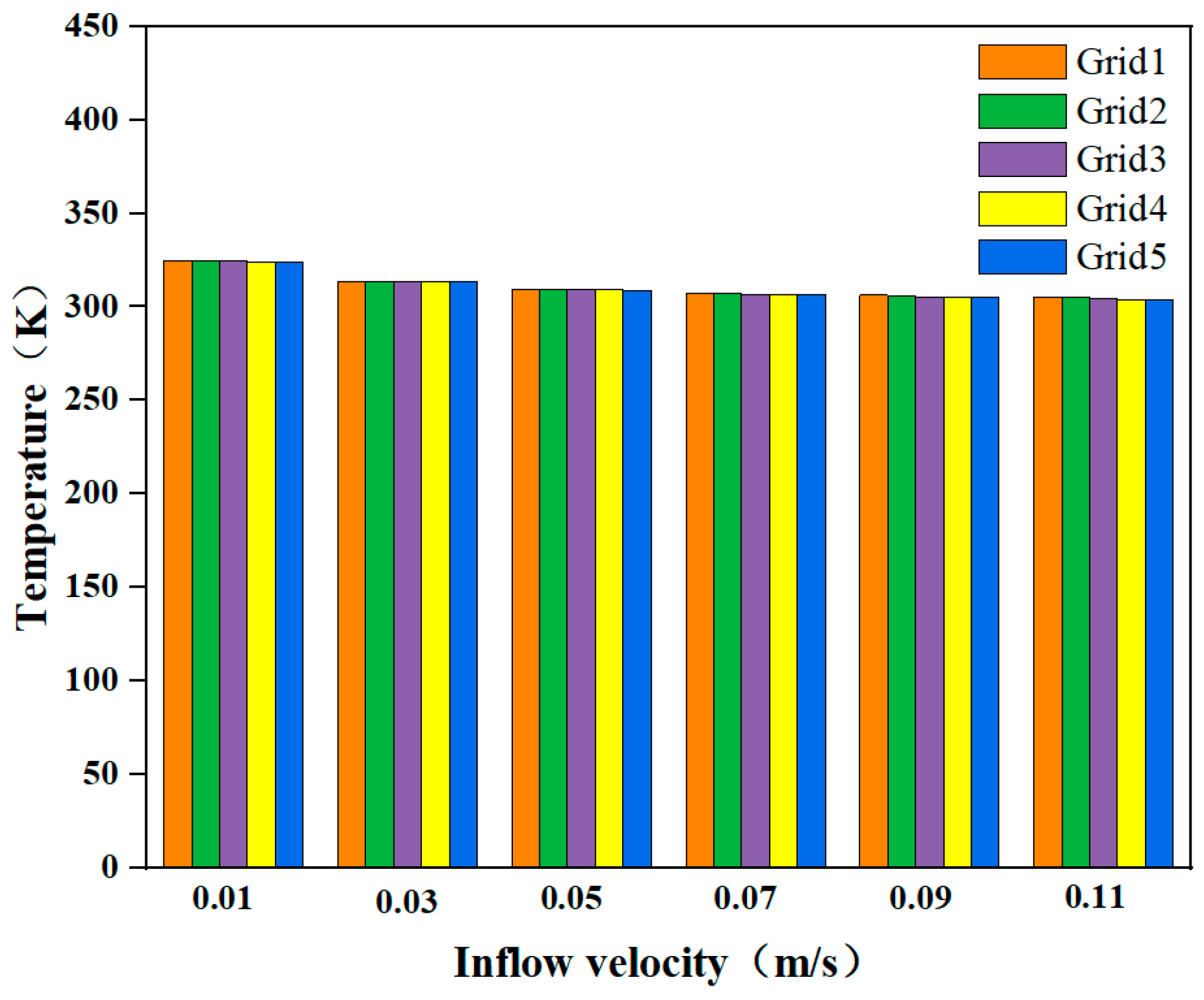
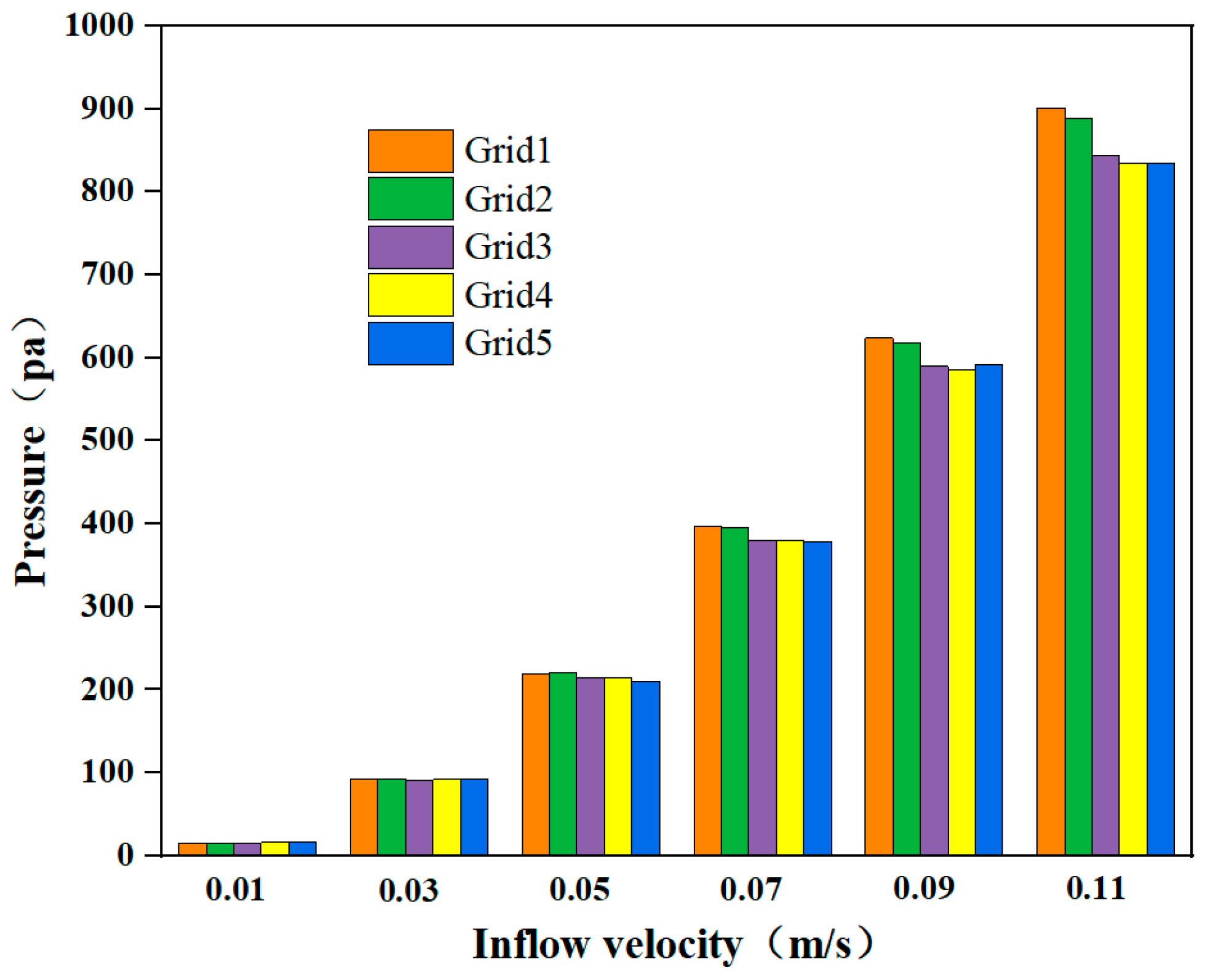
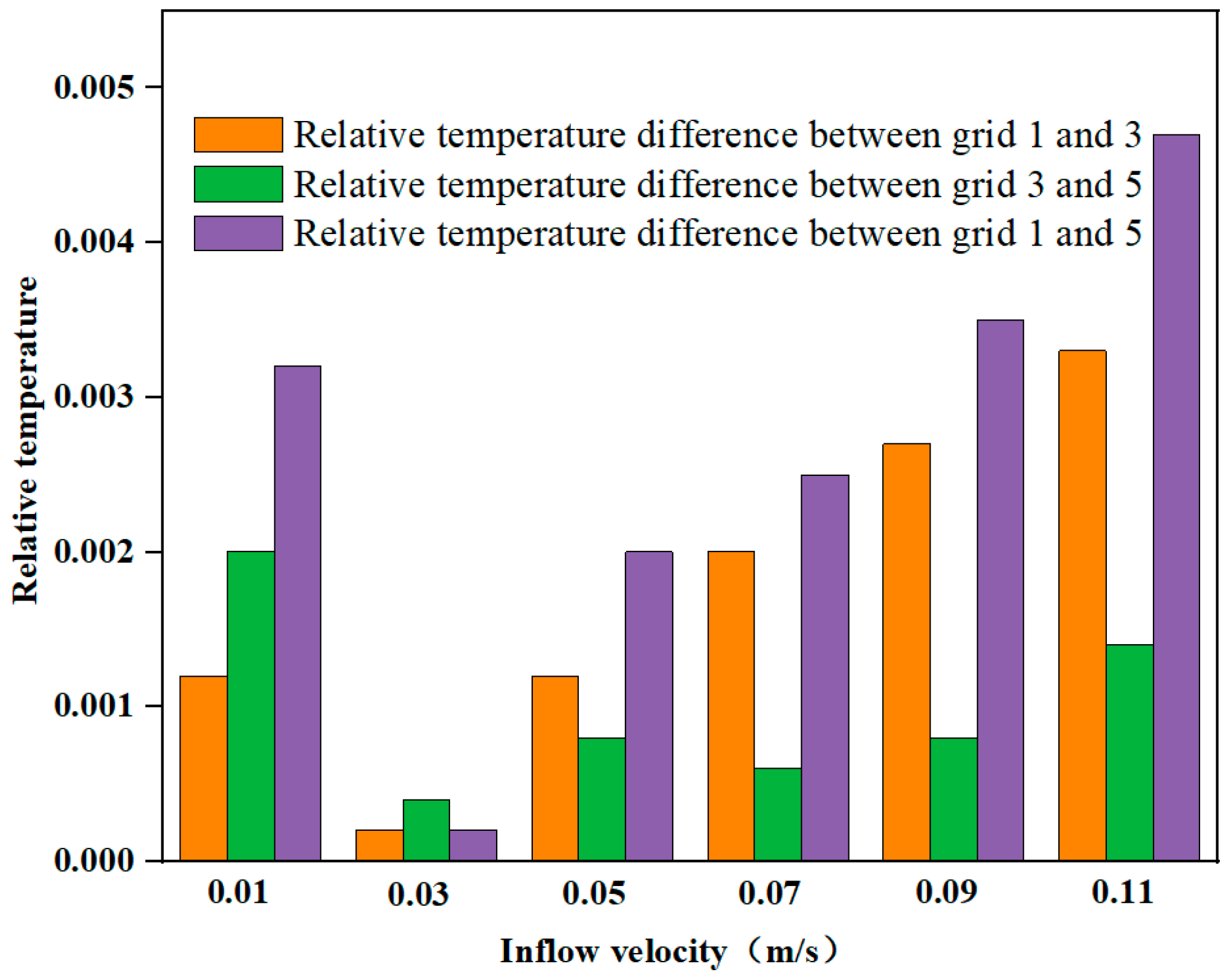
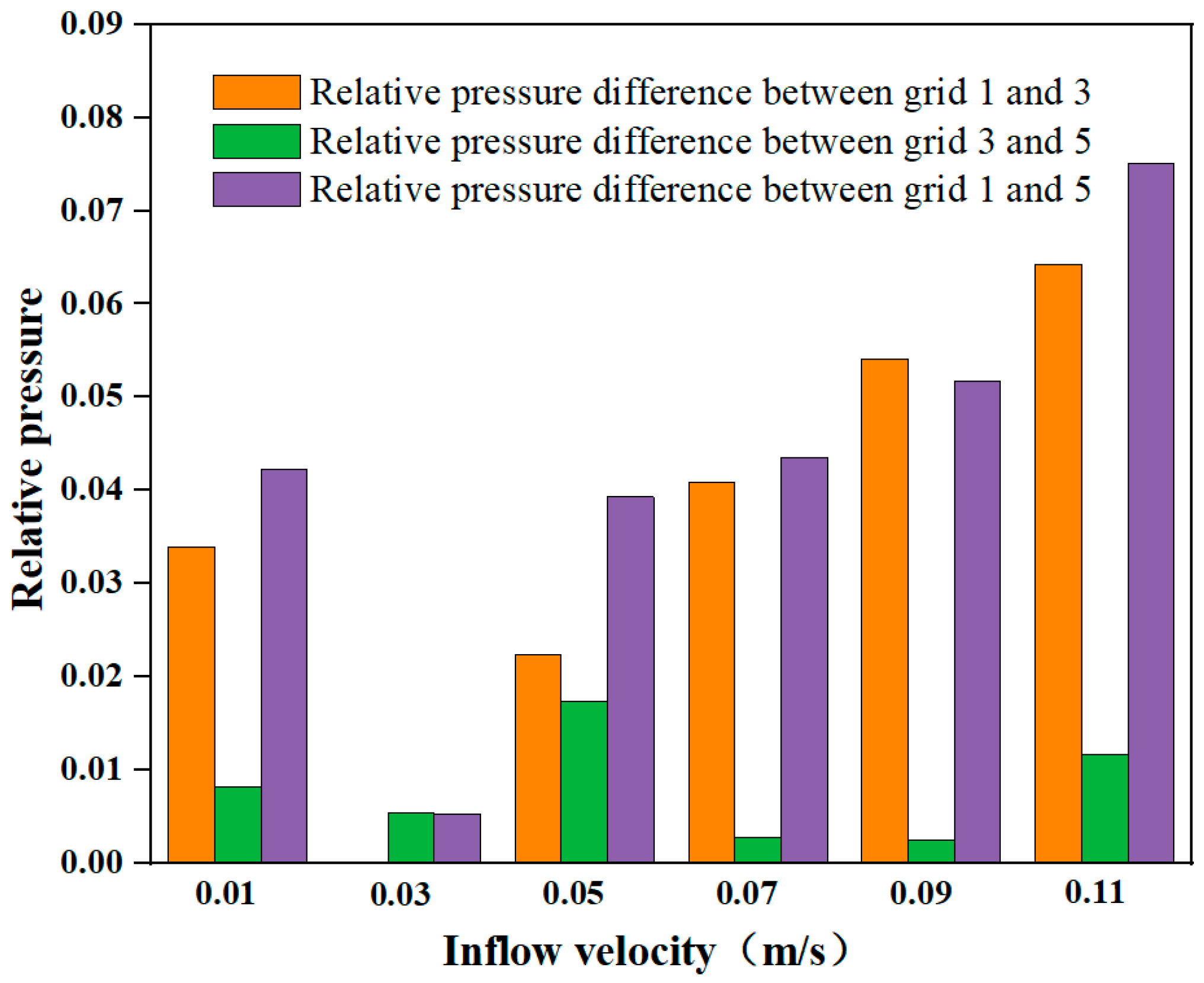
4.3. Grid Independence Test
4.4. Flow and Heat Transfer Processes in TPMS Microfluidic Heat Transfer Model
4.4.1. Flow Characteristic
4.4.2. Heat Transfer Characteristics
5. Numerical Simulation Evaluation of Convective Heat Transfer Performance of the TPMS Microstructure
6. Summary and Conclusions
- (1)
- For the same structure, the inlet velocity increases, pressure , , increase, and outlet temperature , decreases.
- (2)
- Within the speed range studied in this article, this paper finds that D1 and D2 have similar outlet temperatures , and , but D1’s structural pressure and average wall friction factor are far greater than D2. That is, the heat transfer capability is D1 ≈ D2 > G > P. The required power consumption is D1 > D2 > G ≈ P.
- (3)
- When flow velocity is 0.01 m/s, the maximum temperature difference at the outlet of the four structures reached 17.14 °C, and the maximum difference in wall friction had a relative change of 646%. When flow velocity was 0.11 m/s, the maximum pressure difference among the four structures reached 8461.84 Pa, and the maximum difference in had a relative change of 63.36%, The maximum difference between had a relative change of 62.09%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| TPMS | Three Period Minimum Surface |
| G | Gyroid |
| D1 | Diamond 1 |
| D2 | Diamond 2 |
| P | Primitive |
| Average curvature | |
| Real part | |
| Imaginary unit | |
| θ | Bonnet angle |
| Rτ | Weierstrass function |
| c | TPMS threshold |
| Density, Kg/(m3) | |
| The specific heat capacity of the material at constant pressure, J/(Kg·K) | |
| Temperature, K | |
| t | Time, s |
| k | Thermal conductivity, W/(m·K) |
| Heat generation rate, W/(m3) | |
| Gradient, | |
| Laplace operator, | |
| Velocity vector | |
| Pressure, Pa | |
| Identity matrix | |
| Viscous stress tensor, Pa | |
| Volume forces, N | |
| Viscous dissipation term | |
| Reynolds number | |
| Characteristic length, m | |
| μ | Dynamic viscosity coefficient, Pa·s |
| Porosity | |
| Total volume, m3 | |
| Total volume of the pores within the porous structure, m3 | |
| Total volume of the solid portion within the porous structure, m3 | |
| The pore volume of the TPMS unit, m3 | |
| The total volume of the TPMS units, m3 | |
| Average convective heat transfer coefficient, W/(m2·K) | |
| Nusselt number | |
| Wall friction factor | |
| Inlet area, m2 | |
| The temperature difference between the outlet and inlet of the structure, K | |
| Outlet area, m2 | |
| The temperature of the constant temperature wall, K | |
| The qualitative temperature of the fluid, K | |
| Inlet temperature, K | |
| Outlet temperature, K | |
| The length of the flow channel, m |
References
- Deng, Y.; Feng, C.; Jiaqiang, E.; Zhu, H.; Chen, J.; Wen, M.; Yin, H. Effects of different coolants and cooling strategies on the cooling performance of the power lithium-ion battery system: A review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar] [CrossRef]
- Rahman, S.I.; Moghassemi, A.; Arsalan, A.; Timilsina, L.; Chamarthi, P.K.; Papari, B.; Ozkan, G.; Edrington, C.S. Emerging trends and challenges in thermal management of power electronic converters: A state of the art review. IEEE Access 2024, 12, 50633–50672. [Google Scholar] [CrossRef]
- Orville, T.; Tajwar, M.; Bihani, R.; Saha, P.; Hannan, M.A. A review of techniques for effective thermal management in power electronics. SSRN Electron. J. 2024. [Google Scholar] [CrossRef]
- Hamida, M.B.B.; Hatami, M. Optimization of fins arrangements for the square light emitting diode (LED) cooling through nanofluid-filled microchannel. Sci. Rep. 2021, 11, 12610. [Google Scholar] [CrossRef] [PubMed]
- Ben Jaballah, R.; Hamida, M.B.B.; Almeshaal, M.A.; Chamkha, A.J. The influence of hybrid nanofluid and coolant flow direction on bubble mode absorption improvement. Math. Methods Appl. Sci. 2020, 44, 3036–3065. [Google Scholar] [CrossRef]
- Hamida, M.B.B.; Almeshaal, M.A.; Hajlaoui, K.; Rothan, Y.A. A three-dimensional thermal management study for cooling a square light emitting diode. Case Stud. Therm. Eng. 2021, 27, 101223. [Google Scholar] [CrossRef]
- Massoudi, M.D.; Hamida, M.B.B. Enhancement of MHD radiative CNT-50% water + 50% ethylene glycol nanoliquid performance in cooling an electronic heat sink featuring wavy fins. Waves Random Complex Media 2022, 32, 1–26. [Google Scholar] [CrossRef]
- Hamida, M.B. Thermal management of square light emitting diode arrays: Modeling and parametric analysis. Multidiscip. Model. Mater. Struct. 2024, 20, 363–383. [Google Scholar] [CrossRef]
- Hamida, M.B.; Almeshaal, M.A.; Hajlaoui, K. A three-dimensional thermal analysis for cooling a square light emitting diode by multiwalled carbon nanotube-nanofluid-filled in a rectangular microchannel. Adv. Mech. Eng. 2021, 13, 16878140211059946. [Google Scholar] [CrossRef]
- Feng, J.; Fu, J.; Yao, X.; He, Y. Triply periodic minimal surface (TPMS) porous structures from multi-scale design, precise additive manufacturing to multidisciplinary applications. Int. J. Extrem. Manuf. 2022, 4, 022001. [Google Scholar] [CrossRef]
- Han, L.; Che, S. An overview of materials with triply periodic minimal surfaces and related geometry: From biological structures to self-assembled systems. Adv. Mater. 2018, 30, 1705708. [Google Scholar] [CrossRef]
- Hyde, S.; Blum, Z.; Landh, T.; Lidin, S.; Ninham, B.W.; Andersson, S.; Larsson, K. The Language of Shape; Elsevier Science B.V.: Amsterdam, the Netherlands, 1997. [Google Scholar]
- Gado, M.G.; Al-Ketan, O.; Aziz, M.; Al-Rub, R.A.; Ookawara, S. Triply periodic minimal surface structures: Design, fabrication, 3D printing techniques, state-of-the-art studies, and prospective thermal applications for efficient energy utilization. Energy Technol. 2024, 12, 2301287. [Google Scholar] [CrossRef]
- Ali, D.; Ozalp, M.; Blanquer, S.B.; Onel, S. Permeability and fluid flow-induced wall shear stress in bone scaffolds with TPMS and lattice architectures: A CFD analysis. Eur. J. Mech. B/Fluids 2020, 79, 376–385. [Google Scholar] [CrossRef]
- Sean, S.; Phuong, T.; Pier, M. Design and modelling of porous gyroid heatsinks: Influences of cell size, porosity and material variation. Appl. Therm. Eng. 2023, 235, 121296. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, D.Z.; Liu, F.; Jiang, J.; Zhao, M.; Zhang, T. Lattice structures of Cu-Cr-Zr copper alloy by selective laser melting: Microstructures, mechanical properties and energy absorption. Mater. Des. 2020, 187, 108406. [Google Scholar] [CrossRef]
- Cheng, Z.; Xu, R.; Jiang, P. Morphology, flow and heat transfer in triply periodic minimal surface based porous structures. Int. J. Heat Mass Transf. 2021, 170, 120903. [Google Scholar] [CrossRef]
- Wang, J.; Chen, K.; Zeng, M.; Ma, T.; Wang, Q.; Cheng, Z. Investigation on flow and heat transfer in various channels based on triply periodic minimal surfaces (TPMS). Energy Convers. Manag. 2023, 283, 116955. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, H.; Zeng, Y.; Yan, M.; Jiang, C.; Yang, P.; Li, Q.; Li, Z.; Fu, J.; Huang, Y.; et al. Analysis on the convective heat transfer process and performance evaluation of triply periodic minimal surface (TPMS) based on Diamond, Gyroid and IWP. Int. J. Heat Mass Transf. 2022, 201, 123642. [Google Scholar] [CrossRef]
- Tang, W.; Guo, J.; Yang, F.; Zeng, L.; Wang, X.; Liu, W.; Zhang, J.; Zou, C.; Sun, L.; Zeng, Y.; et al. Performance analysis and optimization of the Gyroid-type triply periodic minimal surface heat sink incorporated with fin structures. Appl. Therm. Eng. 2024, 255, 123950. [Google Scholar] [CrossRef]
- Dutkowski, K.; Kruzel, M.; Rokosz, K. Review of the state-of-the-art uses of minimal surfaces in heat transfer. Energies 2022, 15, 7994. [Google Scholar] [CrossRef]
- Yeranee, K.; Rao, Y. A review of recent investigations on flow and heat transfer enhancement in cooling channels embedded with triply periodic minimal surfaces (TPMS). Energies 2022, 15, 8994. [Google Scholar] [CrossRef]
- Qiu, N.; Wan, Y.; Shen, Y.; Fang, J. Experimental and numerical studies on mechanical properties of TPMS structures. Int. J. Mech. Sci. 2024, 261, 108657. [Google Scholar] [CrossRef]
- Savio, G.; Rosso, S.; Meneghello, R.; Concheri, G. Geometric modeling of cellular materials for additive manufacturing in biomedical field: A review. Appl. Bionics Biomech. 2018, 2018, 1654782. [Google Scholar] [CrossRef] [PubMed]
- Lord, E.A.; Mackay, A.L. Periodic minimal surfaces of cubic symmetry. Curr. Sci. 2003, 85, 346–362. [Google Scholar]
- Nitsche, J.C. Lectures on Minimal Surfaces; Cambridge University Press: Cambridge, UK, 1989; Volume 1. [Google Scholar]
- Rajagopalan, S.; Robb, R.A. Schwarz meets Schwann: Design and fabrication of biomorphic and durataxic tissue engineering scaffolds. Med. Image Anal. 2006, 10, 693–712. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Zhu, L.; Li, L.; Li, Z.; Yang, J.; Wang, X. A TPMS-based method for modeling porous scaffolds for bionic bone tissue engineering. Sci. Rep. 2018, 8, 7395. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y. Periodic surface modeling for computer aided nano design. Comput. Aided Des. 2007, 39, 179–189. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R.K. Topology-mechanical property relationship of 3D printed strut, skeletal and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Li, W.; Li, W.; Yu, Z. Heat transfer enhancement of water-cooled triply periodic minimal surface heat exchangers. Appl. Therm. Eng. 2022, 217, 119198. [Google Scholar] [CrossRef]
- Yoo, D.J. Computer-aided porous scaffold design for tissue engineering using triply periodic minimal surfaces. Int. J. Precis. Eng. Manuf. 2011, 12, 61–71. [Google Scholar] [CrossRef]
- Massoudi, M.D.; Hamida, M.B.B.; Mohammed, H.A.; Almeshaal, M.A. MHD heat transfer in W-shaped inclined cavity containing a porous medium saturated with Ag/Al2O3 hybrid nanofluid in the presence of uniform heat generation/absorption. Energies 2020, 13, 3457. [Google Scholar] [CrossRef]
- Ma, S.; Tang, Q.; Feng, Q.; Song, J.; Han, X.; Guo, F. Mechanical behaviours and mass transport properties of bone-mimicking scaffolds consisted of gyroid structures manufactured using selective laser melting. J. Mech. Behav. Biomed. Mater. 2019, 93, 158–169. [Google Scholar] [CrossRef] [PubMed]
- Qian, C.; Wang, J.; Zhong, H.; Qiu, X.; Yu, B.; Shi, J.; Chen, J. Experimental investigation on heat transfer characteristics of copper heat exchangers based on triply periodic minimal surfaces (TPMS). Int. Commun. Heat Mass Transf. 2024, 152, 107292. [Google Scholar] [CrossRef]
- Ali, D.; Sen, S. Finite element analysis of mechanical behavior, permeability and fluid induced wall shear stress of high porosity scaffolds with Gyroid and lattice-based architectures. J. Mech. Behav. Biomed. Mater. 2017, 75, 262–270. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Zhou, W.; Pan, M.Q.; Chen, H.; Liu, W.; Yu, H. Porous copper fiber sintered felts: An innovative catalyst support of methanol steam reformer for hydrogen production. Int. J. Hydrogen Energy 2008, 33, 2950–2956. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, X.; Lu, C.; Wang, Y.; Wen, P.; Shen, Q. Heat transfer efficiency enhancement of gyroid heat exchanger based on multidimensional gradient structure design. Int. Commun. Heat Mass Transf. 2023, 149, 107127. [Google Scholar] [CrossRef]

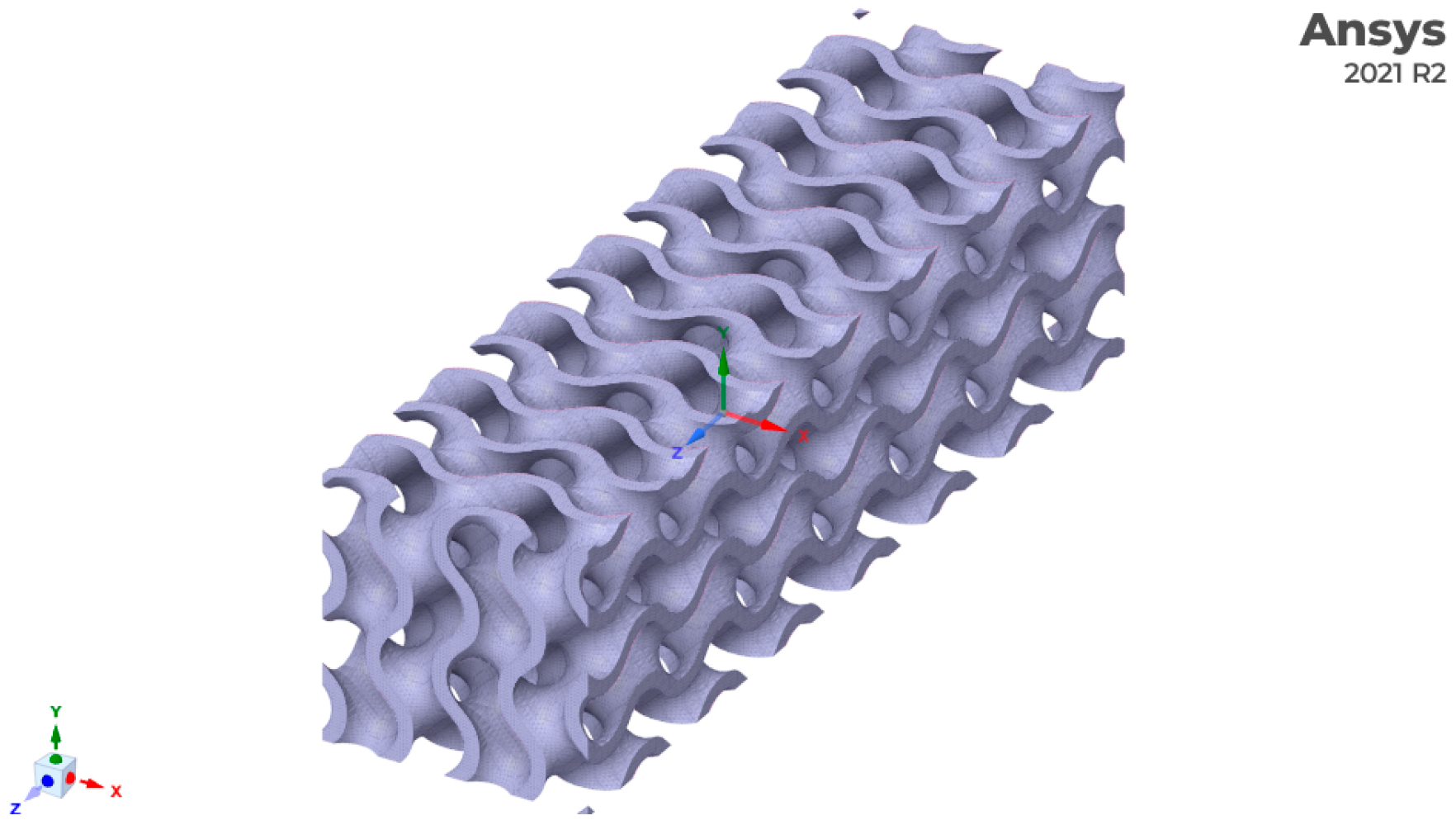

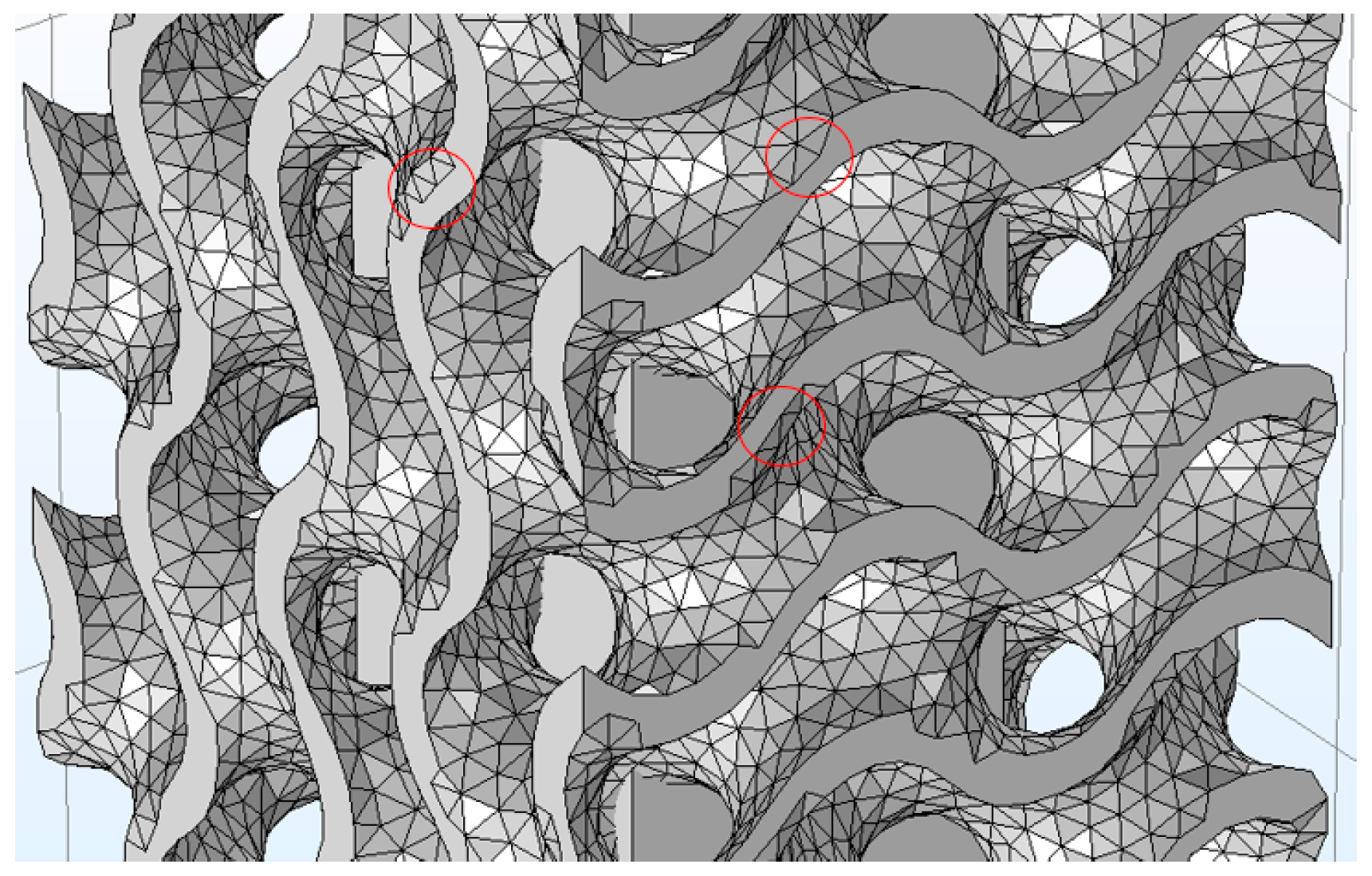
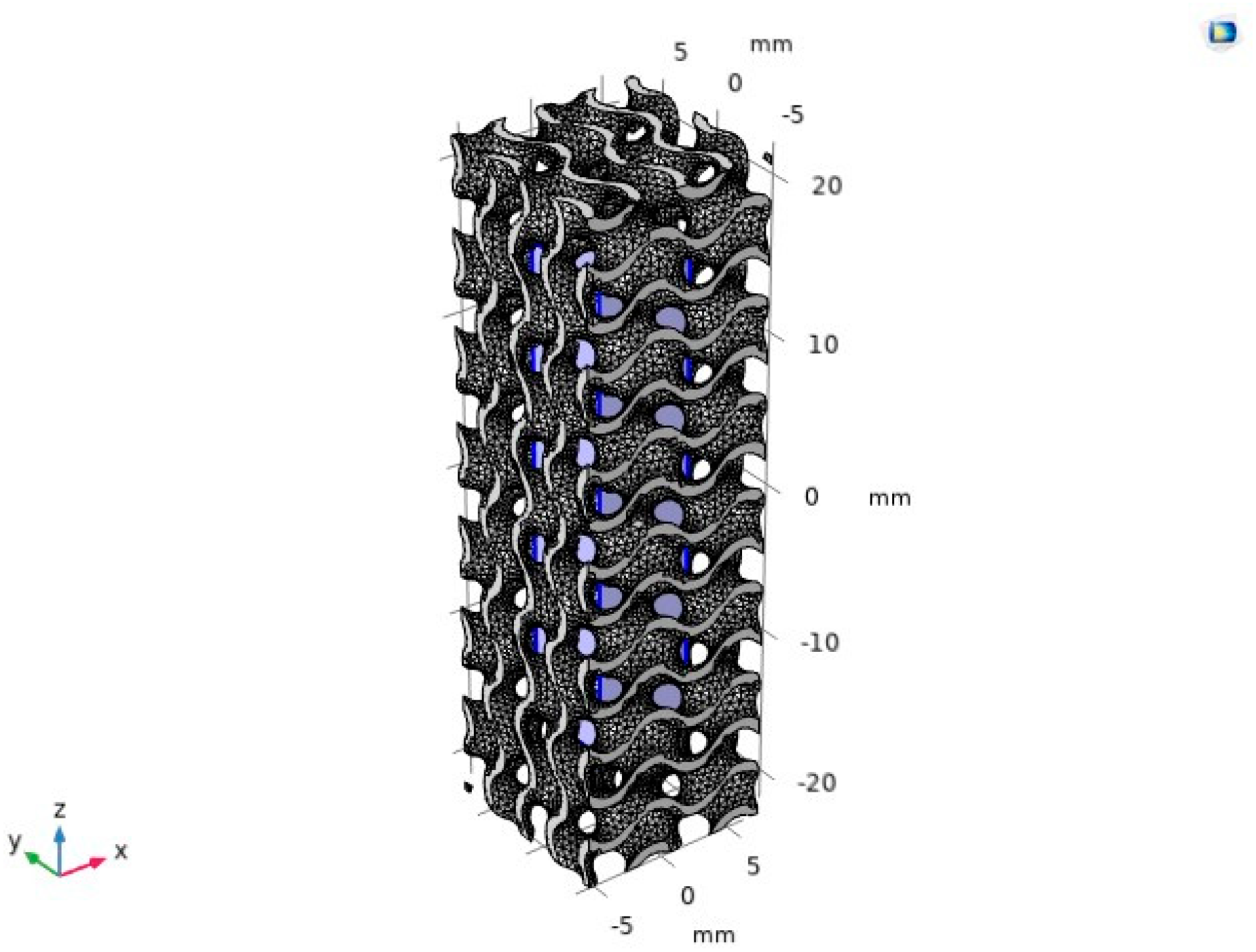
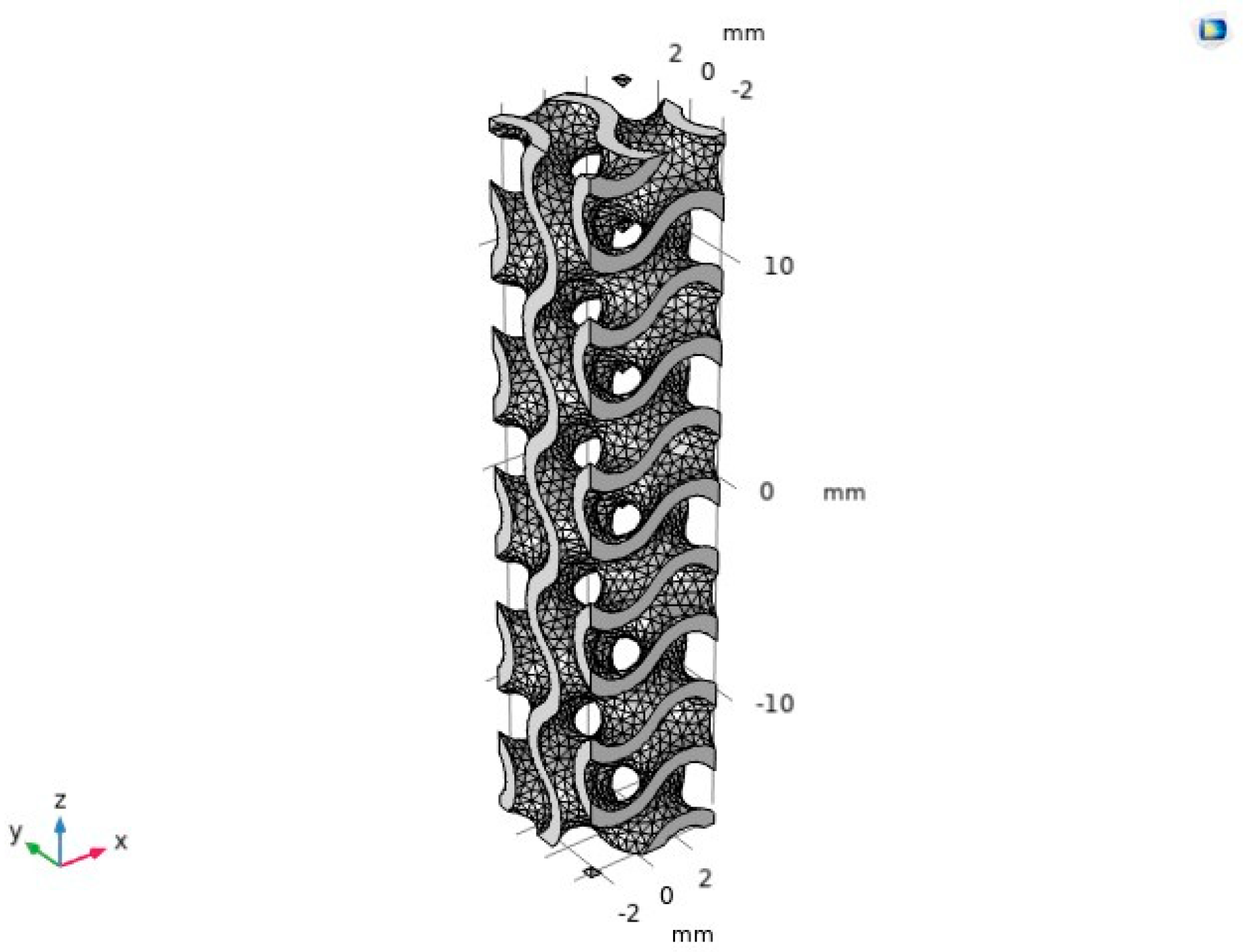
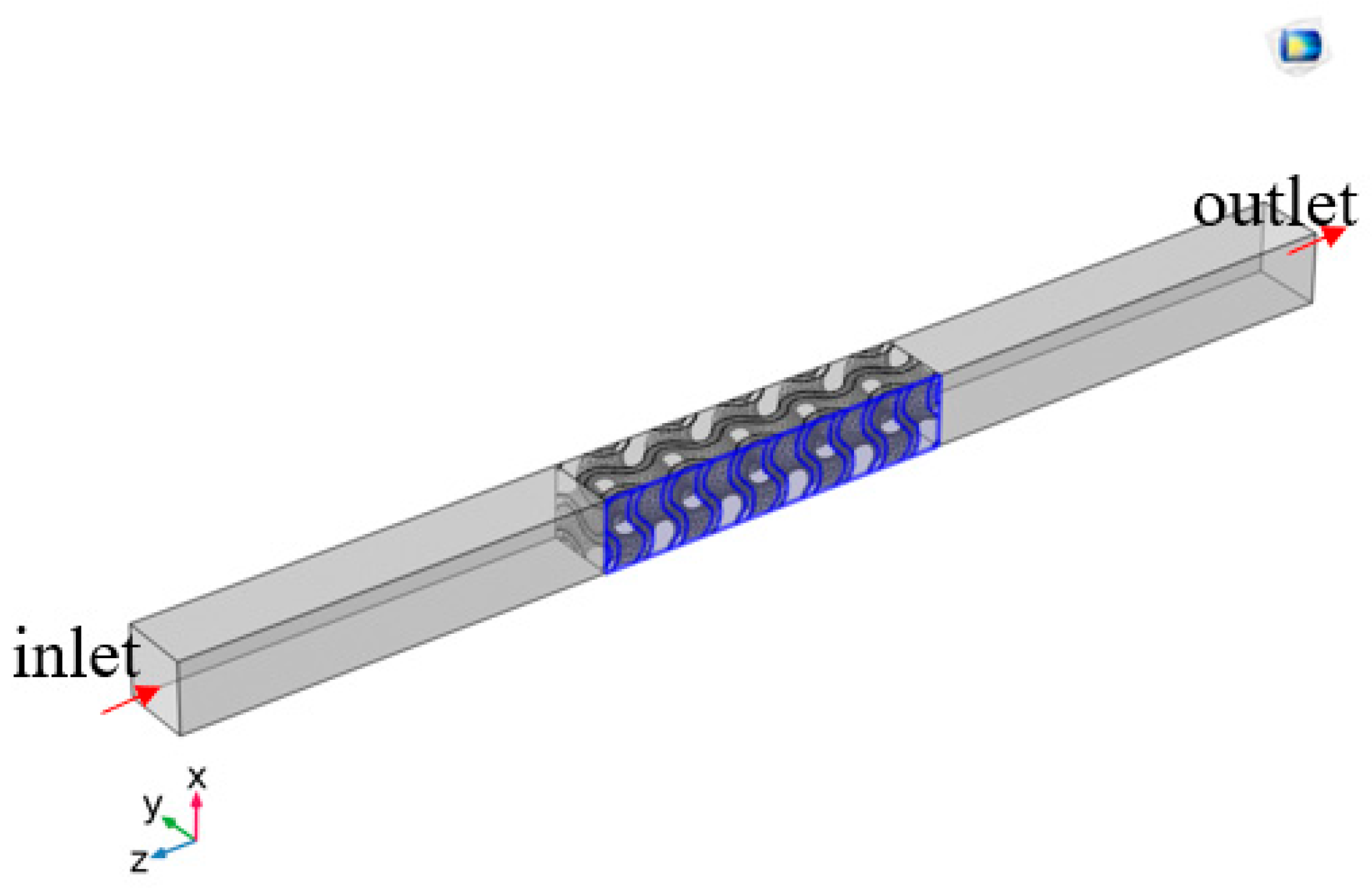


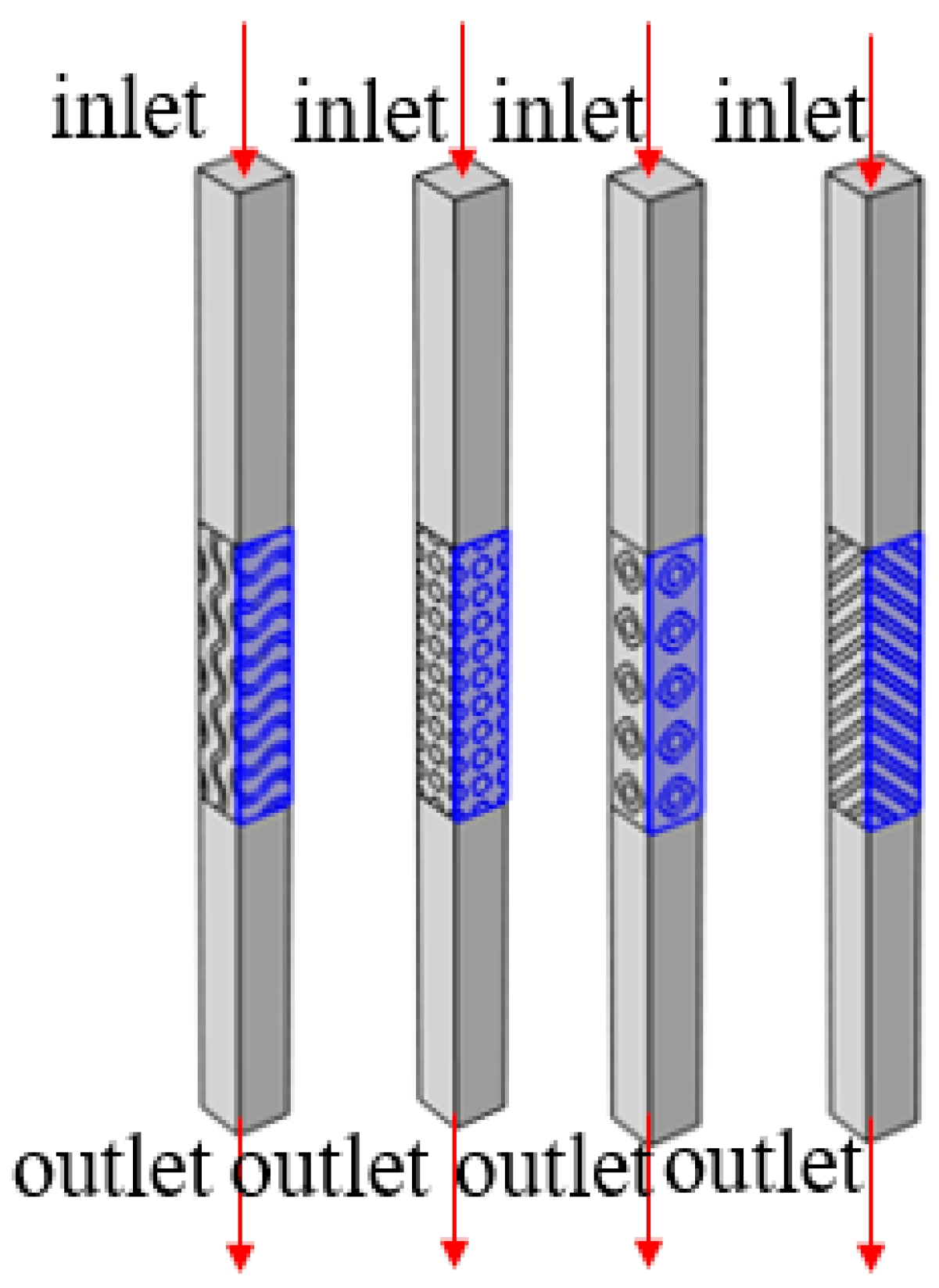


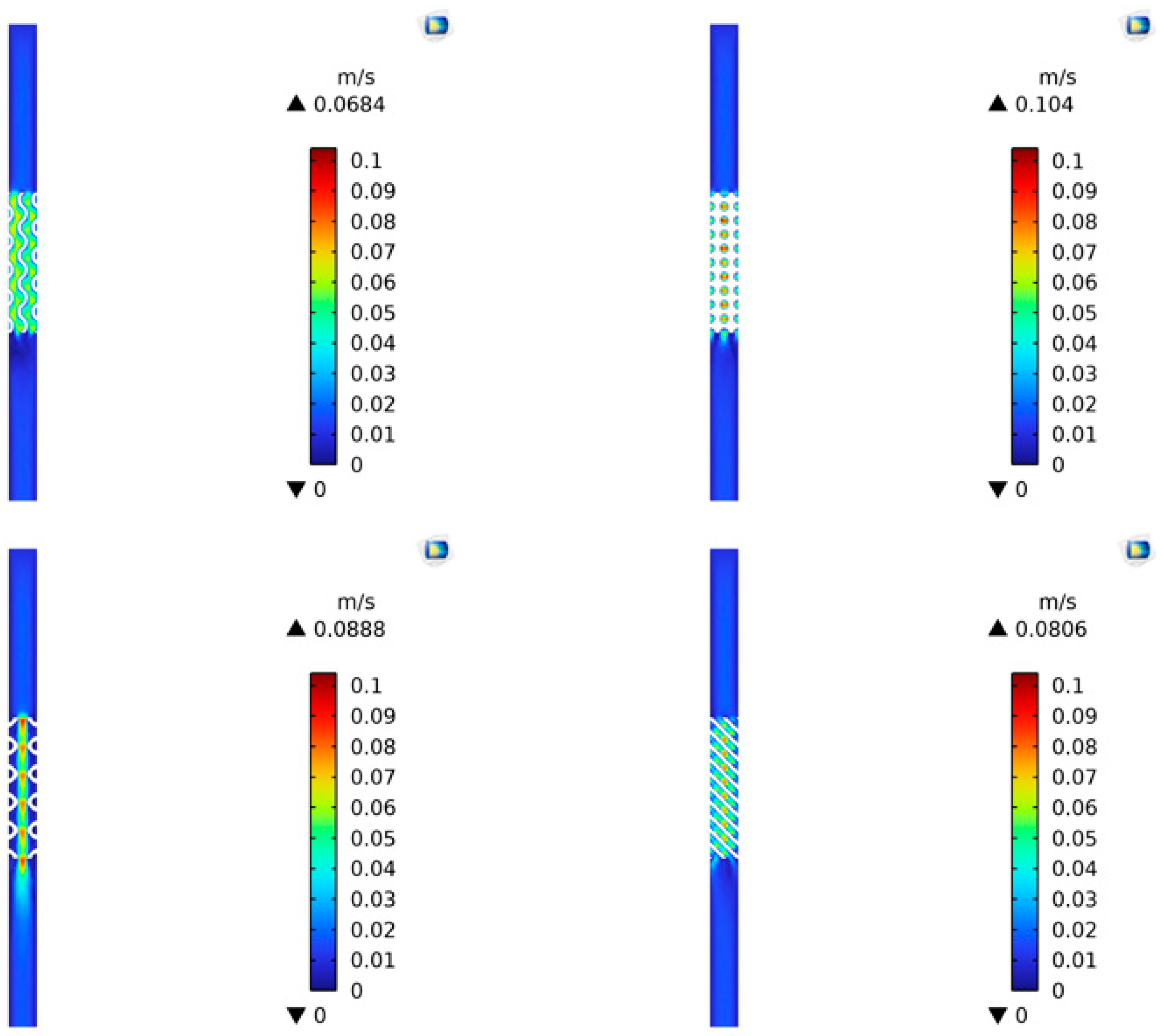
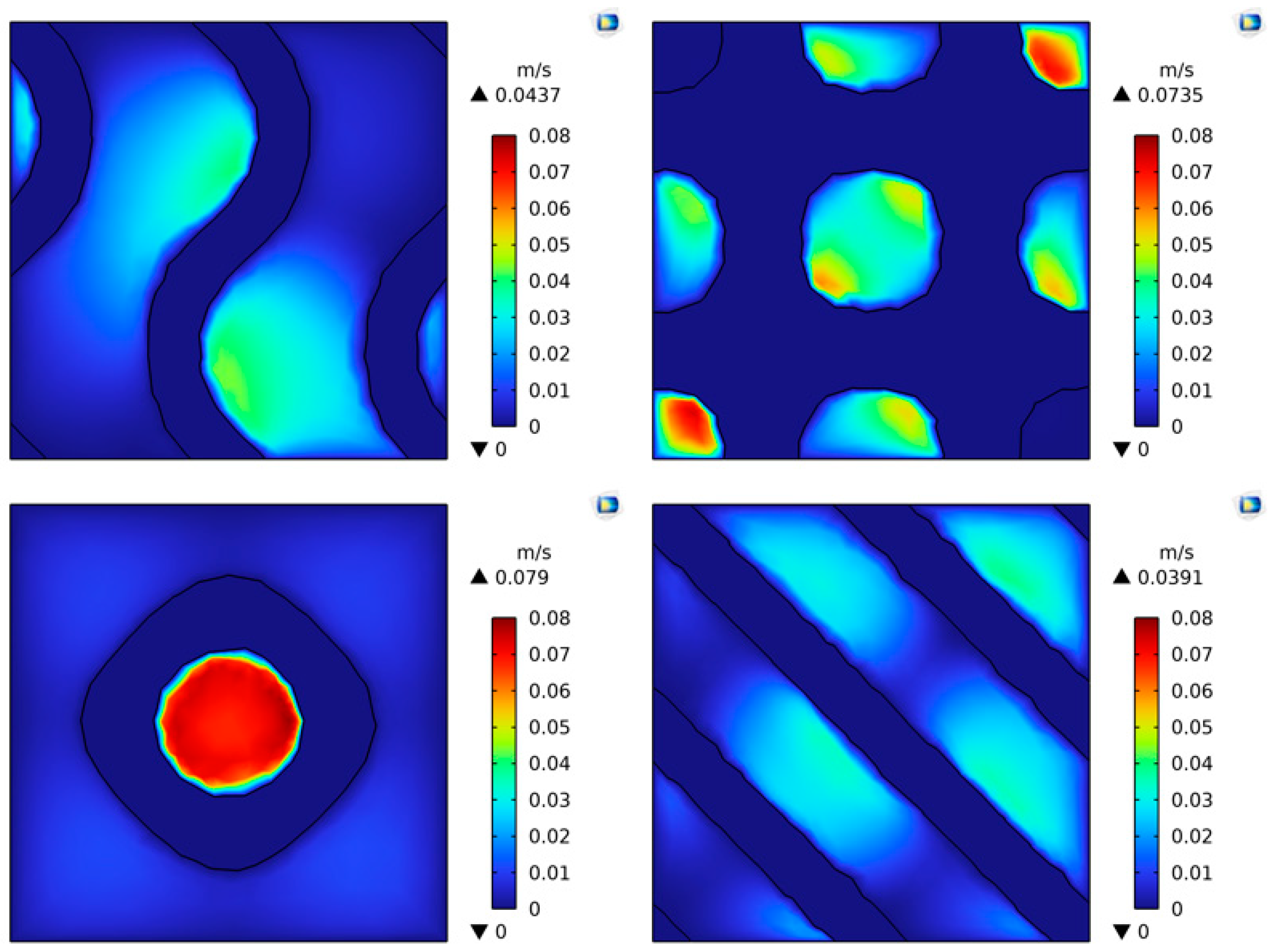

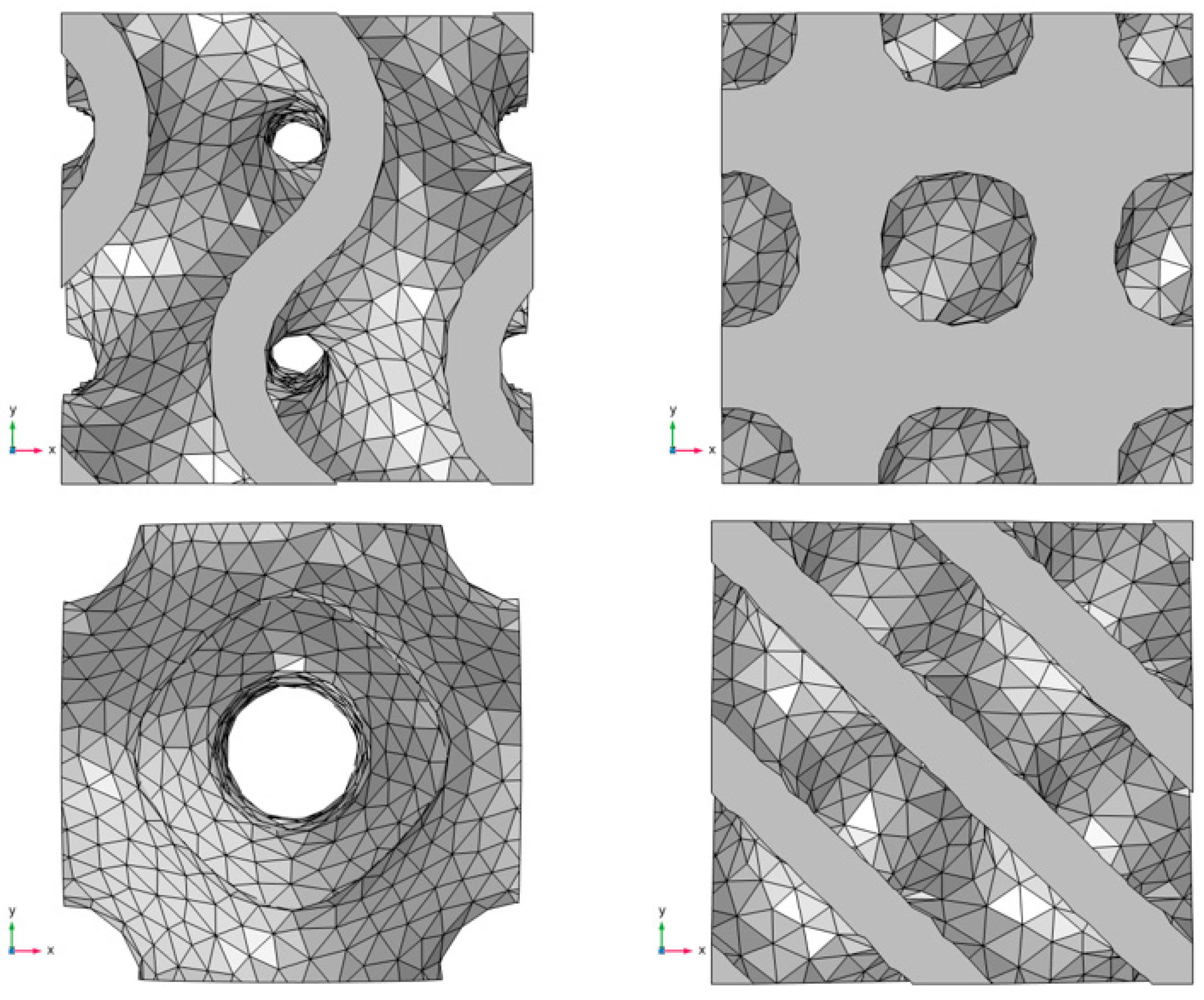
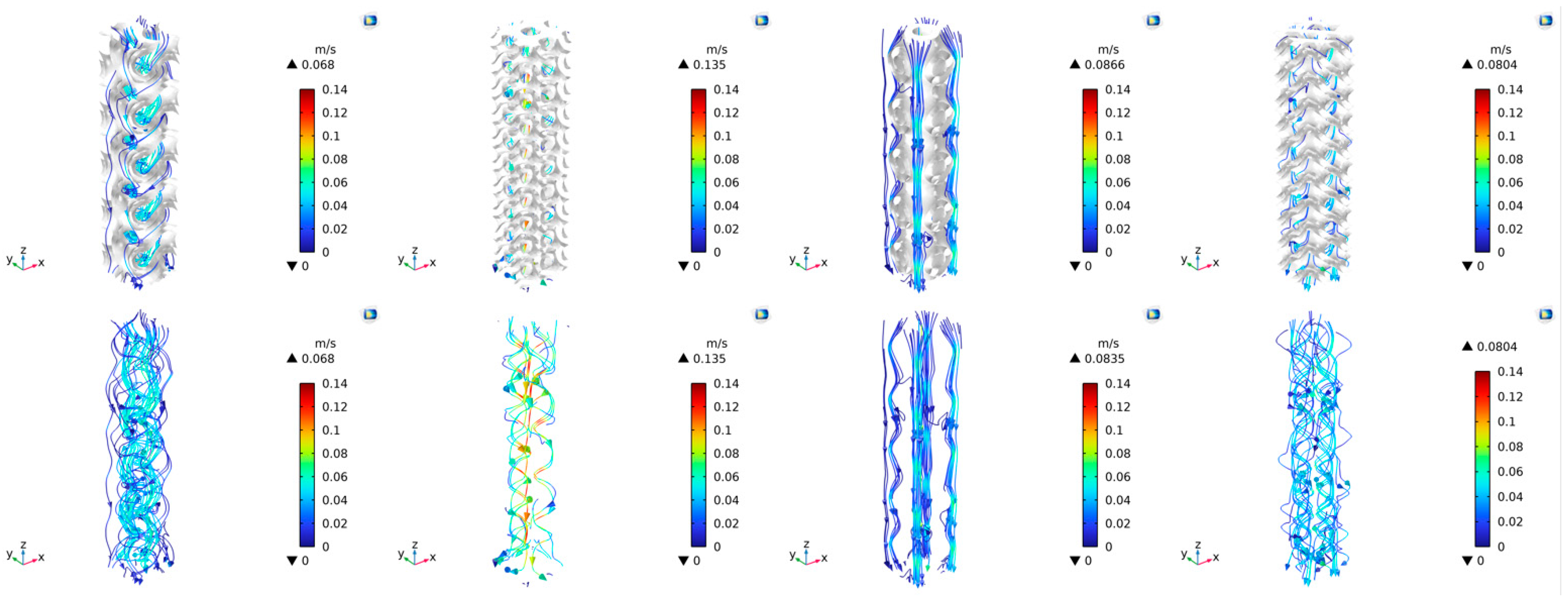
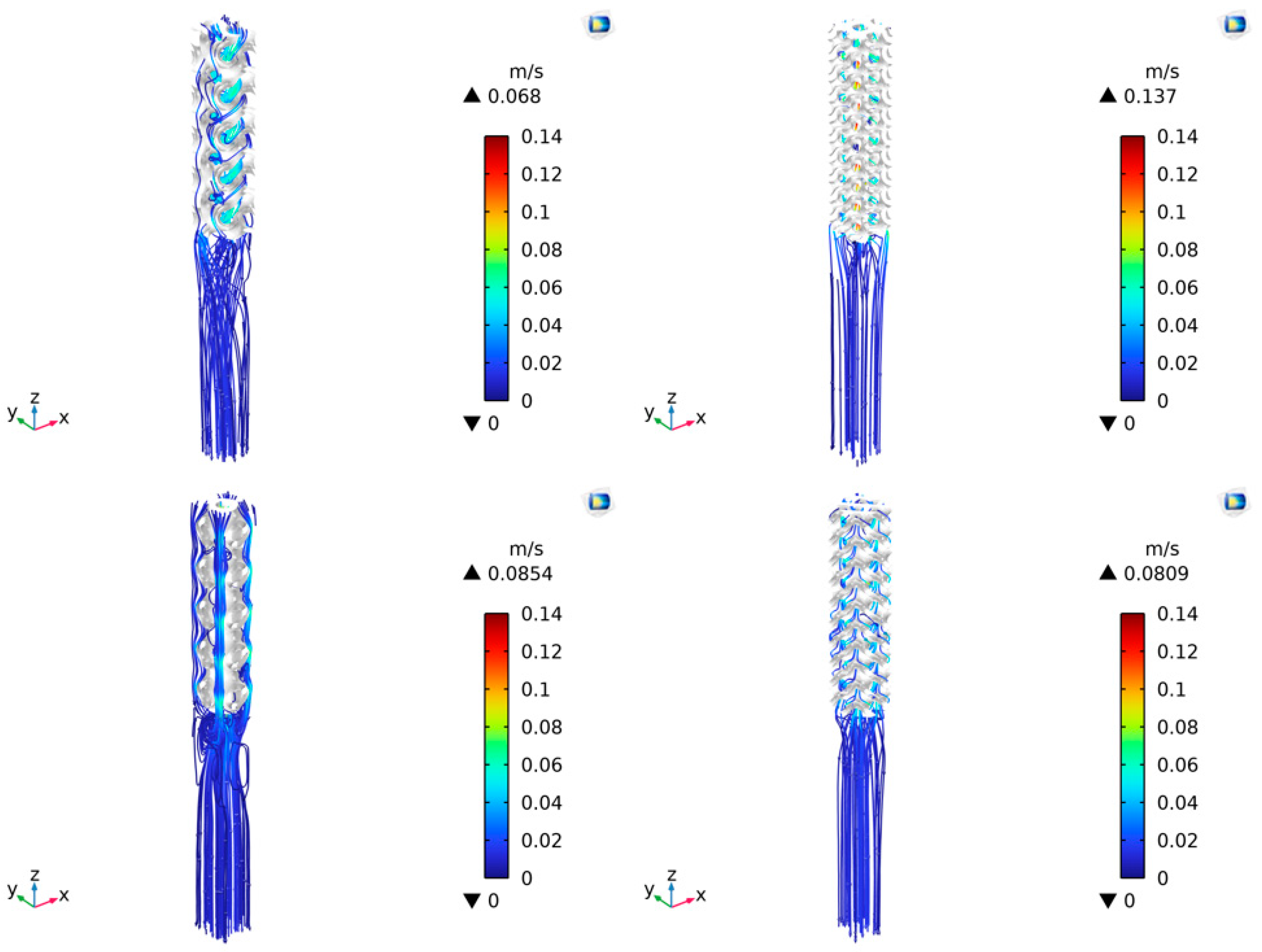

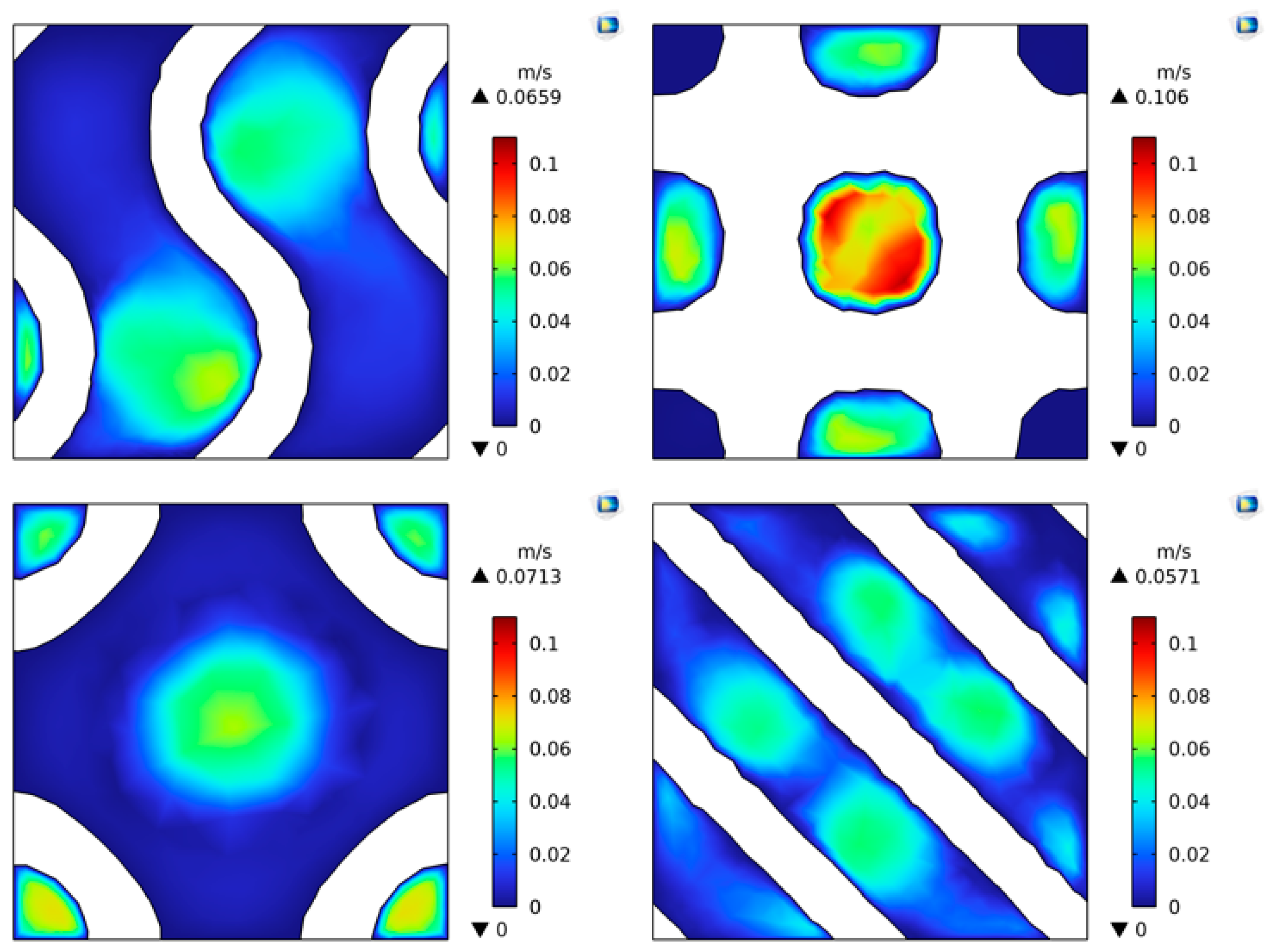

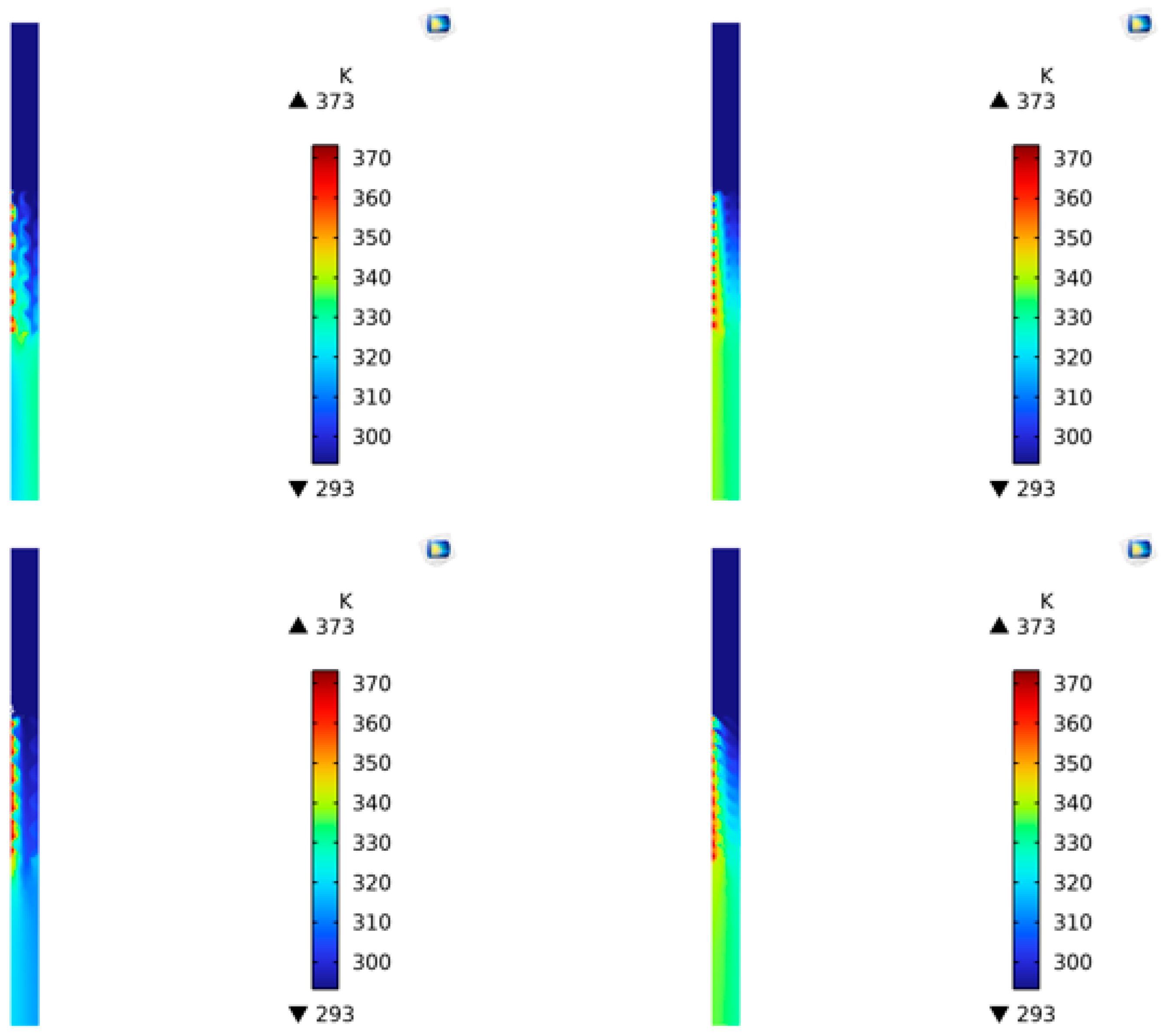

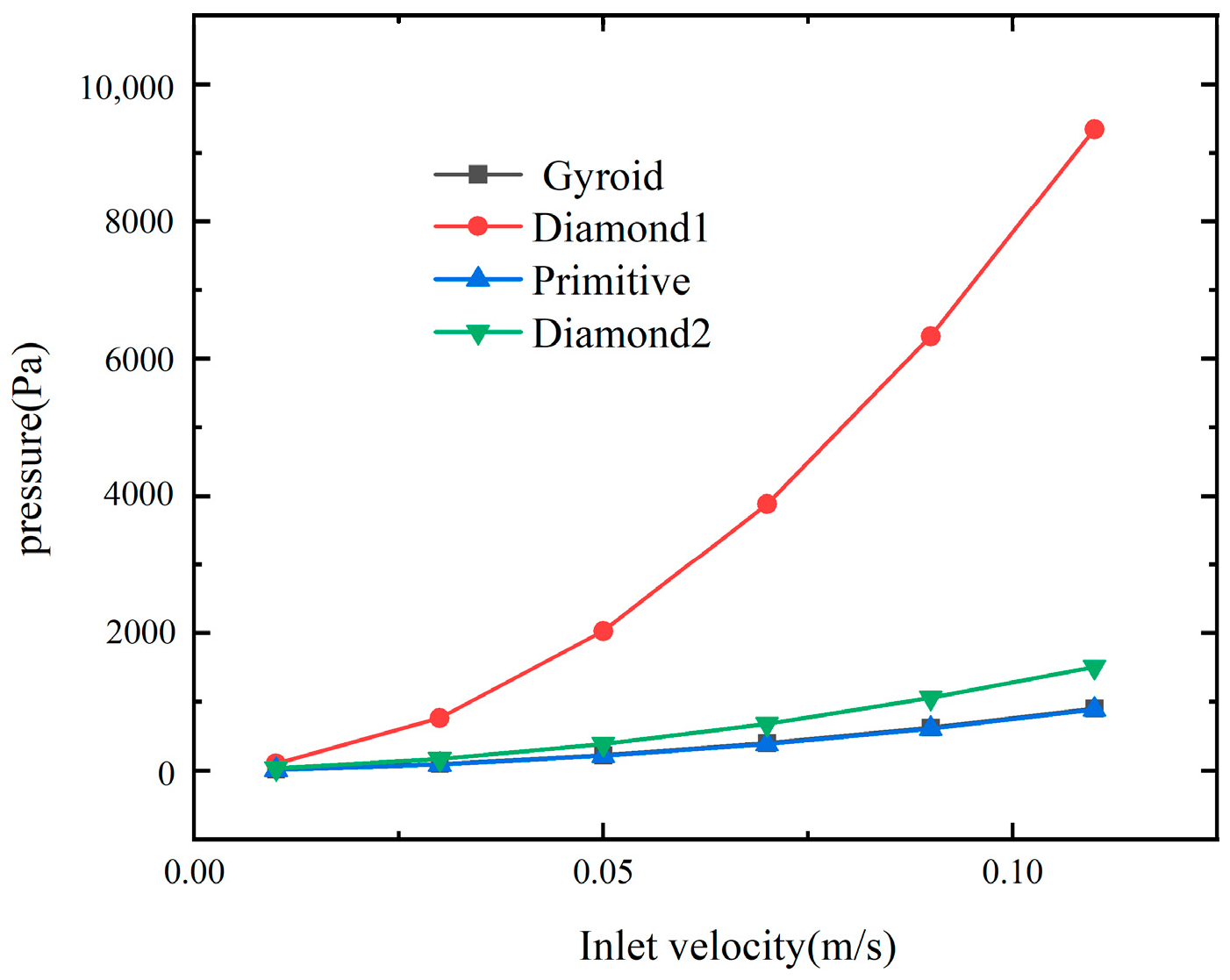
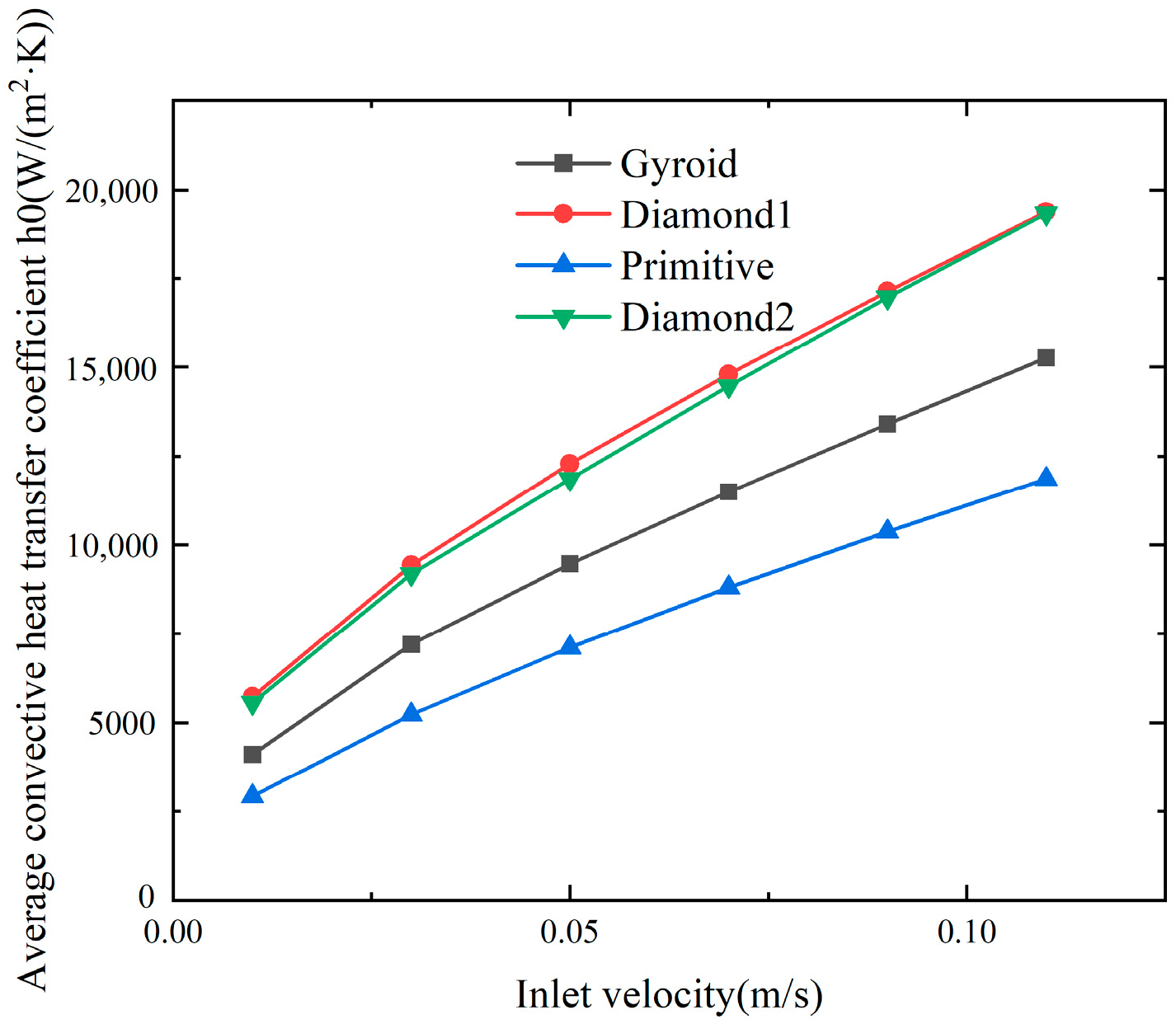


| Type | Gyroid | Diamond 1 | Primitive | Diamond 2 |
|---|---|---|---|---|
| Constant temperature surface area (mm2) | 197.39 | 197.39 | 197.39 | 197.39 |
| Solid contact area (mm2) | 55.166 | 127.800 | 44.442 | 67.682 |
| Solid proportion | 27.95% | 64.74% | 22.51% | 34.29% |
| Porosity | 67.65% | 41.45% | 71.45% | 58.87% |
| SSA (m−1) | 2.923 | 1.731 | 1.886 | 2.652 |
| Type | Gyroid | Diamond | Primitive |
|---|---|---|---|
| Inlet velocity (m/s) | 0.01–0.11 | 0.01–0.11 | 0.01–0.11 |
| Structural outlet pressure (Pa) | 0 | 0 | 0 |
| Constant temperature wall (K) | 373.15 | 373.15 | 373.15 |
| Excluding the surrounding walls of the constant temperature wall | Thermal insulation | Thermal insulation | Thermal insulation |
| Fluid wall conditions | No slip | No slip | No slip |
| TPMS initial temperature (K) | 293.15 | 293.15 | 293.15 |
| Inlet fluid temperature (K) | 293.15 | 293.15 | 293.15 |
| Grid 1 | Grid 2 | Grid 3 | Grid 4 | Grid 5 | |
|---|---|---|---|---|---|
| Number of grids | 813,898 | 953,449 | 2,174,127 | 3,977,522 | 6,519,047 |
| Computing time | 58 min | 1 h 50 min | 2 h 51 min | 13 h 15 min | 16 h 44 min |
| Type | Gyroid | Diamond 1 | Primitive | Diamond 2 |
|---|---|---|---|---|
| Maximum velocity (m/s) | 0.0437 | 0.0735 | 0.079 | 0.0391 |
| Average velocity (m/s) | 0.0134 | 0.0255 | 0.0121 | 0.0148 |
| Liquid area (mm2) | 28.466 | 13.933 | 30.517 | 25.796 |
| Proportion of liquid | 72.11% | 35.29% | 77.30% | 65.34% |
| Name | Inlet Velocity | G Microstructure Outlet Temperature | D1 Microstructure Outlet Temperature | P Microstructure Outlet Temperature | D2 Microstructure Outlet Temperature |
|---|---|---|---|---|---|
| Unit | m/s | K | K | K | K |
| 0.01 | 324.84 | 334.14 | 317.00 | 333.19 | |
| 0.03 | 313.29 | 318.55 | 308.28 | 317.99 | |
| 0.05 | 309.47 | 313.71 | 305.73 | 313.09 | |
| 0.07 | 307.49 | 311.16 | 304.37 | 310.80 | |
| 0.09 | 306.27 | 309.55 | 303.49 | 309.40 | |
| 0.11 | 305.44 | 308.43 | 302.86 | 308.40 |
| Name | Inlet Velocity | G Microstructure Pressure | D1 Microstructure Pressure | P Microstructure Pressure | D2 Microstructure Pressure |
|---|---|---|---|---|---|
| Unit | m/s | Pa | Pa | Pa | Pa |
| 0.01 | 15.34 | 100.51 | 13.52 | 28.89 | |
| 0.03 | 91.78 | 762.06 | 86.33 | 163.66 | |
| 0.05 | 219.11 | 2025.20 | 211.82 | 381.70 | |
| 0.07 | 396.21 | 3882.90 | 386.62 | 678.19 | |
| 0.09 | 623.33 | 6324.70 | 610.74 | 1052.70 | |
| 0.11 | 901.02 | 9346.10 | 884.26 | 1505.90 |
| Name | Inlet Velocity | ||||
|---|---|---|---|---|---|
| Unit | m/s | W/(m2·K) | W/(m2·K) | W/(m2·K) | W/(m2·K) |
| 0.01 | 4105.1 | 5722.1 | 2918.5 | 5549.1 | |
| 0.03 | 7199.8 | 9429.7 | 5221.8 | 9184.7 | |
| 0.05 | 9465.6 | 12,286 | 7112.5 | 11,862 | |
| 0.07 | 11,490 | 14,796 | 8803.9 | 14,465 | |
| 0.09 | 13,401 | 17,133 | 10,368 | 16,958 | |
| 0.11 | 15,264 | 19,371 | 11,858 | 19,315 |
| Name | Inlet Velocity | ||||
|---|---|---|---|---|---|
| Unit | m/s | ||||
| 0.01 | 41.350 | 57.031 | 29.683 | 55.368 | |
| 0.03 | 73.577 | 95.719 | 53.721 | 93.297 | |
| 0.05 | 97.224 | 125.490 | 73.429 | 121.260 | |
| 0.07 | 118.330 | 151.630 | 91.063 | 148.310 | |
| 0.09 | 138.250 | 175.960 | 107.370 | 174.190 | |
| 0.11 | 157.650 | 199.240 | 122.920 | 198.670 |
| Name | Inlet Velocity | ||||
|---|---|---|---|---|---|
| Unit | m/s | ||||
| 0.01 | 18.158 | 119.25 | 15.986 | 34.258 | |
| 0.03 | 12.052 | 100.17 | 11.328 | 21.505 | |
| 0.05 | 10.352 | 95.755 | 10.002 | 18.043 | |
| 0.07 | 9.548 | 93.628 | 9.313 | 16.351 | |
| 0.09 | 9.085 | 92.235 | 8.899 | 15.350 | |
| 0.11 | 8.790 | 91.225 | 8.624 | 14.698 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yang, X. Numerical Simulation of Convective Heat Transfer in Gyroid, Diamond, and Primitive Microstructures Using Water as the Working Fluid. Energies 2025, 18, 1230. https://doi.org/10.3390/en18051230
Zhang J, Yang X. Numerical Simulation of Convective Heat Transfer in Gyroid, Diamond, and Primitive Microstructures Using Water as the Working Fluid. Energies. 2025; 18(5):1230. https://doi.org/10.3390/en18051230
Chicago/Turabian StyleZhang, Jie, and Xiaoqing Yang. 2025. "Numerical Simulation of Convective Heat Transfer in Gyroid, Diamond, and Primitive Microstructures Using Water as the Working Fluid" Energies 18, no. 5: 1230. https://doi.org/10.3390/en18051230
APA StyleZhang, J., & Yang, X. (2025). Numerical Simulation of Convective Heat Transfer in Gyroid, Diamond, and Primitive Microstructures Using Water as the Working Fluid. Energies, 18(5), 1230. https://doi.org/10.3390/en18051230






