Study on the Vibration Characteristics of Wire Rope in Static Testing of Wind Turbine Blades
Abstract
1. Introduction
2. Methodology
2.1. Numerical Model
2.2. Experimental Setup
3. Results and Discussions
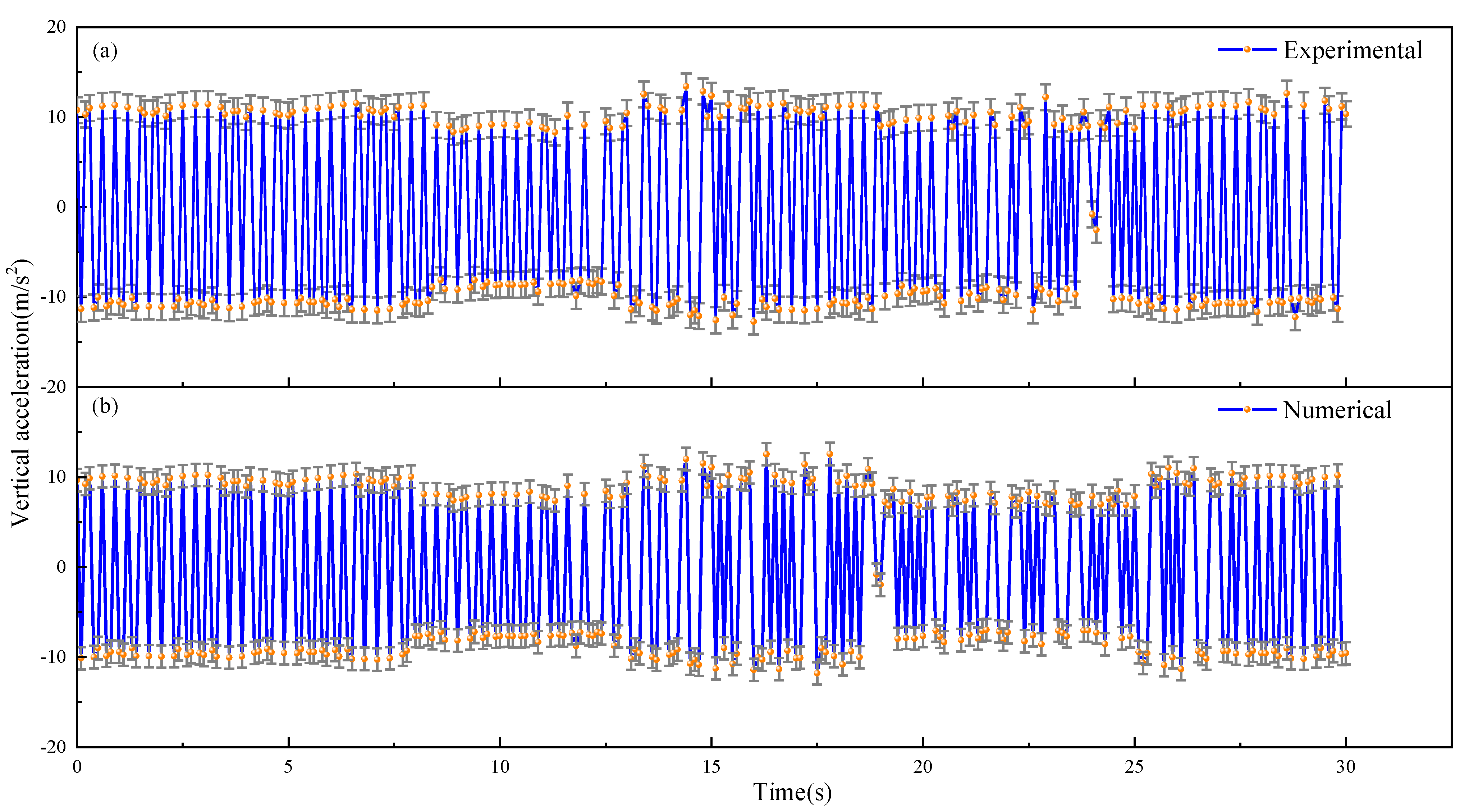
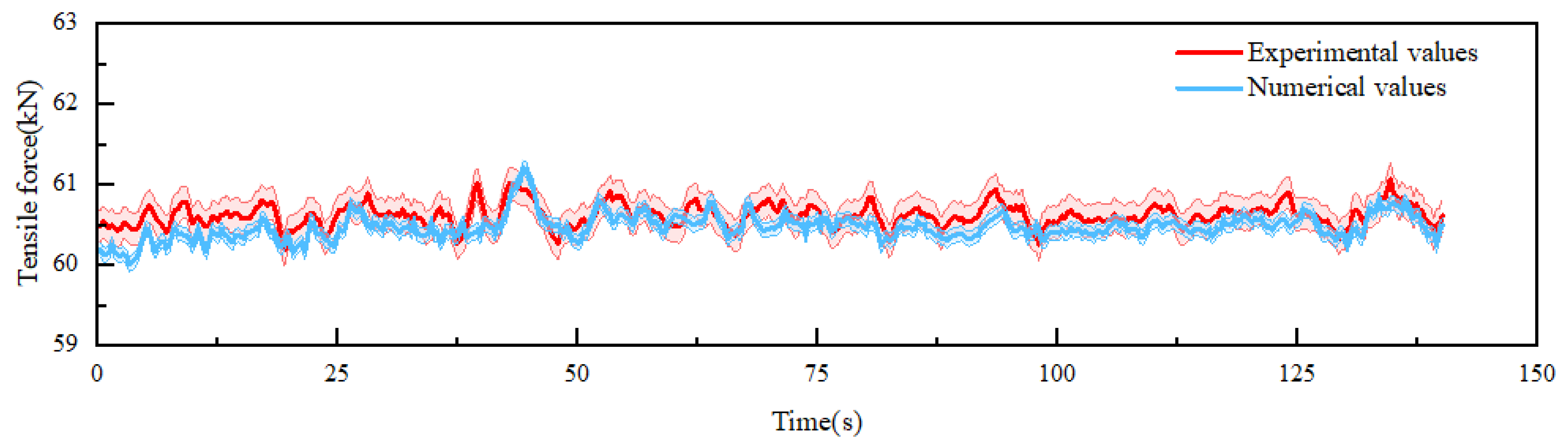
3.1. Numerical Model Validation
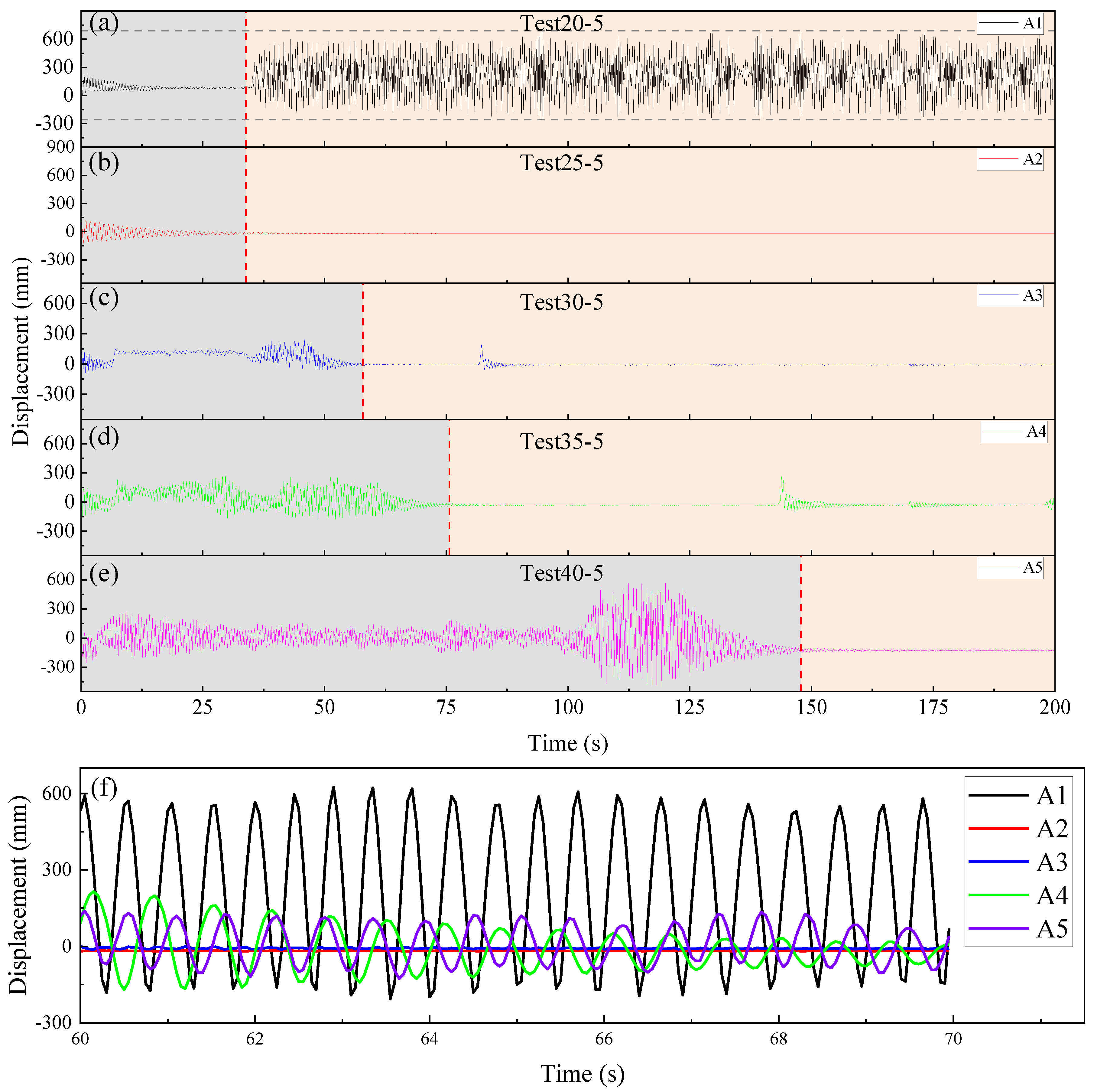
3.2. Influence of Wire Rope Span on Dynamic Vibration Characteristics
3.3. Influence of Pulley Position on Dynamic Vibration Characteristics
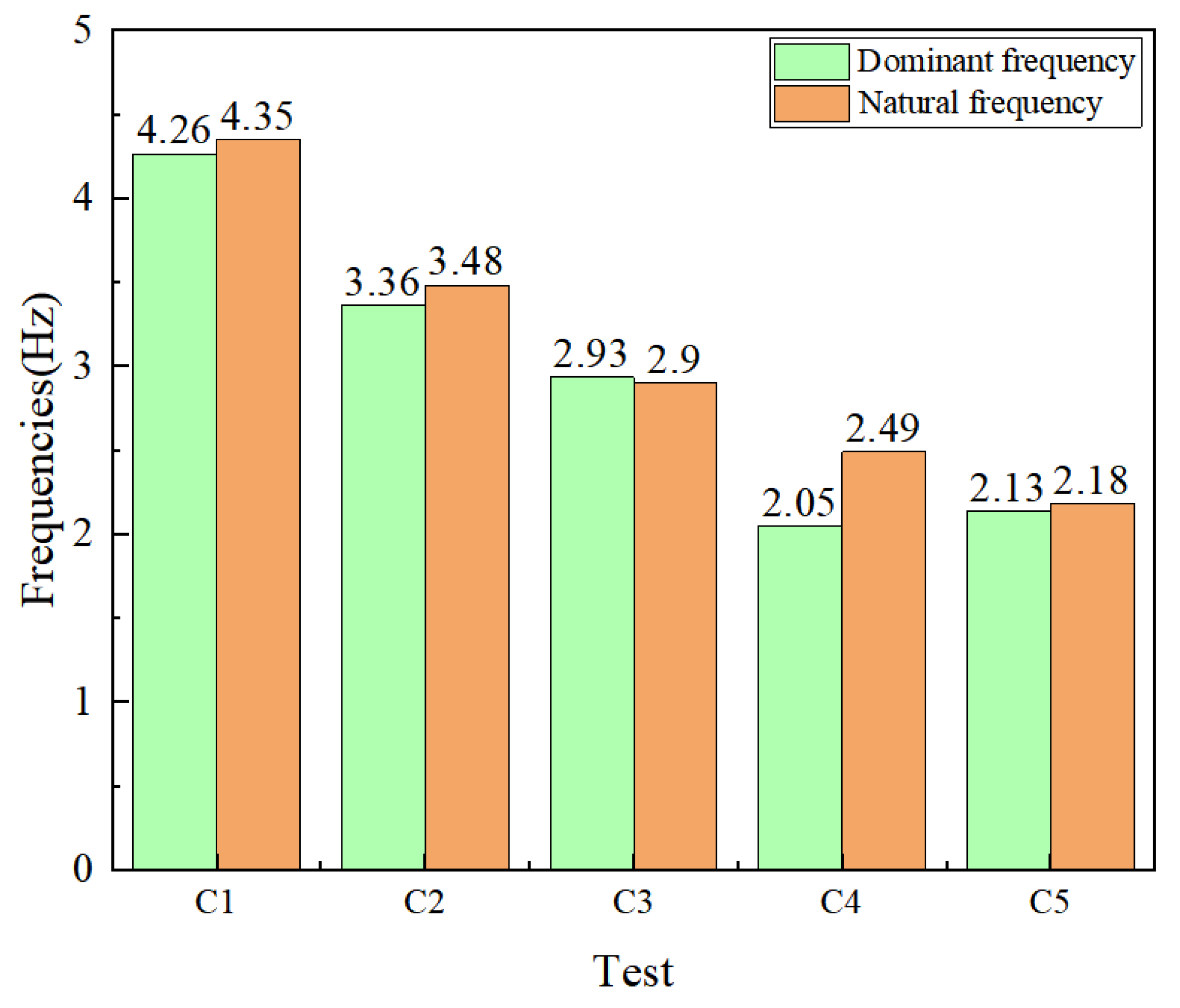
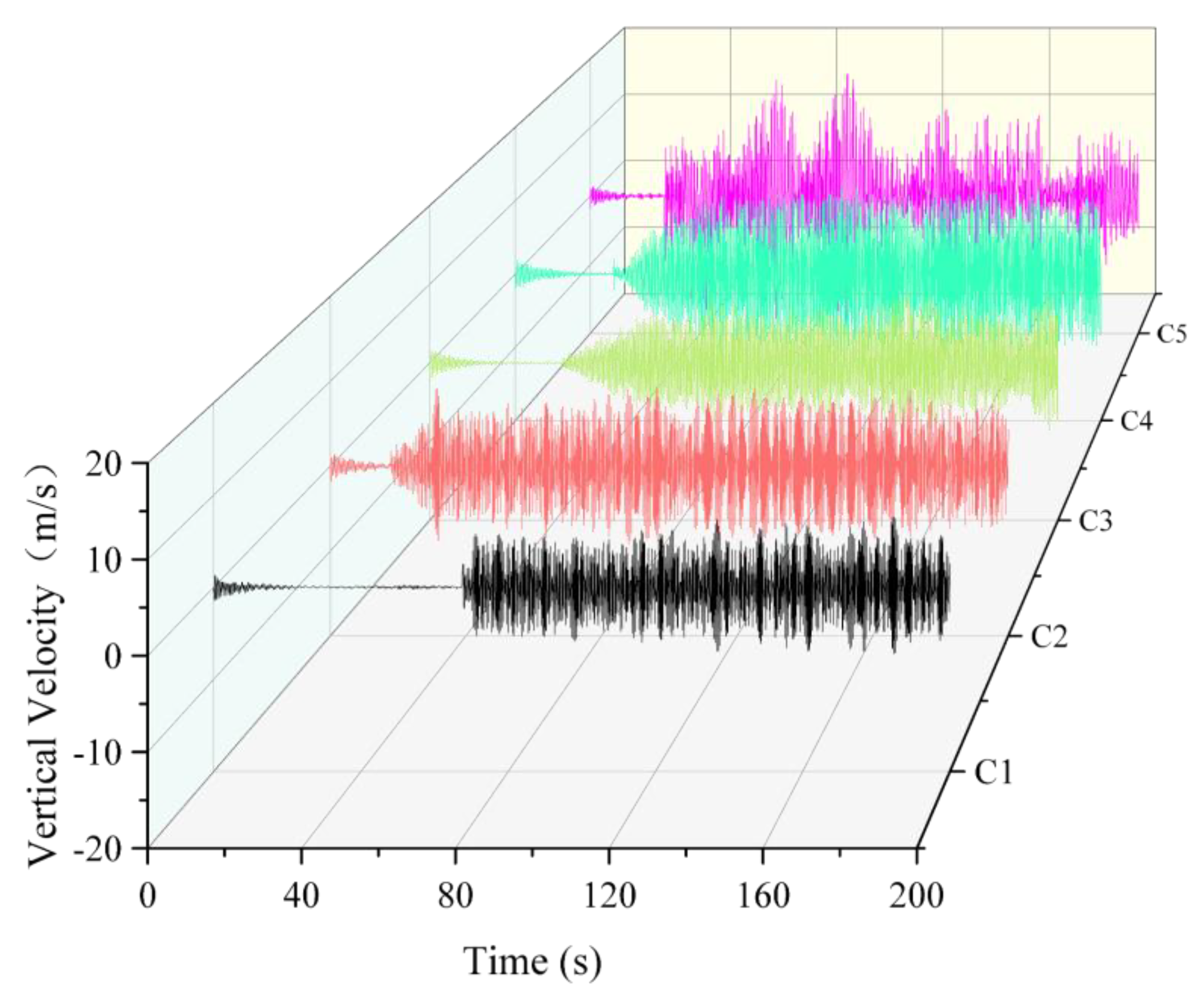
3.4. Influence of Wire Rope Span and Pulley Position on Resonance Characteristics
4. Conclusions
- An increase in the wire rope span from 20 m to 40 m resulted in a corresponding rise in the vibration amplitude of the wire rope. Specifically, within the 30–40 m span range, the displacement amplitude increased from 54.5 mm to 155.4 mm, and the duration of vibrations was significantly prolonged. To optimize static loading tests of wind turbine blades and minimize vibration interference, we recommend employing a two-offset ground track design. This approach ensures that the lateral span of the wire rope remains below 30 m while still satisfying deformation requirements at both the blade root and tip. Such a design effectively mitigates vibrations and resonance effects caused by excessive span, thereby enhancing the accuracy and reliability of the test results.
- Increasing the distance between the pulley and the blade clamp from 5 m to 9 m led to a significant rise in the vibration intensity of the wire rope. With the exception of the resonance test group (B2), the range of tension fluctuations expanded from 7.4 N to 6393.7 N. To effectively control vibrations, it is recommended that the pulley be positioned no more than 7 m away from the blade clamp. By placing the pulley closer to the blade clamp, the vibration amplitude can be significantly reduced, and vibration duration shortened, facilitating faster dissipation of vibration energy in the wire rope. This approach enhances vibration suppression, improving the overall stability of the system.
- The vibration characteristics of the wire rope were affected by the combined influence of span and pulley position. As the span increased and the pulley was positioned further from the blade clamp, system stiffness markedly decreased, resulting in the natural frequency gradually approaching the fundamental vibration frequency. This enhanced frequency alignment significantly increased vibration amplitude, prolonged vibration duration, and heightened the probability of resonance. To avoid resonance, the pulley position and wire rope span should be adjusted in static loading tests to ensure that both are kept away from the resonance frequency range, thereby effectively reducing vibration amplitude and enhancing system stability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sadorsky, P. Wind energy for sustainable development: Driving factors and future outlook. J. Clean. Prod. 2021, 289, 125779. [Google Scholar] [CrossRef]
- Ju, S.-H.; Huang, Y.-C.; Huang, Y.-Y. Study of optimal large-scale offshore wind turbines. Renew. Energy 2020, 154, 161–174. [Google Scholar] [CrossRef]
- Jung, C.; Sander, L.; Schindler, D.J.E.C. Future global offshore wind energy under climate change and advanced wind turbine technology. Energy Convers. Manag. 2024, 321, 119075. [Google Scholar] [CrossRef]
- Boadu, S.; Otoo, E. A comprehensive review on wind energy in Africa: Challenges, benefits and recommendations. Renew. Sustain. Energy Rev. 2024, 191, 114035. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, J.; Chen, X.; Zhao, Y. China in global wind power development: Role, status and impact. Renew. Sustain. Energy Rev. 2020, 127, 109881. [Google Scholar] [CrossRef]
- GWEC. Global Wind Report 2024; GWEC: London, UK, 2024. [Google Scholar]
- McKenna, R.; Leye, P.O.v.d.; Fichtner, W. Key challenges and prospects for large wind turbines. Renew. Sustain. Energy Rev. 2016, 53, 1212–1221. [Google Scholar] [CrossRef]
- de Falani, S.Y.A.; González, M.O.A.; Barreto, F.M.; de Toledo, J.C.; Torkomian, A.L.V. Trends in the technological development of wind energy generation. Int. J. Technol. Manag. Sustain. Dev. 2020, 19, 43–68. [Google Scholar] [CrossRef]
- Hu, Y.; Dai, J.; Liu, D. Research Status and Development Trend on Large Scale Wind Turbine Blades. J. Mech. Eng. 2013, 49, 140. [Google Scholar] [CrossRef]
- Lee, H.G.; Park, J. Static test until structural collapse after fatigue testing of a full-scale wind turbine blade. Compos. Struct. 2016, 136, 251–257. [Google Scholar] [CrossRef]
- Jensen, F.M.; Falzon, B.G.; Ankersen, J.; Stang, H. Structural testing and numerical simulation of a 34m composite wind turbine blade. Compos. Struct. 2006, 76, 52–61. [Google Scholar] [CrossRef]
- Fagan, E.M.; Flanagan, M.; Leen, S.B.; Flanagan, T.; Doyle, A.; Goggins, J. Physical experimental static testing and structural design optimisation for a composite wind turbine blade. Compos. Struct. 2017, 164, 90–103. [Google Scholar] [CrossRef]
- Yang, B.; Sun, D. Testing, inspecting and monitoring technologies for wind turbine blades: A survey. Renew. Sustain. Energy Rev. 2013, 22, 515–526. [Google Scholar] [CrossRef]
- Zhou, H.F.; Dou, H.Y.; Qin, L.Z.; Chen, Y.; Ni, Y.Q.; Ko, J.M. A review of full-scale structural testing of wind turbine blades. Renew. Sustain. Energy Rev. 2014, 33, 177–187. [Google Scholar] [CrossRef]
- Wang, J.; Cao, G.; Zhu, Z.; Wang, Y.; Peng, W. Lateral response of cable-guided hoisting system with time-varying length: Theoretical model and dynamics simulation verification. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2908–2920. [Google Scholar] [CrossRef]
- Kaczmarczyk, S. The passage through resonance in a catenary–vertical cable hoisting system with slowly varying length. J. Sound Vib. 1997, 208, 243–269. [Google Scholar] [CrossRef]
- Kaczmarczyk, S.; Ostachowicz, W. Transient vibration phenomena in deep mine hoisting cables. Part 1: Mathematical model. J. Sound Vib. 2003, 262, 219–244. [Google Scholar] [CrossRef]
- Zhou, B.; Hu, Y.; Zhu, H. Dynamic simulation and experimental investigation of the double-rope winding hoister based on an equivalent mechanical model of wire ropes. Structures 2024, 69, 107237. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, D.; Yang, X.; Feng, C.; Ge, S. Experimental research on effect of wire rope transverse vibration on friction transmission stability in a friction hoisting system. Tribol. Int. 2017, 115, 233–245. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, D.; Chen, K.; Feng, C.; Ge, S. Longitudinal dynamic characteristics of steel wire rope in a friction hoisting system and its coupling effect with friction transmission. Tribol. Int. 2018, 119, 731–743. [Google Scholar] [CrossRef]
- Wu, S.; He, P.; Gong, X. Analysis of transverse vibration of wire rope in flexible hoisting system. J. Vibroeng. 2021, 23, 283–297. [Google Scholar] [CrossRef]
- Wu, S.; He, P.; Gong, X. Transverse vibration analysis of wire rope in deep mining hoisting system. J. Vibroeng. 2021, 23, 1079–1094. [Google Scholar] [CrossRef]
- Zhu, Y.; Xu, T.; Ma, C.; Yao, J. Experimental study on longitudinal vibration of mine hosting rope subjected to disturbance excitations by ADAMS. Adv. Mech. Eng. 2022, 14, 16878132221076818. [Google Scholar] [CrossRef]
- Yang, D.-H.; Kim, K.-Y.; Kwak, M.K.; Lee, S. Dynamic modeling and experiments on the coupled vibrations of building and elevator ropes. J. Sound Vib. 2017, 390, 164–191. [Google Scholar] [CrossRef]
- Zhang, N.; Cao, G.; Zhu, Z.; Wang, K.; Yan, L. Nonlinear dynamics of time-varying curvature balance rope coupled with time-varying length hoisting rope in friction hoisting system. J. Sound Vib. 2023, 567, 117910. [Google Scholar] [CrossRef]
- Ma, C.; Yao, J.; Xiao, X.; Di, X.; Jiang, Y. Vibration Analysis of Winding Hoisting System based on ADAMS/Cable. J. Phys. Conf. Ser. 2021, 1750, 012033. [Google Scholar] [CrossRef]
- Wang, L. Modeling and Analysis of Steel Wire Rope Based on ADAMS Macro Command. Int. Core J. Eng. 2019, 5, 26–29. [Google Scholar] [CrossRef]
- IEC 61400-23; Wind Turbine Generator Systems-Part 23: Full-Scale Structural Testing of Rotor Blades. International Electrotechnical Commission: Geneva, Switzerland, 2012.
- Wang, N.; Cao, G.; Yan, L.; Wang, L. Modelling and passive control of flexible guiding hoisting system with time-varying length. Math. Comput. Model. Dyn. Syst. 2020, 26, 1699121. [Google Scholar] [CrossRef]
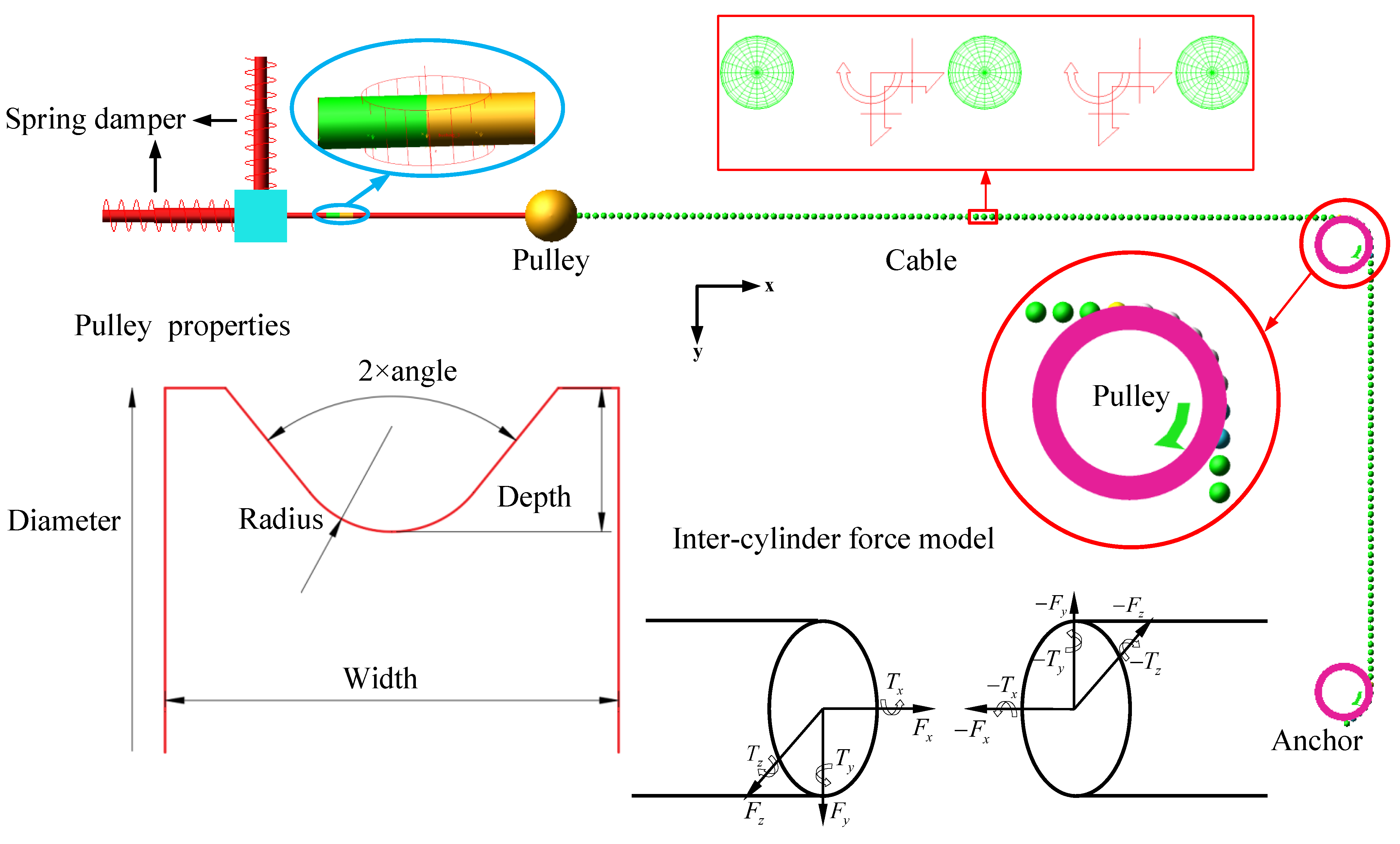
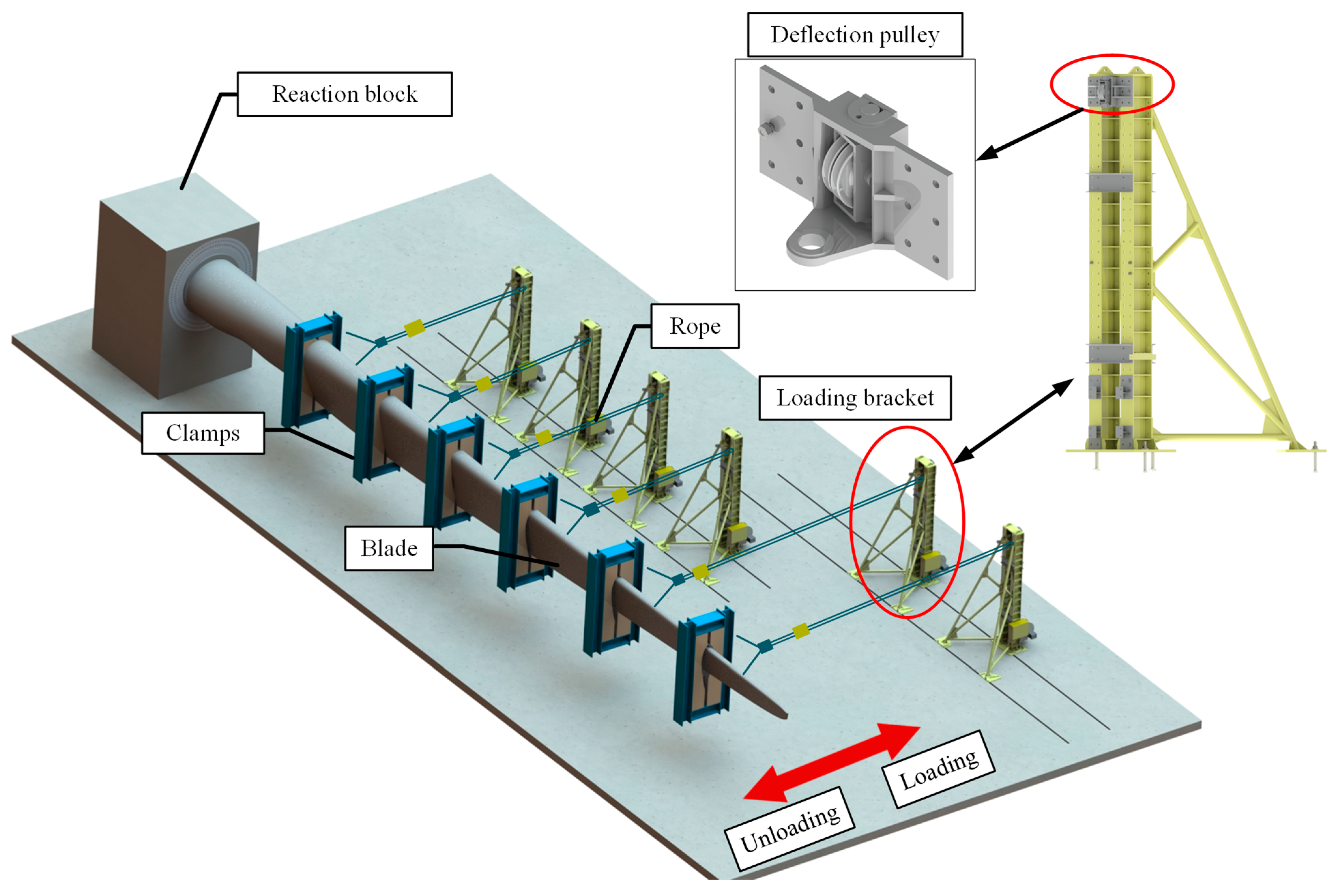
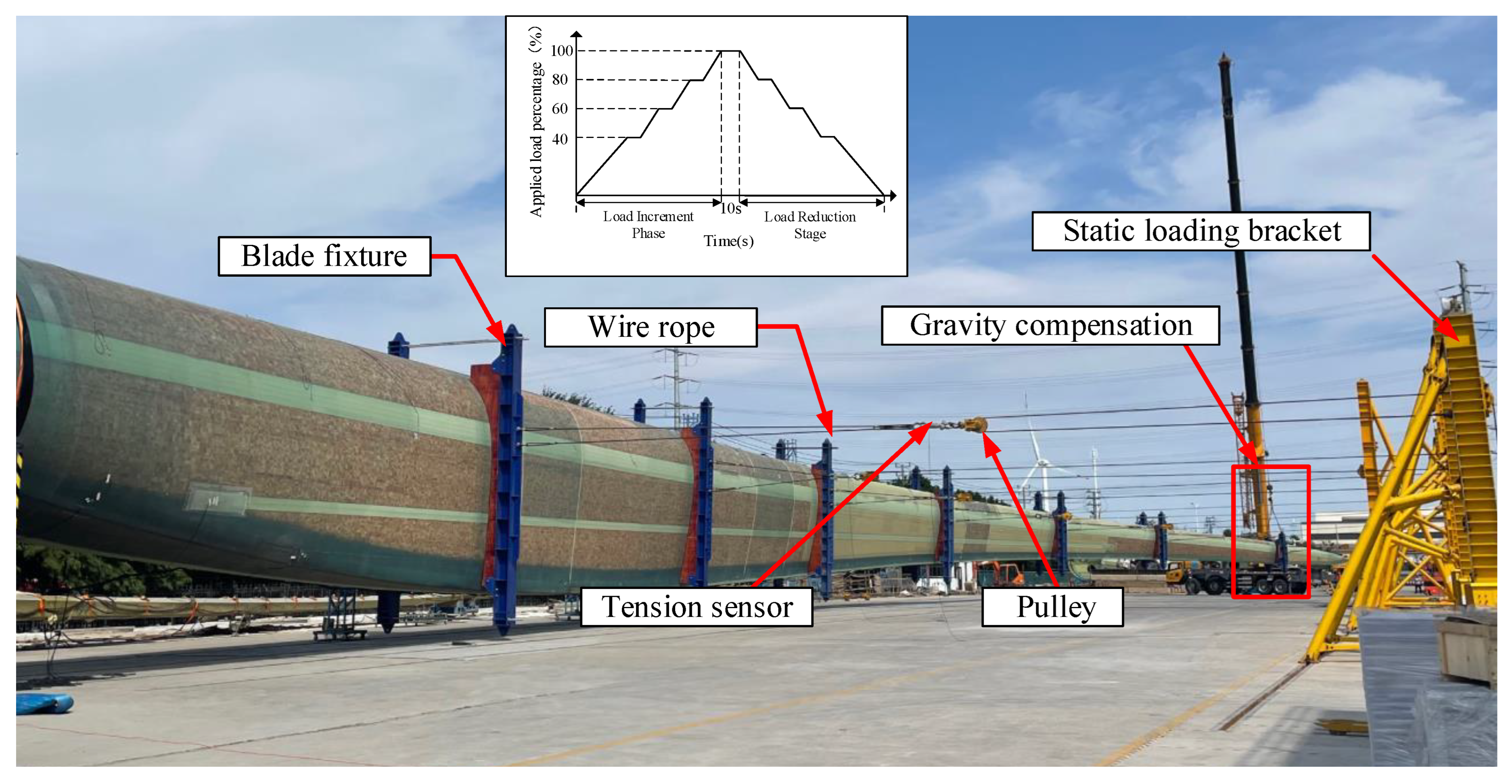

| Component | Parameter | Value |
|---|---|---|
| Wire rope | Diameter (mm) | 24 |
| Density (kg/mm3) | 1.83 × 10−5 | |
| Young’s modulus (N/mm2) | 1.2 × 105 | |
| Damping coefficient | 0.01 | |
| Mesh density | 0.08 | |
| Contact with pulley | Contact stiffness (N·mm) | 10,000 |
| Maximal damping ratio | 0.1 | |
| Friction coefficient | 0.2 |
| Test Group | Experiment ID | Wire Rope Span (m) | Pulley Position (m) |
|---|---|---|---|
| Span variation | A1 | 20 | 5 |
| A2 | 25 | 5 | |
| A3 | 30 | 5 | |
| A4 | 35 | 5 | |
| A5 | 40 | 5 | |
| Pulley position variation | B1 | 25 | 5 |
| B2 | 25 | 6 | |
| B3 | 25 | 7 | |
| B4 | 25 | 8 | |
| B5 | 25 | 9 | |
| Resonance testing | C1 | 20 | 5 |
| C2 | 25 | 6 | |
| C3 | 30 | 7 | |
| C4 | 35 | 8 | |
| C5 | 40 | 9 |
| Parameter | Experimental | Simulation | Percentage of Error (%) |
|---|---|---|---|
| Average acceleration (m/s2) | 11.2 | 10.9 | 2.68% |
| Standard deviation of acceleration (m/s2) | 11.3 | 10.5 | 7.08% |
| Average tension (kN) | 60.6 | 60.4 | 0.33% |
| Standard deviation of tension (kN) | 0.14 | 0.15 | 7.14% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Qin, Z.; Zhang, Y.; Li, J.; Zhang, L.; Yang, P. Study on the Vibration Characteristics of Wire Rope in Static Testing of Wind Turbine Blades. Energies 2025, 18, 1138. https://doi.org/10.3390/en18051138
Zhang Y, Qin Z, Zhang Y, Li J, Zhang L, Yang P. Study on the Vibration Characteristics of Wire Rope in Static Testing of Wind Turbine Blades. Energies. 2025; 18(5):1138. https://doi.org/10.3390/en18051138
Chicago/Turabian StyleZhang, Yingjie, Zhiwen Qin, Yuhuan Zhang, Jialin Li, Leian Zhang, and Panpan Yang. 2025. "Study on the Vibration Characteristics of Wire Rope in Static Testing of Wind Turbine Blades" Energies 18, no. 5: 1138. https://doi.org/10.3390/en18051138
APA StyleZhang, Y., Qin, Z., Zhang, Y., Li, J., Zhang, L., & Yang, P. (2025). Study on the Vibration Characteristics of Wire Rope in Static Testing of Wind Turbine Blades. Energies, 18(5), 1138. https://doi.org/10.3390/en18051138





