Diagnostics of Inter-Turn Short Circuit Fault in Dry-Type Air-Core Reactor Based on Lissajous Graph and Lightweight Network Model
Abstract
1. Introduction
- (1)
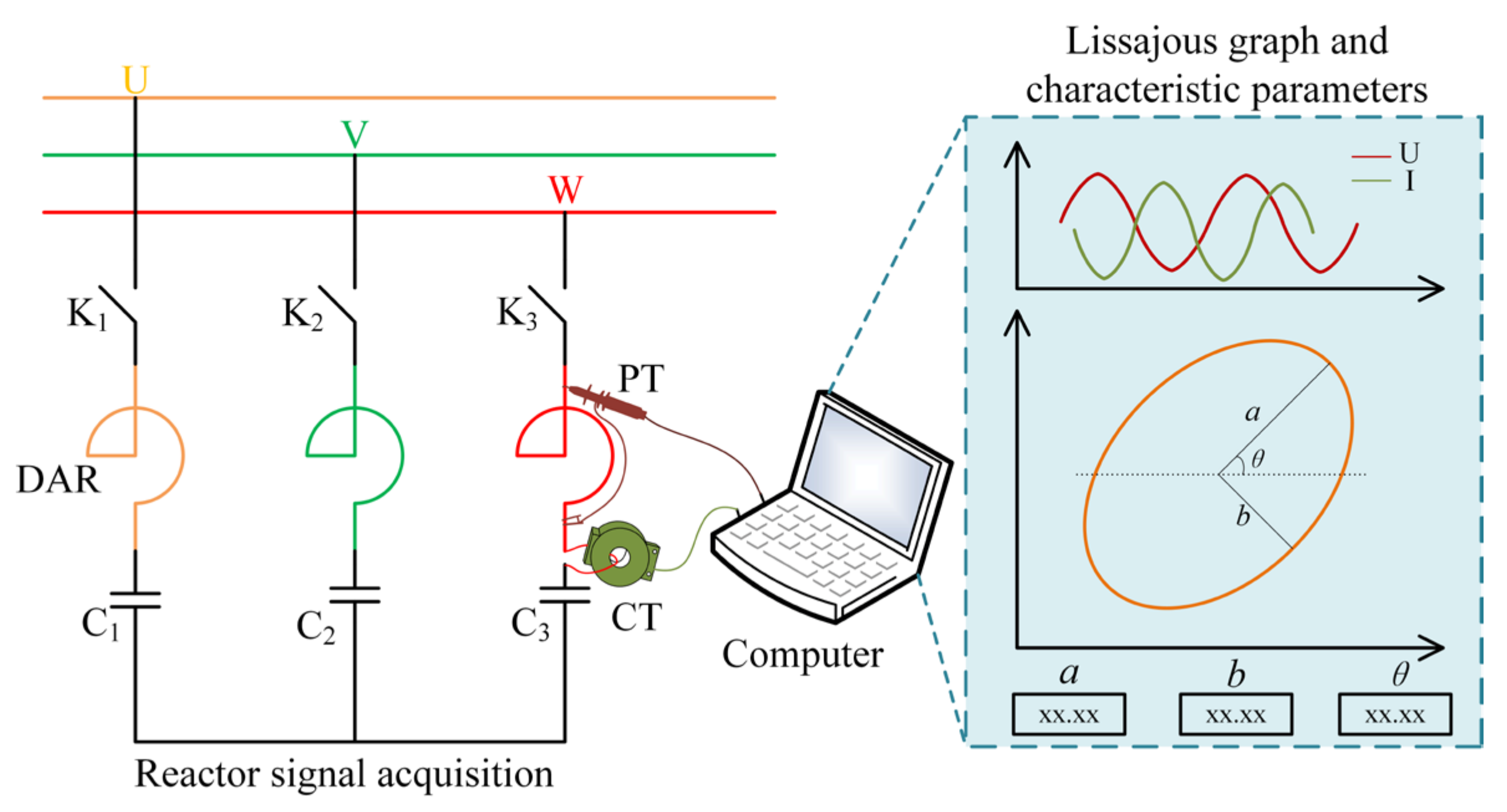
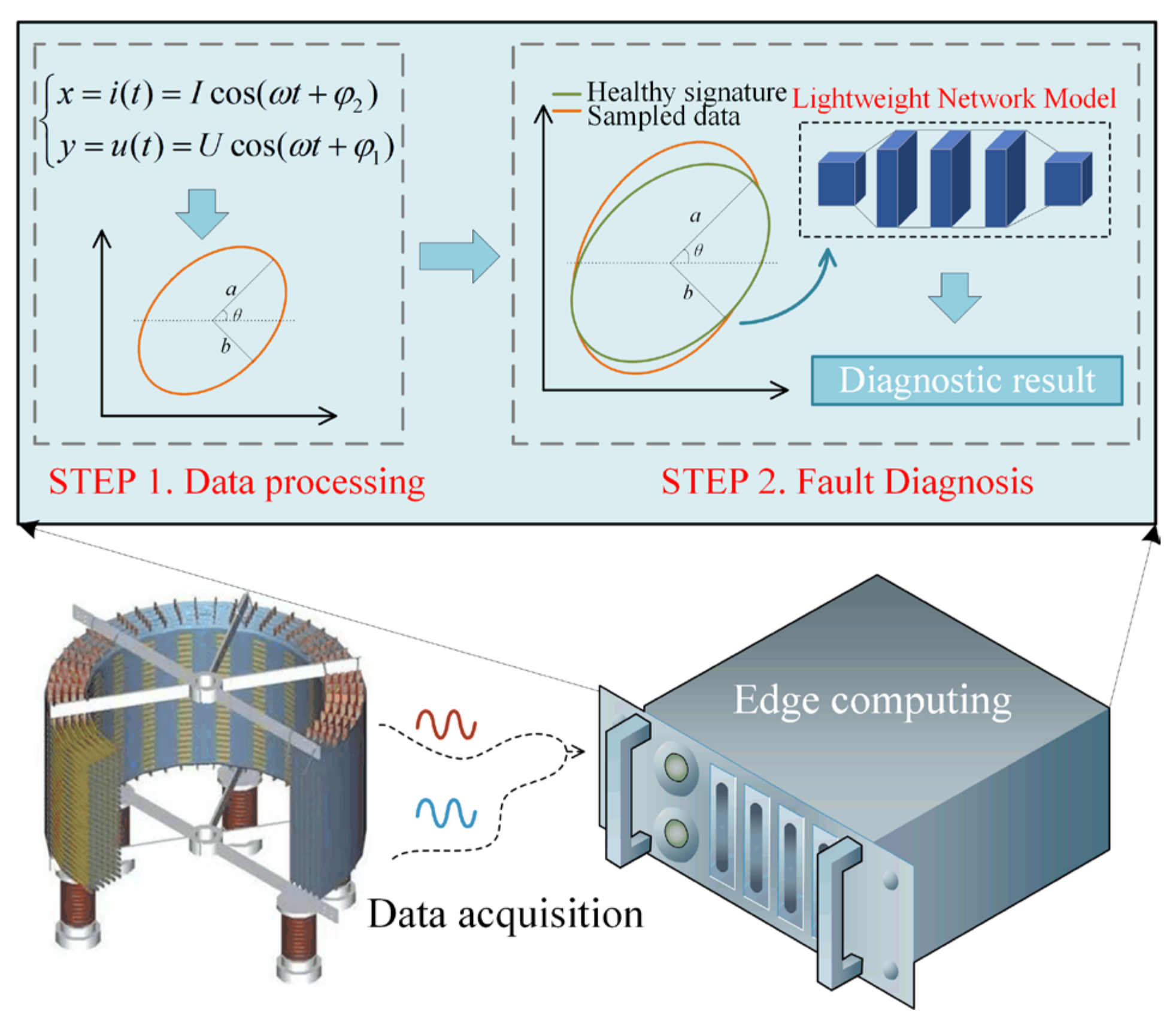
- For the first time, the Lissajous graph is introduced to characterize and detect turn-to-turn short circuit faults of DARs, which only uses existing potential transformers (PTs) and current transformers (CTs) to measure signals of reactors and does not need extra sensors. It is simple and reliable in online situations.
- (2)
- Moreover, a lightweight network MobileNetV3-Small model is used as a new classifier to further diagnose the fault severity of ITSC, which is accurate, intelligent, and can reduce the personnel’s misjudgment. In addition, lightweight network models can better adapt to engineering applications.
2. “Field-Circuit” Coupling Model for ITSC Fault in DAR
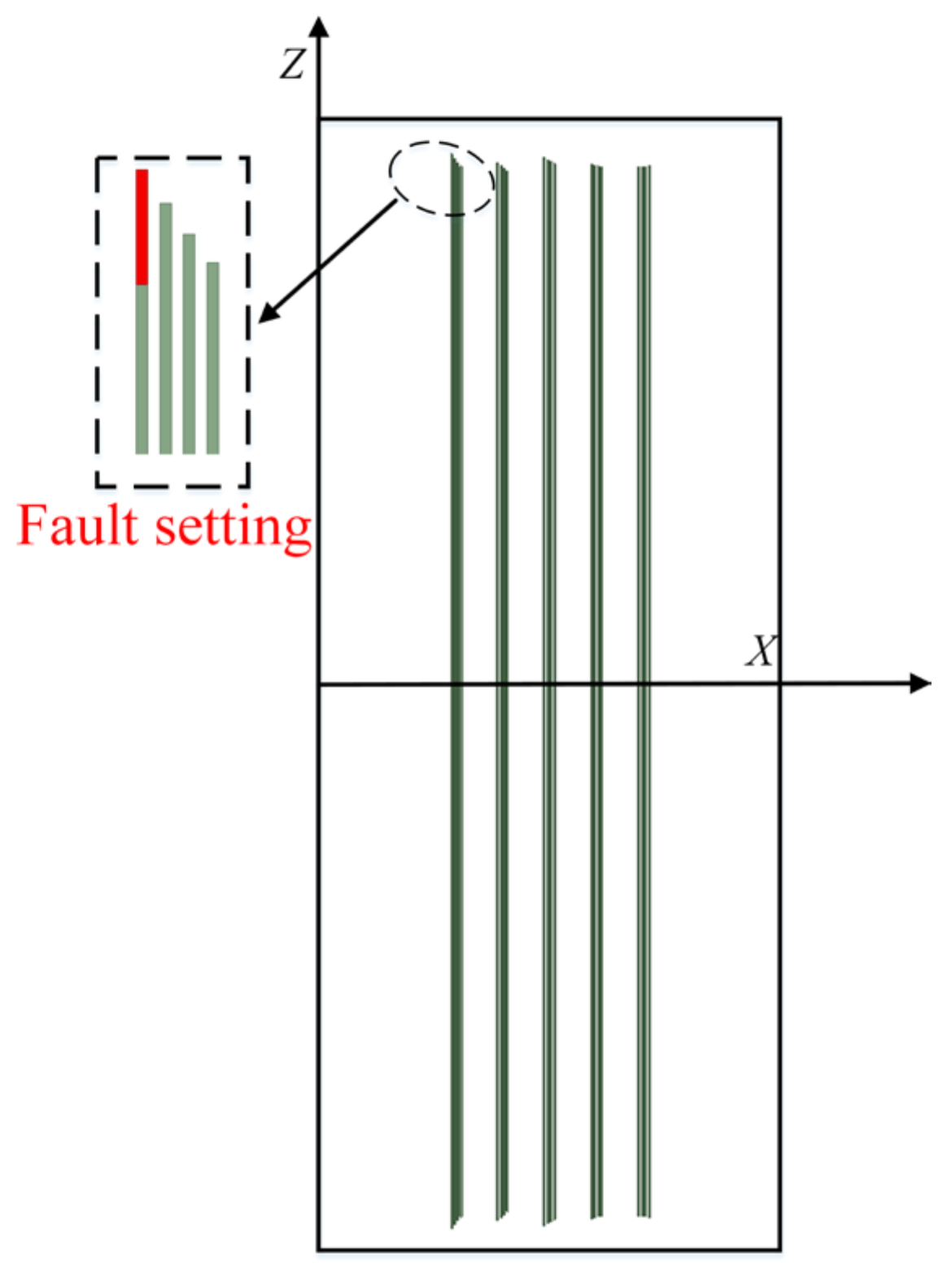
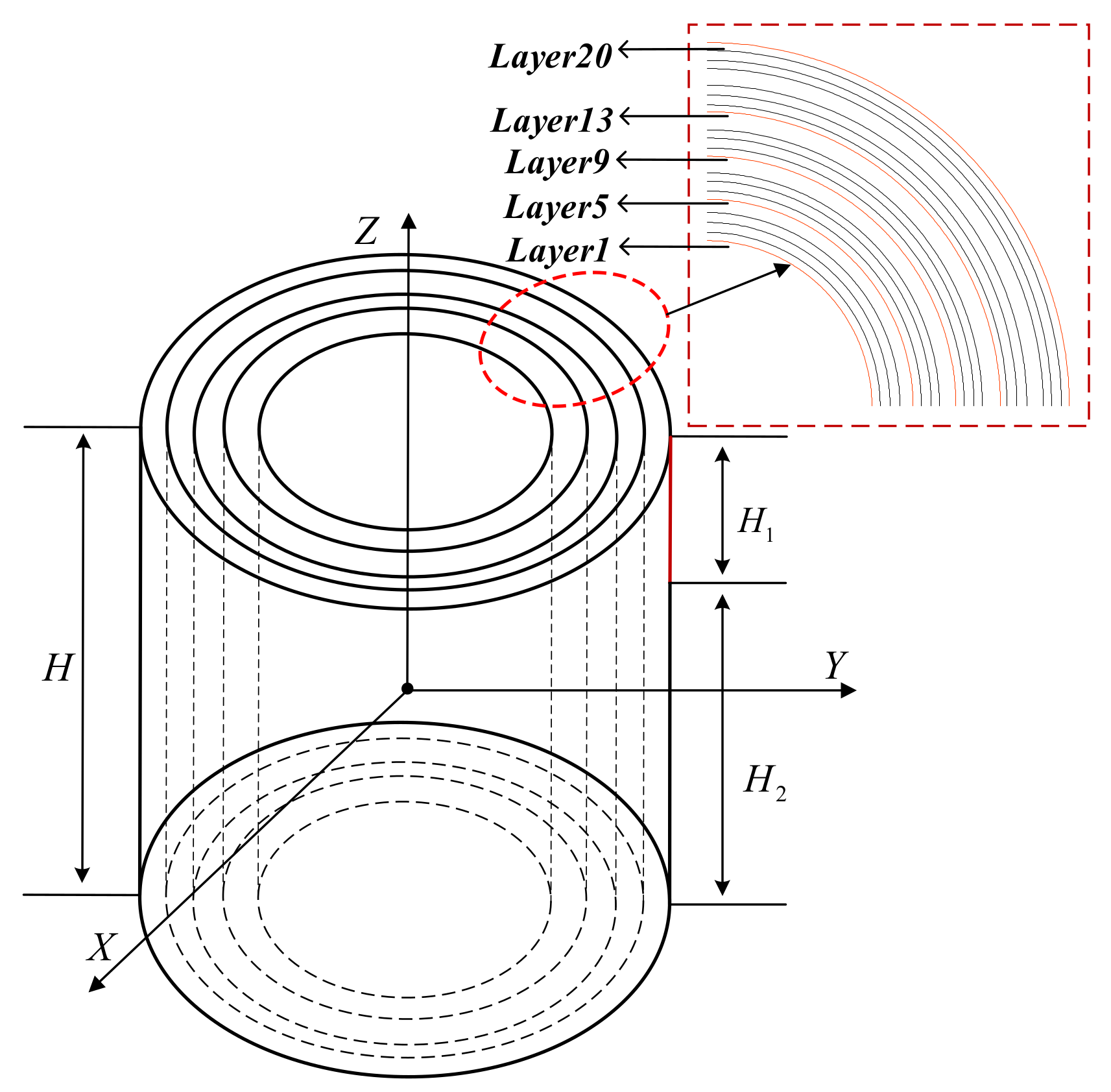
2.1. Two-Dimensional Simulation Model and Fault Setting
2.2. Model Validation
3. Introduction of Online Lissajous Graphic Method Based on Variation in State Parameters
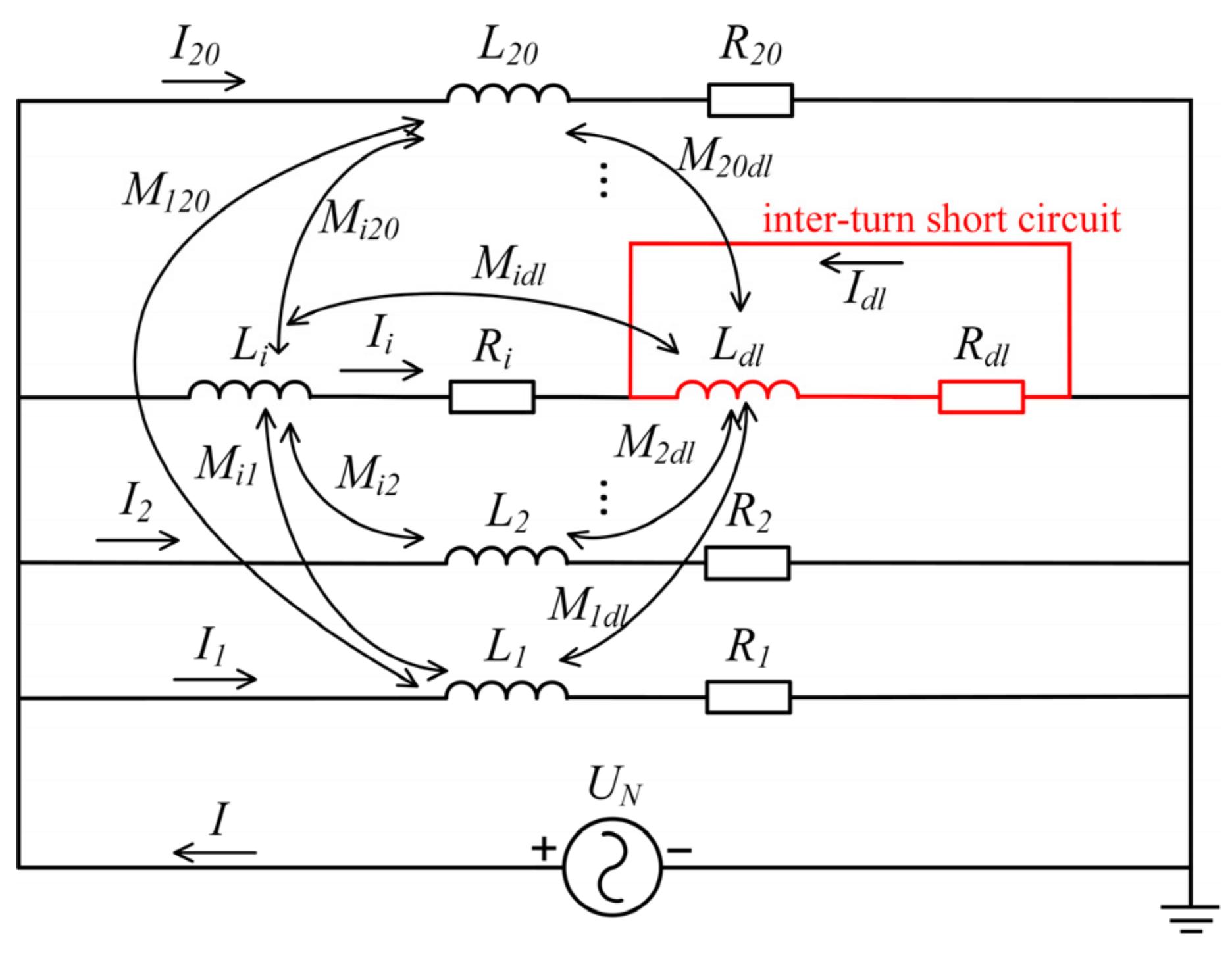
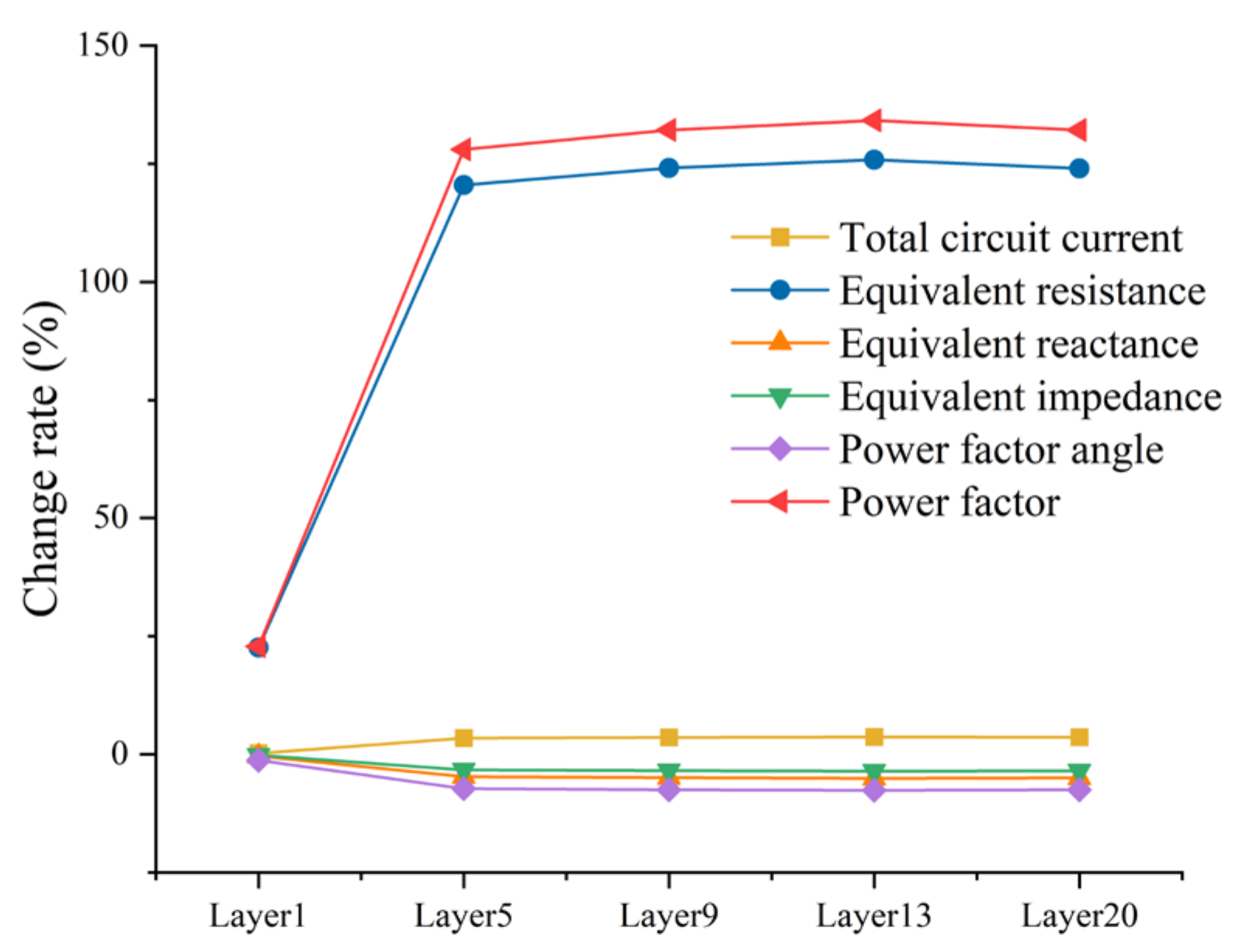
3.1. Impact of ITSC in DAR on Common State Parameters
3.2. Introduction of Online Lissajous Graphical Method
4. Feasibility Analysis of Online Lissajous Graphic Method
4.1. Simulation Validation
- (1)
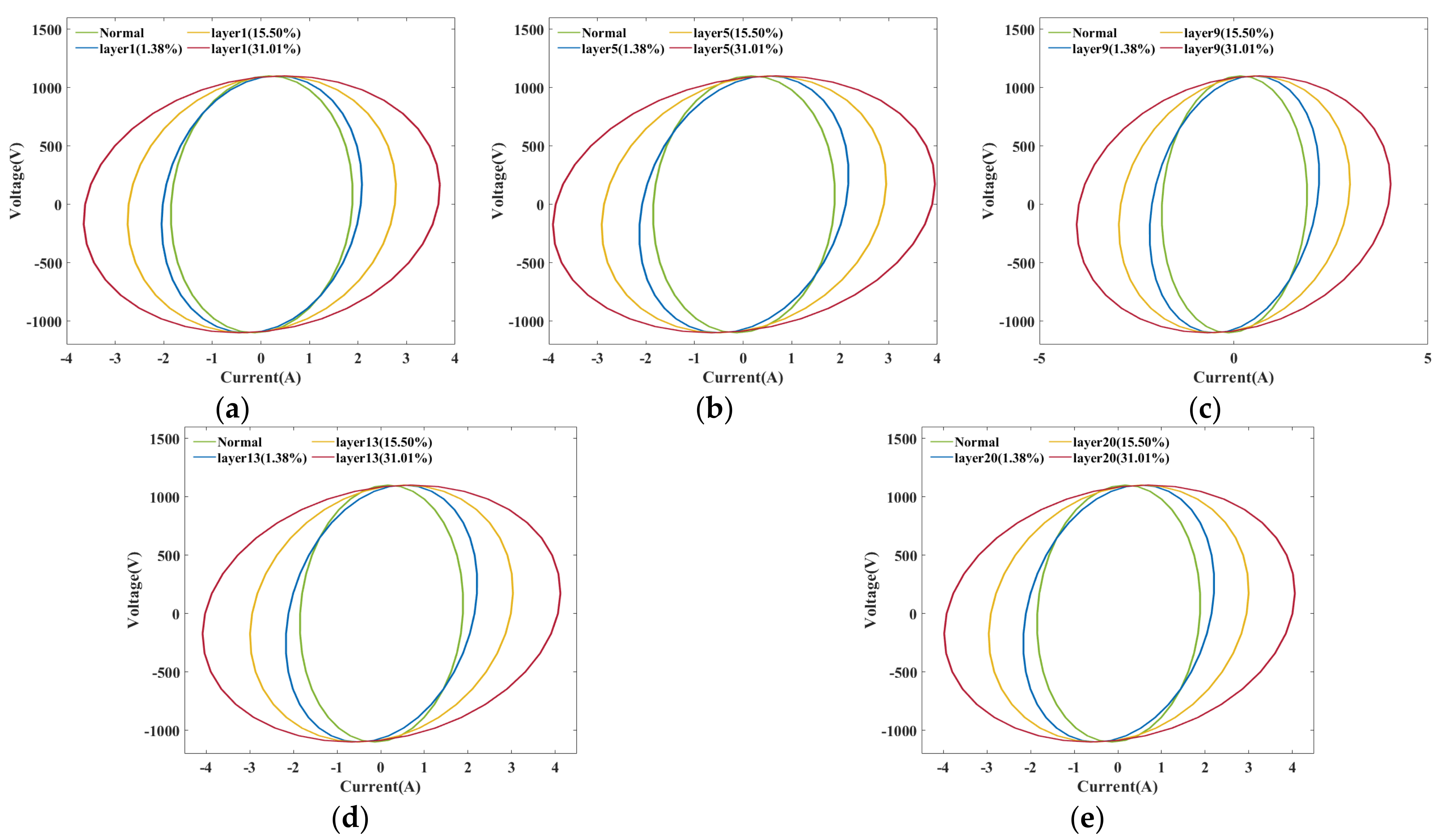
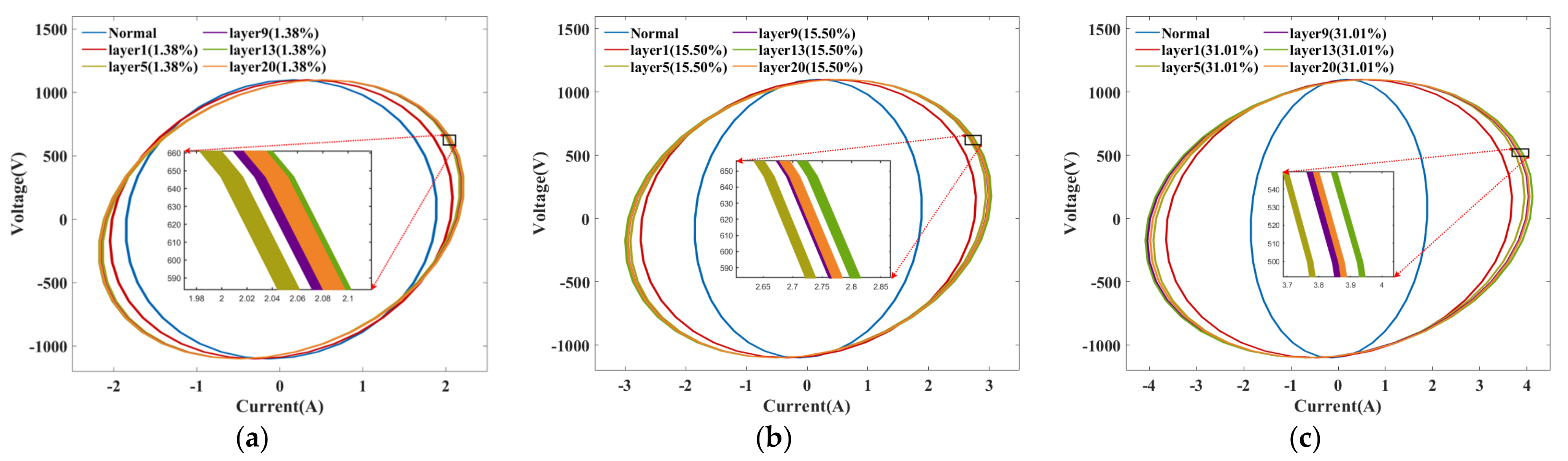
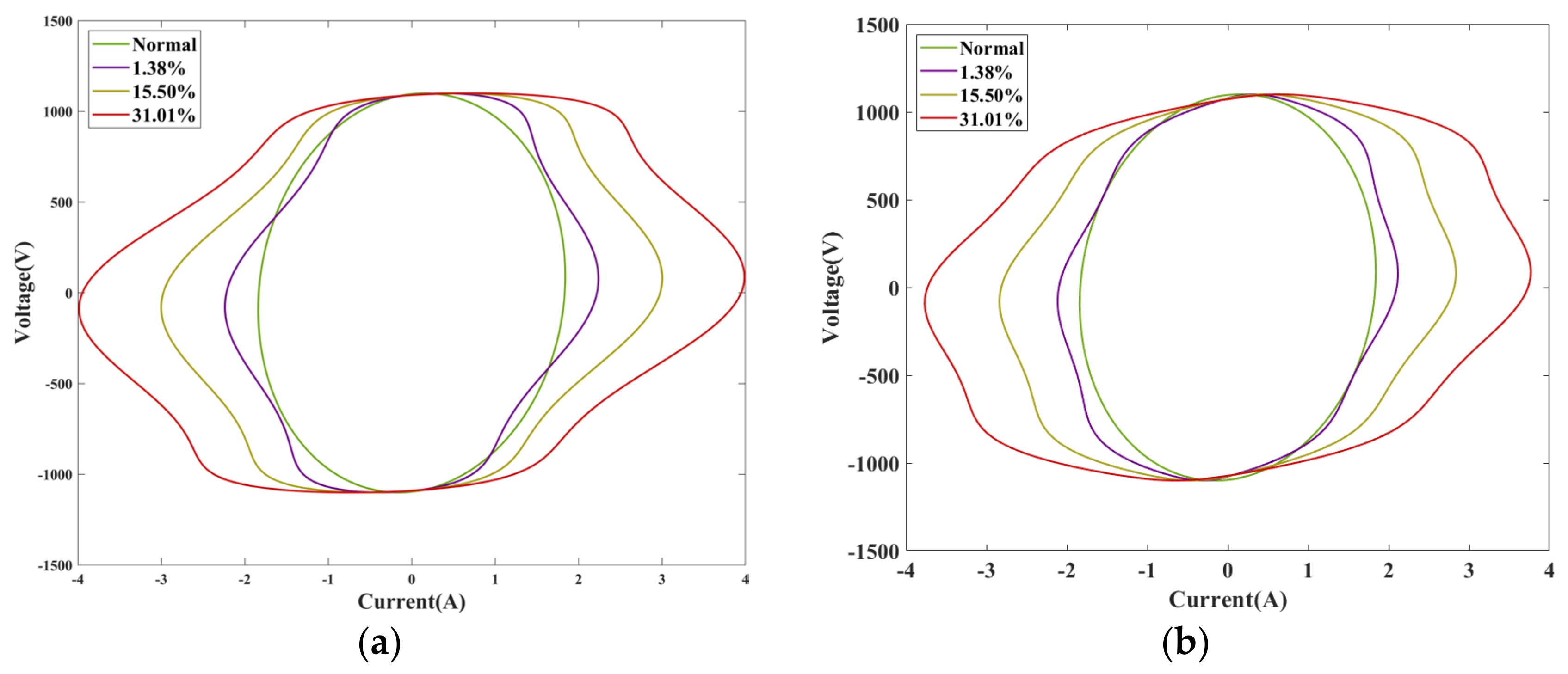
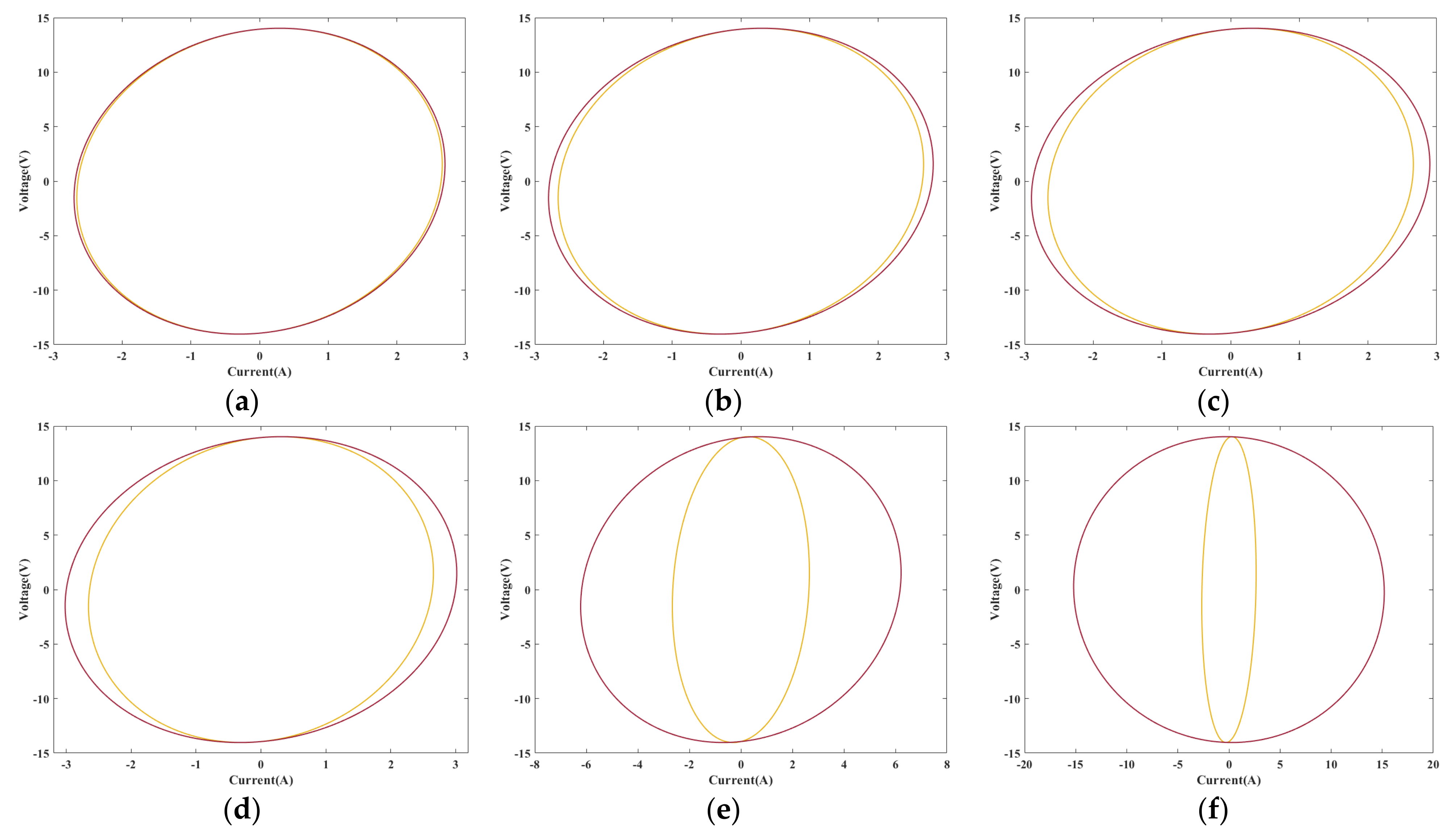
- When an ITSC fault occurs in any layer, as seen in Figure 8, the alteration of the Lissajous graph is strongly correlated with the severity of the ITSC fault. When the fault degree is slight, the graph exhibits noticeable rotational alterations. As the degree of fault escalates, both the area and inclination of the Lissajous graph will markedly expand.
- (2)
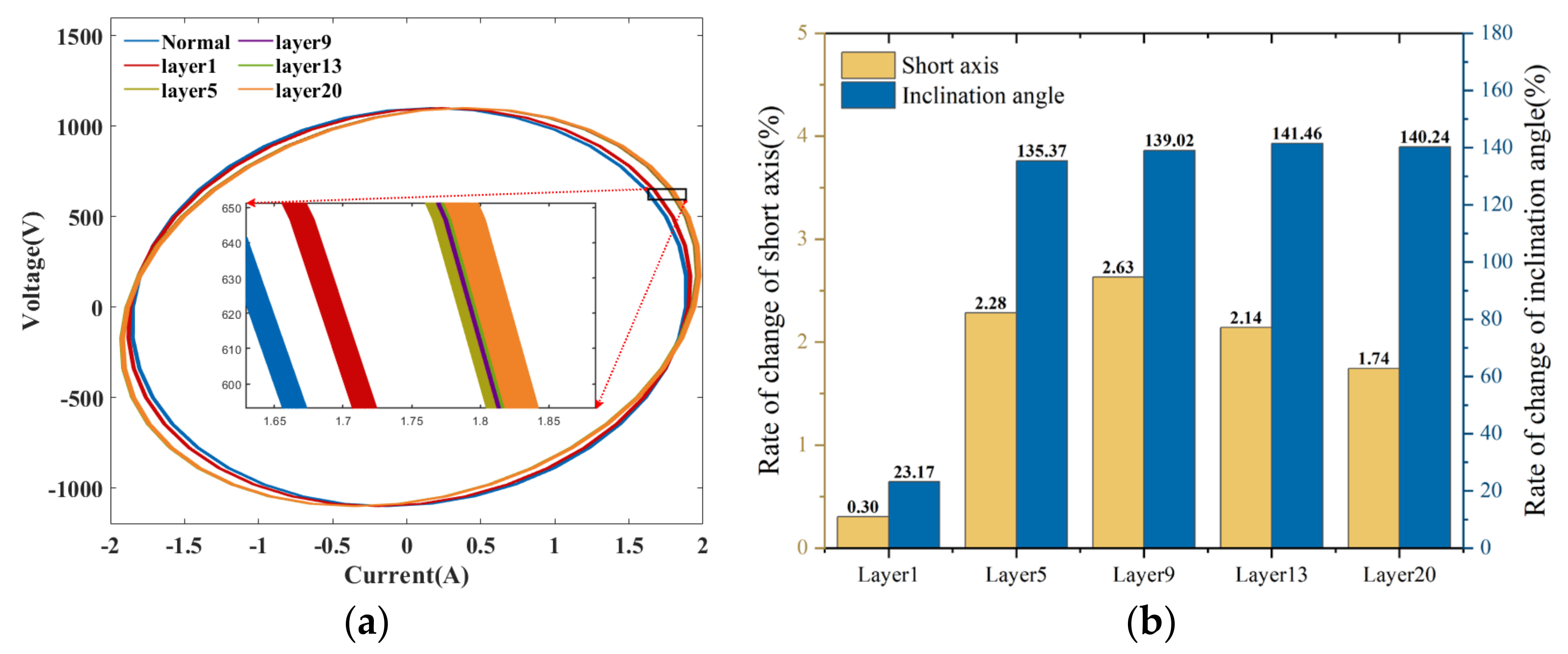
- In Figure 9, it can be observed that when the same degree of fault occurs in different layers, the closer the fault location is to the middle layer of the reactor, the more significant the change in Lissajous graphic is. In contrast, the change in fault pattern at both end layers is slightly weaker. Among them, the closer the fault occurs to the interior, the smaller the rate of change is. The reason is that after a short circuit fault occurs in the middle, the variations in mutual inductances between the fault layer and other normal layers are more significant compared to those that occur at Layer 1 or Layer 20.
- (3)
- The characteristics are greatly influenced by the degree of the fault, regardless of whether a short circuit fault of varying degrees occurs on the same layer or a fault of identical degree occurs on different layers. Table 2 shows that when fault severity escalates, both the short axis b and the inclination angle θ exhibit an upward trend, progressively increasing radially from the interior outward, with a minor reduction observed in the outermost layer. The augmentation in the variation in the inclination angle θ is the most significant, with the rate of change escalating from 114.63% to 475.61%, followed by the short axis, which exhibits a rate of change between 9.39% and 118.52%.
4.2. Sensitivity Verification
4.3. Harmonic and Noise Influence
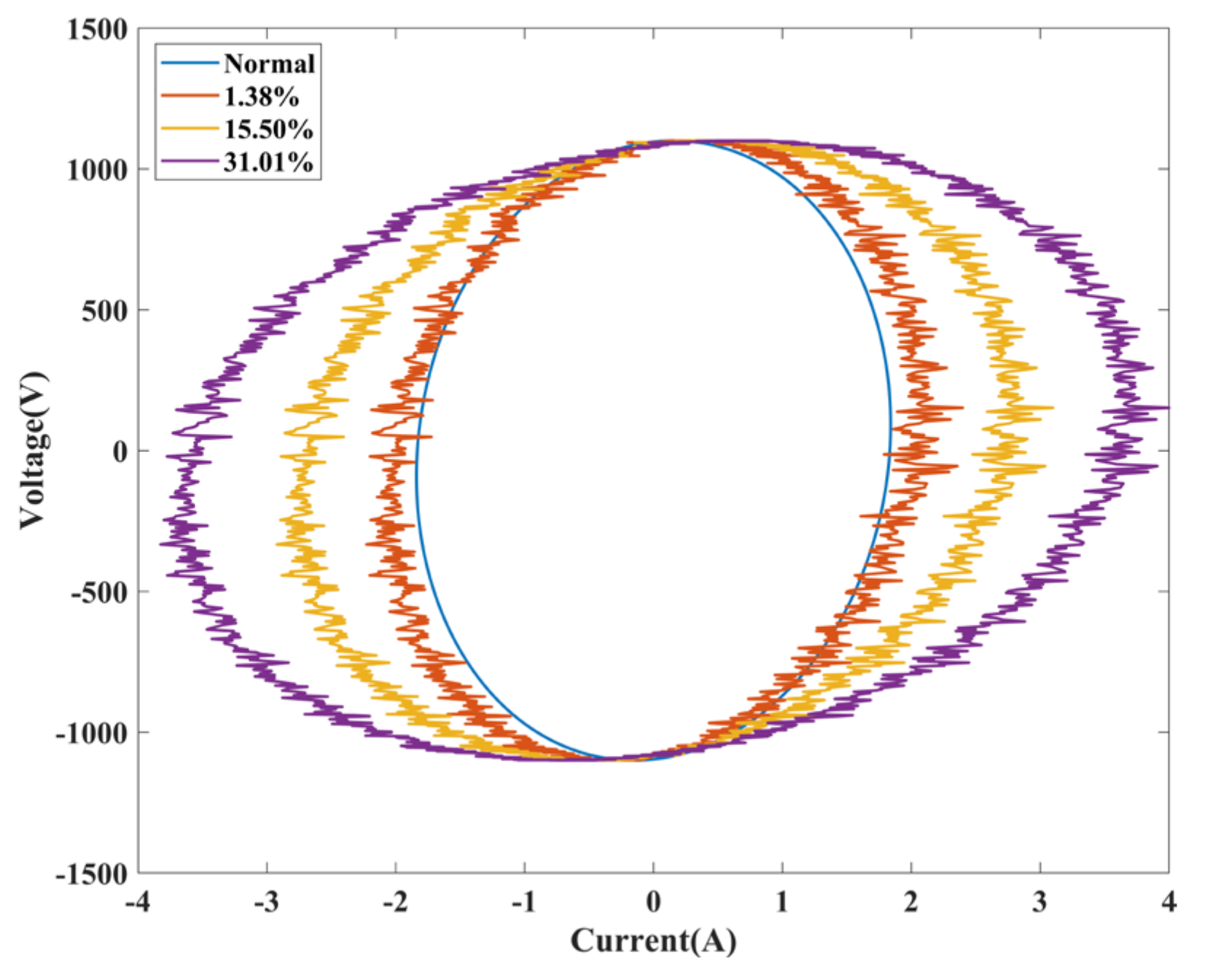
4.4. Experiment Validation
5. Diagnosis of Short-Circuit Fault in DAR Based on Lightweight Network Model
5.1. MobilenetV3-Small Model
5.2. Dataset and Pre-Processing
5.3. Model Performance Evaluation
6. Conclusions
- (1)
- The Lissajous graphs are demonstrated to efficiently characterize the winding status of the DAR. The Lissajous graphs change with the degree of short circuit faults, and the more severe the ITSC, the larger the pattern area will significantly increase and rotate clockwise.
- (2)
- In the characteristic parameters of Lissajous graphs, the short axis b and inclination angle θ change significantly with the degree of fault. Simulation and experimental verification results show that the change rate of inclination angle θ is particularly significant, with variation ranging from 114.63% to 475.61% in simulation cases and variation ranging from 9.78% to 444.80% in experiment cases.
- (3)
- Using the lightweight network model MobileNetV3 Small can significantly improve the ability to diagnose ITSC faults, with a fault diagnosis accuracy of 95.91% and a model parameter of 0.88 M. It also has a faster computation speed and better performance than those of other algorithms, which has the potential to achieve reliable monitoring and identification in the early stages of faults.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, J.; Zhen, W.; Chang, Z.W.; Zhang, M.; Peng, Y.M.; Liu, Y.; Huang, Q. A Detection Method for Slight Inter-Turn Short-Circuit Fault in Dry-Type Air-Core Shunt Reactors. Energies 2024, 17, 1709. [Google Scholar] [CrossRef]
- Hou, Y.M.; Qi, L.; Zhang, X.Y.; Han, S.Y.; Zhang, S.; Cui, X. Analytic calculation of external magnetic field of high voltage toroid-type air-core reactors. IEEE Trans. Power Del. 2023, 38, 3398–3405. [Google Scholar] [CrossRef]
- Yuan, F.T.; Yuan, Z.; Chen, L.X.; Wang, Y.; Liu, J.X.; He, J.J.; Pan, Y. Thermal and Electromagnetic Combined Optimization Design of Dry Type Air Core Reactor. Energies 2017, 10, 1989. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.Y.; Pan, Z.H.; Lu, H.L.; Wen, X.S.; Jiang, Z.P.; Chen, B.; Chen, T.T. Theoretical and Experimental Evaluation of the Temperature Distribution in a Dry Type Air Core Smoothing Reactor of HVDC Station. Energies 2017, 10, 623. [Google Scholar] [CrossRef]
- Wu, J.; Chang, Z.W.; Zhang, H.J.; Zhang, M.; Peng, Y.M.; Liao, J.; Huang, Q. Thermal Simulation and Analysis of Dry-Type Air-Core Reactors Based on Multi-Physics Coupling. Energies 2023, 16, 7456. [Google Scholar] [CrossRef]
- Jin, S.; E, Y.Y.; Zhu, L.; Li, C.; Yang, Y.C.; Wu, Z.W. Research on the diagnosis method of inter-turn short-circuit faults of dry-type air-core reactor winding based on frequency response analysis. AIP Adv. 2024, 14, 065015. [Google Scholar] [CrossRef]
- Chen, Y.H.; Xie, Y.Z.; Li, K.J.; Zhou, Y.; Gao, C.; Zhang, D.Z. Impedance Determination for High Voltage Air-Core Reactor Over Wide Frequency Range Based on Impulse Injection Technique. IEEE Trans. Power Del. 2020, 35, 1909–1917. [Google Scholar] [CrossRef]
- Zhou, X.; Tian, T.; Li, X.G.; Chen, K.; Luo, Y.; He, N.H.; Liu, W.F.; Ma, Y.L.; Bai, J.; Zhang, X.X.; et al. Study on insulation defect discharge features of dry-type reactor based on audible acoustic. AIP Adv. 2022, 12, 025210. [Google Scholar] [CrossRef]
- Zadehgol, A.; Lei, H.T.; Johnson, B.K. A Methodology for Remote Sensing Inter-Turn Fault Events in Power System Air-Core Reactors, via Simulation of Magneto Quasi-Static Fields in 2D FDTD. IEEE Access 2020, 8, 175727–175740. [Google Scholar] [CrossRef]
- Xiao, Y.; Cao, J.A.; Xiong, X.; Zhu, L.Y.; Ji, S.C. Research on Vibration Measurement Method and Analysis of Air-core Reactor. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 6–10. [Google Scholar] [CrossRef]
- Zhu, L.Y.; Du, Y.M.; Lu, G.; Zhuang, Z.; Ji, S.C. Vibration Distribution Detection Method for Turn-to-Turn Short-Circuit Fault of Dry-Type Air-Core Filter Reactors. IEEE Trans. Power Del. 2022, 37, 4474–4476. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Z.Y.; Yu, Y.Q.; Wang, W.; Tang, C. Understanding IFRA for Detecting Synchronous Machine Winding Short Circuit Faults Based on Image Classification and Smooth Grad-CAM++. IEEE Sens. J. 2023, 23, 2422–2432. [Google Scholar] [CrossRef]
- Hechifa, A.; Labiod, C.; Lakehal, A.; Nanfak, A.; Mansour, D.A. A Novel Graphical Method for Interpretating Dissolved Gases and Fault Diagnosis in Power Transformer Based on Dynamique Axes in Circular Form. IEEE Trans. Power Del. 2024, 39, 3186–3198. [Google Scholar] [CrossRef]
- Amaral, T.G.; Pires, V.F.; Foito, D.; Cordeiro, A.; Rocha, J.; Chaves, M. A Fault Detection and Diagnosis Method Based on the Currents Entropy Indexes for the SRM Drive with a Fault Tolerant Multilevel Converter. IEEE Trans. Ind. Appl. 2024, 60, 520–531. [Google Scholar] [CrossRef]
- Zhang, L.H.; Song, J.C.; Wang, X.X.; Lu, J.F.; Lu, S.L. High-Resistance Connection Fault Diagnosis of SRM Based on Multisensor Calibrated Transformer with Shifted Windows. IEEE Sens. J. 2023, 23, 30971–30983. [Google Scholar] [CrossRef]
- Wang, Z.S.; Xuan, J.P.; Shi, T.L. An autonomous recognition framework based on reinforced adversarial open set algorithm for compound fault of mechanical equipment. Mech. Syst. Signal Process. 2024, 219, 111596. [Google Scholar] [CrossRef]
- Wang, Z.S.; Xuan, J.P.; Shi, T.L. Domain reinforcement feature adaptation methodology with correlation alignment for compound fault diagnosis of rolling bearing. Expert Syst. Appl. 2025, 262, 125594. [Google Scholar] [CrossRef]
- Wang, Z.S.; Xuan, J.P.; Shi, T.L.; Li, Y.F. Multi-label domain adversarial reinforcement learning for unsupervised compound fault recognition. Reliab. Eng. Syst. Saf. 2025, 254, 110638. [Google Scholar] [CrossRef]
- Song, H.; Zou, L.; Zhang, X.Q.; Zhang, L.; Zhao, T. Inter-Turn Short-Circuit Detection of Dry-Type Air-Core Reactor Based on Spatial Magnetic Field Distribution. Trans. China Electrotech. Soc. 2019, 34, 105–117. [Google Scholar] [CrossRef]
- Yao, C.G.; Zhao, Z.Y.; Mi, Y.; Li, C.X.; Liao, Y.F.; Qian, G.C. Improved Online Monitoring Method for Transformer Winding Deformations Based on the Lissajous Graphical Analysis of Voltage and Current. IEEE Trans. Power Del. 2015, 30, 1965–1973. [Google Scholar] [CrossRef]
- Li, C.X.; Zhu, T.Y.; Yao, C.G.; Xia, Q.; Mi, Y.; Zhao, Z.Y. Online Diagnosis Method for Transformer Winding Deformation Based on Characteristic of Figure Constructed by Voltage and Current. High Volt. Eng. 2018, 44, 3532–3539. [Google Scholar] [CrossRef]
- Masoum, A.S.; Hashemnia, N.; Abu-Siada, A.; Masoum, M.A.S.; Islam, S.M. Online Transformer Internal Fault Detection Based on Instantaneous Voltage and Current Measurements Considering Impact of Harmonics. IEEE Trans. Power Del. 2017, 32, 587–598. [Google Scholar] [CrossRef]
- Zhou, J.; Cen, B.W.; Cai, Z.X.; Chen, Y.J.; Sun, Y.Y.; Xue, H.L. Workload Modeling for Microservice-Based Edge Computing in Power Internet of Things. IEEE Access 2021, 9, 76205–76212. [Google Scholar] [CrossRef]
- Tan, M.X.; Chen, B.; Pang, R.M.; Vasudevan, V.; Sandler, M.; Howard, A.; Le, Q.V. Mnasnet: Platform-aware neural architecture search for mobile. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2820–2828. [Google Scholar] [CrossRef]
- Yang, T.J.; Howard, A.; Chen, B.; Zhang, X.; Go, A.; Sandler, M.; Sze, V.; Adam, H. Netadapt: Platform-aware neural network adaptation for mobile applications. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 285–300. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.X.; Wang, W.J.; Zhu, Y.K.; Pang, R.M.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar] [CrossRef]








| Parameter | Value | Parameter | Value |
|---|---|---|---|
| System Voltage/kV | 35 | Number of coils | 20 |
| Rated capacity/kV·A | 2000 | Number of encapsulations | 5 |
| Rated current/A | 57.14 | Inner Diameter/mm | 2006.5 |
| Frequency/Hz | 50 | Outer Diameter/mm | 2345.3 |
| Layer | Degree (%) | Short Axis b (%) | Inclination Angle θ (%) |
|---|---|---|---|
| Normal (0.00%) | 1.840 (0.00%) | 0.0082° (0.00%) | |
| Layer 1 | Slight (1.38%) | 2.013 (9.39%) | 0.0176° (114.63%) |
| Moderate (15.50%) | 2.715 (47.57%) | 0.0244° (197.56%) | |
| Severe (31.01%) | 3.611 (96.27%) | 0.0350° (326.83%) | |
| Layer 5 | Slight (1.38%) | 2.071 (12.56%) | 0.0273° (232.97%) |
| Moderate (15.50%) | 2.856 (55.21%) | 0.0345° (320.73%) | |
| Severe (31.01%) | 3.851 (109.32%) | 0.0463° (464.63%) | |
| Layer 9 | Slight (1.38%) | 2.099 (14.06%) | 0.0281° (242.68%) |
| Moderate (15.50%) | 2.902 (57.73%) | 0.0348° (324.39%) | |
| Severe (31.01%) | 3.980 (116.28%) | 0.0465° (467.07%) | |
| Layer 13 | Slight (1.38%) | 2.108 (14.58%) | 0.0286° (248.78%) |
| Moderate (15.50%) | 2.941 (59.87%) | 0.0352° (329.27%) | |
| Severe (31.01%) | 4.021 (118.52%) | 0.0472° (475.61%) | |
| Layer 20 | Slight (1.38%) | 2.102 (14.26%) | 0.0283° (245.12%) |
| Moderate (15.50%) | 2.906 (57.93%) | 0.0345° (320.73%) | |
| Severe (31.01%) | 3.920 (113.03%) | 0.0463° (464.63%) |
| Degree (%) | Long Axis a (%) | Short Axis b (%) | Inclination Angle θ (%) |
|---|---|---|---|
| Normal (0.00%) | 14.0331 (0.00%) | 2.6435 (0.00%) | 1.2357 (0.00%) |
| Slight (3.75%) | 14.0338 (0.005%) | 2.8815 (9.00%) | 1.3566 (9.78%) |
| Moderate (18.75%) | 14.0510 (0.13%) | 6.1724 (133.49%) | 3.5065 (183.77%) |
| Severe (43.00%) | 15.2159 (8.43%) | 14.0128 (430.09%) | 6.7321 (444.80%) |
| Input | Operator | Exp Size | Out Size | SE | NL | s |
|---|---|---|---|---|---|---|
| 224 × 224 × 3 | Conv2d, 3 × 3 | - | 16 | - | HS | 2 |
| 112 × 112 × 16 | bneck, 3 × 3 | 16 | 16 | √ | RE | 2 |
| 56 × 56 × 16 | bneck, 3 × 3 | 72 | 24 | - | RE | 2 |
| 28 × 28 × 24 | bneck, 3 × 3 | 88 | 24 | - | RE | 1 |
| 28 × 28 × 24 | bneck, 5 × 5 | 96 | 40 | √ | HS | 2 |
| 14 × 14 × 40 | bneck, 5 × 5 | 240 | 40 | √ | HS | 1 |
| 14 × 14 × 40 | bneck, 5 × 5 | 240 | 40 | √ | HS | 1 |
| 14 × 14 × 40 | bneck, 5 × 5 | 120 | 48 | √ | HS | 1 |
| 14 × 14 × 48 | bneck, 5 × 5 | 144 | 48 | √ | HS | 1 |
| 14 × 14 × 48 | bneck, 5 × 5 | 288 | 96 | √ | HS | 2 |
| 7 × 7 × 96 | bneck, 5 × 5 | 576 | 96 | √ | HS | 1 |
| 7 × 7 × 96 | bneck, 5 × 5 | 576 | 96 | √ | HS | 1 |
| 7 × 7 × 96 | conv2d, 1 × 1 | - | 576 | √ | HS | 1 |
| 7 × 7 × 576 | pool, 7 × 7 | - | - | - | - | 1 |
| 1 × 1 × 576 | conv2d, 1 × 1, NBN | - | 1024 | - | HS | 1 |
| 1 × 1 × 1024 | conv2d, 1 × 1, NBN | - | k | - | - | 1 |
| Fault Degree | Train Data | Test Data | Total Data |
|---|---|---|---|
| Normal | 554 | 238 | 792 |
| Slight fault | 568 | 244 | 812 |
| Moderate fault | 588 | 252 | 840 |
| Severe fault | 672 | 288 | 960 |
| Fault Degree | Test Accuracy/% | Parameters/M | FLOPs |
|---|---|---|---|
| MobileNetV3-Small | 95.91% | 0.880 M | 3.41 × 107 |
| MobileVIT-Attention | 95.50% | 1.013 M | 2.73 × 108 |
| ShufflenetV2 | 94.38% | 11.824 M | 1.14 × 109 |
| ViT-Small | 84.44% | 21.416 M | 4.59 × 109 |
| Swin-Small | 96.11% | 49.937 M | 8.71 × 109 |
| Fault Degree | Algorithm Model | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|
| Normal | MobileNetV3 | 100.00% | 100.00% | 100.00% |
| ShuffeNetV2 | 100% | 99.16% | 99.58% | |
| MobileVIT-Attention | 100% | 100% | 100% | |
| ViT-Small | 100% | 99.01% | 99.50% | |
| Swin-Small | 100% | 100% | 100% | |
| Slight fault | MobileNetV3 | 96.30% | 95.07% | 95.68% |
| ShuffeNetV2 | 95.26% | 94.85% | 95.05% | |
| MobileVIT-Attention | 95.99% | 94.97% | 95.48% | |
| ViT-Small | 85.47% | 84.03% | 84.74% | |
| Swin-Small | 96.69% | 96.23% | 96.46% | |
| Moderate fault | MobileNetV3 | 95.12% | 95.91% | 95.51% |
| ShuffeNetV2 | 94.90% | 95.08% | 94.99% | |
| MobileVIT-Attention | 95.09% | 94.80% | 94.94% | |
| ViT-Small | 77.46% | 82.13% | 79.73% | |
| Swin-Small | 93.56% | 93.07% | 93.31% | |
| Severe fault | MobileNetV3 | 95.96% | 96.30% | 96.13% |
| ShuffeNetV2 | 95.78% | 96.08% | 95.93% | |
| MobileVIT-Attention | 94.96% | 95.99% | 95.47% | |
| ViT-Small | 74.03% | 72.15% | 73.08% | |
| Swin-Small | 96.03% | 96.15% | 96.09% |
| Fault Degree | Fault Type | Diagnostic Results | |
|---|---|---|---|
| 0.56% | Slight | Slight | √ |
| 2.86% | Slight | Slight | √ |
| 3.75% | Slight | Slight | √ |
| 5.42% | Moderate | Slight | × |
| 18.75% | Moderate | Moderate | √ |
| 43.00% | Severe | Severe | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, B.; Dang, X.; Zhu, J.; Chen, L.; Tang, C.; Zhao, Z. Diagnostics of Inter-Turn Short Circuit Fault in Dry-Type Air-Core Reactor Based on Lissajous Graph and Lightweight Network Model. Energies 2025, 18, 1132. https://doi.org/10.3390/en18051132
Xiang B, Dang X, Zhu J, Chen L, Tang C, Zhao Z. Diagnostics of Inter-Turn Short Circuit Fault in Dry-Type Air-Core Reactor Based on Lissajous Graph and Lightweight Network Model. Energies. 2025; 18(5):1132. https://doi.org/10.3390/en18051132
Chicago/Turabian StyleXiang, Binglong, Xiaojing Dang, Junlin Zhu, Lian Chen, Chao Tang, and Zhongyong Zhao. 2025. "Diagnostics of Inter-Turn Short Circuit Fault in Dry-Type Air-Core Reactor Based on Lissajous Graph and Lightweight Network Model" Energies 18, no. 5: 1132. https://doi.org/10.3390/en18051132
APA StyleXiang, B., Dang, X., Zhu, J., Chen, L., Tang, C., & Zhao, Z. (2025). Diagnostics of Inter-Turn Short Circuit Fault in Dry-Type Air-Core Reactor Based on Lissajous Graph and Lightweight Network Model. Energies, 18(5), 1132. https://doi.org/10.3390/en18051132







