Pathways to Positive Energy Districts: A Comprehensive Techno-Economic and Environmental Analysis Using Multi-Objective Optimization
Abstract
1. Introduction
1.1. Concept of Positive Energy Districts
1.2. Metrics and Benchmarks for Assessing PEDs
1.3. Engaging Multiple Stakeholders of PEDs
1.4. Integration of Technical Solutions
1.5. Tools and Methods for PED Optimal Design
1.6. Scope of This Work
| Reference | KPIs 1 | Evaluation | Solutions 3 | Method 4 | Location | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EnerP | EnviP | EcoP | Metric 2 | RES | Sto | Retro | DSM | Elect | |||
| Marrasso et al. [26] | Y | Y | STC, | TES, | - | Italy | |||||
| PV, WT | PtH2 | ||||||||||
| Bruck et al. [2] | Y | Y | Y | PEF | PV | BAT | MILP | Spain | |||
| Bruck et al. [12] | Y | Y | Y | PEF | PV | Y | Y | MILP | Spain | ||
| Germany | |||||||||||
| Sweden | |||||||||||
| Laitinen et al. [25] | Y | Y | Y | PV, WT | BAT | Y | LP | Finland | |||
| Blumberga et al. [27] | Y | Y | PEF | PV | BAT | - | Latvia | ||||
| An et al. [28] | Y | Y | BIPV | Y | Y | - | South Korea | ||||
| Guarino et al. [6] | Y | Y | PV | Y | - | Spain | |||||
| Gouveia et al. [21] | Y | Y | Y | BIPV | Y | - | Portugal | ||||
| Bambara et al. [29] | Y | Y | PEF | BIPV | Y | Y | - | Canada | |||
| Volpe et al. [13] | Y | Y | PV, BIO | Y | - | Italy | |||||
| Guasselli et al. [22] | Y | Y | PV, GEO | Y | Y | - | Norway | ||||
- Which metrics and benchmarks are used to assess PEDs?
- For a specific case, what are the feasible solutions to achieve PEDs?
- What is the most cost-effective pathway to implementing PEDs in specific scenarios?
2. Methodology
2.1. System Framework
2.2. Mathematical Model
2.3. Objective Functions
2.3.1. Total Annual Cost
2.3.2. Carbon Emissions
2.4. Key Performance Indicators
2.4.1. Evaluation of Financial Profitability
2.4.2. Evaluation of PEDs’ Carbon Neutrality
2.4.3. Self-Sufficient Ratio
2.4.4. Self-Consumption Ratio
2.4.5. LCOEx
2.5. Case Study
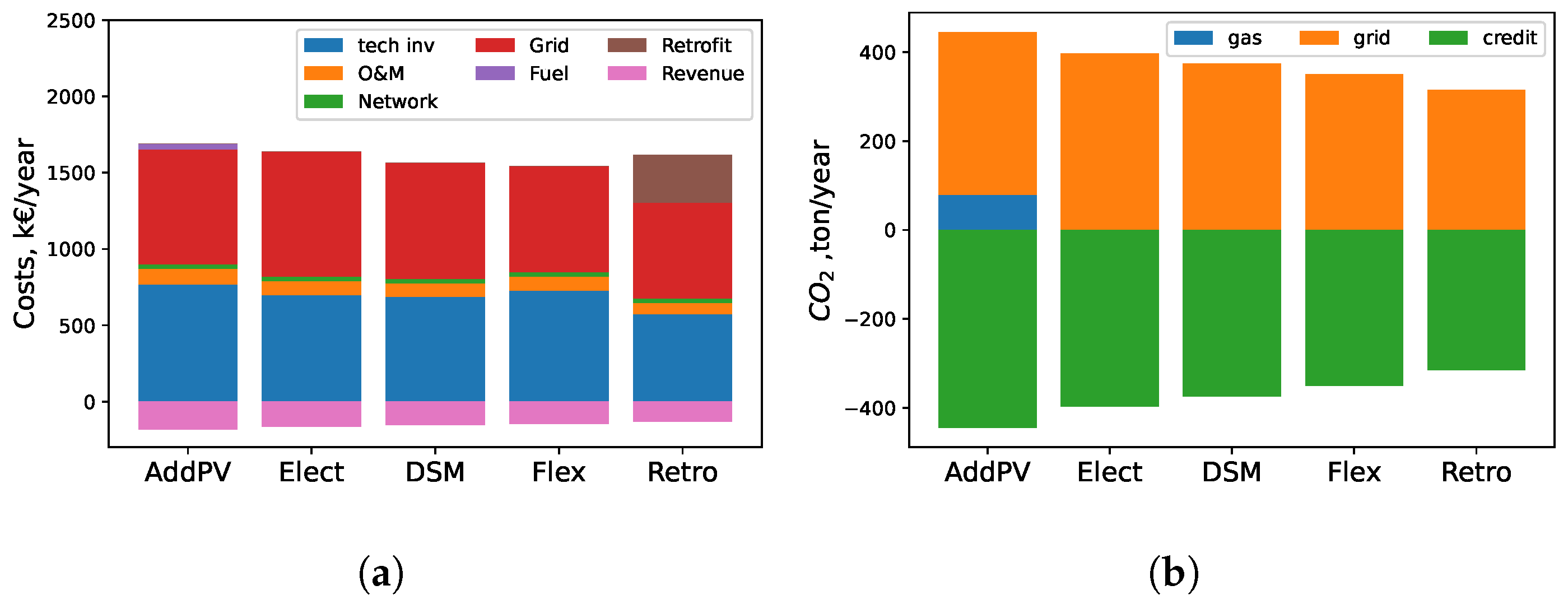
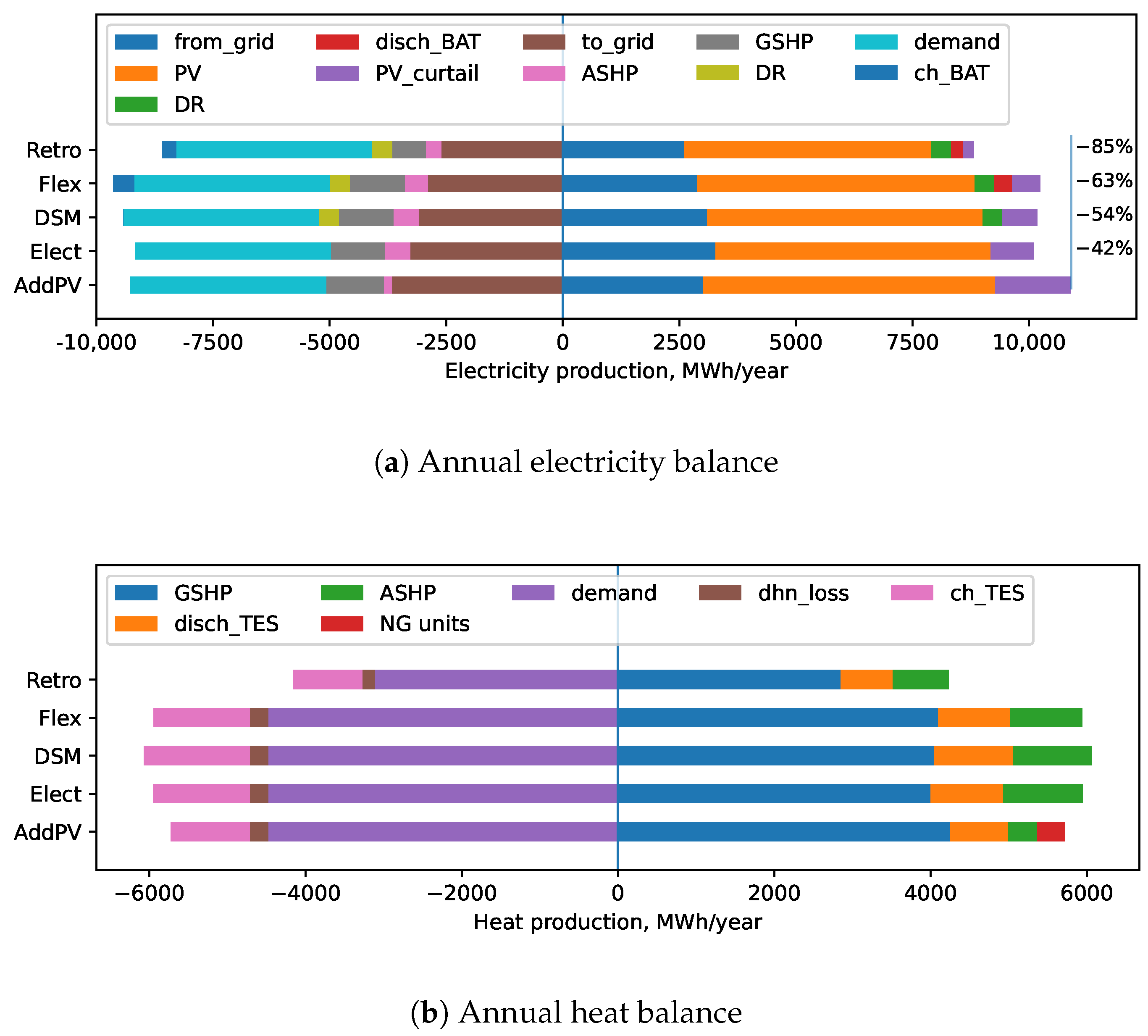
2.6. Investigated Scenarios
- BAU. This scenario represented the status quo, with no PV installations. A natural gas boiler supplied high-temperature heat demand, the grid met all electricity demand, and a compression chiller covered cooling demand.
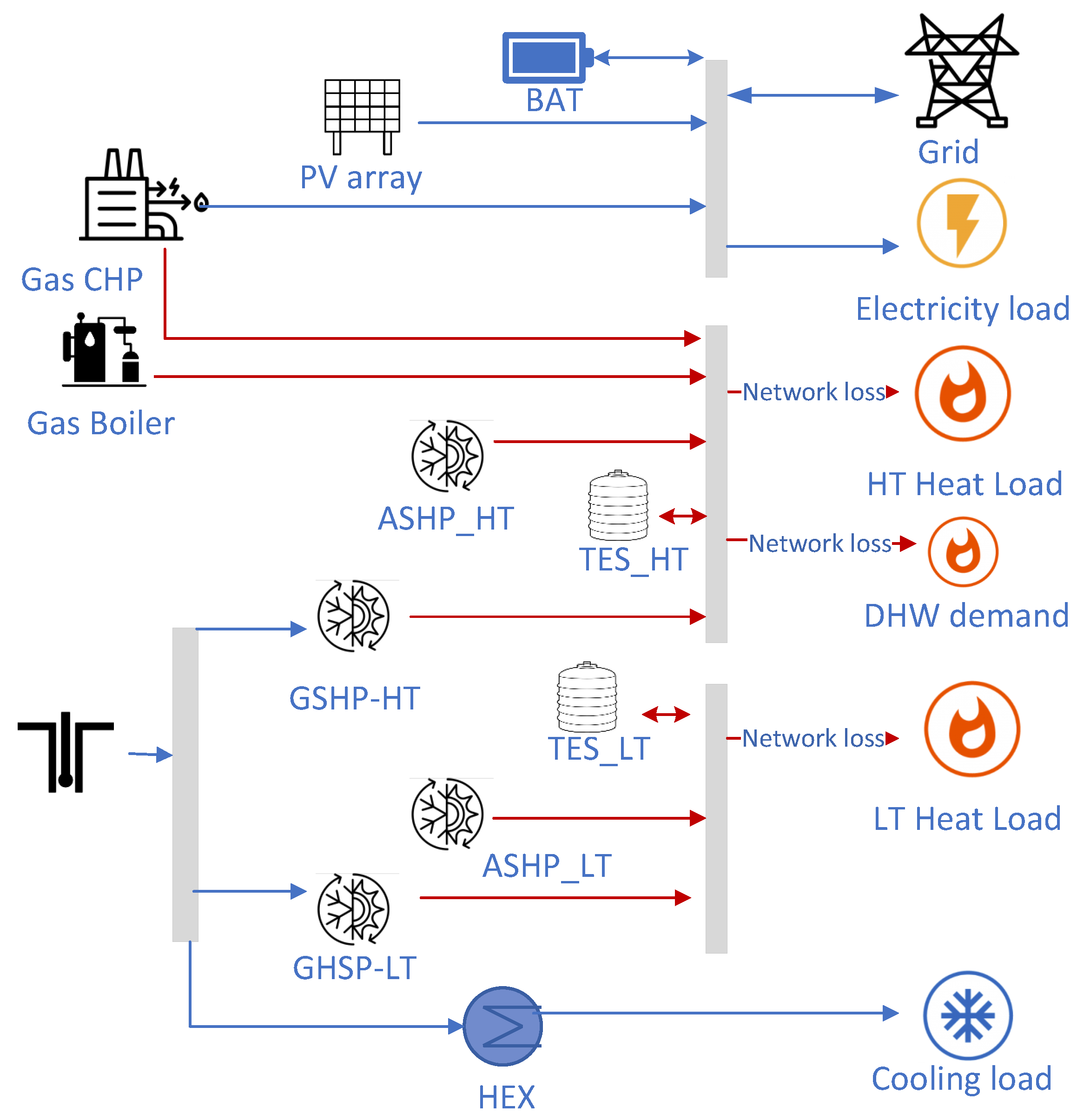
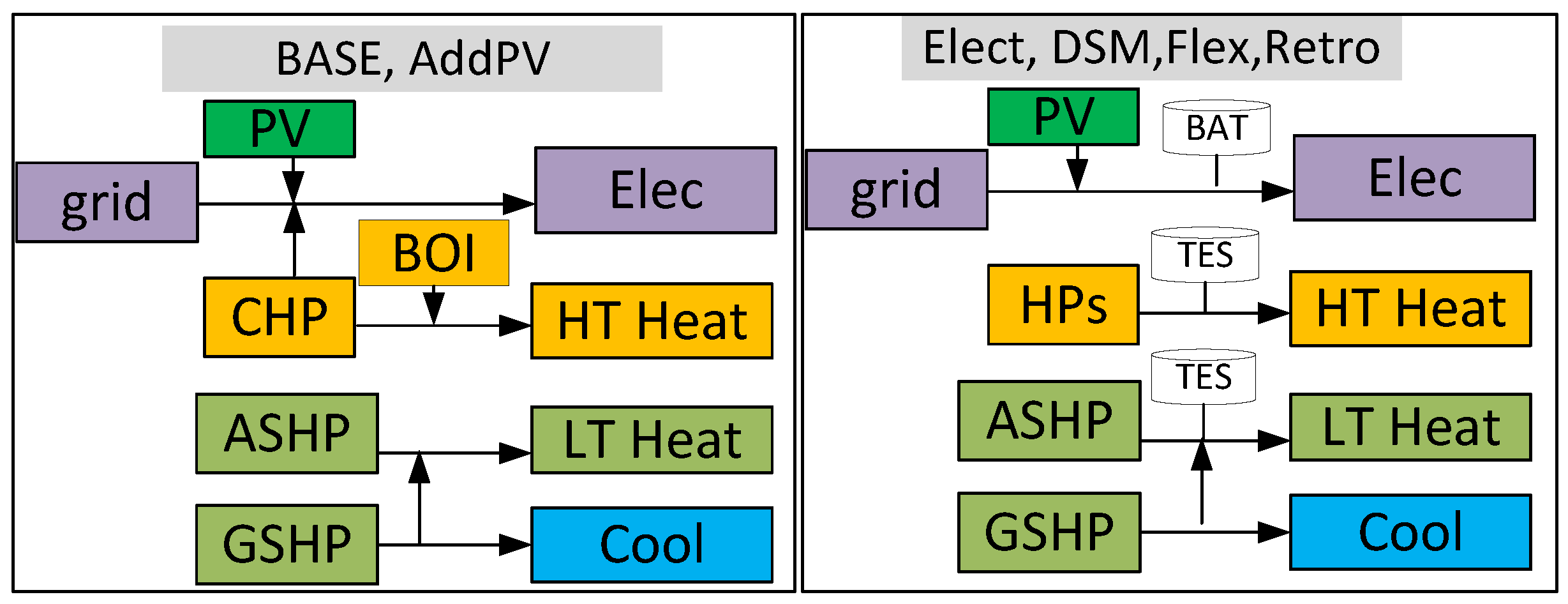
- BASE. The baseline scenario reflected the optimal energy system to be designed, as described in Figure 3. A combination of PV, grid, and a natural-gas CHP met electricity demand. Cooling demand was handled by passive cooling, high-temperature heat demand by a CHP, BOI, and GSHP, and low-temperature heat demand by an ASHP and a GSHP.
- AddPV. In this study, the BASE scenario, limited by available PV roof area, failed to meet carbon-neutral targets. The AddPV scenario addressed this by introducing virtual PEDs, allowing renewable energy imports beyond the geographical boundary. Based on preliminary results, the upper limit of the design variable—the PV roof area—was set at five times the initial capacity to ensure carbon neutrality, although utilizing the maximum area may not be necessary.
- Elect. Additionally to AddPV, this scenario assumed that all energy demands were met by electrical devices, with no NG-based units allowed. Instead, high-temperature heat pumps, including a geothermal heat pump and an air-source heat pump, were utilized to fulfill high-temperature heat demands. This approach is illustrated in Figure 3.
- DSM. In addition to Elect, this scenario incorporated demand response by shifting electricity demand with a dynamic time-of-use (TOU) tariff. A detailed description of the approach is described in Appendix A.4.2.
- Flex. Building on DSM, this scenario included battery storage to utilize energy surplus [10] properly.
- Retro. In addition to the Flex scenario, this approach involved retrofitting the building envelopes of older structures. According to the report by EU Smart Cities Information System (SCIS) [49], and data provided by TABULA [50], after the retrofits, space heating energy needs for the older buildings were assumed to drop by 50% and could be met by a low-temperature heating network (50/40 °C). The spacing heating demands after retrofit is shown in Figure A1i.
3. Results
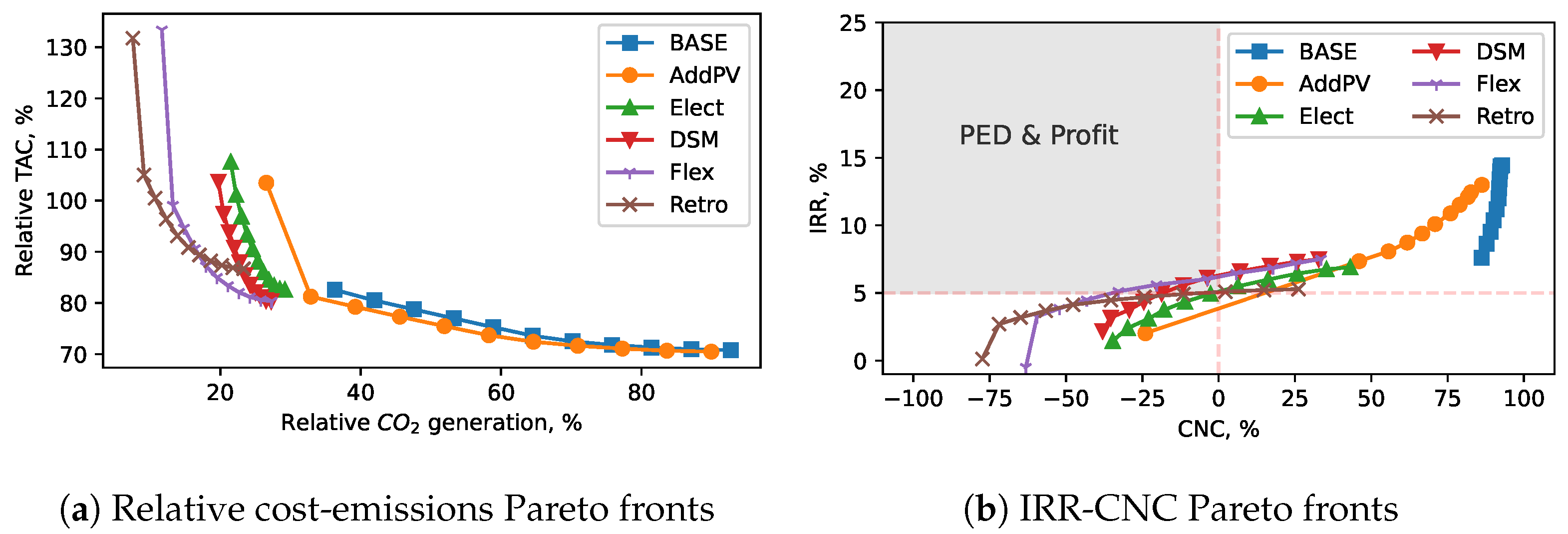
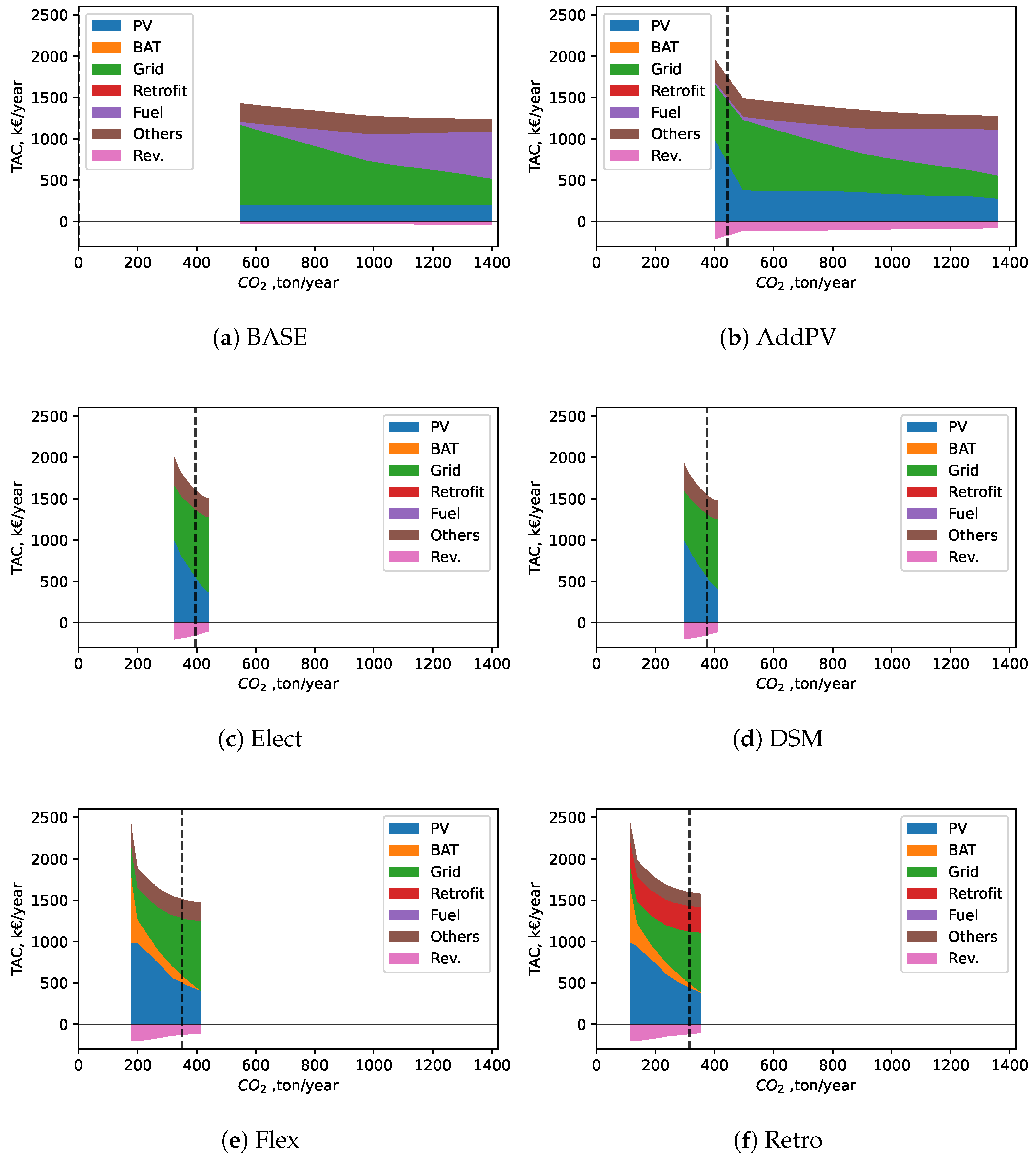
3.1. Results of Pareto Fronts
3.2. Optimal Strategies Towards Positive Energy Districts
3.2.1. Definition of PED Points
3.2.2. Results with PED Constraint Requirements
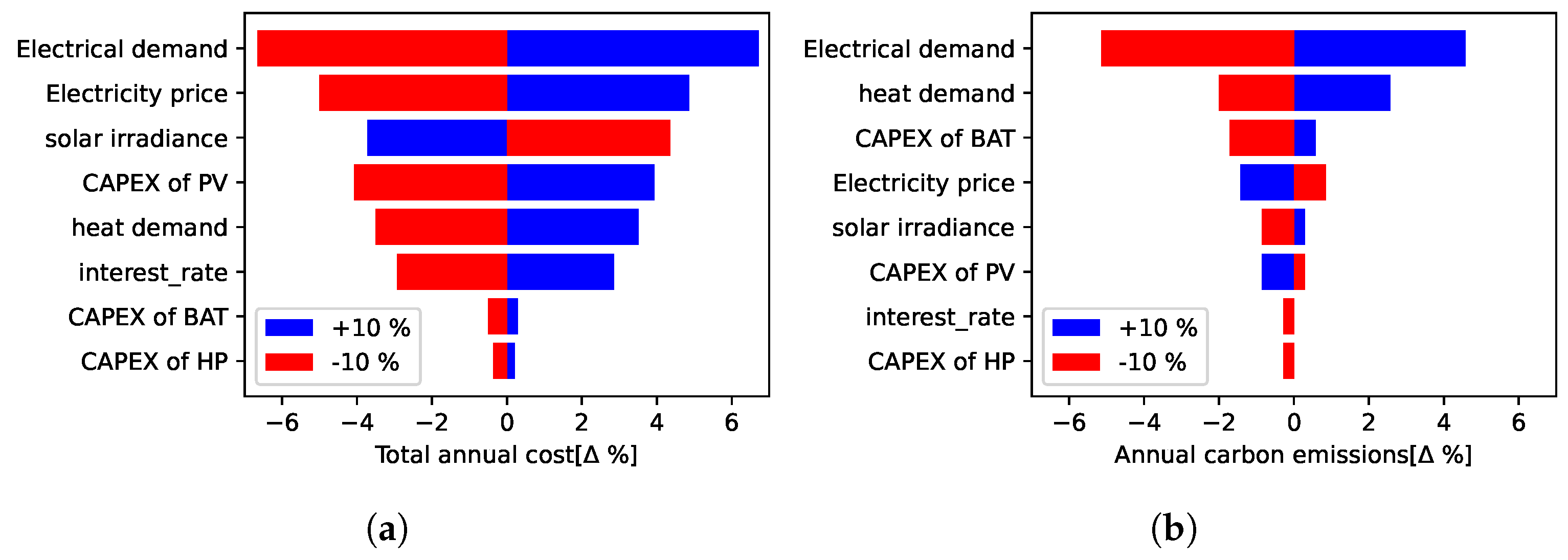
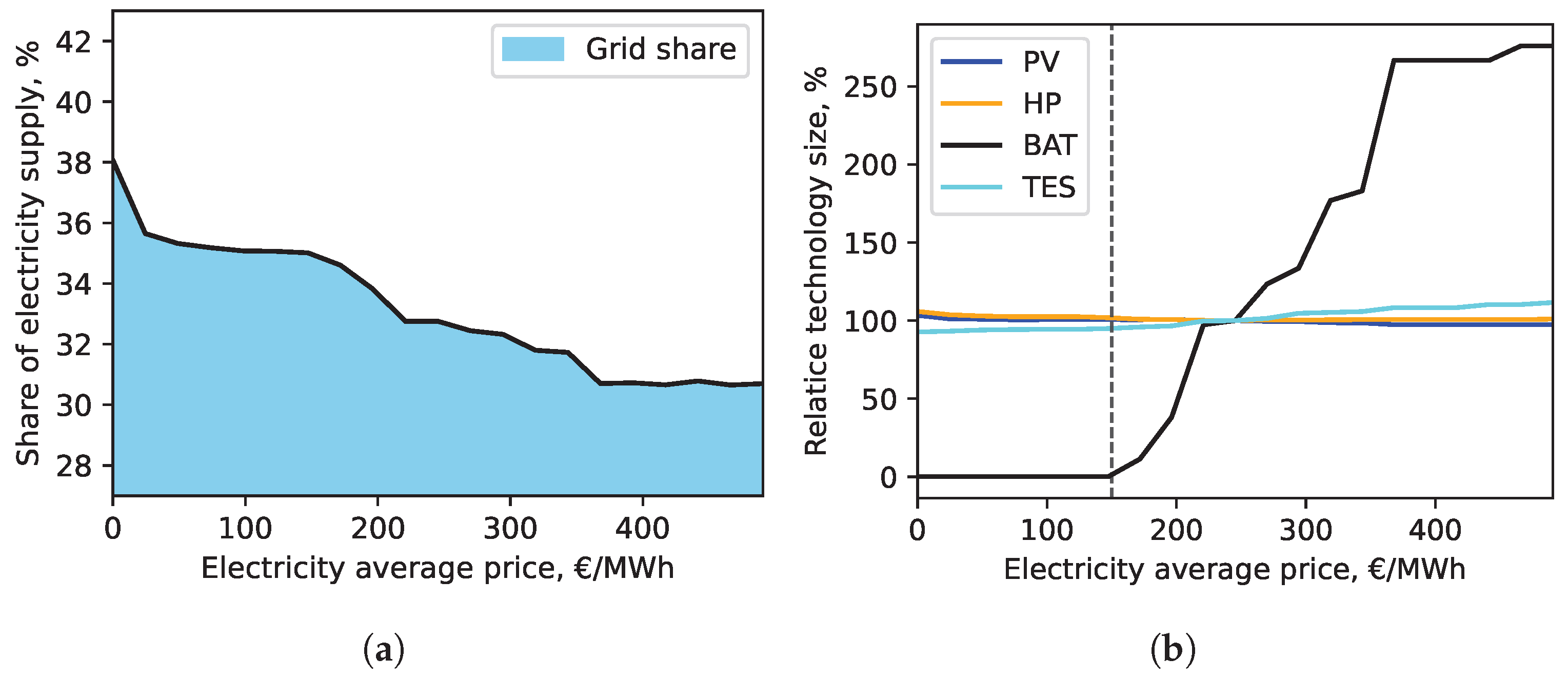
3.3. Sensitivity Analysis
4. Discussion and Limitations
4.1. Discussions of Technical Solutions to PEDs
4.2. Limitations
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BAU | Business-As-Usual |
| CAPEX | Capital expenditure |
| CE | Carbon emissions |
| CF | Cash flow |
| COP | Coefficient of performance |
| CRF | Capital recovery factor |
| CNC | Carbon Neutrality Check |
| DHW | Domestic hot water |
| DR | Demand response |
| DSM | Demand-side management |
| EcoP | Economic performance |
| EnerP | Energy performance |
| EnviP | Environmental performance |
| HRES | Hybrid renewable energy system |
| IRR | Internal rate of return |
| KPI | Key performance indicator |
| LCOEx | Levelized Cost of Exergy |
| MES | Multi-energy system |
| MILP | Mixed-Integer Linear Programming |
| NPV | Net present value |
| OPEX | Operating expenditure |
| Power-to-hydrogen | |
| PCE | Polynomial Chaos Expansion |
| PED | Positive Energy District |
| PEF | Primary Energy Factor |
| PLR | Part-load ratio |
| RES | Renewable energy source |
| SCR | Self-consumption ratio |
| SDGs | Sustainable Development Goals |
| SET | Strategic Energy Technology |
| SH | Space heating |
| SSR | Self-Sufficiency Ratio |
| SV | Salvage value |
| TAC | Total annual cost |
| TES | Thermal energy storage |
| TOU | Time-of-use |
| TRL | Technology readiness level |
Appendix A. Detailed Description of the Optimization Problem
Appendix A.1. System Components
Appendix A.1.1. PV Array
Appendix A.1.2. BOI
Appendix A.1.3. CHP
Appendix A.1.4. Heat Pump
Appendix A.2. Energy Storage
Appendix A.3. Energy Balance
Appendix A.4. Constraints
Appendix A.4.1. Minimum Part Load
Appendix A.4.2. Demand Response Program
Appendix B. Input Data
| Energy Device | Investment Cost | O&M Costs | Lifetime | Ref. |
|---|---|---|---|---|
| [EUR/kW(h)] | [%] | [Years] | ||
| PV array | 1100 | 1 | 15 | Own data |
| Li-ion battery | 285 | 2.2 | 12 | [59] |
| TES | 22 | 2.3 | 20 | Own data |
| CHP | 1100 | 1 | 15 | Own data |
| BOI | 150 | 2.2 | 20 | Own data |
| ASHP | 550 | 1.2 | 20 | Own data |
| GSHP | 430 | 1.2 | 20 | Own data |
| Geothermal drilling | 3365 | 0.75 | 40 | Own data |
| Energy Device | Parameters | Value | Unit |
|---|---|---|---|
| CHP | Elec efficiency | 38 | % |
| Heat efficiency | 56 | % | |
| BOI | Heat efficiency | 90 | % |
| Heat pump | Coefficient of performance | Equation (A9) | % |
| Energy Device | Ref. | ||||||
|---|---|---|---|---|---|---|---|
| [−] | [−] | [] | [−] | [−] | [kWh/] | ||
| TES | 0.95 | 0.005 | 4 | 0 | 1 | 23.2 | [53,61] |
| Li-ion BAT | 0.96 | 0.001 | 3 | 0.2 | 0.8 | 45 | [53,61] |
| Parameter | Unit | Value | Ref. |
|---|---|---|---|
| Peak/off peak electricity price | EUR/kWh | 0.2875/0.2125 | [72] |
| Feed-in tariff | EUR/kWh | 0.05 | [2] |
| Carbon intensity of electricity | kg/kWh | 0.131 | [52] |
| Carbon intensity of NG | kg/kWh | 0.2 | [52] |
| tax | EUR/kg | 0 | |
| Discount rate | % | 5 | [42] |
| Grid exchange limit | kW | 2376 | [24] |
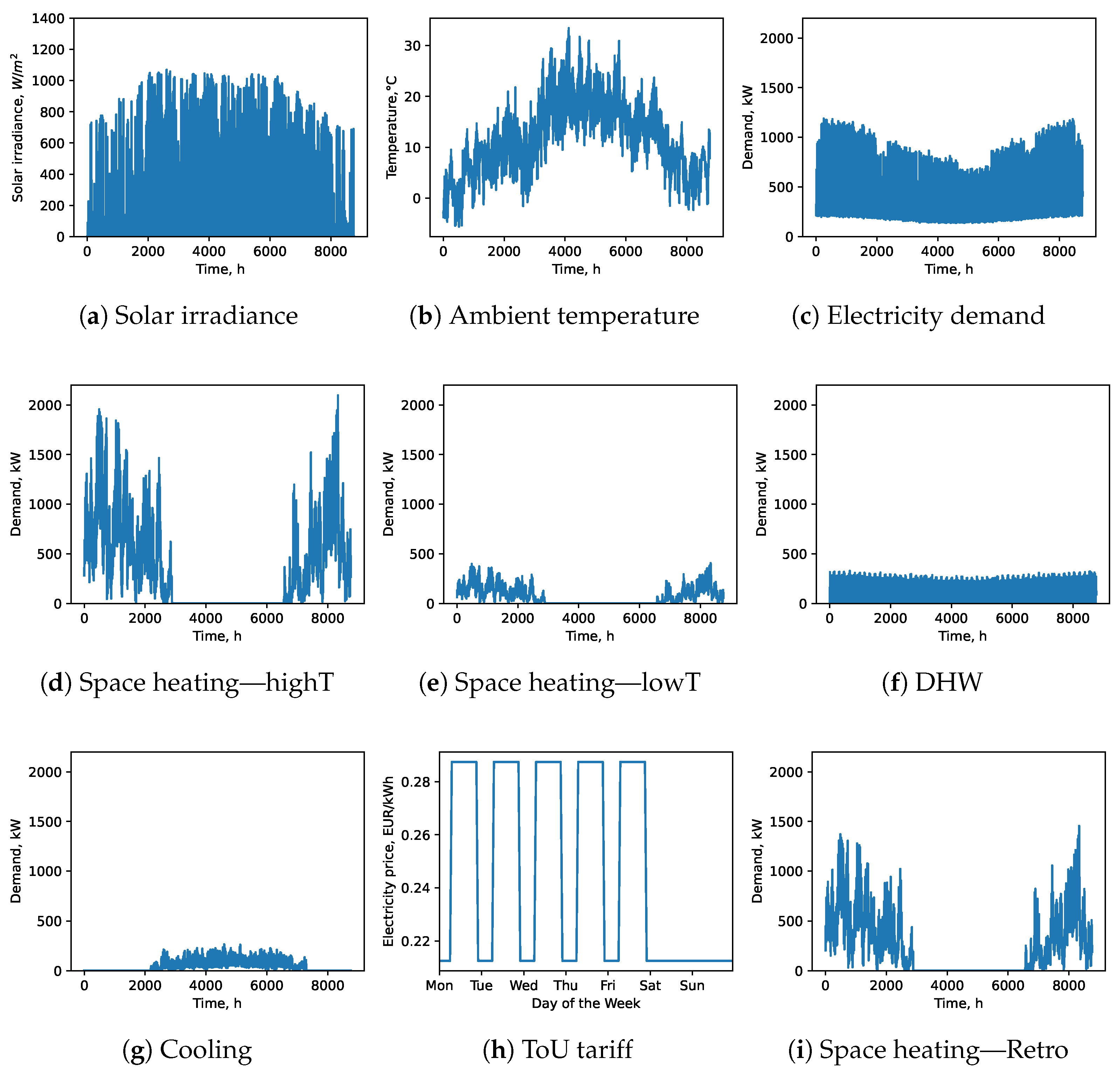
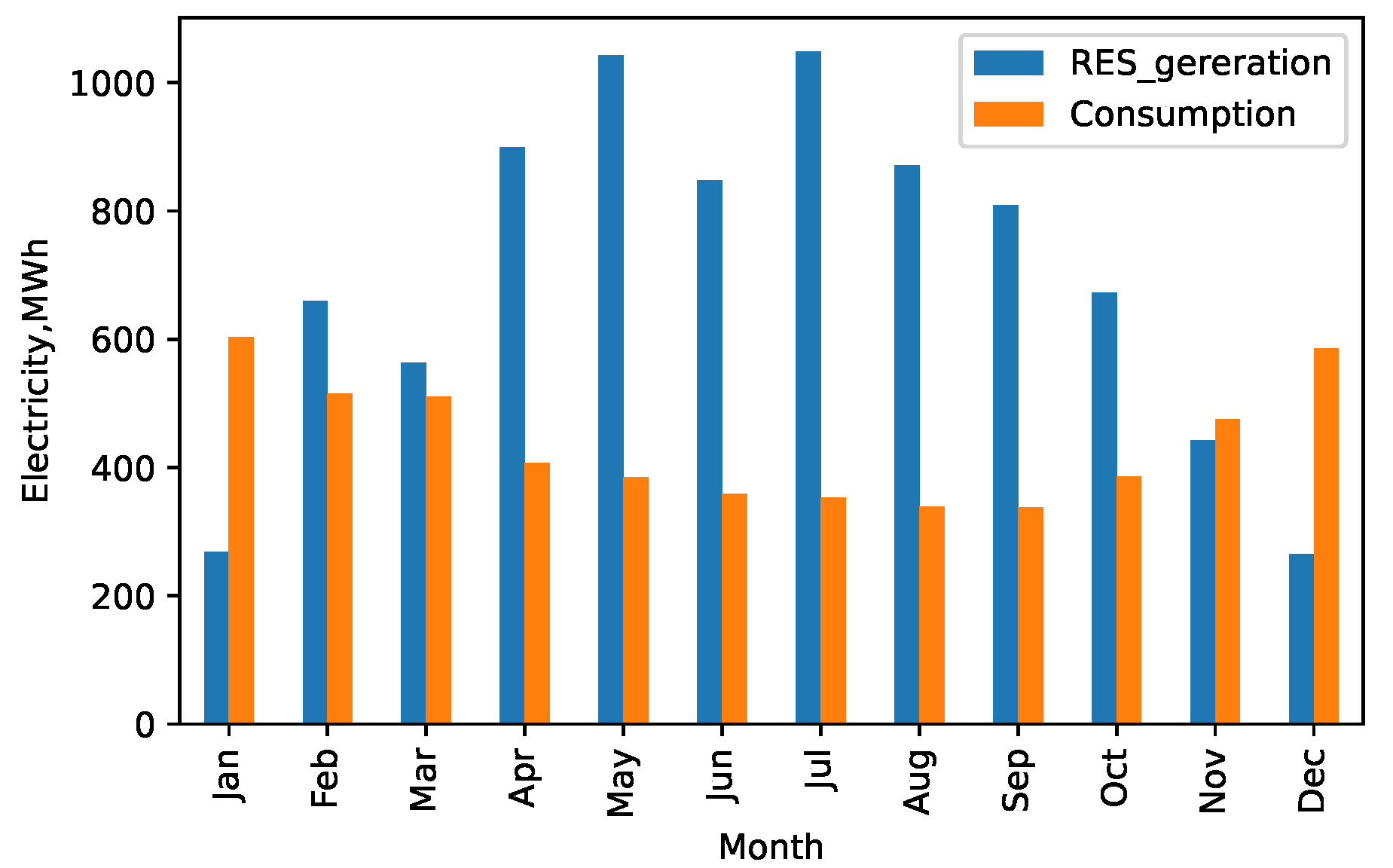
Appendix C. Detailed Results
References
- IEA. Empowering Cities for a Net Zero Future: Unlocking Resilient, Smart, Sustainable Urban Energy Systems; International Energy Agency (IEA): Paris, France, 2021; Available online: https://www.iea.org/reports/empowering-cities-for-a-net-zero-future/ (accessed on 20 February 2025).
- Bruck, A.; Díaz Ruano, S.; Auer, H. A Critical Perspective on Positive Energy Districts in Climatically Favoured Regions: An Open-Source Modelling Approach Disclosing Implications and Possibilities. Energies 2021, 14, 4864. [Google Scholar] [CrossRef]
- SET-Plan Working Group. Europe to become a global role model in integrated, innovative solutions for the planning, deployment, and replication of Positive Energy Districts. SET-Plan Action 2018, 32, 1–72. Available online: https://jpi-urbaneurope.eu/wp-content/uploads/2021/10/setplan_smartcities_implementationplan-2.pdf (accessed on 20 February 2025).
- Hinterberger, R.; Gollner, C.; Noll, M.; Meyer, S.; Schwarz, H.G. Reference Framework for Positive Energy Districts and Neighbourhoods; JPI Urban Europe: Wien, Austria, 2020; Available online: https://jpi-urbaneurope.eu/wp-content/uploads/2020/04/White-Paper-PED-Framework-Definition-2020323-final.pdf (accessed on 20 February 2025).
- Sassenou, L.N.; Olivieri, L.; Olivieri, F. Challenges for positive energy districts deployment: A systematic review. Renew. Sustain. Energy Rev. 2024, 191, 114152. [Google Scholar] [CrossRef]
- Guarino, F.; Rincione, R.; Mateu, C.; Teixidó, M.; Cabeza, L.F.; Cellura, M. Renovation assessment of building districts: Case studies and implications to the positive energy districts definition. Energy Build. 2023, 296, 113414. [Google Scholar] [CrossRef]
- Sassenou, L.N.; Olivieri, F.; Civiero, P.; Olivieri, L. Methodologies for the design of positive energy districts: A scoping literature review and a proposal for a new approach (PlanPED). Build. Environ. 2024, 260, 111667. [Google Scholar] [CrossRef]
- Lindholm, O.; Rehman, H.u.; Reda, F. Positioning Positive Energy Districts in European Cities. Buildings 2021, 11, 19. [Google Scholar] [CrossRef]
- Natanian, J.; Guarino, F.; Manapragada, N.; Magyari, A.; Naboni, E.; De Luca, F.; Cellura, S.; Brunetti, A.; Reith, A. Ten questions on tools and methods for positive energy districts. Build. Environ. 2024, 255, 111429. [Google Scholar] [CrossRef]
- Casamassima, L.; Bottecchia, L.; Bruck, A.; Kranzl, L.; Haas, R. Economic, social, and environmental aspects of Positive Energy Districts—A review. WIREs Energy Environ. 2022, 11, e452. [Google Scholar] [CrossRef]
- Gabaldón Moreno, A.; Vélez, F.; Alpagut, B.; Hernández, P.; Sanz Montalvillo, C. How to Achieve Positive Energy Districts for Sustainable Cities: A Proposed Calculation Methodology. Sustainability 2021, 13, 710. [Google Scholar] [CrossRef]
- Bruck, A.; Diaz Ruano, S.; Auer, H. Values and implications of building envelope retrofitting for residential Positive Energy Districts. Energy Build. 2022, 275, 112493. [Google Scholar] [CrossRef]
- Volpe, R.; Gonzalez Alriols, M.; Martelo Schmalbach, N.; Fichera, A. Optimal design and operation of distributed electrical generation for Italian positive energy districts with biomass district heating. Energy Convers. Manag. 2022, 267, 115937. [Google Scholar] [CrossRef]
- Marrasso, E.; Martone, C.; Pallotta, G.; Roselli, C.; Sasso, M. A novel methodology and a tool for supporting the transition of districts and communities in Positive Energy Districts. Energy Build. 2024, 318, 114435. [Google Scholar] [CrossRef]
- Sareen, S.; Albert-Seifried, V.; Aelenei, L.; Reda, F.; Etminan, G.; Andreucci, M.B.; Kuzmic, M.; Maas, N.; Seco, O.; Civiero, P.; et al. Ten questions concerning positive energy districts. Build. Environ. 2022, 216, 109017. [Google Scholar] [CrossRef]
- Andresen, I.; Healey Trulsrud, T.; Finocchiaro, L.; Nocente, A.; Tamm, M.; Ortiz, J.; Salom, J.; Magyari, A.; Hoes-van Oeffelen, L.; Borsboom, W.; et al. Design and performance predictions of plus energy neighbourhoods—Case studies of demonstration projects in four different European climates. Energy Build. 2022, 274, 112447. [Google Scholar] [CrossRef]
- Salom, J.; Tamm, M.; Andresen, I.; Cali, D.; Magyari, A.; Bukovszki, V.; Balázs, R.; Dorizas, P.V.; Toth, Z.; Zuhaib, S.; et al. An Evaluation Framework for Sustainable Plus Energy Neighbourhoods: Moving Beyond the Traditional Building Energy Assessment. Energies 2021, 14, 4314. [Google Scholar] [CrossRef]
- Volpe, R.; Cutore, E.; Fichera, A. Design and Operational Indicators to Foster the Transition of Existing Renewable Energy Communities towards Positive Energy Districts. J. Sustain. Dev. Energy, Water Environ. Syst. 2024, 12, 1–22. [Google Scholar] [CrossRef]
- Hedman, A.; Rehman, H.U.; Gabaldón, A.; Bisello, A.; Albert-Seifried, V.; Zhang, X.; Guarino, F.; Grynning, S.; Eicker, U.; Neumann, H.M.; et al. IEA EBC Annex83 Positive Energy Districts. Buildings 2021, 11, 130. [Google Scholar] [CrossRef]
- Heller, R. Positive Energy in the City; Eburon Academic Publishers: Delft, The Netherlands, 2022; Available online: https://pure.hva.nl/ws/portalfiles/portal/23920668/positive_energy_in_the_city.pdf (accessed on 20 February 2025).
- Gouveia, J.; Seixas, J.; Palma, P.; Duarte, H.; Luz, H.; Cavadini, G. Positive Energy District: A Model for Historic Districts to Address Energy Poverty. Front. Sustain. Cities 2021, 3, 648473. [Google Scholar] [CrossRef]
- Guasselli, F.; Vavouris, A.; Stankovic, L.; Stankovic, V.; Didierjean, S.; Gram-Hanssen, K. Smart energy technologies for the collective: Time-shifting, demand reduction and household practices in a Positive Energy Neighbourhood in Norway. Energy Res. Soc. Sci. 2024, 110, 103436. [Google Scholar] [CrossRef]
- Marotta, I.; Péan, T.; Guarino, F.; Longo, S.; Cellura, M.; Salom, J. Towards Positive Energy Districts: Energy Renovation of a Mediterranean District and Activation of Energy Flexibility. Solar 2023, 3, 253–282. [Google Scholar] [CrossRef]
- Bruck, A.; Díaz Ruano, S.; Auer, H. One piece of the puzzle towards 100 Positive Energy Districts (PEDs) across Europe by 2025: An open-source approach to unveil favourable locations of PV-based PEDs from a techno-economic perspective. Energy 2022, 254, 124152. [Google Scholar] [CrossRef]
- Laitinen, A.; Lindholm, O.; Hasan, A.; Reda, F.; Hedman, Å. A techno-economic analysis of an optimal self-sufficient district. Energy Convers. Manag. 2021, 236, 114041. [Google Scholar] [CrossRef]
- Marrasso, E.; Martone, C.; Pallotta, G.; Roselli, C.; Sasso, M. Assessment of energy systems configurations in mixed-use Positive Energy Districts through novel indicators for energy and environmental analysis. Appl. Energy 2024, 368, 123374. [Google Scholar] [CrossRef]
- Blumberga, A.; Vanaga, R.; Freimanis, R.; Blumberga, D.; Antužs, J.; Krastiņš, A.; Jankovskis, I.; Bondars, E.; Treija, S. Transition from traditional historic urban block to positive energy block. Energy 2020, 202, 117485. [Google Scholar] [CrossRef]
- An, Y.S.; Kim, J.; Joo, H.J.; woo Han, G.; Kim, H.; Lee, W.; Kim, M.H. Retrofit of renewable energy systems in existing community for positive energy community. Energy Rep. 2023, 9, 3733–3744. [Google Scholar] [CrossRef]
- Bambara, J.; Athienitis, A.K.; Eicker, U. Residential Densification for Positive Energy Districts. Front. Sustain. Cities 2021, 3, 630973. [Google Scholar] [CrossRef]
- Wang, G.; Blondeau, J. Optimal combination of daily and seasonal energy storage using battery and hydrogen production to increase the self-sufficiency of local energy communities. J. Energy Storage 2024, 92, 112206. [Google Scholar] [CrossRef]
- Zheng, N.; Zhang, H.; Duan, L.; Wang, Q.; Bischi, A.; Desideri, U. Techno-economic analysis of a novel solar-driven PEMEC-SOFC-based multi-generation system coupled parabolic trough photovoltaic thermal collector and thermal energy storage. Appl. Energy 2023, 331, 120400. [Google Scholar] [CrossRef]
- Benalcazar, P. Sizing and optimizing the operation of thermal energy storage units in combined heat and power plants: An integrated modeling approach. Energy Convers. Manag. 2021, 242, 114255. [Google Scholar] [CrossRef]
- Coppieters, T.; Blondeau, J. Techno-Economic Design of Flue Gas Condensers for Medium-Scale Biomass Combustion Plants: Impact of Heat Demand and Return Temperature Variations. Energies 2019, 12, 2337. [Google Scholar] [CrossRef]
- Marocco, P.; Ferrero, D.; Lanzini, A.; Santarelli, M. The role of hydrogen in the optimal design of off-grid hybrid renewable energy systems. J. Energy Storage 2022, 46, 103893. [Google Scholar] [CrossRef]
- Coppitters, D.; Verleysen, K.; De Paepe, W.; Contino, F. How can renewable hydrogen compete with diesel in public transport? Robust design optimization of a hydrogen refueling station under techno-economic and environmental uncertainty. Appl. Energy 2022, 312, 118694. [Google Scholar] [CrossRef]
- Ma, T.; Javed, M.S. Integrated sizing of hybrid PV-wind-battery system for remote island considering the saturation of each renewable energy resource. Energy Convers. Manag. 2019, 182, 178–190. [Google Scholar] [CrossRef]
- Mavromatidis, G.; Petkov, I. MANGO: A novel optimization model for the long-term, multi-stage planning of decentralized multi-energy systems. Appl. Energy 2021, 288, 116585. [Google Scholar] [CrossRef]
- Maestre, V.; Ortiz, A.; Ortiz, I. Challenges and prospects of renewable hydrogen-based strategies for full decarbonization of stationary power applications. Renew. Sustain. Energy Rev. 2021, 152, 111628. [Google Scholar] [CrossRef]
- Le, T.S.; Nguyen, T.N.; Bui, D.K.; Ngo, T.D. Optimal sizing of renewable energy storage: A techno-economic analysis of hydrogen, battery and hybrid systems considering degradation and seasonal storage. Appl. Energy 2023, 336, 120817. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef]
- Felice, A.; Rakocevic, L.; Peeters, L.; Messagie, M.; Coosemans, T.; Camargo, L.R. Renewable energy communities: Do they have a business case in Flanders? Appl. Energy 2022, 322, 119419. [Google Scholar] [CrossRef]
- Coppitters, D.; De Paepe, W.; Contino, F. Robust design optimization of a photovoltaic-battery-heat pump system with thermal storage under aleatory and epistemic uncertainty. Energy 2021, 229, 120692. [Google Scholar] [CrossRef]
- de Simón-Martín, M.; Bracco, S.; Piazza, G.; Pagnini, L.C.; González-Martínez, A.; Delfino, F. Levelized Cost of Energy in Sustainable Energy Communities: A Systematic Approach for Multi-Vector Energy Systems; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N.; Graditi, G.; Luh, P.; Mongibello, L.; Naso, V. Multi-objective design optimization of distributed energy systems through cost and exergy assessments. Appl. Energy 2017, 204, 1299–1316. [Google Scholar] [CrossRef]
- Citizens4PED. Our 4 Living Labs. 2023. Available online: https://citizens4ped.eu/index.php/our-living-labs/ (accessed on 6 December 2024).
- Usquare. Bringing People, City and Knowledge Together: Such Is the Ambition of Usquare.Brussels. 2024. Available online: https://usquare.brussels/en/usquarebrussels-bringing-people-city-and-knowledge-together (accessed on 6 December 2024).
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Solar Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Wirtz, M. nPro: A web-based planning tool for designing district energy systems and thermal networks. Energy 2023, 268, 126575. [Google Scholar] [CrossRef]
- Smart Cities Information System. Building Envelope Retrofit Solution Booklet; EU Smart Cities Information System: Brussels, Belgium, 2020; Available online: https://build-up.ec.europa.eu/sites/default/files/content/230113-solution_booklet-building_envelope_retrofit.pdf (accessed on 20 February 2025).
- Loga, T.; Stein, B.; Diefenbach, N. TABULA building typologies in 20 European countries—Making energy-related features of residential building stocks comparable. Energy Build. 2016, 132, 4–12. [Google Scholar] [CrossRef]
- Eurelectric. Decarbonisation Speedways. Eurelectric Electrification Action Plan 2023. Available online: https://www.eurelectric.org/wp-content/uploads/2024/06/extended-full-report_decarbonisation-speedways.pdf (accessed on 20 February 2025).
- Historical Data for Belgium-2022. 2022. Available online: https://www.nowtricity.com/country/belgium/ (accessed on 27 September 2023).
- Gabrielli, P.; Gazzani, M.; Martelli, E.; Mazzotti, M. Optimal design of multi-energy systems with seasonal storage. Appl. Energy 2018, 219, 408–424. [Google Scholar] [CrossRef]
- Vandevyvere, H. Positive Energy Districts Solution Booklet; EU Smart Cities Information System: Brussels, Belgium, 2020; Available online: https://cityxchange.eu/wp-content/uploads/2020/12/1606985144968.pdf (accessed on 20 February 2025).
- Limpens, G.; Moret, S.; Jeanmart, H.; Maréchal, F. EnergyScope TD: A novel open-source model for regional energy systems. Appl. Energy 2019, 255, 113729. [Google Scholar] [CrossRef]
- Borasio, M.; Moret, S. Deep decarbonisation of regional energy systems: A novel modelling approach and its application to the Italian energy transition. Renew. Sustain. Energy Rev. 2022, 153, 111730. [Google Scholar] [CrossRef]
- International Energy Agency. World Energy Outlook; OECD/IEA: Paris, France, 2024; Available online: https://www.iea.org/reports/world-energy-outlook-2024 (accessed on 20 February 2025).
- VREG. Tariefmethodologie 2025–2028. 2024. Available online: https://www.vreg.be/sites/default/files/Tariefmethodologie/2025-2028/besl-2024-41_tariefmethodologie_2025-2028_.pdf (accessed on 20 February 2025).
- Petkov, I.; Gabrielli, P. Power-to-hydrogen as seasonal energy storage: An uncertainty analysis for optimal design of low-carbon multi-energy systems. Appl. Energy 2020, 274, 115197. [Google Scholar] [CrossRef]
- CBRE. Changes to the EPC in Belgium: What Impact on Your Property Investments? 2023. Available online: https://www.cbre.be/insights/articles/changes-to-the-epc-in-belgium-what-impact-on-your-property-investments (accessed on 13 August 2024).
- Wirtz, M.; Kivilip, L.; Remmen, P.; Müller, D. 5th Generation District Heating: A novel design approach based on mathematical optimization. Appl. Energy 2020, 260, 114158. [Google Scholar] [CrossRef]
- Di Somma, M.; Dolatabadi, M.; Burgio, A.; Siano, P.; Cimmino, D.; Bianco, N. Optimizing virtual energy sharing in renewable energy communities of residential users for incentives maximization. Sustain. Energy Grids Netw. 2024, 39, 101492. [Google Scholar] [CrossRef]
- Ceglia, F.; Marrasso, E.; Roselli, C.; Sasso, M. Energy and environmental assessment of a biomass-based renewable energy community including photovoltaic and hydroelectric systems. Energy 2023, 282, 128348. [Google Scholar] [CrossRef]
- Esposito, P.; Marrasso, E.; Martone, C.; Pallotta, G.; Roselli, C.; Sasso, M.; Tufo, M. A roadmap for the implementation of a renewable energy community. Heliyon 2024, 10, e28269. [Google Scholar] [CrossRef] [PubMed]
- European Commission. Energy Efficiency Directive (EU/2023/1791). 2023. Available online: https://energy.ec.europa.eu/topics/energy-efficiency/energy-efficiency-targets-directive-and-rules/energy-efficiency-directive_en (accessed on 3 September 2024).
- Lu, Y.; Wang, S.; Zhao, Y.; Yan, C. Renewable energy system optimization of low/zero energy buildings using single-objective and multi-objective optimization methods. Energy Build. 2015, 89, 61–75. [Google Scholar] [CrossRef]
- Wirtz, M.; Kivilip, L.; Remmen, P.; Müller, D. Quantifying Demand Balancing in Bidirectional Low Temperature Networks. Energy Build. 2020, 224, 110245. [Google Scholar] [CrossRef]
- Hart, W.E.; Laird, C.D.; Watson, J.P.; Woodruff, D.L.; Hackebeil, G.A.; Nicholson, B.L.; Siirola, J.D. Pyomo-Optimization Modeling in Python; Springer: Cham, Switzerland, 2017; Volume 67, Available online: https://link.springer.com/book/10.1007/978-3-030-68928-5 (accessed on 20 February 2025).
- Wirtz, M.; Hahn, M.; Schreiber, T.; Müller, D. Design optimization of multi-energy systems using mixed-integer linear programming: Which model complexity and level of detail is sufficient? Energy Convers. Manag. 2021, 240, 114249. [Google Scholar] [CrossRef]
- Marocco, P.; Ferrero, D.; Martelli, E.; Santarelli, M.; Lanzini, A. An MILP approach for the optimal design of renewable battery-hydrogen energy systems for off-grid insular communities. Energy Convers. Manag. 2021, 245, 114564. [Google Scholar] [CrossRef]
- Iranpour Mobarakeh, A.; Sadeghi, R.; Saghafi Esfahani, H.; Delshad, M. Optimal planning and operation of energy hub by considering demand response algorithms and uncertainties based on problem-solving approach in discrete and continuous space. Electr. Power Syst. Res. 2023, 214, 108859. [Google Scholar] [CrossRef]
- Sibelga. Day and Night Rate. 2024. Available online: https://www.sibelga.be/en/connections-meters/rates/day-and-night-rate (accessed on 20 February 2025).
| Parameter | Peak Load | Annual Demand |
|---|---|---|
| kW | MWh | |
| Electricity | 1188 | 4201 |
| Space heating (70/50 °C) | 2097 | 2739 |
| Space heating (50/40 °C) | 406 | 569 |
| DHW | 328 | 1170 |
| Cooling | 266 | 379 |
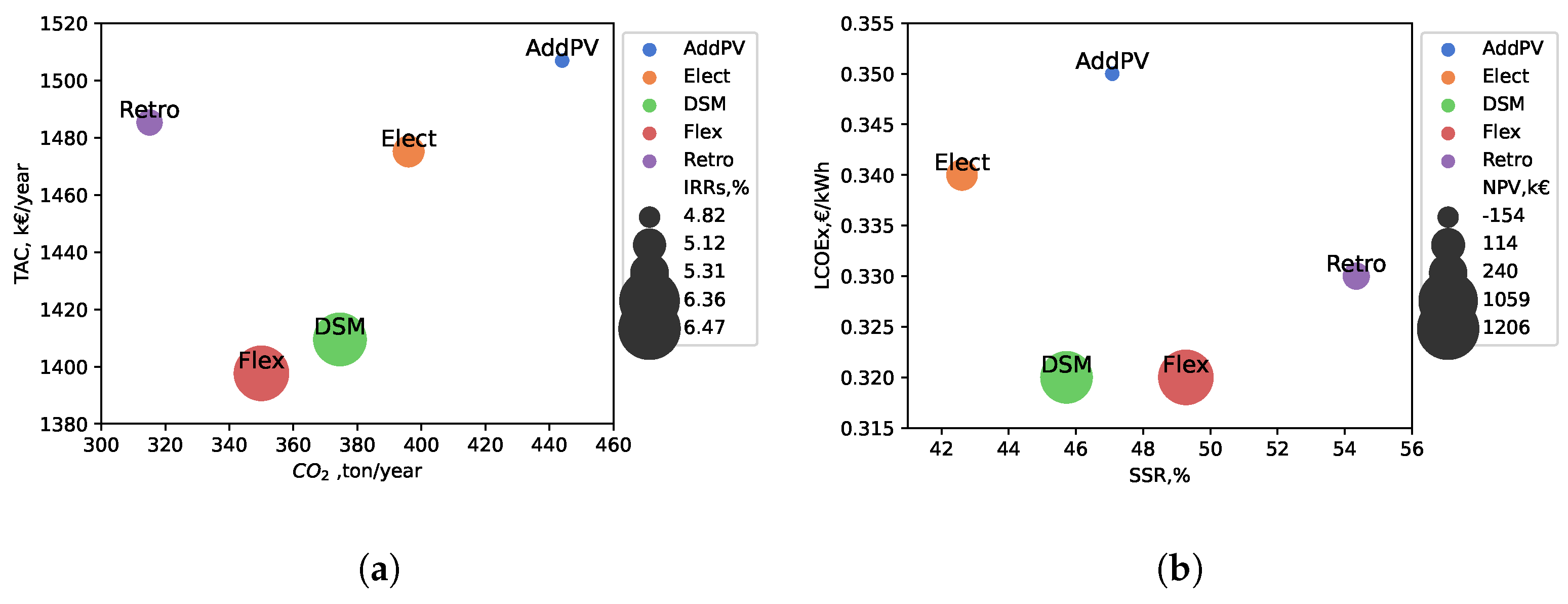
| Parameter | Unit | AddPV | Elect | DSM | Flex | Retro |
|---|---|---|---|---|---|---|
| Objectives | ||||||
| TAC | kEUR/year | 1507 | 1475 | 1410 | 1398 | 1485 |
| CO2 | ton/year | 444 | 396 | 375 | 350 | 315 |
| Main KPIs | ||||||
| IRRs | % | 4.8 | 5.3 | 6.4 | 6.5 | 5.1 |
| NPV | kEUR | −155 | 240 | 1059 | 1206 | 115 |
| LCOEx | EUR/MWh | 348 | 337 | 322 | 317 | 332 |
| SSR | % | 47.1 | 42.6 | 45.7 | 49.3 | 54.3 |
| SCR | % | 32.9 | 38.5 | 42.3 | 46.6 | 48.7 |
| Sizing results | ||||||
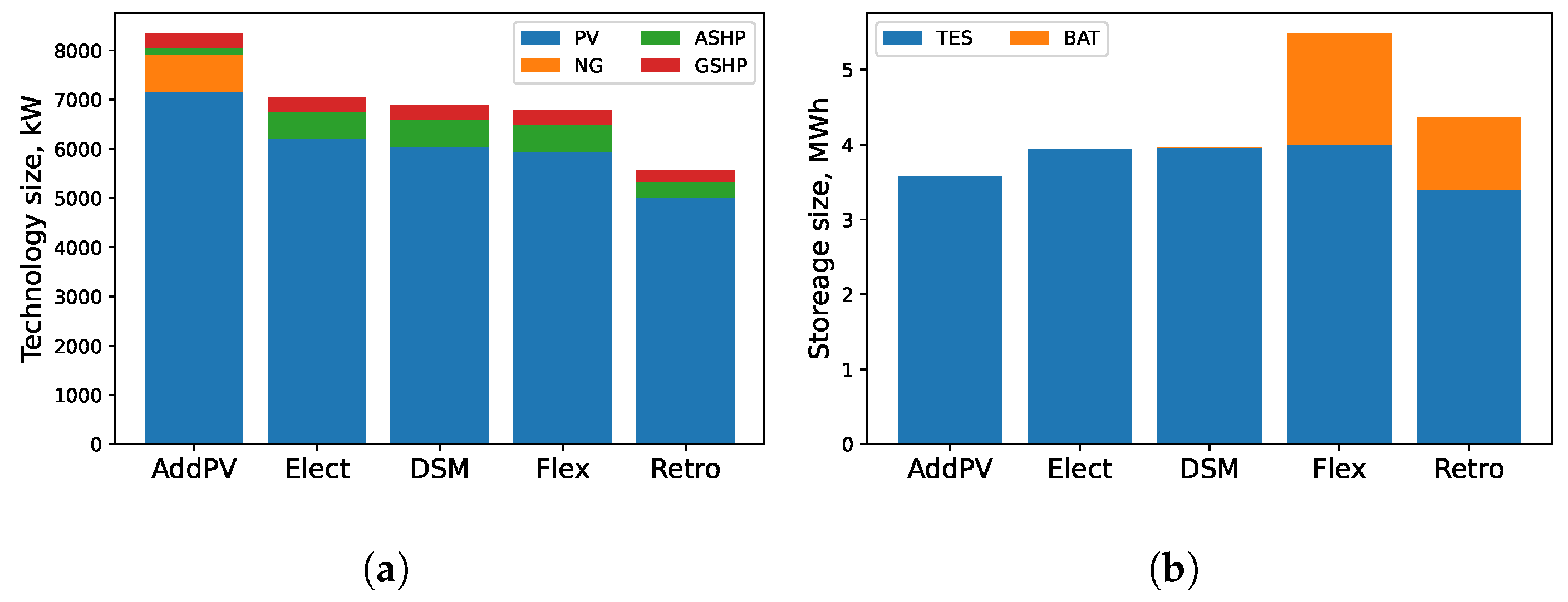
| PV | kWp | 7158 | 6208 | 6049 | 5942 | 5021 |
| BOI | kW | 747 | - | - | - | - |
| GSHP | kW | 301 | 299 | 300 | 299 | 236 |
| ASHP | kW | 140 | 541 | 541 | 546 | 303 |
| TES | MWh | 3.6 | 3.9 | 4.0 | 4.0 | 3.4 |
| BAT | MWh | - | - | - | 1.5 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Gilmont, O.; Blondeau, J. Pathways to Positive Energy Districts: A Comprehensive Techno-Economic and Environmental Analysis Using Multi-Objective Optimization. Energies 2025, 18, 1134. https://doi.org/10.3390/en18051134
Wang G, Gilmont O, Blondeau J. Pathways to Positive Energy Districts: A Comprehensive Techno-Economic and Environmental Analysis Using Multi-Objective Optimization. Energies. 2025; 18(5):1134. https://doi.org/10.3390/en18051134
Chicago/Turabian StyleWang, Guangxuan, Olivier Gilmont, and Julien Blondeau. 2025. "Pathways to Positive Energy Districts: A Comprehensive Techno-Economic and Environmental Analysis Using Multi-Objective Optimization" Energies 18, no. 5: 1134. https://doi.org/10.3390/en18051134
APA StyleWang, G., Gilmont, O., & Blondeau, J. (2025). Pathways to Positive Energy Districts: A Comprehensive Techno-Economic and Environmental Analysis Using Multi-Objective Optimization. Energies, 18(5), 1134. https://doi.org/10.3390/en18051134






