Comparative Study of Voltage and Control Characteristics of Two-Core and Single-Core Step-Up/Down Thyristor-Controlled Phase-Shifting Transformers
Abstract
1. Introduction
2. Basic Principle of TCPST
3. Voltage Step-Down and Phase-Shifting Capability Calculations of the TCSUD-TCPST
3.1. Topology Structure of TCSUD-TCPST
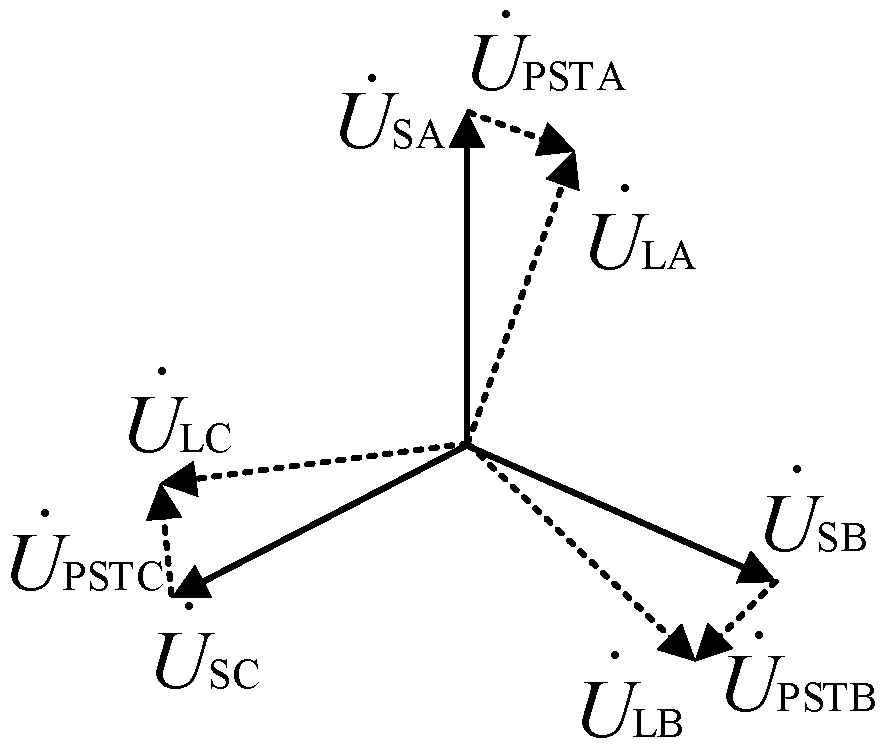
3.2. Calculation of the Phase-Shifting Angle
3.3. Calculation of the Amplitude
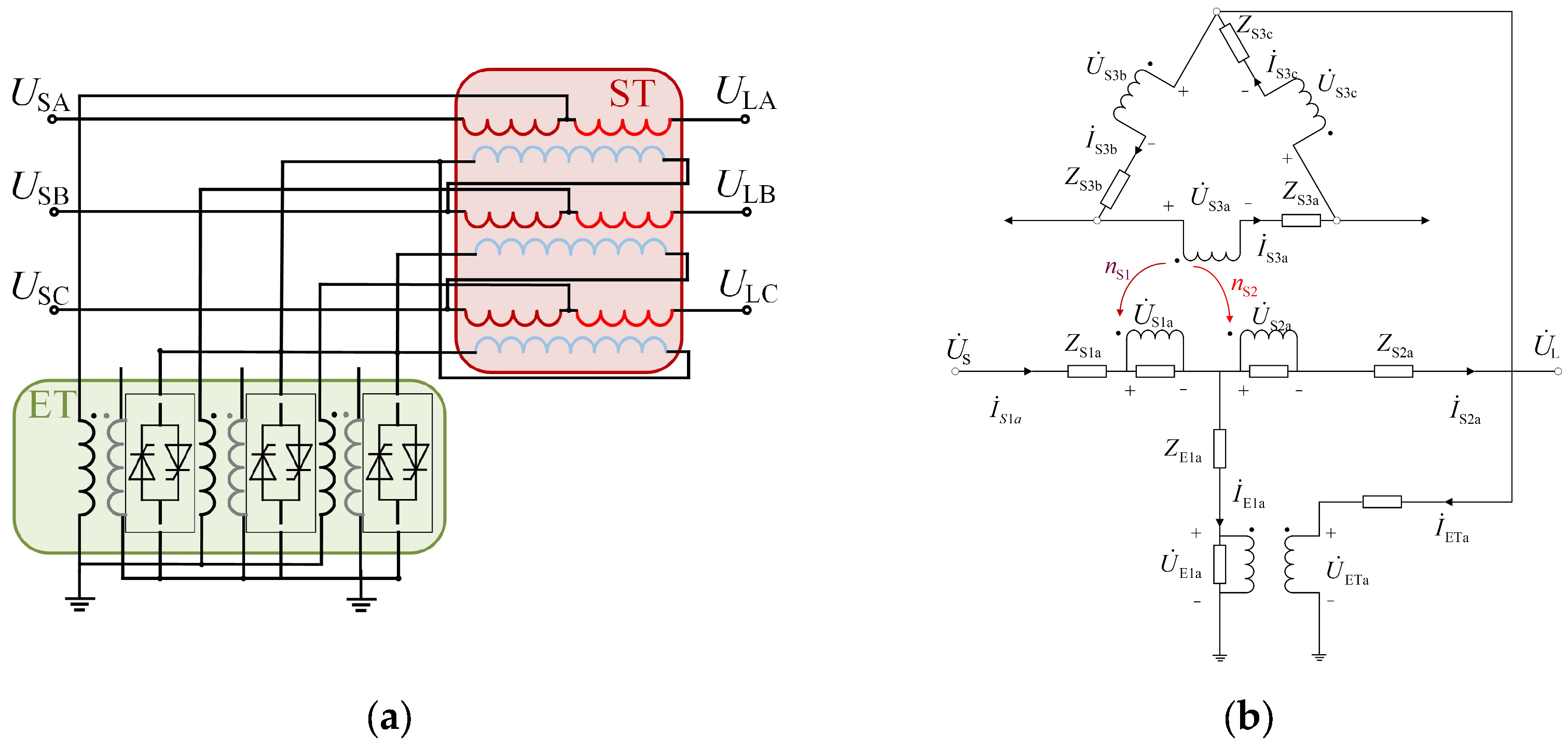
4. Voltage Step-Down and Phase-Shifting Capability Calculations of the SCSUD-TCPST
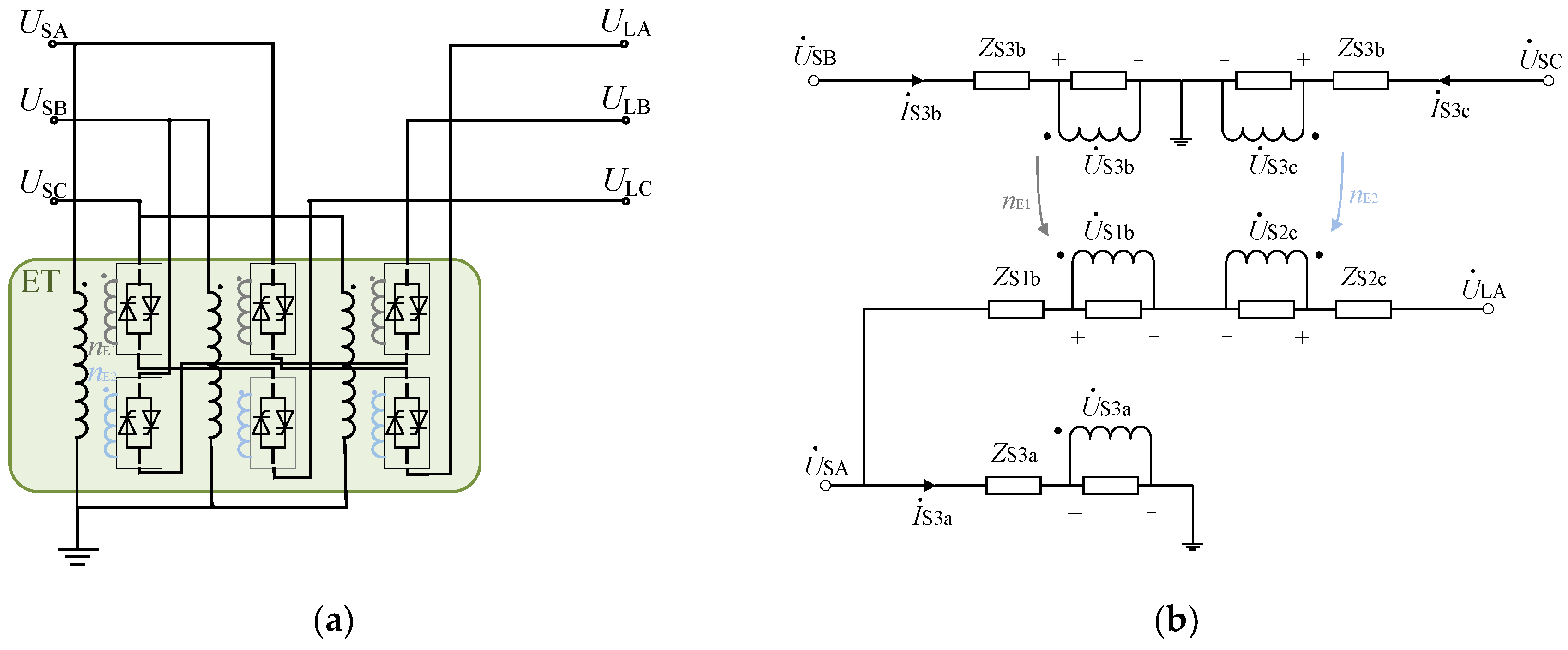
4.1. Topology Structure of SCSUD-TCPST
4.2. Calculation of the Phase-Shifting Angle and the Amplitude
5. Simulations and Experiments
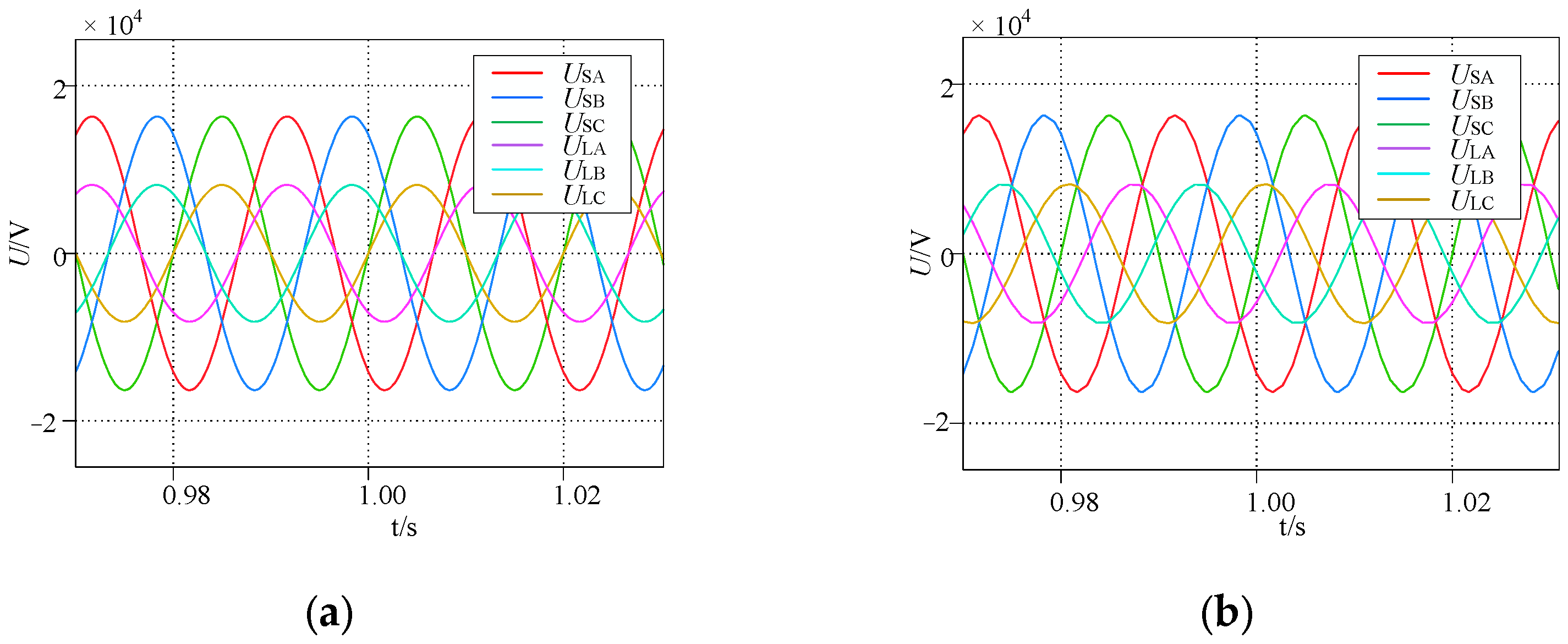
5.1. Comparative Static Performance Simulation of TCSUD-TCPST and SCSUD-TCPST
5.2. Comparative Dynamic Performance Simulation of TCSUD-TCPST and SCSUD-TCPST
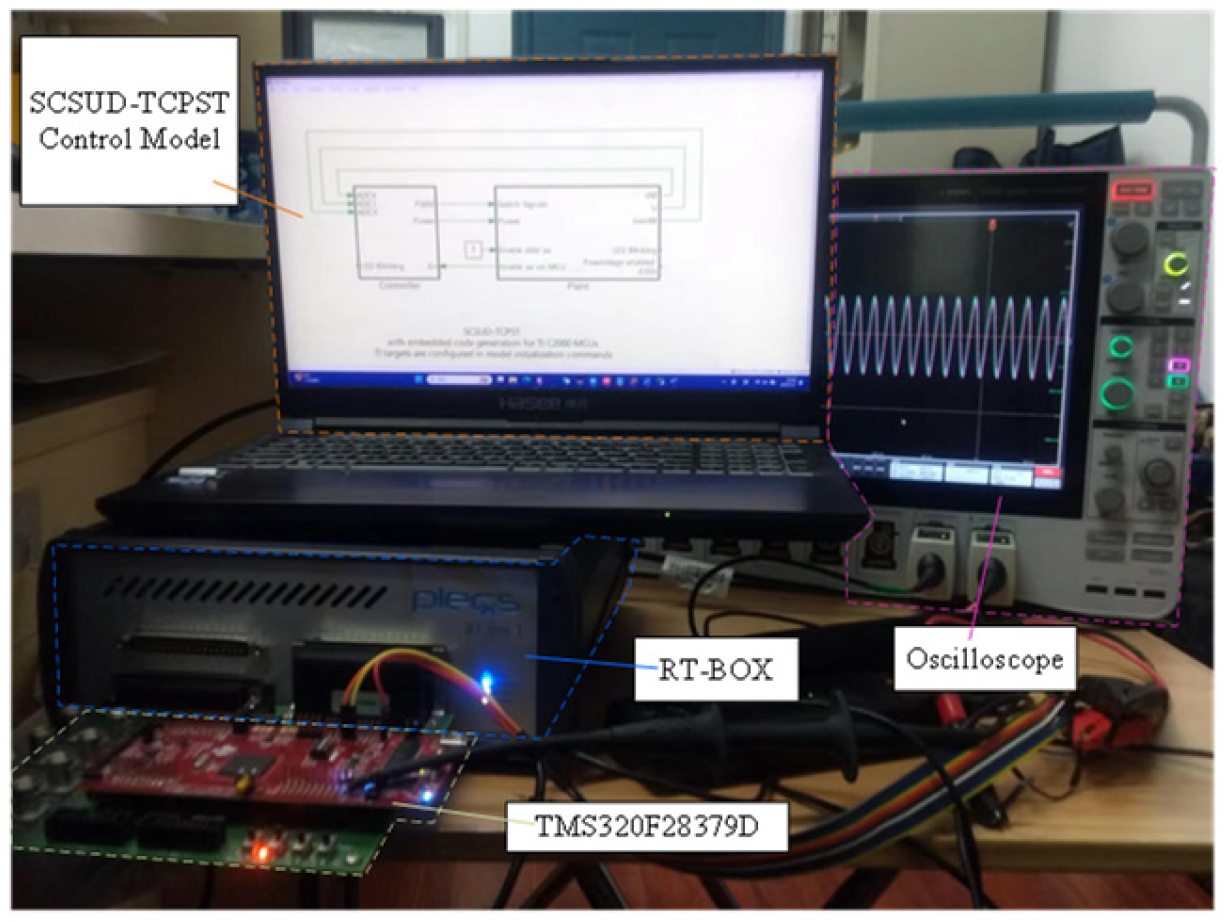
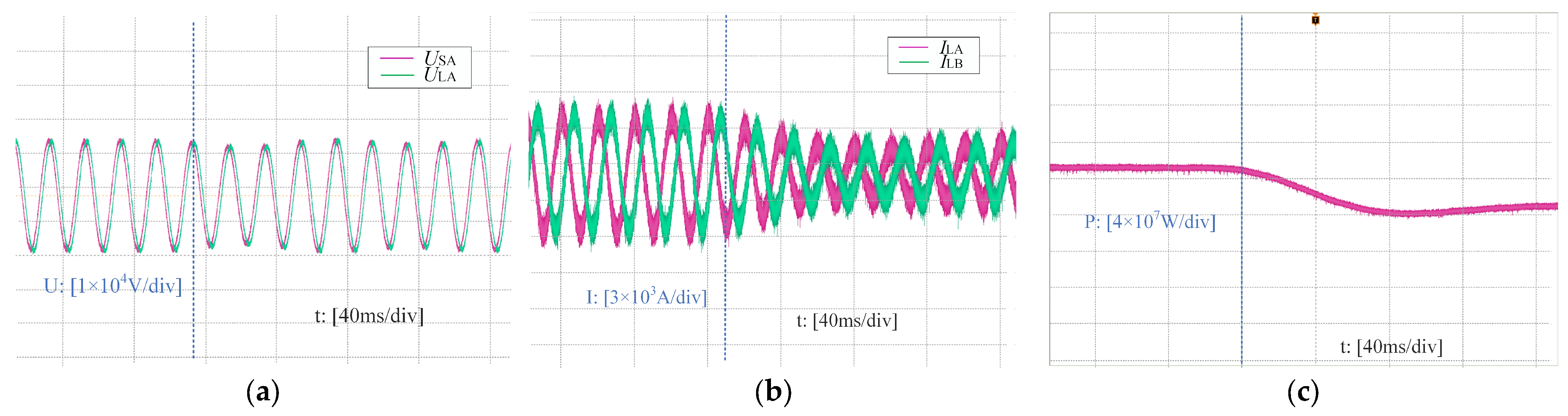
5.3. Hardware-in-Loop Experiments Based on RT-BOX
6. Conclusions
- The coupling relationship between the phase-shifting angle and the amplitude of voltages of the TCSUD-TCPST restricts the range of possible regulation, rendering the regulation process nonlinear;
- The SCSUD-TCPST merges the ST into the ET, thereby simplifying the topology structure, decoupling the relationship between the phase-shifting angle and the amplitude, expanding the range, and linearizing the regulation process;
- Both the TCSUD-TCPST and the SCSUD-TCPST have similar and considerable static and dynamic characteristics in power transmission;
- In conclusion, compared to the TCSUD-TCPST, the SCSUD-TCPST appears to be a more suitable option for power transmission.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gomis-Bellmunt, O.; Sau-Bassols, J.; Prieto-Araujo, E.; Cheah-Mane, M. Flexible Converters for Meshed HVDC Grids: From Flexible AC Transmission Systems (FACTS) to Flexible DC Grids. IEEE Trans. Power Deliv. 2020, 35, 2–15. [Google Scholar] [CrossRef]
- Shan, P.; Sun, Y.; Song, Y.; Zhang, F.; Li, Y.; Sun, K. Adaptive Parameter Tuning and Virtual Impedance Injection Control for Coupled Harmonic Mitigation of Photovoltaic Converter. IEEE Trans. Power Electron. 2025, 1, 162–175. [Google Scholar] [CrossRef]
- Hussain, J.; Huang, Q.; Li, J.; Hussain, F.; Manzoor, K.; Ahmed, S.A. Enhancing Power Quality in Grid Integration of Wind Energy System Using UPFC-BESS. In Proceedings of the 2023 13th International Conference on Power and Energy Systems (ICPES), Chengdu, China, 8–10 December 2023; pp. 453–458. [Google Scholar]
- Jagtap, P.; Chandrakar, V. Advanced UPFC Controllers to Improve Transient and Dynamic Stability of Power System. J. Phys. Conf. Ser. 2024, 1, 2763. [Google Scholar]
- Imdadullah; Ammr, S.M.; Jamil Asghar, M.S.; Ashraf, I.; Meraj, M. A Comprehensive Review of Power Flow Controllers in Interconnected Power System Networks. IEEE Access 2020, 8, 18036–18063. [Google Scholar] [CrossRef]
- Biswas, S.; Nayak, P.K. A Fault Detection and Classification Scheme for Unified Power Flow Controller Compensated Transmission Lines Connecting Wind Farms. IEEE Syst. J. 2021, 15, 297–306. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, J.; Jiang, Y.; Qin, R.; Ma, H.; Yang, Y.; Zhao, C. Analysis of Fault Characteristics of Distribution Network with PST Loop Closing Device Under Small Current Grounding System. Energies 2022, 15, 2307. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, J.; Wang, F.; Tolbert, L.M. DC-Saturated Continuously Variable Series Reactors (CVSRs) for Power Flow Control in Power Transmission Systems. IEEE Trans. Power Deliv. 2022, 37, 268–278. [Google Scholar] [CrossRef]
- Sakallıoğlu, B.; Esenboğa, B.; Demirdelen, T.; Tümay, M. Performance Evaluation of Phase-shifting Transformer for Integration of Renewable Energy Sources. Electr. Eng. 2020, 102, 2025–2039. [Google Scholar] [CrossRef]
- Jin, W.; Liu, H.; Zhang, W.; Yuan, J. Power Flow Regulation Effect and Parameter Design Method of Phase-Shifting Transformer. Energies 2024, 17, 1622. [Google Scholar] [CrossRef]
- Brilinskii, A.S.; Badura, M.A.; Evdokunin, G.A.; Chudny, V.S.; Mingazov, R.I. Phase-Shifting Transformer Application for Dynamic Stability Enhancement of Electric Power Stations Generators. In Proceedings of the 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia, 27–30 January 2020; pp. 1176–1178. [Google Scholar]
- Ding, T.; Bo, R.; Bie, Z.; Wang, X. Optimal Selection of Phase Shifting Transformer Adjustment in Optimal Power Flow. IEEE Trans. Power Syst. 2017, 3, 2464–2465. [Google Scholar] [CrossRef]
- Liang, G.; Wang, L.; Gao, F.; Liu, X. A New Maximum Step Voltage Calculation Method of On-Load Tap-Changer for Symmetrical Two-Core Phase-Shifting Transformer. IEEE Trans. Power Deliv. 2018, 6, 2718–2725. [Google Scholar] [CrossRef]
- Luo, M.; Dujic, D.; Allmeling, J. Leakage Flux Modeling of Medium-Voltage Phase-Shift Transformers for System-Level Simulations. IEEE Trans. Power Electron. 2019, 3, 2635–2654. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, W.; Mei, J.; Gan, D.; Zhou, H.; Zheng, Y. Independent Fast Phase Shifting Transformer: A Flexible and High-Precision Power Flow Controller. IEEE Trans. Power Deliv. 2023, 6, 4410–4421. [Google Scholar] [CrossRef]
- Liu, J.; Hao, X.; Wang, X.; Chen, Y.; Fang, W.; Niu, S. Application of thyristor controlled phase shifting transformer excitation impedance switching control to suppress short-circuit fault current level. J. Mod. Power Syst. Clean Energy 2018, 4, 821–832. [Google Scholar] [CrossRef]
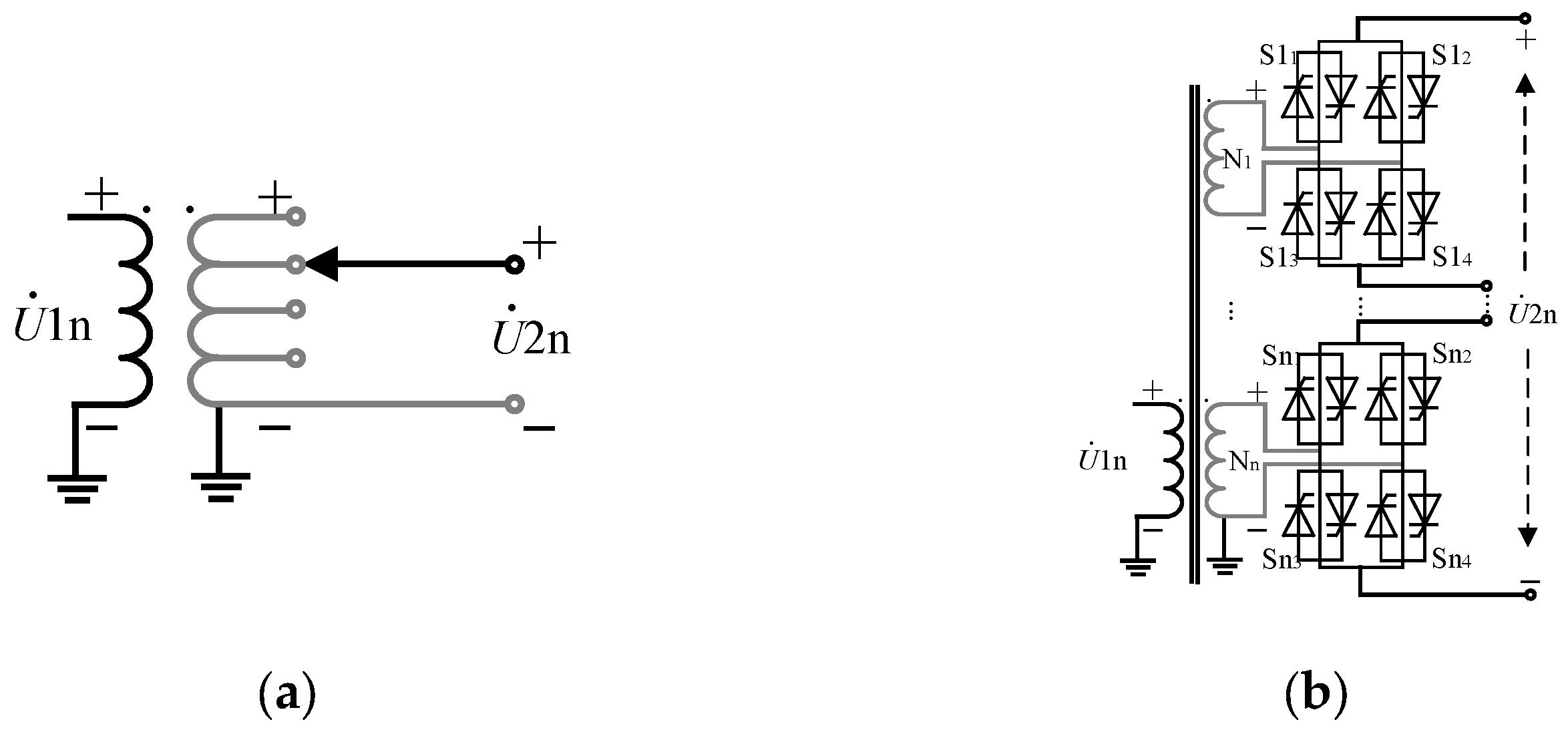
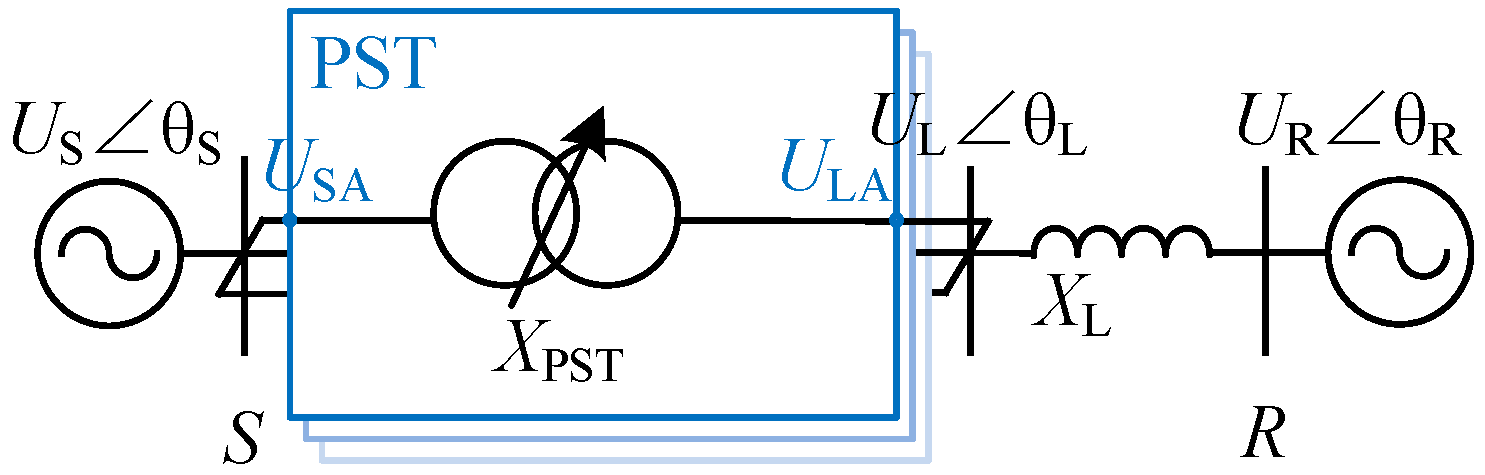




| Sending Voltage US (kV) | Receiving Voltage UR (kV) | Grid Impedance XL (mH) |
|---|---|---|
| 20 | 20 | 0.4 |
| Rated Capacity SPST (MVA) | Power Flow Capacity SP (MVA) | Leakage Inductance L1 (mH) |
|---|---|---|
| 100 | ±60 | 10 |
| Figure | nE1/nS1 | nE2/nS2 |
|---|---|---|
| Figure 7a | −0.155 | 0.423 |
| Figure 7b | 2.155 | 2.155 |
| Figure 8a | 0.467 | 0.467 |
| Figure 8b | −0.155 | 2.155 |
| Figure 9 | 2.155 → 2.066 | 2.155 → 2.155 |
| Figure 10 | −0.155 → −0.066 | 0.6006 → 0.7782 |
| Figure | Actual Angle (°) | Angle Error (%) | Actual Amplitude (p.u.) | Amplitude Error (%) |
|---|---|---|---|---|
| Figure 7a | 29.91 | 0.30 | 1.000 | 0.00 |
| Figure 7b | 29.92 | 0.27 | 1.000 | 0.00 |
| Figure 8a | 0.01 | \ | 0.497 | 0.60 |
| Figure 8b | 97.71 | \ | 0.497 | 0.60 |
| SCSUD-TCPST | TCSUD-TCPST | |
|---|---|---|
| Maximum ratios | 0.7782 | 2.155 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Sending voltage US (kV) | 20 | Receiving voltage UR (kV) | 20 |
| Grid impedance XL (mH) nE1 | 0.40 −0.155 → −0.066 | Active power flow (MW) nE2 | 100 → 50 0.6006 → 0.7782 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Li, H.; Jin, X.; Bi, C.; Wang, J. Comparative Study of Voltage and Control Characteristics of Two-Core and Single-Core Step-Up/Down Thyristor-Controlled Phase-Shifting Transformers. Energies 2025, 18, 837. https://doi.org/10.3390/en18040837
Zhang N, Li H, Jin X, Bi C, Wang J. Comparative Study of Voltage and Control Characteristics of Two-Core and Single-Core Step-Up/Down Thyristor-Controlled Phase-Shifting Transformers. Energies. 2025; 18(4):837. https://doi.org/10.3390/en18040837
Chicago/Turabian StyleZhang, Ningyu, Huarui Li, Xiaokuan Jin, Chongze Bi, and Jianhua Wang. 2025. "Comparative Study of Voltage and Control Characteristics of Two-Core and Single-Core Step-Up/Down Thyristor-Controlled Phase-Shifting Transformers" Energies 18, no. 4: 837. https://doi.org/10.3390/en18040837
APA StyleZhang, N., Li, H., Jin, X., Bi, C., & Wang, J. (2025). Comparative Study of Voltage and Control Characteristics of Two-Core and Single-Core Step-Up/Down Thyristor-Controlled Phase-Shifting Transformers. Energies, 18(4), 837. https://doi.org/10.3390/en18040837





