Composite Power Management Strategy for Hybrid Powered Compound-Wing Aircraft in Level Flight
Abstract
1. Introduction
2. Architecture of Hybrid Power System
2.1. Layout of VTOL and Hybrid Power System
2.2. Modelling of Hybrid Power System
2.3. One Notable Feature of the Architecture
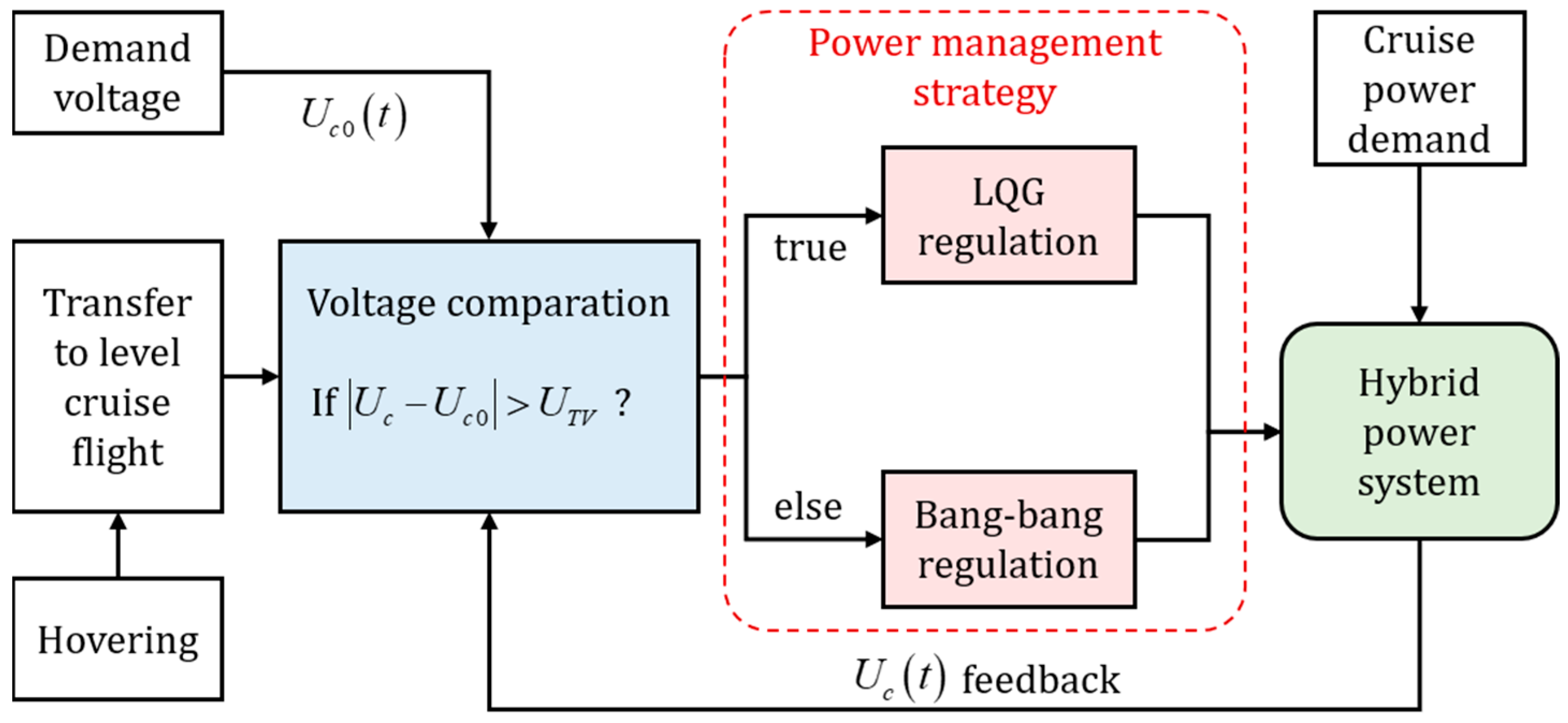
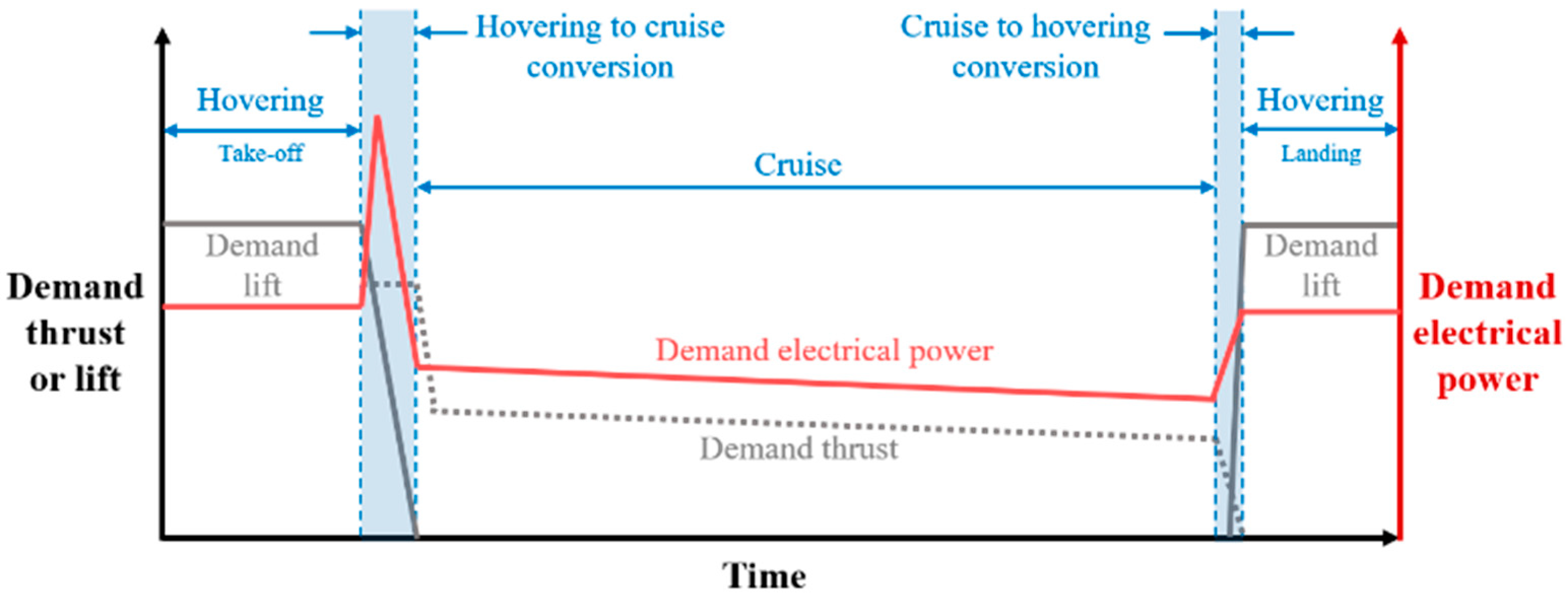
3. Power Management Strategy of Level Cruise Flight
3.1. BANG–BANG Regulation Definition
3.2. Optimal Chasing Regulation Definition
3.3. Power Management Strategy Definition
3.4. Battery Degradation Definition
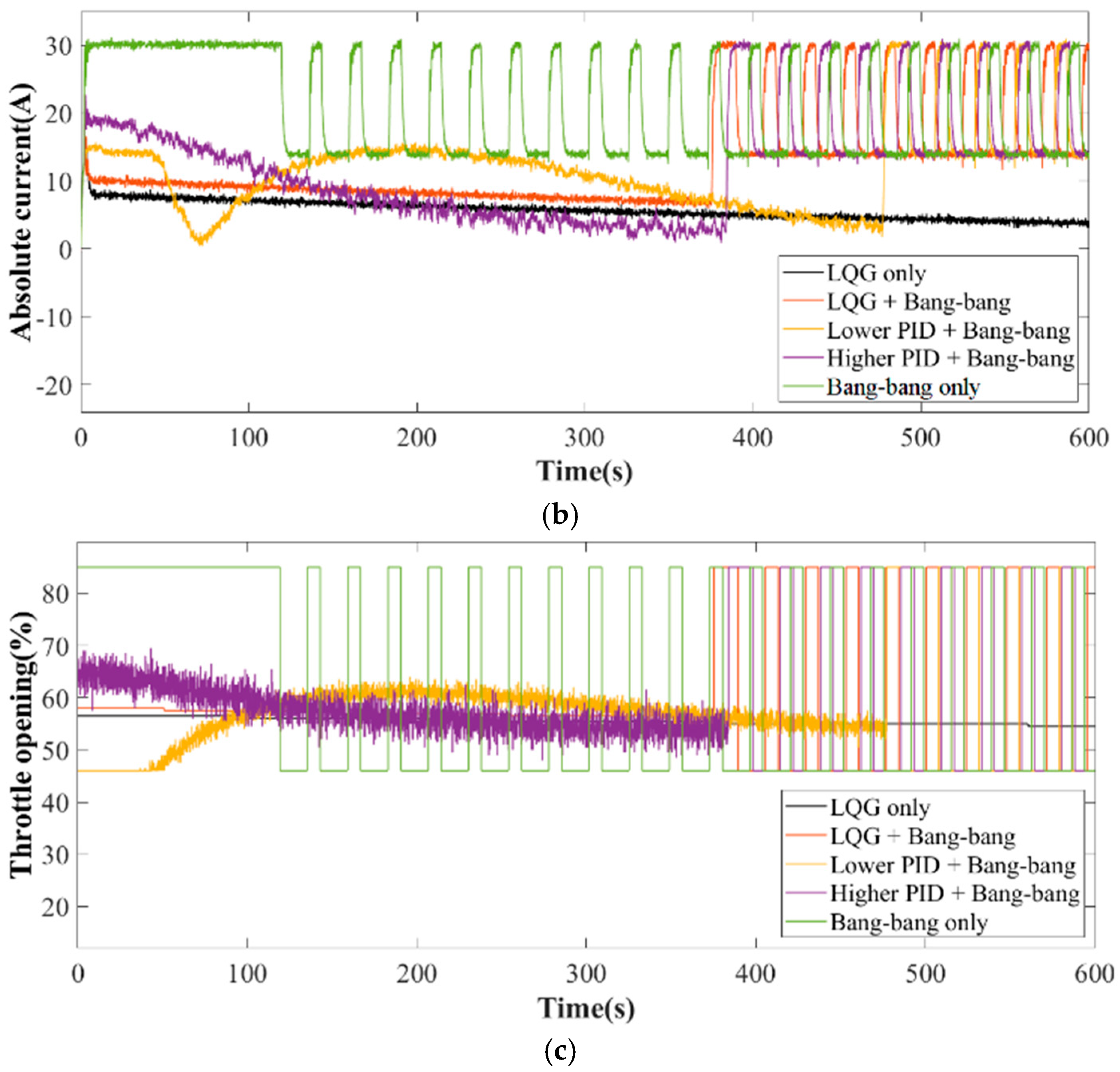
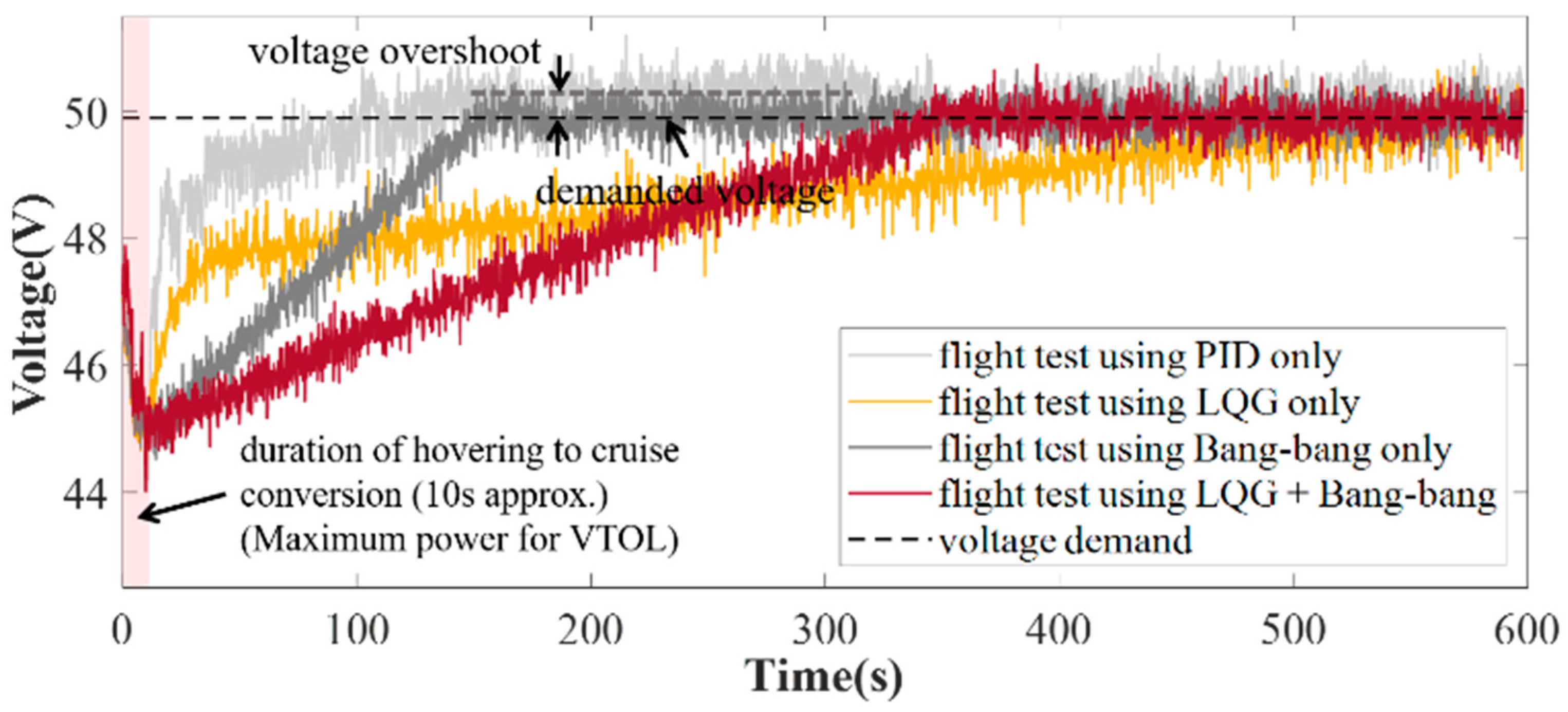
4. Results of the Experiment
4.1. Simulation Verification
4.2. Testbench
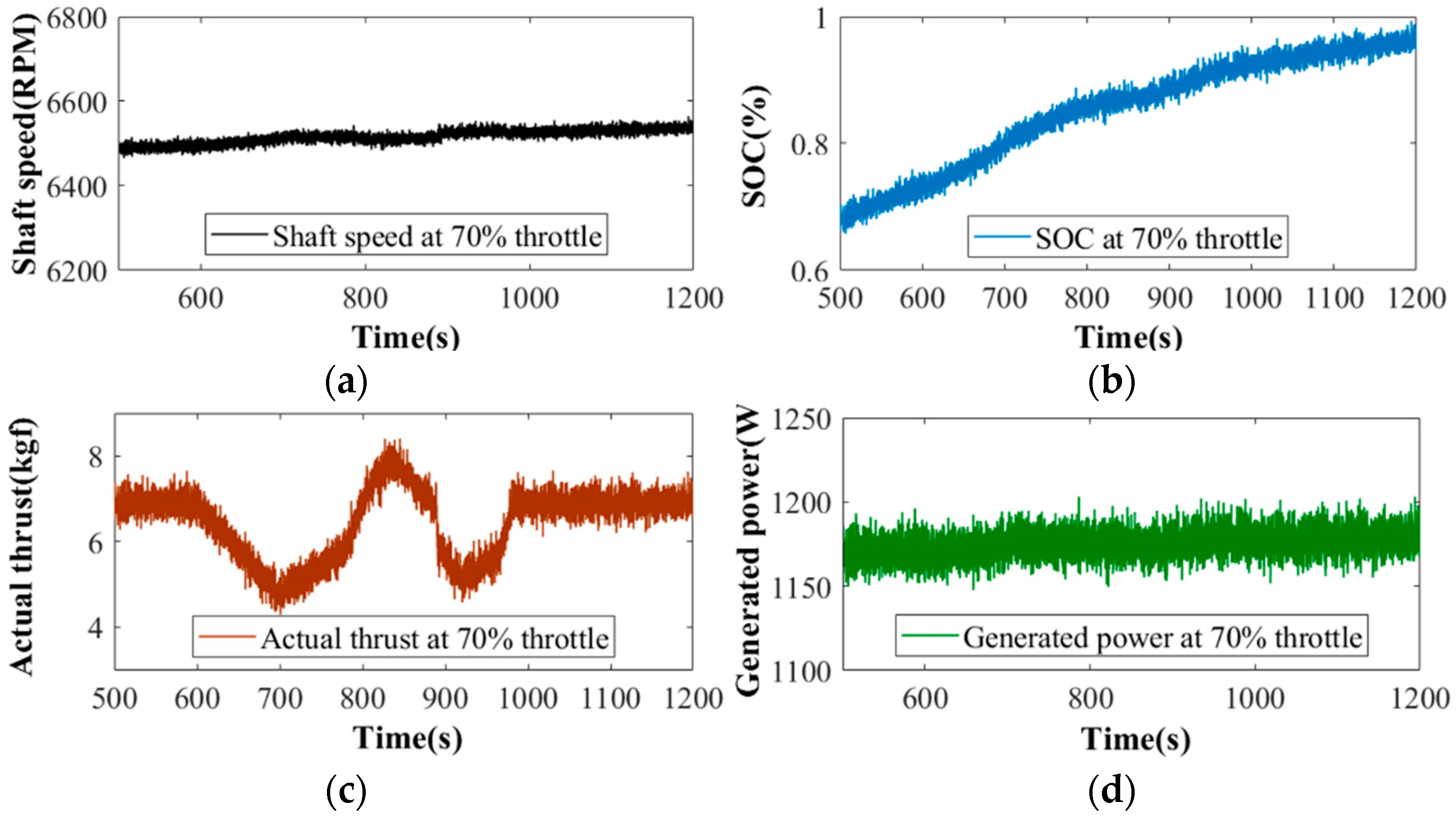
4.3. Typical Operation Conditions
4.4. Result Under Power Management Strategies
5. Conclusions
- (1)
- The complete hybrid power system was modelled and linearized, incorporating the states of shaft speed, voltage, and current. The shaft speed of ICE was primarily determined by the battery voltage, with a secondary influence from current. The validation of semi-fixing the shaft speed through bench testing further confirmed this relationship.
- (2)
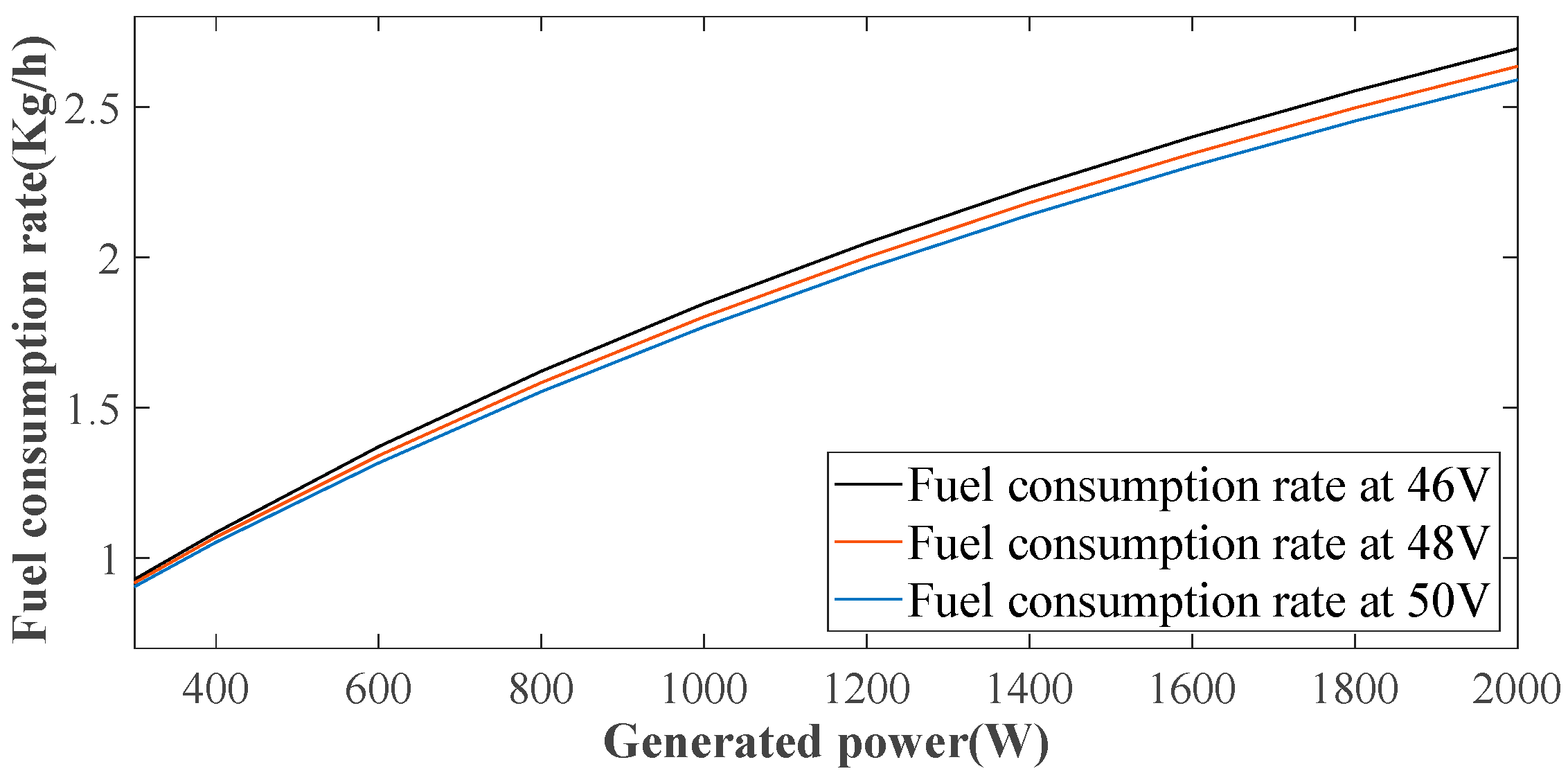
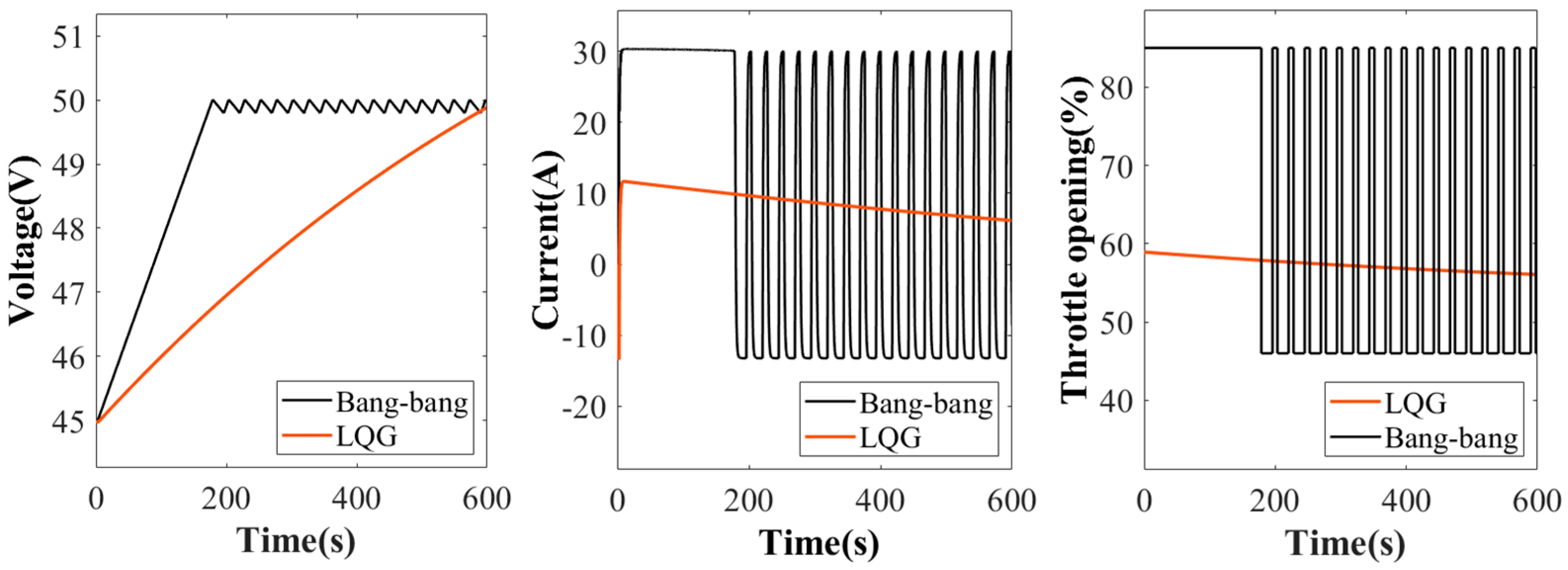
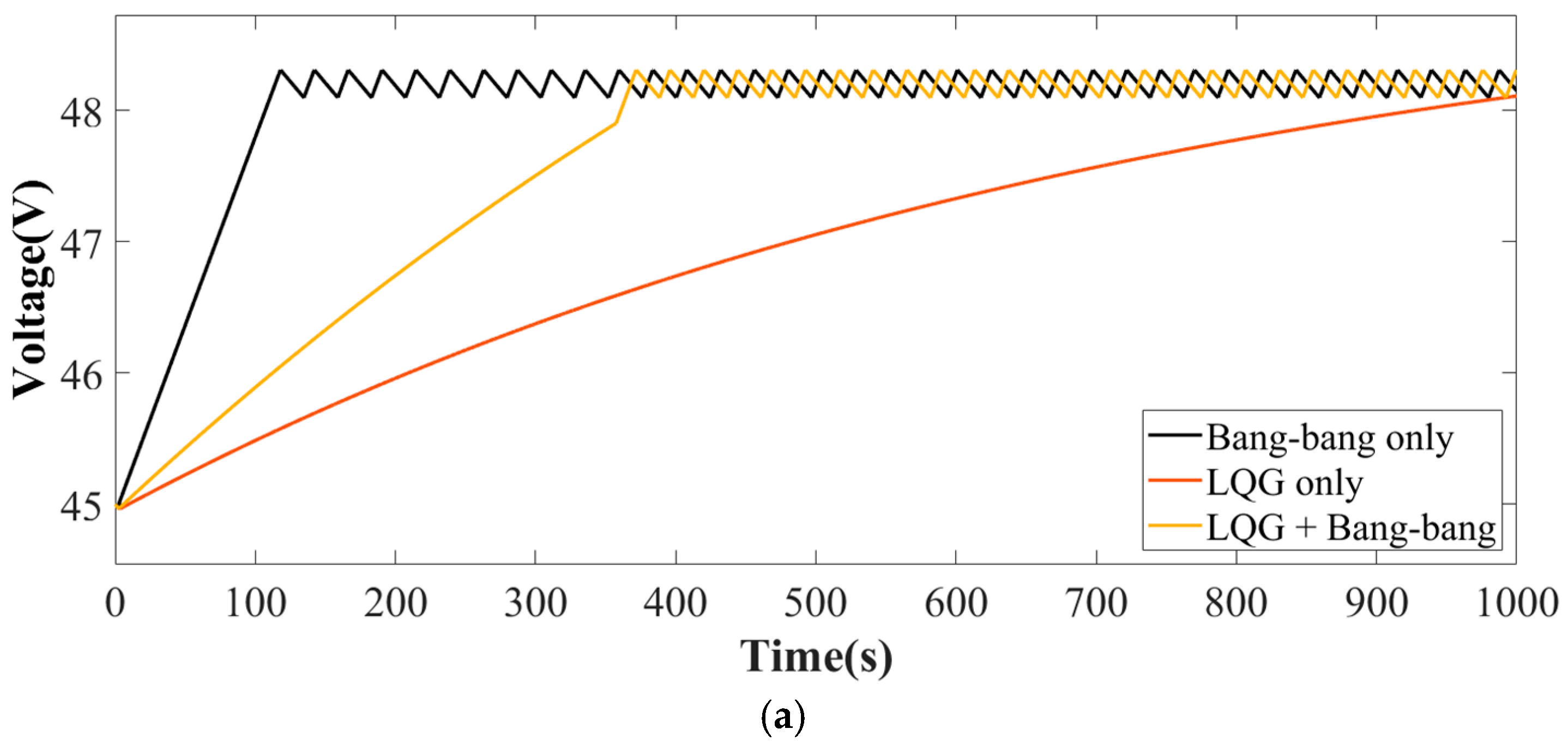
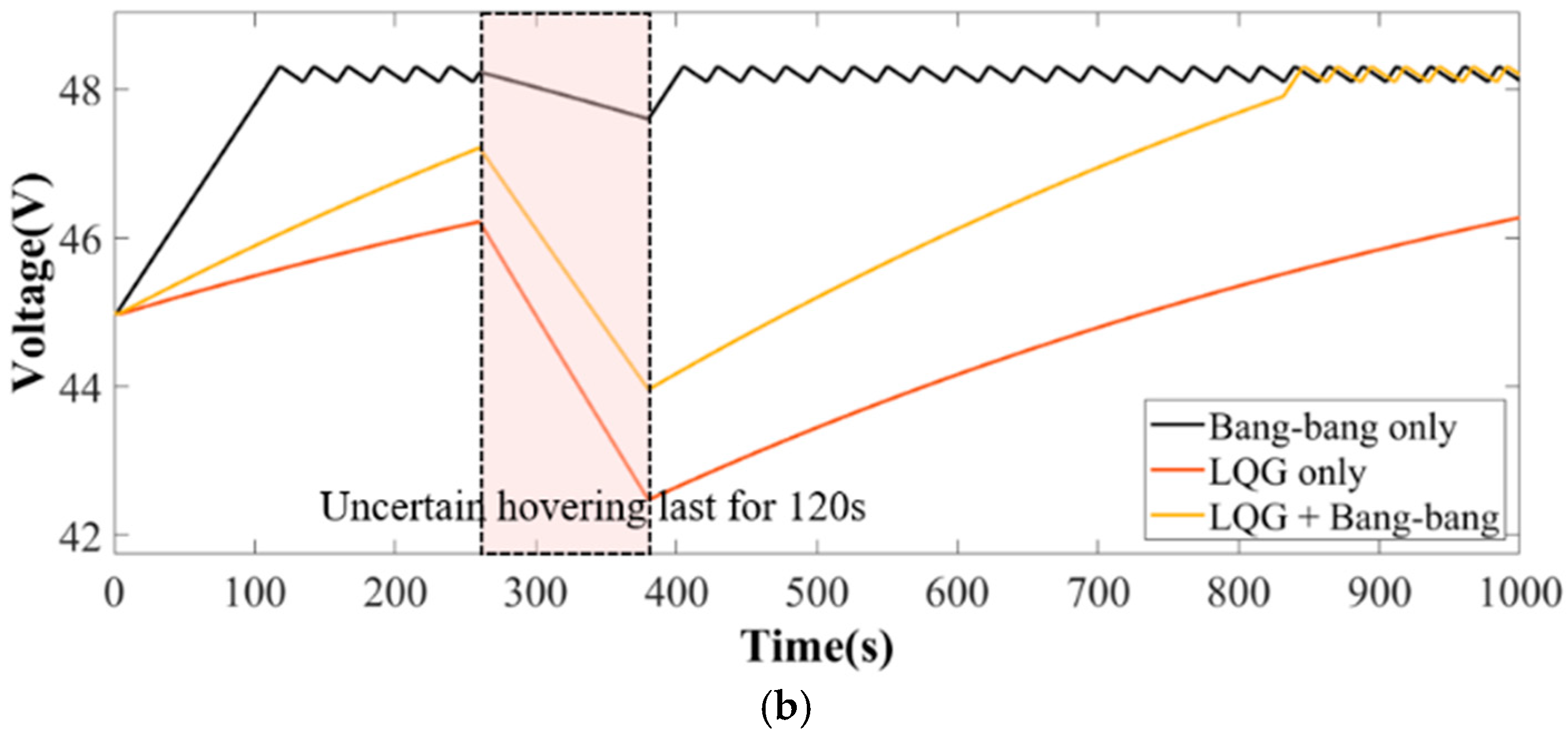
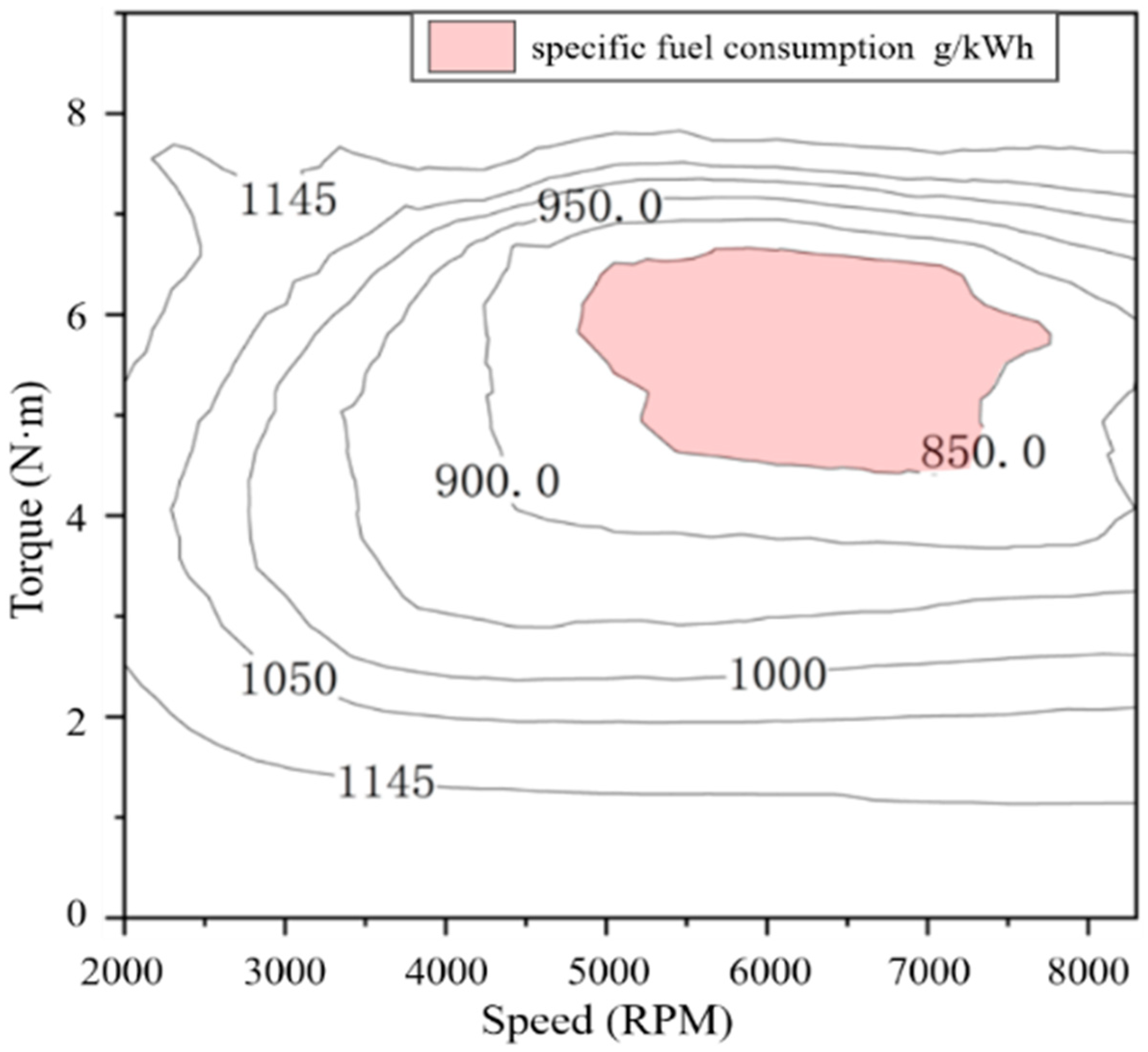
- The fuel consumption chart and battery pack degradation mechanism were provided. The simulation results revealed that the LQG regulation strategy exhibits lower fuel consumption, while the bang–bang regulation strategy performed well in dealing with flight uncertainty. To strike a balance between cost and flight uncertainty, a composite power management strategy combining LQG and bang–bang regulation was devised.
- (3)
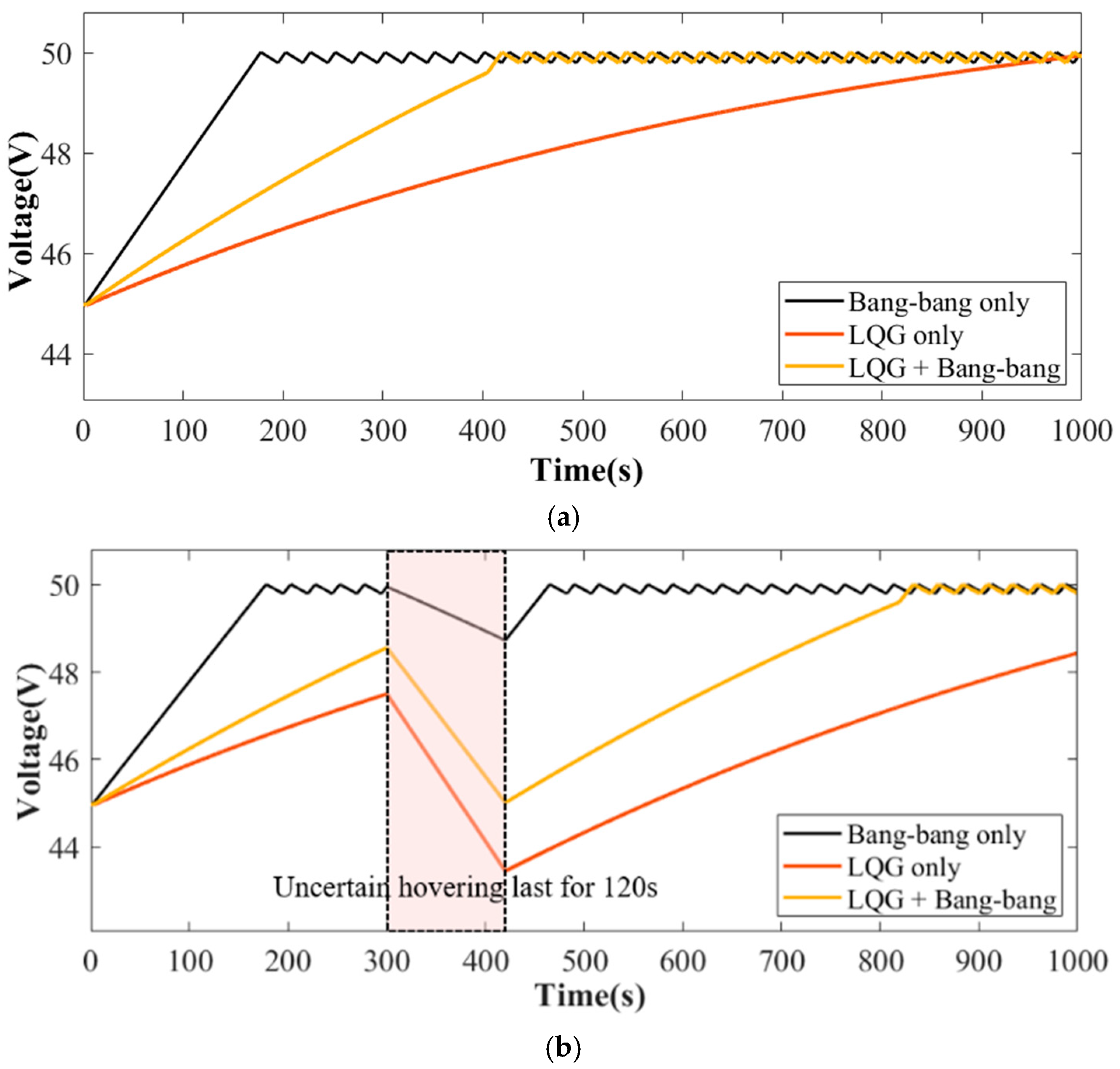
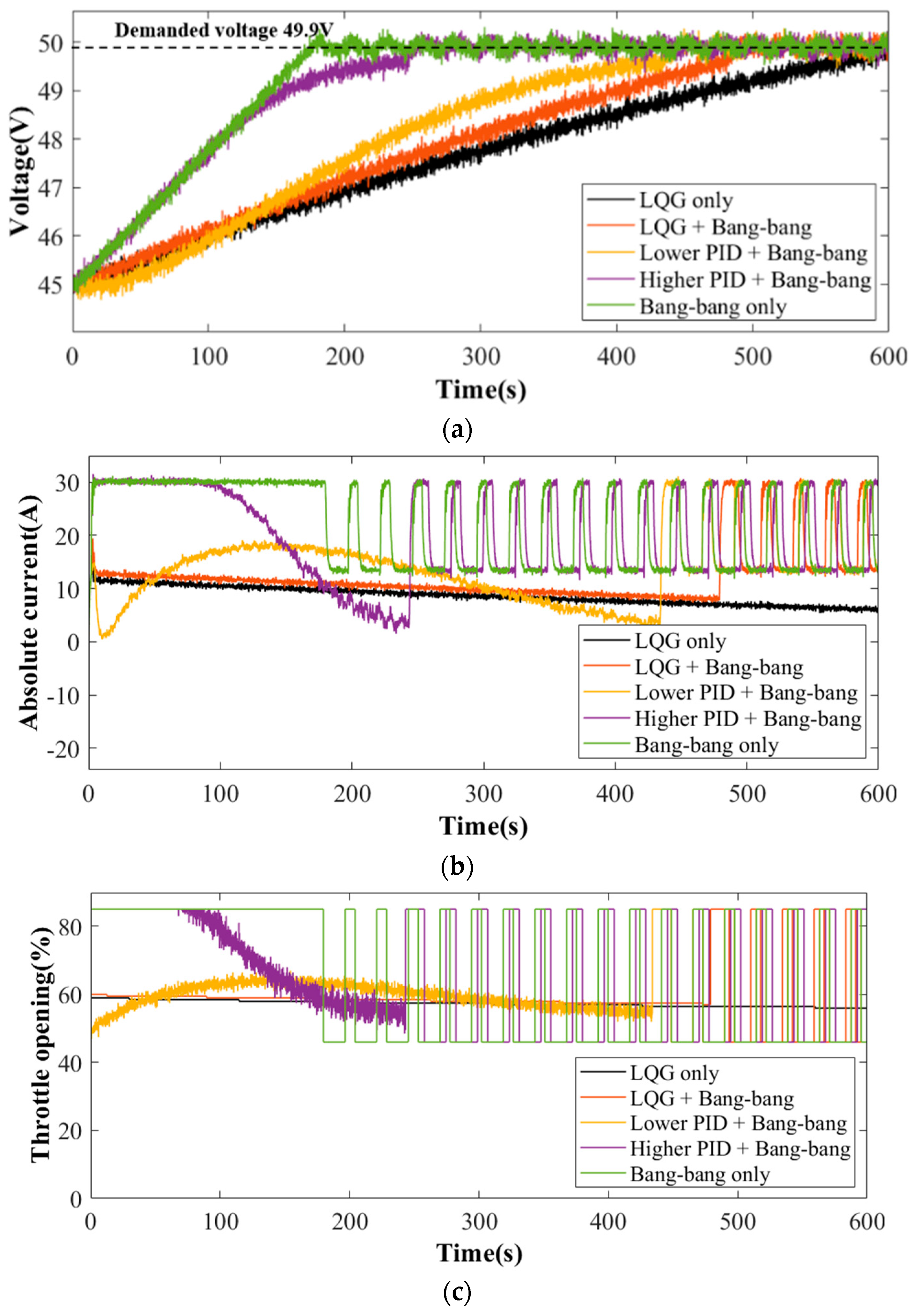
- The proposed composite strategy, integrating LQG and bang–bang regulation, has been validated in both ground testing and flight tests on VTOL prototypes, demonstrating its feasibility and cost-effectiveness. In a comprehensive flight duration of 600 s with uncertainty, this strategy achieved a fuel consumption of 0.310 L, representing a 6.63% reduction compared to the LQG only strategy, which consumed 0.332 L. Battery degradation was reduced to 0.92%, indicating improved battery longevity. This composite strategy not only minimized costs but also enabled the system to achieve desired performance objectives more rapidly.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akhter, M.Z.; Raza, M.; Iftikhar, S.H. Temporal and Economic Benefits of Vertical Take-Off and Landing Vehicles in Urban Transport. In Proceedings of the 2020 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 4 February–9 April 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Arshad, A.; Kallungal, A.J.; Elmenshawy, A.A.A.E. Stability Analysis for a Concept Design of Vertical Take-off and Landing (VTOL) Unmanned Aerial Vehicle (UAV). In Proceedings of the 2021 International Conference on Military Technologies (ICMT), Brno, Czech Republic, 8–11 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yolcu, S.; Akdağ, M. Conceptual Design of a Cargo UAV That Can Take-off and Land Vertically. In Proceedings of the 2021 3rd International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 11–13 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Li, W.; Liang, L.; Liu, W.; Wu, X. State of Charge Estimation of Lithium-Ion Batteries Using a Discrete-Time Nonlinear Observer. IEEE Trans. Ind. Electron. 2017, 64, 8557–8565. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, R.; Pang, S.; Xu, L.; Zhao, D.; Wei, J.; Huangfu, Y.; Gao, F. A Nonlinear Observer SOC Estimation Method Based on Electrochemical Model for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2021, 57, 1094–1104. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Z.; Bian, Z.; Gerada, D.; Gerada, C. Dual-Pulse Mode Control of a High-Speed Doubly Salient Electromagnetic Machine for Loss Reduction and Speed Range Extension. IEEE Trans. Ind. Electron. 2020, 67, 4391–4401. [Google Scholar] [CrossRef]
- Ge, L.; Zhong, J.; Bao, C.; Song, S.; De Doncker, R.W. Continuous Rotor Position Estimation for SRM Based on Transformed Unsaturated Inductance Characteristic. IEEE Trans. Power Electron. 2022, 37, 37–41. [Google Scholar] [CrossRef]
- Mao, S.; Ma, C.; Jiao, N.; Liu, W. Sensorless Starting Control of the Brushless Synchronous Starter/Generator based on Flux and Parameter Estimation of the Main Exciter. IEEE Trans. Power Electron. 2023, 39, 1174–1183. [Google Scholar] [CrossRef]
- Xie, M.; Wang, H.; Zhang, X.; Gao, Z.; Li, W. Study on impedance characteristic of aircraft cables. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; IEEE: New York, NY, USA, 2015; pp. 645–650. [Google Scholar]
- Shan, Z.; Ding, X.; Jatskevich, J.; Tse, C.K. Synthesis of multi-input multi-output DC/DC converters without energy buffer stages. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 712–716. [Google Scholar] [CrossRef]
- Qi, Y.; Li, Y.; Li, W.; Deng, H.; Tang, Y. Autonomous Control of Soft Open Point for Distribution Network Reliability Enhancement. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3127–3137. [Google Scholar] [CrossRef]
- Deng, F.; Li, Y.; Li, X.; Yao, W.; Mattavelli, P.; Zhang, X. A Decentralized Impedance Reshaping Strategy for Balanced, Unbalanced and Harmonic Power Sharing in Islanded Resistive Microgrids. IEEE Trans. Sustain. Energy 2021, 13, 743–754. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Chen, J. Investigation on the Selection of Electric Power System Architecture for Future More Electric Aircraft. IEEE Trans. Transp. Electrif. 2018, 4, 563–576. [Google Scholar] [CrossRef]
- Yang, Z.; Qu, J.; Ma, Y.; Shi, X. Modeling and simulation of power distribution system in more electric aircraft. J. Electr. Comput. Eng. 2015, 2015, 847624. [Google Scholar] [CrossRef]
- Dehesa, D.A.; Menon, S.K.; Monju, M.J. Modeling and Testing of Control Logic Approaches for Series Hybrid-Electric Powertrains for Unmanned Aerial Systems. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Online, 24–26 August 2020; p. 3961. [Google Scholar]
- Hageman, M.D.; McLaughlin, T.E. Considerations for pairing the ic engine and electric motor in a hybrid power system for small uavs. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January, 2018; p. 2132. [Google Scholar]
- Tao, L.; Zhou, Y.; Zicun, L.; Zhang, X. State of art on energy management strategy for hybrid-powered unmanned aerial vehicle. Chin. J. Aeronaut. 2019, 32, 1488–1503. [Google Scholar]
- Campagna, N.; Castiglia, V.; Damiano, A.; Di Noia, L.P.; Miceli, R.; Di Tommaso, A.O. A hybrid energy storage sizing for a vertical take-off and landing electric aircraft. In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Maraschi, L.; Bernabei, L.; Marzioli, P.; Galassi, R.M.; Ciottoli, P.P.; Valorani, M.; Piergentili, F. Hybrid-electric propulsive systems sizing and performance evaluation tool for aircraft and UAV. In Proceedings of the 2022 IEEE 9th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Pisa, Italy, 27–29 June 2022; IEEE: New York, NY, USA, 2022; pp. 43–48. [Google Scholar]
- Martinez-Heredia, J.M.; Colodro, F.; Mora-Jiménez, J.L.; Remujo, A.; Soriano, J.; Esteban, S. Development of GaN technology-based DC/DC converter for hybrid UAV. IEEE Access 2020, 8, 88014–88025. [Google Scholar] [CrossRef]
- Bayrak, Z.U.; Kaya, U.; Oksuztepe, E. Investigation of PEMFC performance for cruising hybrid powered fixed-wing electric UAV in different temperatures. Int. J. Hydrogen Energy 2020, 45, 7036–7045. [Google Scholar] [CrossRef]
- van Nguyen, C.; van Quyen, T.; Le, A.M.; Truong, L.H.; Nguyen, M.T. Advanced hybrid energy harvesting systems for unmanned aerial vehicles (UAVs). Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 34–39. [Google Scholar] [CrossRef]
- Yang, X.; Pei, X. Hybrid system for powering unmanned aerial vehicles: Demonstration and study cases. In Hybrid Technologies for Power Generation; Academic Press: Cambridge, MA, USA, 2022; pp. 439–473. [Google Scholar]
- Zong, J.; Zhu, B.; Hou, Z.; Yang, X.; Zhai, J. Evaluation and comparison of hybrid wing VTOL UAV with four different electric propulsion systems. Aerospace 2021, 8, 256. [Google Scholar] [CrossRef]
- Burgess, J.; Runnels, T.; Johnsen, J.; Drake, J.; Rouser, K. Experimental comparison of direct and active throttle control of a 7-kw turboelectric power system for unmanned aircraft. Appl. Sci. 2021, 11, 10608. [Google Scholar] [CrossRef]
- Hu, C.M.; Yan, D.Y.; Liu, N.; Song, X. Comparison and Simulation Research on Energy Management Strategies of Oil–Electric Hybrid Unmanned Aerial Vehicle. Chin. Intern. Combust. Engine Eng. 2022, 43, 74–83. [Google Scholar]
- He, C.; Tong, Y.; Xia, X.; Chen, G. Integrated optimization of energy management strategy and mission path for hybrid-electric VTOL UAVs in cargo transportation. Acta Aeronaut. Astronaut. Sin. 2024, 45, 229606. [Google Scholar]
- Wu, F.; Wu, Z.; Xu, J.; Hao, Q. Rule-based Transient Power Control Strategy for Hybrid System in Unmanned Aerial Vehicle. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 2425–2429. [Google Scholar]
- Tao, L.; Wang, Y.; Jin, X.; Min, Z.; Zhang, X.; Zhang, X. An optimal fuzzy logic-based energy management strategy for a fuel Cell/Battery hybrid power unmanned aerial vehicle. Aerospace 2022, 9, 115. [Google Scholar] [CrossRef]
- Kittaneh, O. On the Theory of the Arrhenius-Normal Model with Applications to the Life Distribution of Lithium-Ion Batteries. Batteries 2023, 9, 55. [Google Scholar] [CrossRef]




| Flight Profile | Power Management Strategy | Adjusting Time (45.0 V to 49.9 V) | Fuel Consumption (1000 s) | Battery Pack Degradation |
|---|---|---|---|---|
| 45.0–49.9 V | LQG only | none | 0.533 L | 0.73% |
| Bang–bang only | 180 s | 0.456 L | 1.60% | |
| LQG + bang–bang | 820 s | 0.528 L | 1.34% | |
| 45.0–48.2 V | LQG only | none | 0.482 L | 0.68% |
| Bang–bang only | 120 s | 0.407 L | 1.44% | |
| LQG + bang–bang | 840 s | 0.470 L | 1.06% |
| Performance | Value | Performance | Value |
|---|---|---|---|
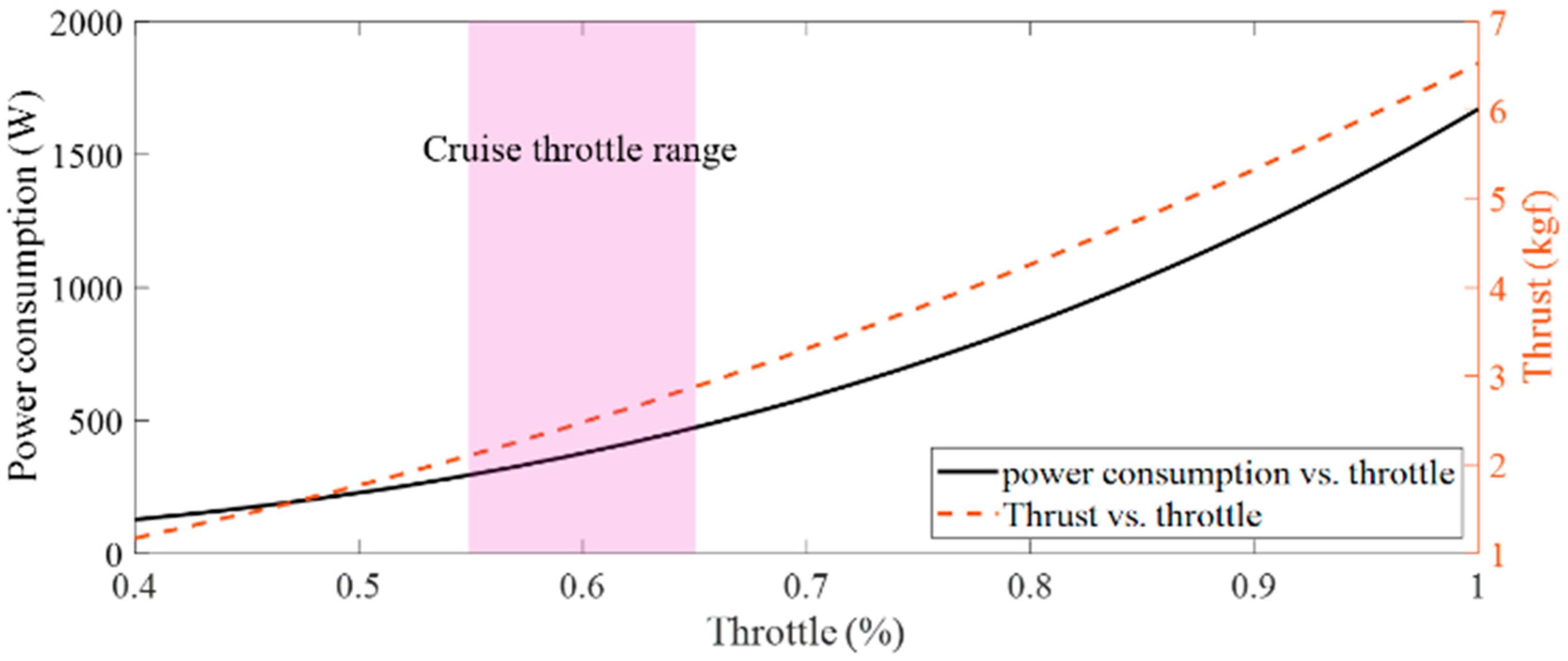
| VTOL take-off weight | 30 kg | Power demand for level cruise flight | 600 W |
| Cruise airspeed | 27 m/s | Generated power (charging) | 1700 W |
| Total cruise thrust (converted at ground) | 8.6 kgf | Thrust on wings (converted at ground) | 2.8 × 2 kgf |
| ICE speed | 6500 RPM |
| Parameter | Q | S | R | Voltage Error (V) |
|---|---|---|---|---|
| LQR-1 | ||||
| LQR-2 |
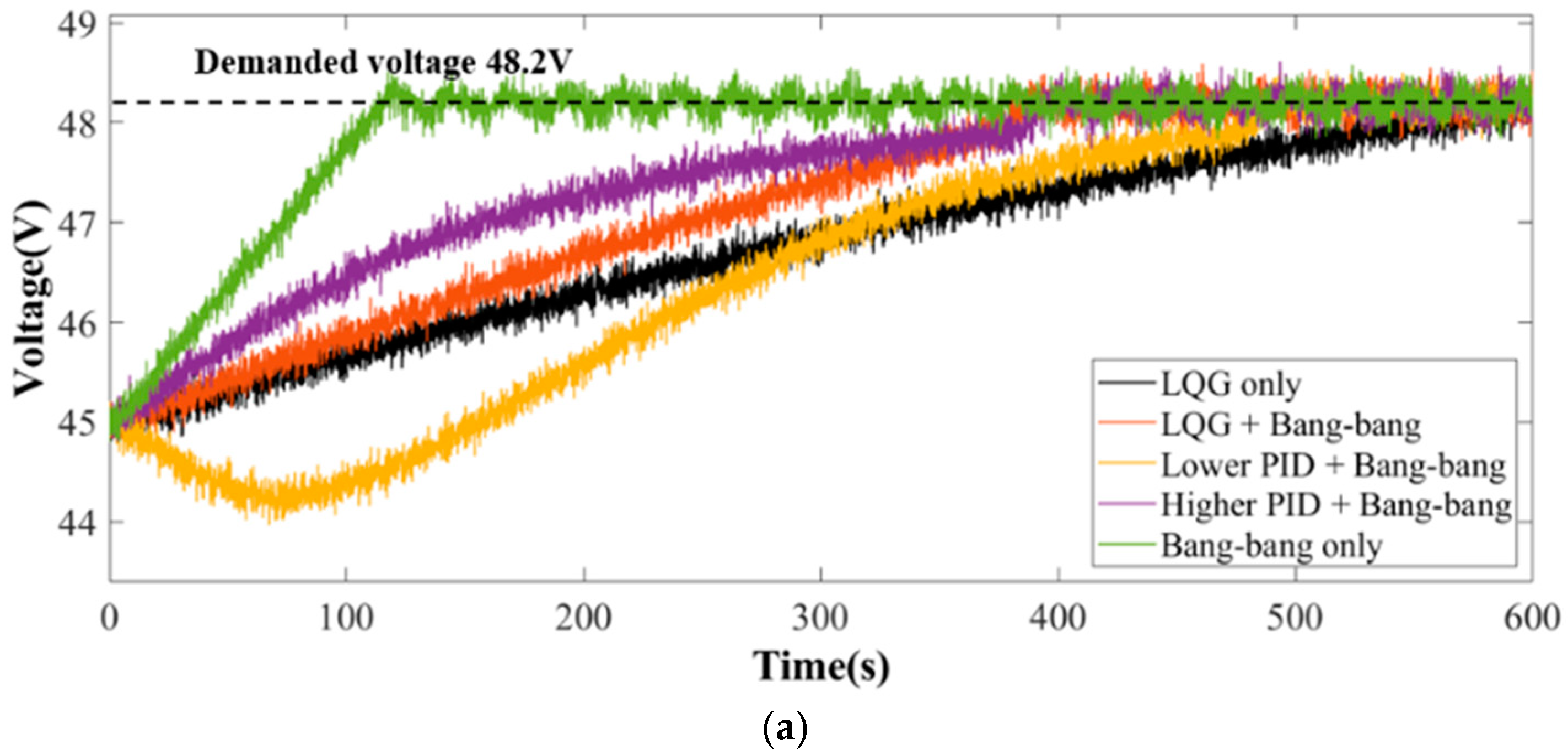
| Demand Voltage | Power Management Strategy | Adjusting Time (45.0 V to 49.9 V) | Fuel Consumption (600 s) | Battery Pack Degradation | Overall Cost ($) |
|---|---|---|---|---|---|
| 49.9 V | LQG only | 600 s | 0.325 L | 0.82% | 1.15 |
| LQG + bang–bang | 480 s | 0.305 L | 0.84% | 1.15 | |
| Lower PI + bang–bang | 450 s | 0.299 L | 0.92% | 1.22 | |
| Higher PI + bang–bang | 260 s | 0.276 L | 1.92% | 2.14 | |
| Bang–bang only | 180 s | 0.266 L | 2.12% | 2.32 | |
| 48.2 V | LQG only | 600 s | 0.262 L | 0.77% | 1.03 |
| LQG + bang–bang | 380 s | 0.255 L | 0.78% | 1.03 | |
| Lower PI + bang–bang | 500 s | 0.299 L | 0.88% | 1.18 | |
| Higher PI + bang–bang | 390 s | 0.276 L | 1.72% | 1.95 | |
| Bang–bang only | 120 s | 0.266 L | 2.01% | 2.22 |
| Power Management Strategy | Adjusting Time (After Conversion) | Overshoot | Fuel Consumption (600 s) | Battery Pack Degradation | Overall Cost ($) |
|---|---|---|---|---|---|
| LQG only | 600 s | None | 0.332 L | 0.85% | 1.23 |
| PID only | 150 s | 0.6 V | 0.378 L | 1.13% | 1.56 |
| Bang–bang only | 150 s | none | 0.267 L | 1.89% | 2.19 |
| LQG + bang–bang | 330 s | none | 0.310 L | 0.92% | 1.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, S.; Peng, X.; Gan, Y.; Yang, J.; Xiang, G.; Dian, S. Composite Power Management Strategy for Hybrid Powered Compound-Wing Aircraft in Level Flight. Energies 2025, 18, 799. https://doi.org/10.3390/en18040799
An S, Peng X, Gan Y, Yang J, Xiang G, Dian S. Composite Power Management Strategy for Hybrid Powered Compound-Wing Aircraft in Level Flight. Energies. 2025; 18(4):799. https://doi.org/10.3390/en18040799
Chicago/Turabian StyleAn, Siqi, Xu Peng, Yuantao Gan, Jingyu Yang, Guofei Xiang, and Songyi Dian. 2025. "Composite Power Management Strategy for Hybrid Powered Compound-Wing Aircraft in Level Flight" Energies 18, no. 4: 799. https://doi.org/10.3390/en18040799
APA StyleAn, S., Peng, X., Gan, Y., Yang, J., Xiang, G., & Dian, S. (2025). Composite Power Management Strategy for Hybrid Powered Compound-Wing Aircraft in Level Flight. Energies, 18(4), 799. https://doi.org/10.3390/en18040799







