Development and Performance Analysis of an Electromagnetic Pump for a Thermal Hydraulic Experimental Loop of a Lead-Cooled Fast Reactor
Abstract
1. Introduction
2. Mathematical and Physical Model
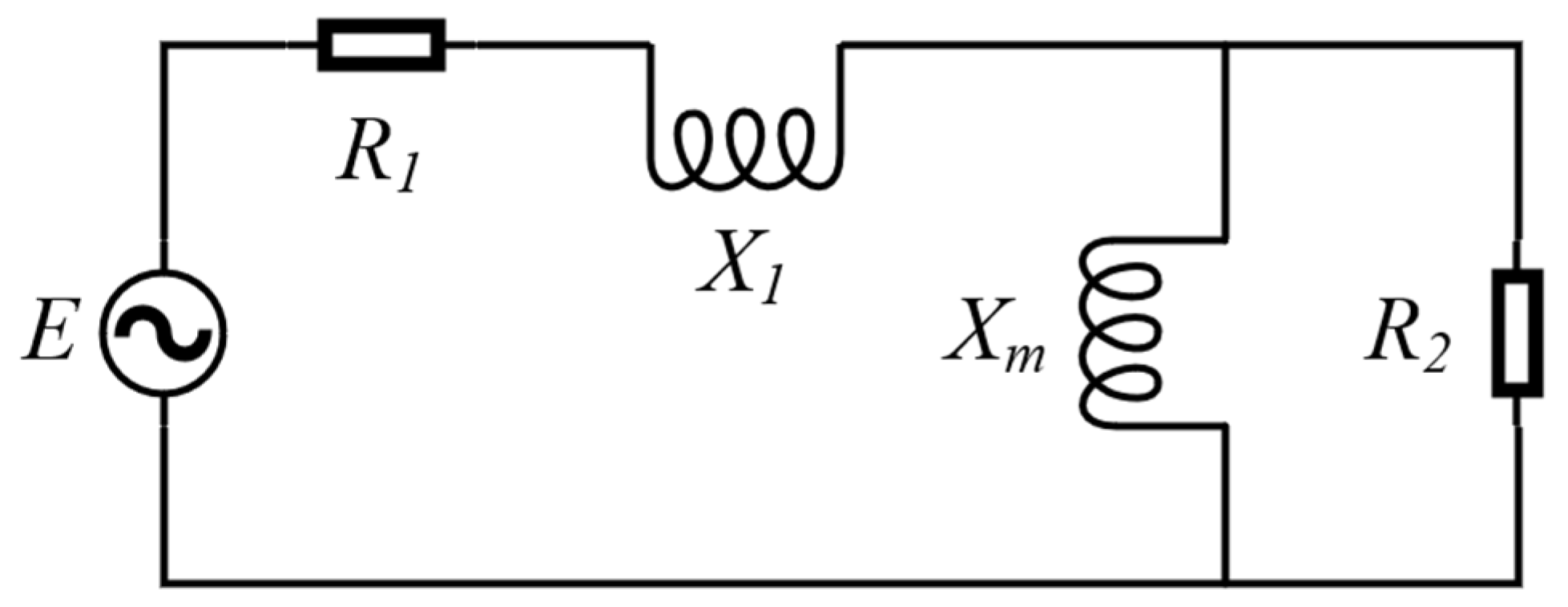
2.1. Equivalent Circuit Model
2.1.1. Primary Equivalent Resistance
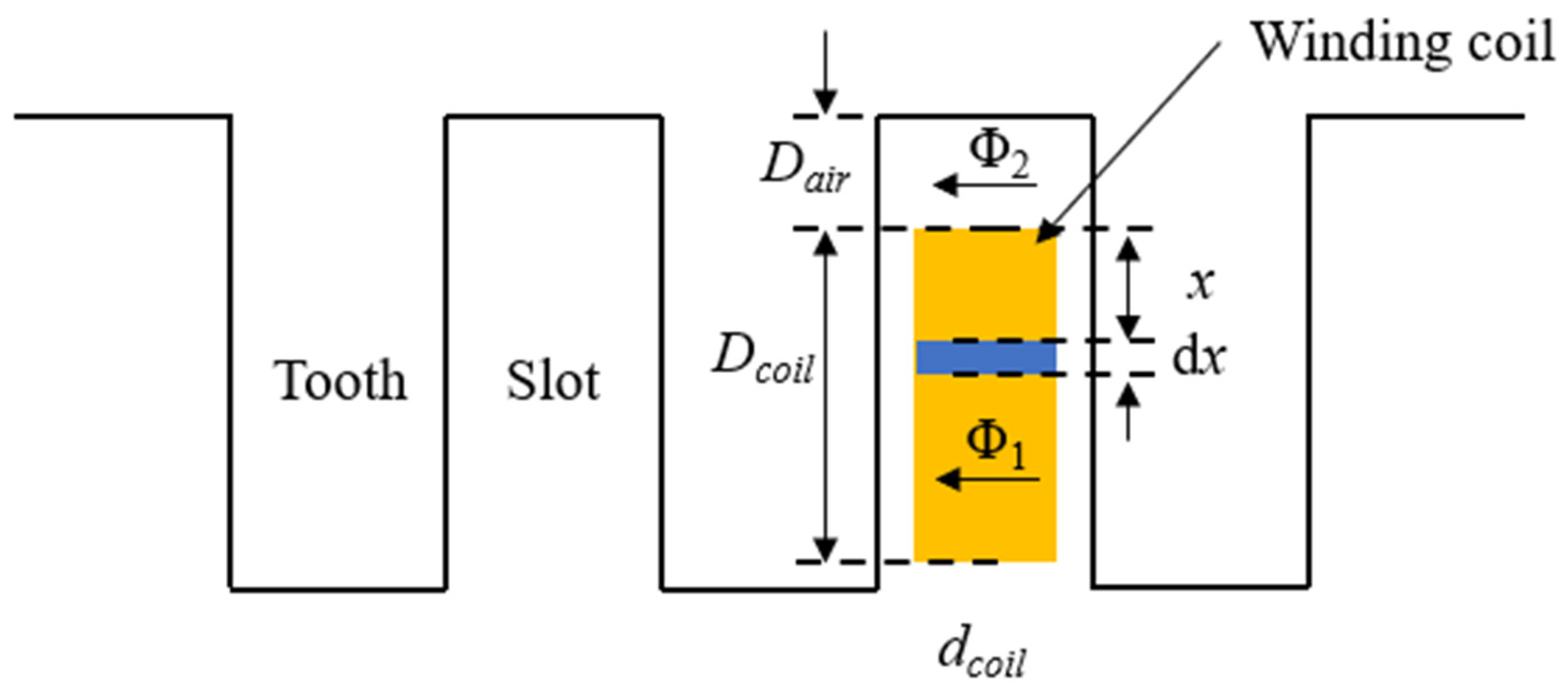
2.1.2. Equivalent Leakage Reactance
2.1.3. Secondary Equivalent Resistance
2.1.4. Magnetizing Reactance
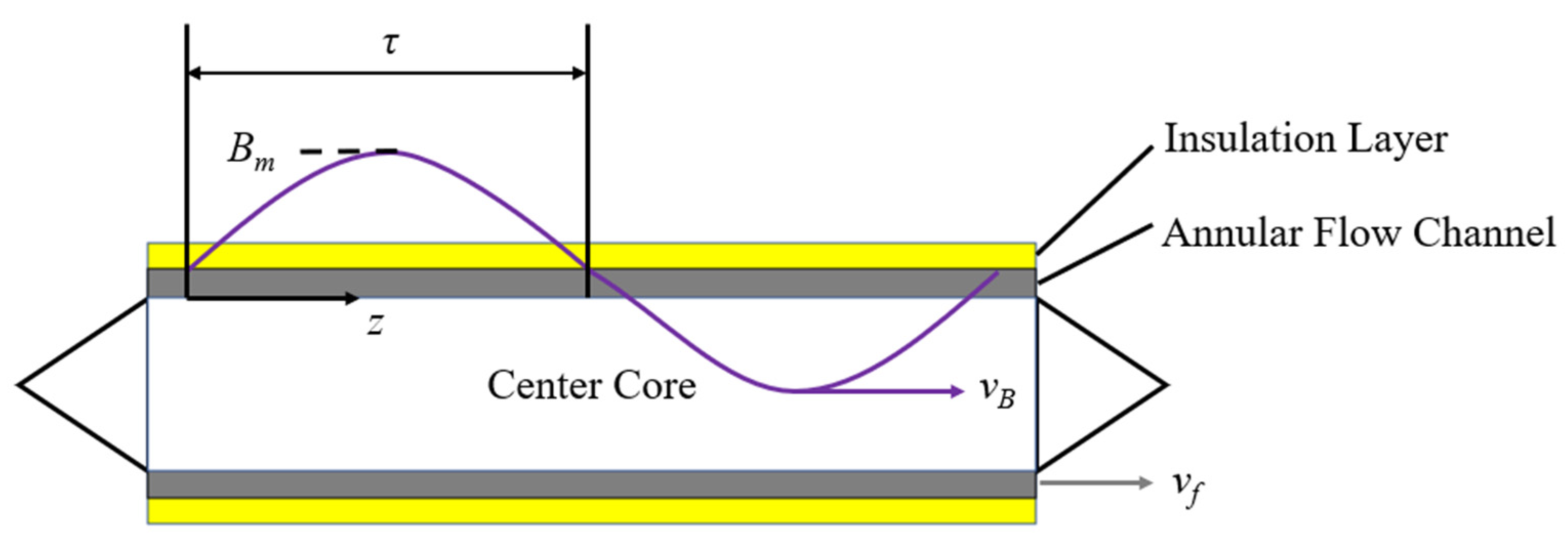
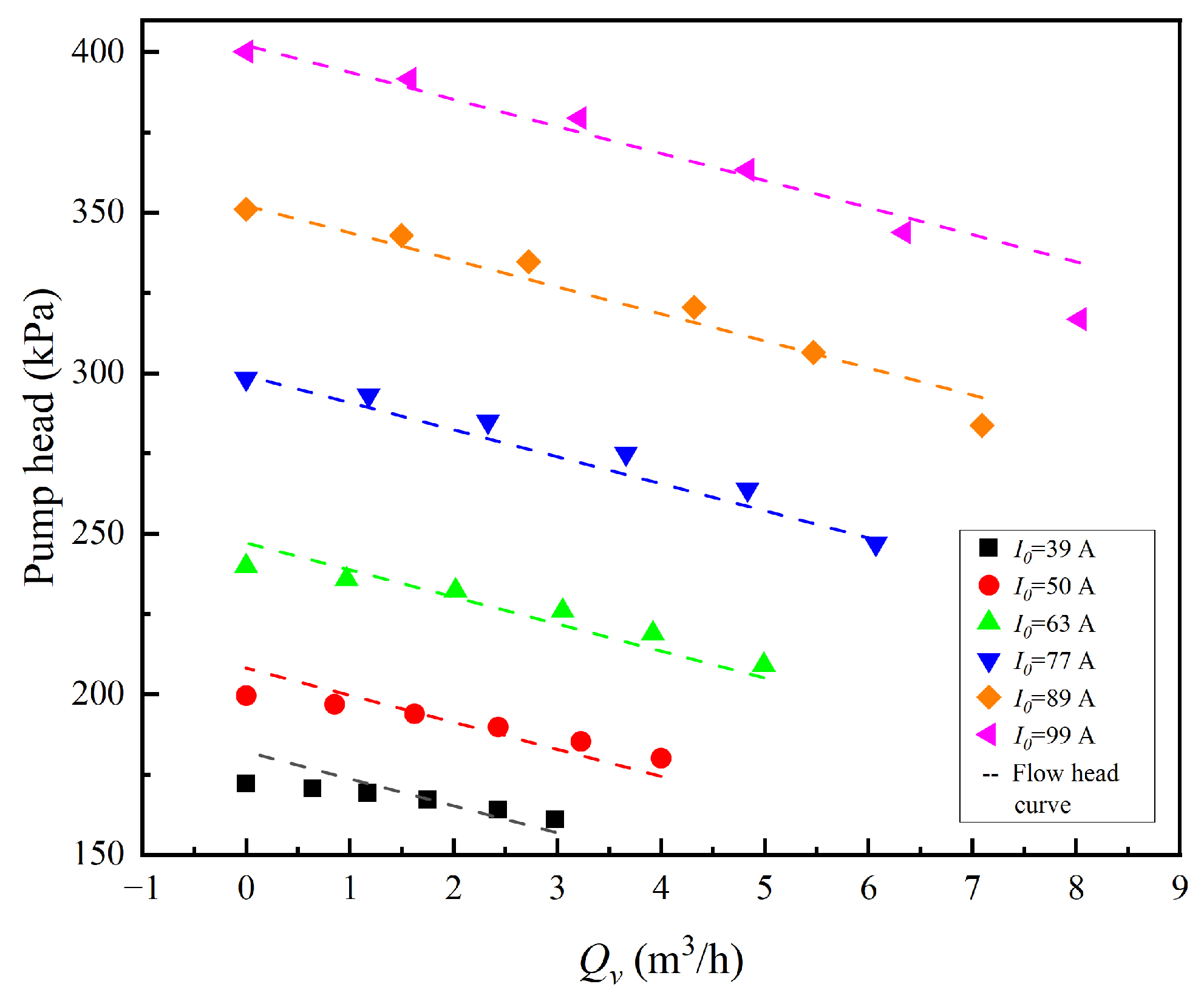
2.2. Flow-Head Model
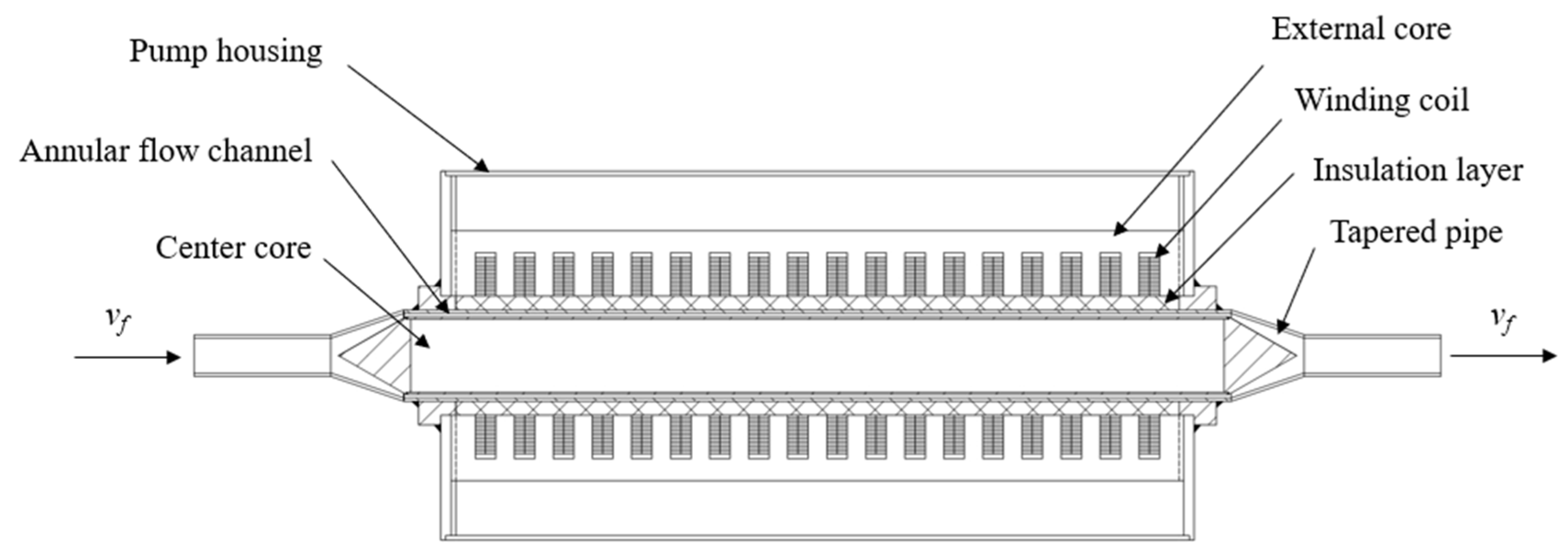
3. Design and Manufacturing
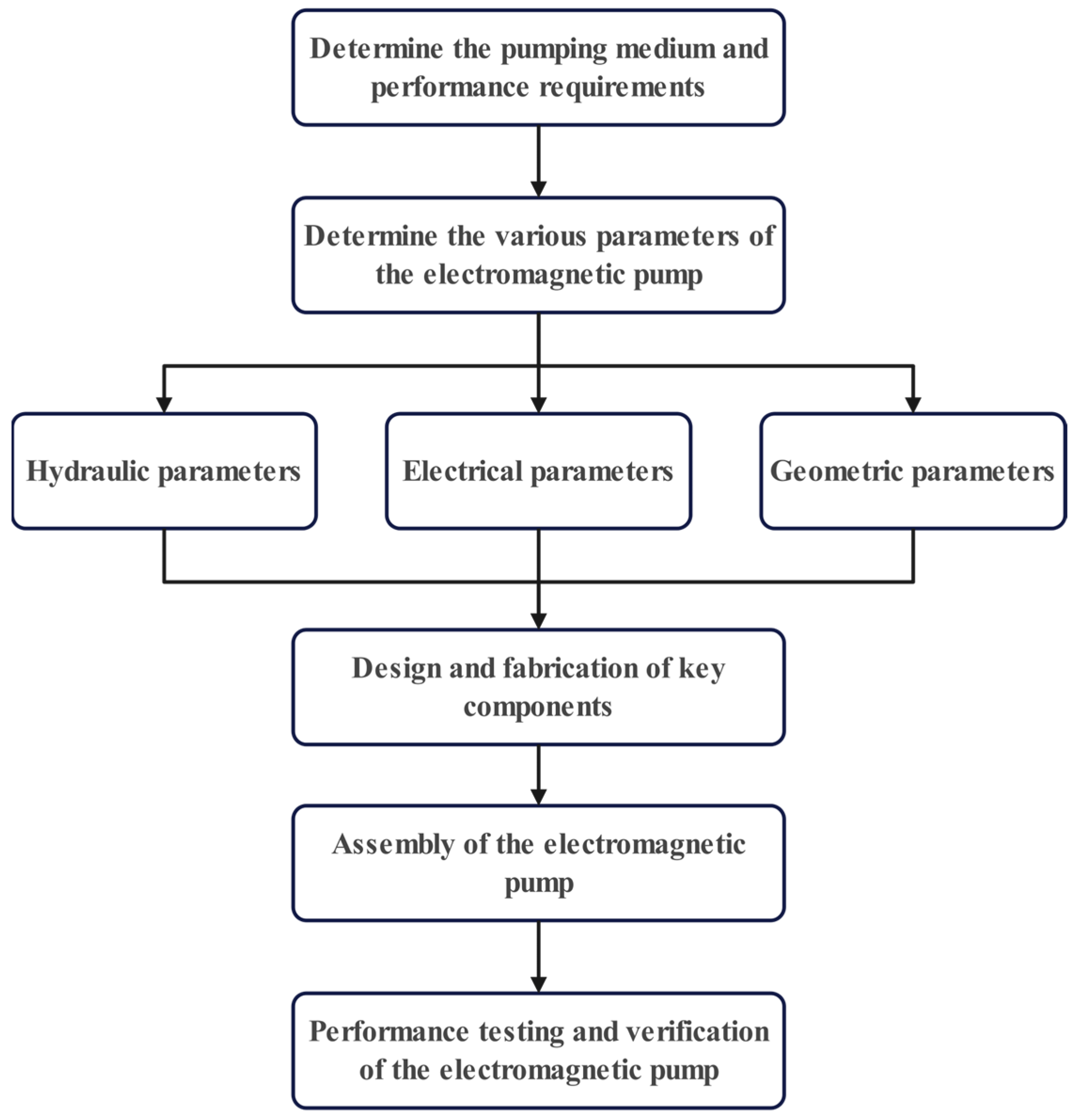
3.1. Parameter Design of the EMP
- (1)
- Hydraulic parameter design: This involves the flow rate range and driving head for the EMP.
- (2)
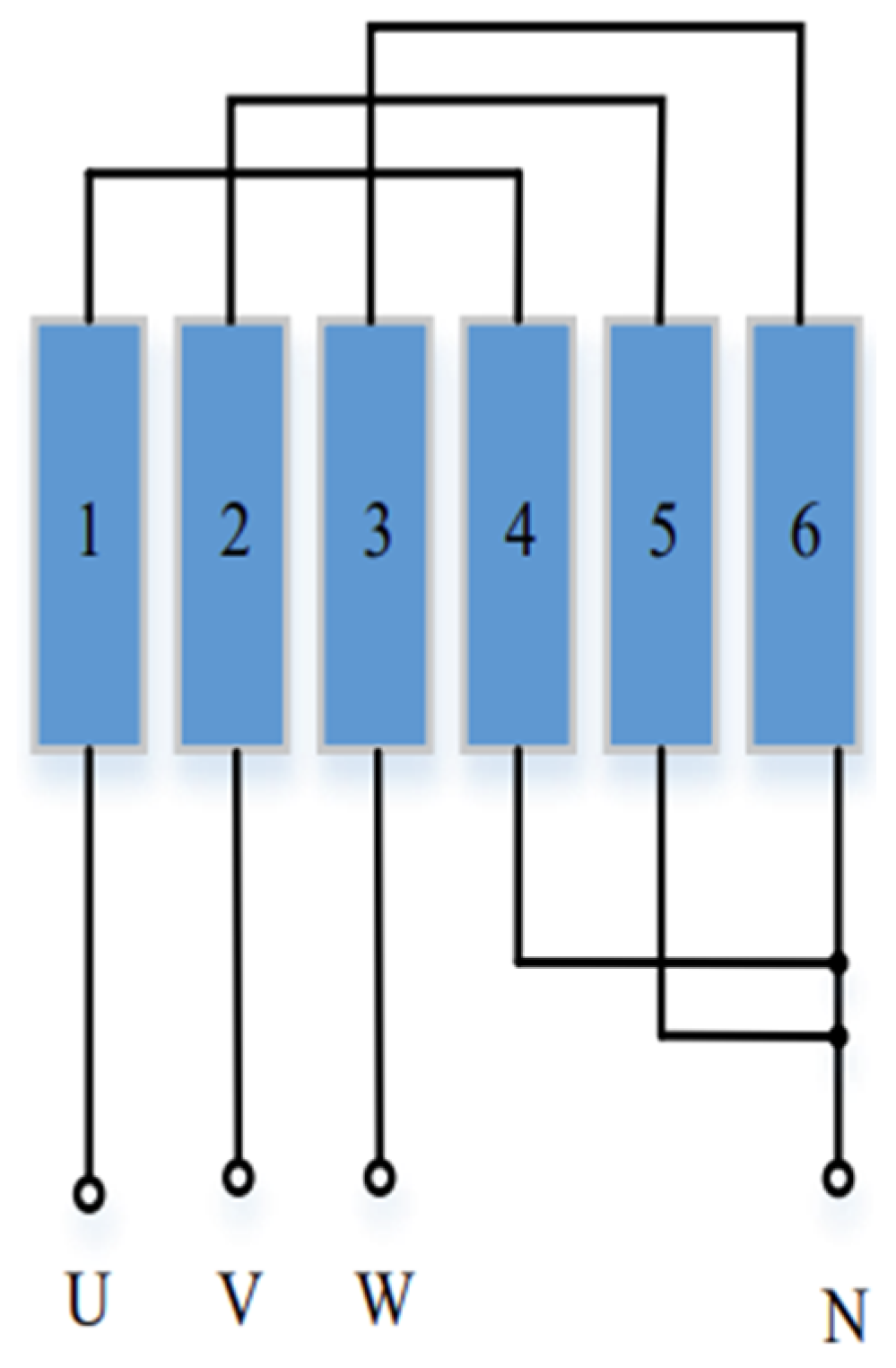
- Electrical parameter design: This involves the input current range, rated voltage, rated frequency, pole pair number, and winding connection method.
- (3)
- Geometric parameter design: This includes the dimensions of the annular flow channel, as well as the center and external iron cores and the solenoid coil.
3.1.1. Hydraulic Parameter Design
3.1.2. Electrical Parameter Design
3.1.3. Geometric Parameter Design
3.2. Fabrication and Manufacturing of the EMP
- (1)
- Securing the center core to the inner wall of the annular channel;
- (2)
- Fixing the inner and outer walls of the annular channel;
- (3)
- Installing insulation layers on the outer surface of the annular channel;
- (4)
- Installing and securing the external core;
- (5)
- Winding and fixing the coils;
- (6)
- Installing the pump casing.
4. Experiments and Results
4.1. Experimental Loop
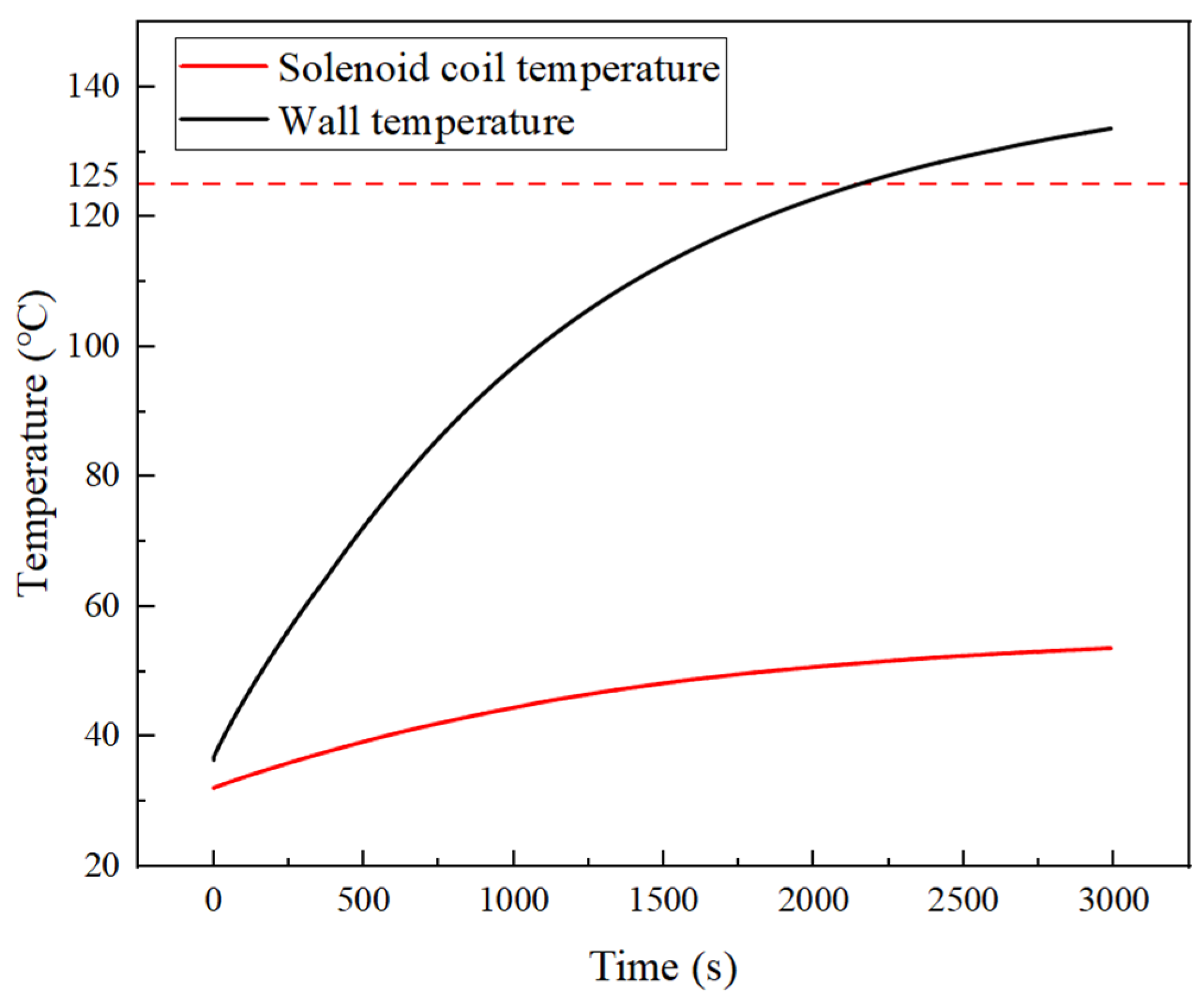
4.2. Start-Up and Preheating Characteristics
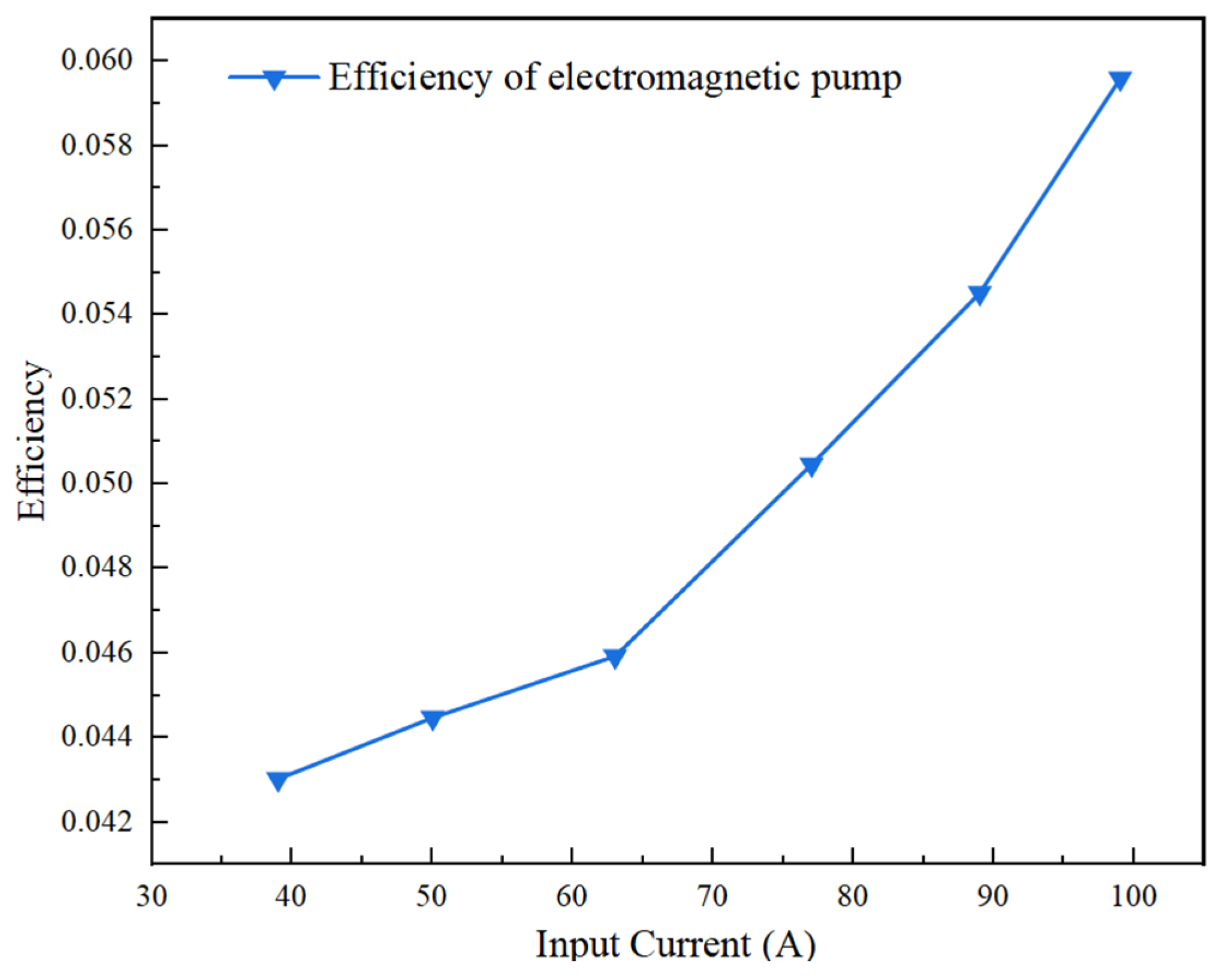
4.3. Drive Performance Characteristics
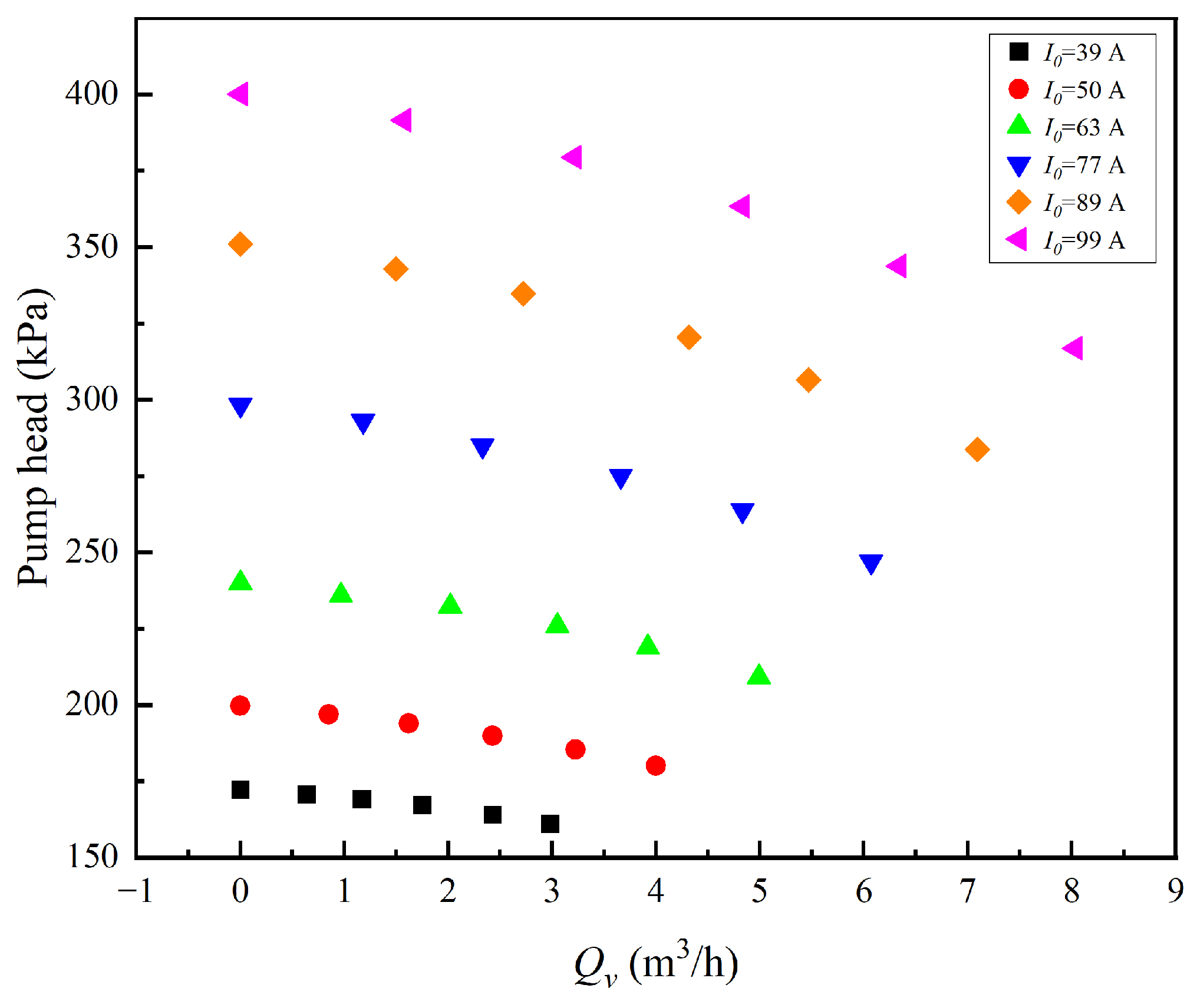
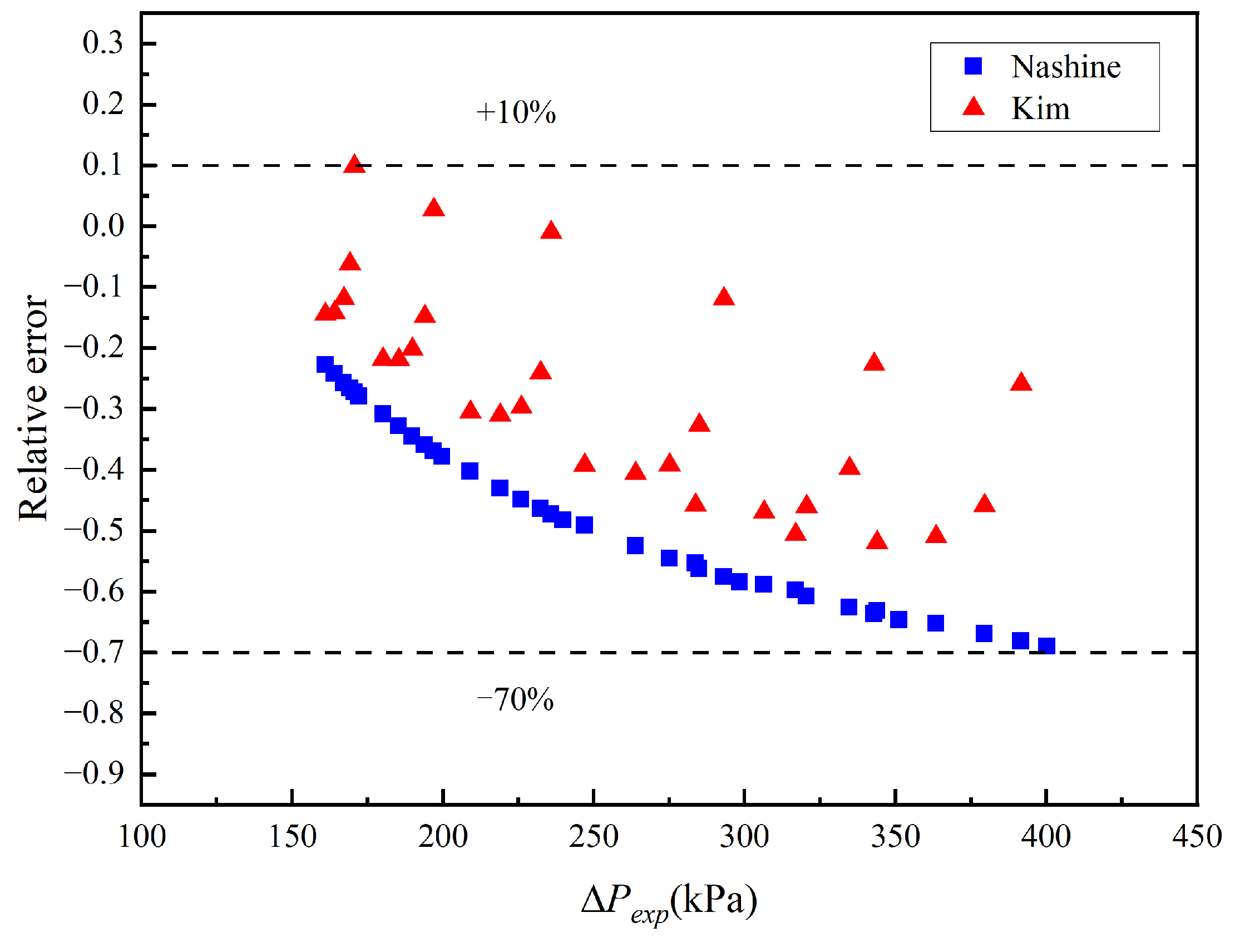
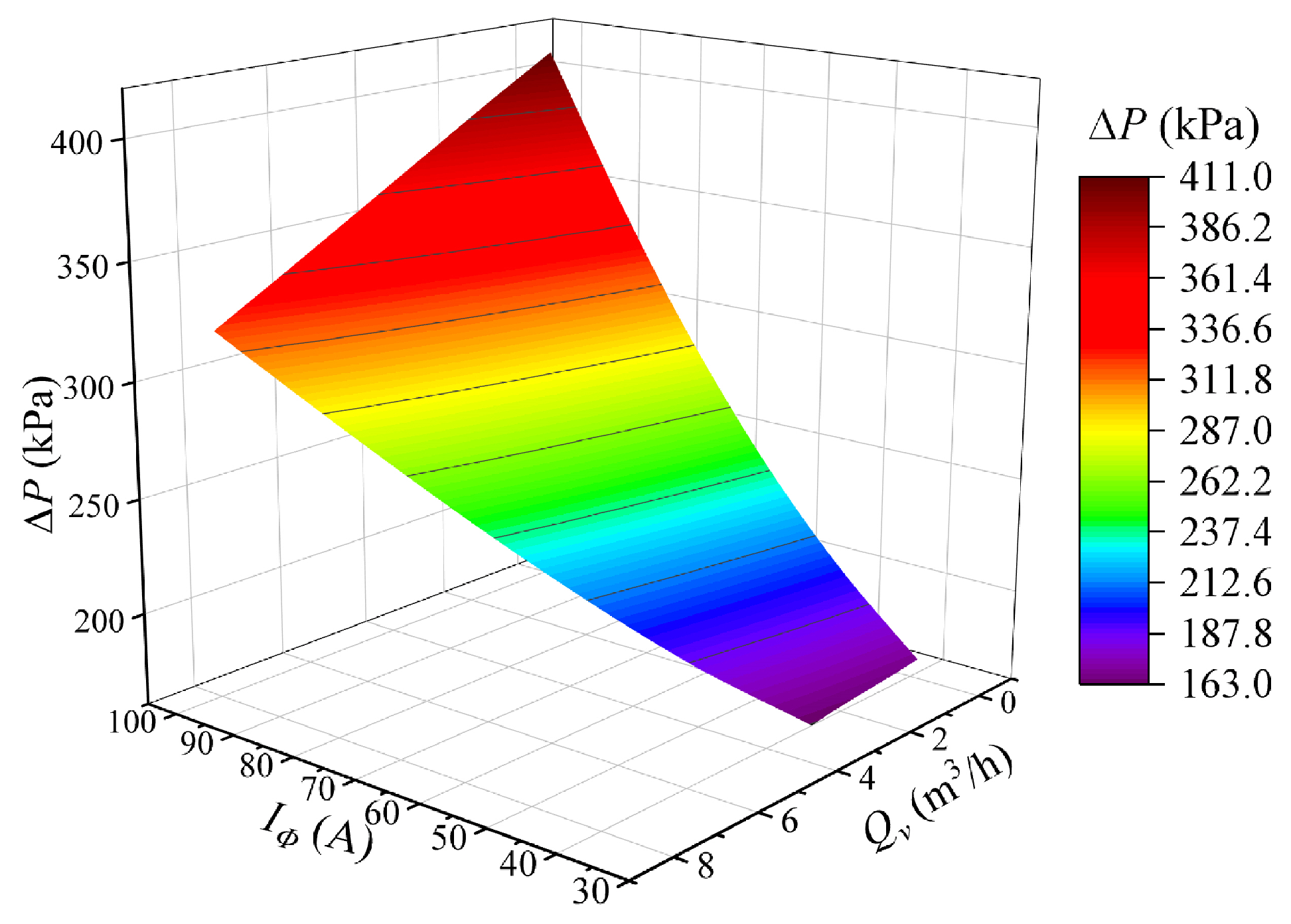
4.4. Flow Rate and Head Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Aannular (m2) | Sectional area of annular flow channel | L2 (H) | Inductance at airgap |
| AB (m2) | Magnetic area of EMP | LB (m) | Magnetic circuit length |
| Acoil (m2) | Cross-sectional area of a single winding coil | Lcoil (m) | Length of coil |
| Bm (T) | Magnetic density amplitude | Lstator (m) | Stator length |
| BP (T) | Magnetic density of single stage | M | Number of phases |
| Bz (T) | Magnetic density at z | N | Turns of coil |
| dairgap (m) | Air layer thickness | Nsc | Effective number of turns in series per phase in stator |
| dannular (m) | Annular channel width | ΔP (kPa) | Pump head |
| dcoil (m) | Winding coil width | p | Pole pairs |
| dw,in (m) | Annular channel inner wall thickness | ∆PM (kPa) | Pressure drop correction factor |
| dw,out (m) | Annular channel outer wall thickness | ∆Pf (kPa) | Friction pressure drop |
| D0 (m) | Diameter of center core | ∆Pel (kPa) | Gravity pressure drop |
| Dair (m) | Air layer outer diameter | ∆Pc (kPa) | Form resistance pressure drop |
| Dannuluar (m) | Annular channel outer diameter | Q | Number of slots |
| Dcoil (m) | Winding coil radial length | Qv (m3/h) | Volume flow rate |
| Dj (m) | Insulation layer outer diameter | Qsyn (m3/h) | Synchronous volume flow rate |
| EA (V) | Induced electromotive force | q | Number of slots per pole pair in a phase |
| EB (V) | Total induced electromotive force | rCu | Resistivity of Cu |
| Ez (V) | Induced electromotive force at z | rLBE | Resistivity of LBE |
| F1 (H) | Fundamental wave MMF of single-phase winding | rss | Resistivity of stainless steel |
| F3 (H) | Fundamental wave MMF of three-phase winding | R1 (Ω) | Primary equivalent resistance |
| Fm (H) | MMF amplitude | R2 (Ω) | Secondary equivalent resistance |
| Fp (N) | Ampere force | Rcoil (Ω) | Resistance of coil |
| Ge (m) | Effective inter-core gap | s | Slip |
| H (T) | Magnetic field strength | TCu (°C) | Temperature of copper coil |
| Iφ (A) | Phase current | TLBE (°C) | Temperature of LBE |
| Iz (A) | Induced current generated by dz | t (s) | Time |
| iφ (A) | Instantaneous phase current | U (V) | Input voltage |
| kw | Winding factor | vsyn (m/s) | Synchronous speed |
| kf | Slot-filling factor | vf (m/s) | Fluid velocity |
| kd | Winding distribution factor | vR (m/s) | Relative speed |
| Kp | Pitch factor | X1 (Ω) | Equivalent leakage reactance |
| L (H) | Total inductance of winding coil | Xm (Ω) | Magnetizing reactance |
| L1 (H) | Inductance at coil | ||
| Greek symbols | |||
| μ0 | Vacuum permeability | τ (m) | Pole distance |
| η | Efficiency | ρc | Resistivity of coil conductor |
| ρr’ | Surface electrical resistivity of fluid | ω | Input angular frequency |
| λc | kd(1 + 3a)/12 (a: chording factor) | Φ | Magnetic flux |
References
- U.S. DOE. A Technology Roadmap for Generation IV Nuclear Energy System. In Nuclear Energy Research Advisory Committee and the Generation IV International Forum; U.S. DOE: Washington, DC, USA, 2002. [Google Scholar]
- Tuček, K.; Tsige-Tamirat, H.; Ammirabile, L.; Lázaro, A.; Grah, A.; Carlsson, J.; Döderlein, C.; Oettingen, M.; Fütterer, M.; D’agata, E.; et al. Generation IV Reactor Safety and Materials Research by the Institute for Energy and Transport at the European Commission’s Joint Research Centre. Nucl. Eng. Des. 2013, 265, 1181–1193. [Google Scholar] [CrossRef]
- Dong, Z.; Qiu, H.; Wang, M.; Tian, W.; Qiu, S.; Su, G. Numerical simulation on the thermal stratification in the lead pool of lead-cooled fast reactor (LFR). Ann. Nucl. Energy 2022, 174, 109176. [Google Scholar] [CrossRef]
- Stanisz, P.; Oettingen, M.; Cetnar, J. Monte Carlo modeling of Lead-Cooled Fast Reactor in adiabatic equilibrium state. Nucl. Eng. Des. 2016, 301, 341–352. [Google Scholar] [CrossRef]
- Gluekler, E.L. US advanced liquid metal reactor (ALMR). Prog. Nucl. Energy 1997, 31, 43–61. [Google Scholar] [CrossRef]
- Baker, R.S.; Tessier, M.J. Handbook of Electromagnetic Pump Technology; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Childs, B.M. Electromagnetic pumps and flowmeters for fast-reactor development. Ann. Nucl. Sci. Eng. 1974, 1, 351I–357I. [Google Scholar] [CrossRef]
- Blake, L.R. Conduction and induction pumps for liquid metals. Proc. IEE-Part A Power Eng. 1957, 104, 49–67. [Google Scholar] [CrossRef]
- Kikuchi, K.; Kurata, Y.; Saito, S.; Futakawa, M.; Sasa, T.; Oigawa, H.; Wakai, E.; Miura, K. Corrosion–erosion test of SS316 in flowing Pb–Bi. J. Nucl. Mater. 2003, 318, 348–354. [Google Scholar] [CrossRef]
- Ota, H.; Katsuki, K.; Funato, M.; Taguchi, J.; Fanning, A.W.; Doi, Y.; Nibe, N.; Ueta, M.; Inagaki, T. Development of 160 m3/min large capacity sodium-immersed self-cooled electromagnetic pump. J. Nucl. Sci. Technol. 2004, 41, 511–523. [Google Scholar] [CrossRef]
- Sharma, P.; Sivakumar, L.; Prasad, R.R.; Saxena, D.; Kumar, V.S.; Nashine, B.; Noushad, I.; Rajan, K.; Kalyanasundaram, P. Design, development and testing of a large capacity annular linear induction pump. Energy Procedia 2011, 7, 622–629. [Google Scholar] [CrossRef]
- Nashine, B.K.; Rao, B. Design, in-sodium testing and performance evaluation of annular linear induction pump for a sodium cooled fast reactor. Ann. Nucl. Energy 2014, 73, 527–536. [Google Scholar] [CrossRef]
- Kim, H.R.; Kwak, J.S. MHD design analysis of an annular linear induction electromagnetic pump for SFR thermal hydraulic experimental loop. Ann. Nucl. Energy 2016, 92, 127–135. [Google Scholar] [CrossRef]
- Wang, L.; Hou, Y.; Shi, L.; Wu, Y.; Tian, W.; Song, D.; Qiu, S.; Su, G. Experimental study and optimized design on electromagnetic pump for liquid sodium. Ann. Nucl. Energy 2019, 124, 426–440. [Google Scholar] [CrossRef]
- Pan, W.; Chen, X.; Wang, X. Generalized design method of the three-phase Y-connected wound rotor for both additive modulation and differential modulation brushless doubly fed machines. IEEE Trans. Energy Convers. 2021, 36, 1940. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, H.; Song, T.; Zhang, Q.; Yang, L.; Bi, K. One dimensional analytical model considering end effects for analysis of electromagnetic pressure characteristics of annular linear induction electromagnetic pump. Ann. Nucl. Energy 2022, 165, 108766. [Google Scholar] [CrossRef]
- Nasar, S.A. Linear Motion Electric Machines; John Wiley & Sons: New York, NY, USA, 1976. [Google Scholar]
- Matula, R.A. Electrical resistivity of copper, gold, palladium, and silver. J. Phys. Chem. Ref. Data 1979, 8, 1147–1298. [Google Scholar] [CrossRef]
- Roman, C.R. Study of the Electromagnetic Pumping Systems of Molten Metals and Molten Salts. Ph.D. Thesis, University Grenoble, Grenoble, France, 2014. [Google Scholar]
- NEA. Handbook on Lead-Bismuth Eutectic Alloy and Lead Properties, Materials Compatibility, Thermal-hydraulics and Technologies, 2007 ed.; OECD Publishing: Paris, France, 2007. [Google Scholar]
- Yan, J.C. Electrical Machinery; Press of University of Science and Technology of China: Hefei, China, 2013. (In Chinese) [Google Scholar]
- Tarantino, M.; Angiolini, M.; Bassini, S.; Cataldo, S.; Ciantelli, C.; Cristalli, C.; Del Nevo, A.; Di Piazza, I.; Diamanti, D.; Eboli, M.; et al. Overview on Lead-Cooled Fast Reactor Design and Related Technologies Development in ENEA. Energies 2021, 14, 5157. [Google Scholar] [CrossRef]











| Design Variables | Units | Values |
|---|---|---|
| Flow rate (Q) | m3·h−1 | 8 |
| Developed pressure (ΔP) | kPa | 500 |
| Design Variables | Unit | Values |
|---|---|---|
| Input voltage (U) | V | 380 |
| Input current (I) | A | 0~150 |
| Power frequency (f) | Hz | 50 |
| Number of slots | - | 18 |
| Number of pole pairs | - | 3 |
| Connection method | - | Y connection |
| Design Variables | Unit | Values |
|---|---|---|
| Core length | mm | 780 |
| Inner core diameter | mm | 89 |
| Flow gap | mm | 4 |
| Channel outer wall thickness | mm | 2 |
| Insulation thickness | mm | 10 |
| Air layer thickness | mm | 5 |
| Tooth width | mm | 22 |
| Slot width | mm | 22 |
| Parameters | Value |
|---|---|
| Design operating pressure/MPa | 0–1.6 |
| Design operating temperature/°C | 150–450 |
| LBE capacity/kg | 800 |
| Pipe material | 316 L |
| Main circuit pipe diameter/mm | Φ45*3.5 |
| Total circuit heating power/kW | 150 |
| Total circuit cooling cower/kW | 150 |
| Maximum flow rate of LBE/m·s−1 | 2.0 |
| Maximum volume flow rate of LBE/m3·h−1 | 8 |
| Volume of the storage tank/L | 200 |
| Maximum pressure of the storage tank/MPa | 1.6 |
| Instrument | Measurement | Range | Accuracy |
|---|---|---|---|
| EMF | Qv (m3/h) | 20 | ±2% |
| Differential pressure transmitter | ∆P (kPa) | 800 | ±0.075% |
| K-type thermocouple | T (°C) | 1300 | ±0.5 K |
| Data acquisition system | - | ±0.02% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Yuan, L.; Wang, C.; Qiu, S.; Li, Y. Development and Performance Analysis of an Electromagnetic Pump for a Thermal Hydraulic Experimental Loop of a Lead-Cooled Fast Reactor. Energies 2025, 18, 750. https://doi.org/10.3390/en18030750
Li Z, Yuan L, Wang C, Qiu S, Li Y. Development and Performance Analysis of an Electromagnetic Pump for a Thermal Hydraulic Experimental Loop of a Lead-Cooled Fast Reactor. Energies. 2025; 18(3):750. https://doi.org/10.3390/en18030750
Chicago/Turabian StyleLi, Zi’ang, Lanfei Yuan, Chenglong Wang, Suizheng Qiu, and Ying Li. 2025. "Development and Performance Analysis of an Electromagnetic Pump for a Thermal Hydraulic Experimental Loop of a Lead-Cooled Fast Reactor" Energies 18, no. 3: 750. https://doi.org/10.3390/en18030750
APA StyleLi, Z., Yuan, L., Wang, C., Qiu, S., & Li, Y. (2025). Development and Performance Analysis of an Electromagnetic Pump for a Thermal Hydraulic Experimental Loop of a Lead-Cooled Fast Reactor. Energies, 18(3), 750. https://doi.org/10.3390/en18030750







