Use of Kinetic Parameters from Thermal Analysis for Balancing Free Energy of Activation Based on Calcite Decomposition
Abstract
1. Introduction
2. Theory
3. The Aim of the Work
4. The Concept of Free Energy Activation According to Equation (11)
5. Thermal Decomposition of Calcite
5.1. The Simplest Decomposition Model
5.2. Thermal Decomposition for Variable Carbonation Activation Energies
5.3. Decomposition in CO2 Atmosphere (E Is Very High)
5.4. Discussion About the Rate Constant for Calcite
- –
- The surface reaction (SR): 67.1 kJ∙mol−1, 1.24 ( in s−1);
- –
- Two-dimensional shrinkage of the reaction interface (PBR(2)): 155.1 kJ∙mol−1, 10.07 ( in s−1).
5.5. Final Remarks
6. Conclusions
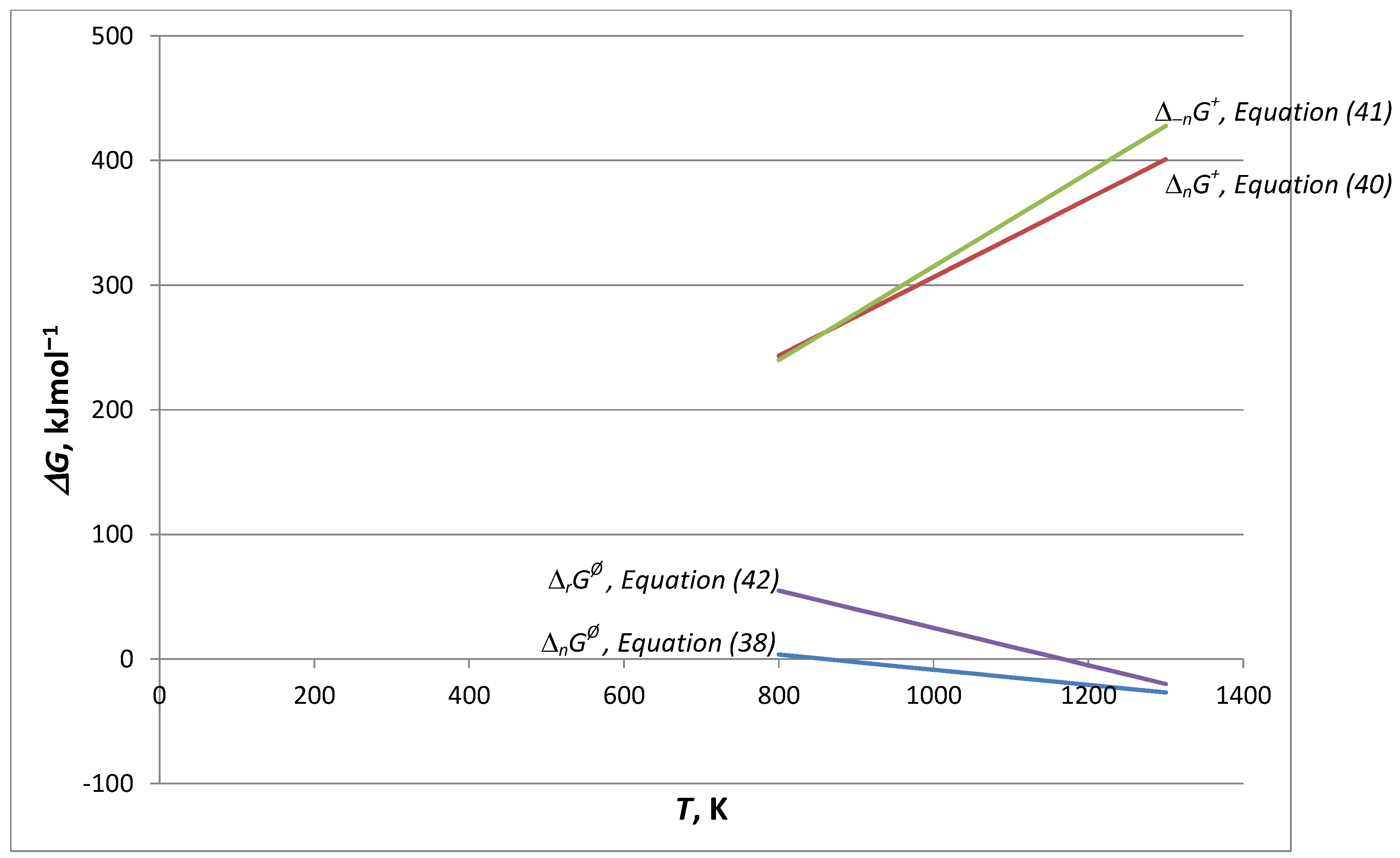
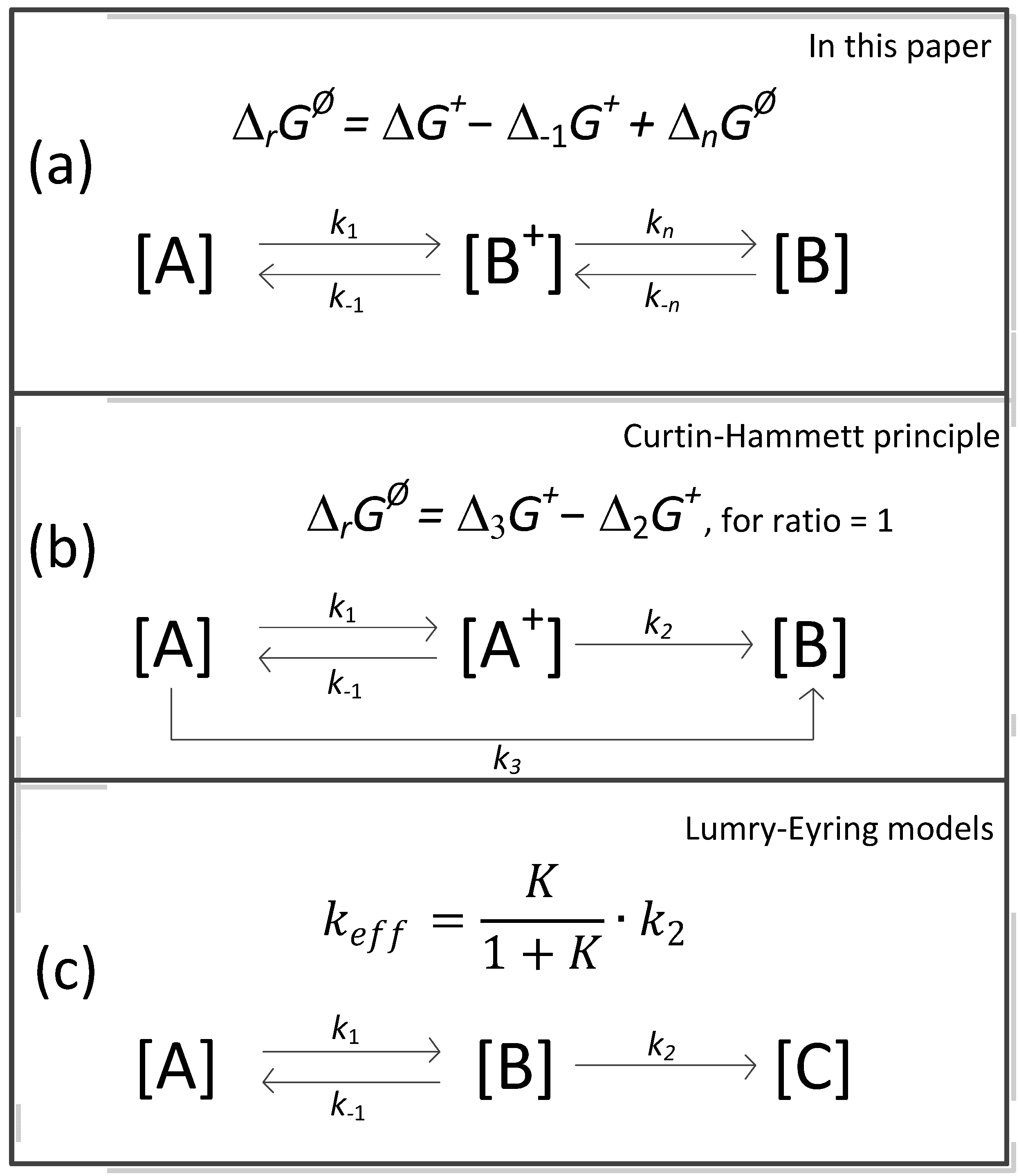
- A comparison of the thermal decomposition reaction/process of calcite in Equation (34) is found, which concerns the reversible reaction according to Equation (35): E−1 = 17.52 kJ∙mol−1 (low), and then we identify only the chemical decomposition rate. In turn, according to Equation (37), E−1 = 70.56 kJ∙mol−1 (high), the structural transformation rate also appears. The reversibility of changes in the structure of the solid phase in these conditions determines the full backwards course of the reaction/process of a complicated cognitive nature. Finally, for a very high activation energy of calcite decomposition/synthesis in the CO2 atmosphere (E = 1362.85 kJ∙mol−1, E−1 = 1187.93 kJ∙mol−1) in these conditions, the full forwards–backwards course of the reaction/process occurs, omitting structural effects.
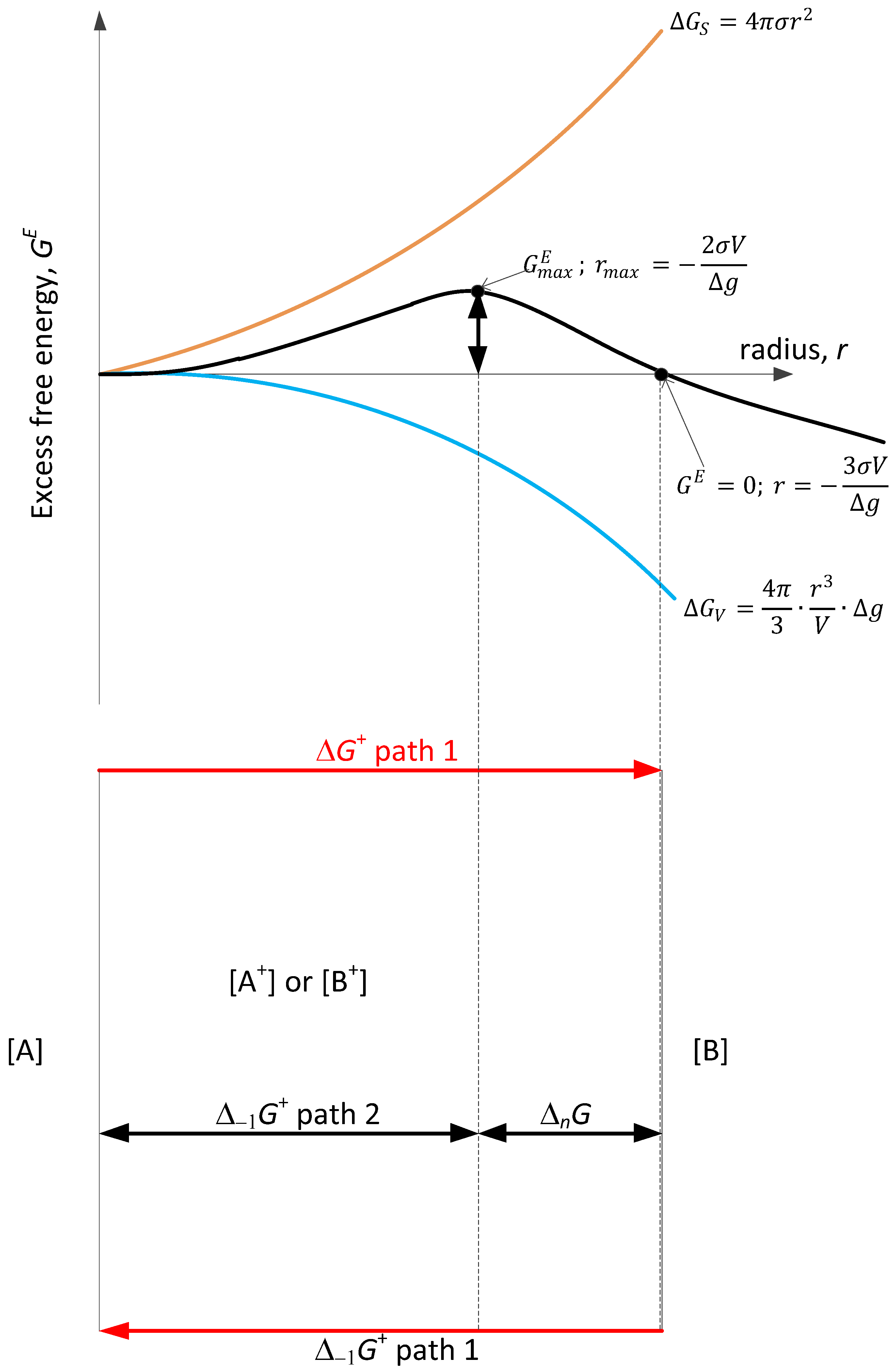
- The structural transformation rate is reduced to the course of the reaction/process according to Equation (34). For the analysis of this case, the excess free energy model known in the literature is used, which is generalized for various conditions, including dynamic ones. For calcite, the maximum constant rate of nucleation is established, which is equal to the pre-exponential constant Equation (31), then the hypothetical activation energy E = 0. For the reversible process, the term in Equation (24) informs either about viscosity changes (negative activation energy) or about the decomposition of a chemical nature (CO2 atmosphere). It should be added that the discussed term is a balance result, not an independent calculation.
- By adding to the Arrhenius kinetic parameters from the surface reaction (SR) model, the two-dimensional shrinkage of the reaction interface (PBR(2)), and data from models [16,23] (sometimes called apparent activation energy), it is established that for T = Teq, we obtain balance agreement, and at this temperature and for Equation (35), structural transformation processes can be neglected and the decomposition is of a chemical nature. Thus, Teq is the isoequilibrium temperature of activation.
- In conclusion No. 3, the four activation energies form a sequence of increasing values (in kJ∙mol−1): 67.1/155.1/184.7 for SR/PBR(2)/TST, respectively. From many possibilities, 191.0 was chosen in [16]. Neglecting at this stage the accompanying increase in the second Arrhenius parameter (lnA), the given sequence justifies the variation of the activation energy with the degree of transformation.
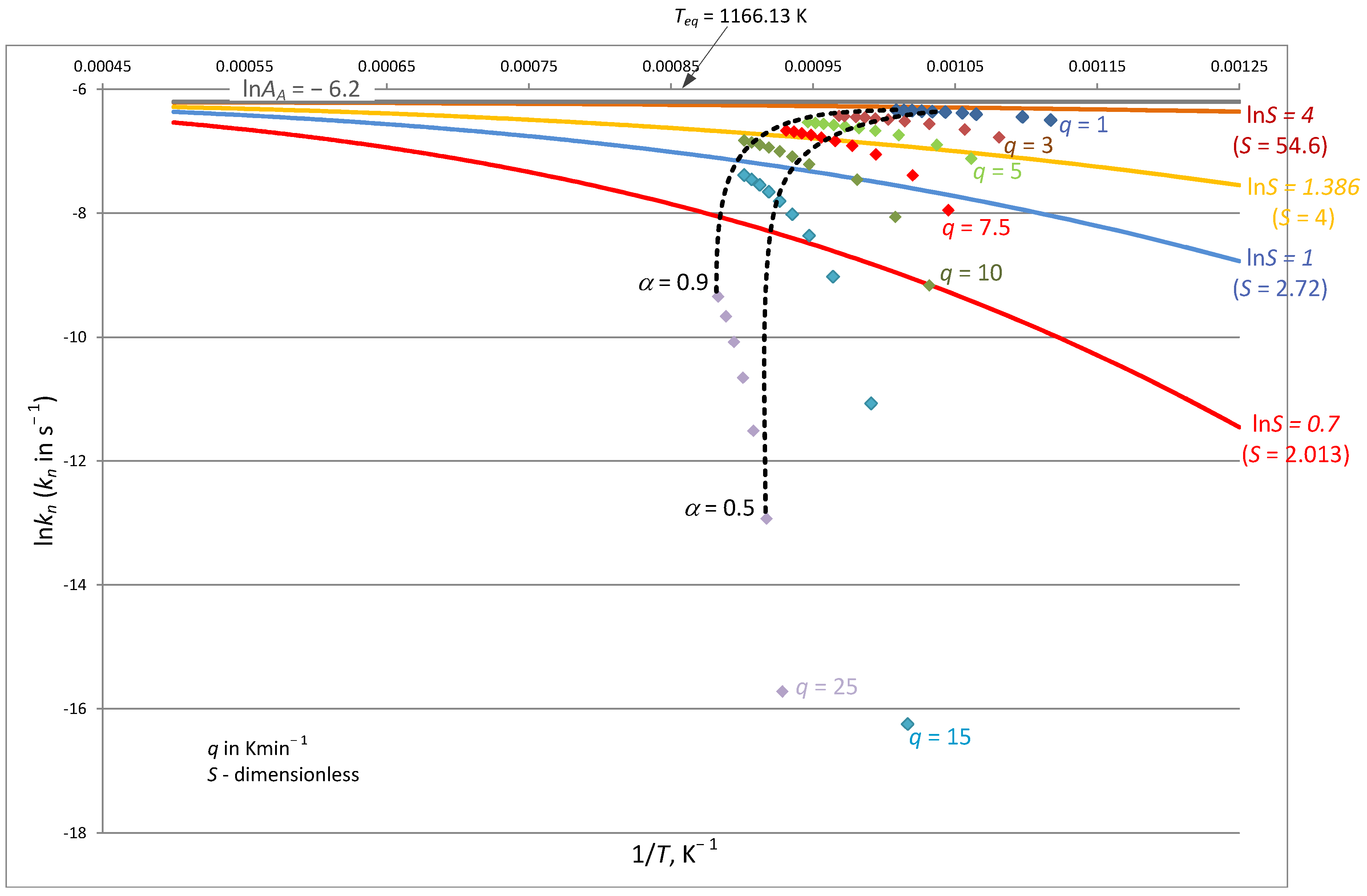
- The free energy balance in terms of phenomenological thermodynamics is the sum of the free energy of activation reactions forwards (sign +), backwards (sign −), and activation terms symmetrically related to nucleation. For the activation process of nucleation, the rate constant can be determined from thermogravimetric studies for dynamic conditions. It is required to control the agreement of the theoretical model Equation (28) with the experimentally determined quantities (Figure 2).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| coefficient: Equation (B8) | |
| A, B, C | chemical compounds |
| A | pre-exponential factor, s−1 |
| b, n | exponents, Equation (7) and Equation (1), respectively |
| 2.08364∙1010 (K∙s)−1 | ratio of Boltzmann to Planck’s constant |
| C | constant |
| E | activation energy, J∙mol−1 |
| kinetic function of conversion degree argument | |
| free energy, J | |
| thermodynamic functions: free energy J∙mol−1, enthalpy J∙mol−1, and entropy J∙(mol∙K)−1, respectively, | |
| h = 6.62607∙10−34 J∙s | Planck constant |
| k | rate constant, s−1 |
| 1.38065∙10−24 J∙K−1 | Boltzmann constant |
| K | equilibrium constant |
| the product of the activities of all components (defined in [3]) | |
| the change in the number of molecules in the active state minus substrates | |
| N = 6.022∙1023 mol−1 | Avogadro constant |
| P | pressure or partial pressure, Pa |
| q | heating rate (Figure 2), K·min−1 |
| r | radius, m |
| R = 8.314 J∙(mol∙K)−1 | universal gas constant |
| S | supersaturation in Equation (29) |
| t | time, s−1 |
| T | absolute temperature, K |
| v | rate of reaction/process |
| V | volume of the CaO, m3 |
| α | conversion degree |
| ν | stoichiometric ratio |
| σ | specific surface energy, J∙m−2 |
| the fraction of active sites filled with adsorbed CO2 | |
| Χ | transmission coefficient, assumed χ = 1 |
| the apparent contact angle between the embryo phase, for calcite acc. [23], θ = 60°, and from Equation (30), f(θ)= 0.15625. | |
| Subscripts | |
| 1, −1 acc. to: forwards, backwards, 01, 02—initial rate of reaction/process in Equations (50) and (51); A, B—chemical compounds; eff—effective rate constant; eq—equilibrium; iso—isokinetic; i—ith point; n—nucleation; —backwards, nucleation inhibition; max—maximum; r—reaction; S—refers to surface; TST—Transition-State Theory; V—refers to volume; and α—refers to conversion degree. | |
| Superscripts | |
| E—excess; +—thermodynamic activation functions; and —standard condition. | |
| Abbreviations | |
| CaL—Calcium Looping; CFD—computational fluid dynamics; CCS—Carbon Capture and Storage; DFE—Distance From Equilibrium (or far from equilibrium); DFT—density functional theory; DSC—differential scanning calorimetry; TGA—thermogravimetric analysis; and TST—Transition-State Theory. | |
Appendix A
Derivation of Equation (29)
Appendix B
Equation for the Relation Equation (3)
References
- IUPAC Gold Book, V. 3.0.1. Available online: https://goldbook.iupac.org/terms/view/O04322 (accessed on 15 January 2025).
- Šesták, J.; Šatava, V.; Wendlandt, W.W. The study of heterogeneous processes by thermal analysis. Thermochim. Acta 1973, 7, 333. [Google Scholar] [CrossRef]
- Blazéjowski, J. Evaluation of kinetic constants for the solid state reactions under linear temperature increase conditions. Thermochim. Acta 1981, 48, 109–124. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N. Determination of pre-exponential factors and of the mathematical functions f(α) or G(α) that describe the reaction mechanism in a model-freeway. Thermochim. Acta 2013, 564, 59–69. [Google Scholar] [CrossRef]
- Lyon, R.E. Isokinetics. J. Phys. Chem. A 2019, 123, 2462–2469. [Google Scholar] [CrossRef] [PubMed]
- Mianowski, A.; Ściążko, M.; Radko, T. Vyazovkin’s isoconversional method as a universal approach. Thermochim. Acta 2020, 696, 178822. [Google Scholar] [CrossRef]
- IUPAC Gold Book, V. 3.0.1. Available online: https://goldbook.iupac.org/terms/view/T06470 (accessed on 15 January 2025).
- Vyazovkin, S. Misinterpretation of Thermodynamic Parameters Evaluated from Activation Energy and Preexponential Factor Determined in Thermal Analysis Experiments. Thermo 2024, 4, 373–381. [Google Scholar] [CrossRef]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Evans, M.G.; Polanyi, M. Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 1935, 31, 875–894. [Google Scholar] [CrossRef]
- Evans, M.G.; Polanyi, M. On the introduction of thermodynamic variables into reaction kinetics. Trans. Faraday Soc. 1937, 33, 448–452. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Garrett, B.C.; Klippenstein, S.J. Current status of transition-state theory. J. Phys. Chem. 1996, 100, 12771–12800. [Google Scholar] [CrossRef]
- Xu, R.; Meisner, J.; Chang, A.M.; Thompson, K.C.; Martíınez, T.J. First principles reaction discovery: From the Schrödinger equation to experimental prediction for methane pyrolysis. Chem. Sci. 2023, 14, 7447. [Google Scholar] [CrossRef] [PubMed]
- Jacquemin, J. A Transitional Phase for Thermo? Thermo 2024, 4, 29–30. [Google Scholar] [CrossRef]
- Li, Z. First-principles-based microkinetic rate equation theory for oxygen carrier reduction in chemical looping. Chem. Eng. Sci. 2022, 47, 117042. [Google Scholar] [CrossRef]
- Mianowski, A.; Radko, T.; Bigda, R. Elements of Transition-State Theory in Relation to the Thermal Dissociation of Selected Solid Compounds. Energies 2024, 17, 2669. [Google Scholar] [CrossRef]
- Mianowski, A.; Szul, M.; Radko, T.; Sobolewski, A.; Iluk, T. Literature Review on Thermodynamic and Kinetic Limitations of Thermal Decomposition of Methane. Energies 2024, 17, 5007. [Google Scholar] [CrossRef]
- Laidler, K.J.; King, M.C. Development of Transition-State Theory. J. Phys. Chem. 1983, 87, 2657–2664. [Google Scholar] [CrossRef]
- Mianowski, A.; Radko, T.; Siudyga, T. Influence of initial assumptions on the kinetic models of CO2 gasification of chars and cokes in solid phase. J. Therm. Anal. Calorim. 2016, 126, 1911–1923. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar] [CrossRef]
- Vyazovkin, S. Isoconversional Kinetics of Thermally Stimulated Processes; University of Alabama at Birmingham: Birmingham, AL, USA, 2015. [Google Scholar] [CrossRef]
- Zeng, Q.; Xu, S. Thermodynamics and Characteristics of Heterogeneous Nucleation on Fractal Surfaces. J. Phys. Chem. C 2015, 119, 27426–27433. [Google Scholar] [CrossRef]
- Cai, J.; Li, Z. First Principle-based Rate Equation Theory for the Calcination Kinetics of CaCO3 in Calcium Looping. Energy Fuels 2024, 38, 8145–8156. [Google Scholar] [CrossRef]
- Martínez, I.; Grasa, G.; Murillo, R.; Arias, B.; Abanades, J.C. Kinetics of Calcination of Partially Carbonated Particles in a Ca-Looping System for CO2 Capture. Energy Fuels 2012, 26, 1432–1440. [Google Scholar] [CrossRef]
- Valverde, J.M.; Medina, S. Reduction of calcination temperature in the Calcium Looping process for CO2 capture by using Helium: In-situ XRD analysis. ACS Sustain. Chem. Eng. 2016, 4, 7090–7097. [Google Scholar] [CrossRef]
- Medina-Carrasco, S.; Valverde, J.M. The Calcium Looping process for energy storage: Insights from in situ XRD analysis. Chem. Eng. J. 2021, 429, 132244. [Google Scholar] [CrossRef]
- Fedunik-Hofman, L.; Bayon, A.; Donne, S.W. Comparative Kinetic Analysis of CaCO3/CaO Reaction System for Energy Storage and Carbon Capture. Appl. Sci. 2019, 9, 4601. [Google Scholar] [CrossRef]
- Romano, M.C.; Martinez, I.; Murillo, R.; Arstad, B.; Blum, R.; Ozcan, D.C.; Ahn, H.; Brandami, S. Guidelines for Modeling and Simulation of Ca-Looping Processes; EERA: Berlin, Germany, 2012. [Google Scholar] [CrossRef]
- Rodriguez-Navarro, C.; Ruiz-Agudo, E.; Luque, A.; Rodriguez-Navarro, A.B.; Ortega-Huertas, M. Thermal decomposition of calcite: Mechanisms of formation and textural evolution of CaO nanocrystals. Am. Miner. 2009, 94, 578–593. [Google Scholar] [CrossRef]
- Maciejewski, M.; Oswald, H.-R.; Reller, A. Thermal transformations of vaterite and calcite. Thermochim. Acta 1994, 234, 315–328. [Google Scholar] [CrossRef]
- Brown, M.E.; Maciejewski, M.; Vyazovkin, S.; Nomen, R.; Sempere, J.; Burnham, A.; Opfermann, J.; Strey, R.; Anderson, H.L.; Kemmler, A.; et al. Computational Aspects of Kinetic Analysis: Part A: The ICTAC Kinetics Project-Data, Methods and Results. Thermochim. Acta 2000, 355, 125–143. [Google Scholar] [CrossRef]
- Mianowski, A.; Radko, T.; Siudyga, T. Kinetic Compensation Effect of Isoconversional Methods. React. Kinet. Catal. Lett. 2021, 132, 37–58. [Google Scholar] [CrossRef]
- Maciejewski, M. Computational Aspects of Kinetic Analysis: Part B. The Decomposition Kinetics of Calcium Carbonate Revisited, Ore Some Tips on Survival in the Kinetic Minefield. Thermochim. Acta 2000, 355, 145–154. [Google Scholar] [CrossRef]
- Maciejewski, M. Somewhere between fiction and reality. The usefulness of kinetic data of solid-state reactions. J. Therm. Anal. Calorim. 1992, 38, 51–70. [Google Scholar] [CrossRef]
- Maciejewski, M.; Bałdyga, J. The influence of the pressure of the gaseous product on the reversible thermal decomposition of solids. Thermochim. Acta 1985, 92, 105–108. [Google Scholar] [CrossRef]
- Maciejewski, M.; Reller, A. How (un)reliable are kinetic data of reversible solid-state decomposition processes? Thermochim. Acta 1987, 110, 145–152. [Google Scholar] [CrossRef]
- Maciejewski, M. The application of kinetic parameters to the investigation of thermal stability determined from rising temperature experiments. Thermochim. Acta 1987, 113, 287–303. [Google Scholar] [CrossRef]
- Powell, E.K.; Searcy, A.W. The Rate and Activation Enthalpy of Decomposition of CaCO3. Met. Trans. B 1980, 11, 427–432. [Google Scholar] [CrossRef]
- Georgieva, V.; Vlaev, L.; Gyurova, K. Non-Isothermal Degradation Kinetics of CaCO3 from Different Origin. J. Chem. 2012, 2013, 872981. [Google Scholar] [CrossRef]
- Britton, H.T.S.; Gregg, S.J.; Winsor, G.W. The calcination of dolomite part I.—The kinetics of the thermal decomposition of calcite and of magnesite. Trans. Faraday Soc. 1952, 48, 63–69. [Google Scholar] [CrossRef]
- Gallagher, P.K.; Johnson, D.W., Jr. The effects of sample size and heating rate on the kinetics of the thermal decomposition of CaCO3. Thermochim. Acta 1973, 6, 67–83. [Google Scholar] [CrossRef]
- L’vov, B.V.; Ugolkov, V.L. Peculiarities of CaCO3, SrCO3 and BaCO3 decomposition in CO2 as a proof of their primary dissociative evaporation. Thermochim. Acta 2004, 410, 47–55. [Google Scholar] [CrossRef]
- Zsako, J.; Arz, H.E. Kinetic analysis of thermogravimetric data. J. Therm. Anal. Calorim. 1974, 6, 651–656. [Google Scholar] [CrossRef]
- Beruto, D.; Searcy, A.W. Use of the Langmuir method for kinetic studies of decomposition reactions: Calcite (CaCO3). J. Chem. Soc. Faraday Trans. 1974, 70, 2145–2153. [Google Scholar] [CrossRef]
- Fedunik-Hofman, L.; Bayon, A.; Hinkley, J.; Lipiński, W.; Donne, S.W. Friedman method kinetic analysis of CaO-based sorbent for high-temperature thermochemical energy storage. Chem. Eng. Sci. 2019, 200, 236–247. [Google Scholar] [CrossRef]
- Gallagher, P.K.; Johnson, D.W., Jr. Kinetics of the thermal decomposition of CaCO3 in CO2 and some observations on the kinetic compensation effect. Thermochim. Acta 1976, 14, 255–261. [Google Scholar] [CrossRef]
- Valverde, J.M.; Medina, S. Crystallographic transformation of limestone during calcination under CO2. Phys. Chem. Chem. Phys. 2015, 17, 21912–21926. [Google Scholar] [CrossRef]
- Valverde, J.M. On the negative activation energy for limestone calcination at high temperatures nearby equilibrium. Chem. Eng. Sci. 2015, 132, 169–177. [Google Scholar] [CrossRef]
- Hotta, M.; Tone, T.; Favergeon, L.; Koga, N. Kinetic Parameterization of the Effects of Atmospheric and Self-Generated Carbon Dioxide on the Thermal Decomposition of Calcium Carbonate. J. Phys. Chem. C 2022, 126, 7880–7895. [Google Scholar] [CrossRef]
- Hotta, M.; Koga, N. Extended kinetic approach to reversible thermal decomposition of solids: A universal description considering the effect of the gaseous product and the kinetic compensation effect. Thermochim. Acta 2024, 733, 179699. [Google Scholar] [CrossRef]
- Hotta, M.; Koga, N. Physicogeometrical Kinetic Insight into the Acceleration Effect of Atmospheric Water Vapor on Thermal Decomposition of Calcium Carbonate. J. Phys. Chem. C 2024, 128, 11583–11597. [Google Scholar] [CrossRef]
- Beruto, D.; Searcy, A.W. Calcium oxides of hight reactivity. Nature 1976, 263, 221–222. [Google Scholar] [CrossRef]
- Towe, K.M. Ultrastructure of calcite decomposition in vacuo. Nature 1978, 274, 239–240. [Google Scholar] [CrossRef]
- Beruto, D.T.; Searcy, A.W.; Kim, M.G. Microstructure, kinetic, structure, thermodynamic analysis for calcite decomposition: Free-surface and powder bed experiments. Thermochim. Acta 2004, 424, 99–109. [Google Scholar] [CrossRef]
- Ma, Y.; Tian, P.; Bounmyxay, M.; Zeng, Y.; Wang, N. Calcium Carbonate@silica Composite with Superhydrophobic Properties. Molecules 2021, 26, 7180. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, S.K.; Perlmutter, D.D. Effect of the Product Layer on the Kinetics of the CO2-Lime Reaction. AIChE J. 1983, 29, 79–86. [Google Scholar] [CrossRef]
- Gupta, H.; Fan, L.-S. Carbonation-Calcination Cycle Using High Reactivity Calcium Oxide for Carbon Dioxide Separation from Flue Ga. Ind. Eng. Chem. Res. 2002, 41, 4035–4042. [Google Scholar] [CrossRef]
- Lee, D.K. An apparent kinetic model for the carbonation of calcium oxide by carbon dioxide. Chem. Eng. J. 2004, 100, 71–77. [Google Scholar] [CrossRef]
- Sun, P.C.; Grace, J.R.; Lim, C.J.; Anthony, E.J. Determination of intrinsic rate constants of the CaO–CO2 reaction. Chem. Eng. Sci. 2008, 63, 47–56. [Google Scholar] [CrossRef]
- Grasa, G.; Murillo, R. Application of the Random Pore Model to the Carbonation Cyclic Reaction. AIChE J. 2009, 55, 1246–1255. [Google Scholar] [CrossRef]
- Rouchon, L.; Favergeon, L.; Pijolat, M. Analysis of the kinetic slowing down during carbonation of CaO by CO2. Therm. Anal. Calorim. 2013, 113, 1145–1155. [Google Scholar] [CrossRef]
- Ooi, B.K.H.; Marek, E.J. Kinetics of CO2 Capture with Calcium Oxide during Direct Air Capture in a Fluidized Bed. Energy Fuels 2024, 38, 22290–22297. [Google Scholar] [CrossRef]
- Mianowski, A.; Urbańczyk, W. Isoconversional Methods in Thermodynamic Principles. J. Phys. Chem. A 2018, 122, 6819–6828. [Google Scholar] [CrossRef]
- Lyon, R.E. A Physical Basis for Kinetic Compensation. J. Phys. Chem. A 2023, 127, 2399–2406. [Google Scholar] [CrossRef] [PubMed]
- Bracken, P. Free Energy Differences in Nonequilibrium Thermodynamic Processes. J. Phys. Chem. A 2024, 128, 6999–7004. [Google Scholar] [CrossRef] [PubMed]
- Ike, E. Arrhenius-Type Relationship of Viscosity as a Function of Temperature for Mustard and Cotton Seed Oils. Niger. Ann. Pure Appl. Sci. 2020, 3, 144–155. [Google Scholar] [CrossRef]
- Mianowski, A.; Baraniec, I. Three-parametric equation in evaluation of thermal dissociation of reference compound. J. Therm. Anal. Calorim. 2009, 96, 179–187. [Google Scholar] [CrossRef]
- Mianowski, A.; Baraniec-Mazurek, I.; Bigda, R. Some remarks on equilibrium state in dynamic condition. J. Therm. Anal. Calorim. 2011, 107, 1155–1165. [Google Scholar] [CrossRef]
- Seeman, J.I. The Curtin-Hammett Principle and the Winstein-Holness Equation, New Definition and Recent Extensions to Classical Concepts. J. Chem. Educ. 1986, 63, 42–48. [Google Scholar] [CrossRef]
- Lumry, R.; Eyring, H. Conformation Changes of Proteins. J. Phys. Chem. 1954, 58, 110–120. [Google Scholar] [CrossRef]
- Sanchez-Ruiz, J.M. Theoretical analysis of Lumry-Eyring models in differentia scanning calorimetry. Biophys. J. 1992, 61, 921–935. [Google Scholar] [CrossRef]
- Lente, G. Deterministic Kinetics in Chemistry and Systems Biology: The Dynamics of Complex Reaction Networks; Springer Briefs in Molecular Science; Springer: Cham, Switzerland, 2014; ISBN 978-3-319-15482-4. [Google Scholar] [CrossRef]
- Błażejowski, J.; Zadykowicz, B. Computational Prediction of the Pattern of Thermal Gravimetry Data for the Thermal Decomposition of Calcium Oxalate Monohydrate. J. Therm. Anal. Calorim. 2013, 113, 1497–1503. [Google Scholar] [CrossRef]
- Uliasz-Bocheñczyk, A.; Mokrzycki, E. Mineralna karbonatyzacja przy zastosowaniu surowców naturalnych metodą redukcji CO2? (Mineral carbonation using natural raw materials as a CO2 reduction method?). Gospod. Surowcami Miner. 2014, 30, 99–110. [Google Scholar] [CrossRef]
- Stec, M.; Tatarczuk, A.; Więcław-Solny, L.; Krótki, A.; Spietz, T.; Wilk, A.; Śpiewak, D. Experimental results of split-flow modification for post-combustion CO2 capture process. In Green Energy and Technology; Springer: Cham, Switzerland, 2018; pp. 441–453. [Google Scholar] [CrossRef]
- Tatarczuk, A.; Tańczyk, M.; Więcław-Solny, L.; Zdeb, J. Pilot plant results of amine-based carbon capture with heat integrated stripper. Appl. Energy 2024, 367, 123416. [Google Scholar] [CrossRef]
- Krótki, A.; Spietz, T.; Dobras, S.; Chwoła, T.; Tatarczuk, A.; Żórawski, D.; Skowron, K.; Skrzyniecki, D.; Hulisz, P. Carbon capture pilot study in Solvay soda ash process. Appl. Energy 2024, 380, 124995. [Google Scholar] [CrossRef]
- Krótki, A.; Chwoła, T.; Więcław-Solny, L.; Tatarczuk, A.; Spietz, T.; Dobras, S.; Zdeb, J. Advancements in CO2 hydrogenation–Investigating a CNG pilot plant in Poland. Fuel 2025, 381, 133599. [Google Scholar] [CrossRef]
- Krótki, A.; Spietz, T.; Dobras, S.; Chwoła, T.; Tatarczuk, A.; Żórawski, D.; Skowron, K.; Kiedzik, Ł.; Kowalska, B.; Skrzyniecki, D. Initial carbon capture pilot study in Solvay soda ash process. Chem. Eng. Res. Des. 2025, 205, 174–187. [Google Scholar] [CrossRef]
- Liendo, F.; Arduino, M.; Deorsola, F.A.; Bensaid, S. Nucleation and growth kinetics of CaCO3 crystals in the presence of foreign monovalent ions. J. Cryst. Growth 2022, 578, 126406. [Google Scholar] [CrossRef]
- Ufnalski, W. Równowagi Chemiczne; Wydawnictwa Naukowo-Techniczne: Warszawa, Poland, 1995. (In Polish) [Google Scholar]
- Mianowski, A.; Urbańczyk, W. Thermal dissociation in terms of the second law of chemical thermodynamics. J. Therm. Anal. Calorim. 2016, 126, 863–870. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mianowski, A.; Bigda, R. Use of Kinetic Parameters from Thermal Analysis for Balancing Free Energy of Activation Based on Calcite Decomposition. Energies 2025, 18, 570. https://doi.org/10.3390/en18030570
Mianowski A, Bigda R. Use of Kinetic Parameters from Thermal Analysis for Balancing Free Energy of Activation Based on Calcite Decomposition. Energies. 2025; 18(3):570. https://doi.org/10.3390/en18030570
Chicago/Turabian StyleMianowski, Andrzej, and Rafał Bigda. 2025. "Use of Kinetic Parameters from Thermal Analysis for Balancing Free Energy of Activation Based on Calcite Decomposition" Energies 18, no. 3: 570. https://doi.org/10.3390/en18030570
APA StyleMianowski, A., & Bigda, R. (2025). Use of Kinetic Parameters from Thermal Analysis for Balancing Free Energy of Activation Based on Calcite Decomposition. Energies, 18(3), 570. https://doi.org/10.3390/en18030570





