Control Parameters of a Wall Heating and Cooling Module with Heat Pipes—An Experimental Study
Abstract
1. Introduction
- -
- fast heat transfer, resulting mainly from the relatively high speed of gas movement under the influence of the temperature difference (or gravitational flow of liquid);
- -
- no moving parts and no additional energy consumption and costs to force the movement of gas or liquid (the thermodynamic medium moves freely);
- -
- lower probability of failure due to the closed space of the heat pipes;
- -
- wide range of operating temperatures of the pipe, resulting from the possibility of using various thermodynamic mediums and their mixtures with different structures;
- -
- a properly selected thermodynamic medium can transfer heat in both directions, i.e., it can transfer heat or receive it from rooms without changing the structure of the exchanger.
- Rotating and revolving Heat Pipes, in which the condensate is returned to the evaporator through centrifugal force, and no capillary wicks are required [8].
- Transient lumped model—the simplest and least accurate.
- One-dimensional transient continuum model.
- Two-dimensional transient continuum model—the most complex, but also the most accurate.
- -
- the construction of the heat exchanger (geometric dimensions, filling building material);
- -
- the number and location of heat pipes in the exchanger material;
- -
- the type and physical properties of the thermodynamic medium filling the pipe;
- -
- the shape of the internal surface of the heat pipe;
- -
- the method of placing the ribs in the building material (in the case of reinforced concrete modules).
- -
- the position of the exchanger (its inclination in relation to the horizontal surface);
- -
- the method and range of change of the exchanger power;
- -
- the method and range of change of the temperature and flow of the supply water.
- -
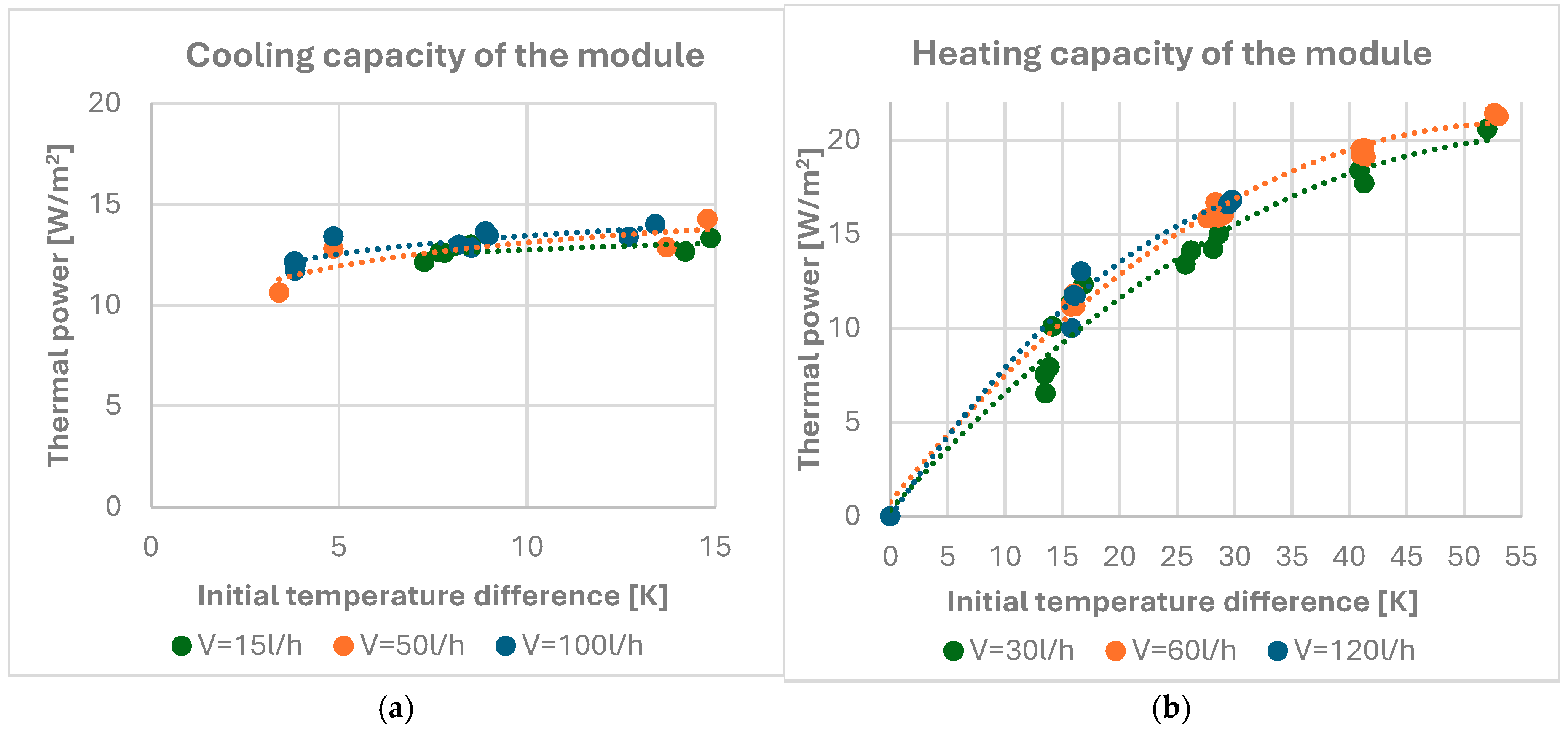
- changes in the thermal power in cooling mode and in heating mode when changing the flow and temperature of the supply water; these results can be used to select heating and cooling modules in the designed room;
- -
- changes in the gain coefficients and time constants of the inertial models, describing the static and dynamic properties of the module as a control object when changing its power during operation; these results will be helpful for correct programming and setting of the module’s power control system for maintaining thermal comfort in the room. The adopted inertial models are most often used to identify the dynamics of thermal objects [34,35,36].
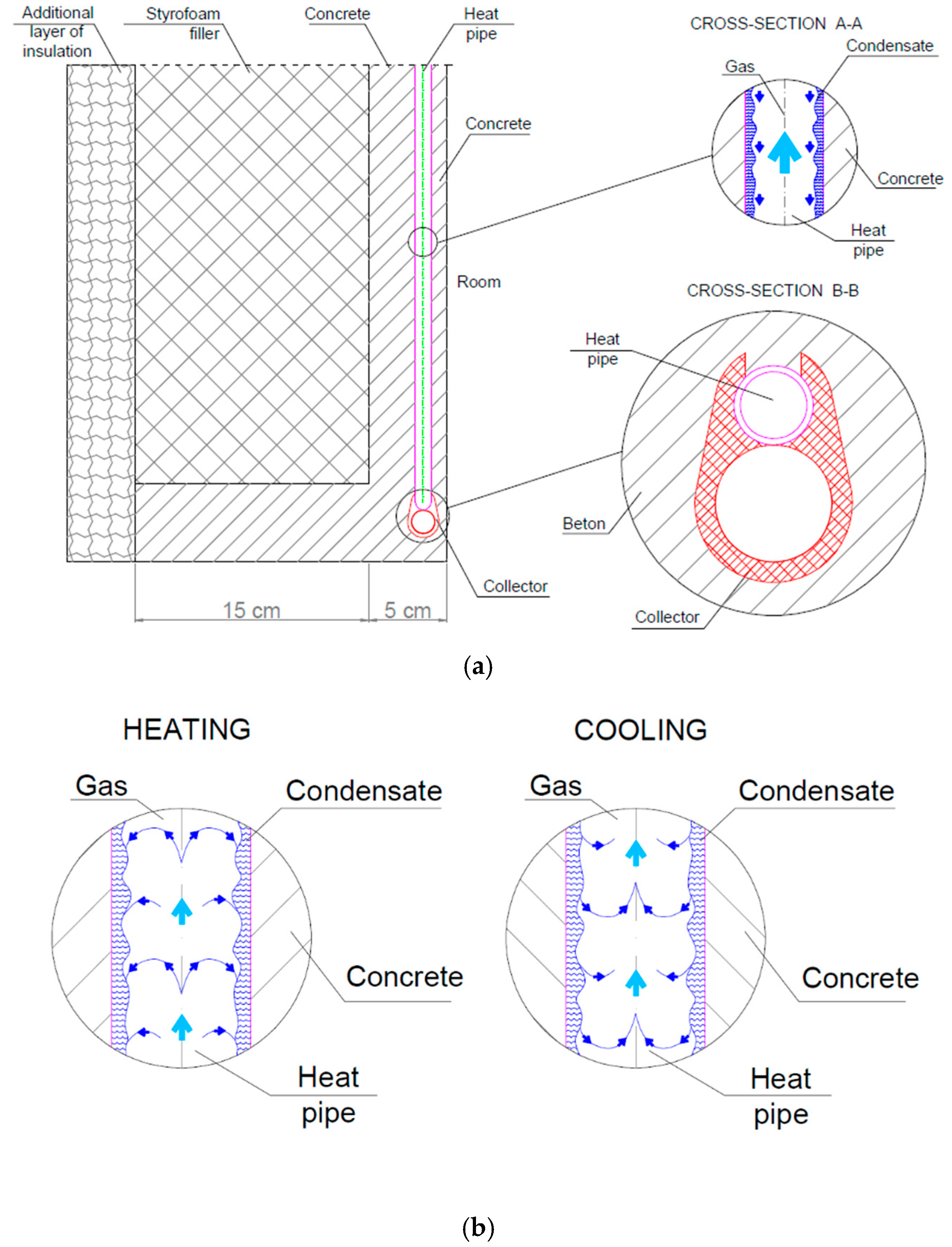
2. Description of the Tested Module
- Heat transfer between the supply water in the collector and the thermodynamic medium in the heat pipe (horizontal section—cross-section B-B in Figure 1a).
- Heat transfer between the thermodynamic medium in the heat pipe and the outer surface of the heat pipe (cross-section A-A in Figure 1a).
- Heat conduction in the module material from the outer surface of the heat pipe wall to the inner surface of the module.
- Heat transfer from the surface of the module to the room (by convention and radiation).
- -
- As an element filling the load-bearing structure of the building (as an external partition);
- -
- As a heating and cooling element, supplying the room with heat or coolness as required to maintain thermal comfort; large heat exchange surfaces allow the use of low-temperature heat sources;
- -
- As an insulating element, limiting heat loss from the room to the external environment; on the external side, the module has additional insulation—a 15 cm thick layer of polystyrene.
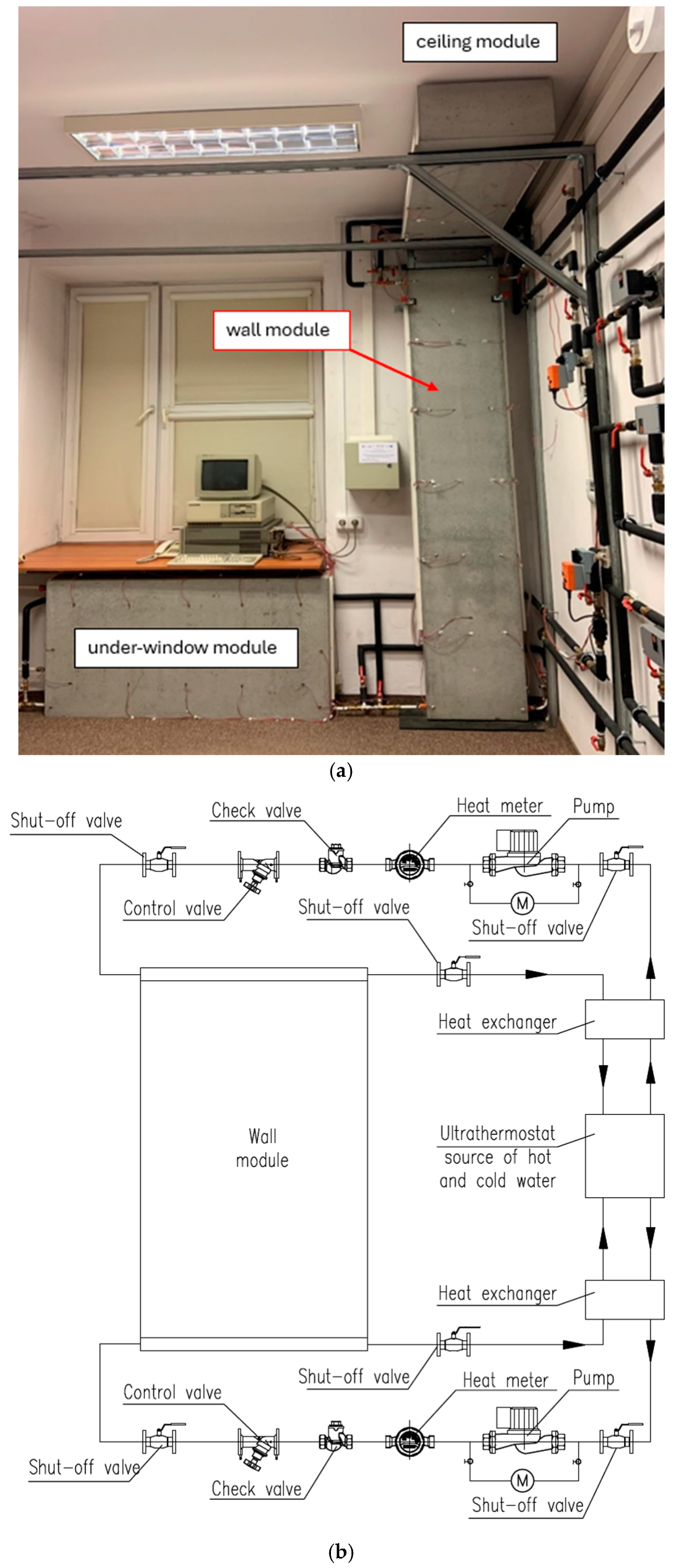
3. Research Site
3.1. Test Site View
3.2. Principles (Description) of Conducting Measurements
- Module surface temperature—11 contact sensors.
- Supply and return water temperature—4 immersion sensors.
- Internal air temperature—2 freely suspended sensors.
- Room wall temperature—1 contact sensor.
- Module supply water flow—2 water meters.
3.3. Calibration of Measuring Sensors
4. Measurements and Results Processing
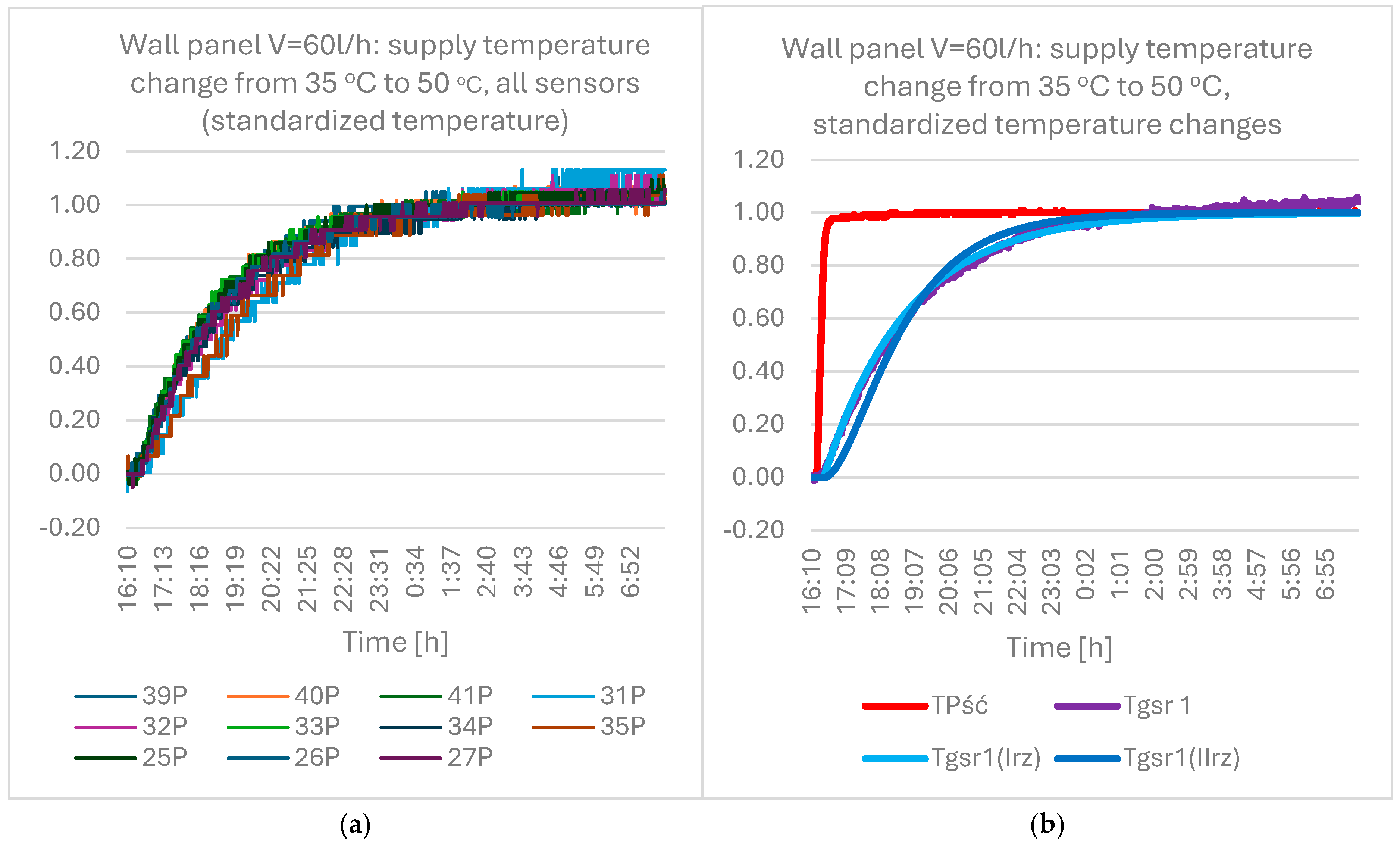
- A graph of the temperature values on the module surface (from all sensors);
- A graph of the internal temperature values and the temperature of the building partition;
- A graph of the temperature values from each row (vertical and horizontal) of sensors;
- A graph of the standardized temperature values on the module surface;
- Calculations (identification) of the values of the amplification coefficients and time constants of the inertial models adopted to describe the transient states (dynamics) of the module;
- Calculations of the heat flux transferred to the room or assimilated from the room in steady states.
- k—amplification factor, dimensionless;
- T, T1, T2—time constants, min;
- T0—delay time, min.
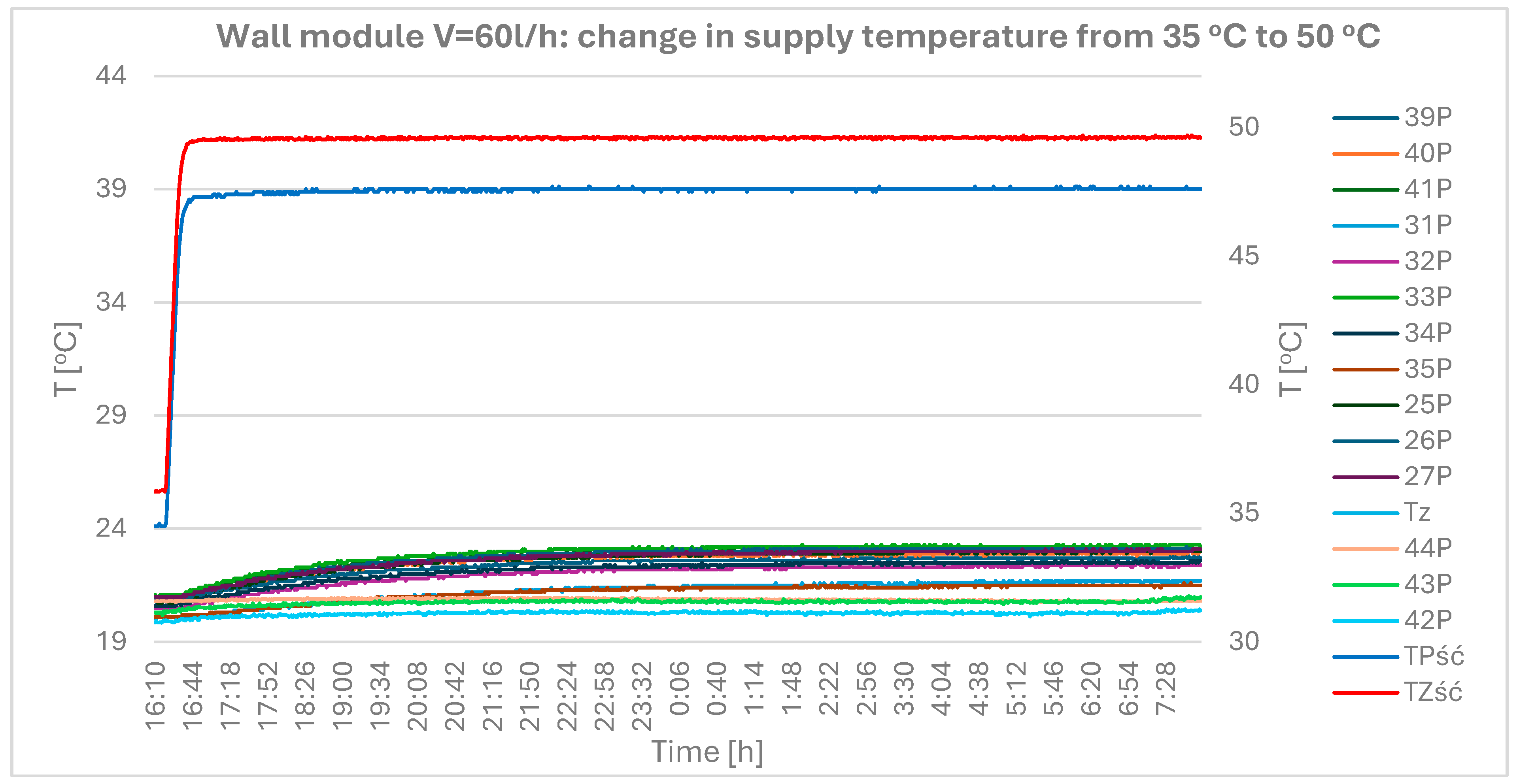
- Relatively small changes in the module surface temperature. As shown in the figure, a change in the module supply water temperature of approx. 15 K causes a temperature change on the module surface of 1.5–2.0 K. This indicates low heat exchange efficiency and low values of the k amplification factor in the adopted inertial models. Low heat exchange efficiency is also the reason for introducing forcing (changes in supply water temperature) of relatively large values, in order to obtain significant changes in the module surface temperature.
- Relatively large variation in the temperature distribution on the module surface. Temperature values at different points on the module surface differ from each other by approx. 1.2 K. Changes in values are particularly visible with the change in module height.
- Relatively slow changes in the module surface temperature. After changing the supply water temperature, it takes 8–10 h to establish a new temperature value on the module surface.
- The nature of the change in the module surface temperature at different measurement points is similar; clear differences occur in the steady-state temperature values.
- t(τ)—temperature value at the analyzed time instant, °C;
- tu1—temperature value in the steady state, before the change in the supply water temperature, °C;
- tu2—temperature value in the final steady state, °C.
- -
- Zero-order for the first-order inertial model (when calculating the time constant T),
- -
- Zero- and first-order for the second-order model (when calculating the time constants T1 and T2).
- k—next time step in measuring the step characteristic;
- n—number of time steps from the initial steady state to the final steady state of the step characteristic;
- ∆τ—data recording step (1 min).
5. Analysis of Measurement Results
5.1. Module Operation in Cooling Mode
- -
- Using measurements from all sensors,
- -
- Using measurements only from the sensors located in the middle of the module (l = 130 cm).
- -
- 22.5 min when decreasing the temperature for all the sensors on the module surface;
- -
- 12.5 min when increasing the temperature for all the sensors on the module surface;
- -
- 20.5 min when decreasing the temperature for the middle-row sensors of the module;
- -
- 16.0 min when increasing the temperature for the middle-row sensors of the module.
- —the averaged standardized temperature value obtained from the measurements;
- —the standardized temperature value obtained from the model;
- n—the number of measurement steps in the characteristics of standardized variables.
5.2. Module Operation in Heating Mode
- -
- 22.7 min when decreasing the temperature for all the sensors on the module surface;
- -
- 10.7 min when increasing the temperature for all the sensors on the module surface;
- -
- 17.0 min when decreasing the temperature for the middle-row sensors of the module;
- -
- 15.8 min when increasing the temperature for the middle-row sensors of the module.
6. Summary and Conclusions
6.1. Influence of Design Parameters on Power of Heat Pipe Module
- The type of thermodynamic medium used in the tubes;
- The thermal resistance and heat exchange surface between the heat pipe and the feedwater collector;
- The spacing (distance from each other) of the heat pipes in the module;
- The arrangement of reinforcing ribs in the concrete of the module (in the case of reinforced concrete modules).
- Methanol—operating range 10–130 °C, melting point −98 °C, boiling point 64 at atm. press. °C;
- Ethanol—operating range 10–130 °C, melting point −112 °C, boiling point 78 at atm. press. °C;
- Water—operating range 30–200 °C, melting point 0 °C, boiling point 100 at atm. press. °C.
6.2. Influence of Operating Conditions on Control Parameters
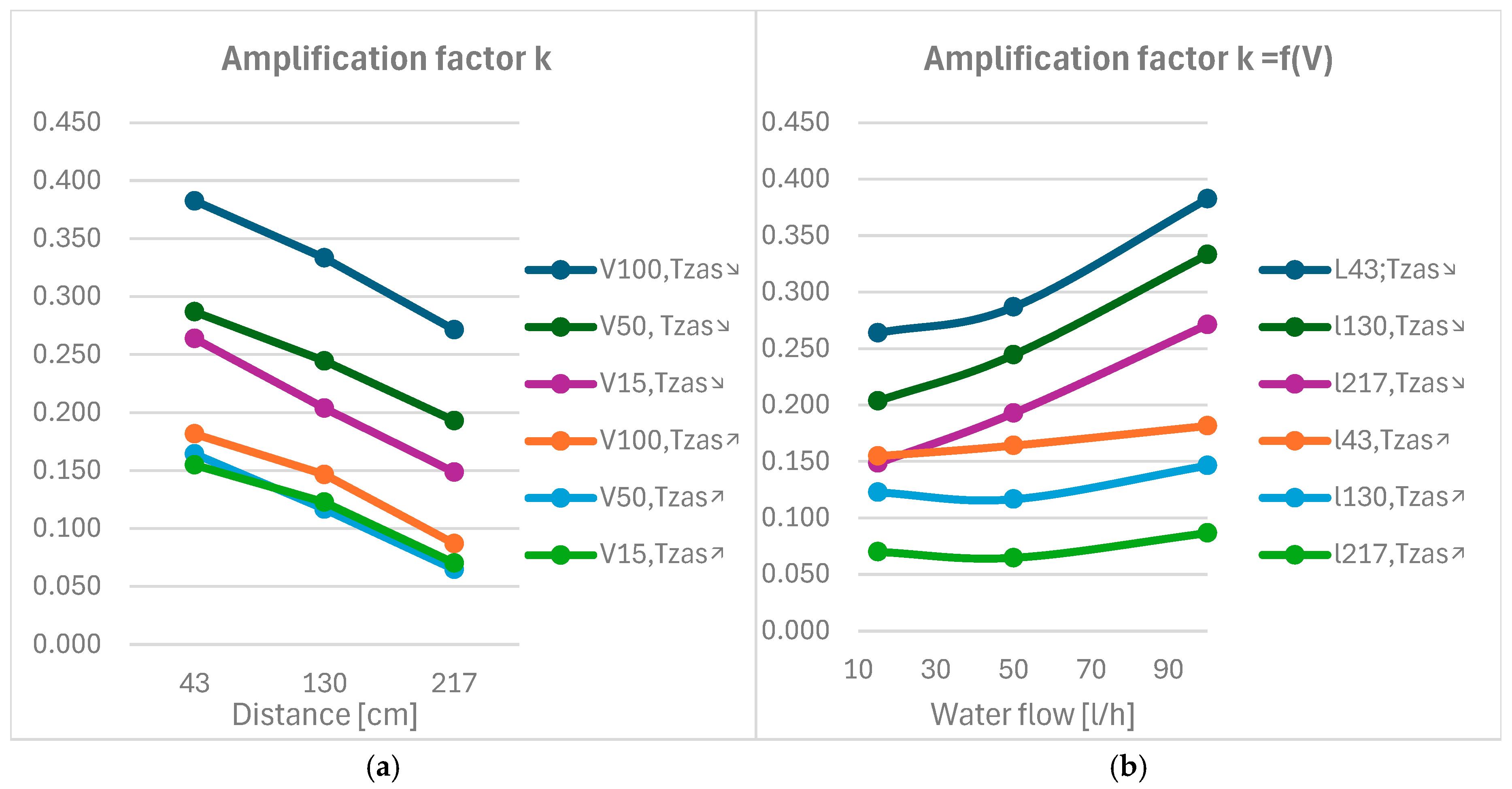
- small values of the gain coefficient allow the use of larger values of the initial temperature difference in operation;
- significantly larger changes in the values of the power and gain coefficients cause larger temperature changes than changes in the feed water flow;
- large changes in control parameters require complex, individual control algorithms; with variable room heat demand, the algorithm should have a procedure for forecasting the required module power in a time horizon of 1–2 h.
- -
- Moisture condensation on the cold surface of the module in cooling mode;
- -
- Deterioration of the thermal comfort of users in heating mode, due to the high radiation temperature of the walls.
- the thermal resistance during heat exchange between the supply water from the heating/cooling system and the thermodynamic medium in the heat pipe—there is a need to reduce this if it is too high in the tested device;
- the proportion of the mixture used as the thermodynamic medium—changing this would reduce the thermal resistance of the heat pipe and improve the thermal efficiency of the module;
- the way the module material is finned—changing this would reduce the thermal resistance of the module material and reduce the time constants, while maintaining the mechanical strength of the module structure.
- -
- Heat exchange between the supply water from the heating/cooling system and the thermodynamic medium in the heat pipe (to reduce the thermal resistance);
- -
- Heat exchange in the heat pipe for various proportions of the mixture used as the thermodynamic medium, which would reduce the thermal resistance of the heat pipe and improve the thermal efficiency of the module;
- -
- Heat exchange in the reinforced concrete material of the module, which would reduce the thermal resistance of the module material and reduce the time constants, while maintaining the mechanical strength of the module structure.
- -
- Changes in the temperature and flow of supply water in heating and cooling mode: in the conditions of the highest thermal load of the room, and in the conditions that most frequently occur during heating and cooling periods;
- -
- Changes in the module operating mode: switching from heating mode to cooling mode, and vice versa.
- -
- Module power in heating and cooling mode;
- -
- Temperature distribution on the module surface;
- -
- Module control parameters (amplification factors and time constants).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krajčík, M.; Šimko, M.; Šikula, O.; Szabó, D.; Petráš, D. Thermal performance of a radiant wall heating and cooling system with pipes attached to thermally insulating bricks. Energy Build. 2021, 246, 111122. [Google Scholar] [CrossRef]
- Saha, A.; Biswas, N.; Ghosh, K.; Manna, N.K. Thermal management with localized heating on enclosure’s wall during thermal convection using different fluids. Mater. Today Proc. 2021, 52, 391–397. [Google Scholar] [CrossRef]
- Todorović, R.; Banjac, M.; Gojak, M. Theoretical and experimental study of heat transfer in wall heating panels. Energy Build. 2015, 98, 66–73. [Google Scholar] [CrossRef]
- Karabay, H.; Arıcı, M.; Sandık, M. A numerical investigation of fluid flow and heat transfer inside a room for floor heating and wall heating systems. Energy Build. 2013, 67, 471–478. [Google Scholar] [CrossRef]
- Koca, A.; Çetin, G. Experimental investigation on the heat transfer coefficients of radiant heating systems: Wall, ceiling and wall-ceiling integration. Energy Build. 2017, 148, 311–326. [Google Scholar] [CrossRef]
- Koca, A.; Gemici, Z.; Topacoglu, Y.; Cetin, G.; Acet, R.C.; Kanbur, B.B. Experimental investigation of heat transfer coefficients between hydronic radiant heated wall and room. Energy Build. 2014, 82, 211–221. [Google Scholar] [CrossRef]
- Reay, D.A.; Kew, P.A.; McGlen, R.J. Heat Pipes: Theory, Design and Applications, 6th ed.; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Zohuri, B. Heat Pipe Design and Technology: Modern Applications for Practical Thermal Management, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Faghri, A. Review and Advances in Heat Pipe Science and Technology. J. Heat Transf. 2012, 134, 123001. [Google Scholar] [CrossRef]
- Shabgard, H.; Allen, M.J.; Sharifi, N.; Benn, S.P.; Faghri, A.; Bergman, T.L. Heat pipe heat exchangers and heat sinks: Opportunities, challenges, applications, analysis, and state of the art. Int. J. Heat Mass Transf. 2015, 89, 138–158. [Google Scholar] [CrossRef]
- Reay, D.; Harvey, A. The role of heat pipes in intensified unit operations. Appl. Therm. Eng. 2012, 57, 147–153. [Google Scholar] [CrossRef]
- Srimuang, W.; Amatachaya, P. A review of the applications of heat pipe heat exchangers for heat recovery. Renew. Sustain. Energy Rev. 2012, 16, 4303–4315. [Google Scholar] [CrossRef]
- Werner, T.C.; Yan, Y.; Karayiannis, T.; Pickert, V.; Wrobel, R.; Law, R. Medium temperature heat pipes—Applications, challenges and future direction. Appl. Therm. Eng. 2024, 236, 121371. [Google Scholar] [CrossRef]
- Seo, J.; Kang, S.; Kim, K.; Lee, J. Compact heat pipe heat exchanger for waste heat recovery within a low-temperature range. Int. Commun. Heat Mass Transf. 2024, 155, 107550. [Google Scholar] [CrossRef]
- Jouhara, H.; Chauhan, A.; Nannou, T.; Almahmoud, S.; Delpech, B.; Wrobel, L. Heat pipe based systems—Advances and applications. Energy 2017, 128, 729–754. [Google Scholar] [CrossRef]
- Jouhara, H.; Bertrand, D.; Axcell, B.; Montorsi, L.; Venturelli, M.; Almahmoud, S.; Milani, M.; Ahmad, L.; Chauhan, A. Investigation on a full-scale heat pipe heat exchanger in the ceramics industry for waste heat recovery. Energy 2021, 223, 120037. [Google Scholar] [CrossRef]
- Kang, S.; Kim, K.; Seo, J.; Lee, J. Empirical modeling and experimental validation of gas-to-liquid heat pipe heat exchanger with baffles. Energy 2024, 303, 131972. [Google Scholar] [CrossRef]
- Moradi, A.; Toghraie, D.; Isfahani, A.H.M.; Hosseinian, A. An experimental study on MWCNT–water nanofluids flow and heat transfer in double-pipe heat exchanger using porous media. J. Therm. Anal. Calorim. 2019, 137, 1797–1807. [Google Scholar] [CrossRef]
- Merlone, A.; Coppa, G.; Bassani, C.; Bonnier, G.; Bertiglia, F.; Dedyulin, S.; Favreau, J.-O.; Fernicola, V.; van Geel, J.; Georgin, E.; et al. Gas-controlled heat pipes in metrology: More than 30 years of technical and scientific progresses. Measurement 2020, 164, 108103. [Google Scholar] [CrossRef]
- He, B.; Li, L.; He, G.; Tian, M.; Zhang, Y.; Tong, W.; Jian, Q.; Yu, X. Experimental study on heat transfer performance of micro-grooved I-shaped aluminum heat pipe for heat pipe heat exchangers. Appl. Therm. Eng. 2024, 253, 123773. [Google Scholar] [CrossRef]
- Aghvami, M.; Faghri, A. Analysis of flat heat pipes with various heating and cooling configurations. Appl. Therm. Eng. 2011, 31, 2645–2655. [Google Scholar] [CrossRef]
- Prado-Montes, P.; Mishkinis, D.; Kulakov, A.; Torres, A.; Pérez-Grande, I. Effects of non condensable gas in an ammonia loop heat pipe operating up to 125 °C. Appl. Therm. Eng. 2014, 66, 474–484. [Google Scholar] [CrossRef]
- Cacua, K.; Buitrago-Sierra, R.; Herrera, B.; Pabón, E.; Murshed, S.M.S. Nanofluids’ stability effects on the thermal performance of heat pipes: A critical review. J. Therm. Anal. Calorim. 2019, 136, 1597–1614. [Google Scholar] [CrossRef]
- Gupta, N.K.; Tiwari, A.K.; Ghosh, S.K. Heat transfer mechanisms in heat pipes using nanofluids—A review. Exp. Therm. Fluid Sci. 2018, 90, 84–100. [Google Scholar] [CrossRef]
- Xu, S.; Ding, R.; Niu, J.; Ma, G. Investigation of air-source heat pump using heat pipes as heat radiator. Int. J. Refrig. 2018, 90, 91–98. [Google Scholar] [CrossRef]
- Chaudhry, H.N.; Hughes, B.R.; Ghani, S.A. A review of heat pipe systems for heat recovery and renewable energy applications. Renew. Sustain. Energy Rev. 2012, 16, 2249–2259. [Google Scholar] [CrossRef]
- Khalil, H.; Saito, T.; Hassan, H. Comparative study of heat pipes and liquid-cooling systems with thermoelectric generators for heat recovery from chimneys. Int. J. Energy Res. 2021, 46, 2546–2557. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Yao, W.; Zhang, W.; Cao, J.; He, H. Research on temperature distribution characteristics and energy saving potential of wall implanted with heat pipes in heating season. Renew. Energy 2022, 195, 1037–1049. [Google Scholar] [CrossRef]
- Amanowicz, Ł. Controlling the Thermal Power of a Wall Heating Panel with Heat Pipes by Changing the Mass Flowrate and Temperature of Supplying Water—Experimental Investigations. Energies 2020, 13, 6547. [Google Scholar] [CrossRef]
- Tan, R.; Zhang, Z. Heat pipe structure on heat transfer and energy saving performance of the wall implanted with heat pipes during the heating season. Appl. Therm. Eng. 2016, 102, 633–640. [Google Scholar] [CrossRef]
- Reay, D.A. Thermal energy storage: The role of the heat pipe in performance enhancement. Int. J. Low-Carbon Technol. 2015, 10, 99–109. [Google Scholar] [CrossRef]
- Vizitiu, R.S.; Burlacu, A.; Abid, C.; Balan, M.C.; Vizitiu, S.E.; Branoaea, M.; Kaba, N.E. Investigating the Efficiency of a Heat Recovery–Storage System Using Heat Pipes and Phase Change Materials. Materials 2023, 16, 2382. [Google Scholar] [CrossRef] [PubMed]
- Robak, C.W.; Bergman, T.L.; Faghri, A. Enhancement of latent heat energy storage using embedded heat pipes. Int. J. Heat Mass Transf. 2011, 54, 3476–3484. [Google Scholar] [CrossRef]
- Douglas, J.M. Process Dynamics and Control; Printice-Hall Inc.: Englewood Cliffs, NJ, USA, 1972. [Google Scholar]
- Friedly, J.C. Dynamic Behavior of Processes; Printice-Hall Inc.: Englewood Cliffs, NJ, USA, 1972. [Google Scholar]
- Zawada, B. Experimental determination of parameters in models of indoor air temperature response to reduction in supplied energy. J. Build. Phys. 2016, 40, 346–371. [Google Scholar] [CrossRef]
- PN-EN 60751:2009; Industrial Platinum Resistance Thermometers and Platinum Temperature Sensors. Polish Committee for Standardization: Warszawa, Poland, 2009.
- PN-EN 1264-2+A1; Water Based Surface Embedded Heating and Cooling Systems—Part 2: Floor Heating: Prove Methods for the Determination of the Thermal Output Using Calculation and Test methods. Polish Committee for Standardization: Warszawa, Poland, 2013.
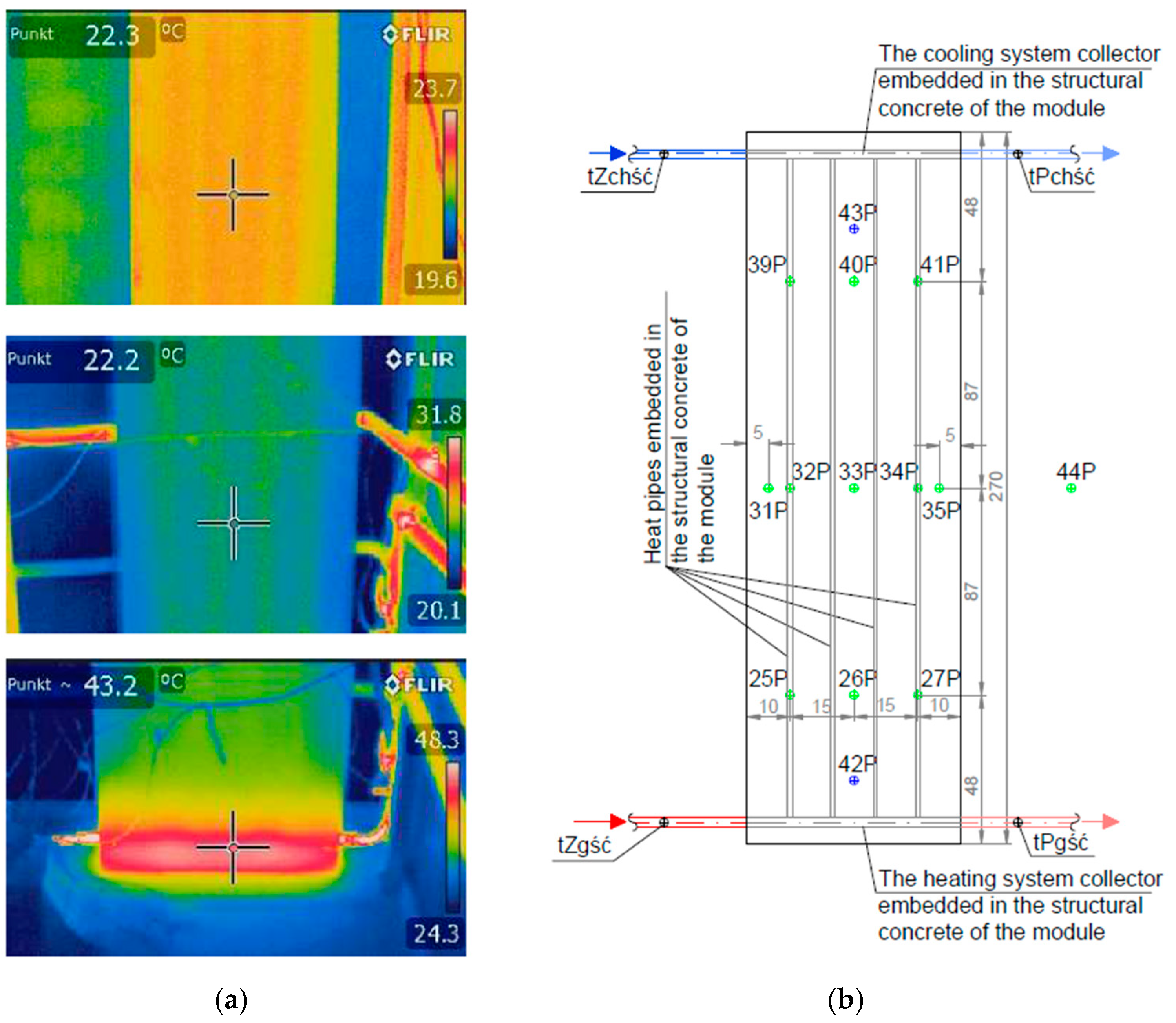
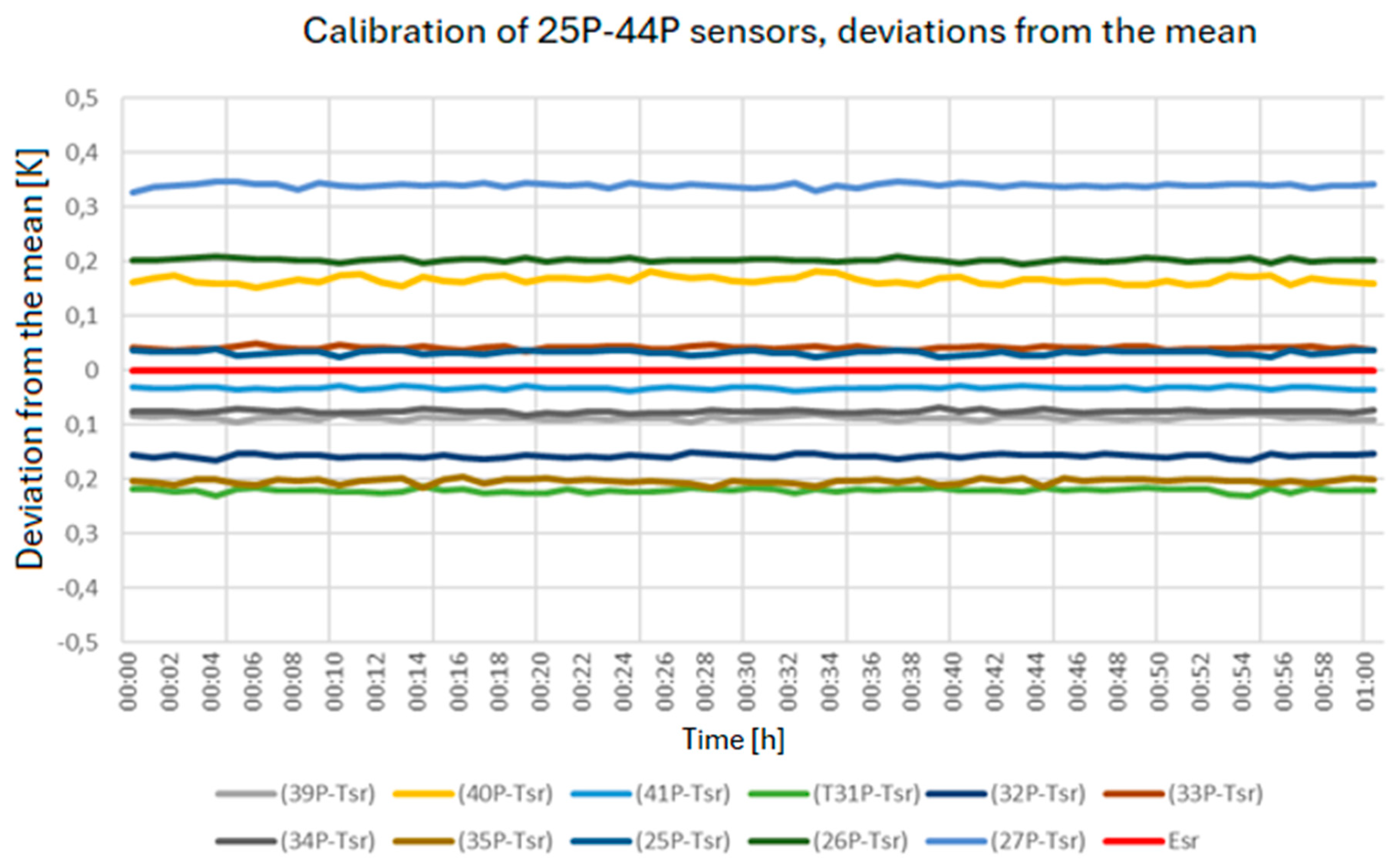

| Sensor Marking | 25P | 26P | 27P | 31P | 32P | 33P | 34P | 35P | 39P | 40P | 41P | 42P | 43P | 44P |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Indication errors [K] | 0.01 | 0.19 | 0.34 | −0.24 | −0.18 | 0.01 | −0.11 | −0.24 | −0.11 | 0.12 | −0.08 | −0.05 | 0.14 | 0.20 |
| No | Cooling Water Flow [L/h] | Reducing the Cooling Water Temperature [Tzas↘] | Increasing the Cooling Water Temperature [Tzas↗] | ||||
|---|---|---|---|---|---|---|---|
| (*) 43 | (*) 130 | (*) 217 | (*) 43 | (*) 130 | (*) 217 | ||
| 1 | 100 | 0.382 | 0.333 | 0.271 | 0.182 | 0.146 | 0.087 |
| 2 | 50 | 0.287 | 0.244 | 0.193 | 0.164 | 0.117 | 0.065 |
| 3 | 15 | 0.264 | 0.204 | 0.149 | 0.155 | 0.123 | 0.070 |
| No | Description | First-Order Model | Second-Order Model | |||
|---|---|---|---|---|---|---|
| T | (*) std | T1 | T2 | (*) std | ||
| min | - | min | min | - | ||
| Cooling—all sensors | ||||||
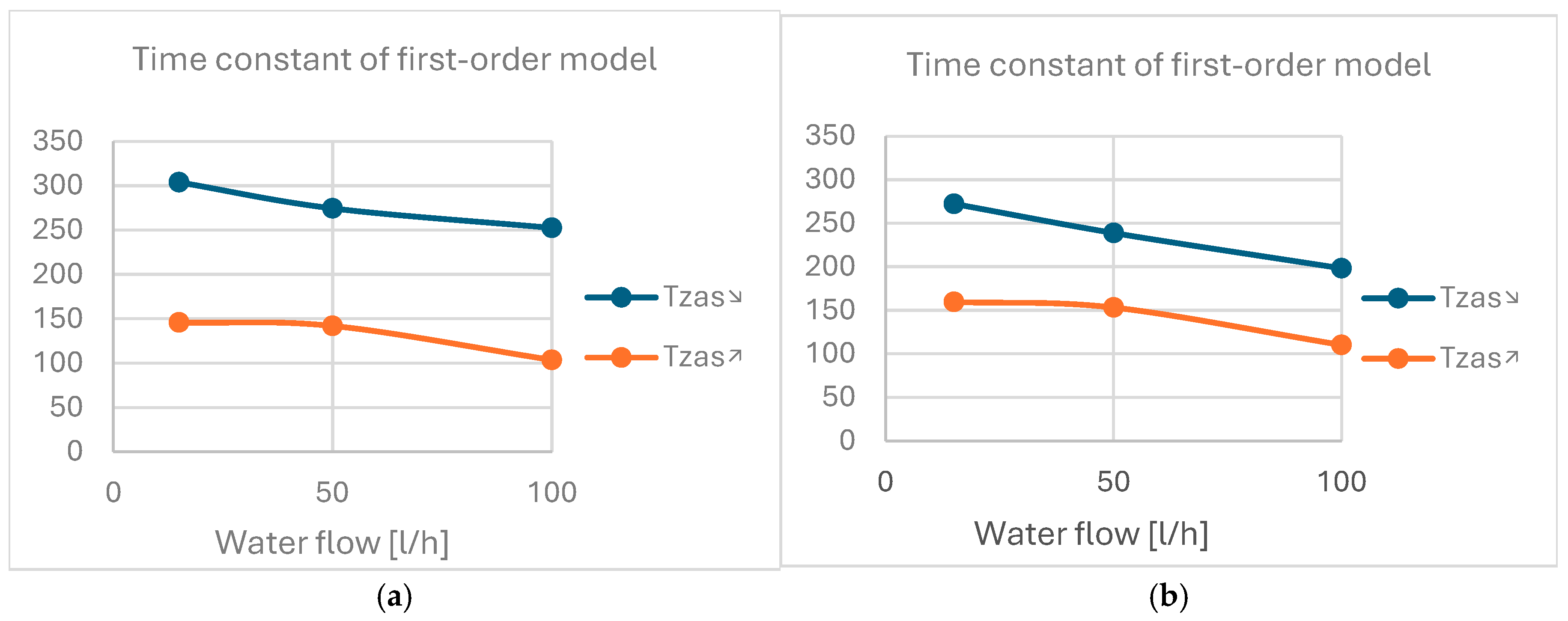
| 1 | V = 100 L/h, Tzas↘ | 252.4 | 0.0477 | 154.2 | 98.2 | 0.0525 |
| 2 | V = 50 L/h, Tzas↘ | 274.5 | 0.0403 | 166.7 | 107.9 | 0.0556 |
| 3 | V = 15 L/h, Tzas↘ | 303.9 | 0.0351 | 183.3 | 120.7 | 0.0650 |
| 4 | V = 100 L/h, Tzas↗ | 103.6 | 0.0758 | 64.7 | 38.8 | 0.0742 |
| 5 | V = 50 L/h, Tzas↗ | 141.9 | 0.0540 | 94.6 | 47.3 | 0.0410 |
| 6 | V = 15 L/h, Tzas↗ | 148.2 | 0.0449 | 96.0 | 52.2 | 0.0516 |
| Cooling—mid-row sensors | ||||||
| 7 | V = 100 L/h, Tzas↘ | 198.3 | 0.0303 | 124.9 | 73.4 | 0.0556 |
| 8 | V = 50 L/h, Tzas↘ | 238.9 | 0.0236 | 147.9 | 91.0 | 0.0591 |
| 9 | V = 15 L/h, Tzas↘ | 272.2 | 0.0284 | 166.4 | 105.8 | 0.0605 |
| 10 | V = 100 L/h, Tzas↗ | 110.3 | 0.0427 | 74.2 | 36.1 | 0.0482 |
| 11 | V = 50 L/h, Tzas↗ | 153.1 | 0.0271 | 99.1 | 54.0 | 0.0469 |
| 12 | V = 15 L/h, Tzas↗ | 159.6 | 0.0349 | 102.9 | 56.7 | 0.0430 |
| No | Heating Water Flow [L/h] | Reducing the Heating Water Temperature | Increasing the Temperature of the Heating Water | ||||
|---|---|---|---|---|---|---|---|
| (*) 43 | (*) 130 | (*) 217 | (*) 43 | (*) 130 | (*) 217 | ||
| 1 | 30 | 0.175 | 0.161 | 0.170 | 0.089 | 0.078 | 0.087 |
| 2 | 60 | 0.199 | 0.179 | 0.178 | 0143 | 0.130 | 0.127 |
| 3 | 120 | 0.211 | 0.192 | 0.198 | 0.156 | 0.153 | 0.163 |
| No | Description | First-Order Model | Second-Order Model | |||
|---|---|---|---|---|---|---|
| T | (*) std | T1 | T2 | (*) std | ||
| min | - | min | min | - | ||
| Heating—all sensors | ||||||
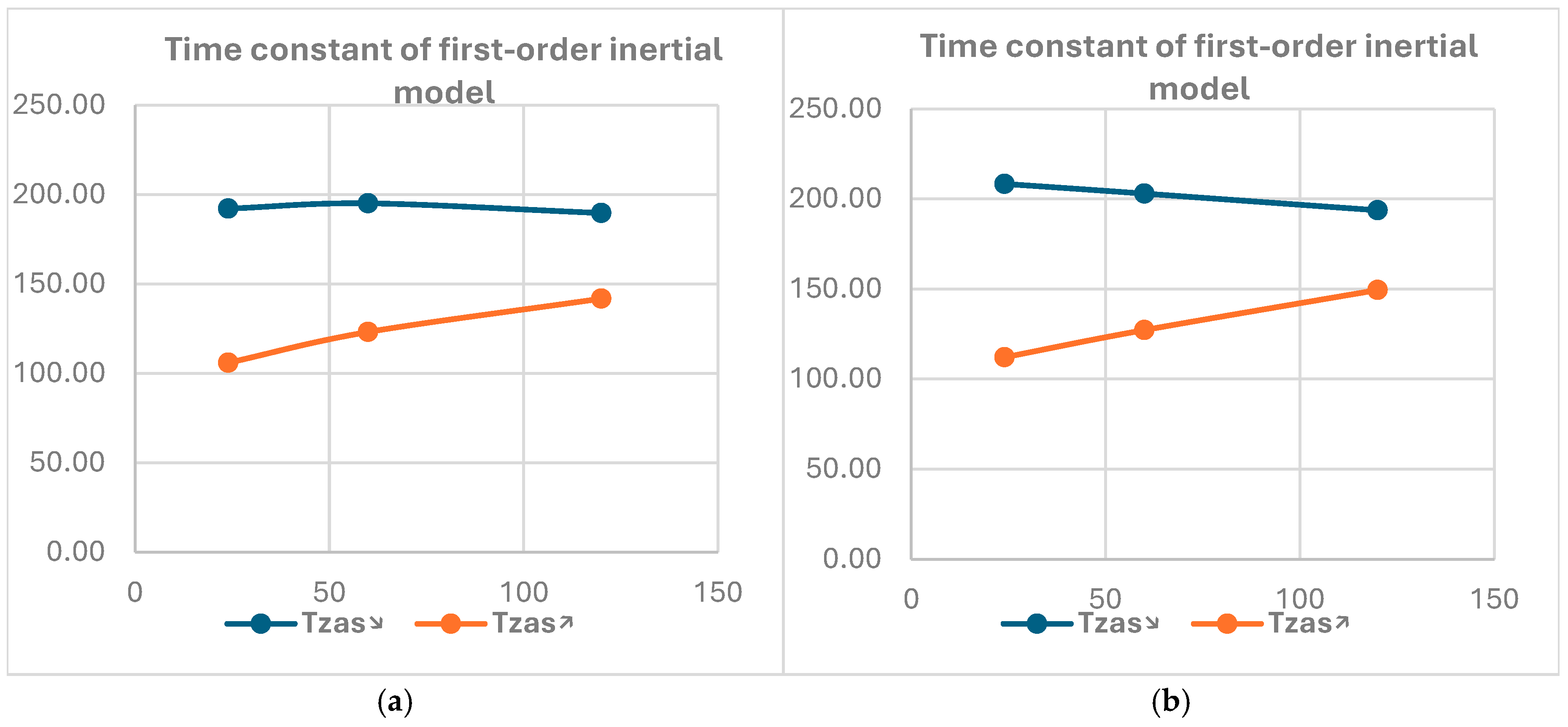
| 1 | V = 120 L/h, Tzas↘ | 189.7 | 0.259 | 120.7 | 69.1 | 0.063 |
| 2 | V = 60 L/h, Tzas↘ | 221.4 | 0.0177 | 138.8 | 82.6 | 0.0574 |
| 3 | V = 30 L/h, Tzas↘ | 192.2 | 0.0173 | 122.9 | 70.3 | 0.0578 |
| 4 | V = 120 L/h, Tzas↗ | 143.1 | 0.0201 | 95.4 | 47.7 | 0.0545 |
| 5 | V = 60 L/h, Tzas↗ | 123.2 | 0.0138 | 82.4 | 40.8 | 0.0410 |
| 6 | V = 30 L/h, Tzas↗ | 106 | 0.0299 | 71.8 | 34.2 | 0.0447 |
| Heating—mid-row sensors | ||||||
| 7 | V = 120 L/h, Tzas↘ | 149.5 | 0.0169 | 98.2 | 51.3 | 0.0556 |
| 8 | V = 60 L/h, Tzas↘ | 217.6 | 0.0218 | 136.9 | 80.7 | 0.0632 |
| 9 | V = 30 L/h, Tzas↘ | 208.4 | 0.0225 | 130.9 | 77.5 | 0.0532 |
| 10 | V = 120 L/h, Tzas↗ | 163.2 | 0.0466 | 103.8 | 59.4 | 0.0261 |
| 11 | V = 60 L/h, Tzas↗ | 127.2 | 0.0157 | 84.7 | 42.6 | 0.0451 |
| 12 | V = 30 L/h, Tzas↗ | 112.1 | 0.0387 | 75.3 | 36.8 | 0.0482 |
| Cooling Period | ||
| Effect | Cause | The power of influence |
| Higher values of k are obtained | -at a smaller distance of the point from the collector | high |
| -when the cold water temperature drops than when it increases | high | |
| -for larger flows of cold water | small | |
| The k values do not change | -with increasing cold water flow | no influence |
| Smaller T values are obtained | -when the cold water temperature increases than when it decreases | high |
| -for larger flows of cold water | small | |
| Heating period | ||
| Effect | Cause | The power of influence |
| Higher values of k are obtained | -when the hot water temperature drops than when it increases | high |
| -for larger flows of hot water | small | |
| The k values do not change | -when changing the distance from the collector | no influence |
| Smaller T values are obtained | -when the hot water temperature increases than when it decreases | high |
| -for larger flows of hot water | small | |
| -with lower flows and increased hot water temperature | small | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zawada, B.; Durczak, K.; Spik, Z. Control Parameters of a Wall Heating and Cooling Module with Heat Pipes—An Experimental Study. Energies 2025, 18, 487. https://doi.org/10.3390/en18030487
Zawada B, Durczak K, Spik Z. Control Parameters of a Wall Heating and Cooling Module with Heat Pipes—An Experimental Study. Energies. 2025; 18(3):487. https://doi.org/10.3390/en18030487
Chicago/Turabian StyleZawada, Bernard, Karolina Durczak, and Zenon Spik. 2025. "Control Parameters of a Wall Heating and Cooling Module with Heat Pipes—An Experimental Study" Energies 18, no. 3: 487. https://doi.org/10.3390/en18030487
APA StyleZawada, B., Durczak, K., & Spik, Z. (2025). Control Parameters of a Wall Heating and Cooling Module with Heat Pipes—An Experimental Study. Energies, 18(3), 487. https://doi.org/10.3390/en18030487





