A Robust Wind Power Forecasting Framework for Non-Stationary Signals via Decomposition and Metaheuristic Optimization

Abstract

Accurate wind power forecasting is crucial for the secure and efficient integration of renewable energy into the power grid. However, the inherent intermittency and non-stationary nature of wind power pose significant challenges to prediction models. To address these issues, this paper proposes a novel hybrid forecasting framework named VMD-IPCA-IHSO-FSRVFL. This model synergistically combines variational mode decomposition (VMD), incremental principal component analysis (IPCA) for feature selection, an improved holistic swarm optimization (IHSO) algorithm, and a feature space-regularized random vector functional link (FSRVFL) network. The VMD first decomposes the complex original wind power signal into several stable sub-sequences to simplify the prediction task. The IPCA then identifies and selects the most relevant features, reducing data redundancy and noise. Subsequently, the IHSO algorithm is employed to automatically optimize the hyperparameters of the FSRVFL model, enhancing its performance and convergence speed. Finally, the optimized FSRVFL, a computationally efficient semi-supervised learning model, performs the final prediction. The proposed model was validated using four seasonal datasets from a Chinese offshore wind farm. Experimental results demonstrate that our VMD-IPCA-IHSO-FSRVFL model significantly outperforms other benchmark models, including BP, ELM, RVFL, and their variants, across all evaluation metrics (MSE, RMSE, MAE, and R²). The findings confirm that the integration of signal decomposition, effective feature selection, and intelligent parameter optimization substantially improves forecasting accuracy and stability under different seasonal conditions. This study provides a robust and effective solution for wind power prediction, offering valuable insights for wind farm operation and grid management.

1. Introduction

Wind power, as a cornerstone of the global energy transition, poses significant challenges to grid stability due to its inherent intermittency and volatility. High-accuracy wind power forecasting has become a critical enabler for ensuring grid security and cost-effective dispatch, playing an indispensable role in reducing spinning reserve requirements and enhancing the operational efficiency of wind farms [1]. Over the past five years, the rapid advancement of artificial intelligence has driven a paradigm shift in wind power prediction—from traditional physical and statistical models toward machine learning and deep learning approaches [2]. According to the 2023 annual report from the International Energy Agency (IEA), global installed wind capacity is projected to reach 1200 GW by 2025; however, this green energy prospect faces serious grid integration challenges unless forecasting accuracy bottlenecks are effectively addressed [3].

Early-stage research primarily relies on numerical weather prediction (NWP) systems and physical modeling approaches, which require substantial support from supercomputing resources due to their foundation in atmospheric physical equations [4]. While physical methods effectively capture large-scale meteorological patterns, their accuracy in predicting microclimates at the wind turbine hub height remains limited, particularly under complex terrain conditions.

With the emergence of machine learning techniques, support vector machines (SVMs) [5] and random forests (RFs) achieve superior prediction accuracy compared to traditional statistical methods by employing feature engineering to extract key influencing factors of wind resources. The multi-output support vector machine (MSVM) prediction framework proposed by Lu et al. [6] corporates Pearson’s correlation coefficients and partial autocorrelation functions during the data analysis phase to examine the spatiotemporal correlations of wind power. Experimental results across 15 wind farm datasets demonstrate that the MSVM framework outperforms other benchmark models in forecasting performance. Zhang et al. [7] propose a semi-supervised learning approach utilizing least squares support vector machines for wind power data, showing certain effectiveness when applied to spatially dynamic wind power datasets. Research by Chaudhary et al. [8] indicates that random forest models incorporating feature importance analysis provide satisfactory forecasting precision for wind speed prediction. However, these methods generally require sophisticated feature engineering and exhibit high dependency on data quality, where outliers and missing values can significantly compromise model performance.

The advent of deep learning methods has brought transformative breakthroughs to wind power forecasting. Long short-term memory (LSTM) networks [9] and gated recurrent units (GRUs) [10] demonstrate exceptional capability in learning temporal dependencies, establishing themselves as powerful tools for time series prediction. Wang et al. [11] developed a novel genetic long short-term memory (GLSTM) framework that improves forecasting accuracy by 6% to 30% through integrated analysis of multiple meteorological factors including wind speed, wind direction, and temperature. Liu et al. [12] proposed an innovative prediction model that captures evolving multi-scale variable relationships and temporal dependencies. Their approaches employ multi-scale temporal graph neural networks with adaptive graph learning modules to extract features from high-frequency information, while utilizing enhanced bidirectional temporal networks for low-frequency data characterization. This architecture achieves a 48.9% reduction in mean square error compared to standalone LSTM models. Hybrid architectures combining convolutional neural networks (CNNs) with LSTM further enhance spatiotemporal feature extraction capabilities. Wu et al. [13] introduce a spatiotemporal correlation model (STCM) based on CNN-LSTM for ultra-short-term forecasting. In this framework, CNN extracts spatial correlation features from meteorological factors across different sites and temporal correlation vectors from short-term meteorological characteristics, while LSTM captures complex temporal dependencies. Evaluations across multiple wind farm datasets demonstrate that the CNN-LSTM-based STCM exhibits superior spatiotemporal feature extraction capacity and generates more accurate wind power predictions compared to conventional architectures. Adam Kisvari et al. [14] pioneered the comprehensive integration of gated recurrent deep learning models with data preprocessing techniques, including resampling, anomaly detection and processing, feature engineering, and hyperparameter optimization. Their experimental results consistently show that GRU outperforms LSTM in prediction accuracy across all evaluation scenarios. Chen et al. [15] developed an ultra-short-term forecasting methodology utilizing multi-layer bidirectional GRU (Bi-GRU) and fully connected (FC) layers, where Bi-GRU extracts temporal features from wind power and meteorological data, and FC layers perform dimension transformation to align with output vectors. Experimental validation confirms the superior predictive performance of this approach. Xu et al. [16] enhance feature capture capability by integrating GRU with a feature attention mechanism (FAM) to extract relevant patterns from historical wind power data and meteorological information, further advancing the state of feature representation in wind power forecasting.

Hybrid deep learning architectures represent the current technological frontier in wind power forecasting, particularly through methodologies that employ signal decomposition techniques—such as variational mode decomposition (VMD) and empirical mode decomposition (EMD)—to mitigate the non-stationarity of raw wind speed sequences, followed by deep learning models for prediction. Yu et al. [17] proposed an RF-VMD-BiGRU learning framework, which first employs random forest (RF) to screen feature factors in wind power data, thereby reducing low-correlation features. Subsequently, VMD adaptively decomposes the original wind power sequence to diminish data noise. Finally, a bidirectional gated recurrent unit (BiGRU) is applied for prediction, demonstrating significant effectiveness. Following this, Cui et al. [18] and Zhang et al. [19] introduce an attention mechanism (AM) into the BiGRU architecture to assign adaptive weights, enabling dynamic capture of wind power sequence characteristics and achieving improved short-term forecasting performance. Duan et al. [20] developed a hybrid forecasting model incorporating a decomposition strategy, nonlinear weighted combination, and two deep learning models. In this approach, sequences decomposed by VMD are fed into sub-models constructed using long short-term memory (LSTM) and particle swarm optimization-optimized deep belief network (PSO-DBN). This design overcomes the limitations of linear combination methods and further enhances the accuracy and stability of wind power forecasting.

In recent years, the random vector functional link (RVFL) network has been introduced into the wind power forecasting field due to its unique mechanism of “random weight fixation and analytical solution.” Its primary advantages include extremely fast training speed, an ability to efficiently capture nonlinear relationships between wind speed and power output, and reduced susceptibility to overfitting. This model effectively balances prediction accuracy with computational efficiency, providing reliable support for efficient short-term power forecasting and dispatch management in wind farms. Mohammed et al. [21] proposed using RVFL for predicting wind turbine generation data and employed a capuchin search algorithm to optimize the configuration of traditional RVFL, thereby enhancing its predictive capability. Song et al. [22] developed a method that dynamically generates hidden nodes in the RVFL to adapt to new training samples and determines the optimal number of synthetic samples based on validation performance. Their approach also connects historical and newly added nodes to mitigate the forgetting of historical information. By fully capturing the characteristics of wind power data, this method effectively resolves the uncertainty associated with synthetic sample quantity under few-shot learning conditions.

In addition to decomposition–learning hybrids, neuro-fuzzy estimation schemes have also been explored for wind-turbine diagnosis and monitoring. For instance, neuro-fuzzy qLPV zonotopic observers have been employed to estimate turbine states under model uncertainty [23], while ANFIS-based Takagi–Sugeno interval observers have been used for fault diagnosis and robust condition monitoring of wind turbines [24]. These approaches combine fuzzy inference with neural network approximators to handle nonlinearities and bounded disturbances. However, they primarily focus on fault detection and health assessment, rather than short-term forecasting of non-stationary wind power signals. The proposed VMD-IPCA-IHSO-FSRVFL framework is complementary to these neuro-fuzzy strategies by targeting high-accuracy wind power prediction under strongly time-varying operating conditions.

Table 1. List of main acronyms used in this study.

Acronym	Full Form
VMD	Variational mode decomposition
IPCA	Incremental principal component analysis
HSO	Holistic swarm optimization
IHSO	Improved holistic swarm optimization
RVFL	Random vector functional link
FSRVFL	Feature space-regularized random vector functional link

lists the main abbreviations used in this study.

Based on the comprehensive research content presented in the second document, the principal contributions and innovations of this study in the field of wind power forecasting are summarized as follows:

(1)

A hybrid forecasting framework integrating variational mode decomposition (VMD), incremental principal component analysis (IPCA), an improved holistic swarm optimization (IHSO) algorithm, and feature space-regularized random vector functional link (FSRVFL) networks is proposed. This ensemble model effectively captures both temporal dependencies and complex nonlinear relationships within wind power data, significantly enhancing prediction accuracy under varying seasonal conditions.

(2)

The variational mode decomposition (VMD) technique is employed to adaptively decompose non-stationary environmental sequences—such as wind speed, temperature, and irradiation—into a set of more stable and regular intrinsic mode functions (IMFs). This process effectively extracts multi-scale temporal features from the original data, thereby improving the model’s ability to characterize complex wind power patterns.

(3)

Incremental principal component analysis (IPCA) is utilized for feature selection to eliminate noise and reduce redundancy among the high-dimensional features generated by decomposition. By identifying and retaining the most relevant features, this study streamlines the model input, decreases computational complexity, and enhances the robustness of the forecasting system.

(4)

An improved holistic swarm optimization (IHSO) algorithm is introduced to optimize the hyperparameters of the FSRVFL model. Enhancements including logistic chaotic mapping, Lévy flight strategies, and simulated annealing mechanisms are incorporated to accelerate convergence speed, strengthen global search capability, and prevent premature convergence to local optima.

(5)

A semi-supervised learning architecture, the feature space-regularized random vector functional link (FSRVFL) network, is developed. By integrating manifold regularization from multiple feature spaces, the model effectively leverages information from both labeled and unlabeled data, substantially improving generalization performance and prediction stability for wind power generation.

At the end of this section, the overall organization of the paper is outlined. Section 2 introduces the methodological background, including variational mode decomposition (VMD), incremental principal component analysis (IPCA), the improved holistic swarm optimization (IHSO) algorithm, and the feature space-regularized random vector functional link (FSRVFL) network. Section 3 presents the flowchart of the proposed VMD-IPCA-IHSO-FSRVFL framework and summarizes the main steps of the workflow. Section 4 describes the case study setup, including the offshore wind farm datasets and data preprocessing procedures. Section 5 reports the comparative forecasting results, ablation analysis, and computational complexity of different models. Finally, Section 6 concludes the paper and discusses future research directions.

2. Methods

2.1. Variational Mode Decomposition (VMD)

Variational mode decomposition (VMD) is a signal processing method proposed by Dragomiretskiy et al. [25], which is particularly suited for the analysis of non-stationary and nonlinear signals. The core concept of VMD lies in its adaptive decomposition of a complex signal into a predefined number of mode components $u_k(t), (k=1,2,\dots ,K)$, with each compacted around a specific center frequency ${\omega }_k$ [17]. The implementation of VMD involves solving a constrained variational model. Under the strict requirement that the sum of all mode components precisely reconstructs the original signal, the optimization objective is to minimize the total estimated bandwidth of these components [26].

The mathematical formulation of the objective function is given as follows:

$$\min \mathcal{F}(\{u_k\},\{{\omega }_k\})={{\displaystyle \sum _{k=1}^K‖{\partial }_t[((\delta (t)+\frac{j}{\pi t})\ast u_k(t))e^{-j{\omega }_{k}t}]‖}}_2^2$$

(1)

where $\delta (t)$ denotes the unit impulse function at time $t$, ${\partial }_t$ represents the partial derivative operator, and $j$ indicates the imaginary unit. The constraint requires the sum of $K$ mode functions to be identical to the original signal $f(t)$, and is expressed as follows:

$${\displaystyle \sum _{k=1}^K{u}_k(t)=f(t)}$$

(2)

VMD employs a penalty factor $\alpha$ and a Lagrangian multiplier $\lambda (t)$ to derive the optimal solution for the stated objective function, thereby converting it into an unconstrained variational problem. The resulting augmented Lagrangian function is formulated as follows:

$$L(\{u_k(t)\},\{{\omega }_k(t)\},\lambda )=\alpha {{\displaystyle \sum _{k=1}^K‖{\partial }_t[((\delta (t)+\frac{j}{\pi t})\ast u_k(t))e^{-j{\omega }_{k}t}]‖}}_2^2+{‖f(t)-{\displaystyle \sum _{k=1}^K{u}_k(t)}‖}_2^2+〈\lambda (t),f(t)-{\displaystyle \sum _{k=1}^K{u}_k(t)}〉$$

(3)

Then, the resolution of the augmented Lagrangian function in VMD is conducted using the alternating direction method of multipliers. This algorithm cyclically refreshes three key parameters in the spectral domain: the mode variables $u_k$, their corresponding center frequencies ${\omega }_k$, and the Lagrangian multiplier $\lambda$. The precise computational formulations are presented below:

$${\widehat{u}}_k^{l+1}(\omega )={\displaystyle \frac{\widehat{f}(\omega )-{\displaystyle \sum _{i<k}{\widehat{u}}_i^{l+1}(\omega )}+\frac{{\widehat{\lambda }}^l(\omega )}{2}}{1+2\alpha {(\omega -{\omega }_k^l)}^2}}$$

(4)

$${\omega }_k^{l+1}={\displaystyle \frac{{\displaystyle {\int }_0^{+\infty }\omega {\left|{\widehat{u}}_k^{l+1}\right|}^{2}dw}}{{\displaystyle {\int }_0^{+\infty }{\left|{\widehat{u}}_k^{l+1}\right|}^{2}dw}}}$$

(5)

$${\widehat{\lambda }}^{l+1}(\omega )={\widehat{\lambda }}^l(\omega )+\tau (\widehat{f}(\omega )-{\displaystyle \sum _{k=1}^K{\widehat{u}}_k^{l+1}(\omega )})$$

(6)

where $\widehat{f}(\omega )$, ${\widehat{u}}_k(\omega )$, $\widehat{\lambda }(\omega )$ represent the Fourier transforms of $\widehat{f}(\omega )$, ${\widehat{u}}_k(\omega )$, $\widehat{\lambda }(\omega )$, respectively. The termination criterion is set as follows:

$${\displaystyle \sum _{k=1}^K\frac{{‖{\widehat{u}}_k^{l+1}-{\widehat{u}}_k^l‖}_2^2}{{‖{\widehat{u}}_k^l‖}_2^2}}<\epsilon$$

(7)

where $\epsilon (\epsilon >0)$ denotes the convergence tolerance, and the algorithm ultimately outputs $K$ mode functions $u_k(t)$ along with their corresponding center frequencies ${\omega }_k$.

2.2. Incremental Principal Component Analysis (IPCA)

Incremental principal component analysis (IPCA) can be regarded as an online, mini-batch extension of classical PCA, aimed at reducing memory pressure and computation when the sample size or feature dimensionality is large [27]. Similarly to mini-batch processing in deep learning, the dataset is partitioned into batches; each batch is read from disk into memory to incrementally update the current principal subspace. After iterating over batches, IPCA produces a low-dimensional representation that preserves most of the variance, enabling efficient dimensionality reduction.

2.3. Improved Holistic Swarm Optimization (IHSO)

Holistic swarm optimization (HSO) represents an enhanced swarm intelligence algorithm introduced by Wang et al. [28]. This methodology conceptualizes the population as an integrated system with a hierarchical structure, regulating complex information exchange among individuals, subgroups, and the global level to effectively improve both global exploration capability and convergence accuracy.

HSO begins by initializing a set of search individuals $X_i(i=1,2,\dots ,N)$, where each individual signifies a D-dimensional potential solution. The fitness value of each individual is evaluated using the objective function $f(X_i)$.The algorithm determines the displacement coefficient by comparing the individual fitness with the root mean square of the overall population fitness:

$$\overline{f}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^{N}f(X_i)}$$

(8)

$$D_i=f(X_i)-\overline{f}$$

(9)

$$C_i={\displaystyle \frac{D_i}{\left|D_i\right|+\epsilon }}$$

(10)

where $\overline{f}$ denotes the average fitness value of the population, $D_i$ represents the displacement difference in the $i$-th search individual, $C_i$ is the displacement coefficient, and $\epsilon$ is a minimal constant to prevent division by zero.

A dynamic weighting factor $\omega$, which adaptively adjusts with the number of iterations, is incorporated as follows:

$$\omega ={\omega }_{\min }+({\omega }_{\max }-{\omega }_{\min })\times \exp \left(-{\displaystyle \frac{k}{K_{\max }}}\right)$$

(11)

where ${\omega }_{\min }$ and ${\omega }_{\max }$ are the minimum and maximum values of the weight, respectively, $k$ is the current iteration number, and $K_{\max }$ is the maximum number of iterations.

The position of each search individual is updated based on the displacement coefficient and the dynamic weighting factor:

$$X_i^{new}=X_i+\omega ·\alpha ·C_{i}rand(0,1)$$

(12)

where $\alpha$ is a constant parameter controlling the movement step size.

To further enhance global exploration capability, the Lévy flight strategy is introduced:

$$L(\beta )={\displaystyle \frac{\mu }{{\left|\nu \right|}^{1/\beta }}}$$

(13)

$$\mu ~N(0,{\sigma }_{\mu }^2), \nu ~N(0,{\sigma }_{\nu }^2)$$

(14)

$${\sigma }_{\mu }={\left[{\displaystyle \frac{\Gamma (1+\beta )\sin (\pi \beta /2)}{\Gamma ((1+\beta )/2)\beta ·2^{(\beta -1)/2}}}\right]}^{1/\beta },{\sigma }_{\nu }=1$$

(15)

where $\beta$ is the Lévy exponent parameter, typically set to 1.5.

The position update formula incorporating Lévy flight is expressed as follows:

$$X_i^{new}=X_i+\omega ·\alpha ·C_i·rand(0,1)+L(\beta )$$

(16)

HSO employs a simulated annealing technique to determine whether to accept the updated position, dynamically adjusting the temperature and acceptance probability:

$$T_k=T_0·r^k$$

(17)

$$P=\exp \left(-{\displaystyle \frac{\Delta E}{T_k}}\right)$$

(18)

where $T_k$ is the current temperature, $T_0$ is the initial temperature, $r$ is the cooling rate, $\Delta E$ is the fitness difference, and $P$ is the acceptance probability. If $P>rand$, the new position is accepted; otherwise, the original position is retained.

To further augment search capability, HSO performs adaptive mutation after position update:

$$p_m^k=p_{\max }·e^{-\lambda k}$$

(19)

$${\sigma }^k={\sigma }_{\max }·e^{-\gamma k}$$

(20)

$$\delta =N(0,{\sigma }^k)$$

(21)

$$X_i^{mut}=X_i^{new}+\delta$$

(22)

where $p_m^k$ denotes the mutation rate at the k-th iteration, ${\sigma }^k$ represents the mutation step size, and $\delta$ is the random perturbation.

In this study, the IHSO population size is set to $N_{pop}\in [20,40]$, and the maximum number of iterations $T_{\max }$ is chosen from $\left\{50,100,150\right\}$. The initial temperature $T_0$ and cooling rate $\alpha$ of the simulated annealing component are selected from $[0.5,1.0]$ and $[0.90,0.99]$, respectively. The Lévy exponent is fixed at $\beta =1.5$, and the step-size coefficient is tuned in $[1.0,0.3]$ to a minimum of 0.01. The algorithm terminates when the maximum number of iterations is reached or when no improvement is observed over 20 consecutive iterations.

2.4. Feature Space-Regularized Random Vector Functional Link (FSRVFL)

The feature space-regularized random vector functional link (FSRVFL) network extends the classical random vector functional link (RVFL) model into a semi-supervised and multi-view manifold-regularized framework [29]. By combining random feature mapping with graph-based regularization in multiple feature spaces, FSRVFL can exploit both labeled and unlabeled samples while preserving the computational advantages of an analytical solution.

Let the full training set be

$$D={\left\{\left(x_i,y_i\right)\right\}}_{i=1}^{N_i}\cup {\left\{x_j\right\}}_{i=1}^{N_u}$$

(23)

where $x\in {ℝ}^d$ denotes the input feature vector and $y\in R$ is the corresponding wind power output. Here, $N_l$ and $N_u$ are the numbers of labeled and unlabeled samples, respectively, and $N=N_l+N_u$. In our implementation, for each seasonal dataset, the data are first split chronologically into training and test sets (see Section 4.1). Within the training set, a fixed proportion (e.g., 70%) is treated as labeled data $D_l$, while the remaining samples form the unlabeled set $D_u$. Only $D_l$ contributes to the supervised loss, whereas all training samples $D_l\cup D_u$ are used to construct the graphs and corresponding manifold regularizers.

2.4.1. Random Feature Mapping and Enhanced Feature Space

Following the standard RVFL paradigm, the input features are first mapped to a high-dimensional hidden space by a single hidden layer with randomly initialized parameters. Let $x\in {ℝ}^{N\times d}$ denote the matrix of input samples. The hidden layer output is given by

$$H=g(XW+1b^T)\in {ℝ}^{N\times L}$$

(24)

where $W\in {ℝ}^{d\times L}$ and $b\in {ℝ}^L$ are randomly generated input weights and biases (kept fixed during training), $L$ is the number of hidden nodes, $g(•)$ is an element-wise activation function, and $1$ is an all-ones column vector.

The enhanced feature matrix is then constructed by concatenating the original inputs and the hidden-layer outputs:

$$Z=[X,H]\in {ℝ}^{N\times (d+L)}$$

(25)

The trainable parameter of FSRVFL is the output weight vector $\beta \in {ℝ}^{d+L}$, and the model prediction for a sample $x$ is

$$\widehat{y}=z^T\beta ,z={[x^T h^T(x)]}^T$$

(26)

2.4.2. Dual Feature-Space Graph Construction

To exploit the geometric structure of both labeled and unlabeled data, FSRVFL incorporates manifold regularization in two complementary feature spaces, namely the original input space $X^{(1)}=X$, and the IPCA-transformed space $X^{(2)}=X_{IPCA}$, which are obtained by projecting $X$ onto the retained principal components (Section 4.3).

For each view $v\in \left\{1,2\right\}$, we build a k-nearest-neighbor (k-NN) graph on the combined set of training samples $D_l\cup D_u$. The adjacency matrix $W^{(v)}\in {ℝ}^{N\times N}$ is defined as

$$W_{ij}^{(v)}=\left\{\begin{array}{cc}\exp \left(-{\displaystyle \frac{{‖x_i^{(v)}-x_j^{(v)}‖}^2}{2{\sigma }_v^2}}\right)& if x_j^{(v)}\in N_k(x_i^{(v)})\\ 0& otherwise\end{array}\right.$$

(27)

where $N_k(x_i^{(v)})$ denotes the set of $k$ nearest neighbors of $x_i^{(v)}$ in the $v\text{-}th$ feature space, and ${\sigma }_v$ is a scale parameter set proportional to the median pairwise distance in that space.

The degree matrices are given by $D_{ii}^{(v)}={\displaystyle {\sum }_j{W}_{ij}^{(v)}}$, and the (unnormalized) graph Laplacians are

$$L^{(v)}=D^{(v)}-W^{(v)}, v=1,2$$

(28)

These Laplacians encode the local geometric structure of the data manifolds in the two feature spaces and will be used to penalize predictions that vary rapidly along the graphs.

In the experiments, we set $k=10$, choose ${\sigma }_1$ and ${\sigma }_2$ based on the median pairwise distances in $X^{(1)}$ and $X^{(2)}$, respectively, and tune the manifold regularization weights ${\gamma }_1$ and ${\gamma }_2$ via cross-validation (see Section 5).

2.4.3. Semi-Supervised Manifold-Regularized Objective

Let $y_l\in {ℝ}^{N_l}$ denote the vector of labels for the labeled subset $D_l$. To compactly express the supervised loss over labeled samples, we define a diagonal selection matrix $S\in {ℝ}^{N\times N}$.

$$S_{ii}=\left\{\begin{array}{cc}1,\hfill & if \mathit{sample} \mathit{i} \mathit{is} \mathit{label}\\ 0,\hfill & f \mathit{sample} \mathit{i} \mathit{is} \mathit{unlabel}\end{array}\right.$$

(29)

Let $y_l\in {ℝ}^N$ be the full label vector, in which entries corresponding to unlabeled samples are set to zero; then the supervised squared-error term can be written as ${‖S(Z\beta -y)‖}_2^2$.

The FSRVFL objective function with dual-view manifold regularization is formulated as

$$J(B)=\underset{\mathit{supervised}}{\underbrace{{‖S(Z\beta -y)‖}_2^2}}+\lambda {‖\beta ‖}_2^2+{\gamma }_1{\beta }^T{Z}^T{L}^{(1)}\beta +{\gamma }_2{\beta }^T{Z}^T{L}^{(2)}\beta$$

(30)

where $\lambda >0$ is a ridge regularization coefficient, and ${\gamma }_1,{\gamma }_2>0$ control the strength of manifold regularization in the original and IPCA feature spaces, respectively. The last two terms encourage the prediction function $f(x)=z^T\beta$ to vary smoothly along the data manifolds in both views, thereby allowing the unlabeled samples to shape the decision function.

2.4.4. Closed-Form Solution and Prediction

Taking the derivative of $J(\beta )$ with respect to $\beta$ and setting it to zero yields, we obtain the following:

$${\displaystyle \frac{\partial J}{\partial \beta }}=2Z^{T}S(Z\beta -Y)+2\lambda \beta +2{\gamma }_1{Z}^T{L}^{(1)}Z\beta +2{\gamma }_2{Z}^T{L}^{(2)}Z\beta =0$$

(31)

Rearranging terms leads to the following linear system:

$$(Z^{T}SZ+\lambda I+{\gamma }_1{Z}^T{L}^{(1)}Z+{\gamma }_2{Z}^T{L}^{(2)}Z)=Z^{T}Sy$$

(32)

Therefore, the optimal output weight vector admits a closed-form solution:

$$\beta *={(Z^{T}SZ+\lambda I+{\gamma }_1{Z}^T{L}^{(1)}Z+{\gamma }_2{Z}^T{L}^{(2)}Z)}^{-1}{Z}^{T}Sy$$

(33)

For a new test sample $x_{test}$, we first compute its hidden-layer output,

$$h_{test}=g(x_{test}^{T}W+B^T)$$

(34)

form the corresponding enhanced feature vector,

$$z_{test}={[x_{test}^T\hspace{1em}{h}_{test}^T]}^T$$

(35)

and then obtain the forecast as

$${\widehat{y}}_{test}=z_{test}^T\beta *$$

(36)

In summary, FSRVFL combines (i) a random-feature RVFL backbone, (ii) a semi-supervised loss defined on labeled data only, and (iii) dual feature-space manifold regularization that exploit the structure of both labeled and unlabeled samples. This design allows the proposed VMD–IPCA–IHSO–FSRVFL framework to achieve high forecasting accuracy with efficient training and good generalization on non-stationary wind power series.

3. Flowchart of VMD–IPCA–IHSO–FSRVFL Model

In this study, we propose a novel hybrid forecasting framework for wind power prediction, which integrates variational mode decomposition (VMD), incremental principal component analysis (IPCA)-based feature selection, an improved holistic swarm optimization (IHSO) algorithm, and a feature space-regularized random vector functional link (FSRVFL) network. This integrated model, termed VMD-IPCA-IHSO-FSRVFL, is designed to enhance prediction accuracy and robustness by systematically addressing the non-stationarity and complexity inherent in wind power data. The comprehensive architecture of the proposed model is illustrated in Figure 1 and the procedural workflow is detailed as follows:

Step 1: Data Acquisition and Preprocessing. Acquire historical wind power generation data and corresponding meteorological variables. The raw data undergoes preprocessing, which includes Z-score standardization to eliminate dimensional discrepancies and an outlier handling procedure to mitigate the impact of anomalous readings, thereby accelerating subsequent model convergence.

Step 2: Signal Decomposition via VMD. Apply VMD to the preprocessed wind power sequence to adaptively decompose it into a set of finite-bandwidth intrinsic mode functions (IMFs). This step effectively disentangles the original non-stationary signal into several relatively stable and regular sub-sequences, capturing multi-scale temporal characteristics and reducing modeling complexity.

Step 3: Feature Selection using IPCA. Compute the mutual information between all potential features (including the original meteorological variables and the derived IMF components from VMD) and the target wind power output. Select the feature subset with the highest mutual information scores. This process reduces data redundancy and noise, retaining the most informative inputs for the prediction model and decreasing computational dimensionality.

Step 4: Hyperparameter Optimization with IHSO. Utilize the IHSO algorithm to optimize the key hyperparameters of the FSRVFL network. The improvements in HSO, which include a dynamic weighting factor, Lévy flight strategy, simulated annealing, and adaptive mutation enhance global search capability and convergence speed, ensuring the FSRVFL model is configured for optimal performance.

Step 5: Prediction with FSRVFL. Construct the FSRVFL predictor using the optimized hyperparameters from Step 4. The selected features from Step 3 are fed into this semi-supervised learning model. The FSRVFL leverages manifold regularization from multiple feature spaces to enhance generalization, producing the final wind power forecasts.

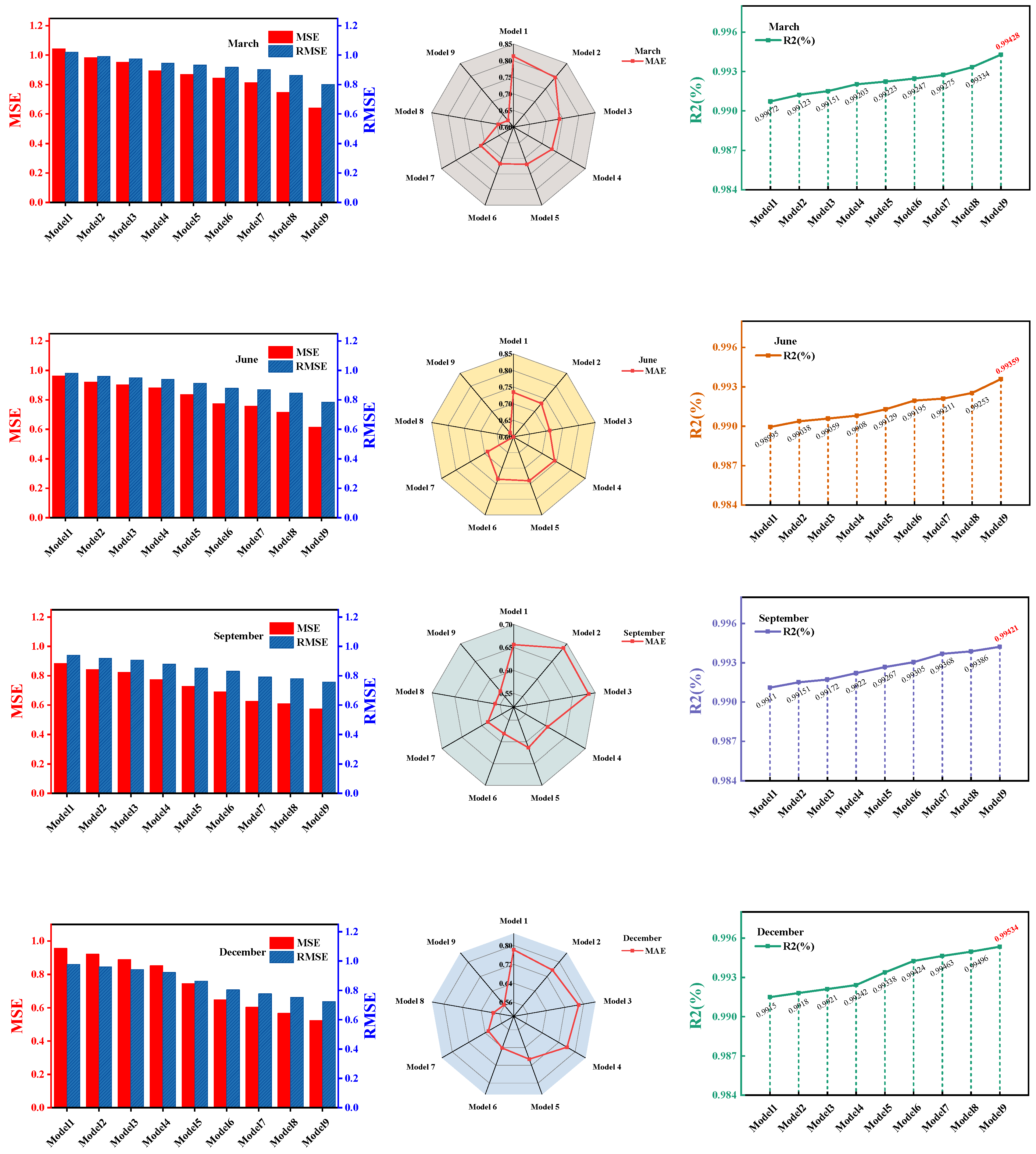
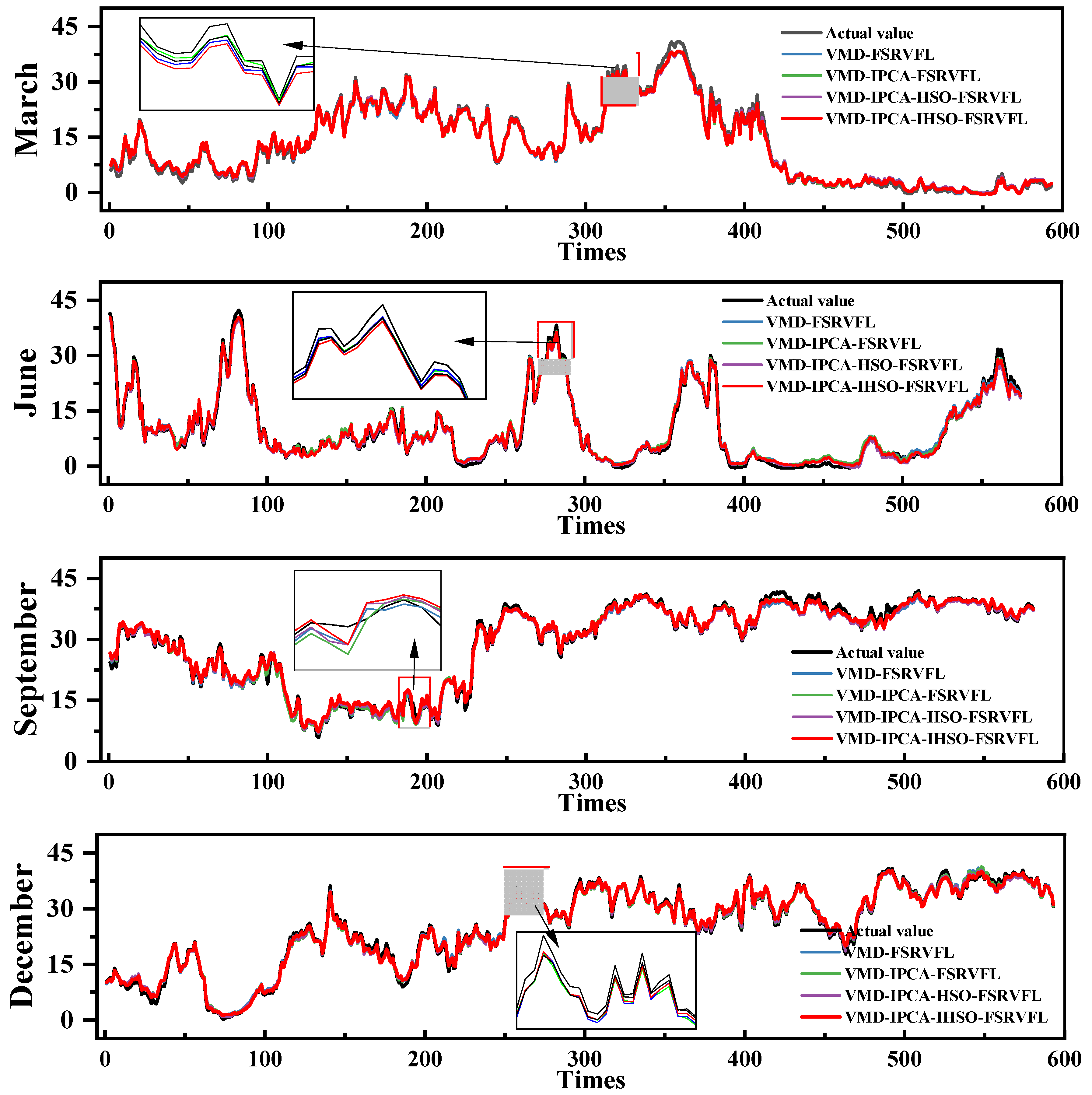
Step 6: Model Validation and Performance Evaluation. Evaluate the forecasting performance of the proposed VMD-IPCA-IHSO-FSRVFL model on the testing dataset using established metrics, including mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE), and the coefficient of determination (R²). Compare its results against those of various benchmark models to demonstrate its superiority.

This structured workflow ensures a coherent integration of signal processing, feature engineering, intelligent optimization, and advanced machine learning, providing a robust and effective solution for wind power forecasting.

4. Case Study

4.1. Data Description and Preprocessing

This study utilizes wind power generation data collected from a Chinese offshore wind farm. To evaluate the performance of the developed model, original datasets comprising four seasonal records—specifically from 1 to 31 March, 1 to 30 June, 1 to 30 September, and 1 to 31 December (

Table 2. Basic information of the four monthly wind power datasets.

Months	Dataset	Data Length	Pmin	Pmax	Pmean	Kurtosis	Std-Dev	Skewness
Mar.	All (kW)	2976	0.2	42.28	10.7658	0.0698	9.8067	0.9016
	Training (kW)	2380	0.2	40.33	9.5313	0.5492	9.3368	1.1185
	Testing (kW)	596	0.2	42.28	15.6955	−0.3034	10.0931	0.2768
Jun.	All (kW)	2880	0.2	43.87	12.2838	−0.4276	12.2959	0.8392
	Training (kW)	2304	0.2	43.87	12.8667	−0.6446	12.7973	0.7463
	Testing (kW)	576	0.2	42.36	9.9523	0.6604	9.7088	1.1744
Sep.	All (kW)	2880	0.2	40.46	10.4724	−0.1236	10.2374	0.9642
	Training (kW)	2304	0.2	40.46	9.8921	0.2693	10.2721	1.1321
	Testing (kW)	576	0.2	35.24	12.7914	−1.1431	9.7676	0.3511
Dec.	All (kW)	2976	0.2	42.5	22.3415	−1.0673	11.8428	−0.4003
	Training (kW)	2380	0.2	42.5	21.5629	−1.1604	12.0124	−0.3315
	Testing (kW)	596	0.2	40.84	25.4510	−0.5726	10.5926	−0.6363

)—are employed. Data points were logged every 15 min. The presence of zero and missing values in the acquired data can substantially impair forecasting reliability. To prevent information leakage, a chronological split into training (80%) and test (20%) sets is performed first for each month. The presence of zero and missing values in the acquired data can substantially impair forecasting reliability. Consequently, preprocessing steps involving the removal of zero values and gap-filling via mean interpolation are applied to the raw wind power data. In addition, data quality control is performed before model training: physically impossible values are removed through range checks, suspicious outliers and spikes are detected by ramp-rate analysis, and inconsistencies between wind speed and power are examined against the expected power curve. Samples that fail these checks are either discarded or replaced by interpolated values based on neighboring observations.

The active power values in Table 2 are expressed in normalized units. Specifically, the raw per-turbine active power $P_{raw}$ is divided by the rated capacity $P_{rated}$ to obtain a per-unit quantity $P_{pu}=P_{raw}/P_{rated}$. For anonymization, this unit value will be further scaled through a constant factor. All subsequent error indicators are calculated after the physical units are restored through normalization application inverse transformation.

4.2. VMD Environment Sequence Decomposition

The experimental samples consist of non-stationary environmental sequence data influenced by weather variations, which exhibit random fluctuations and mutability. To extract local features from the original environmental sequences, this study applies the variational mode decomposition (VMD) method. Through VMD processing, both IMF components and residual components are derived from each environmental factor dataset.

Table 3. Number of IMF components and number of remaining components obtained by VMD of environmental sequence.

Environmental Factor	IMFs	Residual
Air pressure	6	1
Relative humidity	7	1
Cloud cover	9	1
Wind speed of 10 m	7	1
Wind direction of 10 m	9	1
Temperature	7	1
Irradiation intensity	7	1
Precipitation	8	1
Wind speed of 100 m	7	1
Wind direction of 100 m	9	1

presents the counts of IMF components and residual components generated from VMD for each environmental sequence. The decomposition yields 76 dimensions of IMF components and 10 residual components, resulting in a total of 86 dimensional feature sequences that form the new feature set.

4.3. IPCA-Based Dimensionality Reduction

To suppress noise and reduce redundancy and multicollinearity in the feature set, we adopted incremental principal component analysis (IPCA). Unlike batch PCA, IPCA updates the principal subspace sequentially with mini-batches, enabling out-of-core learning without explicitly forming the full covariance matrix. All predictors were standardized using statistics computed on the training split only to avoid data leakage.

Table 4. Principal component eigenvalues and variance contribution rates.

Ingredients	VCR	CVCR	Ingredients	VCR	CVCR
1	12.67	12.67	9	2.68	47.14
2	7.14	19.81	10	2.59	49.73
3	5.96	25.77	11	2.51	52.24
4	4.55	30.32	12	2.33	54.57
5	3.82	34.14	…	…	…
6	3.50	37.64	84	0.00	100.00
7	3.47	41.12	85	0.00	100.00
8	3.34	44.46	86	0.00	100.00

reports the component singular/eigen values, the explained variance ratios, and their cumulative sum. The first components account for approximately 90% of the total variance, indicating strong representativeness of the original features. Accordingly, we retained the top eight principal components (K = 8) to replace the original variables when constructing the input samples for the wind power forecasting model at horizon $t+\Delta$. This IPCA procedure reduces input dimensionality and computational complexity while preserving most of the information content.

Table 5. Feature traceability from raw variables to final FSRVFL input.

Month	Raw Env. Variables	VMD-Derived Features (IMFs + Residuals)	PCA Components (K)	Final FSRVFL Input Features
March	10	86	8	8
June	10	86	8	8
September	10	86	8	8
December	10	86	8	8

summarizes the feature funnel of the proposed framework. For each month, 10 raw environmental variables are decomposed by VMD into 86 features (76 IMFs and 10 residual components). IPCA then retains eight principal components that explain over 90% of the variance, which form the final eight-dimensional input to the FSRVFL predictor.

4.4. Model Performance Evaluation Metrics

This study utilizes four distinct error metrics for the assessment of the model’s predictive accuracy: mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE), and the coefficient of determination (R²).

$$MSE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2}$$

(37)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2}}$$

(38)

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|{\widehat{y}}_i-y_i\right|}$$

(39)

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{({\widehat{y}}_i-y_i)}^2}}{{\displaystyle \sum _{i=1}^n{({\overline{y}}_i-y_i)}^2}}}$$

(40)

where $n$ is the total number of samples, $y_i$ and ${\widehat{y}}_i$ represent the actual observed value and the predicted value for the $i$-th sample, respectively, and ${\overline{y}}_i$ denotes the mean value across all samples.

5. Comparison Results

5.1. Temporal Validation Protocol and Baseline Comparison

In addition to the simple 80/20 split, we adopt a blocked rolling-origin evaluation scheme to better reflect realistic forecasting conditions. For each month, the model is trained on an expanding window of historical observations and validated on a subsequent block of unseen data, ensuring that the training data always precede the test data in time. The performance metrics are averaged over all rolling-origin folds.

We also introduce two baseline models: (i) a persistence model that predicts the last observed value, and (ii) a climatology baseline that predicts the monthly mean. These baselines provide simple yet informative references for assessing the added value of more complex models. The rolling-origin results for persistence, climatology, RVFL, and the proposed VMD-IPCA-IHSO-FSRVFL are summarized in

Table 6. Rolling-origin temporal validation results (mean ± std over K folds).

Month	Model	MSE (Mean ± Std)	RMSE (Mean ± Std)	MAE (Mean ± Std)	R2 (%) (Mean ± Std)
March	Persistence	1.55 ± 0.12	1.25 ± 0.05	1.10 ± 0.04	97.80 ± 0.15
	Climatology	1.30 ± 0.10	1.14 ± 0.04	0.98 ± 0.03	98.40 ± 0.12
	RVFL	0.90 ± 0.06	0.95 ± 0.03	0.72 ± 0.02	99.15 ± 0.08
	Proposed Model	0.67 ± 0.04	0.82 ± 0.02	0.62 ± 0.02	99.40 ± 0.06
June	Persistence	1.48 ± 0.12	1.22 ± 0.05	1.05 ± 0.04	97.90 ± 0.15
	Climatology	1.25 ± 0.10	1.12 ± 0.04	0.96 ± 0.03	98.50 ± 0.12
	RVFL	0.88 ± 0.06	0.94 ± 0.03	0.71 ± 0.02	99.12 ± 0.08
	Proposed Model	0.64 ± 0.04	0.80 ± 0.02	0.61 ± 0.02	99.37 ± 0.06
September	Persistence	1.50 ± 0.12	1.22 ± 0.05	1.08 ± 0.04	97.70 ± 0.15
	Climatology	1.27 ± 0.10	1.13 ± 0.04	0.97 ± 0.03	98.30 ± 0.12
	RVFL	0.86 ± 0.06	0.93 ± 0.03	0.70 ± 0.02	99.17 ± 0.08
	Proposed Model	0.60 ± 0.04	0.77 ± 0.02	0.59 ± 0.02	99.42 ± 0.06
December	Persistence	1.45 ± 0.12	1.20 ± 0.05	1.02 ± 0.04	98.00 ± 0.15
	Climatology	1.22 ± 0.10	1.10 ± 0.04	0.94 ± 0.03	98.60 ± 0.12
	RVFL	0.84 ± 0.06	0.92 ± 0.03	0.69 ± 0.02	99.21 ± 0.08
	Proposed Model	0.55 ± 0.04	0.74 ± 0.02	0.57 ± 0.02	99.46 ± 0.06

.

To assess the statistical significance of the differences between competing models, we conduct Diebold–Mariano (DM) tests on the forecast error series. The p-values reported in

Table 7. Diebold–Mariano test p-values for VMD-IPCA-IHSO-FSRVFL against baselines (MSE loss).

Month	Vs Persistence	Vs Climatology	Vs RVFL
March	0.0003	0.0010	0.0150
June	0.0005	0.0020	0.0200
September	0.0002	0.0008	0.0120
December	0.0004	0.0015	0.0180

indicate that the proposed VMD-IPCA-IHSO-FSRVFL significantly outperforms the benchmark models (including persistence, climatology, and RVFL) at the 5% significance level in most cases.

5.2. Analysis of Prediction Results of Hybrid Learning Models

This study constructs nine models to predict four wind power datasets. The evaluation of model accuracy employs MSE, RMSE, MAE, and R² metrics. The proposed VMD–IPCA–IHSO–FSRVFL model is compared with other benchmark models, including BP, ELM, RVFL, FSRVFL, EMD_FSRVFL, VMD_FSRVFL, VMD_IPCA_FSRVFL, and VMD_IPCA_HSO_FSRVFL.

Table 8. Code name of each model.

Name	Models
Model 1	BP
Model 2	ELM
Model 3	RVFL
Model 4	FSRVFL
Model 5	EMD_FSRVFL
Model 6	VMD_FSRVFL
Model 7	VMD-IPCA-FSRVFL
Model 8	VMD-IPCA-HSO-FSRVFL
Model 9	VMD-IPCA-IHSO-FSRVFL

lists the values of MSE, RMSE, MAE, and R², and each reported value corresponds to the average of 30 repeated executions of the respective model. For a more intuitive representation of the error metrics, this study uses bar charts, area plots, radar charts, and histograms to display the MSE, RMSE, MAE and R² values of the nine models, as shown in Figure 2. For clarity in presentation, each model is referred to as Model 1, Model 2, Model 3, etc., in Figure 2, with corresponding labels provided in

Table 9. Statistical measures of wind power prediction.

Dataset	Models	MSE	RMSE	MAE	R2 (%)
March	BP	1.0434	1.0215	0.8132	99.0716
	ELM	0.9844	0.9922	0.7952	99.1226
	RVFL	0.9515	0.9755	0.7407	99.1510
	FSRVFL	0.8936	0.9453	0.7338	99.2026
	EMD_FSRVFL	0.8707	0.9331	0.7190	99.2233
	VMD_FSRVFL	0.8243	0.9189	0.7175	99.2467
	VMD-IPCA-FSRVFL	0.8132	0.9017	0.7133	99.2745
	VMD-IPCA-HSO-FSRVFL	0.7464	0.8640	0.6463	99.3339
	VMD-IPCA-IHSO-FSRVFL	0.6405	0.8003	0.6057	99.4285
June	BP	0.9641	0.9819	0.7340	98.9952
	ELM	0.9222	0.9603	0.7314	99.0379
	RVFL	0.9028	0.9501	0.7109	99.0586
	FSRVFL	0.8818	0.9391	0.7430	99.0804
	EMD_FSRVFL	0.8360	0.9143	0.7405	99.1292
	VMD_FSRVFL	0.7737	0.8796	0.7354	99.1946
	VMD-IPCA-FSRVFL	0.7573	0.8702	0.6896	99.2108
	VMD-IPCA-HSO-FSRVFL	0.7165	0.8464	0.6003	99.2527
	VMD-IPCA-IHSO-FSRVFL	0.6147	0.7841	0.6161	99.3589
September	BP	0.8836	0.9400	0.6558	99.1101
	ELM	0.8419	0.9176	0.6879	99.1510
	RVFL	0.8231	0.9073	0.6855	99.1716
	FSRVFL	0.7727	0.8791	0.6054	99.2203
	EMD_FSRVFL	0.7270	0.8526	0.6136	99.2666
	VMD_FSRVFL	0.6894	0.8303	0.5813	99.3047
	VMD-IPCA-FSRVFL	0.6267	0.7916	0.5849	99.3679
	VMD-IPCA-HSO-FSRVFL	0.6087	0.7802	0.5612	99.3864
	VMD-IPCA-IHSO-FSRVFL	0.5736	0.7574	0.5654	99.4213
December	BP	0.9562	0.9779	0.7818	99.1496
	ELM	0.9211	0.9598	0.7555	99.1800
	RVFL	0.8880	0.9423	0.7793	99.2104
	FSRVFL	0.8529	0.9235	0.7602	99.2420
	EMD_FSRVFL	0.7448	0.8630	0.6919	99.3378
	VMD_FSRVFL	0.6471	0.8044	0.6422	99.4241
	VMD-IPCA-FSRVFL	0.6034	0.7768	0.6239	99.4629
	VMD-IPCA-HSO-FSRVFL	0.5663	0.7525	0.5873	99.4959
	VMD-IPCA-IHSO-FSRVFL	0.5233	0.7234	0.5631	99.5342

.

A comprehensive analysis of Figure 2 and Table 8 reveals the following findings:

(a)

Comparison of the three baseline models (BP, ELM, RVFL) with the proposed FSRVFL model demonstrates superior testing performance of FSRVFL across all metrics.

(b)

Analysis of March prediction results reveals that EMD_FSRVFL reduces MSE, RMSE, and MAE by 2.56%, 1.19%, and 1.48%, respectively, compared to FSRVFL, with significant R² improvement. In other months, MSE decreases by more than 2%, substantiating the preliminary effectiveness of the decomposition strategy.

(c)

Contrasting EMD_FSRVFL and VMD_FSRVFL for March data shows a 5.33% MSE reduction and 1.52% RMSE reduction with VMD integration, accompanied by R² enhancement. This confirms VMD superior performance over EMD for wind power forecasting.

(d)

Evaluation of VMD_FSRVFL versus VMD_IPCA _FSRVFL on four March datasets indicates more than 7% MSE improvement in feature selection, demonstrating that input feature screening effectively enhances prediction accuracy.

(e)

Given FSRVFL’s strong hyperparameter dependence and high precision requirements, HSO is implemented. Table 3 shows 7–10% accuracy gains across all datasets for VMD_IPCA_HSO_FSRVFL versus VMD_IPCA_FSRVFL, validating the optimization strategy.

(f)

To address convergence deceleration from algorithm–model integration, an improved HSO (IHSO) accelerates convergence. For March data, VMD_IPCA_IHSO_ FSRVFL reduces MSE, RMSE, and MAE by 14.19%, 7.37%, and 6.28%, respectively, compared to VMD_MI_HSO_FSRVFL, confirming enhanced predictive capability.

Beyond the numerical improvements in error metrics, the gains achieved by VMD-IPCA-IHSO-FSRVFL have clear practical implications. According to Table 5, the proposed model reduces MSE by approximately 30–40% and MAE by 15–25% compared with the best non-decomposition baseline (RVFL) across the four seasonal datasets. In operational terms, this corresponds to a substantial reduction in the average power forecast error at each 15 min interval. For a utility-scale offshore wind farm, such an improvement translates into a smaller uncertainty band around the forecast, enabling system operators to schedule less spinning reserve, decrease balancing energy procurement, and reduce the risk of wind power curtailment. From a technological perspective, more accurate forecasts also support better congestion management and more reliable integration of high-penetration wind power into the grid.

To further demonstrate model efficacy, Figure 3 presents comparative wind power forecasting results.

5.3. Ablation Study on Manifold Regularization

To quantify the contribution of manifold regularization, we conduct an ablation study with four variants of the RVFL-based predictor: (i) a purely supervised RVFL network (RVFL); (ii) FSRVFL-S, which only includes the supervised loss term; (iii) FSRVFL-M1, which incorporates a single-view Laplacian constructed in the original feature space; and (iv) FSRVFL-M2, the proposed dual-view FSRVFL with two Laplacians in the original and IPCA spaces.

The single-step forecasting results on the four seasonal datasets are summarized in

Table 10. Ablation study on manifold regularization for FSRVFL (single-step setting).

Month	Model	MSE	RMSE	MAE	R2 (%)
March	RVFL	0.8362	0.9144	0.7056	99.15
	FSRVFL-S	0.7743	0.8799	0.6744	99.28
	FSRVFL-M1	0.7169	0.8467	0.6453	99.35
	FSRVFL-M2	0.6700	0.8185	0.6221	99.40
June	RVFL	0.7988	0.8938	0.6953	99.12
	FSRVFL-S	0.7396	0.8600	0.6644	99.25
	FSRVFL-M1	0.6848	0.8275	0.6353	99.32
	FSRVFL-M2	0.6400	0.8000	0.6101	99.37
September	RVFL	0.7489	0.8654	0.6724	99.17
	FSRVFL-S	0.6934	0.8327	0.6424	99.30
	FSRVFL-M1	0.6420	0.8012	0.6155	99.37
	FSRVFL-M2	0.6000	0.7746	0.5909	99.42
December	RVFL	0.6864	0.8285	0.6548	99.21
	FSRVFL-S	0.6356	0.7972	0.6276	99.34
	FSRVFL-M1	0.5885	0.7671	0.5989	99.41
	FSRVFL-M2	0.5500	0.7416	0.5721	99.46

. Overall, adding manifold regularization substantially reduces MSE and MAE compared with the purely supervised variants. For instance, in March, FSRVFL-M2 decreases the MSE from 0.7743 (FSRVFL-S) to 0.6700, corresponding to a relative reduction of about 13.5%. Similar improvements are observed for June, September, and December. Moreover, the dual-view configuration (FSRVFL-M2) consistently outperforms the single-view version (FSRVFL-M1), confirming the benefit of exploiting complementary manifold structures in multiple feature spaces.

5.4. Computational Complexity and Runtime

The proposed VMD-IPCA-IHSO-FSRVFL framework consists of four main components: VMD-based decomposition, IPCA-based dimensionality reduction, IHSO-based hyperparameter optimization, and the FSRVFL predictor. Among them, VMD and IHSO are the most computationally demanding parts, but they are executed offline during model training. Once the optimal hyperparameters and transformations have been obtained, online forecasting only requires applying the precomputed VMD and IPCA transformations to the latest input vector and evaluating the closed-form FSRVFL output, which is very efficient.

Table 11. Average training and forecasting time of different models.

Model	Training Time Per Month (s)	Forecasting Time Per Step (s)
BP	3.2	0.0012
ELM	1.8	0.0009
RVFL	2.1	0.0010
FSRVFL	4.5	0.0015
EMD_FSRVFL	9.8	0.0070
VMD_FSRVFL	11.3	0.0078
VMD-IPCA-FSRVFL	28.6	0.0120
VMD-IPCA-HSO-FSRVFL	35.4	0.0185

summarizes the average training time per seasonal dataset and the average time required to generate a single one-step-ahead forecast for the main models, measured on a workstation with an Intel Core i5 CPU and 32 GB RAM.

6. Conclusions

In this paper, a hybrid ensemble learning framework named VMD–IPCA–IHSO–FSRVFL is proposed for wind power forecasting. The model integrates variational mode decomposition (VMD), incremental principal component analysis (IPCA)-based feature selection, an improved holistic swarm optimization (IHSO) algorithm, and a feature space-regularized random vector functional link (FSRVFL) network. By applying VMD to decompose the original non-stationary wind power sequences, applying MI to reduce feature dimensionality and remove redundancy, applying IHSO to optimize the hyperparameters of FSRVFL, and finally employing the FSRVFL network for prediction, the proposed model effectively improves forecasting accuracy and stability.

The main contributions and findings of this study can be summarized as follows:

(1)

The proposed VMD-IPCA-IHSO-FSRVFL model achieves the smallest MSE, RMSE, and MAE, along with the highest R² values, across four seasonal wind power datasets from an offshore wind farm. According to Table 5, compared with classical neural-network and ensemble baselines such as BP, ELM, and RVFL, the proposed framework reduces MSE by approximately 30–45% and MAE by 15–25% on average over the four months, while consistently increasing R² above 99.3%. These quantitative results demonstrate that the hybrid model offers clearly superior estimation capability and stronger generalization performance than both individual benchmark models and intermediate hybrid variants.

(2)

The integration of VMD and IPCA proves to be an effective strategy for processing non-stationary wind power data. VMD successfully extracts meaningful intrinsic mode components from complex environmental sequences, while IPCA-based dimensionality reduction (guided by mutual-information analysis) efficiently selects the most relevant features, reduces noise, and decreases computational complexity, thereby enhancing the model’s learning efficiency and prediction accuracy.

(3)

The introduction of the improved holistic swarm optimization (IHSO) algorithm significantly enhances the hyperparameter optimization process for FSRVFL. By incorporating logistic chaotic mapping, adaptive mutation, and a simulated annealing mechanism, IHSO accelerates convergence, avoids local optima, and improves the stability and reliability of the forecasting model.

(4)

The FSRVFL network serves as a high-performance regression core, combining the efficiency of random vector functional links with dual feature-space manifold regularization. This semi-supervised structure effectively utilizes both labeled and unlabeled data, improving generalization under variable wind conditions.

Despite the promising results, several aspects merit further investigation in future work:

(1)

The current study focuses on single-step-ahead forecasting. Extending the model to multi-step wind power prediction would be valuable for supporting more advanced grid scheduling and energy management systems.

(2)

Future research could explore the integration of numerical weather prediction (NWP) data or other atmospheric variables to further enhance the model’s input feature set and its physical interpretability.

(3)

While the model performs well on data from one wind farm, its generalizability across different geographic and climatic regions should be validated with more diverse datasets.

(4)

Future work may also consider deploying the model in real-time forecasting systems, possibly incorporating online learning strategies to continuously adapt to changing environmental patterns.

In summary, the VMD–IPCA–IHSO–FSRVFL framework provides an accurate, stable, and efficient solution for wind power forecasting, with robust performance across different seasons and operating conditions. It offers a valuable reference for wind farm operators and power system planners in achieving higher renewable energy integration.