Improvement and Validation of Transient Analysis Code FRTAC for Liquid Metal-Cooled Fast Reactors

Abstract

Transient safety analysis is a critical aspect of ensuring the safe design of Liquid Metal-cooled Fast Reactors (LMRs), relying heavily on advanced system analysis programs. To this end, the China Institute of Atomic Energy (CIAE) independently developed the Fast Reactor Transient Analysis Code (FRTAC) system analysis code for LMRs, which has been applied to the safety analysis of several reactor types. However, long-term use has revealed certain limitations, such as complex control system modeling and numerical dissipation from the first-order numerical scheme. This study analyzes the current limitations of the code and carries out systematic improvements and validation. The main improvements include enhancing the system compilation architecture and refactoring functional modules to improve computational efficiency, scalability, and usability; introducing a second-order accurate numerical scheme based on a limiter to reduce numerical dissipation in the convection term while ensuring computational stability; and optimizing the solution procedure to accommodate the new architecture and algorithms. The improved code’s computational stability and accuracy were validated using the Edwards blowdown experiment and the Energy Technology Engineering Center (ETEC) once-through steam generator steady-state test, respectively. The validation results show that the improved code maintains excellent numerical stability in problems with rapid transient pressure changes. In steady-state convective heat transfer problems, the computational accuracy and grid convergence are significantly improved, with the relative deviation of the water-side outlet temperature reduced from −3.56% to −0.59%. Under the same computational conditions, the computational efficiency was increased by up to 36.1%. The results of this study will provide a more accurate and efficient system analysis code for the transient safety analysis of LMRs.

1. Introduction

As one of the main reactor types in fourth-generation nuclear energy systems, Liquid Metal-cooled Fast Reactors (LMRs) [1,2] play a pivotal role in global nuclear energy development due to their inherent passive safety features, efficient nuclear fuel breeding capabilities, and potential for transmuting nuclear waste. However, compared to traditional light-water reactors, the physical processes in LMRs under transient accident conditions are more complex, involving tightly coupled multi-physics effects between neutron kinetics, thermal–hydraulics, and structural mechanics. This presents severe challenges to the accuracy and reliability of their safety analysis. Therefore, the development and validation of high-fidelity system transient analysis codes are crucial for accurately predicting reactor system responses and ensuring their design and operational safety.

Internationally, several mature system analysis codes have been widely applied and validated in the field of fast reactors. For instance, the SAS4A/SASSYS-1 [3] code from the United States has been successfully used in the design of various fast reactors, such as the Experimental Breeder Reactor-II (EBR-II) [4], and has undergone extensive experimental validation. Similarly, Japan’s SPECTRA [5], France’s CATHARE [6], and Russia’s EUCLID/V1 [7] codes have provided essential safety analysis support for their respective fast reactor projects. The successful development and application of these codes underscore the fundamental role of system analysis programs in fast reactor safety research.

Against this backdrop, the China Institute of Atomic Energy, after years of research and development, has successfully developed the Fast Reactor Transient Analysis Code (FRTAC) [8], a system analysis program for LMRs. FRTAC integrates a rich set of physical models, with functionalities covering transient heat transfer and fluid dynamics simulations for the core, heat exchangers, pumps, pipes, and other primary and secondary circuit systems, coupled with key physical processes such as neutron kinetics and reactivity feedback. The FRTAC has been successfully applied to safety analysis and design verification for projects like CFR600, providing vital technical support for the design, safety assessment, and licensing of subsequent fast reactors.

As the engineering application of FRTAC deepens and faces increasingly complex safety analysis demands, its limitations in model accuracy, numerical algorithms, and user-friendliness have become apparent. The current upwind first-order discretization scheme is also the numerical scheme adopted by mainstream analysis programs, such as RELAP5 [9] and TRACE [10]. Although it largely ensures computational stability, it simultaneously introduces significant numerical dissipation. The current technological development trend is shifting towards high-precision discrete schemes, such as programs developed based on the MOOSE framework [11] (e.g., SAM [12]) or precision improvements to existing programs [13,14]. Furthermore, the original data structure and functional architecture of the program have room for optimization when handling complex conditions, constraining computational efficiency and the flexibility for future functional expansion. These issues directly impact the precise assessment of system safety margins under specific conditions.

This study aims to systematically address the aforementioned limitations of the FRTAC. At the program architecture level, improvements in computational performance, compatibility, and scalability are achieved through refactoring and optimization. At the numerical method level, higher-order differencing schemes are introduced to suppress numerical dissipation, combined with limiter techniques [15,16] to avoid non-physical oscillations that may arise from high-order schemes, thus improving solution accuracy while maintaining computational stability. Finally, internationally recognized benchmark experiments are selected to comprehensively validate and evaluate the computational stability, accuracy, and efficiency of the improved code.

2. Overview of FRTAC

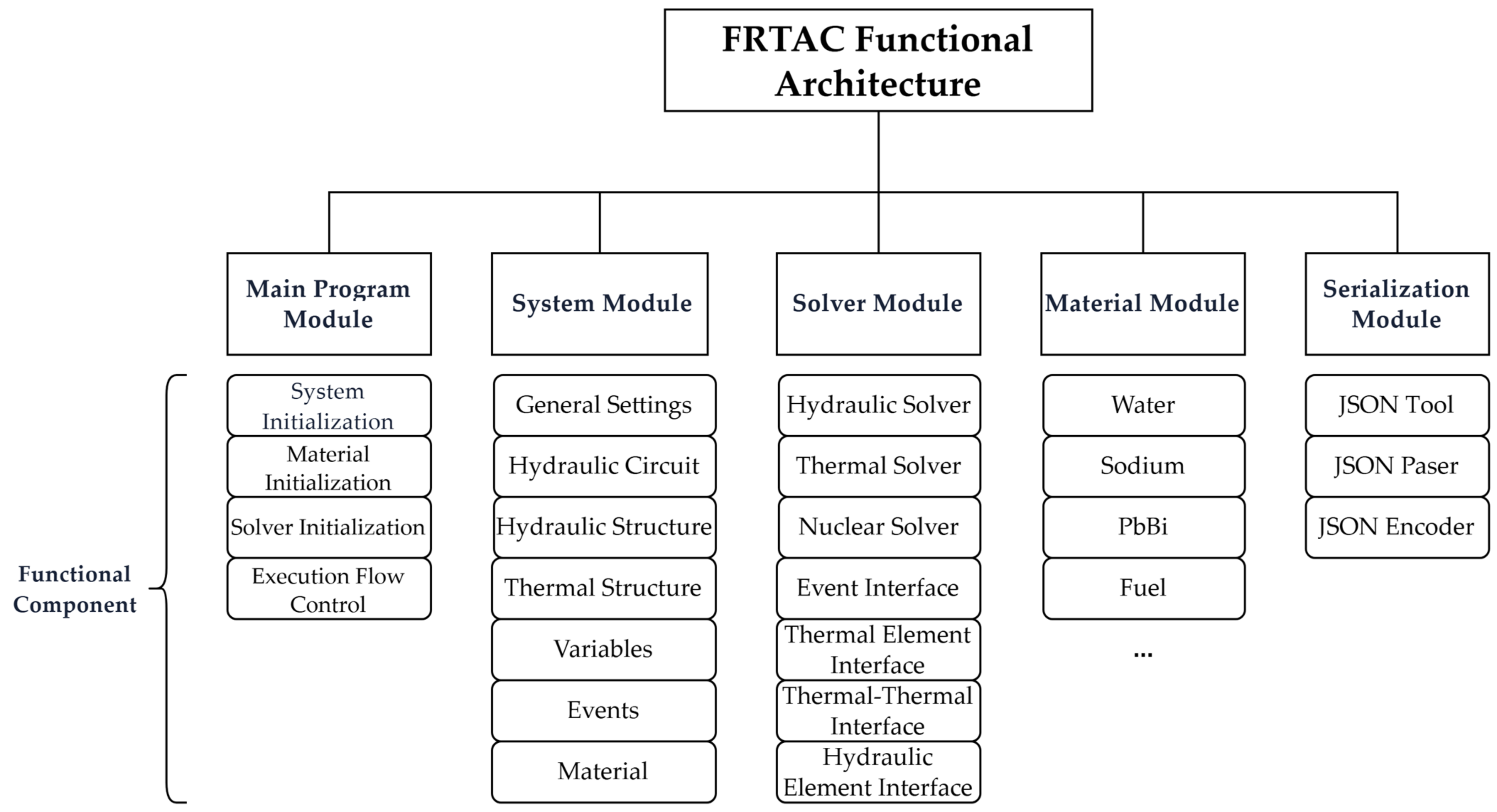
2.1. System Functional Architecture

FRTAC is a system safety analysis code for LMRs that supports thermal–hydraulic simulations for both steady-state and transient conditions, capable of analyzing system responses during normal operation, startup/shutdown, and various design basis accidents. The code has multi-scale modeling capabilities, allowing for detailed modeling of key components such as the reactor core, primary coolant system, intermediate loop, and steam generator. Many studies have used FRTAC as a tool for accident analysis and safety assessment of nuclear facilities, such as EBR-II [17] and small lead-cooled reactors [18].

The program is developed in the object-oriented C++ language, adhering to modular design principles to ensure its extensibility, maintainability, and robustness. The entire program consists of five core modules, each with clear responsibilities, working collaboratively to complete complex system transient analysis tasks. Its original functional architecture is shown in Figure 1.

• Main Program Module: As the program’s entry point, it is responsible for system initialization, configuration loading, coordination between modules, and controlling the overall calculation flow, ensuring all modules operate efficiently in the prescribed order.
• System Module: Stores all state-related system variables; constructs and manages the physical models of the entire reactor system, including hydraulic circuits, thermal structures, and nuclear parameters; builds the control system, setting control variables and trigger events; loads built-in and externally defined material information.
• Solver Module: As the core computational unit responsible for transient analysis in FRTAC, this module integrates multiple sub-solvers and coupled calculation interfaces. The hydraulic solver is based on a staggered-grid finite volume method and employs a semi-implicit discretization scheme to solve the one-dimensional mass, momentum, and energy conservation equations for the fluid. The thermal conduction solver uses a fully implicit finite volume formulation on a two-dimensional mesh to resolve transient heat conduction in thermal components. The nuclear solver solves the point kinetics model together with the decay heat model, with time integration carried out using a first-order Taylor expansion. The event interface updates the function values associated with triggered events at the current time level. The inter-component coupling interface handles the coupled calculations between thermal structures and hydraulic component. Furthermore, reactivity feedback is computed within the nuclear solver: after the hydraulic and thermal solvers complete their calculations at each time step, the nuclear solver evaluates various reactivity feedback terms based on the geometric and thermophysical properties of the fluid and thermal components.
• Material Module: Provides a library of physical properties for various built-in materials such as sodium, water, fuel, and structural steel.
• Serialization Module: Responsible for the program’s input/output, parsing user-input configuration files, and generating formatted result files for subsequent processing.

2.2. Thermal–Hydraulic Models

2.2.1. Hydrodynamic Model

The code uses a one-dimensional homogeneous flow model [19] to describe the flow characteristics of the coolant circuit. This model treats two-phase flow as an equivalent homogeneous fluid, assuming that both phases have the same velocity and temperature, i.e., they are in thermodynamic equilibrium. The form of its basic conservation equations is the same as for single-phase flow, but the physical properties therein are obtained by weighted averaging of each phase according to the void fraction. For one-dimensional flow in a pipe, the mass, momentum, and energy conservation equations are expressed as:

Mass Conservation Equation:

$${\displaystyle \frac{\partial \mathit{\rho }}{\partial \mathit{t}}} + {\displaystyle \frac{\partial \mathit{\rho }\mathit{v}}{\partial \mathit{z}}} = 0$$

(1)

Momentum Conservation Equation:

$$\mathit{\rho }{\displaystyle \frac{\partial \mathit{v}}{\partial \mathit{t}}} + \mathit{\rho }\mathit{v}{\displaystyle \frac{\partial \mathit{v}}{\partial \mathit{z}}} =- {\displaystyle \frac{\partial \mathit{p}}{\partial \mathit{z}}} - \mathit{\rho }\mathit{g}\mathit{sin}\mathit{\theta } - {\mathit{F}}_{\mathit{wj}} - L_{\mathit{j}}$$

(2)

Energy Conservation Equation:

$${\displaystyle \frac{\partial \mathit{\rho }\mathit{h}}{\partial \mathit{t}}} + {\displaystyle \frac{\partial \mathit{\rho }\mathit{vh}}{\partial \mathit{z}}} = \mathit{q} + {\displaystyle \frac{\partial \mathit{p}}{\partial \mathit{t}}} + \mathit{v}{\displaystyle \frac{\partial \mathit{p}}{\partial \mathit{z}}} + \mathit{v}{\mathit{F}}_{\mathit{wv}}$$

(3)

where ρ, v, p are the density, velocity, and pressure of the fluid. F_wj is the wall friction resistance term at the junction, and $L_{\mathit{j}}$ is the local resistance at the junction. F_wv is the distributed friction resistance term for the control volume. If the fluid is single-phase, the distributed resistance can be calculated using the Darcy-Weisbach Formula based on wall roughness and fluid velocity. For two-phase flow, the distributed resistance is the two-phase frictional pressure drop containing a two-phase multiplier. $\mathit{v}{\mathit{F}}_{\mathit{wv}}$ represents the energy dissipation due to friction. q is the heat source term, including internal heat sources from direct heating and heat transfer from convection between circuits.

With pressure and density as independent variables, the equation of state for specific enthalpy is:

$$\mathit{h} = \mathit{h}(\mathit{\rho },\mathit{p})$$

(4)

When dealing with liquid metal coolant, it is treated as a single-phase liquid. When the coolant is water, the density is expressed as:

$$\mathit{\rho } = \mathit{\alpha }{\mathit{\rho }}_{\mathit{g}} + (1-\mathit{\alpha }){\mathit{\rho }}_{\mathit{l}}$$

(5)

where ${\mathit{\rho }}_{\mathit{g}}$ is the gas phase density, ${\mathit{\rho }}_{\mathit{l}}$ is the liquid phase density, $\mathit{\alpha }$ is the void fraction.

The void fraction $\mathit{\alpha }$ is calculated using the following formula:

$$\mathit{\alpha } = {\displaystyle \frac{\mathit{x}\hspace{0.17em}{\mathit{v}}_{\mathit{g}}}{\mathit{x}\hspace{0.17em}{\mathit{v}}_{\mathit{g}} + (1-\mathit{x})\hspace{0.17em}{\mathit{v}}_{\mathit{l}}}}$$

(6)

where $\mathit{x}$ is the vapor quality, $\hspace{0.17em}{\mathit{v}}_{\mathit{g}}$ is the specific volume of saturated vapor, ${\mathit{v}}_{\mathit{l}}$ is the specific volume of saturated liquid.

2.2.2. Heat Conduction Model

The unsteady heat conduction process within a thermal structure is described as:

$$\mathit{\rho }\mathit{c}{\displaystyle \frac{\partial \mathit{T}}{\partial \mathit{t}}} = \nabla ·(\mathit{\lambda }\nabla \mathit{T}) + \mathit{S}$$

(7)

where $\mathit{\rho }$ is the density, $\mathit{c}$ is the specific heat capacity, $\mathit{T}$ is the temperature, $\mathit{\lambda }$ is the thermal conductivity, the above all represent the thermophysical properties of thermal component materials, and $\mathit{S}$ is the heat source term.

Three types of boundary conditions for the thermal structure are considered:

• First-kind boundary condition (Dirichlet): The boundary temperature ${\mathit{T}}_{\mathit{f}}$ is a known constant.
• Second-kind boundary condition (Neumann): The heat flux density ${\mathit{q}}_{\mathit{f}}$ at the boundary is specified. A value of zero indicates an adiabatic condition.
• Third-kind boundary condition (Robin): Describes the heat exchange between the boundary and the surrounding fluid by providing the heat transfer coefficient ${\mathit{h}}_{\infty }$ and the fluid temperature ${\mathit{T}}_{\infty }$.

2.2.3. Heat Transfer Model

A single-phase heat transfer model is employed in the code to describe the heat exchange process between the fluid and the surface of thermal structures, which is essential for achieving thermal–hydraulic coupling. This process is illustrated in Figure 2.

The heat transfer between the thermal component and the fluid is described by a simplified engineering model that embodies the empirical Newton’s law of cooling:

$${\mathit{q}}_{\mathit{w}}^{″} = \mathit{h}\left({\mathit{T}}_{\mathit{w}}- \mathit{T}\right)$$

(8)

where ${\mathit{q}}_{\mathit{w}}^{″}$ is the heat flux density at the wall where the thermal component contacts the hydraulic component, h is the convective heat transfer coefficient, ${\mathit{T}}_{\mathit{w}}$ is the wall temperature of the thermal component, and $\mathit{T}$ is the fluid temperature.

h is not a fixed physical property; rather, it depends on fluid properties, flow regime (e.g., forced or natural convection), and geometric configuration. The Nusselt number Nu can be calculated using either empirical correlations from the code’s built-in fluid property library or dedicated heat transfer correlations, and h is then derived inversely from the definition of Nu:

$$\mathit{h} = {\displaystyle \frac{\mathit{Nu}\cdot \mathit{\lambda }}{{\mathit{D}}_{\mathit{h}}}}$$

(9)

where λ is the thermal conductivity of the fluid and ${\mathit{D}}_{\mathit{h}}$ is the hydraulic diameter.

2.3. Numerical Solution Methods

2.3.1. Discretization of Fluid Equations

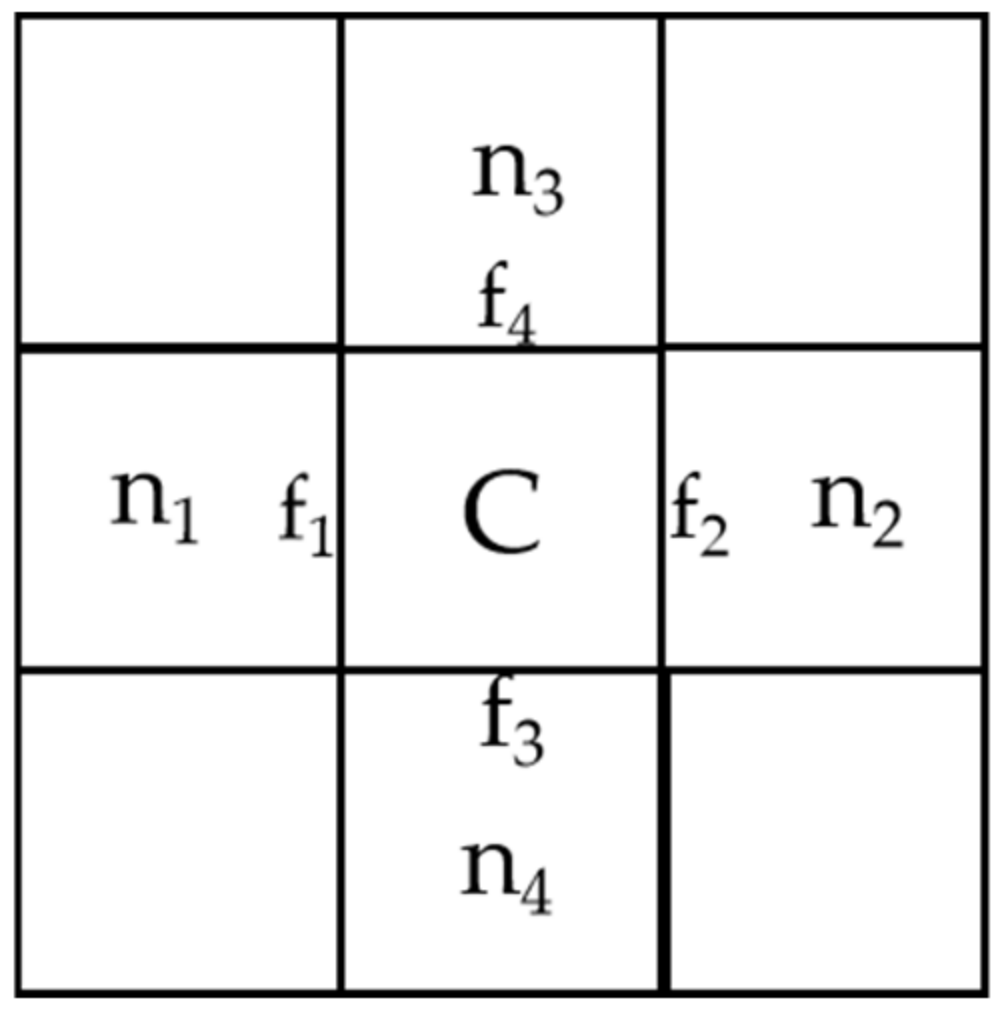
The fluid equations are discretized using the staggered grid finite volume method. Scalar quantities like density, enthalpy (or temperature), and pressure are solved at the center of the grid cells, while velocity is solved at the junctions between grid cells. A schematic of the grid division is shown in Figure 3.

The mass and energy equations are discretized for the control volume j. The momentum equation is discretized at the j + 1/2 junction. A semi-implicit scheme is used for the discretization of the control equations.

Discretizing and simplifying the mass equation yields:

$${\mathit{\rho }}_{\mathit{j}}^{\mathit{n}+1} = {\mathit{\rho }}_{\mathit{j}}^{\mathit{n}} - {\displaystyle \frac{\Delta \mathit{t}}{\Delta \mathit{z}}}\left({\mathit{\rho }}_{\mathit{j}+1/2}^{\mathit{n}}{\mathit{v}}_{\mathit{j}+1/2}^{\mathit{n}+1} - {\mathit{\rho }}_{\mathit{j}-1/2}^{\mathit{n}}{\mathit{v}}_{\mathit{j}-1/2}^{\mathit{n}+1}\right)$$

(10)

Differencing and simplifying the momentum equation gives:

$${\mathit{v}}_{\mathit{j}+1/2}^{\mathit{n}+1} = {\mathit{v}}_{\mathit{j}+1/2}^{\mathit{n}} + {\displaystyle \frac{\Delta \mathit{t}}{\Delta \mathit{z}{\mathit{\rho }}_{\mathit{j}+1/2}^{\mathit{n}}}} \times \left({\mathit{p}}_{\mathit{j}}^{\mathit{n}+1}-{\mathit{p}}_{\mathit{j}+1}^{\mathit{n}+1}\right) + {\displaystyle \frac{\Delta \mathit{t}}{\Delta \mathit{z}}}{\mathit{v}}_{\mathit{j}+1/2}^{\mathit{n}} \times \left({\mathit{v}}_{\mathit{j}}^{\mathit{n}}-{\mathit{v}}_{\mathit{j}+1}^{\mathit{n}}\right)-\Delta \mathit{t}\cdot \mathit{g}\mathit{sin}\mathit{\theta }-{\displaystyle \frac{\Delta \mathit{t}}{{\mathit{\rho }}_{\mathit{j}+1/2}^{\mathit{n}}}} \times {\mathit{F}}_{\mathit{w}}$$

(11)

Discretizing the energy conservation equation results in:

$${\left(\mathit{\rho }\mathit{h}\right)}_{\mathit{j}}^{\mathit{n}+1}-{\left(\mathit{\rho }\mathit{h}\right)}_{\mathit{j}}^{\mathit{n}}+{\displaystyle \frac{\Delta \mathit{t}}{\Delta \mathit{z}}}\left[{\left(\mathit{\rho }\mathit{h}\right)}_{\mathit{j}+1/2}^{\mathit{n}}{\mathit{v}}_{\mathit{j}+1/2}^{\mathit{n}+1}-{\left(\mathit{\rho }\mathit{h}\right)}_{\mathit{j}-1/2}^{\mathit{n}}{\mathit{v}}_{\mathit{j}-1/2}^{\mathit{n}+1}\right]-\left({\mathit{p}}_{\mathit{j}}^{\mathit{n}+1}- {\mathit{p}}_{\mathit{j}}^{\mathit{n}}\right)- \Delta \mathit{t}\cdot {\mathit{q}}_{\mathit{j}}^{\mathit{n} }- \Delta \mathit{t}\cdot {\mathit{v}}_{\mathit{j}}^{\mathit{n}}\cdot {\displaystyle \frac{\left({\mathit{p}}_{\mathit{j}+1/2}^{\mathit{n}}- {\mathit{p}}_{\mathit{j}-1/2}^{\mathit{n}}\right)}{\Delta \mathit{z}}} - \Delta \mathit{t}\cdot {\mathit{v}}_{\mathit{j}}^{\mathit{n}}\cdot {\mathit{F}}_{\mathit{w}}^{\mathit{n}}= 0$$

(12)

Substituting the discretized mass Equation (8) and momentum Equation (9) into the energy Equation (10) gives:

$$\mathit{f}({\mathit{p}}_{\mathit{j}-1},{\mathit{p}}_{\mathit{j}},{\mathit{p}}_{\mathit{j}+1}) = 0$$

(13)

Finally, a system of non-linear equations is obtained that depends only on the control volume pressures. Let the left side of Equation (11) be denoted as E_j. The Newton-Raphson method [20] is used to solve this system of equations:

$${{\displaystyle \frac{\partial {\mathit{E}}_{\mathit{j}}}{\partial {\mathit{p}}_{\mathit{j}-1}^{\mathit{n}+1}}}}^{\left(\mathit{k}\right)}\mathit{\delta }{\mathit{p}}_{\mathit{j}-1} + {{\displaystyle \frac{\partial {\mathit{E}}_{\mathit{j}}}{\partial {\mathit{p}}_{\mathit{j}}^{\mathit{n}+1}}}}^{\left(\mathit{k}\right)}\mathit{\delta }{\mathit{p}}_{\mathit{j}} + {{\displaystyle \frac{\partial {\mathit{E}}_{\mathit{j}}}{\partial {\mathit{p}}_{\mathit{j}+1}^{\mathit{n}+1}}}}^{\left(\mathit{k}\right)}\mathit{\delta }{\mathit{p}}_{\mathit{j}+1} +{ \mathit{E}}_{\mathit{j}}^{\left(\mathit{k}\right)} = 0$$

(14)

After obtaining the pressure changes $\mathit{\delta }{\mathit{p}}_{\mathit{j}-1}$, $\mathit{\delta }{\mathit{p}}_{\mathit{j}}$, $\mathit{\delta }{\mathit{p}}_{\mathit{j}+1}$, taking ${\mathit{p}}_{\mathit{j}}$ as an example, the pressure for the k + 1 iteration is updated as follows

$${\mathit{p}}_{\mathit{j}}^{\left(\mathit{k}+1\right)}={ \mathit{p}}_{\mathit{j}}^{\left(\mathit{k}\right)}+\mathit{\delta }{\mathit{p}}_{\mathit{j}}$$

(15)

By substituting the final calculated pressure values into the mass, momentum, and state equations, other quantities such as control volume density, junction velocity, control volume specific enthalpy, fluid temperature, and void fraction can be obtained.

2.3.2. Discretization of Heat Conduction Equation

A two-dimensional grid system is used for thermal structures, with its mesh structure shown in Figure 4. The interfaces between grid cells in the thermal structure are divided into internal interfaces and boundary interfaces, with the latter corresponding to the three types of boundary conditions.

Taking control volume C as an example, the heat conduction equation is discretized using a fully implicit scheme, forming a system of linear equations for temperature.

When control volume C is an internal control volume, i.e., all four sides are internal interfaces, the discretized heat conduction equation is:

$$\left({\displaystyle \frac{\mathit{\rho }\mathit{c}\mathit{\delta }\mathit{\tau }}{\mathit{\delta }\mathit{t}}} +\sum _{\mathit{i}=1}^4{\displaystyle \frac{{\mathit{s}}_{\mathit{fi}}{\mathit{\lambda }}_{\mathit{fi}}}{\mathit{\delta }{\mathit{x}}_{\mathit{fi}}}}\right){\mathit{T}}^1-\sum _{\mathit{i},\mathit{n}=1}^4{\displaystyle \frac{{\mathit{s}}_{\mathit{fi}}{\mathit{\lambda }}_{\mathit{fi}}}{\mathit{\delta }{\mathit{x}}_{\mathit{fi}}}}{\mathit{T}}_{\mathit{n}}^1 = \mathit{S}\mathit{\delta }\mathit{\tau } + {\displaystyle \frac{\mathit{\rho }\mathit{c}\mathit{\delta }\mathit{\tau }}{\mathit{\delta }\mathit{t}}}\mathit{T}$$

(16)

For the first-kind boundary condition, assuming f₁ is the boundary surface with temperature ${\mathit{T}}_{\mathit{f}1}$, the discretized equation is:

$$\left({\displaystyle \frac{\mathit{\rho }\mathit{c}\mathit{\delta }\mathit{\tau }}{\mathit{\delta }\mathit{t}}} +\sum _{\mathit{i}=2}^4{\displaystyle \frac{{\mathit{s}}_{\mathrm{fi}}{\mathit{\lambda }}_{\mathrm{fi}}}{\mathit{\delta }{\mathit{x}}_{\mathrm{fi}}}} + {\displaystyle \frac{{\mathit{s}}_{\mathit{f}1}{\mathit{\lambda }}_{\mathit{f}1}}{\mathit{\delta }{\mathit{x}}_{\mathit{f}1}}}\right){\mathit{T}}^1-\sum _{\mathit{i},\mathit{n}=2}^4{\displaystyle \frac{{\mathit{s}}_{\mathrm{fi}}{\mathit{\lambda }}_{\mathrm{fi}}}{\mathit{\delta }{\mathit{x}}_{\mathrm{fi}}}}{\mathit{T}}_{\mathit{n}}^1 = \mathit{S}\mathit{\delta }\mathit{\tau }+{\displaystyle \frac{\mathit{\rho }\mathit{c}\mathit{\delta }\mathit{\tau }}{\mathit{\delta }\mathit{t}}}\mathit{T} + {\displaystyle \frac{{\mathit{s}}_{\mathit{f}1}{\mathit{\lambda }}_{\mathit{f}1}{\mathit{T}}_{\mathit{f}1}}{\mathit{\delta }{\mathit{x}}_{\mathit{f}1}}}$$

(17)

For the second-kind boundary condition, assuming f₁ is the boundary surface with heat flux ${\mathit{q}}_{\mathit{f}1}$, the discretized equation is:

$$\left({\displaystyle \frac{\mathit{\rho }\mathit{c}\mathit{\delta }\mathit{\tau }}{\mathit{\delta }\mathit{t}}} +\sum _{\mathit{i}=2}^4{\displaystyle \frac{{\mathit{s}}_{\mathrm{fi}}{\mathit{\lambda }}_{\mathrm{fi}}}{\mathit{\delta }{\mathit{x}}_{\mathrm{fi}}}}\right){\mathit{T}}^1 -\sum _{\mathit{i},\mathit{n}=2}^4{\displaystyle \frac{{\mathit{s}}_{\mathrm{fi}}{\mathit{\lambda }}_{\mathrm{fi}}}{\mathit{\delta }{\mathit{x}}_{\mathrm{fi}}}}{\mathit{T}}_{\mathit{n}}^1 = \mathit{S}\mathit{\delta }\mathit{\tau }+{\displaystyle \frac{\mathit{\rho }\mathit{c}\mathit{\delta }\mathit{\tau }}{\mathit{\delta }\mathit{t}}}\mathit{T} + {\mathit{q}}_{\mathit{f}1}{\mathit{s}}_{\mathit{f}1}$$

(18)

For the third-kind boundary condition, assuming f₁ is the boundary surface, with external fluid temperature ${\mathit{T}}_{\infty }$, and convective heat transfer coefficient ${\mathit{h}}_{\infty }$:

$$\left({\displaystyle \frac{\mathit{\rho }\mathit{c}\mathit{\delta }\mathit{\tau }}{\mathit{\delta }\mathit{t}}} + \sum _{\mathit{i}=2}^4{\displaystyle \frac{{\mathit{s}}_{\mathrm{fi}}{\mathit{\lambda }}_{\mathrm{fi}}}{\mathit{\delta }{\mathit{x}}_{\mathrm{fi}}}} + {\displaystyle \frac{{\mathit{s}}_{\mathit{f}1}{\mathit{\lambda }}_{\mathit{f}1}{\mathit{h}}_{\infty }}{\left(\mathit{\delta }{\mathit{x}}_{\mathit{f}}{\mathit{h}}_{\infty }+{\mathit{\lambda }}_{\mathit{f}1}\right)}}\right){\mathit{T}}^1 -\sum _{\mathit{i},\mathit{n}=2}^4{\displaystyle \frac{{\mathit{s}}_{\mathrm{fi}}{\mathit{\lambda }}_{\mathrm{fi}}}{\mathit{\delta }{\mathit{x}}_{\mathrm{fi}}}}{\mathit{T}}_{\mathit{n}}^1 = \mathit{S}\mathit{\delta }\mathit{\tau } + {\displaystyle \frac{\mathit{\rho }\mathit{c}\mathit{\delta }\mathit{\tau }}{\mathit{\delta }\mathit{t}}}\mathit{T} + {\displaystyle \frac{{\mathit{s}}_{\mathit{f}1}{\mathit{\lambda }}_{\mathit{f}1}{\mathit{h}}_{\infty }{\mathit{T}}_{\infty }}{\left(\mathit{\delta }{\mathit{x}}_{\mathit{f}}{\mathit{h}}_{\infty }+{\mathit{\lambda }}_{\mathit{f}1}\right)}}$$

(19)

where ρ is the nodal density, δτ is the nodal volume, S is the nodal volumetric power density, δx is the nodal length, λ is the nodal thermal conductivity, T is the nodal temperature, ${\mathit{s}}_{\mathit{f}}$ is the interface area, ${\mathit{\lambda }}_{\mathit{f}}$ is the interface thermal conductivity, and $\mathit{\delta }{\mathit{x}}_{\mathit{f}}$ is the interface length.

The coefficient matrix for temperature is constructed based on Equations (16) to (19). It is necessary to traverse every node and determine the coefficients of its corresponding equation based on the type of each of its interfaces, placing them into the appropriate positions in the coefficient matrix and source vector.

Ultimately, the following standard form is obtained:

$${\mathit{a}}_{\mathit{c}}{\mathit{T}}_{\mathit{c}} -\sum _{\mathit{nb}}{\mathit{a}}_{\mathit{nb}}{\mathit{T}}_{\mathit{nb}} = \mathit{b}$$

(20)

where T_c is the temperature of the central node, T_nb is the temperature of its neighboring nodes, a_c is the diagonal element of the coefficient matrix, −a_nb is the off-diagonal element of the coefficient matrix, and b is the source vector. This linear system is solved using a direct method, requiring no iteration.

2.4. Solution Procedure

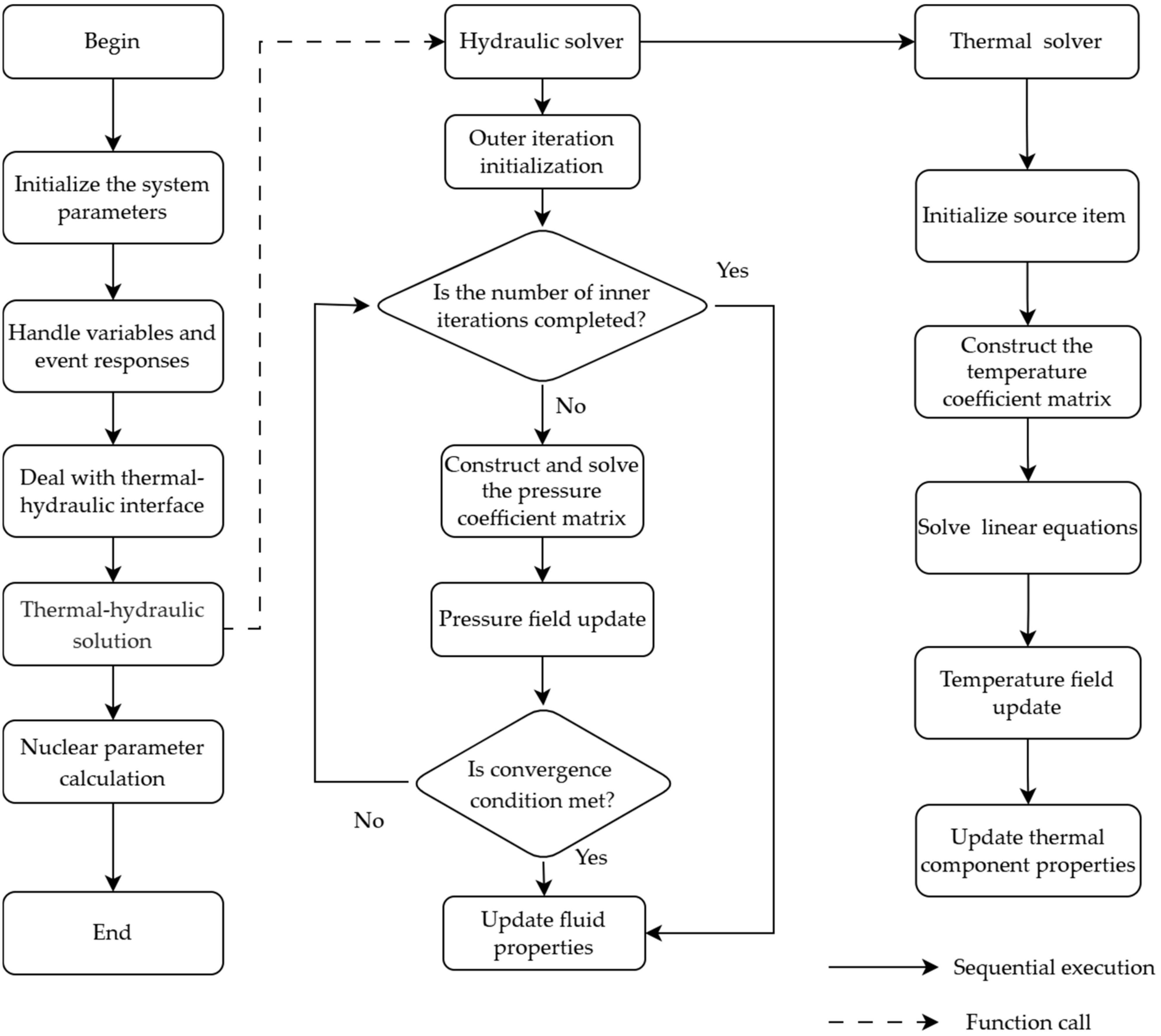
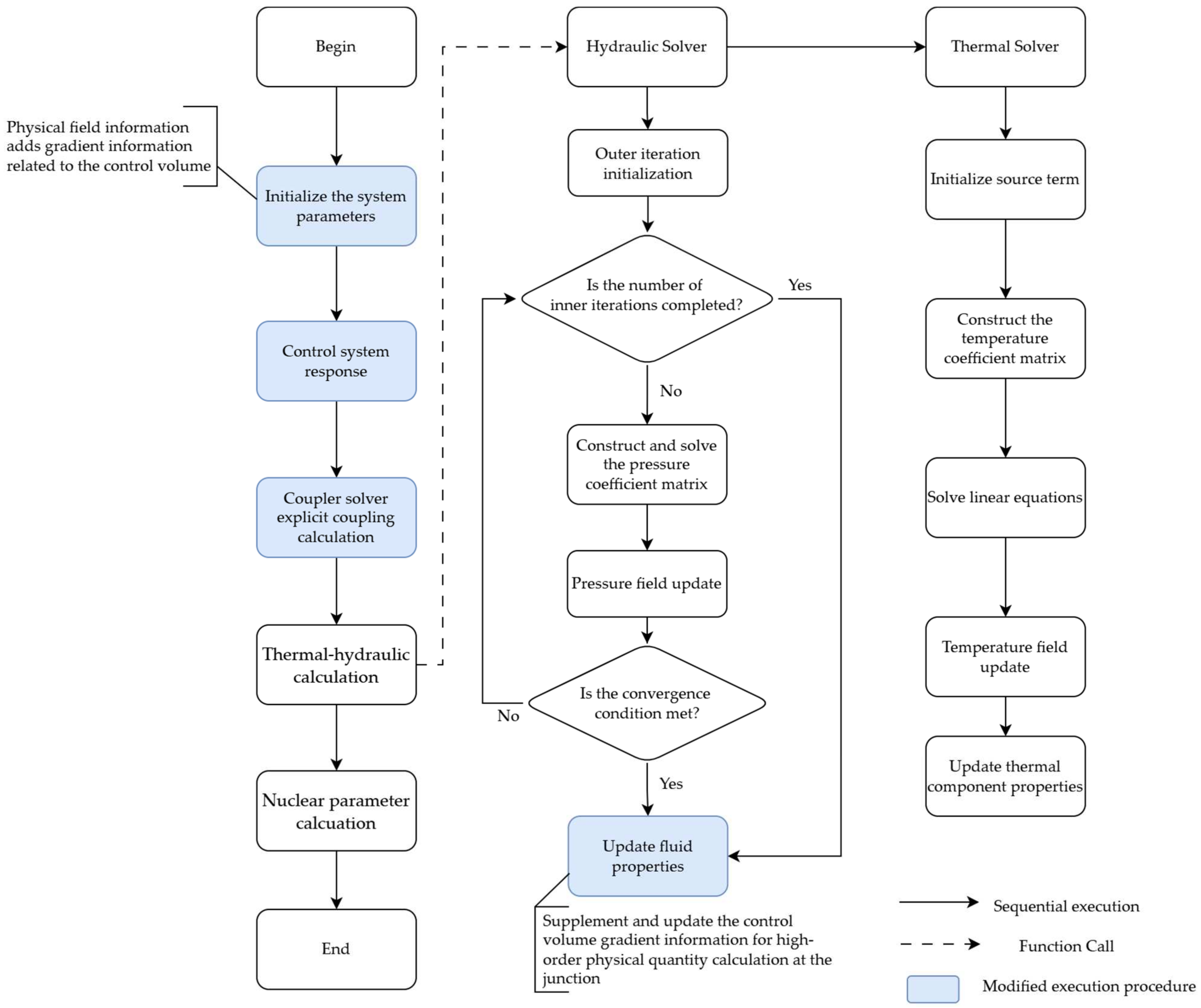
The main solution procedure of the program is shown in Figure 5, where the thermal–hydraulic calculation provides detailed subroutine call information.

After the program starts, it first initializes various system parameters, such as system configuration information, material information, and solver information. Before calculation, event handling is performed to determine if any event meeting the trigger conditions has occurred, modifying the physical field properties of the triggered objects. Next, the thermal–hydraulic interface heat transfer process is handled; this process explicitly treats the thermal power generated by convective heat transfer as an external heat source for the fluid and updates the boundary values of the third-kind boundary conditions on the thermal component surfaces coupled with the fluid.

After handling the above processes, the hydraulic solver subroutine is called to solve the pressure non-linear system, and the thermal solver is called to solve the temperature linear system.

The hydraulic solver involves outer and inner iteration processes. Outer iteration initialization calculates the source terms needed for solving the pressure matrix, including calculating the control volume frictional resistance, then averaging to obtain the junction frictional resistance based on the calculated control volume friction; calculating local frictional resistance, involving four types: sudden enlargement, sudden contraction, bends, and valves; and finally updating inter-grid heat conduction for the fluid. The inner iteration constructs the pressure coefficient matrix and uses the Newton-Raphson method [20] to iteratively solve and update pressure values. The inner iteration process ends when the residual meets the convergence criterion or the maximum number of inner iterations is reached. The values calculated in the last inner iteration are the results for the new time level. The outer iteration process continues, using the pressure values from the inner iteration to update the fluid properties for the next time level, concluding the outer iteration loop.

Compared to the hydraulic solver, the thermal solver is simpler. It first initializes explicit source terms, then constructs the temperature coefficient matrix. Since the linear system obtained using the fully implicit discretization scheme is solved using a direct method, no iteration is required. The temperature field is updated based on the calculation results, which in turn updates other properties of the thermal components, such as density and specific heat capacity.

After all thermal–hydraulic solvers have completed their calculations, if an update of core reactivity and decay heat power is required, nuclear parameters are further solved by the nuclear solver. First, various reactivity feedback mechanisms—including coolant density feedback, Doppler feedback, fuel axial expansion feedback, cladding axial expansion feedback, and core radial expansion feedback—are evaluated to compute their individual contributions to reactivity, which are then accumulated into the corresponding reactivity terms. Subsequently, a coupled solution of the point kinetics neutron dynamics model and the decay heat model is performed based on the updated total reactivity, yielding key nuclear parameters for the current time step, such as neutron flux density, precursor concentrations for each delayed neutron group, fission product concentrations, and decay heat power fractions.

3. Program Improvement Measures

Long-term engineering applications have revealed FRTAC’s limitations in computational accuracy, efficiency, and usability. Specifically, computational accuracy limitations constrain its capability for high-fidelity analysis of complex accident scenarios. The original first-order numerical scheme introduces significant numerical dissipation, leading to insufficient accuracy in large-scale steady-state convective heat transfer problems. Additionally, inadequate spatial resolution exists; the first-order method exhibits large errors on coarse grids, necessitating grid refinement that substantially increases computational costs. Furthermore, the original 32-bit compilation architecture and data structure create performance bottlenecks when handling large-scale problems, while the fragmented functional design increases user modeling complexity and hinders subsequent maintenance and functional expansion. To address these specific shortcomings, this study implemented targeted improvements in both system architecture and computational methods.

3.1. Improvement of System Architecture

System architecture improvements considered program user-friendliness, scalability, maintainability, and computational efficiency enhancement. Specific improvements include:

• Compilation Architecture Upgrade: Upgraded the program from a 32-bit to a 64-bit compilation architecture, breaking the original memory addressing space limitations. This enables the program to handle larger-scale, more refined models, enhances execution speed for data-intensive computations, and improves compatibility with modern operating systems.
• Separation of Physical and Configuration Data: Decoupled dynamically changing physical field information (e.g., temperature, pressure) during iterative solving from static configuration information (e.g., component indices, connection relationships), storing them separately in dedicated global arrays and static structures. This enables direct memory access for physical variables, reducing inefficient queries during computation and boosting performance.
• Functional Architecture Refactoring: The original control logic and component interfaces were fragmented across different modules, making complex scenario setup cumbersome and hindering maintenance. The architecture was refactored into three unified systems:
  • Unified Control System: Refactored Hydraulic Structure, Variables, and Events from the System Module into a Control System. Correspondingly, merged Event Interface, Hydraulic Element Interface, and Thermal Element Interface from the Solver Module into a Control Solver. This integrates original event handling and variable control functions, forming centralized control logic and simplifying the user workflow for setting up complex scenarios.
  • Unified Coupling Solver: Refactored Thermal Element Interface and Thermal-Thermal Interface into a Coupler Solver. This consolidates all heat transfer processes (including thermal–hydraulic convective heat transfer and conduction between thermal components) into a unified coupling solver, clarifying the coupling logic.
  • Unified Mesh System: With physical field information stripped out, the mesh system contains only configuration information. A unified mesh data structure was designed for both hydraulic and thermal components, simplifying model construction and information transfer.
• More Efficient Serialization Module: Replaced the original custom JSON parser with the high-performance open-source library nlohmann/json to improve input file processing efficiency and usability. Added JSON Optimizer and JSON Operator functional components to preprocess model information during deserialization, further reducing initialization time.

The refactored FRTAC functional architecture is shown in Figure 6.

3.2. Computational Method Improvements

For the density (ρ), pressure (p), and the product of density and specific enthalpy (ρ·h) at hydraulic junctions, the original program used first-order upwind interpolation. To enhance the discretization accuracy of convection terms, a second-order extension of the first-order upwind scheme was implemented. As higher-order schemes can cause numerical oscillations, improving numerical accuracy must be balanced with computational stability. The computational method improvement involves adopting a second-order accurate discretization scheme combined with a limiter for interpolating junction physical quantities. For unified representation, $\mathit{\varphi }$ denotes these physical quantities.

Taking junction j + 1/2 in the mesh division of Figure 3 as an example, the second-order discretization scheme with a limiter is as follows:

$${\mathit{\varphi }}_{\mathit{j}+1/2} = \left\{\begin{array}{cc}{\mathit{\varphi }}_{\mathit{j}} + \mathit{\psi }({\mathit{r}}_{\mathit{j},\mathit{j}+1})\cdot (\nabla \mathit{\varphi }{)}_{\mathit{j}}\cdot {\displaystyle \frac{\Delta \mathit{z}}{2}}& \left({\mathit{v}}_{\mathit{j}+{\displaystyle \frac{1}{2}}} \ge 0\right)\\ {\mathit{\varphi }}_{\mathit{j}+1} - \mathit{\psi }({\mathit{r}}_{\mathit{j},\mathit{j}+1})\cdot (\nabla \mathit{\varphi }{)}_{\mathit{j}+1}\cdot {\displaystyle \frac{\Delta \mathit{z}}{2}}& \left({\mathit{v}}_{\mathit{j}+{\displaystyle \frac{1}{2}}} < 0\right)\end{array}\right.$$

(21)

where $\mathit{\psi }\left({\mathit{r}}_{\mathit{j},\mathit{j}+1}\right)$ is the limiter. Its function is to maintain second-order accuracy in smooth flow regions while degrading to first-order accuracy in regions containing extrema of $\mathit{\varphi }$ to avoid numerical oscillations. $\mathit{\psi }\left({\mathit{r}}_{\mathit{j},\mathit{j}+1}\right)$ is expressed as:

$${\mathit{\psi }(\mathit{r}}_{\mathit{j},\mathit{j}+1}) = \left\{\begin{array}{c}\begin{array}{cc}1& \left({\mathit{r}}_{\mathit{j},\mathit{j}+1\ge 0}\right)\end{array}\\ \begin{array}{cc}0& \left({\mathit{r}}_{\mathit{j},\mathit{j}+1<0}\right)\end{array}\end{array}\right.$$

(22)

where ${\mathit{r}}_{\mathit{j},\mathit{j}+1}$ measures whether the change in $\mathit{\varphi }$ at junction j + 1/2 is smooth, i.e., whether an extremum point of $\mathit{\varphi }$ exists between control volumes j and j + 1. Its calculation process is: First, determine the upwind control volume based on the fluid flow direction at junction j + 1/2, assumed to be control volume j. Pre-calculate the second-order accurate flux ${\mathit{\varphi }}_{\mathit{j}+1/2}^{\left(2\right)}$ according to Equation (19). The expression for ${\mathit{r}}_{\mathit{j},\mathit{j}+1}$ is:

$${\mathit{r}}_{\mathit{j},\mathit{j}+1} = \left({\mathit{\varphi }}_{\mathit{j}+1/2}^{\left(2\right)} - {\mathit{\varphi }}_{\mathit{j}}\right) \times \left({\mathit{\varphi }}_{\mathit{j}+1} - {\mathit{\varphi }}_{\mathit{j}+1/2}^{\left(2\right)}\right)$$

(23)

Additionally, the physical field information needs to be supplemented with gradient information corresponding to the control volume. The calculation expression is:

$$\nabla \mathit{\varphi } = {\displaystyle \frac{1}{\mathit{V}}}\sum _{\mathit{f}\in \mathit{in}}\left(\mathit{sign}\left({\mathit{v}}_{\mathit{f}}\right)\cdot {\mathit{\varphi }}_{\mathit{f}}\cdot {\mathit{A}}_{\mathit{f}}\right) - {\displaystyle \frac{1}{\mathit{V}}}\sum _{\mathit{f}\in \mathit{out}}\left(\mathit{sign}\left({\mathit{v}}_{\mathit{f}}\right)\cdot {\mathit{\varphi }}_{\mathit{f}}\cdot {\mathit{A}}_{\mathit{f}}\right)$$

(24)

where ${\mathit{\varphi }}_{\mathit{f}}$ is the value of the physical quantity $\mathit{\varphi }$ on the junction connected to the control volume, V is the volume of control volume, ${\mathit{A}}_{\mathit{f}}$ is the junction area, and ${\mathit{v}}_{\mathit{f}}$ is the fluid velocity on the junction. sign(${\mathit{v}}_{\mathit{f}}$) is the sign function of the velocity ${\mathit{v}}_{\mathit{f}}$, used to calculate the net change in the physical quantity.

3.3. Solution Procedure Update

The updated solution procedure is shown in Figure 7.

To accommodate the above improvements, the original solution procedure was updated. Main changes include: adding initialization of gradient fields and new data structures during the initialization phase; updating the original event handling to respond to the unified control system; updating the thermal–hydraulic interface calculation to invoke the unified coupling solver; and adding steps for updating gradient fields and higher-order fluxes after the hydraulic solver iteration completes.

4. Program Validation

4.1. Computational Stability Validation: Edwards Blowdown Experiment

The Edwards blowdown experiment [21] was selected to validate the numerical stability of the improved method. It simulates the instantaneous rupture of a high-temperature, high-pressure water-filled pipe and features a simple geometry, well-defined boundary conditions and high-fidelity transient pressure data during rapid depressurization. It is therefore commonly used in recent studies as a reference case for assessing numerical approaches to simulate blowdown behavior in blowdown piping [22,23,24]. The experiment effectively tests whether the method maintains numerical stability under severe transient conditions. The experimental parameters are summarized in

Table 1. Parameter settings for Edwards blowdown experiment.

Parameter Name	Parameter Name
Pipe Length (m)	4.09
Pipe Area (m2)	1.0956 × 10−4
Break Area (m2)	0.95317 × 10−4
Initial Temperature (°C)	228.85
Initial Pressure (MPa)	7

.

Referencing the modeling approach used by Carlson et al. with the RELAP5 program [25] for simulating the experiment, the model employed a 4.09 m hydraulic component pipe to simulate the test pipe. Initial pressure was 7 MPa, temperature was 228.85 °C, divided into 20 control volumes. The local friction coefficient of the outlet junction of the last control volume was set to simulate the break. A pressure boundary condition (TDV) was used to simulate the environment with a pressure of 0.1 MPa and temperature of 20 °C. The model mesh division is shown in Figure 8.

Figure 9 shows the transient pressure variations at different locations in the pipe. Figure 9a, Figure 9b and Figure 9c, respectively, show the transient pressure changes within 0.5 s at the pipe break head location (GS1), the pipe tail location (GS7), and the middle location (control volume 7, instrument position GS5). The comparison plots for the break head and tail locations include transient pressure changes within 0.02 s.

From Figure 9a, it can be seen that the pressure at the break end drops rapidly at the instant of rupture, decreasing to around 2.4 MPa within a very short time. The simulated pressure drop speed is faster than the measured experimental drop speed, mainly because the program simulates ideal test conditions, whereas friction and measurement errors exist in the actual experiment. From Figure 9b, it can be seen that the calculated pressure wave propagation speed is faster than the experimental value. Furthermore, when the pressure wave reaches the tail in the experiment, the tail pressure oscillates up and down within an extremely short time. Since this pressure undershoot process occurs only during a very short transient period, its impact on long-term calculations is minimal. For the long-term calculation results, Figure 9a–c show that the pressure change trend simulated by the FRTAC program after the break is basically consistent with the experimental measurements, with the best simulation effect at the middle observation location (GS5).

It can be seen that the numerical results from both schemes agree reasonably well with the experimental values, correctly predicting the pressure change trend of the Edwards blowdown experiment. Although the original first-order numerical scheme is unconditionally stable, the improved calculation results show no numerical oscillations or even divergence, indicating that the improved numerical method maintains good stability when calculating such problems with severe transients.

The adaptivity of the numerical scheme was also quantitatively validated during the experiment. The average usage rate of the second-order scheme throughout the transient calculation was 66.84%. This key indicator indicates that when faced with the steep pressure gradient generated instantaneously at the break, the limiter in the scheme was effectively activated, causing the scheme to adaptively degrade from second-order to the more stable first-order upwind scheme, thereby successfully suppressing numerical oscillations and ensuring computational stability. This dynamic adaptability is the core mechanism enabling the new module to balance stability and accuracy in complex transient calculations, demonstrating its good applicability.

To quantitatively assess the impact of program optimization on computational efficiency, it is essential to minimize the influence of environmental fluctuations—such as CPU resource contention from background processes, transient memory scheduling delays, and other stochastic factors—on measured execution times. In this study, all simulations were conducted under identical hardware and software conditions. Five consecutive runs were performed for each of the three test cases: Original Program-First Order, Improved Program-First Order, and Improved Program-Second Order. The average computation time for each case was recorded, and the results are presented in

Table 2. Program running time comparison for the Edwards Blowdown Experiment.

Test Object	Calculation Time (ms)					Average Calculation Time (ms)
Original program-First Order	417.0	441.0	431.0	466.0	427.0	436.4
Improved program-First Order	390.0	366.0	366.0	381.0	387.0	378.0
Improved program-Second Order	403.0	376.0	385.0	385.0	383.0	386.4

.

From Table 2, it can be seen that the efficiency of the improved program is significantly enhanced. System architecture improvements alone (both using first-order schemes) reduced the average calculation time from 436.4 ms to 378.0 ms, a reduction of 13.4%. The second-order method in the improved program is slightly slower than the first-order method, but the difference is small, incurring only about 2.2% additional computational overhead.

4.2. Computational Accuracy Validation: ETEC Steam Generator Steady-State Experiment

To validate the accuracy of the new module in steady-state convective heat transfer problems, the steady-state test of the ETEC once-through steam generator [26] was selected. This evaluated the advantages of the improved numerical method in suppressing numerical dissipation and enhancing prediction accuracy, and assessed the impact of introducing thermal–hydraulic coupling calculations on computational efficiency. The basic design parameters of the ETEC once-through steam generator are shown in

Table 3. Basic design parameters of the ETEC steam generator.

Component Name	Parameter Name	Value
Sodium Side	Flow Rate (kg·s−1)	114.01
	Inlet Temperature (°C)	502.45
	Hydraulic Diameter (m)	0.52
Water Side	Flow Rate (kg·s−1)	0.0411355
	Inlet Temperature (°C)	205.75
	Inlet Pressure (MPa)	14.1819
Heat Transfer Tube	Length (m)	14.021
	Number of Tubes	757
	Inner/Outer Diameter (m)	0.10338/0.015875

.

To reduce modeling errors and enable a clearer assessment of numerical accuracy, the A7 operating condition was selected. It features a high flow velocity and produces fully superheated steam, both of which ensure good validity of the homogeneous equilibrium model. The controlled parameters for A7 are given in

Table 4. Controlled Parameters for the A7 Operating Condition.

Water Side			Sodium Side
Flow Rate (kg·s−1·Tube)	Inlet Temp. (°C)	Inlet Pressure (MPa)	Flow Rate (kg·s−1·Tube)	Inlet Temp. (°C)
0.057099	283.15	14.3171	0.539456	456.75

.

Before formal calculation, a grid independence study was performed. Three different mesh resolutions were employed for the hydraulic component: a coarse mesh with 30 control volumes, a medium mesh with 60 control volumes, and a fine mesh with 90 control volumes. Identical solver parameters were used for all cases. To ensure that steady-state conditions were fully achieved, each simulation was run for 1200 s. The results of the grid independence verification for both the original first-order and the improved second-order numerical schemes are summarized in

Table 5. Grid independence verification results.

Order	Outlet Temperature	Number of Control Volumes			Relative Deviation
		30	60	90	30 → 60	60 → 90
First-Order	Sodium Side (°C)	322.64	321.57	321.10	0.33%	0.15%
	Water Side (°C)	369.68	372.36	373.57	0.72%	0.32%
Second-Order	Sodium Side (°C)	321.10	320.84	320.76	0.08%	0.02%
	Water Side (°C)	374.43	375.10	375.23	0.18%	0.03%

.

A relative deviation threshold of 0.5% between successive grid refinements was adopted as the convergence criterion for grid independence. Given that the code requires identical grid resolutions on both the sodium and water sides, the first-order numerical scheme required 60 control volumes to achieve grid independence, whereas the second-order scheme satisfied the same criterion with only 30 control volumes. This demonstrates that the second-order method exhibits significantly faster grid convergence. Its higher-order discretization effectively reduces truncation error and diminishes sensitivity to grid resolution, enabling high-fidelity predictions even on coarser meshes.

On the premise of ensuring computational accuracy, to conduct a fair comparison of the computational efficiency between the two numerical schemes, all cases adopt the same mesh resolution: the hydraulic component is discretized into 60 control volumes, while the thermal component uses a mesh of 5 × 60 (radial × axial) control volumes.

The formula for calculating the relative deviation of the hydraulic component outlet temperature is defined as follows for comparing the computational deviation of different numerical methods:

$$\mathit{RD} = {\displaystyle \frac{{\mathit{T}}_{\mathit{calculated},\mathit{out}}-{\mathit{T}}_{\mathit{measured},\mathit{out}}}{{\mathit{T}}_{\mathit{measured},\mathit{out}}-{\mathit{T}}_{\mathit{measured},\mathit{in}}}} \times 100\%$$

(25)

where $\mathit{RD}$ is the relative deviation, ${\mathit{T}}_{\mathit{calculated},\mathit{out}}$ is the calculated fluid outlet temperature, ${\mathit{T}}_{\mathit{measured},\mathit{out}}$ is the measured fluid outlet temperature, and ${\mathit{T}}_{\mathit{measured},\mathit{in}}$ is the measured inlet temperature.

Calculating the relative deviation according to Equation (23), the comparison between simulated calculation results and measured values for the sodium and water side outlet temperatures under the A7 condition is shown in

Table 6. Comparison of steady-state experimental and calculation results for ETEC steam generator.

2nd-Order Usage Rate	Sodium Side Outlet Temperature				Water Side Outlet Temperature
	Measured (°C)	Order	Calculated (°C)	RD	Measured (°C)	Order	Calculated (°C)	RD
90.85%	320.95	First-Order	321.57	−0.46%	375.55	First-Order	372.36	−3.56%
		Second-Order	320.84	0.08%		Second-Order	375.10	−0.59%

.

During the calculation process, the usage rate of the second-order scheme reached 90.85%, indicating that in smooth steady-state problems involving flow and temperature fields, the designed second-order scheme can operate in high-precision mode to the maximum extent, consistent with the method’s theoretical design. The second-order scheme also significantly improved computational accuracy, reducing the relative deviation of the water side outlet temperature from −3.56% (first-order) to −0.59%, and the sodium side deviation from −0.46% to 0.08%.

Similarly, the calculation time before and after program improvement was compared. Following the same testing protocol described earlier—under identical operating conditions and solver settings. The average computation time from five consecutive runs was recorded, as shown in

Table 7. Program running time comparison for ETEC Steam Generator Steady-State Experiment.

Test Object	Calculation Time (s)					Average Calculation Time (s)
Original program-First Order	73.47	72.89	73.16	73.16	74.51	73.44
Improved program-First Order	46.81	46.70	46.99	46.43	46.92	46.77
Improved program-Second Order	47.88	47.38	47.65	47.44	47.56	47.58

.

The results in Table 7 further highlight the advantages of the architecture improvements. With increased grid count and the introduction of thermal–hydraulic coupling calculations, the calculation time for the first-order scheme decreased from the original 73.44 s to 46.77 s after improvement, a performance enhancement of 36.32%. The additional computational overhead for the improved second-order scheme was only 1.74%.

5. Conclusions

This study successfully implemented and validated a series of improvement measures targeting FRTAC’s limitations in computational efficiency, accuracy, and usability. The main contributions are summarized as follows:

• System Architecture Optimization: By upgrading to a 64-bit compilation architecture, refactoring functional modules, and optimizing data structures, the program’s computational efficiency (up to 36.1% improvement) and maintainability were significantly enhanced, and user-friendliness was optimized.
• Numerical Method Improvement: A second-order accurate numerical method based on a limiter was designed and implemented, effectively reducing computational dissipation while ensuring computational stability through an adaptive switching strategy. Its computational stability under severe transients was validated in the Edwards blowdown experiment, and its computational accuracy was validated in the ETEC steady-state heat transfer experiment, reducing the prediction deviation of the water side outlet temperature from −3.56% to −0.59%.
• Solution Process Update: The solution process was optimized to efficiently support the new functional architecture and higher-order numerical schemes.

Future work will focus on further refinement of the FRTAC program, particularly supplementing the two-phase flow model. The current program is primarily based on the homogeneous two-phase flow model, limiting its analysis capability for conditions involving two-phase flow. Subsequent research plans to introduce more comprehensive two-phase flow models to expand FRTAC’s applicability in fast reactor system analysis and to extend parallel computing capabilities to improve computational efficiency for complex scenarios. Furthermore, validation and analysis of more typical accident conditions will be conducted to further enhance the reliability and applicability scope of the FRTAC program.