Controller Hardware-in-the-Loop Simulation of SOFC-GT Hybrid System

Abstract

The solid oxide fuel cell–gas turbine (SOFC-GT) hybrid system is confronted with challenges related to system integration and coordinated control. In this study, a Controller Hardware-in-the-Loop Simulation (C-HILS) platform is constructed to validate its digital solutions. The C-HILS platform integrates the Advanced Process Simulation System (APROS), LabVIEW 2020 programming software, NI PXI hardware, and a distributed control system (DCS). Specifically, bidirectional data transmission between the simulation software and the DCS is facilitated through LabVIEW and PXI, leveraging the OLE for Process Control (OPC) protocol and physical Input and Output (I/O) channels. The dynamic SOFC-GT model developed in APROS demonstrates good consistency with design values, with relative errors below 4%. The DCS configuration employs PID controllers to achieve control over total power, SOFC fuel utilization, and gas turbine rotational speed. Experiments under transient conditions reveal that, despite discrepancies in dynamic responses between C-HILS and full-digital simulations, both can achieve stable control. This C-HILS platform effectively integrates virtual models with physical hardware, offering a reliable environment for verifying SOFC-GT control strategies and digital solutions, and thus facilitating the digital transformation of energy systems.

1. Introduction

The global transition toward low-carbon energy systems has spurred intensive research into high-efficiency, low-emission power generation technologies. The solid oxide fuel cell–gas turbine (SOFC-GT) hybrid system has thus emerged as a highly promising solution, integrating the high electrochemical efficiency of SOFCs with the thermodynamic advantages of gas turbines (GTs) [1,2]. Its theoretical efficiency can exceed 70% [3]. Capable of flexibly employing a range of fuels (e.g., hydrogen, natural gas, and biogas) and mitigating greenhouse gas emissions, this hybrid system holds significant importance in distributed power generation and industrial combined heat and power (CHP) applications [4,5].

However, the commercialization of SOFC-GT systems is hindered by challenges in dynamic coordination and stable control [6]. SOFCs are slow-response electrochemical devices, characterized by gradual changes in temperature and electrochemical state, with a time constant ranging from minutes to even hours. In contrast, GTs are fast-response mechanical systems, exhibiting rapid rotational speed and pressure dynamics with a time constant on the order of seconds [7]. The strong coupling between SOFCs and GTs gives rise to complex transient behaviors, including thermal inertia mismatch, pressure fluctuations, and fuel utilization imbalance [8]. These issues compromise system stability during load changes, start-stop cycles, or fuel switching events. Consequently, in-depth research on SOFC-GT hybrid systems—particularly focusing on their control strategies and operational stability—is critical for advancing the technology’s commercialization and enabling the development of future sustainable energy systems.

Since the conceptualization of the SOFC-GT hybrid system, global researchers have conducted extensive studies on its modeling, simulation, and control strategies. Current research on SOFC-GT control primarily relies on two approaches: full digital simulation and physical experimentation. Full digital simulation, leveraging professional simulation software, enables system modeling and control strategy testing under diverse operating conditions with low cost and high flexibility [9]. For instance, Chen et al. developed an SOFC temperature control system based on an adaptive multi-model predictive control (MMPC) approach, where all identified linear models achieved an accuracy exceeding 95% [10]. Wang et al. proposed a novel control method integrating multiple control loops with a coordinated protection loop, which adjusts the transient behavior of operating parameters online to prevent undesirable operational failures [11]. Zhang et al. implemented a 50% load transition within 10 s using a simple yet innovative strategy: during the transition, the power demands of both the SOFC and GT decreased synchronously, while the SOFC anode fuel flow was regulated to maintain fuel utilization, and the cathode inlet air flow and temperature were adjusted to provide thermal protection for the SOFC [12]. To address load disturbances caused by uncertainties, Wang et al. designed a control system combining fuzzy logic theory, temperature feedforward, and online adjustment of coordination factors; this strategy reduced the thermal response time inside the fuel cell stack by nearly 49.97% [13]. Despite their utility for preliminary control algorithm testing, simulation tools often simplify the dynamic characteristics of physical hardware (e.g., sensor delays, actuator nonlinearities) and fail to capture interactions between virtual models and real-world control systems [14]. This discrepancy between simulated and actual system performance limits the reliability of simulation results in scaling up industrial applications.

Physical experiments, conducted on real prototypes, accurately reflect system dynamic responses but suffer from inherent limitations: high costs, prolonged experimental cycles, and elevated risks. These constraints make in-depth studies under transient or fault conditions particularly challenging [15]. Thus, developing a verification platform with both high fidelity and flexibility is essential for the design and optimization of SOFC-GT control strategies. For bridging the gap between full digital simulation and physical experimentation, Hardware-in-the-Loop Simulation (HILS) technology has been developed and applied [16]. In the energy systems domain, HILS has been preliminarily implemented in power generation systems such as wind turbines and fuel cells, demonstrating its feasibility and advantages [17,18,19,20,21].

Controller Hardware-in-the-Loop Simulation (C-HILS) refers to a specific implementation of HILS where the controller functions as the physical entity [22,23]. It enables the integration of a real-world control system into the simulation loop, thereby facilitating the closed-loop validation of control strategies and physical hardware. For example, Wang et al. proposed a dynamic modeling method based on the integration of mass balance and energy balance analyses; this model was connected to a distributed control system (DCS) via the OLE for Process Control (OPC) communication protocol to construct a digital twin of a roaster [24]. Yan et al. focused on a 1000 MW coal-fired power unit, using the Emerson OIF platform as an interface between the DCS and a digital twin platform to develop a multi-scale, multi-dimensional thermal twin of physical equipment [25]. For networked microgrids (NMGs), Kandasamy et al. validated the effectiveness of a DCS under diverse scenarios (e.g., normal operation, communication delays/failures, large-scale systems) via OPAL-RT-based HILS, showing that the DCS outperformed conventional control schemes [26].

SOFC-GT hybrid systems have made substantial progress in modeling, steady-state analysis, and control strategy development. Additionally, institutions such as NETL have established relevant HILS platforms, such as the Hyper facility [27]. However, the construction of such facilities is extremely challenging, resulting in a lack of a platform that can be rapidly established to conduct C-HILS for such systems [28]. The traditional control program development process requires first developing control programs in digital simulation software, followed by porting them to physical controllers. Yet this workflow fails to guarantee the effectiveness after transplantation, and may require multiple rounds of repeated testing to develop an effective control program. This study constructs a C-HILS platform by integrating Advanced Process Simulation Software V6.07 (APROS V6.07), NI LabVIEW 2020 programming software, NI PXI hardware, and the HOLLiAS MACS-FM series DCS. The NI PXI is manufactured by National Instruments, a company headquartered in Austin, TX, USA. The HOLLiAS MACS-FM Series DCS is produced by Hollysys Automation Co., Ltd., with its headquarters located in Hangzhou, Zhejiang Province, China. This platform serves as an auxiliary tool for addressing the challenges of system coupling and control strategy verification in SOFC-GT hybrid systems. It enables the in-depth integration of virtual models with real DCS, allowing the evaluation and testing of system coupling characteristics and control strategies without damaging expensive components, thereby reducing Research and Development (R&D) risks. The main contributions of this paper can be summarized as follows:

(1)

This study presents a rapidly deployable C-HILS platform. By integrating four core components, namely APROS V6.07 software, NI PXI hardware, LabVIEW 2020 software, and a DCS, this platform not only retains the flexibility and safety inherent to digital simulation but also replicates the real dynamic behaviors of physical control hardware (e.g., sensor delays and actuator nonlinearities).

(2)

A dynamic model of the SOFC-GT bottoming cycle hybrid system was established based on APROS, encompassing core components such as the solid oxide fuel cell (SOFC), gas turbine (GT), compressor, and heat exchanger. This model exhibits a steady-state relative error of less than 4%. Three transient experiments were conducted to compare the control performance of C-HILS and full-digital simulation.

(3)

A standardized program for converting between digital parameters and voltage signals is developed based on the NI PXI system. This program not only effectively addresses compatibility issues in cross-device data interaction but also boasts high transferability: it is not dependent on the specific SOFC-GT system, can be directly migrated to other energy systems, and thus provides a universal technical solution for the digital testing of various energy systems.

The remainder of this paper is organized as follows: Section 2 presents the composition of the SOFC-GT hybrid system and the design of the C-HILS platform. Section 3 elaborates on the modeling of key components (e.g., fuel cells, turbines, compressors, and shafting) in APROS. Section 4 describes the DCS configuration, including point configuration, control logic configuration, and human–machine interface (HMI) configuration. Section 5 presents the C-HILS experimental results under transient conditions (e.g., total power reduction, fuel utilization reduction, and GT speed reduction) and compares them with full digital simulation results. Section 6 summarizes the research and proposes future application prospects of the platform.

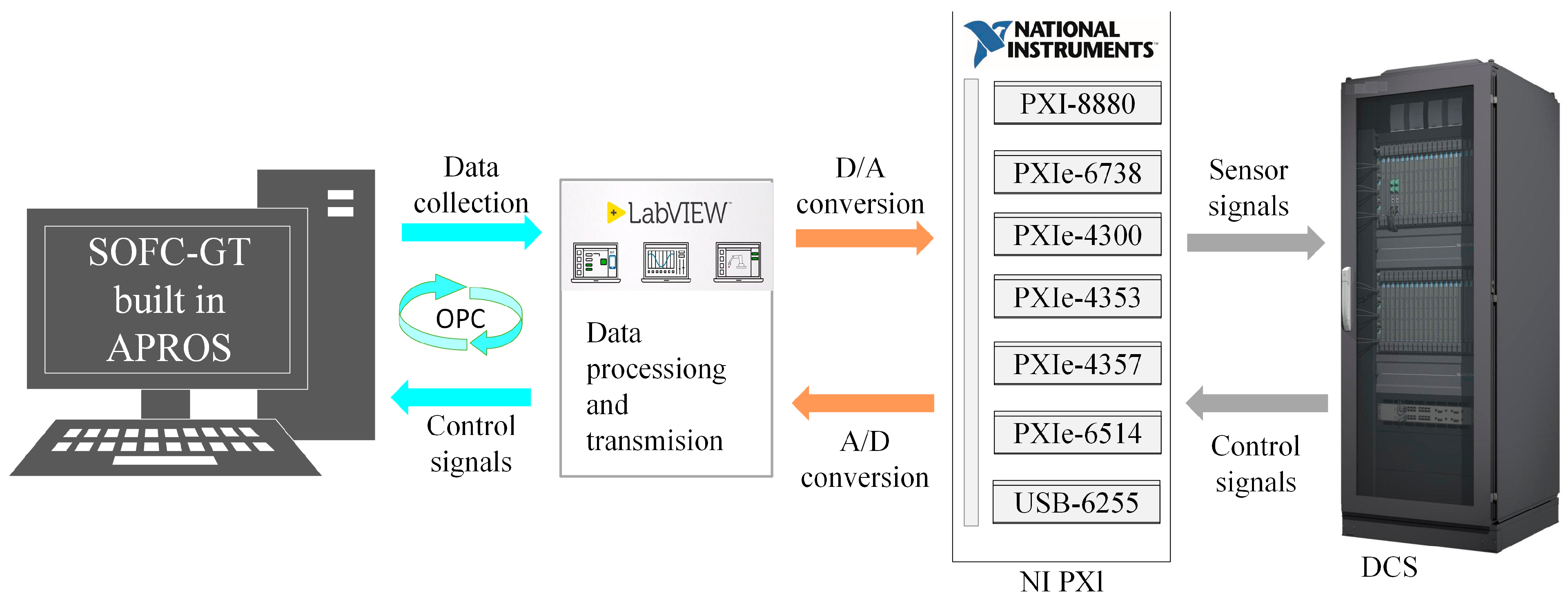
2. C-HILS Platform Description

2.1. Description of the SOFC-GT Hybrid System

The SOFC-GT hybrid system model was constructed using APROS, a modular modeling tool specialized in dynamic modeling and simulation of complex industrial systems. It is widely utilized for system analysis and optimization in fields such as energy, chemical engineering, and power systems, with core features including support for multi-physics coupling, dynamic process simulation, and high modularity and expandability [29]. These capabilities enable accurate modeling of multi-dimensional behaviors in industrial processes, such as thermal-hydraulics, chemical reactions, and electrical system dynamics [30].

APROS software features mature modules for SOFCs, turbines, compressors, and other components, allowing this study to rapidly develop the SOFC-GT hybrid system model. More importantly, it supports the OPC communication protocol and enables real-time simulation, including even faster-than-real-time simulation [31,32,33].

The SOFC-GT bottoming cycle hybrid system investigated in this study is illustrated in Figure 1. Its key components comprise a solid oxide fuel cell, gas turbine (GT), compressor, generator, combustion chamber, and shell-and-tube heat exchanger. The SOFC operates on hydrogen as fuel, which is fed into the anode channel, while oxygen (serving as the oxidant) is supplied to the cathode channel for reaction participation. Exhaust streams from the SOFC anode and cathode are directed to the afterburner for secondary combustion. The resulting combustion gases first heat the air upstream of the GT, followed by preheating the SOFC inlet air and fuel. Compressed air from the compressor enters the shell-and-tube heat exchanger for heat exchange with the afterburner exhaust, after which it is directed into the GT. The turbine exhaust is additionally employed to preheat the SOFC inlet air and fuel.

Table 1. Design Values and Steady-State Values of the SOFC-GT Hybrid System.

Parameters	Unit	Design Value	Simulation Value	Relative Error (%)
SOFC electrical power	kW	98.00	97.53	0.48
SOFC fuel utilization	%	85.00	85.01	0.01
SOFC electrical efficiency	%	62.00	62.11	0.18
GT mechanical power	kW	36.00	36.06	0.17
GT efficiency	%	85.00	85.07	0.08
GT rotational speed	rpm	48,000.00	48,000.01	0.00
Compressor power consumption	kW	24.00	23.58	1.75
Generator output power	kW	12.00	12.47	3.92
Combustion chamber temperature	°C	900.00	900.01	0.00

presents the design and simulation values of each parameter for the SOFC-GT hybrid system under rated operating conditions. With the exception of the compressor power consumption and generator output power, the steady-state relative error of the rest of the equipment is less than 0.5%. The maximum relative error, which stands at 3.92%, stems from the generator output power.

2.2. C-HILS Platform Design and Construction

2.2.1. C-HILS Platform Frame Design

The basic structure of the C-HILS platform is illustrated in Figure 2. This platform comprises four key components: APROS, NI PXI hardware, LabVIEW graphical programming software, and the HOLLiAS MACS-FM DCS. In this study, the SOFC-GT bottoming cycle hybrid power generation system, constructed within APROS, functions as the digital simulation module. The DCS is integrated into the simulation loop as the control hardware, where HMI configuration and control logic configuration are implemented to enable real-time monitoring and control. NI PXI hardware and LabVIEW software serve as the data transmission interface between APROS and the DCS.

The operational workflow of the C-HILS is as follows: Digital signals generated by the APROS model are first transmitted to the LabVIEW platform via the OPC communication protocol. LabVIEW then converts these digital signals into analog electrical signals (D/A conversion), which are output to the DCS through NI PXI hardware. Concurrently, LabVIEW acquires analog electrical signals from the DCS using NI PXI hardware, converts them into digital signals (A/D conversion), and feeds these data back to the SOFC-GT simulation model via OPC. This bidirectional data exchange mechanism completes the C-HILS with the DCS hardware integrated into the loop.

2.2.2. Physical Equipment Composition

The photographs of the C-HILS platform are presented in Figure 3. The platform utilizes a total of four computers: one hosting the APROS, and the remaining two functioning as the operator station and engineer station of the DCS, respectively. The NI PXI system employs the NI PXI-8880 as its embedded controller, which integrates all functionalities required for PXI system operation without the need for an external PC. This controller operates as a standalone computer, pre-installed with the Windows operating system and LabVIEW programming environment.

Within the NI PXI system, the NI PXIe-6738 serves as the signal generation module, paired with the NI SCB-68A shielded I/O connector junction box. Copper conductors link the analog output ports of the junction box to the input ports of the DCS’s FM-148C functional module. Since the NI PXIe-6738 is limited to outputting ±10 V voltage signals, while the FM-148C exclusively accepts 0~20 mA current signals, an intermediate signal isolation and conversion module is incorporated to facilitate the conversion of ±10 V voltage signals to 0~20 mA current signals.

For signal acquisition, the NI platform utilizes the NI USB-6255 multifunctional I/O device, which is capable of acquiring ±10 V voltage signals. Its analog input ports are connected via copper conductors to the output ports of the DCS’s FM-151A functional module. The FM-151A, configured as the signal output module in the DCS, generates 4~20 mA current signals. Correspondingly, an additional signal isolation and conversion module is deployed between these components to convert the 4~20 mA current signals to ±10 V voltage signals.

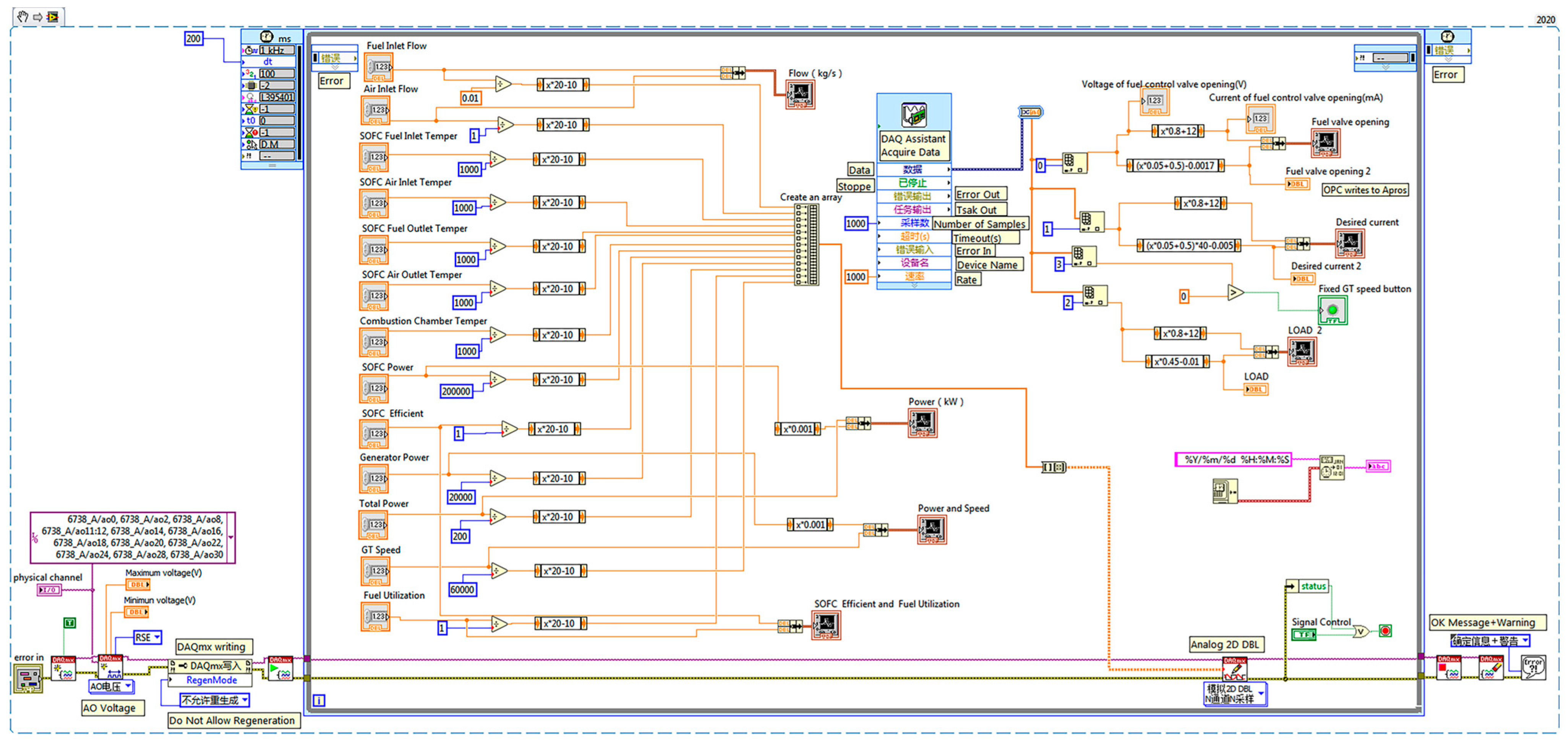
2.3. LabVIEW Configuration

In this C-HILS, OPC communication technology is employed for data reading from and writing to the APROS simulation model. Specifically, APROS functions as the OPC server, while LabVIEW software provides an OPC client to access data within the APROS model. Since LabVIEW and APROS operate on separate computers, prior to establishing OPC DA communication, both devices must be added to the same domain. Additionally, Distributed Component Object Model (DCOM) configurations and firewall settings need to be configured on each computer, respectively. Only after these configurations are completed can a remote OPC connection between the two computers be realized. The OPC client integrated in LabVIEW’s Datalogging and Supervisory Control (DSC) module is utilized to access the OPC server of APROS.

Upon successful establishment of the OPC DA connection, a While loop is created in the LabVIEW block diagram to enable continuous data access to APROS. Within this loop, digital signals are converted into analog signals, which are then transmitted to the input terminals of the DCS via the physical channels of NI PXI hardware. Concurrently, the loop continuously acquires output signals from the DCS, converts these analog signals back into digital signals, and writes them to the APROS model through the OPC client. This bidirectional process completes data communication between the APROS model and the physical DCS.

The block diagram of the LabVIEW program is shown in Figure 4, which is designed to implement two core functions: analog signal output and analog signal acquisition. Both functions adopt the continuous sampling mode with a sampling frequency of 1 kHz. Additionally, it is necessary to set the time required for one iteration of the While loop, and a value of 200 s is adopted here. All parameters within the While loop are bound to the data of the APROS simulation model using DataSocket (provided by NI), thereby enabling real-time data reading and writing.

Equation (1) is used to convert the parameter values in the simulation model into corresponding voltage values. Considering that the voltage output range of the NI PXI-6738 is −10 V to 10 V, Equation (1) can be derived through a simple linear transformation. Equation (2) is employed to convert the voltage values acquired by the NI USB-6255 into corresponding parameter values. Given that the voltage acquisition range of the NI USB-6255 is −10 V to 10 V, Equation (2) is obtained via a simple linear transformation.

$${\displaystyle \frac{ParameterValue}{UpperLimit}}\times 20-10=VoltageValue$$

(1)

$$\left({\displaystyle \frac{VoltageValue}{20}}+0.5\right)\times UpperLimit=ParameterValue$$

(2)

3. SOFC-GT Hybrid System Dynamical Model Based on APROS

3.1. SOFC Model

3.1.1. Mathematical Model

A SOFC is composed of an anode, a cathode, and a solid oxide electrolyte. At the cathode, oxygen, acting as an oxidant, accepts electrons and undergoes a reduction reaction to form oxide ions, which are then transported to the anode through the solid oxide electrolyte. Hydrogen and oxide ions undergo an oxidation reaction at the anode, generating water and electrons. Both electrodes contain catalysts to accelerate the rate of the redox reactions. A planar solid oxide fuel cell is selected as the subject for mathematical modeling. To accelerate the simulation runtime, the following assumptions are made prior to model establishment:

(1)

The air entering the cell cathode is composed of 79% nitrogen and 21% oxygen;

(2)

All gases are ideal gases;

(3)

The pressures in the anode and cathode inside the fuel cell are assumed to be constant and balanced;

(4)

The effects of kinetic energy and potential energy are neglected.

For the SOFC, the chemical reactions in the anode adhere to Equation (3), and those in the cathode conform to Equation (4).

$$H_2+O^{2-}\to H_{2}O+2e^{-}$$

(3)

$${\displaystyle \frac{1}{2}}{O}_2+2e^{-}\to O^{2-}$$

(4)

The performance of a cell is characterized by calculating the ideal voltage and electrochemical losses. The Nernst potential, which represents the maximum possible voltage achievable, is a function of temperature and the partial pressures of the substances involved in the electrochemical reaction. The ideal voltage, i.e., the maximum Nernst voltage, is determined by the change in Gibbs free energy and is expressed by the thermodynamic Nernst equation as:

$$E_{Nernst}=-{\displaystyle \frac{\Delta G(T_{cell},P_{cell})}{nF}}$$

(5)

after derivation, it can be written as:

$$E_{Nernst}=E_{Nernst}^0+{\displaystyle \frac{R{T}_{cell}}{2F}}\ln ({\displaystyle \frac{p_{H_2}{p}_{O_2}^{0.5}}{p_{H_{2}O}{p}_0}})$$

(6)

where $E_{Nernst}$ is the Nernst electromotive force, $E_{Nernst}^0$ is the standard electromotive force related to temperature, $R$ is the universal gas constant, $T$ is the temperature, $F$ is the Faraday constant, $p_i$ is the partial pressure of component $i$, and $p_0$ represents the reference pressure.

The operating voltage of the cell is obtained by subtracting the electrochemical barriers, the potential drops caused by the ohmic resistance of each component, and the potential drops due to changes in reactant concentrations from the Nernst electromotive force:

$$V_{cell}=E_{Nernst}-V_{act}-V_{ohm}-V_{conc}$$

(7)

This equation shows three polarization loss terms related to electrochemical reactions. Activation polarization $V_{act}$ is associated with reaction kinetics. The electrochemical reactions on the electrode surface need to overcome energy barriers, which results in voltage loss. Ohmic polarization $V_{ohm}$ is related to the internal current resistance of the cell. During charge transport, the resistance of the electrolyte, electrodes, and other connecting components causes voltage loss, which is determined by the materials and cell structure. Concentration polarization $V_{conc}$ is affected by the diffusion rate of gases.

The activation polarization loss is derived by calculating the difference between the anodic and cathodic reactions, namely the Butler-Volmer (BV) equation:

$$i=i_0\left\{\exp \left(z\mu F{V}_{act}/R{T}_{cell}\right)-\exp \left[zF{V}_{act}\left(\mu -1\right)/R{T}_{cell}\right]\right\}$$

(8)

where i and i₀ are the fuel cell current density and the exchange current density of the fuel cell, respectively, z is the reaction electron constant, and μ is the electron transfer coefficient, which is generally 0.5 in SOFCs.

The ohmic polarization loss can be obtained via Ohm’s law:

$$V_{ohm}=i\left[{\displaystyle \sum _{\mathrm{k}}{\delta }_{\mathrm{k}}}\exp \left(B_{\mathrm{k}}/T_{cell}\right)+r_{int}\right]$$

(9)

where ${\displaystyle \sum _{\mathrm{k}}{\delta }_{\mathrm{k}}}\exp \left(B_{\mathrm{k}}/T_{cell}\right)$ represents the sum of resistances of all parts in the fuel cell, $T_{cell}$ is the SOFC temperature, k denotes the cathode, anode, and electrolyte of the cell, $r_{int}$ is the interconnector resistance, and ${\delta }_{\mathrm{k}}$ and $B_{\mathrm{k}}$ are empirical constants related to the resistivity of the cell’s cathode, anode, and electrolyte.

$$V_{conc}=-{\displaystyle \frac{R{T}_{cell}}{zF}}\ln {\displaystyle \frac{c_s}{c_b}}$$

(10)

where $c_s$ is the concentration at the reaction site, and $c_b$ is the bulk concentration. According to Fick’s first law and Faraday’s law, the above equation can be rewritten as:

$$V_{conc}=-{\displaystyle \frac{R{T}_{cell}}{zF}}\ln \left(1-{\displaystyle \frac{i}{i_{lim}}}\right)$$

(11)

where $i_{lim}$ is the limiting current density.

The single-cell power is the product of its operating voltage and operating current, where the operating current is calculated using the current density and active surface area:

$$P_{cell}=V_{cell}\times i\times A_{active}$$

(12)

where $A_{active}$ is the active surface area of one cell.

The SOFC model employs a lumped parameter model, in which the temperature is uniform across all components of the fuel cell. Additionally, assuming no heat transfer between the SOFC and the ambient environment, its temperature can be derived from the energy balance equation:

$$c_{p,cell}{\displaystyle \frac{\partial T_{cell}}{\partial t}}=Q_{cell,gen}-h_{HT}{A}_{HT}(T_{cell}-T_{air,ave})$$

(13)

where $c_{p,cell}$ denotes the single cell average specific heat capacity for the temperature range, $h_{HT}$ represents convective heat transfer coefficient between cathode airflow and cell, and $A_{HT}$ stands for heat transfer surface area of cathode airflow channels, and $T_{air,ave}$ is the average cathode airflow temperature. The expression for the heat generation term is provided as follows:

$${\stackrel{•}{Q}}_{cell,gen}={\stackrel{•}{H}}_{fuel,in}-{\stackrel{•}{H}}_{fuel,out}-P_{cell}$$

(14)

where ${\stackrel{•}{H}}_{fuel,in}$ is the enthalpy flow rate of fuel at anode inlet, ${\stackrel{•}{H}}_{fuel,out}$ denotes the enthalpy flow rate of fuel at anode outlet, and $P_{cell}$ is the electrical power generated by a single cell.

The temperature at the cathode inlet is set by the operating conditions, whereas the outlet temperature remains to be determined. Assuming the air temperature operates in a quasi-steady state, the outlet air temperature can be derived via a simple energy balance calculation for the airflow, given that the heat capacity of air is considerably smaller than that of the battery materials:

$$m_{air}{c}_{p,air}(T_{air,out}-T_{air,in})=h_{HT}{A}_{HT}(T_{cell}-T_{air,ave})$$

(15)

where $m_{air}$ is the air mass flow rate and $c_{p,air}$ is the air average specific heat capacity for the temperature range. The aforementioned equation can be rearranged as:

$$T_{air,out}=\left({\displaystyle \frac{h_{HT}{A}_{HT}-2m_{air}{c}_{p,air}}{2m_{air}{c}_{p,air}{h}_{HT}{A}_{HT}}}\right){\stackrel{•}{Q}}_{cell,gen}+T_{cell}$$

(16)

This formulation yields the quasi-steady outlet air temperature as a function of the cell operating temperature, yet fails to capture the dynamic characteristics of the outlet air temperature [34]. The term is thus defined as the steady-state additive temperature:

$$T_{add,ss}=\left({\displaystyle \frac{h_{HT}{A}_{HT}-2m_{air}{c}_{p,air}}{2m_{air}{c}_{p,air}{h}_{HT}{A}_{HT}}}\right){\stackrel{•}{Q}}_{cell,gen}$$

(17)

However, the objective is to predict a dynamic temperature response. Therefore, to incorporate dynamic behavior, a first-order differential equation is introduced with a temperature time constant similar to the cell material:

$${\displaystyle \frac{\partial T_{add,dyn}}{\partial t}}={\displaystyle \frac{h_{HT}{A}_{HT}}{c_{p,cell}}}(T_{add,ss}-T_{add,dyn})$$

(18)

This differential equation establishes the dynamic additive term, $T_{add,dyn}$, which will always, over time, approach the steady-state additive, $T_{add,ss}$. Finally, the exit air temperature can be computed using the following equation:

$$T_{air,out}=T_{add,dyn}+T_{cell}$$

(19)

3.1.2. Parameter Settings

The APROS offers three simulation models (zero-dimensional, one-dimensional, and two-dimensional) for SOFC simulations [35]. These models can be flexibly selected based on simulation objectives to balance accuracy and computational efficiency. The key parameters that can be set for SOFC components include geometric parameters, electrochemical properties, heat transfer parameters, etc. Additionally, the desired current and voltage can be defined.

For the SOFC-GT Bottoming Cycle Hybrid System studied in this paper, the zero-dimensional SOFC module provided by APROS is selected for modeling. The fuel composition is set to 30% hydrogen and 70% water vapor by mass fraction. The zero-dimensional SOFC is a simplified model based on macroscopic adiabatic energy balance, which ignores spatial distribution and is suitable for system-level fast simulations (such as integrated analysis of SOFC with the entire power plant). It mainly calculates overall parameters (such as total power, average efficiency, and fuel utilization) and does not involve the spatial distribution of internal temperature or concentration.

The zero-dimensional SOFC module is defined in the APROS according to the parameters in

Table 2. Parameter settings of the SOFC zero-dimensional module.

Parameter	Value	Unit	Description of Property
Width of a fuel channel	2	mm	The width of a fuel channel perpendicular to the fuel flow direction.
Height of a fuel channel	2	mm	The height of a fuel channel.
Width of an air channel	2	mm	The width of an air channel perpendicular to the fuel flow direction.
Height of an air channel	2	mm	The height of an air channel.
Number of fuel cells in one stack	3600	/	The number of fuel cells in one stack.
Number of parallel stacks	1	/	The number of parallel stacks.
Thickness of electrolyte	2 × 10−4	m	The thickness of the electrolyte.
Active surface area of one cell	0.01	m2	The active surface area of one fuel cell.
Calculation mode of ASR	1	/	The calculation mode of the area-specific resistance. The calculation mode 1 is the theoretical electromotive force.
Function used to calculate ASR	4	/	The function defines the calculation of the area-specific resistance.
Coefficient ALFA	0.61	/	The first coefficient of the function defining ASR.
Coefficient BETA	0.79	/	The second coefficient of the function defining ASR.

, with other parameters remaining at their default values.

When the value of the attribute Function used to calculate ASR is 4, the form of the function is:

$$ASR={\displaystyle \frac{\alpha }{33400\cdot \exp (-10300/T)}}\cdot {\displaystyle \frac{\Delta E}{\beta }}$$

(20)

where $\Delta E$ is the thickness of the electrolyte.

3.2. Turbine Model

The turbine is modeled using subroutines that compute the enthalpy at the outlet of the turbine module. These calculations rely on the inlet enthalpy, the turbine’s efficiency, and its nominal operating parameters. The mechanical power generated by the turbine is also computed and fed into the generator model for system-level analysis [36].

The solution process for the turbine model can be segregated into two primary segments: pressure calculations and enthalpy calculations. When resolving the pressure-flow dynamics, the turbine is treated as a flow resistance component. This resistance induces a pressure drop across the turbine stage, with the magnitude of the drop being a function of the mass flow rate.

Given that extraction pressures are dependent on mass flow rates, the Stodola equation is employed to determine the pressures upstream and downstream of the turbine model. This equation establishes the turbine coefficient, as shown below:

$$K=m\sqrt{{\displaystyle \frac{p_{in}\cdot v_{in}}{{(p_{in})}^2-{(p_{out})}^2}}}=m_0\sqrt{{\displaystyle \frac{p_{0,in}\cdot v_{0.in}}{{(p_{0.in})}^2-{(p_{0,out})}^2}}}$$

(21)

where $K$ represents the Stodola coefficient, $p_{in}$ denotes the pressure before the turbine module, and $p_{out}$ is the pressure after the turbine module. m stands for the mass flow through the turbine module, while $v_{in}$ is the specific volume of the inlet. $p_{0,in}$, $p_{0,out}$, $m_0$, $v_{0,in}$ represent the values of the corresponding parameters at the optimal load.

Equation (19) enables the calculation of either the pressure upstream or downstream of the turbine, as well as the mass flow passing through the turbine. The mass flow through the turbine is obtained as:

$$m_c=K\cdot \sqrt{{\displaystyle \frac{{(p_{in})}^2-{(p_{out})}^2}{P_{in}\cdot v_{in}}}}$$

(22)

where $m_c$ represents the calculated mass flow through the turbine branch. Hence, the resistance coefficient used in the pressure-flow solution can be calculated with the equation:

$$\xi =2\cdot (p_{out}-p_{in})/m_c^2$$

(23)

The thermodynamic process within the turbine may be approximated as a polytropic process, and its enthalpy drop can be calculated by the following equations:

$${\displaystyle \frac{h_{in}-h_0}{h_{out}-h_0}}={\left({\displaystyle \frac{p_{in}}{p_{out}}}\right)}^{1-1/k}$$

(24)

$$\Delta h=m_c\left(h_{in}-h_{out}\right)$$

(25)

where $h_0$ is the stagnation enthalpy, $k$ is the polytropic exponent, and $\Delta h$ is the enthalpy drop.

The mechanical power generated by the turbine can be calculated using the mass flow through the turbine and the enthalpy drop:

$$P_{GT}={\displaystyle \sum (m\cdot \Delta h)}$$

(26)

3.3. Compressor Model

A compressor is used to increase the gas pressure by transferring energy from its rotating blades to the flowing substance. The compressor model in APROS is particularly suitable for axial compressors, which are typically used in gas turbine power plants.

The simplest way to define a compressor is through one operating point (nominal point), requiring the following physical parameters: inlet pressure and temperature, pressure ratio, mass flow, isentropic efficiency, mechanical efficiency, rotational speed, inertia moment, and a performance map from the stalling limit to the choke point.

The pressure of the compressor is solved using a performance map. Based on the inlet pressure and rotational speed of the compressor, the values of the reduced flow rate and isentropic efficiency are obtained from the performance map. The compressor module uses these equations to calculate the reduced mass flow rate and rotational speed:

$$m_{red}=m\sqrt{T_{in}/T_{0,in}}\cdot (p_{0,in}/p_{in})$$

(27)

$$n_{red}=(n/n_0)\cdot \sqrt{T_{0,in}/T_{in}}$$

(28)

where $m_{red}$ is the reduced mass flow, $m$ is the mass flow, $T_{in}$ is the input temperature, $T_{0,in}$ is the input temperature at the nominal point, $p_{0,in}$ is the input pressure at the nominal point, and $p_1$ is the input pressure, $n_{red}$ is the reduced rotational speed, $n$ is the rotational speed, $n_0$ is the rotational speed at the nominal point. The pressure ratio over the compressor is obtained as:

$$\mathsf{\Pi }=p_{out}/p_{in}$$

(29)

where $p_{in}$ and $p_{out}$ are the pressures before and after the compressor, respectively.

In actual operation, considering factors such as heat generation from friction, a compressor does not undergo an isentropic compression process, and the thermodynamic process during operation is more complex than the ideal process. The adiabatic efficiency is introduced and defined as the ratio of the actual power consumption to the power consumption in the isentropic process:

$${\eta }_{ise}=P_{C,ise}/P_C$$

(30)

The power consumption of the compressor in the isentropic compression process can be calculated by:

$$P_{C,ise}={\displaystyle \frac{1}{\gamma -1}}R{T}_{in}\left[1-{\left({\displaystyle \frac{p_{out}}{p_{in}}}\right)}^{{\displaystyle \frac{\gamma -1}{\gamma }}}\right]$$

(31)

where $T_{in}$ is the inlet temperature of the compressor, $\gamma$ is the specific heat ratio, and $R$ is the gas constant. The outlet temperature of the compressor $T_{out}$ can be calculated by:

$$T_{out}=T_{in}\left({\displaystyle \frac{{\mathsf{\Pi }}^{\frac{\gamma -1}{\gamma }}-1}{{\eta }_{ise}}}+1\right)$$

(32)

3.4. Shaft Model

The SHAFT module type is used to connect different rotating components (generator, motor, turbine section, compressor, and basic pump). The turbine drives the rotating shaft, which in turn enables the compressor and generator to operate in tandem. Under ideal conditions, the output power of the system balances the input power, allowing the rotating shaft to maintain a constant rotational speed. However, any imbalance between power supply and demand will induce dynamic acceleration or deceleration of the rotating shaft. For single-shaft micro gas turbines, the equilibrium state of the rotating shaft can be precisely described by the following equation:

$${\displaystyle \frac{dn}{dt}}={\displaystyle \frac{900}{J{\pi }^{2}n}}\left(P_{GT}-P_C-P_G\right)$$

(33)

where $J$ denotes the moment of inertia of the rotating shaft, while $P_{GT}$, $P_C$, and $P_G$ represent the turbine mechanical power, the actual power consumed by the compressor, and the generator mechanical power, respectively.

3.5. Heat Exchanger Model

The heat transfer of the hot-side fluid inside the heat exchanger satisfies Equation (34), and the heat transfer of the cold-side fluid inside the heat exchanger satisfies Equation (35).

$$m_h{c}_{p,h}{\displaystyle \frac{d{T}_h}{dt}}=m_{h,in}{c}_{p,h,in}{T}_{h,in}-m_{h,out}{c}_{p,h,out}{T}_{h,out}-Q_h$$

(34)

$$m_c{c}_{p,c}{\displaystyle \frac{d{T}_c}{dt}}=m_{c,in}{c}_{p,c,in}{T}_{c,in}-m_{c,out}{c}_{p,c,out}{T}_{c,out}+Q_c$$

(35)

The heat storage of the metal material of the heat exchanger satisfies Equation (36). The heat transfer between the hot-side fluid and the metal material of the heat exchanger satisfies Equation (37), and the heat transfer between the cold-side fluid and the metal material of the heat exchanger satisfies Equation (38).

$$m_{metal}{c}_{p,metal}{\displaystyle \frac{d{T}_{metal}}{dt}}=Q_h-Q_c$$

(36)

$$Q_h={\lambda }_h{A}_h\left(T_h-T_{metal}\right)$$

(37)

$$Q_c={\lambda }_c{A}_c\left(T_{metal}-T_c\right)$$

(38)

where $\lambda$ is the heat transfer coefficient and $A$ is the heat transfer area.

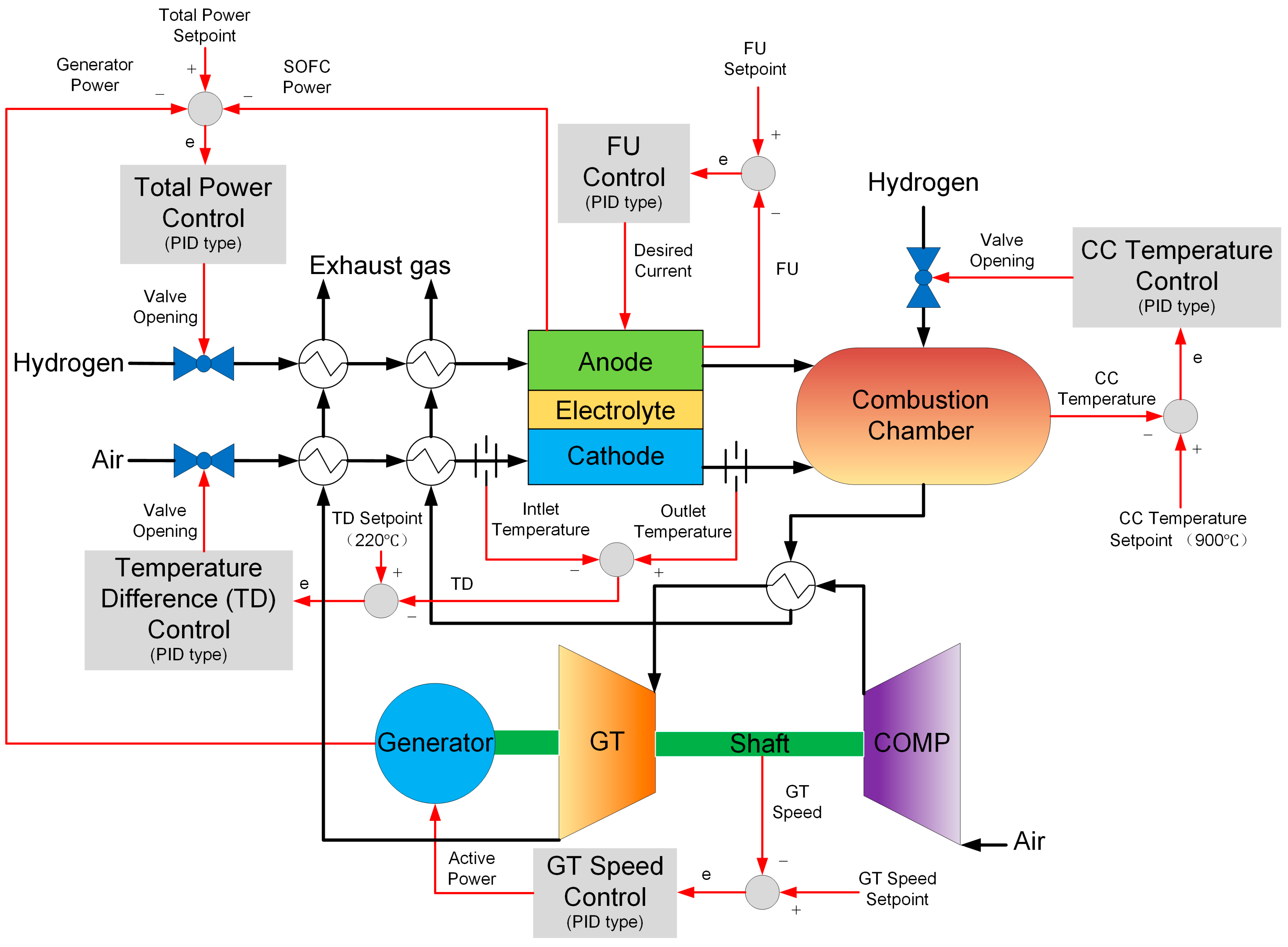
3.6. Control System Design

After constructing the SOFC-GT hybrid system in APROS, the subsequent step is to build an automatic control system within the same software environment. As illustrated in Figure 5, this control system will employ five PID controllers to regulate five critical parameters of the SOFC-GT hybrid system, specifically: the total output power of the hybrid system, the fuel utilization (FU) of the SOFC, the GT speed, the temperature of the combustion chamber (CC), and the temperature difference (TD) between the inlet and outlet of the SOFC cathode. Each control loop will be outfitted with a dedicated PID controller to ensure the precision and stability of system operation.

Notably, the regulation of combustion chamber temperature and the cathode temperature difference serve solely to maintain the stable operation of the hybrid system. The following section will therefore focus on elaborating the three control loops that are directly associated with the transient tests of the hybrid system.

3.6.1. Total Power Control

To enable the SOFC-GT hybrid system to operate under partial loads, the control strategy must incorporate at least a power controller. The total output power of the SOFC-GT hybrid power generation system is supplied by both the SOFC and the generator. For a given fuel flow rate, the ratio between the SOFC output power and the GT output power is directly influenced by the SOFC fuel utilization. While the fuel utilization allows for small-scale load tracking of power, significant load demand fluctuations necessitate power control through adjustments to the fuel flow rate. Consequently, two control schemes exist for the power control strategy of the hybrid power generation system:

(1)

Maintain a constant SOFC fuel utilization by controlling the SOFC desired current, and adjust the total output power of the hybrid system by regulating the SOFC fuel inlet valve.

(2)

Keep the SOFC fuel utilization constant by adjusting the SOFC fuel inlet valve, and modulate the total output power by controlling the SOFC desired current.

This paper selects Scheme (1) as the control strategy for the system. In the APROS model, a PID controller measures the combined output power of the SOFC and GT. The setpoint is the target total power, and the output of the PID controller directly adjusts the opening of the SOFC fuel inlet valve. The PID controller in APROS software employs the following calculation formulas:

$$O(s)=K_p\ast \left[\left(1+1/T_i\ast s\right)+\left(T_d\ast s\right)/(T_d\ast V_d\ast s+1)\right]\ast E(s)+K_{ff}\ast F(s)$$

(39)

where $O(s)$ denotes the output of the controller, while $E(s)$, $F(s)$, $K_p$, $T_i$, $T_d$, $V_d$, and $K_{ff}$ represent the control deviation of the controller, the feed forward signal of the controller, the controller gain, the integration time (s), the derivation time (s), the derivation gain, and the feed forward coefficient, respectively, and the $s$ is the Laplace operator.

3.6.2. Fuel Utilization (FU) Control

Corresponding to the two power control schemes for the hybrid system, when Scheme (1) is selected, the fuel utilization (FU) is regulated by controlling the desired current of the SOFC. In the APROS model, a PID controller measures the actual fuel utilization of SOFC, with the setpoint being the target fuel utilization. The output of this PID controller is the desired current for the SOFC.

3.6.3. GT Speed Control

Within the APROS, the GT model is constructed using the TURBINE module, whose rotational speed is dynamically adjusted in response to changes in the SHAFT module. The rotational speed of the SHAFT module is determined by the interplay between three key parameters: turbine mechanical power, compressor power consumption, and generator mechanical power, with the underlying calculation methodology detailed in Equation (33).

To regulate the GT rotational speed, the critical intervention is to modify the generator’s mechanical power. This is achieved by connecting a LOAD module to the generator (serving as a load source) within APROS: adjusting the active power of the LOAD module induces a corresponding change in the generator’s active power, which in turn alters the generator’s mechanical power, ultimately stabilizing the SHAFT module at a new steady-state rotational speed.

The GT speed control loop in APROS is implemented using a PID controller, which continuously measures the rotational speed of the SHAFT module. The controller’s setpoint is defined as the target shaft speed, and its output directly dictates the active power of the LOAD module (which is connected to the generator). Specifically, an increase in active power leads to a decrease in SHAFT rotational speed, whereas a decrease in active power results in an increase in rotational speed.

Parameter settings for the three PID controllers are shown in

Table 3. Parameter settings for three PID controllers.

PID Controller Name	Controller Gain	Integration Time (s)	Derivation Time (s)	Derivation Gain
Total power control	0.003	18	10	0.5
Fuel utilization control	15	20	40	0.3
GT Speed control	−0.005	35	8	0.5

.

4. DCS Configuration

In this paper, the DCS selected is the HOLLiAS MACS-FM series developed by Hangzhou Hollysys Automation Co., Ltd. (Hangzhou, China). It is equipped with mature advanced control algorithms, fully complies with the IEC61131-3 standard [37], and realizes computer-based monitoring of the control system.

For achieving control over the SOFC-GT hybrid system via the DCS, it is essential to sequentially complete the point configuration, control logic configuration, and HMI configuration for the DCS.

4.1. Points Configuration

DCS point configuration encompasses the configuration of I/O devices and databases. The DCS acquires field data via I/O devices. Prior to control logic configuration, it is essential to complete this point configuration. The DCS collects field data via I/O devices.

In the point configuration, analog input and output points required for the control loops involved in this research are individually mapped to and defined against the I/O channels of the DCS functional module, thereby forming the point information of the control station.

When setting upper and lower limits for each data item in DCS points configuration, mere consistency with the corresponding limits configured in the LabVIEW program ensures accurate conversion of analog electrical signals to digital data. The analog quantities acquired and output by the DCS are presented in

Table 4. Analog input of FM-148C.

Point Name	Point Description	Upper Limit	Unit
FUEL_FLOW_INLET	Fuel inlet flow rate of SOFC	0.01	kg/s
AIR_FLOW_INLET	Air inlet flow rate of SOFC	1.00	kg/s
FUEL_TEMPER_INLET	Fuel inlet temperature of SOFC	1000.00	°C
AIR_TEMPER_INLET	Air inlet temperature of SOFC	1000.00	°C
FUEL_TEMPER_OUTLET	Fuel outlet temperature of SOFC	1000.00	°C
AIR_TEMPER_OUTLET	Air outlet temperature of SOFC	1000.00	°C
MIX_TEMPERTURE	Temperature of the afterburner in SOFC	1000.00	°C
POWER_SOFC	Electric power of SOFC	200.00	kW
EFFICIENCY_SOFC	Electrical efficiency of SOFC	1.00	\
FUEL_UTILIZATION	Fuel utilization of SOFC	1.00	\
G_POWER	Mechanical power of the generator	20.00	kW
FULLPOWER	Total power of the hybrid system	200.00	kW
TURBINE_SPEED	Rotational speed of the gas turbine	60,000.00	rpm

and

Table 5. Analog output of FM-151A.

Point Name	Point Description	Upper Limit	Unit
Fuel_Valve	Opening degree of the SOFC fuel inlet valve	1.00	\
Desired_Current	Desired current of SOFC	40	A
Load	Active power of the LOAD module	450	kW

. It should be noted that among these analog quantities, all have a lower limit of 0 except for LOAD, which has a lower limit of −450 kW.

4.2. Control Configuration

DCS control configuration is primarily composed of three components: logic editing pages, variables, and algorithmic function blocks. For the HOLLiAS MACS V6.5.3 system, control configuration is implemented by creating a Program Organization Unit (POU) within user programs via AutoThink V6.5.3 software, utilizing the graphical Continuous Function Chart (CFC) as the programming language. A POU consists of three fundamental elements: programs, function blocks, and functions.

Control algorithm configuration requires pre-definition of all variables involved, a step that has already been completed in the points configuration. Once all variables are defined, the control algorithm can be formulated by graphically describing the control loop logic using CFC.

As previously established, the automatic control logic for the SOFC-GT hybrid system was developed in APROS. Now, it is necessary to configure the control logic illustrated in Figure 5 within the DCS. Equation (40) corresponds to the PID calculation formula of the HOLLiAS DCS, which incorporates an additional multiplication factor when compared with Equation (39). Therefore, a simple linear conversion of the parameter values presented in Table 3 is required prior to their application as the PID parameters for the DCS, thereby ensuring the consistency of the two equations.

$$O(s)={\displaystyle \frac{M_U-M_D}{P_U-P_D}}\ast K_p\ast \left[\left(1+1/T_i\ast s\right)+\left(T_d\ast s\right)/(T_d\ast V_d\ast s+1)\right]\ast E(s)$$

(40)

where $M_U$ denotes the upper limit of the PID output range, $M_D$ represents the lower limit of the PID output range, $P_U$ stands for the upper limit of the PID measured value range, and $P_D$ refers to the lower limit of the PID measured value range.

4.3. HMI Configuration

The HOLLiAS MACS V6.5.3 system leverages its built-in graphic editing software to edit and generate process flow diagrams, enabling real-time supervision and control of unit operating parameters via the DCS operator station. HMI configuration includes two categories of graphics: static graphics, which are non-operable and unassociated with the system’s point configuration; and dynamic graphics, which can update in response to changes in system point values and support modifications to their numerical data or graphical attributes.

For the SOFC-GT hybrid system under investigation, screen creation and dynamic graphic binding were implemented to achieve remote monitoring of the APROS model through the DCS. Moreover, the setpoints of the PID controllers in the three control loops can be adjusted individually to modulate the operating state of the hybrid system.

5. Results and Discussion

Within the APROS software, the mathematical model and automatic control system for the solid oxide fuel cell–gas turbine (SOFC-GT) hybrid system have been successfully established, enabling full-digital simulations. The platform illustrated in Figure 2 facilitates the implementation of Controller Hardware-in-the-Loop Simulation (C-HILS) experiments. Subsequently, the full-digital simulation method and the C-HILS method will be utilized individually to conduct step change tests on the total power setpoint, fuel utilization setpoint, and rotational speed setpoint. Furthermore, a comparative analysis of the PID controller output values derived from the two approaches will be performed, with the output results of APROS serving as the reference values. This study seeks to validate whether the DCS of the C-HILS platform can attain consistent control effectiveness when equipped with the same control system as that integrated in APROS.

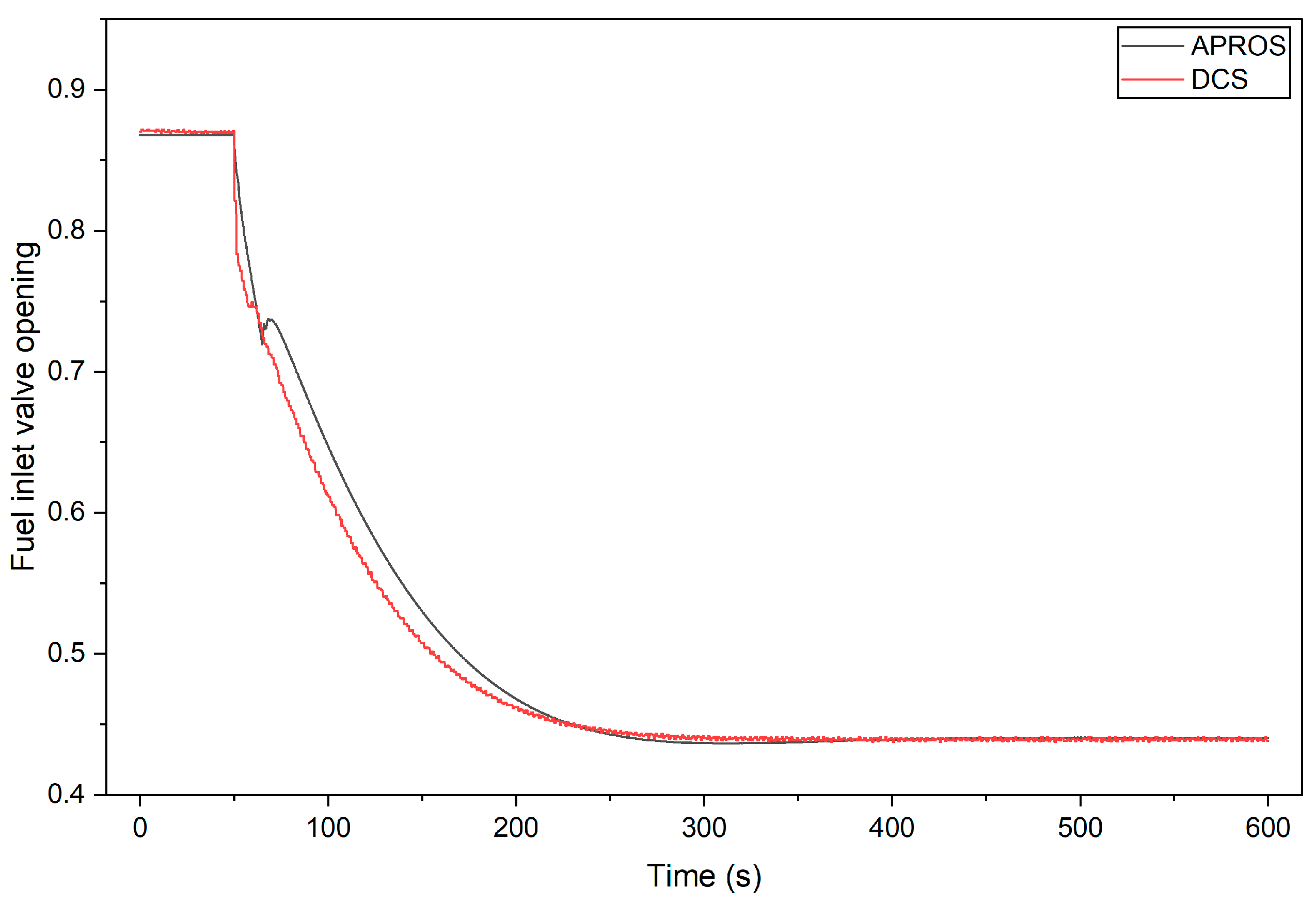
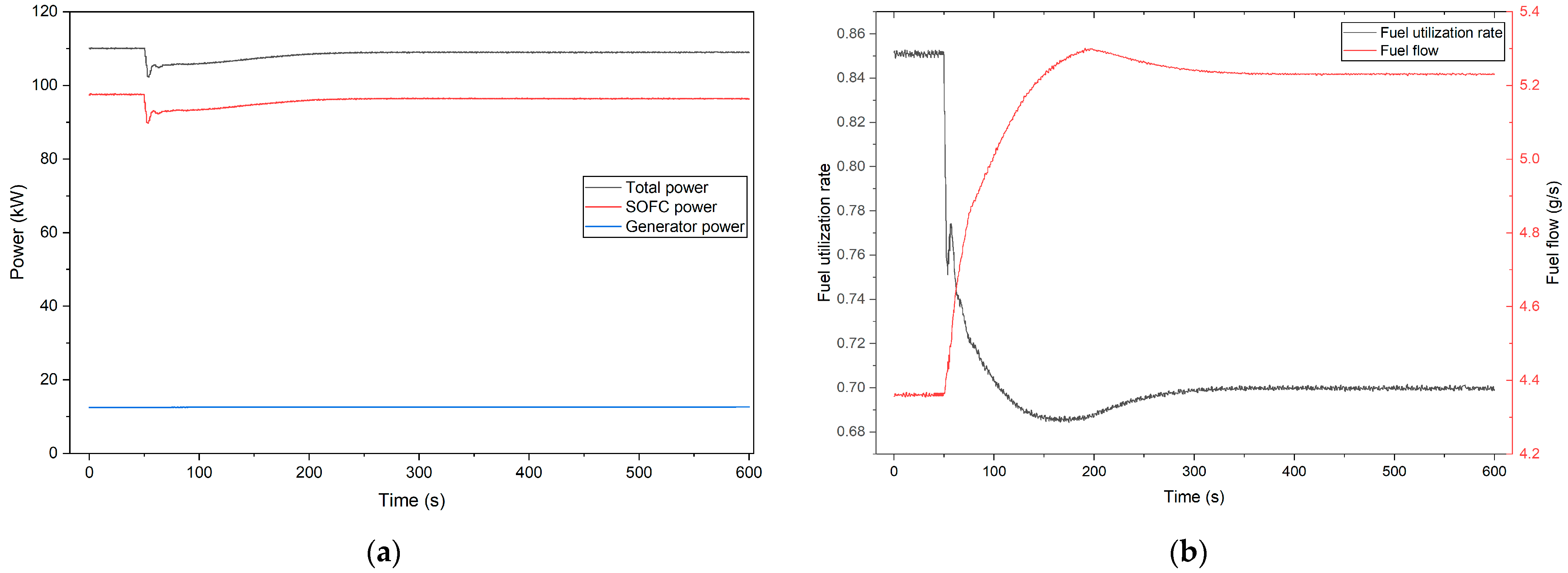
5.1. Total Power Turndown

Following 50 s of operation at its rated power of 110 kW, the total power setpoint of the SOFC-GT hybrid system was adjusted from 110 kW to 80 kW via the DCS. Figure 6 presents the dynamic response curves of the C-HILS. Figure 6a illustrates the power response: given that the total power control loop of the hybrid system achieves its target by regulating the opening of the SOFC fuel inlet valve, the variation in total power during this process is primarily determined by changes in SOFC power, while the generator power remains largely unaffected. Figure 6b shows the response curves of SOFC fuel utilization and fuel flow rate.

After the total power setpoint is adjusted, the fuel flow rate begins to decrease, inducing a rapid rise in fuel utilization. However, due to the concurrent operation of the fuel utilization control loop, the fuel utilization is eventually re-stabilized around 0.85. Since data transmission between the DCS and the APROS simulation model relies on analog signals, electrical signal fluctuations may occur during transmission, which can induce significant oscillations in sensitive parameters such as fuel utilization.

The black curve in Figure 7 denotes the output of the PID controller within APROS during full digital simulation, while the red curve represents the output of the PID controller within DCS during C-HILS. The key divergence between the two curves manifests in the initial phase of load variation (50–70 s): the valve opening output by the PID controller within DCS exhibits a more abrupt decrease, whereas that by APROS declines more gradually. This discrepancy arises primarily from the distinct output limiting mechanisms employed by the two PID controllers.

The HOLLiAS DCS directly imposes constraints on the rate of change in the PID controller’s output: the PID module monitors the rate of change in its computed output, and if this rate exceeds a preset threshold, the system constrains the current output of the PID module to lie within the allowable range of change. In contrast, APROS applies its rate-of-change limitation to the PID controller’s setpoint, confining it to the maximum allowable rate.

Limiting the rate of output change prevents excessive fluctuations in the output. Nevertheless, when initial calculation errors are substantial, significant step changes may still arise between consecutive output values. Conversely, constraining the rate of setpoint change mitigates excessive calculation errors within the PID controller, thereby contributing to a smoother overall control process.

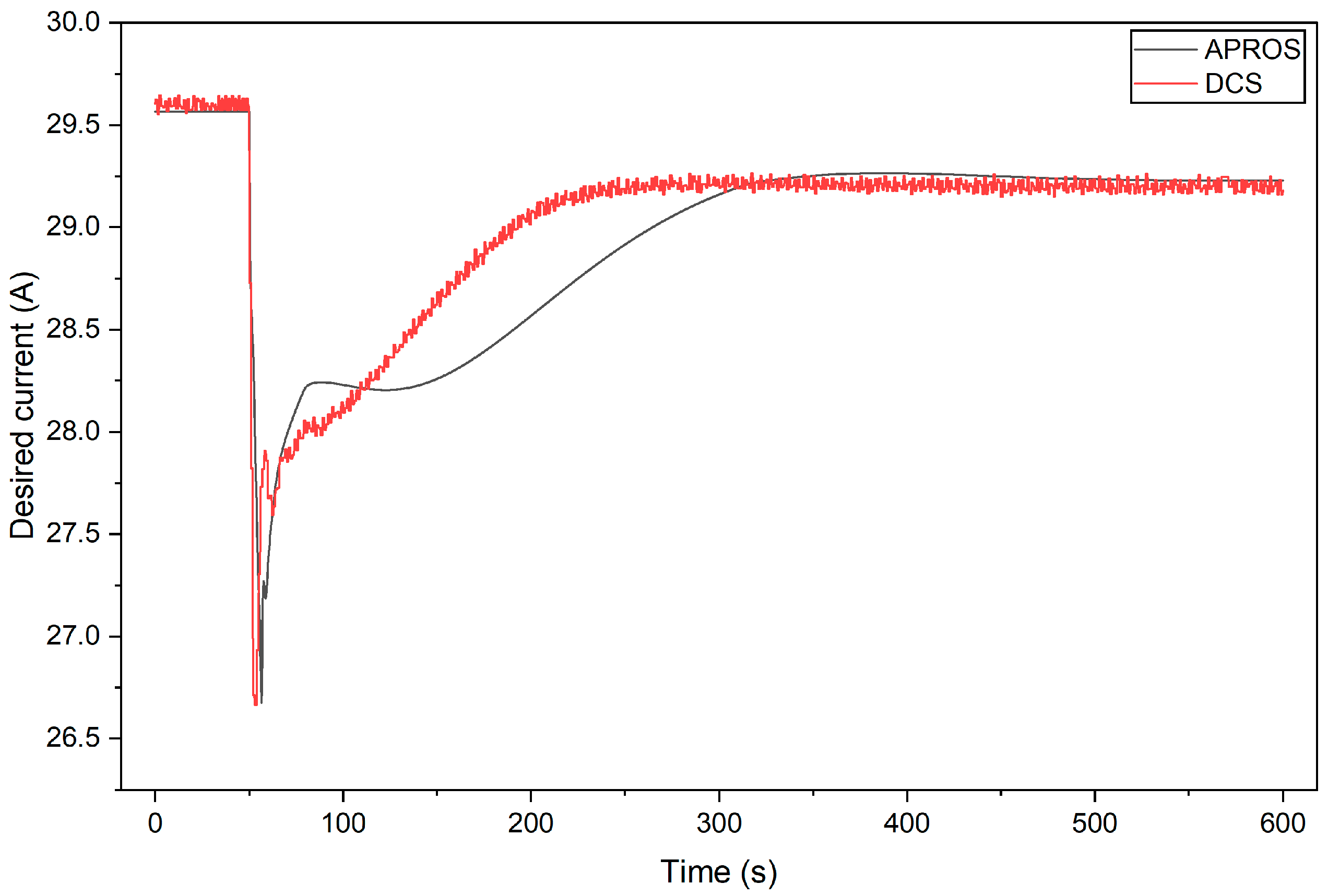
5.2. Fuel Utilization Turndown

After operating at its rated power of 110 kW for 50 s, the setpoint for SOFC fuel utilization in the SOFC-GT hybrid system was adjusted from 0.85 to 0.7 via the DCS. Figure 8 presents the dynamic response curves of the C-HILS. Figure 8a illustrates the power response characteristics: since the fuel utilization control loop of the hybrid system achieves its regulatory objective by adjusting the SOFC’s desired current, a decrease in the desired current leads to reductions in both fuel utilization and SOFC power output. Meanwhile, due to the concurrent operation of the power control loop, the total power is restored to 110 kW. Figure 8b shows the response curves of SOFC fuel utilization and fuel flow rate. As the fuel utilization control loop operates, fuel utilization stabilizes at approximately 0.7 after 300 s, while the power control loop increases the opening of the fuel control valve to bring the total power back to around 110 kW.

The black curve in Figure 9 represents the output of the PID controller within APROS during full digital simulation, whereas the red curve represents the output of the PID controller within DCS during C-HILS. The two curves exhibit significant discrepancies throughout the entire response process, except for the initial 5 s, which again arises from the distinct output limiting mechanisms employed by the two PID controllers. As observed in Figure 7, although the two curves differ in the initial stage, the discrepancy is minor, and their output trends remain consistent. However, the two curves in Figure 9 display divergent response characteristics to the same transient process, primarily because the proportional gain of the PID controller in this control loop is set to 15, which not only strongly amplifies calculation errors but also magnifies the differences between the two PID limiting methods.

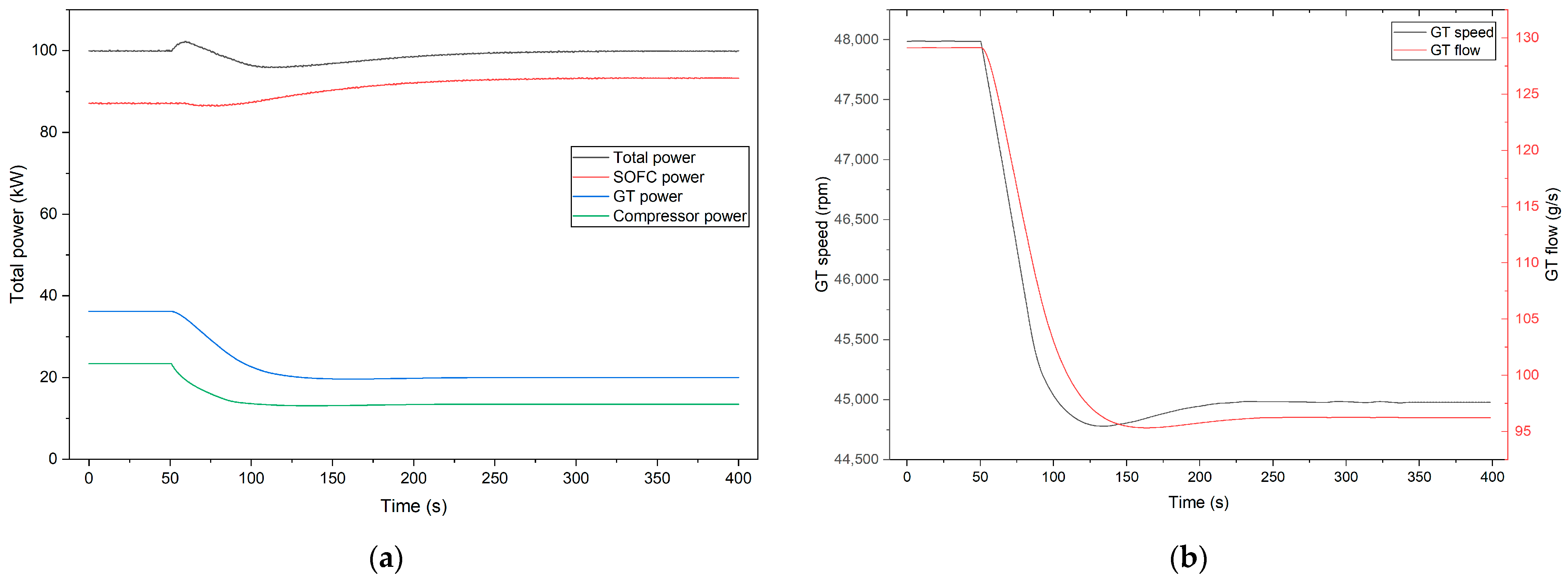
5.3. GT Speed Ramp-Down

Following 50 s of operation at 100 kW, the setpoint for GT rotational speed in the SOFC-GT hybrid system was adjusted from 48,000 rpm to 45,000 rpm via the DCS. Figure 10a illustrates the power response characteristics: between 50 s and 75 s, both the gas turbine and compressor power decreased, with the compressor power exhibiting a more significant reduction. This resulted in the total power of the hybrid system exceeding 100 kW. After 75 s, the GT power dropped more substantially, causing the total power to fall below 100 kW. In response, the total power control loop initiated an increase in the opening of the fuel control valve, thereby restoring the total power to 100 kW. Figure 10b shows the response curves of GT rotational speed and flow rate, where the GT inlet flow rate commenced a decrease as the rotational speed declined.

The black curve in Figure 11 represents the output of the PID controller during full digital simulation in APROS, while the red curve corresponds to the output of the PID controller during C-HILS. The two curves display certain discrepancies only between 50 s and 100 s, with their subsequent trends showing substantial consistency.

6. Conclusions

This study proposes a platform and method for developing control strategies directly based on a physical DCS. Based on APROS, this study developed a dynamic model for the solid oxide fuel cell–gas turbine (SOFC-GT) bottoming cycle hybrid system, encompassing core components such as the solid oxide fuel cell (SOFC), gas turbine (GT), compressor, and heat exchanger, with a steady-state relative error of less than 4%. Meanwhile, a C-HILS platform was constructed leveraging NI virtual instrument equipment and DCS control hardware. To validate the control performance of the C-HILS platform, control systems illustrated in Figure 5 were established within both the APROS software and the HOLLiAS DCS, respectively. Finally, three sets of transient experiments were conducted using the C-HILS method and the full-digital simulation method, with the experimental results from APROS serving as the reference to validate the control effectiveness of the DCS. Although the two methods exhibit differences in dynamic responses, both can achieve stable control, and the time required to reach a new steady state is nearly identical. This ultimately verifies the effectiveness of the C-HILS platform in the context of SOFC-GT hybrid systems. Favorable experimental results demonstrate that the platform can provide a realistic, flexible, and safe testing environment for validating digital solutions in energy and power systems. Based on the research presented herein, the following conclusions are drawn:

(1)

The C-HILS method proposed in this paper enables the coordinated operation of virtual generator sets and physical distributed control systems (DCS), accomplishing the dual objectives of control system verification and unit online virtual simulation. This method not only facilitates the rapid development of control logic within the DCS but also allows for real-time online simulation by replacing the corresponding equipment in the C-HILS platform with the DCS of an actual power plant, thereby transmitting on-site DCS control signals to the simulation model.

(2)

The proposed data signal acquisition and conversion platform can simulate real measurement and control signals. For research on the C-HILS, the signal conversion center built using NI virtual instrument equipment in this study serves as a valuable reference for rapidly constructing experimental platforms.

(3)

As a reliable verification and development platform for the digitization of energy and power systems, the proposed C-HILS scheme not only provides a high-fidelity testing environment for the control strategy optimization of SOFC-GT hybrid systems but also exhibits strong scalability and adaptability. It can be flexibly migrated to other energy systems (e.g., wind-solar hybrid power plants, hydrogen energy storage systems) by adjusting model parameters and signal conversion protocols, supporting the validation of digital solutions and advanced control algorithms for diverse energy scenarios.