Diagnosis of Cascaded Open/Short-Circuit Fault in Three-Phase Inverter Using Two-Stage Interval Sliding Mode Observer

Abstract

A three-phase inverter faces the risk of open-circuit (OC) and short-circuit (SC) faults in operation and requires real-time fault diagnosis. However, existing diagnosis methods have the following limitations: (1) insufficient rapid diagnosis capability for multi-switch cascaded faults; (2) inability to achieve diagnosis for hybrid OC and SC faults. To address these issues, this paper proposes a diagnosis method for cascaded switch open/short-circuit fault in a three-phase inverter based on a two-stage interval sliding mode observer (ISMO). First, by establishing a mixed logic dynamic (MLD) model considering open- and short-circuit faults, the different fault operating states of the three-phase inverter can be fully characterized. Furthermore, a two-stage cascaded ISMO was designed. The pre-stage ISMO rapidly detects abnormal status and fault phase, while the post-stage ISMO accurately isolates OC and SC faults. After diagnosis, the corresponding fault identification of the observer is set for the next fault diagnosis, achieving the sequential diagnosis of cascaded faults. The proposed diagnosis method was tested to validate its effectiveness.

1. Introduction

As a common DC–AC converter, the three-phase inverter is widely used in various fields such as industrial automation, electric vehicles, and renewable energy generation. As core components in three-phase inverters, power switching devices such as insulated gate bipolar transistors (IGBTs) and metal oxide semiconductor field effect transistor (MOSFETs) are subjected to high-frequency switching actions, high current surges, and thermal stress under complex operating conditions for a long time, resulting in parameter degradation and finally failure. If such faults are not diagnosed and handled in a timely manner, they will cause abnormal output, reduced efficiency, and compromised safety, leading to significant economic losses and hazards [1]. According to statistics, power switching devices are the most vulnerable components in power electronic converters [2,3]. Therefore, being able to quickly diagnose faults in switching devices is very helpful in improving the reliability of the system.

There have been many studies on the diagnosis of switch faults in power electronic converters, which can be mainly divided into signal-based, data-driven, and model-based methods [4,5]. Signal-based methods mainly use various signal processing methods to obtain fault characteristics and perform fault diagnosis by comparing the characteristics before and after the fault. Fault characteristics include the slope, the spectrogram, the wavelet packet transform, the modal decomposition, etc. [6,7,8]. In power electronic converters, signal-based fault diagnosis methods can be divided into voltage signal-based methods and current signal-based methods [9,10,11,12,13]. In [14], an SC fault diagnosis method for a three-phase current source inverter is proposed, using the amplitude and phase of the output current vector. Voltage signal-based fault diagnosis methods usually require additional circuits and increase costs, while current signal-based fault diagnosis methods have a longer delay in capturing fault characteristics, due to the presence of inductive components, which cannot change the current instantly, thereby prolonging the fault diagnosis time and affecting the reliable operation of power electronic devices [15].

Data-driven methods are suitable for situations where there is already a large amount of historical information, and the principle of data-driven methods is to extract the mapping relationship between the measurement data and fault labels. First, fault-related data are collected and processed to extract discriminative features, which are systematically organized into a comprehensive fault database. Subsequently, these extracted fault features are utilized to train fault diagnosis models through machine learning or deep learning techniques. The trained fault diagnosis models can obtain fault mode classification results based on input feature data [16,17,18,19,20,21]. In [22], manifold feature learning is used to process current signals to obtain fault features, and then an extreme learning machine is used to train a fault diagnosis model for IGBT open circuit fault diagnosis in a three-phase inverter. A novel pooling layer was designed using discrete wavelet transform and an adaptive sparse attention mechanism for OC fault diagnosis in PMSM drives in [23], which improves the robustness of the diagnostic model by filtering out high-frequency components of the current data and redundant information of the attention mechanism. However, data-driven methods typically use waveform data of at least one AC cycle; so, the response time for fault diagnosis is relatively long, resulting in lower efficiency in fault diagnosis.

Model-based methods establish a system model through physical laws or system identification, monitor the consistency between actual system output and model predicted output, and detect and locate deviations to identify faults. These methods typically require a relatively accurate mathematical model of the system. However, the mathematical model often deviates from reality to a certain extent, and it is necessary to use actual measured values to correct the estimated values, usually using observers for correction. Currently, many types of observers have been used in the field of fault diagnosis, including Luenberger observers [24], sliding mode observers [25,26], Kalman filters [27], and other types of observers [28,29]. Among them, the sliding mode observer has stability against system model inaccuracy and external disturbances and can maintain stable estimation performance even in the presence of system parameter deviation or measurement result interference [11]. Meanwhile, it has the advantages of a fast-tracking speed, a small estimation error after stabilization, a simple structure, and low computational complexity [30]. A novel discrete disturbance sliding mode observer is used to quickly and accurately estimate the three-phase current of grid-connected three-phase inverters in [31], and adaptive fault diagnosis detection variables are designed to diagnose OC faults in grid-connected three-phase inverters. The interval estimation method can effectively improve the accuracy of the observation values. Combining interval estimation with a sliding mode observer can not only improve the convergence speed of the sliding mode observer but also effectively reduce chattering and enhance the robustness of fault diagnosis system. Ref. [32] proposed an OC fault diagnosis method for inverters based on ISMO, which has strong anti-interference ability and can diagnose single-switch and multi-switch OC faults.

In summary, there are currently many fault diagnosis methods for three-phase inverters. However, most of these methods are limited to diagnosing only one type of fault, either an OC or SC fault, and cannot diagnose both simultaneously. In addition, in the actual three-phase inverter applications, if one switch has an OC or SC fault, another switch may be broken down by voltage or current surge, resulting in a new OC fault or SC fault, which is called a cascaded fault. For a cascaded fault situation, existing diagnosis methods such as signal-based methods may encounter situations where the fault characteristics counteract each other, making it impossible to diagnose. In response to this issue, this paper proposes a diagnosis method based on ISMO for three-phase inverter cascaded open/short-circuit faults, with universality. The main contributions of this paper are as follows.

(1) A modified MLD model of a three-phase inverter was established based on the state–space method, considering an OC fault and an SC fault of the switch, including single-switch faults and multi- switch faults, which can accurately reflect the operating state of the three-phase inverter when various types of faults occur.

(2) A two-stage ISMO used for fault diagnosis was designed based on the modified MLD model of the three-phase inverter, with consideration of the disturbance during the measurement process and parameter uncertainties. Compared to conventional sliding mode observers, the ISMO can improve the robustness of the observed value output. Furthermore, a cascaded open/short-circuit fault diagnosis method for three-phase inverter based on a two-stage ISMO was designed. On the basis of the traditional observer-based fault diagnosis method to implement the capability of open- and short-circuit diagnosis, the method can further implement the diagnosis of cascaded faults that occur successively in two or more switches in a short time.

The remaining parts of this paper are arranged as follows: Section 2 presents the fault analysis and MLD modeling of open/short-circuit faults in a three-phase inverter, Section 3 presents the cascaded fault diagnosis method for a three-phase inverter based on ISMO. The simulation analysis and experimental verification results are presented in Section 4. Finally, Section 5 summarizes the paper.

2. Fault Analysis and Modeling

The typical two-level three-phase inverter studied in this paper is shown in Figure 1. The inverter has a three-phase Y connection resistive inductive load and a neutral point of n.

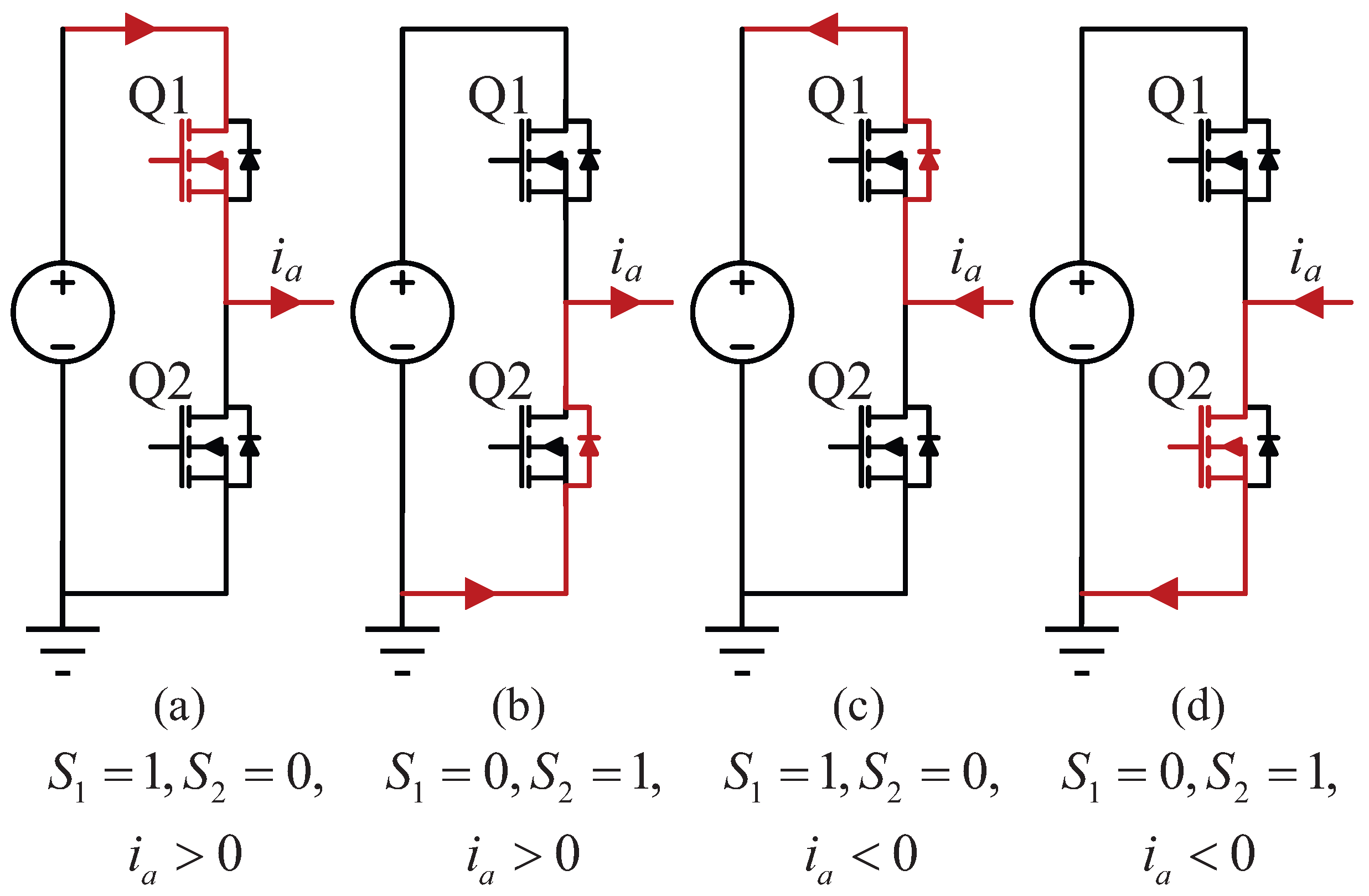
2.1. Operating Status and Fault Analysis of Three-Phase Inverter

In the healthy state, the upper and lower switches of one phase in a three-phase inverter conduct alternately. Taking one phase as an example, the relationship between the current path and the switch state is shown in Figure 2. In the figure, $S_1$ is the switch signal of Q1, $S_2$ is switch signal of Q2, and $i_a$ is the phase current. When the switch is conducting, the forward current flows through the switch, and the reverse current flows through the body diode.

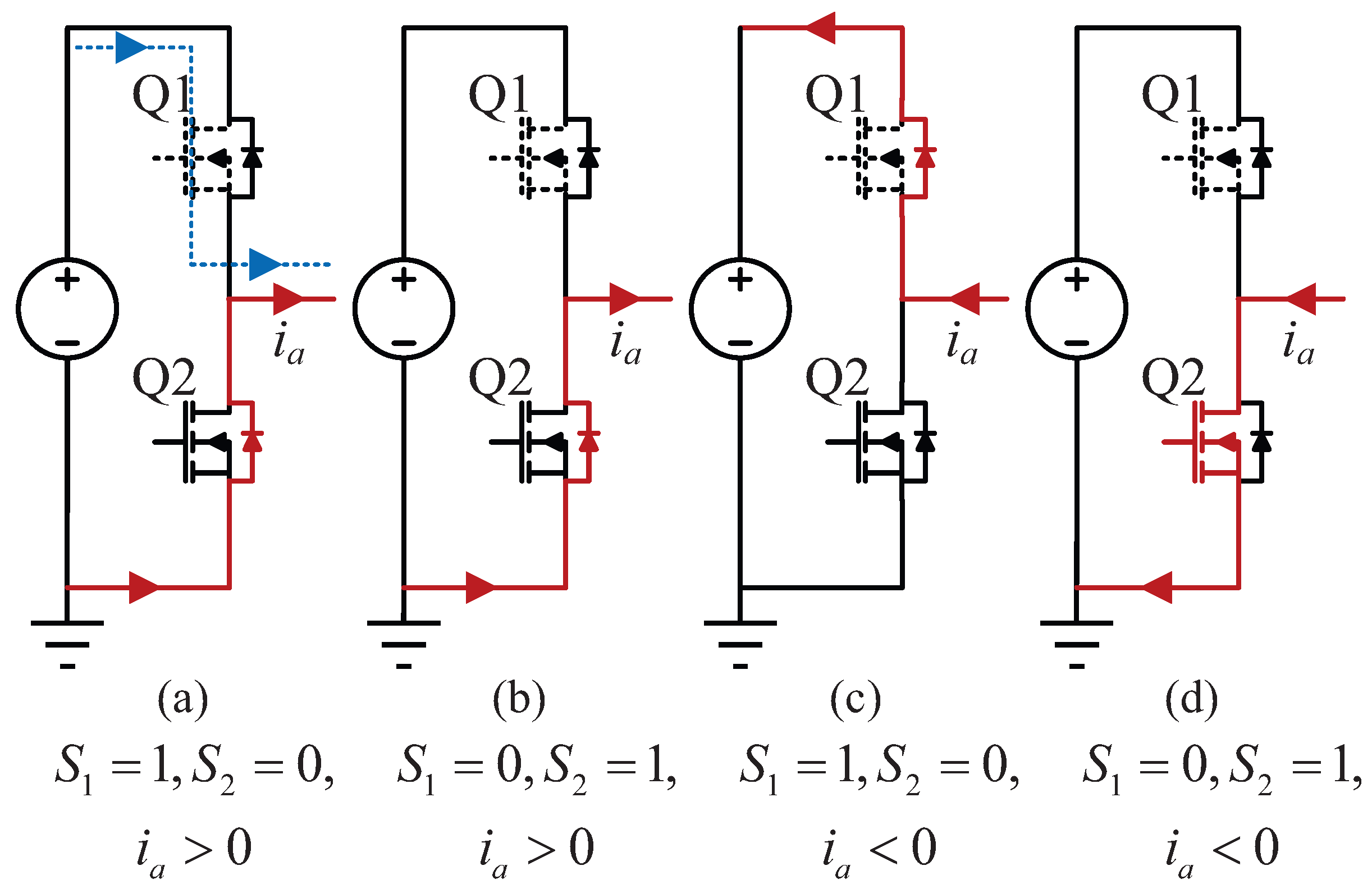
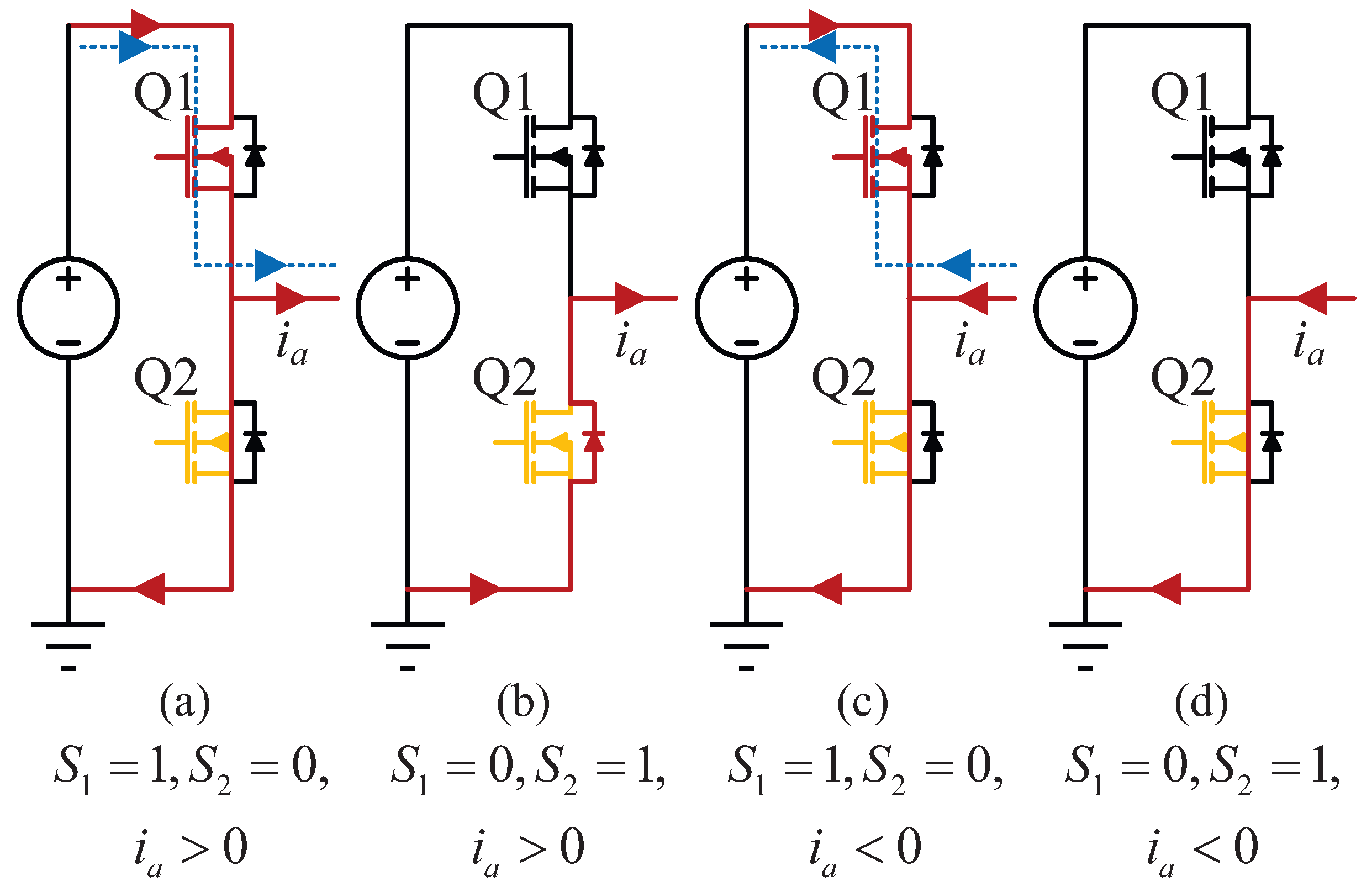
2.1.1. OC Fault Analysis

Taking a Q1 OC fault as an example, the relationship between the current path and the switch state is shown in Figure 3. When the current direction is positive, as shown in Figure 3a, the forward current that should have flowed through Q1 can only flow through the body diode of Q2, which is consistent with the situation when Q2 is conducting, and the positive half cycle of the output current is lost, while the negative half cycle is not affected, as shown in Figure 3c,d. Similarly, when a Q2 OC fault occurs, the negative half cycle of the output current is lost, while the positive half cycle is not affected.

2.1.2. SC Fault Analysis

Taking a Q2 SC fault as an example, the relationship between the current path and the switch state is shown in Figure 4. If Q1 is in a conducting state, the phase is in a shoot-through state, the current flow through Q1 and Q2 increases sharply, and the output current shows a negative offset. When a Q1 SC fault occurs, the output current shows a positive offset.

Distinguishing between one switch OC fault and another switch in same phase SC fault simply based on the output current waveform is challenging, as both faults induce a similar positive or negative current bias under most operating conditions. Therefore, developing more reliable fault diagnosis methods is necessary.

2.2. Modeling of Three-Phase Inverters Considering Faults

According to the Y connection, the sum of three-phase currents is zero; so, we have

$$\left[\begin{array}{c}{u}_{an}\\ u_{bn}\\ u_{cn}\end{array}\right]={\displaystyle \frac{1}{3}}\left[\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right]\left[\begin{array}{c}{u}_{ag}\\ u_{bg}\\ u_{cg}\end{array}\right],$$

(1)

where $u_{an}$, $u_{bn}$, and $u_{cn}$ are phase voltages, and $u_{ag}$, $u_{bg}$, and $u_{cg}$ are terminal voltages.

Assuming that the filter inductance is L, the load resistance is R, and the three phase currents are $i_a$, $i_b$, and $i_c$, according to Kirchhoff’s law, the phase voltages can be described as

$$\left\{\begin{array}{cc}\hfill u_{an}& =i_{a}R+L{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{i}_a\hfill \\ \hfill u_{bn}& =i_{b}R+L{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{i}_b\hfill \\ \hfill u_{cn}& =i_{c}R+L{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{i}_c\hfill \end{array}\right..$$

(2)

In a healthy state, switches in the three-phase inverter are in an alternating conduction state; therefore, $s_2=\overline{s_1}$, $s_4=\overline{s_3}$, and $s_6=\overline{s_5}$, where $s_x$ represents the switch state of ${\mathrm{Q}}_{\mathrm{x}}$ ($x=1,2,3,4,5,6$), $s_x=1$ denotes that ${\mathrm{Q}}_{\mathrm{x}}$ state is “ON”, and $s_x=0$ denotes that ${\mathrm{Q}}_{\mathrm{x}}$ state is “OFF”. Taking phase A as an example, the relationship between the terminal voltage, switch state, and current direction can be obtained as shown in

Table 1. Relationship between switch status, current direction, and terminal voltage in phase A under health status.

${\mathit{\delta }}_{\mathit{a}}$	${\mathit{s}}_1$	${\mathit{s}}_2$	${\mathit{u}}_{\mathit{a}\mathit{g}}$
0	0	1	0
0	1	0	$v_{dc}$
1	0	1	0
1	1	0	$v_{dc}$

, where ${\delta }_a$ represents the current direction, ${\delta }_a=0$ denotes $i_a<0$, and ${\delta }_a=1$ denotes $i_a>0$. Therefore, $u_{ag}=s_1{v}_{dc}$. Similarly, $u_{bg}=s_3{v}_{dc}$ and $u_{cg}=s_5{v}_{dc}$ can be obtained.

Combining Equations (1) and (2), the MLD model of three-phase inverter in a healthy state can be summarized as follows:

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]=-{\displaystyle \frac{R}{L}}\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]+{\displaystyle \frac{v_{dc}}{3L}}\left[\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right]\left[\begin{array}{c}{s}_1\\ s_3\\ s_5\end{array}\right].$$

(3)

When a three-phase inverter has an OC fault in the switch, taking phase A as an example, there will be a situation where both Q1 and Q2 are not conducting. When the current direction is positive, $u_{ag}=0$; when the current direction is negative, $u_{ag}=v_{dc}$. When the three-phase inverter has a switch SC fault, there will be a situation where the phase is shoot-through, and the SC current is much higher than the load current. Ignoring the influence of the internal resistance of the switch, it can be approximately assumed that $u_{ag}=v_{dc}/2$. The relationship between the terminal voltage, switch state, and current direction under fault conditions is shown in

Table 2. Relationship between switch status, current direction, and terminal voltage in phase A under fault status.

${\mathit{\delta }}_{\mathit{a}}$	${\mathit{s}}_1$	${\mathit{s}}_2$	${\mathit{u}}_{\mathit{ag}}$
0	0	0	$v_{dc}$
0	1	1	$v_{dc}/2$
1	0	0	0
1	1	1	$v_{dc}/2$

.

By combining the relationship between the switch status, current direction, and terminal voltage under health and fault conditions, taking phase A as an example, the logical relationship can be organized as follows:

$$u_{ag}=v_{dc}(\overline{s_2}(s_1+\overline{s_1}\overline{{\delta }_a})+{\displaystyle \frac{1}{2}}{s}_1{s}_2).$$

(4)

Similarly, the following equations can be obtained:

$$u_{bg}=v_{dc}(\overline{s_4}(s_3+\overline{s_3}\overline{{\delta }_b})+{\displaystyle \frac{1}{2}}{s}_3{s}_4),$$

(5)

$$u_{cg}=v_{dc}(\overline{s_6}(s_5+\overline{s_5}\overline{{\delta }_c})+{\displaystyle \frac{1}{2}}{s}_5{s}_6).$$

(6)

Finally, an MLD model of a three-phase inverter considering open and short circuit faults can be obtained as follows:

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]=-{\displaystyle \frac{R}{L}}\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]+{\displaystyle \frac{v_{dc}}{3L}}\left[\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right]\left[\begin{array}{c}\overline{s_2}(s_1+\overline{s_1}\overline{{\delta }_a})+{\displaystyle \frac{1}{2}}{s}_1{s}_2\\ \overline{s_4}(s_3+\overline{s_3}\overline{{\delta }_b})+{\displaystyle \frac{1}{2}}{s}_3{s}_4\\ \overline{s_6}(s_5+\overline{s_5}\overline{{\delta }_c})+{\displaystyle \frac{1}{2}}{s}_5{s}_6\end{array}\right].$$

(7)

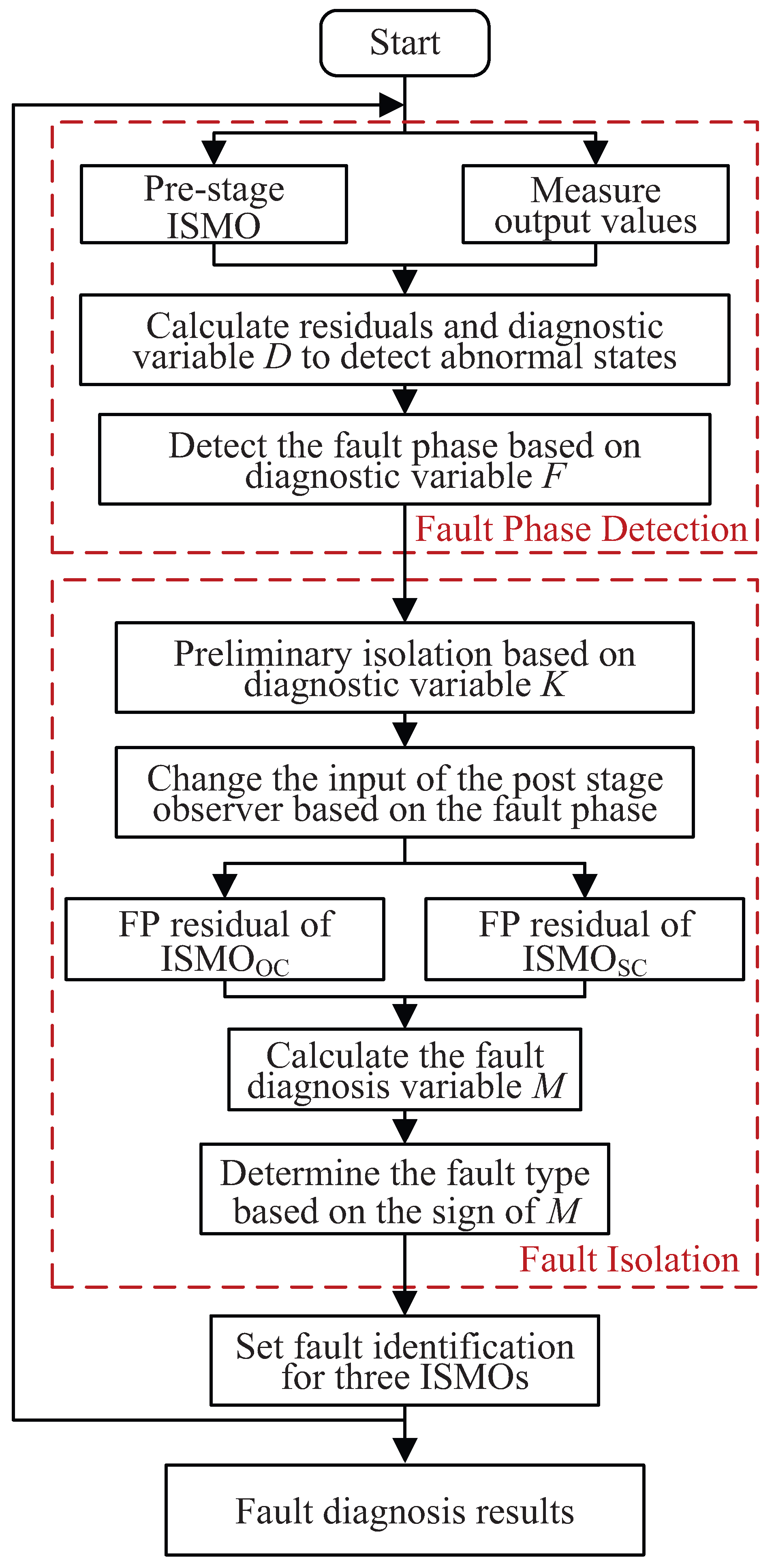
3. Fault Diagnosis Method

The fault diagnosis method proposed in this paper consists of three main components: observer design, fault phase detection strategy, and fault isolation strategy. Initially, an ISMO is designed to accurately estimate the output current. Subsequently, fault phase detection and fault isolation strategies are developed based on the residuals generated by ISMOs. The complete procedure of this method is illustrated in Figure 5.

3.1. Design of Observer

When using the MLD model to reflect the actual working state of a three-phase inverter, there may be a certain gap between the model output and the actual output, due to measurement noise and parameter uncertainty. In this case, using an observer can more accurately estimate the output. To better estimate the output of the actual system, reduce the impact of system parameter uncertainty, and effectively distinguish between healthy and faulty states, this paper designs an ISMO, which combines a sliding mode observer with interval estimation to improve the robustness of the estimated values. According to (7), considering the uncertainty of system parameters and disturbance, it can be written as follows:

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]=-{\displaystyle \frac{R}{L}}\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]+\mathsf{\theta }{\displaystyle \frac{v_{dc}}{3L}}\left[\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right]\left[\begin{array}{c}\overline{s_2}(s_1+\overline{s_1}\overline{{\delta }_a})+{\displaystyle \frac{1}{2}}{s}_1{s}_2\\ \overline{s_4}(s_3+\overline{s_3}\overline{{\delta }_b})+{\displaystyle \frac{1}{2}}{s}_3{s}_4\\ \overline{s_6}(s_5+\overline{s_5}\overline{{\delta }_c})+{\displaystyle \frac{1}{2}}{s}_5{s}_6\end{array}\right]+\left[\begin{array}{c}{v}_a\\ v_b\\ v_c\end{array}\right].$$

(8)

The above equation can be also written in the form of a state–space equation as follows:

$$\left\{\begin{array}{cc}\hfill \dot{\mathit{x}}& =\mathit{Ax}+\mathsf{\theta }\mathit{Bu}+\mathit{Dv}\hfill \\ \hfill \mathit{y}& =\mathit{Cx}\hfill \end{array}\right.,$$

(9)

where $\mathit{x}=\mathit{y}={\left[\begin{array}{ccc}{i}_a& i_b& i_c\end{array}\right]}^T$, $\mathit{v}={\left[\begin{array}{ccc}{v}_a& v_b& v_c\end{array}\right]}^T$, $\mathit{A}=-{\displaystyle \frac{R}{L}}{\mathit{I}}_{3\times 3}$, $\mathit{B}={\displaystyle \frac{1}{3L}}\left[\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right]$, $\mathit{C}={\mathit{I}}_{3\times 3}$, $\mathit{D}={\left[\begin{array}{ccc}1& 1& 1\end{array}\right]}^T$, $\mathit{u}=v_{dc}\left[\begin{array}{c}\overline{s_2}(s_1+\overline{s_1}\overline{{\delta }_a})+s_1{s}_2/2\\ \overline{s_4}(s_3+\overline{s_3}\overline{{\delta }_b})+s_3{s}_4/2\\ \overline{s_6}(s_5+\overline{s_5}\overline{{\delta }_c})+s_5{s}_6/2\end{array}\right],$ and $\mathsf{\theta }$ is an uncertain parameter vector with known upper and lower bounds. $\mathit{I}$ is the identity matrix of the corresponding dimension.

According to the proposed ISMO in [33], the system meets the following criteria:

(1)

$(\mathit{A},\mathit{C})$ is observable.

(2)

Matrix $\mathit{A}$ is Metzler matrix.

(3)

The input $\mathit{u}\left(t\right)$ and the disturbance $\mathit{v}\left(t\right)$ is positive at any time.

(4)

$\mathsf{\theta }$ satisfies ${\mathsf{\theta }}_{-}\mathit{Bu}\left(t\right)<\mathsf{\theta }\mathit{Bu}\left(t\right)<{\mathsf{\theta }}_{+}\mathit{Bu}\left(t\right)$.

The original system state variables can be better observed by designing an ISMO.

If there exists a matrix $\mathit{E}$, so that the matrix $\mathit{F}=\mathit{A}-\mathit{EC}$ meets the Hurwitz condition and Metzler condition, and ${\displaystyle K_s>{\displaystyle \frac{∥\mathit{D}∥v_{min}+3∥\mathit{D}∥v_{max}}{∥\mathit{C}∥}}}$, then the ISMO can be designed as follows:

$$\left\{\begin{array}{cc}\hfill {\dot{\widehat{\mathit{x}}}}^{+}& =\mathit{A}{\widehat{\mathit{x}}}^{+}+{\theta }_{+}\mathit{Bu}+\mathit{E}(\mathit{y}-\mathit{C}{\widehat{\mathit{x}}}^{+})\hfill \\ \hfill & +K_s\left(sign(\mathit{y}-\mathit{C}{\widehat{\mathit{x}}}^{+})\right)+{\mathit{Dv}}_{max}\hfill \\ \hfill {\dot{\widehat{\mathit{x}}}}^{-}& =\mathit{A}{\widehat{\mathit{x}}}^{-}+{\theta }_{-}\mathit{Bu}+\mathit{E}(\mathit{y}-\mathit{C}{\widehat{\mathit{x}}}^{-})\hfill \\ \hfill & +K_s\left(sign(\mathit{y}-\mathit{C}{\widehat{\mathit{x}}}^{-})\right)+{\mathit{Dv}}_{min}\hfill \end{array}\right..$$

(10)

Then, the estimated value can be obtained:

$$\widehat{\mathit{x}}=\alpha {\widehat{\mathit{x}}}^{-}+(1-\alpha ){\widehat{\mathit{x}}}^{+},$$

(11)

where $\alpha$ is the weight factor, and $\alpha ={\displaystyle \frac{\mathit{y}-\mathit{C}{\widehat{\mathit{x}}}^{+}}{\mathit{C}({\widehat{\mathit{x}}}^{-}-{\widehat{\mathit{x}}}^{+})}}={\displaystyle \frac{\mathit{x}-{\widehat{\mathit{x}}}^{+}}{{\widehat{\mathit{x}}}^{-}-{\widehat{\mathit{x}}}^{+}}}$.

The convergence and stability of the observer are demonstrated as follows:

Define the observation error:

$$\mathit{e}\left(t\right)=\mathit{x}\left(t\right)-\widehat{\mathit{x}}\left(t\right).$$

(12)

Derive the state observation error:

$$\begin{array}{cc}\hfill \dot{\mathit{e}}\left(t\right)=& (\mathit{A}-\mathit{EC})\mathit{e}\left(t\right)+\mathit{Dv}\left(t\right)-K_s(\alpha sign(\mathit{Cx}\left(t\right)-\mathit{C}{\widehat{\mathit{x}}}^{-}\left(t\right))+\hfill \\ \hfill & (1-\alpha )sign(\mathit{Cx}\left(t\right)-\mathit{C}{\widehat{\mathit{x}}}^{+}(t)))-\alpha \mathit{D}{\mathit{v}}_{min}-(1-\alpha )\mathit{D}{\mathit{v}}_{max}.\hfill \end{array}$$

(13)

Construct Lyapunov functions:

$$\mathit{V}\left(t\right)={\mathit{e}}^T\left(t\right)\mathit{P}\mathit{e}\left(t\right),$$

(14)

where $\mathit{P}$ is a positive-definite matrix, and $\mathit{Q}$ is a positive definite matrix and satisfies the Lyapunov equation:

$${(\mathit{A}-\mathit{EC})}^T\mathit{P}+\mathit{P}(\mathit{A}-\mathit{EC})=-\mathit{Q}.$$

(15)

According to the second Lyapunov method, the system is asymptotically stable within a finite time when $\mathit{V}\dot{\mathit{V}}<0$. We derive $\mathit{V}\left(t\right)$ as follows:

$$\begin{array}{cc}\hfill \dot{\mathit{V}}=& -{\mathit{e}}^T\mathit{Qe}+2{\mathit{e}}^T\mathit{P}(\mathit{Dv}\left(t\right)-\alpha \mathit{D}{\mathit{v}}_{min}-(1-\alpha )\mathit{D}{\mathit{v}}_{max}-\hfill \\ \hfill & K_s(\alpha sign(\mathit{Cx}\left(t\right)-\mathit{C}{\widehat{\mathit{x}}}^{-}\left(t\right))+(1-\alpha )sign(\mathit{Cx}\left(t\right)-\mathit{C}{\widehat{\mathit{x}}}^{+}\left(t\right)))).\hfill \end{array}$$

(16)

Applying the Rayleigh inequality,

$$0<{\lambda }_{min}\left(\mathit{Q}\right){∥\mathit{e}∥}^2\le {\mathit{e}}^T\mathit{Qe}\le {\lambda }_{max}\left(\mathit{Q}\right){∥\mathit{e}∥}^2,$$

(17)

where ${\lambda }_{min}\left(\mathit{Q}\right)$ and ${\lambda }_{max}\left(\mathit{Q}\right)$ are the minimum eigenvalue and maximum eigenvalue of matrix $\mathit{Q}$, respectively.

From (11) and (12), it can be concluded that

$$\mathit{Ce}=\alpha (\mathit{Cx}-\mathit{C}{\widehat{\mathit{x}}}^{-})+(1-\alpha )(\mathit{C}{\widehat{\mathit{x}}}^{+}-\mathit{Cx}).$$

(18)

Therefore,

$$sign\left(\mathit{Ce}\right)\le \alpha sign(\mathit{Cx}-\mathit{C}{\widehat{\mathit{x}}}^{-})+(1-\alpha )sign(\mathit{C}{\widehat{\mathit{x}}}^{+}-\mathit{Cx}).$$

(19)

From (16), (17), and (19), it can be concluded that

$$\dot{\mathit{V}}<-{\lambda }_{min}\left(\mathit{Q}\right){∥\mathit{e}∥}^2+2{\mathit{e}}^T\mathit{P}(\mathit{Dv}\left(t\right)-\alpha \mathit{D}{\mathit{v}}_{min}-(1-\alpha )\mathit{D}{\mathit{v}}_{max})-2{\mathit{e}}^T\mathit{P}{K}_{s}sign\left(\mathit{Ce}\right).$$

(20)

By applying the norm inequality, it can be obtained that

$$\dot{\mathit{V}}<-{\lambda }_{min}\left(\mathit{Q}\right){∥\mathit{e}∥}^2+2{\lambda }_{max}\left(\mathit{P}\right)∥\mathit{e}∥(∥\mathit{D}∥{\mathit{v}}_{min}+3∥\mathit{D}∥{\mathit{v}}_{max}-∥\mathit{C}∥∥K_s∥).$$

(21)

Therefore, when ${\displaystyle K_s>{\displaystyle \frac{∥\mathit{D}∥v_{min}+3∥\mathit{D}∥v_{max}}{∥\mathit{C}∥}}}$, $\dot{\mathit{V}}<0$ holds. Since $\mathit{V}={\mathit{e}}^T\mathit{P}\mathit{e}>0$, $\mathit{V}\dot{\mathit{V}}<0$ holds, and the system is asymptotically stable.

In this paper, the ISMO parameters are as follows: $\mathit{E}=500·I_{3\times 3}$, $K_s=500$.

3.2. Fault Phase Detection Strategy

Fault phase detection first requires abnormal detection, and this part is implemented using an ISMO called the pre-stage ISMO. The residual output current of the pre-stage observer is denoted as $\mathit{r}$, $\mathit{r}=\left[\begin{array}{c}{r}_a\\ r_b\\ r_c\end{array}\right]$, where $\left\{\begin{array}{cc}\hfill r_a& ={\widehat{i}}_a-i_a\hfill \\ \hfill r_b& ={\widehat{i}}_b-i_b\hfill \\ \hfill r_c& ={\widehat{i}}_c-i_c\hfill \end{array}\right.$.

We define abnormal state detection variable:

$${\displaystyle D={\displaystyle \frac{1}{T}}{\int }_{t-T}^t{∥\mathit{r}∥}_1\mathrm{d}t.}$$

(22)

An abnormal state threshold is set and denoted as ${\theta }_1$. When $D>{\theta }_1$ occurs, it indicates that a fault has occurred in the three-phase inverter. The selection of ${\theta }_1$ has a great impact on the accuracy of fault diagnosis as well as the occurrence of false alarms and missed alarms. The appropriate value of ${\theta }_1$ can be obtained through the following deduction process.

We discretize the state space equation using the Euler method as follows:

$$\mathit{x}(\mathrm{k}+1)={\mathit{A}}_z\mathit{x}\left(\mathrm{k}\right)+{\mathit{B}}_z\mathit{u}\left(\mathrm{k}\right),$$

(23)

where ${\mathit{A}}_z=T\mathit{A}+\mathit{I}$, ${\mathit{B}}_z=T\mathit{B}$, $\mathit{I}$ is the identity matrix, and T is the time step.

The discrete form of the sliding mode observer is

$$\begin{array}{cc}\hfill \widehat{\mathit{x}}(\mathrm{k}+1)& ={\mathit{A}}_z\widehat{\mathit{x}}\left(\mathrm{k}\right)+{\mathit{B}}_z\mathit{u}\left(\mathrm{k}\right)+{\mathit{E}}_z(\mathit{y}\left(\mathrm{k}\right)-\mathit{C}\widehat{\mathit{y}}\left(\mathrm{k}\right))\hfill \\ \hfill & +K_z·sign(\mathit{y}\left(\mathrm{k}\right)-\mathit{C}\widehat{\mathit{y}}\left(\mathrm{k}\right)),\hfill \end{array}$$

(24)

where ${\mathit{E}}_z=T\mathit{E}$, and $K_z=T{K}_s$.

The discretized residual current can be expressed as

$$\begin{array}{cc}\hfill \mathit{r}(\mathrm{k}+1)& =\widehat{\mathit{x}}(\mathrm{k}+1)-\mathit{x}(\mathrm{k}+1)\hfill \\ \hfill & =({\mathit{A}}_z-{\mathit{E}}_z)\mathit{r}\left(\mathrm{k}\right)-K_z·sign\left(\mathit{r}\left(\mathrm{k}\right)\right).\hfill \end{array}$$

(25)

The threshold ${\theta }_1$ selection can be obtained based on the residuals. By taking the norm on both sides of the residual expression, we have

$$∥\mathit{r}(\mathrm{k}+1)∥=∥({\mathit{A}}_z-{\mathit{E}}_z)\mathit{r}\left(\mathrm{k}\right)-K_z·sign(\mathit{r}\left(\mathrm{k}\right))∥.$$

(26)

From the norm triangle inequality, it can be concluded that

$$∥\mathit{r}(\mathrm{k}+1)∥\le ∥{\mathit{A}}_z-{\mathit{E}}_z∥∥\mathit{r}\left(\mathrm{k}\right)∥+∥K_z∥.$$

(27)

Therefore, the threshold can be set as follows:

$${\theta }_1=\zeta (∥{\mathit{A}}_z-{\mathit{E}}_z∥∥\mathit{r}\left(\mathrm{k}\right)∥+∥K_z∥),$$

(28)

where $\zeta$ is the coefficient considering the robustness of the fault diagnosis method, usually $\zeta >1$. If the coefficient is too high, it will lead to missed alarms in the fault diagnosis method. If it is too low, it will lead to false alarms in the fault diagnosis method. To ensure the stability and reliability of the fault diagnosis methods, $\zeta \in (1.5,3)$ is suggested, and the specific values can be obtained through simulation.

When $D>{\theta }_1$ occurs, we start detecting the fault phase. We define the fault phase detection variable as

$${\displaystyle F_x=\sqrt{{\displaystyle \frac{1}{T}}{\int }_{t-T}^t{r}_x^2\mathrm{d}t},}$$

(29)

where $x=a,b,c$. The corresponding phase of the largest among $F_a$, $F_b$, and $F_c$ is the fault phase.

3.3. Fault Isolation Strategy

The fault isolation strategy is divided into two parts: feature-based preliminary isolation and residual-based fault isolation. According to the operating mode analysis in Section 2, the fault feature variable can be defined as

$${\displaystyle K={\displaystyle \frac{1}{T}}{\int }_{t-T}^t{r}_f\mathrm{d}t,}$$

(30)

where $r_f$ is the residual of the fault phase. $K>0$ indicates that there may be an OC fault in the upper switch or an SC fault in the lower switch, and $K<0$ indicates that there may be an OC fault in the lower switch or an SC fault in the upper switch. Therefore, six possible scenarios for the first step of fault isolation can be obtained, as shown in

Table 3. Criteria of preliminary isolation.

Fault Phase	K	Possible Fault Type
A	$K>0$	O1 or S2
	$K<0$	S1 or O2
B	$K>0$	O3 or S4
	$K<0$	S3 or O4
C	$K>0$	O5 or S6
	$K<0$	S5 or O6

.

Each situation includes two possible fault modes, OC or SC, which require further isolation. To distinguish fault modes, two post-stage ISMOs are used, which are noted as ISMO_OC and ISMO_SC, respectively. These two ISMOs are completely identical in structure and parameters to the pre-stage ISMO, with only different input. They simulate open- or short-circuit faults by resetting or setting the switch control signal. Simulating possible OC faults in ISMO_OC and possible SC faults in ISMO_SC and calculating the residual output of the two ISMOs, the residual of ISMO_OC is $\left\{\begin{array}{cc}\hfill r_{Oa}& ={\widehat{i}}_{Oa}-i_{Oa}\hfill \\ \hfill r_{Ob}& ={\widehat{i}}_{Ob}-i_{Ob}\hfill \\ \hfill r_{Oc}& ={\widehat{i}}_{Oc}-i_{Oc}\hfill \end{array}\right.$, and the residual of ISMO_SC is $\left\{\begin{array}{cc}\hfill r_{Sa}& ={\widehat{i}}_{Sa}-i_{Sa}\hfill \\ \hfill r_{Sb}& ={\widehat{i}}_{Sb}-i_{Sb}\hfill \\ \hfill r_{Sc}& ={\widehat{i}}_{Sc}-i_{Sc}\hfill \end{array}\right.$. We select the residual of the corresponding phase based on the fault phase, namely $r_{Of}$ and $r_{Sf}$. We define residual diagnostic variable:

$$M=\left|r_{Sf}\right|-\left|r_{Of}\right|.$$

(31)

$M>0$ indicates an OC fault, and $M<0$ indicates an SC fault. Considering the stability of the diagnosis, a threshold ${\theta }_2$ is set, and the second step of diagnosis will only begin when $\left|M\right|>{\theta }_2$. According to the residual of ISMO, ${\theta }_2$ can be set to 10∼20% of the expected output current amplitude to ensure robustness. The final fault diagnosis method is shown in

Table 4. Criteria of proposed fault diagnosis method.

D	Fault Phase	K	M	Diagnostic Result
$D<{\theta }_1$	−			Health
$D>{\theta }_1$	A	$K>0$	$M>{\theta }_2$	O1
			$M<-{\theta }_2$	S2
		$K<0$	$M>{\theta }_2$	O2
			$M<-{\theta }_2$	S1
	B	$K>0$	$M>{\theta }_2$	O3
			$M<-{\theta }_2$	S4
		$K<0$	$M>{\theta }_2$	O4
			$M<-{\theta }_2$	S3
	C	$K>0$	$M>{\theta }_2$	O5
			$M<-{\theta }_2$	S6
		$K<0$	$M>{\theta }_2$	O6
			$M<-{\theta }_2$	S5

.

When a fault is diagnosed, we set or reset the corresponding switch signal of the three ISMO inputs and reset the two post-stage ISMO input signals used for fault type isolation, and the three ISMOs are completely consistent, so that the ISMOs can continue to track the output status of the system, diagnose the next incoming fault, and thus complete the diagnosis of cascaded open/short-circuit faults.

4. Simulation and Experiment Verification

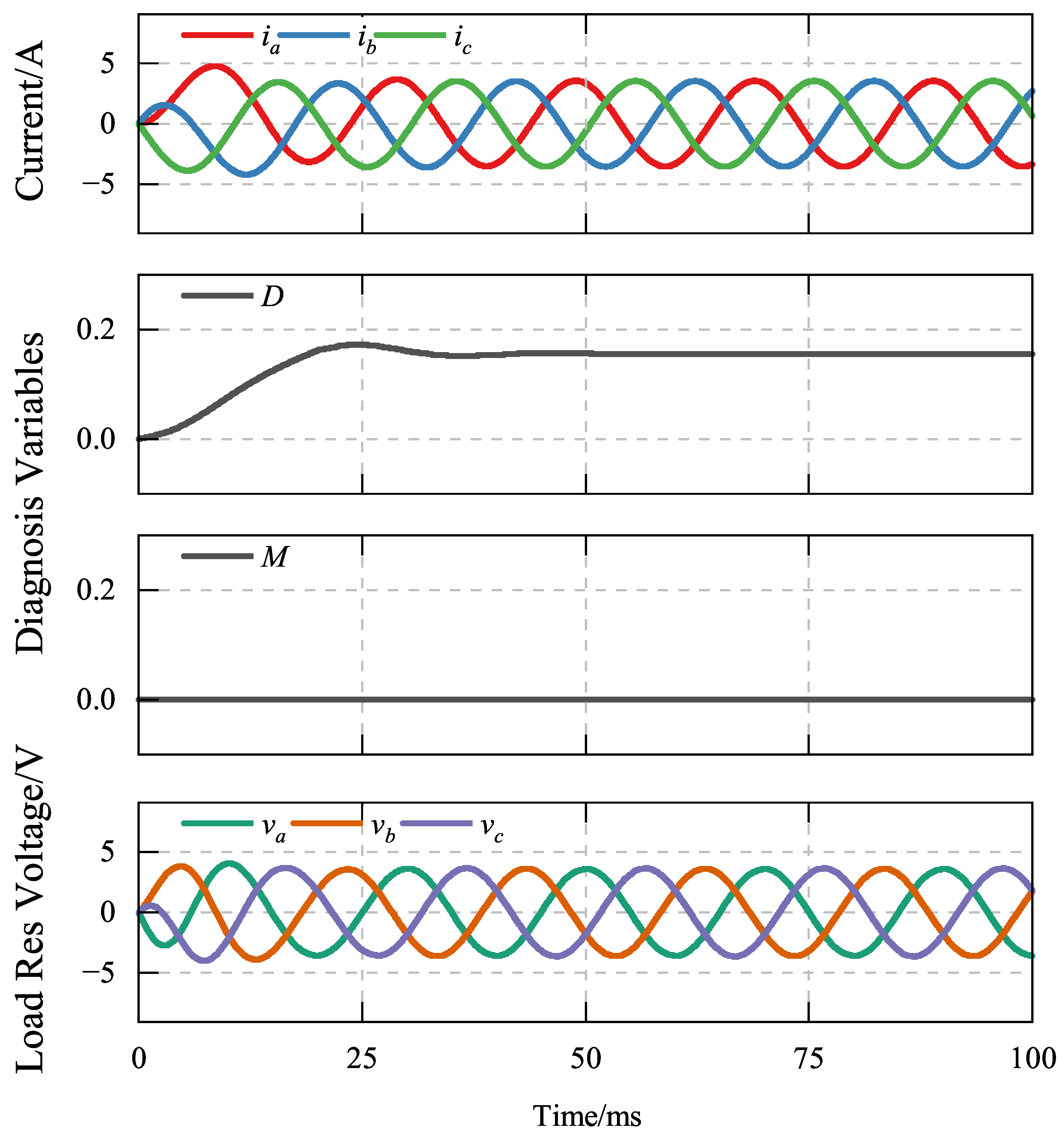
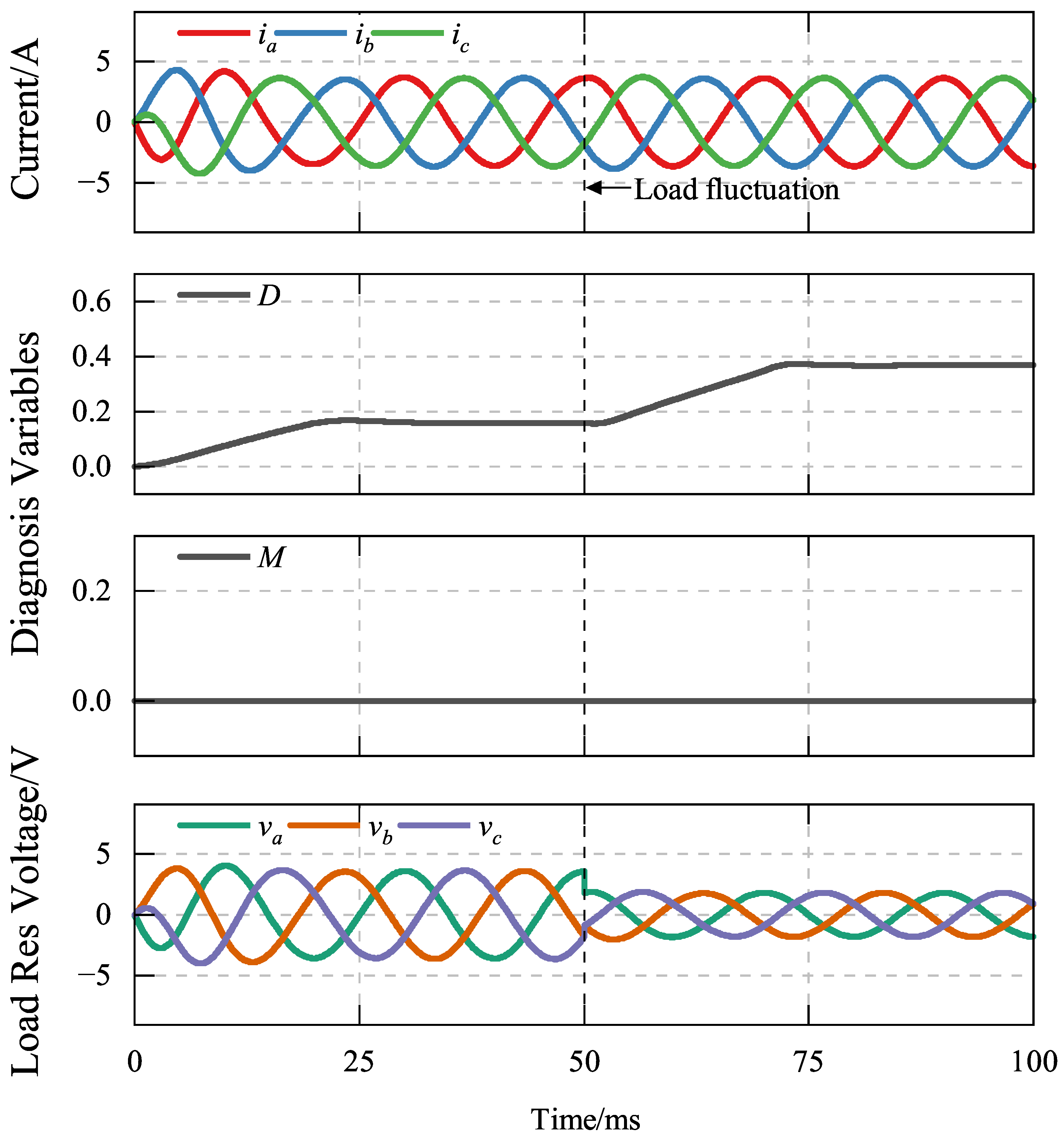
4.1. Simulation Analysis

To verify the effectiveness of the proposed fault diagnosis method, simulation analysis was conducted. A three-phase inverter circuit was built in the simulation, and a fault diagnosis algorithm module was constructed using model-based design methods to simplify the development process. The circuit parameters used in the simulation are shown in

Table 5. Component parameters of simulation circuit.

Parameter	Value
Output frequency	50 Hz
DC input voltage	20 V
Switching frequency	10 kHz
Load resistance	1 $\Omega$
Inductance	5 mH
Output current	3.6 A

. The current control method is to decouple the three-phase current into d-axis current and q-axis current, controlling the d-axis current to 0 A and the q-axis current to 3.6 A. The d-axis and q-axis currents are controlled by a PI controller, with $K_p=0.08$ and $K_i=0.005$.

To simulate the measurement noise of current sensors in an actual three-phase inverter circuit, white noise with a mean value of 0.1A was added to the current measurement results transmitted to the fault diagnosis algorithm in the simulation circuit. In the healthy state, according to the previous definition, considering measurement errors, D will not be larger than 0.3. Therefore, ${\theta }_1$ can be taken as 0.5, to ensure robustness under uncertain parameter conditions. In addition, based on the amplitude of the current, we set the threshold ${\theta }_2$ to 0.6. The waveform of the output current, phase voltage, and fault diagnosis variables in the healthy state is shown in Figure 6. To demonstrate the current control effect, a waveform of the voltage across the load resistor is added.

Since D has not reached ${\theta }_1$, the subsequent fault classification algorithm is not triggered, and M remains zero.

4.1.1. Robustness Verification

To simulate the robustness of the observer under different load conditions, the load resistance was reduced by half at 50 ms in the simulation. To test the convergence speed of the observer, the current controller parameters were modified to $K_p=0.2$ and $K_i=0.08$ to improve the response speed. The results obtained in a healthy state are shown in Figure 7. After the load suddenly changes, D will increase, but it has not reached ${\theta }_1$; so, fault detection will not be triggered. The above simulation of load fluctuations can verify the rationality of the threshold selection and will not cause false alarms.

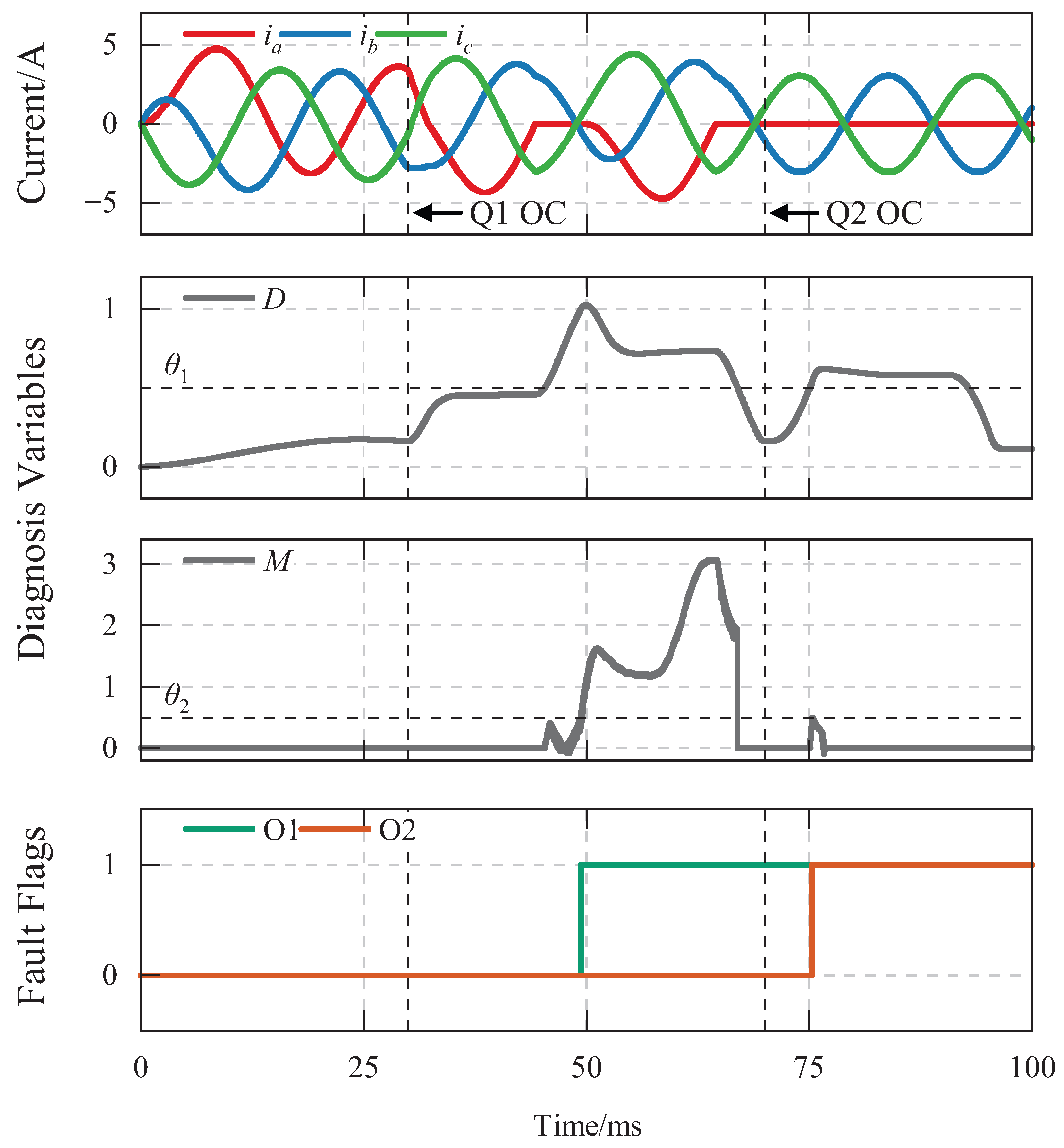
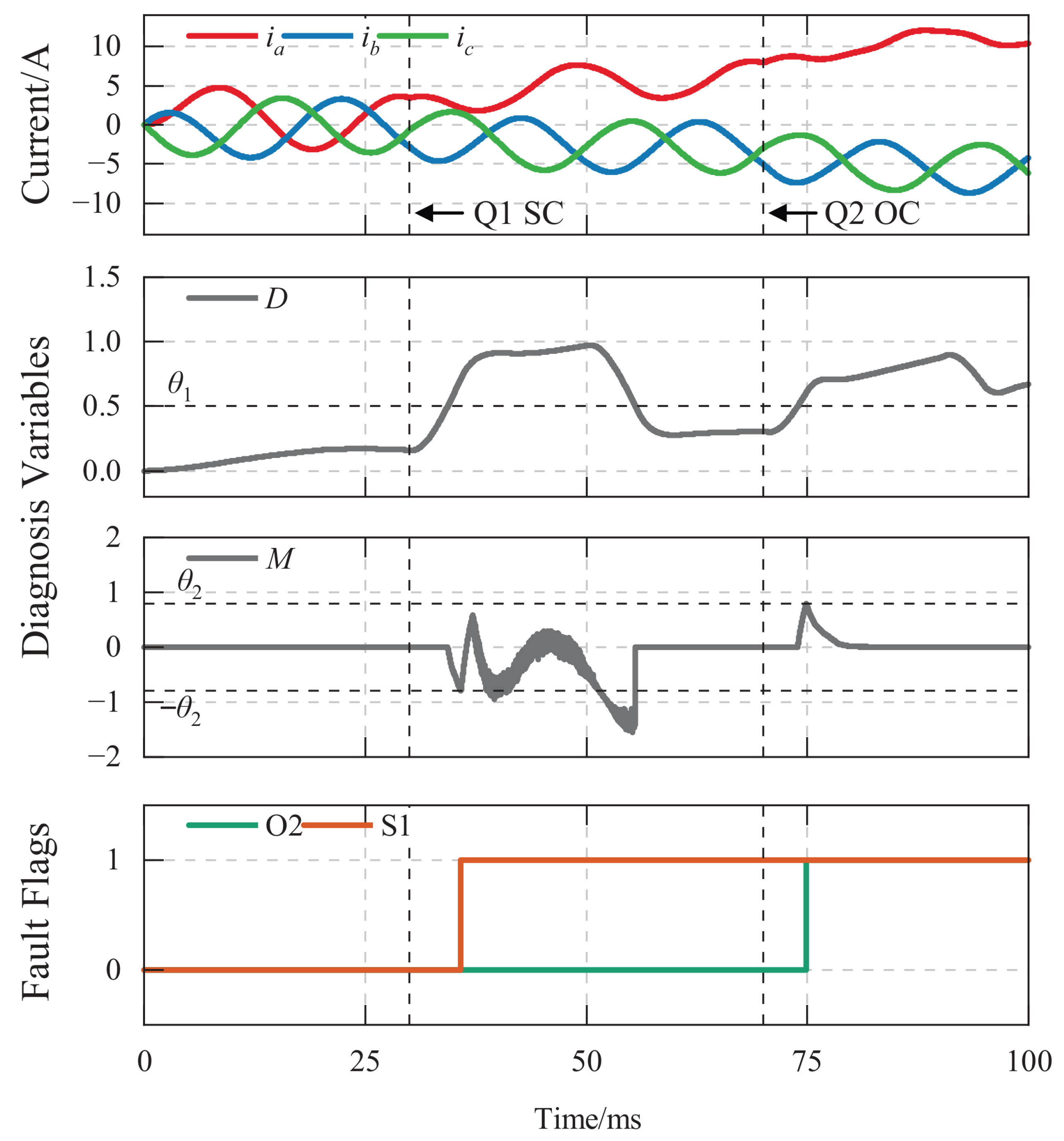
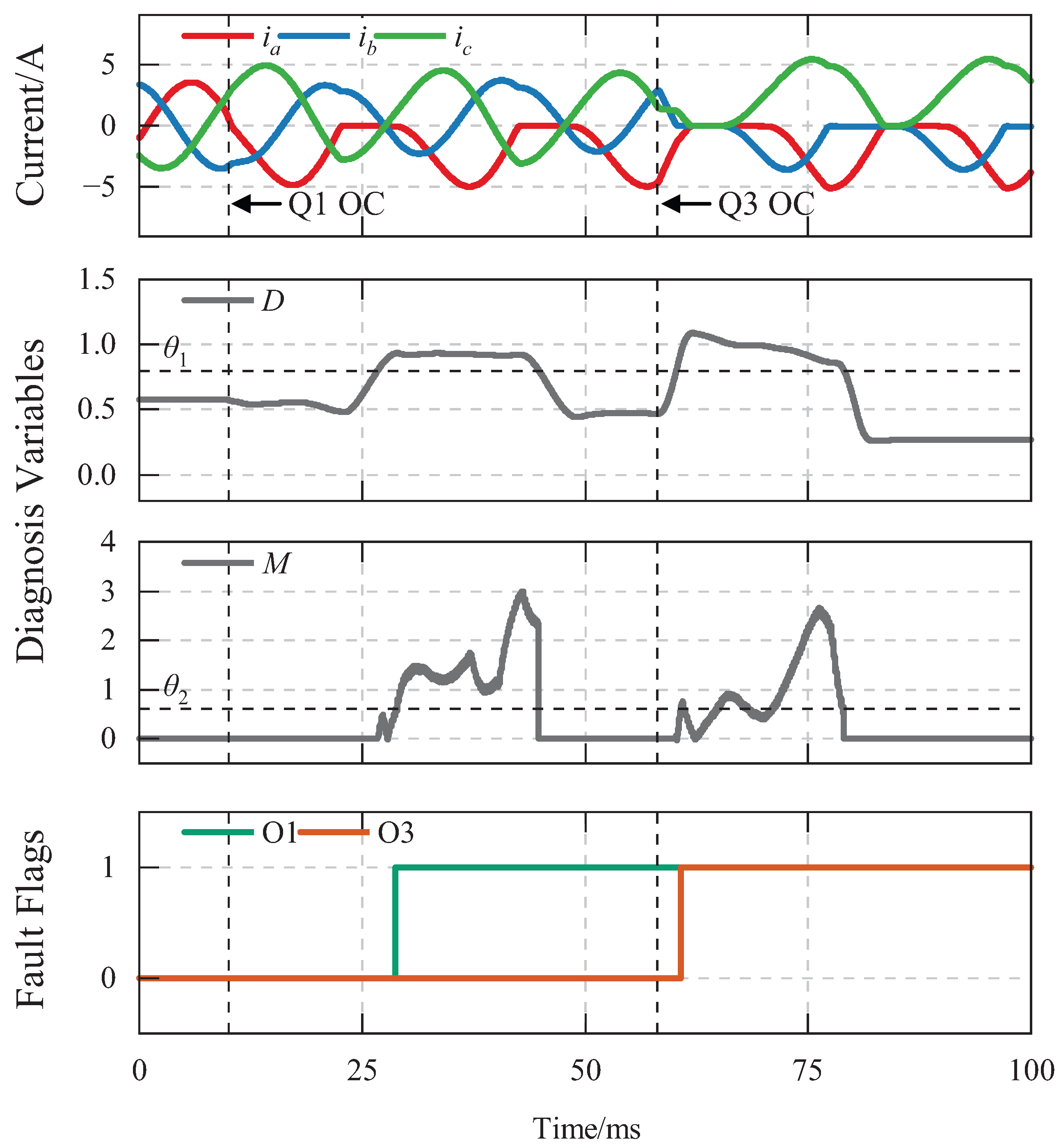
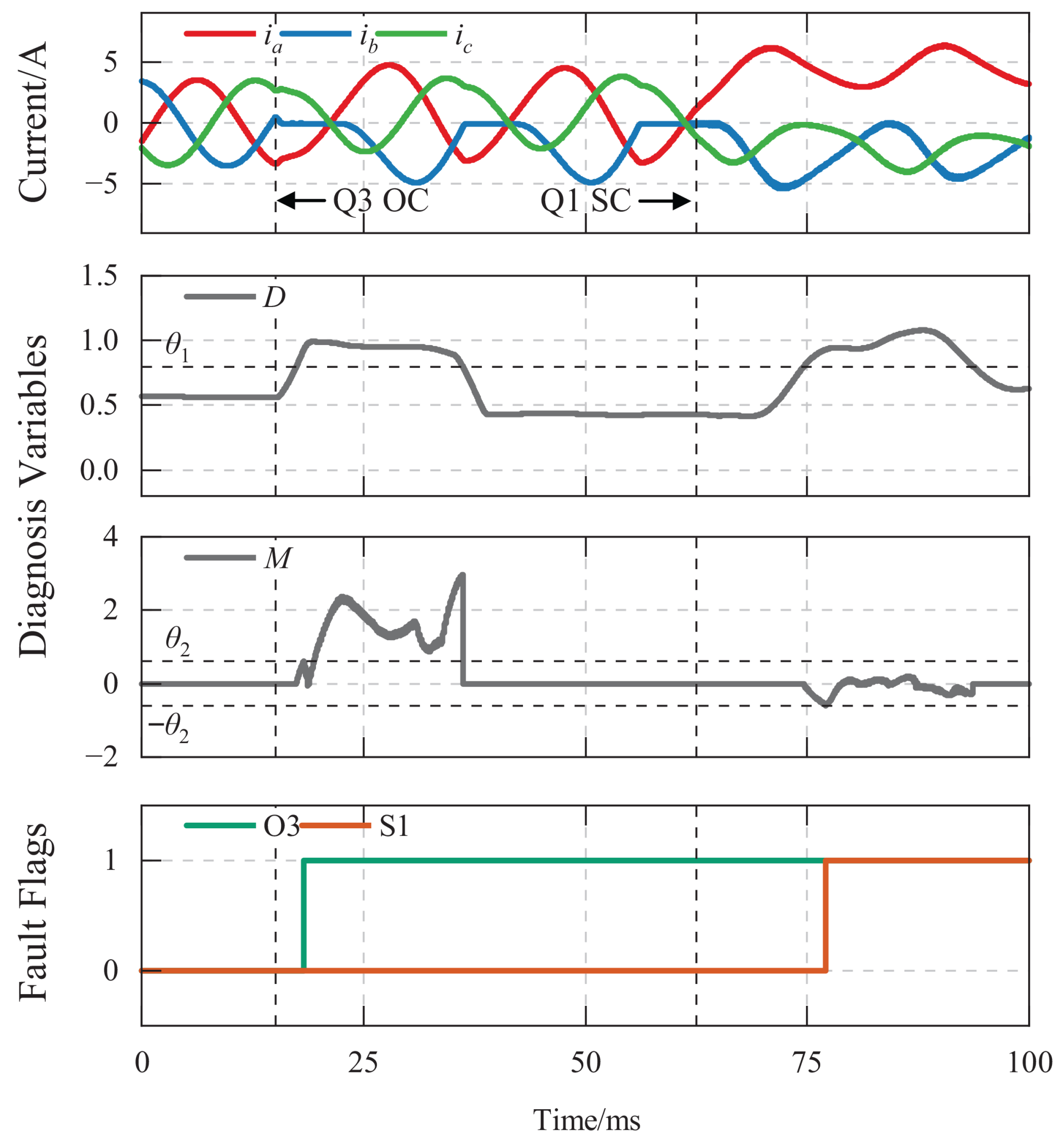
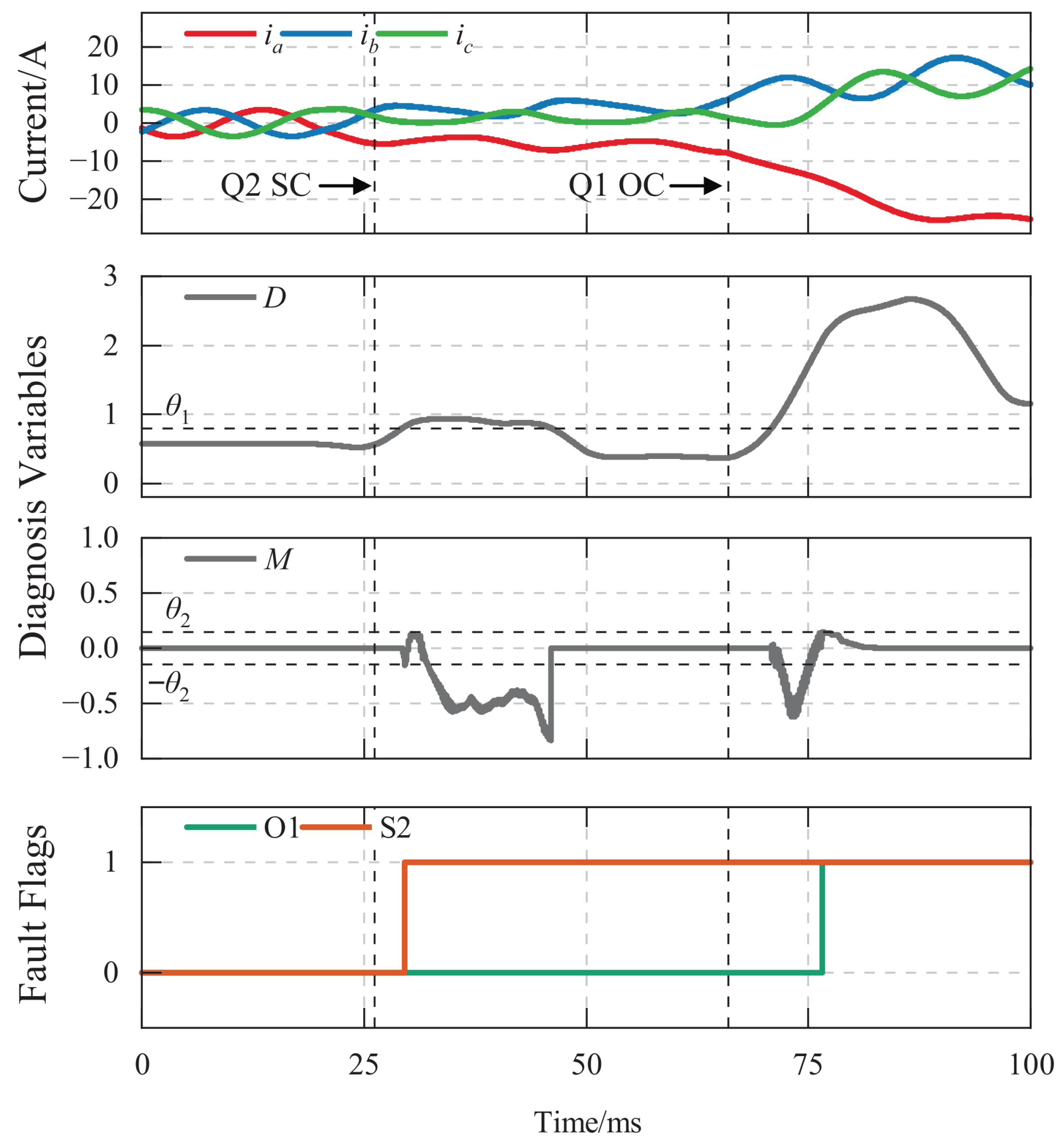
4.1.2. OC–OC Cascaded Fault Simulation

In the case of an OC and OC cascaded fault, taking a Q1 and Q2 OC fault as an example, the waveforms of the output current and diagnosis variables are shown in Figure 8. The Q1 OC fault is triggered at 30 ms. However, at this time, the current of phase A is in the positive half cycle decreasing part, and the current waveform of phase A is not much different from the healthy state until the next positive half cycle arrives. Therefore, no fault is diagnosed. After the positive half cycle arrives, the positive half cycle of phase A’s current is missing, and D rapidly rises, triggering two ISMOs in the fault isolation part. M is positive and reaches ${\theta }_2$, diagnosing a Q1 OC fault. After diagnosing the fault, D decreases and exits the fault isolation, and M becomes 0. A Q2 OC fault triggers at 70 ms, like before, diagnosing the fault at around 5 ms.

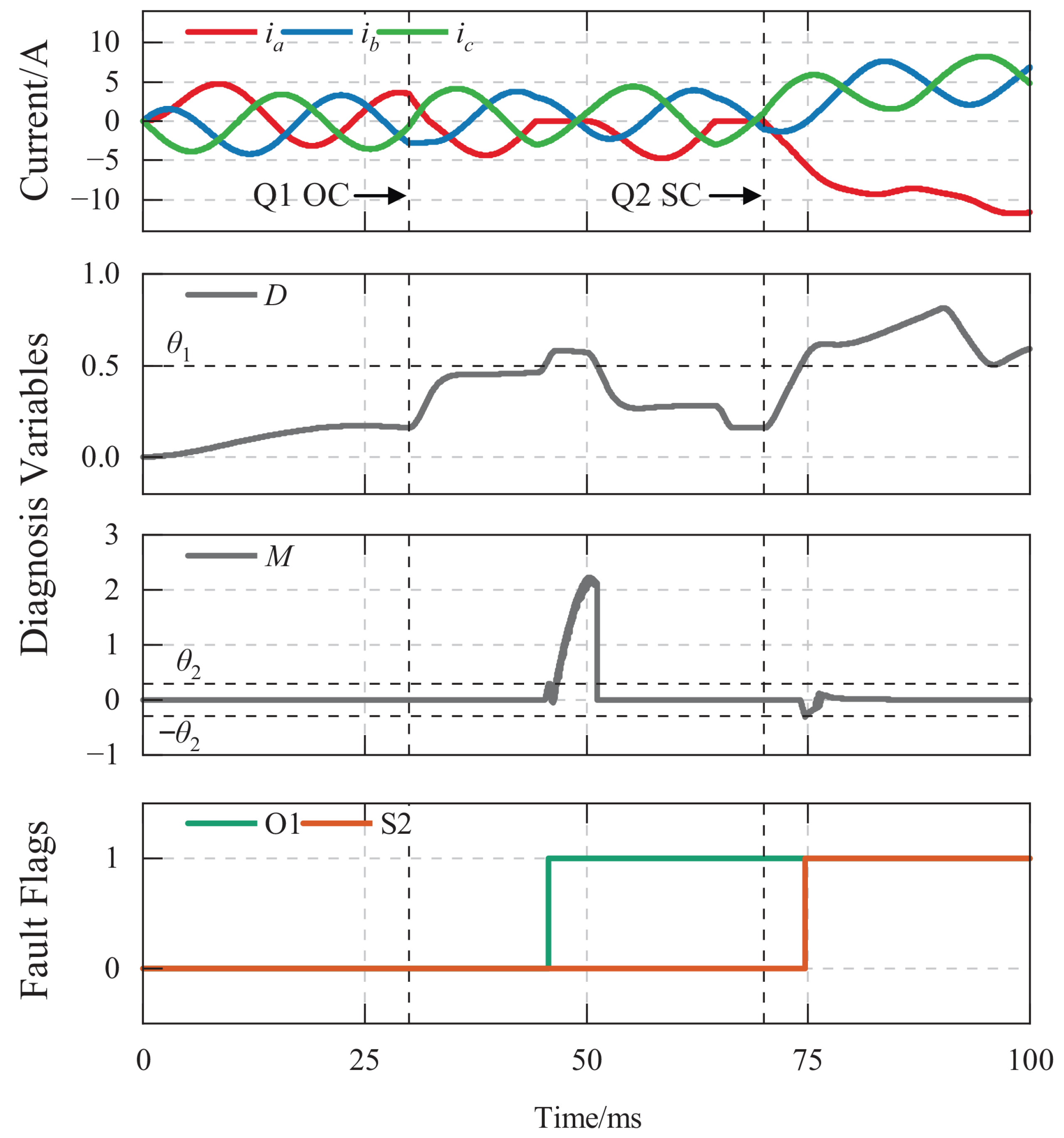
4.1.3. OC–SC Cascaded Fault Simulation

Under an OC and SC cascaded fault, taking a Q1 OC fault and a Q2 SC fault as an example, the waveforms of the output current and diagnosis variables are shown in Figure 9. The Q1 OC fault diagnosis is the same as in the previous section. At 70 ms, a Q2 SC fault occurs, and D rapidly increases to reach ${\theta }_1$. Then, M is negative and reaches $-{\theta }_2$. The fault is diagnosed at around 5 ms.

4.1.4. SC–OC Cascaded Fault Simulation

Under the cascaded fault of SC and OC, taking a Q1 SC fault and Q2 OC fault as an example, the waveforms of the output current and diagnosis variables are shown in Figure 10. The Q1 SC fault is first triggered. After the fault occurs, M becomes negative and reaches $-{\theta }_2$. After about one cycle, D decreases to less than ${\theta }_1$, and the fault diagnosis ends. Then, Q2 has an OC fault, with D exceeding ${\theta }_1$ and M reaching the ${\theta }_2$, diagnosing Q2 as an OC fault.

4.2. Experimental Verification

To verify the effectiveness of the fault diagnosis method proposed in this paper, the experimental platform is set up as shown in Figure 11, mainly including a three-phase inverter circuit, three-phase load, current sensor, signal conditioning circuit, ADC module, and a Zynq core board. The parameters of the three-phase inverter and load are shown in

Table 6. Three-phase inverter and load parameters.

Parameter	Value
Output frequency	50 Hz
DC input voltage	20 V
Switching frequency	10 kHz
Load resistance	1 $\Omega$
Inductance	5 mH
Output current	3.6 A

. The control parameters are the same as for the simulation. Due to the need for simulated SC experiments, higher voltages can cause damage to the MOSFETs of the three-phase inverter. Therefore, lower voltage and current levels were used during the experiment, and the output current of the DC power supply was limited.

The three-phase inverter is controlled by a microcontroller, and the driving signal output by the microcontroller is converted through an optical fiber and connected to the Zynq. The ADC collects the conditioned three-phase current signal and DC bus voltage signal, which are also sent to the Zynq for processing. All signals are synchronously sampled. For current sampling, a hall sensor with a bandwidth of 25 kHz is used. The fault diagnosis method proposed in this paper is an online operation that can diagnose while the three-phase inverter is working. The method is deployed in the programmable logic part of the Zynq, with an execution frequency of 1 MHz. The processing system part is responsible for implementing ethernet communication with the host PC to obtain the measured current waveforms, diagnosis variable waveforms, and diagnosis results. The simulated fault command is sent to the microcontroller through host PC, and the microcontroller drives the three-input logic gate to pull the driving signal of the switching device low or high, to simulate the open- or short-circuit fault. Due to the difference between the residuals obtained from the experimental measurements and simulations, the threshold for diagnostic variables has also been adjusted. The threshold ${\theta }_1$ for the experimental part can be calculated as 0.8 using Equation (28), and threshold ${\theta }_2$ remains at 0.6.

4.2.1. OC–OC Cascaded Fault Experiment

The waveform of the Q1 OC and Q3 OC cascaded fault diagnosis process is shown in Figure 12. After a Q1 OC fault occurs, D increases over ${\theta }_1$. At this time, the phase with the largest residual three-phase current is taken as phase A. The input signal of the post-stage ISMO changes, and M is the difference between the outputs of the two post-stage ISMOs in phase A. M is positive and reaches ${\theta }_2$, and the diagnosis result is a Q1 OC fault. After changing the corresponding input signal of the pre-stage ISMO, D decreases to a level less than ${\theta }_1$, and the fault diagnosis is completed. Similarly, Q3 is diagnosed with an OC fault.

4.2.2. OC–SC Cascaded Fault Experiment

The waveform of the Q3 OC and Q1 SC cascaded fault diagnosis process is shown in Figure 13. The process of diagnosing the Q3 OC fault is similar to that in the previous section. When the Q1 SC fault occurs, D increases over ${\theta }_1$, and the residual current of phase A is the largest. M is the difference between phase A’s outputs of post-stage ISMOs, and M is negative, reaching $-{\theta }_2$, and a Q1 SC fault is diagnosed.

4.2.3. SC–OC Cascaded Fault Experiment

The waveform of the Q2 SC fault and Q1 OC fault cascaded fault diagnosis process is shown in Figure 14. After the SC fault occurred in Q2, the current of phase A fluctuated rapidly, D increased beyond ${\theta }_1$, $M<-{\theta }_2$, and the SC fault was diagnosed. The diagnosis variable D decreased after one cycle. Subsequently, a Q1 OC fault occurred, and D increased again. Due to the Q2 SC fault, M was negative, and the fault had been diagnosed; so, it was ignored. Then, M reached ${\theta }_2$, and the Q1 OC fault was diagnosed.

4.3. Accuracy of Proposed Fault Diagnosis Method

In order to verify the universality of the proposed method, experiments covering possible types of faults have been conducted. Cascaded faults can be divided into two switch faults of the same phase and two switch faults of different phases. These two types of faults can be divided into three categories: two switch OC, SC first and then OC, and OC first and then SC. Due to the severe overcurrent that may cause device damage when both switches are short-circuited simultaneously, the experiment was not conducted. The faults of two switches in the same phase can be divided into two categories: upper switch fault followed by lower switch fault and lower switch fault followed by upper switch fault, while the faults of two switches in different phases can be divided into four categories: upper switch fault, lower switch fault, upper switch fault followed by lower switch fault, and lower switch fault followed by upper switch fault. Overall, there are 18 possible types of cascading faults. Due to only protecting Q1 and Q2, only Q1 and Q2 are used to simulate short-circuit faults. To verify the repeated testing accuracy of the proposed fault diagnosis method, a fault diagnosis experiment on twelve types of faults was conducted, simulating each type of fault 20 times. The diagnosis results are shown in

Table 7. Statistics of fault diagnosis results.

Fault Type	T/MA/FA	Fault Type	T/MA/FA
O1O2	20/0/0	O2O1	20/0/0
O1S2	20/0/0	S2O1	19/1/0
S1O2	18/2/0	O2S1	20/0/0
O1O3	20/0/0	O2O4	20/0/0
O1O4	20/0/0	O2O3	20/0/0
S1O3	19/0/1	S2O4	19/1/0
S1O4	18/2/0	S2O3	18/1/1
O3S1	19/1/0	O4S2	19/0/1
O3S2	19/1/0	O4S1	19/0/1

, where T represents correct diagnosis, MA represents a missed alarm, and FA represents a false alarm. For OC–OC cascaded faults, the accuracy of the fault diagnosis is relatively high. When it comes to SC faults, due to inconsistent triggering timing, the fault diagnosis results may include a missed alarm and a false alarm. However, the diagnosis accuracy of a single fault is always above or equal to 90%. In this experiment, the overall accuracy of the fault diagnosis method proposed in this paper was 96.39%.

4.4. Comparison with Existing Fault Diagnosis Methods

The fault diagnosis method proposed in this paper was compared with existing fault diagnosis methods in terms of diagnosable fault types, fault diagnosis time, consideration of multi-switch faults and load change, and microcontroller realizability. The results are shown in

Table 8. Comparison with other fault diagnosis methods.

Diagnosis Method	Fault Type	Diagnosis Time	Consider Multi-Switch Faults	Consider Load Change	Microcontroller Realizability
Signal-based [34]	OC	0.05$T_p$∼0.55$T_p$	Yes	Yes	Easy
Signal-based [14]	SC	<$T_p$	Yes	Yes	Yes
Data-driven [35]	OC	>$T_p$	Yes	Yes	Hard
Model-based [25]	OC and Sensor fault	<$T_p$	No	Yes	Yes
Model-based [24]	OC	<$T_p$	No	No	Yes
Proposed	OC and SC	≤$T_p$	Yes	Yes	Medium

, where $T_p$ stands for the fundamental period. The author of [34] conducted fault diagnosis based on voltage signals, with a relatively short diagnosis time, and also considered multi-switch faults. However, the above four methods only considered OC faults. The author of [14] diagnosed SC faults in a three-phase current source inverter based on current signals, requiring only a threshold and a small computational burden, and the algorithm can run on the microcontroller. The author used a data-driven fault diagnosis method in [35], but due to the need to collect a waveform of the fundamental current cycle, the fault diagnosis time is long. Despite using feature extraction methods, the computational burden is still significant, and it requires the use of Raspberry Pi as hardware implementation, making it difficult to deploy on traditional controllers. The author studied single-switch OC faults in grid-connected NPC inverters without considering multi-switch faults in [25]. The author studied the single-switch OC fault of parallel inverters in [24], but did not consider the multi-switch fault, and used a fixed threshold for fault diagnosis, resulting in limited robustness for load change. Both articles used a model-based method, which requires calculating the estimated output current value, and the computational burden is moderate. Compared with other existing fault diagnosis methods, the method proposed in this paper can diagnose OC and SC faults of a switch and can diagnose multi-switch cascaded faults. The diagnosis thresholds can be set according to the control need, reducing the dependence on prior experience. Compared with data-driven methods, it has a moderate computational burden and can be deployed on embedded microcontrollers for real-time operation, improving the applicability of fault diagnosis methods.

5. Conclusions

The diagnosis of switching device faults in three-phase inverters is crucial for improving reliability and safety. This paper proposes a diagnosis method for three-phase inverter cascaded switch open/short-circuit faults based on an ISMO. First, an MLD model of three-phase inverters is built, taking open-and short-circuit faults of a switch into account. A cascaded ISMO is used to detect abnormal status and distinguish between OC faults and SC faults. The effectiveness of the method has been verified through simulation and experiments. Compared with existing fault diagnosis methods, the proposed method not only can simultaneously diagnose OC faults and SC faults in switches but also can diagnose cascaded faults that occur continuously for a short period of time. The experiment simulated 18 possible types of cascading faults, the comprehensive diagnostic accuracy reached 96.39%, and the required diagnostic time for each fault was less than one current fundamental cycle, which greatly helps optimize the reliability of the inverter. This paper investigates cascaded open/short-circuit fault diagnosis methods for three-phase inverters with resistive inductive loads. For scenarios such as grid-connected inverters and nonlinear loads, corresponding modifications can be made to the load part of the MLD model, and the ISMO parameters can be redesigned to continue using the two-stage observer approach proposed in this paper for fault diagnosis.