Quantifying Overload Risk: A Parametric Comparison of IEC 60076-7 and IEEE C57.91 Standards for Power Transformers

Abstract

Modern power grids face increasing stress from volatile, high-dynamics loads, such as Electric Vehicle (EV) charging clusters and intermittent renewable energy sources. Accurate transformer thermal monitoring via the International Electrotechnical Commission (IEC) 60076-7 and the Institute of Electrical and Electronics Engineers (IEEE) C57.91 standards is crucial, yet their methodologies differ significantly. This study develops a comprehensive MATLAB simulation framework to quantify these differences. The analysis compares physical thermal models across multi-stage cooling—Oil Natural Air Natural (ONAN), Oil Natural Air Forced (ONAF), and Oil Forced Air Forced (OFAF)—and insulation aging models. It is demonstrated that divergence in transformer life estimation stems primarily from the physical thermal models. A ‘reversal of conservatism’ is identified, where ‘conservative’ is defined as predicting higher hot-spot temperatures and enforcing a larger safety margin. Results prove that while the IEC model is thermally more conservative during cooling failures (static mode), the IEEE model is consistently more conservative during normal active cooling. Additionally, 2D “heat maps” are presented to define safe operational zones, and the catastrophic impact of cooling system failures is quantified. These findings provide a quantitative outline for managing transformer state under increasingly demanding loading schemes.

1. Introduction

Power transformers are critical and high-cost assets essential for the reliability of electrical transmission and distribution systems. The operational life of these assets is primarily dictated by the degradation of their cellulose insulation [1,2], an irreversible chemical reaction dependent on temperature, moisture, and oxygen content [1,3,4,5]. Historically, transformers were often over-rated and operated under light loads. However, modern power grids face increasing stress from grid development, the integration of volatile renewable energy sources, and the expansion of high-dynamics loads such as Electric Vehicle (EV) charging clusters [6,7,8]. Along with the emergency cases, these factors force transformers to operate closer to their nameplate ratings and increasingly under temporary overload conditions [9,10,11,12,13].

This new operational pattern makes the accurate monitoring and prediction of the winding hot-spot temperature (HST) and the resulting insulation aging a critical task for operators to ensure reliability and avoid expensive replacements. To manage this, system operators rely on two main international loading guides: the International Electrotechnical Commission (IEC) 60076-7 [14] and the Institute of Electrical and Electronics Engineers (IEEE) C57.91 [15]. While both standards share the common goal of calculating thermal aging, they utilize fundamentally different physical models and are not interchangeable [16].

A significant challenge arises because these standards propose different mathematical approaches for calculating the winding hot-spot gradient and insulation aging. Furthermore, while advanced dynamic thermal–hydraulic models have been proposed to account for oil viscosity and transient “overshoot” phenomena [17,18,19], utility operators predominantly rely on the simplified differential equations provided in the standards, which only highlights how important the topic is.

The core problem addressed in this study is the inconsistency in risk assessment caused by these differing methodologies. Although the standards provide ranges for key parameters (such as winding exponents) that technically overlap, they prescribe different default values for identical cooling modes. Consequently, an operator assessing a specific overload event may receive contradictory safety signals depending on which standard is applied. Understanding the magnitude and direction of this divergence—specifically under modern multi-stage cooling scenarios—is essential for grid reliability.

The purpose of this study is to quantify these differences. A comprehensive MATLAB simulation framework was developed to compare the standards across a wide range of parametric and transient scenarios, including multi-stage active cooling (Oil Natural Air Natural (ONAN), Oil Natural Air Forced (ONAF), and Oil Forced Air Forced (OFAF)) [20]. It is demonstrated that for modern transformers using Thermally Upgraded (TU) paper, the significant difference in life estimation stems solely from the physical thermal models rather than the aging mathematics.

The remainder of this paper is organized as follows: Section 2 details the mathematical modeling methodology, defining the specific thermal differential equations and default exponent parameters used for the IEC and IEEE simulations. Section 3 presents the simulation results, beginning with foundational parameter sensitivities and progressing to complex multi-stage cooling scenarios. Section 4 discusses the implications of the “reversal of conservatism” finding, and Section 5 summarizes the conclusions.

2. Modeling Methodology

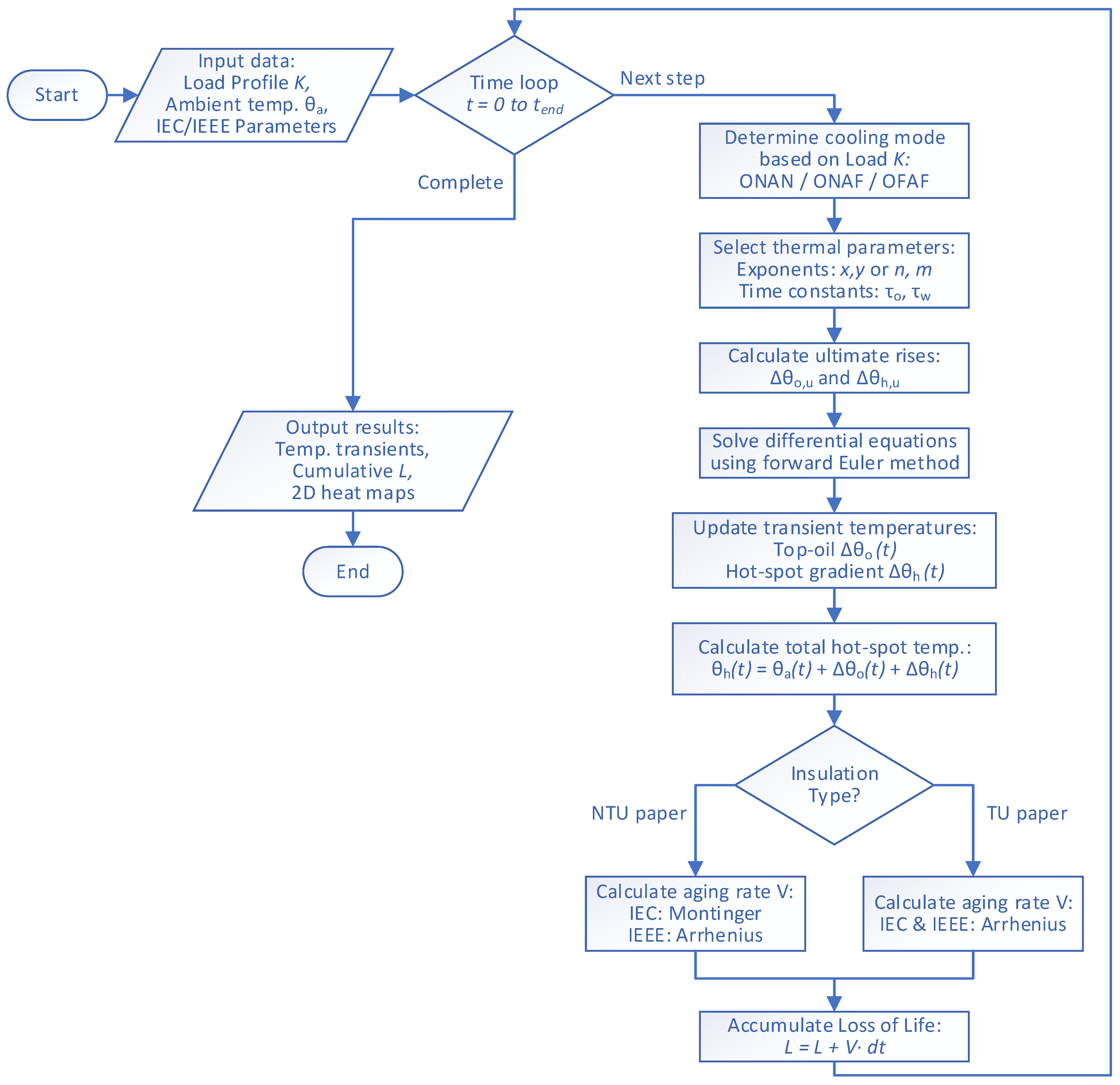
This study is based on a comprehensive thermal-aging simulation framework developed in MATLAB R2024b, which implements the transient thermal models of both the International Electrotechnical Commission (IEC) 60076-7 and the Institute of Electrical and Electronics Engineers (IEEE) C57.91. The overall computational logic of this framework is illustrated in Figure 1. The simulation operates on a discrete time-step basis, processing the input load profile K(t) and ambient temperature θ_a(t). At each calculation step, the algorithm first determines the active cooling mode (Oil Natural Air Natural (ONAN), Oil Natural Air Forced (ONAF), or Oil Forced Air Forced (OFAF)) based on the instantaneous load factor. Subsequently, the appropriate thermal parameters are selected, and the differential equations (detailed in Section 2.1 and Section 2.2) are solved using the forward Euler method. Finally, the instantaneous aging rate is computed based on the specific insulation type (Non-Thermally Upgraded paper (NTU) or Thermally Upgraded paper (TU)) and accumulated to determine the total Loss of Life. It is important to notice that the cooling control logic implemented in this simulation utilizes ideal load-based thresholds without hysteresis. The cooling stage transitions occur instantaneously when the load factor K crosses the defined limits (e.g., switching from ONAN to ONAF at K = 0.8, and to OFAF at K = 1.2) to strictly isolate the thermal models response from any control lag.

2.1. IEC 60076-7 Model Realization

The developed MATLAB script implements the steady-state equations from the IEC 60076-7 standard, solving the transient response with a simplified first-order dynamic model using the forward Euler method.

2.1.1. Calculation of Ultimate Top-Oil Temperature Rise

Ultimate top-oil temperature rise is the steady-state top-oil temperature rise the transformer would reach if the current load (K) was held indefinitely.

$$\Delta {\theta }_{o,u}=\Delta {\theta }_{or}\cdot {\left[{\displaystyle \frac{1+R\cdot K^2}{1+R}}\right]}^x$$

(1)

where ∆θ_o,u is the ultimate top-oil temperature rise, ∆θ_or is the top-oil temperature rise at rated load (K), R is the ratio of load losses at rated current to no-load losses, K is the load factor (per unit of rated load), and x is the specified oil exponent (e.g., 0.8 for ONAN).

2.1.2. Calculation of Ultimate Hot-Spot Gradient

The ultimate hot-spot gradient is the steady-state hot-spot-to-top-oil gradient for the current load:

$$\Delta {\theta }_{h,u}=\Delta {\theta }_{hr}\cdot K^y$$

(2)

where ∆θ_h,u is the ultimate hot-spot gradient, ∆θ_hr is the hot-spot-to-top-oil gradient at rated load, K is the load factor (per unit of rated load), and y is the specified winding exponent (e.g., 1.3 for ONAN).

In the IEC model, the winding exponent y in Equation (2) dictates the non-linear rise in the winding gradient. While the standard allows y to range from 1.3 to 2.0 depending on the specific design, this study utilizes the standard default value of y = 1.3 for ONAN and ONAF cooling modes, as typically prescribed for distribution transformers [14]. This parameter is a primary differentiator from the IEEE model.

2.1.3. Calculation of Transient Temperatures

The transient response is calculated at each time step (Dt) using a discrete difference equation based on the forward Euler method. The top-oil rise is calculated according to Equation (3) and the hot-spot gradient according to Equation (4):

$$\Delta {\theta }_o(t)=\Delta {\theta }_o(t-1)+\left[{\displaystyle \frac{\Delta {\theta }_{o,u}-\Delta {\theta }_o(t-1)}{{\tau }_o}}\right]\cdot Dt$$

(3)

$$\Delta {\theta }_h(t)=\Delta {\theta }_h(t-1)+\left[{\displaystyle \frac{\Delta {\theta }_{h,u}-\Delta {\theta }_h(t-1)}{{\tau }_w}}\right]\cdot Dt$$

(4)

where ∆θ_o(t) is the top-oil rise in current calculation step, ∆θ_o(t − 1) is the top-oil rise in the previous calculation step, ∆θ_o,u is the ultimate top-oil temperature rise, τ_o is the oil time constant [min], ∆θ_h(t) is the hot-spot gradient in the current calculation step, ∆θ_h(t − 1) is the hot-spot gradient in the previous calculation step, ∆θ_h,u is the ultimate hot-spot temperature, and τ_w is the winding time constant [min].

2.1.4. Calculation of Final Hot-Spot Temperature

The final hot-spot temperature is the sum of the ambient temperature and the two calculated values above:

$${\theta }_h\left(t\right)={\theta }_a\left(t\right)+\Delta {\theta }_o\left(t\right)+\Delta {\theta }_h\left(t\right)$$

(5)

where θ_h(t) is the final hot-spot temperature, θ_a(t) is the ambient temperature, ∆θ_o(t) is the top-oil rise temperature, and ∆θ_h(t) is the hot-spot gradient.

2.1.5. Calculation of Insulation Aging (Loss of Life)

The IEC model relative aging rate (V) calculation for Non-Thermally Upgraded paper is based on Montsinger’s empirical ‘6-degree rule’, stating that the rate of aging doubles for every 6 °C increase above the reference temperature of 98 °C (Equation (6)), while for Thermally Upgraded paper, it is based on chemical kinetics and utilizes the Arrhenius Equation (7):

$$V\left(t\right)=2^{({\theta }_h\left(t\right)-98)/6}$$

(6)

$$V\left(t\right)=e^{\left[{\displaystyle \frac{\mathrm{15,000}}{110+273}}-{\displaystyle \frac{\mathrm{15,000}}{{\theta }_h\left(t\right)+273}}\right]}$$

(7)

where V(t) is the relative aging rate, and θ_h(t) is the hot-spot temperature.

The cumulative Loss of Life (L) is the sum of relative aging rates for each calculation instant t according to Equation (8):

$$L={\displaystyle \sum (V\left(t\right)\cdot Dt)}$$

(8)

2.2. IEEE C57.91-2011 Model Realization

The developed Matlab script implements the thermal model described in Chapter 7 of the IEEE standard [15].

2.2.1. Calculation of Ultimate Top-Oil Temperature Rise

Ultimate top-oil temperature rise is the steady-state top-oil temperature rise the transformer would reach if the current load (K) was held indefinitely:

$$\Delta {\Theta }_{TO,U}=\Delta {\Theta }_{TO,R}\cdot {\left[{\displaystyle \frac{K_U^{2}R+1}{R+1}}\right]}^n$$

(9)

where ∆ϴ_TO,U is the ultimate top-oil temperature rise, ∆ϴ_TO,R is the top-oil temperature rise at rated load (K), R is the ratio of load losses at rated current to no-load losses, K is the load factor (per unit of rated load), and n is the specified oil exponent (e.g., 0.8 for ONAN).

2.2.2. Calculation of Ultimate Hot-Spot Gradient

The IEEE model calculates the ultimate hot-spot gradient using the winding exponent m. It is important to note that while the IEEE exponent m typically ranges from 0.8 to 1.0, it is applied as 2m in the gradient calculation (Equation (10)). For this study, the standard default of m = 0.8 is used, resulting in an effective exponent of 1.6 [15]. Although this value (1.6) falls within the theoretical range of the IEC parameter y (1.3–2.0), the distinct default selection (1.6 for IEEE vs. 1.3 for IEC) creates the structural divergence in risk assessment analyzed in this paper:

$$\Delta {\Theta }_{H,U}=\Delta {\Theta }_{H,R}{K}_U^{2m}$$

(10)

where ∆ϴ_H,U is the ultimate hot-spot gradient, ∆ϴ_H,R is the hot-spot rise over top-oil at rated load (K), K_U is the load factor (per unit of rated load), and m is the specified winding exponent (e.g., 0.8 for ONAN/ONAF).

2.2.3. Calculation of Transient Temperatures

The developed MATLAB script calculates the transient behavior by solving the first-order differential equations provided in the IEEE standard [15] using a discrete difference equation based on the forward Euler method. This approach is applied to Equation (11) for top-oil rise and Equation (12) for the hot-spot gradient.

$$\Delta {\Theta }_{TO}(t)=\Delta {\Theta }_{TO}(t-1)+\left[{\displaystyle \frac{\Delta {\Theta }_{TO,U}-\Delta {\Theta }_{TO}(t-1)}{{\tau }_{TO}}}\right]\cdot Dt$$

(11)

$$\Delta {\Theta }_H(t)=\Delta {\Theta }_H(t-1)+\left[{\displaystyle \frac{\Delta {\Theta }_{H,U}-\Delta {\Theta }_H(t-1)}{{\tau }_W}}\right]\cdot Dt$$

(12)

where ∆ϴ_TO(t) is the top-oil rise in the current calculation step, ∆ϴ_TO(t − 1) is the top-oil rise in the previous calculation step, ∆ϴ_TO,U is the ultimate top-oil temperature rise, τ_TO is the oil time constant, ∆ϴ_H(t) is the hot-spot gradient in the current calculation step, ∆ϴ_H(t − 1) is the hot-spot gradient in previous calculation step, ∆ϴ_H,U is the ultimate hot-spot temperature, and τ_w is the winding time constant.

2.2.4. Calculation of Final Hot-Spot Temperature

The final hot-spot temperature is the sum of the ambient temperature and the two calculated above values:

$${\Theta }_H\left(t\right)={\Theta }_A\left(t\right)+\Delta {\Theta }_{TO}\left(t\right)+\Delta {\Theta }_H\left(t\right)$$

(13)

where ϴ_H(t) is the final hot-spot temperature, θ_A(t) is the ambient temperature, ∆θ_TO(t) is the top-oil rise temperature, and ∆ϴ_H(t) is the hot-spot gradient.

2.2.5. Calculation of Insulation Aging (Loss of Life)

The IEEE standard uses the Aging Acceleration Factor (F_AA) expression for relative aging rate (V), which is presented in the IEC standard. For better clarity, in this paper all the results will be presented uniformly with use of relative aging rate (V) and Loss of Life (L) notation for both standards. The relative aging rate (V) calculation in the IEEE standard utilizes the Arrhenius equation for both types of insulation paper but with different reference temperatures (ϴ_H,R):

$$V\left(t\right)=e^{\left[{\displaystyle \frac{\mathrm{15,000}}{{\Theta }_{H,R}+273}}-{\displaystyle \frac{\mathrm{15,000}}{{\Theta }_H\left(t\right)+273}}\right]}$$

(14)

where V(t) is the relative aging rate, ϴ_H,R is the reference temperature (95 °C for NTU and 110 °C for TU), and ϴ_H(t) is the hot-spot temperature.

The cumulative Loss of Life (L) is a sum of relative aging rate for each calculation step—exactly as in the IEC approach, presented with Equation (8) in Section 2.1.5.

3. Results

This section presents the comprehensive comparative analysis of the IEC 60076-7 and IEEE C57.91 standards, based on the simulation scenarios developed, and equations presented in the Methodology Section 2. The results are structured to build from foundational parameter sensitivities to more complex applications, finally comparing the standards across their full operational maps.

3.1. Foundational Model Behavior and Parameters

3.1.1. Impact of Insulation Paper Type on Thermal Aging

The analysis first isolates the core components influencing the models, starting with one of the most decisive factors in the entire aging calculation: the type of insulation paper. The distinction between Non-Thermally Upgraded (NTU) and Thermally Upgraded (TU) paper not only impacts thermal endurance but, in the case of the IEC standard, fundamentally alters the aging equation itself. Figure 2 illustrates this comparison under a 48 h representative cyclic load profile constructed using a periodic double-peak Gaussian function. This profile simulates a typical heavy residential loading scheme with distinct morning (around 09:00) and evening (around 19:00) peaks, ensuring a realistic assessment of the transformer’s thermal inertia and the phase shift between the electrical load and the top-oil temperature.

The most important observation, visible in Figure 2b, is the difference in cumulative Loss of Life (LOL) between the two paper types. The solid lines (NTU paper) show significant, non-linear aging. The LOL accumulates rapidly as the hot-spot temperature (from Figure 2a) exceeds its nominal limits of 98 °C for IEC and 95 °C for IEEE during the daily peak load.

The dashed lines (TU paper), in contrast, remain nearly flat. This demonstrates that for the exact same thermal-load profile, the superior thermal endurance of TU paper (rated for 110 °C) results in a negligible Loss of Life.

Figure 2a also reveals a key difference in the thermal models themselves. For this specific ONAN scenario, the IEC model (red line) calculates a peak hot-spot temperature that is consistently a few degrees higher than the IEEE model (blue line).

This thermal discrepancy, combined with the standards’ different aging equations for NTU paper, explains the divergence in Figure 2b. The IEC model (red solid line) is shown to be more conservative, predicting a higher total LOL than the IEEE model (blue solid line) under these conditions.

3.1.2. Thermal–Hydraulic Response of Cooling Modes (ONAN vs. ONAF)

Following the insulation analysis, it comes now to isolate the impact of the physical cooling system. Figure 3 compares the performance of a transformer with standard Oil Natural Air Natural (ONAN) cooling against the one with Oil Natural Air Forced (ONAF) cooling. Both models are exposed to an identical load step change, increasing from 0.8 p.u. to a 1.3 p.u. at the 10 h duration. This scenario allows for a comparison of both the steady-state thermal limits and the transient response of the two cooling modes.

The results clearly demonstrate the benefits of forced-air cooling. As shown in Figure 3a, the ONAF models (dashed lines) achieve a significantly lower steady-state hot-spot temperature—approximately 15 °C lower than their ONAN corresponding item (solid lines) during the overload phase.

Furthermore, the ONAF models exhibit a faster thermal response, as evidenced by the steeper temperature rise and quicker leveling-off. This is a direct result of the lower top-oil time constant (τ_o) associated with forced-air flow (120 min vs. 180 min for ONAN).

The direct consequence for transformer aging is quantified in Figure 3b. The lower operating temperature of the ONAF system results in a reduced accumulation of Loss of Life. For the 48 h duration of this simulation, the ONAN-cooled transformer aged significantly more than the ONAF-cooled one. This test confirms the model’s correct thermal–hydraulic behavior and quantifies the critical role of active cooling systems in mitigating thermal stress and aging during overloads.

It should also be noted from Figure 3b that for ONAF cooling, the situation has inversed, and now the IEEE standard is more conservative (blue dashed line) than that of the IEC (red dashed line). This phenomenon is caused by the various approaches to exponent factors that both standards used in various ways for forced cooling.

3.1.3. Analysis of Transient Thermal Components and Response Dynamics

Beyond cyclic loads, the transformer’s response to sudden, transient events is critical for understanding short-term overload aging. The dynamic components of the hot-spot temperature are now investigated. Figure 4 analyzes the thermal response to a step-load (from 0.8 p.u. to 1.5 p.u. at t = 2 h) under constant ambient temperature. This scenario is designed to isolate and visualize the different time constants that govern the thermal model.

Figure 4 reveals the fundamental “two-stage” thermal response of the transformer, which is a key concept in both standards. Figure 4a, using the IEC model as an example, decomposes the total hot-spot temperature (θ_h) into its fundamental parts. The total temperature is the sum of the ambient temperature (θ_a black dotted line), the top-oil rise (∆θ_o, blue dashed line), and the hot-spot gradient (∆θ_h, red shaded area).

The top-oil temperature rises slowly, ruled by the large oil time constant (τ_o approx. 180 min). The hot-spot gradient, however, rises very quickly, controlled by the short winding time constant (τ_w approx. 7 min). This leads to important finding from the transient analysis: transformer aging is not delayed. Since the hot-spot temperature is the sum of these components, it rises almost immediately with the fast winding gradient. Significant aging, therefore, begins within minutes of the overload, long before the oil temperature has reached its peak.

Figure 4b compares the total hot-spot response of the IEC and IEEE models. While both exhibit the same two-stage behavior, their differing winding exponents (y vs. 2m) and oil exponents (n) result in different final steady-state temperatures, again highlighting the differences in the standards thermal–hydraulic calculations.

3.1.4. Active Multi-Stage Cooling vs. Static (Failure) Mode

The analyses so far have focused on single, fixed cooling modes (ONAN-only). However, a real transformer operates with an active, multi-stage cooling system that engages fans and pumps (ONAF, OFAF) as the load increases [20].

Before comparing the standards across a full operational map, it is essential to first present the simulation of this cooling logic. Figure 5 demonstrates the behavior of the multi-stage thermal model when subjected to a step-load profile designed to trigger all three cooling stages (ONAN, ONAF, and OFAF).

Figure 5 presents results expected from the active cooling logic operation. Figure 5a shows the hot-spot temperature (solid lines) reacting to the load steps (green line). The temperature is effectively limited and controlled as the load increases.

Figure 5b provides the developed model’s “Cooling Mode” (black line), switching from ONAN (Stage 1) to ONAF (Stage 2) and OFAF (Stage 3) at the precise load-factor setpoints.

The resulting aging, shown in Figure 5c, is minimal and occurs only during the brief 1.5 p.u. peak.

With the active multi-stage model presented, it can now be used to quantify the criticality of the cooling system itself. The following analysis compares this “Active” model against a “Static ONAN” (cooling failure) scenario, where the transformer is fixed in its least effective cooling mode.

Figure 6 provides a continued comparison for the exact same load profile as Figure 5. The active models (solid lines) successfully manage the overload, keeping the temperature around 130 °C and resulting in a negligible, acceptable Loss of Life.

The static ONAN models (dashed lines), representing a cooling failure, are quickly overwhelmed. Figure 6a shows the temperature exceeding 150 °C. This leads to worse outcomes in Figure 6b, where the cumulative LOL for the static models takes values of over 120 h of transformer life consumed, while the active cooling provides much better results of around 23 and 33 h (IEC and IEEE, respectively) of Loss of Life, proving the IEEE standard to be more conservative in the case of active cooling operation.

This finding proves that the active cooling system is a safety-critical system. Even a seemingly small thermal gain (the 15–20 °C difference at the peak) results in a four- to five-fold reduction in life-loss during this 4 h overload event. This justifies analyzing the standards under these two distinct cases: the designed “Active Cooling” map and the failure “Static Cooling” map, in the later part of this work.

3.2. Parametric Comparison of Thermal and Aging Models

Following the time-based dynamic simulations, this section presents the core parametric comparison of the standards. Comprehensive steady-state analysis is presented, mapping the models’ behavior across the full operational range of load factors (K) and ambient temperatures (θ_a). Building on the conclusions from Section 5, this comparison is performed for the two operating cases: the “Static ONAN” (failure) mode and the “Active Multi-Stage” mode.

3.2.1. Hot-Spot Temperatures for Active Multi-Stage Cooling vs. Static (Failure) Mode

The first point of the parametric comparison is to focus on the core thermal models. This section compares the steady-state hot-spot temperature (θ_h) calculated by each standard across the full operational map. Figure 7a,b present the direct difference between the models: θ_{h_IEC} − θ_{h_IEEE}. A positive value (yellow/green) indicates that the IEC model calculates higher steady-state temperature values, while a negative value (blue/green) indicates that the IEEE model is “hotter”.

This side-by-side comparison of static and active cooling presented in Figure 7 reveals that in the cooling failure scenario, the difference is almost entirely positive, reaching up to 4.5 °C. This demonstrates that for the static ONAN mode, the IEC thermal model is consistently more conservative, predicting higher transformer hot-spot temperatures than the IEEE model, while the for active cooling scenario, the finding is the complete opposite. The presented difference is almost entirely negative, resulting in the IEEE model temperatures being higher by as much as 9 °C. This proves that when multi-stage cooling is active, the IEEE model is consistently more conservative.

It is worth noticing that the relative conservatism of the thermal standards is not fixed but is dependent on the cooling system’s operational state and specific working conditions.

3.2.2. Loss of Life for Active Multi-Stage Cooling vs. Static (Failure) Mode

After presenting the fundamental differences in the thermal models in Figure 7, it is now possible to analyze the aging consequences. Figure 8 and Figure 9 present the 3D surface maps for the calculated steady-state Loss of Life per day.

These surfaces plots in Figure 8 and Figure 9 are the resulting aging as a function of load factor (K) and ambient temperature (θ_a). The Z-axis is presented in a logarithmic scale (log10) to visualize the exponential nature of thermal aging. These figures directly correspond to the thermal maps from Figure 7, whereas Figure 8 shows the LOL for the static cooling case, and Figure 9 shows the LOL for the active cooling case.

Figure 8, presenting transformer daily Loss of Life during the static cooling scenario, visualizes a fast aging rate during cooling failure. The most critical aging rate is found for the IEC model and NTU paper. This is due to the afore-mentioned fact of utilizing Equation (3) for the calculation. The IEC model (Figure 8a) is far more conservative, with a maximum log(LOL) of 8, while the IEEE model (Figure 8b) is significantly less severe, with a maximum log(LOL) of 6. This demonstrates a major discrepancy in the standards’ aging models for traditional NTU paper.

For TU paper (Figure 8c,d), the results are much closer, with both models showing a maximum log(LOL) of 5. This suggests that when both standards use the Arrhenius equation (common for TU paper), their predictions are more aligned, with differences primarily reflecting the thermal differences from Figure 7.

Figure 9 presents the Loss of Life of the transformer during an active cooling scenario and shows a completely different picture. The first finding, when comparing Figure 9 to Figure 8, is a reduction in aging values. The active cooling, effectively dissipating the heat, is able to protect the transformer from excessive aging. For NTU paper, the maximum log(LOL) has dropped from 8 (IEC) and 6 (IEEE) down to 6 (IEC) and 5 (IEEE), respectively, which proves that the active cooling system is essential for protecting the transformer’s life.

The surfaces in Figure 9 are not as smooth as in Figure 8 but exhibit visible breakpoints or ridges (e.g., at K = 1.2). These breakpoints correspond to the activation points of the ONAF and OFAF cooling stages, which suppress the temperature and, in turn, limit the aging rate.

3.2.3. Relative Aging Difference for Active Multi-Stage Cooling vs. Static (Failure) Mode

To directly and quantitatively summarize the disagreement in aging calculations, Figure 10 and Figure 11 presents the relative difference in daily Loss of Life. The surfaces are calculated as (IEC_LOL − IEEE_LOL)/IEEE_LOL, expressed as a percentage.

The plots presented in Figure 10 and Figure 11 allow us to make a final conclusion for each operating case presenting a positive surface (yellow/green), indicating transformer operating conditions for which the IEC standard is more conservative (predicts more aging), while a negative surface (blue) indicates the conditions for which the IEEE standard is more conservative.

Comparing Figure 10 and Figure 11, one may easily notice that for the static cooling (failure), the IEC standard is much more conservative, calculating higher aging values for both types of insulation paper (over 500% for NTU and up to 40% for TU), while under active cooling conditions (which are a healthy transformer’s normal operating conditions), the IEEE standard is more conservative across vast number of cases (up to 100% for NTU paper and up to 60% for TU paper). It should be noted that there are some regions in Figure 11 where the IEC standard is more conservative. However, these values are only for load factors (K) over 1.6 and simultaneously very high ambient temperatures for NTU paper, and below the nominal load for TU paper (reaching only up to 20%).

After careful examination of Figure 10 and Figure 11, it can be stated that for the common transformer operating conditions (i.e., fully operating active cooling, typical range of load factors, and typical ambient temperature), the IEEE standard operates more conservatively, calculating higher rates of transformer aging.

3.2.4. Practical Operational Aging Maps for Active Cooling

To make the 3D aging data from Figure 8 more practical for operational use, Figure 12 presents the same information as a 2D “heat map”. These maps correspond to the active multi-stage cooling cases as the most common transformer operating conditions.

In Figure 12, the x-axis represents the steady-state load factor (K), and the y-axis represents the ambient temperature (θ_a). The color and contour lines show the resulting relative aging rate (V). A value of V = 1 is the nominal rate, meaning one hour of life is consumed per 1 h of transformer operation, values over 1 mean increased wear (e.g., 5 means 5 times higher than nominal), and values under 1 mean decreased wear of the insulation (e.g., 0.1 means 10 times less that nominal).

The operational maps presented in Figure 12 show the “safe” (white and green), “nominal” (yellow), and “danger” (red) zones for the transformer operation.

The noticeable finding is the difference between the NTU paper and the TU paper. The safe (V < 1) operating area is larger for the TU paper models (Figure 12c,d). This visually quantifies the benefit of using thermally upgraded insulation, as it can handle much higher loads and ambient temperatures before significant aging begins.

Comparing the left column (IEC) to the right (IEEE), the safe (green) area for the IEC models (Figure 12a,c) is slightly larger than for the corresponding IEEE models (Figure 12b,d). This confirms the conclusion from Figure 11 that the IEEE standard is more conservative, as it predicts a higher aging rate for the same operating point and thus defines a smaller safe operational zone.

4. Discussion

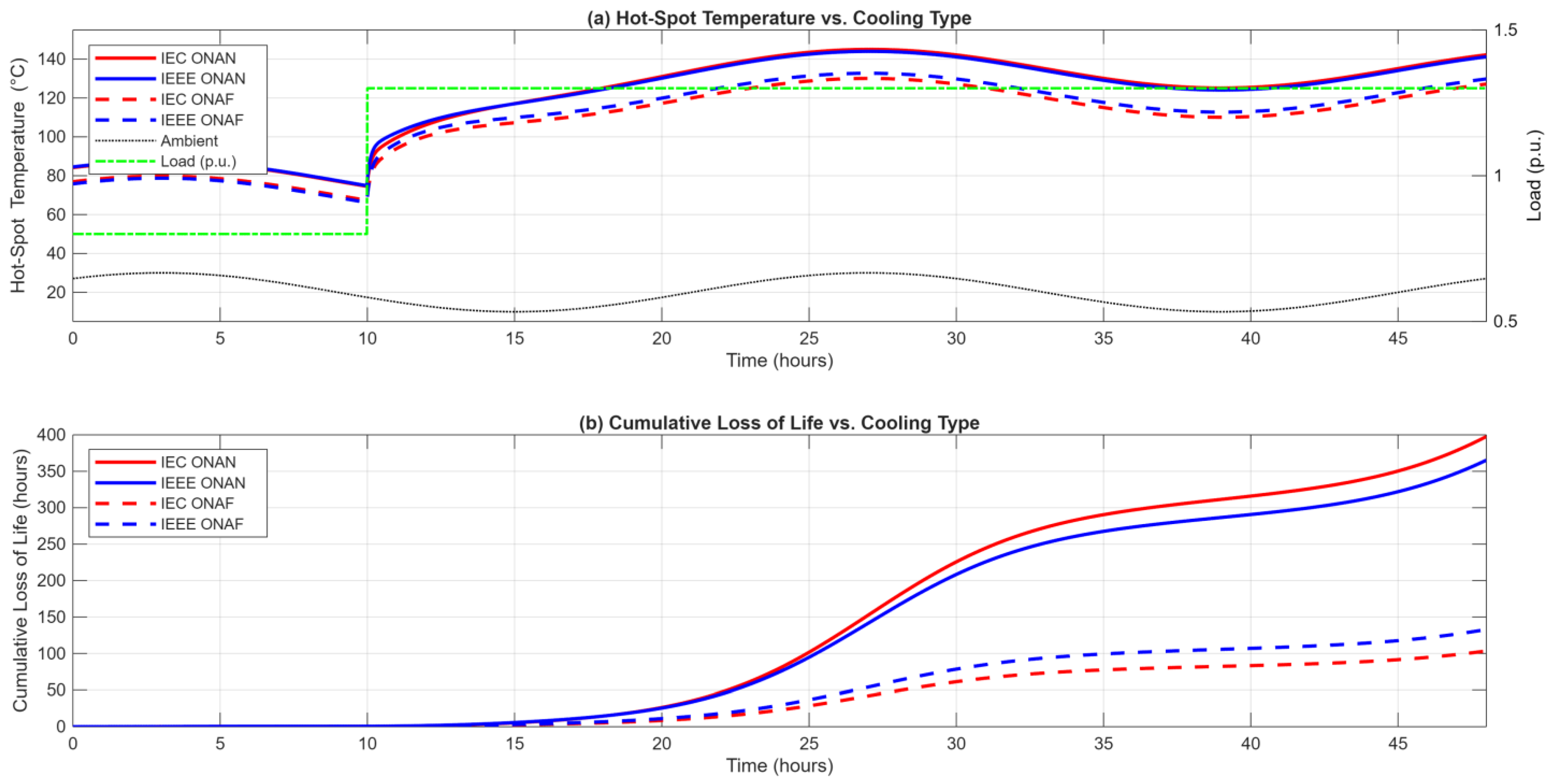
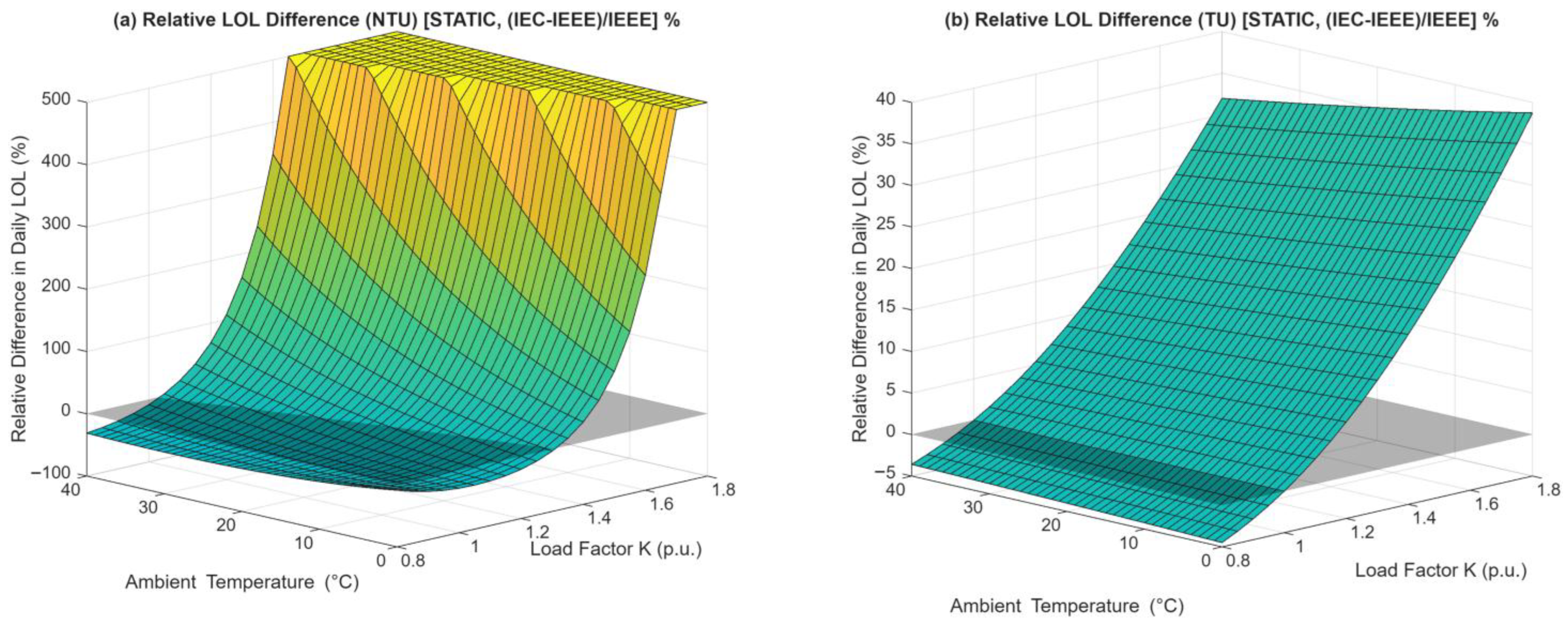
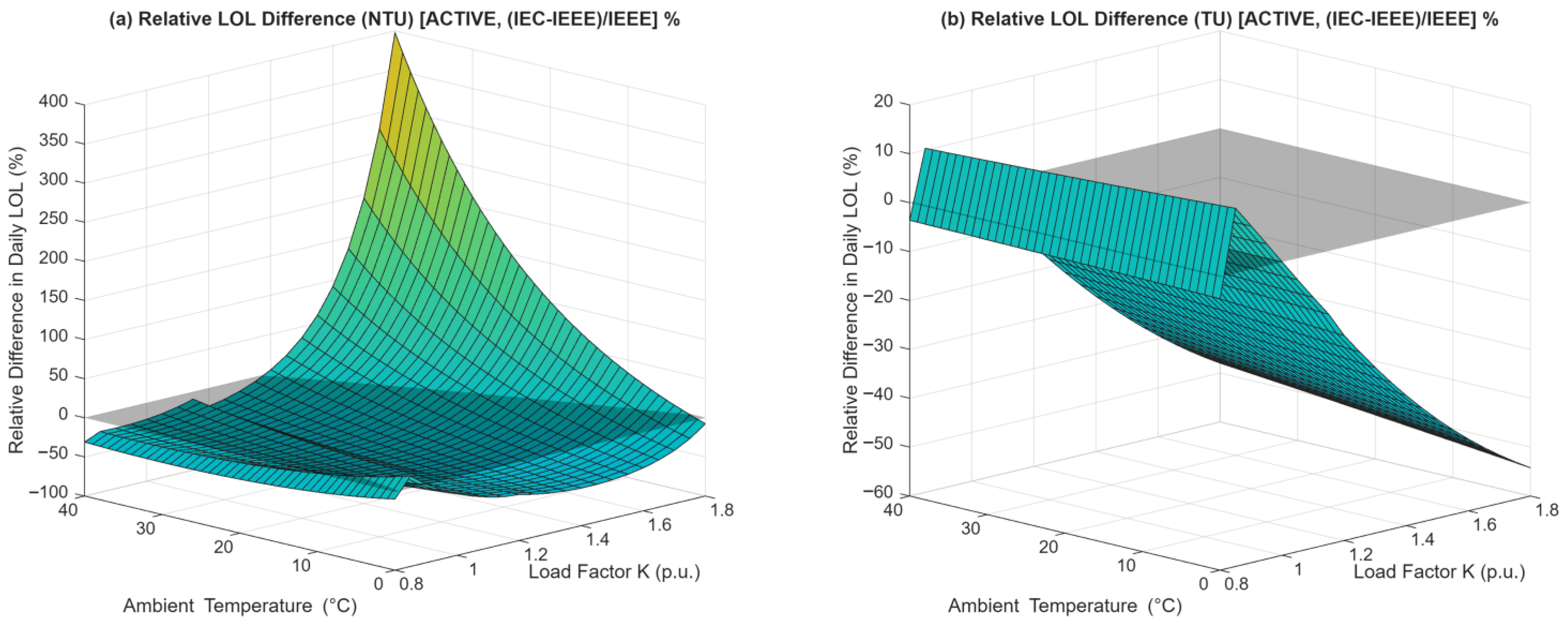
The results of this comparative study provide a detailed, quantitative answer to the uncertainties between the IEC 60076-7 and IEEE C57.91 standards. The findings confirm the working hypothesis that the standards are not interchangeable. More importantly, this work proves that the primary source of disagreement in modern transformers is not the aging mathematics, but the fundamental differences in the physical thermal models themselves. The potential effects of this are significant and depend entirely on the operational state of the transformer’s cooling system.

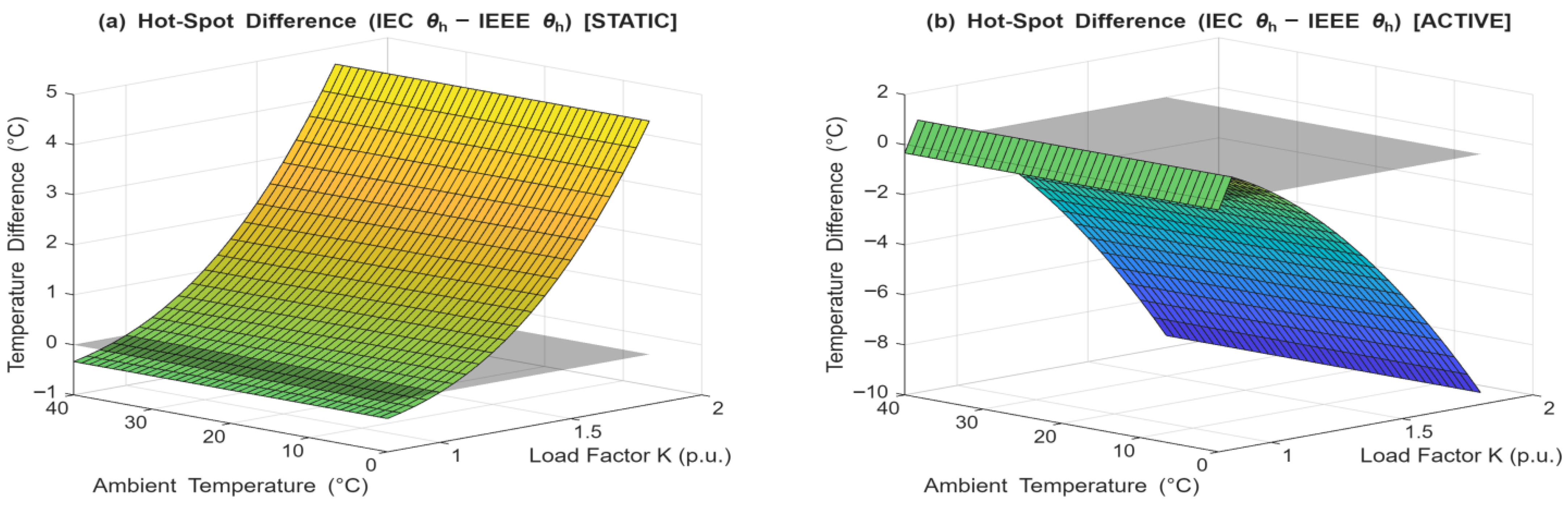
The first important finding of this paper is the “reversal of conservatism” shown in Figure 7. The analysis of the steady-state operational maps proved that in a static ONAN (failure) mode, the IEC thermal model is more conservative, predicting higher transformer hot-spot temperatures (Figure 7a), while in an Active Multi-Stage cooling mode, the IEEE thermal model is more conservative (Figure 7b).

The study also revealed the cause of this reversal. In the static ONAN mode, the IEC model’s higher oil exponent (n = 0.9) is the dominant factor, leading to a higher calculated top-oil temperature. However, when the active cooling stages (ONAF/OFAF) engage, the oil exponents of both standards equalize (to n = 0.9 and n = 1.0, respectively). This neutralization of the oil model difference leaves the winding-to-oil gradient as the primary differentiator. In this case, the IEEE model’s more aggressive winding exponent (2m = 1.6) becomes the decisive factor, dominating the thermal calculation and resulting in a consistently hotter hot-spot prediction.

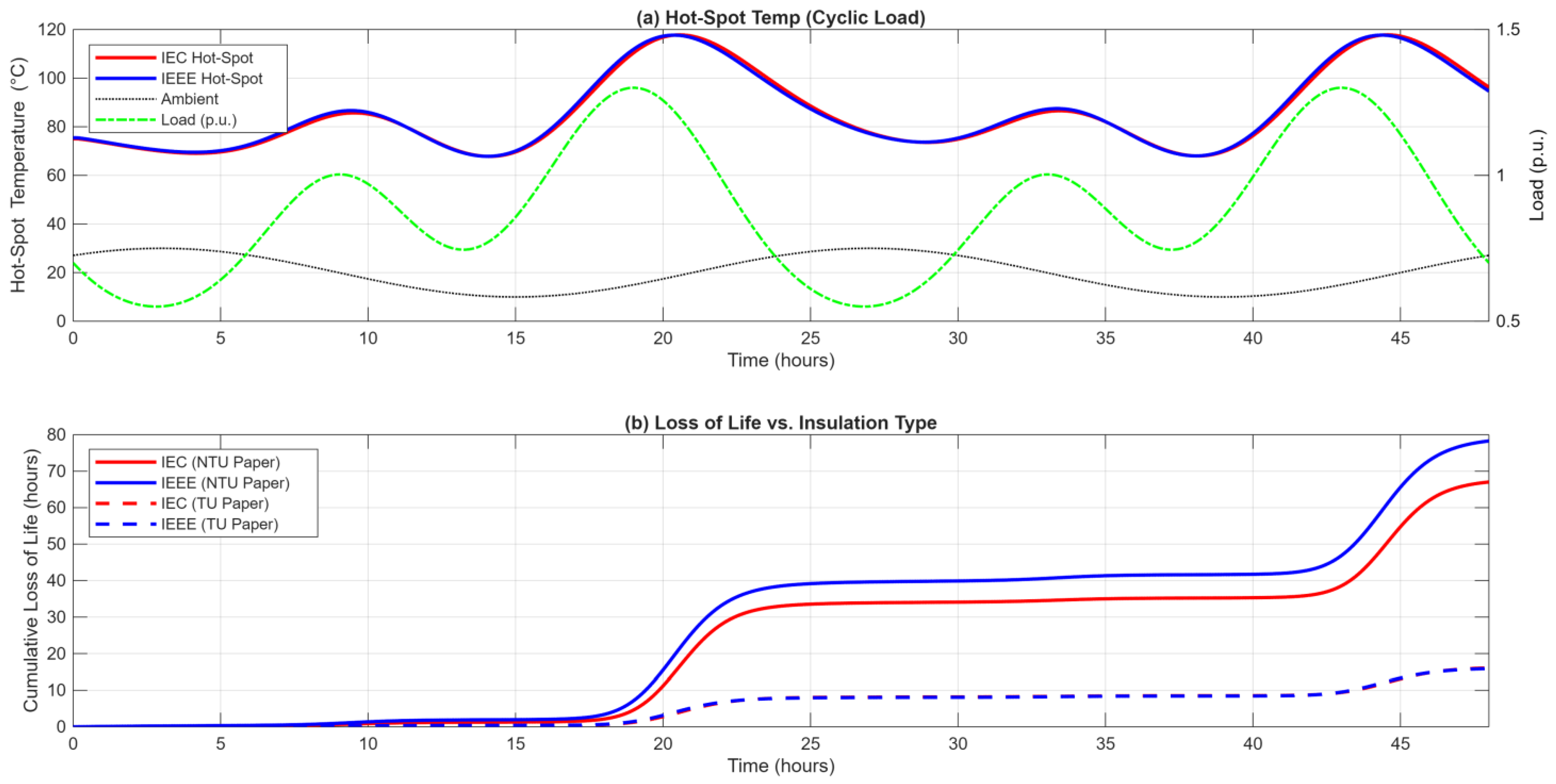
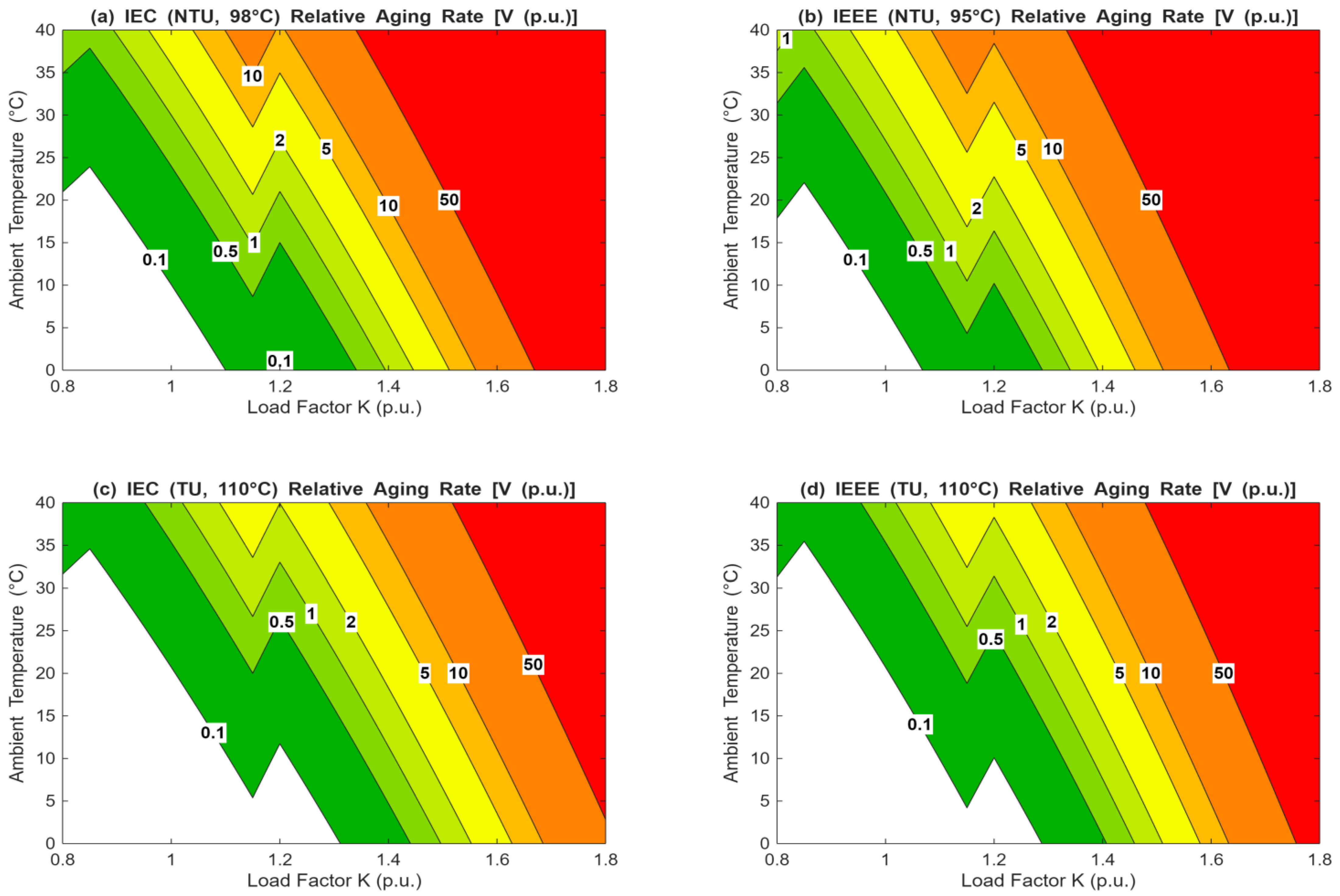
This finding has a significant implication for modern transformers using Thermally Upgraded (TU) paper. As it was shown in Figure 8c,d and Figure 10b, when both standards use the same Arrhenius aging equation, their Loss of Life predictions are very similar. This proves that for modern transformers the differences due to aging mathematics are secondary, and the thermal model itself is the main source of this nonconformity. The major discrepancy in aging calculations for NTU paper (Figure 10a) confirms that the IEC “6-degree rule” is far more punitive than the IEEE Arrhenius model, but this is primarily relevant to older, NTU-equipped transformers.

The practical implications for a utility operator are two-fold. First, the conservatism of the chosen standard is not fixed but is conditional on the health of the cooling system. An operator relying on the IEEE standard (Figure 11) might set conservative loading limits for a healthy transformer, while an operator using the IEC standard (Figure 10a) would be far more conservative when assessing a cooling failure. Second, the 2D operational heat maps (Figure 12) provide a practical, visual tool for this risk assessment. They confirm that for a healthy transformer, the IEEE standard defines a smaller “safe operating area” (white and green zone) than the IEC standard.

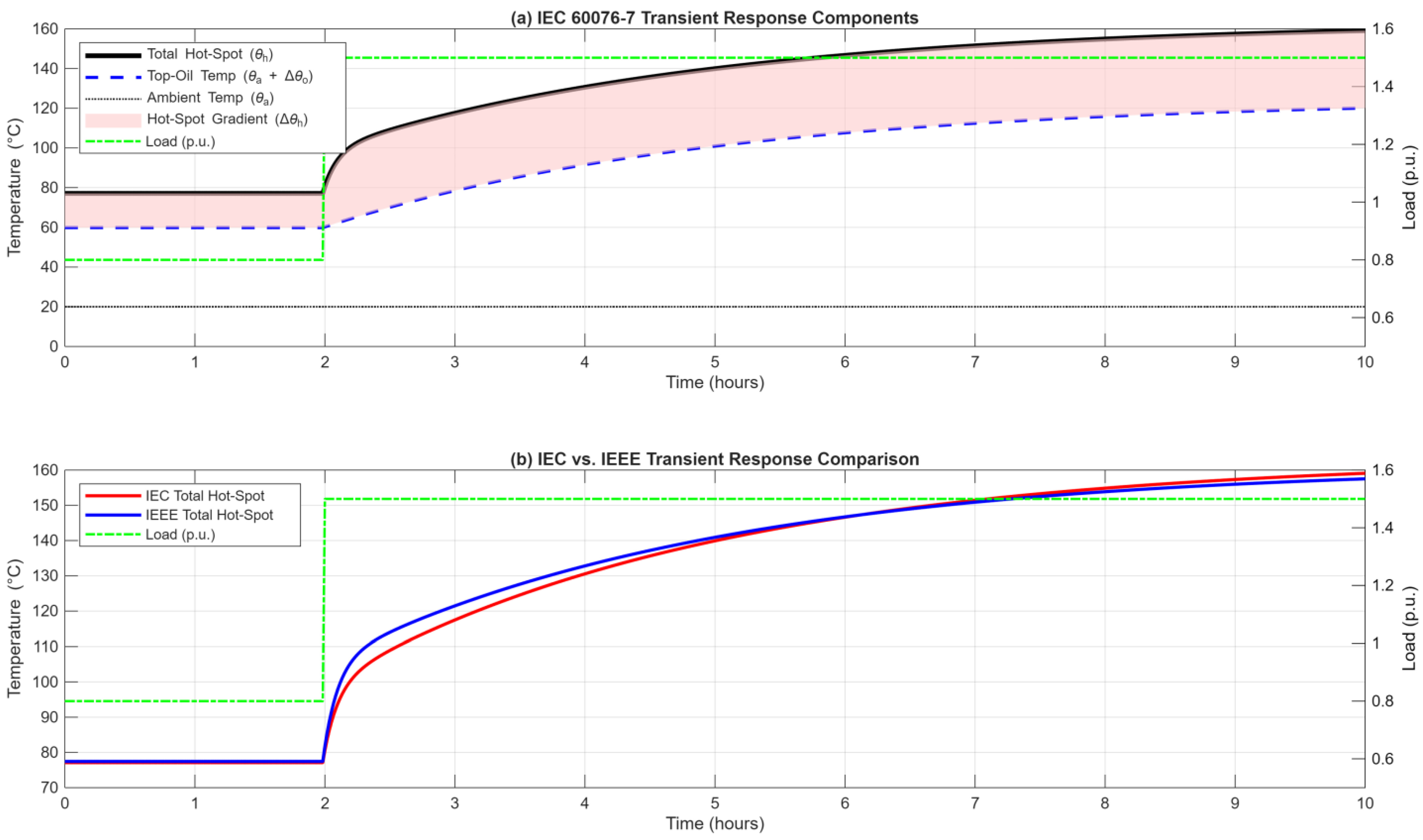
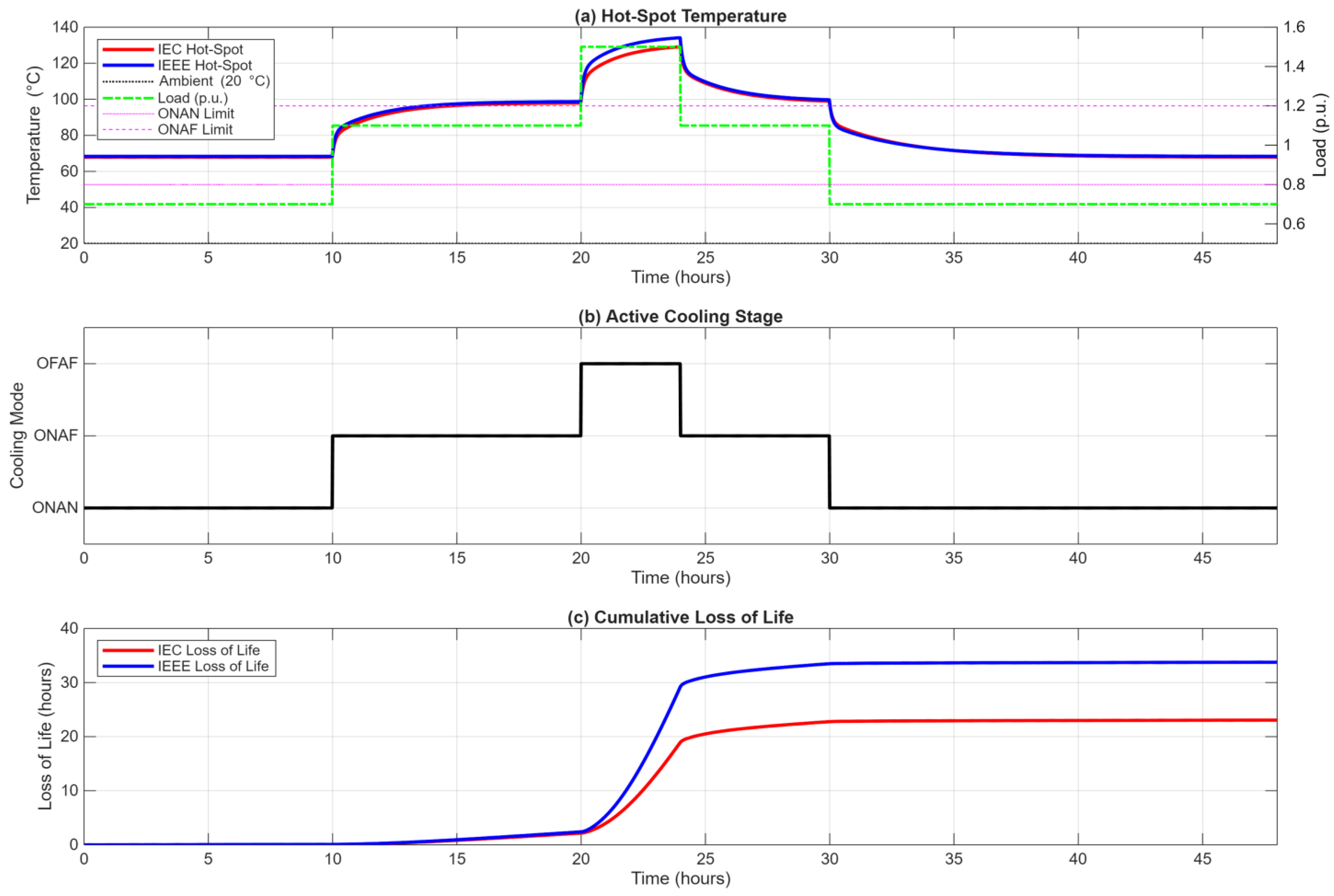
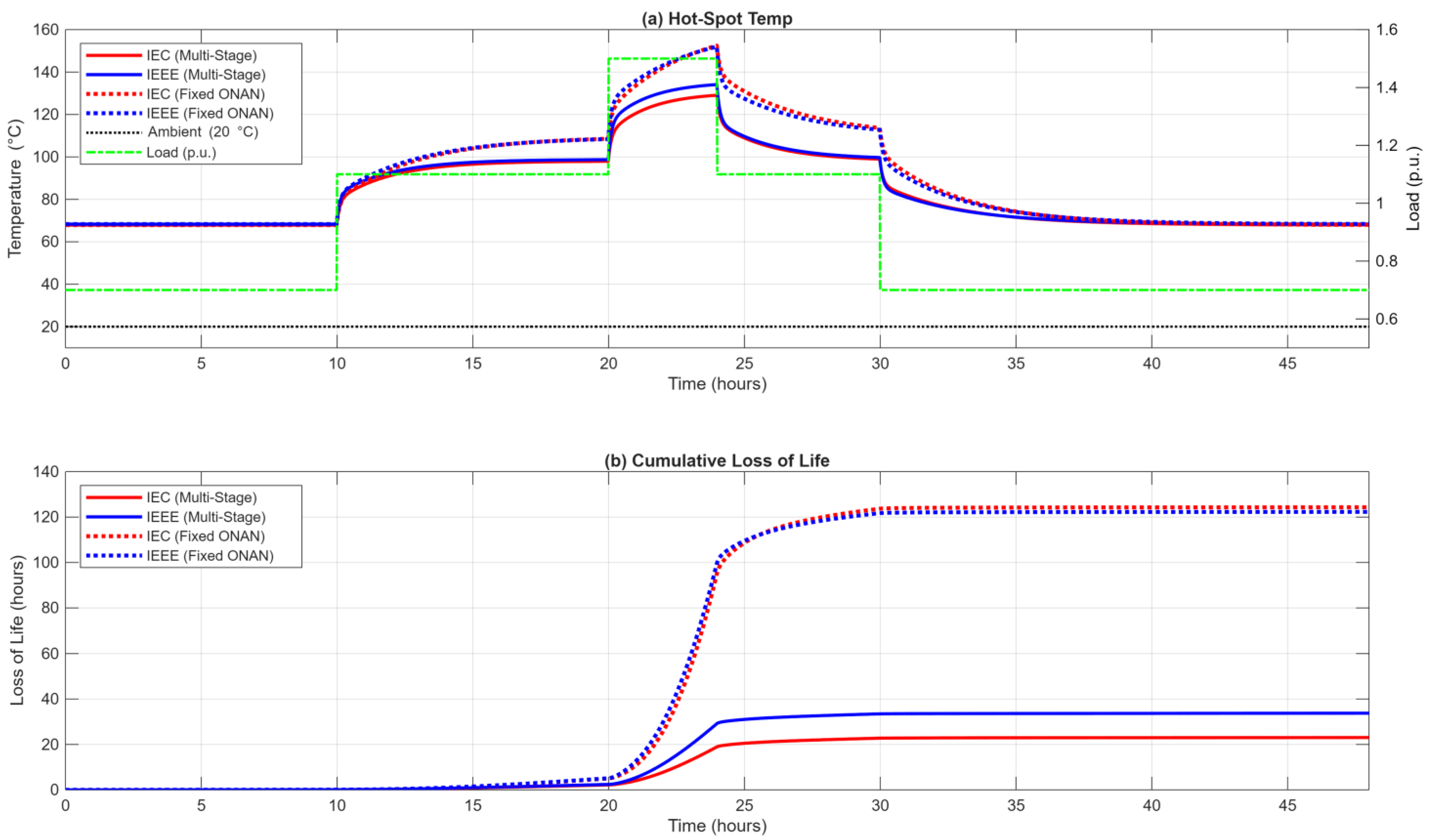
Finally, this study reinforced two other important concepts. The active vs. static cooling scenario analysis (Figure 6) quantitatively proved that a cooling system failure is a high-impact event, acting as a four- to five-fold multiplier on life-loss for a 4 h overload. This validates classifying the cooling system as a safety-critical component. Furthermore, the transient analysis (Figure 4) demonstrated the two-stage thermal response, proving that aging begins almost immediately with the short winding time constant (τ_w). This implies that short-duration, high-impact overloads (e.g., from EV charging or renewable in-feeds) must be accounted for in aging calculations, as they will consume life long before the top-oil temperature has risen significantly.

For future research, these findings should be validated against field data from transformers equipped with fiber-optic winding sensors. This would provide the necessary proofs to determine which standard’s thermal model—and specifically, which set of exponents—more accurately represents physical reality. Further modeling could also incorporate the dynamic oil-viscosity effects proposed by Susa et al. [17,18] to refine the transient response for these new, volatile load profiles.

5. Conclusions

This study proves that the IEC and IEEE standards are not interchangeable. For modern transformers using TU paper, the primary source of differences is not the aging mathematics (as both use the Arrhenius equation) but the fundamental differences in their physical thermal models. The core finding is a “reversal of conservatism” dependent on the cooling system’s health: the IEC model is thermally more conservative in a static mode, while the IEEE model is consistently more conservative in the active mode. For practical application, this means that for a healthy transformer, the IEEE standard is more conservative and defines a smaller safe operating area, as visualized in the 2D operational heat maps. The study also quantified that a cooling system failure is a high-impact event, acting as a four- to five-fold multiplier on life-loss even for short overloads.